Politechnika Częstochowska

Instytut Fizyki

Ćwiczenie nr 1:

Wyznaczanie oporu elektrycznego metodą mostka Wheastone'a.

Oczkowicz Paweł

Kliszcz Piotr

Cel ćwiczenia.

Celem ćwiczenia jest wyznaczenie oporu elektrycznego metodą mostka Wheastone'a.

Prawa przepływu prądu stałego.

Warunkiem przepływu prądu elektrycznego w przewodniku jest pole elektryczne, będące wynikiem wytworzenia w różnych punktach przewodnika różnych potencjałów. Do tego służą urządzenia zwane źródłami napięć, czyli ogniwa galwaniczne, akumulatory, prądnice itp. W tych źródłach w wyniku przekształcenia energii mechanicznej lub chemicznej na energię elektryczną następuje przemieszczenie dopływających do źródeł ładunków i nagromadzenie się elektronów na jednym z jego biegunów (ujemnym) zaś ich niedomiar na drugim biegunie (dodatnim). Wskutek czego dochodzi do wytworzenia między dodatnim i ujemnym biegunem różnica potencjałów.

Podstawowymi prawami rządzącymi przepływem prądu w przewodniku są:

• prawo Ohma, pozwalające wyznaczyć zależności w elementarnym obwodzie elektrycznym;

• prawa Kirchhoffa, mające większe zastosowanie szczególnie w przypadku obwodów rozgałęzionych.

I prawo Kirchhoffa wynika z zasady zachowania ładunku i mówi, że w każdym punkcie węzłowym sieci algebraiczna suma prądów równa się zeru:

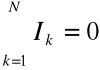
II prawo Kirchhoffa można sformułować następująco: W oczku algebraiczna suma napięć źródłowych i odbiornikowych równa się zeru.

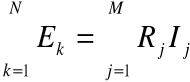
Opór elektryczny.

Rezystancją czyli oporem elektrycznym nazywa się idealny element elektryczny, w którym zachodzi jednostronna zamiana energii elektrycznej na energię cieplną według relacji:

W=RI­²t

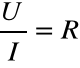
Należy zaznaczyć, że termin rezystancja (opór elektryczny) i odpowiadające jej umowne oznaczenie R stosuje się do oznaczania samego elementu, w którym zachodzi nieodwracalny proces dyssypacji (rozpraszania ) energii elektromagnetycznej, jak również do ilościowego oznaczania wielkości równej stosunkowi napięcia na danym elemencie do prądu przepływającego przez ten element:

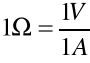
Powyższa formuła wyraża prawo Ohma, odkryte doświadczalnie w 1826 r. Jednostką rezystancji jest om [ 1 Ω ]:

Om jest to rezystancja istniejąca między dwoma punktami przewodnika, gdy napięcie 1V, panujące między tymi punktami, wywołuje prąd 1A.

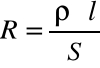
Rezystancja przewodu jest tym większa, im większa jest jego długość l i im mniejszy przekrój poprzeczny S. Te zależności można zapisać za pomocą równania:

Współczynnik proporcjonalności ρ jest stałą, której wartość zależy od rodzaju materiału przewodu. Stała ta nazywa się rezystywnością materiału lub oporem właściwym.

Rezystancja elektryczna materiału zależy nie tylko od wielkości występujących w powyższych równaniach, ale także od temperatury. W praktyce przyjęto podawać wartość rezystancji dla temperatury 293K ( 20°C ). Jeżeli temperatura odbiega od 293K, to występuje przyrost rezystancji ΔR, który wynosi:

ΔR = αR­­₂₀Δσ,

gdzie: α - temperaturowy współczynnik rezystancji,

Δσ - przyrost temperatury w stosunku do 20°C

Rezystancję zależną od temperatury określa się również z wyrażenia:

R = R₂₀+α₂₀R₂₀Δσ

lub

R = R₂₀(1+α₂₀Δσ).

Zasada działania mostka Wheatstone'a.

Obwód mostka Wheatstone'a składa się z dwóch równolegle połączonych gałęzi ACB i ADB. Punkty A i B połączone są źródłem prądu stałego przez opornik R_z, a punkty C i D z galwanometrem lub czułym mikroamperomierzem. Oporniki R_p i R₂ mogą być dwiema częściami potencjometru dekadowego, wtedy

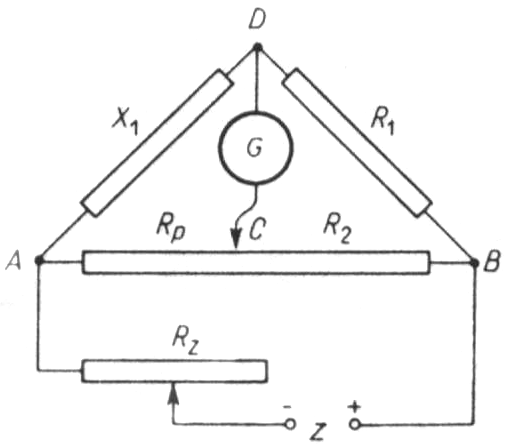
punkt C odpowiada suwakowi potencjometru. Suma oporów R_p i R₂ jest wielkością stałą. Pomiar polega na takim dobraniu położenia punktu C, by przez galwanometr nie płynął prąd, czyli by mostek był zrównoważony. Przy zrównoważonym mostku pomiędzy punktami C i D nie ma różnicy potencjałów (U_CD = 0), a przez oporniki X₁ i R₁ płynie prąd o takim samym natężeniu I₁. Również przez oporniki R_p. i R₂ płynie prąd o takim samym natężeniu I₂. Wtedy, zgodnie z II prawem Kirchhoffa, możemy napisać następujące związki: X₁I₁ = R_pI₂, R₁I₁ = R₂I₂. Dzieląc pierwsze równanie przez drugie otrzymujemy:

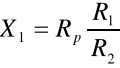
Metody pomiaru oporu elektrycznego.

Pomiar oporu elektrycznego można dokonać na kilka sposobów:

• w sposób bezpośredni - przez użycie omomierza;

• w sposób pośredni, mierząc napięcie i natężenie prądu i stosując prawo Ohma dla obwodu elementarnego, przy czym pomiar ten może być przeprowadzony z dokładnością do napięci lub natężenia;

• stosując inne mierniki lub multimetry elektroniczne.

Schemat układu pomiarowego.

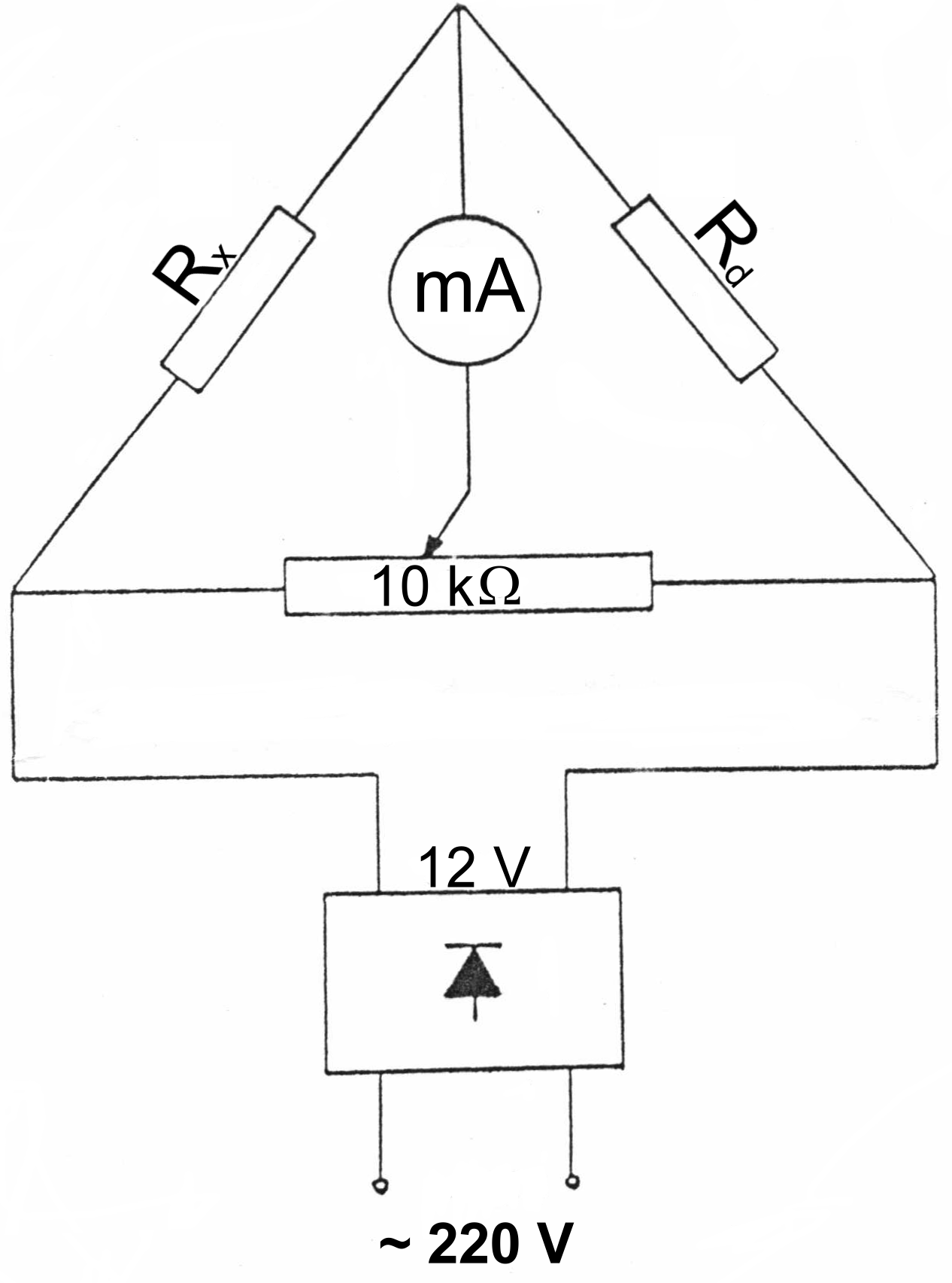
Tabela pomiarów.

Lp.	Nr   oporu i    rodzaj połączenia	Opór dekadowy Rd [Ω]	Wartość na dzielniku		Opór zmierzony Rx[Ω]	Opór obliczony Rx[Ω]	ΔRx[Ω]
									R1[Ω]	R2[Ω]
1.	R1	320	5000	5000	320	320±1	1
2.	R2	2232	5000	5000	2232	2232±6,7	6,7
3.	R3	4680	5000	5000	4680	4680±14	14
4.	R1	206	4000	6000	309	309±1	1
5.	R2	1500	4000	6000	2250	2250±6,75	6,75
6.	R3	3150	4000	6000	4725	4725±14,17	14,17
7.	Szereg R1+ R2	2532	5000	5000	2532	2552±7	20
8.	Szereg R2+ R3	7052	5000	5000	7052	6912±20	120
9.	Szereg R1+ R2+ R3	7400	5000	5000	7400	7232±21,7	147
10.	Równolegle R1 + R2	290	5000	5000	290	280±7,7	2,3
11.	Równolegle R2 + R3	1490	5000	5000	1490	1511,25±20,7	0,55
12.	Równolegle R1 + R2+ R3	260	5000	5000	260	329,78±21,7	48,08
13.	Szereg R1 + R2+ R3	5000	4000	6000	7500	7232±21,7	246,3
14.	Szereg R1+ R2	1690	4000	6000	2535	2552±7,75	9,25

Opór zmierzony     -   wartość oporu zmierzona przy pomocy mostka;

Opór obliczony - wartość oporu zastępczego obliczona dla połączeń                                   szeregowego i równoległego .

Wyprowadzenie wzoru na wartość oporu mierzonego mostkiem Wheatstone'a.

Wiedząc o zależności, że U_CA = U_CB oraz U_AD = U_BD Możemy spokojnie napisać, że:

I₁ ^. R­­₁ = I_{2 ­­}^. R_d oraz I₁ ^. R₂ = I₂ ^. R_x.

Dzieląc równania obustronnie przez siebie otrzymujemy: R₁ ^. R_x = R₂ ^. R_d.

Po przekształceniu obliczmy Rx

R_x = (R₂ ^. R_d) / R₁

Wyprowadzenie wzorów na obliczanie oporu zastępczego dla połączenia oporników szeregowego i równoległego

Przy szeregowym połączeniu oporników R1 i R2 całkowity ich opór zastępczy będzie równać się sumie ich oporów Rx=R1+R2.

Natomiast przy połączeniu równoległym suma ich całkowitego oporu zastępczego będzie równa sumie odwrotności ich oporów. 1/R=1/R1+1/R2 z czego wynika 1/Rx=(R2+R1) / (R1*R2)

a to się równa Rx=(R1*R2) / (R2+R1)

Opracować metodę obliczania błędów i przeprowadzić dyskusję dokładności pomiarów.

Na podstawie metody mostka Wheatstone'a obliczamy Rx czyli opór mierzony . Przyjmując następujące wartości:

Rd=320[Ω]

R1=5000[Ω]

R2=5000[Ω]

Podstawiając do wzoru otrzymujemy:

Rx=(5000[Ω]*320[Ω]) / 5000[Ω]=320[Ω].

Niepewności pomiarowe |dR1|, |dR2| są sobie równe i wynoszą:

1,5 / 100=0.015≈0.02[Ω]

Obliczenia niepewności rezystancji obliczonej: metoda różniczki zupełnej:

Rx=(R2*Rd) / R1

|dRx|=(∂Rx/∂R2)*dR2 + (∂Rx/∂Rd)*dRd + (∂Rx/∂rR1)*dR1

|dRx|=(Rd*dR2) / R1 + (R2*dRd) / R1 - (R2*Rd*dR1) / R1^2 podstawiając wartości liczbowe otrzymujemy:

|dR|=(320*0.02) / 5000 + (5000*1) / 5000 - (5000*320*0.02) / 5000^2= 0,00132 + 1 - 0,00132 = 1[Ω].

Rx=(320+/-1) [Ω]

Względna niepewność pomiarowa jest bardzo niska δR=|dR/R| = 1/320 = 0,0030(30)

Na podstawie obserwacji wyników z tabelki dochodzimy do wniosku, że „coś” przyczyniło się do powstania małych ale zawsze błędów. Np. w pomiarze nr 1 Rx mierzone wynosi 320 omów a w pomiarze nr 2, 2232, czyli w sumie 2552.(Tak jak w połączeniu szeregowym). Teraz proszę porównać wynik Rx mierzonego w pomiarze nr 7. Różnica jest spora, bo aż 20 . Naszym zdaniem obecność błędów jest czymś normalnym w laboratorium fizycznym. Przyczyną tego typu błędów może być praktycznie wszystko począwszy od niezbyt nowego sprzętu po temperaturę powietrza w pracowni, nie wyłączając także czynnika ludzkiego, takiego jak np.: bezwładność ludzkiego oka, czy nie dokładność ustawień galwanometru. Zdajemy sobie sprawę iż to właśnie przez nas powstały niektóre błędy ale z pewnością nie były one zamierzone

2

8

---