Projekt „Inżynier mechanik – zawód z przyszłością”

współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego

Zajęcia wyrównawcze z fizyki -Zestaw 13 -Teoria

Drgania i fale. Ruch drgający harmoniczny, równanie fali płaskiej, efekt Dopplera, fale stojące.

Siła harmoniczna, ruch drgający harmoniczny

Siłą harmoniczną (sprężystości) nazywamy siłę działającą na ciało proporcjonalną do wychylenia ciała
z położenia równowagi i skierowaną przeciwnie do wychylania.

Dla przesunięcia wzdłuż osi x siła sprężystości jest dana równaniem

x

k

F











gdzie x jest wychyleniem (przesunięciem) ciała z jego położenia równowagi. Stałą k nazywamy
współczynnikiem sprężystości.

Siła taka wywołuje ruch drgający harmoniczny, tzn. ruch powtarzający się w czasie w sposób
okresowy, gdzie zależność wychylenia ciała z położenia równowagi w funkcji czasu jest opisana
funkcją sinus lub cosinus, przykładowo:

 

t

A

x



sin





,

A oznacza amplitudę drgań, czyli maksymalne wychylenie z położenia równowagi,



jest częstością

kołową drgań, powiązaną z okresem drgań wzorem:

,

, f oznacza częstotliwość.

Prędkość i przyspieszenie w ruchu drgającym harmonicznym.

Gdy w ruchu drgającym harmonicznym wychylenie ciała z położenia równowagi opisane jest w
funkcji czasu wzorem:

, to prędkość i przyspieszenie liczymy w sposób następujący:





2



T

 

 

t

A

t

x



sin





 

 

t

A

dt

x

d

dt

dv

t

a





sin

2

2

2











 

 

t

A

dt

dx

t

v





cos







f

T







2

2





T

f

1



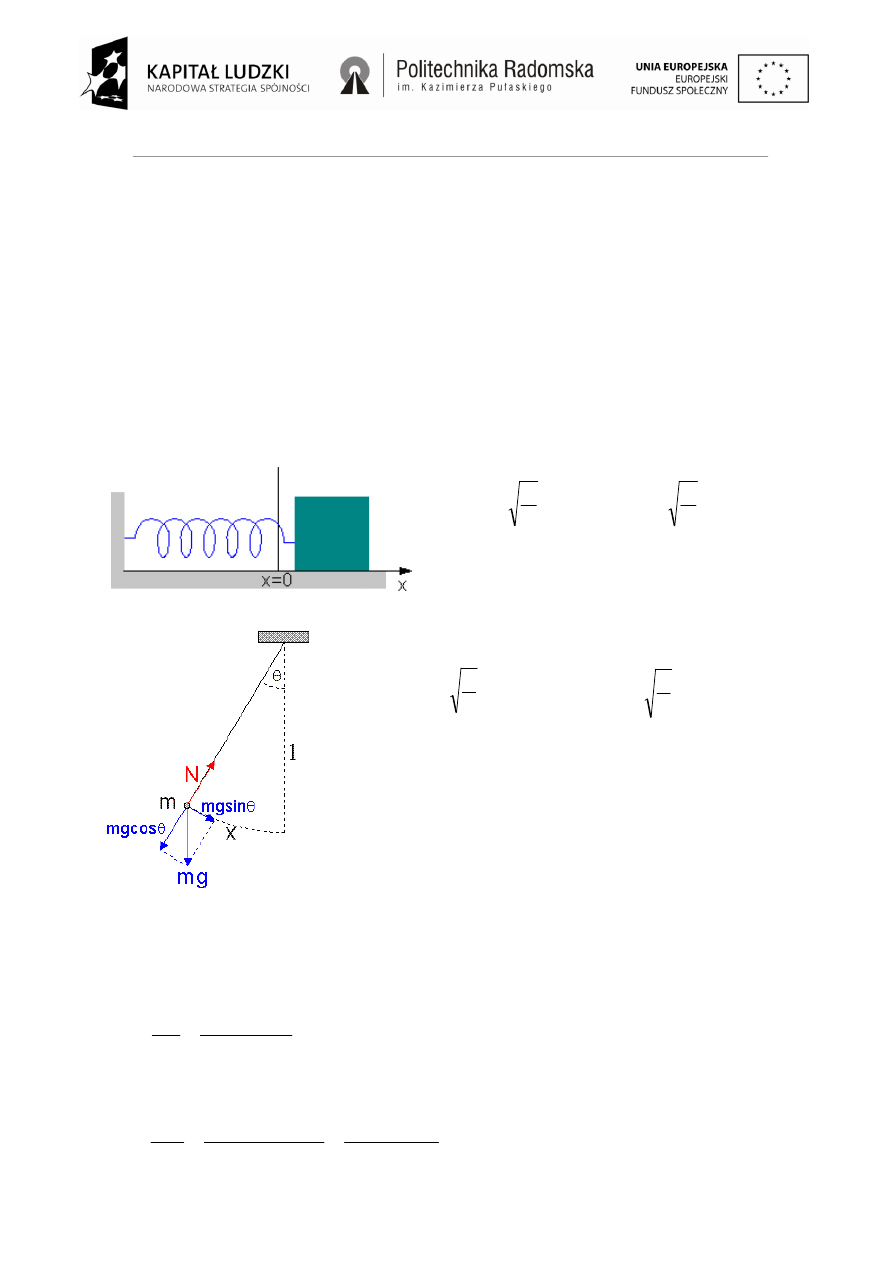
Projekt „Inżynier mechanik – zawód z przyszłością”

współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego

Z powyższych wzorów wynika, że maksymalne wartości prędkości i przyspieszenia wynoszą
odpowiednio:

Ponadto w każdej chwili czasu spełniona jest następująca zależność pomiędzy
przyspieszeniem i wychyleniem:

Przykłady drgań harmonicznych, wzory na częstość drgań:

Ciężarek na sprężynie.

Wahadło matematyczne.

Energia w ruchu drgającym harmonicznym.

W ruchu drgającym harmonicznym energia potencjalna obiektu wykonującego drgania wynosi:

Natomiast energia kinetyczna wynosi:



A

v



max

2

max



A

a



x

a

2







m

k





k

m

T



2



l

g





g

l

T



2



 

2

sin

2

2

2

2

t

kA

kx

E

p







 

 

2

cos

2

cos

2

2

2

2

2

2

2

t

kA

t

mA

mv

E

k













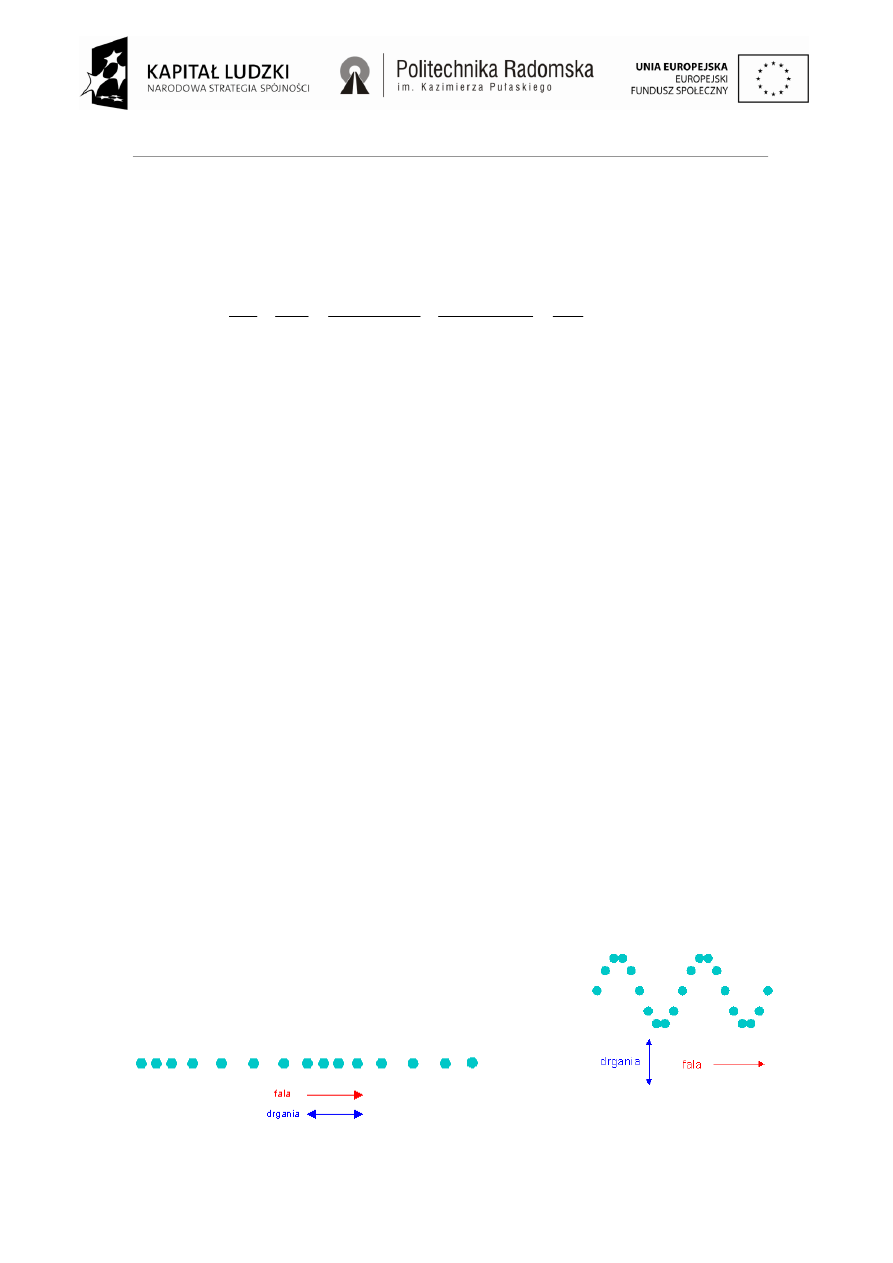
Projekt „Inżynier mechanik – zawód z przyszłością”

współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego

Można udowodnić, że w ruchu drgającym harmonicznym energia całkowita obiektu jest stała.

Wniosek ten jest słuszny gdy drgania zachodzą jedynie pod wpływem siły sprężystości, przy braku
siły tarcia, sił oporu ruchu.

Fale mechaniczne

Ruch falowy jest bardzo rozpowszechniony w przyrodzie. Przykładami fal mechanicznych są między
innymi fale rozchodzące się na powierzchni wody, a także fale dźwiękowe.

Jeżeli wychylimy jakiś fragment ośrodka sprężystego z jego położenia równowagi to w następstwie
będzie on wykonywał drgania wokół tego położenia. Te drgania, dzięki właściwościom sprężystym
ośrodka, są przekazywane na kolejne części ośrodka, które zaczynają drgać. W ten sposób zaburzenie
(fala) rozchodzi się w ośrodku.

Zwróćmy uwagę, że sam ośrodek nie przesuwa się, a jedynie jego elementy wykonują drgania.
Dobrym przykładem są tu fale na powierzchni wody: przedmioty pływające na powierzchni wody
wykonują niewielkie drgania wokół swojego położenia równowagi, natomiast same fale rozchodzą się
ruchem jednostajnym na duże odległości. Jest to możliwe dzięki przekazywaniu energii kolejnym
cząsteczkom ośrodka, które w ten sposób są pobudzane do drgań przez swoich „poprzedników”.

Rodzaje fal

Ze względu na kierunek drgań cząstek ośrodka względem kierunku rozchodzenia się fale dzielimy na
fale podłużne i fale poprzeczne .

Fala jest podłużna gdy kierunek drgań cząstek ośrodka jest równoległy do kierunku rozchodzenia się
fali i zarazem kierunku transportu energii. Przykładem są tu fale dźwiękowe w powietrzu czy też
drgania naprzemiennie ściskanej i rozciąganej sprężyny.

Fala jest poprzeczna gdy kierunek drgań cząstek ośrodka jest
prostopadły do kierunku rozchodzenia się fali i zarazem kierunku
transportu energii. Przykładem mogą tu być drgania naprężonego

sznura, którego końcem poruszamy cyklicznie w górę i w dół.

Fala podłużna.

Fala poprzeczna.

 

 

2

2

cos

2

sin

2

2

2

2

2

2

2

2

2

kA

t

kA

t

kA

mv

kx

E

E

E

k

p

C



















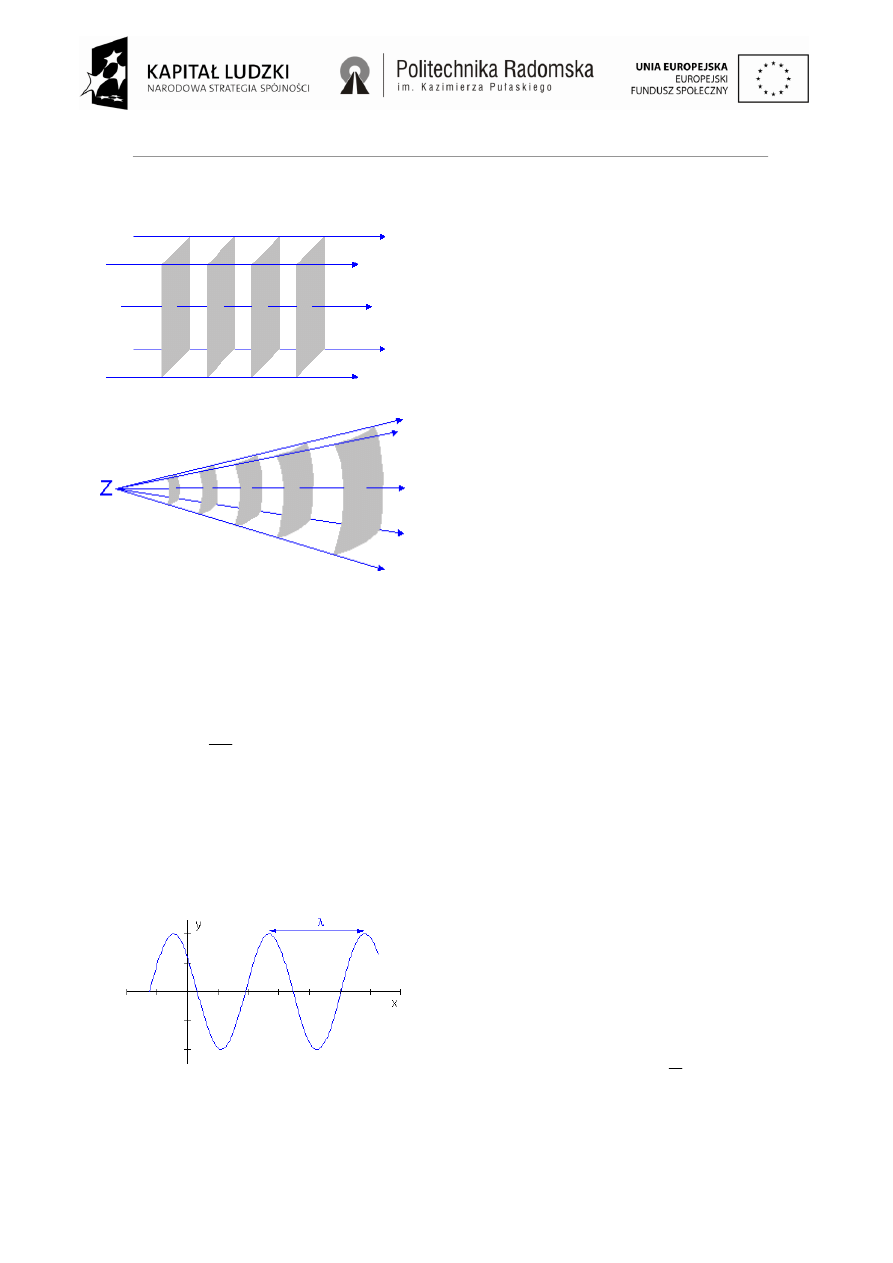
Projekt „Inżynier mechanik – zawód z przyszłością”

współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego

Ze względu na kształt powierzchni falowej możemy wyróżnić fale płaskie i fale kuliste .

Powierzchnie falowe (płaszczyzny) i promienie fali
płaskiej

Fala kulista rozchodząca się ze źródła Z; wycinki
powłok sferycznych przedstawiają powierzchnie
falowe.

Równanie fali płaskiej:

Następujące równanie opisuje poprzeczną falę płaską rozchodzącą się w dodatnim kierunku osi x.

 





vt

x

A

t

x

y









2

sin

,

,

w powyższym wzorze:

A oznacza amplitudę (maksymalne wychylenie drgającego punktu z położenia równowagi),



to długość fali, a v to prędkość rozchodzenia się fali w ośrodku.

x to odległość rozważanego punktu drgającego od źródła fali.

Długość fali λ

Czas, w którym fala przebiega odległość równą λ
nazywamy

okresem T .

v

T





Projekt „Inżynier mechanik – zawód z przyszłością”

współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego

Fale stojące –W przypadku nakładania się fal biegnących w dwóch przeciwnych kierunkach,
posiadających te samą częstotliwość i amplitudę, w ośrodku może powstać fala stojąca. Położenie
punktów charakteryzujących się maksymalną i minimalną amplitudą drgań tej fali nie zmienia się

wraz z upływem czasu.

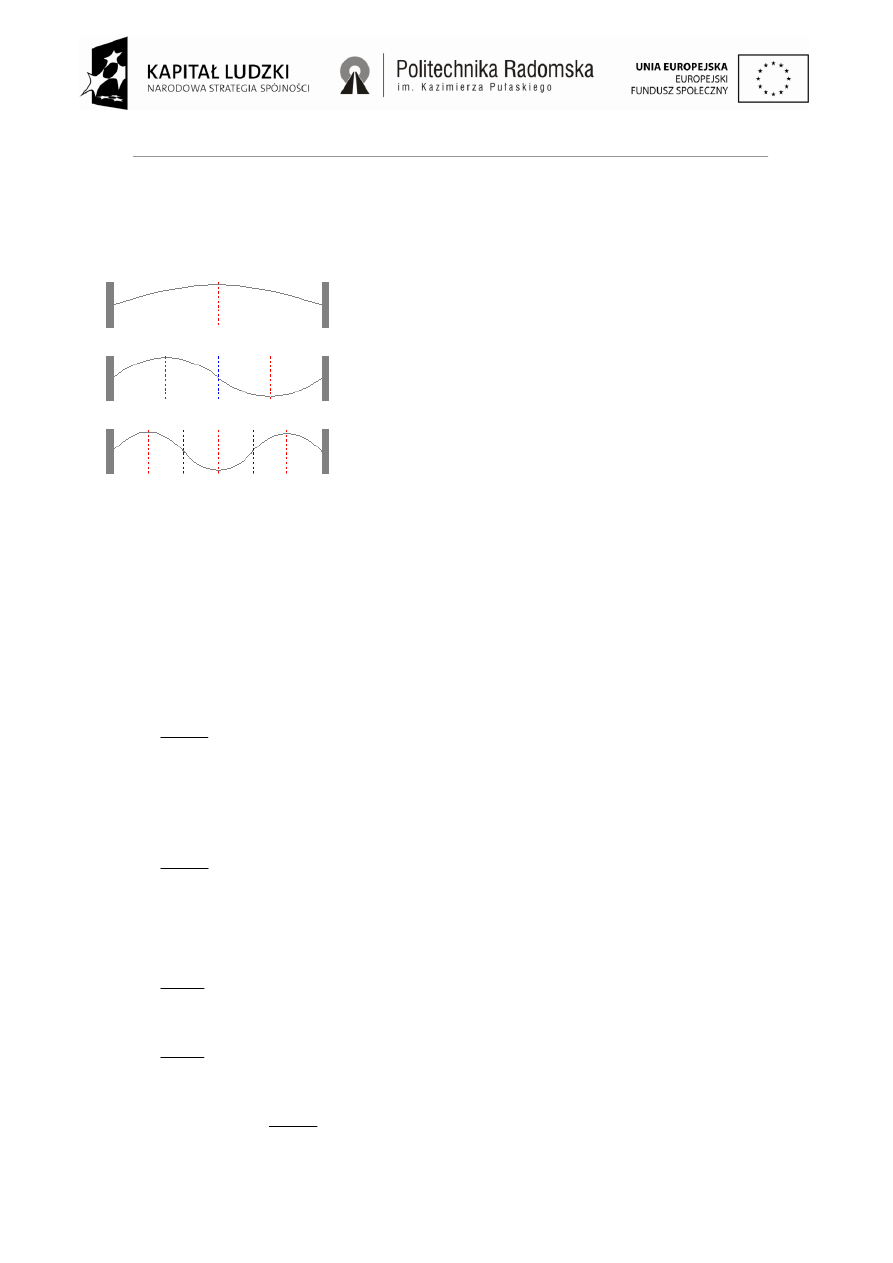
Przykład fal stojących:

Fale stojące dla struny zamocowanej na

obu końcach; węzły są
zaznaczone niebieskimi liniami, a strzałki czerwonymi.

Punkty znajdujące się w położeniach x = λ/4, 3λ/4, 5λ/4 itd. mają
maksymalną amplitudę. Punkty te nazywamy

strzałkami

, a punkty

takie, że x = λ/2, λ, 3λ/2 itd. mają zerową amplitudę i nazywane są

węzłami

. Widać, że odległości między kolejnymi węzłami i

strzałkami wynoszą pół długości fali.

Zjawisko Dopplera

Zjawisko Dopplera (efekt Dopplera) polega na zmianie częstotliwości fali z powodu ruchu
obserwatora lub źródła fali.

Zjawisko to możemy zaobserwować np. gdy słyszymy dźwięk poruszającej się karetki pogotowia.

Gdy karetka zbliża się do obserwatora –częstotliwość odbieranego dźwięku jest wyższa, niż
częstotliwość dźwięku wysyłanego przez syrenę karetki.

zr

v

v

v

f

f







Gdy karetka oddala się do obserwatora –częstotliwość odbieranego dźwięku jest niższa, niż
częstotliwość dźwięku wysyłanego przez syrenę karetki.

zr

v

v

v

f

f







Gdy źródło dźwięku jest nieruchome, a porusza się obserwator, obowiązują następujące wzory:

v

v

v

f

f

o







, obserwator zbliża się do nieruchomego źródła.

v

v

v

f

f

o







, obserwator oddala się od nieruchomego źródła.

Wzór ogólny:

zr

o

v

v

v

v

f

f









.

Projekt „Inżynier mechanik – zawód z przyszłością”

współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego

Natężenie fali dźwiękowej.

Natężeniem fali dźwiękowej nazywamy energię fali dźwiękowej podzieloną przez czas i
powierzchnię, przez którą ta energia przenika.

S

P

S

t

W

I







I - natężenie dźwięku - jednostką jest "wat na metr kwadrat" [W/m

2

].

t - czas w sekundach [s]
S - pole powierzchni, na którą pada energia dźwiękowa wyrażone w "metrach kwadratowych" [m

2

].

P - moc fali dźwiękowej w watach [W]

Natężenie progu słyszalności

Minimalna wartość natężenia fali dźwiękowej, którą człowiek może jeszcze usłyszeć wynosi: 10

-12

W/m

2

(jedna bilionowa wata na metr kwadrat). Moc związana z tym natężeniem jest niezwykle mała, a

fakt że w ogóle może być przez ucho rejestrowania świadczy bardzo dobrze o możliwościach naszych
zmysłów.

Natężenie progu bólu

Gdy natężenie fali dźwiękowej przekroczy wartość ok. 1 W/m

2

, wtedy dźwięk staje się zbyt silny jak

na możliwości ludzkiego ucha. Wtedy przestaje ono rozróżniać cechy tego dźwięku i reaguje bólem.

Poziom natężenia dźwięku, decybel

Ucho ludzkie działa "nieliniowo". Oznacza to, że 2 razy większe natężenie dźwięku wcale nie jest
przez nas odbierane jako 2 razy głośniejszy dźwięk. Ucho dokonuje silnego "spłaszczenia"
odczuwania głośności - dźwięk, który odczuwamy jako kilka razy głośniejszy od początkowego, ma w
rzeczywistości energię dziesiątki, a nawet setki razy większą. Dokładniej - nasz narząd słuchu
logarytmuje natężenie dźwięku, co powoduje, że 2 razy większe natężenie dźwięku odpowiada
zwiększeniu głośności o wartość proporcjonalną do "logarytmu z dwóch".

Wprowadza się wielkość zwaną poziomem natężenia dźwięku - uwzględniającą logarytmiczny
charakter odczuwania głośności.

o

I

I

log

10







,

gdzie

Β- jest poziomem natężenia wyrażanym w decybelach [dB],
I - jest natężeniem badanej fali dźwiękowej w W/m

2

.

I

0

- jest natężeniem tzw. "progu słyszalności" czyli wielkości równej 10

-12

W/m

2

.

Przykłady:

2 - krotny wzrost natężenia oznacza wzrost poziomu głośności o ok. 3 dB

Projekt „Inżynier mechanik – zawód z przyszłością”

współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego

10 - krotny wzrost natężenia daje wzrost poziomu głośności o 10 dB

100 - krotny wzrost natężenia daje wzrost poziomu głośności o 20 dB

1000 - krotny wzrost natężenia daje wzrost poziomu głośności o 30 dB

itd...

Ponieważ logarytm z jedynki ma wartość zero, więc od razu widać, że (po podstawieniu do wzoru I =
I

0

) natężenie progu słyszalności daje poziom natężenia 0 dB. Z kolei bardzo głośny słyszalny dźwięk

ma poziom głośności w okolicy 100 dB; 120 dB to tzw. próg bólu.