Materiały do wykładów
Fizyka (Informatyka - EEIiA 2011/12)
23 października 2011
c
Mariusz Krasiński 2011
Spis treści
III
DRGANIA cd.
1
1
Przypominacz (?) matematyczny
1
2
Drgania a liczby zespolone
2
3
Drgania harmoniczne tłumione
2
3.1
Założenia modelu . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2
3.2
Rozwiązanie równania dla drgań tłumionych . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3
3.3
Dyskusja możliwych postaci rozwiązania . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4
3.4
Energia oscylatora tłumionego
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
6
3.5
Dobroć oscylatora
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
6
3.6
Dekrement logarytmiczny tłumienia
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7
4
Drgania harm. wymusz. z tłum.
7
4.1
Wymuszenie harmoniczne . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7
4.2
Rozwiązanie równania (4.1) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7
4.3
Rezonans . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
8
4.4
Ruch wymuszony na wykresie fazowym . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
9
4.5
Dynamiczny tłumik drgań . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
9
UWAGA! Większość rysunków wymaga własnoręcznego dopisania oznaczeń!
Część III
DRGANIA cd.
1
Przypominacz (?) matematyczny
(x
n
)
0
=
d
dx
(x
n
) = n x
n−1
[sin(x)]
0
=
d
dx
[sin(x)] = cos(x)
[cos(x)]
0
=
d
dx
[cos(x)] = − sin(x)
(e
x
)
0
=
d
dx
(e
x
) = e
x
1
3
DRGANIA HARMONICZNE TŁUMIONE
d
dt
[sin(ωt + φ)] = cos(ωt + φ)
d
dt
(ωt + φ) = cos(ωt + φ) ω
d
dt
[cos(ωt + φ)] = − sin(ωt + φ)
d
dt
(ωt + φ) = − sin(ωt + φ) ω
d
dt
e
i(ωt+φ)
= e
i(ωt+φ)
d
dx
[i(ωt + φ)] = e
i(ωt+φ)
iω
2
Drgania a liczby zespolone
Ogólna postać liczby zespolonej
z = X + iY
gdzie
i =
p
(−1)
Trygonometryczna postać liczby zespolonej
z = R[cos(φ) + i sin(φ)]
Wykładnicza postać liczby zespolonej
z = Re
iφ
= R[cos(φ) + i sin(φ)]
Drganie harmoniczne można więc przedstawić w postaci:
x = Ae
i(ωt+φ)
Obliczmy, korzystając z zapisu przy pomocy liczb zespolonych, prędkość i przyspieszenie w ruchu
harmonicznym
v =
dx
dt
=
d
dt
Ae
i(ωt+φ)
= −Aωe
i(ωt+φ)
a =
d
2
x
dt
2
=
d
dt
dx
dt
=
d
dt
−Aωe
i(ωt+φ)
= −Aω
2
e
i(ωt+φ)
= −ω
2
x
Otrzymaliśmy więc identyczną jak na poprzednim wykładzie zależność pomiędzy przyspieszeniem i
wychyleniem ciała drgającego ruchem harmonicznym prostym
d
2
x
dt
2
= −ω
2
x
3
Drgania harmoniczne tłumione
3.1
Założenia modelu
Rozpatrzymy jedynie przypadek gdy siła oporu (tłumienia) jest proporcjonalna do prędkości.
~
F
op
= −β~
v
(3.1)
(!! Kiedy wolno tak napisać?)
c
Mariusz Krasiński 2011
2
3.2
Rozwiązanie równania dla drgań tłumionych
3
DRGANIA HARMONICZNE TŁUMIONE
Równanie ruchu drgającego z tłumieniem przyjmie wtedy postać
m
d
2
x
dt
2
= −kx − βv
czyli
d
2
x
dt
2
+
β
m
dx
dt
+
k
m
x = 0
(3.2)
albo po wprowadzeniu oznaczenia
k
m
= ω
o
2
(dlaczego tak? )
d
2
x
dt
2
+
β
m
dx
dt
+ ω
2
o
x = 0
(3.3)
3.2
Rozwiązanie równania dla drgań tłumionych
Postulujemy, że rozwiązanie równania (3.3) ma postać (czyli zakładamy, że będzie to drganie harmoniczne)
x = Be
iωt
(3.4)
Odpowiednie pochodne wyrażenia (3.4) wynoszą
dx
dt
= Biωe
iωt
= iωx
(3.5)
d
2
x
dt
2
=
d
dt
dx
dt
= (iω)
2
Be
iωt
= −ω
2
x
(3.6)
Podstawiając (3.5) i (3.6) do równania (3.3) otrzymujemy
−ω
2
x +
β
m
iωx + ω
o
2
x = 0
czyli
ω
2
−
iβ
m
ω − ω
o
2
= 0
(3.7)
Równanie (3.7) jest zwykłym równaniem kwadratowym, z którego można wyliczyć ω
“Delta” dla tego równania wynosi
∆ =
iβ
m
2
+ 4ω
2
o
= 4ω
2
o
−
β
m
2
a rozwiązania równania (3.7) mają postać
ω
1,2
=
β
m
i ±
r
4ω
2
o
−
β
m
2
2
=
β
2m
i ±
s
ω
2
o
−
β
2m
2
(3.8)
Ponieważ zapostulowaliśmy, że rozwiązanie równania (3.3) ma postać jak w równaniu (3.4) więc ogólna postać
rozwiązania równania (3.3) jest
x = Ae
iω
1
t
+ Be
iω
2
t
(3.9)
gdzie A, B są stałymi zaś ω
1
, ω
2
możemy wziąć z równania (3.8)
x = Ae
i
β
2m
i +
q
ω
2
o
−
(
β
2m
)
2
t
+ Be
i
β
2m
i −
q
ω
2
o
−
(
β
2m
)
2
t
(3.10)
c
Mariusz Krasiński 2011
3
3.3
Dyskusja możliwych postaci rozwiązania
3
DRGANIA HARMONICZNE TŁUMIONE
3.3
Dyskusja możliwych postaci rozwiązania
3.3.1
Przypadek 1 (małe tłumienie)
Kiedy spełniony jest warunek
ω
2
o
−
β
2m
2
> 0
rozwiązanie równania (3.3) ma postać
x = Ae
−
β
2m
t
cos
s
ω
2
o
−
β
2m
2
t
(3.11)
Uzasadnienie zależności (3.11)
Oznaczając
ω
0
=
s
ω
2
o
−
β
2m
2
> 0
i podstawiając do równania (3.10) otrzymujemy (przy założeniu A = B = C)
x = Ce
−
β
2m
t
e
iω
0
t
+ Ce
−
β
2m
t
e
−iω
0
t
= Ce
−
β
2m
t
[e
iω
0
t
± e
−iω
0
t
)] =
= Ce
−
β
2m
t
{[cos(ω
0
t) + i sin(ω
0
t)] + [cos(ω
0
t) − i sin(ω
0
t)]} =
= Ce
−
β
2m
t
[2 cos(ω
0
t)] = 2Ce
−
β
2m
t
cos(ω
0
t)
Ponieważ amplituda drgań zależy od warunków początkowych a nie od parametrów
układu więc możemy oznaczyć sobie
Amp = 2C
a wtedy rozwiązanie ma postać
x = Amp e
−
β
2m
t
cos
s
ω
2
o
−
β
2m
2
t
(3.12)
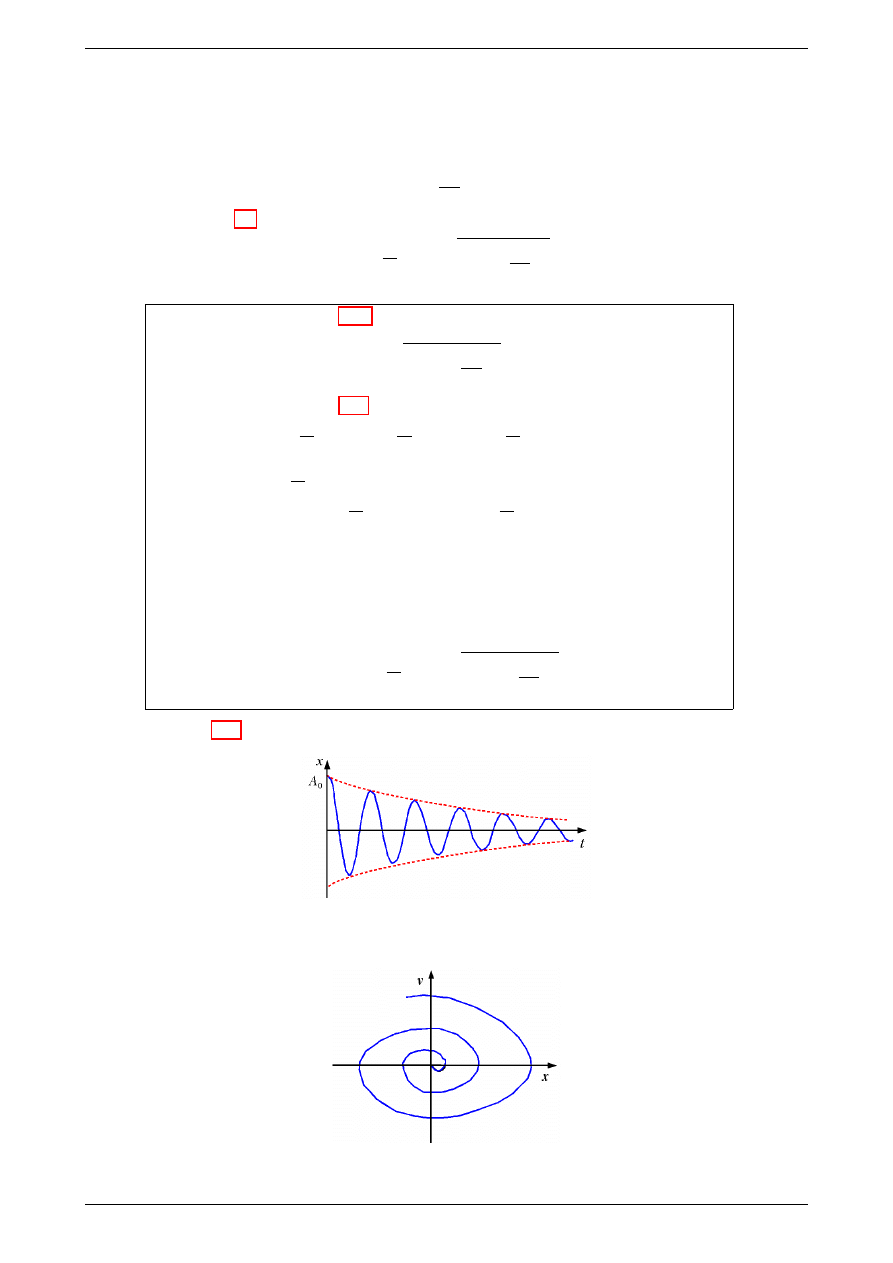
Wykres zależności (3.11) przedstawiono poniżej
Rysunek 1: Zależność wychylenia od czasu dla drgań tłumionych przy małym tłumieniu.
Rysunek 2: Drgania harmoniczne tłumione w przestrzeni fazowej.
c
Mariusz Krasiński 2011
4
3.3
Dyskusja możliwych postaci rozwiązania
3
DRGANIA HARMONICZNE TŁUMIONE
3.3.2
Przypadek 2 (tłumienie krytyczne)
Kiedy spełniony jest warunek
ω
2
o
−
β
2m
2
= 0
(3.13)
wtedy rozwiązanie równania (3.3) ma postać
x =
A − B
b
2m
t
e
−
β
2m
t
(3.14)
i przedstawia ruch aperiodyczny. Tłumienie odpowiadające warunkowi (3.13) nazywamy tłumieniem kryty-
cznym.
Aby zrozumieć skąd wzięła się taka postać rozwiązania równania (3.3) w przypadku (3.13) trzeba niestety wiedzieć
trochę więcej o równaniach różniczkowych.
3.3.3
Przypadek 3 (układ przetłumiony)
Kiedy tłumienie jest duże i spełniony jest warunek
ω
2
o
−
β
2m
2
< 0
wtedy rozwiązanie równania (3.3) przyjmuje postać
x = Ae
−
β
2m
t
e
±ω
00
t
(3.15)
i to także nie jest równanie ruchu periodycznego (dyskusja wykład ). Układ, którego zachowanie może być
opisane równaniem (3.15) nazywamy układem przetłumionym.
Uzasadnienie zależności (3.15)
Ponieważ wyrażenie
ω
2
o
−
β
2m
2
< 0
jest ujemne więc możemy je przekształcić w następujący sposób
s
ω
2
o
−
β
2m
2
=
v
u
u
t
−1
β
2m
2
− ω
2
o
!
=
√
−1
s
β
2m
2
− ω
2
o
= iω
00
(3.16)
gdzie
ω
00
=
s
β
2m
2
− ω
2
o
jest wielkością dodatnią.
Podstawiając (3.16) do (3.9) otrzymujemy
x = Ae
i
(
β
2m
i∓iω
00
)
t
= Ae
−
β
2m
t
e
±ω
00
t
(3.17)
3.3.4
Porównanie
Rysunek poniżej przedstawia na jednym wykresie zachowanie układu tłumionego, układu z tłumieniem kryty-
cznym oraz układu przetłumionego.
c
Mariusz Krasiński 2011
5
3.4
Energia oscylatora tłumionego
3
DRGANIA HARMONICZNE TŁUMIONE
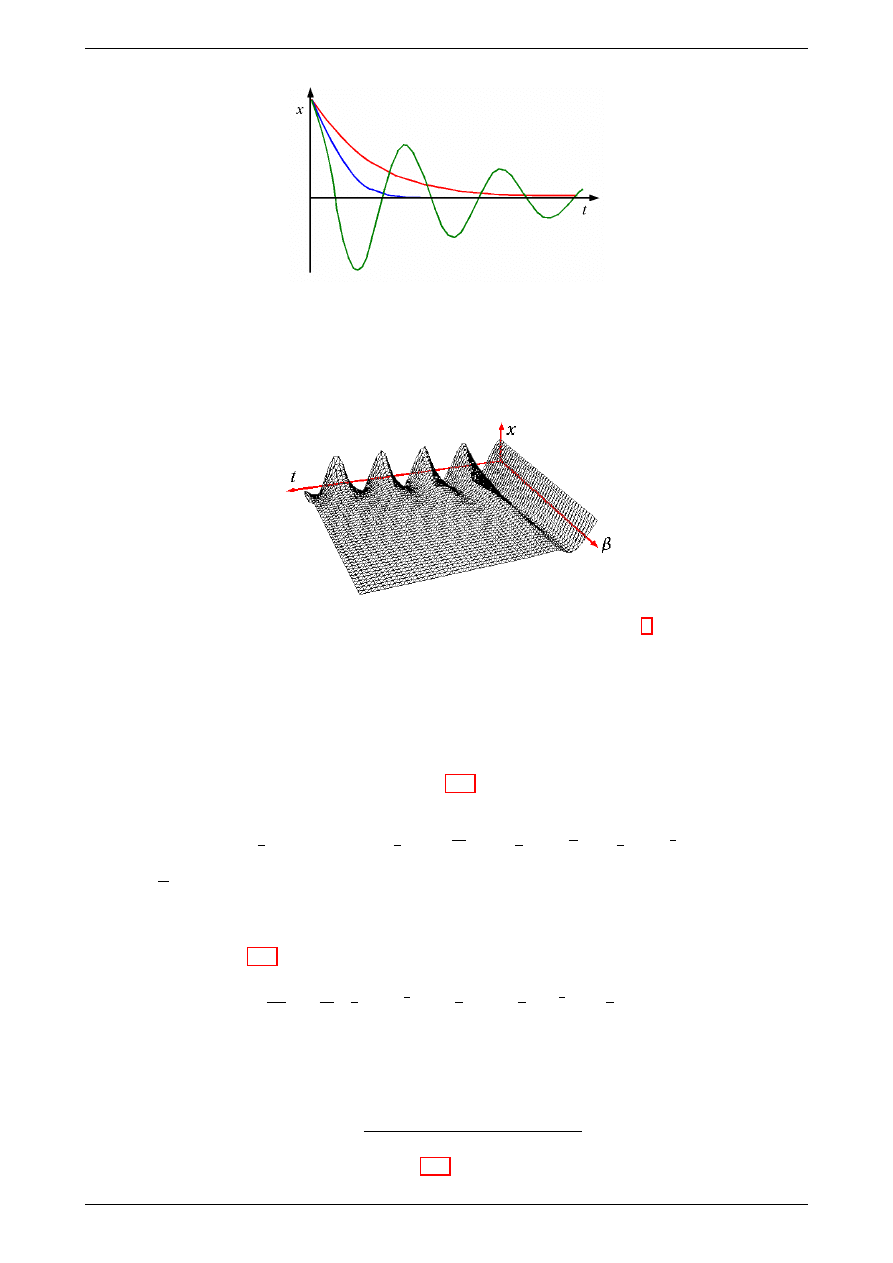
Rysunek 3: Zależność wychylenia od czasu dla ciała wykonującego drgania harmoniczne, tłumione. Wykresy
odpowiadają różnym współczynnikom tłumienia. Uzupełnij opisy na wykładzie.
Sposób w jaki drga układ tłumiony, w zależności od wielkości tłumienia β, można przedstawić na trójwymi-
arowym wykresie
Rysunek 4: Rysunek przedstawia te same dane, które przedstawiono na rysunku 3 ale w postaci wykresu
trójwymiarowego.
W dalszym ciągu zajmiemy się tylko przypadkiem 1 czyli ruchem drgającym (periodycznym)
3.4
Energia oscylatora tłumionego
Korzystając z równania na energię oscylatora harmonicznego oraz z postaci zależności wychylenia od czasu,
dla ruchu tłumionego w przypadku małego tłumienia (3.11), możemy zapisać, że całkowita energia oscylatora
tłumionego wynosi
E =
1
2
k(Amplituda)
2
=
1
2
k
Ae
−
β
2m
t
2
=
1
2
kA
2
e
−
β
m
t
=
1
2
kA
2
e
−
t
τ
(3.18)
gdzie τ =
m
β
jest czasem relaksacji
3.4.1
Szybkość zmian energii
Na podstawie równania (3.18) możemy obliczyć szybkość zmian energii w ruchu harmonicznym tłumionym.
dE
dt
=
d
dt
1
2
kA
2
e
−
t
τ
=
1
2
kA
2
−
1
τ
e
−
t
τ
= −
1
τ
E
(3.19)
3.5
Dobroć oscylatora
Dobrocią oscylatora nazywamy wielkość zdefiniowaną jako
Q = 2π
energia zmagazynowana
energia tracona w jednym okresie
Biorąc pod uwagę definicję dobroci oraz zależność (3.19) możemy zapisać
c
Mariusz Krasiński 2011
6
3.6
Dekrement logarytmiczny tłumienia
4
DRGANIA HARM. WYMUSZ. Z TŁUM.
Q = 2π
E
dE
dt
T
= 2π
E
1
τ
ET
=
2π
T
τ = ω
0
τ
3.6
Dekrement logarytmiczny tłumienia
Dekrementem logarytmicznym tłumienia nazywamy wielkość będącą logarytmem stosunku amplitudy występu-
jącej w dowolnej chwili t podczas drgania tłumionego do amplitudy w chwili t + T . Wielkość ta wynosi więc
Λ = ln
A
n
A
n+1
= ln
Ae
−
β
2m
t
Ae
−
β
2m
(t+T )
!
= ln
e
β
2m
T
=
β
2m
T
i jest niezależna od czasu.
4
Drgania harmoniczne wymuszone z tłumieniem
4.1
Wymuszenie harmoniczne
Rozpatrzymy najprostszy przypadek gdy siła wymuszająca jest harmoniczna czyli ma postać
F = F
0
cos(ωt)
lub stosując zapis przy pomocy liczb zespolonych
F = F
0
e
iωt
Równanie ruchu będzie miało wtedy postać:
m
d
2
x
dt
2
+ β
dx
dt
+ kx = F
0
e
iωt
(4.1)
4.2
Rozwiązanie równania (4.1)
Postulujemy rozwiązanie postaci:
x = Ce
iωt
dlaczego?
(4.2)
Licząc podobnie jak w przypadku ruchu tłumionego odpowiednie pochodne położenia (zależność (4.2)) otrzy-
mamy:
dx
dt
= Ciωe
iωt
= iωx
(4.3)
d
2
x
dt
2
=
d
dt
dx
dt
= (iω)
2
Ce
iωt
= −ω
2
x
(4.4)
Po podstawieniu zależności (4.3) i (4.4) do równania głównego (4.1) otrzymamy:
−mω
2
x + βiωx + kx = F
0
x
C
a stąd
C =
F
0
m
k
m
− ω
2
+ iωβ
=
F
0
m(ω
0
2
− ω
2
) + iωβ
(4.5)
c
Mariusz Krasiński 2011
7
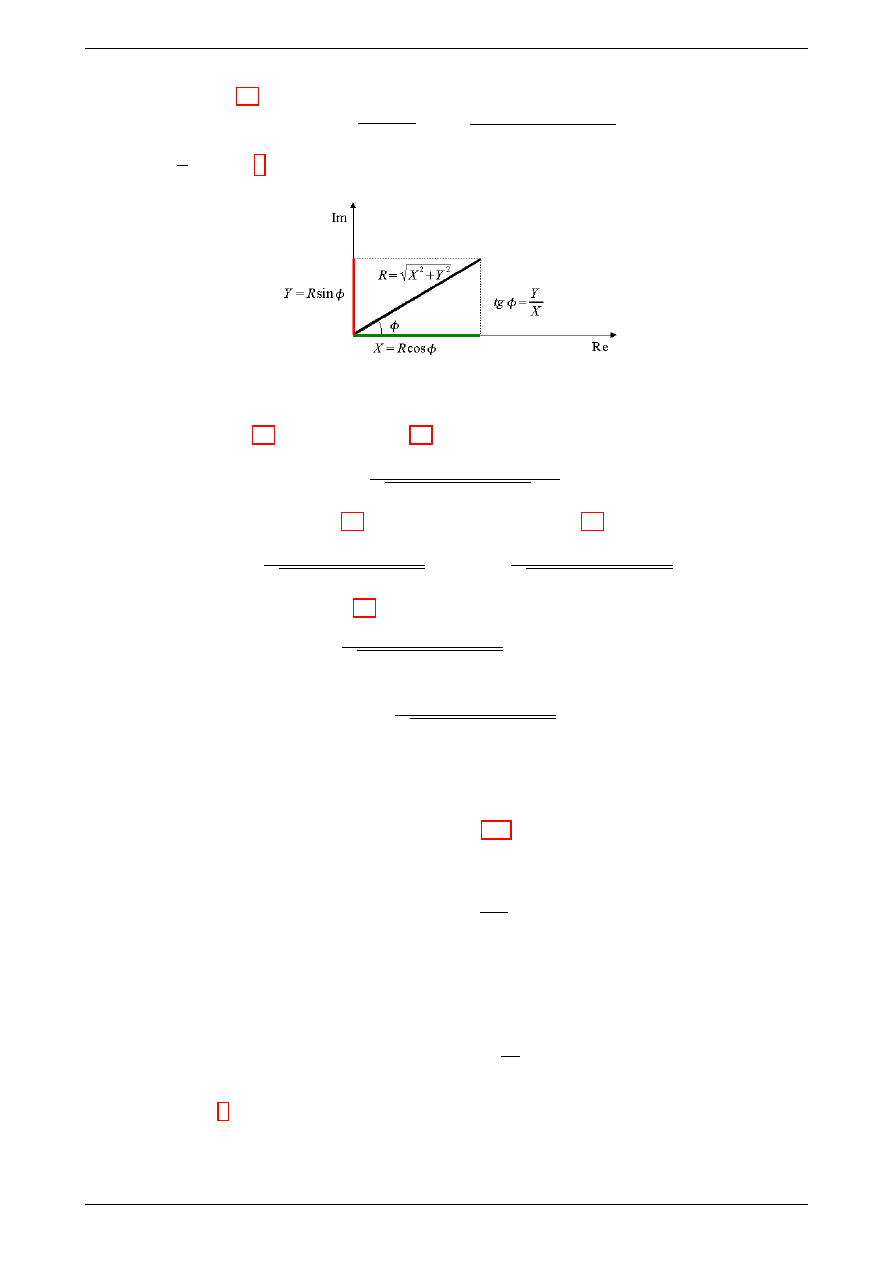
4.3
Rezonans
4
DRGANIA HARM. WYMUSZ. Z TŁUM.
Mianownik zależności (4.5) jest liczbą zespoloną i ma postać X + iY . Można go więc zapisać w inny sposób
jako
mianownik =
p
X
2
+ Y
2
e
iφ
=
p
m
2
(ω
0
2
− ω
2
)
2
+ ω
2
β
2
e
iφ
(4.6)
gdzie tg φ =
Y
X
(rysunek 5)
Rysunek 5: Trygonometryczna postać liczby zespolonej.
Korzystając z zależności (4.6) możemy równanie (4.5) przepisać w postaci:
C =
F
0
pm
2
(ω
0
2
− ω
2
)
2
+ ω
2
β
2
e
iφ
(4.7)
Podstawiając B wyliczone z równania (4.7) do ogólnej postaci rozwiązania (4.2) otrzymamy ostateczne
x = Ce
iωt
=
F
0
pm
2
(ω
0
2
− ω
2
)
2
+ ω
2
β
2
e
−iφ
e
iωt
=
F
0
pm
2
(ω
0
2
− ω
2
)
2
+ ω
2
β
2
e
i(ωt−φ)
(4.8)
Czyli ostatecznie, rozwiązanie równania (4.1) ma postać
x =
F
0
pm
2
(ω
0
2
− ω
2
)
2
+ ω
2
β
2
cos(ωt + φ)
(4.9)
gdzie
A
wym
=
F
0
pm
2
(ω
0
2
− ω
2
)
2
+ ω
2
β
2
(4.10)
jest po prostu amplitudą drgań wymuszonych.
4.3
Rezonans
Amplituda drgań przedstawionych przy pomocy równania (4.10) będzie największa gdy wyrażenie pod pier-
wiastkiem będzie najmniejsze. Łatwo policzyć, że nastąpi to dla częstotliwości (rezonansowej) drgań spełniającej
zależność
ω
2
rez
= ω
2
0
−
β
2
2m
2
W przypadku małego tłumienia (małe β) otrzymamy
ω
rez
2
≈ ω
0
2
Amplituda drgań będzie wynosić wtedy
(Amplituda)
max
=
F
0
ωβ
Wielkość ta może przyjmować bardzo duże wartości, często niemożliwe z uwagi na ograniczoną wytrzymałość
obiektu drgającego (6).
Porównując wzory dla siły wymuszającej
F = F
0
e
iωt
c
Mariusz Krasiński 2011
8
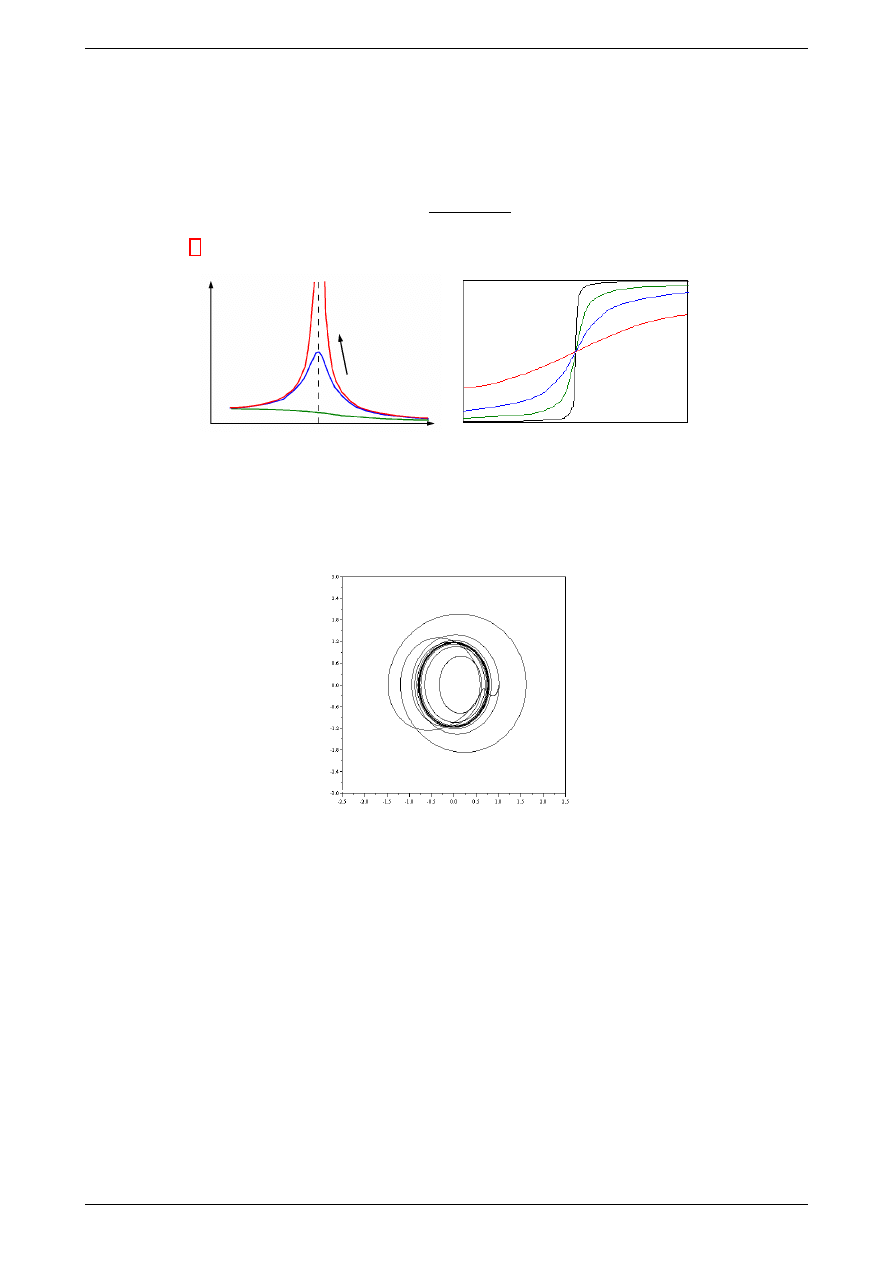
4.4
Ruch wymuszony na wykresie fazowym
4
DRGANIA HARM. WYMUSZ. Z TŁUM.
i wychylenia
x = x
0
e
i(ωt−φ)
zauważyć można, iż drgania układu są przesunięte w fazie względem siły wymuszającej o φ
tgφ =
ωβ
m(ω
0
2
− ω
2
)
Zobacz rysunek 6.
Rysunek 6: Rezonans. Amplituda oraz przesunięcie fazowe pomiędzy siłą wymuszającą i wychyleniem. (dopisz
oznaczenia! )
4.4
Ruch wymuszony na wykresie fazowym
Rysunek 7: Typowy portret fazowy drgania wymuszonego z tłumieniem. Dopisz samodzielnie oznaczenia osi!
4.5
Dynamiczny tłumik drgań
Opis dynamicznego tłumika drgań zostanie przedstawiony na wykładzie.
c
Mariusz Krasiński 2011
9
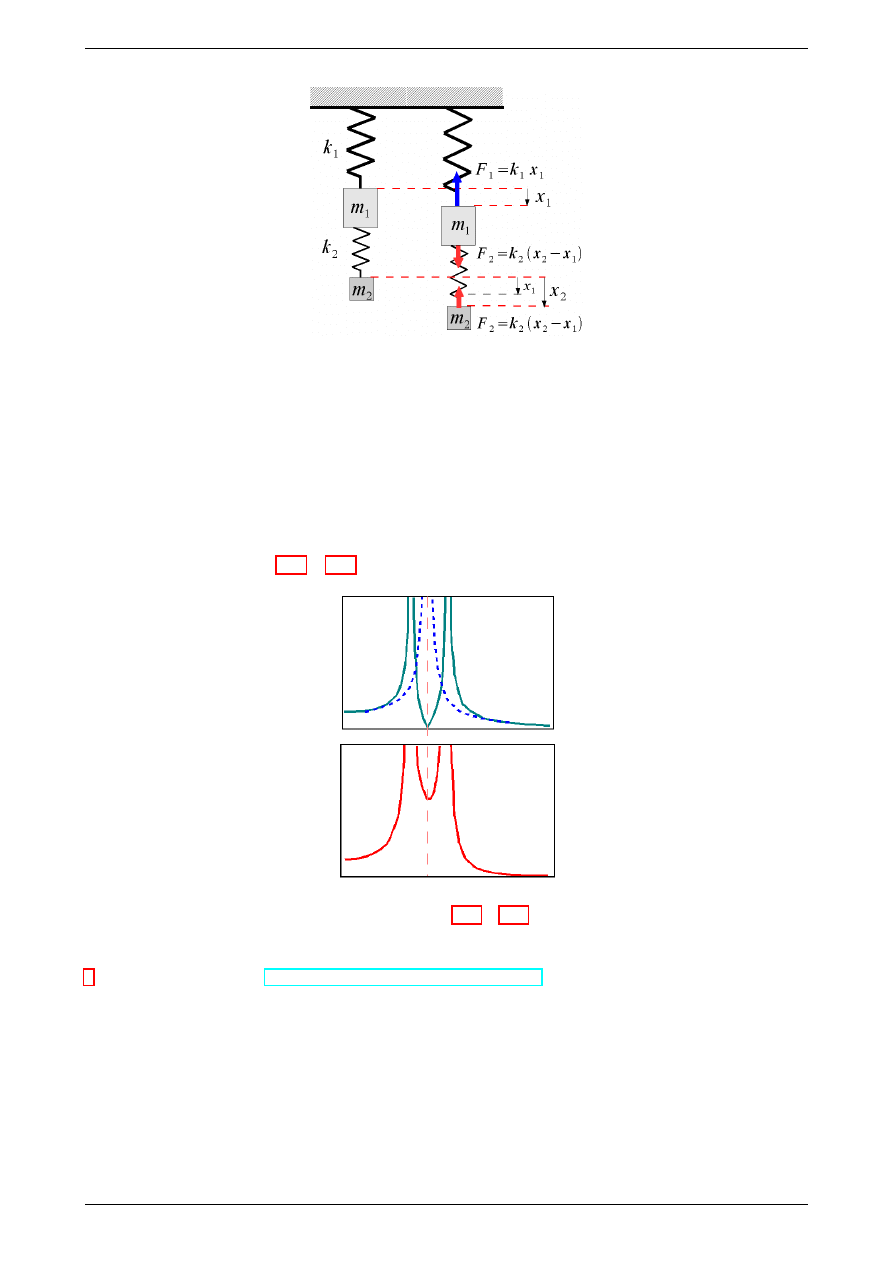
4.5
Dynamiczny tłumik drgań
4
DRGANIA HARM. WYMUSZ. Z TŁUM.
Rysunek 8: Siły działające na układ dwóch mas drgających. Ilustracja do opisu dynamicznego tłumika drgań.
Równania ruchu dla układu powyżej mają postać:
m
1
a
1
= −k
1
x
1
+ k
2
(x
2
− x
1
) + F
0
cos(ωt)
(4.11)
m
2
a
2
= −k
2
(x
2
− x
1
)
(4.12)
Rozwiązanie układu równań (4.11), (4.12) przedstawiono poniżej
Rysunek 9: Rozwiązanie układu równań (4.11), (4.12). Dodaj opisy na wykładzie.
Symulację pt. „Dynamiczny tłumik drgań”, przedstawiającą jak zachowuje się układ przedstawiony na rysunku
8 można znaleźć na stronie http://cmf.p.lodz.pl/markras/fizyka.
c
Mariusz Krasiński 2011
10
Document Outline