WYTRZYMAŁOŚĆ MATERIAŁÓW – wiadomości podstawowe
- 1/11 -
W Y T R Z Y M A Ł O Ś Ć M A T E R I A Ł Ó W
1. WIADOMOŚCI PODSTAWOWE
Wytrzymałość Materiałów
nauka o trwałości spotykanych w praktyce typowych elementów konstrukcji
poddanych działaniu sił
1. 1. Zadania i metody wytrzymałości materiałów
Stosowane w W.M. metody umożliwiają dokonanie stosunkowo prostych
obliczeń dających ilościową ocenę wytrzymałości i podatności w stosunku do
postawionych wymagań.
Główny nacisk położony jest na stronę praktyczną i dla ułatwienia analizy
przyjmuje się metody przybliżone i upraszczające założenia.
Wytrzymałość Materiałów opiera się na:
− przesłankach doświadczalnych (własności materiałów - szczególnie
odkształcenie, w funkcji obciążeń przy różnych warunkach zewnętrznych),
− przesłankach teoretycznych (prawa i zasady statyki! )
Dyscypliny pokrewne W.M.:
− teoria sprężystości,
− teoria plastyczności,
−
reologia.
Z a d a n i a
Wytrzymałości Materiałów
określenie
wytrzymałości elementu
(odporności na zniszczenie)
aby konstrukcja spełniała wymóg
dostatecznego bezpieczeństwa
określenie
podatności elementu
(rodzaju i wartości odkształceń)
aby konstrukcja spełniała wymóg
dostatecznej sztywności
WYTRZYMAŁOŚĆ MATERIAŁÓW – wiadomości podstawowe
- 2/11 -
1.2. Uproszczony model ciała
Uproszczenia dotyczą:
1) materiału
a) jednorodność (dowolnie mała kostka ma takie same właściwości
fizyczne)
b) sprężystość (odkształcenia wywołane obciążeniem znikają całkowicie -
ciało idealnie sprężyste - lub częściowo - ciało częściowo sprężyste - po
odciążeniu)
c) izotropia (w większości materiałów)
2) opisu kształtu
a) pręty (jeden wymiar jest o wiele większy od dwóch pozostałych)
♦ proste
♦ zakrzywione
− płasko zakrzywione
(pierścień tłokowy, spinacz biurowy)
− przestrzennie zakrzywione (sprężyna)
b) powłoki ( jeden wymiar - grubość - jest mniejszy od pozostałych)
c) bryły (wszystkie wymiary są tego samego rzędu)
Powstaje schemat obliczeniowy, w którym zostają zachowane istotne cechy
obiektu.
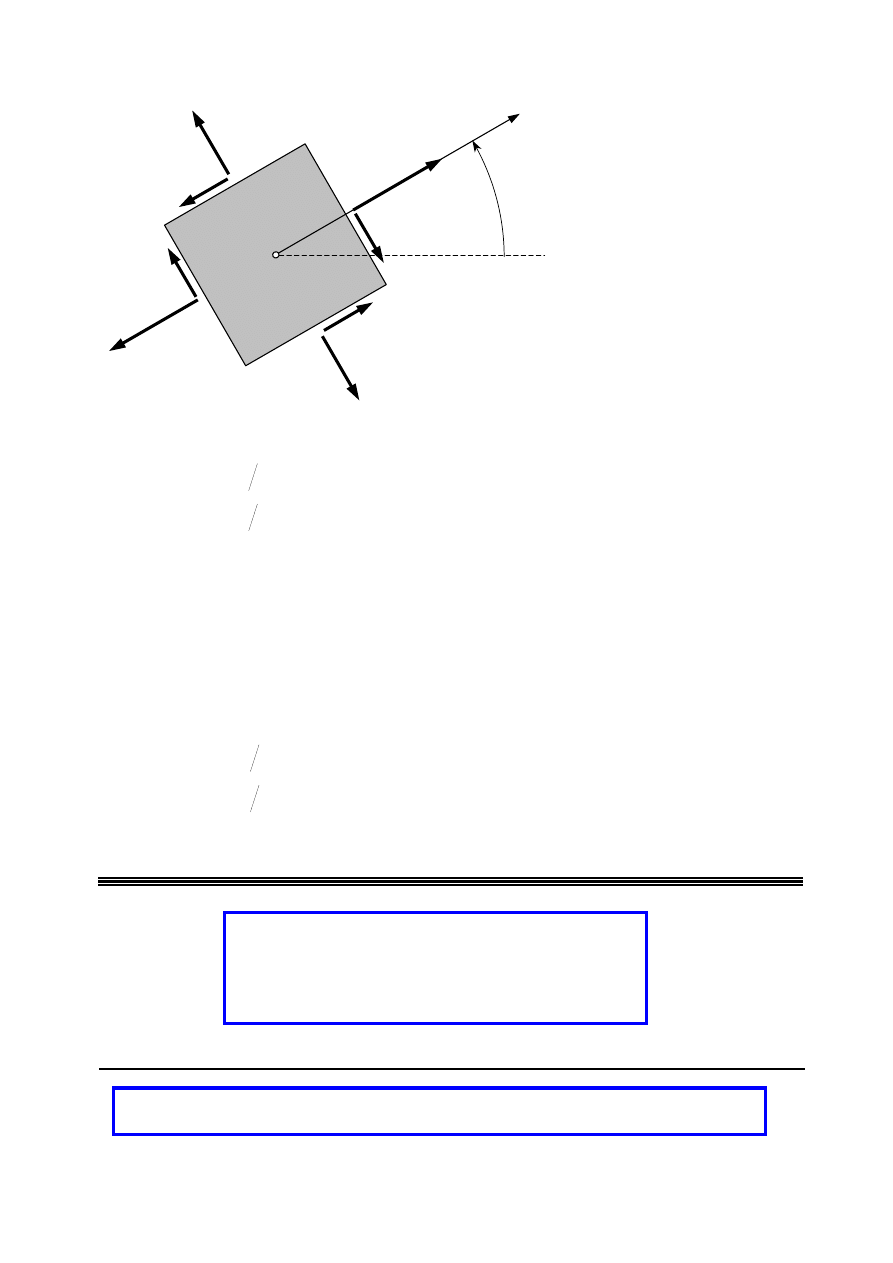
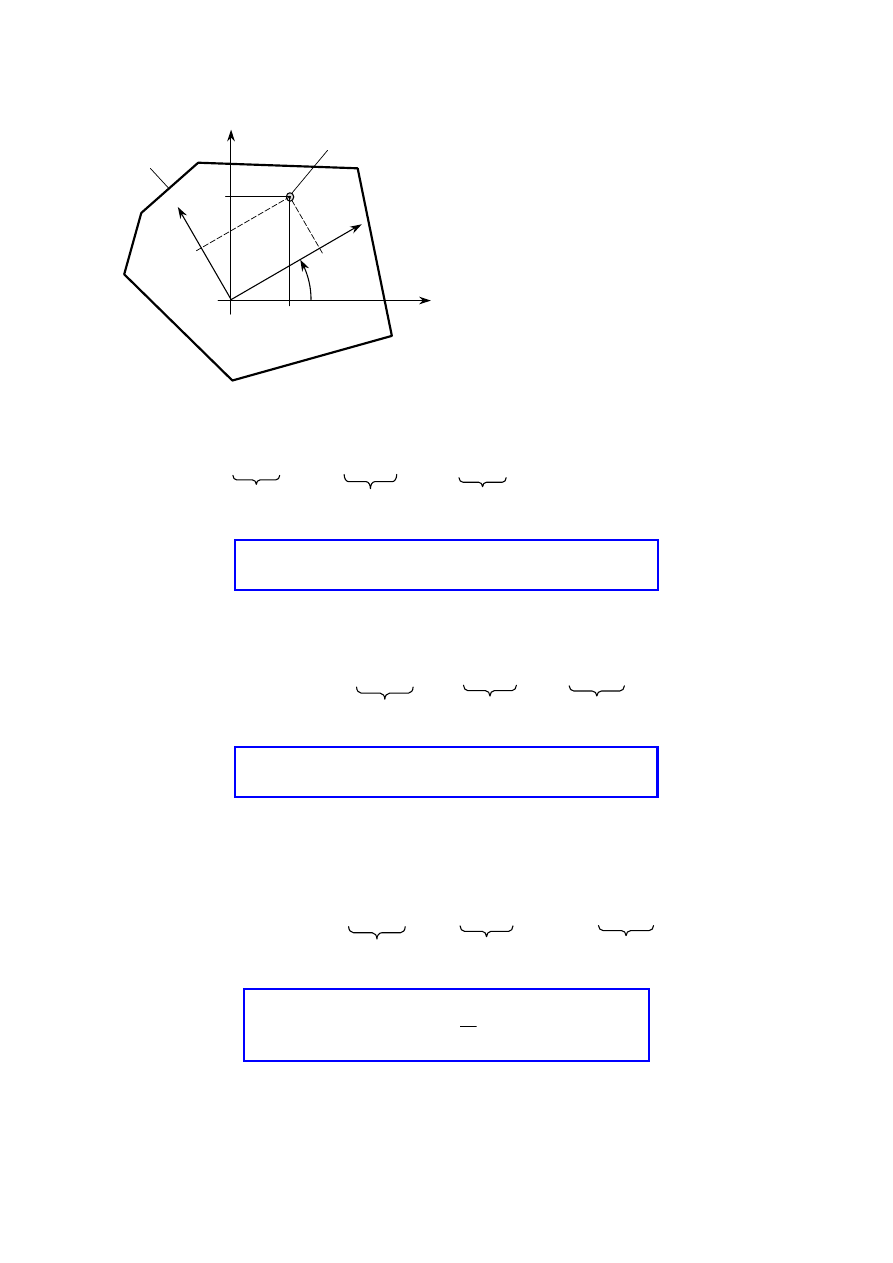
1.3. Siły wewnętrzne i zewnętrzne
− skupione
−
−
−
− skupione
− powierzchniowe
−
−
−
− powierzchniowe
−
objętościowe
Siły
miara mechanicznego oddziaływania
ciał między sobą
Wewnętrzne
oddziaływanie między częściami
konstrukcji
Zewnętrzne
obciążenie konstrukcji
Bierne
reakcje więzów
Czynne
znane wartości
dla ich ujawnienia stosujemy
metodę myślowych przecięć
podział na siły czynne i bierne zależy od tego,
gdzie poprowadzimy granicę podziału
obiekt-otoczenie
WYTRZYMAŁOŚĆ MATERIAŁÓW – wiadomości podstawowe
- 3/11 -
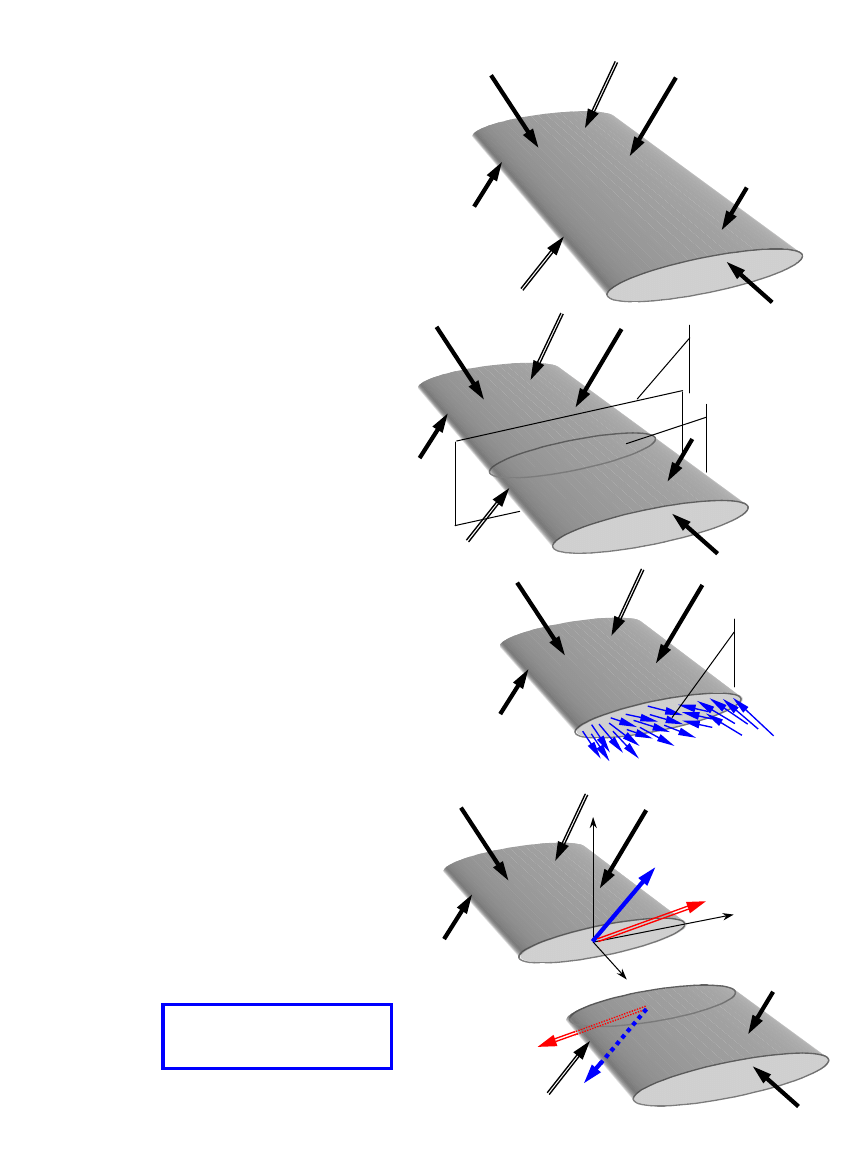
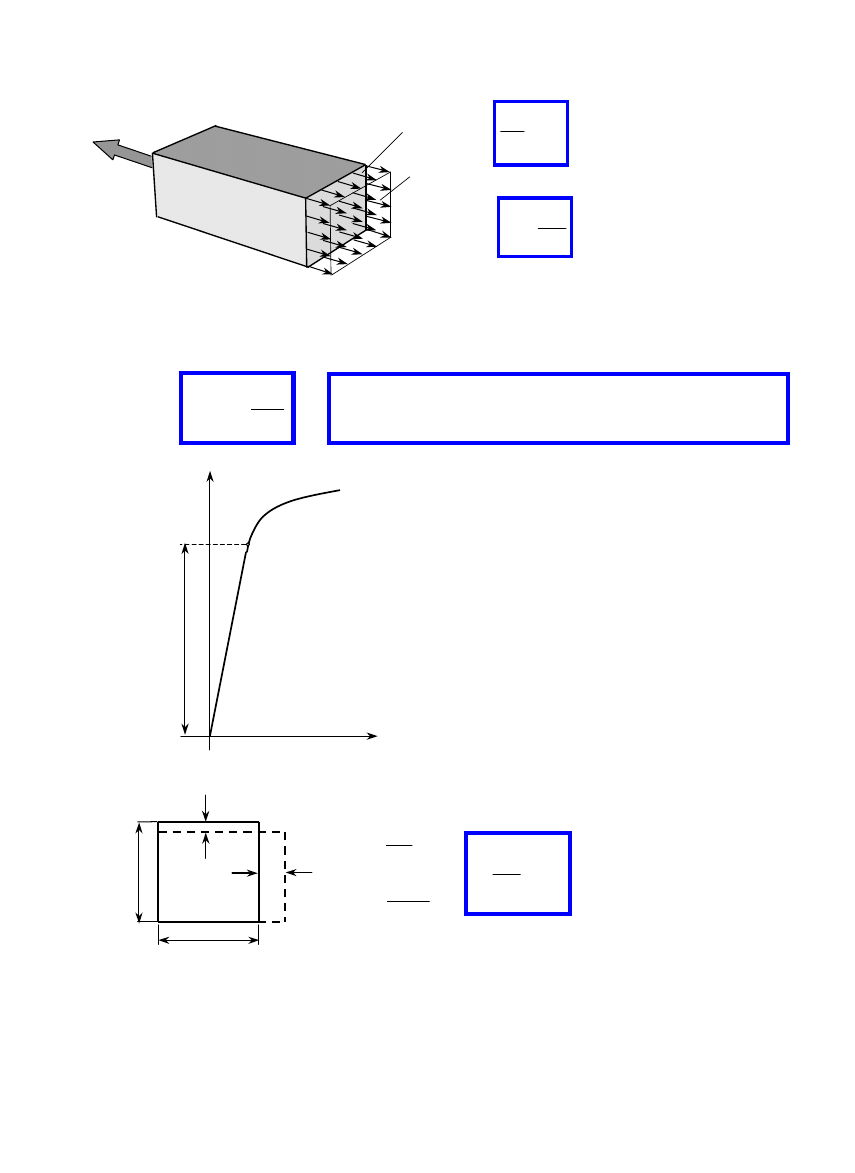
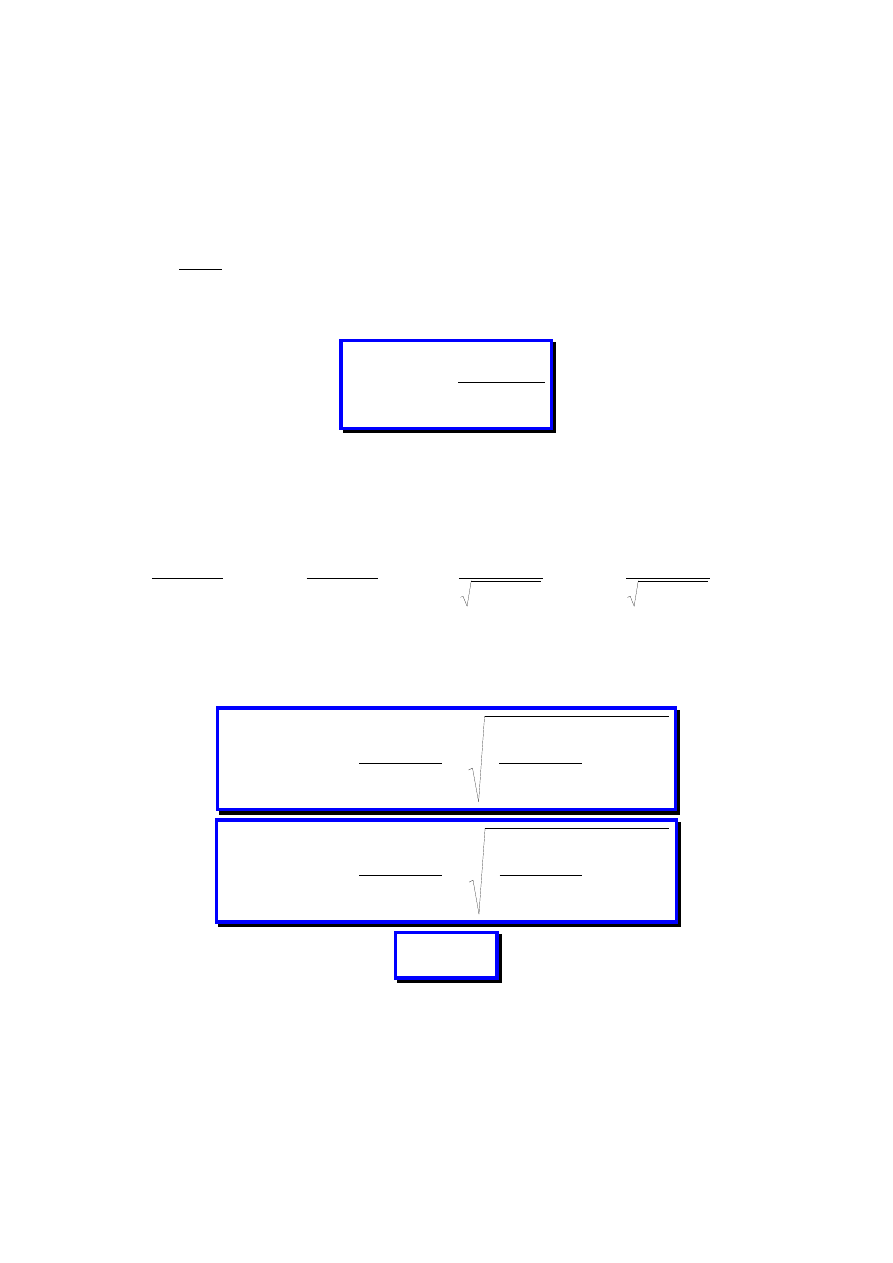
1.4. Wysiłek przekroju
1. Zakładamy, że badany ustrój
znajdujący się pod działaniem
znanego obciążenia zewnętrznego:
− sił (objętościowych,
powierzchniowych, skupionych),
− momentów sił,
pozostaje w równowadze.
2. Dokonujemy myślowego
przekroju ustroju płaszczyzną
(metoda przecięć)
3. Odsuwając od siebie myślowo obie
części ujawniamy na przekroju siły
wewnętrzne jako siły oddziaływania
między nimi. Siły te rozłożone są na
przekroju w sposób ciągły. Jednym z
głównych zadań wytrzymałości
materiałów jest określenie rozkładu sił
wewnętrznych.
4. Siły wewnętrzne redukujemy do
wybranego punktu (zazwyczaj
środka ciężkości przekroju sc)
otrzymując wektor wypadkowej
siły
W
oraz wypadkowego
momentu
M
.
M
x
y
z
sc
W
-
W
-
M
siły
wewnętrzne
płaszczyzna
myślowego
przekroju
myślowy
przekrój
Zespół
W
i
M
nazywamy
wysiłkiem przekroju.
WYTRZYMAŁOŚĆ MATERIAŁÓW – wiadomości podstawowe
- 4/11 -
2
z
2
y
T
T
T
+
=
2
gz
2
gy
g
M
M
M
+
=
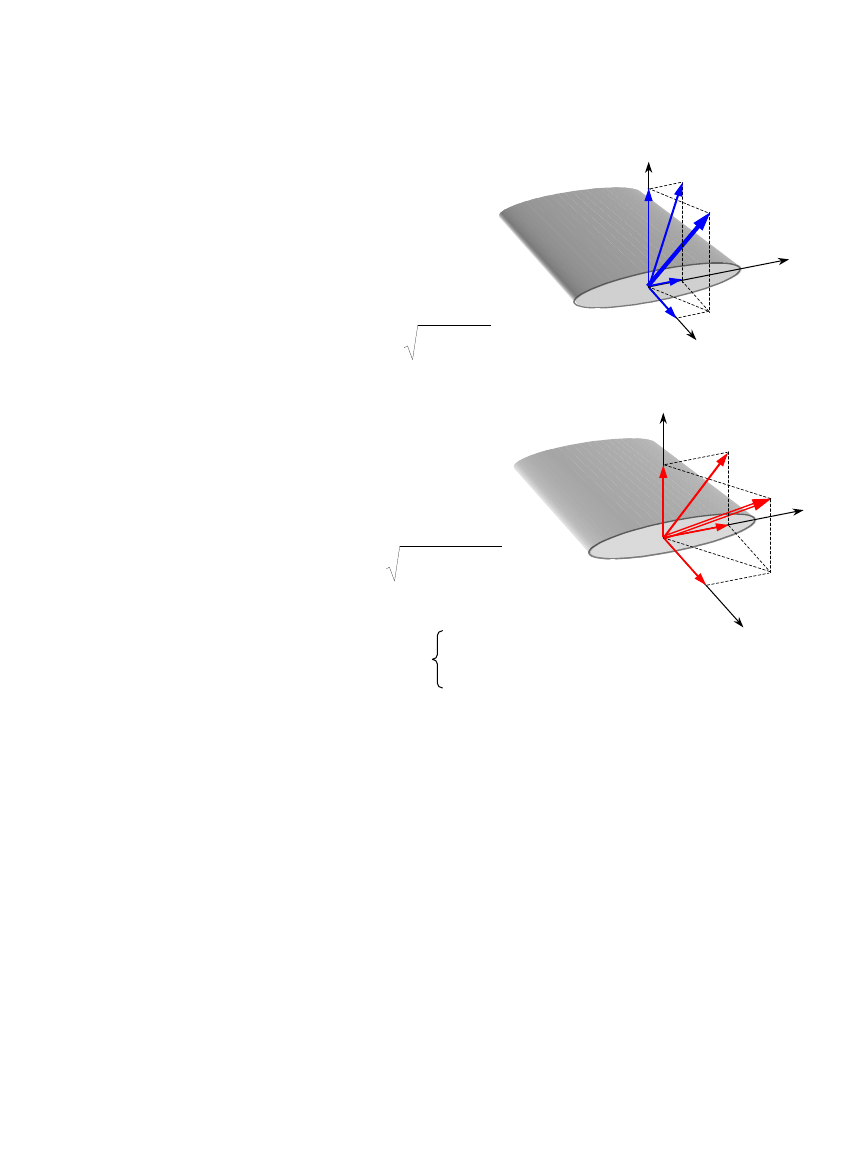
5. Wektory wysiłku przekroju rozkładamy na składowe:
W
=W
x
+W
y
+W
z
W
x
=
N
− siła
normalna
(wzdłużna)
W
y
=
T
y
− siła
tnąca
(poprzeczna) w kierunku
osi y
W
z
=
T
z
− siła
tnąca
(poprzeczna) w kierunku
osi z
wypadkowa siła tnąca
M=M
x
+M
y
+M
z
M
x
=
M
s
− moment
skręcający
M
y
=
M
gy
− moment
gnący
w kierunku osi y
M
z
=
M
gz
− moment
gnący
w kierunku osi z
wypadkowy moment
gnący
N T
y
T
z
M
s
M
gy
M
gz
Elementy wysiłku przekroju wyznaczamy z warunków równowagi jednej lub
drugiej części. Rozwiązujemy w tym celu odpowiednie równania równowagi sił
i momentów:
0
0
0
0
0
0
=
=
=
=
=
=
∑
∑
∑
∑
∑
∑
z
y
x
z
y
x
M
M
M
F
F
F
Nie ma przy tym żadnego znaczenia, której części równowagę będziemy badać,
gdyż na zasadzie akcji i reakcji, siły wewnętrzne działające na obie części mają
jednakowe wartości. Są jedynie przeciwnie skierowane.
Reguła wymiarów początkowych − przy formułowaniu równań równowagi
przyjmuje się, że obciążenie ciała nie zmienia jego geometrii.
Nie wolno jej stosować przy badaniu zagadnień stateczności oraz w wypadku, gdy nawet
małe odkształcenia zmieniają istotnie charakter pracy ustroju.
x
y
z
sc
W
N
T
y
T
z
T
M
x
y
z
sc
M
g
M
s
M
gy
M
gz
elementy wysiłku przekroju
WYTRZYMAŁOŚĆ MATERIAŁÓW – wiadomości podstawowe
- 5/11 -
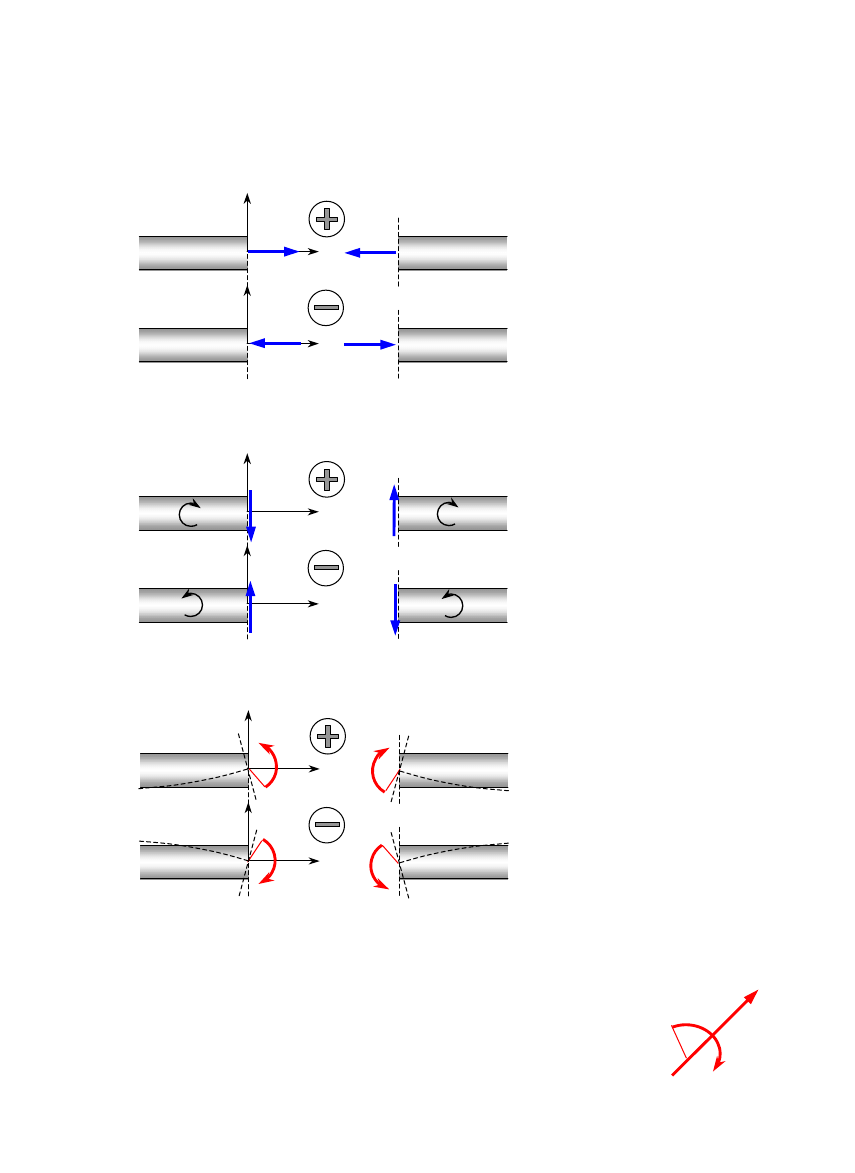
Umowa dotycząca znaku elementów wysiłku przekroju
SIŁA NORMALNA
DODATNIA – skierowana od
przekroju
UJEMNA – skierowana do
przekroju
SIŁA TNĄCA
DODATNIA – stara się obrócić
rozpatrywaną część zgodnie z
ruchem wskazówek zegara
UJEMNA – stara się obrócić
rozpatrywaną część przeciwnie
do ruchu wskazówek zegara
MOMENT GNĄCY
DODATNI – stara się wygiąć
belkę wypukłością w dół
UJEMNY – stara się wygiąć
belkę wypukłością w górę
MOMENT SKRĘCAJĄCY – jak dla siły normalnej
UWAGA: wektor momentu prostopadły do płaszczyzny rysunku
przedstawiamy za pomocą zagiętej strzałki stosując się przy tym
do reguły śruby prawoskrętnej.
x
z
x
z
N
N
N
N
x
z
x
z
T
T
T
T
x
z
x
z
M
g
M
g
M
g
M
g
góra
dół
góra
dół

WYTRZYMAŁOŚĆ MATERIAŁÓW – wiadomości podstawowe
- 6/11 -
Wyodrębnienie poszczególnych elementów wysiłku przekroju pozwala na
rozbicie złożonego stanu obciążenia na przypadki proste:
− rozciąganie (ściskanie) – siła normalna N,
− skręcanie – moment skręcający M
s
.
− czyste zginanie – moment gnący M
g
,
− zginanie poprzeczne – moment gnący M
g
i siła tnąca T,
− ścinanie – siła tnąca T,
stosunkowo łatwe do analizy rachunkowej.
Rozbicie złożonego stanu na przypadki proste a następnie zsumowanie wyników
poszczególnych analiz to zasada superpozycji (metoda bardzo często
stosowana w wytrzymałości materiałów).
Zasada superpozycji nie może być stosowana tam, gdzie działanie jednych sił
mogłoby zmienić charakter działania innych (np. przy utracie stateczności
konstrukcji).
Wartości elementów wysiłku przekroju zależą m.in. od położenia myślowego
przekroju. Stanowią zatem funkcje współrzędnej x:
N(x), T(x), M
g
(x), M
s
(x).
Wyznaczenie tych funkcji jest pierwszym, niezbędnym etapem
analizy wytrzymałościowej konstrukcji.
WYTRZYMAŁOŚĆ MATERIAŁÓW – wiadomości podstawowe
- 7/11 -
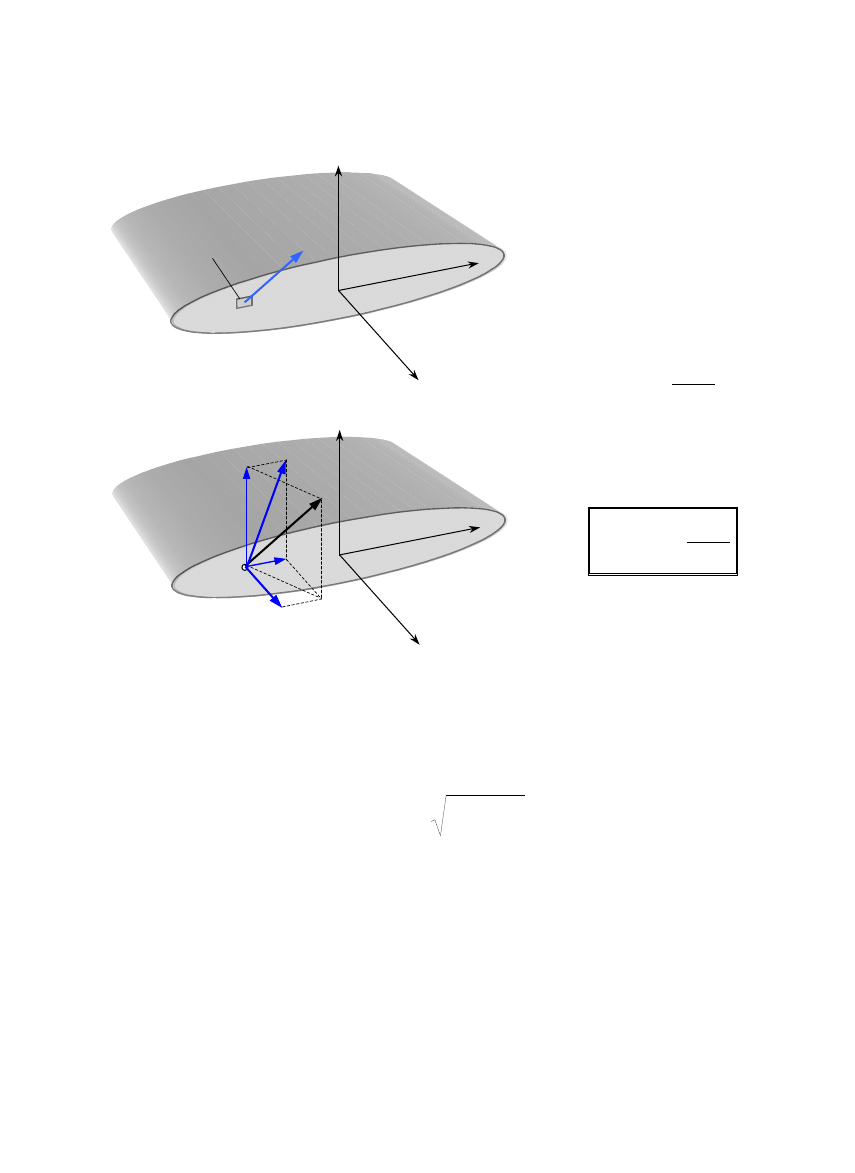
1.5. Naprężenia, odkształcenia
NAPRĘŻENIE (natężenie
sił wewnętrznych) – miara
sił wewnętrznych działają-
cych na wybranym polu
przekroju.
Średnie wypadkowe
naprężenie na polu
∆
A
A
W
p
ś
r
∆
∆
=
Wypadkowe naprężenie
w punkcie B
A
W
p
A
∆
∆
=
→
∆
0
lim
Naprężenie wypadkowe p rozkładamy na składowe:
− prostopadłą do przekroju:
σ
σ
σ
σ
– naprężenie normalne
− w płaszczyźnie przekroju:
ττττ
y
,
ττττ
z
– naprężenia styczne
Wypadkowe naprężenie styczne
2
2
z
y
τ
τ
τ
+
=
jednostka
σ
σ
σ
σ
,
ττττ
:
Pa=N/m
2
w praktyce
MPa=10
6
N/m
2
=1N/mm
2
paskal megapaskal
Jednym z głównych zadań wytrzymałości materiałów jest wyznaczenie
rozkładu naprężeń w wybranym przekroju ciała poddanego działaniu sił.
UWAGA
Naprężenia normalne
σ
σ
σ
σ
i styczne
ττττ
w danym punkcie ciała zależą od kierunku
poprowadzenia przez ten punkt płaszczyzny myślowego przekroju.
x
y
z
∆
∆
∆
∆
W
∆
∆
∆
∆
A
x
y
z
p
B
σ
σ
σ
σ
ττττ
ττττ
y
ττττ
z
WYTRZYMAŁOŚĆ MATERIAŁÓW – wiadomości podstawowe
- 8/11 -
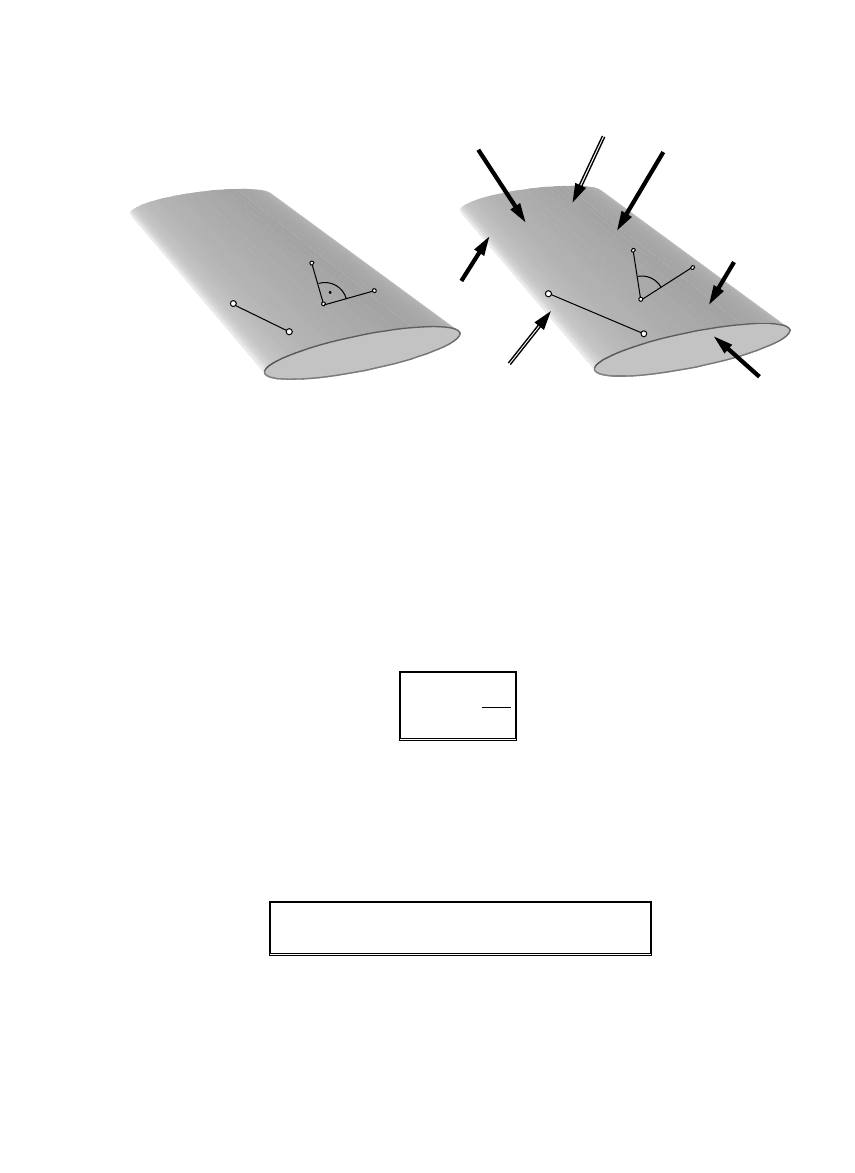
Pod wpływem odkształceń ciała spowodowanych działaniem sił
odcinek A-B przechodzi w odcinek A’-B’
kąt prosty CDE przechodzi w kąt C’D’E’
Następuje zmiana długości odcinka A-B o ∆s i zmiana kąta prostego CDE o γ.
∆
s – wydłużenie bezwzględne odcinka A-B
ε
ś
r
=∆s/s – średnie wydłużenie względne odcinka A-B
wydłużenie względne w punkcie A w kierunku A-B
s
s
s
∆
=
→0
lim
ε
[liczba niemianowana]
Pełny obraz odkształceń poznamy, jeśli w otoczeniu punktu A będą znane
wydłużenia względne we wszystkich możliwych kierunkach.
kąt odkształcenia postaciowego w punkcie D
(
)
'
'
'
lim
0
,
0
E
D
C
CDE
E
D
D
C
∠
−
∠
=
→
−
→
−
γ
[rad]
Pełny obraz odkształceń postaciowych w otoczeniu punktu D poznamy, gdy
będą znane kąty odkształceń postaciowych przy wszystkich możliwych
kierunkach ustawień ramion CD i DE.
A
B
s
A’
B’
s+∆s
C
E
D
C’
E’
D’
90
o
-γ
przed obciążeniem po obciążeniu
WYTRZYMAŁOŚĆ MATERIAŁÓW – wiadomości podstawowe
- 9/11 -
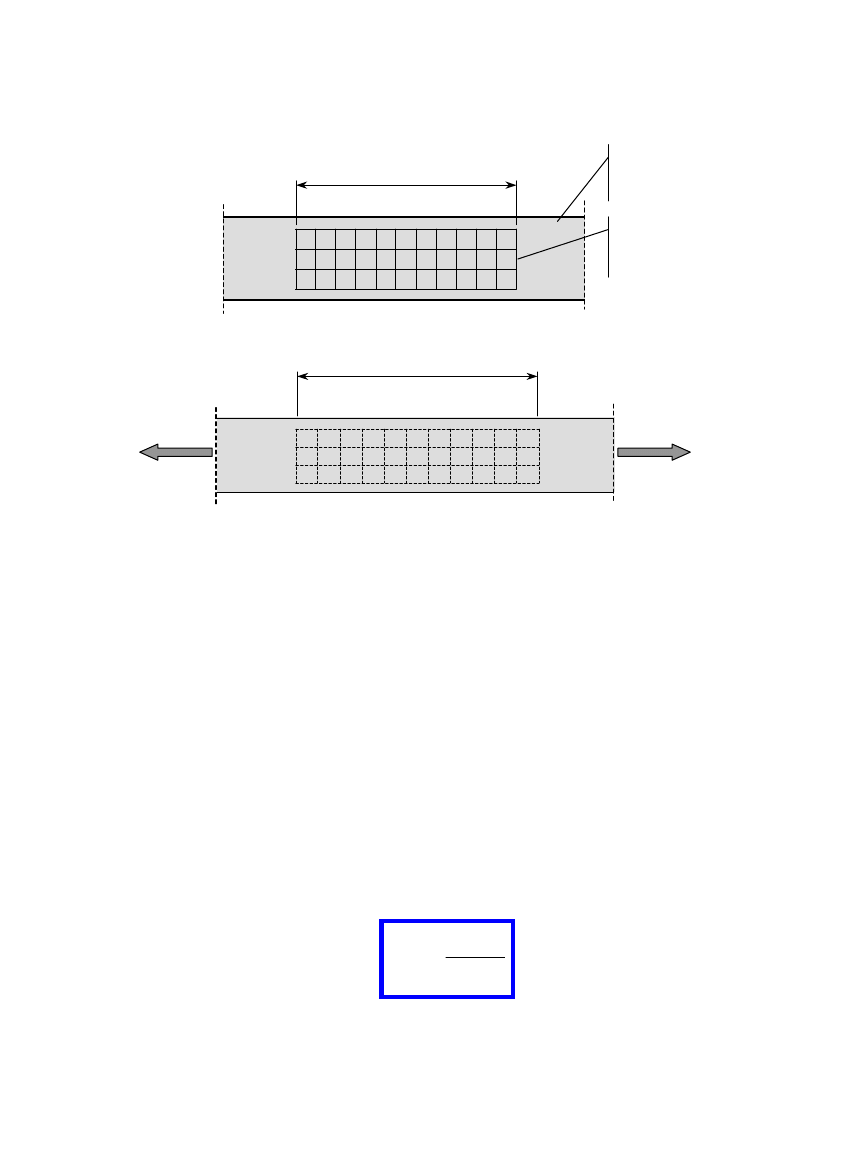
1.6. Prawo Hooke'a, moduł Younga, współczynnik Poissona
Przed obciążeniem
Po obciążeniu
Fakty doświadczalne:
−
oś pręta po obciążeniu pozostaje prosta,
− odcinek pomiarowy L zwiększa swoją długość o ∆L,
− narysowana przed obciążeniem na powierzchni pręta prostokątna siatka
zachowuje po obciążeniu kąty proste i proste krawędzie bez względu na
geometrię przekroju pręta,
− długości boków siatki zwiększają się w kierunku działającej siły i
zmniejszają w kierunku poprzecznym,
− jednakowe oczka siatki zmieniają się po obciążeniu w ten sam sposób bez
względu na ich położenie,
−
o ile siła F nie jest za duża, to dla większości materiałów konstrukcyjnych
wydłużenie ∆L odcinka pomiarowego jest proporcjonalne do jego
długości L, siły F, zaś odwrotnie proporcjonalne do pola powierzchni
przekroju poprzecznego S
0
,
− wydłużenie ∆L zależy od materiału, z którego wykonany jest pręt.
prawo Hooke’a
E [MPa]
– moduł Younga (współczynnik sprężystości wzdłużnej)
– stała materiałowa
L+
∆
∆
∆
∆
L
F
F
L
pręt
pryzmatyczny
kwadratowa siatka
naniesiona na powierzchni
E
S
L
F
L
⋅
⋅
=
∆
0
WYTRZYMAŁOŚĆ MATERIAŁÓW – wiadomości podstawowe
- 10/11 -
S
0
σ
σ
σ
σ
=const
F
E
σ
ε
=
naprężenie normalne
(rozciągające,
ś
ciskające)
wydłużenie względne
Prawo Hooke’a w przypadku rozciągania:
wydłużenie względne
εεεε
jest wprost proporcjonalne
do naprężenia normalnego
σ
σ
σ
σ
Prawo Hooke’a (liniowy związek między
wydłużeniem względnym εεεε a naprężeniem
normalnym σ
σ
σ
σ) zazwyczaj nie obowiązuje w
całym zakresie obciażeń materiału.
Zakres stosowalności prawa Hooke’a
wyznaczony jest przez naprężenia
R
p
zwane
granicą proporcjalności
(maksymalna wartość naprężeń, przy których
zachowany jest jeszcze liniowy związek σ(ε) ).
− współczynnik Poissona jest dla danego materiału stały w granicach
stosowalności prawa Hooke’a
− dla materiałów izotropowych 0<ν<0.5 (stal: ν≈0.3)
x
y
∆
∆
∆
∆
y
∆
∆
∆
∆
x
y
y
x
x
y
x
∆
−
=
∆
=
ε
ε
,
ν
ε
ε
=
−
x
y
współczynnik (liczba)
Poissona – stała materiałowa
σ
σ
σ
σ
ε
εε
ε
R
p
za
kr
es
s
to
so
w
al
no
śc
i p
ra
w
a
H
oo
ke
’a
σ
=
0
S
F
L
L
∆
=
ε
WYTRZYMAŁOŚĆ MATERIAŁÓW – wiadomości podstawowe
- 11/11 -
Orientacyjne wartości modułu Younga E i współczynnika Poissona ν
dla różnych materiałów
Materiał
E [MPa]
ν
stal sprężynowa
2.10×10
5
0.30
stal konstrukcyjna zwykłej jakości
2.06×10
5
0.29
brąz
1.0÷1.2×10
5
0.32
ż
eliwo szare
1.0×10
5
0.23÷0.27
stopy aluminium
0.67÷0.74×10
5
0.33
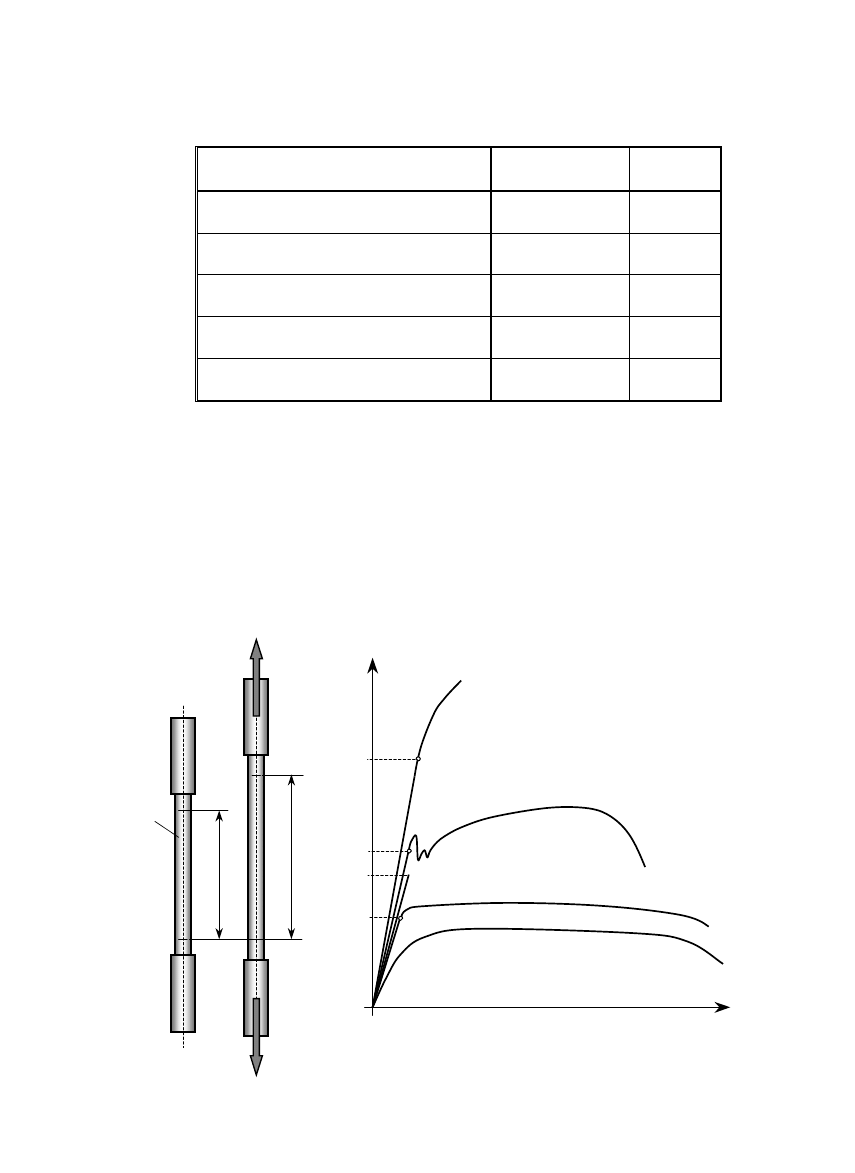
1.7. Wykres rozciągania
Podstawowe własności mechaniczne materiału możemy poznać dzięki
statycznej próbie rozciągania.
Polega ona na powolnym rozciąganiu specjalnie przygotowanej próbki
zazwyczaj aż do zerwania. Podczas tego procesu rejestrowany jest wykres
rozciągania F(∆
∆
∆
∆L), będący podstawą do wyznaczenia szeregu własności
mechanicznych materiału.
F
F
L
L
+∆
L
S
0
F
∆
∆
∆
∆L
aluminium
miedź
stal niskowęglowa
stal sprężynowa
ż
eliwo
2. Rozciąganie (ściskanie) pręta
- 1/ 9 -
2. ROZCIĄGANIE (ŚCISKANIE) PRĘTA
Rozciąganie (ściskanie) –
przypadek obciążenia pręta, w
którym w myślowym przekroju,
prostopadłym do osi pręta, istnieje
siła normalna N(x).
Wynikiem działania siły normalnej
są naprężenia normalne
( )
( )
( )
x
S
x
N
x
=
σ
posiadające w danym przekroju
rozkład równomierny (w każdym
punkcie mają jednakowe wartości).
W praktyce założenie o równomierności rozkładu naprężeń normal-
nych nie zawsze jest spełnione.
Obszary rozciąganych prętów rzeczywistych, gdzie nie jest spełnione
założenie o równomierności naprężeń normalnych
(Zb.Brzoska, Wytrzymałość Materiałów, PWN Warszawa 1979)
x
z
y
x
S(x)
N(x)
σ
σ
σ
σ
(x)
2. Rozciąganie (ściskanie) pręta
- 2/ 9 -
2.1. Analiza wytrzymałościowa pręta rozciąganego (ściskanego)
Założenia:
− pręt jest prosty,
− pręt obciążony jest siłami działającymi osiowo:
o
skupionymi P
i
[N],
o
rozłożonymi w sposób ciągły q
i
[N/m],
− pręt znajduje się w równowadze,
− pręt może posiadać zmienne pole powierzchni przekroju poprzecznego
(skokowo lub w sposób ciągły),
− pręt może być odcinkami zbudowany z różnych materiałów.
Pełna analiza wytrzymałościowa obejmuje:
1. wyznaczenie funkcji siły normalnej N(x)
na podstawie analizy równowagi myślowo odciętej części,
2. wyznaczenie funkcji naprężeń normalnych
σ
σ
σ
σ
(x),
( )
( )
( )
x
S
x
N
x
=
σ
S
(x) – pole powierzchni przekroju poprzecznego pręta w miejscu
określonym współrzędną x,
3. wyznaczenie funkcji wydłużenia względnego
εεεε
(x)
z prawa Hooke’a
( )
( )
( )
x
E
x
x
σ
ε
=
E
– moduł Younga materiału,
4. wyznaczenie funkcji przemieszczenia przekrojów u(x)
( )
( )
dx
x
x
u
x
∫
=
0
ε
y
x
P
i
q
i
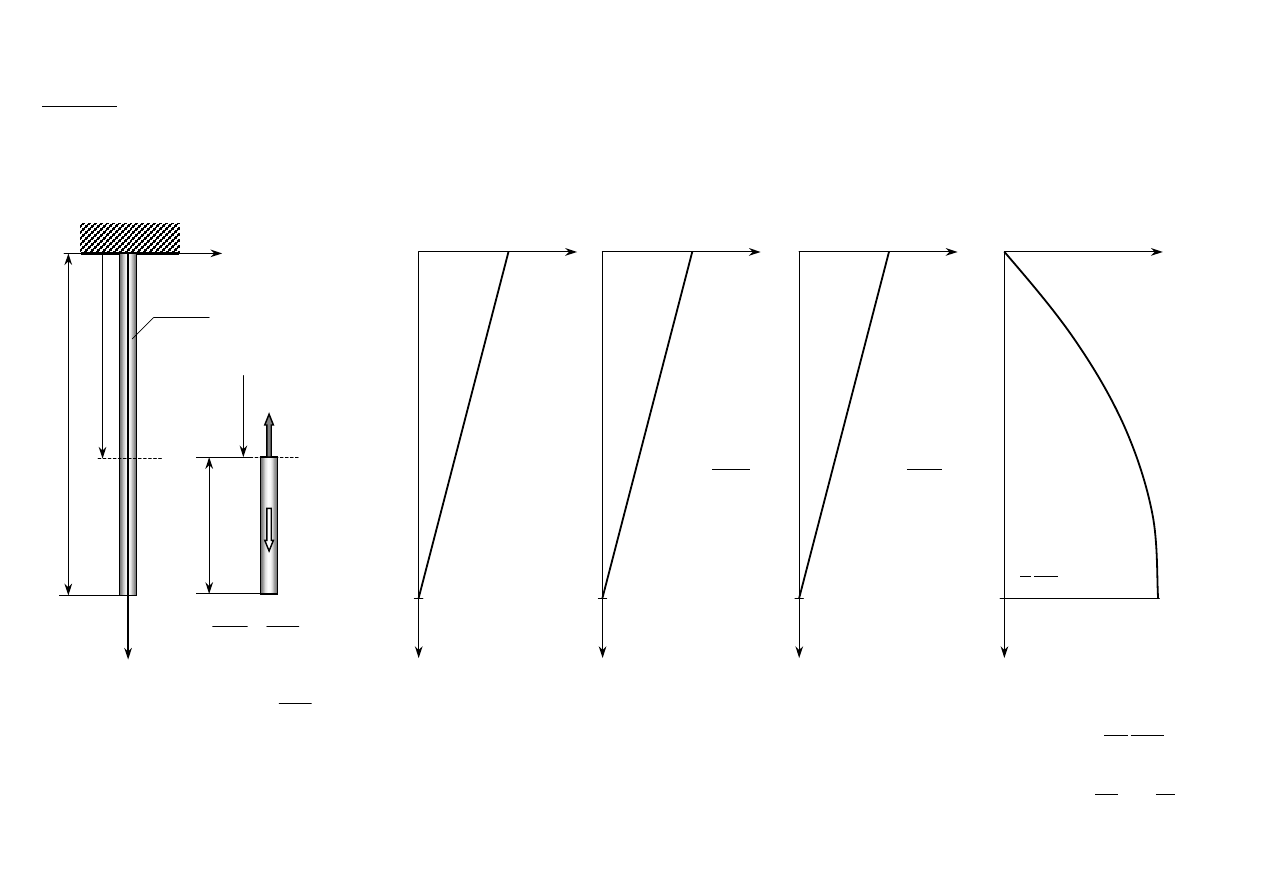
2. Rozciąganie (ściskanie) pręta
- 3/ 9 -
Przykład
Wykonać pełną analizę wytrzymałościową pręta OA o długości l, polu przekroju poprzecznego S, gęstości materiału
ρ
ρ
ρ
ρ
, zawieszonego
pionowo i obciążonego własnym ciężarem. Moduł Younga materiału pręta równy jest E.
Dane: l=100m, S=1cm
2
,
ρ
ρ
ρ
ρ
=7850kg/m
3
, E=2.1⋅10
5
MPa, g≈10m/s
2
.
ciężar pręta
g
lS
G
ρ
=
G
=100m⋅10
-4
m
2
⋅7850kg/m
3
⋅9.81m/s
2
=770N
O
l
A
x
y
ρ
, S, E
x
α
α
x
α
α
l-x
G(x)
N(x)=G(x)
( )
( )
l
x
l
G
x
G
l
x
l
G
x
G
−
=
⇓
−
=
x
N(x)
l
G=770N
x
σ
σ
σ
σ
(x)
l
G/S=
=7.7MPa
( )
( )
S
x
N
x
=
σ
l
x
εεεε
(x)
G/(SE)=
=3.67
⋅⋅⋅⋅
10
-5
( )
( )
E
x
x
σ
ε
=
( )
( )
−
=
=
−
=
=
=
∫
∫
l
x
x
SE
G
dx
l
x
l
SE
G
dx
x
x
u
x
x
2
2
0
0
ε
l
x
u(x)
mm
l
SE
G
84
.
1
2
1
=
2. Rozciąganie (ściskanie) pręta
- 4/ 9 -
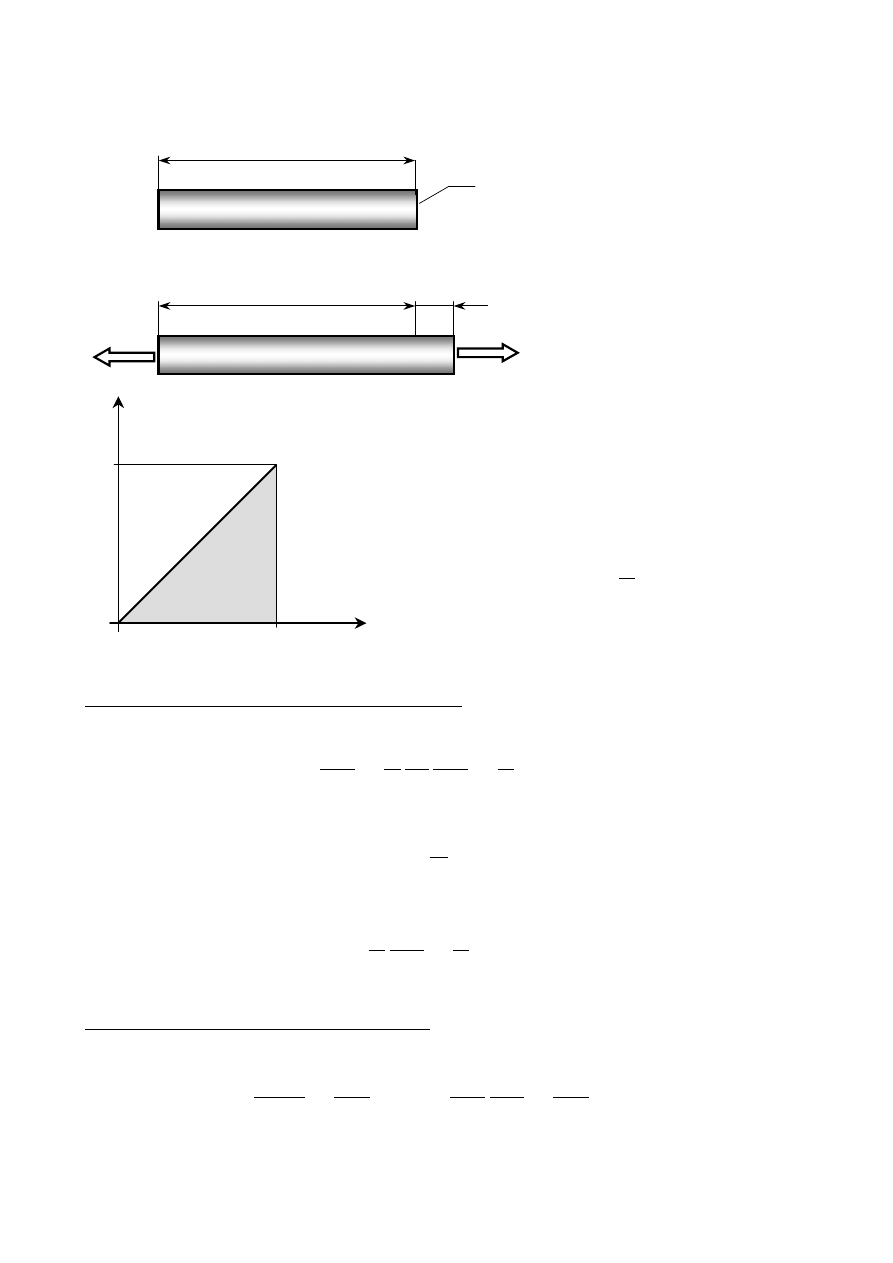
2.2. Energia odkształcenia przy rozciąganiu
Założenia:
− siła rozciągająca narasta od
zera do swojej maksymalnej
wartości F
− spełnione jest prawo Hooke’a
Energia odkształcenia
U
zgromadzona
w pręcie równa jest pracy
W
siły F
[ ]
J
L
F
W
U
∆
⋅
=
=
2
1
Energia odkształcenia na jednostkę objętości
[
]
3
/
2
1
2
1
m
J
L
L
S
F
LS
U
U
v
ε
σ
⋅
=
∆
=
=
po uwzględnieniu prawa Hooke’a
E
σ
ε
=
[
]
3
2
2
/
2
1
2
1
m
J
E
E
U
v
ε
σ
=
=
Energia odkształcenia na jednostkę masy
[
]
kg
J
E
E
LS
U
U
m
/
2
1
2
1
2
1
2
2
ε
ρ
σ
ρ
ε
σ
ρ
ρ
=
=
⋅
=
=
ρ
- gęstość materiału pręta
L
S
L
∆
∆
∆
∆
L
F
F
siła rozciągająca
wydłużenie
bezwzględne
F
∆
∆
∆
∆
L
W
2. Rozciąganie (ściskanie) pręta
- 5/ 9 -
σ
σ
σ
σ
εεεε
σ
σ
σ
σ
εεεε
R
e
R
m
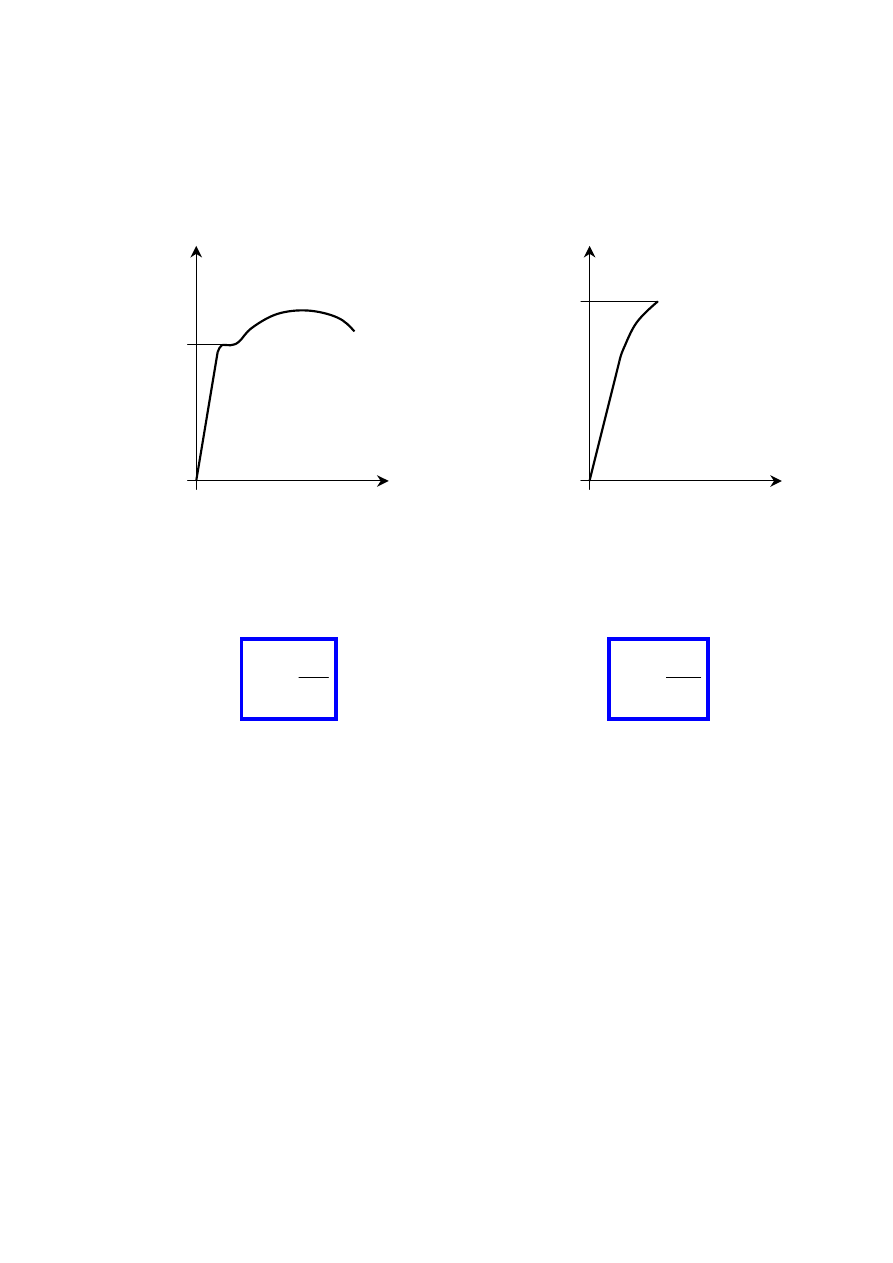
2.3. Współczynnik bezpieczeństwa
Naprężenia w żadnym miejscu konstrukcji
nie mogą przekroczyć dopuszczalnych wartości
k
r
(metoda naprężeń dopuszczalnych)
σ
σ
σ
σ
max
≤ k
r
przykładowy wykres rozciągania przykładowy wykres rozciągania
dla materiału plastycznego dla materiału kruchego
R
e
–
granica plastyczności
R
m
–
wytrzymałość na rozciąganie
współczynnik bezpieczeństwa
n
e
, n
m
>1
Wartość współczynnika bezpieczeństwa przyjmuje się w zależności od:
− dokładności, z jaką znane są obciążenia zewnętrzne,
− charakteru obciążeń (stałe, zmienne),
− jakości technologii,
− warunków użytkowania,
− dokładności danych materiałowych,
− skutków awarii (koszty naprawy, ew. ofiary) itd. ⇒ normy
e
e
r
n
R
k
=
m
m
r
n
R
k
=
2. Rozciąganie (ściskanie) pręta
- 6/ 9 -
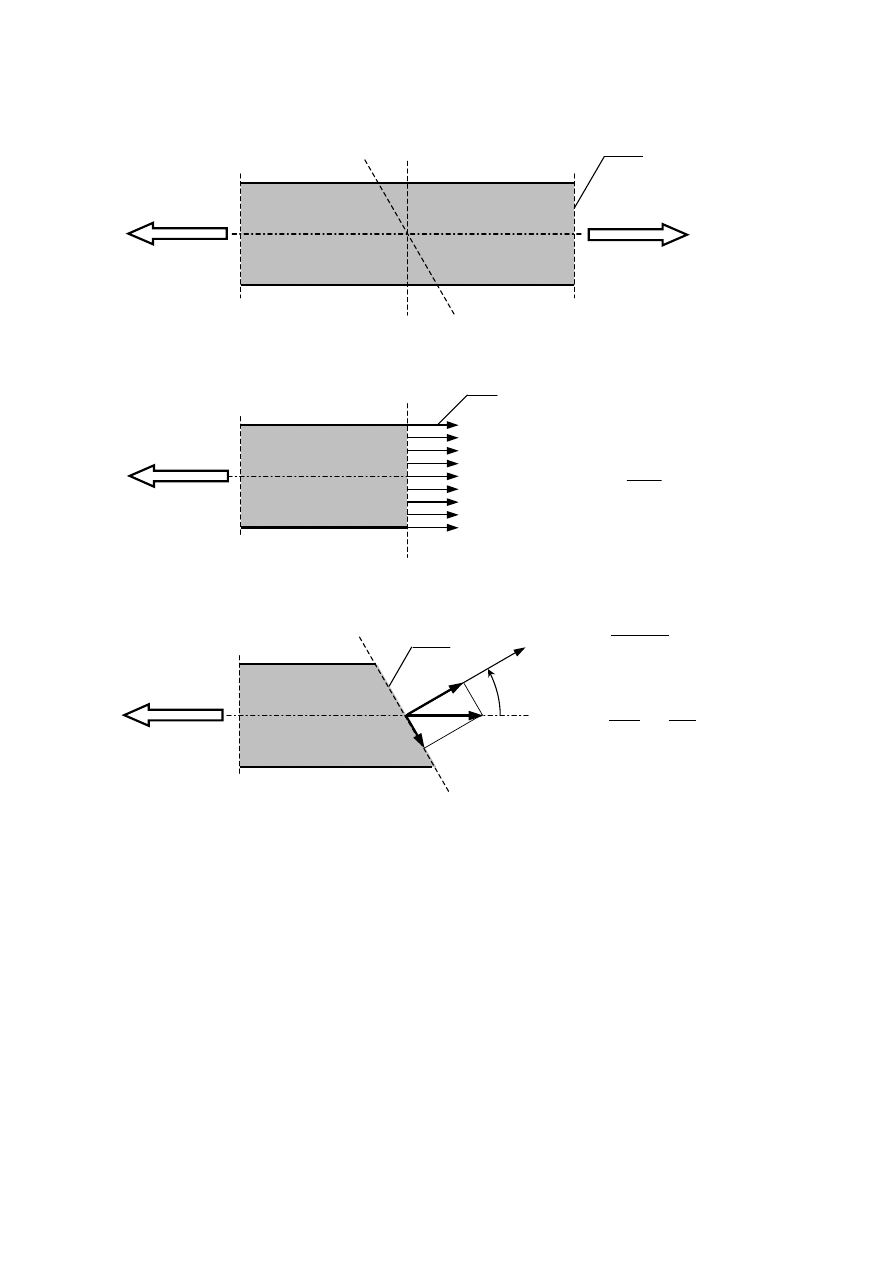
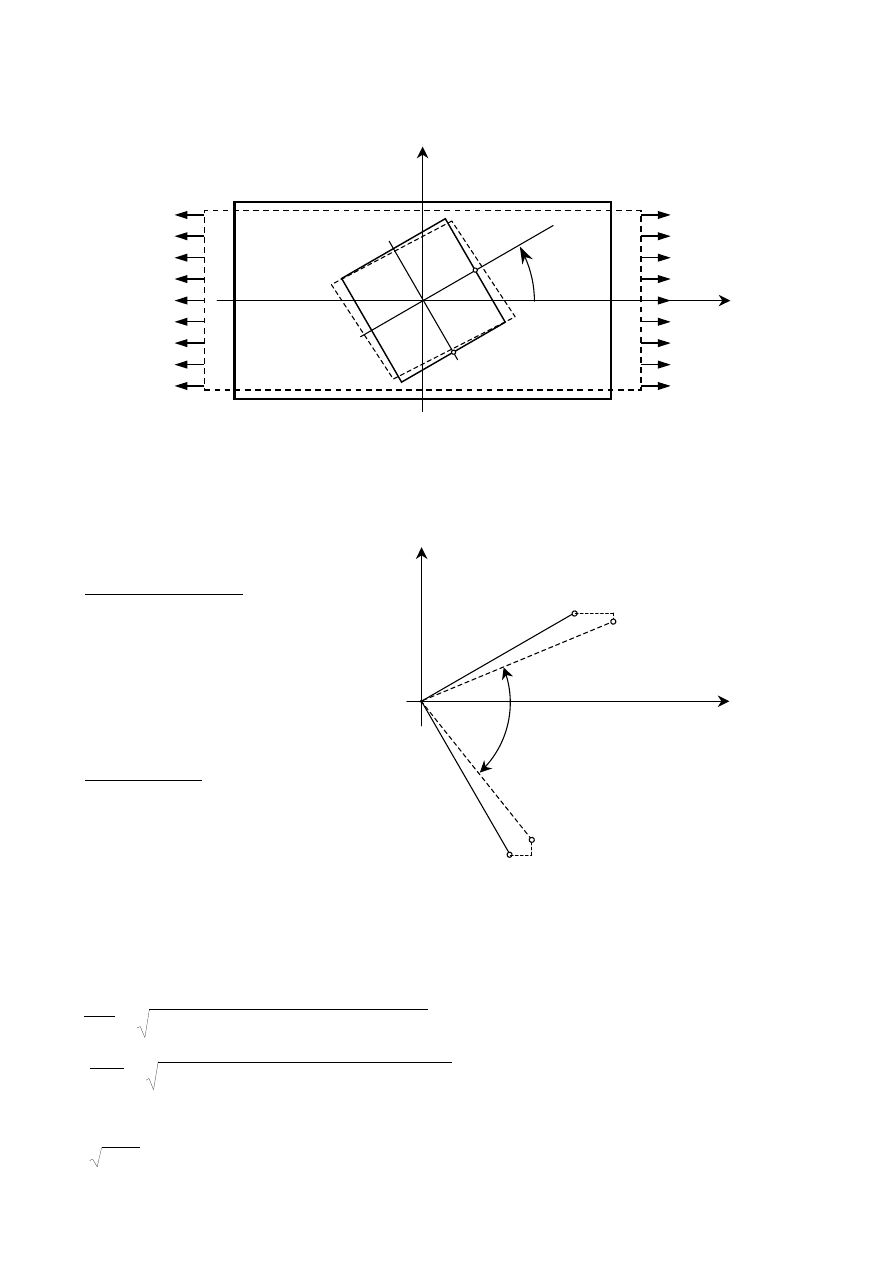
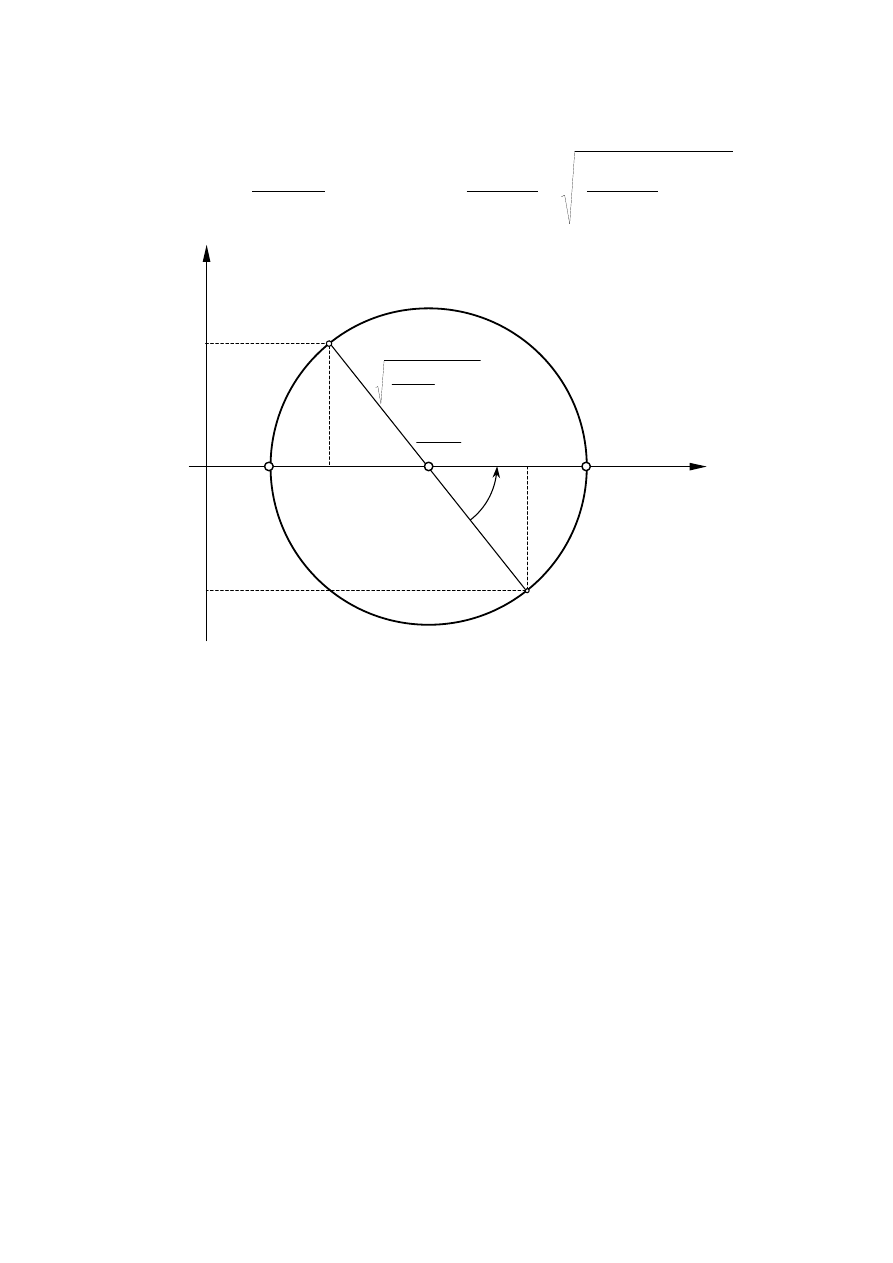
2.4. Analiza stanu naprężenia
σ
σ
σ
σ
α
α
α
α
− dodatnie, gdy działa na zewnątrz rozpatrywanej części
ττττ
α
α
α
α
− dodatnie, gdy daje współzegarowy obrót rozpatrywanej części
F
F
S
0
A
A
B
B
O
0
0
S
F
=
σ
A
A
F
σ
o
O
F
B
B
n
α
S
α
α
α
α
O
p
σ
σ
σ
σ
α
α
α
α
ττττ
α
α
α
α
α
α
cos
S
S
0
=
α
σ
α
α
cos
cos
S
F
S
F
p
0
0
=
=
=
=
α
σ
α
σ
α
2
0
cos
cos
p
=
=
α
α
σ
α
τ
α
cos
sin
sin
p
0
=
=
2. Rozciąganie (ściskanie) pręta
- 7/ 9 -
n
α
σ
σ
σ
σ
α
α
α
α
+
π
π
π
π
/2
σ
σ
σ
σ
α
α
α
α
ττττ
α
α
α
α
ττττ
α
α
α
α
+
π
π
π
π
/2
σ
σ
σ
σ
α
α
α
α
+
π
π
π
π
ττττ
α
α
α
α
+
π
π
π
π
σ
σ
σ
σ
α
α
α
α
+3
π
π
π
π
/2
ττττ
α
α
α
α
+3
π
π
π
π
/2
O
(
)
(
)
α
π
α
α
π
α
sin
2
cos
cos
2
sin
−
=
+
=
+
(
)
(
)
α
π
α
α
π
α
cos
cos
sin
sin
=
+
−
=
+
(
)
(
)
α
π
α
α
π
α
sin
2
3
cos
cos
2
3
sin
=
+
−
=
+
α
α
σ
τ
α
σ
σ
α
α
cos
sin
cos
0
2
0
=
=
α
α
σ
τ
α
σ
σ
π
α
π
α
cos
sin
sin
0
2
/
2
0
2
/
−
=
=
+
+
α
α
σ
τ
α
σ
σ
π
α
π
α
cos
sin
cos
0
2
0
=
=
+
+
α
α
σ
τ
α
σ
σ
π
α
π
α
cos
sin
sin
0
2
/
3
2
0
2
/
3
−
=
=
+
+
α
σ
σ
σ
α
σ
σ
σ
π
α
π
α
π
α
α
2
0
2
/
3
2
/
2
0
sin
cos
=
=
=
=
+
+
+
α
α
σ
τ
τ
τ
τ
π
α
π
α
π
α
α
cos
sin
0
2
/
3
2
/
=
−
=
=
−
=
+
+
+
zasada symetrii naprężeń stycznych
2. Rozciąganie (ściskanie) pręta
- 8/ 9 -
(
)
[
]
(
)
[
]
(
)
[
]
α
ν
α
ε
νε
α
ε
α
2
2
2
2
1
sin
cos
1
a
1
sin
a
1
cos
a
OA
−
+
≈
−
+
+
=
(
)
[
]
(
)
[
]
(
)
[
]
α
ν
α
ε
νε
α
ε
α
2
2
2
2
1
cos
sin
1
a
1
cos
a
1
sin
a
OD
−
+
≈
−
−
+
+
=
2
/
c
1
c
1
+
≈
+
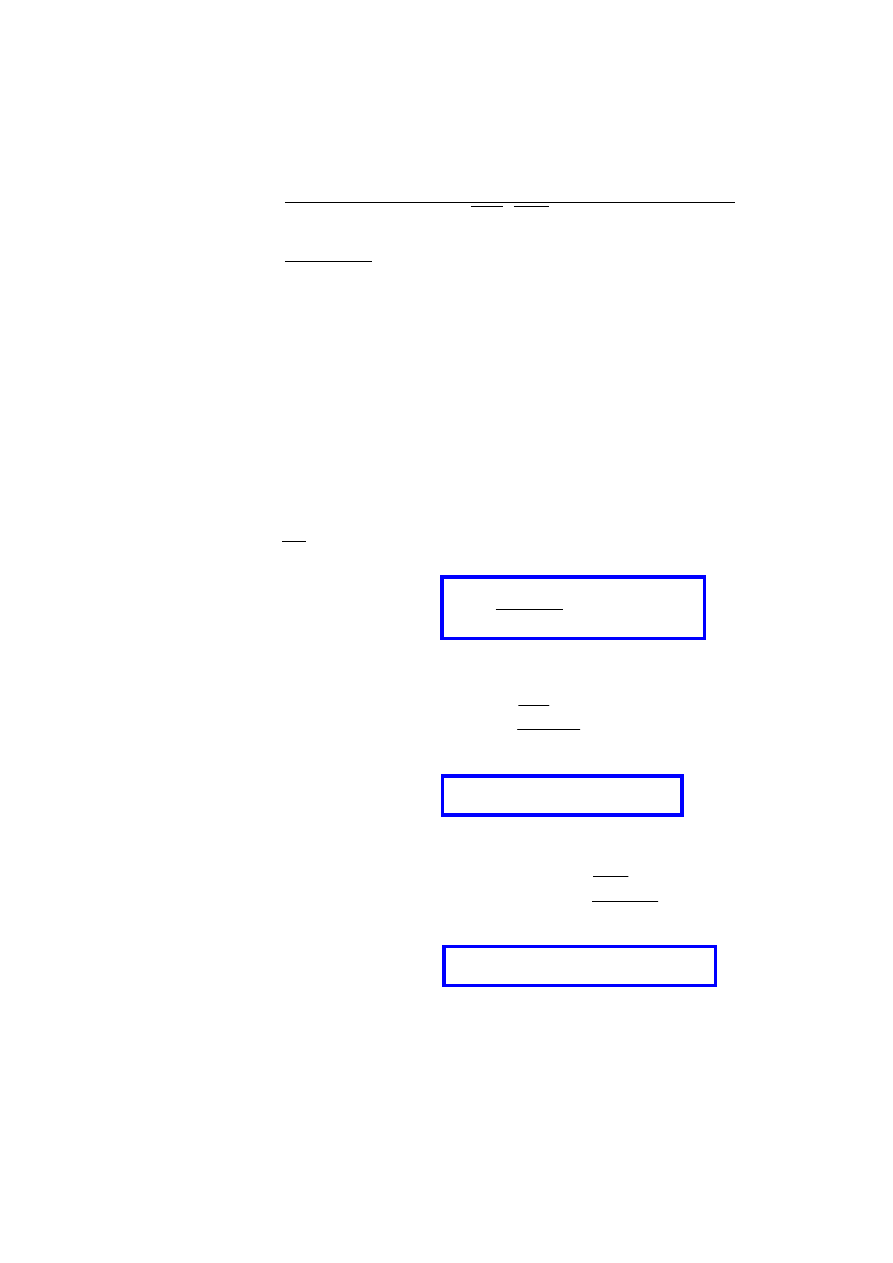
2.5. Analiza stanu odkształcenia
Po obciążeniu wszystkie wymiary na kierunku osi Ox doznają wydłużenia względnego
εεεε
, zaś na kierunku osi Oy skrócenia względnego
ν
ν
ν
νεεεε
.
przed obciażeniem
A
[acosα; asinα]
D
[asinα; −acosα]
kąt AOD jest prosty
po obciażeniu
punkt A przechodzi w A
1
A
1
[acosα(1+
ε
); asinα(1−
νε
)]
punkt D przechodzi w D
1
D
1
[asinα(1+
ε
); −acosα(1−
νε
)]
kąt A
1
OD
1
jest mniejszy od prostego o wartość
γ
α
(pomini
ę
to człony
ε
2
jako małe drugiego rz
ę
du oraz przyj
ę
to przybli
ż
enie
gdy c<<1)
y
x
O
D
A
a
a
A
1
D
1
90
0
-
γ
α
y
x
O
σ
o
σ
o
D
A
α
2. Rozciąganie (ściskanie) pręta
- 9/ 9 -
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
α
α
ν
ε
α
α
ν
ε
ν
ε
νε
α
νε
α
ε
α
ε
α
γ
α
cos
sin
1
2
cos
sin
1
1
1
2
OD
OA
1
cos
a
1
sin
a
1
sin
a
1
cos
a
90
cos
1
1
o
+
≈
−
+
+
=
=
⋅
−
−
−
+
+
=
−
(
)
1
1
<<
−
ν
ε
bo
dla małych kątów
z prawa Hooke'a
kąt odkształcenia postaciowego
wydłużenie względne na kierunku α
α
α
α
wydłużenie względne na kierunku α
α
α
α−
−
−
−π
π
π
π/2
(
)
α
α
γ
γ
sin
90
cos
o
=
−
α
α
γ
γ
=
sin
(
)
α
α
ν
ε
γ
α
cos
sin
1
2
+
=
E
o
σ
ε
=
(
)
α
α
σ
ν
γ
α
cos
sin
1
2
o
E
+
=
a
a
OA
1
−
=
α
ε
a
a
OD
1
2
/
−
=
−
π
α
ε
(
)
α
ν
α
ε
ε
α
2
2
sin
cos
−
=
(
)
α
ν
α
ε
ε
π
α
2
2
2
/
cos
sin
−
=
−
3. Skręcanie pręta
- 1/13 -
3. SKRĘCANIE PRĘTA
3.1. Stan czystego ścinania
σ
σ
σ
σ
α
α
α
α
+
π
π
π
π
/2
σ
σ
σ
σ
α
α
α
α
σ
σ
σ
σ
α
α
α
α
+
π
π
π
π
σ
σ
σ
σ
α
α
α
α
+3
π
π
π
π
/2
O
rozciąganie
σ
σ
σ
σ
α
α
α
α
+
π
π
π
π
/2
σ
σ
σ
σ
α
α
α
α
ττττ
α
α
α
α
ττττ
α
α
α
α
+
π
π
π
π
/2
σ
σ
σ
σ
α
α
α
α
+
π
π
π
π
ττττ
α
α
α
α
+
π
π
π
π
σ
σ
σ
σ
α
α
α
α
+3
π
π
π
π
/2
ττττ
α
α
α
α
+3
π
π
π
π
/2
O
złożony stan naprężeń
ττττ
α
α
α
α
ττττ
α
α
α
α
+
π
π
π
π
/2
ττττ
α
α
α
α
+
π
π
π
π
ττττ
α
α
α
α
+3
π
π
π
π
/2
O
czyste
ścinanie
złożony stan
odkształceń
O
O
wydłużenie
(skrócenie)
O
odkształcenie
postaciowe
odkształcenie
spowodowane
działaniem
naprężeń
normalnych
σ
odkształcenie
spowodowane
działaniem
naprężeń
stycznych
τ
3. Skręcanie pręta
- 2/13 -
dla stali: E≈2.1⋅10
5
MPa,
ν≈0.3 ⇒
⇒
⇒
⇒
G
≈
≈
≈
≈0.81⋅⋅⋅⋅10
5
MPa
przykład: τ=200MPa, G≈0.81⋅10
5
MPa ⇒
⇒
⇒
⇒ γ=2.47
⋅
10
-3
rad=0.14
o
≈8.5’
3.2. Energia wewnętrzna w stanie czystego ścinania
τ
⋅
= bh
T
AB
- wypadkowa siła działająca na brzegu
AB
(
h
– grubość kostki)
Energia wewnętrzna
U
zgromadzona w kostce równa jest pracy siły
T
AB
na
przemieszczeniu
∆
a=
γ
a
]
[
2
1
2
1
J
a
bh
a
T
U
AB
τγ
=
∆
=
Energia wewnętrzna na jednostkę objętości
]
/
[
2
2
2
1
3
2
2
m
J
G
G
abh
U
U
v
γ
τ
τγ
=
=
=
=
kąt odkształcenia postaciowego
α
α
σ
τ
cos
sin
0
=
(
)
α
α
σ
ν
γ
cos
sin
1
2
0
E
+
=
(
)
(
)
ν
τ
τ
ν
γ
+
=
+
=
1
2
1
2
E
E
(
)
G
E
=
+
ν
1
2
moduł sztywności
postaciowej
(moduł Kirchhoffa)
G
τ
γ
=
prawo Hooke’a
przy ścinaniu
ττττ
γγγγ
ττττ
ττττ
ττττ
∆
a
a
b
D
C
B
A
A’
B’
T
AB
3. Skręcanie pręta
- 3/13 -
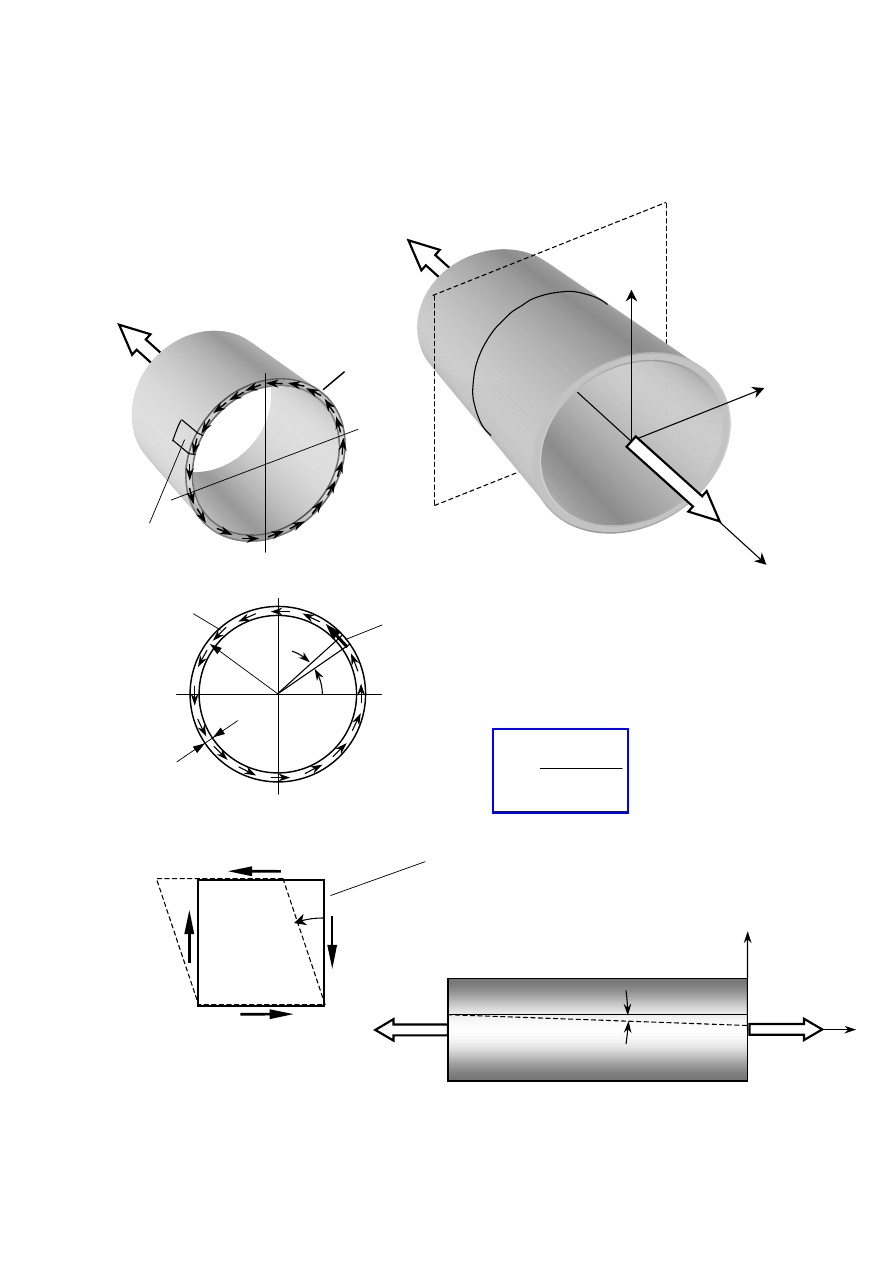
3.3. Skręcanie rury cienkościennej
realizacja stanu czystego ścinania
O
x
y
z
M
s
M
s
β
dF=
τδ
Rd
β
O
d
β
R
δ
τ
2
2
0
2
2
0
2
R
d
R
RdF
M
s
πτδ
β
τδ
π
π
=
=
=
∫
∫
2
2
R
M
s
πδ
τ
=
M
s
ττττ
elementarna
kostka
elementarna kostka
wycięta ze ścianki rury
stan czystego
ścinania
ττττ
τ
τ
τ
γγγγ
x
z
M
s
M
s
γγγγ
ilustracja kąta odkształcenia postaciowego
na powierzchni skręcanej rury
3. Skręcanie pręta
- 4/13 -
γγγγ
ττττ
ττττ
e
ττττ
p
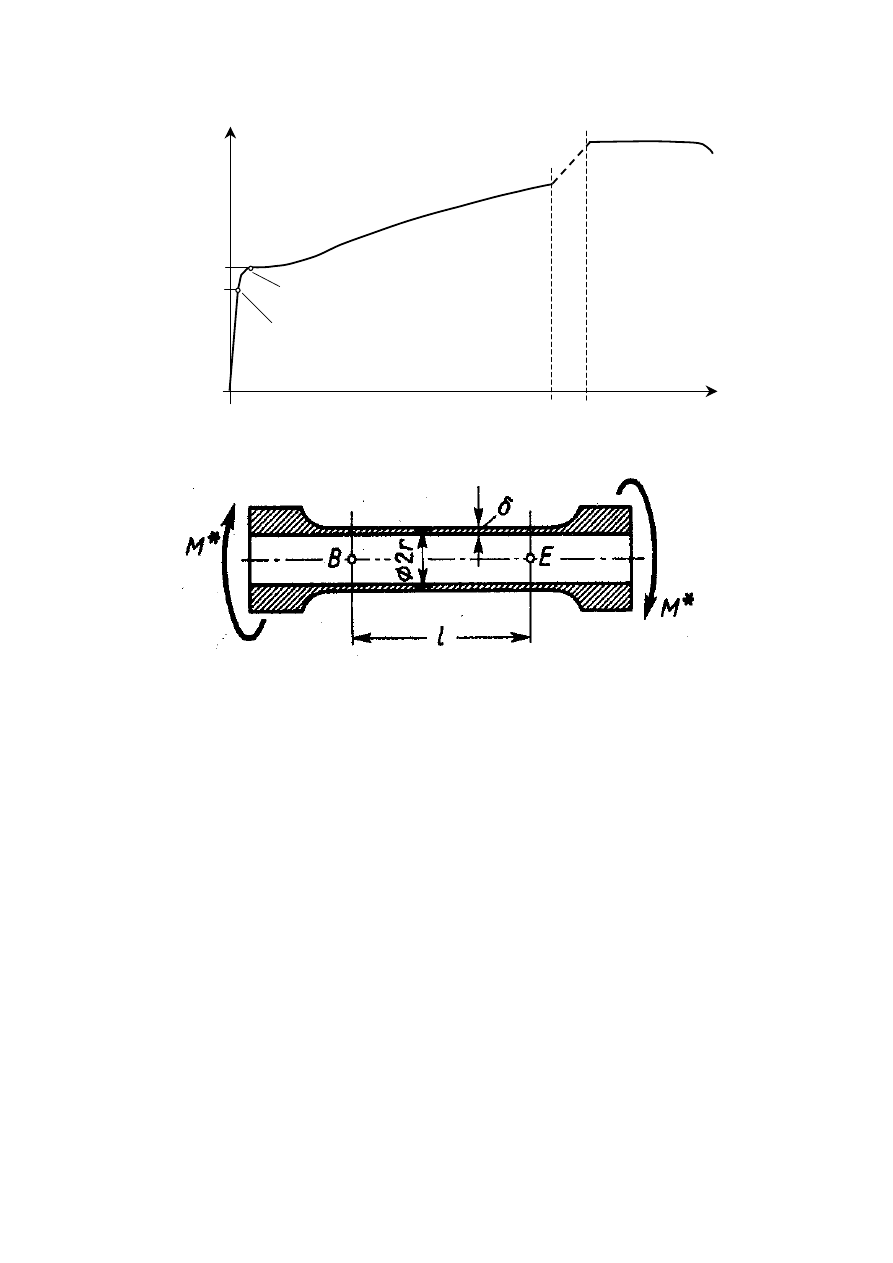
Przykładowy wykres skręcania
granica proporcjonalności
(granica stosowalności prawa
Hooke’a) przy skręcaniu
granica plastyczności przy skręcaniu
Próbka do statycznej próby skręcania
(Zb.Brzoska, Wytrzymałość Materiałów, PWN Warszawa, 1979)
3. Skręcanie pręta
- 5/13 -
3.4. Skręcanie pręta o przekroju kołowym
Skręcanie – przypadek obciążenia konstrukcji, gdy w myślowym
przekroju istnieje moment skręcający
M
s
.
Hipoteza płaskich przekrojów:
Przy skręcaniu pręta kołowego przekroje poprzeczne nie doznają
żadnych odkształceń, a jedynie obracają się wokół osi pręta.
z
y
x
d
z
=
2
r
z
d
w
=
2
r
w
l
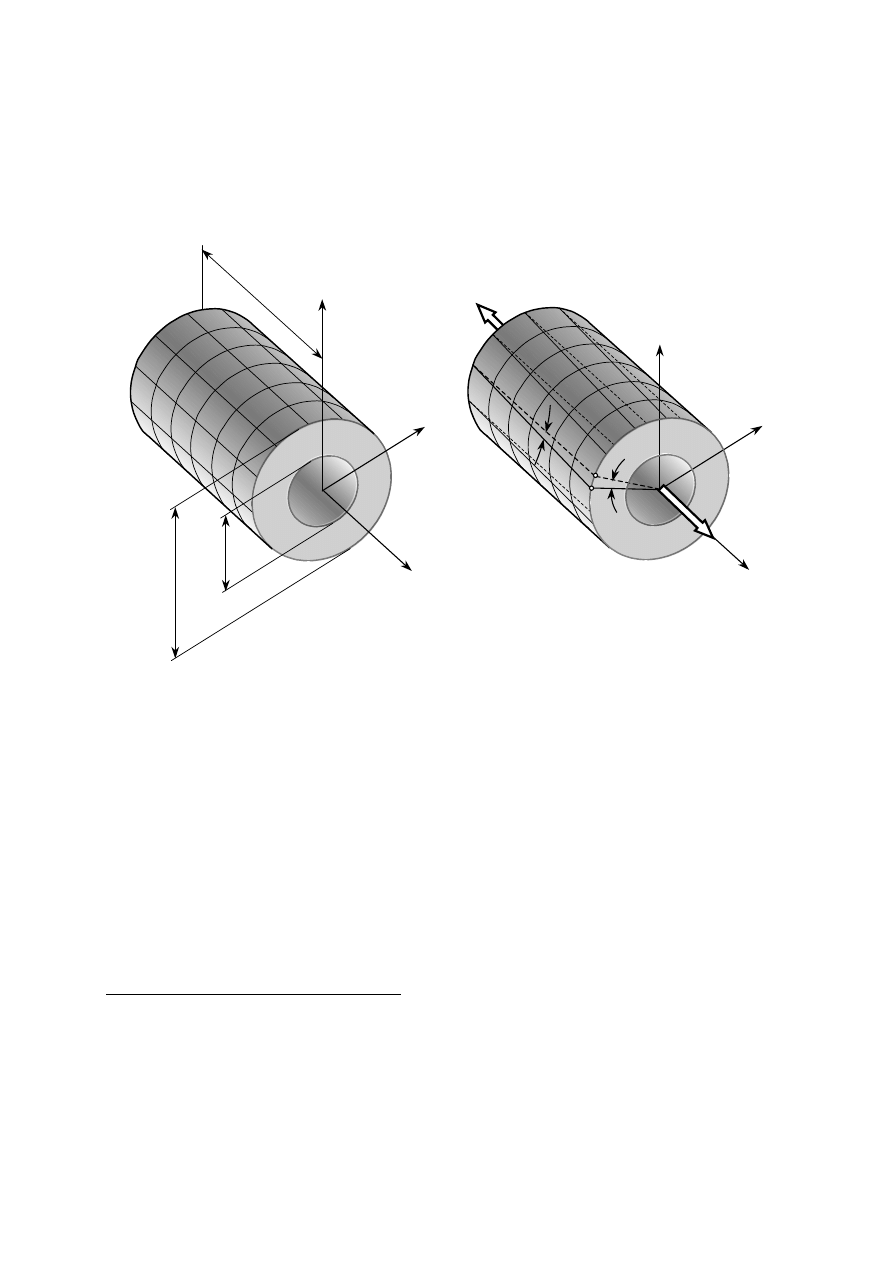
przed obciążeniem
− na powierzchni pręta
narysowano prostokątną siatkę
o krawędziach równoległych do
osi pręta
po obciążeniu pręta momentem
skręcającym M
s
− siatka prostokątna zmienia się na
ukośnokątną
− łuki kół pozostają nie zmienione
− linie równoległe do osi zmieniają
się na linie śrubowe nachylone
pod kątem
γγγγ
− przekroje końcowe odcinka pręta
skręcają się względem siebie o
kąt
ϕ
ϕ
ϕ
ϕ
M
s
z
y
x
M
s
ϕ
ϕ
ϕ
ϕ
A
A’
γγγγ

3. Skręcanie pręta
- 6/13 -
Elementarna współśrodkowa rura o
promieniu
r
i grubości
dr
ulega skręceniu
o ten sam kąt
ϕ
, co i cały pręt.
γ
r
– kąt odkształcenia postaciowego
elementarnej rury
r
l
BB
r
ϕ
γ
=
=
'
⇒
l
r
r
ϕ
γ
=
z prawa Hooke’a dla ścinania
l
r
G
G
r
r
ϕ
γ
τ
=
=
Elementarny moment
dM
, jaki naprężenia
τ
r
rozwijają względem punktu O
wynosi
dr
l
r
G
dr
r
dM
r
3
2
2
2
ϕ
π
π
τ
=
=
(patrz: skręcanie rury cienkościennej).
Moment względem punktu
O
od wszystkich myślowo wyciętych, współśrodko-
wych rur, pokrywających całe pole powierzchni
S
przekroju pręta, musi być
równoważny momentowi skręcającemu
M
s
s
r
r
r
r
S
M
dr
r
l
G
dr
l
r
G
dM
z
w
z
w
=
=
=
∫
∫
∫
3
3
2
2
π
ϕ
ϕ
π
biegunowy moment bezwładności
przekroju kołowego [m
4
]
z
y
dr
r
ϕ
elementarna
współśrodkowa
rura
τ
r
A
A’
B
B’
O
(
)
(
)
32
2
2
4
4
4
4
3
0
w
z
w
z
r
r
d
d
r
r
dr
r
J
z
w
−
=
−
=
=
∫
π
π
π
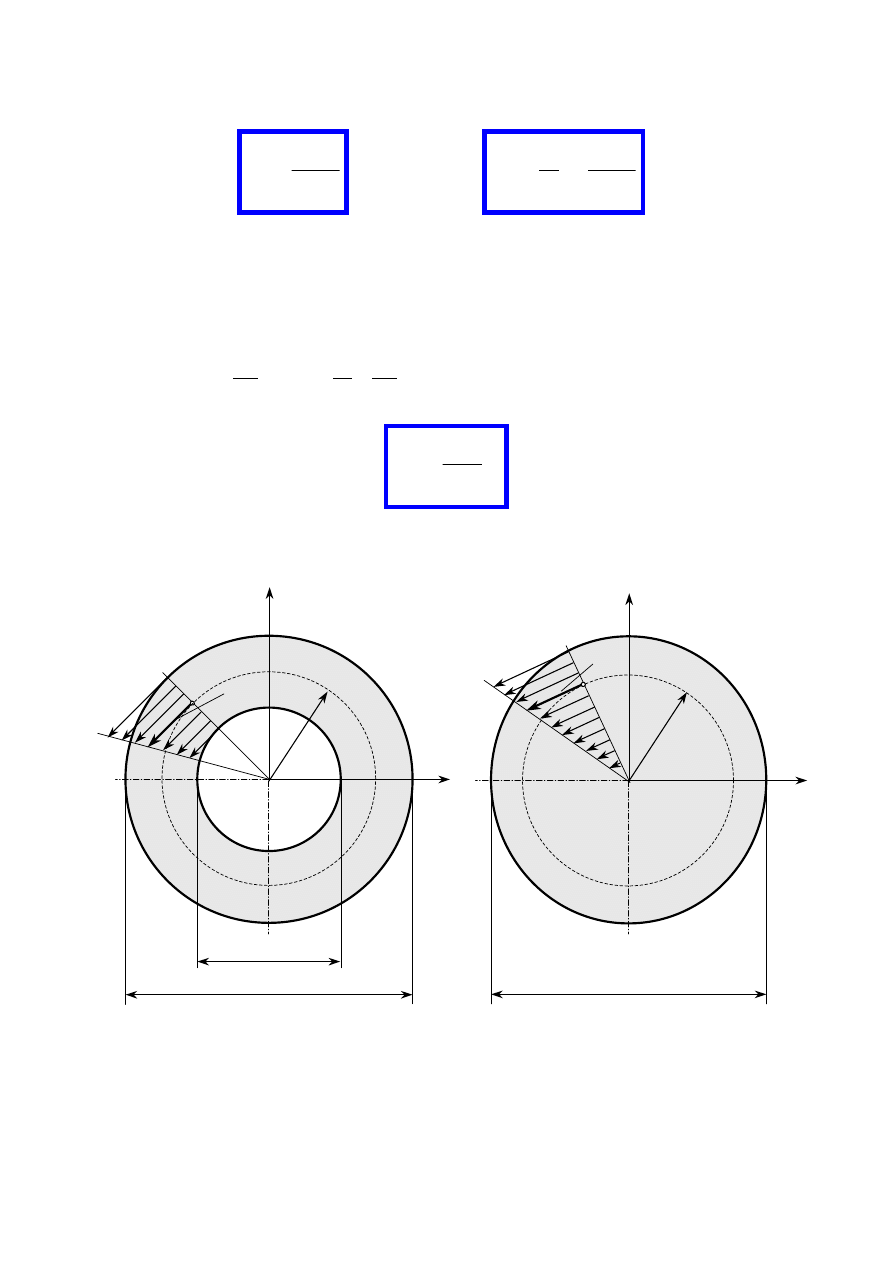
3. Skręcanie pręta
- 7/13 -
kąt skręcenia jednostkowy kąt skręcenia
[rad] (skręcenie względne) [rad/m]
GJ
0
[Nm
2
]
– sztywność pręta na skręcanie
analogia do
ES
Fl
l
=
∆
oraz
ES
F
l
l
=
∆
=
ε
przy rozci
ą
ganiu pr
ę
ta
naprężenia styczne
przy skręcaniu przekroju kołowego
rozkład naprężeń stycznych
w przekroju skręcanego pręta kołowego
O
z
y
r
ττττ
max
ττττ
min
ττττ
r
C
d
z
=2r
z
d
w
=2r
w
O
z
y
r
ττττ
max
ττττ
r
d
z
=2r
z
d
w
=0
0
GJ
l
M
s
=
ϕ
0
GJ
M
l
s
=
=
Θ
ϕ
r
J
M
s
r
0
=
τ
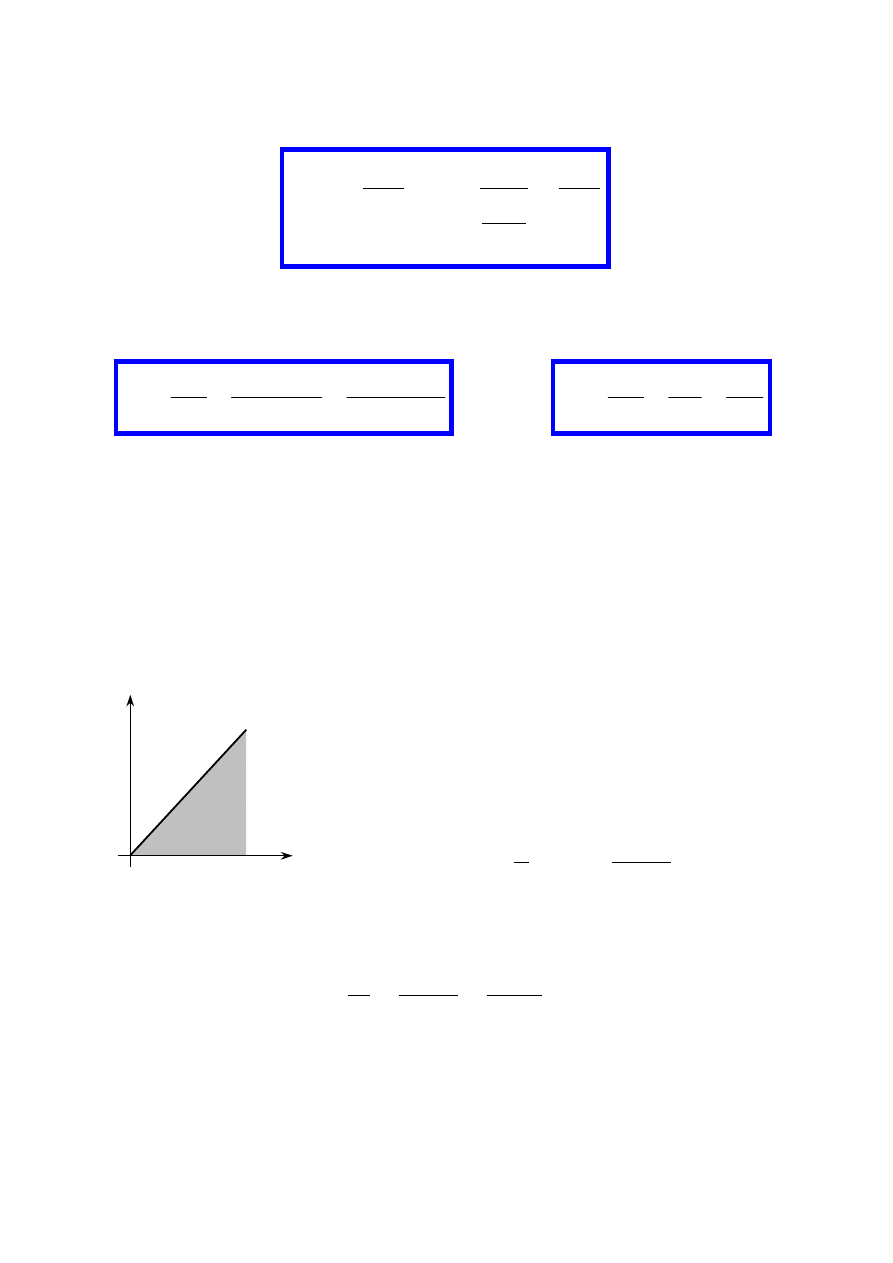
3. Skręcanie pręta
- 8/13 -
maksymalne naprężenia styczne
dla przekroju drążonego dla przekroju pełnego
wskaźnik wytrzymałości na skręcanie
3.5. Energia wewnętrzna w skręcanym pręcie
Jeśli zachowane jest prawo Hooke'a przy skręcaniu,
to energia wewnetrzna
U
zgromadzona w pręcie
równa jest pracy zewnętrznej wykonanej przez
moment skręcający
M
s
na przemieszczeniu
ϕ
ϕ
ϕ
ϕ
0
2
s
s
GJ
2
l
M
M
2
1
W
U
=
=
=
ϕ
[J]
Energia wewnętrzna na jednostkę długości pręta
2
M
GJ
2
M
l
U
U
s
0
2
s
l
Θ
=
=
=
[J/m]
ϕ
M
s
W
0
max
0
max
0
max
W
M
r
J
M
r
J
M
s
s
s
=
=
=
τ
(
)
(
)
z
w
z
z
w
z
d
d
d
r
r
r
r
J
W
16
2
4
4
4
4
max
0
0
−
=
−
=
=
π
π
16
2
3
3
max
0
0
z
z
d
r
r
J
W
π
π
=
=
=
3. Skręcanie pręta
- 9/13 -
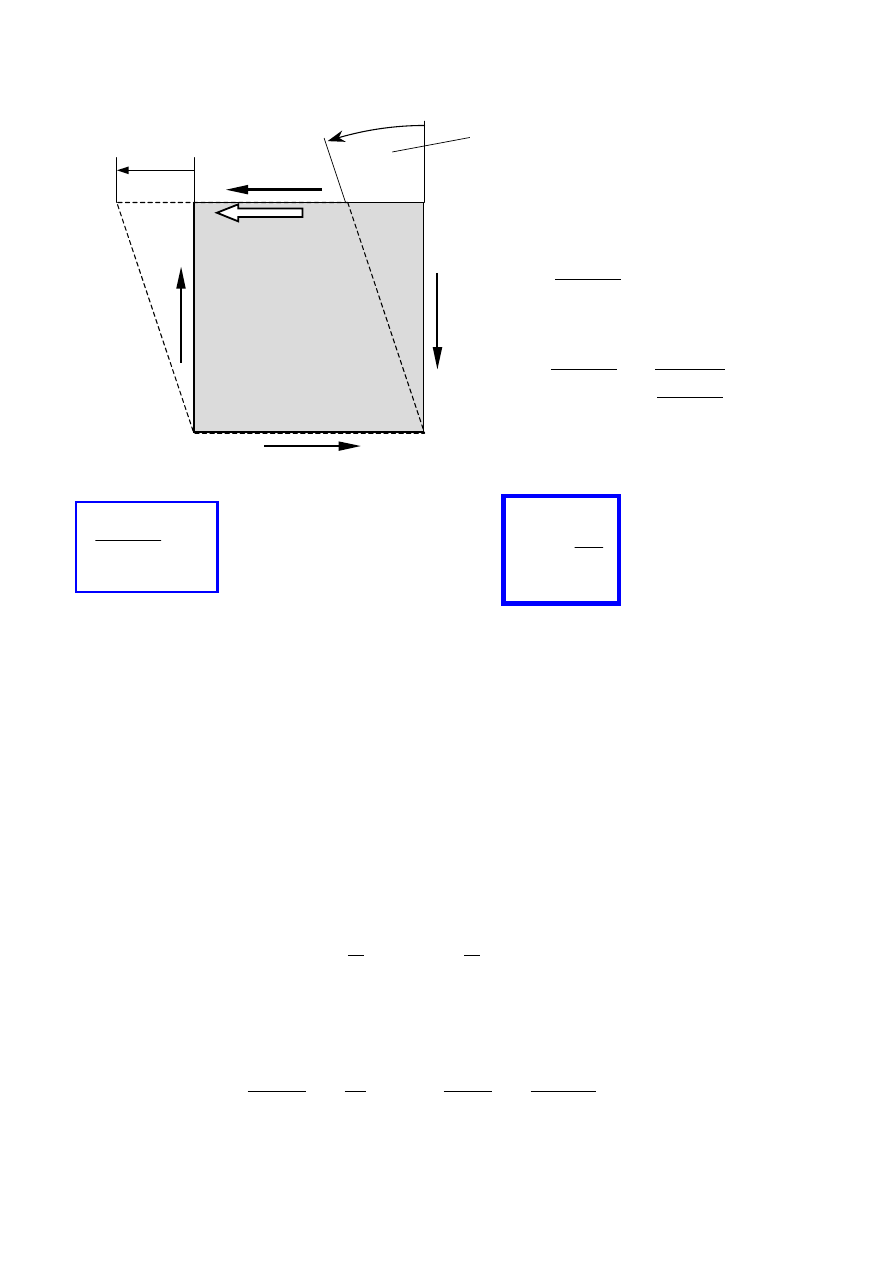
przed obciążeniem
−
prostokątna siatka
naniesiona na bocznej
powierzchni pręta
3.6. Skręcanie prętów o przekrojach niekołowych
Obraz odkształceń przy skręcaniu pręta prostokątnego
(Zb.Brzoska, Wytrzymałość Materiałów, PWN Warszawa, 1979)
z Teorii Sprężystości:
1. przy skręcaniu pryzmatycznego pręta w jego przekroju poprzecz-
nym istnieją tylko naprężenia styczne
ττττ
,
2. kierunki naprężeń stycznych wykazują analogię do kierunku ruchu
cząstek cieczy krążącej w płaskim naczyniu o kształcie przekroju
danego pręta (analogia hydrodynamiczna),
3. skręcenie względne
Θ
Θ
Θ
Θ
pręta zależy od kształtu i wymiarów prze-
kroju i jest proporcjonalne do momentu skręcającego
M
s
, a odwrot-
nie proporcjonalne do modułu
G
.
po obciążeniu momentem
skręcającym
−
siatka odkształca się
niejednakowo
−
linie proste i prostopadłe do osi
pręta stają się zakrzywione
(pierwotnie płaski przekrój nie
pozostaje płaski)
płaskie
naczynie
linie prądu krążącej
cieczy (tory cząstek)
prędkość cząstki
przekrój
pręta
M
s
ττττ
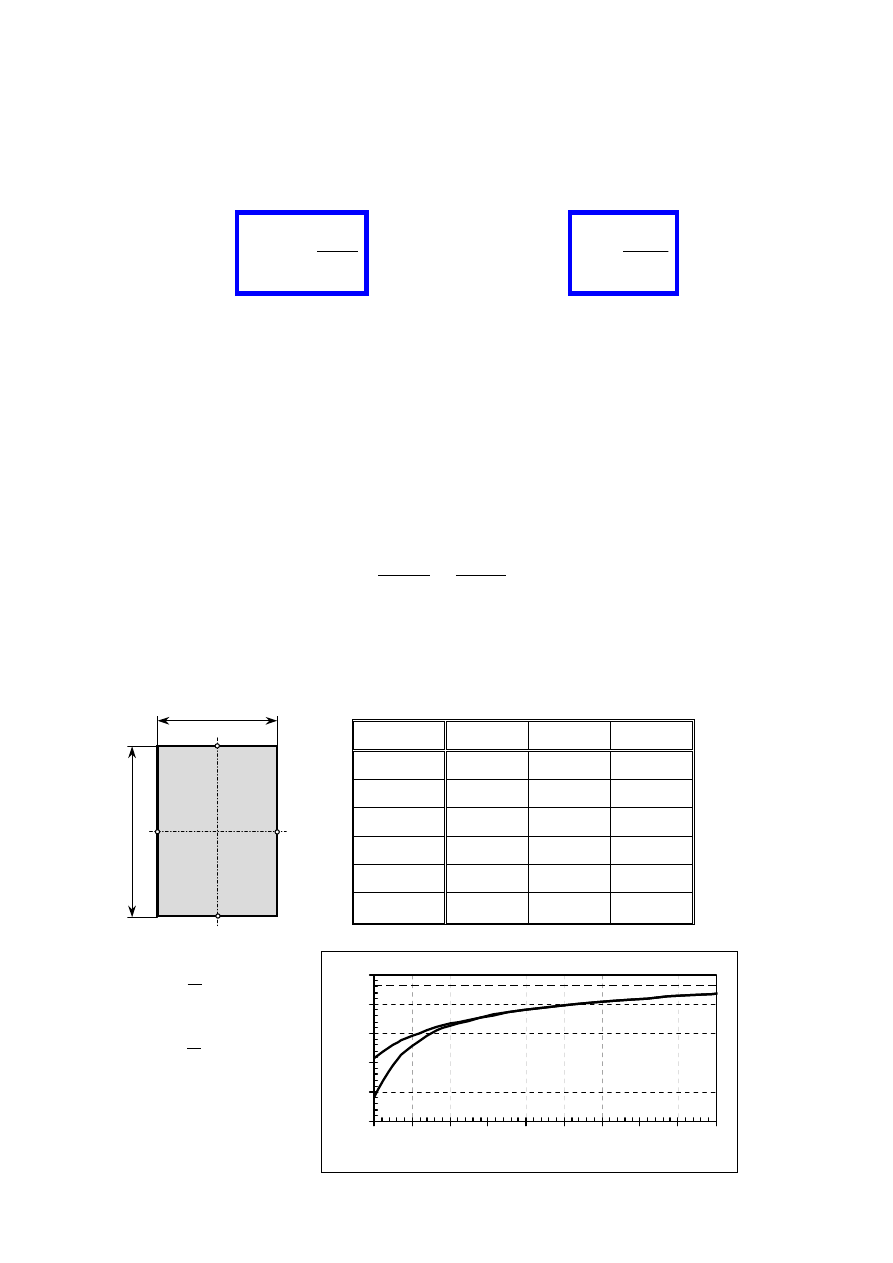
3. Skręcanie pręta
- 10/13 -
Maksymalne naprężenia styczne
ττττ
max
oraz jednostkowy kat skręcenia
θ
θθ
θ
oblicza się ze wzorów:
maksymalne naprężenia jednostkowy
styczne kąt skręcenia
W
s
[m
3
],
J
s
[m
4
]
– wielkości czysto geometryczne zależne od kształtu i wymia-
rów przekroju
(odpowiadaj
ą
parametrom W
0
i J
0
przy skr
ę
caniu przekroju kołowego)
GJ
s
[Nm
2
] – sztywność na skręcanie
Energia wewnętrzna na jednostkę długości pręta
2
2
2
Θ
=
=
s
s
s
l
M
GJ
M
U
[J/m]
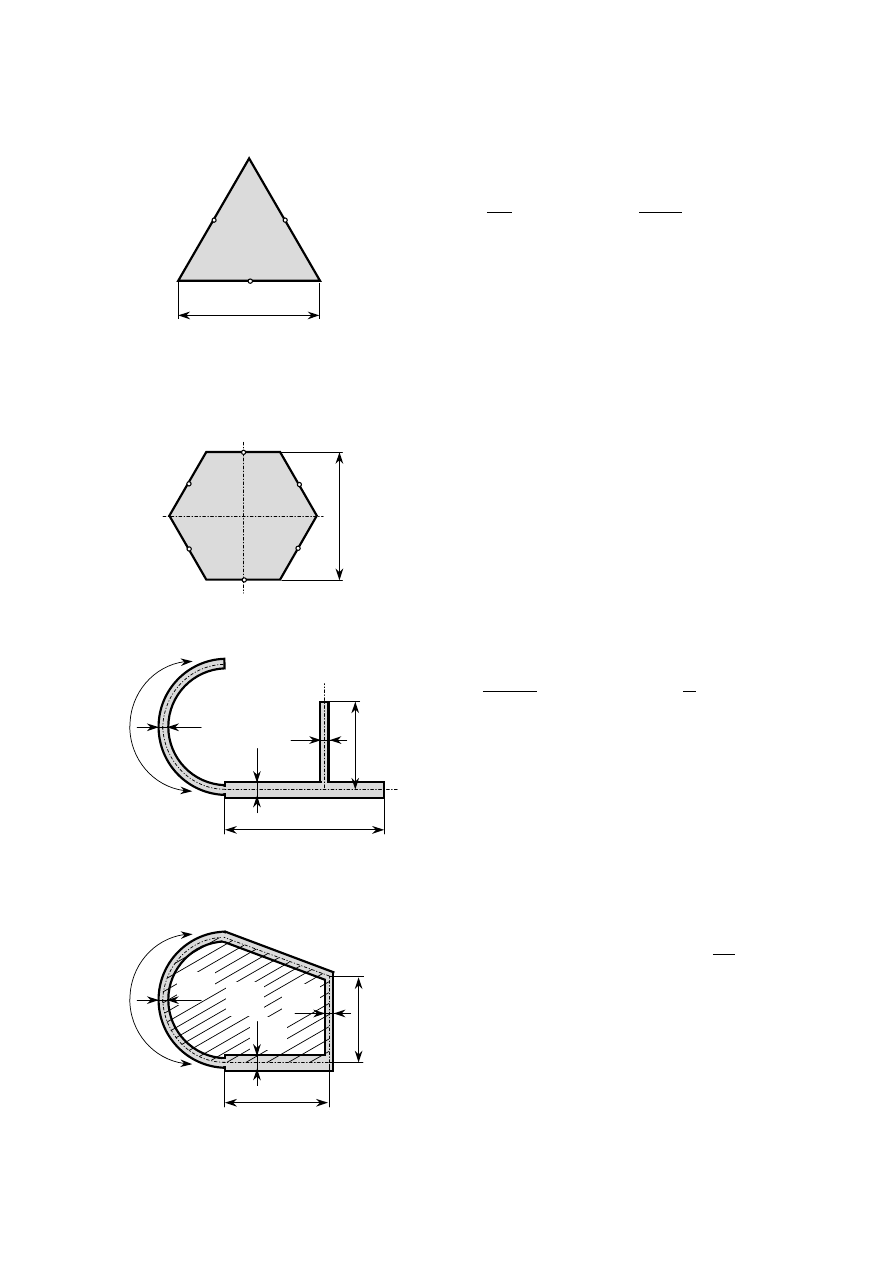
PROSTOKĄT
h/b
c
1
c
2
c
3
1.0
0.208
0.141
1.000
1.5
0.231
0.196
0.858
2.0
0.246
0.229
0.796
3.0
0.267
0.263
0.753
6.0
0.299
0.298
0.743
∞
0.333
0.333
0.743
3
1
b
b
h
c
W
s
=
4
2
b
b
h
c
J
s
=
τ
A
=
τ
max
τ
B
=c
3
τ
max
τ
=
0
w narożach
b
h
A
A
B
B
h
≥
≥
≥
≥ b
0.10
0.15
0.20
0.25
0.30
0.35
1
2
3
4
5
6
7
8
9
10
h/b
c
1
c
2
0.333
s
s
W
M
=
max
τ
s
s
GJ
M
=
Θ
3. Skr
ę
canie pr
ę
ta
- 11/13 -
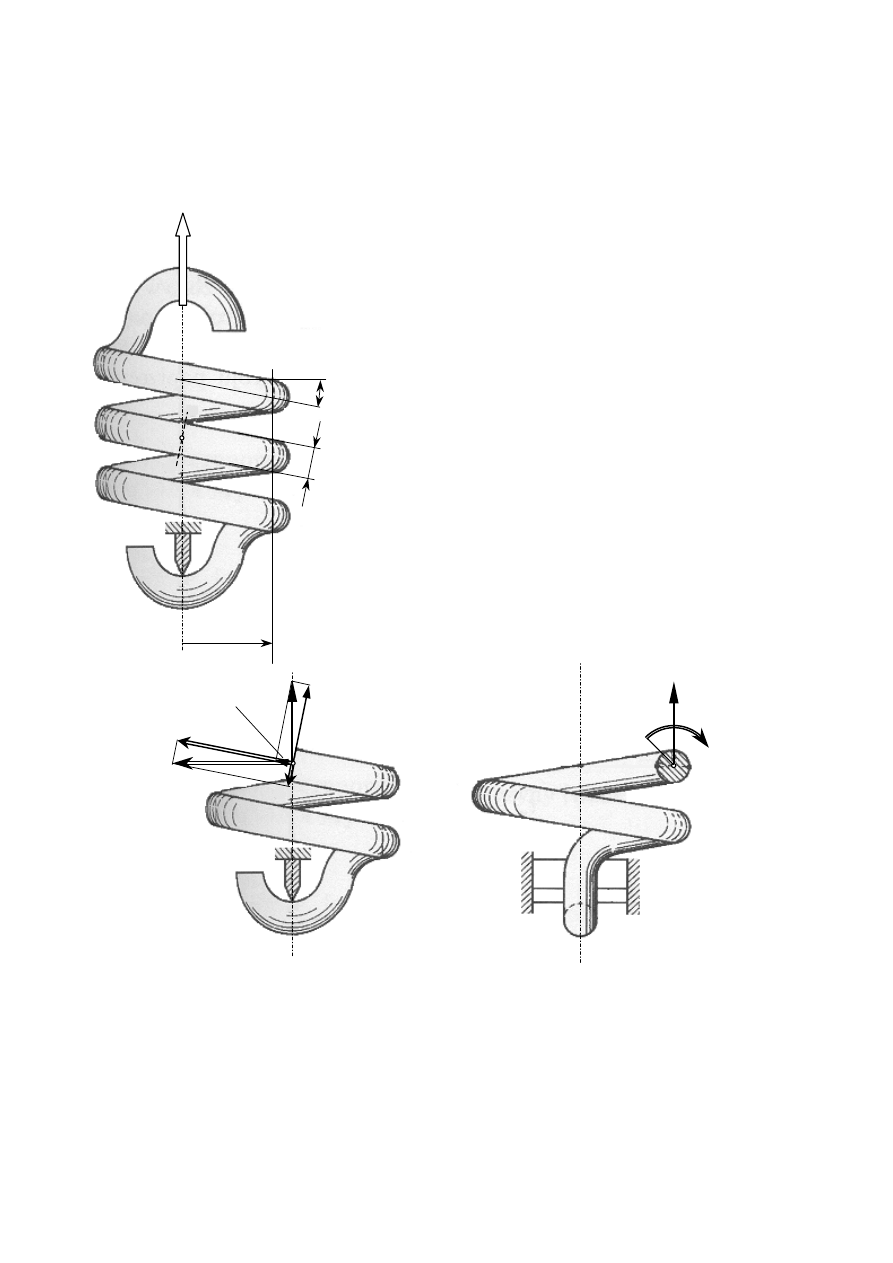
TRÓJKĄT RÓWNOBOCZNY
20
3
a
W
s
=
2
.
46
4
a
J
s
=
τ
A
=
τ
max
τ
=
0
w narożach
SZEŚCIOKĄT FOREMNY
3
189
.
0
a
W
s
=
4
115
.
0
a
J
s
=
τ
A
=
τ
max
τ
=
0
w narożach
CIENKOŚCIENNY PROFIL OTWARTY
∑
=
=
n
i
i
i
s
s
W
1
3
max
3
1
δ
δ
∑
=
=
n
i
i
i
s
s
J
1
3
3
1
δ
τ
max
– w środku dlugich boków odcinka
o grubości
δ
max
CIENKOŚCIENNA DOWOLNA RURA
min
2
δ
F
W
s
=
∑
=
=
n
i
i
i
s
s
F
J
1
2
4
δ
τ
max
– w miejscu, gdzie grubość ścianki jest
najmniejsza
F
– pole ograniczone linią środkową
a
A
A
A
A
a
A
A
A
A
A
δ
1
δ
i
δ
n
s
1
s
i
s
n
s
1
s
i
s
n
δ
1
δ
n
δ
i
F
3. Skr
ę
canie pr
ę
ta
- 12/13 -
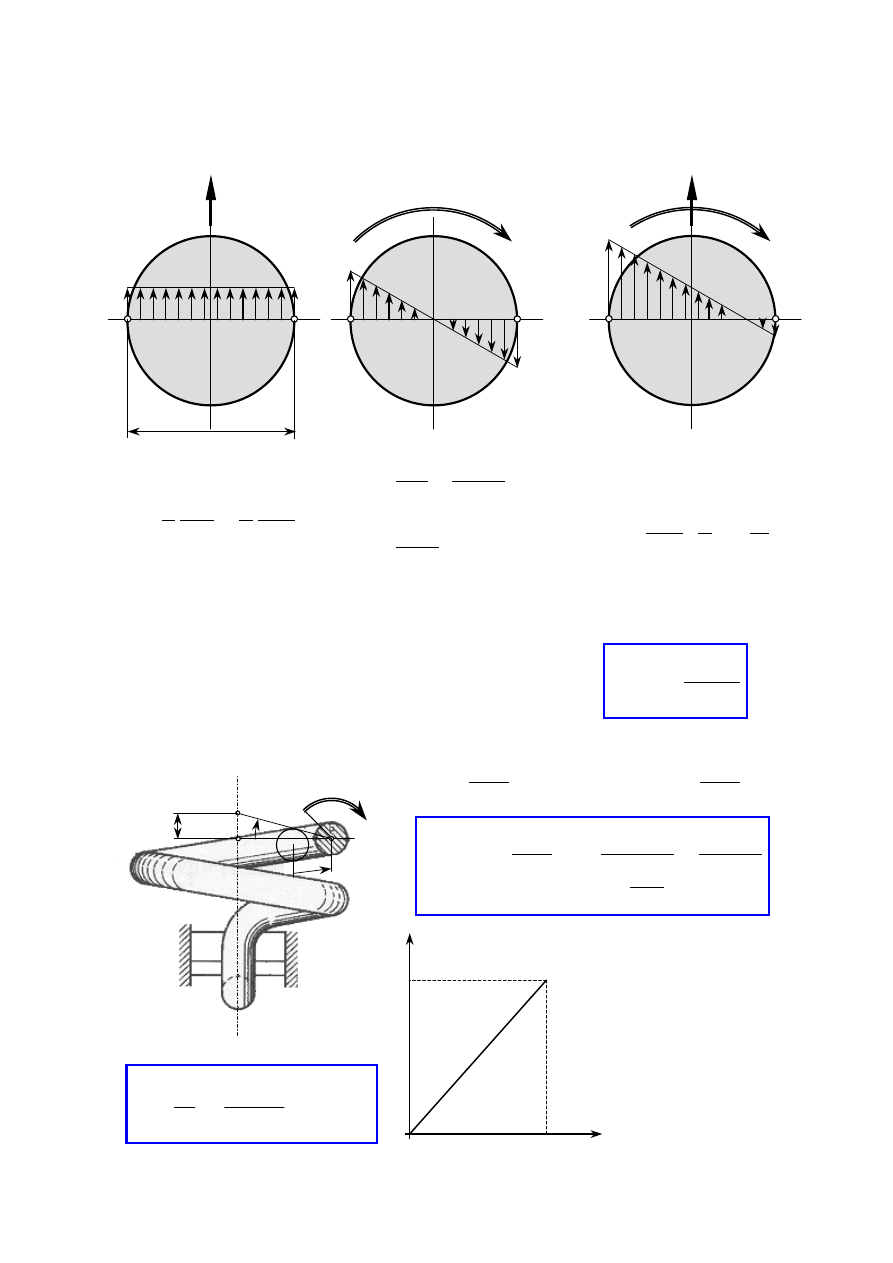
3.7. Naprężenia i odkształcenia sprężyny śrubowej
D
=2R
– średnica sprężyny
d
=2r
– średnica drutu
n
– liczba zwojów
α
– kąt nachylenia zwojów (mały)
P
– siła rozciągająca sprężynę
(rysunki spr
ęż
yn zaczerpni
ę
to z:
Niezgodzi
ń
ski M.E., Niezgodzi
ń
ski T.:
Wytrzymało
ść
materiałów
, PWN Warszawa 2002)
W myślowym przekroju
Dla małych kątów
α
α
α
α
drutu sprężyny działają:
można przyjąć:
− siła normalna
Psin
α
,
0
− siłą tnąca
Pcos
α
,
P
− moment skręcający
Mcos
α
,
M
s
− moment gnący
Msin
α
,
0
R
P
d=2r
α
O
O
P
Pcos
α
O
Psin
α
M=PR
Mcos
α
Msin
α
O
P
M
s
=PR
3. Skr
ę
canie pr
ę
ta
- 13/13 -
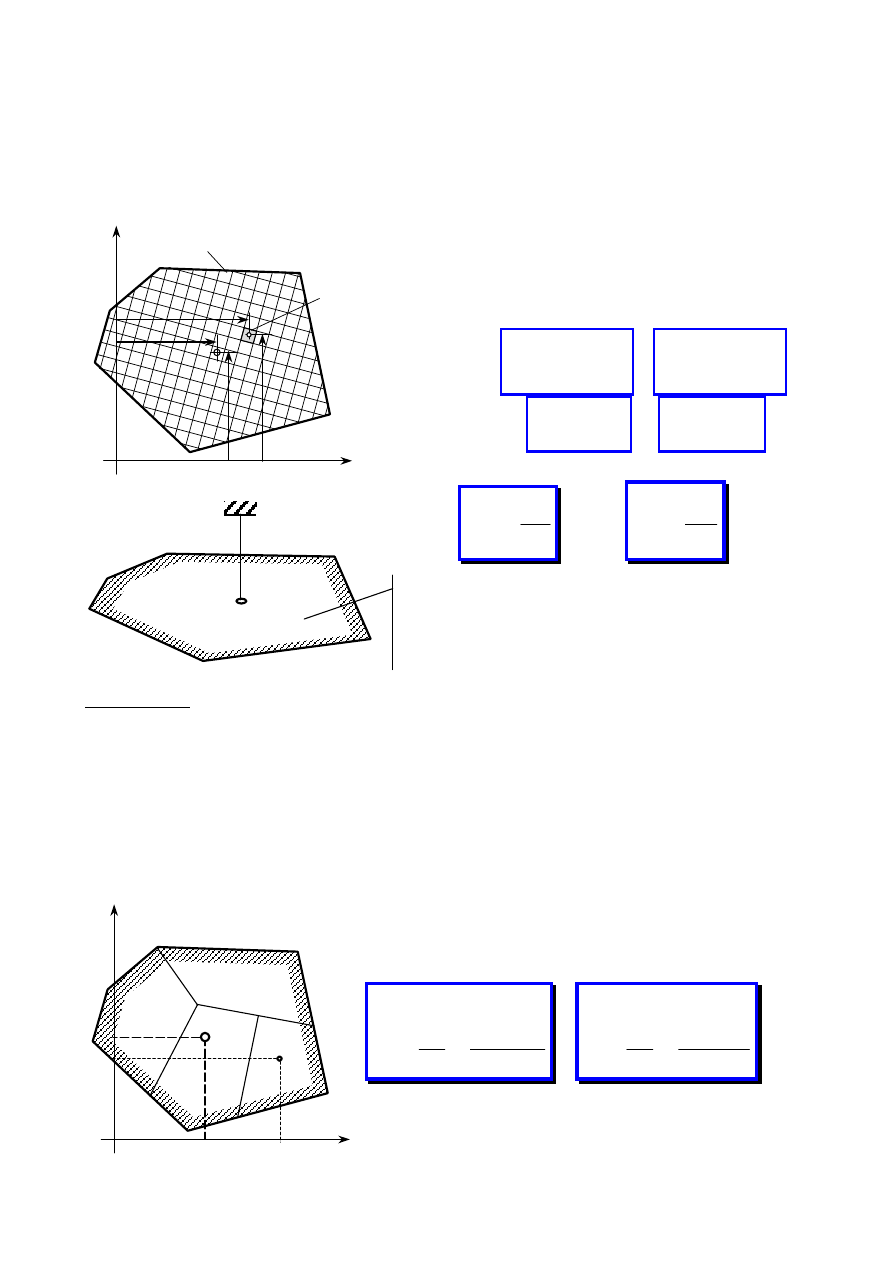
Naprężenia istniejące w myślowym przekroju drutu sprężyny są sumą naprężeń
od ścinania siłą P i skręcania momentem M
s
2
2
4
3
4
3
4
d
P
r
P
P
π
π
τ
=
=
3
3
0
8
16
d
PD
d
M
W
M
s
s
M
π
π
τ
=
=
=
=
+
=
=
+
=
d
D
d
P
M
P
2
3
4
4
2
max
π
τ
τ
τ
jeśli
D
>>
d
to
Odkształcenie sprężyny śrubowej
ds
GJ
M
d
s
0
=
ϕ
ds
GJ
M
R
Rd
d
s
0
=
=
ϕ
λ
4
3
4
3
2
0
0
8
2
2
Gd
n
PD
r
G
n
PR
ds
GJ
M
R
Rn
s
=
=
=
∫
π
π
λ
π
ττττ
M
M
s
ττττ
max
M
s
P
P
ττττ
P
d=2r
O
M
s
d
λ
d
ϕ
A’
A
ds
λ
P
const
n
D
Gd
P
k
=
=
=
3
4
8
λ
sztywność sprężyny
sprężyna śrubowa
o małym skoku jest
sprężyną liniową
3
max
8
d
PD
π
τ
≅
4. Zginanie pręta
- 1/26 -
4. ZGINANIE PRĘTA
4.1. Wielkości charakteryzujące geometrię przekroju
4.1.1. Środek ciężkości przekroju
Całe pole
A
powierzchni przekroju podzielono na
n
części o polach powierzchni
∆
A
i
Momenty statyczne przekroju względem osi y i z
∑
=
∆
=
n
i
i
i
y
A
z
S
1
∑
=
∆
=
n
i
i
i
z
A
y
S
1
gdy n
→∞ i
∆
A
i
→0
∫
=
A
y
zdA
S
∫
=
A
z
ydA
S
Współrzędne środka ciężkości przekroju
A
S
y
z
c
=
A
S
z
y
c
=
Twierdzenia
1. Moment statyczny względem osi przechodzącej przez środek ciężkości
przekroju równy jest zeru.
2. Jeśli przekrój posiada oś symetrii to środek ciężkości leży na tej osi.
3. Moment statyczny sumy pól względem wybranej osi równy jest sumie
momentów statycznych tych pól względem tejże osi.
Przekrój dzielimy na
n
części o polach powierzchni
A
i
, dla których znane są
współrzędne
y
ci
,
z
ci
położenia ich środków ciężkości
c
i
.
Współrzędne środka ciężkości całego przekroju
obliczamy ze wzorów
A
y
A
A
S
y
n
i
ci
i
z
c
∑
=
=
=
1
A
z
A
A
S
z
n
i
ci
i
y
c
∑
=
=
=
1
gdzie:
∑
=
=
n
i
i
A
A
1
- pole powierzchni całej przekroju
A
y
O
z
∆
A
i
z
i
y
i
c
z
c
y
c
c
gdyby z cienkiej blachy wyciąć element o kształcie
danego przekroju i zawiesić go na nici w środku
ciężkości to będzie on pozostawał w równowadze
w każdym położeniu
A
1
y
O
z
y
c
c
z
c
A
2
A
i
A
n
z
ci
y
ci
c
i
4. Zginanie pr
ę
ta
- 2/26 -
r
R
α
c
r
c
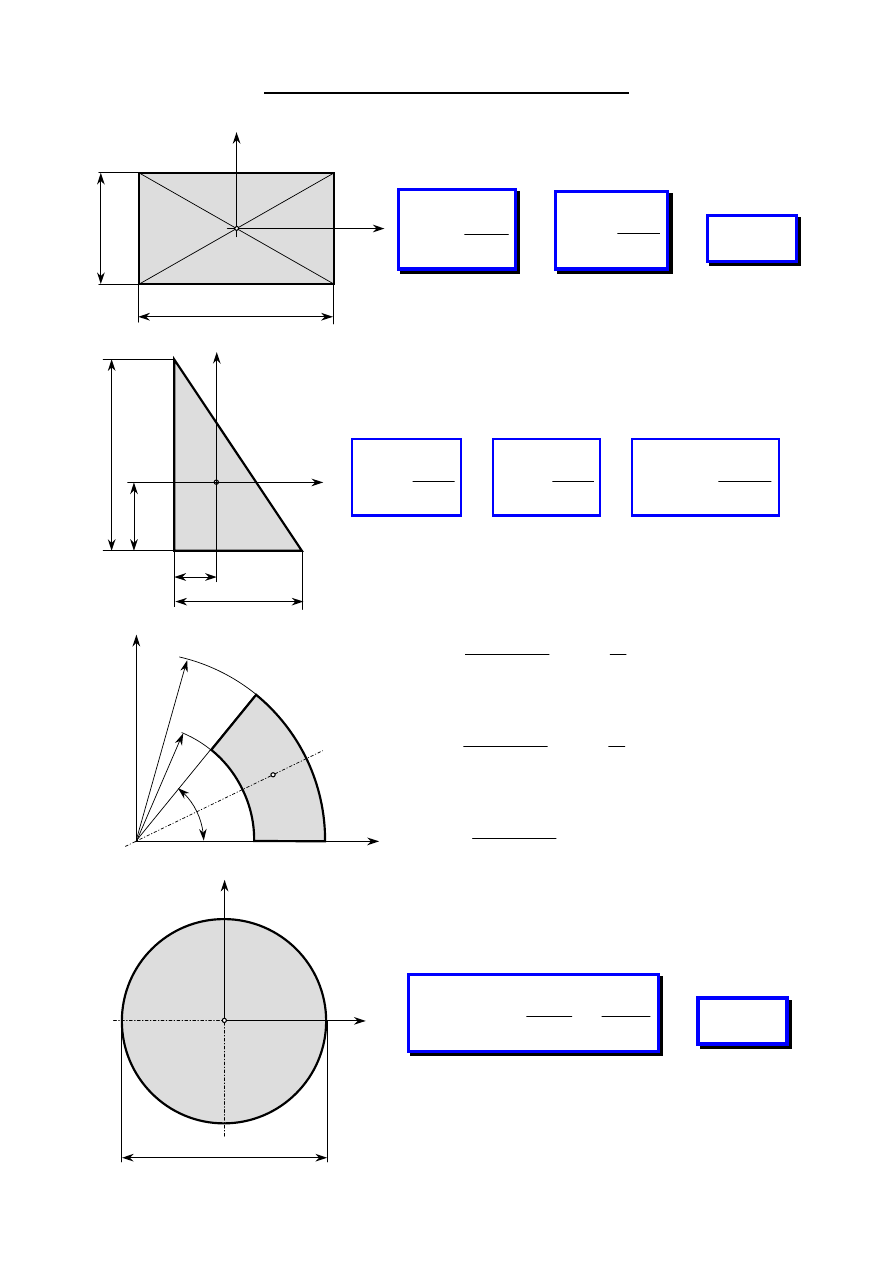
Położenie środka ciężkości wybranych figur
wycinek pierścienia
2
2
sin
3
2
2
2
α
α
r
R
r
Rr
R
r
c
+
+
+
=
α
[rad]
przypadki szczególne
α
α
α
α
=
π
π
π
π/2
α
α
α
α
=
π
π
π
π/2
r=0
π
3
4R
r
R
r
Rr
R
r
c
+
+
+
=
2
2
3
2
4
π
R
r
c
π
3
2
4
=
r
R
c
r
c
r
c
c
R
c
prostokąt
h
h/3
c
trójkąt
h
b
a
b
b
a
a
c
trapez
4. Zginanie pr
ę
ta
- 3/26 -
Przykład:
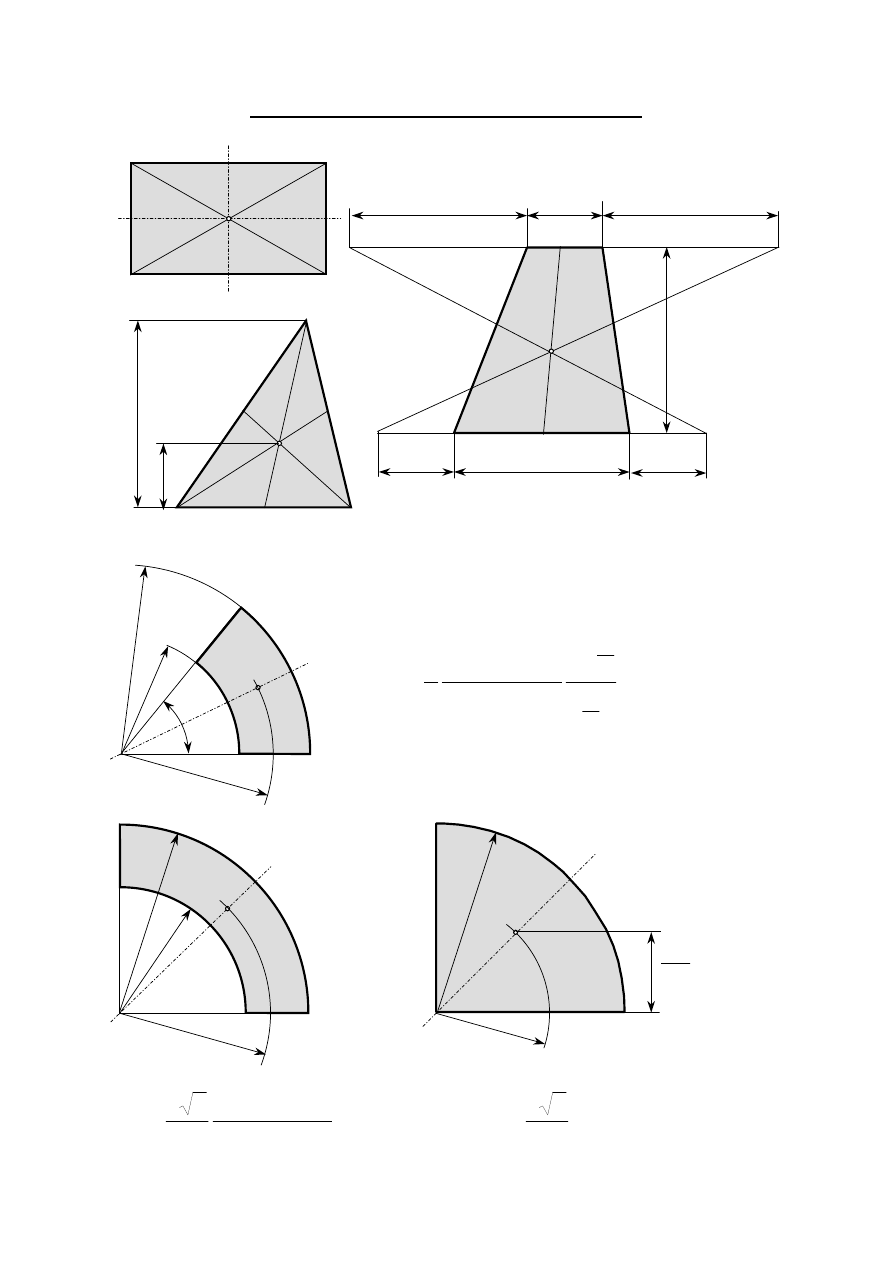
Wyznaczyć współrzędne środka ciężkości przekroju ABCDEFGH pokazanego na
rysunku (wymiary podano w mm).
Kolejność postępowania:
1) obieramy układ współrzędnych y,z,
2) dzielimy przekrój na części, których
współrzędne środków ciężkości można
łatwo obliczyć,
3) numerujemy te części od 1 do n,
4) przygotowujemy tabelkę według
podanego niżej wzoru,
5) do tabelki wpisujemy pola powierzchni A
i
kolejnych części oraz współrzędne y
ci
, z
ci
ich środków ciężkości,
6) wykonujemy obliczenia w tabeli (kolumny
5 i 6),
7) kolumny 2, 5 i 6 podsumowujemy,
8) obliczamy współrzędne środka ciężkości całego przekroju według podanych
wzorów, położenie środka ciężkości nanosimy na rysunku.
i
A
i
[mm
2
]
y
ci
[mm]
z
ci
[mm]
A
i
y
ci
[mm
3
]
A
i
z
ci
[mm
3
]
1
2
3
4
5
6
1
100
20
47.5
2000
4750
2
500
5
25
2500
12500
3
300
20
7.5
6000
2250
Σ
900
10500
19500
y
c
=10500/900
≅11.67mm
z
c
=19500/900
≅21.67mm
Metoda „pól ujemnych”
Rozpatrywany przekrój możemy potraktować jako złożony z dwóch figur:
1 – prostokąta ABGH, 2 – prostokąta CDEF ale o polu ujemnym.
i
A
i
[mm
2
]
y
ci
[mm]
z
ci
[mm]
A
i
y
ci
[mm
3
]
A
i
z
ci
[mm
3
]
1
2
3
4
5
6
1
1500
15
25
22500
37500
2
– 600
20
30
–12000
–18000
Σ
900
10500
19500
y
c
=10500/900
≅11.67mm
z
c
=19500/900
≅21.67mm
5
50
H
G
F
30
10
15
E
D
C
B
A
y
z
1
2
3
c
(
11.67, 21.67)
4. Zginanie pr
ę
ta
- 4/26 -
A
y
O
z
∆
A
i
z
i
y
i
r
i
4.1.2. Momenty bezwładności przekroju
Całe pole
A
powierzchni przekroju podzielono na
n
części o polach powierzchni
∆
A
i
Momenty bezwładności względem osi
gdy n
→∞ i
∆
A
i
→0
∑
=
∆
=
n
i
i
i
y
A
z
J
1
2
∫
=
A
y
dA
z
J
2
∑
=
∆
=
n
i
i
i
z
A
y
J
1
2
∫
=
A
z
dA
y
J
2
Biegunowy moment bezwładności
gdy n
→∞ i
∆
A
i
→0
∑
=
∆
=
n
i
i
i
O
A
r
J
1
2
∫
=
A
O
dA
r
J
2
(
)
y
z
A
A
A
A
O
J
J
dA
z
dA
y
dA
z
y
dA
r
J
+
=
+
=
=
+
=
=
∫
∫
∫
∫
2
2
2
2
2
Twierdzenie
Biegunowy moment bezwładności równy jest sumie momentów bezwładności
względem dwóch wzajemnie prostopadłych osi przecinających się w biegunie.
Moment odśrodkowy (dewiacji, zboczenia)
gdy n
→∞ i
∆
A
i
→0
∑
=
∆
=
n
i
i
i
i
yz
A
z
y
J
1
∫
=
A
yz
yzdA
J
Definicje
1. Osie y,z zaczepione w środku ciężkości przekroju nazywamy osiami
centralnymi.
2. Osie y,z, względem których momenty bezwładności
J
y
oraz
J
z
osiągają
ekstremalne wartości nazywamy osiami głównymi.
3. Osie centralne, będące równocześnie osiami głównymi nazywamy głównymi
centralnymi osiami bezwładności (GCOB)
Główne centralne osie bezwładności mają szczególne znaczenie
przy analizie rozkładu naprężeń w prętach zginanych.
Twierdzenie
Jeśli któraś z osi y,z jest osią symetrii
przekroju, to moment odśrodkowy J
yz
względem tych osi równy jest zeru.
4. Zginanie pręta
- 5/26 -
Momenty bezwładności względem osi równoległych
y
c
, z
c
– osie centralne (zaczepione w
ś
rodku ciężkości przekroju)
y
, z – osie równoległe do osi centralnych,
przesunięte o y
0
, z
0
Elementarne pole dA posiada
współrzędne (y
c
, z
c
) w układzie
centralnym oraz współrzędne (y, z) w
układzie przesuniętym.
0
y
y
y
c
−
=
0
z
z
z
c
−
=
A
z
J
J
c
y
y
2
0
+
=
wzory
Steinera
A
y
J
J
c
z
z
2
0
+
=
Twierdzenie Steinera
Moment bezwładności względem osi jest równy sumie momentu bezwładności
względem równoległej osi centralnej oraz iloczynu pola A figury przez kwadrat
odległości między tymi osiami.
A
z
y
J
J
c
c
z
y
yz
0
0
+
=
Twierdzenie
Moment odśrodkowy względem osi układu przesuniętego jest równy sumie
momentu odśrodkowego względem osi układu centralnego oraz iloczynu pola A
figury przez iloczyn współrzędnych środka układu przesuniętego.
A
y
c
0
z
c
c
y
0
y
z
z
0
d
A
z
c
y
c
y
z
(
)
∫
∫
∫
+
−
=
+
−
=
=
−
=
=
A
A
c
A
c
y
c
c
c
y
dA
z
dA
z
z
dA
z
J
dA
z
dA
z
z
dA
z
dA
z
z
dA
z
dJ
2
0
0
2
2
0
0
2
2
0
2
2
2
(
)
∫
∫
∫
+
−
=
+
−
=
=
−
=
=
A
A
c
A
c
z
c
c
c
z
dA
y
dA
y
y
dA
y
J
dA
y
dA
y
y
dA
y
dA
y
y
dA
y
dJ
2
0
0
2
2
0
0
2
2
0
2
2
2
c
y
J
c
z
J
A
0
0
A
c
c
z
y
J
A
0
(
)(
)
∫
∫
∫
∫
+
−
−
=
+
−
−
=
=
−
−
=
=
A
A
A
A
c
c
c
c
yz
c
c
c
c
c
c
yz
dA
z
y
dA
z
y
dA
y
z
dA
z
y
J
dA
z
y
dA
z
y
dA
y
z
dA
z
y
z
z
y
y
yzdA
dJ
0
0
0
0
0
0
0
0
0
0
0
4. Zginanie pr
ę
ta
- 6/26 -
A
y
z
0
y
1
z
1
d
A
z
1
y
y
1
z
α
Momenty bezwładności względem osi obróconych
y
1
, z
1
– osie obrócone w stosunku do osi
y
, z o kąt
α
Elementarne pole dA posiada współrzę-
dne (y, z) w układzie y, z oraz współrzę-
dne (y
1
, z
1
) w układzie obróconym.
α
α
sin
cos
1
z
y
y
+
=
α
α
cos
sin
1
z
y
z
+
−
=
α
α
α
2
sin
sin
cos
2
2
1
yz
z
y
y
J
J
J
J
−
+
=
α
α
α
2
sin
cos
sin
2
2
1
yz
z
y
z
J
J
J
J
+
+
=
(
)
α
α
2
sin
2
1
2
cos
1
1
z
y
yz
z
y
J
J
J
J
−
+
=
(
)
∫
∫
∫
+
+
=
+
+
=
+
=
=
A
A
A
y
z
dA
z
yzdA
dA
y
J
dA
z
dA
yz
dA
y
dA
z
y
dA
y
dJ
2
2
2
2
2
2
2
2
2
2
1
sin
2
sin
cos
sin
cos
sin
2
cos
sin
cos
1
1
α
α
α
α
α
α
α
α
α
J
z
J
y
J
yz
J
z
J
y
J
yz
(
)
∫
∫
∫
+
−
=
+
−
=
+
−
=
=
A
A
A
y
y
dA
z
yzdA
dA
y
J
dA
z
dA
yz
dA
y
dA
z
y
dA
z
dJ
2
2
2
2
2
2
2
2
2
2
1
cos
2
sin
sin
cos
cos
sin
2
sin
cos
sin
1
1
α
α
α
α
α
α
α
α
α
(
)(
)
∫
∫
∫
+
+
−
=
+
−
+
−
=
=
+
−
+
=
=
A
A
A
z
y
z
y
dA
z
yzdA
dA
y
J
dA
z
yzdA
yzdA
dA
y
dA
z
y
z
y
dA
z
y
dJ
2
2
2
2
2
2
1
1
cos
sin
2
cos
cos
sin
cos
sin
sin
cos
cos
sin
cos
sin
sin
cos
1
1
1
1
α
α
α
α
α
α
α
α
α
α
α
α
α
α
α
J
z
J
y
J
yz
4. Zginanie pr
ę
ta
- 7/26 -
Osie główne i główne momenty bezwładności
Zadanie
Należy znaleźć taki kąt
α
=
α
0
obrotu osi, aby momenty
1
y
J
oraz
1
z
J
osiągały
ekstremalne wartości.
(
)
0
2
cos
2
2
sin
0
2
cos
2
cos
sin
2
cos
sin
2
1
=
−
−
=
−
+
−
=
yz
y
z
yz
z
y
y
J
J
J
J
J
J
d
dJ
α
α
α
α
α
α
α
α
y
z
yz
J
J
J
tg
−
= 2
2
0
α
Osie obrócone o tak określony kąt
α
0
nazywamy osiami głównymi.
Po podstawieniu k
ą
ta
α
=
α
0
do wyra
ż
e
ń
na momenty bezwładno
ś
ci w układzie obróconym i
wykorzystaniu nast
ę
puj
ą
cych zale
ż
no
ś
ci trygonometrycznych
α
α
α
α
α
α
α
α
α
2
1
1
2
cos
2
1
2
2
sin
2
2
cos
1
cos
2
2
cos
1
sin
2
2
2
2
tg
tg
tg
+
=
+
=
+
=
−
=
otrzymujemy
główne momenty bezwładności
(momenty względem osi głównych)
2
2
min
2
2
1
yz
y
z
y
z
y
J
J
J
J
J
J
J
+
−
−
+
=
=
2
2
max
2
2
1
yz
y
z
y
z
z
J
J
J
J
J
J
J
+
−
+
+
=
=
0
1
1
=
z
y
J
Momenty główne osiągają wartości ekstremalne (największą i najmniejszą)
spośród wszystkich możliwych wartości uzyskanych przy obrocie układu
współrzędnych o dowolny kąt.
Moment odśrodkowy (dewiacji) względem osi głównych osiąga wartość 0.
4. Zginanie pr
ę
ta
- 8/26 -
Koło Mohra dla momentów bezwładności
(geometryczna interpretacja wzorów)
y
z
yz
J
J
J
tg
−
= 2
2
0
α
2
2
max
min,
2
2
yz
y
z
y
z
J
J
J
J
J
J
+
−
+
=
m
Kolejność postępowania:
1) rysujemy układ współrzędnych: oś pozioma
J
y
J
z
, oś pionowa
J
yz
,
2) zaznaczamy punkty: A
(J
y
, J
yz
)
, B
(J
z
,
–
J
yz
),
3) punkty A i B łączymy odcinkiem, który przecinając się z poziomą osią wyznacza
ś
rodek C koła Mohra,
4) zakreślamy koło Mohra promieniem CA,
5) aby otrzymać główne momenty bezwładności
J
min
,
J
max
należy średnicę AB
obrócić o kąt 2
α
α
α
α
tak, aby stała się średnicą poziomą,
6) aby otrzymać kierunki osi głównych należy osie y,z obrócić na rysunku przekroju
o kąt
α
α
α
α
w tę samą stronę, co średnicę AB.
J
y
J
z
J
yz
J
z
J
y
- J
yz
J
yz
J
min
J
max
2
z
y
J
J
+
2
2
2
yz
y
z
J
J
J
+
−
2
α
0
A
B
C
4. Zginanie pręta
- 9/26 -
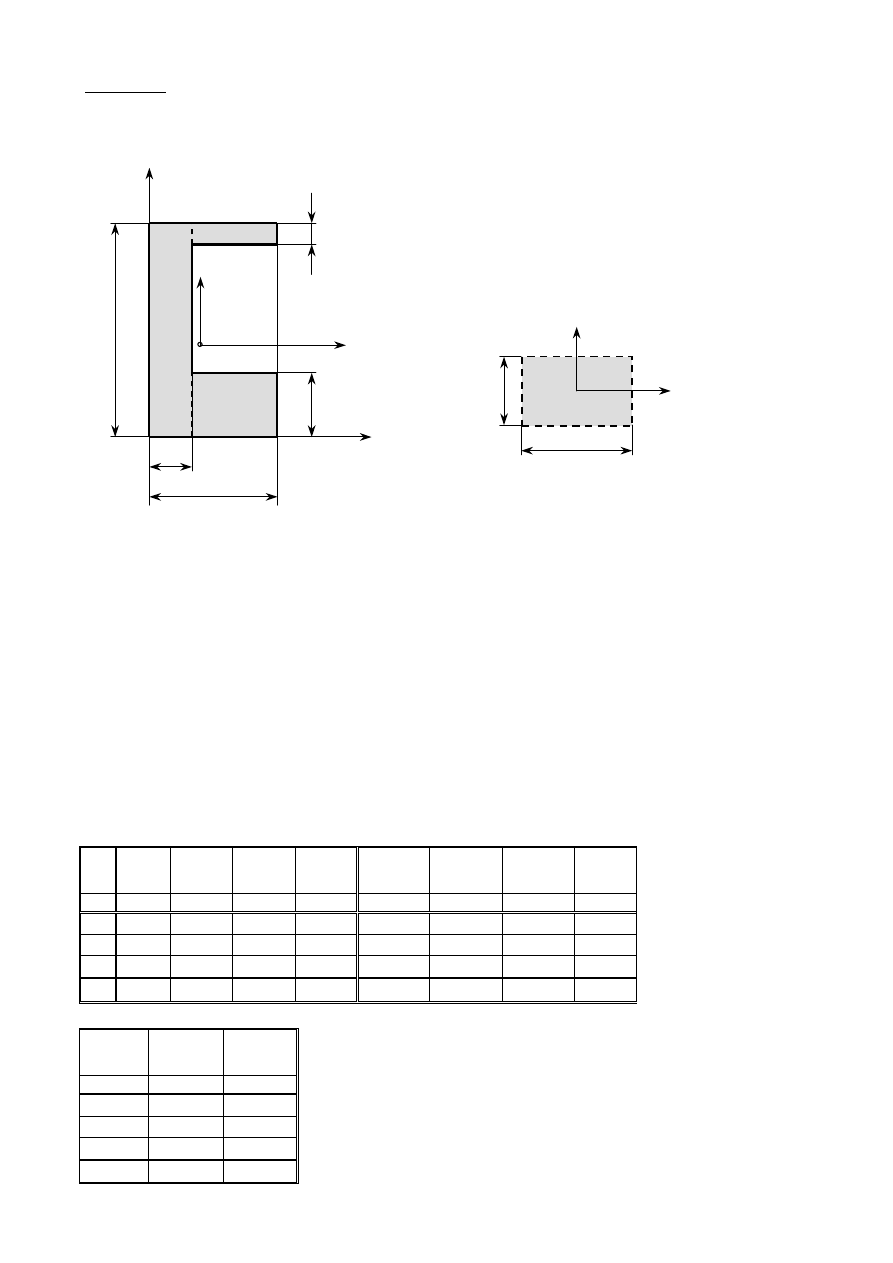
prostokąt
c
y
z
a
b
b
b/3
c
trójkąt
prostokątny
z
y
a
a/3
r
R
α
c
y
z
wycinek
pierścienia
y
c
D=2R
z
Momenty bezwładności wybranych figur
12
3
ab
J
y
=
12
3
ba
J
z
=
0
=
yz
J
36
3
ab
J
y
=
36
3
ba
J
z
=
72
2
2
b
a
J
yz
−
=
−
−
=
α
α
2
sin
2
1
8
4
4
r
R
J
y
+
−
=
α
α
2
sin
2
1
8
4
4
r
R
J
z
(
)
α
2
cos
1
16
4
4
−
−
=
r
R
J
yz
64
4
4
4
D
R
J
J
z
y
π
π
=
=
=
0
=
yz
J
4. Zginanie pręta
- 10/26 -
b
i
a
i
c
i
u
i
v
i
Przykład:
Wyznaczyć momenty główne i główne centralne osie bezwładności przekroju
ABCDEFGH pokazanego na rysunku (wymiary podano w mm).
Kolejność postępowania:
1) wyznaczamy położenie środka ciężkości
przekroju (patrz poprzedni przykład)
2) wprowadzamy dla każdej części pola lokalny
okład współrzędnych u
i
,v
i
zaczepiony w jej
środku ciężkości i osiach równoległych do
osi układu globalnego y,z
3) przygotowujemy tabelkę według podanego
niżej wzoru,
4) do tabelki wpisujemy pola powierzchni wymiary a
i
, b
i
kolejnych części oraz
współrzędne ich środków ciężkości y
ci
, z
ci
w układzie globalnym y,z,
5) obliczamy pola powierzchni A
i
części oraz ich momenty bezwładności względem
lokalnych osi u
i
,v
i
:
12
/
3
i
i
ui
b
a
J
=
,
12
/
3
i
i
vi
a
b
J
=
,
0
=
uvi
J
6) korzystając z twierdzenia Steinera obliczamy momenty bezwładności części
względem osi układu y,z (kolumny 10, 11 i 12)
2
ci
i
ui
yi
z
A
J
J
+
=
2
ci
i
vi
zi
y
A
J
J
+
=
ci
ci
i
uvi
yzi
z
y
A
J
J
+
=
,
7) kolumny 10, 11 i 12 podsumowujemy,
8) korzystając z twierdzenia Steinera obliczamy momenty bezwładności względem
osi centralnych y
c
, z
c
∑
∑
−
=
i
c
yi
yc
A
z
J
J
2
∑
∑
−
=
i
c
zi
zc
A
y
J
J
2
∑
∑
−
=
i
c
c
yzi
yzc
A
z
y
J
J
i
a
i
[mm]
b
i
[mm]
y
ci
[mm]
z
ci
[mm]
A
i
[mm
2
]
J
ui
[mm
4
]
J
vi
[mm
4
]
J
uvi
[mm
4
]
1
2
3
5
6
4
7
8
9
1
20
5
20
47.5
100
208
3333
0
2
10
50
5
25
500
104167
4167
0
3
20
15
20
7.5
300
5625
10000
0
Σ
900
J
yc
=665000
−21.67
2
⋅900=242370mm
4
J
zc
=190000
−11.67
2
⋅900=67430mm
4
J
yzc
=202500
−11.67⋅21.67⋅900=−25100mm
4
J
yi
[mm
4
]
J
zi
[mm
4
]
J
yzi
[mm
4
]
10
11
12
225833
43333
95000
416667
16667
62500
22500
130000
45000
665000 190000 202500
5
50
H
G
F
30
10
15
E
D
C
B
A
y
z
1
2
3
c
(
11.67, 21.67)
y
c
z
c
4. Zginanie pręta
- 11/26 -
9) w celu znalezienia położenia osi głównych i momentów głównych możemy
wykorzystać koło Mohra
154900
2
=
+
zc
yc
J
J
mm
4
J
min
=J
z0
=
154900-91000=63900 mm
4
91000
2
2
2
=
+
−
yzc
yc
zc
J
J
J
mm
4
J
max
=J
y0
= 154900+91000=245900 mm
4
tg2
α=0.287
⇒
2
α=15.4
0
J
yc
J
zc
J
yzc
154900
J
zc
=67430
J
yc
=
242370
91000
J
min
= 63900
J
max
= 245900
J
yzc
=
-25100
15.4
0
5
50
30
10
15
c
y
0
z
0
7.7
0
11.67
2
1
.6
7
4. Zginanie pręta
- 12/26 -
4.2. Rodzaje zginania
Zginanie
– sposób obciążenia pręta,
który powoduje istnienie w myślowym
przekroju prostopadłym do jego osi
momentu gnącego
M
g
Momentowi gnącemu towarzyszy
zazwyczaj siła tnąca
T
.
y,z
– główne centralne osie
bezwładności przekroju
Zginanie:
− czyste – w myślowym przekroju istnieje jedynie moment gnący
M
g
− poprzeczne – momentowi
M
g
towarzyszy siła tnąca
T
Zginanie:
− proste – wypadkowy moment gnący
M
g
ma kierunek jednej z głównych
centralnych osi bezwładności przekroju
y,z
− ukośne – wypadkowy moment gnący daje niezerowe składowe na obie osie y,z
Inny sposób przedstawienia wektora momentu gnącego
x
z
c
y
T
T
y
T
z
M
g
M
gz
M
gy
x
z
c
y
M
gz
M
gy
x
z
M
gy
4. Zginanie pręta
- 13/26 -
q(x)
T(x)
M
g
(x)
dx
x
T(x)+dT(x)
M
g
(x)+d M
g
(x)
K
4.3. Wykresy momentów gnących i sił tnących
Pręt obciążony siłami oraz momentami sił, których wektory są prostopadłe do jego
osi, nazywamy belką.
Obciążenie belki:
1. siły czynne
− siły skupione P
i
[N]
− skupione momenty gnące M
gi
[Nm]
− obciążenie ciągłe q
i
(x)
[N/m]
2. siły bierne
− reakcje podpór
Związek między obciążeniem ciągłym, momentem gnącym i siłą tnącą
( )
( )
( )
( )
[
]
0
0
=
+
−
−
=
∑
x
dT
x
T
dx
x
q
x
T
F
z
⇓
( )
( )
x
q
dx
x
dT
−
=
( )
( )
( )
( )
[
]
( )
( )
[
]
0
2
0
=
+
−
+
+
+
=
∑
x
dM
x
M
dx
x
dT
x
T
dx
dx
x
q
x
M
M
g
g
g
K
po pominięciu małych drugiego rzędu: dxdx, dT(x)dx otrzymujemy
( )
( )
x
T
dx
x
dM
g
=
x
z
q
i
(x)
P
i
A
B
M
gi
dx
x
4. Zginanie pręta
- 14/26 -
Aby wykonać wykresy momentów gnących M
g
(x)
oraz sił tnących T(x) w ogólnym
przypadku należy:
1. wyznaczyć reakcje podpór
2. dokonać myślowego przekroju belki
α
-
α
w miejscu określonym
współrzędną x
3. wyznaczyć siły wewnętrzne M
g
(x), T(x) z warunków równowagi lewej lub
prawej myślowo odciętej części
x
z
q
i
(x)
P
i
A
B
M
gi
R
A
R
B
x
x
z
q
i
(x)
P
i
A
B
M
gi
R
A
R
B
α
α
x
x
z
q
i
(x)
P
i
A
B
M
gi
R
A
R
B
α
α
x
α
α
M
g
(x)
M
g
(x)
T(x)
T(x)
4. Zginanie pręta
- 15/26 -
x
z
q
P
A
B
M
g
D
C
E
l
1
l
2
l
3
l
4
Przykład:
Wykonać wykres momentów gnących M
g
(x)
oraz sił tnących T(x) dla belki pokaza-
nej na rysunku.
l
1
=1m
l
2
=1m
l
3
=2m
l
4
=2m
M
g
=5kNm
q
=2kN/m
P
=10kN
Uwaga:
W ogólnym przypadku nie da się opisać jednym równaniem przebiegu funkcji M
g
(x)
oraz T(x) na całej belce. Równania te trzeba pisać niezależnie dla poszczególnych
przedziałów belki. Granice przedziałów wyznaczone są przez punkty przyłożenia sił
skupionych i momentów skupionych jak również początek i koniec obciążenia
ciągłego.
1) Obliczenia reakcji
(
)
(
)
(
)
0
2
0
4
3
2
1
3
2
1
4
3
2
1
4
3
=
+
+
+
+
+
+
+
+
+
+
+
−
=
∑
l
l
l
l
P
l
l
l
R
l
l
l
l
l
l
q
M
M
D
g
A
R
D
=
−8.25kN
(
)
0
0
4
3
=
+
+
+
−
=
∑
P
R
l
l
q
R
F
D
A
z
R
A
=6.25kN
x
z
q
P
A
B
M
g
D
C
E
l
1
l
2
l
3
l
4
R
A
R
D
q
(l
3
+l
4
)
4. Zginanie pręta
- 16/26 -
q
A
B
M
g
C
l
1
l
2
R
A
γ
γ
M
g
(x)
T(x)
K
x
2) W kolejnych przedziałach belki wykonujemy myślowe przekroje i z warunków
równowagi lewej lub prawej części wyznaczamy funkcje M
g
(x)
oraz T(x)
przedział A-B
( )
0
0
=
−
=
∑
x
T
R
F
A
z
⇒
( )
25
.
6
=
=
A
R
x
T
kN
( )
0
0
=
−
=
∑
x
R
x
M
M
A
g
K
⇒
( )
x
x
R
x
M
A
g
25
.
6
=
=
kNm
przedział B-C
( )
0
0
=
−
=
∑
x
T
R
F
A
z
⇒
( )
25
.
6
=
=
A
R
x
T
kN
( )
0
0
=
+
−
=
∑
g
A
g
K
M
x
R
x
M
M
( )
(
)
5
25
.
6
−
=
−
=
x
M
x
R
x
M
g
A
g
kNm
przedział C-D
(
)
[
]
( )
0
0
2
1
=
−
+
−
−
=
∑
x
T
l
l
x
q
R
F
A
z
( )
(
)
[
]
2
1
l
l
x
q
R
x
T
A
+
−
−
=
( )
(
)
[
]
2
2
25
.
6
−
−
=
x
x
T
kN
( )
(
)
[
]
(
)
[
]
0
2
0
2
1
2
1
=
+
−
+
−
+
+
−
=
∑
l
l
x
l
l
x
q
M
x
R
x
M
M
g
A
g
K
( )
(
)
[
]
2
2
2
1
l
l
x
q
M
x
R
x
M
g
A
g
+
−
−
−
=
( )
(
)
2
2
5
25
.
6
−
−
−
=
x
x
x
M
g
kN
x
z
q
=2kN/m
P
=10kN
A
B
M
g
=5kNm
D
C
E
l
1
=1m
l
2
=1m
l
3
=2m
l
4
=2m
R
A
=6.25kN
R
D
=8.25kN
α
β
γ
δ
α
β
γ
δ
x
A
R
A
α
α
M
g
(x)
T(x)
K
x
A
B
M
g
l
1
=1m
R
A
β
β
M
g
(x)
T(x)
K

4. Zginanie pręta
- 17/26 -
x
P
E
δ
δ
l
1
+l
2
+l
3
+l
4
M
g
(x)
T(x)
K
q
przedział D-E
( )
(
)
[
]
0
0
4
3
2
1
=
+
−
+
+
+
−
=
∑
P
x
l
l
l
l
q
x
T
F
z
( )
(
)
[
]
P
x
l
l
l
l
q
x
T
−
−
+
+
+
=
4
3
2
1
( )
[
]
10
6
2
−
−
=
x
x
T
kN
0
=
∑
K
M
( )
(
)
[
]
(
)
[
]
(
)
[
]
0
2
4
3
2
1
4
3
2
1
4
3
2
1
=
−
+
+
+
−
−
+
+
+
−
+
+
+
+
x
l
l
l
l
P
x
l
l
l
l
x
l
l
l
l
q
x
M
g
( )
(
)
[
]
(
)
[
]
2
2
4
3
2
1
4
3
2
1
x
l
l
l
l
q
x
l
l
l
l
P
x
M
g
−
+
+
+
−
−
+
+
+
=
( )
[
] [
]
2
6
6
10
x
x
x
M
g
−
−
−
=
kNm
3) Wykonujemy wykresy
Otrzymane wykresy sił wewnętrznych stanowią podstawę dalszej analizy
wytrzymałościowej belki.
x
T [kN]
A
B
D
C
E
6.25
2.25
−6
−10
x
M
g
[kNm]
A
B
D
C
E
6.25
16
1.25
7.5
4. Zginanie pręta
- 18/26 -
x
M
g
(x)
P
A
B
a
a
P
C
D
M
g
=Pa=
const
odcinek belki poddany
czystemu zginaniu
Przed obciążeniem:
−
na powierzchni pręta narysowano
prostokątną siatkę
z
x
l
Po obciążeniu momentem gnącym M
g
:
−
linie siatki równoległe do osi pręta
(wzdłużne) stają się fragmentami
współśrodkowych okręgów,
−
linie siatki prostopadłe do osi pozostają
proste i prostopadłe do linii wzdłużnych.
4.4. Odkształcenia i naprężenia przy czystym zginaniu belki
pryzmatycznej
Czyste zginanie – taki sposób obciążenia belki, że w przekrojach na pewnym jej
odcinku panuje jedynie moment gnący M
g
(siła tnąca T=0).
Ponieważ dM
g
/dx=T, to przy czystym zginaniu M
g
=const.
Przykład realizacji stanu czystego zginania belki
Założenia:
− zginanie następuje w płaszczyźnie rysunku
(oś z jest osią główną)
Wnioski:
− przekroje płaskie prostopadłe do osi belki przed odkształceniem pozostają płaskie
i prostopadłe do zakrzywionej po odkształceniu osi belki,
− jedne wzdłużne włókna belki ulegają wydłużeniu, inne skróceniu,
− istnieje warstwa obojętna, której włókna nie zmieniają swojej długości.
z
x
M
g
M
g
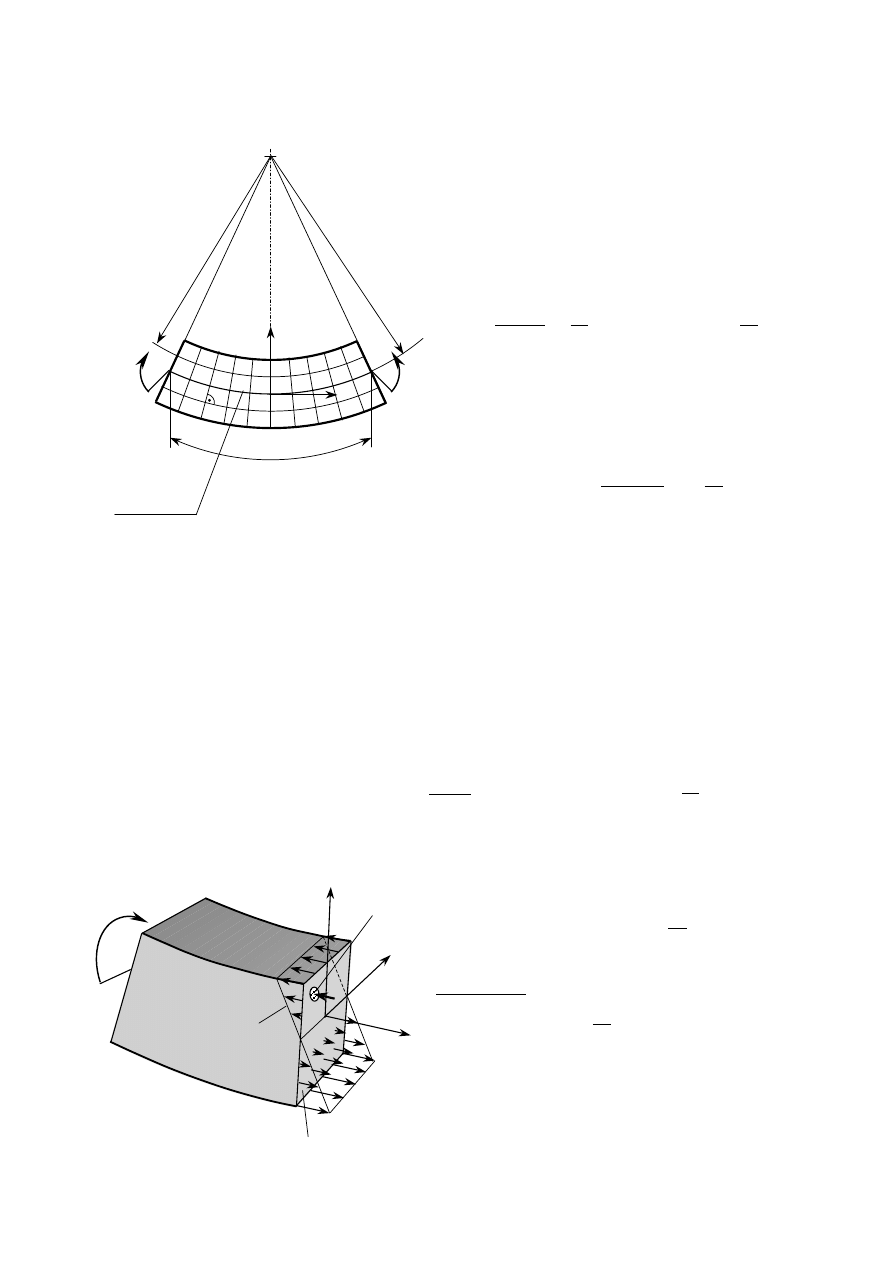
4. Zginanie pręta
- 19/26 -
l
– długość włókien warstwy obojętnej
ρ
– promień warstwy obojętnej
l(z)
– długość włókien warstwy, której
położenie określone jest współrzędną z
(promieniem
ρ
-z
)
( )
ρ
ρ
l
z
z
l
=
−
⇒
( )
−
=
ρ
z
l
z
l
1
ε
(z)
– odkształcenie względne włókien
o współrzędnej z
( )
( )
ρ
ε
z
l
l
z
l
z
−
=
−
=
Przy czystym zginaniu odkształcenia względne włókien belki są proporcjonalne
do ich odległości od warstwy obojętnej:
− dla z>0 (powyżej warstwy obojętnej)
ε
(z)
<0 (ściskanie)
− dla z<0 (poniżej warstwy obojętnej)
ε
(z)
>0 (rozciąganie)
Założenia:
− naprężenia w kierunku poprzecznym do włókien belki można zaniedbać – każde
włókno pracuje na rozciąganie lub ściskanie jak elementarny pręt (z Teorii
Sprężystości),
− spełnione jest prawo Hooke’a:
( )
( )
E
z
z
σ
ε
=
⇒
( )
( )
ρ
ε
σ
z
E
z
E
z
−
=
=
siła wypadkowa od naprężeń
σ
działających
na elementarnym polu dA:
zdA
E
dA
dF
x
ρ
σ
−
=
⋅
=
0
=
∑
x
F
∫
∫
=
−
=
⋅
=
A
A
x
zdA
E
dA
F
0
ρ
σ
a zatem moment statyczny przekroju
względem osi y:
∫
=
A
zdA
0
x
warstwa
oboj
ę
tna
ρ
z
l
ρ
-z
x
M
g
M
g
z
y
x
σ
σ
σ
σ
(z
)
M
g
dA
σ
A
– pole powierzchni
przekroju poprzecznego
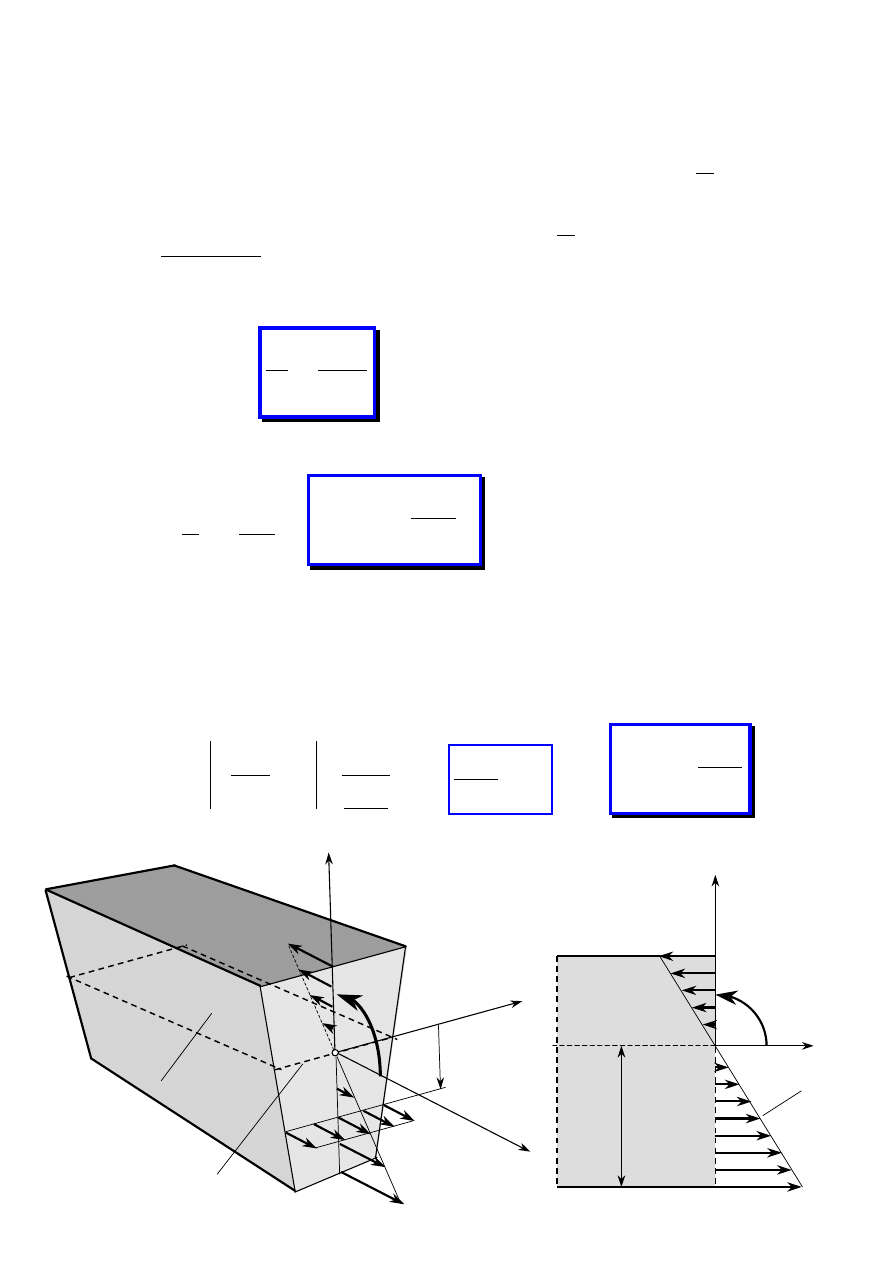
4. Zginanie pręta
- 20/26 -
wniosek: oś y przechodzi przez środek
ciężkości przekroju (jest osią
centralną)
elementarny moment względem osi y od siły dF
x
:
dA
z
E
zdF
dM
x
y
2
ρ
−
=
−
=
0
=
∑
y
M
⇒
0
=
+
∫
g
A
y
M
dM
⇒
0
2
=
+
−
∫
g
A
M
dA
z
E
ρ
y
A
J
dA
z
=
∫
2
− moment bezwładności pola przekroju względem osi y
y
g
EJ
M
=
ρ
1
( )
z
J
M
z
E
z
y
g
−
=
−
=
ρ
σ
( )
z
J
M
z
y
g
−
=
σ
Wnioski:
− przy czystym zginaniu belki pryzmatycznej oś obojętna (włókna belki, w
których naprężenia
σ=0) przechodzi przez środek ciężkości przekroju,
− naprężenia rosną liniowo wraz z odległością włókien od osi obojętnej
(ekstremalne naprężenia występują we włóknach, których odległość od osi
obojętnej jest największa i mają przeciwne znaki)
max
max
max
z
J
M
z
J
M
y
g
y
g
=
−
=
σ
y
y
W
z
J
=
max
y
g
W
M
=
max
σ
związek między:
obciążeniem M
g
,
sztywnością na zginanie EJ
y
,
i promieniem krzywizny warstwy obojętnej
ρ
ρ
ρ
ρ
przy czystym zginaniu belki pryzmatycznej
naprężenia przy czystym zginaniu
belki pryzmatycznej
c
z
y
x
M
g
z
σ
σ
σ
σ
(z )
warstwa obojętna
oś obojętna
x
z
σ
σ
σ
σ
(z )
z
max
σ
σ
σ
σ
max
M
g
y, z
– główne centralne
osie bezwładności
przekroju pręta
W
y
– wskaźnik wytrzymałości na zginanie
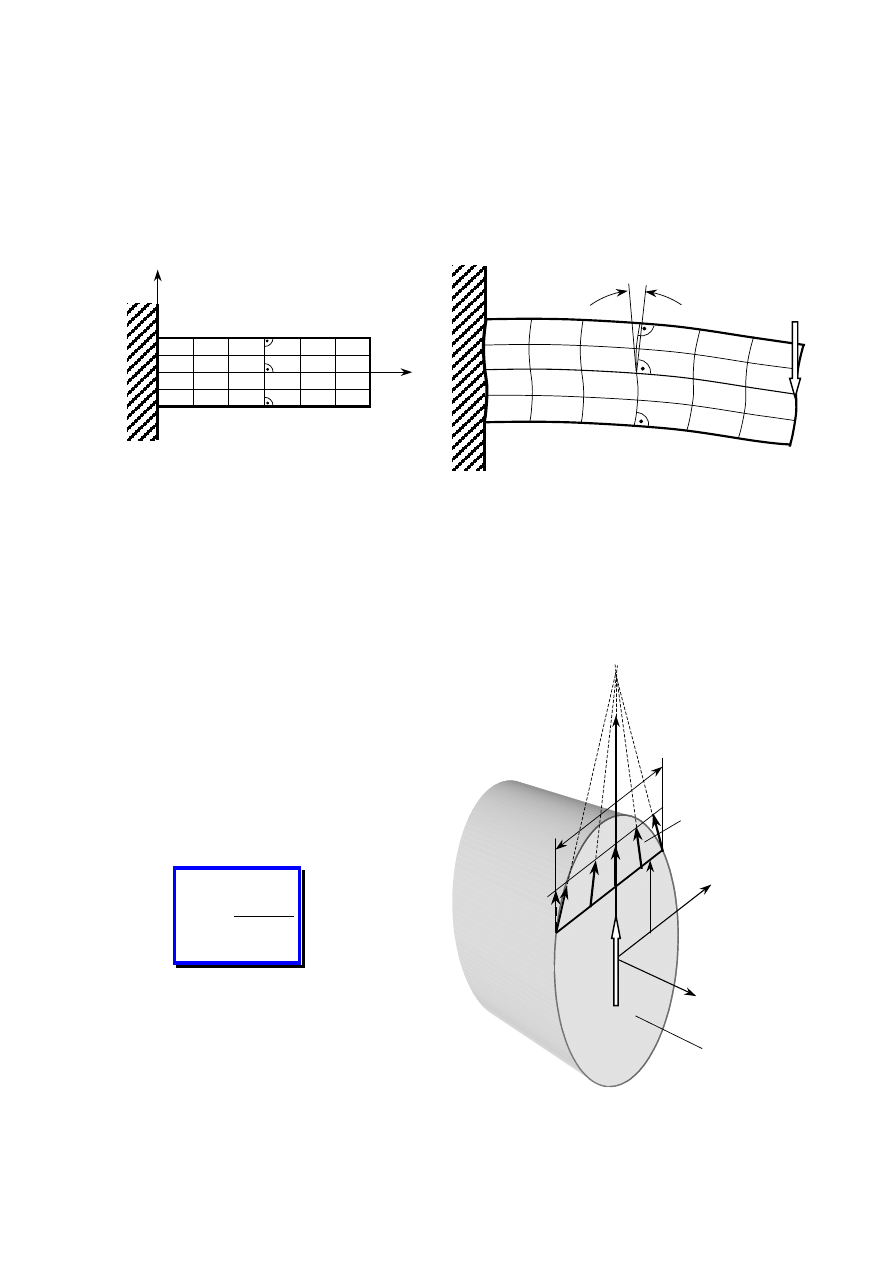
4. Zginanie pręta
- 21/26 -
Przed obciążeniem:
−
na powierzchni pręta narysowano
prostokątną siatkę
Po obciążeniu siłą poprzeczną P:
−
kąty między bokami odkształconej siatki
nie są na ogół proste,
−
najbardziej zmienione zostają kąty w
pobliżu osi pręta,
−
zmiana katów przy włóknach skrajnych
jest prawie niezauważalna
4.5. Naprężenia styczne przy zginaniu poprzecznym
belki pryzmatycznej
Zginanie poprzeczne – zginanie belki z udziałem siły tnącej T.
Wniosek:
ponieważ naprężenia styczne
τ
są proporcjonalne
do kata odkształcenia postaciowego
γ
to rozkład
naprężeń stycznych w przekroju poprzecznym
pręta nie jest równomierny.
wzór Żurawskiego
y
z
z
y
z
J
b
TS
)
(
=
τ
τ
z
– średnia wartość z-owej składowej
naprężeń stycznych w warstwie
o współrzędnej z
T
– siła tnąca w przekroju
)
( z
y
S
– moment statyczny pola przekroju odciętego współrzędną z
b
z
– szerokość warstwy
J
y
– moment bezwładności przekroju względem osi y
γ
P
z
x
z
y
x
T
z
τ
z
b
z
pole odci
ę
te lini
ą
o współrz
ę
dnej z
przekrój
zwarty
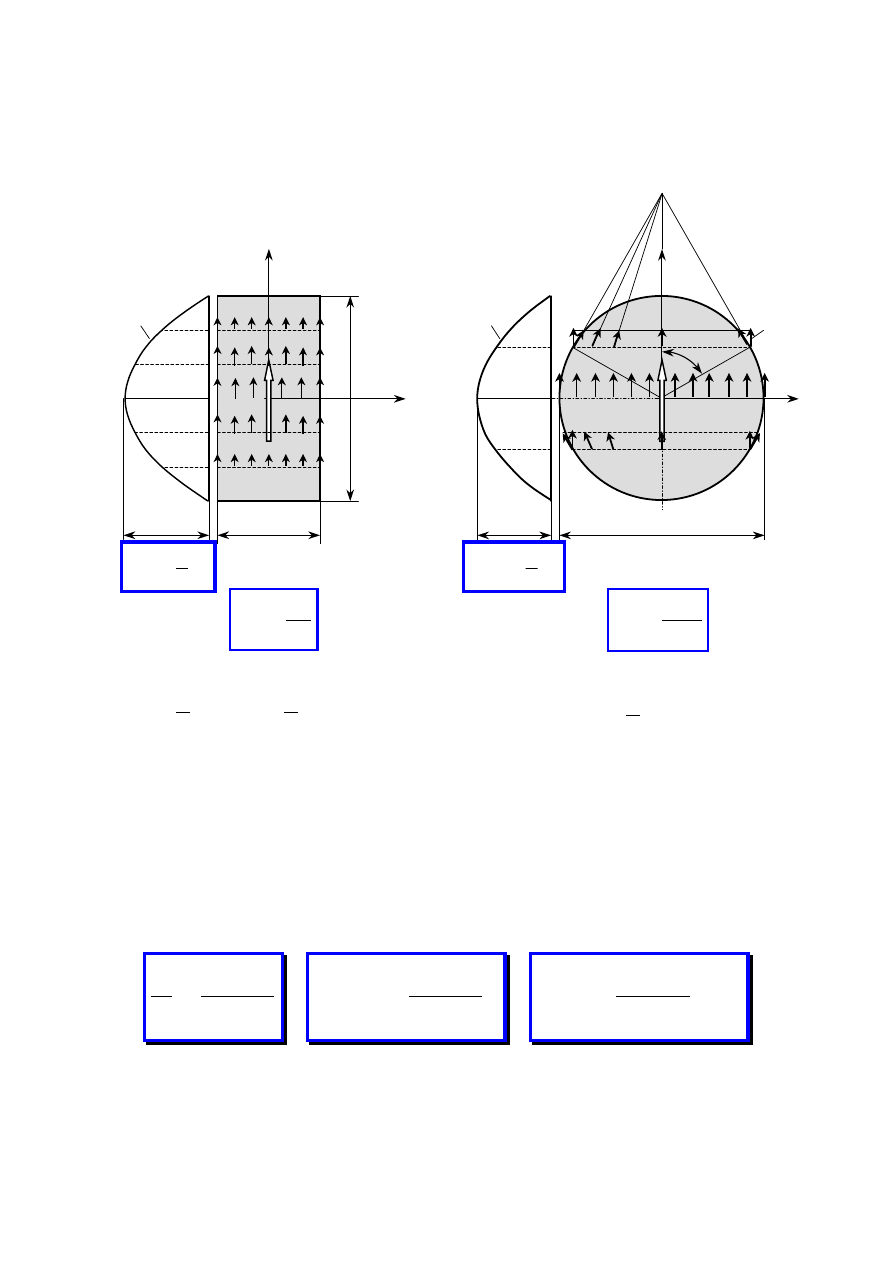
4. Zginanie pręta
- 22/26 -
rozkład naprężeń stycznych rozkład naprężeń stycznych
w przekroju prostokątnym w przekroju kołowym
bh
T
ś
r
=
τ
2
4
d
T
ś
r
π
τ
=
−
=
2
2
1
2
3
h
z
ś
r
z
τ
τ
α
τ
τ
2
sin
3
4
ś
r
z
=
Przy zginaniu poprzecznym z techniczną dokładnością można stosować wzory
na naprężenia i promień krzywizny belki jak przy czystym zginaniu:
( )
y
g
EJ
x
M
=
ρ
1
( )
( )
z
J
x
M
z
y
g
−
=
σ
( )
g
y
g
k
W
x
M
≤
=
max
σ
k
g
– dopuszczalne naprężenia na zginanie
y
z
h
b
T
ττττ
z
T
ττττ
z
y
z
d
τ
z
α
ś
r
τ
τ
2
3
max
=
ś
r
z
τ
τ
3
4
max
=
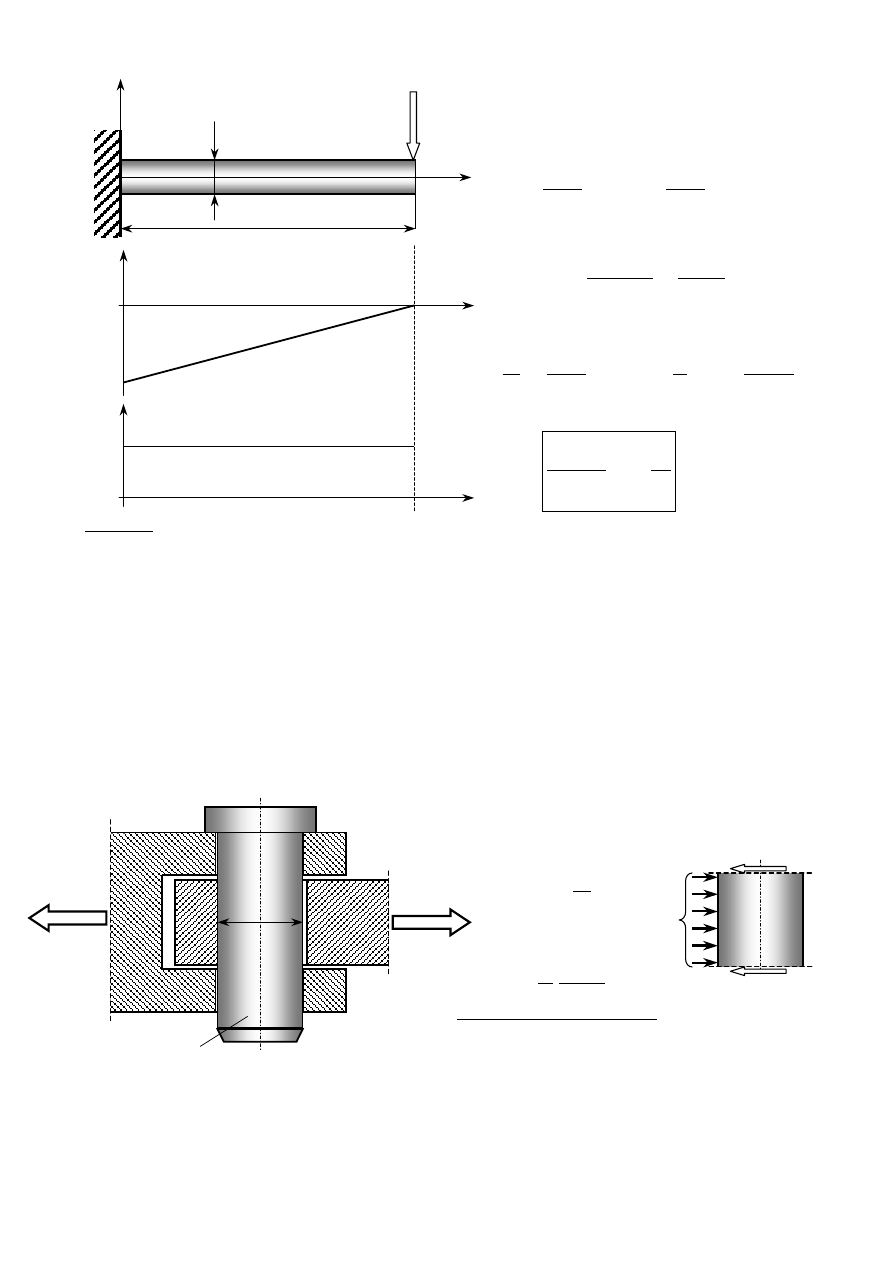
4. Zginanie pr
ę
ta
- 23/26 -
x
z
P
d
l
x
M
g
(x)
-Pl
A
B
x
T(x)
P
4
2
d
A
π
=
32
3
d
W
y
π
=
3
max
max
32
d
Pl
W
M
y
g
π
σ
=
−
=
2
4
d
P
A
T
ś
r
π
τ
=
=
2
max
3
16
3
4
d
P
ś
r
π
τ
τ
=
=
d
l
6
max
max
=
τ
σ
przykład: dla l/d=10
τ
max
≈1.7%σ
max
Wniosek: w belkach smukłych, gdzie długość jest dużo większa od
wymiaru poprzecznego, naprężenia od ścinania są pomijalnie małe w
porównaniu z naprężeniami od zginania.
Za pominięciem naprężeń stycznych w belkach smukłych przemawia również fakt, że
w punktach przekroju gdzie panują największe naprężenia normalne (punkty
najbardziej oddalone od osi obojętnej) naprężenia styczne są równe zeru – a zatem
wzajemne działanie naprężeń stycznych i normalnych „sumuje się” w bardzo małym
stopniu.
2
P
T
=
t
k
d
P
≤
=
2
max
3
8
π
τ
k
t
– naprężenia dopuszczalne na ścinanie
Przykład konstrukcji, w której naprężenia styczne pełnią rolę dominującą
(połączenie sworzniowe)
P
T
T
d
P
P
sworze
ń
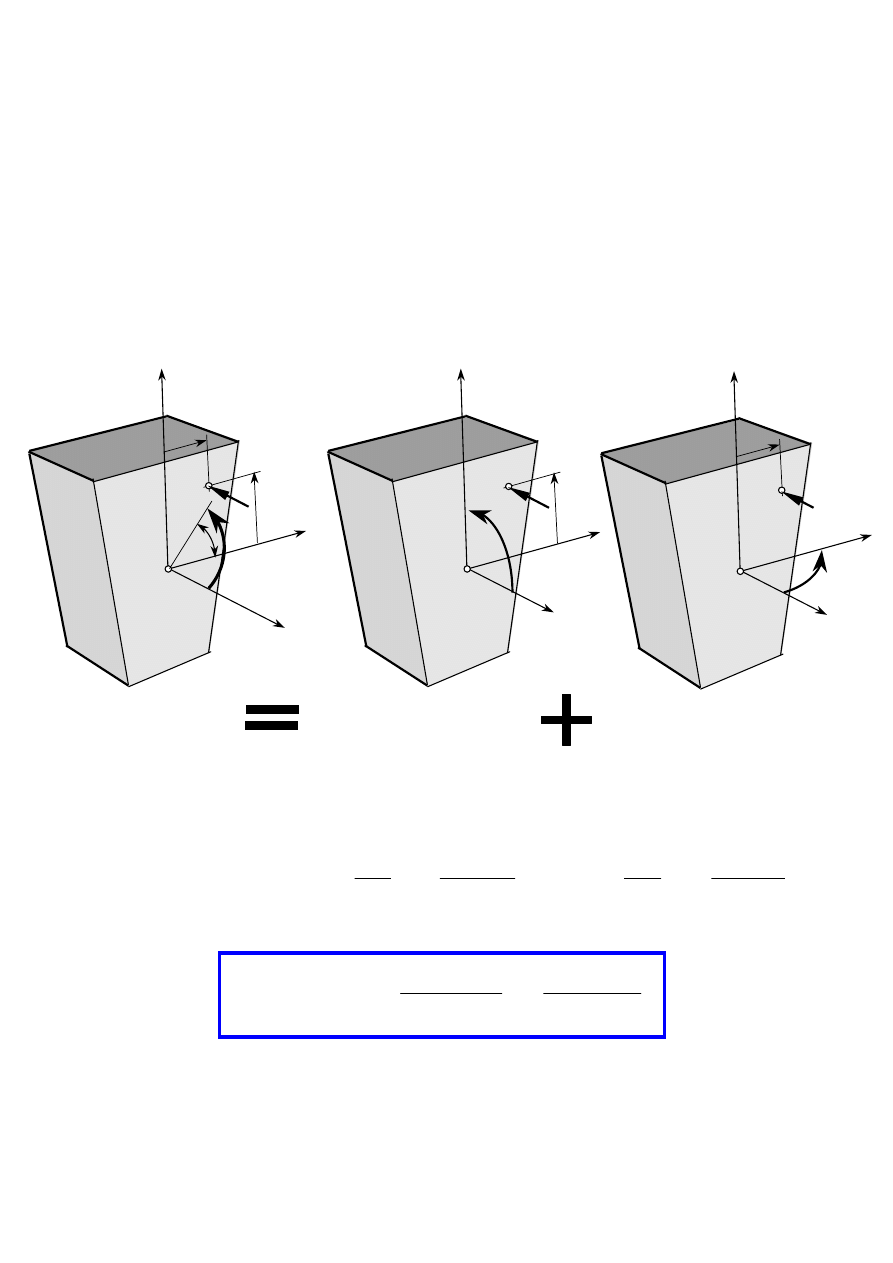
4. Zginanie pr
ę
ta
- 24/26 -
z
J
cos
M
z
J
M
y
g
y
gy
1
α
σ
−
=
−
=
y
J
sin
M
y
J
M
z
g
z
gz
2
α
σ
−
=
−
=
y
J
sin
M
z
J
cos
M
z
g
y
g
2
1
α
α
σ
σ
σ
−
−
=
+
=
4.6. Zginanie ukośne
Zginanie ukośne − przypadek zginania belki, w którym wypadkowy moment gnący
M
g
w przekroju nie pokrywa się z żadną z głównych centralnych
osi bezwładności
Zginanie ukośne traktuje się jako superpozycję dwóch stanów zginania prostego:
1. momentem
M
gy
2. momentem
M
gz
zginanie zginanie zginanie
momentem M
g
momentem M
gy
momentem M
gz
(zginanie ukośne) (zginanie proste) (zginanie proste)
M
gy
=M
g
cos
α
M
gz
=M
g
sin
α
α
- kąt nachylenia płaszczyzny działania momentu gnącego M
g
do płaszczyzny x-y
c
z
y
x
M
gz
y
B
σ
2
c
z
y
x
M
gy
z
B
σ
1
c
z
y
x
M
g
y
z
B
σ
α
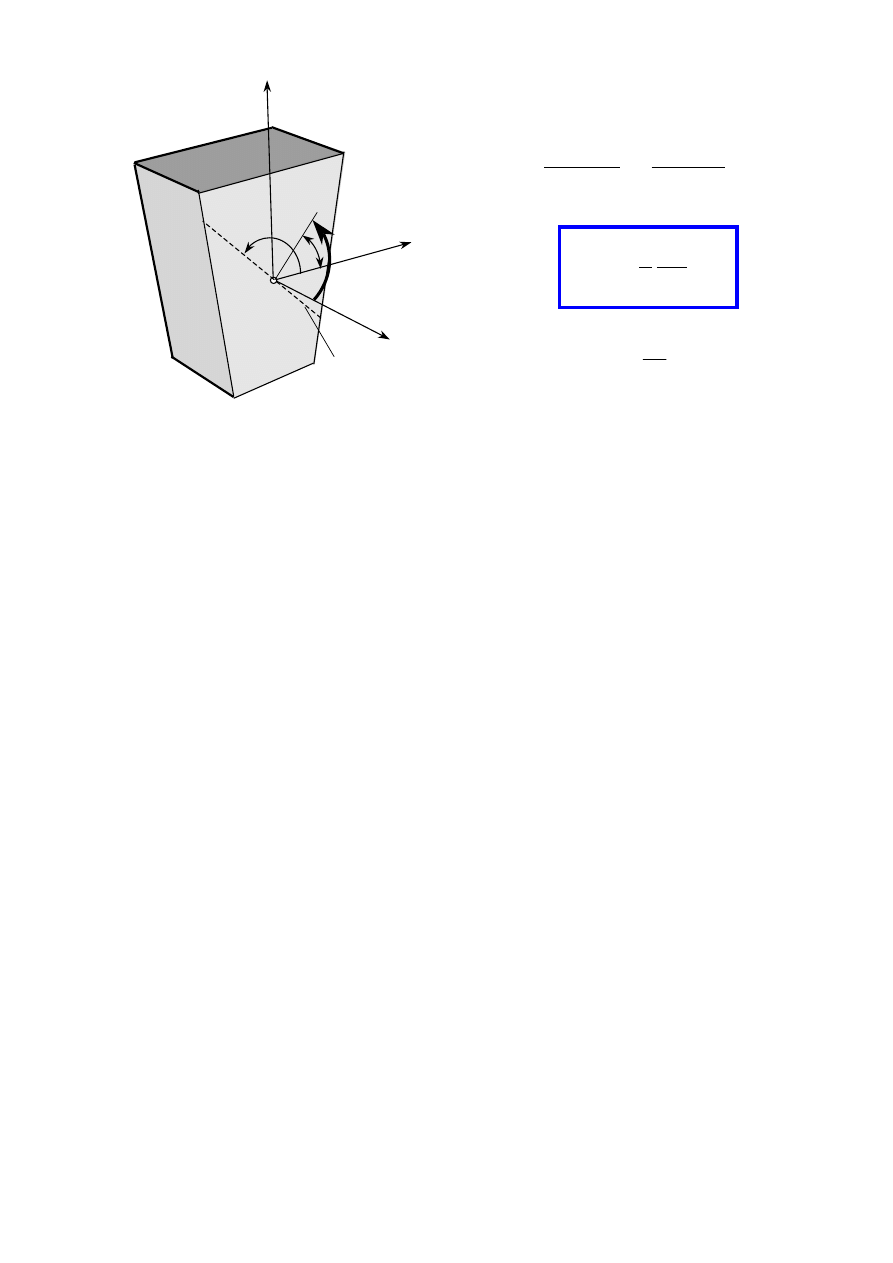
4. Zginanie pr
ę
ta
- 25/26 -
0
y
J
sin
M
z
J
cos
M
z
g
y
g
=
−
−
α
α
α
tg
J
J
y
z
z
y
−
=
α
β
tg
J
J
tg
z
y
−
=
Równanie osi obojętnej (
σ
=0)
⇓
Oś obojętna przy zginaniu ukośnym przechodzi przez środek ciężkości przekroju
i w przypadku ogólnym nie jest prostopadła do płaszczyzny działania momentu M
g
.
Ekstremalne naprężenia występują w punktach najbardziej oddalonych od osi
obojętnej.
c
z
y
x
M
g
α
β
oś obojętna
przekroju
4. Zginanie pr
ę
ta
- 26/26 -
4.7. Linia ugięcia belki
C
− punkt na osi belki
określony współrzędną x
z(x)
− ugięcie belki w
punkcie C
ϕ
(x)
− kąt ugięcia belki
w punkcie C
ρ
(x)
− promień krzywi-
zny belki w punkcie C
dla małych kątów ugięcia
Przykład: Wyznaczyć równanie linii ugięcia belki wspornikowej pokazanej powyżej.
stałą całkowania c
1
wyznaczamy z warunków brzegowych: dla x=0
ϕ
(x)=
0
⇒ c
1
=0
stałą całkowania c
2
wyznaczamy z warunków brzegowych: dla x=0 z(x)=0
⇒ c
2
=0
Ostatecznie Ugięcie na końcu
x
z
P
l
A
B
z(x)
x
C
ϕ
(x)
ρ
(x)
( )
2
2
dx
z
d
x
1
=
ρ
( )
( )
dx
EJ
x
M
dx
dz
x
y
g
∫
=
=
ϕ
( )
y
g
2
2
EJ
x
M
dx
z
d
=
( )
( )
dx
x
x
z
∫
=
ϕ
x
M
g
(x)
A
B
M
g
(x)=P(l-x)
( )
(
)
1
2
y
y
c
2
x
lx
EJ
P
dx
EJ
x
l
P
dx
dz
x
+
−
=
−
=
=
∫
ϕ
1
c
0
0
+
=
( )
2
3
2
y
2
y
c
6
x
2
x
l
EJ
P
dx
2
x
lx
EJ
P
x
z
+
−
=
−
=
∫
2
c
0
0
+
=
( )
−
=
6
x
2
x
l
EJ
P
x
z
3
2
y
( )
y
3
B
EJ
3
Pl
l
z
z
=
=
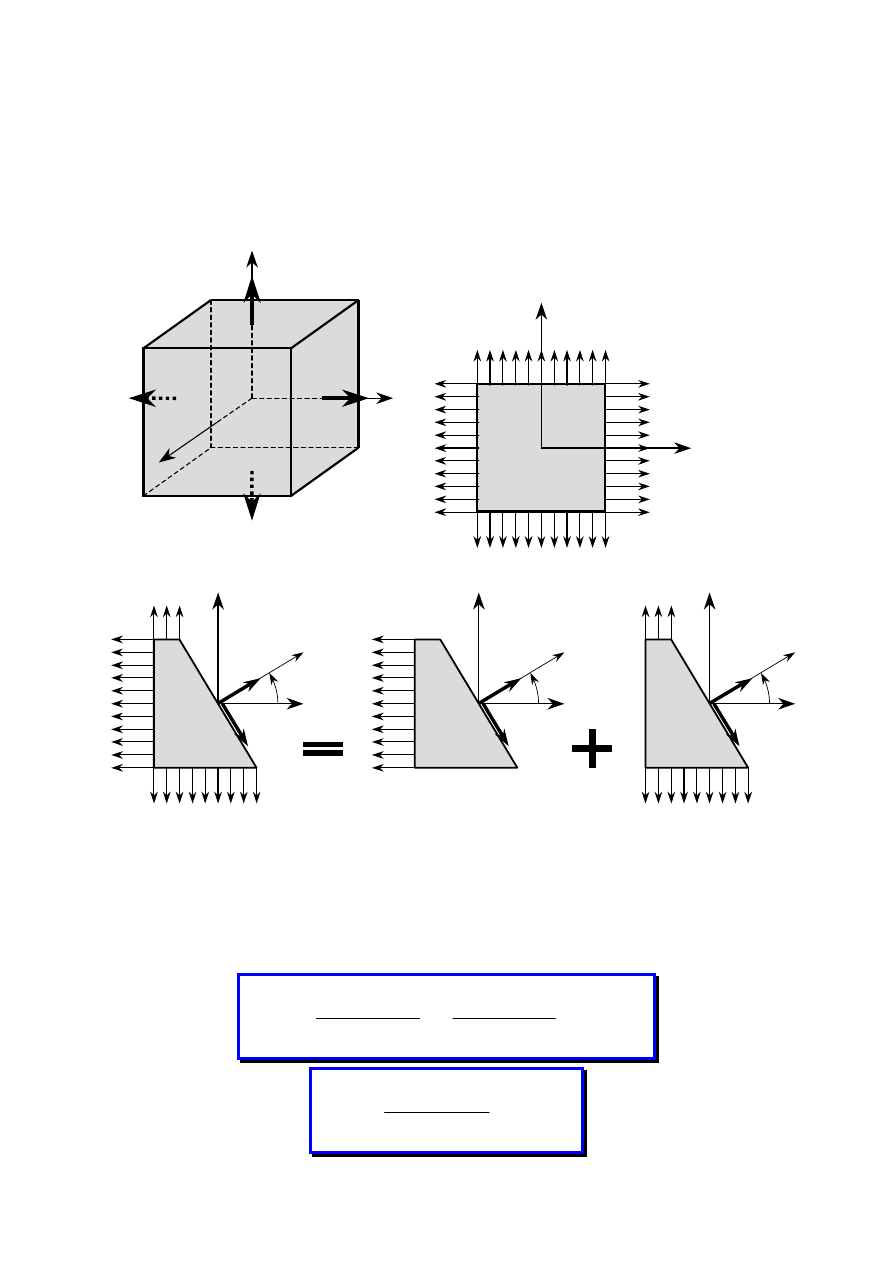
5. Analiza stanu naprężenia i odkształcenia
- 1/6 -
5. ANALIZA STANU NAPRĘŻENIA I ODKSZTAŁCENIA
5.1. Analiza płaskiego stanu naprężenia
Płaski stan naprężenia - na myślowo
wyciętą, elementarną kostkę działają
naprężenia w jednej płaszczyźnie (1-2)
α
σ
σ
σ
σ
σ
α
2
cos
2
2
2
1
2
1
−
+
+
=
α
σ
σ
τ
α
2
sin
2
2
1
−
=
1
2
3
σ
σ
σ
σ
1
σ
σ
σ
σ
2
σ
σ
σ
σ
2
σ
σ
σ
σ
1
2
1
σ
σ
σ
σ
1
σ
σ
σ
σ
1
σ
σ
σ
σ
2
σ
σ
σ
σ
2
2
1
σ
1
σ
2
σ
2
α
σ
α
τ
α
2
1
σ
1
α
σ
'
α
τ
'
α
2
1
σ
2
σ
2
α
σ
"
α
τ
"
α
α
σ
σ
α
2
1
'
cos
=
α
σ
σ
α
2
2
"
sin
=
α
α
σ
τ
α
cos
sin
1
'
=
α
α
σ
τ
α
cos
sin
2
"
−
=
"
'
α
α
α
σ
σ
σ
+
=
"
'
α
α
α
τ
τ
τ
+
=
1
, 2 – osie główne
σ
σ
σ
σ
1
,
σ
σ
σ
σ
2
– naprężenia
główne
(brak naprężeń
stycznych)
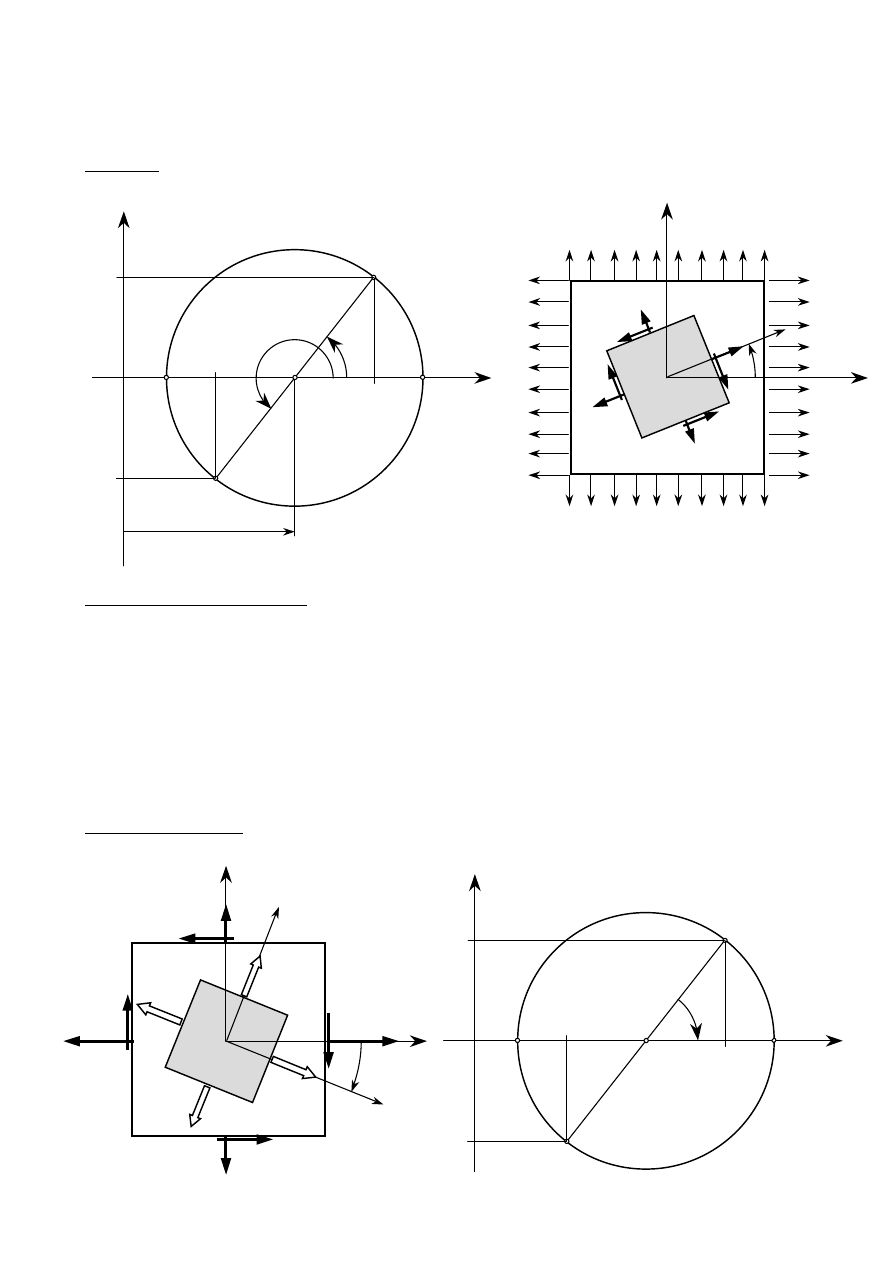
5. Analiza stanu naprężenia i odkształcenia
- 2/6 -
Koło Mohra dla naprężeń
Zadanie: Dane są naprężenia główne
σ
1
,
σ
2
. Znaleźć naprężenia na ściankach kostki
obróconej o kąt
α
.
Kolejność postępowania:
1. rysujemy układ współrzędnych
σ
,
τ
,
2. na osi poziomej zaznaczamy naprężenia
σ
1
i
σ
2
,
3. ze środka (
σ
1
+
σ
2
)/2 rysujemy okrąg przechodzący przez punkty
σ
1
i
σ
2
,
4. poziomą średnicę koła obracamy o kąt 2
α
,
5. odczytujemy naprężenia
− dla krawędzi nachylonej pod kątem
α
:
σ
α
,
τ
α
,
− dla krawędzi prostopadłej :
σ
α
+
π
/2
,
τ
α
+
π
/2
.
Zadanie odwrotne: Na ściankach kostki dane są naprężenia
σ
x
,
σ
y
,
τ
. Znaleźć
położenie osi głównych i naprężenia główne.
σ
σ
2
σ
α
τ
α
σ
1
τ
2
α
2
α
+
π
σ
α
+
π
/2
τ
α
+
π
/2
(
σ
1
+
σ
2
)/2
σ
2
σ
1
σ
1
σ
2
2
1
σ
α
τ
α
σ
α
+
π
/2
τ
α
+
π
/2
α
σ
σ
2
σ
x
τ
x
σ
1
τ
2
α
σ
y
-
τ
σ
y
σ
x
σ
x
σ
y
y
x
τ
τ
τ
τ
σ
1
2
1
σ
1
σ
2
σ
2
α
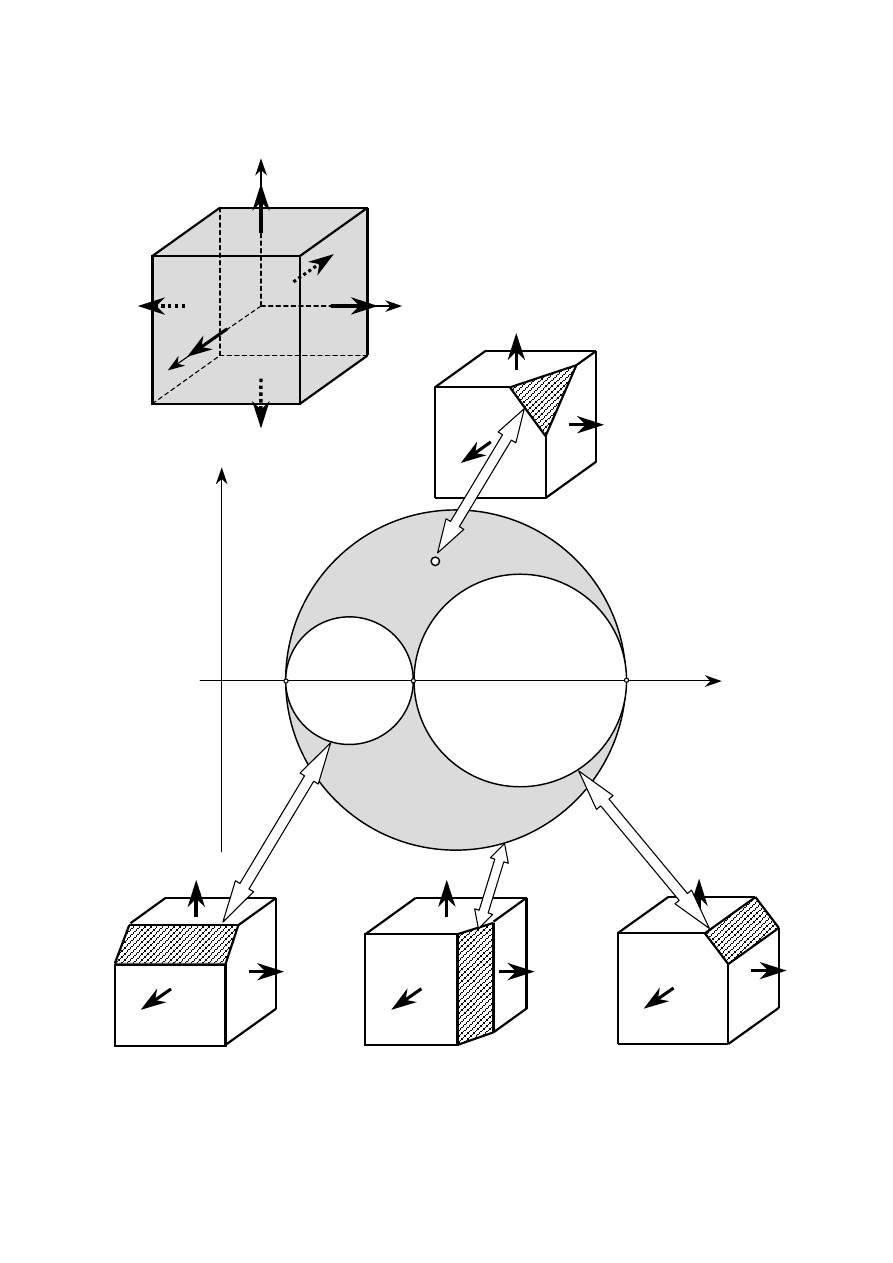
5. Analiza stanu naprężenia i odkształcenia
- 3/6 -
5.2. Uproszczona analiza trójosiowego stanu naprężenia
Trójosiowy stan naprężenia – na
wszystkich ścianach kostki działają
naprężenia
1
,2,3 – osie główne
σ
σ
σ
σ
1
,
σ
σ
σ
σ
2
,
σ
σ
σ
σ
3
– naprężenia główne
1. Poszczególne koła reprezentują stan naprężeń w płaszczyznach równoległych do
odpowiednich osi.
2. Punkt wewnątrz wyróżnionego obszaru reprezentuje stan naprężeń w dowolnie
ustawionym przekroju (z Teorii Sprężystości).
3. Maksymalne naprężenia styczne równe są promieniowi największego koła.
1
2
3
σ
σ
σ
σ
1
σ
σ
σ
σ
2
σ
σ
σ
σ
2
σ
σ
σ
σ
1
σ
σ
σ
σ
3
σ
3
τ
σ
σ
1
σ
2
σ
3
σ
σ
σ
σ
2
σ
σ
σ
σ
1
σ
σ
σ
σ
3
σ
σ
σ
σ
2
σ
σ
σ
σ
1
σ
σ
σ
σ
3
σ
σ
σ
σ
1
σ
σ
σ
σ
2
σ
3
σ
σ
σ
σ
1
σ
σ
σ
σ
3
σ
σ
σ
σ
2
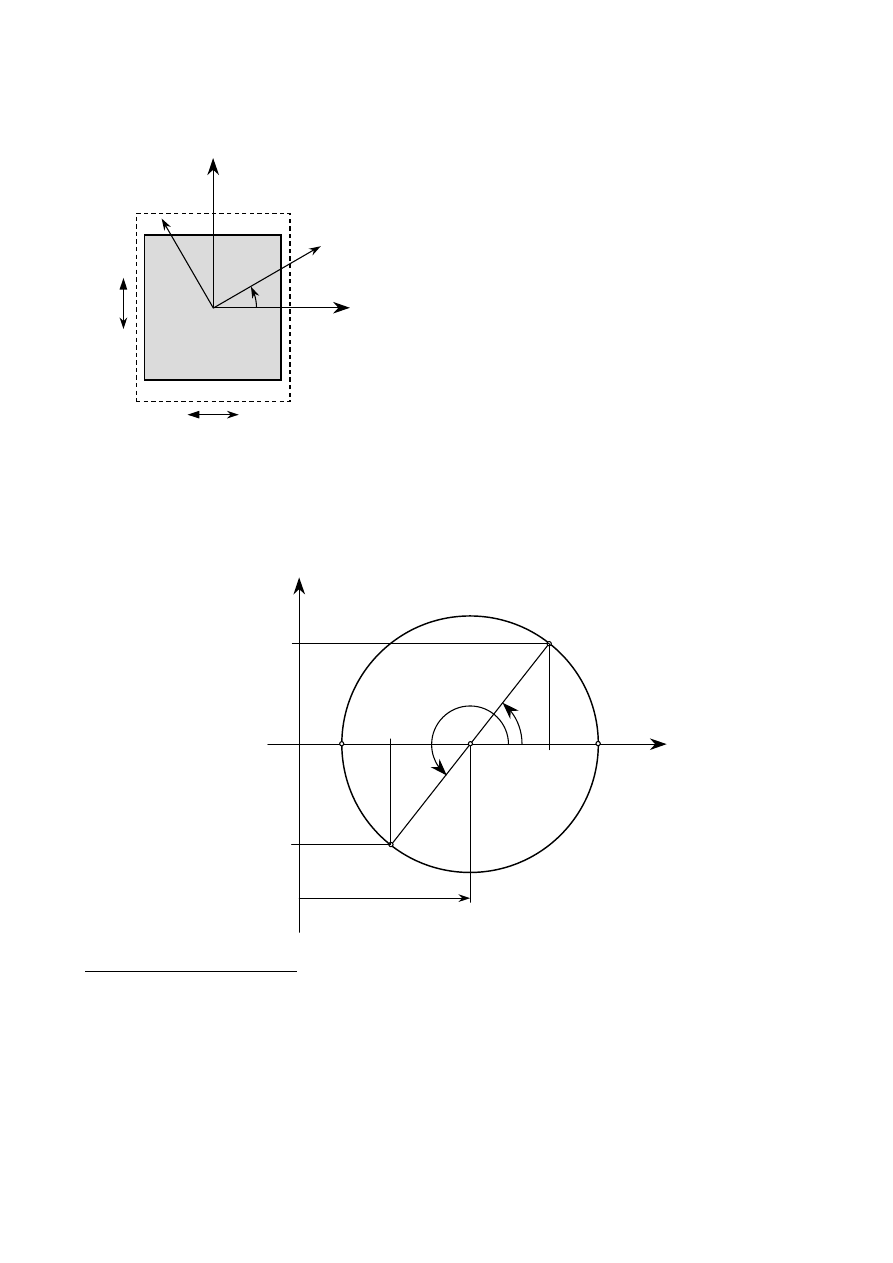
5. Analiza stanu naprężenia i odkształcenia
- 4/6 -
5.3. Uproszczona analiza stanu odkształcenia
Elementarna myślowo wycięta kostka, znajdująca
się w płaskim stanie odkształcenia, doznaje
wydłużeń względnych jak na rysunku:
− na kierunku 1:
ε
1
− na kierunku 2:
ε
2
Na kierunku nachylonym pod kątem
α
α
α
α
odkształcenia kostki wyniosą:
− wydłużenie względne
α
ε
α
ε
ε
α
2
2
2
1
sin
cos
+
=
− kąt odkształcenia postaciowego
(
)
α
α
ε
ε
γ
α
cos
sin
2
2
1
−
=
(patrz: Analiza stanu odkształcenia rozciąganego pręta)
Koło Mohra dla płaskiego stanu odkształcenia
Kolejność postępowania:
1. rysujemy układ współrzędnych
ε
,
γ
/2,
2. na osi poziomej zaznaczamy wydłużenia
ε
1
i
ε
2
,
3. ze środka (
ε
1
+
ε
2
)/2 rysujemy okrąg przechodzący przez punkty
ε
1
i
ε
2
,
4. poziomą średnicę koła obracamy o kąt 2
α
,
5. odczytujemy odkształcenia
− dla krawędzi nachylonej pod kątem
α
:
ε
α
,
γ
α
/2 ,
− dla krawędzi prostopadłej:
ε
α
+
π
/2
,
γ
α
+
π
/2
/2 .
ε
ε
2
ε
α
γ
α
/2
ε
1
γ
/2
2
α
2
α
+
π
ε
α
+
π
/2
γ
α
+
π
/2
/2
(
ε
1
+
ε
2
)/2
2
1
ε
1
ε
2
α
1
,2 – główne osie odkształcenia
εεεε
1
,
εεεε
2
– odkształcenia główne
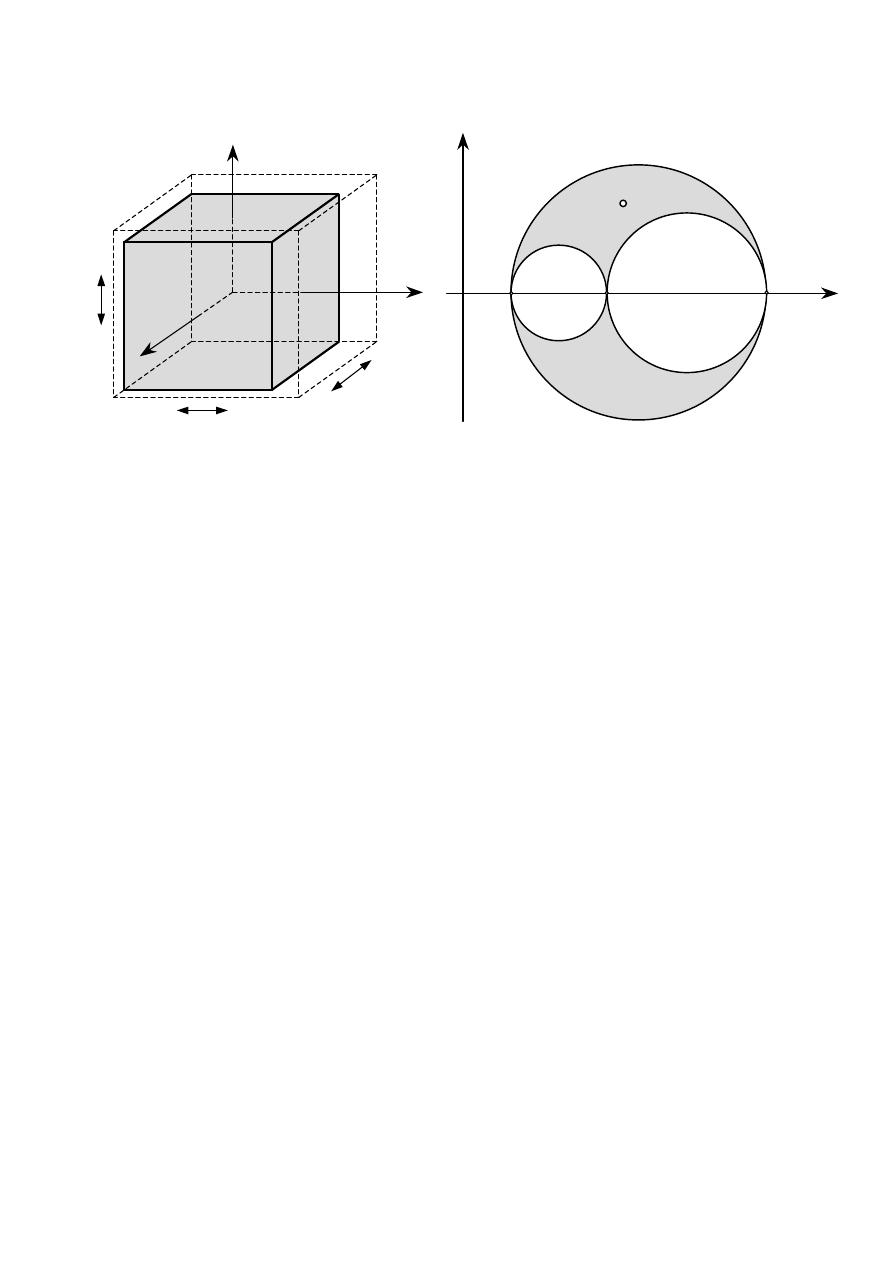
5. Analiza stanu naprężenia i odkształcenia
- 5/6 -
Trójwymiarowy stan odkształcenia
1
,2,3 – osie główne
εεεε
1
,
εεεε
2
,
εεεε
3
– odkształcenia główne
1. Poszczególne koła reprezentują stan odkształcenia w płaszczyznach
równoległych do odpowiednich osi.
2. Punkt wewnątrz wyróżnionego obszaru reprezentuje stan odkształcenia w
dowolnie ustawionym przekroju (z Teorii Sprężystości).
3. Maksymalny kąt odkształcenia postaciowego równy jest średnicy
największego koła.
4. W każdym stanie odkształcenia istnieją tylko 3 kierunki główne (1, 2, 3), między
którymi pierwotne kąty proste nie ulegają zmianie. Odpowiadające tym
kierunkom odkształcenia
εεεε
1
,
εεεε
2
,
εεεε
3
zwane są odkształceniami głównymi.
1
2
3
εεεε
2
εεεε
1
εεεε
3
γ
/2
ε
ε
1
ε
2
ε
3
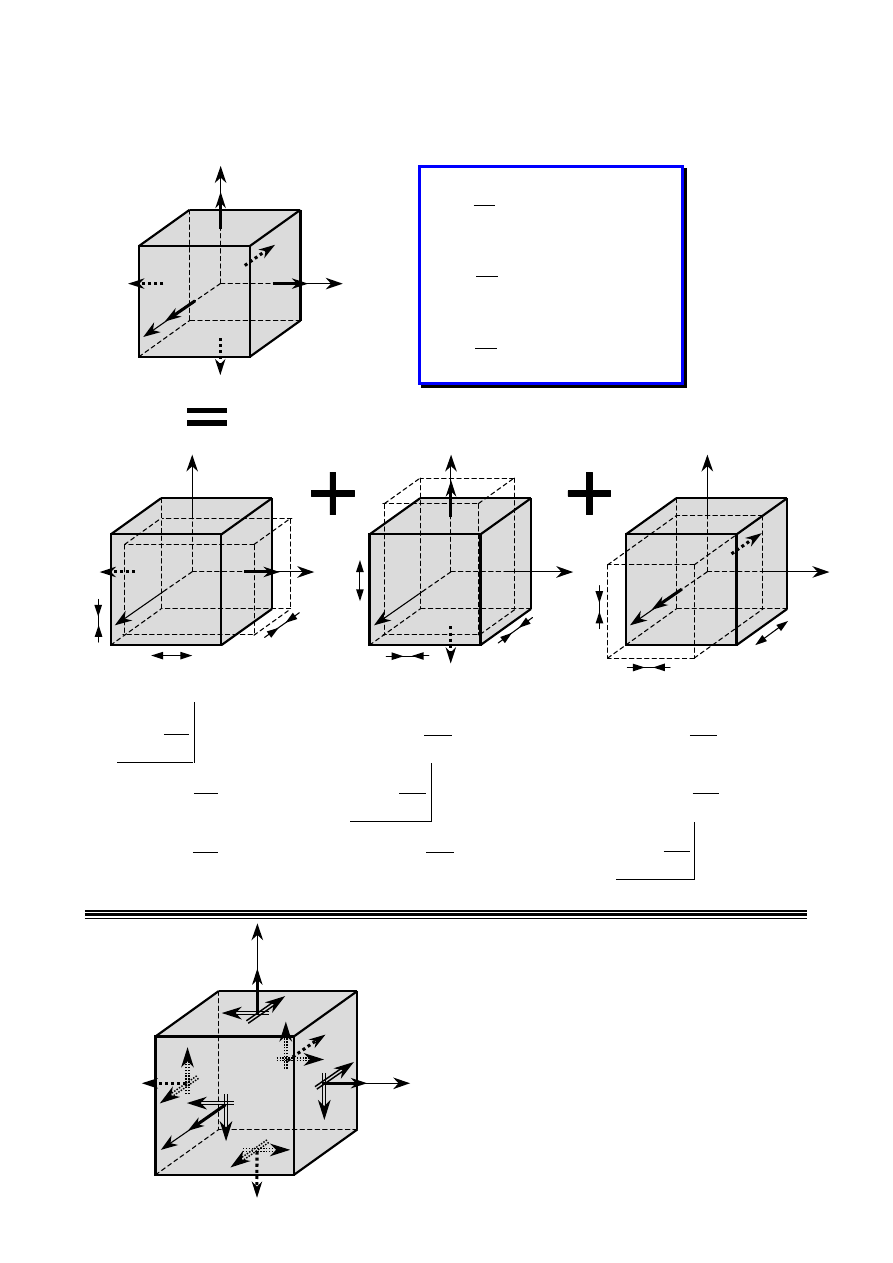
5. Analiza stanu naprężenia i odkształcenia
- 6/6 -
5.4. Uogólnione prawo Hooke’a
(
)
[
]
(
)
[
]
(
)
[
]
2
1
3
3
3
1
2
2
3
2
1
1
1
1
1
σ
σ
ν
σ
ε
σ
σ
ν
σ
ε
σ
σ
ν
σ
ε
+
−
=
+
−
=
+
−
=
E
E
E
E
1
1
σ
ε
=
E
2
1
σ
ν
ε
−
=
E
3
1
σ
ν
ε
−
=
E
1
2
σ
ν
ε
−
=
E
2
2
σ
ε
=
E
3
2
σ
ν
ε
−
=
E
1
3
σ
ν
ε
−
=
E
2
3
σ
ν
ε
−
=
E
3
3
σ
ε
=
Ogólny przypadek obciążenia elementarnej kostki
(gdy osie x,y,z nie są osiami głównymi)
Stan naprężenia opisany jest
jednoznacznie przez 6 składowych:
σ
σ
σ
σ
x
σ
σ
σ
σ
y
σ
σ
σ
σ
z
– naprężenia normalne
ττττ
x
ττττ
y
ττττ
z
– naprężenia styczne
1
2
3
σ
σ
σ
σ
1
σ
σ
σ
σ
2
σ
σ
σ
σ
2
σ
σ
σ
σ
1
σ
σ
σ
σ
3
σ
3
1
2
3
σ
σ
σ
σ
1
σ
σ
σ
σ
1
εεεε
1
εεεε
3
εεεε
2
1
2
3
σ
σ
σ
σ
2
σ
σ
σ
σ
2
εεεε
1
εεεε
3
εεεε
2
1
2
3
σ
σ
σ
σ
3
σ
3
εεεε
1
εεεε
3
εεεε
2
x
y
z
σ
σ
σ
σ
x
σ
σ
σ
σ
y
σ
σ
σ
σ
y
σ
σ
σ
σ
x
σ
σ
σ
σ
z
σ
z
ττττ
z
τ
z
τ
z
ττττ
z
ττττ
x
τ
x
τ
x
ττττ
x
ττττ
y
ττττ
y
τ
y
τ
y

6. Hipotezy wytrzymałościowe i wytrzymałość złożona pręta
- 1/5 -
6. HIPOTEZY WYTRZYMAŁOŚCIOWE
I WYTRZYMAŁOŚĆ ZŁOŻONA PRĘTA
6.1. Hipotezy wytrzymałościowe
Hipotezy wytrzymałościowe – przybliżone ujęcie ilościowe złożonych zjawisk
towarzyszących pojawieniu się w materiale ma-
kroskopowych odkształceń trwałych.
Hipoteza
energii odkształcenia postaciowego
(Hubera)
miarą niebezpieczeństwa, jakie przedstawia dany stan naprężenia
z uwagi na pojawienie się pierwszych makroskopowych trwałych
odkształceń jest
efektywne naprężenie styczne
τ
ττ
τ
ef
jeśli znane są naprężenia główne
(
)
(
)
(
)
[
]
2
1
3
2
3
2
2
2
1
15
1
σ
σ
σ
σ
σ
σ
τ
−
+
−
+
−
=
ef
w przypadku ogólnego stanu naprężeń
(
) (
)
(
)
(
)
[
]
2
2
2
2
2
2
6
15
1
z
y
x
x
z
z
y
y
x
ef
τ
τ
τ
σ
σ
σ
σ
σ
σ
τ
+
+
+
−
+
−
+
−
=
Hipoteza
maksymalnych naprężeń stycznych
(τ
max
, Coulomba-Treski)
miarą niebezpieczeństwa, jakie przedstawia dany stan naprężenia
z uwagi na pojawienie się pierwszych makroskopowych trwałych
odkształceń jest
maksymalne naprężenie styczne
τ
ττ
τ
max
(podejście uproszczone)
Ten stan naprężenia jest dla materiału bardziej niebezpieczny, dla którego
efektywne naprężenie styczne τ
ef
(wg hipotezy Hubera)
lub
maksymalne naprężenie styczne τ
max
(wg hipotezy τ
max
)
jest większe.
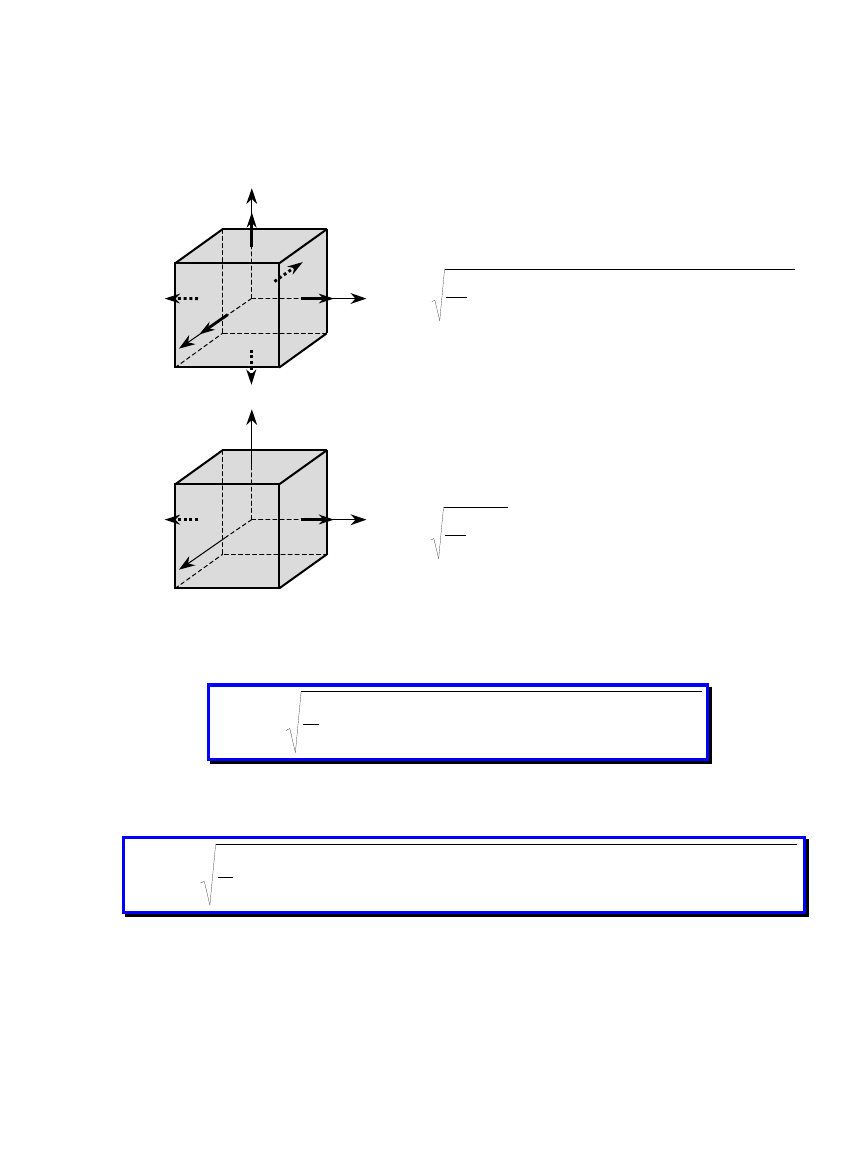
6. Hipotezy wytrzymałościowe i wytrzymałość złożona pręta
- 2/5 -
6.2. Naprężenia zredukowane
złożony stan naprężeń
(
)
(
)
(
)
[
]
2
1
3
2
3
2
2
2
1
15
1
σ
σ
σ
σ
σ
σ
τ
−
+
−
+
−
=
ef
(hip. Hubera)
JEDNAKOWO NIEBEZPIECZNY
stan prostego rozciągania
(statyczna próba rozciągania)
2
15
2
red
ef
σ
τ
=
(hip. Hubera)
Z założenia efektywne naprężenia styczne obu stanów są jednakowe, skąd
naprężenia zredukowane
(
)
(
)
(
)
[
]
2
1
3
2
3
2
2
2
1
2
1
σ
σ
σ
σ
σ
σ
σ
−
+
−
+
−
=
red
w przypadku najbardziej ogólnym
(
) (
)
(
)
(
)
[
]
2
2
2
2
2
2
6
2
1
z
y
x
x
z
z
y
y
x
red
τ
τ
τ
σ
σ
σ
σ
σ
σ
σ
+
+
+
−
+
−
+
−
=
Naprężenia zredukowane – naprężenia w stanie prostego rozciągania tak samo
niebezpieczne dla materiału, jak dany złożony stan
naprężeń
Umożliwiają porównanie złożonego stanu naprężeń z wynikami statycznej próby
rozciągania.
1
2
3
σ
σ
σ
σ
1
σ
σ
σ
σ
2
σ
σ
σ
σ
2
σ
σ
σ
σ
1
σ
σ
σ
σ
3
σ
3
1
2
3
σ
σ
σ
σ
red
σ
σ
σ
σ
red
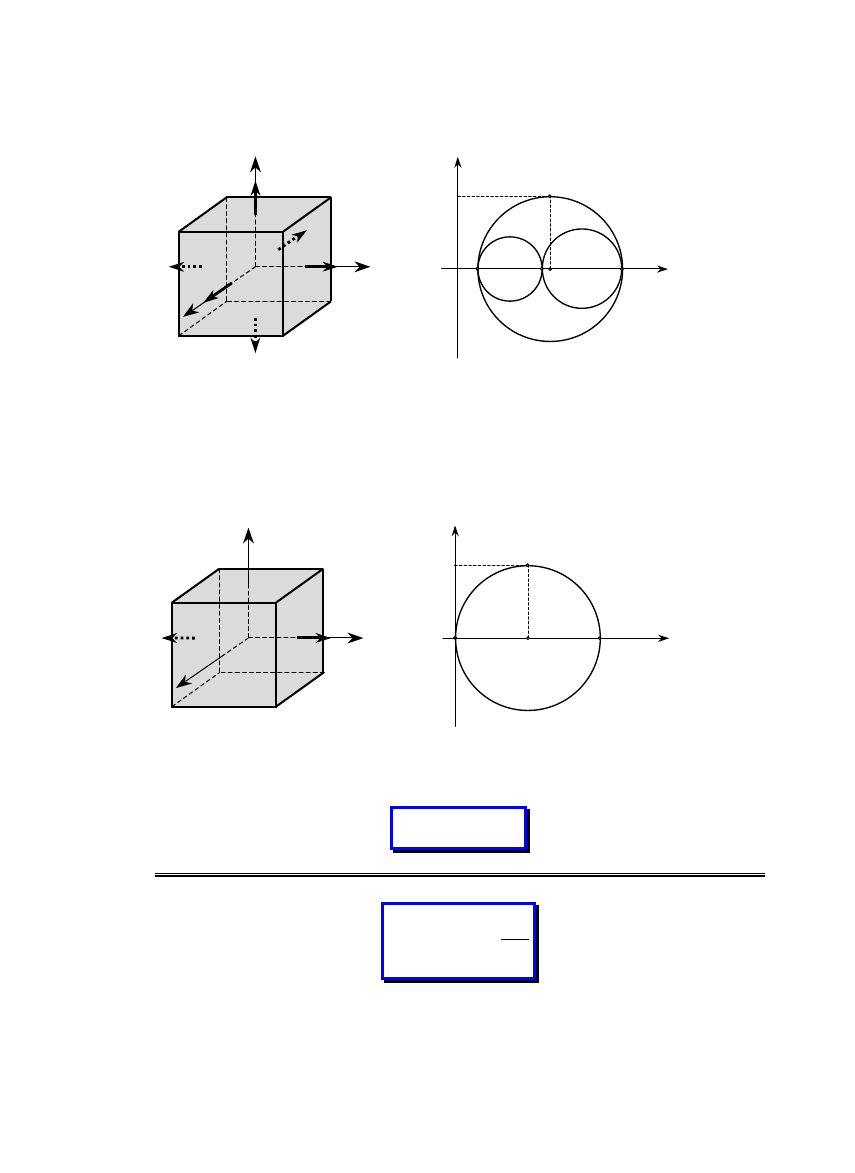
6. Hipotezy wytrzymałościowe i wytrzymałość złożona pręta
- 3/5 -
Naprężenia zredukowane według hipotezy
τ
ττ
τ
max
τ
ττ
τ
max
= promień największego koła Mohra
JEDNAKOWO NIEBEZPIECZNY
stan prostego rozciągania
(statyczna próba rozciągania)
2
/
max
red
σ
τ
=
Ponieważ z założenia oba stany są dla materiału jednakowo niebezpieczne, to
max
2
τ
σ
=
red
e
e
r
red
n
R
k =
≤
σ
k
r
– naprężenia dopuszczalne na rozciąganie
R
e
– granica plastyczności materiału
n
e
>1
– współczynnik bezpieczeństwa
1
2
3
σ
σ
σ
σ
1
σ
σ
σ
σ
2
σ
σ
σ
σ
2
σ
σ
σ
σ
1
σ
σ
σ
σ
3
σ
3
τ
max
τ
σ
1
2
3
σ
σ
σ
σ
red
σ
σ
σ
σ
red
τ
max
τ
σ
σ
red
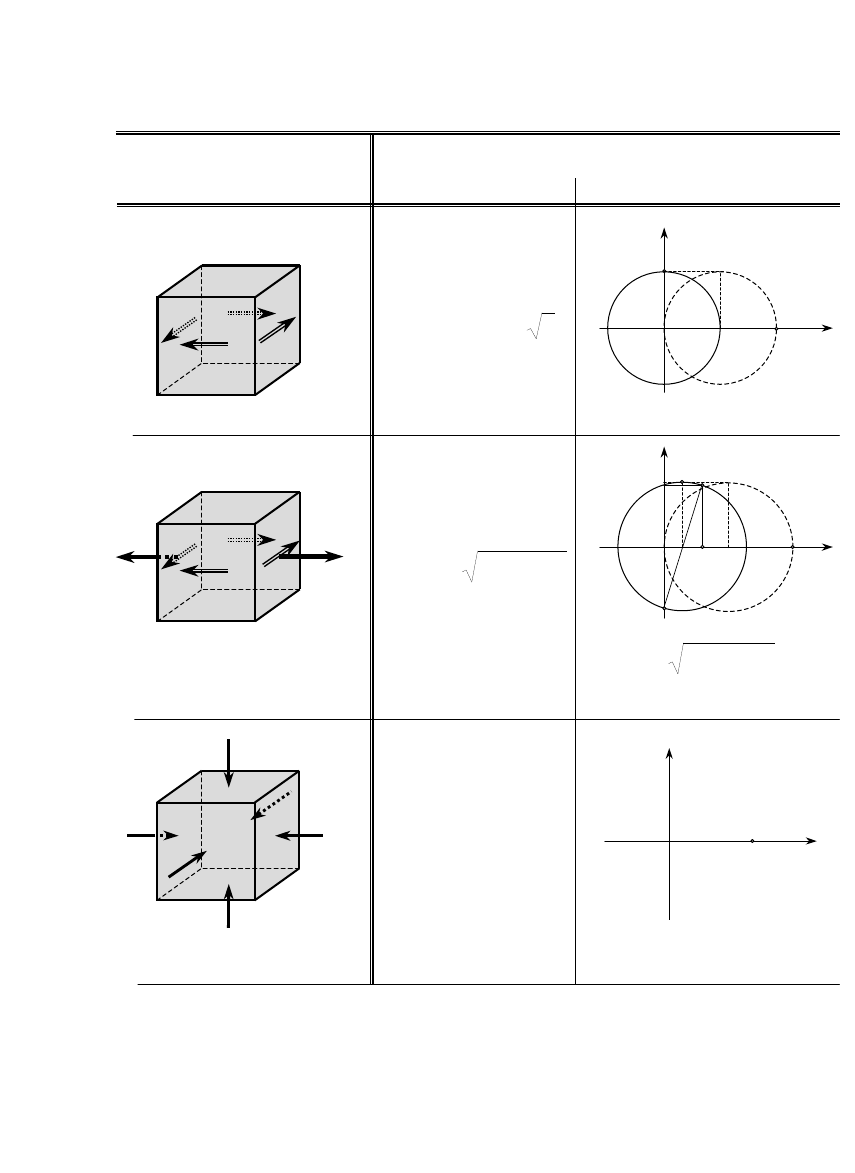
6. Hipotezy wytrzymałościowe i wytrzymałość złożona pręta
- 4/5 -
Porównanie wyników hipotez wyrtzymałościowych Hubera i ττττ
max
Przypadki szczególne
Naprężenia zredukowane
złożonych stanów naprężenia wg hipotezy Hubera wg hipotezy τ
max
3
τ
σ
=
red
czyste ścinanie
τ
σ
2
=
red
2
2
3
τ
σ
σ
+
=
red
ś
cinanie z rozciąganiem
2
2
4
τ
σ
σ
+
=
red
(ściskaniem)
0
=
red
σ
hydrostatyczne ściskanie
0
=
red
σ
τ
τ
τ
τ
τ
σ
τ
max
=
τ
σ
red
τ
τ
τ
τ
σ
σ
τ
σ
τ
max
σ
red
τ
−τ
σ
σ
σ
σ
σ
σ
σ
σ
σ
σ
σ
σ
σ
τ
σ
σ
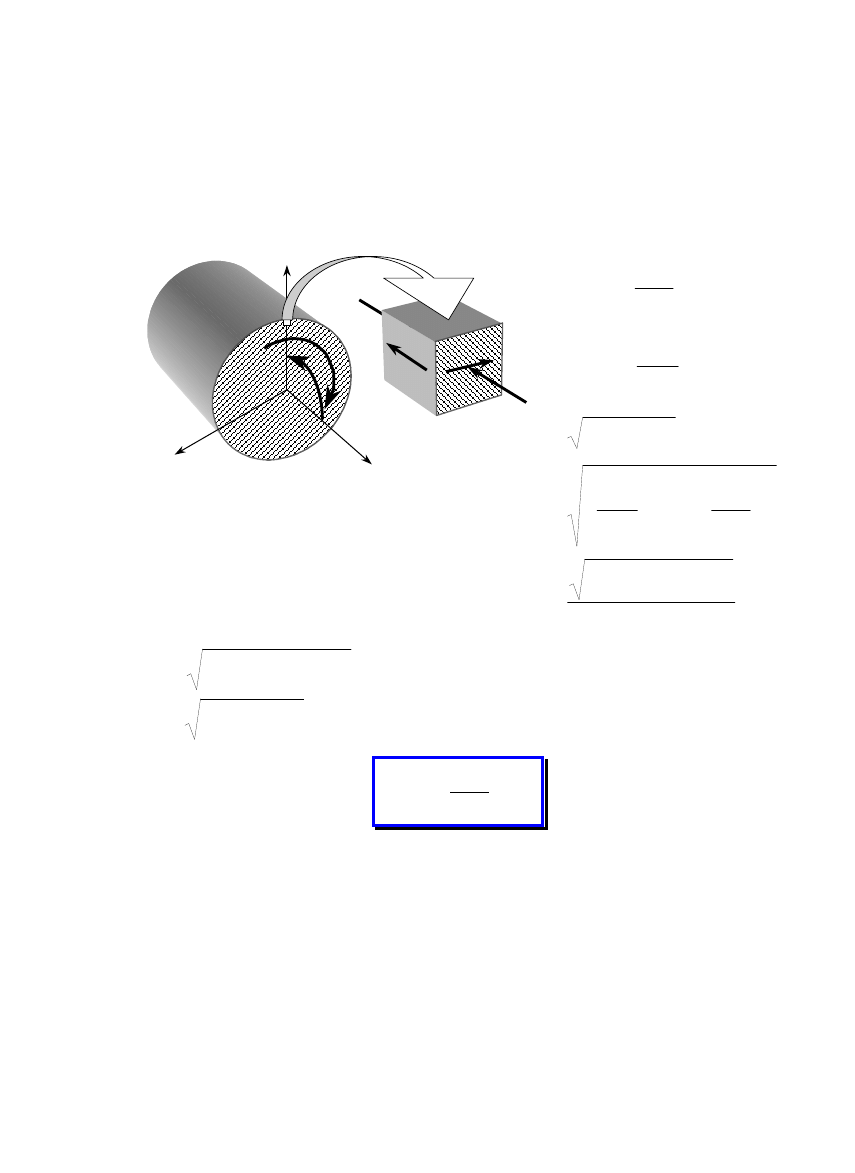
6. Hipotezy wytrzymałościowe i wytrzymałość złożona pręta
- 5/5 -
6.3. Wytrzymałość złożona pręta
O wytrzymałości złożonej mówimy wówczas, gdy w myślowym przekroju pręta
istnieje więcej niż jeden element wysiłku przekroju.
Zginanie ze skręcaniem
(wały z kołami zębatymi)
W
z
=W
y
=W
- wskaźnik wytrzymałości na zginanie
W
0
– wskaźnik wytrzymałości na skręcanie
W
0
=
2W
–
moment zastępczy (na podst. hipotezy Hubera)
–
moment zastępczy (na podst. hipotezy
τ
max
)
g
z
red
k
W
M
≤
=
σ
k
g
– naprężenia dopuszczalne na zginanie
x
z
y
M
s
M
g
σ
σ
σ
σ
τ
ττ
τ
W
M
M
W
M
W
M
s
g
s
g
red
2
2
2
2
2
2
75
.
0
2
3
3
+
=
=
+
=
=
+
=
τ
σ
σ
W
M
g
=
σ
0
W
M
s
=
τ
2
2
75
.
0
s
g
z
M
M
M
+
=
2
2
s
g
z
M
M
M
+
=
7. Wyboczenie pręta
- 1/6 -
7. WYBOCZENIE PRĘTA
7.1. Mimośrodowe ściskanie pręta
Pręt ściskany momośrodowo (e
y
- mimośród)
Odkształcona oś pręta Równowaga myślowo
odciętej części
(
)
y
y
e
P
M
B
y
z
−
+
=
(
)
z
B
y
z
z
EJ
y
y
e
P
EJ
M
dx
y
d
−
+
=
=
=
2
2
1
ρ
Podstawiając
z
z
EJ
P
k
=
otrzymujemy równanie
(
)
B
z
z
z
y
e
k
y
k
dx
y
d
+
=
+
2
2
2
2
.
Rozwiązanie tego równania różniczkowego ma postać
B
y
z
z
y
e
x
k
C
x
k
C
y
+
+
+
=
cos
sin
2
1
.
Stałe C
1
i C
2
wyznaczany z warunków brzegowych:
dla
0
/
0
0
=
=
=
dx
dy
y
x
dla
B
y
y
l
x
=
=
otrzymując:
(
)
B
y
y
e
C
C
+
−
=
=
2
1
0
Ostatecznie równanie linii ugięcia przyjmuje postać
−
=
x
EJ
P
l
EJ
P
e
y
z
z
y
cos
1
cos
. Przy
∞
→
→
y
l
EJ
P
z
2
π
.
x
y
A
B
P
l
EJ
z
=const
e
y
y
C
x
y
A
B
P
x
e
y
y
B
M
z
C
B
P
T
N
7. Wyboczenie pr
ę
ta
- 2/6 -
Siłę
P=P
kr
, przy której
2
π
=
l
EJ
P
z
nazywamy
siłą eulerowską
lub siłą
krytyczną.
Siła krytyczna
( )
2
2
2l
EJ
P
z
kr
π
=
Siła krytyczna - siła, przy której ściskany (bez mimośrodu) pręt może mieć
dwie postacie równowagi:
− pierwotną − o osi prostoliniowej,
−
nową
− o osi wygiętej.
Pręt obciążony siłą krytyczną znajduje się w stanie równowagi obojętnej.
Zjawisko wyginania się pręta pod wpływem siły ściskającej nosi nazwę
utraty stateczności lub wyboczenia pręta.
Ponieważ przy obciążeniu siłą krytyczną ugięcie
y
pręta wzrasta
nieograniczenie to siła krytyczna jest siłą niszczącą pręt.
7.2. Wyboczenie pręta w zakresie sprężystym
równowaga
trwała obojętna chwiejna
P<P
kr
P=P
kr
P>P
kr
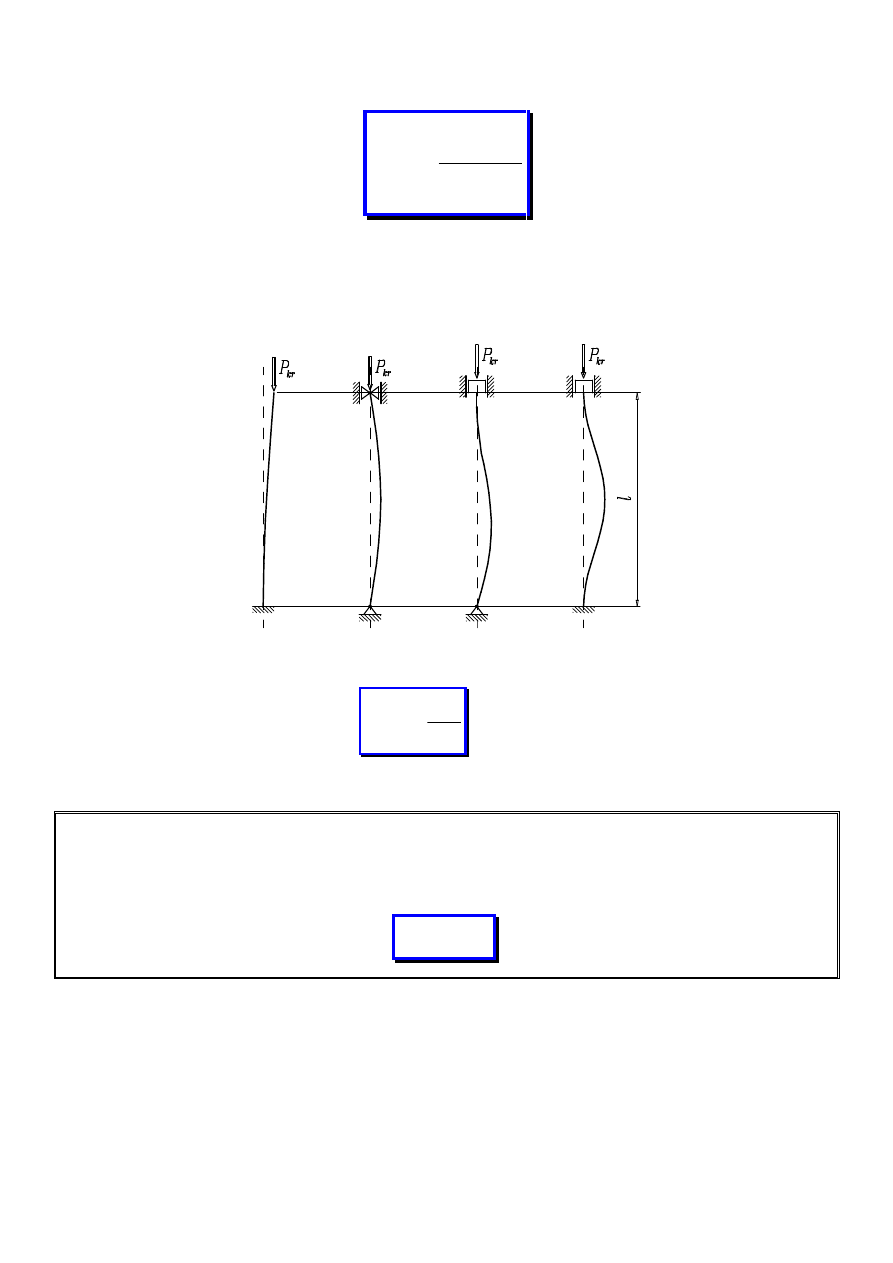
7. Wyboczenie pr
ę
ta
- 3/6 -
nl
l
w
=
2
w
z
2
kr
l
EJ
P
π
=
wzór Eulera na siłę krytyczną
l
w
- długość wyboczeniowa
n
- współczynnik zależny od sposobu mocowania końców pręta
n=2 n=1 n
≈
0.7 n=0.5
Naprężenia krytyczne:
A
P
kr
kr
=
σ
A
− pole powierzchni przekroju poprzecznego pręta.
Wzór Eulera wolno stosować, jeśli naprężenia krytyczne nie przekraczają granicy
proporcjonalności
R
p
(granicy stosowalności prawa Hooke'a)
p
kr
R
≤
σ
.
Jeśli
σ
σ
σ
σ
kr
≤
≤
≤
≤
R
p
to wyboczenie nazywamy sprężystym (po odciążeniu pręt powraca do
swojej prostoliniowej postaci).
Jeśli
σ
σ
σ
σ
kr
>R
p
to wyboczenie nazywamy sprężysto-plastycznym lub plastycznym (po
odciążeniu pręt nie powróci do swojej prostoliniowej postaci).
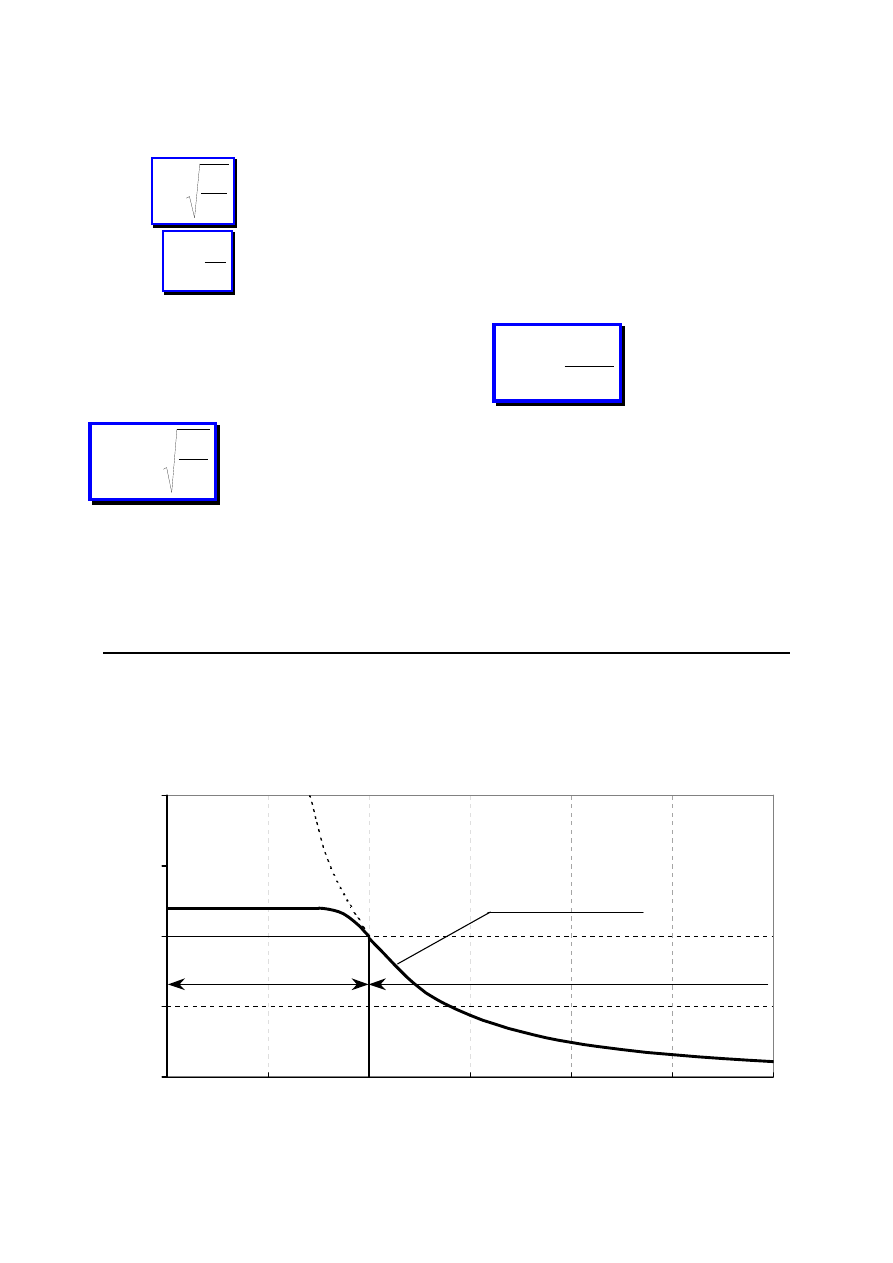
7. Wyboczenie pr
ę
ta
- 4/6 -
Wprowadzając oznaczenia:
A
J
i
z
=
i
l
w
=
λ
2
2
kr
E
λ
π
σ
=
p
gr
R
E
π
λ
=
Smukłość graniczna – parametr zależny wyłącznie od materiału pręta
(dla stali
λ
gr
≈100)
Inna postać kryterium stosowalności wzoru Eulera na siłę krytyczną:
λ
λ
λ
λ
≥
≥
≥
≥
λ
λ
λ
λ
gr
(
σ
kr
≤R
p
–
wyboczenie sprężyste
) – wzór wolno stosować
λ
λ
λ
λ
<
λ
λ
λ
λ
gr
(
σ
kr
>R
p
–
wyboczenie sprężysto-plastyczne
) – wzoru nie wolno stosować
0
100
200
300
400
0
50
100
150
200
250
300
λ
σσσσ
k
r
[M
P
a]
R
p
λ
λ
λ
λ
gr
zakres stosowalności wzoru Eulera
(wyboczenie sprężyste)
materiał: stal konstrukcyjna
(0.15%C E=2
.
10
5
MPa)
hiperbola Eulera
wyboczenie
sprężysto-plastyczne
Przykładowa zależność naprężeń krytycznych
σ
σ
σ
σ
kr
od smukłości pręta
λ
λ
λ
λ
Smukłość pręta, przy której naprężenia krytyczne osiągają wartość
granicy proporcjonalności nazywamy smukłością graniczną
smukłość pręta – parametr zależny od geometrii pręta
i sposobu zamocowania końców,
ramię bezwładności przekroju poprzecznego
otrzymujemy wzór na naprężenia krytyczne
w postaci hiperboli Eulera
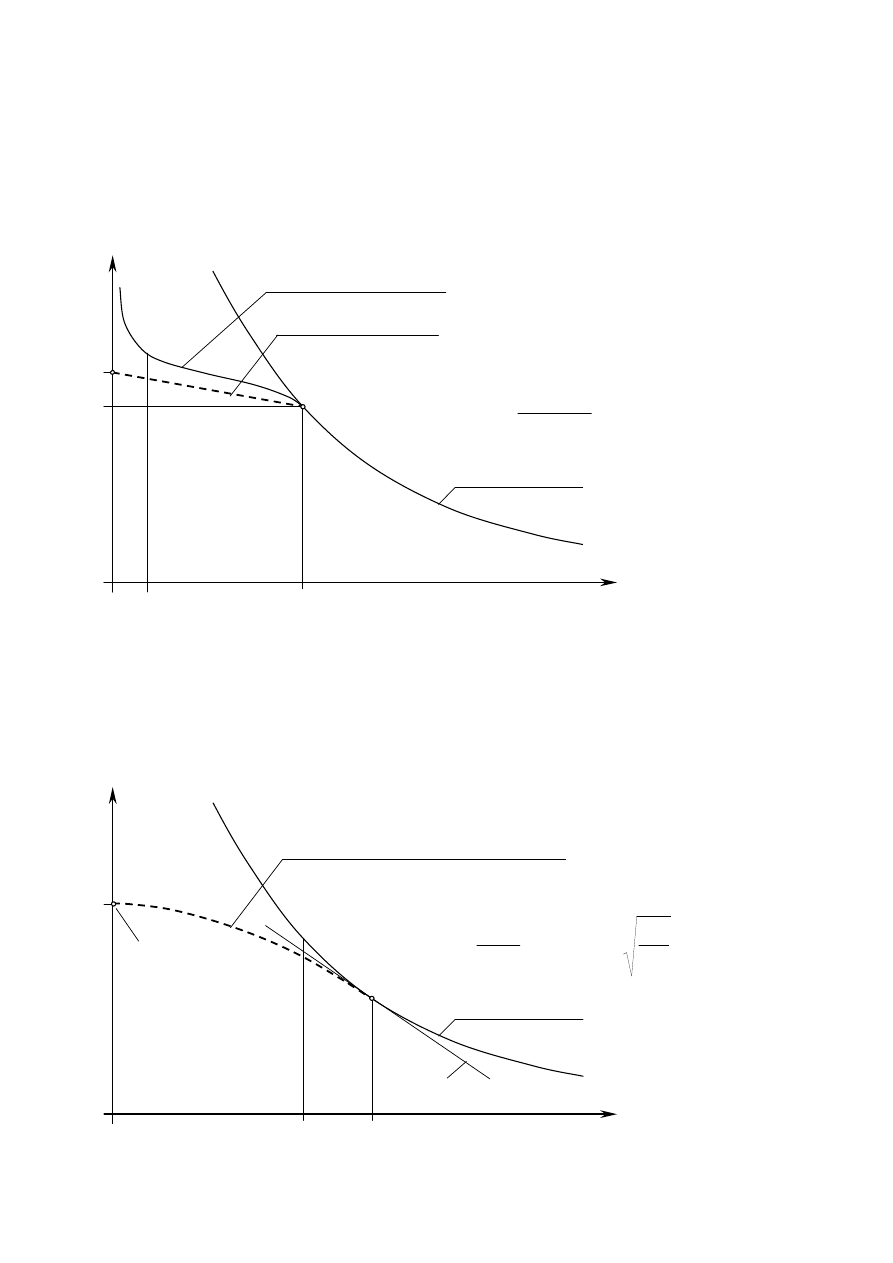
7. Wyboczenie pr
ę
ta
- 5/6 -
Dla stali konstrukcyjnej
naprężenia krytyczne w zakresie
smukłości (
∼20,
λ
gr
)
przybliżyć
można
prostą Tetmajera
durale,
mosiądze,
brązy
7.3. Wyboczenie pręta w zakresie sprężysto-plastycznym
(
σ
σ
σ
σ
kr
>R
p
λ
λ
λ
λ<λ
λ
λ
λ
gr
)
Wzory, tabele, wykresy do obliczeń konstrukcji stalowych na wyboczenie
PN-90/B-03200
σ
λ
λ
gr
R
e
R
p
prosta Tetmajera
λ
σ
b
a
kr
−
=
gr
p
e
R
R
b
λ
−
−
=
e
R
a
=
krzywa do
ś
wiadczalna
hiperbola Eulera
∼20
A
B
σ
λ
λ
gr
R
e
parabola Johnsona-Ostenfelda
2
λ
σ
b
a
kr
−
=
4
0
2
λ
π
E
b
=
e
R
a
=
hiperbola Eulera
λ
0
e
R
E
2
0
π
λ
=
wierzchołek
wspólna
styczna
A
B
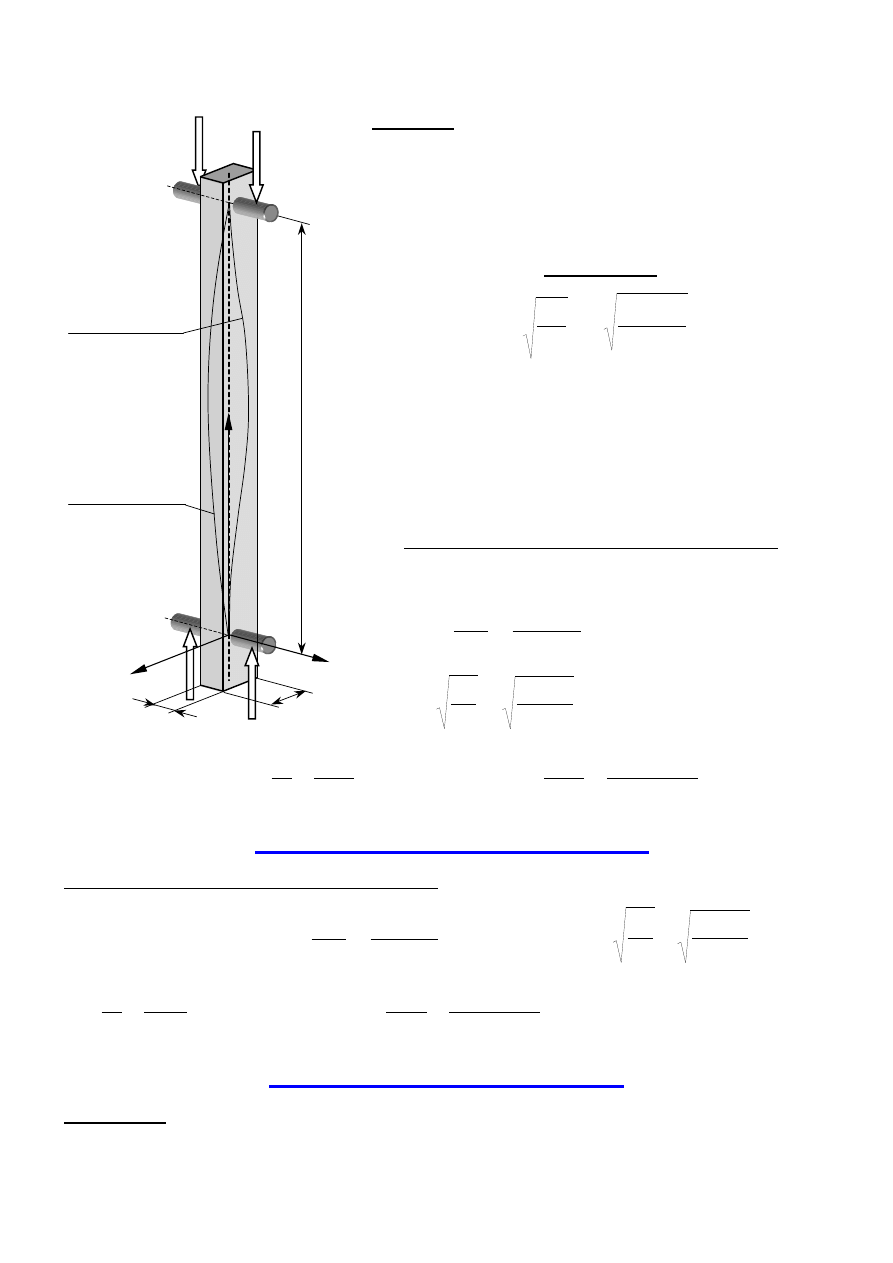
7. Wyboczenie pr
ę
ta
- 6/6 -
Przykład
Wyznaczyć siłę krytyczną dla pokazanego pręta.
Materiał St3: E=2.1
⋅10
5
MPa, R
p
=R
e
=400MPa.
l
=1m a=20mm b=30mm
Rozwiązanie
72
400
10
1
.
2
5
=
⋅
=
=
π
π
λ
p
gr
R
E
600
30
20
=
⋅
=
= ab
A
mm
2
Istnieją 2 możliwe postacie wyboczenia pręta:
1.
− w płaszczyźnie y-z
2.
− w płaszczyźnie x-z
Wariant 1 (wyboczenie w płaszczyźnie y-z)
n
=0.5 l
w
=0.5l=500mm
4
3
3
20000
12
20
30
12
mm
ba
J
x
=
⋅
=
=
77
.
5
600
20000
=
=
=
A
J
i
x
gr
w
i
l
λ
λ
>
=
=
=
7
.
86
77
.
5
500
MPa
E
kr
276
7
.
86
10
1
.
2
2
5
2
2
2
=
⋅
=
=
π
λ
π
σ
kN
N
A
P
kr
kr
6
.
165
165600
276
600
=
=
⋅
=
=
σ
Wariant 2 (wyboczenie w płaszczyźnie x-z)
n
=1 l
w
=l=1000mm
4
3
3
45000
12
30
20
12
mm
ab
J
y
=
⋅
=
=
66
.
8
600
45000
=
=
=
A
J
i
y
gr
w
i
l
λ
λ
>
=
=
=
5
.
115
66
.
8
1000
MPa
E
kr
155
5
.
115
10
1
.
2
2
5
2
2
2
=
⋅
=
=
π
λ
π
σ
kN
N
A
P
kr
kr
93
93000
155
600
=
=
⋅
=
=
σ
Odpowiedź
Wyboczenie nastąpi w płaszczyźnie x-z a siła krytyczna wynosi 93kN
x
z
y
l
b
a
P/2
P/2
P/2
P/2
1-sza postać
wyboczenia
(y-z)
2-ga postać
wyboczenia
(x-z)
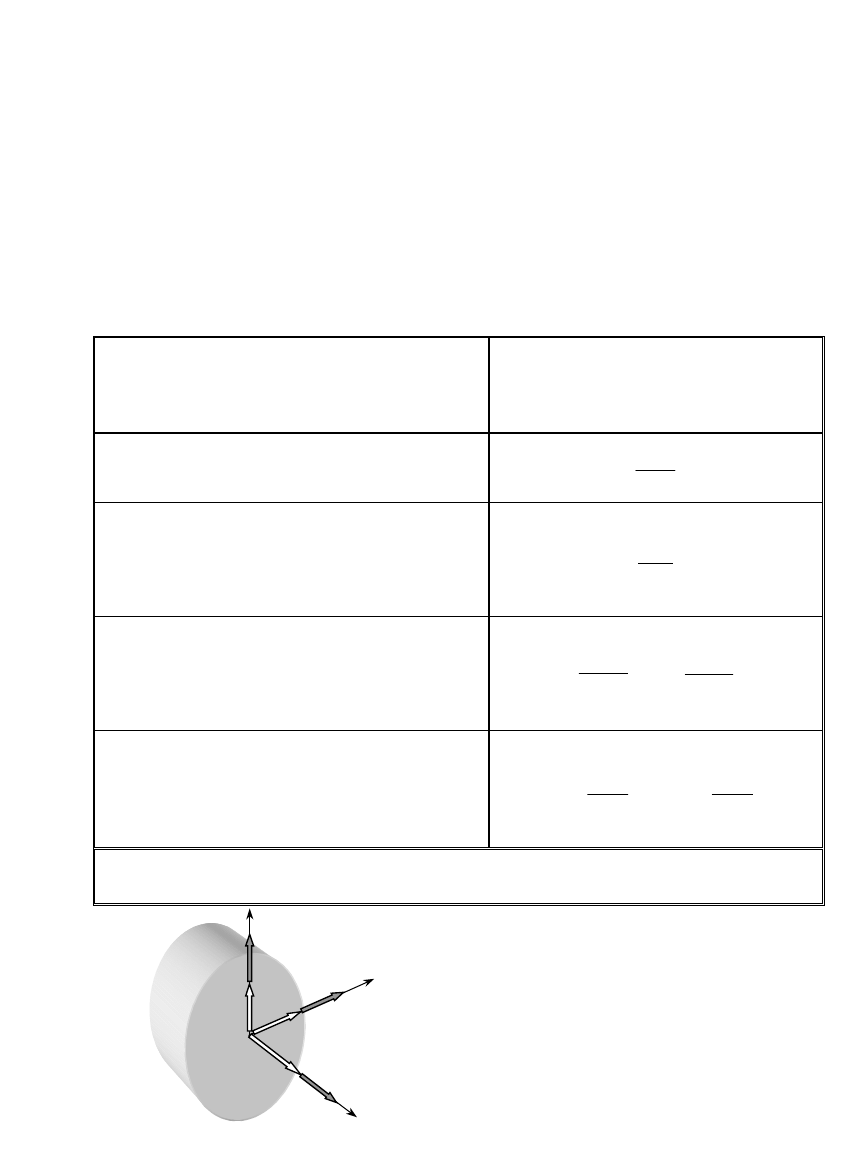
8. Metody energetyczne
- 1/23 -
8. METODY ENERGETYCZNE
Metody energetyczne – metody analizy odkształceń konstrukcji prętowych na podstawie
energii potencjalnej zgromadzonej w obciążonej konstrukcji
8.1. Energia sprężysta w konstrukcji prętowej
Energia potencjalna (sprężysta, odkształcenia) równa jest pracy sił zewnętrznych
obciążających konstrukcję.
Sposób obciążenia przekroju pręta
Energia sprężysta w pręcie
na jednostkę jego długości
[J/m]
rozciąganie
N
[N] – siła normalna w przekroju
A
[m
2
] – pole powierzchni przekroju
EA
N
2
2
skręcanie
M
s
[Nm] – moment skręcający
C
[Nm
2
] – sztywność na skręcanie
C
=GJ
0
– dla przekroju kołowego
C
=GJ
s
– dla przekroju niekołowego
C
M
s
2
2
zginanie
M
gy
, M
gz
[Nm] – momenty gnące w kierunku osi
y
i z
J
y
, J
z
[m
4
] – momenty bezwładności przekroju
względem osi y i z
y
gy
EJ
M
2
2
z
gz
EJ
M
2
2
ścinanie
T
y
, T
z
[N] – siły tnące w kierunku osi y i z
ψ
y
,
ψ
z
– bezwymiarowe współczynniki zależne
od kształtu przekroju
(dla przekroju kołowego
ψ
y
=
ψ
z
=32/27)
GA
T
y
y
2
2
ψ
GA
T
z
z
2
2
ψ
E
[Pa] – moduł Younga, G [Pa] – moduł sztywności postaciowej
y,z
– główne centralne osie bezwładności przekroju
W przypadku ogólnym elementy wysiłku
przekroju N, M
s
, M
gy
, M
gz
, T
y
, T
z
zależą od
położenia przekroju, a zatem są funkcjami
współrzędnej x:
N(x)
, M
s
(x)
, M
gy
(x)
, M
gz
(x)
, T
y
(x)
, T
z
(x).
x
y
z
N(x)
M
s
(x)
M
gy
(x)
T
y
(x)
T
z
(x)
M
gz
(x)
8. Metody energetyczne
- 2/23 -
do pominięcia
w przypadku konstrukcji zbudowanej
z prętów smukłych
na ogół do pominięcia
w konstrukcjach
zginanych i skręcanych
Energia zgromadzona w konstrukcji prętowej
dx
EA
T
dx
EA
T
dx
EJ
M
dx
EJ
M
dx
C
M
dx
EA
N
U
l
z
z
l
y
y
l
z
gz
l
y
gy
l
s
l
∫
∫
∫
∫
∫
∫
+
+
+
+
+
=
0
2
0
2
0
2
0
2
0
2
0
2
2
2
2
2
2
2
ψ
ψ
x
–
współrzędna określająca położenie przekroju,
l
– długość całej konstrukcji prętowej
dx
EJ
M
dx
EJ
M
dx
C
M
dx
EA
N
U
l
z
gz
l
y
gy
l
s
l
∫
∫
∫
∫
+
+
+
=
0
2
0
2
0
2
0
2
2
2
2
2
8.2. Siły uogólnione, współrzędne uogólnione, układ Clapeyrona
(Benoit Paul Emil Clapeyron 1799-1864)
siła uogólniona
dowolne obciążenie działające na ciało
współrzędna uogólniona
przemieszczenie odpowiadające sile
uogólnionej
siła skupiona P
przemieszczenie f
punktu przyłożenia siły
na kierunku linii działania siły
moment skręcający M
s
kąt skręcenia wywołany działaniem
momentu skręcającego M
s
moment gnący M
g
kąt ugięcia wywołany działaniem
momentu gnącego M
g
obciążenie ciągłe q
pole zakreskowane na rysunku
P
f
A
A
1
8. Metody energetyczne
- 3/23 -
A
B
P
1
f
C1
f
D1
C
D
Układ Clapeyrona to układ mechaniczny, w którym:
1. materiał jest idealnie sprężysty,
2. w żadnym punkcie naprężenia nie przekraczają granicy proporcjonalności,
3. można stosować zasadę superpozycji (działanie jednych sił uogólnionych nie
zmienia charakteru działania innych sił)
Jeśli siły uogólnione działające na układ przykładane są jednocześnie, wzrastają
równomiernie i osiągają swoje końcowe wartości w tej samej chwili
to
energia sprężysta układu równa jest pracy sił uogólnionych
∑
=
=
+
+
+
+
+
=
n
i
i
i
n
n
i
i
f
P
f
P
f
P
f
P
f
P
U
1
2
2
1
1
2
1
2
1
...
2
1
...
2
1
2
1
8.3. Zasada wzajemności prac i zasada wzajemności przemieszczeń
układ Clapeyrona (belka)
Stan 1
W punkcie C belka
obciążona zostaje siłą P
1
,
która wywołuje ugięcie f
C1
w punkcie C oraz f
D1
w
punkcie D.
energia sprężysta
Stan 2
W punkcie D belka zostaje
dodatkowo obciążona siłą
P
2
, która wywołuje
dodatkowe ugięcia belki f
C2
,
f
D2
.
końcowa energia sprężysta
2
1
2
2
1
1
2
2
1
2
1
C
D
C
f
P
f
P
f
P
U
+
+
=
Gdyby siły przykładane były w odwrotnej kolejności (najpierw P
2
, potem P
1
) to końcowa
energia sprężysta układu wyraziłaby się wzorem
1
2
1
1
2
2
2
2
1
2
1
D
C
D
f
P
f
P
f
P
U
+
+
=
1
1
1
2
1
C
f
P
U
=
A
B
P
1
f
C2
f
D2
C
D
P
2
bez czynnika ½ bo cała siła o wartości P
1
wykonuje pracę na drodze f
C2
8. Metody energetyczne
- 4/23 -
Pionowa siła P
B
wywołuje poziome
przesunięcie punktu C o wartość f
C
.
Jakie będzie pionowe przemieszczenie
punktu B, jeśli do punktu C przyłożona
zostanie pozioma siła P
C
?
Ponieważ końcowa energia sprężysta nie może zależeć od kolejności przykładania sił, to
1
2
1
1
2
2
2
1
2
2
1
1
2
1
2
1
2
1
2
1
D
C
D
C
D
C
f
P
f
P
f
P
f
P
f
P
f
P
+
+
=
+
+
⇓
⇓
⇓
⇓
zasada wzajemności prac
1
2
2
1
D
C
f
P
f
P
=
(Bettiego)
(Enrico Betti 1823-1892)
Praca sił pierwszego stanu obciążenia
na przemieszczeniach uogólnionych wywołanych przez stan drugi
równa jest
pracy sił drugiego stanu obciążenia
na przemieszczeniach uogólnionych wywołanych przez stan pierwszy.
Jeśli
P
1
=P
2
to
zasada wzajemności przemieszczeń
1
2
D
C
f
f
=
(Maxwella)
(James Clark Maxwell 1831-1879)
Siła uogólniona przyłożona na kierunku pierwszym
wywoła na kierunku drugim przemieszczenie
równe przemieszczeniu,
jakie na kierunku pierwszym
wywoła ta siła przyłożona na kierunku drugim
Przykład
Rozwiązanie
Z zasady wzajemności prac
C
C
B
B
f
P
f
P
=
⇒
C
B
C
B
f
P
P
f
=
A
B
P
B
C
A
B
f
B
C
P
C
f
C
8. Metody energetyczne
- 5/23 -
A
B
P
1
f
1
f
n
f
i
P
n
P
i
A
B
P
1
f
i
P
n
P
i
δ
f
i
δδδδ
P
i
8.4. Twierdzenie Castigliano
(Carlo Alberto Castigliano 1847-1884)
energia sprężysta układu
i
n
i
i
f
P
U
∑
=
=
1
2
1
energia sprężysta układu
i
i
P
P
U
U
U
δ
∂
∂
+
=
1
Ten sam efekt końcowy uzyskać można przykładając siły w innej kolejności
energia sprężysta układu
i
i
f
P
U
δ
δ
δ
2
1
=
energia sprężysta układu
i
i
i
i
f
P
U
f
P
U
δ
δ
δ
+
+
=
2
1
2
układ Clapeyrona
(belka obciążona
siłami P
1
÷P
n
)
siła P
i
doznaje
przyrostu o małą
wartość
δδδδ
P
i
A
B
δ
f
i
δδδδ
P
i
obciążamy układ
małą siłą
δδδδ
P
i
dodajemy
zasadniczy układ sił
P
1
÷P
n
A
B
P
1
f
i
P
n
P
i
δ
f
i
δδδδ
P
i
f
n
f
1
bez czynnika ½ bo cała siła o wartości
δ
P
i
wykonuje pracę na drodze f
i

8. Metody energetyczne
- 6/23 -
Końcowe energie sprężyste układu są równe
U
1
=U
2
i
i
i
i
i
i
f
P
U
f
P
P
P
U
U
δ
δ
δ
δ
+
+
=
∂
∂
+
2
1
⇓
⇓
⇓
⇓
twierdzenie Castigliano
i
i
f
P
U
=
∂
∂
Pochodna cząstkowa energii sprężystej układu względem siły uogólnionej
równa jest współrzędnej uogólnionej odpowiadającej tej sile.
do pominięcia (mała drugiego rzędu)
8. Metody energetyczne
- 7/23 -
Obliczamy energię
sprężystą układu
(uwzględniamy jedynie
moment gnący, ścinanie
pomijamy)
Przykład
Stosując twierdzenie
Castigliano wyznaczyć
ugięcia f
B
i f
C
w punktach B
i C oraz kąt ugięcia
υ
C
w
punkcie C belki wsporniko-
wej pokazanej na rysunku.
Rozwiązanie
Aby móc obliczyć współrzędne uogólnione w punkcie C (ugięcie, kąt ugięcia) musimy
chwilowo przyłożyć tam siły uogólnione odpowiadające tym współrzędnym: siłę R
i moment gnący M (ostatecznie przyjmiemy, że R=0 oraz M=0)
EJ
Pa
P
U
f
B
3
3
=
∂
∂
=
(
)
EJ
a
l
Pa
R
U
f
C
6
3
2
−
=
∂
∂
=
EJ
Pa
M
U
C
2
2
=
∂
∂
=
υ
przy R=0, M=0
A
B
C
P
y
x
R
M
dx
EJ
M
dx
EJ
M
U
l
a
C
gB
a
B
gA
∫
∫
−
−
+
=
2
2
2
0
2
A
B
M
g
x
M
gB-C
=
−
R
(l
−
x
)
−
M
C
M
gA-B
=
−
P
(a
−
x
)
−
R
(l
−
x
)
−
M
a
l
(
)
(
)
[
]
(
)
[
]
(
)
(
)(
)
(
)
[
]
(
)
(
)
(
)
(
)(
)
[
]
2
2
2
2
3
3
2
2
2
3
2
0
2
3
3
6
1
3
3
6
1
2
2
M
Rl
a
l
M
Rl
R
a
l
R
a
l
EJ
M
Rl
Pa
a
M
Rl
Pa
R
P
a
R
P
a
EJ
dx
EJ
M
x
l
R
dx
EJ
M
x
l
R
x
a
P
U
l
a
a
+
−
+
+
−
−
−
+
+
+
+
+
+
+
+
−
+
=
=
−
−
−
+
−
−
−
−
−
=
∫
∫
A
B
C
P
a
l
y
x
EJ=
const
f
B
f
C
υ
υ
υ
υ
C
8. Metody energetyczne
- 8/23 -
równań tego rodzaju można napisać tyle,
ile jest reakcji statycznie niewyznaczalnych
8.5. Twierdzenie Menabrea
(Luigi Federico Menabrea 1809-1896)
Belka trójpodporowa – przykład ustroju statycznie niewyznaczalnego
Należy wyznaczyć 3 niewiadome reakcje: R
A
, R
B
, R
C
.
Do dyspozycji mamy 2 równania równowagi:
0
=
∑
y
F
0
=
∑
K
M
albo
0
=
∑
K
M
0
=
∑
J
M
(K, J – dowolnie wybrane punkty płaszczyzny)
Trzecie równanie wyrażające równowagę sił w kierunku osi x:
0
=
∑
x
F
jest spełnione.
Liczba niewiadomych przewyższa o 1 liczbę równań równowagi. Układ jest zatem
jednokrotnie statycznie niewyznaczalny.
Przy wyznaczaniu reakcji w układach statycznie niewyznaczalnych
wykorzystujemy informacje dotyczące odkształceń konstrukcji.
1. Jedną z poszukiwanych reakcji, np. R
C
uznajemy za statycznie niewyznaczalną.
2. Belkę traktujemy tak, jakby była podparta na 2 podporach (A i B) – a więc jak
statycznie wyznaczalną – i obciążona dodatkowo chwilowo nieznaną siłą R
C
=X.
3. Siłę X wyznaczamy z warunku, że ugięcie belki na podporze równe jest 0.
4. Wykorzystujemy twierdzenie Castigliano
twierdzenie Menabrea
0
=
∂
∂
X
U
Pochodna cząstkowa energii sprężystej układu
względem reakcji statycznie niewyznaczalnej jest równa zeru.
A
B
P
C
f
R
A
R
C
R
B
x
y
A
B
P
C
f
R
A
R
C
=X
R
B
x
y
8. Metody energetyczne
- 9/23 -
Przykład
Wykorzystując twierdzenie
Menabrea wyznaczyć reakcje
podpór belki pokazanej na
rysunku i wykonać wykres
momentów gnących.
Rozwiązanie
1. Uwalniamy układ od
więzów.
2. Stwierdzamy, że belka
jest jednokrotnie staty-
cznie niewyznaczalna.
3. Dowolną z reakcji uzna-
jemy za statycznie
niewyznaczalną (R
C
).
4. Wykonujemy „roboczy” wykres momentów gnących.
5. Obliczamy energię sprężystą
∫
∫
−
−
+
=
l
a
C
gB
a
B
gA
dx
EJ
M
dx
EJ
M
U
2
2
2
0
2
Uwaga: jeżeli
∫
=
l
g
dx
EJ
M
U
0
2
2
to
∫
∂
∂
=
∂
∂
l
g
g
dx
X
M
M
EJ
X
U
0
1
a zatem
0
1
1
0
=
∂
∂
+
∂
∂
∫
∫
−
−
−
−
dx
X
M
M
EJ
dx
X
M
M
EJ
l
a
C
gB
C
gB
a
B
gA
B
gA
(
)
(
)
[
]
(
)
(
)(
)
0
0
=
−
−
+
−
−
−
−
∫
∫
dx
x
l
x
l
X
dx
x
l
x
a
P
x
l
X
l
a
a
stąd otrzymujemy:
(
)
3
2
2
3
l
a
l
a
P
X
−
=
A
B
C
P
a
l
y
x
EJ=
const
M
A
A
B
C
P
M
g
x
R
A
R
C
=X
M
gB-C
=X(l
−x)
M
gA-B
=X(l
−x)−P(a−x)
„Roboczy” wykres momentów gnących
A
B
C
M
g
x
Wykres momentów gnących
a
l
(
)(
)
3
2
2
3
l
a
l
a
l
a
P
M
B
−
−
=
(
)
−
−
=
1
2
3
2
l
a
l
a
Pa
M
A
(
)
−
−
=
−
=
3
2
2
3
1
l
a
l
a
P
X
P
R
A
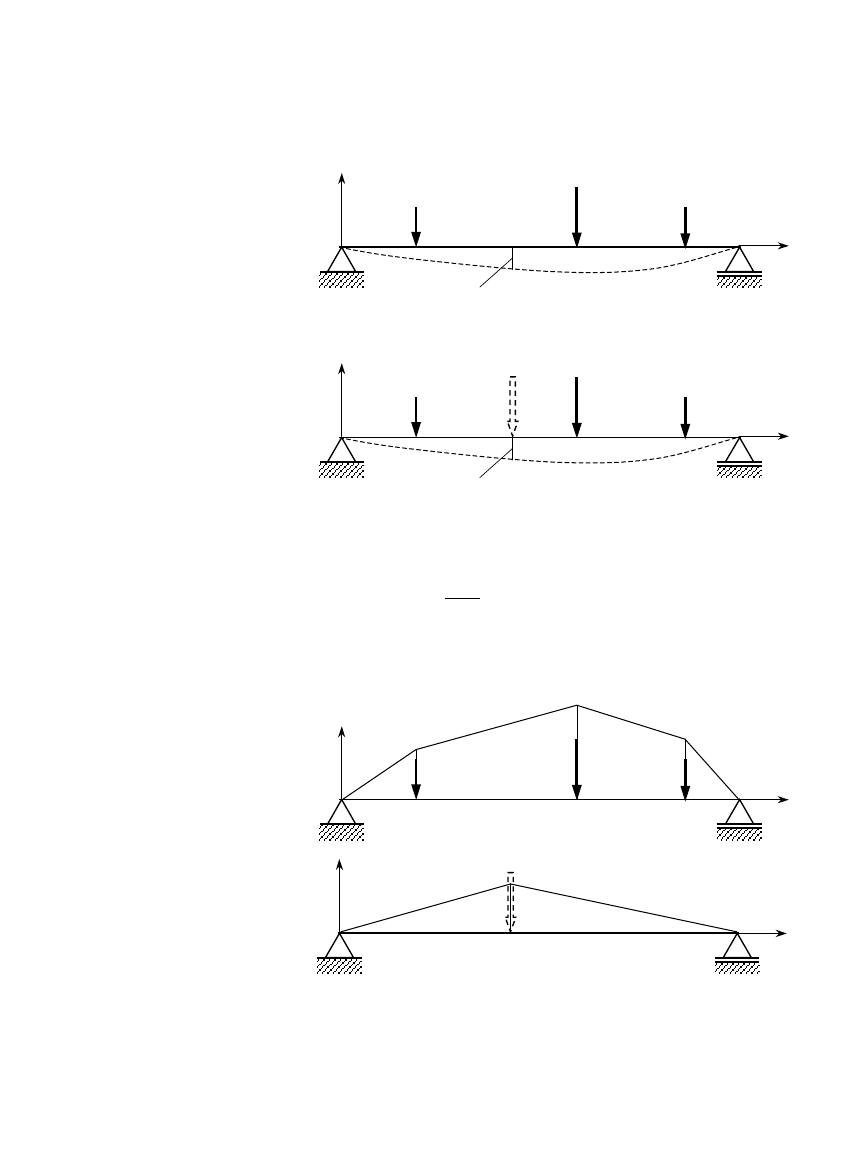
8. Metody energetyczne
- 10/23 -
8.6. Obliczanie przemieszczeń w konstrukcji prętowej na podstawie wzoru
Maxwella-Mohra
(Christian Otto Mohr 1835-1918)
Celem jest obliczenie przemieszczenia w punkcie K belki
Stosujemy twierdzenie
Castigliano:
1. W punkcie K
przykładamy siłę
uogólnioną P
K
,
odpowiadającą
przemieszczeniu f
K
.
2. Obliczamy energię sprężystą układu U i różniczkujemy po sile P
K
, ostatecznie
przyjmując P
K
=0
0
=
∂
∂
=
K
P
K
K
P
U
f
Energię sprężystą obliczamy na podstawie momentu gnącego panującego na belce.
Moment gnący wyznaczamy jako superpozycję dwóch stanów:
1. obciążenia zasadniczego
(siłami P
1
÷P
n
)
2. obciążenia dodatkowego
uogólnioną siłą
P
K
=1
Wykres m
g
(x) wykonujemy dla jednostkowej wartości
P
K
=1
siły uogólnionej.
W przypadku dowolnej siły P
K
wartości momentu gnącego od tej siły będą równe
m
g
(x)
⋅⋅⋅⋅
P
K
układ Clapeyrona
(belka obciążona
siłami P
1
÷P
n
)
A
B
P
1
f
K
P
n
P
i
K
x
y
A
B
P
1
f
K
P
n
P
i
K
P
K
=0
x
y
A
B
P
1
P
n
P
i
K
x
M
g
(x)
A
B
K
P
K
=1
x
m
g
(x)
8. Metody energetyczne
- 11/23 -
Sumaryczny moment gnący panujący na belce równy jest
M
g
(x)+m
g
(x)P
K
Energia sprężysta
( )
( )
(
)
∫
+
=
l
K
g
g
dx
EJ
P
x
m
x
M
U
0
2
2
Przemieszczenie w punkcie K
W rzeczywistości
P
K
=0, ostatecznie otrzymujemy
wzór Maxwella-Mohra
( ) ( )
∫
=
l
g
g
K
dx
EJ
x
m
x
M
f
0
W ogólnym wypadku, gdy energia sprężysta pochodzi od:
− rozciągania (ściskania) ⇒ N(x) − rozkład siły normalnej wzdłuż konstrukcji prętowej
wywołany obciążeniem rzeczywistym,
− ścinania
⇒ T(x)
− rozkład siły tnącej ...,
− skręcania
⇒ M
s
(x)
− rozkład momentu skręcającego ...,
− zginania
⇒ M
g
(x)
− rozkład momentu gnącego ...
wzór Maxwella-Mohra przyjmuje postać:
( ) ( )
( ) ( )
( ) ( )
( ) ( )
∫
∫
∫
∫
+
+
+
=
l
g
g
l
s
s
s
l
l
K
dx
EJ
x
m
x
M
dx
GJ
x
m
x
M
dx
GA
x
t
x
T
dx
EA
x
n
x
N
f
0
0
0
0
ψ
gdzie:
− n(x) − rozkład siły normalnej wzdłuż konstrukcji prętowej wywołany jednostkową siłą
uogólnioną P
K
odpowiadającą przemieszczeniu f
K
,
− t(x) − rozkład siły tnącej ...,
− m
s
(x)
− rozkład momentu skręcającego ...,
− m
g
(x)
− rozkład momentu gnącego ... .
( )
( )
(
)
( )
∫
+
=
∂
∂
=
l
g
K
g
g
K
K
dx
x
m
P
x
m
x
M
EJ
P
U
f
0
1
8. Metody energetyczne
- 12/23 -
8.7. Metoda Wereszczagina obliczania całek typu
( ) ( )
∫
b
a
dx
x
m
x
M
( ) ( )
h
dx
x
m
x
M
b
a
⋅
Ω
=
∫
Ω
− zakreskowane pole
sc
− środek ciężkości pola
Ω
h
=m(x
sc
)
− wartość funkcji
liniowej dla argumentu
x
sc
W podręcznikach do Wytrzymałości Materiałów podane są tabele ułatwiające obliczanie
całek metodą Wereszczagina dla wybranych przebiegów funkcji podcałkowych.
M
(x)
x
a
b
Ω
sc
x
sc
m
(x)
x
a
b
x
sc
h
dowolna funkcja
całkowalna
funkcja liniowa
d
e
l
a
b
l
(
)
(
)
[
]
e
d
b
e
d
a
l
2
2
6
1
+
+
+
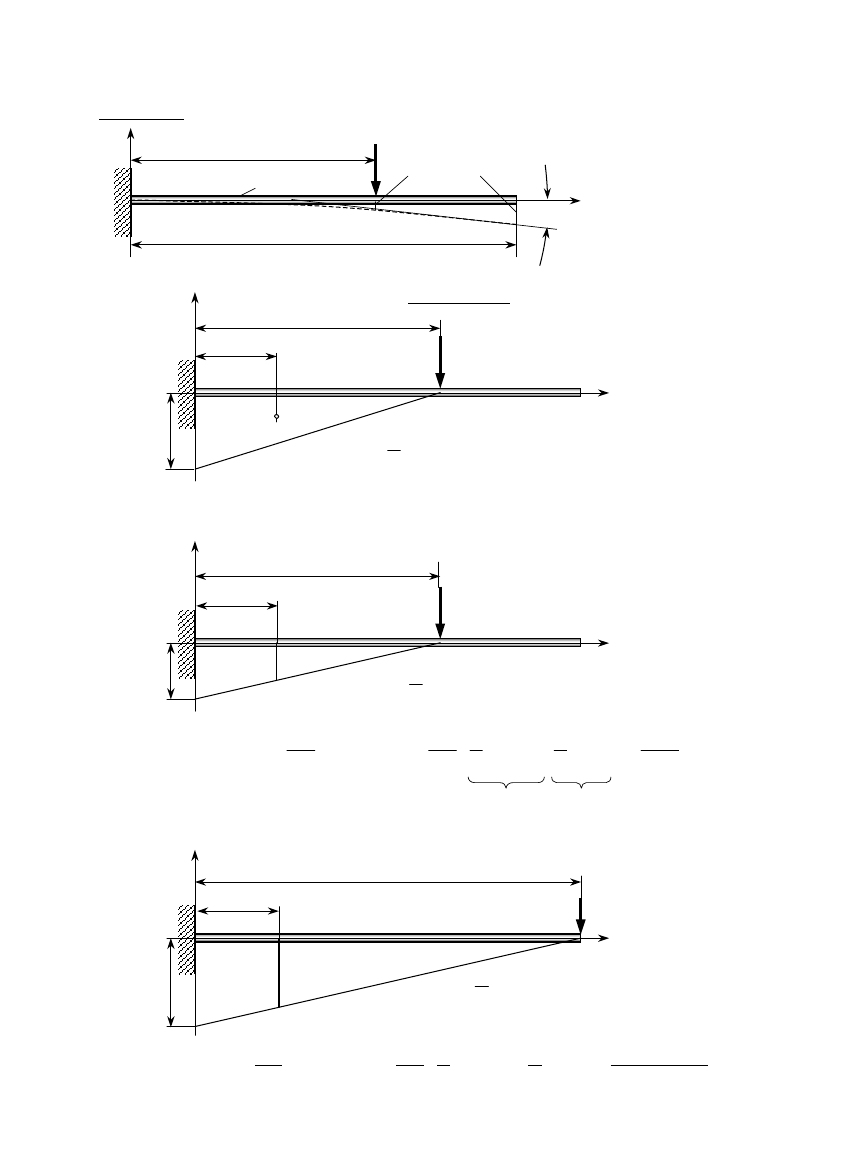
8. Metody energetyczne
- 13/23 -
Przykład 1
Stosując wzór Maxwella-
Mohra wyznaczyć ugięcia f
B
i f
C
w punktach B i C oraz
kąt ugięcia
υ
C
w punkcie C
belki wspornikowej
pokazanej na rysunku.
Rozwiązanie
„Stan 0”
Obliczenia ugięcia w punkcie B
„stan 1”
Obliczenia ugięcia w punkcie C
„stan 1”
(
)
(
)
EJ
a
l
Pa
l
a
a
Pa
EJ
dx
m
M
EJ
f
l
g
g
C
6
3
3
2
1
1
1
2
0
−
=
−
−
=
=
∫
A
B
C
P
a
l
y
x
EJ=
const
f
B
f
C
υ
υ
υ
υ
C
A
B
C
P
a
M
g
x
-Pa
a
/3
sc
Ω
(
)
a
Pa
−
=
Ω
2
1
A
B
C
1
a
m
g
x
-a
a
/3
h
(
)
a
h
−
=
3
2
Ω h
(
)
( )
EJ
Pa
a
a
Pa
EJ
dx
m
M
EJ
f
l
g
g
B
3
3
2
2
1
1
1
3
0
=
−
−
=
=
∫
A
C
1
l
m
g
x
-l
a
/3
h
l
a
h
−
=
3

8. Metody energetyczne
- 14/23 -
Obliczenia kąta ugięcia w punkcie C
„stan 1”
(
) ( )
EJ
Pa
a
Pa
EJ
dx
m
M
EJ
l
g
g
C
2
1
2
1
1
1
2
0
=
−
−
=
=
∫
ϑ
A
C
1
l
m
g
x
−1
a
/3
h
=
−1
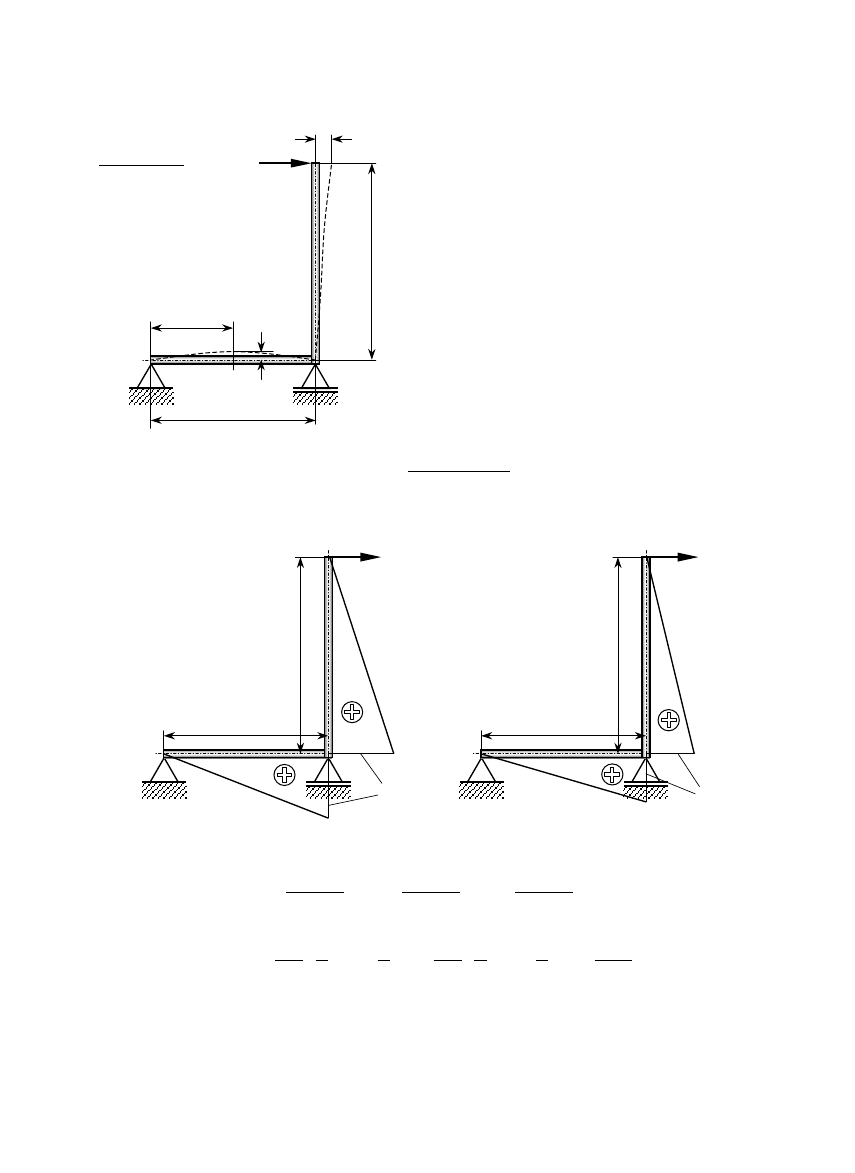
8. Metody energetyczne
- 15/23 -
Przykład 2
Korzystając ze wzoru Maxwella-Mohra
obliczyć ugięcia f
C
i f
D
ramy pokazanej na
rysunku.
Rozwiązanie
Obliczenia ugięcia ramy w punkcie C
Stan "0" stan "1"
(
)
b
a
EJ
Pb
b
bPb
EJ
b
aPb
EJ
dx
EJ
m
M
dx
EJ
m
M
dx
EJ
m
M
f
b
g
g
a
g
g
l
g
g
C
+
=
⋅
+
⋅
=
=
+
=
=
∫
∫
∫
3
3
2
2
1
1
3
2
2
1
1
2
0
0
0
A
B
C
a
P
b
f
C
D
a
/2
f
D
EJ
=const
A
B
C
P
Pb
a
b
M
g
A
B
C
1
b
a
b
m
g
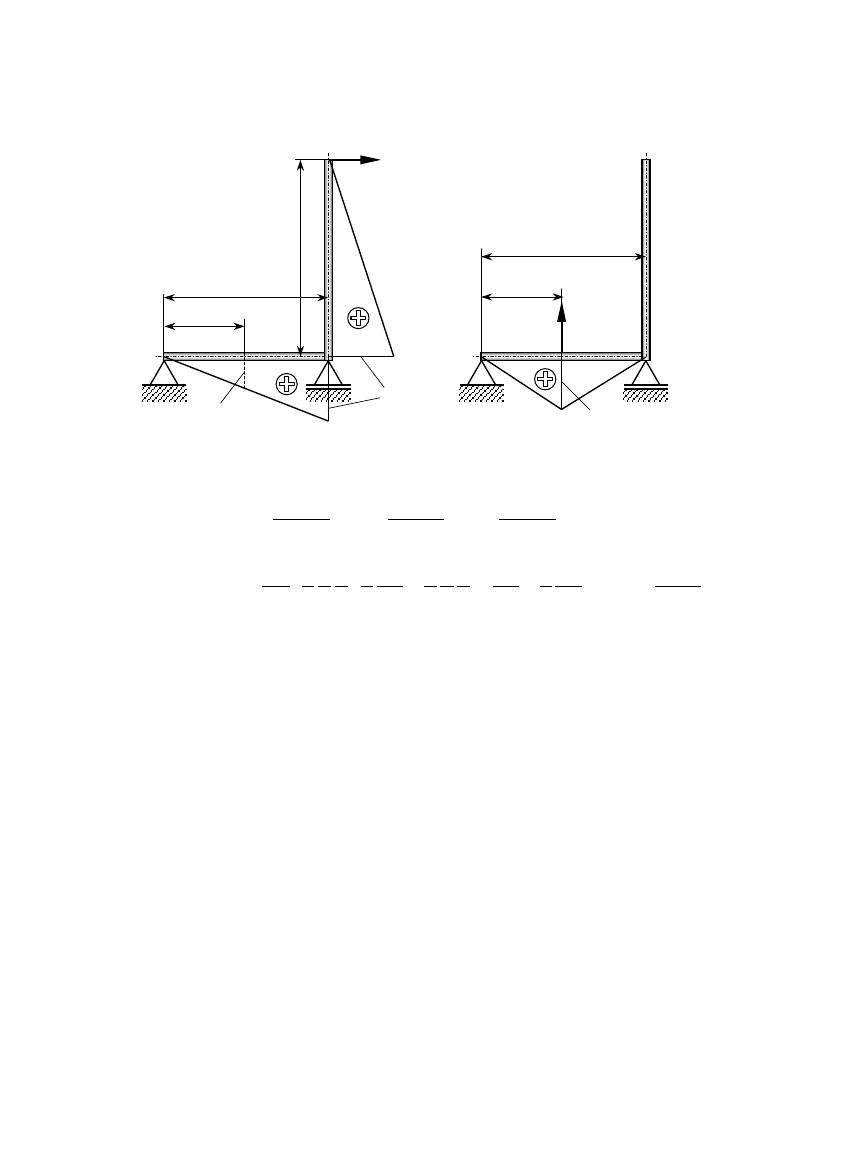
8. Metody energetyczne
- 16/23 -
Obliczenia ugięcia ramy w punkcie D
Stan "0" stan "1"
EJ
Pba
Pb
Pb
a
a
Pb
a
a
EJ
dx
EJ
m
M
dx
EJ
m
M
dx
EJ
m
M
f
b
g
g
a
g
g
l
g
g
D
16
0
2
3
1
2
4
2
2
1
2
3
2
4
2
2
1
1
2
0
0
0
=
+
+
⋅
+
⋅
=
=
+
=
=
∫
∫
∫
A
B
C
1
a
/4
a
m
g
D
a
/2
P
A
B
C
Pb
a
b
M
g
Pb
/2
a
/2
D
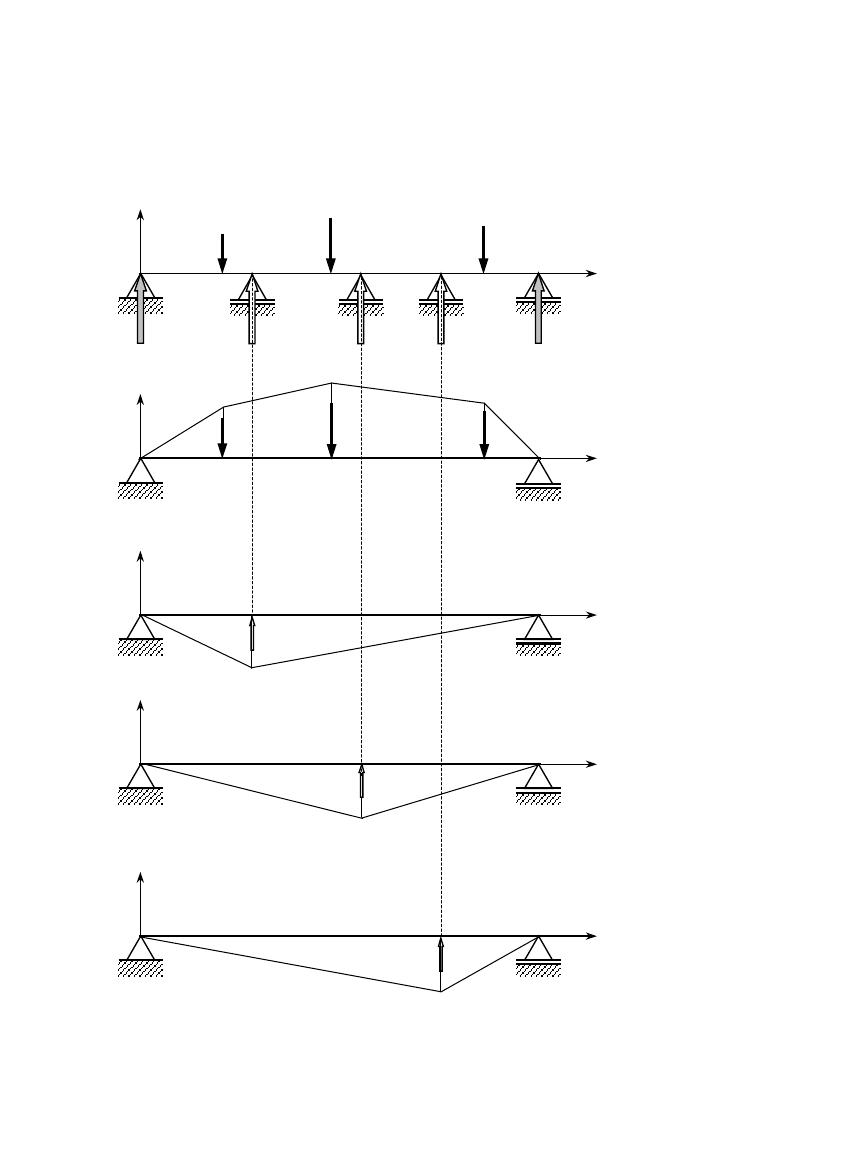
8. Metody energetyczne
- 17/23 -
8.8. Równania Maxwella-Mohra (równania kanoniczne metody sił)
Układ Clapeyrona
belka na
n
+2
podporach
(układ n-krotnie
statycznie
niewyznaczalny)
Stan „0”
stan „1”
1
)
1
(
)
1
(
X
m
M
g
g
=
stan „i”
i
i
g
i
g
X
m
M
)
(
)
(
=
stan „n”
n
n
g
n
g
X
m
M
)
(
)
(
=
A
B
P
1
R
A
X
1
R
B
x
y
P
2
P
k
X
i
X
n
A
B
P
1
x
)
0
(
g
M
M
P
2
P
k
A
B
1
x
)
1
(
g
m
A
B
x
)
(i
g
m
1
A
B
x
)
(n
g
m
1
8. Metody energetyczne
- 18/23 -
Sumaryczny moment gnący na belce
n
n
g
i
i
g
g
g
g
X
m
X
m
X
m
M
M
)
(
)
(
1
)
1
(
)
0
(
...
...
+
+
+
+
+
=
Energia sprężysta układu
dx
EJ
M
U
l
g
∫
=
0
2
2
Z twierdzenia Menabrea wynika, że
0
1
=
∂
∂
X
U
...
0
=
∂
∂
i
X
U
...
0
=
∂
∂
n
X
U
Równanie jak wyżej można napisać dla każdej z wielkości
X
1
, ...,X
n
, otrzymuje się więc
tyle równań, ile jest reakcji statycznie niewyznaczalnych.
0
0
0
0
1
1
0
1
1
10
1
1
1
11
=
+
+
+
+
+
=
+
+
+
+
+
=
+
+
+
+
+
n
n
nn
i
ni
n
i
n
in
i
ii
i
n
n
i
i
X
X
X
X
X
X
X
X
X
α
α
α
α
α
α
α
α
α
α
α
α
L
L
M
L
L
M
L
L
∫
=
l
i
g
j
g
ij
dx
EJ
m
m
0
)
(
)
(
α
ji
ij
α
α
=
∫
=
l
i
g
g
i
dx
EJ
m
M
0
)
(
)
0
(
0
α
Rozwiązując układ równań Maxwella-Mohra
wyznacza się reakcje statycznie niewyznaczalne X
1
, ...,X
n
0
...
...
1
1
0
)
(
)
(
0
)
(
)
(
0
)
(
)
1
(
1
0
)
(
)
0
(
)
(
0
0
=
+
+
+
+
+
=
=
=
∂
∂
=
∂
∂
∫
∫
∫
∫
∫
∫
l
i
g
n
g
n
l
i
i
i
i
i
l
i
g
g
l
i
g
g
i
g
g
l
i
g
g
l
i
dx
EJ
m
m
X
dx
EJ
m
m
X
dx
EJ
m
m
X
dx
EJ
m
M
dx
m
M
EJ
dx
X
M
M
EJ
X
U
α
i0
α
in
α
ii
α
i1
układ
równań
Maxwella
-Mohra
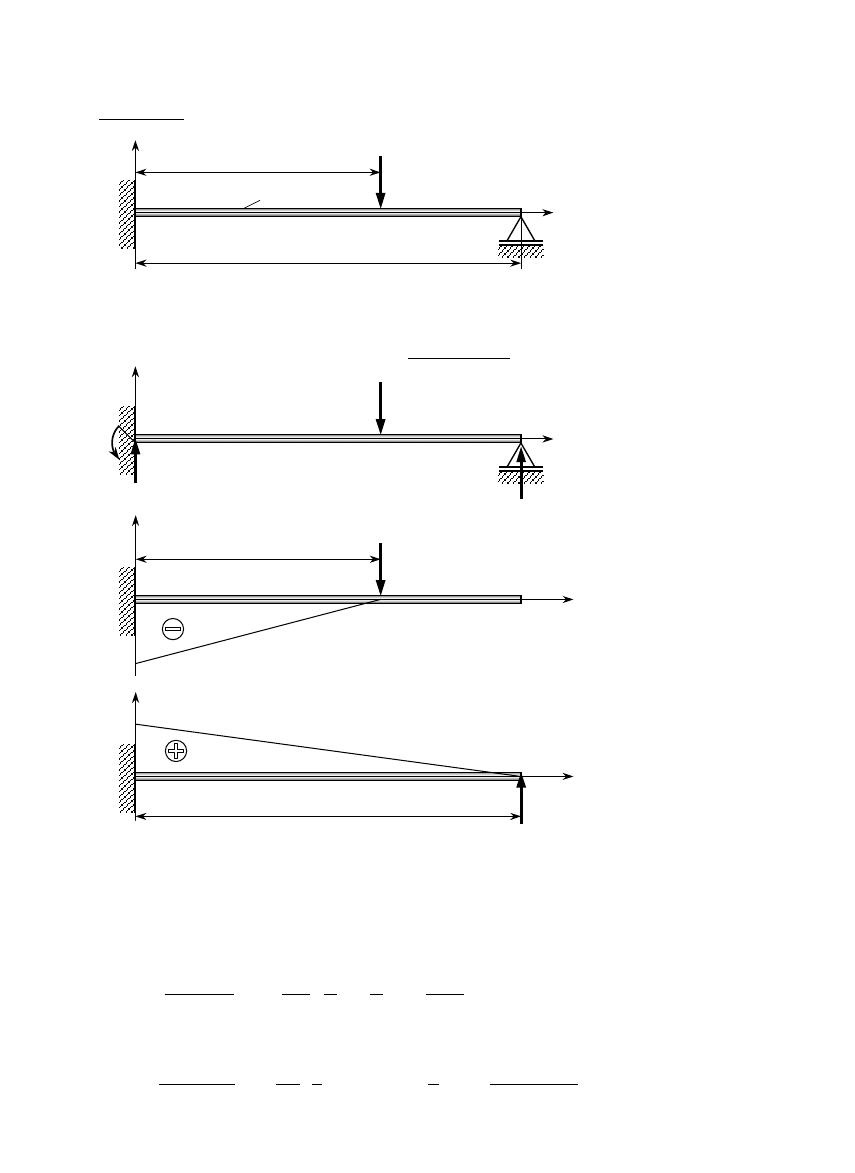
8. Metody energetyczne
- 19/23 -
Przykład 1
Wykorzystując równania
Maxwella-Mohra wyznaczyć
reakcje podpór belki
pokazanej na rysunku
i narysować wykres
momentów gnących
Rozwiązanie
Belka jest 1-krotnie
statycznie niewyznaczalna.
Jako wielkość statycznie
niewyznaczalną
przyjmujemy reakcję na
podporze B.
Stan „0”
stan „1”
0
10
1
11
=
+
α
α
X
Współczynniki
α
ij
obliczamy metodą Wereszczagina:
EJ
l
l
l
EJ
dx
EJ
m
m
l
g
g
3
3
2
2
1
1
3
2
0
)
1
(
)
1
(
11
=
⋅
=
=
∫
α
(
)
(
)
EJ
a
l
Pa
a
l
Pa
a
EJ
dx
EJ
m
M
l
)
(
g
)
(
g
6
3
3
2
1
1
2
0
1
0
10
−
−
=
−
⋅
−
=
=
∫
α
A
C
B
P
a
l
y
x
EJ=
const
A
C
B
P
y
x
R
A
M
A
R
B
=X
1
A
B
C
P
x
)
0
(
g
M
-
Pa
a
A
B
1
x
)
1
(
g
m
l
l
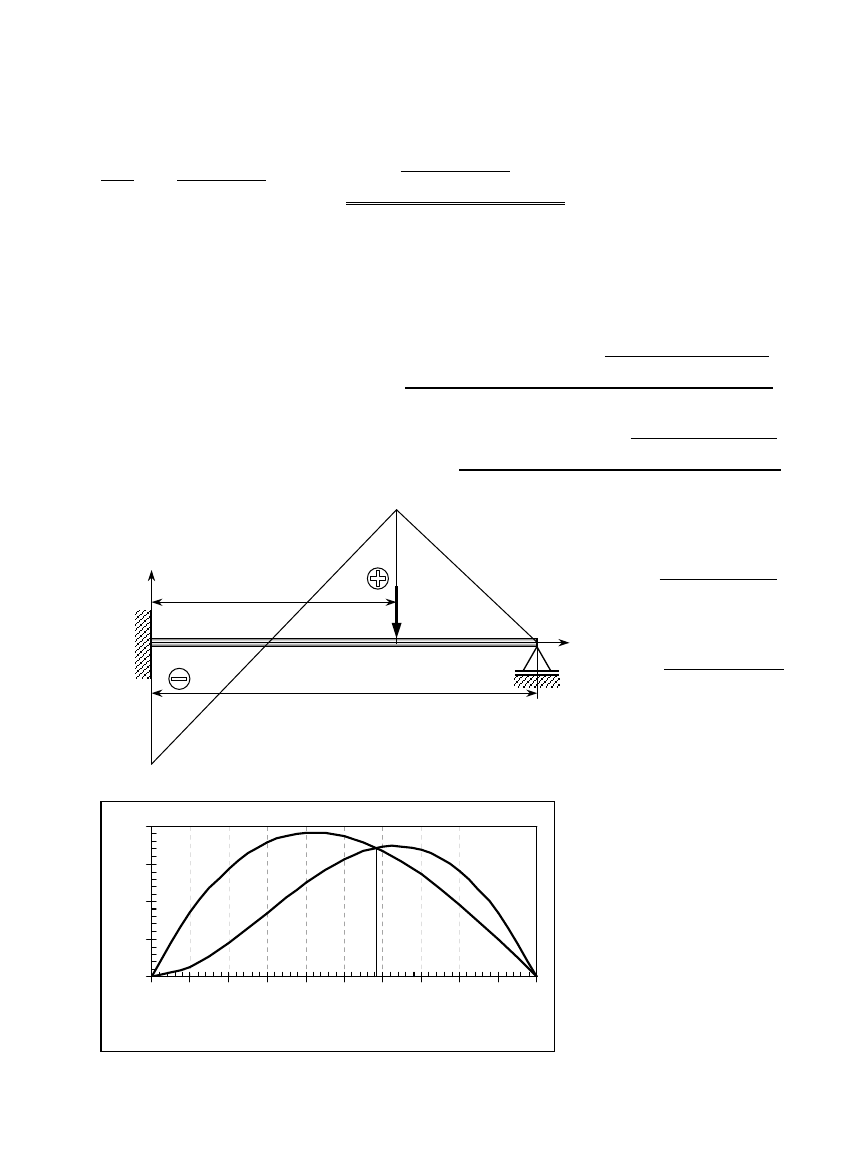
8. Metody energetyczne
- 20/23 -
(
)
0
6
3
3
2
1
3
=
−
−
EJ
a
l
Pa
X
EJ
l
⇒
(
)
B
R
l
a
l
Pa
X
=
−
=
3
2
1
2
3
Po wyznaczeniu reakcji statycznie niewyznaczalnej R
B
belka staje się statycznie
wyznaczalna i niewiadome reakcje R
A
, M
A
obliczamy z warunków równowagi:
0
=
∑
A
M
⇒
0
=
+
−
l
R
Pa
M
B
A
⇒
(
)
2
2
2
2
3
2
l
a
al
l
a
P
l
R
Pa
M
B
A
+
−
=
−
=
0
=
∑
F
⇒
0
=
+
−
B
A
R
P
R
⇒
3
3
2
3
2
3
2
l
a
l
a
l
P
R
P
R
B
A
+
−
=
−
=
(
)
2
2
2
2
3
2
l
a
al
l
a
P
M
A
+
−
=
(
)
(
)(
)
3
2
2
3
l
a
l
a
l
a
P
a
l
R
M
B
C
−
−
=
=
−
=
Rozkład momentu gnącego na belce
C
C
A
A
k
Pl
M
k
Pl
M
⋅
=
⋅
=
dla a/l
≈0.586
M
A
=M
C
≈0.172Pl
A
C
B
P
a
l
M
g
x
M
C
M
A
0.00
0.05
0.10
0.15
0.20
0.0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
a/l
k
A
k
C
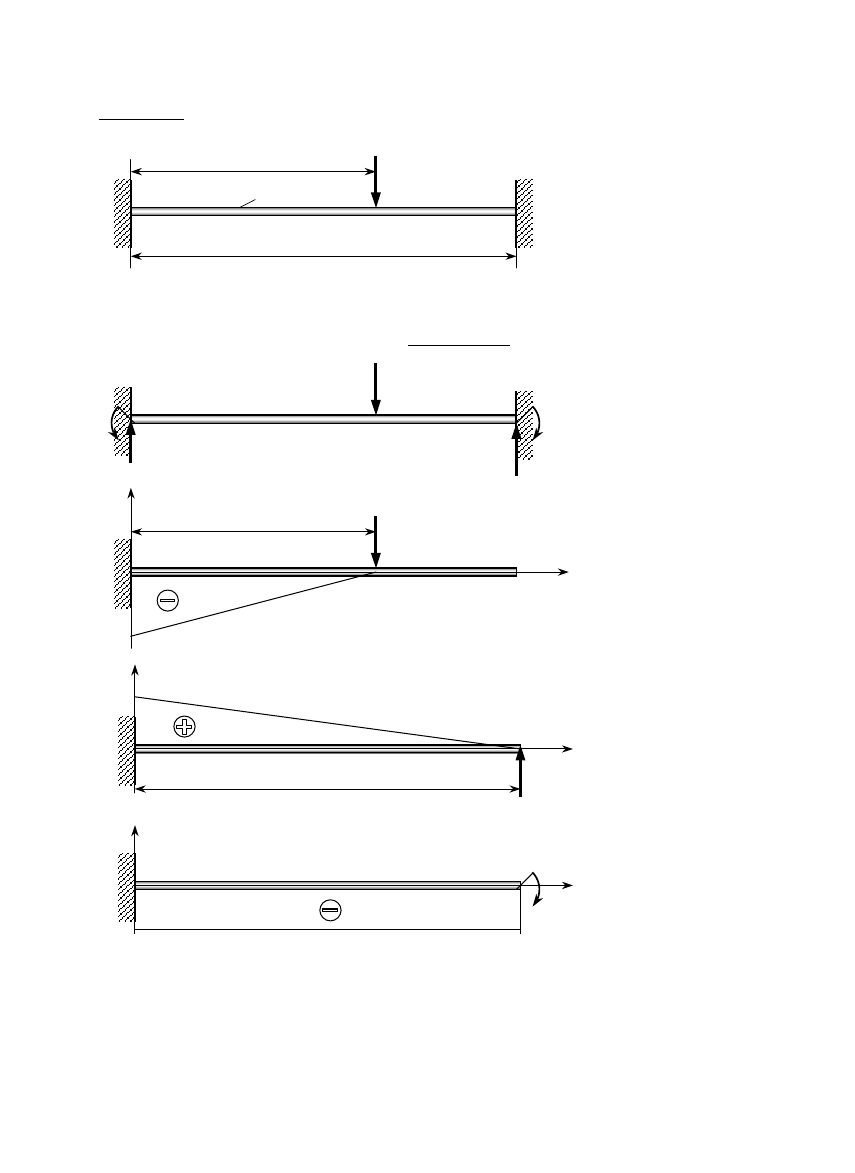
8. Metody energetyczne
- 21/23 -
Przykład 2
Wykorzystując układ równań
Maxwella-Mohra wyznaczyć
reakcje w belce pokazanej na
rysunku i wykonać wykres
momentów gnących.
Rozwiązanie
Belka jest 2-krotnie
statycznie niewyznaczalna.
Jako wielkości
statycznie
niewyznaczalne
przyjmujemy R
B
i M
B
.
Stan „0”
stan „1”
stan „2”
0
0
20
2
22
1
21
10
2
12
1
11
=
+
+
=
+
+
α
α
α
α
α
α
X
X
X
X
A
B
C
P
a
l
EJ=
const
A
B
C
P
R
A
M
A
M
B
=X
2
R
B
=X
1
A
B
C
P
x
)
0
(
g
M
-
Pa
a
A
B
1
x
)
1
(
g
m
l
l
A
B
1
x
-
1
)
2
(
g
m
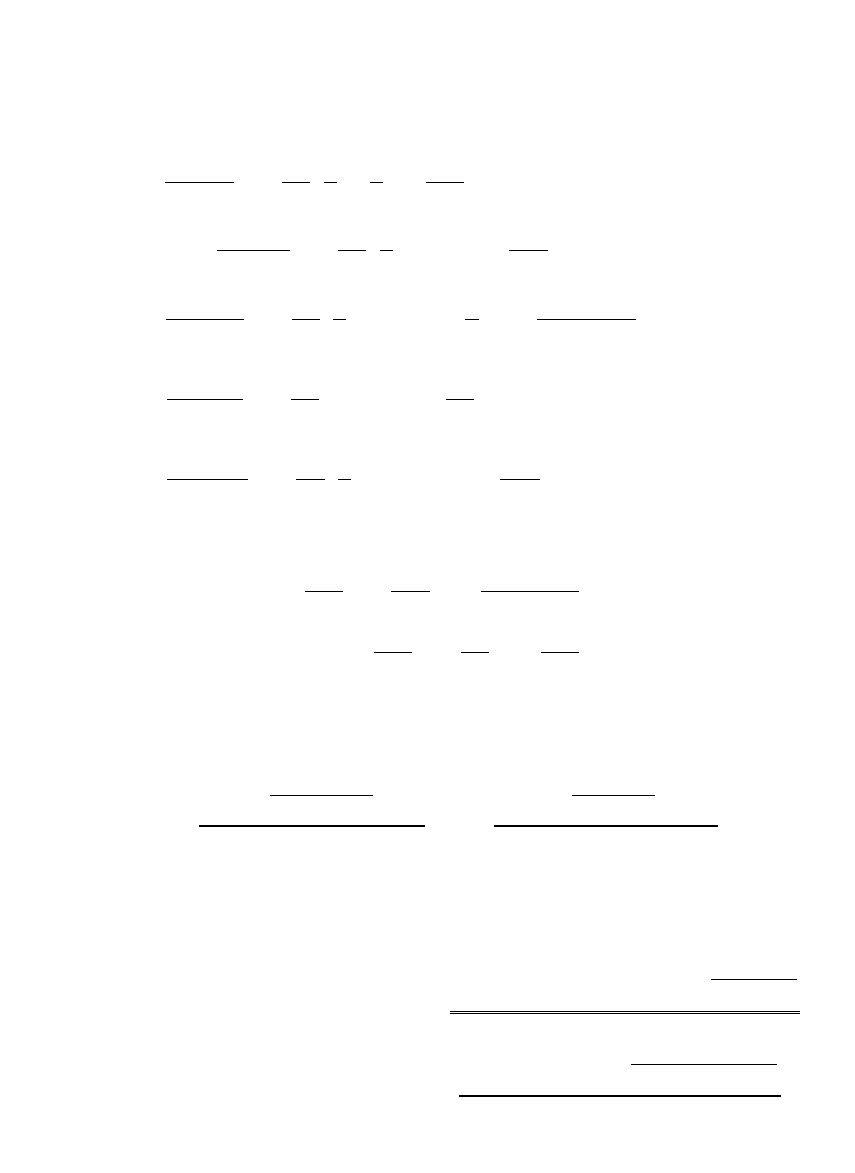
8. Metody energetyczne
- 22/23 -
Współczynniki
α
ij
obliczamy metodą Wereszczagina:
EJ
l
l
l
EJ
dx
EJ
m
m
l
g
g
3
3
2
2
1
1
3
2
0
)
1
(
)
1
(
11
=
⋅
=
=
∫
α
( )
EJ
l
l
EJ
dx
EJ
m
m
l
g
g
2
1
2
1
1
2
2
0
)
2
(
)
1
(
21
12
−
=
−
⋅
=
=
=
∫
α
α
(
)
(
)
EJ
a
l
Pa
a
l
Pa
a
EJ
dx
EJ
m
M
l
g
g
6
3
3
2
1
1
2
0
)
1
(
)
0
(
10
−
−
=
−
⋅
−
=
=
∫
α
( ) ( )
[
]
EJ
l
l
EJ
dx
EJ
m
m
l
g
g
=
−
⋅
−
=
=
∫
1
1
1
0
)
2
(
)
2
(
22
α
(
) ( )
EJ
Pa
Pa
a
EJ
dx
EJ
m
M
l
g
g
2
1
2
1
1
2
0
)
2
(
)
0
(
20
=
−
⋅
−
=
=
∫
α
(
)
0
2
2
0
6
3
2
3
2
2
1
2
2
2
2
1
3
=
+
+
−
=
−
−
−
EJ
Pa
X
EJ
l
X
EJ
l
EJ
a
l
Pa
X
EJ
l
X
EJ
l
Po rozwiązaniu układu równań otrzymujemy
(
)
B
R
l
a
l
a
P
X
=
−
=
3
2
1
2
3
(
)
B
M
l
a
l
a
P
X
=
−
=
2
2
2
Po wyznaczeniu reakcji statycznie niewyznaczalnych R
B
, M
B
belka staje się statycznie
wyznaczalna i niewiadome reakcje R
A
, M
A
obliczamy z warunków równowagi:
0
=
∑
A
M
⇒
0
=
−
+
−
B
B
A
M
l
R
Pa
M
⇒
(
)
2
2
l
a
l
a
P
M
l
R
Pa
M
B
B
A
−
=
+
−
=
0
=
∑
F
⇒
0
=
+
−
B
A
R
P
R
⇒
(
) (
)
3
2
2
l
l
a
a
l
P
R
P
R
B
A
+
−
=
−
=
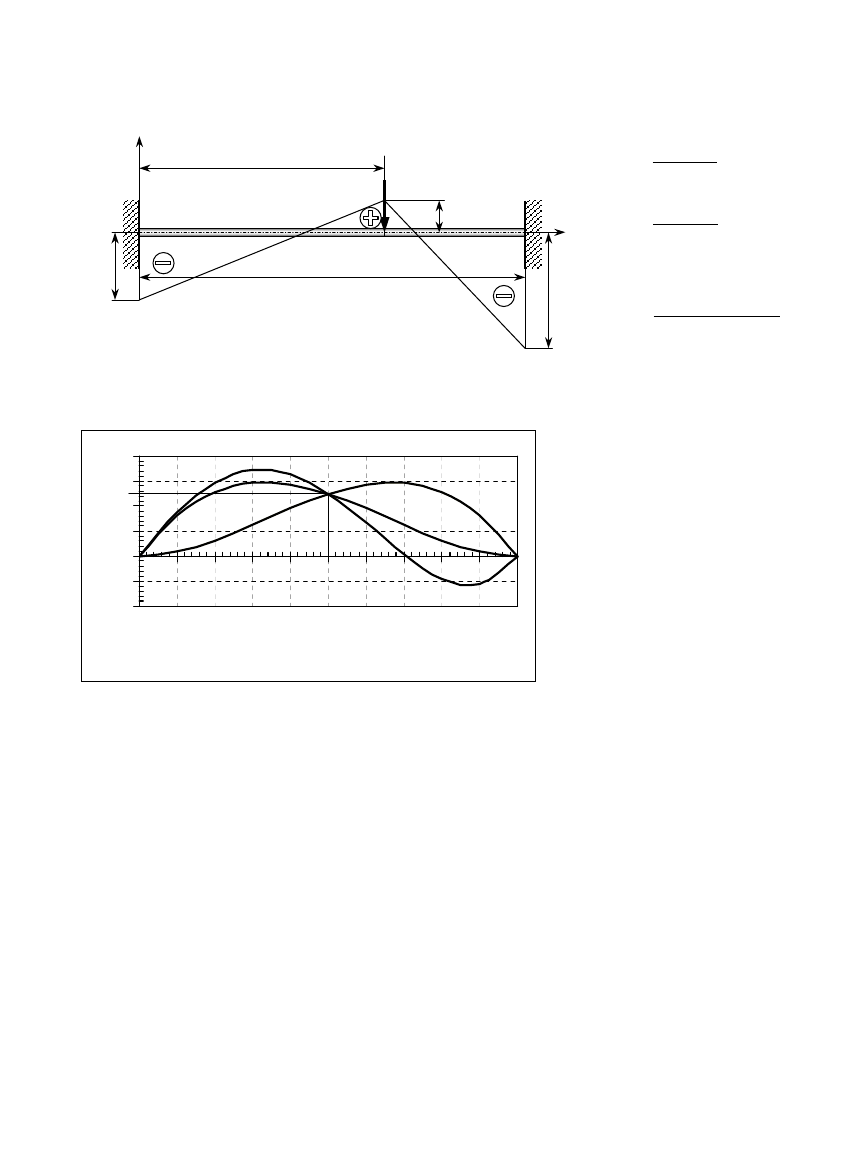
8. Metody energetyczne
- 23/23 -
(
)
2
2
l
a
l
a
P
M
A
−
=
(
)
2
2
l
a
l
a
P
M
B
−
=
(
)
(
)
3
2
2
2
l
a
l
a
l
a
P
M
a
R
M
A
A
C
−
−
=
=
−
=
Rozkład momentu gnącego na belce
C
C
B
B
A
A
k
Pl
M
k
Pl
M
k
Pl
M
⋅
=
⋅
=
⋅
=
dla a=l/2
M
A
=M
B
=M
C
=Pl
/8
A
B
C
P
a
l
M
C
M
B
M
A
x
M
g
-0.10
-0.05
0.00
0.05
0.10
0.15
0.20
0.0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
a/l
k
A
k
C
k
B
Wyszukiwarka
Podobne podstrony:
Ekologia wykłady nie potwierdzone
geologia wyklad nie kompletny
fizykochemia 6 str[1]. wykład nie nasz, sgsp, Fizykochemia
Negocjacje w biznesie [ opracowanie z książki] [ wykłady dr Marek Datko], Negocjacje w biznesie - wy
Negocjacje w biznesie [ opracowanie z książki] [ wykłady dr Marek Datko], Negocjacje w biznesie - wy
Politologia Książka - Wykład 1 i 2, Studia - politologia, Podstawy politologii
matka do fiz[1]. 6 st. wykład nie nasz, sgsp, Fizykochemia
obyna3.pl-259 notatki - ksiazki wyklady cwiczenia, Cz
Negocjacje w biznesie [ opracowanie z książki] [ wykłady dr Marek Datko], Negocjacje w biznesie - wy
Zarządzanie Dziedzictwem Kulturowym wykład 4 NIE CAŁY!!, Studia
wykład 1, nie uzupełniony
Psychofizjologia - książka i wykłądy (razem), psychofizjologia
podatkowa książka wykład
ekonometria fir wyklady nie umk! id 155326
Negocjacje w biznesie [ opracowanie z książki] [ wykłady dr Marek Datko], Negocjacje w biznesie - wy
Negocjacje w biznesie [ opracowanie z książki] [ wykłady dr Marek Datko], Negocjacje w biznesie - wy
Modlitwy do odmawiania przed i w czasie Mszy Sw z ksiazki Wykład o Mszy Świętej
więcej podobnych podstron