Zarz

ą

dzanie przedsi

ę

wzi

ę

ciami budowlanymi

Mgr in

ż

. Anna Jakubczyk

1

Zarz

ą

dzanie przedsi

ę

wzi

ę

ciem budowlanym

Materiały do kolokwium.

1

1. PODSTAWOWE POJ

Ę

CIA

Optymalizacja

- obszar dopuszczalnych decyzji + kryterium oceny, które zale

ż

y od

celu działania.

Celem

jest po

żą

dany wynik odnosz

ą

cy si

ę

do przyszło

ś

ci przedsi

ę

wzi

ę

cia lub

działalno

ś

ci.

Uporz

ą

dkowanie rozwi

ą

za

ń

dopuszczalnych z uwagi na kryterium oceny jest to

Funkcja

Celu

(Z; Z(x); FC; FC(x))

2.

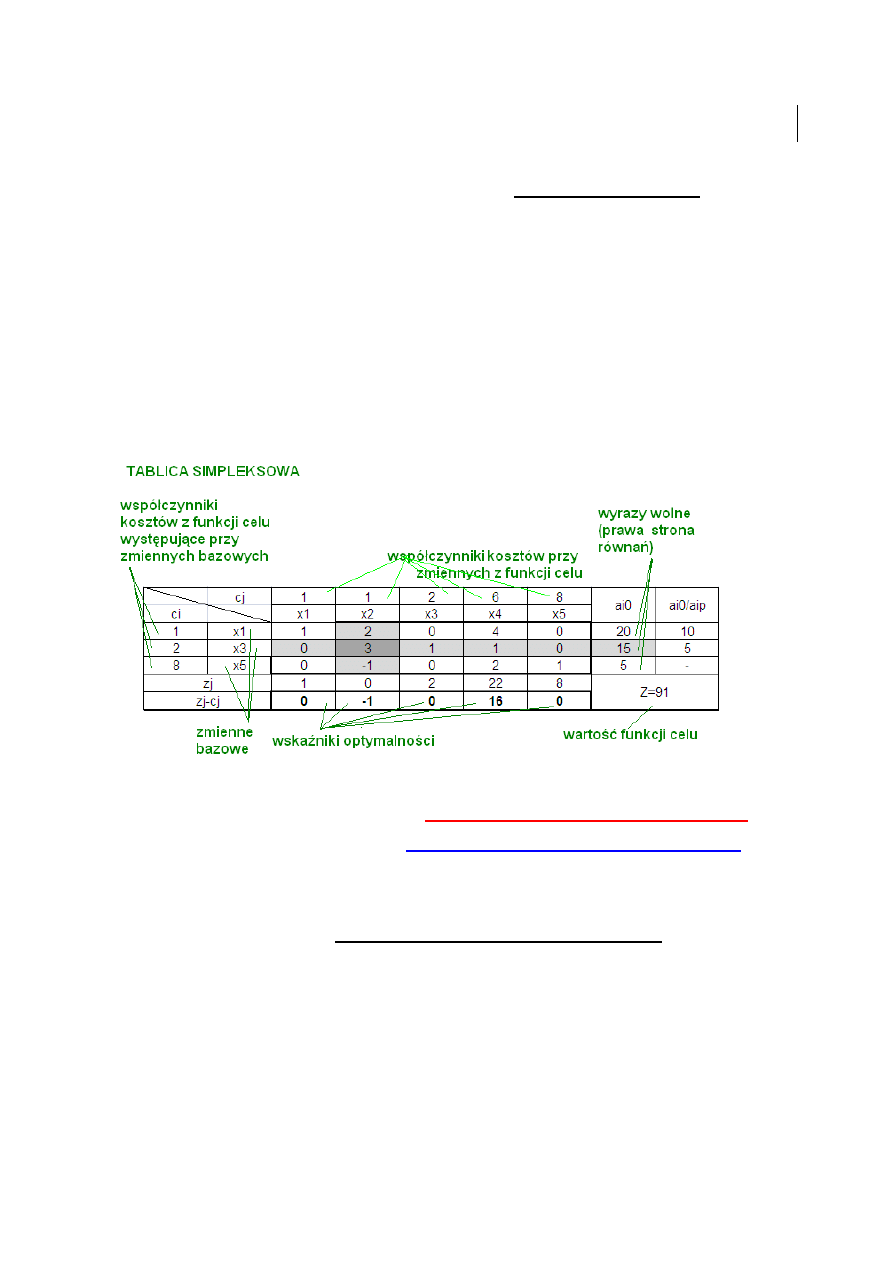
METODA SIMPLEKSOWA

Metoda polega na znalezieniu rozwi

ą

zania (lub rozwi

ą

za

ń

) optymalnych - czyli

najlepszych.

Istniej

ą

dwa rodzaje zagadnie

ń

:

MINIMALIZACJA

(np. kosztów) i

MAKSYMALIZACJA

(np. zysków).

Algorytm metody simpleksowej polega na:

1. Stworzeniu modelu matematycznego - zapis zadania w postaci matematycznej:

Z=c

1

x

1

+c

2

x

2

+…+c

n

x

n

-> max (min) (np. Z= x

1

+x

2

+3x

3

+6x

4

+8x

5

->max)

przy ograniczeniach (przykładowo):

x

1

+2x

2

-x

3

≥

20

x

2

+3x

3

+x

4

=15

3x

2

+x

3

≥

5

Warunki nieujemno

ś

ci:

x

i

≥

0; i=(1;2;3;4)

2. Zapisie w postaci standardowej:

Wyrazy wolne ai0 musz

ą

by

ć

wi

ę

ksze lub równe zero. Je

ś

li nie s

ą

, nale

ż

y równanie

pomno

ż

y

ć

przez (-1)

[uwaga: zmienne, które były przed pomno

ż

eniem przez (-1) w bazie, to

wykonaniu mno

ż

enia mog

ą

ju

ż

nie by

ć

bazowe!]

1

Do przygotowania materiałów wykorzystano własn

ą

wiedz

ę

oraz skrypt: Metody matematyczne w ekonomice, organizacji, i

zarz

ą

dzaniu w budownictwie, prof. Zdzisław Kowalczyk

Zarz

ą

dzanie przedsi

ę

wzi

ę

ciami budowlanymi

Mgr in

ż

. Anna Jakubczyk

2

Ograniczenia, które s

ą

w postaci nierówno

ś

ci nale

ż

y zamieni

ć

na równania poprzez

dodanie do danych nierówno

ś

ci zmiennych bilansuj

ą

cych:

•

dla nierówno

ś

ci typu

≥

odejmujemy

od lewej strony nierówno

ś

ci zmienn

ą

z kolejnym

indeksem; dodatkowa zmienna jest zmienn

ą

NIEDOBORU

- brakuj

ą

ca ilo

ść

(np. zasobu)

do pełnego wykorzystania;

•

dla nierówno

ś

ci typu

≤

dodajemy

zmienn

ą

z kolejnym indeksem; dodatkowa zmienna

jest zmienn

ą

NADMIARU

- niewykorzystana cz

ęść

zasobu ilo

ść

(np. zasobu)

3. Utworzeniu tablicy simpleksowej i znalezieniu rozwi

ą

zania optymalnego

4.Ocena optymalno

ś

ci:

-w przypadku

maksymalizacji

wszystkie

wska

ź

niki "zj-cj" musz

ą

by

ć

nieujemne

-w przypadku

minimalizacji

wszystkie

wska

ź

niki "zj-cj" musz

ą

by

ć

niedodatnie

je

ś

li taki fakt zaistnieje- rozwi

ą

zanie jest optymalne.

-Je

ś

li istnieje wska

ź

nik

ujemny

w przypadku

maksymalizacji

(lub

dodatni

w przypadku

minimalizacji

), to rozwi

ą

zanie nie jest optymalne i nale

ż

y je poprawi

ć

.

Poprawa rozwi

ą

zania:

-Jako

kolumn

ę

główn

ą

wybieramy ten wektor zmiennej swobodnej, dla której wska

ź

nik

jest

najmniejszy z ujemnych

w przypadku

maksymalizacji

lub w przypadku

minimalizacji

jest

najwi

ę

kszy z dodatnich.

Zarz

ą

dzanie przedsi

ę

wzi

ę

ciami budowlanymi

Mgr in

ż

. Anna Jakubczyk

3

-Dla wybranego wektora(kolumny głównej) obliczamy iloraz wyrazów wolnych ai0 przez

wyrazy z wybranej kolumny głównej aip (interesuj

ą

nas warto

ś

ci ilorazu > 0). Ze

wszystkich wyników ilorazów wybieramy warto

ść

najmniejsz

ą

(ale wi

ę

ksz

ą

od zera!).

Ten wybór wskazuje na

wiersz główny

.

-Elementy kolejnej iteracji obliczamy wg wzorów:

•

Wiersz główny:

Wiersz główny w nast

ę

pnej iteracji aik’ powstaje przez podzielenie wiersza z poprzedniej

iteracji a

ik

przez wyraz a

ij

≠

0

•

Kolumna główna:

aqj’

=0, q

≠

0

Wszystkie elementy z kolumny głównej nast

ę

pnej iteracji poza elementem głównym s

ą

równe zero.

•

Pozostałe elementy (poza kolumn

ą

główn

ą

i wierszem głównym)

Rozwi

ą

zania alternatywne:

Je

ś

li istnieje wi

ę

cej ni

ż

jedno rozwi

ą

zanie optymalne, to nazywamy je

alternatywnymi

.

-ka

ż

de rozwi

ą

zanie alternatywne musi by

ć

optymalne (tj. "zj-cj" musz

ą

spełnia

ć

w/w

warunek) i warto

ś

ci funkcji celu "Z" jest zawsze jednakowa (tzn. je

ś

li dla rozwi

ą

zania

optymalnego warto

ść

funkcji celu wynosiła np. Z = 35j.p., to je

ś

li istnieje rozwi

ą

zanie

alternatywne to warto

ść

funkcji celu równie

ż

musi by

ć

Z=35j.p.

-je

ś

li

rozwi

ą

zanie jest optymalne i wska

ź

nik optymalno

ś

ci zj-cj jest równy 0 dla

chocia

ż

jednej zmiennej swobodnej

(nie bazowej), to istnieje rozwi

ą

zanie alternatywne

optymalne, które znajdziemy poprzez kolejn

ą

iteracj

ę

: jako kolumn

ę

główn

ą

trzeba

przyj

ąć

wła

ś

nie t

ę

zmienn

ą

swobodn

ą

, dla której zj-cj=0.

Brak rozwi

ą

zania optymalnego:

W przypadku, kiedy ze znaków wska

ź

ników " zj-cj" wynika,

ż

e rozwi

ą

zanie nie jest

optymalne, a nie mo

ż

na wybra

ć

kolumny głównej, poniewa

ż

jej wszystkie elementy s

ą

niedodatnie, to rozwi

ą

zanie optymalne nie istnieje.

Zarz

ą

dzanie przedsi

ę

wzi

ę

ciami budowlanymi

Mgr in

ż

. Anna Jakubczyk

4

Iteracja zerowa składa si

ę

z:

-przepisanie współczynników przy zmiennych z warunków ograniczaj

ą

cych, wyrazów

wolnych, współczynników przy zmiennych w funkcji celu

-obliczenie zj czyli iloczynu wektora ci oraz xj

-obliczenie wska

ź

ników optymalno

ś

ci zj-cj

-wybór kolumny głównej i wiersza głównego

-przej

ś

cie do kolejnej iteracji

Iteracja kolejna składa si

ę

z:

-obliczenie warto

ś

ci współczynników stoj

ą

cych przy zmiennych oraz wyrazów wolnych

na podstawie w/w wzorów

-obliczenie zj czyli iloczynu wektora ci oraz xj

-obliczenie wska

ź

ników optymalno

ś

ci zj-cj

-wybór kolumny głównej i wiersza głównego

-przej

ś

cie do kolejnej iteracji

Zarz

ą

dzanie przedsi

ę

wzi

ę

ciami budowlanymi

Mgr in

ż

. Anna Jakubczyk

5

3. METODA KAR - METODA SZTUCZNEJ BAZY

Jest to metoda poszukiwania rozwi

ą

zania optymalnego, która

ś

ci

ś

le bazuje na metodzie

simpleksowej.

Metod

ę

kar musimy zastosowa

ć

wtedy, kiedy na wst

ę

pie nie mo

ż

emy ustali

ć

rozwi

ą

zania bazowego tj. nie ma BAZY.

Baz

ę

mamy wtedy, kiedy mamy tyle wektorów bazowych ile jest warunków

ograniczaj

ą

cych (równa

ń

).

W ka

ż

dym równaniu musimy mie

ć

jedn

ą

zmienn

ą

bazow

ą

- czyli tak

ą

, której

współczynnik w tym równaniu jest równy "1" a w pozostałych ta zmienna nie wyst

ę

puje

czyli jej współczynniki s

ą

równe "0".

Do równa

ń

, które nie posiadaj

ą

zmiennej bazowej nale

ż

y doda

ć

sztuczn

ą

zmienn

ą

bazow

ą

z kolejnym indeksem, któr

ą

wprowadzamy równie

ż

do funkcji celu ze

szczególnie niekorzystnym współczynnikiem kosztów:

-w przypadku

maksymalizacji

zmienna sztuczna musi mie

ć

współczynnik

-M

, gdzie M>>0

-w przypadku

minimalizacji

zmienna sztuczna musi mie

ć

współczynnik

+M

, gdzie M>>0.

Dalsza procedura jest ju

ż

znana: mamy baz

ę

i przechodzimy do budowania tablicy

simpleksowej, pami

ę

taj

ą

c, aby nad sztuczn

ą

zmienn

ą

w wierszu "cj" zapisa

ć

współczynnik

M

lub

-M

. W rozwi

ą

zaniu automatycznie d

ąż

y si

ę

do usuni

ę

cia sztucznych

zmiennych z bazy i znalezienia optymalnego rozwi

ą

zania.

Zarz

ą

dzanie przedsi

ę

wzi

ę

ciami budowlanymi

Mgr in

ż

. Anna Jakubczyk

6

4. ZAGADNIENIE TRANSPORTOWE

Z zagadnieniem transportowym mamy do czynienia wtedy, gdy mamy problem typu:

Z m punktów dostaw nale

ż

y dostarczy

ć

towar (jednego typu) do n punktów odbioru.

Dla ka

ż

dego punktu dostaw jest okre

ś

lona ilo

ść

transportowanego towaru, analogicznie

dla ka

ż

dego z punktów odbioru jest okre

ś

lona ilo

ść

towaru, jak

ą

nale

ż

y tam dostarczy

ć

.

Dla ka

ż

dego transportu jest okre

ś

lony koszt przewozu c

ij

.

Je

ś

li ilo

ść

towaru dostarczanego = ilo

ś

ci towaru odbieranego mamy do czynienia z

zagadnieniem

zbilansowanym

. W przeciwnym przypadku zagadnienie jest

niezbilansowane

(patrz str. 14)

m-ilo

ść

dostawców

i-nr kolejnego dostawcy, i=(1,m)

n- ilo

ść

odbiorców

j- nr kolejnego odbiorcy, j=(1,n)

c

ij

- koszt transportu towaru z punktu „i” do punktu „j” [jednostki pieni

ęż

ne j.p.]

x

ij

- ilo

ść

towaru przewo

ż

ona z punktu „i” do punktu „j”

W zagadnieniu transportowym

zawsze

mamy do czynienia z MINIMALIZACJ

Ą

(KOSZTÓW).

Funkcja celu przyjmie zatem posta

ć

:

∑ ∑

=

=

→

=

m

i

n

j

xij

cij

Z

1

1

min

*

Wyznaczenie x

ij

– problem zagadnienia transportowego: jak dobra

ć

x

ij

, aby koszty

całego transportu były minimalne?

Istnieje kilka szybkich metod rozkładu towaru. S

ą

to metody pozwalaj

ą

ce znale

źć

rozwi

ą

zanie dopuszczalne, ale

niekoniecznie optymalne

! Czyli rozwi

ą

zanie mo

ż

e

mie

ć

rzeczywiste zastosowanie ( dostawcy pozb

ę

d

ą

si

ę

całego towaru, a odbiorcy

otrzymaj

ą

potrzebn

ą

im ilo

ść

towaru), ale nie zawsze to rozwi

ą

zanie jest najta

ń

sze =

optymalne!

Zarz

ą

dzanie przedsi

ę

wzi

ę

ciami budowlanymi

Mgr in

ż

. Anna Jakubczyk

7

ALGORYTM ROZWI

Ą

ZANIA ZAGADNIENIA TRANSPORTOWEGO:

1. Znalezienie wst

ę

pnego rozwi

ą

zania bazowego

2. Ocena optymalno

ś

ci:

a) wyznaczenie potencjałów (ui) i (-vj)

b) wyznaczenie ocen

δ

δ

δ

δ

ij

3. Ewentualna poprawa rozwi

ą

zania poprzez dodanie warto

ś

ci "

θ

θ

θ

θ

" i przej

ś

cie do

punktu 2.

Ad1. Metody wyznaczania rozwi

ą

zania dopuszczalnego:

1. Metoda k

ą

ta północno-zachodniego

2. Metoda minimalnego elementu w wierszu

3. Metoda minimalnego elementu w kolumnie

4. Metoda minimalnego elementu w macierzy

5. Metoda VAM

2

Nale

ż

y pami

ę

ta

ć

o zasadzie:

Ilo

ść

w

ę

złów bazowych= ilo

ść

wypełnionych kratek: m+n-1, Gdzie:

m - liczba dostawców
n - liczba odbiorców

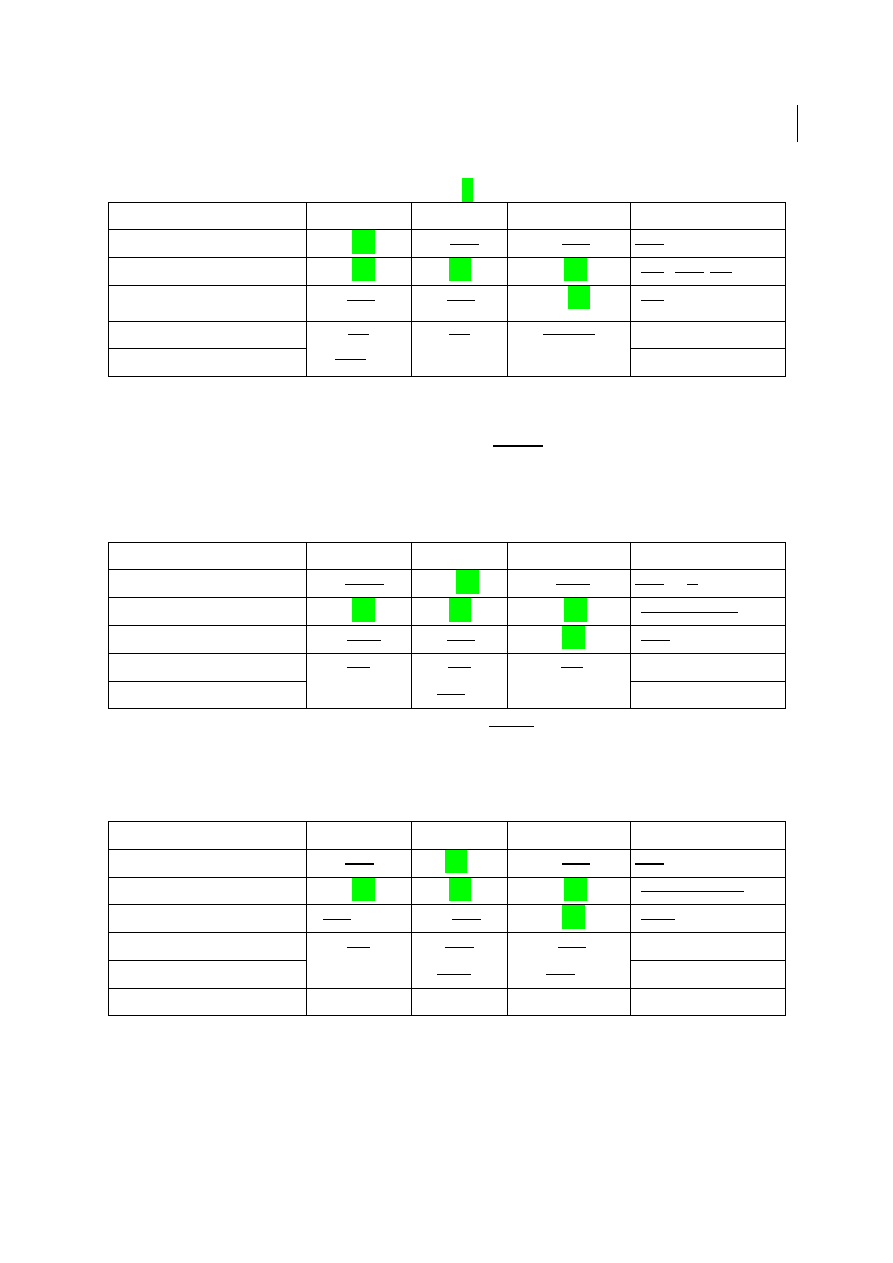
1. METODA K

Ą

TA PÓŁNOCNO-ZACHODNIEGO

-zaczynamy uzupełnia

ć

tabel

ę

od klatki poło

ż

onej najbardziej na górze i po lewej.

Uwaga: Je

ś

li wykre

ś

lamy naraz kolumn

ę

i wiersz nale

ż

y wpisa

ć

„zero bazowe” w

klatce o najmniejszym koszcie, je

ś

li istniej

ą

dwie lub wi

ę

cej takich klatek to

„zero” wpisujemy najbardziej na lewo lub najwy

ż

ej!

O1

O2

O3

Zasób dostawców

D1

5

2

8

10

D2

1

4

6

60

D3

3

7

2

20

Potrzeby odbiorców

20

40

30

Zasób dostawców: 20+40+30=90
Potrzeby odbiorców: 10+60+20=90,
90

≡

90 czyli D=O => zadanie jest zbilansowane

2

Metoda nie omawiana na zaj

ę

ciach

Zarz

ą

dzanie przedsi

ę

wzi

ę

ciami budowlanymi

Mgr in

ż

. Anna Jakubczyk

8

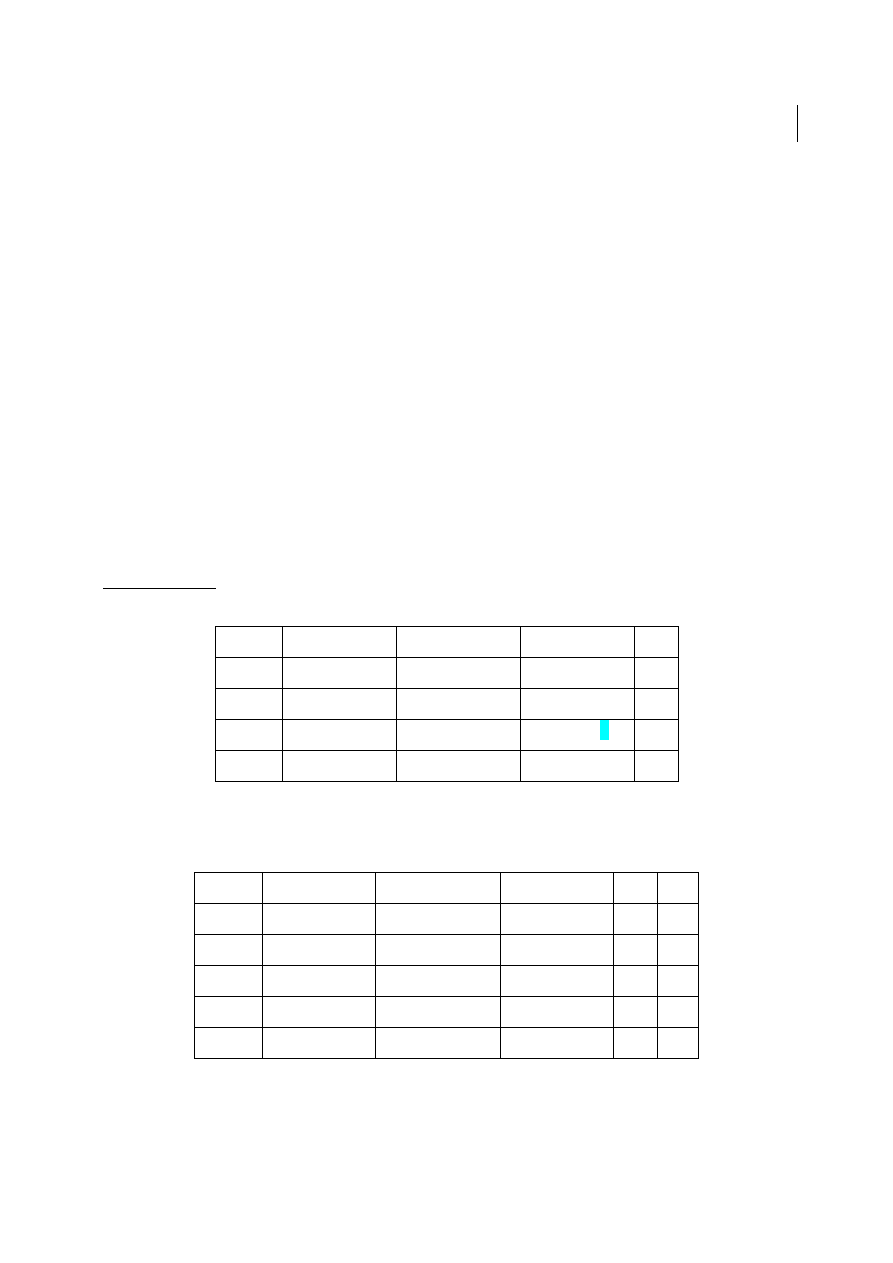
Ilo

ść

w

ę

złów bazowych m+n-1= 3+3-1=5

O1

O2

O3

Zasób dostawców

D1

10

5

2

8

10 0

D2

10

1

40

4

10

6

60; 50; 10

D3

3

7

20

2

20

Potrzeby odbiorców

20

10; 0

40

0

30; 20

0

Jest to wst

ę

pne rozwi

ą

zanie bazowe znalezione metod

ą

k

ą

ta północno-zachodniego. Na tym

etapie niewiadomo, czy jest optymalne, chocia

ż

warto

ść

funkcji celu mo

ż

emy wyliczy

ć

:

Z= 10*5+10*1+40*4+10*6+20*2= 50+10+160+60+40= 320j.p.

2.METODA MINIMALNEGO ELEMENTU W WIERSZU

-rozpoczynamy wpisywanie od klatek o najmniejszym koszcie w wierszu

O1

O2

O3

Zasób dostawców

D1

5

10

2

8

10 ; 0

D2

20

1

30

4

10

6

60; 40; 10; 0

D3

3

7

20

2

20; 0

Potrzeby odbiorców

20

0

40

30; 0

30

0

Z= 10*2+20*1+30*4+10*6+20*2=20+20+120+60+40= 260j.p. (nie wiadomo, czy optymalne, ale
na pewno ta

ń

sze = lepsze ni

ż

poprzednie)

3.METODA MINIMALNEGO ELEMENTU W KOLUMNIE

-rozpoczynamy wpisywanie od klatek o najmniejszym koszcie w kolumnie

O1

O2

O3

Zasób dostawców

D1

5

10

2

8

10 ; 0

D2

20

1

30

4

10

6

60; 40; 10; 0

D3

3

7

20

2

20; 0

Potrzeby odbiorców

20

0

40;

30; 0

30;

10; 0

Zarz

ą

dzanie przedsi

ę

wzi

ę

ciami budowlanymi

Mgr in

ż

. Anna Jakubczyk

9

4.METODA MINIMALNEGO ELEMENTU W MACIERZY

-rozpoczynamy wpisywanie od klatek o najmniejszym koszcie w całej tablicy

O1

O2

O3

Zasób dostawców

D1

5

10

2

8

10 ; 0

D2

20

1

30

4

10

6

60; 40; 10; 0

D3

3

7

20

2

20; 0

Potrzeby odbiorców

20;

0

40;

30; 0

30;

10; 0

3 ostatnie metody dały taki sam wynik, co nie oznacza,

ż

e zawsze taka zale

ż

no

ść

wyst

ą

pi!

Ad2. Ocena optymalno

ś

ci:

Oceny

δ

ij = ui+(-vj)+cij,

zało

ż

enie: dla zmiennych bazowych(czyli wypełnionych

klatek) ocena wynosi zero.

Nale

ż

y wyznaczy

ć

warto

ś

ci potencjałów (ui) i (-vj) wg nast

ę

puj

ą

cej zasady:

-Przyjmujemy u1= 0.

-obliczamy potencjały bazuj

ą

c na wypełnionych klatkach i wiedz

ą

c,

ż

e oceny s

ą

dla tych

klatek równe zero.

-po wyznaczeniu potencjałów obliczamy oceny dla klatek pustych.

Rozwi

ą

zanie jest optymalne, je

ś

li wszystkie oceny s

ą

nieujemne.

Rozwi

ą

zania alternatywne - istniej

ą

, je

ś

li dla chocia

ż

jednej klatki pustej ocena równa

si

ę

zeru. Rozwi

ą

zanie to mo

ż

na znale

źć

poprzez zmian

ę

rozwi

ą

zania przez

wprowadzenie warto

ś

ci

Θ

Θ

Θ

Θ

zaczynaj

ą

c cykl w miejscu klatki pustej (zmiennej swobodnej),

dla której ocena wynosiła zero.

Ad3. Poprawa rozwi

ą

zania:

Kiedy istnieje ujemna ocena

δ

δ

δ

δ

ij, rozwi

ą

zanie jest nieoptymalne i mo

ż

na je poprawi

ć

poprzez budow

ę

cyklu:

-wybieramy klatk

ę

pust

ą

o najmniejszej ujemnej warto

ś

ci. Je

ś

li istniej

ą

dwie klatki o

takiej samej ujemnej ocenie to wybieramy klatk

ę

z

mniejszym

kosztem

-w t

ę

klatk

ę

wstawiamy warto

ść

Θ

Θ

Θ

Θ

≥

0 (czyli ta zmienna ze swobodnej zamienia si

ę

w

Zarz

ą

dzanie przedsi

ę

wzi

ę

ciami budowlanymi

Mgr in

ż

. Anna Jakubczyk

10

bazow

ą

) - powstaje nowa trasa, ale jednocze

ś

nie jedn

ą

inn

ą

tras

ę

trzeba usun

ąć

-

zmienna bazowa wychodzi z bazy i staje si

ę

swobodn

ą

(musi by

ć

zachowany warunek:

m+n-1). Je

ś

li wi

ę

cej ni

ż

jedna zmienna wychodzi z bazy, to wprowadzamy zero bazowe

w klatce o mniejszym

3

koszcie a klatk

ę

o wi

ę

kszym koszcie wykre

ś

lamy).

-budujemy cykl: w kolumnie i wierszu, w którym dodali

ś

my

Θ

Θ

Θ

Θ

musimy zrobi

ć

bilans wi

ę

c

musimy te

ż

odj

ąć

Θ

Θ

Θ

Θ

w tym wierszu i kolumnie.

Warto

ść

Θ

Θ

Θ

Θ

mo

ż

emy dodawa

ć

i

odejmowa

ć

tylko po zaj

ę

tych klatkach

czyli na poł

ą

czeniach (trasach), które istniej

ą

.

Nie mo

ż

na odj

ąć

ani doda

ć

Θ

Θ

Θ

Θ

do klatki pustej, gdy

ż

to poł

ą

czenie (ta trasa) nie istnieje!

Wyj

ą

tkiem jest pierwszy krok cyklu kiedy to wprowadzamy zmienn

ą

do bazy. Dodajemy i

odejmujemy

Θ

Θ

Θ

Θ

a

ż

b

ę

d

ą

zbilansowane wszystkie wiersze i kolumny(zamkni

ę

cie cyklu),

przy czym w jednej kolumnie(wierszu)

Θ

Θ

Θ

Θ

mo

ż

e by

ć

odj

ę

ta i dodana jednokrotnie.

Zawsze mo

ż

na utworzy

ć

tylko jeden cykl. Je

ś

li nie mo

ż

na utworzy

ć

cyklu oznacza to,

ż

e rozwi

ą

zanie optymalne nie istnieje.

-warto

ść

Θ

Θ

Θ

Θ

= min

p.k.c

. {xij} z klatek parzystych cyklu, czyli tych w których

odejmowali

ś

my

Θ

Θ

Θ

Θ

.

Podajemy nowe rozwi

ą

zanie w nast

ę

pnej tabeli i wyznaczamy warto

ś

ci potencjałów i

ocen, aby stwierdzi

ć

, czy jest optymalne. Je

ś

li nie, trzeba je dalej poprawi

ć

itd.

3

Je

ś

li wstawimy zero bazowe w klatce o najwi

ę

kszym lub

ś

rednim koszcie to nie b

ę

dzie to bł

ą

d jednak wg literatury [1] lepiej jednak

wstawia

ć

zero w klatce o najmniejszym koszcie, wtedy prawdopodobnie szybciej dojdziemy do rozwi

ą

zania. Du

ż

ym bł

ę

dem jest

pomini

ę

cie zera bazowego.

Zarz

ą

dzanie przedsi

ę

wzi

ę

ciami budowlanymi

Mgr in

ż

. Anna Jakubczyk

11

ZAGADNIENIE TRASY ZABLOKOWANEJ - ZAKAZ PRZEWOZU

Nakładamy dodatkowy warunek np. trzeci odbiorca nie mo

ż

e dosta

ć

ż

adnego towaru od

trzeciego dostawcy (powiedzmy,

ż

e nagle stało si

ę

to nieopłacalne, poniewa

ż

np. trasa

przewozu si

ę

wydłu

ż

yła, droga jest remontowana, b

ą

d

ź

dostawca przeniósł swoj

ą

placówk

ę

itp.).

Dla tej trasy nakładamy bardzo du

ż

y koszt przewozu

c

33

=M, M>>0.

Takie zagadnienie mo

ż

na rozwi

ą

za

ć

dla 2 przypadków::

1. Znale

źć

rozwi

ą

zanie optymalne dla normalnych kosztów (c

33

=2 )i potem wstawi

ć

koszt c

33

=M, M>>0 (przypadek, kiedy mamy ju

ż

wyznaczone trasy i nagle co

ś

si

ę

wydarzyło i musimy zablokowa

ć

tras

ę

)

2. Zacz

ąć

rozwi

ą

zywa

ć

zadanie od razu z kosztem c

33

=M, M>>0 (przypadek, kiedy

przed planowaniem mamy informacj

ę

,

ż

e dane poł

ą

czenie b

ę

dzie bardzo

nieopłacalne)

Zagadnienie 1:

Znale

źć

optymalne rozwi

ą

zanie zagadnienia a nast

ę

pnie uwzgl

ę

dni

ć

zablokowan

ą

tras

ę

3-3.

O1

O2

O3

D1

1

3

2

30

D2

4

2

6

20

D3

5

1

2

20

10

20

40

Zagadnienie jest zbilansowane D: 30+20+20=70, O:10+20+40=70.

Liczba zmiennych bazowych (wypełnionych klatek): m+n-1=5

O1

O2

O3

ui

D1

0 10 1

2 / 3

0 20 2

30

0

D2

2 / 4

0 20 2

3 / 6

20

-1

D3

4 / 5

0 0 1

0 20 2

20

0

10

20

40

-vj

-1

-1

-2

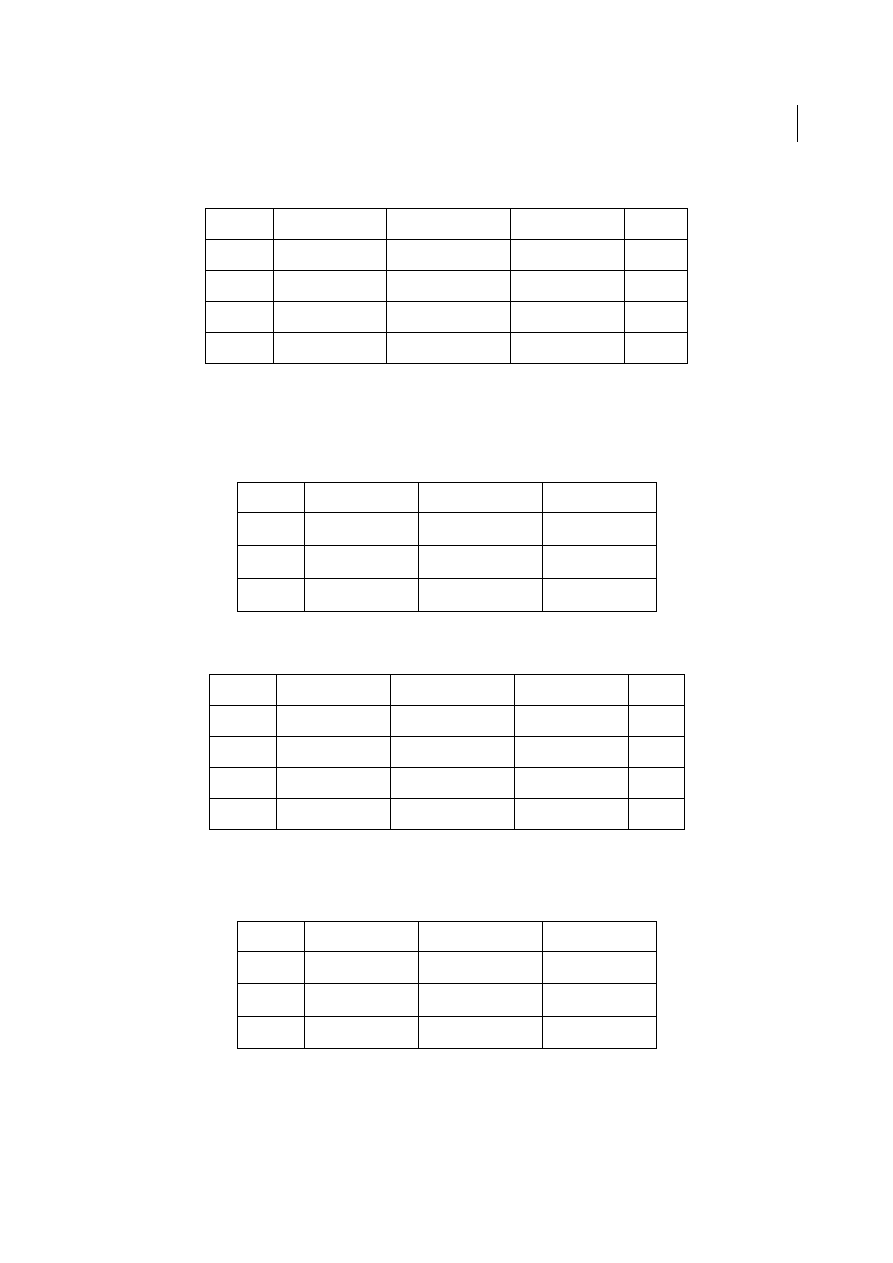
Zarz

ą

dzanie przedsi

ę

wzi

ę

ciami budowlanymi

Mgr in

ż

. Anna Jakubczyk

12

Rozwi

ą

zanie jest optymalne, nakładamy koszt c

33

=M, M>>0

O1

O2

O3

ui

D1

0 10 1

M / 3

0 20 2

0

D2

-M+4

/ 4

0 20 2

-M+5

/ 6

-M+1

D3

-M+6

/ 5

0 0 1

0 20

M

-M+2

-vj

-1

M-3

-2

To samo rozwi

ą

zanie przy wprowadzonym dodatkowym warunku ju

ż

nie jest optymalne,

poniewa

ż

-M+4<0;

-M+5<0;

-M+6<0, najmniejsza ocena to -M+4

, wi

ę

c tam rozpoczynamy cykl

+

Θ

Θ

Θ

Θ

:

O1

O2

O3

D1

0 10

-

Θ

Θ

Θ

Θ

1

M / 3

0 20

+

Θ

Θ

Θ

Θ

2

D2

-M+4 /

+

Θ

Θ

Θ

Θ

4

0 20

-

Θ

Θ

Θ

Θ

2

-M+5 / 6

D3

-M+6 / 5

0 0

+

Θ

Θ

Θ

Θ

1

0 20

-

Θ

Θ

Θ

Θ

M

Θ

Θ

Θ

Θ

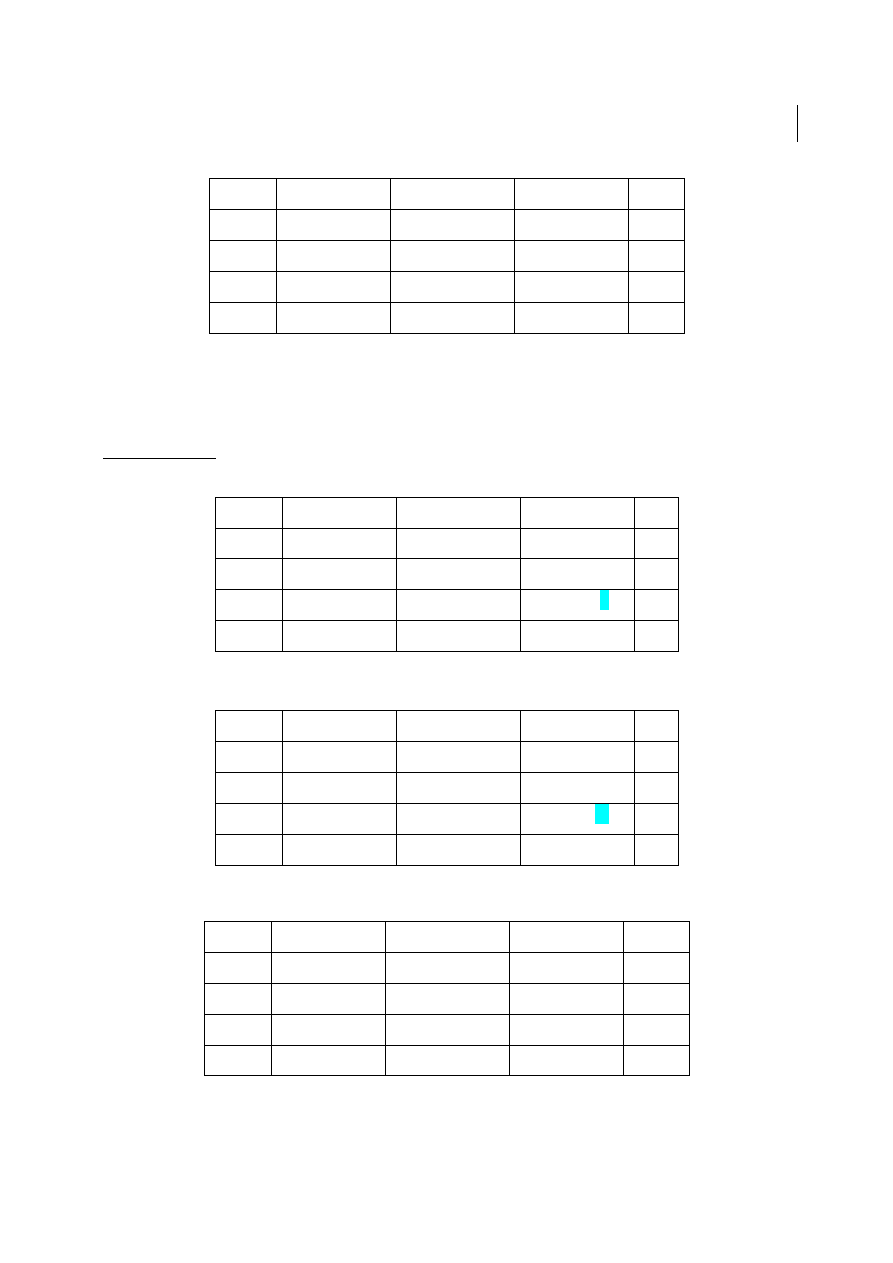
= min{10; 20; 20} = 10

O1

O2

O3

ui

D1

M-4 / 1

M / 3

0 30 2

0

D2

0 10 4

0 10 2

-M+5

/ 6

-M+1

D3

2 / 5

0 10 1

0 10 M

-M+2

-vj

M-5

M-3

-2

Nadal rozwi

ą

zanie nie jest optymalne, poniewa

ż

-M+5

<0, wi

ę

c w tej klatce

rozpoczynamy cykl:

O1

O2

O3

D1

M-4 / 1

M / 3

0 30 2

D2

0 10 4

0 10

-

Θ

Θ

Θ

Θ

2

-M+5

/

+

Θ

Θ

Θ

Θ

6

D3

2 / 5

0 10

+

Θ

Θ

Θ

Θ

1

0 10

-

Θ

Θ

Θ

Θ

M

Θ

Θ

Θ

Θ

=

min {10; 10} = 10

Zarz

ą

dzanie przedsi

ę

wzi

ę

ciami budowlanymi

Mgr in

ż

. Anna Jakubczyk

13

O1

O2

O3

ui

D1

1 / 1

5 / 3

0 30 2

0

D2

0 10 4

0 0 2

0 10 6

-4

D3

2 / 5

0 20 1

M-5 / M

-3

-vj

0

2

-2

Teraz wszystkie oceny

δ

ij

≥

0, wi

ę

c rozwi

ą

zanie jest optymalne. Brak rozwi

ą

za

ń

alternatywnych,

poniewa

ż

ż

adna ocena nie jest równa zeru dla zmiennych swobodnych (

δ

ij >0).

Zagadnienie 2:

Znale

źć

rozwi

ą

zanie optymalne uwzgl

ę

dniaj

ą

c warunek,

ż

e trasa 3-3 jest niemo

ż

liwa.

O1

O2

O3

D1

1

3

2

30

D2

4

2

6

20

D3

5

1

2

20

10

20

40

Zmieniamy od razu koszt c33 z 2 jednostek na M, M>>0:

O1

O2

O3

D1

1

3

2

30

D2

4

2

6

20

D3

5

1

M

20

10

20

40

I znajdujemy rozwi

ą

zanie wst

ę

pne np. metod

ą

minimalnego elementu w wierszu:

O1

O2

O3

ui

D1

0 10 1

M / 3

0 20 2

0

D2

-M+4 / 4

0 20 2

-M+5 / 6

-M+1

D3

-M+6 / 5

0 0 1

0 20 M

-M+2

-vj

-1

M-3

-2

Dalsze rozwi

ą

zanie jak wcze

ś

niej.

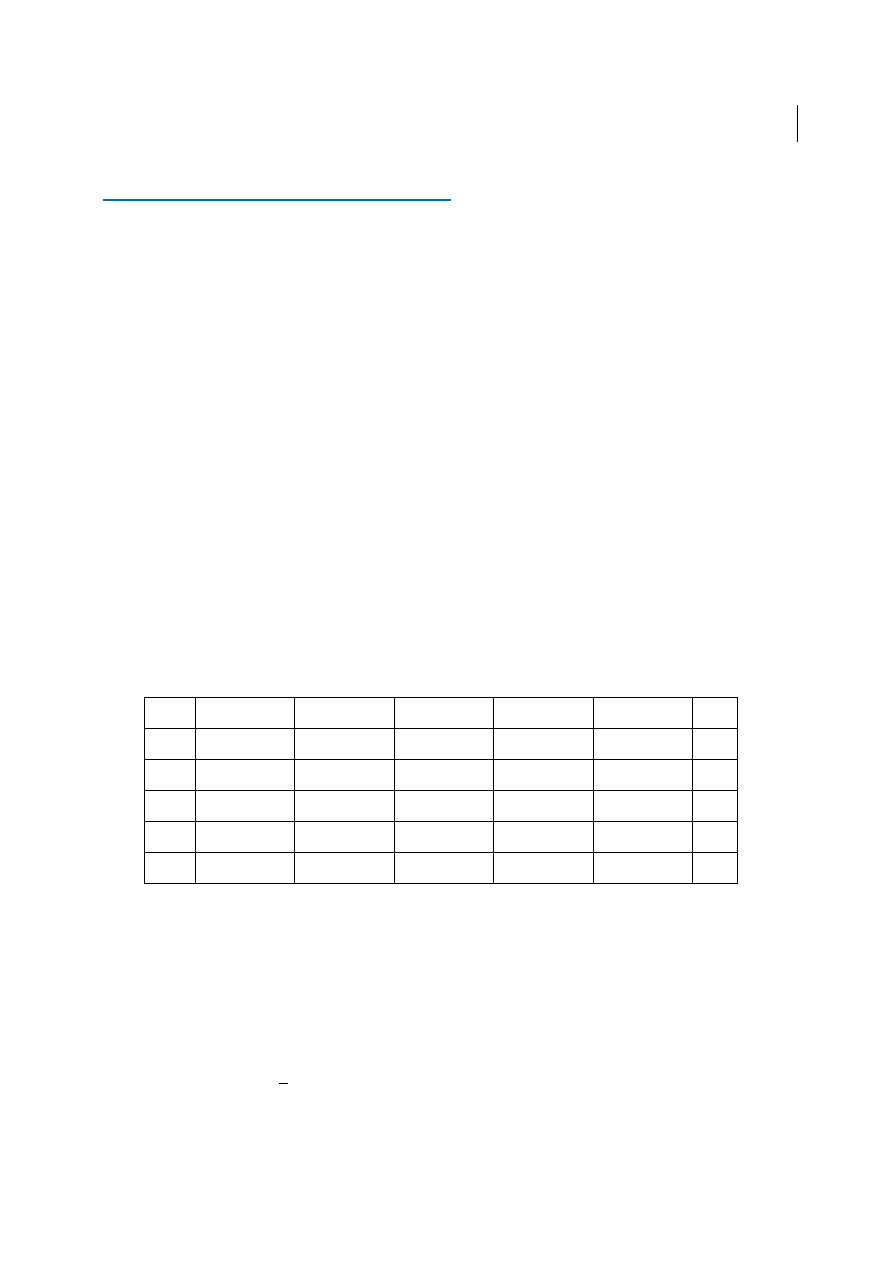
Zarz

ą

dzanie przedsi

ę

wzi

ę

ciami budowlanymi

Mgr in

ż

. Anna Jakubczyk

14

ZAGADNIENIE NIEZBILANSOWANE

Mamy do czynienia z 2 przypadkami zagadnienia niezbilansowanego:

1. Sumaryczna ilo

ść

towaru u dostawców jest wi

ę

ksza od ł

ą

cznego

zapotrzebowania odbiorców

2. Sumaryczna ilo

ść

towaru u dostawców jest mniejsza od ł

ą

cznego

zapotrzebowania odbiorców

Ad1. Wprowadzamy

FIKCYJNEGO ODBIORC

Ę

, któremu przydzielamy

zapotrzebowanie równe nadmiarowi towaru

Ad2. Wprowadzamy

FIKCYJNEGO DOSTAWC

Ę

, któremu przydzielamy zapas równy

niedoborowi towaru

Koszty fikcyjnych transportów s

ą

równe zeru, poniewa

ż

tak naprawd

ę

towar nie

zostanie przetransportowany. W pierwszym przypadku niektórzy z dostawców nie

pozb

ę

d

ą

si

ę

nadmiaru towaru, a w drugim przypadku niektórzy z odbiorców nie

zostan

ą

w cało

ś

ci zaopatrzeni. Wprowadzaj

ą

c fikcyjne punkty odszukujemy

rozwi

ą

zanie najbardziej korzystne (np. komu mo

ż

na nie dostarczy

ć

całego towaru

tak, aby było to najta

ń

sze).

Zad: Rozwi

ą

za

ć

zagadnienie transportowe:

O1

O2

O3

O4

O5

D1

4

8

1

5

7 100

D2

5

2

1

9

2 60

D3

3

3

2

1

6 40

D4

3

4

6

8

1 50

30

70

20

60

40

SD = 100+60+40+50=250

SO=30+70+20+60+40=220

Jest to przypadek 1) wi

ę

c wprowadzamy FIKCYJNEGO ODBIORC

Ę

o

zapotrzebowaniu 250-220=30 i znajdujemy wst

ę

pne rozwi

ą

zanie bazowe.

Nast

ę

pnie wyznaczamy potencjały i oceny sprawdzaj

ą

c czy rozwi

ą

zanie jest

optymalne, je

ś

li nie musimy je poprawi

ć

:

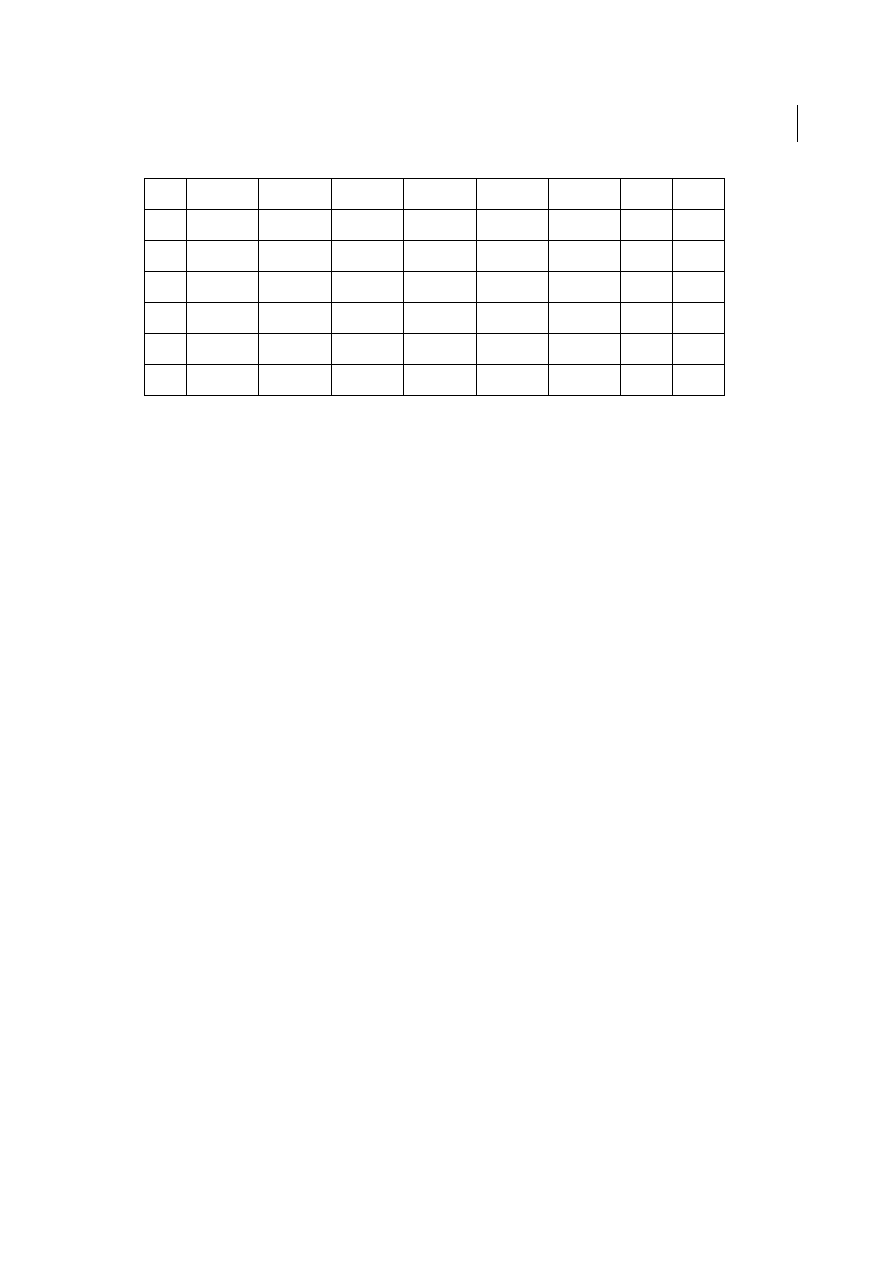
m+n-1= 4+6-1=9

Zarz

ą

dzanie przedsi

ę

wzi

ę

ciami budowlanymi

Mgr in

ż

. Anna Jakubczyk

15

O1

O2

O3

O4

O5

OF

ui

D1

0 30 4

1 / 8 0 20 1 0 20 5 3 / 7 0 30 0 100

0

D2

6 / 5 0 60 2 5 / 1 9 / 9 3 / 2 5 / 0 60

5

D3

3 / 3 0 0 3 5 / 2 0 40 1 6 / 6 4 / 0 40

4

D4

2 / 3 0 10 4 8 / 6 6 / 8 0 40 1 3 / 0 50

3

30

70

20

60

40

30

-vj

-4

-7

-1

-5

-4

0

Optymalna warto

ść

funkcji celu:

Z

min

= 30*4+20*1+20*5+30*0+60*2+0*3+40*1+10*4+40*1 = 480j.p.

Odp. Rozwi

ą

zanie jest optymalne. Koszt całego transportu wynosi 480j.p.

Zadanie nie jest zbilansowane, mamy nadmiar towaru (30j.). Najbardziej

korzystnym rozwi

ą

zaniem jest, aby pierwszy dostawca nie pozbył si

ę

30

jednostek towaru.

Zalecana literatura:

1. Z. Kowalczyk: Metody matematyczne w ekonomice, organizacji, i zarz

ą

dzaniu w

budownictwie, Wydawnictwo Politechniki Gda

ń

skiej, Gda

ń

sk 1982

2. Z. Kowalczyk, J. Zabielski: Kosztorysowanie i normowanie w budownictwie, WSiP,

Warszawa 2005

3. K.M. Jaworski: Podstawy organizacji budowy, PWN Warszawa 2004

4. K.M. Jaworski: Metodologia projektowania realizacji budowy, PWN Warszawa 1999

5. C.L. Pritchard: Zarz

ą

dzanie ryzykiem w projektach. Teoria i praktyka, Management

Training & Development Center, WIG – PRESS, Warszawa 2002

6. Praca zbiorowa pod red. E. Ignasiaka: Badania operacyjne, PWE, Warszawa 2001.

Zarz

ą

dzanie przedsi

ę

wzi

ę

ciami budowlanymi

Mgr in

ż

. Anna Jakubczyk

16

Zadania do samodzielnego rozwi

ą

zania:

Zad.1. Rozwi

ą

za

ć

:

Z = 2x1+x2-4x3+x4+10x5+5x6+8x7->max

Przy ograniczeniach:

x1-2x5+4x6+2x7=15

x2+4x5+x6+5x7=10

x3+x5+2x6-2x7=12

x4+2x5-x6+x7=20

xi

≥

0, i=

Є

(1,7)

Odpowied

ź

:

Z=50,89

X1=0, x2=0, x3=1,72, x4=21,67, x5=1,39, x6=4,44, x7=0

Zad.2 Rozwi

ą

za

ć

:

Z=2x1-x2+x3-2x4+2x5->min

Przy ograniczeniach:

-2x1+x2+x3=4

x1+4x2+x3+x4=32

x1+x5=8

xi

≥

0, i=

Є

(1,5)

Odpowied

ź

:

Z= -36

X1=0, x2=0, x3=4, x4=28, x5=8

Zad.3. Rozwi

ą

za

ć

:

Z=x1+2x2+x3+3x4->max

Przy ograniczeniach:

X1+2x3+3x4=30

2x1+x2+2x3=40

x3+x4

≤

10

xi

≥

0, i=

Є

(1,4)

Odpowied

ź

:

Z = 110

X1=0, x2=40, x3=0, x4=10, x5=0

Zarz

ą

dzanie przedsi

ę

wzi

ę

ciami budowlanymi

Mgr in

ż

. Anna Jakubczyk

17

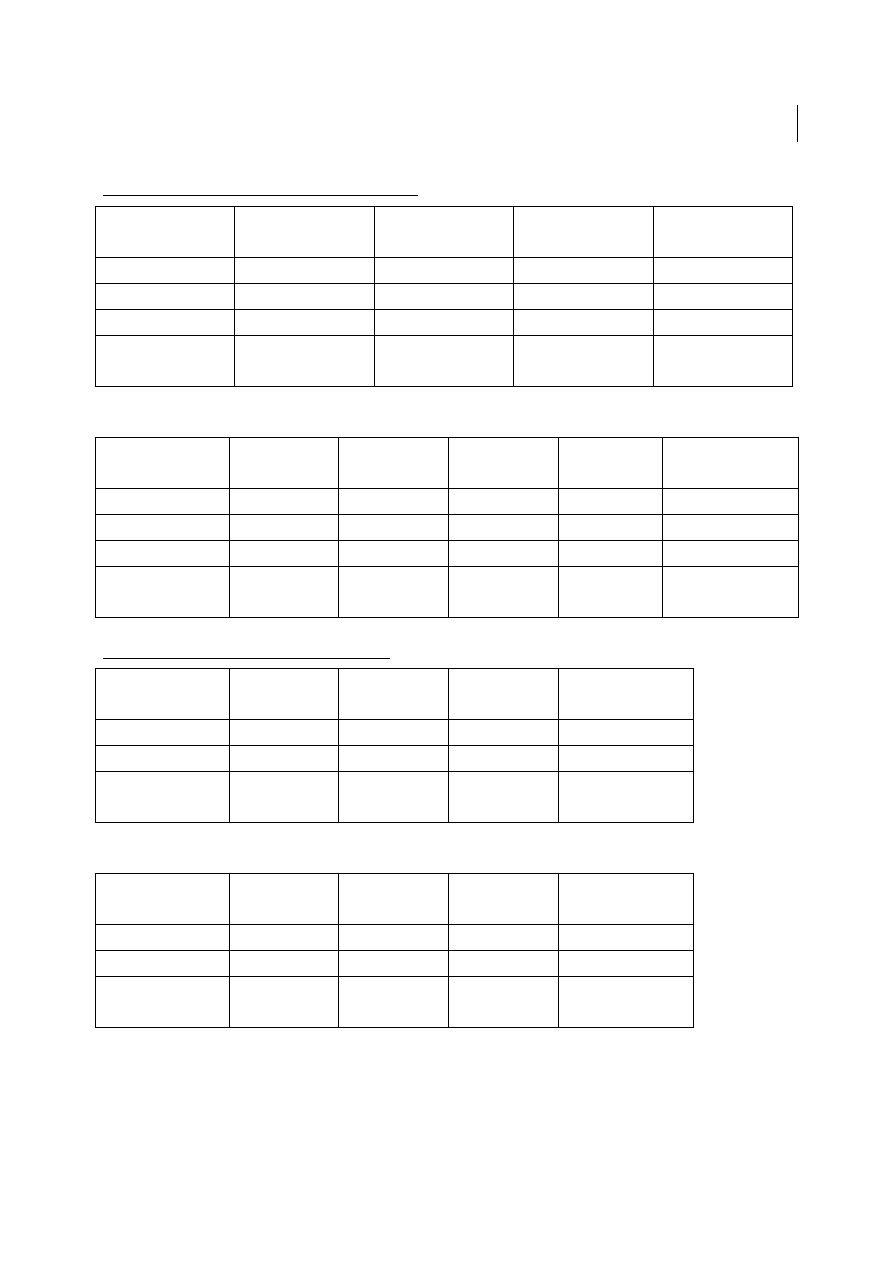
Zad4. Znale

źć

optymalny plan przewozu:

O1

O2

O3

ZASÓB

DOSTAWCÓW

D1

7

3

6

75

D2

4

8

2

40

D3

1

5

9

35

POTRZEBY

ODBIORCÓW

20

45

30

Odp.:

O1

O2

O3

OF

ZASÓB

DOSTAWCÓW

D1

/ 7

45 3

/ 6

30 0

75

D2

/ 4

/ 8

30 2

10 0

40

D3

20 1

/ 5

/ 9

15 0

35

POTRZEBY

ODBIORCÓW

20

45

30

55

Zad5. Znale

źć

optymalny plan przewozu:

O1

O2

O3

ZASÓB

DOSTAWCÓW

D1

6

8

2

60

D2

3

5

10

30

POTRZEBY

ODBIORCÓW

25

45

20

Odp.:

O1

O2

O3

ZASÓB

DOSTAWCÓW

D1

25 6

15 8

20 2

60

D2

/ 3

30 5

/ 10

30

POTRZEBY

ODBIORCÓW

25

45

20

Zarz

ą

dzanie przedsi

ę

wzi

ę

ciami budowlanymi

Mgr in

ż

. Anna Jakubczyk

18

Istnieje równie

ż

rozwi

ą

zanie alternatywne:

O1

O2

O3

ZASÓB

DOSTAWCÓW

D1

/ 6

40 8

20 2

60

D2

25 3

5 5

/ 10

30

POTRZEBY

ODBIORCÓW

25

45

20

Zad.6 Znale

źć

optymalny plan przewozu, wiedz

ą

c z góry,

ż

e trasa 2-2 (od drugiego

dostawcy do 2 odbiorcy) jest nieczynna/nieopłacalna.

O1

O2

O3

O4

ZASÓB

DOSTAWCÓW

D1

3

2

3

2

70

D2

5

1

9

4

40

D3

1

5

7

1

30

POTRZEBY

ODBIORCÓW

20

30

40

50

Sugerowana metoda: minimalnego elementu w kolumnie

Rozwi

ą

za

ć

te

ż

metod

ą

minimalnego elementu w wierszu i minimalnego elementu w

macierzy, aby utrwali

ć

algorytm i sprawdzi

ć

swoje rozwi

ą

zanie.

Odp.

O1

O2

O3

O4

ZASÓB

DOSTAWCÓW

D1

/ 3

30 2

40 3

0 2

70

D2

/ 5

/ M

/ 9

40 4

40

D3

20 1

/ 5

/ 7

10 1

30

POTRZEBY

ODBIORCÓW

20

30

40

50