1/10
Archives of Foundry,
Ye ar 2003, Volume 3, № 10
Archiwum Odlewnictwa,
Rok 2003, Rocznik 3, Nr 10
PAN – Katowice PL ISSN 1642-5308
OCENA FRAKTALNA POWIERZCHNI KRZEPNIĘCIA
M. MAREK
1
Politechnika Częstochowska
Instytut Mechaniki i Podstaw Konstrukcji Maszyn
ul. Dąbrowskiego 73, 42-201 Częstochowa, Polska
STRESZCZENIE
Artykuł dotyczy możliwości zastosowania geometrii fraktalnej do opisu
powierzchni krzepnięcia. Głównym przedmiotem badań są struktury dendrytyczne –
zwrócono uwagę na ich samopodobieńs two i oszacowano wymiar fraktalny na
wybranym przykładzie.
Keywords: fractal, dendrite, solidification, surface
1. WSTĘP
Od czasu ukazania się książki B. Mandelbrota „The Fractal Geometry of Nature”
(„Fraktalna geometria natury”) [1] pojęcie fraktala zrobiło zawrotną karierę w wielu
dziedzinach nauki, a nawet sztuki. Nieczęsto zdarza się by jakaś koncepcja
matematyczna spotkała się z tak szerokim oddźwiękiem. Wydaje się, że główną tego
przyczyną jest uderzające podobieństwo niektórych fraktali do kształtów pojawiających
się w naturze – roślin, linii brzegowych, meandrów rzecznych czy struktur
dendrytycznych. Niniejszy artykuł jest próbą ukazania możliwości zastosowania metod
geometrii fraktalnej do opisu powierzchni krzepnięcia.
2. DENDRYTY
Po utworzeniu zarodków krystalizacji dalszy wzrost kryształu i jego struktura
uzależnione są od stabilności uformowanej powierzchni rozdziału ciecz-ciało stałe.
1
mgr inż., macmar@imipkm.pcz.czest.pl
18
W przypadku, gdy niewielkie zaburzenia powierzchni (powstałe na skutek np.
nierozpuszczonych domieszek, fluktuuacji temperatury, granicy ziarn) zostają z czasem
zredukowane poprzez proces jej wzrostu, uważa się ją za stabilną. Bardzo często zdarza
się jednak, że powierzchnia krzepnięcia traci stabilność i każde jej zaburzenie jest
dodatkowym bodźcem do jej rozbudowy. Dzieje się tak, gdy kierunek wzrostu kryształu
pokrywa się z kierunkiem odpływu ciepła (gradientu temperatury). Kryształ przybiera
wtedy złożoną, drzewopodobną formę nazywaną dendrytem.
Struktura dendrytu
podyktowana jest głównie kierunkiem gradientu temperatury oraz anizotropią kryształu
wynikającą z uprzywilejowania określonych osi krystalograficznych (np. (100) dla
metali regularnych). Rozgałęzienia boczne powstają ze względu na utratę stabilności
przez powierzchnię pnia dendrytu [2, 3].
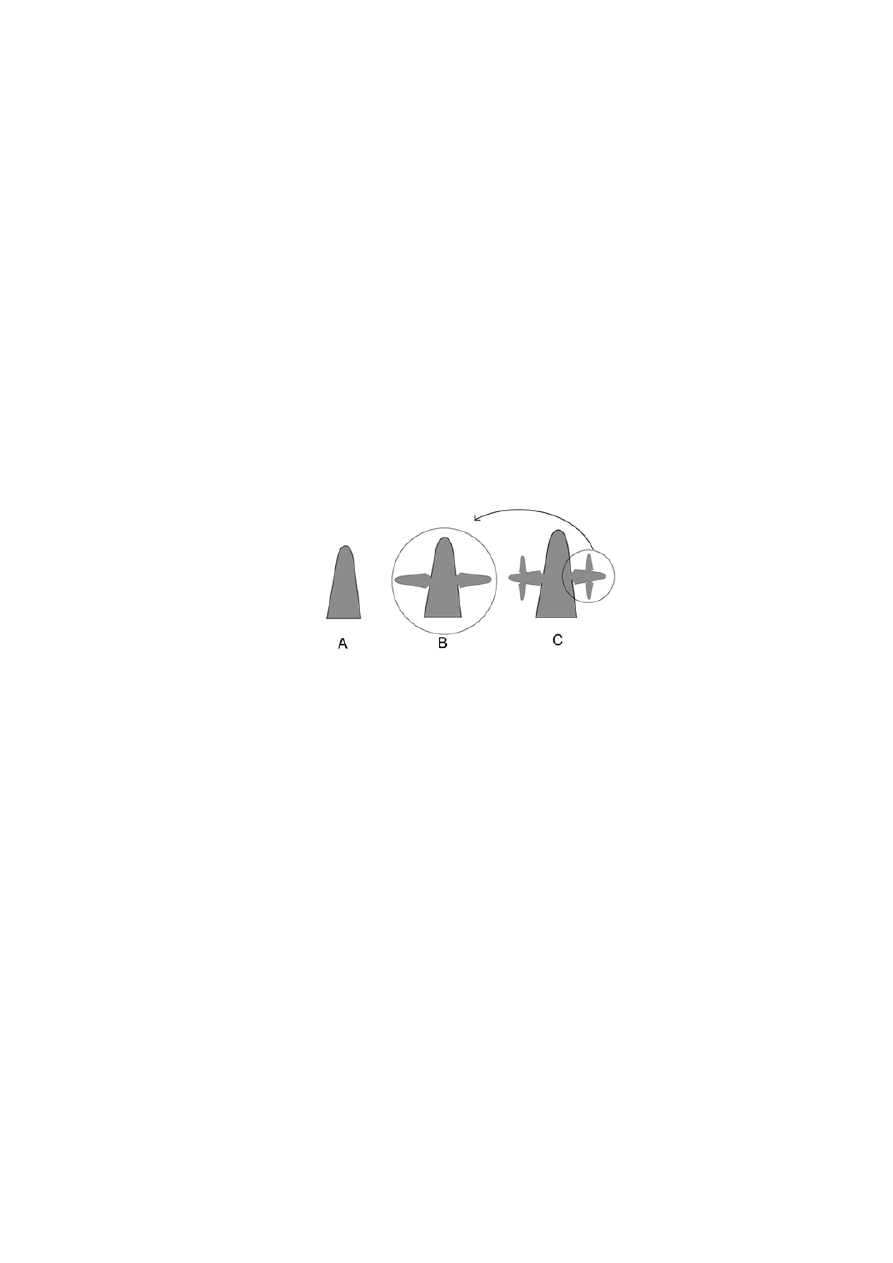
Rysunek 1 przestawia schematycznie kolejne etapy wzrostu dendrytu [4] – od
powstania pnia, po pojawienie się rozgałęzień coraz to wyższych rzędów.
Rys. 1. Wzrost dendrytu: A – pień główny; B- pojawienie się odgałęzień
pierwszego rzędu; C – wzrost odgałęzień drugiego rzędu
Fig. 1. Growth of dendrite: A – trunk; B – appearence of branches of first
order; C- growth of branches of second order
Jeśli porównamy struktury powstałe w następujących po sobie etapach, możemy
zauważyć szczególnego rodzaju własność: istnieje część dendrytu, która po
odpowiednim przeskalowaniu jest bardzo podobna do kształtu dendrytu w poprzednim
etapie – np. odgałęzienia boczne z etapu B po przeskalowaniu są zbliżone kształtem do
pnia dendrytu, zaś zaznaczona część z etapu C – do kształtu z etapu B. Własność tą
nazywamy samopodobieństwem (część dendrytu podobna jest całości) i jest ona jedną
z podstawowych cech charakteryzujących matematyczne obiekty nazywane fraktalami.
W przypadku dendrytu nie można oczywiście mówić o podobieństwie w śc isłym,
geometrycznym sensie, ale przekonamy się, że nawet w tym przypadku geometria
fraktalna dostarcza narzędzi do opisu obiektów o rozważanej własności.
Fraktale określa się jako obiekty geometryczne, których wymiar Hausdorffa jest
różny od wymiaru topologicznego [5]. Ponieważ wymiar Hausdorffa jest zazwyczaj
trudny do wyznaczenia, w praktyce stosuje się inne miary, jak np. wymiar pudełkowy
lub wymiar korelacyjny (nazywane po prostu wymiarami fraktalnymi).
Mówiąc krótko – wymiar pudełkowy określa zależność między najmniejszą liczbą
N(
) figur o liniowym rozmiarze
, które pokrywają dany obiekt, a ich rozmiarem. Ze
19
względu na prostotę implementacji zwykle pokrywa się kwadratami (lub w trzech
wymiarach – sześcianami - stąd nazwa „wymiar pudełkowy”). Wtedy jako
należy
rozmieć długość boku kwadratu (krawędzi sześcianu).
W przypadku obiektów samopodobnych zależność ta określona jest prostym
prawem potęgowym:
gdzie c jest pewną stałą, a d
ƒ
poszukiwanym wymiarem pudełkowym. Jeśli
zlogartymujemy obie strony, to otrzymamy:
z czego widać, że przedstawienie na wykresie zależności między log N(
) a log
prowadzi do linii prostej o współczynniku kierunkowym równym (z dokładnością co do
znaku) wymiarowi pudełkowemu. Jest to najczęściej spotykana metoda wyznaczenia
tego wymiaru.
Procedura postępowania dla dowolnych figur na płaszczyźnie może być
następująca („box counting method”, zobacz np. [8]):
1. pokrywamy obraz jednorodną siatką kwadratową (wymiar oczka -
1
);
2. zliczamy oczka sieci mające niepustą część wspólną z b adaną figurą – oznaczmy
wynik przez N(
1
);
3. zagęszczamy siatkę przez zmniejszenie wymiarów oczek do
2
<
1;
4. postępujemy jak w pkt.2 otrzymując N(
2
)
5. powtarzamy czynność z pkt.3 i 4 otrzymując N(
i
) dla coraz to gęstszych siatek
o rozmiarach oczek
i
.
6. wykreślamy zależność log N(
i
) od log
i
- otrzymanie linii prostej świadczy
o samopodobieństwie badanej figury, a współczynnik kierunkowy tej prostej równy
jest jej wymiarowi pudełkowemu;
Dla zwykłych figur geometrycznych takich jak odcinek, kwadrat, wymiar fraktalny
pokrywa się z wymiarem topologicznym (odpowiednio d
ƒ
=1, d
ƒ
=2) i dlatego, mimo
ich samopodobieństwa, nie uważa się ich za fraktale.
Spróbujmy przykładowo wyznaczyć wymiar fraktalny struktury dendrytycznej
wziętej z literatury [3].
f
d
c
N
)
(
log
log
)
(
log
f
d
c
N
20
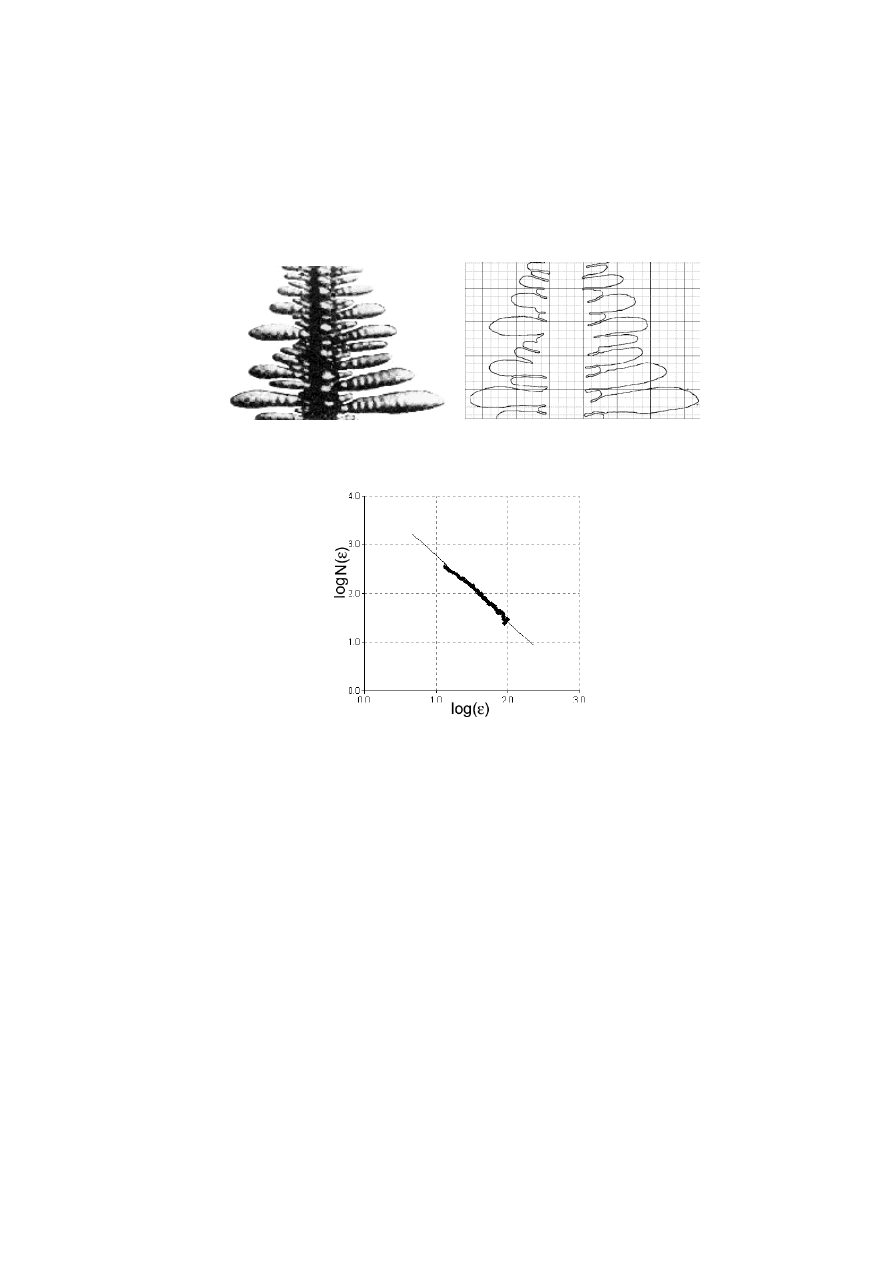
Rys. 2. Część dendrytu [3] i jego kontur pokryty siatką kwadratową
Fig. 2. Part of dendrite [3] and its contour covered by square grid
Rys. 3. Wykres zależności log N(
) od log
aproksymowany
linią prostą o nachyleniu –1.34
Fig. 3. Log-log plot of N(
) dependence approximated by straight
line (slope –1.34)
Wykres otrzymany dla konturu przekroju dendrytu z rys. 2 ukazany jest na rys. 3,
dla takiego zakresu zmian
, w którym można z dobrą dokładnością (współczynnik
korelacji ok.0.99) dokonać aproksymacji linią prostą o nachyleniu –1.34. Oznacza to, że
w tym zakresie mian
, kontur dendrytu jest obiektem samopodobnym o wymiarze
fraktalnym 1.34. Z kolei dla bardzo małych wartości
własności konturu są takie same
jak gładkiej krzywej o wymiarze 1 (stąd wynika zmniejszenie nachylenia wykresu
w części początkowej).
Bisang i Bilgram [6] użyli tej samej metody do wyznaczenia wymiaru fraktalnego
konturu dendrytu ksenonu. Wykres zależności logarytmu N(
) od logarytmu
dla tego
konturu można z dobrym przybliżeniem aproksymować linią prostą o nachyleniu –1.4,
21
zatem w zakresie dwóch rzędów wielkości w
możemy dany kontur uznać za fraktal o
wymiarze d
ƒ
1.4.
Wymiar korelacyjny (w wielu przypadkach równy wymiarowi pudełkowemu)
otrzymuje się badając własności skalowania funkcji korelacji [7]:
gdzie H(x) jest funkcją Heaviside’a (równa 1 dla x
0, zaś 0 dla x<0), zaś punkty x
i
, x
j
należą do zbioru wybranych m punktów konturu (równomiernie rozmieszczonych).
Funkcję korelacji można rozumieć jako stosunek liczby par punktów odd alonych
wzajemnie o nie więcej niż r do liczby wszystkich par punktów. Jak pokazał
Grassberger:
gdzie
jest wymiarem korelacyjnym.
Punkty na wykresie C(r) w skali logarytmicznej (log C(r)
log r) z dobrą
dokładnością układają się na linii prostej, a jej nachylenie jest równe (w granicy błędu)
wartości otrzymanej dla wymiaru pudełkowego.
Badania Bisanga i Bilgrama [6] wykazały, że wymiar fraktalny jest jednym z tych
integralnych parametrów dendrytu, które zachowują swoje wartości w różnych
realizacjach eksperymentalnych przy tych samych warunkach zewnętrznych (w
przeciwieństwie np. do długości i odstępie między gałęziami dendrytu), a nawet przy
różnych przechłodzeniach i rozmiarach dendrytu (po krótkim okresie początkowego
wzrostu). Średni wymiar fraktalny dla różnych wartości przechłodzenia to d
ƒ
=1.42
0.05.
Modelem wzrostu dendrytycznego może być jeden z klasycznych fraktali –
krzywa von Kocha (rys. 4)[5,8], przy czym podstawową cechą którą on akcentuje jest
nie zmiana rozmiarów, a pojawianie się rozgałęzień wyższych rzędów.
Krzywa von Kocha jest tzw. deterministycznym fraktalem – samopodobieństwo w
jej przypadku jest dokładne – granica ciągu konstrukcji z rys.4 rozpada się na cztery
trzykrotnie pomniejszone kopie całości, a jej wymiar fraktalny d
ƒ
=log(4)/log(3)
1.26.
Rys. 4. Pierwsze trzy etapy konstrukcji krzywej von Kocha
Fig. 4. First three steps of construction of van Koch curve
|)
|
(
lim
)
(
1
,
2
j
m
j
i
i
m
x
x
r
H
m
r
C
r
r
C
)
(
22
4. ZAKOŃCZENIE
Główną korzyścią z zastosowania geometrii fraktalnej w procesach krzepnięcia
jest możliwość dogodnego opisu powstających struktur, takich jak dendryty czy
nierówne powierzchnie. Ujęcie fraktalne pozwala nie tylko scharakteryzować je
jakościowo (poprzez własność samopodobieństwa), ale również ilościowo – wprowadza
parametry odnoszące się do obiektu jako całości, daje możliwość łatwej klasyfikacji
oraz oceny wpływu czynników zewnętrznych na jego morfologię.
LITERATURA
[1]
Mandelbrot B.B.: The Fractal Geometry of Nature. New York, W.H.Fredman
and Comp.,1983;
[2]
Kurz W., Fisher D.J.: Fundamentals of Solidifcation. Trans Tech.,
Aedermannsdorf, 1986;
[3]
Fraś E.: Krystalizacja metali. WNT, Warszawa, 2003;
[4]
Guy A.G.: Wprowadzenie do nauk i o materiałach. PWN, Warszawa, 1977;
[5]
Kudrewicz J.: Frak tale i chaos. WNT, Warszawa, 1996;
[6]
Bisang U., Bilgram J.H.: The fractal dimension of xenon dendrites. J. Cryst.
Growth 166 (1966) 207-211;
[7]
Grassberger P., Procaccia I., Phys. Rev. Lett. 50 (1983) 346;
[8]
Peitgen H.-O, Jurgens H., Saupe D.: Granice chaosu – frak tale. PWN,
Warszawa 1997;
FRACTAL ESTIMATION OF SOLIDIFICATION SURFACE
SUMMARY
Article deals with possibility of describing solidification surface using methods
of fractal geometry. The main subject of interest are dendritic structures – their self-
similarity is pointed out and fractal dimension of selected dendrite is estimated.
Recenzował dr hab. Jan Szajnar