
Zestaw 11- Działania na wektorach i macierzach,
wyznacznik i rząd macierzy
1
PRZYKŁADOWE ZADANIA Z ROZWIAZANIAMI
Dodaj
ą
c( b
ą
d
ź
odejmuj
ą
c) do siebie dwa wektory (lub wi
ę
cej), dodajemy (b
ą
d
ź
odejmujemy) ich odpowiednie współrz
ę
dne. Mno
żą
c wektor przez liczb
ę
rzeczywist
ą
, mno
ż
ymy ka
ż
d
ą
współrz
ę
dn
ą
danego wektora przez t
ę
liczb
ę
.
Zadanie 1
Oblicz sum
ę
i ró
ż
nic
ę
podanych wektorów:
[
]
3
,
2
,
1
1
−
=
→
u
,
[
]
6
,
5
,
2
2
−
=
→
u
.
Rozwi
ą
zanie:
Mamy:
[
] [
]
( )
[
] [
]
9
,
3
,
1
6
3
,
5
2
,
2
1
6
,
5
,
2
3
,
2
,
1
2
1
−
=
+
−
+
+
−
=
−
+
−
=
+
→
→
u
u
[
] [
]
( )
[
] [
]
3
,
7
,
3
6
3
,
5
2
,
2
1
6
,
5
,
2
3
,
2
,
1
2
1
−
−
=
−
−
−
−
−
=
−
−
−
=
−
→
→
u
u
.
Zadanie 2
Dane s
ą
wektory
[
]
3
,
1
,
1
1
−
=
→
u
,
[
]
5
,
1
,
4
2
−
=
→
u
,
[
]
5
,
3
,
2
3
−
=
→
u
.
Wyznacz wektor
→
→
→
→
+
−
=
1
2
3
2
3
u
u
u
u
.
Rozwi
ą
zanie:
Mo
ż
emy obliczy
ć
po kolei :
→
→
→
−
1
2
3
2
,
,
3
u
u
u
, a nast
ę
pnie doda
ć
do siebie otrzymane
wektory.
Mamy zatem:
[
]
15
,
9
,
6
3
3
−
=
→
u
,
[
]
9
,
3
,
3
2
−
=
−
→
u
,
[
]
6
,
2
,
2
2
1
−
=
→
u
,
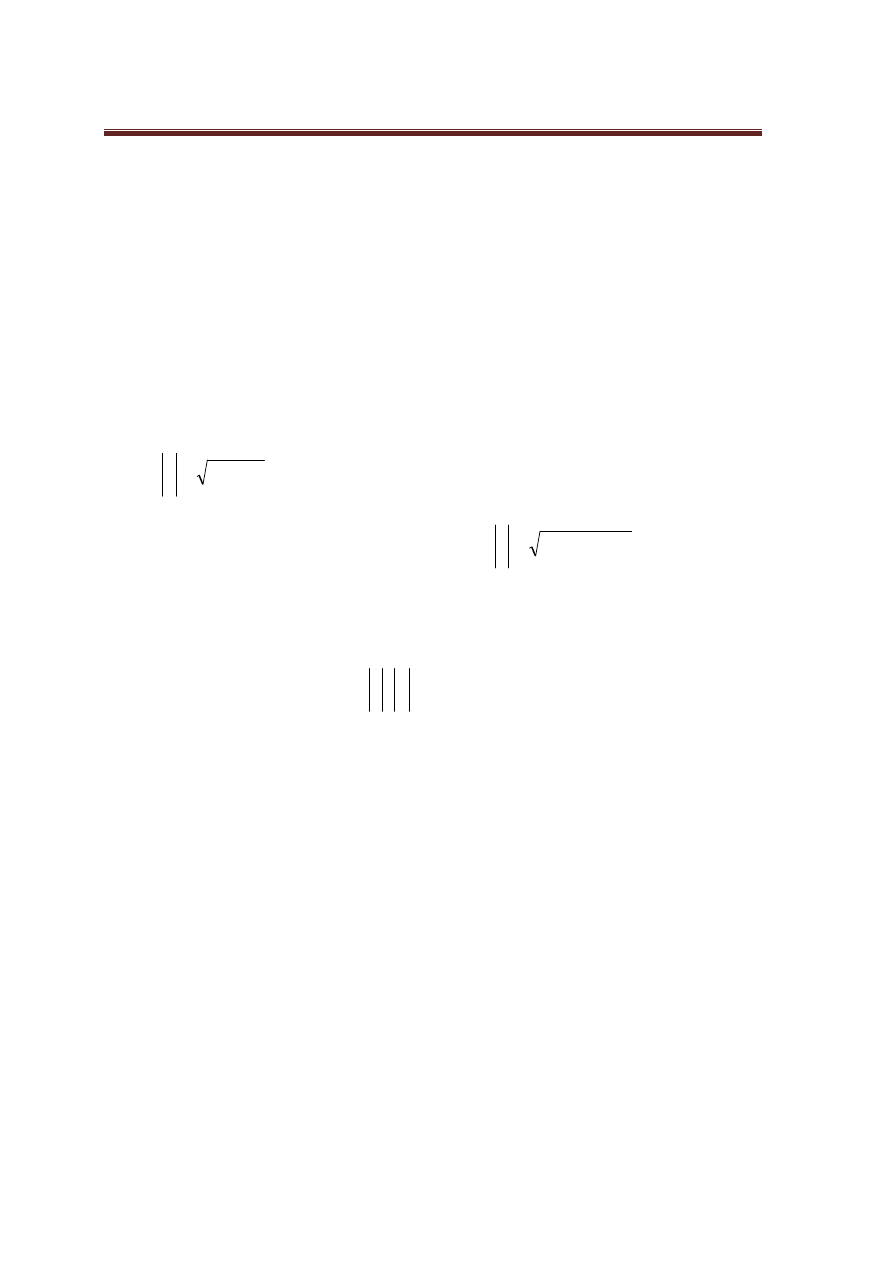
Zestaw 11- Działania na wektorach i macierzach,
wyznacznik i rząd macierzy
2
i dalej:
( ) ( )
[
] [
]
0
,
4
,
11
6
9
15
,
2
3
9
,
2
3
6
2
3
1
2
3
=
+
+
−
−
+
−
+
+
+
=
+
−
=
→
→
→
→
u
u
u
u
Długo
ść
wektora
[ ]
2
,
R
y
x
u
∈
=
→
obliczamy korzystaj
ą
c z nast
ę
puj
ą
cego wzoru:
2
2
y
x
u
+
=
→
. Oczywi
ś
cie dla wektorów z przestrzeni
3
R
wzór jest
analogiczny, czyli je
ś
li
[
]
3
,
,
R
z
y
x
u
∈
=
→
, to
2
2
2
z
y
x
u
+
+
=
→
.
Iloczynem skalarnym pary wektorów niezerowych
→
→
w
u,
nazywamy liczb
ę
rzeczywist
ą
równ
ą
α
cos
⋅
⋅
=
→
→
→
→
w
u
w
uo
, gdzie
α
jest k
ą
tem zawartym mi
ę
dzy
tymi wektorami. Je
ś
li przynajmniej jeden z wektorów jest zerowy, to
przyjmujemy,
ż
e iloczyn skalarny tych wektorów jest równy
0
. Innym
sposobem na obliczenie iloczynu skalarnego jest nast
ę
puj
ą
cy wzór:
Je
ś
li
[
]
[
]
2
1
2
1
,
,
,
w
w
w
u
u
u
=
=
→
→
, to
2
2
1
1
w
u
w
u
w
u
⋅
+
⋅
=
→
→
o
;
Je
ś
li
[
]
[
]
3
2
1
3
2
1
,
,
,
,
,
w
w
w
w
u
u
u
u
=
=
→
→
, to
3
3
2
2
1
1
w
u
w
u
w
u
w
u
⋅
+
⋅
+
⋅
=
→
→
o
.
Zauwa
ż
my,
ż
e iloczyn skalarny dwóch wektorów niezerowych jest równy
0
wtedy i tylko wtedy, gdy wektory te s
ą
prostopadłe. Mówimy równie
ż
w takiej
sytuacji,
ż
e wektory te s
ą
ortogonalne.
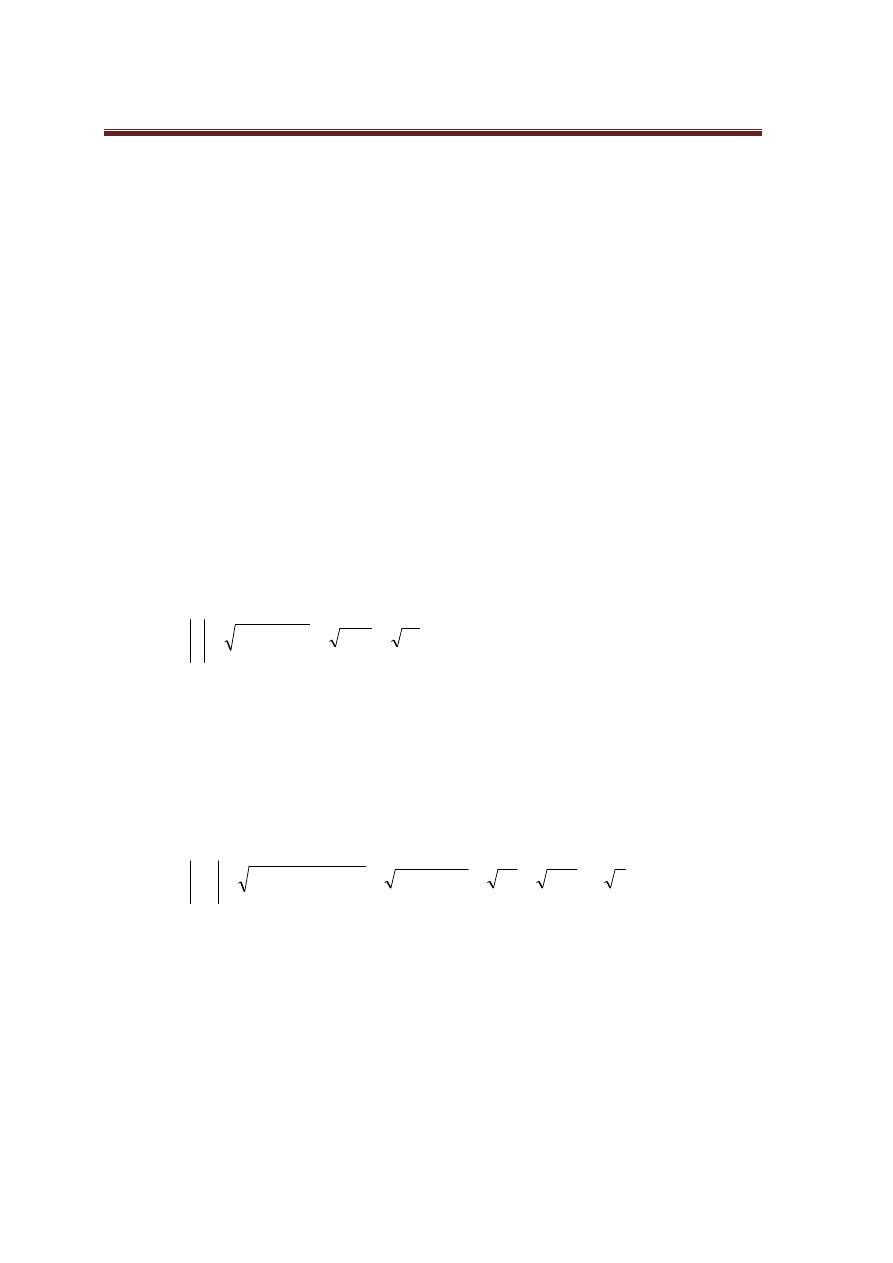
Zestaw 11- Działania na wektorach i macierzach,
wyznacznik i rząd macierzy
3
Zadanie 6.
Oblicz długo
ś
ci nast
ę
puj
ą
cych wektorów:
a)
[ ]
1
,
3
−
=
→
u
b)
PQ
→
;
(
)
(
)
1
,
3
,
2
;
5
,
0
,
1
−
=
−
=
Q
P
Rozwi
ą
zanie:
a)
( )
10
1
9
1
3
2
2
=
+
=
−
+
=
→
u
b) Aby obliczy
ć
długo
ść
wektora, korzystaj
ą
c z podanego powy
ż
ej wzoru,
obliczymy najpierw jego współrz
ę
dne:
( )
[
] [
]
6
,
3
,
3
5
1
,
0
3
,
1
2
−
=
−
−
−
−
−
=
→
PQ
, i
dalej:
( )
6
3
6
9
54
36
9
9
6
3
3
2
2
2
=
⋅
=
=
+
+
=
−
+
+
=
→
PQ
.
Zadanie 7.
Oblicz iloczyn skalarny nast
ę
puj
ą
cych par wektorów. Czy podane wektory s
ą
ortogonalne?

Zestaw 11- Działania na wektorach i macierzach,
wyznacznik i rząd macierzy
4
a)
[ ]
4
,
1
−
=
→
u
,
[ ]
1
,
2
−
=
→
v
b)
[
]
2
,
6
,
2
=
→
u
,
[
]
1
,
1
,
2
−
−
=
→
v
Rozwi
ą
zanie:
a) Aby sprawdzi
ć
, czy podane wektory s
ą
ortogonalne, obliczymy ich iloczyn
skalarny:
( ) ( )
6
1
4
2
1
−
=
⋅
−
+
−
⋅
=
→
→
v
uo
, zatem wektory nie s
ą
ortogonalne.
b) Mamy :
( )
( )
0
2
6
4
1
2
1
6
2
2
=
−
+
−
=
−
⋅
+
⋅
+
−
⋅
=
→
→
v
uo
, zatem wektory te s
ą
ortogonalne.
Je
ś
li macierz
A
ma
n
kolumn oraz
l
wierszy, to mówimy,
ż
e jest ona wymiaru
l
n
×
. Wyraz tej macierzy, znajduj
ą
cy si
ę
w
i
-tym wierszu i
j
-tej kolumnie,
oznaczamy symbolem
ij
a
.
Sum
ą
(ró
ż
nic
ą
) macierzy
A
i
B
jest macierz
C
, której ka
ż
dy wyraz jest sum
ą
(ró
ż
nic
ą
) odpowiednich wyrazów macierzy
A
i
B
, tj.
ij
ij
ij
b
a
c
+
=
w przypadku
sumy, oraz
ij
ij
ij
b
a
c
−
=
w przypadku ró
ż
nicy. Oczywi
ś
cie, aby dało si
ę
doda
ć
(odj
ąć
) dwie macierze
A
i
B
, musz
ą
by
ć
one tego samego wymiaru.
Iloczynem macierzy
A
przez liczb
ę
rzeczywist
ą
a
nazywamy macierz
A
a
⋅
,
której ka
ż
dy wyraz jest iloczynem odpowiedniego wyrazu macierzy
A
przez
liczb
ę
a
.
Macierz
ą
transponowan
ą
do macierzy
A
wymiaru
l
n
×
nazywamy macierz
T
A
, która powstaje przez zast
ą
pienie
−
i
tej kolumny macierzy
A
−
i
tym
wierszem , dla ka
ż
dego
l
i
...,
,
2
,
1
=
. W wyniku takiej zamiany miejscami wierszy
i kolumn, otrzymujemy macierz o wymiarze
n
l
×
.
Macierz kwadratowa to ka
ż
da macierz, w której liczba kolumn jest równa
liczbie wierszy. Główn
ą
przek
ą
tn
ą
macierzy kwadratowej
A
wymiaru
n
n
×
(w
skrócie- wymiaru
n
) nazywamy wyrazy
nn
a
a
a
,...,
,
22
11
.

Zestaw 11- Działania na wektorach i macierzach,
wyznacznik i rząd macierzy
5
Macierz
ą
jednostkow
ą
nazywamy macierz kwadratow
ą
dowolnego wymiaru, w
której ka
ż
dy wyraz na głównej przek
ą
tnej jest równy
1
, za
ś
wszystkie pozostałe
s
ą
równe
0
. Oznaczamy j
ą
I
.
Zadanie 8.
Dla podanych macierzy:
−
−
=
2
0
3
4
5
1
A
,
−
−
−
=
1
2
0
3
1
3
B
, oblicz
a)
T
B
A
+
,
b)
B
A
T
3
−
.
Rozwi
ą
zanie:
a) Wyznaczymy najpierw macierz transponowan
ą
do
B
:
−
−
−
=
1
3
2
1
0
3
T
B
,
a nast
ę
pnie wykonamy dodawanie:
( )
( )
( )
−
−
−
=
−
+
−
+
+
−
+
+
−
+
−
=
+
1
3
1
5
5
4
1
2
3
0
2
3
1
4
0
5
3
1
T
B
A
.
b) Wyznaczymy najpierw macierz transponowan
ą
do
A
:
−
−
=
2
3
5
0
4
1
T
A
,

Zestaw 11- Działania na wektorach i macierzach,
wyznacznik i rząd macierzy
6
oraz obliczymy iloczyn macierzy
B
przez liczb
ę
3
:
−
−
−
=
3
6
0
9
3
9
3
B
.
Mamy nast
ę
pnie:
( )
( )
( )
−
=
−
−
−
−
−
−
−
−
−
−
−
=
−
5
9
5
9
1
8
3
2
6
3
0
5
9
0
3
4
9
1
3
B
A
T
.
Iloczynem dwóch macierzy:
A
o wymiarze
l
n
×
, oraz
B
o wymiarze
k
l
×
,
nazywamy macierz
C
wymiaru
k
n
×
, w której ka
ż
dy wyraz
ij
c
liczymy
posługuj
ą
c si
ę
nast
ę
puj
ą
cym wzorem:
lj
il
j
i
j
i
ij
b
a
b
a
b
a
c
⋅
+
+
⋅
+
⋅
=
...
2
2
1
1
.
Zadanie 8.
Dla podanych macierzy
−
−
=
3
1
2
3
0
1
A
,
−
=
2
4
2
1
B
, oblicz:
a)
T
A
B
⋅
,
b)
B
A
⋅
c)
(
)
T
A
I
B
⋅
−
4

Zestaw 11- Działania na wektorach i macierzach,
wyznacznik i rząd macierzy
7
d)
2
B
Rozwi
ą
zania:
a) Zaczniemy od wyznaczenia macierzy
T
A
:
−
−
=
3
2
0
1
3
1
T
A
. Macierz
t
A
B
⋅
ma wymiar
3
2
×
; obliczymy wg. wzoru wyrazy
ij
c
macierzy
T
A
B
⋅
: ( przez
a
b
ę
dziemy oznacza
ć
odpowiednie wyrazy macierzy
T
A
, za
ś
b
- wyrazy
macierzy
B
)
( ) ( )
1
0
1
0
2
1
1
21
12
11
11
11
−
=
+
−
=
⋅
−
+
−
⋅
=
⋅
+
⋅
=
a
b
a
b
c
,
( )
1
4
3
2
2
3
1
22
12
12
11
12
−
=
−
=
⋅
−
+
⋅
=
⋅
+
⋅
=
a
b
a
b
c
,
( ) ( )
7
6
1
3
2
1
1
23
12
13
11
13
=
+
=
−
⋅
−
+
⋅
=
⋅
+
⋅
=
a
b
a
b
c
,
( )
4
0
4
0
2
1
4
21
22
11
21
21
−
=
+
−
=
⋅
+
−
⋅
=
⋅
+
⋅
=
a
b
a
b
c
,
16
4
12
2
2
3
4
22
22
12
21
22
=
+
=
⋅
+
⋅
=
⋅
+
⋅
=
a
b
a
b
c
,
( )
2
6
4
3
2
1
4
23
22
13
21
23
−
=
−
=
−
⋅
+
⋅
=
⋅
+
⋅
=
a
b
a
b
c
.
Mamy wi
ę
c:
−
−
−
−
=
⋅
2
16
4
7
1
1
T
A
B
.
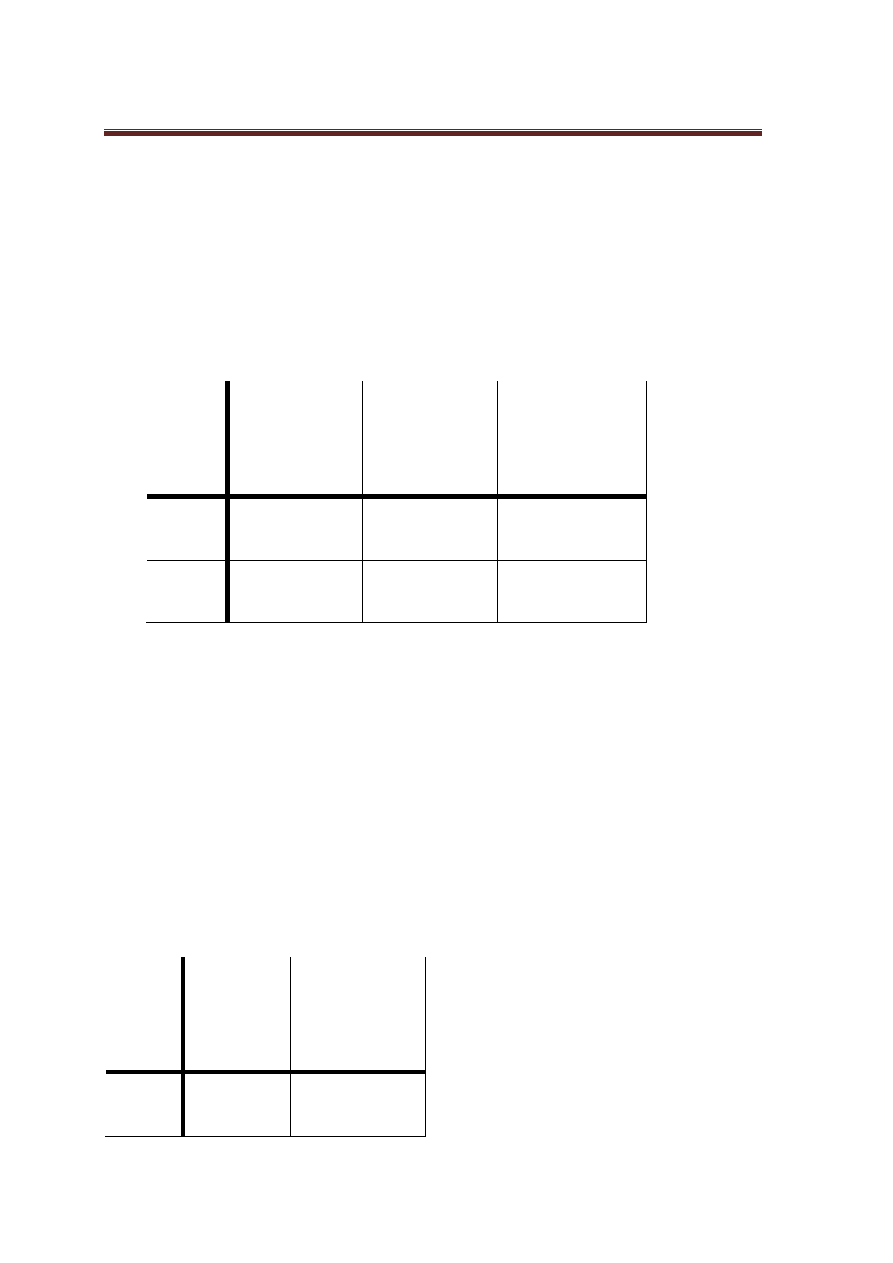
Zestaw 11- Działania na wektorach i macierzach,
wyznacznik i rząd macierzy
8
Mno
ż
enie macierzy wydaje si
ę
prostsze, gdy zapiszemy dane macierze w
tabeli takiej jak poni
ż
ej; wówczas w ka
ż
dym z sze
ś
ciu pól wpisujemy sum
ę
iloczynów odpowiednich wyrazów :
-1
0
3
2
1
-3
1 -2
( ) ( )
0
2
1
1
⋅
−
+
−
⋅
( )
2
2
3
1
⋅
−
+
⋅
( ) ( )
3
2
1
1
−
⋅
−
+
⋅
4 2
( )
0
2
1
4
⋅
+
−
⋅
2
2
3
4
⋅
+
⋅
( )
3
2
1
4
−
⋅
+
⋅
Wykonuj
ą
c teraz obliczenia w ka
ż
dym z pól, polegaj
ą
ce na pomno
ż
eniu przez
siebie ka
ż
dego wyrazu wiersza pierwszej macierzy, przez odpowiedni wyraz
kolumny drugiej macierzy, otrzymujemy wynik taki sam, jak wtedy, gdy
posługiwali
ś
my si
ę
definicj
ą
iloczynu macierzy. Metoda pokazana tutaj zmniejsza
mo
ż
liwo
ść
pomyłki przy podstawianiu do wzoru.
b) Skorzystamy z tabeli:
1
4
-2
2
-1 0
( )
4
0
1
1
⋅
+
⋅
−
( ) ( )
2
0
2
1
⋅
+
−
⋅
−
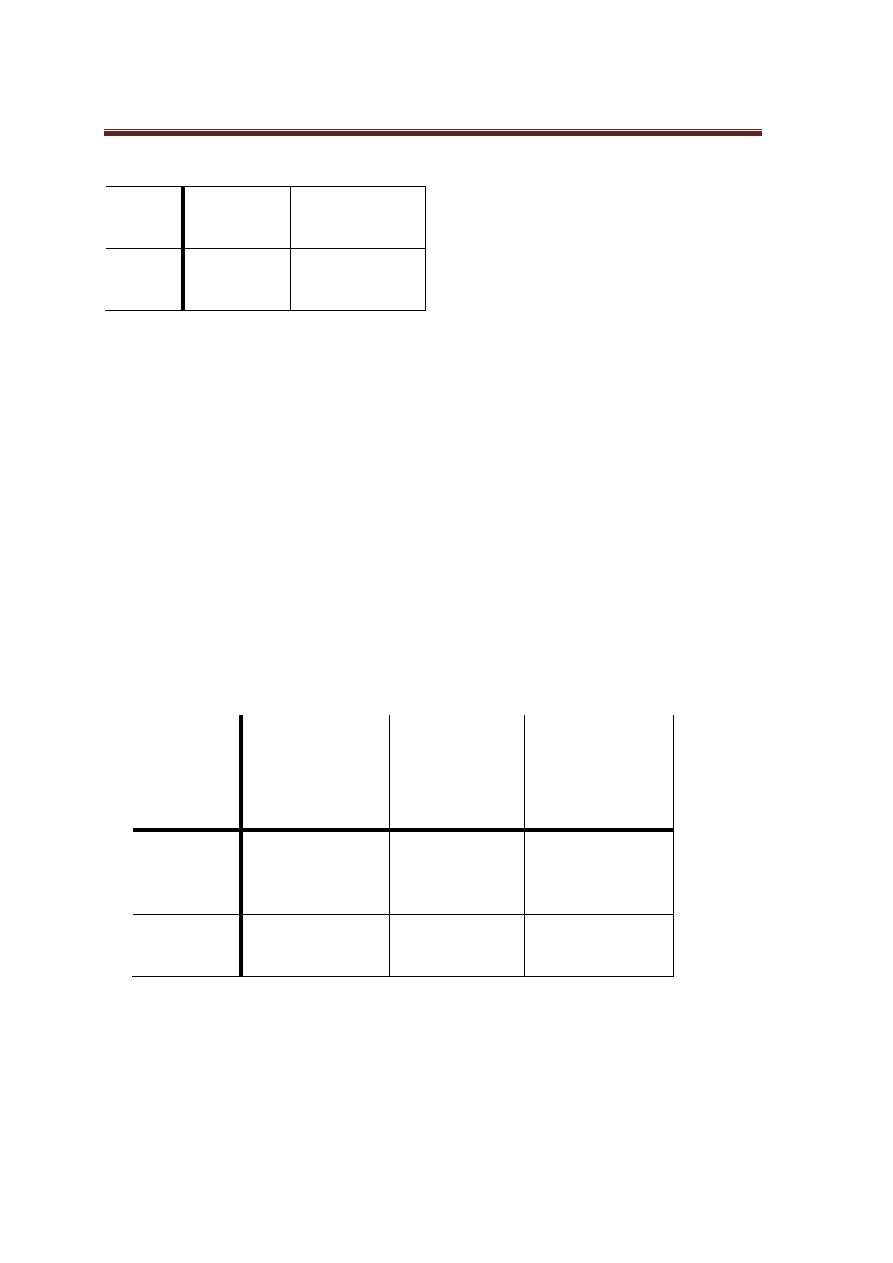
Zestaw 11- Działania na wektorach i macierzach,
wyznacznik i rząd macierzy
9
3 2
4
2
1
3
⋅
+
⋅
( )
2
2
2
3
⋅
+
−
⋅
1 -3
( )
4
3
1
1
⋅
−
+
⋅
( ) ( )
2
3
2
1
⋅
−
+
−
⋅
Z tabeli odczytujemy,
ż
e
−
−
−
−
=
⋅
8
11
2
11
2
1
B
A
.
c) Obliczymy najpierw macierz
−
−
−
=
−
−
=
⋅
−
−
=
−
1
4
2
3
4
0
0
4
2
4
2
1
1
0
0
1
4
2
4
2
1
4I
B
, a nast
ę
pnie
zapiszemy macierze w odpowiedniej tabeli:
-1
0
3
2
1
-3
-3 -2
( ) ( ) ( )
0
2
1
3
⋅
−
+
−
⋅
−
( ) ( )
2
2
3
3
⋅
−
+
⋅
−
( ) ( ) ( )
3
2
1
3
−
⋅
−
+
⋅
−
4 -1
( ) ( )
0
1
1
4
⋅
−
+
−
⋅
( )
2
1
3
4
⋅
−
+
⋅
( ) ( )
3
1
1
4
−
⋅
−
+
⋅
sk
ą
d odczytujemy,
ż
e
(
)
−
−
=
⋅
−
7
10
4
3
13
3
4
T
A
I
B
.
Zestaw 11- Działania na wektorach i macierzach,
wyznacznik i rząd macierzy
10
d) Symbol
2
B
rozumiemy jako iloczyn
B
B
⋅
.
1
4
-2
2
1 -2
( )
4
2
1
1
⋅
−
+
⋅
( ) ( )
2
2
2
1
⋅
−
+
−
⋅
4 2
4
2
1
4
⋅
+
⋅
( )
2
2
2
4
⋅
+
−
⋅
czyli
−
−
−
=
4
12
6
7
2
B
.
Wyznacznik macierzy kwadratowej jest liczb
ą
rzeczywist
ą
, któr
ą
obliczamy w
nast
ę
puj
ą
cy sposób:
1) Je
ś
li
=
d
c
b
a
A
, to
bc
ad
A
−
=
det
;
2) Je
ś
li
=
33
32
31
23
22
21
13
12
11
a
a
a
a
a
a
a
a
a
A
, to
12
21
33
23
32
11
13
22
31
23
12
31
32
21
13
33
22
11
det
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
A
−
−
−
+
+
=
.
Uwaga!

Zestaw 11- Działania na wektorach i macierzach,
wyznacznik i rząd macierzy
11
Wyznacznik, b
ę
d
ą
cy pewn
ą
liczb
ą
rzeczywist
ą
, posiada ka
ż
da macierz
kwadratowa, jednak sposoby obliczania wyznaczników macierzy wi
ę
kszego
wymiaru, s
ą
bardziej skomplikowane; pomijamy je tutaj .
Je
ś
li macierz jest wymiaru
2
2
×
, mówimy o wyznaczniku drugiego stopnia; je
ś
li
3
3
×
-
to trzeciego, itd
Zadanie 10.
Oblicz wyznaczniki macierzy:
a)
−
−
=
2
3
1
5
A
b)
−
−
=
2
2
0
6
1
2
3
0
1
A
Rozwi
ą
zania:
a) Zgodnie z powy
ż
szym, prostym wzorem, mamy:
( ) ( )
7
1
3
2
5
det
−
=
−
⋅
−
−
⋅
=
A

Zestaw 11- Rząd macierzy, układy równań liniowych
12
b) Aby łatwiej było wykona
ć
podane obliczenia, zapiszemy raz jeszcze dan
ą
macierz, dopisuj
ą
c dodatkowo dwie pierwsze kolumny:
2
0
1
2
0
1
2
2
0
6
1
2
3
0
1
det
−
−
−
−
=
A
B
ę
dziemy nast
ę
pnie mno
ż
y
ć
przez siebie wyrazy znajduj
ą
ce si
ę
na głównej
przek
ą
tnej macierzy
A
oraz wzdłu
ż
dwóch kolejnych linii równoległych do
głównej przek
ą
tnej; otrzymane iloczyny dodajemy. Podobne działania
wykonamy zaczynaj
ą
c od drugiej przek
ą
tnej macierzy
A
, otrzymane w ten
sposób iloczyny iloczyny b
ę
dziemy odejmowa
ć
od sumy poprzednich:
( ) ( )
( )
( )
=
⋅
−
⋅
−
⋅
⋅
−
−
⋅
⋅
−
−
⋅
−
⋅
+
⋅
⋅
+
⋅
⋅
=
−
−
−
−
=
0
2
2
1
6
2
3
1
0
2
2
3
0
6
0
2
1
1
2
0
1
2
0
1
2
2
0
6
1
2
3
0
1
det A
26
12
12
2
=
+
+
=
.
Rz
ę
dem dowolnej macierzy
A
nazywamy stopie
ń
najwi
ę
kszego ( w sensie
wymiaru) podwyznacznika niezerowego macierzy
A
.
Zadanie 11
Oblicz rz
ą
d macierzy
A
.
a)
−
−
=
3
1
2
2
2
4
A

Zestaw 11- Rząd macierzy, układy równań liniowych
13
b)
−
−
=
2
1
1
1
0
3
3
1
2
A
c)
−
−
−
=
1
1
3
0
3
1
1
0
2
A
Rozwi
ą
zania:
a) Rz
ą
d tej macierzy mo
ż
e by
ć
równy co najwy
ż
ej
2
; zapiszemy wszystkie
podwyznaczniki drugiego stopnia:
1
2
2
4
−
−
,
3
1
2
2
−
oraz
3
2
2
4
−
. Mamy:
0
4
4
1
2
2
4
=
−
=
−
−
;
0
8
2
6
3
1
2
2
≠
−
=
−
−
=
−
, zatem nie ma potrzeby
obliczania trzeciego podwyznacznika drugiego stopnia; stwierdzamy,
ż
e rz
ą
d
macierzy
A
jest równy 2; piszemy
2
=
rzA
.
b) Rz
ą
d tej macierzy mo
ż
e by
ć
równy co najwy
ż
ej
3
; jedynym jej
podwyznacznikiem trzeciego stopnia jest wyznacznik macierzy
A
. Mamy
zatem:
( )
0
6
2
0
9
1
0
1
1
0
3
1
2
2
1
1
1
0
3
3
1
2
det
=
−
−
−
+
−
+
=
−
−
−
=
A
, zatem
3
<
rzA
.
Spróbujemy teraz znale
źć
podwyznacznik drugiego stopnia, ró
ż
ny od zera:
( )
0
3
3
0
0
3
1
2
≠
=
−
−
=
−
, zatem
2
=
rzA
.
c) Podobnie jak poprzednio,
3
≤
rzA
. Aby stwierdzi
ć
, czy zachodzi równo
ść
,
obliczymy wyznacznik macierzy
A
:

Zestaw 11- Działania na wektorach i macierzach;
wyznacznik i rząd macierzy.
14
( ) ( )
0
14
0
0
9
1
0
6
1
3
3
1
0
2
1
1
3
0
3
1
1
0
2
det
≠
=
−
−
−
−
−
+
+
=
−
−
−
−
=
A
,
zatem
3
=
rzA
.
ZADANIA DO SAMODZIELNEGO ROZWI
Ą
ZANIA
Zadanie 1
Dane s
ą
wektory
[
]
2
,
1
,
3
1
−
=
→
u
,
[
]
2
,
1
,
5
2
−
−
=
→
u
,
[
]
4
,
8
,
2
3
−
=
→
u
Wyznacz wektor
→
u
a)
→
→
→
→
+
−
=
3
2
1
2
1
3
2
u
u
u
u
b)
→
→
→
→
+
−
=
1
2
3
2 u
u
u
u
c)
→
→
→
→
−
+
−
=
3
2
1
2
u
u
u
u
Zadanie 2
Wyznacz wektor
→
→
→
→
+
−
=
3
2
1
5
3
2
u
u
u
u
, je
ż
eli
a)
[
]
1
,
2
1
−
=
→
u
,
[ ]
2
,
0
2
=
→
u
,
[ ]
3
,
1
3
−
=
→
u
b)
[
]
2
,
1
,
0
1
=
→
u
,
[
]
4
,
3
,
2
2
−
=
→
u
,
[
]
1
,
1
,
1
3
−
=
→
u
Zestaw 11- Działania na wektorach i macierzach;
wyznacznik i rząd macierzy.
15
c)
[
]
0
,
2
,
4
1
−
=
→
u
,
[
]
1
,
2
,
3
2
−
=
→
u
,
[
]
0
,
2
,
1
3
=
→
u
Zadanie 3
Oblicz długo
ś
ci nast
ę
puj
ą
cych wektorów:
c)
[
]
4
,
2
−
=
→
u
d)
[ ]
1
,
3
,
1
=
→
u
e)
[
]
6
,
1
,
2
=
→
u
f)
[
]
5
,
3
,
1
−
=
→
u
g)
PQ
→
;
( )
(
)
4
,
2
;
3
,
1
−
=
=
Q
P
h)
PQ
→
;
(
)
(
)
1
,
0
,
0
;
2
,
3
,
1
=
−
=
Q
P
i)
PQ
→
;
(
)
(
)
7
,
3
,
1
;
4
,
3
,
1
−
=
−
=
Q
P
j)
PQ
→
;
(
)
(
)
2
,
2
,
1
;
1
,
3
,
0
=
=
Q
P
Zadanie 4
Oblicz iloczyn skalarny nast
ę
puj
ą
cych par wektorów. Czy podane wektory s
ą
ortogonalne?
c)
[
]
4
,
2
−
=
→
u
,
[ ]
1
,
3
−
=
→
v
d)
[ ]
2
,
1
−
=
→
u
,
[ ]
2
,
4
=
→
v
e)
[ ]
2
,
0
=
→
u
,
[ ]
1
,
1
−
=
→
v
f)
[
]
2
,
4
,
2
−
=
→
u
,
[
]
5
,
1
,
3
−
=
→
v
g)
[
]
0
,
1
,
1
−
=
→
u
,
[
]
0
,
1
,
2
−
=
→
v
h)
[
]
2
,
1
,
3
−
=
→
u
,
[
]
6
,
4
,
2
−
=
→
v
Zadanie 5

Zestaw 11- Działania na wektorach i macierzach;
wyznacznik i rząd macierzy.
16
Dla podanych macierzy:
−
−
=
2
1
2
0
3
1
A
,
−
=
1
0
7
8
5
1
B
, oblicz
c)
B
A
+
,
d)
B
A
−
2
,
e)
B
A
5
3
+
−
,
f)
T
T
B
A
3
2
−
,
g)
B
A
2
3
2
1
+
Zadanie 6
Dla podanych macierzy
−
=
1
0
0
2
3
1
A
,
−
=
1
3
2
1
B
, oblicz:
e)
A
B
⋅
,
f)
B
A
T
⋅
g)
(
)
A
I
B
⋅
−
2
h)
(
)
I
B
A
T
3
+
⋅
Zadanie 7
Oblicz
B
A
⋅
, je
ż
eli
a)
−
=
4
2
1
0
1
3
A
,
=
3
2
1
B
b)
=
2
3
0
1
A
,
=
0
3
1
2
0
1
B
c)
−
=
2
1
2
3
0
1
A
,
−
=
0
1
1
0
2
1
B
d)
[
]
4
2
1
−
=
A
,
−
=
2
3
0
1
2
1
B

Zestaw 11- Działania na wektorach i macierzach;
wyznacznik i rząd macierzy.
17
e)
−
=
4
3
1
4
2
1
A
,
−
=
2
1
3
0
1
0
2
1
B
Zadanie 8
Oblicz wyznaczniki macierzy:
c)
5
3
2
1
−
d)
4
1
1
0
−
e)
2
1
1
1
3
0
2
1
1
−
f)
1
2
1
1
3
0
1
1
3
−
−
g)
3
0
1
1
2
1
3
4
5
−
−
h)
1
1
0
5
4
3
2
1
2
−
i)
2
1
1
0
5
3
4
2
1
−
j)
1
2
3
0
1
5
3
2
1
k)
1
5
2
1
1
3
4
0
2
−
−
l)
3
1
4
2
0
1
4
3
1
−
−
−

Zestaw 11- Rząd macierzy, układy równań liniowych
18
Zadanie 9
Oblicz rz
ą
d macierzy
A
.
d)
−
−
=
3
4
2
0
2
1
A
e)
−
−
−
=
0
1
1
1
1
0
1
2
1
A
f)
−
−
=
2
2
3
1
0
0
1
2
3
A
g)
−
−
−
=
1
2
6
4
3
1
3
2
A
h)
−
−
=
0
2
0
1
0
1
1
2
1
A
ODPOWIEDZI
Zadanie 1
a)
[
]
12
,
9
,
22
−
b)
[
]
10
,
11
,
13
−
c)
[
]
10
,
11
,
13
−
−
Zadanie 2
a)
[
]
11
,
9
−
b)
[
]
3
,
12
,
11
−
−
c)
[
]
3
,
0
,
4
Zestaw 11- Rząd macierzy, układy równań liniowych
19
Zadanie 3
a)
5
2
=
→
u
b)
11
=
→
u
c)
3
=
→
u
d)
3
=
→
u
e)
2
5
=
→
u
f)
11
=
→
u
g)
3
=
→
u
h)
3
=
→
u
Zadanie 4
a)
10
−
=
→
→
v
uo
, nie
b)
0
=
→
→
v
uo
, tak
c)
2
=
→
→
v
uo
, nie
d)
0
=
→
→
v
uo
, tak
e)
3
−
=
→
→
v
uo
, nie
f)
2
=
→
→
v
uo
, nie
Zadanie 5
a)
−
3
1
9
8
8
0
b)
−
−
−
−
3
2
3
8
1
3
c)
−
1
3
29
40
16
8
d)
−
−
−
−
−
1
24
2
9
17
5
e)
−
2
5
2
1
2
23
12
9
1
Zadanie 6
a)
−
−
7
9
3
0
3
1
b)
−
−
5
1
6
3
2
1
c)
−
−
−
5
9
3
4
9
3
d)
−
−
8
7
6
6
2
2

Zestaw 11- Rząd macierzy, układy równań liniowych
20
Zadanie 7
a)
−
17
1
b)
6
6
5
2
0
1
c)
−
−
5
0
2
4
d)
−
10
13
e)
−
−
11
4
6
3
2
1
11
4
5
2
4
1
Zadanie 8
a)
11
det
=
A
b)
1
det
=
A
c)
2
det
−
=
A
d)
19
det
=
A
e)
40
det
=
A
f)
7
det
=
A
g)
30
det
−
=
A
h)
12
det
=
A
i)
40
det
=
A
j)
13
det
=
A
Zadanie 9
a)
2
=
rzA
b)
2
=
rzA
c)
3
=
rzA
d)
2
=
rzA
e)
2
=
rzA
Wyszukiwarka
Podobne podstrony:
Zestaw 11- Działania na wektorach i macierzach
Temat lementy działań na wektorach
Dzialania na wektorach Zastoso zadania id 146885
Cwiczenia dzialania na wektorach
Cwiczenia dzialania na wektorach
Przykłady działań na wektorach
Działania na wektorach
Wektory definicja i działania na wektorach
,algebra 1,wektor i działanie na wektorach
nt podstawy dzialan na wektorach odejmowanie
anestezjologia ZESTAW 11, OPIEKA PALIATYWNA - pytania na zaliczenie pisemne
3 Zadania do wykladu Dzialania na macierzach rzad macierzy
3.Zadania do wykladu Dzialania na macierzach rzad macierzy
Wzór nr 11, zestawienie zbiorcze wyd na wyżywienie
więcej podobnych podstron