Do   obliczania   całki  Mohra  można   wykorzystać   formułę
Simpsona. Sposób ten daje dokładne wartości rozwiązania, jeżeli
jedna   z   funkcji   jest   funkcją   liniową   (

2

1

, M

M

są   takie   zawsze),

a druga z funkcji jest, co najwyżej drugiego stopnia (M

p

  w tych

przedziałach, co obciążenie q równomiernie rozłożone).

Układ równań MS ma postać:

0







p

Δ

X

Δ

Macierz podatności układu jest równa:

M

A

M

Δ







T

gdzie:







,

,

2

1

M

M

M



 – macierz momentów jednostkowych

A – jest quasi diagonalną macierzą zbudowaną z macierzy A

p 

podatności na zginanie:

 















2

1

1

2

6EI

p

p

p

l

A

tam gdzie wykres M

p

 jest

liniowy























1

0

0

0

4

0

0

0

1

6EI

p

p

p

l

A

tam gdzie wykres M

p

 jest 

2-go stopnia

Wektor wyrazów wolnych jest równy:

p

T

p

M

A

M

Δ







gdzie:  M

p

 – wektor momentu zginającego powstającego jako

skutek działania obciążenia zewnętrznego na UP

Rozwiązaniem jest wektor:

p

1

Δ

Δ

X









Moment zginający w układzie statycznie niewyznaczalnym:

X

M

M

M







p

Politechnika Rzeszowska, Katedra Mechaniki Konstrukcji, 10'2003

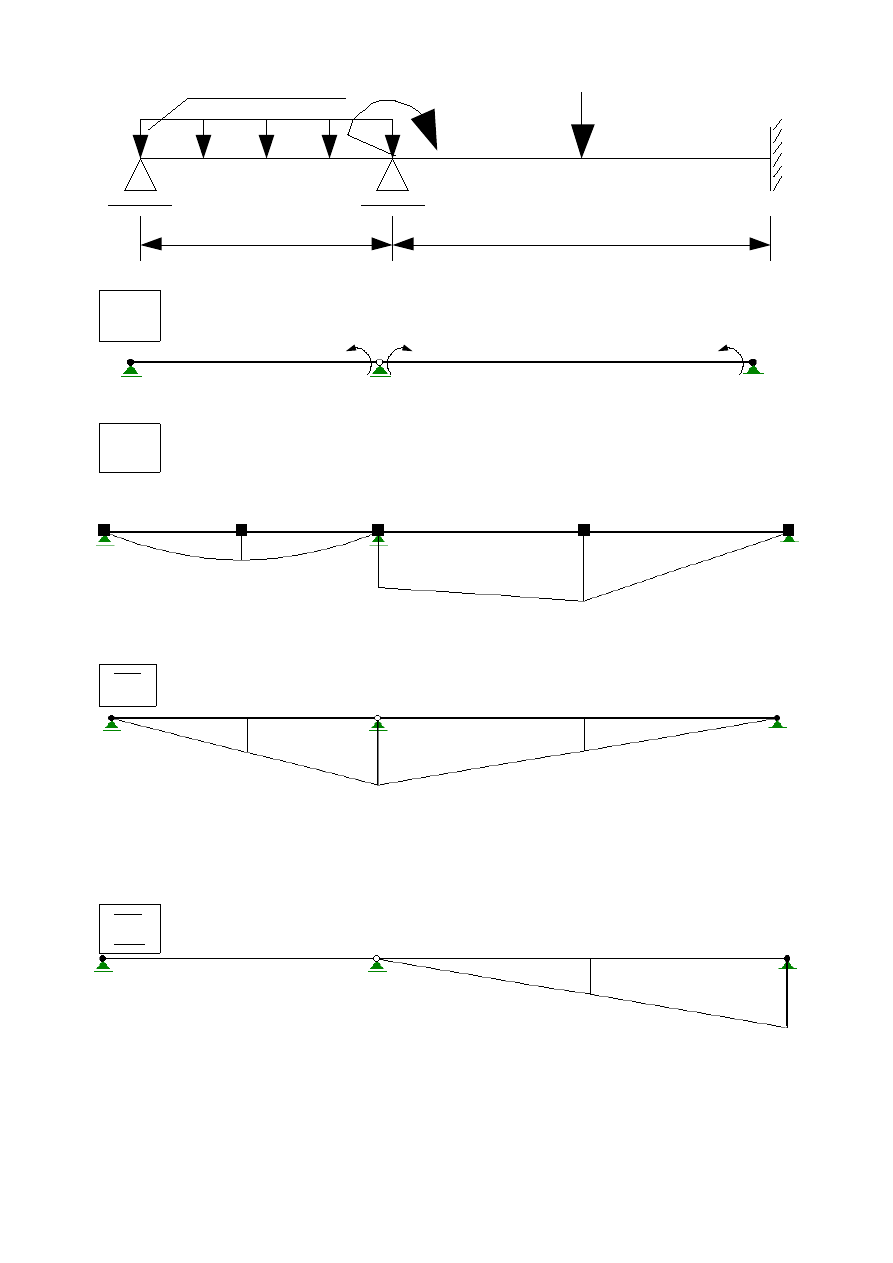
q=1,0 kN/m

4,0 m

6,0 m

EI

2EI

M=4 kNm

P=2 kN

X

1

X

1

X

2

I przedział 

II przedział

III przedział

wykres opisany jedną

wykres liniowy

inny wykres liniowy

funkcją 2go stopnia

1

3 4

5 6

7

2

2,0

5,0

4,0

0]

 

5;

 

5;

 

4;

 

0;

 

2;

 

[0;



p

M

0,5

1,0

0,5

0]

 

1/2;

 

1/2;

 

1;

 

1;

 

1/2;

[0;



M1

0,5

1,0

1]

 

1/2;

 

1/2;

 

0;

 

0;

 

0;

 

[0;



M2

Politechnika Rzeszowska, Katedra Mechaniki Konstrukcji, 10'2003

UP

1

M

2

M

1

M

p

M

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Metoda sil w ujeciu macierzowym
% Belka dwukrotnie stat. niewyzn.
% Matlab: G. Piatkowski 10.2002
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

clear all

% Wektory momentow jednostkowych
% ##### Wprowadzic rzedne wykresow jednostkowych Mi
M1 = [0; 0.5;  1;  1;  0.5;  0.5;  0]
M2 = [0;   0;  0;  0;  0.5;  0.5;  1]

% Wektor momentu od obciazenia zewnetrznego
% ##### Wprowadzic rzedne wykresu Mp
Mp = [0;  2;  0;  4;  5;  5;  0]

% Utworzenie macierzy momentow jednostkowych
% ##### Uwzglednic liczbe macierzy Mi
M = [M1  M2]

% Wspolcz. do calk. wg formuly Simpsona
% ##### Uwzglednic liczbe przedzialow, 
% ##### ich dlugosci i sztywnosc 
% ##### oraz stopien wykresu
A1 = 4/(6*1)*[1 0 0; 0 4 0; 0 0 1];
A2 = 3/(6*2)*[2 1; 1 2];
A3 = 3/(6*2)*[2 1; 1 2];

% Deklaracja macierzy A
wym = length(M1);
A = zeros(wym);

ip = 1;
% Zbudowanie quasi diagonalnej macierzy podatnosci
% Petla powtarza obliczenia dla kolejnych macierzy A1, A2, A3, ...
% ##### Zmienic liczbe powtorzen „i” adekwatnie do liczby przedzialow
for i=1:3
% okreslenie rozmiaru kolejnej macierzy A1, A2, A3, ...

r = eval(['length(','A',int2str(i),')']);

% Obliczenie indeksu koncowego

ik = ip + (r - 1)

% wbudowanie na przekatna macierzy A kolejnej macierzy A1, A2, A3, ..

A(ip:ik, ip:ik) = eval(['A',int2str(i)])

% aktualizacja indeksu poczatkowego

ip = ik + 1;

end

% Obliczenie macierzy podatnosci
d = M'*A*M

% Obliczenie wektora wyrazow wolnych
dp = M'*A*Mp

% Rozwiazanie rownania MS
X = -inv(d)*dp

% Obliczenie rzednych wykresu momentu zginajacego
Mk = Mp + M*X

Politechnika Rzeszowska, Katedra Mechaniki Konstrukcji, 10'2003