Janusz KOWAL

Janusz KOWAL

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza

Hutnicza

Podstawy Automatyki

Podstawy Automatyki

Wykład 7

Stabilność liniowych

stacjonarnych układów

sterowania

Wykład 7

Wykład 7

Stabilno

Stabilno

ść

ść

liniowych

liniowych

stacjonarnych uk

stacjonarnych uk

ł

ł

ad

ad

ó

ó

w

w

sterowania

sterowania

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

2

9

Ogólne warunki stabilności

9

Matematyczne warunki stabilności

9

Kryterium Hurwitza

9

Kryterium Michajłowa

9

Kryterium Nyquista

9

Logarytmiczne kryterium stabilności

Plan wykładu:

Plan wykładu:

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

3

9

Stabilność

układu sterowania jest

najważniejszą jego cechą charakteryzującą
zdolność układu do wykonywania zadań dla
których został on zbudowany.

Ogólne warunki stabilności

9

Stabilność

jest pojęciem określającym - w

potocznym znaczeniu - zdolność układu do
zachowania pewnego stanu.

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

4

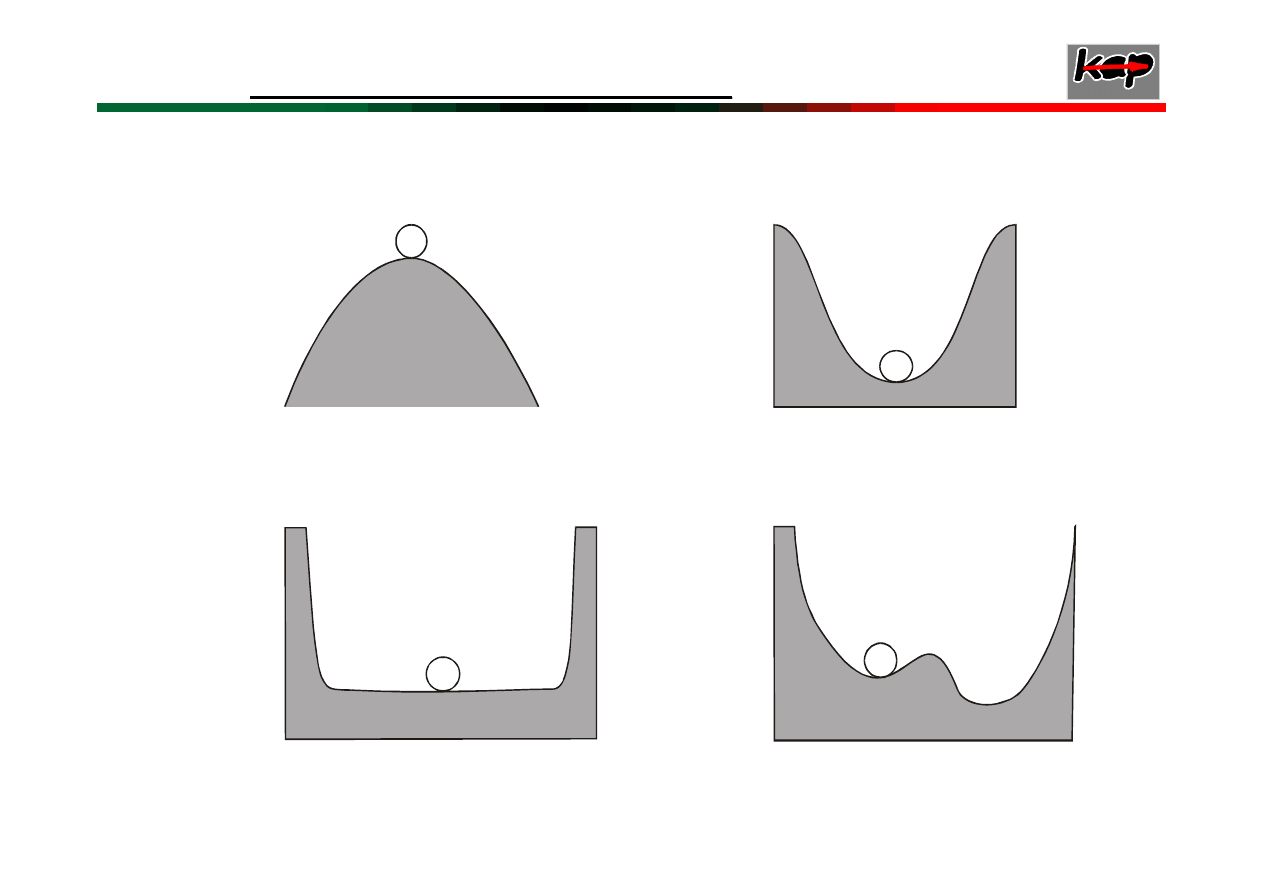
stabilna lokalnie

a)

c)

b)

d)

Rodzaje równowagi:

niestabilna

stabilna asymptotycznie

stabilna nieasymptotycznie

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

5

Przez

stabilność

układu automatycznej

regulacji (UAR), rozumiemy właściwość układu
polegającą na:

9

powrocie do stanu równowagi stałej po ustaniu

działania wymuszenia, które wytrąciło układ z
tego stanu, lub

9

osiągnięciu nowego stanu równowagi stałej,

jeśli wymuszenie pozostało na stałym poziomie.

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

6

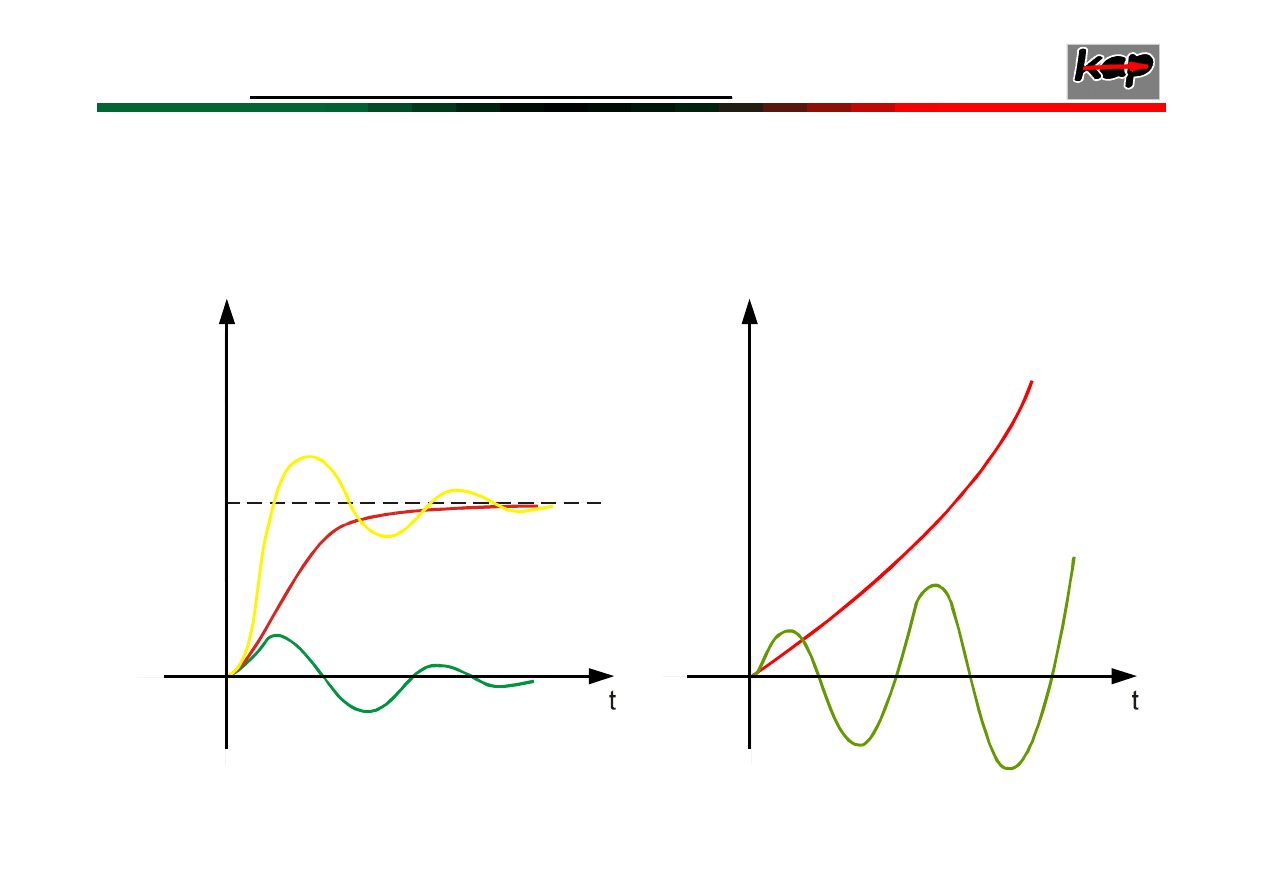
układów niestabilnych

y

y

Przykładowe charakterystyki czasowe

układów stabilnych

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

7

9

ogólnego

y

0

(t)

0

lim

0

=

∞

→

(t)

y

t

Analityczne sformułowanie warunków

stabilności -

korzystamy z równania różniczkowego opisującego
dynamikę układu

x

b

dt

dx

b

....

dt

x

d

b

y

a

dt

dy

a

....

dt

y

d

a

dt

y

d

a

m

m

n

n

n

n

n

n

0

1

0

0

1

1

1

+

+

+

=

+

+

+

+

−

−

Rozwiązanie tego równania jest sumą dwóch rozwiązań

Ponieważ rodzaj sygnału wejściowego nie ma znaczenia
przy badaniu stabilności, układ będzie stabilny gdy

9

szczególnego

y

s

(t)

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

8

0

0

1

1

1

=

+

+

+

+

−

−

a

s

a

...

s

a

s

a

n

n

n

n

0

0

1

1

1

1

=

+

+

+

+

−

−

−

y

a

dt

dy

a

...

dt

dy

a

dt

dy

a

n

n

n

n

n

n

W celu sprawdzenia czy układ jest stabilny,
należy zbadać rozwiązanie ogólne równania
różniczkowego jednorodnego

Korzystając z przekształcenia Laplace’a
otrzymamy równanie

algebraiczne

zwane

równaniem charakterystycznym

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

9

Pierwiastki równania charakterystycznego mogą
przybrać wartości:

t

s

n

t

s

t

s

n

e

C

...

e

C

e

C

(t)

y

+

+

+

=

2

1

2

1

0

Rozwiązanie możemy zapisać w postaci

∑

=

=

n

i

t

s

i

i

e

C

(t)

y

1

0

gdzie: C

i

- stałe całkowania wynikające z warunków

początkowych

s

i

- pierwiastki równania charakterystycznego

9

rzeczywiste dodatnie lub ujemne,

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

10

9

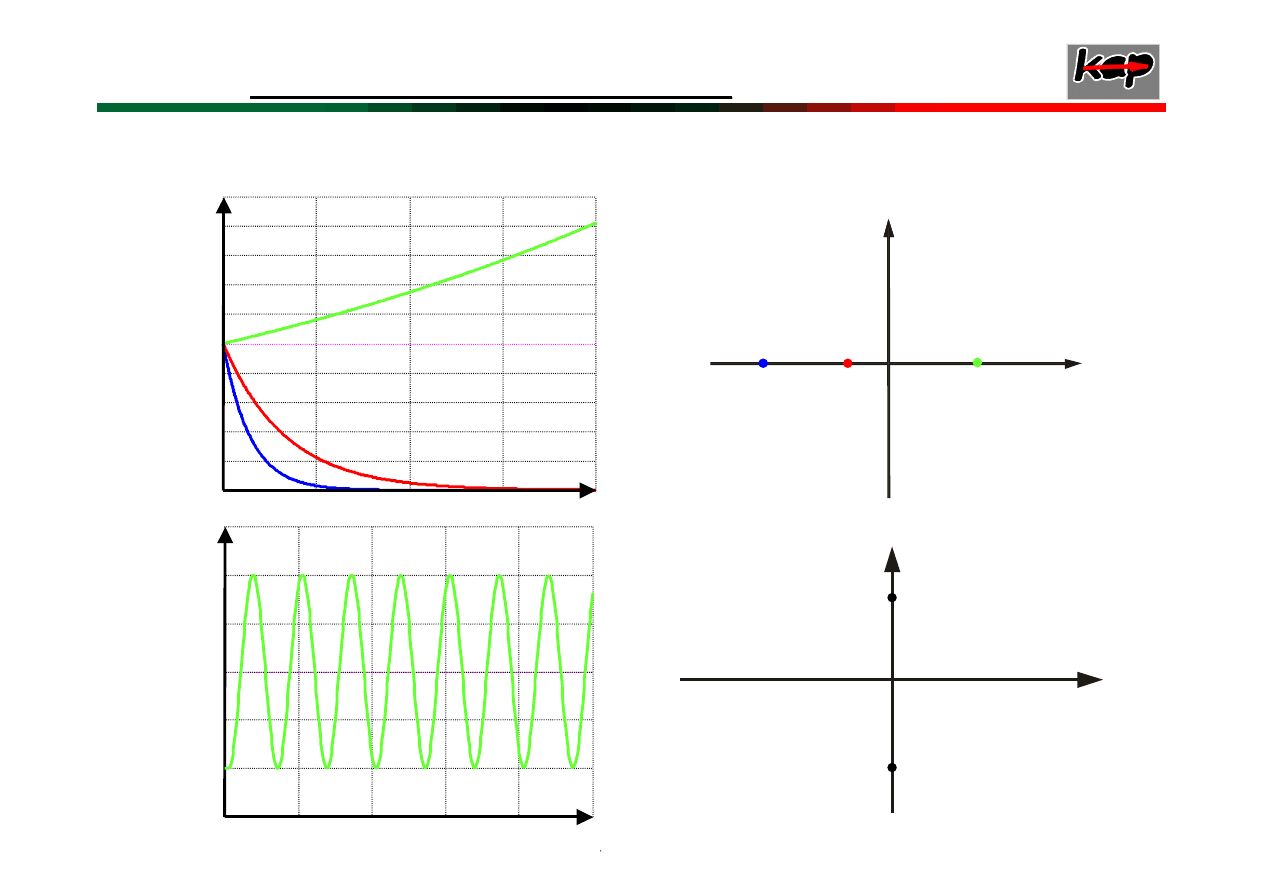
zespolone z częścią rzeczywistą dodatnią,

zerową lub ujemną

W zależności od wartości pierwiastków
otrzymujemy różne przebiegi

t)

ω

A

t

ω

(A

e

t

ω

A

t

ω

(A

e

(t)

y

t

α

t

α

2

4

2

3

1

2

1

1

0

sin

cos

sin

cos

2

1

+

+

+

+

=

Jeżeli są pierwiastkami
tego równania to rozwiązanie ma postać:

2

2

3,4

1

1

2

,

1

s

,

ω

α

ω

α

j

j

s

±

=

±

=

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

11

0

t

1

A

Im

Re

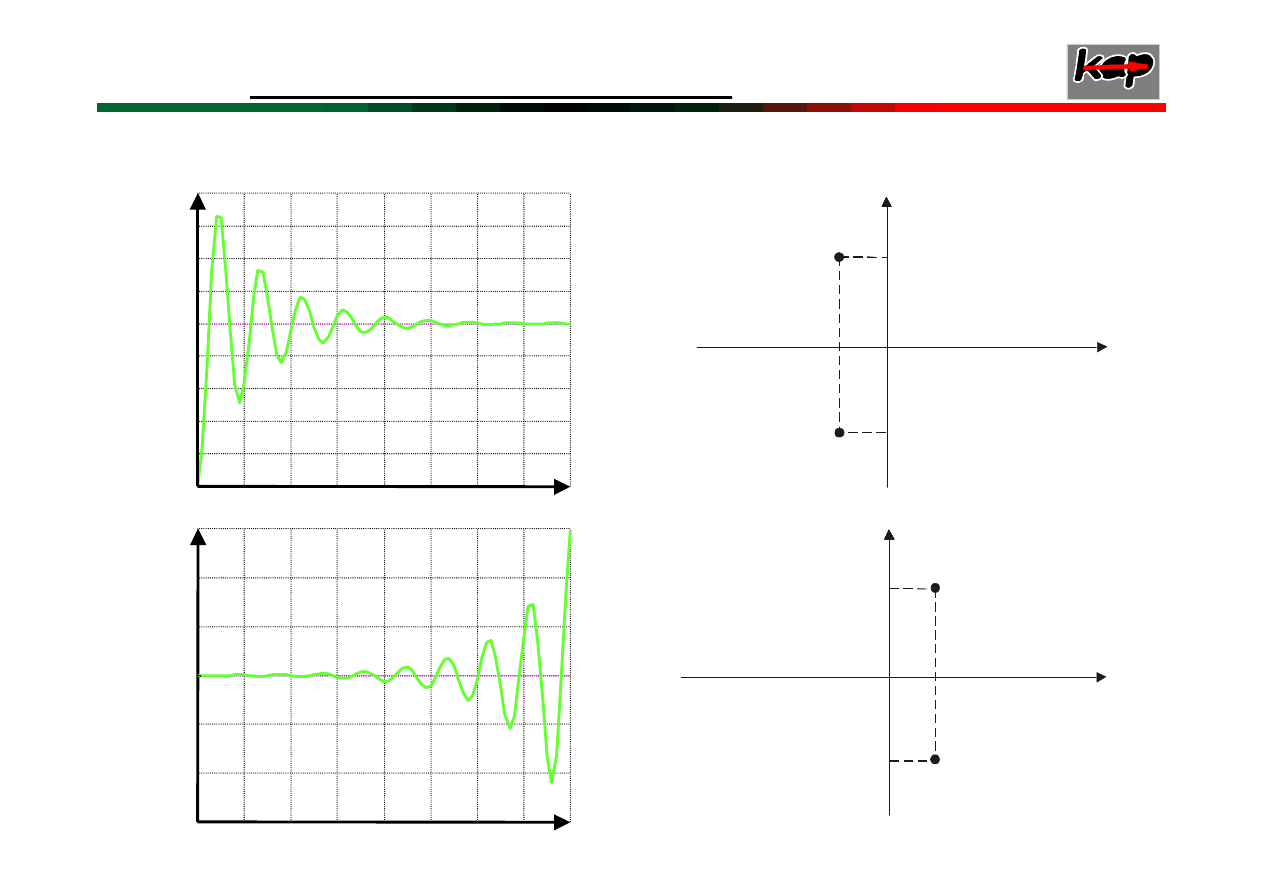
Wpływ lokalizacji pierwiastków na stabilność układu

0

t

1

A

t

s

e

3

t

s

e

2

−

t

s

e

1

−

s

1

s

2

s

3

Im

Re

-j

ω

+j

ω

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

12

0

t

1

A

Im

Re

-j

ω

+j

ω

α

α

Wpływ lokalizacji pierwiastków na stabilność układu

Im

Re

-j

ω

+j

ω

-

α

-

α

0

1

A

t

t

ω

sin

t

α

e

−

t

ω

sin

e

t

α

−

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

13

9

jeżeli chociażby jedna z części rzeczywistych s

i

jest dodatnia to

y

0

(t)

zmierza do nieskończoności

czyli układ jest niestabilny

9

przebiegi y

o

(t) zanikają w funkcji czasu, jeżeli

pierwiastki równania charakterystycznego są
rzeczywiste ujemne lub zespolone o częściach
rzeczywistych ujemnych.

Z przedstawionych wykresów wynika, że:

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

14

9

Koniecznym i dostatecznym warunkiem stabilności
asymptotycznej układu jest aby pierwiastki równania
charakterystycznego układu zamkniętego leżały w
lewej półpłaszczyźnie płaszczyzny zmiennej
zespolonej s (miały ujemne części rzeczywiste)

9

jeżeli równanie charakterystyczne ma pierwiastki w lewej
półpłaszczyźnie oraz jednokrotne na osi liczb urojonych, to
układ jest na granicy stabilności (nie jest stabilny
asymptotycznie)

9

jeżeli pierwiastki są zerowe lub są wielokrotne to układ jest
niestabilny

Re(s

k

)<0 i wtedy

0

lim

0

=

∞

→

(t)

y

t

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

15

Matematyczne warunki stabilności

9

stabilność układu w stanie swobodnym (gdy na

układ nie działają

sygnały zewnętrzne,

zarówno sterujące jak i zakłócające)

9

stabilność

układu poddanego działaniom

zewnętrznym

Wyróżniamy dwa rodzaje stabilności:

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

16

Przyjmijmy, że jeżeli układ swobodny znajduje się
w

stanie równowagi

czyli

0

=

(t)]

t),...,y

F[y(t),y'(

(n)

Stan dynamiczny układu mo

ż

emy określić na

podstawie znajomości wektora y(t) w przestrzeni
fazowej.

to odpowiadający temu

punkt równowagi

w

przestrzeni fazowej umieszczamy w początku jej
układu współrzędnych.

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

17

9

Jeżeli dla t

→∞

trajektoria nie wychodzi poza

pewien ograniczony obszar otaczający początek
układu współrzędnych, to układ jest

stabilny w

sensie Lapunowa

.

9

Jeżeli dla t

→∞

trajektoria oddala się

nieskończenie do początku układu
współrzędnych to układ jest

niestabilny.

9

Jeżeli dla t

→∞

trajektoria dąży do początku

układu współrzędnych (punkt równowagi) to
układ jest

stabilny asymptotycznie.

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

18

Stabilność Lapunowa

zachodzi gdy dla liczby

dodatniej

ε

można znaleźć taką liczbę

δ

, żeby

przy

obowiązywała nierówność:

Przez

||

y

||

będziemy oznaczać w przestrzeni

fazowej będącej liniową przestrzenią wektorową,

normę wektora

y o składowych y

1

,y

2

,.....,y

n

równą:

[

]

(t)

y

...

(t)

y

(t)

y

(t)

y

y(t)

n

n

k

k

2

2

2

2

1

1

2

+

+

+

=

=

∑

=

||

y(t

0

)

|| <

δ

||

y(t)

|| <

ε

dla t>t

0

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

19

i dla t>t

0

trajektoria dążyła do początku układu

współrzędnych tzn.

Stabilność asymptotyczna

zachodzi gdy można

dobrać dodatnią liczbę

δ

żeby przy spełnionym

warunku

δ

)

y(t

<

0

0

→

+∞

→

t

y(t)

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

20

9

lub dochodzi do obszaru określonego wzorem

Stabilność globalna

zachodzi w przypadku gdy układ

jest stabilny dla dowolnych warunków początkowych.

9

osiąga początek układu współrzędnych

(stabilność globalna asymptotyczna),

Wtedy trajektoria układu swobodnego wychodząca z
dowolnego punktu przestrzeni fazowej:

i pozostaje w nim (stabilność globalna w sensie
Lapunowa).

||

y(t)

|| <

ε

dla

t>t

0

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

21

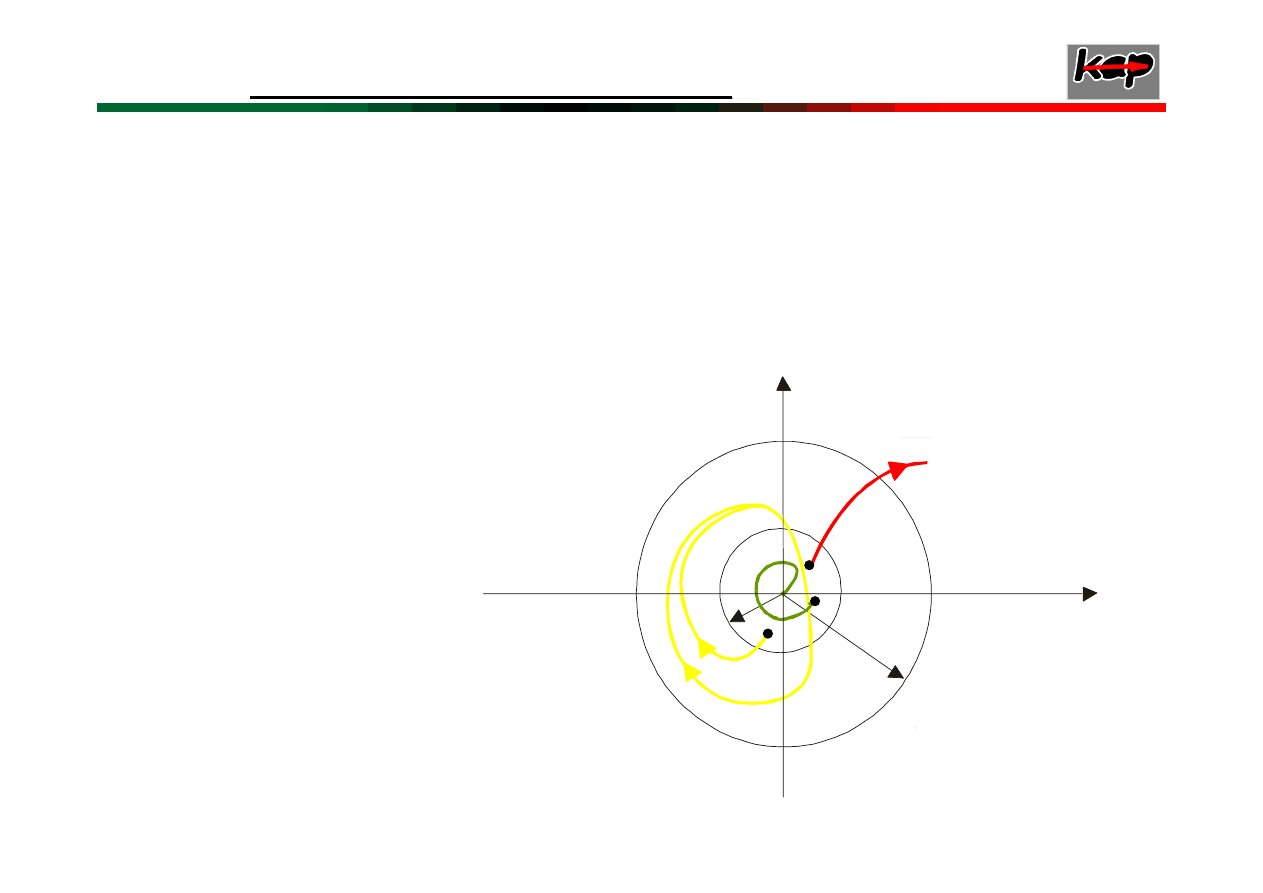
Przebiegi trajektorii fazowej dla układu II-go rzędu
wychodzące z punktu:

9

A

0

- dla układu stabilnego

w sensie Lapunowa,

9

B

0

- dla układu stabilnego

asymptotycznie,

9

C

0

- dla układu niestabilnego

B

0

0

C

C

0

A

0

δ

8

0

y

2

y

1

ε

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

22

W przypadku

układu liniowego

stan swobodny

jest opisany jednorodnym równaniem liniowym o
stałych współczynnikach

Rozwiązanie ogólne równania różniczkowego n-go
rzędu, zwyczajnego liniowego o stałych
współczynnikach i jednorodnego

zależy od

pierwiastków równania charakterystycznego

0

0

1

1

1

=

+

+

+

+

−

−

−

y(t)

a

dt

dy(t)

...

dt

y(t)

d

a

dt

y(t)

d

a

n

n

n

n

n

n

0

0

1

1

1

+

+

+

+

+

−

−

a

s

a

...

s

a

s

a

n

n

n

n

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

23

9

Równanie charakterystyczne ma wyłącznie
pojedyncze pierwiastki rzeczywiste ujemne

czyli układ jest stabilny asymptotycznie.

Dla przykładu rozpatrzymy szereg przypadków:

t

t

Be

Ae

s

B

s

A

L

)

)(s

(s

L(s)

L

g(t)

2

1

1

2

1

2

1

−

−

−

−

+

=









+

+

+

=













+

+

=

0

lim

=

∞

→

g(t)

t

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

24

9

Równanie charakterystyczne ma oprócz

pojedynczych ujemnych pierwiastków

rzeczywistych ma również wielokrotne
pierwiastki rzeczywiste ujemne

wtedy układ jest również stabilny asymptotycznie.

t

t

t

Cte

Be

Ae

s

C

s

B

s

A

L

)

)(s

(s

L(s)

L

g(t)

2

2

1

2

1

2

2

1

2

1

−

−

−

−

−

+

=









+

+

+

+

+

=













+

+

=

0

lim

=

∞

→

g(t)

t

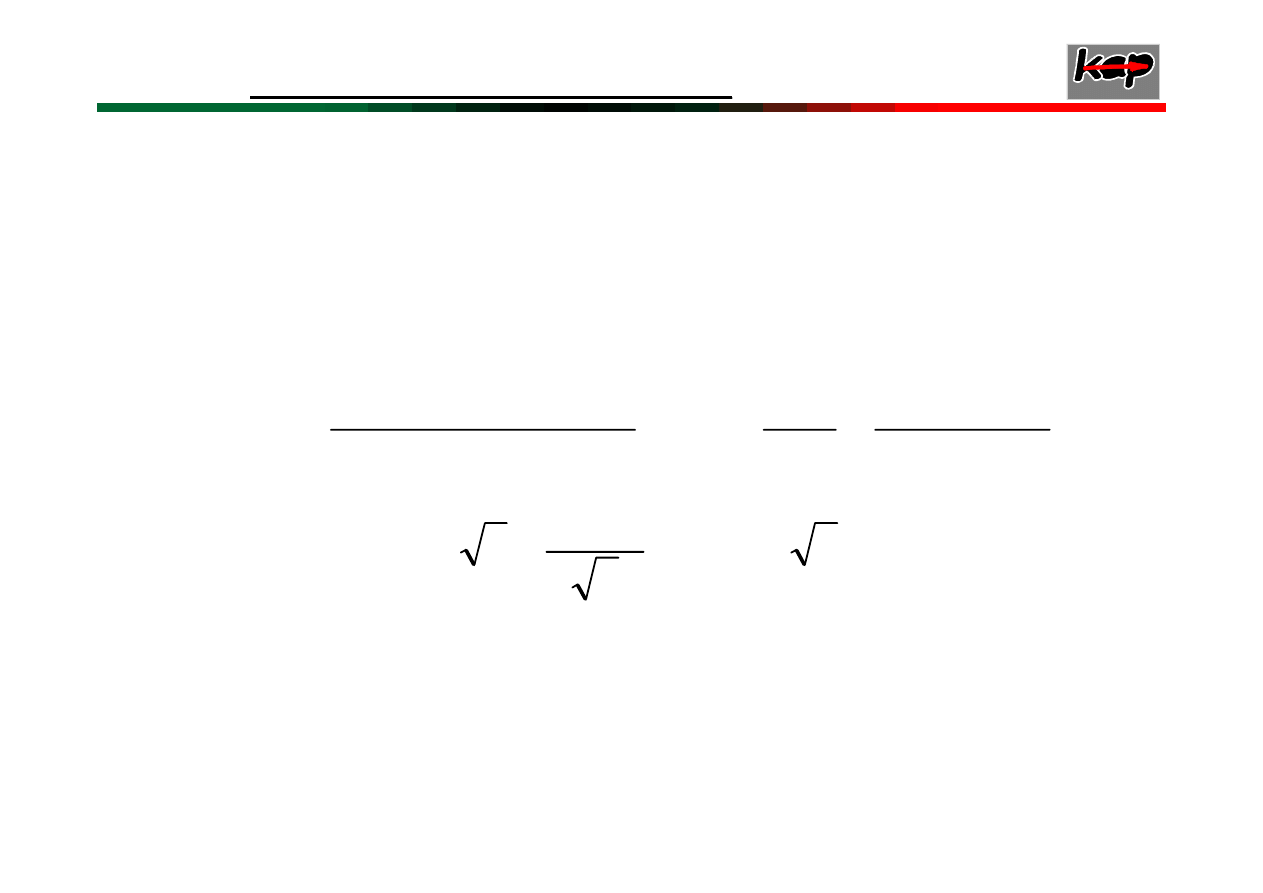
Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

25

9

Równanie charakterystyczne ma rzeczywiste

pierwiastki ujemne i pierwiastki zespolone o
częściach rzeczywistych ujemnych

wtedy układ jest stabilny asymptotycznie, bo
występują sinusoidy o gasnącej amplitudzie.

3

sin

3

3

cos

4

2

1

4

2

1

2

1

2

1

⋅

−

+

+

=

=









+

+

+

+

+

=













+

+

+

=

−

−

−

−

−

t

e

B

C

t

Be

Ae

s

s

C

Bs

s

A

L

)

s

)(s

(s

L(s)

L

g(t)

t

t

t

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

26

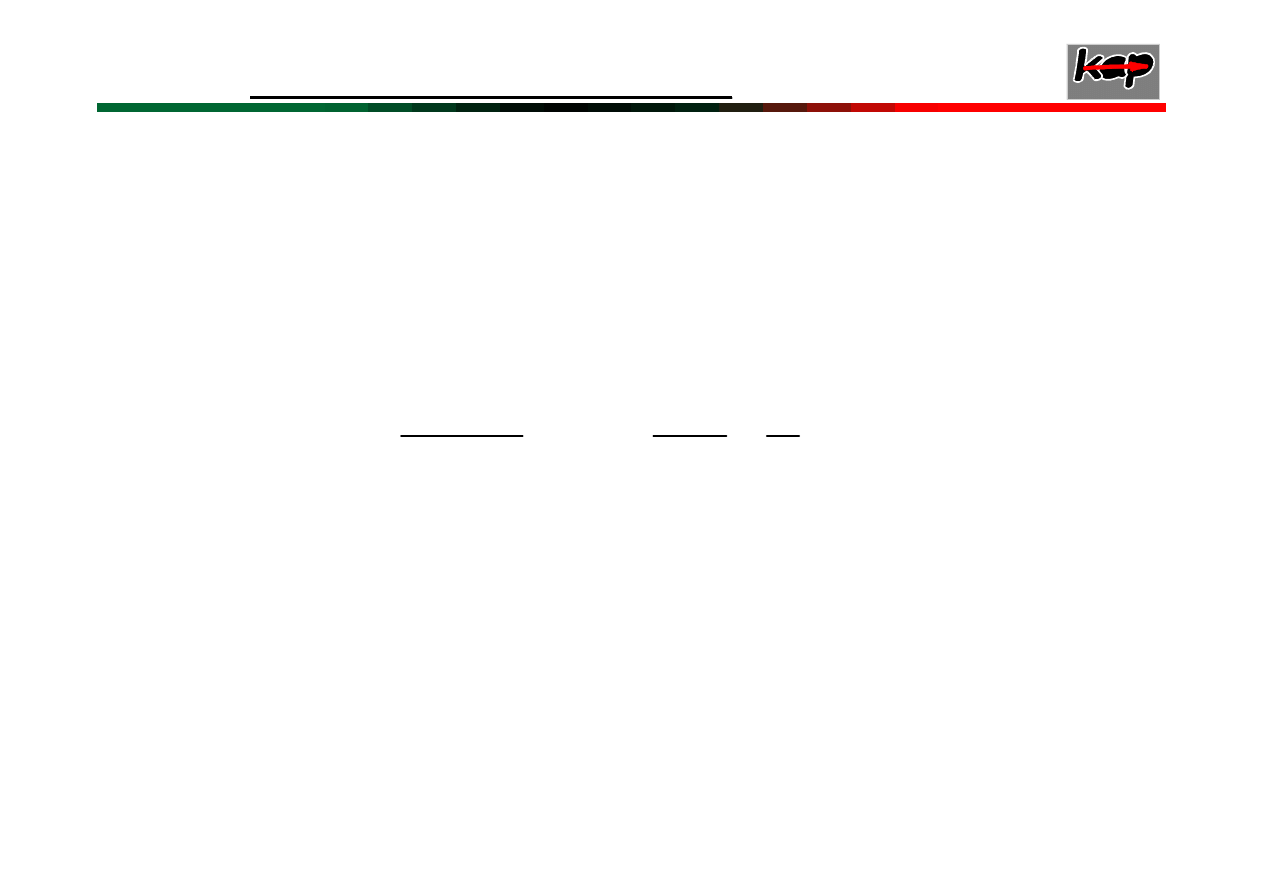
9

Równanie charakterystyczne ma oprócz
pierwiastków o ujemnych częściach
rzeczywistych jeden pierwiastek zerowy

Stabilność nieasymptotyczna związana jest z
występowaniem jednego pierwiastka zerowego;
układ stabilny w sensie Lapunowa.

B

Ae

s

B

s

A

L

)s

(s

L(s)

L

g(t)

t

+

=









+

+

=













+

=

−

−

−

1

1

1

2

1

B

g(t)

t

=

∞

→

lim

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

27

9

Równanie charakterystyczne oprócz pierwiastków

ujemnych ma wielokrotny pierwiastek zerowy

wtedy układ jest niestabilny

Ct

B

Ae

s

C

s

B

s

A

L

)s

(s

L(s)

L

g(t)

t

+

+

=









+

+

+

=













+

=

−

−

−

2

1

2

1

1

1

∞

=

∞

→

g(t)

t

lim

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

28

9

Równanie charakterystyczne oprócz
pierwiastków ujemnych ma pierwiastki dodatnie

wtedy układ jest niestabilny

t

-

t

Be

Ae

s-

B

s

A

L

)

)(s-

(s

L(s)

L

g(t)

2

1

1

2

1

2

1

+

=









+

+

=













+

=

−

−

−

∞

=

∞

→

g(t)

t

lim

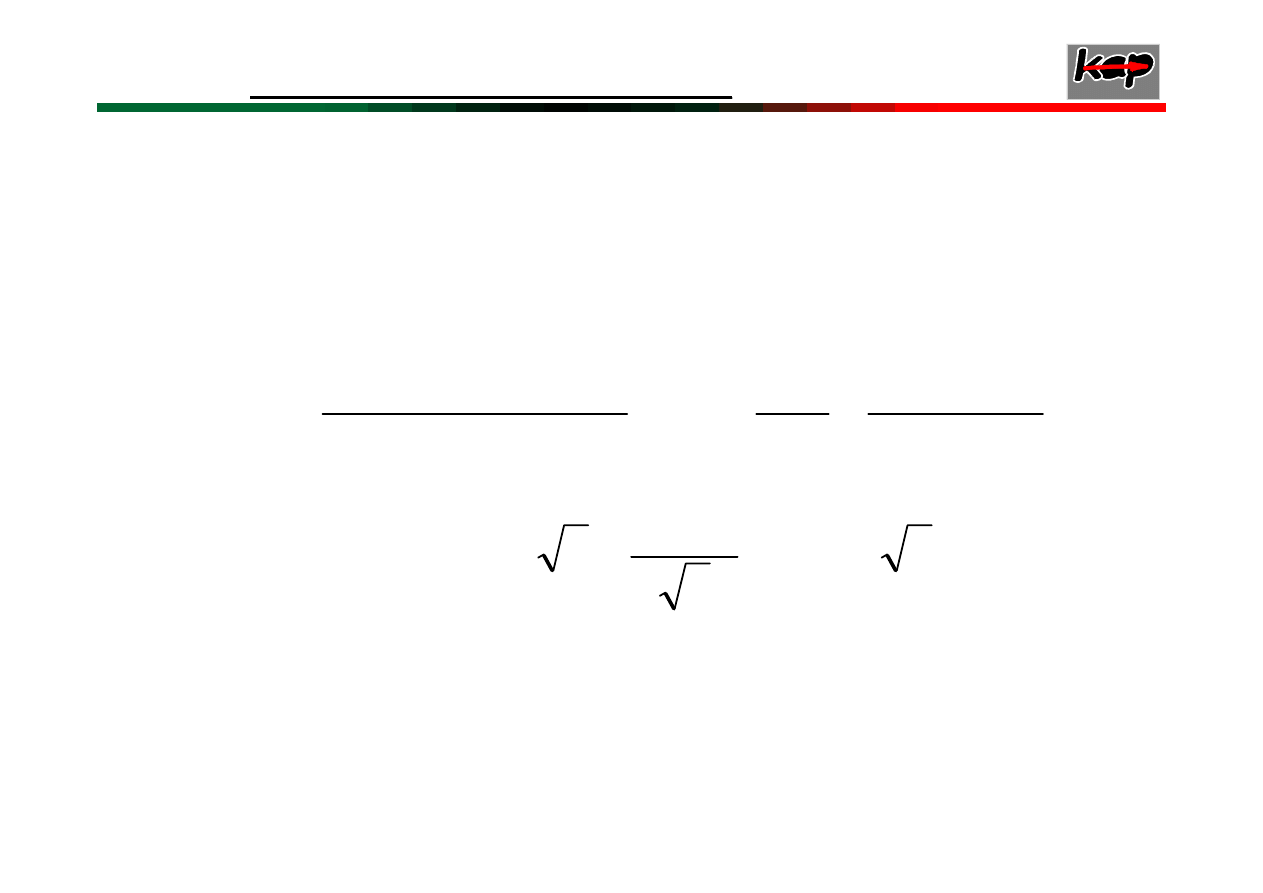
Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

29

9

Równanie charakterystyczne oprócz
pierwiastków ujemnych ma pierwiastki
zespolone o dodatniej części rzeczywistej

wtedy układ jest niestabilny

=









+

−

+

+

+

=













+

−

+

=

−

−

4

2

1

4

2

1

2

1

2

1

s

s

C

Bs

s

A

L

)

s

)(s

(s

L(s)

L

g(t)

∞

=

∞

→

g(t)

t

lim

3

sin

3

3

cos

1

⋅

+

+

+

=

−

t

e

B

C

t

Be

Ae

t

t

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

30

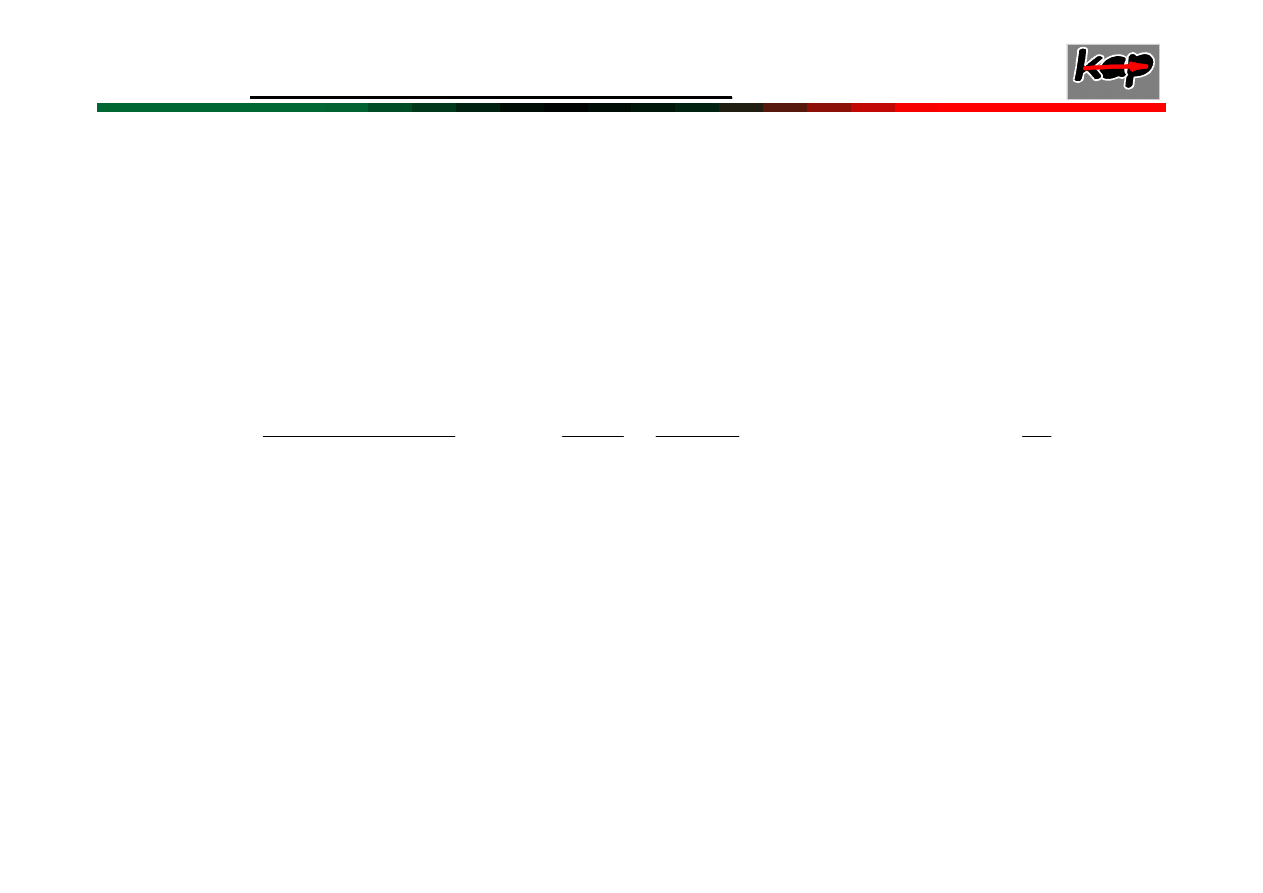
9

Równanie charakterystyczne oprócz

pierwiastków ujemnych ma pierwiastki zespolone
o zerowych częściach rzeczywistych

wtedy występują

drgania niegasnące

- układ

stabilny w sensie Lapunowa.

t

C

t

B

Ae

s

B

s

A

L

)

)(s

(s

L(s)

L

g(t)

t

2

sin

2

2

cos

4

1

4

1

2

1

2

1

+

+

=









+

+

+

=













+

+

=

−

−

−

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

31

Warunek konieczny stabilności Lapunowa jest

następujący:

9

krotność par pierwiastków urojonych powinna

być co najwyżej równa jedności.

9

krotność pierwiastków rzeczywistych równych

zeru,

9

wszystkie pierwiastki rzeczywiste i

części

rzeczywiste pierwiastków zespolonych powinny
być ujemne,

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

32

9

występuje jeden pierwiastek rzeczywisty równy
zeru,

9

występują pojedyncze (nie wielokrotne) pary

pierwiastków urojonych,

9

przy jednym pierwiastku rzeczywistym równym
zeru występują pojedyncze (nie wielokrotne)
pary pierwiastków urojonych.

Gdy spełniony jest powyższy warunek konieczny,
układ jest stabilny w sensie Lapunowa gdy:

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

33

Warunkiem koniecznym i wystarczającym

stabilności asymptotycznej jest, aby wszystkie
pierwiastki rzeczywiste oraz części rzeczywiste
pierwiastków urojonych były ujemne, możemy
zapisać:

Globalna stabilność asymptotyczna występuje
gdy układ jest stabilny asymptotycznie

0

)

Re(

<

k

s

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

34

Najbardziej znanymi są kryteria :

9

analityczne

Hurwitza

9

analityczne

Routha

9

kryterium graficzne

Michajłowa

9

analityczno-graficzne

Nyquista

Pierwsze dwa kryteria wymagają znajomości
transmitancji układu w postaci analitycznej.

Kryteria graficzne oparte są na charaktery-
stykach częstotliwościowych.

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

35

Kryterium Hurwitza

Warunkiem koniecznym i wystarczającym

, żeby

układ liniowy stacjonarny ciągły był

stabilny

asymptotycznie jest aby:

1) wszystkie współczynniki równania charakterystycznego

0

0

1

1

1

=

+

+

+

+

−

−

a

s

a

...

s

a

s

a

n

n

n

n

,...,n

,

,

,i

a

i

2

1

0

0

=

>

były różne od zera i jednakowego znaku

2) wszystkie podwyznaczniki główne (

minory

) wyznacznika

Hurwitza były większe od zera.

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

36

0

2

4

1

3

0

2

1

3

1

3

1

4

2

5

3

1

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

a

a

a

a

a

a

a

a

a

a

a

a

a

a

a

a

a

a

n

n

n

n

n

n

n

n

n

n

n

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

=

∆

−

−

−

−

−

−

−

−

−

0

1

1

>

=

∆

−

n

a

0

2

3

1

2

>

=

∆

−

−

−

n

n

n

n

a

a

a

a

0

0

3

1

4

2

1

5

3

1

3

>

=

∆

−

−

−

−

−

−

−

−

n

n

n

n

n

n

n

n

a

a

a

a

a

a

a

a

;

;

Kryterium Hurwitza pozwala na sprawdzenie czy równanie
algebraiczne dowolnego stopnia ma wyłącznie pierwiastki
ujemne lub o ujemnych częściach rzeczywistych.

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

37

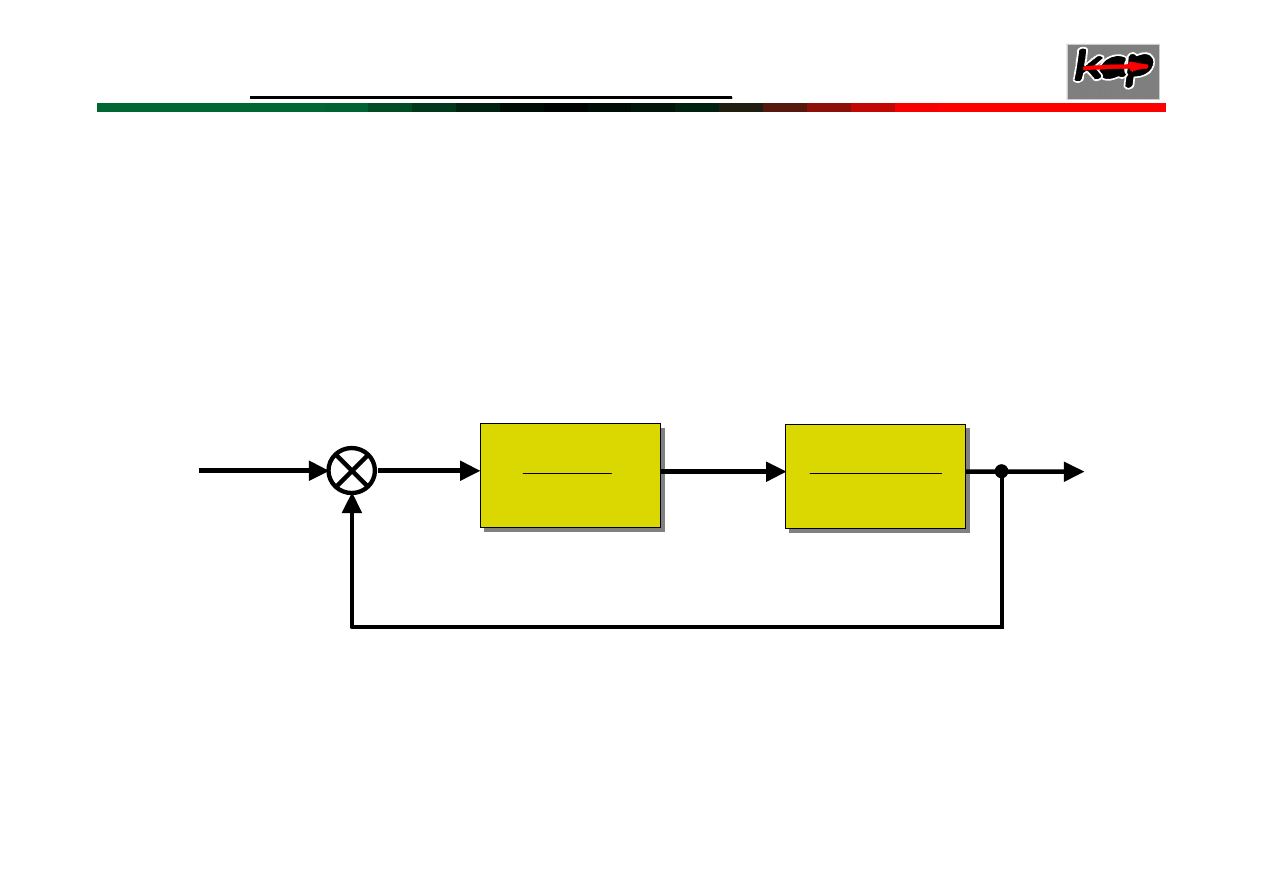
Przykład 1

Dany jest układ regulacji automatycznej o
schemacie przedstawionym na rysunku i
transmitancjach:

E(s)

U(s)

1

s

T

K

1

1

+

Y(s)

)

1

s

T

(

s

K

2

2

+

–

W(s)

Wyznaczyć zakresy parametrów K

1

, K

2

, T

1

, i T

2

,

przy których układ jest stabilny.

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

38

Transmitancja operatorowa

układu zamkniętego

2

1

2

1

2

1

0

0

1

1

1

K

K

)

s

)(T

s

s(T

K

K

G

G

G

G

G(s)

R

R

+

+

+

=

+

=

Równanie charakterystyczne

ma postać

a po przekształceniu

0

2

1

2

2

1

3

2

1

=

+

+

+

+

K

K

s

)s

T

(T

s

T

T

W tym przypadku n=3, należy więc zbadać tylko
wyznacznik drugiego stopnia

0

1

1

2

1

2

1

=

+

+

+

K

K

)

s

)(T

s

s(T

2

1

2

1

2

1

2

1

2

1

2

1

1

0

3

2

2

1

T

T

K

K

T

T

K

K

T

T

T

T

a

a

a

a

∆

−

+

=

+

=

=

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

39

Aby układ był stabilny, parametry regulatora T

1

i K

1

muszą spełniać warunek

2

1

2

1

1

1

K

K

T

T

>

+

Aby układ był na

granicy stabilności

, musi

zachodzić zależność

2

1

2

1

1

1

K

K

T

T

=

+

Wówczas równanie charakterystyczne ma postać

0

1

2

1

2

2

1

=

+

+

)

K

K

)(s

s

T

(T

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

40

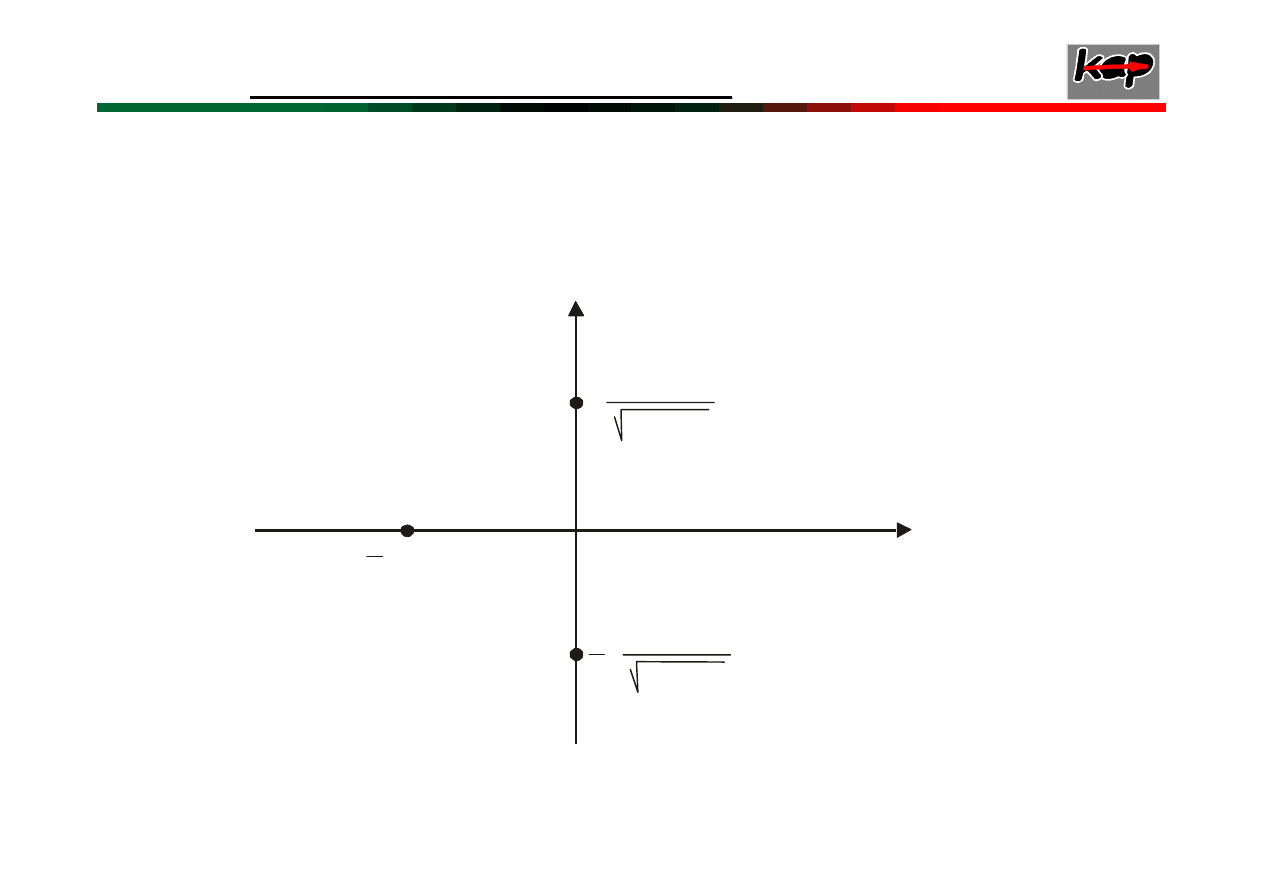
Rozkład

pierwiastków

tego równania pokazano

na poniższym rysunku

Im

Re

1

K

1

K

2

1

T

1

T

2

T

1

T

2

j

j

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

41

Kryterium Hurwitza umożliwia stwierdzenie
stabilności:

Możliwość wystąpienia stabilności nieasympto-
tycznej zachodzi wtedy, kiedy w równaniu
charakterystycznym współczynnik a

0

=0.

9

asymptotycznej

9

nieasymptotycznej

Po podzieleniu stron równania przez s,
otrzymujemy równanie stopnia n-1 w odniesieniu
do którego stosujemy kryterium Hurwitza.

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

42

Kryterium Michajłowa

Kryterium Michajłowa

służy do oceny stabilności

układu liniowego jednowymiarowego, a właściwie
do uzyskania

metodą graficzną odpowiedzi na

pytanie:

ile pierwiastków równania charaktery-

stycznego leży w prawej półpłaszczyźnie?

Umożliwia ono badanie stabilności na podstawie
przebiegu na płaszczyźnie zmiennej zespolonej
wykresu funkcji N(j

ω

), otrzymanej z wielomianu

charakterystycznego po podstawieniu s=j

ω

0

1

1

1

a

s

a

...

s

a

s

a

N(s)

n

n

n

n

+

+

+

+

=

−

−

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

43

Wyrażenie to zapiszemy w postaci

)

s

.(s

).........

s

)(s

s

(s

a

N(s)

k

n

−

−

−

=

2

1

gdzie: s

k

(k=1,2,...,n)

po obraniu s= j

ω

otrzymujemy

m)π

(n

mπ

m)π

(n

)

N(jω

arg

∆

2

−

=

−

−

=

lub inaczej

jΦ

e

)

N(j ω

)

N(j ω

=

gdzie:

n

n

s

jω

...

s

jω

a

)

N(j ω

−

−

=

2

n

s

jω

arg

....

s

jω

arg

)

N(jω

arg

Φ

−

+

+

−

=

=

1

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

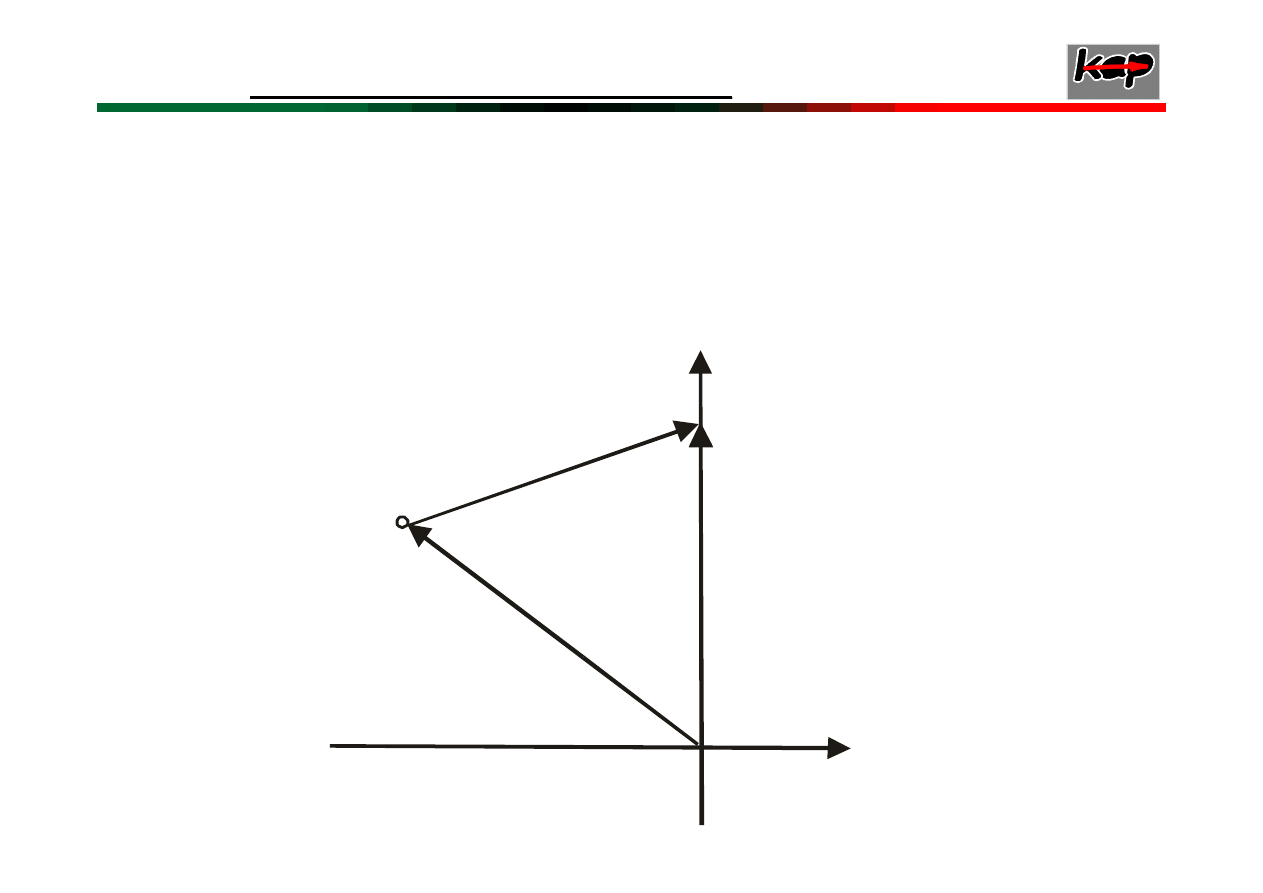
44

Wektor

odpowiadający j

ω

jest położony na osi

urojonej i końce poszczególnych wektorów
przedstawiających czynniki (j

ω−

s

k

) znajdują się

na tej osi na rysunku poniżej.

S

Re

Im

k

S

k

jω−

j

ω

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

45

Jeżeli będziemy zmieniać pulsację

ω

, w zakresie

od

−

∞

do

+

∞

, to stwierdzimy, że

zmiana

argumentu wektora

(j

ω−

s

k

) zależy od położenia

punktu odpowiadającego s

k

na płaszczyźnie

zmiennej zespolonej.

9

W przypadku gdy punkt ten leży w

lewej

półpłaszczyźnie

wektor (j

ω−

s

k

) przy zmianie

−

∞

<ω<+

∞

obróci się w kierunku przeciwnym do

ruchu wskazówek zegara o kąt

+π

9

Natomiast gdy punkt odpowiadający s

k

leży w

prawej półpłaszczyźnie

to wektor (j

ω−

s

k

) przy

zmianie

−

∞

<ω<+

∞

obróci się w kierunku

zgodnym z ruchem wskazówek zegara o kąt

− π

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

46

Jeżeli z liczby wszystkich pierwiastków n, m
pierwiastków znajduje się

w

prawej

półpłaszczyźnie

a (n-m) w lewej to zmiana

argumentu N(j

ω

) przy

−

∞

<ω<+

∞

Ponieważ

warunkiem stabilności jest aby

wszystkie pierwiastki miały

ujemne części

rzeczywiste

(czyli m=0), to:

m)π

(n

mπ

m)π

(n

)

N(jω

arg

∆

2

−

=

−

−

=

−

∞

<ω<+

∞

−

∞

<ω<+

∞

R

e

s

k

<

0

jeżeli

∆

argN(j

ω

)=n

π

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

47

Układ regulacji automatycznej jest stabilny

wtedy i tylko wtedy, gdy zmiana argumentu
krzywej N(j

ω

) przy zmianie pulsacji

−

∞

<ω<+

∞

wynosi n(

π

/2) gdzie n oznacza stopień równania

charakterystycznego tzn.

Kryterium Michajłowa

można sformułować

następująco :

2

nπ

)

N(jω

arg

∆

=

−

∞

<ω<+

∞

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

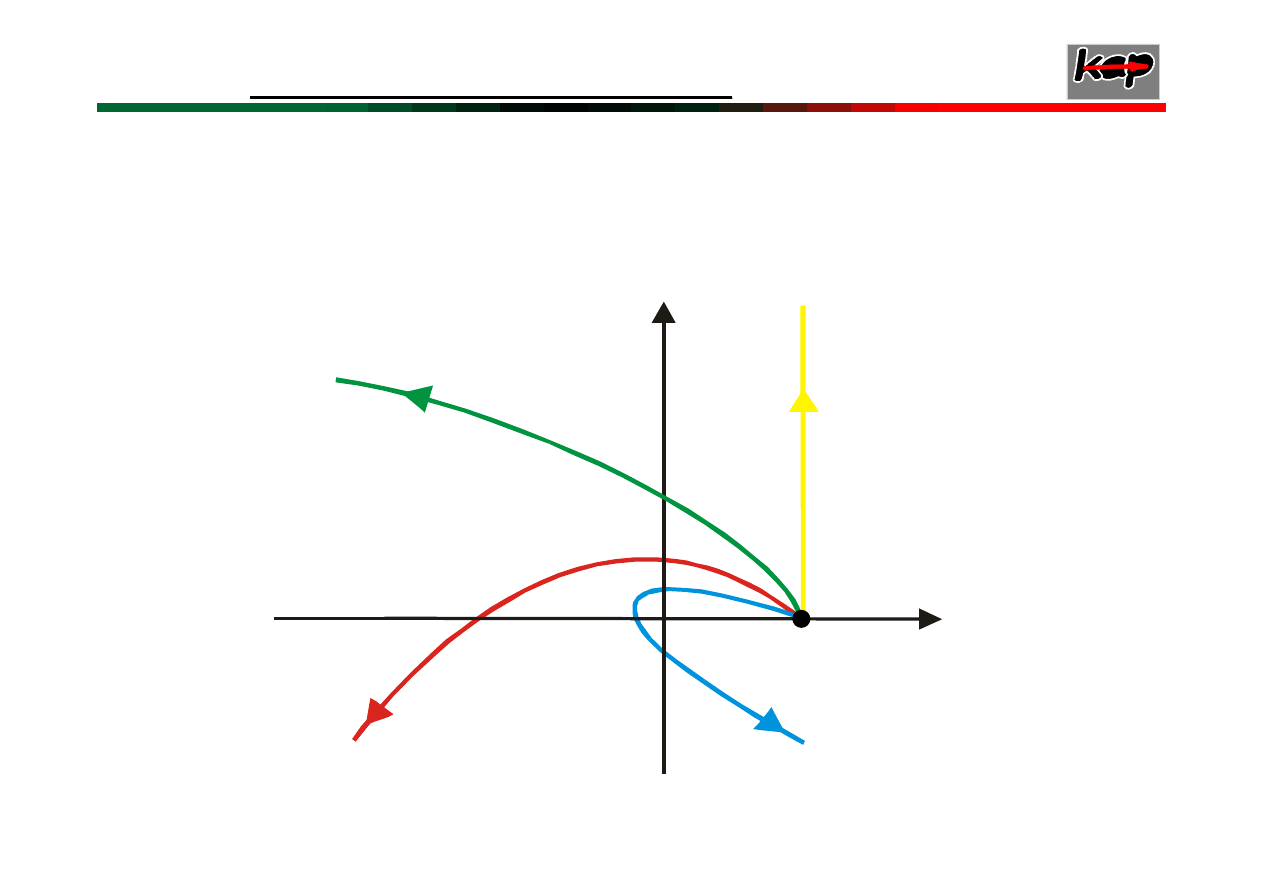
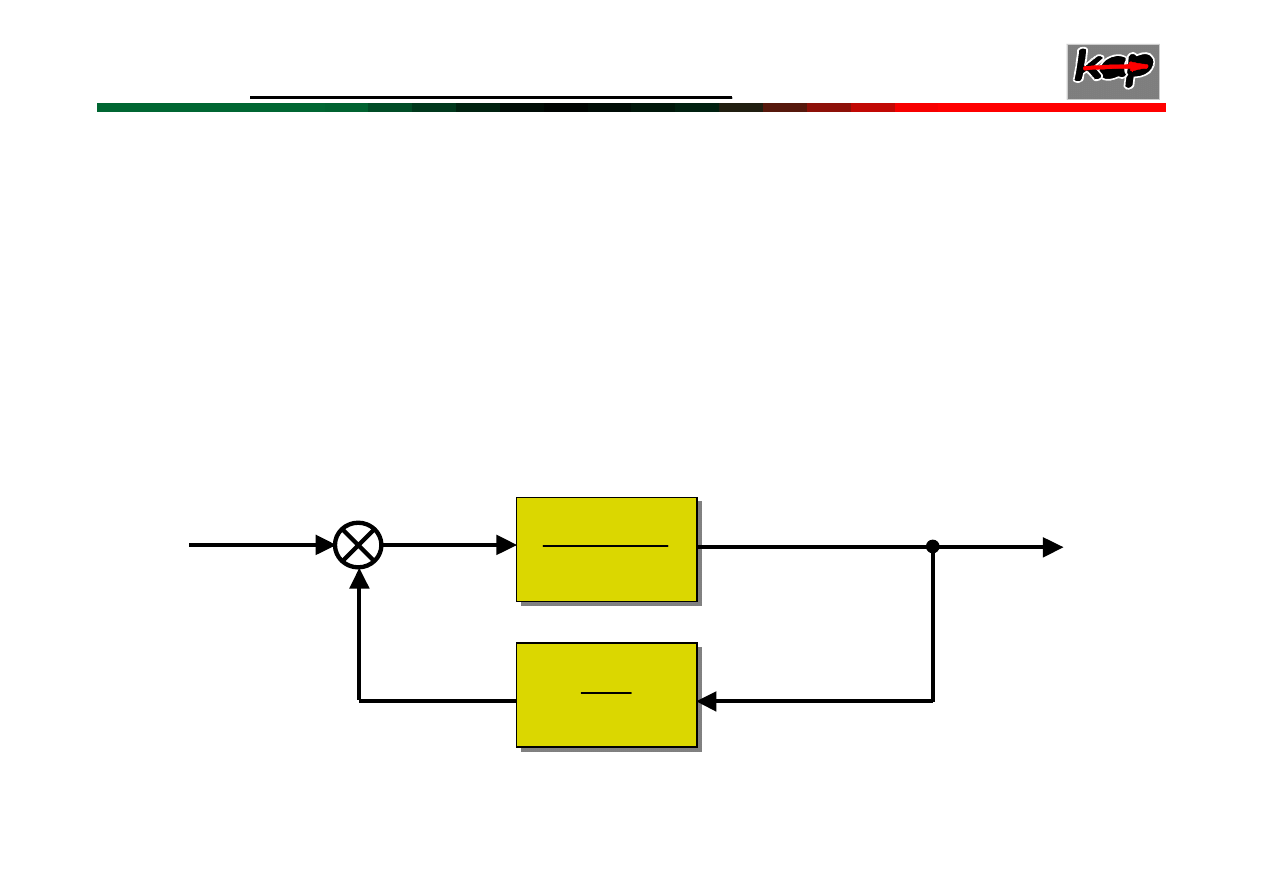
48

Przykładowe wykresy

Michajłowa

układów

stabilnych asymptotycznie rzędu od n=4 do n=1

n=4

n=3

n=2

n=1

0

=

ω

(

)

(

ω

jQ

)

ω

P

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

49

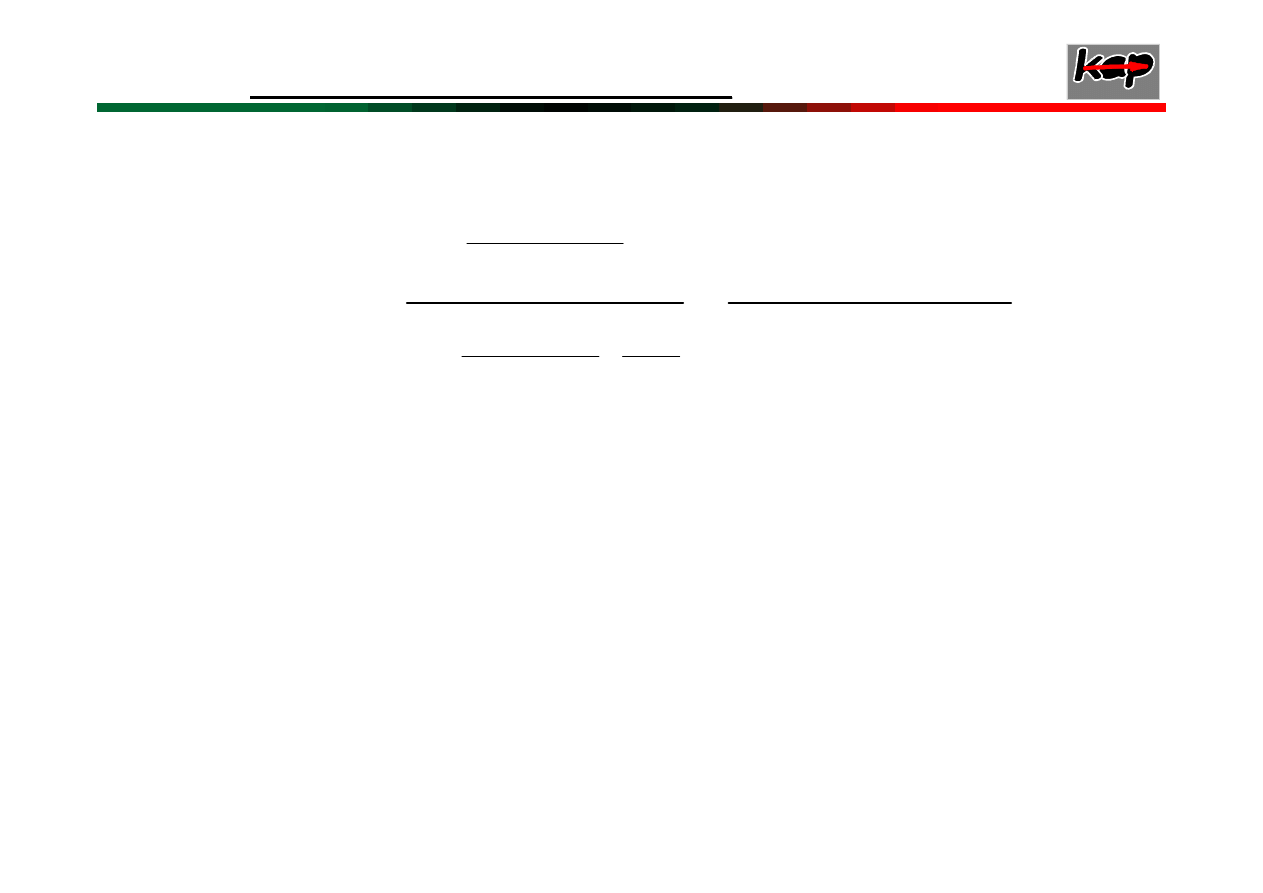
Przykład 2

Dany jest układ regulacji automatycznej jak na
rysunku. Zbadać stabilność układu, wykorzystując
kryterium Michajłowa, jeśli T

1

=0.14s, T

2

=2s i

K=10. Jakie powinno byś K by układ znalazł się na
granicy stabilności?

Schemat blokowy układu regulacji

U(s)

2

1

)

1

s

T

(

K

+

Y(s)

s

T

1

2

–

W(s)

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

50

Transmitancja zastępcza układu zamkniętego

Przekształcając

mianownik

transmisji

G

z

(s),

otrzymujemy wielomian charakterystyczny układu

po podstawieniu danych

10

2

56

0

04

0

2

3

+

+

+

=

s

s

,

s

,

N(s)

K

)

s

s(T

T

s

KT

s

T

)

s

(T

K

)

s

(T

K

(s)

G

z

+

+

=

⋅

+

+

+

=

2

1

2

2

2

1

2

1

1

1

1

1

1

K

s

T

s

T

T

s

T

T

N(s)

+

+

+

=

2

2

2

1

3

2

2

1

2

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

51

Podstawiając s=j

ω

oraz wyodrębniając część

rzeczywistą i urojoną

otrzymamy

Następnie rozwiązujemy równania P(

ω

)=0

i

Q(

ω

)=0 znajdując w ten sposób punkty, przy

których wykres Michajłowa przecina osie.

)

ω

,

(

jω

ω

,

)

jQ(ω

)

P(ω

)

N(jω

2

2

04

0

2

56

0

10

−

+

−

=

+

=

Wykres krzywej N(j

ω

) przedstawiono na rysunku

poniżej.

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

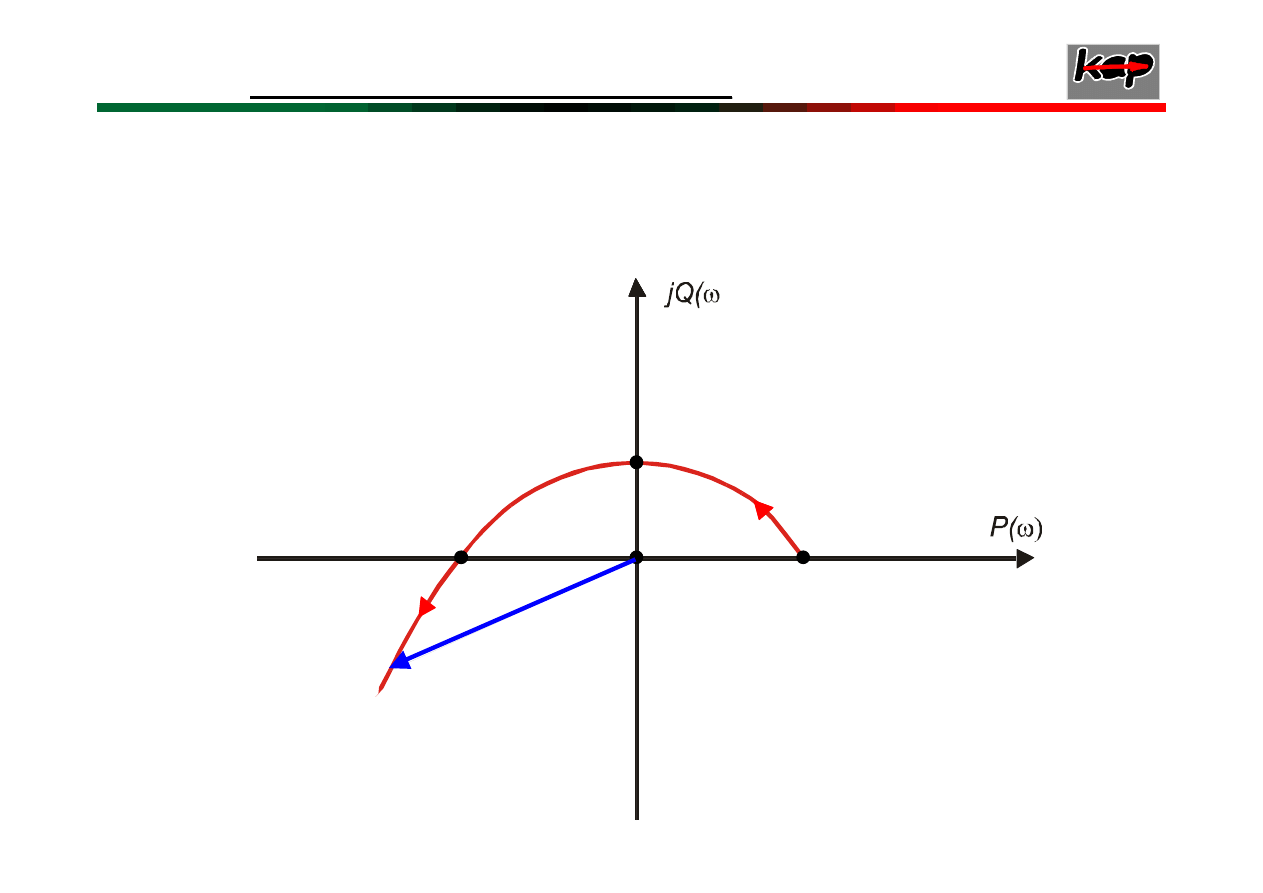
52

0

)

Wykres tego przechodzi kolejno przez trzy ćwiartki
płaszczyzny zmiennej zespolonej, więc układ jest
stabilny.

ω

1

5,44

-18

ω

3

ω

2

= 0

10

ω =

8

N j

)

( ω

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

53

Uzupełnieniem

kryterium Michajłowa

jest

następujące twierdzenie:

)

,

(

ω

π

m)

(n

N(jω(

∆

∞

∈

⋅

−

=

0

2

2

arg

Całkowita

zmiana argumentu

wielomianu

charakterystycznego N(j

ω

) niestabilnego układu

liniowego

jednowymiarowego rzędu n-tego,

którego m pierwiastków leży w prawej
półpłaszczyźnie wynosi:

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

54

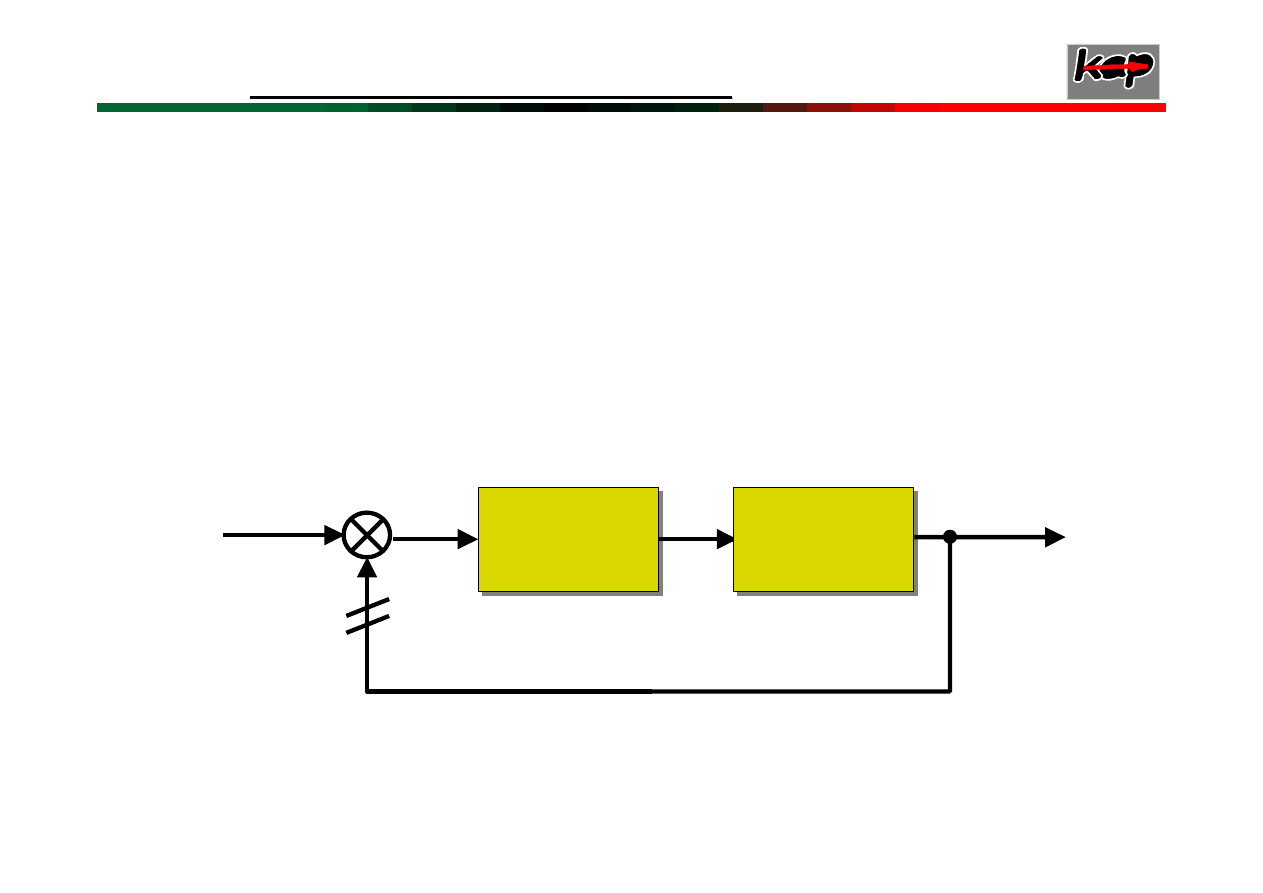
Kryterium Nyquista

Kryterium Nyquista

jest graficznym sposobem

oceny stabilności układu zamkniętego na podstawie
znajomości

charakterystyki częstotliwościowej

układu otwartego.

Schemat blokowy układu regulacji

)

s

(

G

R

Y(s)

)

s

(

G

O

–

W(s)

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

55

Transmitancja operatorowa

układu otwartego,

otrzymanego poprzez przerwanie pętli sprzężenia
zwrotnego wynosi:

(s)

(s)G

G

W(s)

Y(s)

G(s)

R

0

=

=

Przedstawiając tę transmitancję w postaci ilorazu
wielomianów zmiennej s, otrzymamy

N(s)

M(s)

G(s)

=

(s)

N

(s)

M

G(s)

G(s)

(s)

(s)G

G

(s)

(s)G

G

G(s)

Z

Z

R

R

+

=

+

=

1

1

0

0

przy czym N(s)=0 jest

równaniem charaktery-

styczne

n-tego stopnia układu otwartego.

Transmitancja układu zamkniętego wynosi:

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

56

lub po uwzględnieniu wyrażenia

otrzymujemy

Równanie charakterystyczne układu zamkniętego

jest również stopnia n.

(s)

N

(s)

M

G(s)

=

M(s)

(s)

N

(s)

M

G(s)

+

=

0

=

+

=

M(s)

N(s)

(s)

N

Z

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

57

Wnioskujemy zatem, że równanie charakterystyczne N

z

(s)

ma te same miejsca zerowe co wyrażenie w mianowniku
transmitancji

czyli:

(s)

N

(s)

M

G(s)

G(s)

(s)

(s)G

G

(s)

(s)G

G

(s)

G

Z

Z

R

R

Z

=

+

=

+

=

1

1

0

0

[

]

)

arg

)

arg

)

1

arg

0

0

(j ω

N

∆

(j ω

N

∆

(j ω

G

∆

Z

−

=

+

[

]

[

]

)

arg

)

)

arg

)

1

arg

0

0

(jω

N

∆

(jω

N

(jω

M

∆

(jω

G

∆

Z

Z

−

+

=

+

Przyrost

argumentu

wyrażenia 1+G

0

(j

ω

) przy zmianach

częstości

ω

od 0 do +

∞

wyniesie:

0

<ω<

∞

0

<ω<

∞

0

<ω<

∞

0

<ω<

∞

0

<ω<

∞

0

<ω<

∞

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

58

Rozpatrzmy teraz dwa przypadki:

9

Układ otwarty jest stabilny

Układ zamknięty będzie

stabilny

, jeżeli

2

)

arg

π

n

N(jω

∆

⋅

=

2

)

arg

π

n

(jω

N

∆

Z

⋅

=

Równanie charakterystyczne układu otwartego
posiada wszystkie pierwiastki w lewej
półpłaszczyźnie

s.

Zgodnie z kryterium

Michajłowa

0

<ω<

∞

0

<ω<

∞

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

59

Warunek stabilności układu zamkniętego można
wtedy zapisać:

Ten sam warunek odniesiony do charakterystyki

amplitudowo-fazowej

układu otwartego G

0

(j

ω

)

będzie sformułowany następująco:

[

]

0

)

1

arg

=

+ G(jω

∆

Jeżeli otwarty układ regulacji jest stabilny i jego
charakterystyka amplitudowo-fazowa G

0

(j

ω

) dla

pulsacji 0

<ω< ∞

nie obejmuje punktu

(-1,j0) to

wtedy i tylko wtedy po zamknięciu będzie on
również stabilny.

0

<ω<

∞

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

60

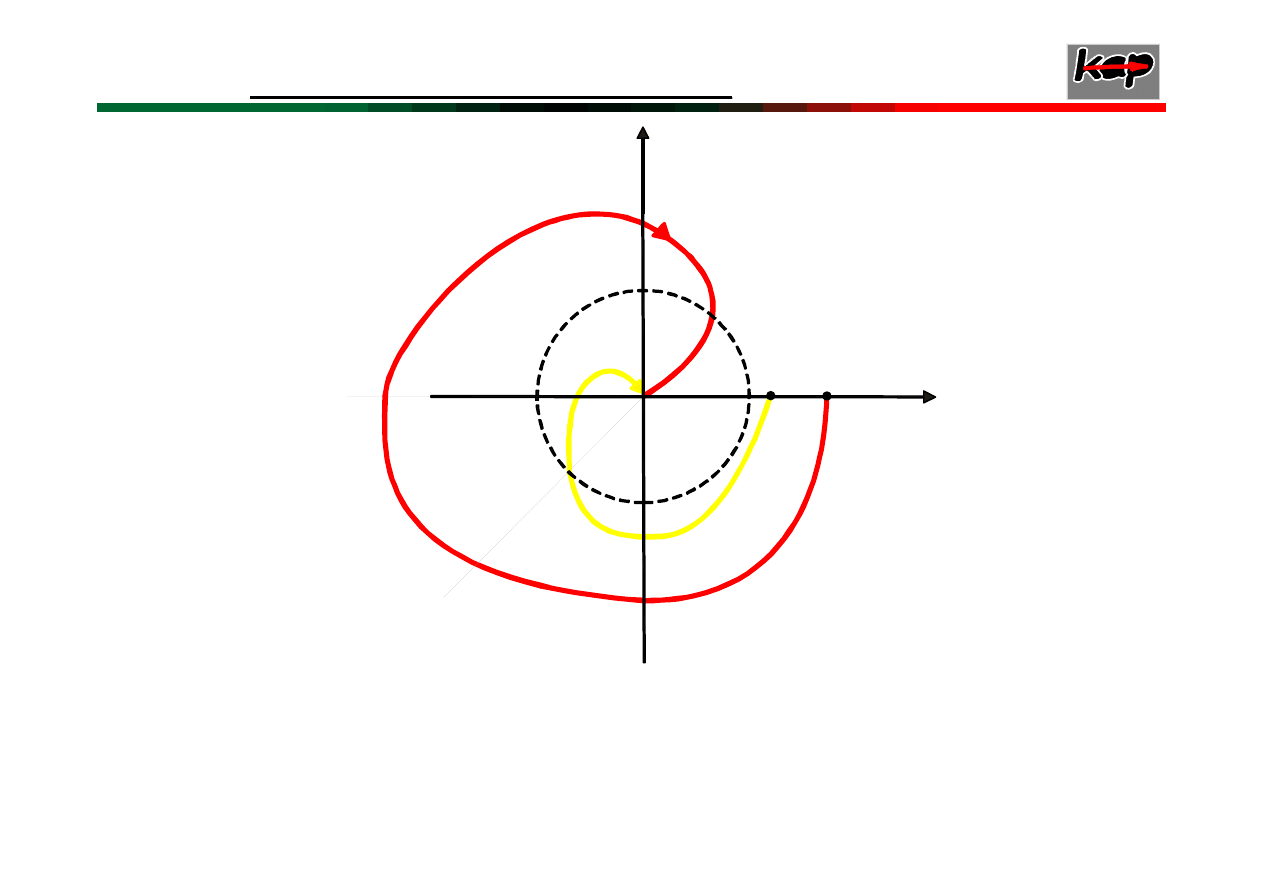
Charakterystyki amplitudowo fazowe:

b) układów

niestabilnych

a) układów

stabilnych

)

(

ω

jQ

)

(

ω

P

0

=

ω

0

=

ω

(-1,j0)

a

b

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

61

9

Układ otwarty jest niestabilny.

2

2

)

arg

π

m)

(n

N(jω

∆

−

=

Równanie charakterystyczne układu otwartego ma
(n-m) pierwiastków w

lewej półpłaszczyźnie

zmiennej s oraz m pierwiastków w

prawej

półpłaszczyźnie

. Zgodnie ze wzorem:

0

<ω<

∞

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

62

Warunek stabilności układu zamkniętego można
więc zapisać

Układ zamknięty będzie

stabilny

, jeżeli

2

2

)

arg

π

m)

(n

(jω

N

∆

Z

−

=

[

]

π

m

G(jω

∆

2

2

)

1

arg

⋅

=

+

0

<ω<

∞

0

<ω<

∞

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

63

Warunek

ten odniesiony do charakterystyki

amplitudowo-fazowej układu otwartego

G(j

ω

)

możemy sformułować następująco:

Jeżeli otwarty układ automatyki jest niestabilny i
posiada m pierwiastków w

prawej półpłaszczyźnie

zmiennej s, to po zamknięciu będzie on stabilny,
wtedy i tylko wtedy, gdy charakterystyka
amplitudowo-fazowa

układu

otwartego

dla

częstości zmieniającej się od 0 do

∞

, okrąża

razy m/2 punkt (-1,j0) w kierunku dodatnim
(przeciwnym do ruchu wskazówek zegara).

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

64

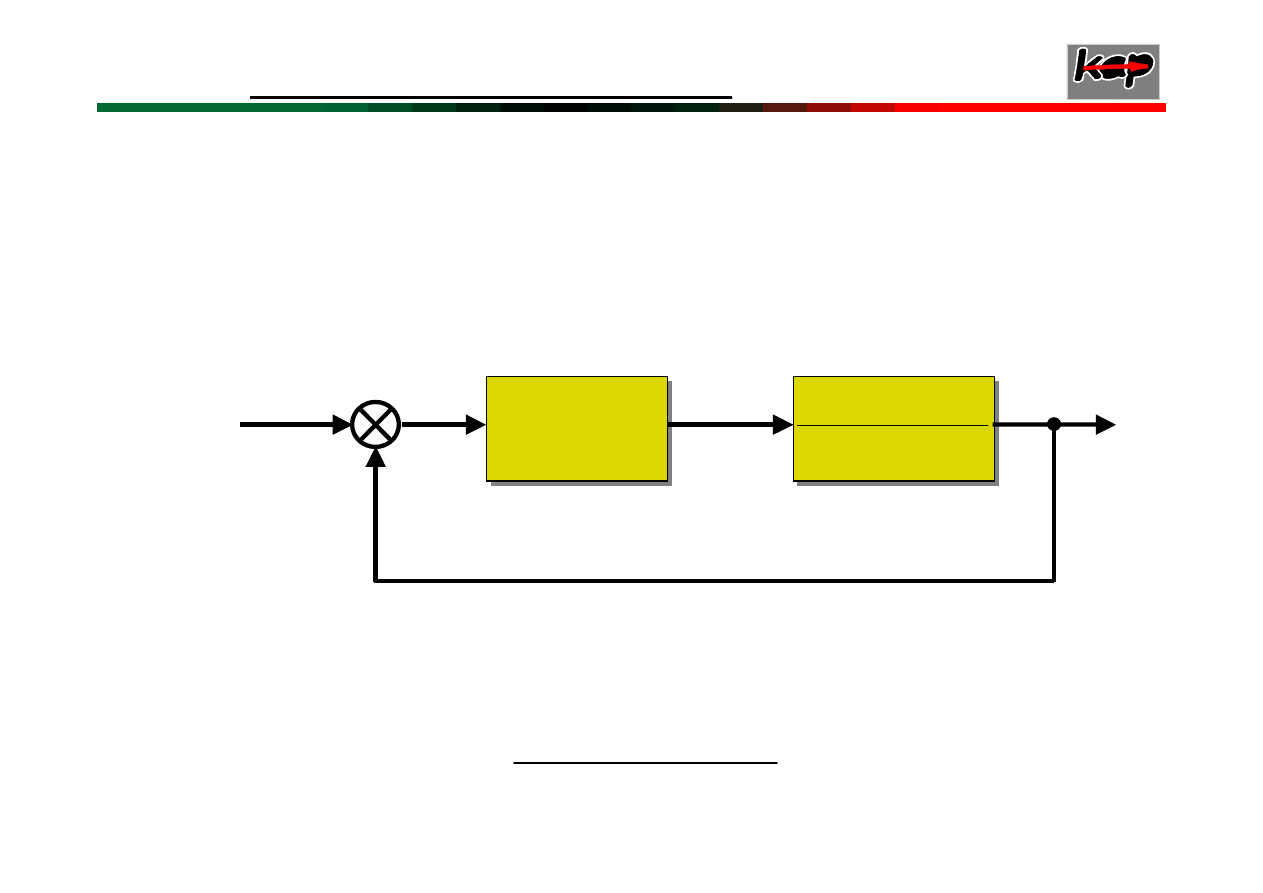
Przykład 3

Transmitancja układu otwartego :

1

2

2

2

3

+

+

+

=

s

s

s

K

G(s)

P

Sprawdzić na podstawie kryterium Nuquista, czy
układ zamknięty, którego schemat podano na
rysunku jest stabilny przy K

p

= 10.

E(s)

U(s)

p

K

Y(s)

1

s

2

s

2

s

1

2

3

+

+

+

–

W(s)

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

65

Stosując

kryterium Hurwitza

sprawdzamy czy układ

otwarty jest stabilny:

0

3

1

4

2

1

1

2

2

>

=

−

=

=

∆

Układ otwarty jest

stabilny

.

2)

1)

1 , 2 , 2 , 1 > 0

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

66

Transmitancja widmowa

układu otwartego

2

2

2

2

2

2

2

2

1

1

)

Im

)

ω

(

ω

)

ω

(

)

ω

(

K

G(jω

P

−

+

−

−

=

2

2

2

2

2

2

2

2

1

2

1

)

Re

)

ω

(

ω

)

ω

(

)

ω

(

K

G(jω

P

−

+

−

−

=

2

2

2

2

2

2

2

2

1

1

)

Im

)

ω

(

ω

)

ω

(

)

ω

(

K

G(jω

P

−

+

−

−

=

stąd

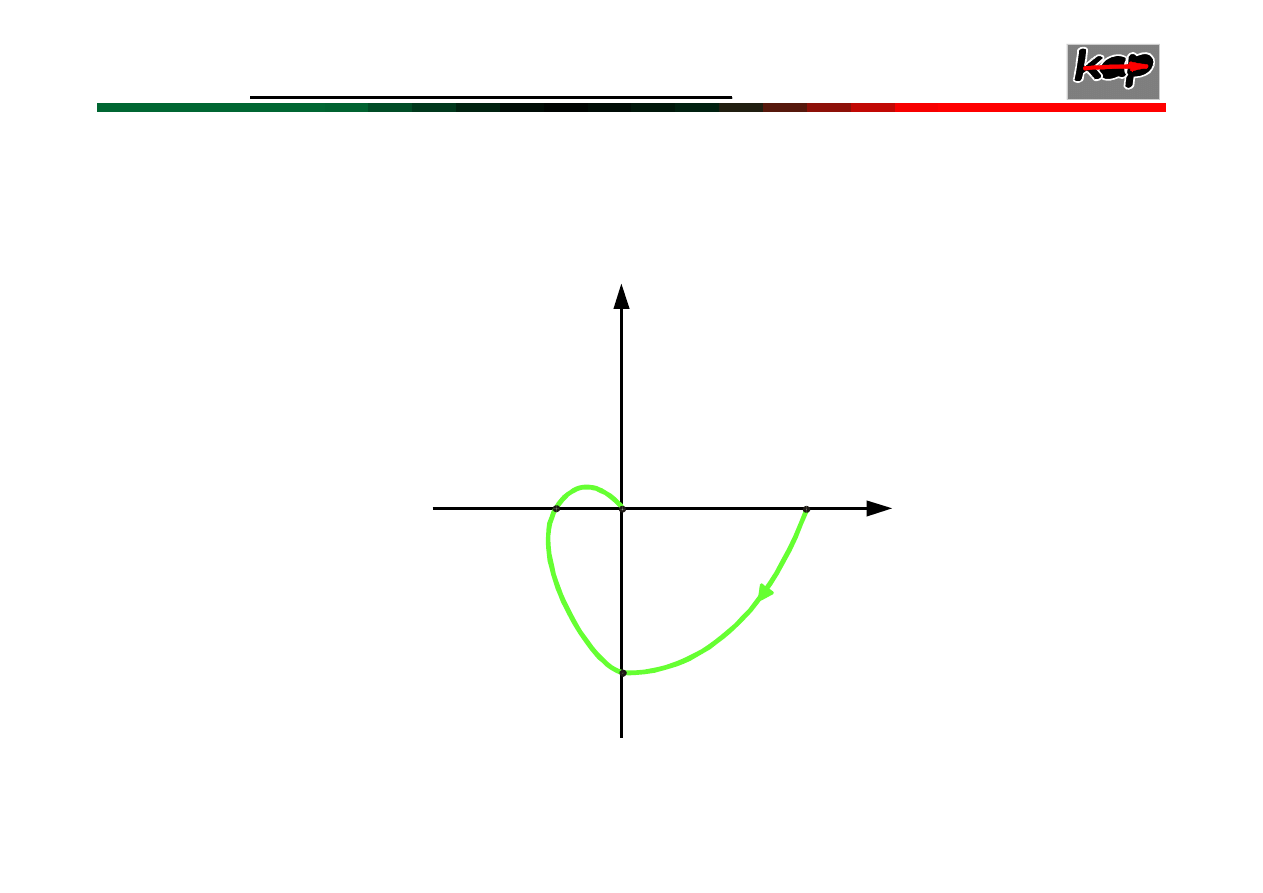
Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

67

Im

Re

Po podstawieniu K

p

= 10 wykreślono poniżej

charakterystykę amplitudowo-fazową.

-3,3

-9,45

ω=

8

ω=

10

ω=0

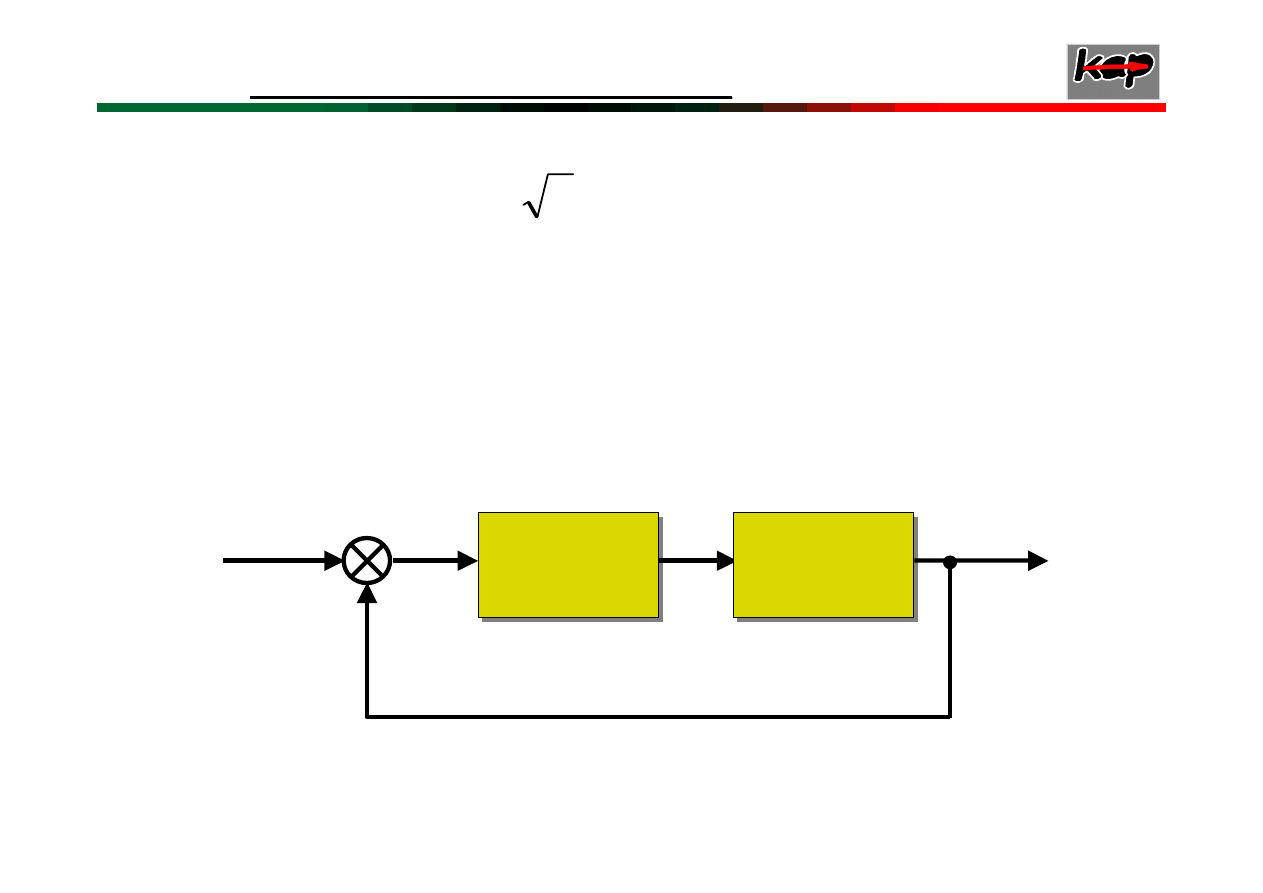
Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

68

Wykres G(j

ω

) przecina oś rzeczywistą przy

częstości

w punkcie (-3.3,j0) i w

związku z tym obejmuje punkt (-1,j0). Układ
zamknięty będzie więc niestabilny.

2

=

p

ω

Jedną z zalet

kryterium Nyquista

jest, iż można

je stosować

dla układów zamkniętych

zawierających elementy opóźniające

Schemat blokowy układu zamkniętego z elementem

opóźniającym

τ

−s

e

Y(s)

)

s

(

G

–

W(s)

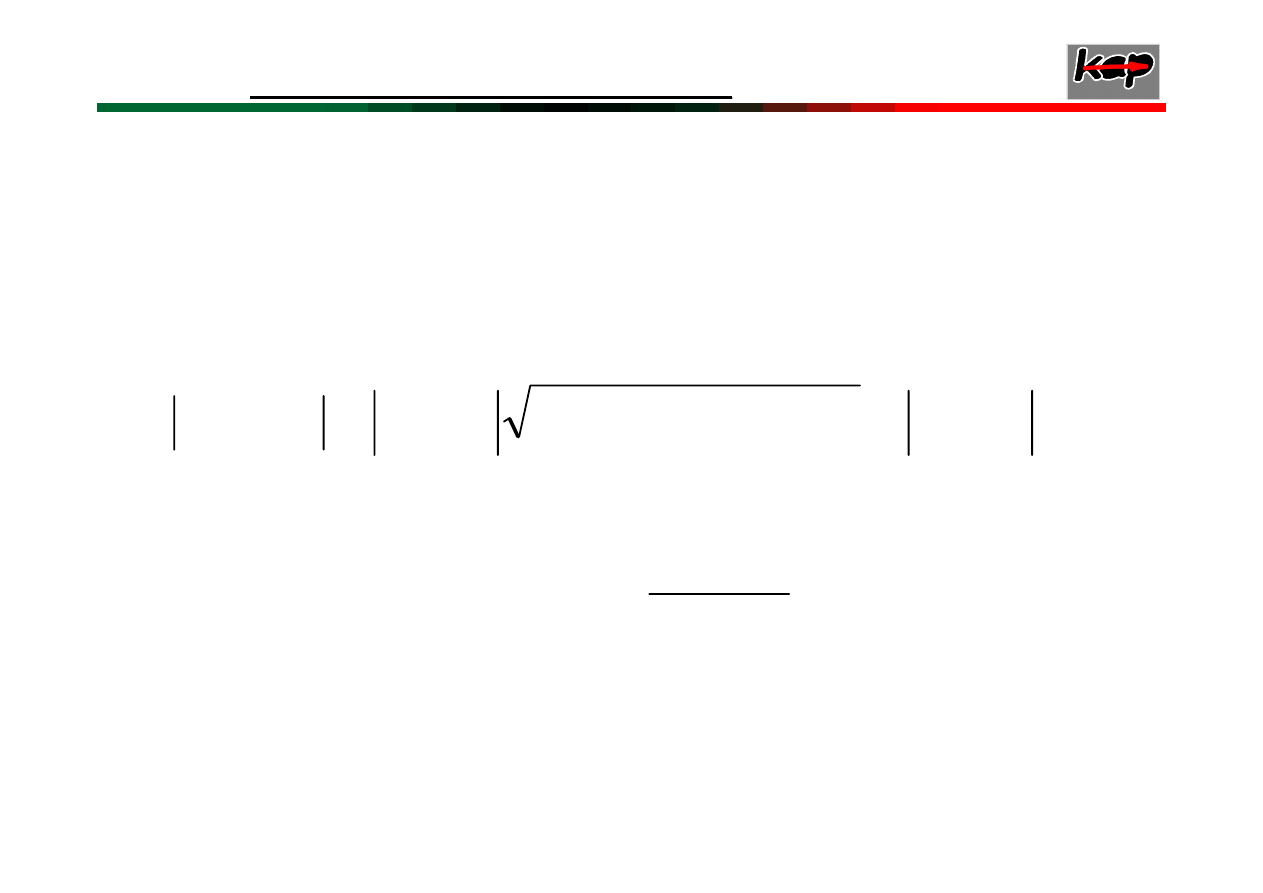
Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

69

Transmitancja widmowa

układu otwartego

ma postać

Moduł

transmitancji widmowej

Kąt przesunięcia fazowego

gdzie: |G

otw

(j

ω

)| i |

ϕ

otw

(j

ω

)| są modułem i fazą

układu otwartego bez opóźnienia.

ωτ)

j

ωτ

(jω

G

e

(jω

G

(jω

G

jω

otw

sin

)(cos

)

)

−

=

=

−

τ

)

sin

cos

)

)

2

2

(jω

G

ω

ωτ

(jω

G

(jω

G

otw

=

+

=

τ

ωτ

(ω

ωτ

ωτ

arctg

(ω

(ω

otw

otw

−

=

−

=

)

cos

sin

)

)

ϕ

ϕ

ϕ

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

70

Dla pewnej częstości

ω

x

, dla której |G(j

ω

x

)|=1

istnieje krytyczna stała czasowa opóźnienia

τ

kr

taka, że:

czyli

Wtedy wykres przechodzi przez punkt (-1,j0) a
układ zamknięty znajduje się

na granicy

stabilności.

π

τ

ω

)

(ω

kr

x

x

otw

−

=

−

ϕ

x

x

otw

kr

ω

π

)

(ω

τ

+

=

ϕ

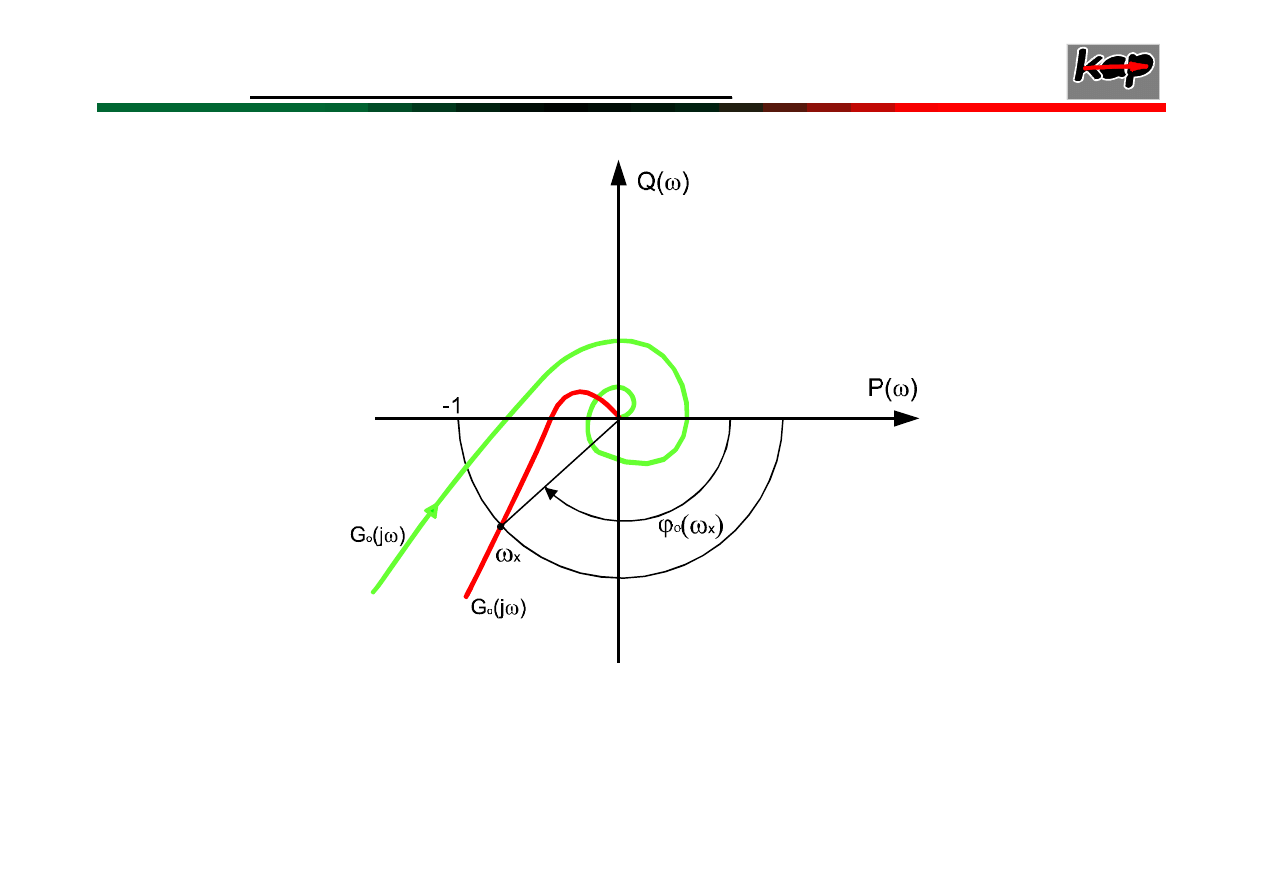
Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

71

Wpływ elementu opóźniającego na przebieg

charakterystyki amplitudowo-fazowej układu otwartego

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

72

Logarytmiczne kryterium stabilności

Z kryterium Nyquista

wynika, że moduł

transmitancji widmowej układu otwartego dla
częstości

ω

x

, dla której argument tej transmitancji

jest równy

−π

, powinien być mniejszy od jedności.

Wtedy bowiem charakterystyka amplitudowo-
fazowa nie obejmuje punktu (-1,j0).

Zapas stabilności

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

73

Otrzymujemy zatem warunki:

oraz

Warunek |G(j

ω

x

)|

<

1 w skali logarytmicznej przyjmie

postać

1

)

<

G(jω

-π

)

G(jω

x

=

arg

0

lg

20

<

=

)

G(jω

)

(ω

L

x

x

m

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

74

Na podstawie przedstawionych zależności można
sformułować

kryterium Nyquista

oparte na

charakterystykach logarytmicznych :

Jeśli

układ otwarty

jest

stabilny

, a jego

charakterystyka amplitudowa logarytmiczna
przecina oś 0 dB przy częstości mniejszej od
częstości przecięcia osi

−π

przez charakterystykę

fazową, to układ zamknięty jest

stabilny

.

W przeciwnym razie układ zamknięty jest

niestabilny

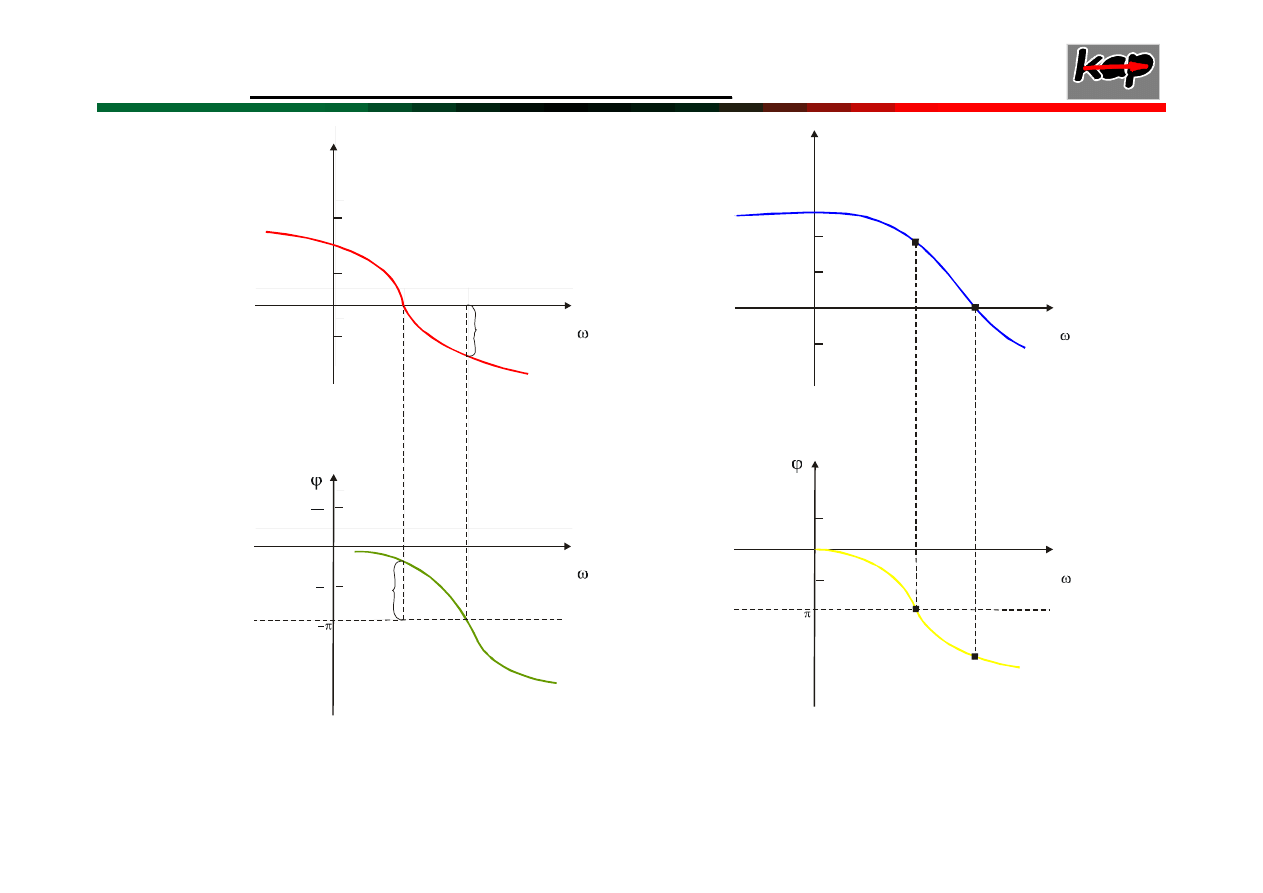
Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

75

Charakterystyki logarytmiczne: a) układu

stabilnego

b) układu

niestabilnego

Lm G
dB

Lg

0

0

Lg

0

ϕ

∆

m

L

∆

π

2

1

π

2

1

−

X

ω

a)

Lm G
dB

Lg

0

Lg

0

π

2

1

π

2

1

−

b)

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

76

Na podstawie przebiegu charakterystyk
logarytmicznych można również określić tzw.
„

zapas stabilności

”. Jest to pewien margines

bezpieczeństwa, dający projektantowi układu
regulacji pewność, że układ pozostanie stabilny,
pomimo pewnych zmian jego parametrów

Wyróżnia się przy tym dwa rodzaje zapasu
stabilności:

9

zapas modułu:

9

zapas fazy:

0

m

∆L

0

ϕ

∆

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

77

Zapas modułu

zwany też zapasem wzmocnienia

określa wartość, o którą może być zwiększone
wzmocnienie układu otwartego aby układ znalazł
się na

granicy stabilności

Zapas fazy

określa wartość zmiany argumentu

transmitancji widmowej przy stałym wzmocnieniu,
które spowodowałoby że układ zamknięty
znalazłby się na

granicy stabilności

)

lg

20

0

G(jω

∆L

m

−

=

π

∆

−

=

0

ϕ

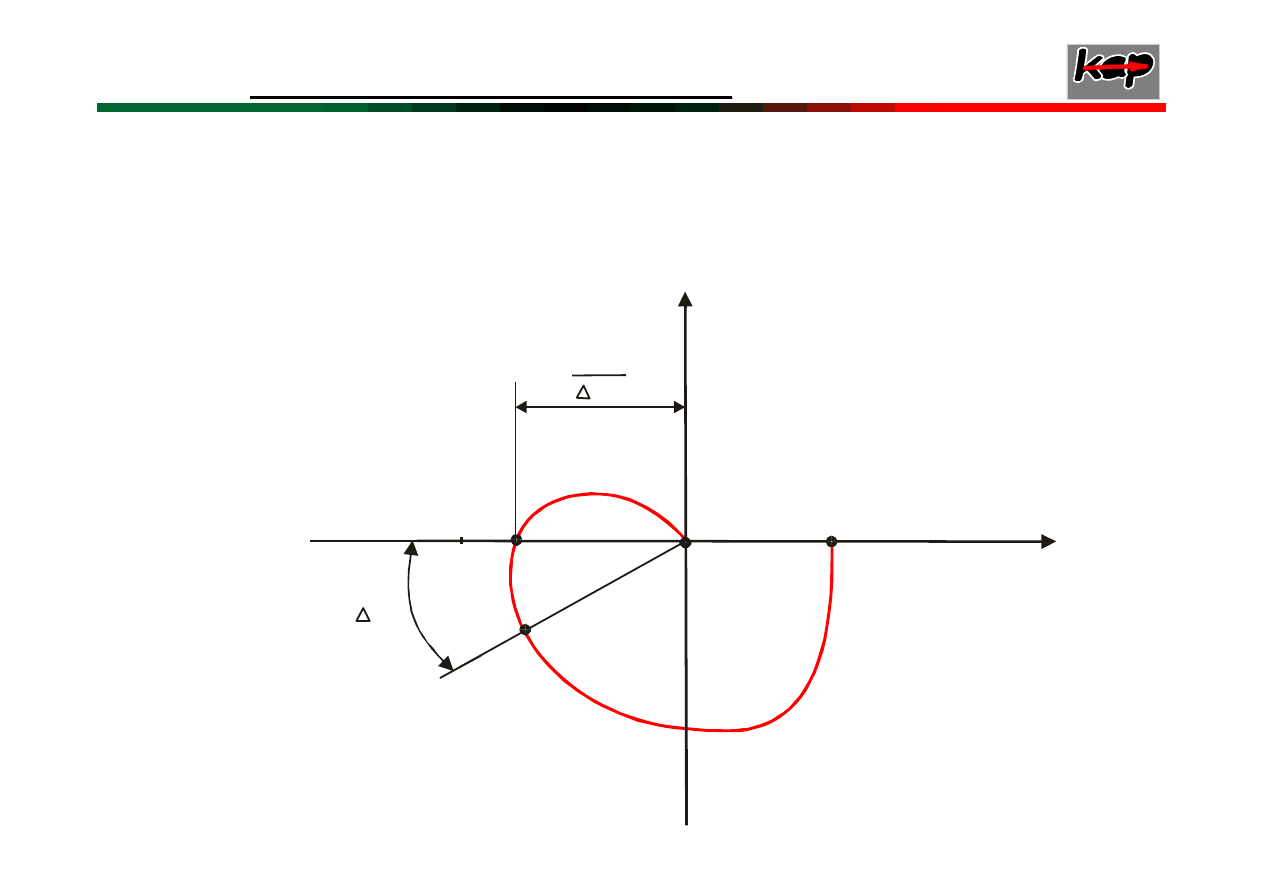
Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

78

Zapas stabilności

można również określić na

podstawie charakterystyki amplitudowo-fazowej
układu otwartego

Im

Re

8

ω=

ω=0

ο

-1

ω

x

ϕ

K

1

Katedra Automatyzacji Procesów

Katedra Automatyzacji Procesów

Wydział Inżynierii Mechanicznej i Robotyki

Wydział Inżynierii Mechanicznej i Robotyki

Akademia Górniczo

Akademia Górniczo

-

-

Hutnicza w Krakowie

Hutnicza w Krakowie

Prof. dr hab. inż. Janusz KOWAL

Prof. dr hab. inż. Janusz KOWAL

Temat wykładu: Stabilność liniowych stacjonarnych układów sterowania

Temat wykładu:

Temat wykładu:

Stabilność liniowych stacjonarnych układów sterowania

Stabilność liniowych stacjonarnych układów sterowania

Podstawy Automatyki

Podstawy Automatyki

79

Zapas modułu

można wyznaczyć

W tym przypadku

miarą zapasu stabilności

układu jest oddalenie charakterystyki amplitudowo-
fazowej od punktu krytycznego (-1,j0).

)

1

G(jω

∆K

=

π

−

=

ϕ