www.hakin9.org

hakin9 Nr 01/2008

36

Atak

P

rzesyłanie informacji za pośrednic-
twem Internetu jest złożonym proce-
sem regulowanym przez zestaw pro-

tokołów. Protokoły te implementowane są
obecnie zgodnie z globalnym standardem
– określającym warstwy funkcjonalne wymaga-
ne do obsługi połączeń – o nazwie OSI (Open
System Interconnection). Kiedy użytkownik
wpisuje do swojej przeglądarki internetowej ad-
res URL w celu obejrzenia strony WWW, prze-
glądarka nawiązuje połączenie przy wykorzy-
staniu protokołu TCP (Transmission Control
Protocol). W następnej kolejności, przy wy-
korzystaniu istniejącego połączenia TCP, wy-
syłane jest żądanie za pośrednictwem pro-
tokołu HTTP (Hyper Text Transfer Protocol).
Pakiet TCP jest przesyłany przez sieć za po-
średnictwem protokołu IP (Internet Protocol).
Przesyłany komunikat może zostać podzielo-
ny na mniejsze pakiety, które przesłane zosta-
ną niezależnie przez szereg routerów znajdu-
jących się między źródłem a miejscem docelo-
wym. Kiedy żądanie HTTP dotrze do miejsca
przeznaczenia, odpowiedź odsyłana jest tym
samym połączeniem TCP, jakie zostało nawią-
zane przez przeglądarkę użytkownika.

Mechanizmy zaimplementowane w proto-

kołach TCP/IP rekonstruują oryginalny komu-

nikat ze zbioru pakietów, jakie zostały przesła-
ne przez sieć. Komunikat ten jest ostatecznie
przetwarzany w warstwie aplikacji przez proto-
kół HTTP. Po zinterpretowaniu żądania przez
serwer WWW zostaje wygenerowana odpo-
wiedź (może to być właściwa strona, komuni-
kat o błędzie itd.).

Jak widać, prosty z pozoru proces wymaga

dosyć znacznej liczby obliczeń – zarówno po
stronie wysyłającej, jak i odbierającej żądanie.
Niezawodność komunikacji, jaką zapewnia do-

Obliczenia pasożytnicze

Michał Styś

stopień trudności

Niezawodne przesyłanie danych w Internecie gwarantowane

jest przez zestaw protokołów sieciowych implementowanych

w systemach komputerowych. Artykuł ten pokaże, w jaki sposób

protokoły te mogą zostać wykorzystane w celu zmuszenia

zdalnych systemów do nieświadomego wykonania użytecznych

z punktu widzenia napastnika obliczeń.

Z artykułu dowiesz się

• w jaki sposób wykorzystać protokoły sieciowe,

aby wykonywać obliczenia na komputerach
podłączonych do Sieci,

• jakie znaczenie dla bezpieczeństwa kompu-

terowego ma trudność rozwiązywania proble-
mów klasy NP.

Co powinieneś wiedzieć

• powinieneś mieć podstawową wiedzę o modelu

OSI,

• powinieneś rozumieć, jak działają protokoły

sieciowe.

Techniki obliczeń pasożytniczych

hakin9 Nr 01/2008

www.hakin9.org

37

datkowo protokół TCP, wprowadza
takie elementy jak trójfazowe uzgad-
nianie połączenia, potwierdzanie
otrzymania pakietu, sumy kontrolne
oraz numery sekwencyjne. Elementy
zapewniające niezawodność komu-
nikacji można jednak wykorzystać
w zupełnie innym celu niż ten, do
którego zostały zaprojektowane.

Pasożytniczy komputer

Termin pasożytniczy komputer odno-
si się do realizacji abstrakcyjnej ma-
szyny składającej się z rozproszo-
nych w sieci komputerów. Podobnie
jak w przypadku standardowych pro-
jektów realizujących obliczenia roz-
proszone, maszyna ta zbudowana
jest w oparciu o protokoły sieciowe.
W odróżnieniu jednak od nich, układ
pasożytniczy wykonuje obliczenia
bez wiedzy i pozwolenia właścicie-
la komputera ofiary, wykorzystywa-
nego jako węzeł obliczeniowy. Infor-
matyka pasożytnicza nie musi zakła-
dać również konieczności ingerencji
w oprogramowanie działające na
komputerze ofiary. Nie dochodzi tu-
taj do włamania do zdalnego systemu
ani też instalowania na nim jakiego-
kolwiek złośliwego oprogramowania.

Realizacja

pasożytniczego

komputera

Protokół TCP dobrze nadaje się do
zrealizowania idei pasożytniczego
komputera w praktyce. Do tego ce-
lu posłużyć może mechanizm sumy
kontrolnej.

Pakiet przesyłany przez Inter-

net może w którymś momencie ulec

uszkodzeniu. Przykładowo, seria sy-
gnałów elektrycznych reprezentu-
jących bity może zostać zmieniona
w czasie przepływu przez kabel kon-
centryczny wskutek tłumienia lub in-
terferencji wywołanych przez źródła
pól elektromagnetycznych znajdują-
cych się w pobliżu medium transmi-
syjnego. Aby zapewnić niezawod-
ność w tego typu sytuacjach, proto-
kół TCP wprowadza mechanizm su-
my kontrolnej. Komputer wysyłający
pakiet oblicza jego sumę kontrolną
i dołącza ją do pakietu. Następnie
operację obliczenia sumy kontrolnej
odbiorca wykonuje na otrzymanym
pakiecie. Jeśli suma kontrolna zapi-
sana w pakiecie zgadza się z sumą
obliczoną dla tego pakietu, oznacza
to, że dane są poprawne i mogą być
przekazane do wyższych warstw
protokołów modelu OSI. Jeśli wy-
stąpiła niezgodność, pakiet uznawa-
ny jest za uszkodzony, a warstwa TCP
usuwa go i nie wysyła do odbiorcy
potwierdzenia otrzymania danych.

Interesującą nas właściwością

tego mechanizmu jest fakt, że suma
kontrolna TCP wyliczana jest przy
wykorzystaniu operacji wystarcza-
jących do wykonania każdej ope-
racji mieszczącej się w zakresie al-
gebry Boole'a. Istnieje zatem możli-
wość wykorzystania go jako bram-
ki logicznej. To z kolei otwiera drzwi
do wykonywania operacji arytme-
tycznych.

Implementacja układu obliczeń

pasożytniczych wykorzystujących
protokół TCP polega na zbudowa-
niu pakietu ze specjalnie sprepa-
rowaną sumą kontrolną. Kompu-

ter ofiary w procesie przetwarza-
nia żądania i generowania odpowie-
dzi automatycznie wykona zlecone
obliczenie – podczas wykonywania
algorytmu sprawdzania sumy kon-
trolnej. Zakres działania omawia-
nych mechanizmów wystarcza do
zbudowania pasożytniczego układu
obliczeniowego.

Informatyka

pasożytnicza

W obliczu omówionego potencjału
związanego z możliwością korzy-
stania z zasobów obliczeniowych
komputerów w Internecie pojawia
się pytanie: do czego można taki
mechanizm zastosować?

W roku 2001 czterech naukow-

ców – Albert Laszlo Barabasi, Vin-
cent W. Freeh, Hawoong Jeong
oraz Jay B. Brockman – zapropo-
nowało mechanizm rozwiązywa-
nia problemu klasy NP (non-poly-
nomial) przy wykorzystaniu obli-
czeń pasożytniczych. Ich publika-
cja wzbudziła spore zainteresowa-
nie, jako że na trudności rozwiązy-
wania problemów tej klasy opiera
się całe bezpieczeństwo współcze-
snych mechanizmów kryptograficz-
nych. Gdyby znaleziony został spo-
sób na rozwiązywanie problemów
NP w rozsądnym czasie, większość
znanych technik kryptograficznych
stałaby się bezużyteczna.

Aby rozwiązywać problemy

matematyczne przy wykorzystaniu
sumy kontrolnej TCP, konieczna je-
stodpowiednia reprezentacja proble-
mu. Dla problemów NP stosowna
w tym przypadku jest reprezen-

Listing 1.

Program dla pasożytniczej maszyny wirtualnej napisany w mikroassemblerze 4IA (plik sub.4ia)

ARCH

8

10

;

Definicja

architektury

.

Rejestry

o

d

ł

ugo

ś

ci

8

bit

ó

w

,

liczba

rejestr

ó

w

–

10

00

:

SET

r3

,

0xFF

;

Do

rejestru

r3

ł

adujemy

warto

ść

-

1

01

:

SET

r2

,

5

;

Do

rejestru

r2

ł

adujemy

5

.

B

ę

dzie

to

ilo

ść

iteracji

w

p

ę

tli

02

:

SET

r9

,

100

;

Rejestr

r9

przechowa

warto

ść,

od

kt

ó

rej

b

ę

dziemy

odejmowa

ć

03

:

SET

r0

,

4

;

Do

rejestru

instrukcji

ł

adujemy

numer

,

od

kt

ó

rego

zacznie

si

ę

p

ę

tla

04

:

ADD

r9

,

r3

;

Wykonujemy

operacj

ę

odejmowania

na

rejestrze

r9

(

100

+

(

-

1

))

05

:

SET

r1

,

0

;

Reset

flagi

przepe

ł

nienia

06

:

ADD

r2

,

r3

;

Zmniejszamy

licznik

p

ę

tli

o

1

07

:

ADD

r0

,

r1

;

Je

ś

li

flaga

przepe

ł

nienia

==

1

,

skaczemy

do

instrukcji

09

08

:

SET

r0

,

9

;

Koniec

p

ę

tli

,

skok

do

linii

10

09

:

SET

r0

,

3

;

P

ę

tla

trwa

,

skok

do

linii

04

10

:

HLT

;

Koniec

dzia

ł

ania

programu

hakin9 Nr 01/2008

www.hakin9.org

Atak

38

tacja problemu jako Boole'owskie
równanie spełnialności. Równania
takie określa się jako SAT. Równa-
nia spełnialności SAT pozwalają
na zapis problemu przy wykorzy-
staniu operatorów logiki Boole'a.
Jako przykład równania SAT może
posłużyć następująca konstrukcja:

P=(x1 XOR x2) AND (~x2 AND x3)

P

oznacza tu problem, natomiast

x1

,

x2

oraz

x3

są parametrami. W pre-

zentowanym przykładzie istnieje 23
potencjalnych rozwiązań, ale rów-
nanie będzie spełnione tylko dla jed-
nego z nich – w tym przypadku

x1=1

,

x2=0

,

x3=1

. Rozwiązywanie proble-

mów SAT polega na odnalezieniu
takiej wartości wszystkich parame-
trów, aby całe równanie mogło być
spełnione. Zaprezentowany przy-
kład równania SAT jest trywialny
i może być rozwiązany bardzo łatwo.
W przypadku bardziej złożonych rów-
nań zawierających więcej parame-
trów problem staje się NP-zupełny.

Z uwagi na swoją specyfikę, rów-

nanie SAT może zostać zapisane
jako sekwencja bitów, która zosta-
je następnie uformowana w pakiet
TCP i wysłana do ofiary jako ele-
ment problemu do policzenia.

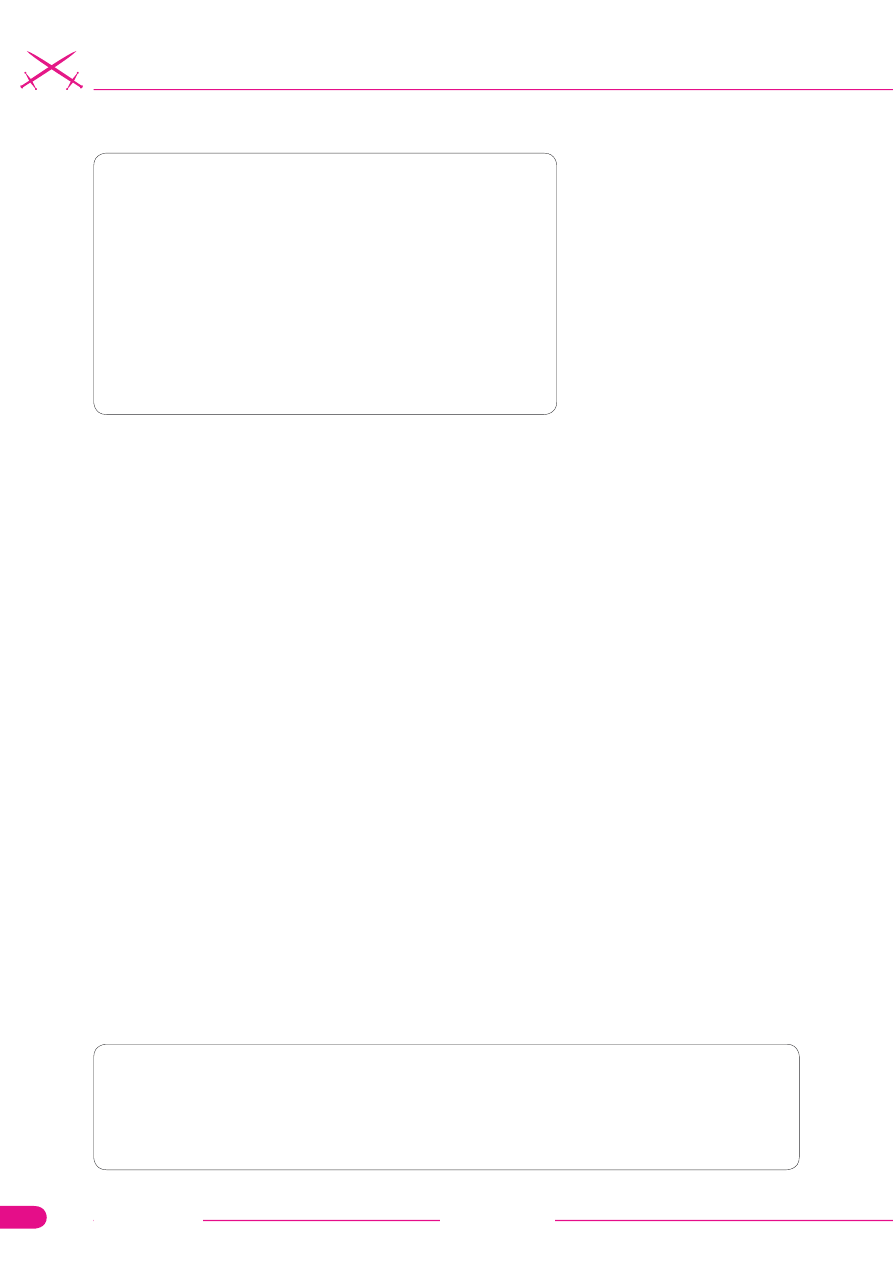
Scenariusz pasożytniczego kom-

putera zilustrowany został na Ry-
sunkach 1 oraz 2. W pierwszym
kroku komputer-pasożyt, nadzo-
rujący proces wykonywania obli-
czeń, przygotowuje 2n specjalnie
skonstruowanych pakietów zawie-
rających wszystkie możliwe kom-
binacje parametrów równania SAT.
Następnie wysyła spreparowane
pakiety TCP do pewnej liczby ma-
szyn-ofiar. Maszyny te wyposażo-
ne są w jednostki arytmetyczno-
logiczne, umożliwiające wykony-
wanie obliczeń oraz w interfejsy
sieciowe umożliwiające zdalne po-
łączenia (warunki te spełnia każ-
dy komputer podłączony do Inter-
netu). Pakiety zawierające błęd-
ne rozwiązania nie posiadają
prawidłowej sumy kontrolnej i zosta-
ją odrzucone (ilustruje to strzałka
z opisująca błędne rozwiązanie).
W przypadku, gdy rozwiązanie
problemu jest poprawne, oblicze-
nie sumy kontrolnej zakończy się
sukcesem, a pakiet trafi w górę
stosu protokołów.

Ponieważ protokół HTTP za-

kłada generowanie odpowiedzi na
wszystkie, nawet niepoprawne, żą-
dania, zostanie ona wysłana, gdy
tylko pakiet dotrze do warstwy apli-

kacji. Dzięki temu można rozpo-
znać, który zestaw parametrów
jest poprawnym rozwiązaniem pro-
blemu SAT.

Po wysłaniu wszystkich pakie-

tów do milionów komputerów w In-
ternecie odpowiedziałyby tylko te,
które otrzymały pakiety zawiera-
jące parametry równania SAT bę-
dące prawidłowym rozwiązaniem.
Reszta pakietów zostałaby po pro-
stu odrzucona. Możliwe jest zatem
odnalezienie rozwiązania bez wy-
konywania obliczeń na lokalnym
komputerze.

Barabasi, Freeh, Jeong oraz

Brockman przeprowadzili udaną pró-
bę rozwiązania równania SAT przy
wykorzystaniu omawianej techni-
ki. Udowodnili tym samym tezę, że
możliwe jest zmuszanie kompute-
rów w Internecie do wykonywania
konkretnych obliczeń bez koniecz-
ności naruszania ich infrastruktury
i instalowania na nich dodatkowego
oprogramowania. Dodatkowo spo-
re problemy stwarza zabezpiecze-
nie się przed tego typu technikami.
Ponieważ wykorzystywane są stan-
dardowe mechanizmy zapewniające
funkcjonowanie komputera w sieci,
uniemożliwienie takich obliczeń jest
praktycznie nierealne.

Obliczenia pasożytnicze

w praktyce

Czy opisane techniki wystarcza-
ją do praktycznego zastosowania
obliczeń pasożytniczych w posta-
ci skonstruowania gigantycznego
superkomputera i zagrożenia tech-
nikom kryptograficznym? Okazuje się,
że nie do końca. Omawiane podej-
ście prezentuje jak najbardziej god-
ny uwagi, wręcz rewolucyjny sposób
spojrzenia na możliwości prowadze-
nia obliczeń rozproszonych, ale spra-
wa komplikuje się po rozważeniu kilku
dodatkowych czynników.

Listing 3.

Polecenie sh do wylistowania hosta

sh
Hostname Address Packets Timeouts Enabled Falsepos.
-------------------- --------------- ------- -------- ------- -----------
192.168.0.2 192.168.0.2 0 0 yes untested
192.168.0.3 192.168.0.3 0 0 yes untested

Listing 2.

Stan rejestrów pasożytniczej maszyny wirtualnej po

zakończeniu wykonywania zadania obliczeniowego

Register Decimal Hex Comment
-------- ------- ------- ---------------------------
r0000000 10 0x000a Instruction pointer (ip)
r0000001 0 0x0000 Flag register (fl)
r0000002 255 0x00ff XIA error register
r0000003 255 0x00ff XIA carry register
r0000004 0 0x0000
r0000005 0 0x0000
r0000006 0 0x0000
r0000007 0 0x0000
r0000008 0 0x0000
r0000009 95 0x005f
r0000010 0 0x0000

Techniki obliczeń pasożytniczych

hakin9 Nr 01/2008

www.hakin9.org

39

Pierwszy problem rodzi mecha-

nizm identyfikowania prawidłowych
rozwiązań. W przypadku niepo-
prawnego obliczenia sumy kontro-
lnej pakietu przez komputer-ofia-
rę, TCP usuwa pakiet i nie generuje
żadnej odpowiedzi. W efekcie trud-
ne jest ustalenie, czy nie otrzymali-
śmy odpowiedzi wskutek faktycznie
niepoprawnej sumy kontrolnej, czy
też na przykład w wyniku zmiany
polityki firewalla lub po prostu odłą-
czenia komputera-ofiary od sieci.

Drugim aspektem trudności wy-

korzystania informatyki pasożytni-
czej w obecnej postaci jest fakt du-
żego zapotrzebowania na pasmo
potrzebne do rozesłania wielkiej ilo-
ści pakietów SAT. Samo przygoto-
wanie takich pakietów również wy-
maga sporej mocy obliczeniowej.
Czynniki te powodują, że na dzień
dzisiejszy opisywane podejście nie
jest wystarczająco wydajne, aby
mogło służyć budowie i praktycz-
nemu wykorzystaniu gigantyczne-
go klastra zbudowanego z milionów
komputerów znajdujących się w In-
ternecie.

Przykładowa

aplikacja pasożytnicza

Dobrym przykładem aplikacji reali-
zującej obliczenia pasożytnicze przy
wykorzystaniu omawianej metodolo-

gii jest stworzona przez Jürga Reus-
sera oraz Luziana Scherrera maszy-
na wirtualna. Oprogramowanie to
jest publicznie dostępne pod adre-
sem http://szene.ch/parasit/. Oma-
wiana maszyna jest w pełni progra-
mowalna i zdolna rozwiązać dowol-
ny znany problem matematyczny.

W celu zainstalowania oprogra-

mowania pasożytniczej maszyny wir-
tualnej, należy pobrać kod źródłowy.
Dostępny jest on pod adresem http://
szene.ch/parasit/code/parasitic_
computing.tar.gz Niniejszy artykuł za-
wiera opis wykorzystania omawianej
aplikacji w systemie Linux. Po pobra-
niu archiwum należy je rozpakować.
Można to zrobić poleceniem:

tar -zxf parasitic_computing.tar.gz

Następnie przechodzimy do instalacji:

make
make install

Aplikacja instaluje się domyślnie
w katalogu

/usr/local

, a więc wa-

riant ten wymaga uprawnień do zapi-
suw tym katalogu. Aby zmienić doce-
lowy katalog, należy zmienić wartość
zmiennej PREFIX w pliku Makefile.

Do korzystania z programu ko-

nieczne jest zrozumienie podstaw
jego działania. Maszyna wirtualna

wyposażona została w zestaw reje-
strów, które wykorzystywane są do
wykonywania zadań. Rejestry po-
siadają oznaczenia

rn

gdzie

n

okre-

śla numer rejestru. Wyróżnić można
tu trzy typy rejestrów:

• r0 – rejestr instrukcji. Przeznaczo-

ny do przechowywania numeru
aktualnie wykonywanej instrukcji.
Manipulacja jego zawartością po-
zwala na sterowanie przebiegiem
zadania,

• r1 – rejestr flagi. Pozwala na wy-

krywanie warunku zakończenia
działania pętli. Przyjmuje wartość

1

, gdy w którymś z rejestrów ogól-

nego przeznaczenia dojdzie do
przepełnienia wywołanego dzia-
łaniem instrukcji ADD (instrukcje
omówione zostały poniżej),

• r2...rn – rejestry ogólnego prze-

znaczenia. Można przechowy-
wać w nich wartości oraz wyko-
nywać operacje arytmetyczne.

Autorzy aplikacji stworzyli zestaw in-
strukcji pozwalający na definiowanie
zadań obliczeniowych realizowanych
na zdalnych maszynach. Język ten
bazuje na klasycznym assemblerze.
Określony został jako

4IA

, co ozna-

cza czteroinstrukcyjny assembler
(4 Instruktionen Assembler). Zgod-
nie z nazwą, posiada on cztery pod-
stawowe instrukcje:

• HLT – instrukcja przerywa wyko-

nanie zadania obliczeniowego,

• SET dst, const – instrukcja

umieszcza wartość const w reje-
strze określonym na pozycji dst,

• MOV dst, src – instrukcja ta ko-

piuje wartość rejestru src do reje-
stru określonego jako dst,

• ADD dst, src – instrukcja ADD po-

zwala na dodanie wartości prze-
chowywanej w rejestrze src do
wartości rejestru dst. Wynik zapisa-

Problemy wielomianowe

Problemy wielomianowe to takie zadania, dla których na maszynie Turinga możliwe
jest wygenerowanie rozwiązania w czasie wielomianowo proporcjonalnym do długo-
ści danych wejściowych. Czas potrzebny do rozwiązania takiego problemu jest bezpo-
średnio zależny od długości danych wejściowych podniesionych do stałej potęgi. Dla
problemów klasy NP (niewielomianowych) nie ma takich rozwiązań. Dla tej klasy pro-
blemów niewielki wzrost długości danych wejściowych wywołuje znaczne wydłużenie
czasu rozwiązywania problemu (czas może rosnąć wykładniczo).

Dla problemów NP-zupełnych będących podzbiorem problemów klasy NP udo-

wodniono brak rozwiązań w czasie proporcjonalnym do wielomianowego.

W przypadku nietrywialnych danych wejściowych problemy NP są trudne w roz-

wiązywaniu.

Listing 4.

Ilość pakietów pasożytniczych

sh
Hostname Address Packets Timeouts Enabled Falsepos.
-------------------- --------------- ------- -------- ------- -----------
192.168.0.2 192.168.0.2 817 0 yes untested
192.168.0.3 192.168.0.3 809 0 yes untested

hakin9 Nr 01/2008

www.hakin9.org

Atak

40

ny zostaje w rejestrze dst. Jeśli doj-
dzie do przepełnienia zakresu reje-
stru, ustawiona zostaje flaga

r1

.

Zestaw powyższych instrukcji wystar-
cza do realizacji każdej operacji aryt-
metycznej. Jako przykład zrealizowa-
na zostanie prosta operacja odejmo-
wania. Trywialny problem

100 - 5

zde-

finiować można w następujący sposób:
Tak przygotowany program gotowy jest
do uruchomienia na pasożytniczej ma-
szynie. Sama maszyna uruchamiana
jest przy wykorzystaniu polecenia:

/usr/local/bin/pshell

Najpierw należy przygotować plik
z adresami IP komputerów, które
wykorzystane zostaną jako ofia-
ry. Adresy rozdzielane są znakami
nowej linii. Po przygotowaniu pliku
i uruchomieniu

pshell

, należy go

załadować:

lh /sciezka/do/pliku/adresow_IP

Przykład:

lh /home/parasite/hosts
Hostlist loaded

Hosty wylistować można przy wyko-
rzystaniu polecenia

sh

: W celu wyko-

nania napisanego zadania posłużyć
należy się następującym poleceniem:

xp /home/parasite/sub.4ia

Jeśli wszystko zakończy się po-
wodzeniem (hosty – ofiary po-

winny być włączone), otrzymamy
komunikat:

Execution successfully terminated.

Wyniki (stan rejestrów) obejrzeć
można przy wykorzystaniu polece-
nia

sr

. Rejestr

r9

przechowuje zgod-

ną z oczekiwaniami wartość

100 – 5

= 95

. Obliczenia powiodły się.

Teraz zobaczyć można także, ile

pasożytniczych pakietów wysłanych
zostało do poszczególnych kompute-
rów. Szczegółowe statystyki obejrzeć
można po wydaniu polecenia

ss

.

Przykłady bardziej skompliko-

wanych zadań dostarczone są wraz
z maszyną wirtualną i po instalacji
znaleźć je można w katalogu

/usr/

local/share/parasit/4ia/

.

Strukturę wysyłanych pakietów

można obejrzeć na maszynach-
ofiarach przy wykorzystaniu dowol-
nego sniffera sieciowego (najlepiej
Wireshark). Obserwować należy
pakiety ICMP przesyłane między
ofiarą i pasożytem, ponieważ pa-
sożytniczy mechanizm obliczeń zo-
stał zaimplementowany przy wyko-
rzystaniu właśnie tego protokołu.

Aspekty legalności

Mimo, że informatyka pasożytni-
cza nie narusza integralności sys-
temów wykonujących zlecone ob-
liczenia, może powodować opóź-
nienia ich działania. Duże ilości
pakietów przesyłane do interfejsów
sieciowych powodują efekty po-
dobne do ataku typu Denial of Se-
rvice. Z tego powodu powstaje sze-
reg pytań natury etyczno-prawnej

dotyczących wykorzystywania mo-
cy obliczeniowej maszyn znajdują-
cych się w Internecie bez pozwo-
lenia ich właścicieli. Wszystko to
skłania do refleksji na temat okre-
ślenia granic własności zasobów
Internetu.

Podsumowanie

Podsumowując, da się zauważyć,
że informatyka pasożytnicza za-
ciera granice pomiędzy komunika-
cją a obliczeniami w sieci. Udowod-
niono, że możliwe jest wymusze-
nie użytecznych obliczeń na zdal-
nych komputerach przy wykorzy-
staniu samej infrastruktury obec-
nego Internetu. Mimo, iż w prakty-
ce zastosowanie obliczeń pasożyt-
niczych w ich obecnej formie jest
mocno ograniczone, otwiera drogę
do kolejnych eksperymentów i zna-
cząco wpływa na aspekty spojrze-
nia na Internet. l

Rysunek 1.

Prototyp

pasożytniczego komputera

Pasożyt

Ofiara

HTTP

HTTP

TCP

TCP

IP

IP

Sieć

Sieć

Interfejs fizyczny

Poprawne rozwiązanie

Błędne rozwiązanie – brak odpowiedzi

Pakiet odrzucony z powodu

błędnej sumy kontrolnej

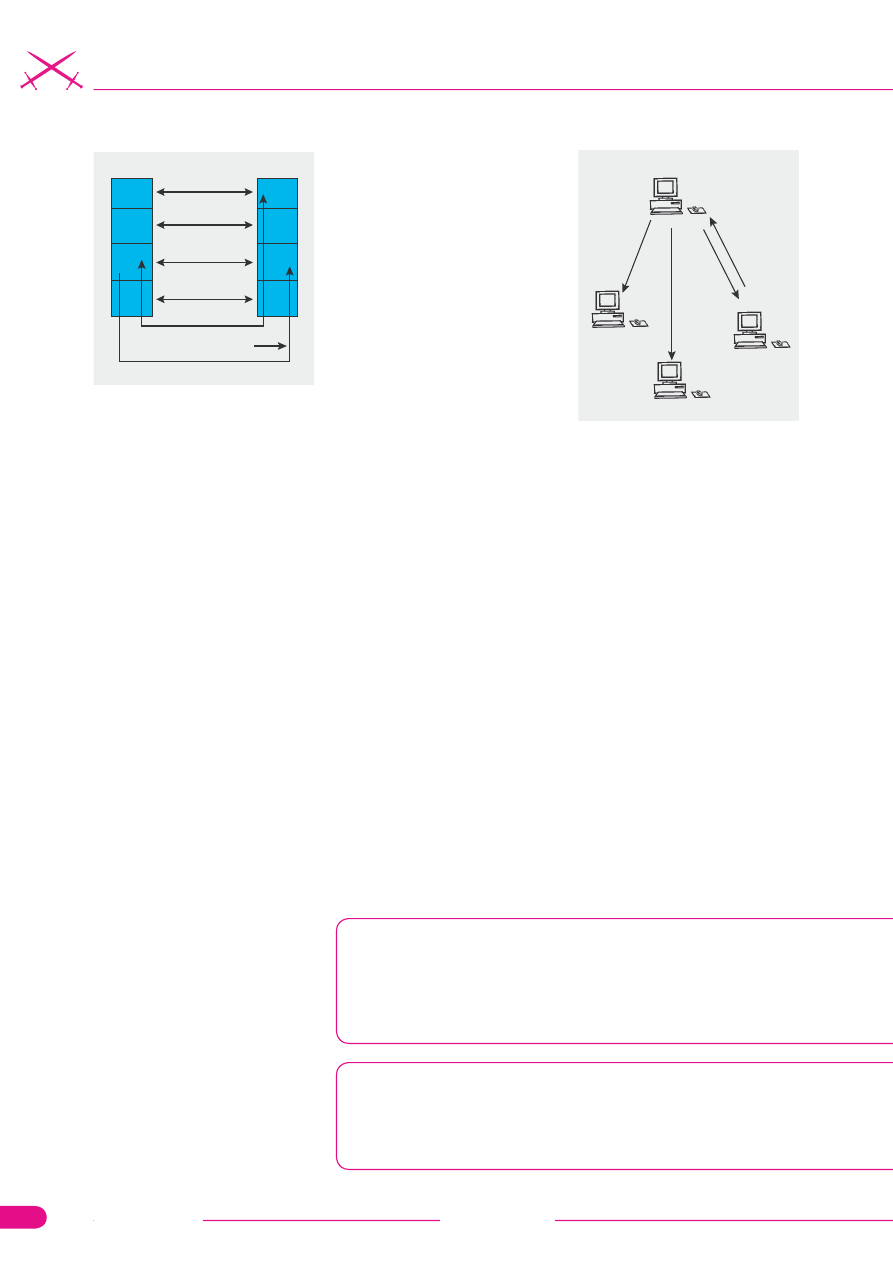
Rysunek 2.

Działania mechanizmu

obliczeń pasożytniczych

Pasożyt

niepoprawna

suma kontrolna

(brak odpowiedzi)

niepoprawna

suma kontrolna

(brak odpowiedzi)

Ofiara

Ofiara

Ofiara

Poprawna

suma

kontrolna

(odpowiedź)

Znaleziono

poprawne

rozwiązanie!

O autorze

Aktualnie jest studentem drugiego roku SUM Informatyki na Akademii Górniczo-Hutni-
czej w Krakowie. Do jego głównych zainteresowań należy programowanie, administra-
cja systemów komputerowych oraz aspekty bezpieczeństwa informatycznego.
Kontakt z autorem: [e-mail]

W Sieci

• http://www.nd.edu/~parasite/ – strona twórców idei informatyki pasożytniczej wyko-

rzystującej mechanizmy protokołów internetowych,

• http://szene.ch/parasit/ – strona z implementacjami oprogramowania wykorzystu-

jącego techniki obliczeń pasożytniczych.