
Wykłady z matematyki
Anna Witaszczyk
1
Logistyka – Studia niestacjonarne I Stopnia Zaoczne
I rok
Semestr zimowy 2011/12
WYKŁADY Z MATEMATYKI
I. LOGIKA
1. RACHUNEK ZDAŃ
Zdaniem w logice nazywamy każde wyrażenie, o którym można orzec, czy jest
prawdziwe, czy fałszywe. Pośród wyrażeń języka potocznego zdaniami mogą być jedynie
wyrażenia oznajmujące (np.: „Jan lubi jabłka”, „Warszawa jest stolicą Islandii”). Nie są
zdaniami pytania, polecenia, prośby czy też wyrażenia ustalające pewne normy (np.: „Należy
jeść jabłka”). Zdaniami nie są też prognozy (np.: „Jutro będzie padał deszcz”). W logice
matematycznej poszczególne zdania oznaczać będziemy przy pomocy małych liter, np.: p, q,
r, s itp.
Wartością logiczną zdania p nazywamy liczbę równą liczbie 1 lub 0 w zależności od
tego, czy zdanie uznajemy za prawdziwe, czy fałszywe. To, czy dane zdanie uznajemy za
prawdziwe, czy nie, zależy od stanu naszej wiedzy potocznej lub naukowej.
Przykład 1.1.1. Następujące wyrażenia są – z punktu logiki – przykładami zdań:
„3=4” (zdanie fałszywe, wartość logiczna – 0)
„2+5>7” (zdanie fałszywe, wartość logiczna – 0)
„
{
}
4
,
3
,
2
,
1
3
∈
” (zdanie prawdziwe, wartość logiczna -1)
„Arystoteles był uczniem Platona” (zdanie prawdziwe, wartość logiczna -1)
Pojedyncze zdania mogą być połączone spójnikami logicznymi ‘i”, „lub”,
„jeżeli…to”, „wtedy i tylko wtedy, gdy”, „nieprawda, że”, oznaczanymi odpowiednio za
pomocą symboli:
,
,
,
,
⇔
⇒
∨
∧
~. Zdanie, w którym nie wyróżnia się spójników logicznych,
będziemy nazywali
zdaniem prostym, natomiast zdanie z wyróżnionymi spójnikami
logicznymi –
zdaniem złożonym.
W matematyce i innych naukach dedukcyjnych zakłada się z góry, że pewne zdania są
prawdziwe (tego rodzaju zdania nazywa się aksjomatami i za pomocą dedukcji dowodzi się
prawdziwości innych zdań (nazywanych twierdzeniami).
Aby móc poprawnie przeprowadzić dedukcję, trzeba umieć jednoznacznie
odpowiedzieć na pytanie: Jaka jest wartość logiczna zdania złożonego w zależności od
wartości logicznej składających się na nie zdań prostych. Aby odpowiedzieć na to pytanie,
będziemy się posługiwali tzw.
schematami zdaniowymi, tzn. wyrażeniami zawierającymi
symbole p, q, r, … itp. Oznaczające pewne, nieokreślone bliżej zdania oraz spójniki logiczne.
Najprostsze schematy zdaniowe mogą być przedstawione za pomocą wyrażeń:
negacja
p
~
,
koniunkcja
q
p
∧
,
alternatywa
q
p
∨
,
implikacja
q
p ⇒
,
równoważność
q
p
⇔
.
W tabeli 1.1.1 podane są wartości logiczne wyżej wymienionych zdań złożonych w
zależności od wartości logicznych zdań p i q. Tabela ta jednoznacznie definiuje spójniki
logiczne.

Wykłady z matematyki
Anna Witaszczyk
2
Tabela 1.1.1
p
q
p
~
q
p
∧
q
p
∨
q
p ⇒
q
p
⇔
1
1
0
0
1
0
1
0
0
0
1
1
1
0
0
0
1
1
1
0
1
0
1
1
1
0
0
1
Dla dowolnego zdania złożonego (przedstawionego za pomocą pewnego schematu
zdaniowego) można, posługując się podobną tabelą, określić jego wartości logiczne w
zależności od wartości logicznych wchodzących w jego skład zdań prostych.
Przykład 1.1.2. W tabeli 1.1.2 określono wartości logiczne zdania przedstawionego za
pomocą schematu:
(
) (
)
q
p
q
p
~
⇒
⇒
∧
Tabela 1.1.2
p q
q
p
∧
~q
q
p
~
⇒
(
) (
)
q
p
q
p
~
⇒
⇒
∧
1
1
0
0
1
0
1
0
1
0
0
0
0
1
0
1
0
1
1
1
0
1
1
1
Z powyższej tabeli wynika, że jeżeli zdania p oraz q są prawdziwe, to zdanie
(
) (
)
q
p
q
p
~
⇒
⇒
∧
jest fałszywe.
Metoda sprawdzania prawdziwości zdania złożonego przedstawiona w powyższym
przykładzie nazywa się
metodą zero-jedynkową.
Tautologią (prawem) rachunku zdań będziemy nazywać taki schemat zdaniowy,
który określa zdanie prawdziwe, niezależnie od wartości logicznej wchodzących w jego skład
zdań prostych. Inaczej mówiąc, tautologie są to schematy zdań zawsze prawdziwych.
Schemat zdaniowy z przykładu 1.1.2 nie jest tautologią.
Poniżej przedstawiona jest lista najbardziej znanych praw rachunku zdań. O tym, że
rzeczywiście są to prawa rachunku zdań można się przekonać przy pomocy metody zero-
jedynkowej. Symbol 1 przyjęto dla prawdziwego zdania prostego, zaś symbol 0 dla
fałszywego zdania prostego.
Prawa rachunku zdań
1. prawo tożsamości
p
p
⇔
2. prawo sprzeczności
(
)
0
~
⇔
∧
p
p
(zdanie
nie
może
być
prawdziwe wraz ze swym zaprzeczeniem)
3. prawo wyłączonego środka
p
p
~
∨
(z dwóch zdań sprzecznych jedno
jest prawdziwe)
4. prawo podwójnego przeczenia
( )
p
p
~
~
⇔

Wykłady z matematyki
Anna Witaszczyk
3
5. prawa De Morgana
(
) (
)
q
p
q
p
~
~
~
∨
⇔
∧
(zaprzeczenie
koniunkcji jest równoważne alternatywie
zaprzeczeń)
(
) (
)
q
p
q
p
~
~
~
∧
⇔
∨
(zaprzeczenie
alternatywy jest równoważne koniunkcji
zaprzeczeń)
6. zaprzeczenie implikacji
(
) (
)
q
p
q
p
~
~
∧
⇔
⇒
7. prawo kontrapozycji
(
) (
)
p
q
q
p
~
~
⇒
⇔
⇒
8. prawa przemienności
(
) (
)
p
q
q
p
∧
⇔
∧
(przemienność koniunkcji)
(
) (
)
p
q
q
p
∨
⇔
∨
(przemienność
alternatywy)
9. prawa łączności
(
)
[
]
(
)
[
]
r
q
p
r
q
p
∧
∧
⇔
∧
∧
(łączność
koniunkcji)
(
)
[
]
(
)
[
]
r
q
p
r
q
p
∨
∨
⇔
∨
∨
(łączność
alternatywy)
10. prawa rozdzielności
(
)
[
]
(
) (
)
[
]
r
p
q
p
r
q
p
∧
∨
∧
⇔
∨
∧
(rozdzielność
koniunkcji
względem
alternatywy)
(
)
[
]
(
) (
)
[
]
r
p
q
p
r
q
p
∨
∧
∨
⇔
∧
∨
(rozdzielność
alternatywy
względem
koniunkcji)
11. prawa tautologii
(
)
p
p
p
⇔
∧
(
)
p
p
p
⇔
∨
12. prawa pochłaniania (absorpcji)
(
)
p
p
⇔
∧
1
(
)
1
1
⇔
∨
p
13. prawa konfabulacji
(
)
0
0
⇔
∧
p
(
)
p
p
⇔
∨
0
14. prawo odrywania (modus ponens)
(
)
[
]
q
q
p
p
⇒
⇒
∧
15. prawo podnoszenia (modus tollens)
(
)
[
]
p
q
q
p
~
~
⇒
∧
⇒
16. prawo sprowadzania do niedorzeczności
(reductio ad absurdum, prawo Claviusa)
(
)
p
p
p
⇒
⇒
~
17.
prawo
sylogizmu
(przechodniości
implikacji)
(
) (
)
[
]
(
)
r
p
r
q
q
p
⇒
⇒
⇒
∧
⇒
18. prawo dodawania
(
)
q
p
p
∨
⇒
19. prawo specjalizacji
(
)
p
q
p
⇒
∧
20.prawo redukcji
(
) (
)
[
]
(
)
[
]
r
q
p
r
q
r
p
⇒
∨
⇒
⇒
∧
⇒
21. prawo implikacji
p
p ⇒
22. prawo Dunsa Szkota
(
)
q
p
p
⇒
⇒
~
(zdanie fałszywe implikuje
dowolny sąd)
Jeśli dla pewnych dwóch zdań p oraz q zdanie
q
p ⇒
jest prawdziwe, to mówimy, że
zdanie p jest warunkiem dostatecznym dla zdania q oraz że zdanie q jest warunkiem
koniecznym dla zdania p.

Wykłady z matematyki
Anna Witaszczyk
4
Kwadrat logiczny:
q
p ⇒
odwrotność
p
q ⇒
przeciwieństwo
przeciwieństwo
q
p
~
~
⇒
odwrotność
p
q
~
~
⇒
Jeżeli
q
p ⇒
nazwiemy implikacją prostą, to:
p
q ⇒
nazywa się implikacją
odwrotną,
q
p
~
~
⇒
- implikacją przeciwną,
p
q
~
~
⇒
- implikacją przeciwstawną (
transpozycją, kontrapozycją).
Implikacje przeciwstawne, a więc
q
p ⇒
i
p
q
~
~
⇒
oraz
p
q ⇒
i
q
p
~
~
⇒
, tzn.
napisane na końcach przekątnych kwadratu logicznego są równoważne, a więc jednocześnie
prawdziwe lub jednocześnie fałszywe.
Z prawdziwości implikacji prostej nie wynika ani prawdziwość implikacji odwrotnej,
ani przeciwnej, ale jeżeli któraś z nich, wraz z implikacją prostą jest prawdziwa, to prawdziwe
są wszystkie cztery implikacje.
2. FUNKCJA ZDANIOWA I KWANTYFIKATORY
Funkcja zdaniowa (forma zdaniowa) jest to takie wyrażenie P(x,y,z,…) zawierające
pewne zmienne x, y, z,…, które staje się zdaniem po podstawieniu za te zmienne konkretnych
wartości (np. liczb albo nazw osób lub przedmiotów). Na ogół zakłada się, że wartości
zmiennych występujących w funkcji zdaniowej należą do pewnych zbiorów X, Y, Z,…(tzn.
X
x
∈
,
Y
y
∈
,
Z
z
∈
,…) nazywanych zakresami zmienności zmiennych zdaniowych x, y,
z,…
Przykład 1.2.1. Wyrażenie „Pan X ma samochód” jest funkcją zdaniową, która staje
się zdaniem, jeśli za X podstawimy nazwisko konkretnego człowieka, np. „Pan Nowak ma
samochód”. Jeśli „Nowak” oznacza konkretną osobę, to o powyższym zdaniu możemy
rozstrzygnąć, czy jest prawdziwe, czy też fałszywe.
Przykład 1.2.2. Wyrażenie „x+y=4” jest funkcją zdaniową o zakresie zmienności
(R,R). Jeśli podstawimy x=2, y=2, to otrzymamy zdanie prawdziwe 2+2=4, natomiast po
podstawieniu x=3, y=4 otrzymujemy zdanie fałszywe 3+4=4.
Funkcja zdaniowa P(x,y,z,…) – gdzie
X
x
∈
,
Y
y
∈
,
Z
z
∈
,… - jest nazywana
tożsamością, jeśli dla dowolnych ustalonych wartości
X
x
∈
0
,
Y
y
∈
0
,
Z
z
∈
0
,… zdanie
P(x
0
,y
0
,z
0
,…) jest prawdziwe.
Przykład 1.2.3. Funkcja zdaniowa „x+y=y+x”, o zakresie zmienności (R,R), jest
tożsamością.
Dwie funkcje zdaniowe P(x,y,z,…) i Q(x,y,z,…) są równoważne, jeśli funkcja
zdaniowa
P(x,y,z,…)
⇔
Q(x,y,z,…)
jest tożsamością.

Wykłady z matematyki
Anna Witaszczyk
5
Przykład 1.2.4. Funkcja zdaniowa „x+5=9” jest równoważna funkcji zdaniowej „x=4.
Z danej funkcji zdaniowej można otrzymać zdanie również poprzez użycie
kwantyfikatorów określających wzajemne związki pomiędzy funkcją zdaniową a zakresami
zmienności jej zmiennych zdaniowych. Najczęściej używa się dwóch rodzajów
kwantyfikatorów:
- kwantyfikator duży (ogólny), oznaczony symbolem
∧
lub
∀
oznaczający wyrażenie „dla
każdego”,
- kwantyfikator mały (szczegółowy, egzystencjalny), oznaczony symbolem
∨
lub
∃
oznaczający wyrażenie „istnieje”.
Zapisy
( )
x
P
x
∀
,
( )
x
P
x :
∀
oznaczają jedno ze zdań: „Dla każdego x P(x) jest
prawdziwe”, „Dla każdego x zachodzi P(x)”. Można również uwzględnić zakres zmienności
X funkcji P(x):
( )
x
P
X
x
∈
∀
. Zapisy
( )
x
P
x
∃
,
( )
x
P
x :
∃
oznaczają jedno ze zdań: ”Istnieje takie x,
ż
e P(x) jest prawdziwe”, „Istnieje takie x, że zachodzi P(x)”. W razie potrzeby również w tym
przypadku można uwzględnić zakres zmienności zmiennej x.
Przykład 1.2.5. Niech L będzie zbiorem wszystkich ludzi, zaś P(x) – wyrażeniem „x
jest inteligentny”. Wówczas poniższe zdania można odczytać następująco:
1.
( )
x
P
L
x
∈
∀
- „Każdy człowiek jest inteligentny”,
2.
( )
x
P
L
x
∈
∃
- „Istnieją ludzie inteligentni”,
3.
( )
x
P
L
x
∈
∀
~
- „Nie wszyscy ludzie są inteligentni”,
4.
( )
x
P
L
x
∈
∃
~
- „Nie ma ludzi inteligentnych”,
5.
( )
x
P
L
x
~
∈
∀
- „śaden człowiek nie jest inteligentny”,
6.
( )
x
P
L
x
~
∈
∃
- „Istnieją ludzie nieinteligentni”.
Zauważmy, że w powyższym przykładzie zdania 3 i 6 oraz 4 i 5 są równoważne. Jest
to zgodne z ogólną zasadą, która mówi, że aby zaprzeczyć zdaniu z kwantyfikatorem, należy
zmienić rodzaj kwantyfikatora, a znak negacji włączyć pod kwantyfikator. Inaczej mówiąc,
prawdziwe są równoważności:
( )
x
P
L
x
∈
∀
~
⇔
( )
x
P
L
x
~
∈
∃
( )
x
P
L
x
∈
∃
~
⇔
( )
x
P
L
x
~
∈
∀
Są to
prawa De Morgana dla kwantyfikatorów.
Ważnymi regułami wnioskowania, w których występują kwantyfikatory są:
( )
( )
x
P
x
a
P
:
∃
⇒
( )
( )
a
P
x
P
x
⇒
∀
:
Przykład 1.2.6. Jeśli wiemy, że pan Nowak jest inteligentny, to wnioskujemy, że
istnieją ludzie inteligentni (istnieje przynajmniej jeden człowiek inteligentny). Jeśli natomiast
wiemy, że wszyscy ludzie są inteligentni, to automatycznie wiemy, że również pan Nowak
jest inteligentny (nawet go nie znając).

Wykłady z matematyki
Anna Witaszczyk
6
II. ZBIORY
1. ZBIORY I DZIAŁANIA NA ZBIORACH
W matematyce nie istnieje precyzyjna definicja zbioru, jest to pojęcie pierwotne
(niedefiniowalne). Elementy zbiorów będziemy oznaczać małymi literami, np. a, b, c,…,
natomiast same zbiory dużymi literami, np. A, B, C,… Pewnym zbiorom przypisywać
będziemy standardowe oznaczenia: N – zbiór liczb naturalnych, C – zbiór liczb całkowitych,
W – zbiór liczb wymiernych, R – zbiór liczb rzeczywistych, R
+
- zbiór dodatnich liczb
rzeczywistych, R
-
- zbiór ujemnych liczb rzeczywistych, NW – zbiór liczb niewymiernych.
Fakt, że a jest elementem zbiory A (należy do zbioru A) będziemy zapisywać w
postaci
A
a
∈
. Zaprzeczenie tego zdania, czyli zdanie
(
)
A
a
∈
~
, zapisuje się
następująco:
A
a
∉
(element a nie należy do zbioru A).
Zbiór A składający się z elementów a
1
, a
2
,…,a
n
będziemy zapisywać w postaci
{
}
n
a
a
a
A
,...,
,
2
1
=
.
Zbiory mogą też być przedstawiane w postaci
( )
{
}
x
P
x
A
:
=
, gdzie P(x) jest pewną
funkcją zdaniową charakteryzującą własność, którą posiadają wszystkie elementy zbioru A
(czytamy: ”A jest zbiorem wszystkich x, które spełniają warunek P(x)”).
Zauważmy, że każdy zbiór A może być zapisany w postaci
{
}
A
x
x
A
∈
=
:
.
Równość dwóch zbiorów definiuje się następująco:
[
]
B
x
A
x
B
A
x
∈
⇔
∈
∀
⇔
=
- dwa zbiory A i B są równe wtedy i tylko wtedy,
gdy mają te same elementy.
Przykład 2.1.1.
{1, 2, 3, 4}={3, 1, 4, 2}
{
}
{ }
1
,
0
:
2
=
=
∧
∈
x
x
R
x
x
Zawieranie się dwóch zbiorów definiuje się następująco:
[
]
B
x
A
x
B
A
x
∈
⇒
∈
∀
⇔
⊂
- zbiór A zawiera się w zbiorze B, jeśli każdy
element zbioru A jest jednocześnie elementem zbioru B, A nazywa się podzbiorem zbioru B.
To samo oznacza zapis
A
B
⊃
, który czytamy: „zbiór B zawiera zbiór A”.
Analogicznie:
[
]
A
x
B
x
A
B
x
∈
⇒
∈
∀
⇔
⊂
i
B
A
⊃
.
Przykład 2.1.2.
{1, 2, 3, 4}
⊂
{1, 2, 3, 4, 5}
{
} {
}
5
:
5
:
≤
∧
∈
⊂
<
∧
∈
x
R
x
x
x
R
x
x
Prawdziwa jest równoważność:
A
B
B
A
B
A
⊂
∧
⊂
⇔
=
.
Zbiór pusty definiujemy jako zbiór nie zawierający żadnych elementów i
oznaczamy go symbolem Ø. Spełnia on w teorii zbiorów rolę podobną do roli liczby 0 w
arytmetyce.
Działania na zbiorach:
Wspólną częścią (przekrojem, iloczynem) dwóch zbiorów A i B nazywamy zbiór,
który składa się z elementów należących zarówno do A, jak i do B. Zapis formalny:
{
}
B
x
A
x
x
B
A
∈
∧
∈
=
∩
:
lub
B
x
A
x
B
A
x
∈
∧
∈
⇔
∩
∈
.
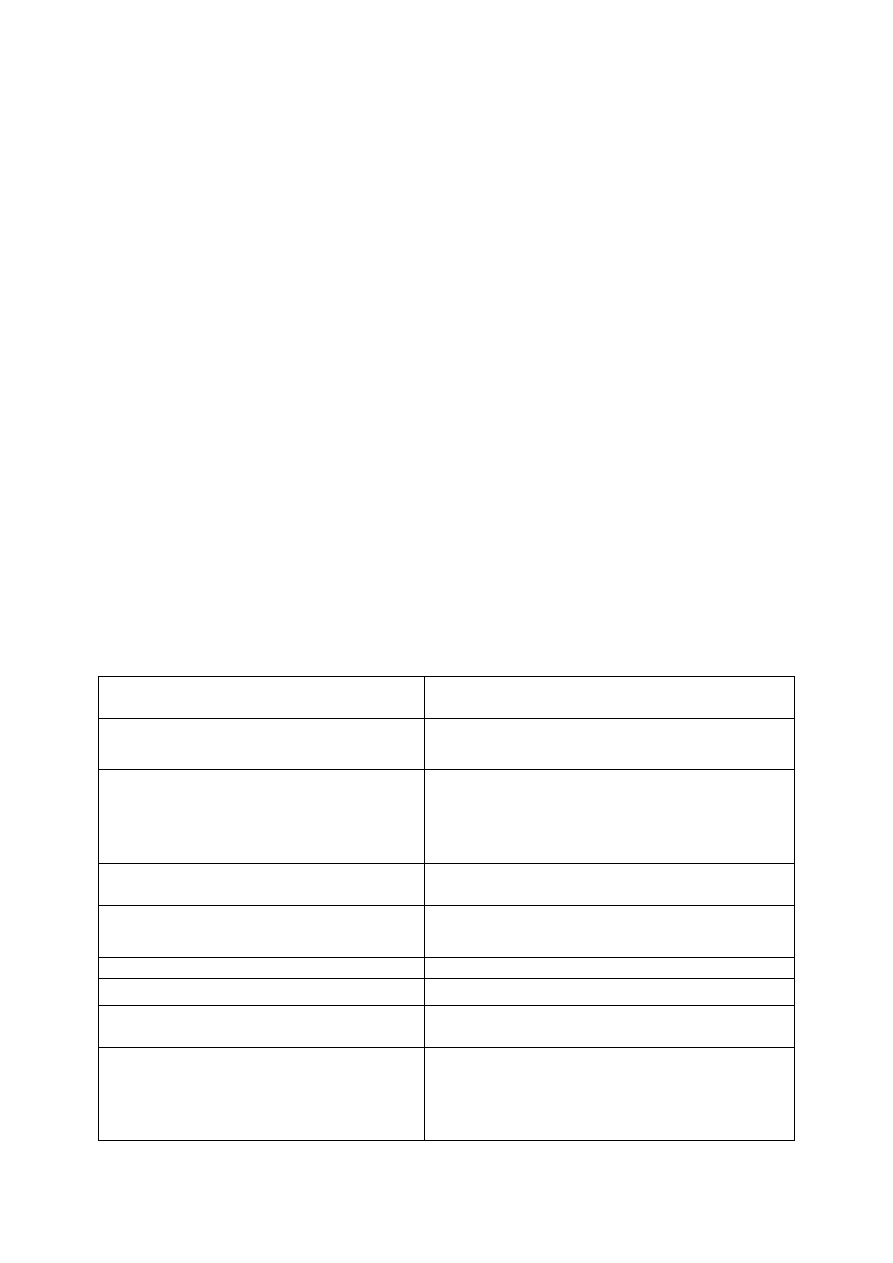
Wykłady z matematyki
Anna Witaszczyk
7
Dwa zbiory nazywamy rozłącznymi, jeśli ich wspólna część jest zbiorem pustym, tzn.
=
∩
B
A
Ø. Mówimy, że zbiory A
1
, A
2
, …, A
n
są parami rozłączne, jeśli
=
∩
j
i
A
A
Ø dla
j
i
≠
.
Sumą (unią, złączeniem) dwóch zbiorów A i B nazywamy zbiór złożony z
elementów należących do zbioru A lub do zbioru B:
{
}
B
x
A
x
x
B
A
∈
∨
∈
=
∪
:
,
B
x
A
x
B
A
x
∈
∨
∈
⇔
∪
∈
.
Różnicą dwóch zbiorów A i B nazywamy zbiór złożony z tych elementów zbioru A,
które nie należą do zbioru:
{
}
B
x
A
x
x
B
A
∉
∧
∈
=
:
\
,
B
x
A
x
B
A
x
∉
∧
∈
⇔
∈
\
.
Oczywiście:
{
}
A
x
B
x
x
A
B
∉
∧
∈
=
:
\
oraz
A
x
B
x
A
B
x
∉
∧
∈
⇔
∈
\
.
Dla dowolnego zbioru A możemy też zdefiniować jego dopełnienie oznaczane
symbolem A’. Dopełnienie musi być zawsze określone względem jakiegoś większego zbioru
nazywanego zbiorem uniwersalnym, uniwersum lub przestrzenią. Jeśli przestrzeń oznaczymy
symbolem
Ω
Ω
Ω
Ω
, to
dopełnienie zbioru A do
Ω
Ω
Ω
Ω
składa się z tych elementów zbioru
Ω
Ω
Ω
Ω
, które
nie należą do zbioru A, czyli:
{
}
A
x
x
x
A
∉
∧
∈
=
Ω
Ω
Ω
Ω
:
'
lub
A
x
x
A
x
∉
∧
∈
⇔
∈
Ω
Ω
Ω
Ω
'
.
To, jakie jest dopełnienie danego zbioru zależy od tego, względem jakiej przestrzeni
określamy to dopełnienie.
Zauważmy, że
A
A
\
'
Ω
Ω
Ω
Ω
=
.
Poniżej podane są ważniejsze prawa działań na zbiorach (prawa rachunku zbiorów,
prawa algebry zbiorów).
Prawa rachunku zbiorów
1. prawa przemienności
A
B
B
A
∪
=
∪
(przemienność sumy)
A
B
B
A
∩
=
∩
(przemienność iloczynu)
2. prawa łączności
(
) (
)
C
B
A
C
B
A
∩
∩
=
∩
∩
(łączność iloczynu)
(
) (
)
C
B
A
C
B
A
∪
∪
=
∪
∪
(łączność sumy)
3. prawa rozdzielności
(
) (
) (
)
B
A
B
A
C
B
A
∩
∪
∩
=
∪
∩
(rozdzielność
iloczynu względem sumy)
(
) (
) (
)
C
A
B
A
C
B
A
∪
∩
∪
=
∩
∪
9rozdzielność
sumy względem iloczynu)
4. idempotentność
A
A
A
=
∩
A
A
A
=
∪
5. prawa pochłaniania
(
)
A
B
A
A
=
∪
∩
(
)
A
B
A
A
=
∩
∪
6. antytoniczność
'
'
A
B
B
A
⊂
⇒
⊂
7. prawo inwolucji
( )
A
A
=
'
'
8. prawa Boole’a
=
∩
'
A
A
Ø
Ω
Ω
Ω
Ω
=
∪
'
A
A
9. prawa De Morgana
(
)
'
'
'
B
A
B
A
∩
=
∪
(dopełnienie sumy równe jest
iloczynowi dopełnień)
(
)
'
'
'
B
A
B
A
∪
=
∩
(dopełnienie iloczynu równe
jest sumie dopełnień)
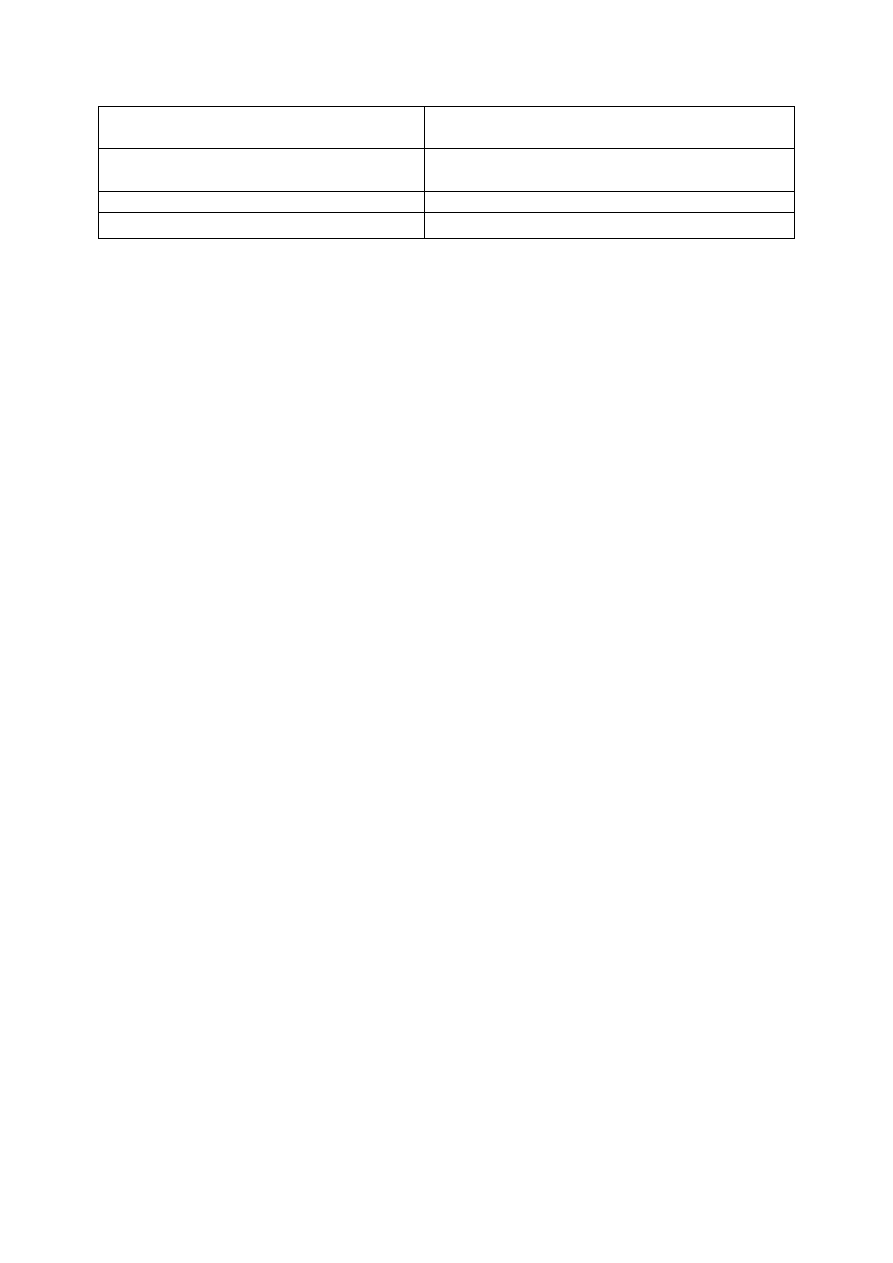
Wykłady z matematyki
Anna Witaszczyk
8
10. działania ze zbiorem pustym
A
∩
Ø=Ø
A
∪
Ø=A
11. działania z uniwersum
A
A
=
∩ Ω
Ω
Ω
Ω
Ω
Ω
Ω
Ω
Ω
Ω
Ω
Ω =
∪
A
12.
'
\
B
A
B
A
∩
=
13.
=
∩
B
A
Ø
'
B
A
⊂
⇔
Prawa działań na zbiorach na ogół wynikają z odpowiednich praw logiki.
2. ILOCZYN KARTEZJAŃSKI
Dla dowolnych (niekoniecznie różnych) elementów a i b przez
parę uporządkowaną
utworzoną z a i b będziemy rozumieli ustawienie tych elementów w pewnej kolejności, tzn.
tak, że jeden z nich jest traktowany jako pierwszy, a pozostały jako drugi. Parę
uporządkowaną, w której element a jest pierwszy, oznaczamy symbolem (a,b).
Mamy więc:
( ) ( )
a
b
b
a
b
a
,
,
≠
⇒
≠
;
( ) ( ) {
}
d
b
c
a
d
c
b
a
=
∧
=
⇔
=
,
,
.
Dla dowolnego elementu a możemy utworzyć parę (a,a).
Iloczynem kartezjańskim (produktem) dowolnych zbiorów A i B nazywamy zbiór
( )
{
}
B
b
A
a
b
a
B
A
∈
∧
∈
=
×
:
,
.
Jeśli
B
A
≠
oraz A i B są niepuste, to
A
B
B
A
×
≠
×
(iloczyn kartezjański nie jest
przemienny).
III. ZNAK
∑
I
∑∑
Na oznaczenie sumy S=a
1
+a
2
+…+a
n
wprowadza się symbol
∑
(sigma). Przy jego
użyciu sumę tą zapisuje się w postaci:
∑
=
=
n
k
k
a
S
1
i czyta się: „suma a
k
od k=1 do n”. Wyraz a
k
jest ogólnym wyrazem sumy, a litera k jest tu
wskaźnikiem sumowania i przyjmuje kolejne wartości całkowite od 1 do n. Wskaźnikiem
sumowania może być dowolna litera, jego pierwszą wartością może być dowolna liczba
całkowita, nie tylko 1. Stąd też:
∑
∑
∑
=
=
=
=
=
n
p
p
n
i
i
n
k
k
a
a
a
1
1
1
n
m
m
n
m
k
k
a
a
a
a
+
+
+
=
+
=
∑
...
1
,
n
m
≤
.
Znak
∑
zachowuje wszystkie własności dodawania, m. in.:
(3.1)
(
)
∑
∑
∑
=
=
=
±
=
±
n
m
k
k
n
m
k
k
n
m
k
k
k
b
a
b
a
,
n
m
≤
,
(3.2)
∑
∑
∑
+
=
=
=
+
=
n
p
k
k
p
m
k
k
n
m
k
k
a
a
a
1
dla
n
p
m
≤
≤
,

Wykłady z matematyki
Anna Witaszczyk
9
(3.3)
∑
∑
=
=
=
n
m
k
k
n
m
k
k
a
c
ca )
(
,
n
m
≤
,
R
c
∈
, (stałą można wyłączyć przed znak sumy)
(3.4)
(
)
c
m
n
c
n
m
k
1
+
−
=
∑
=
,
n
m
≤
,
R
c
∈
.
Przykład 3.1. Posługując się znakiem sumy, zapiszmy sumę dodatnich liczb
parzystych nie większych od stu.
Liczbę parzystą można zapisać w postaci 2k, gdzie
+
∈
N
k
, zatem:
∑
=
=
+
+
+
+
50
1
2
100
...
6
4
2
k
k .
Przykład 3.2. Obliczmy wartości sum:
1.
90
36
25
16
9
4
6
5
4
3
2
2
2
2
2
2
6
2
2
=
+
+
+
+
=
+
+
+
+
=
∑
=
k
k
;
2.
( )
0
1
1
1
1
1
1
)
1
(
)
1
(
)
1
(
)
1
(
)
1
(
)
1
(
1
5
4
3
2
1
0
5
0
=
−
+
−
+
−
=
−
+
−
+
−
+
−
+
−
+
−
=
−
∑
=
j
j
;
3.
30
5
6
5
5
5
5
5
5
5
2
3
=
⋅
=
+
+
+
+
+
=
∑
−
=
j
lub
( )
(
)
30
5
6
5
1
3
2
5
)
4
.
3
(
2
3
=
⋅
=
+
−
−
=
∑
−
=
j
;
4.
(
)
260
3
10
)
16
...
8
7
(
2
3
)
1
7
16
(
2
3
2
3
2
16
7
)
4
.
3
(
),
3
.
3
(
16
7
16
7
)
1
.
3
(
16
7
=
⋅
+
+
+
+
=
+
−
+
=
+
=
+
∑
∑
∑
∑
=
=
=
=
i
i
i
i
i
i
i
.
Przykład 3.3. Wielkość produkcji (np. w tonach) fabryki X w i-tym miesiącu
oznaczmy przez x
i
. Wielkość produkcji w pierwszym kwartale możemy wówczas zapisać
jako
∑
=
3
1
i
i
x , wielkość produkcji w ostatnim kwartale roku jako sumę
∑
=
12
10
i
i
x , a całość produkcji
w ciągu roku jako sumę
∑
=
12
1
i
i
x .
Niech teraz składniki będą postaci
∑
∑
∑
=
=
+
=
m
t
j
jn
m
t
j
jp
m
t
j
jp
a
a
a
,...,
,
1
,
gdzie
C
n
p
m
t
∈
,
,
,
i
m
t
≤
,
n
p
≤
wtedy
∑∑
∑ ∑
∑
∑
∑
=
=
=
=
=
=
+
=
=
=
+
+
+
n
p
k
m
t
j
jk
n
p
k
m
t
j
jk
m
t
j
jn
m
t
j
jp
m
t
j
jp
a
a
a
a
a
...
1
,
a więc sumowanie jest podwójne.
Sumowanie podwójne ma następujące własności:
(3.5)
∑
∑∑
∑
=
=
=
=
=
m
t
j
n
p
k
m
t
j
jk
n
p
k
jk
a
a
(kolejność sumowania jest dowolna),
(3.6)
∑
∑
∑∑
∑
∑
=
=
=
=
=
=
±
=
±
m
t
j
m
t
j
m
t
j
n
p
k
jk
n
p
k
jk
n
p
k
jk
jk
b
a
b
a
)
(
,
(3.7)
∑
∑∑
∑
=
=
=
=
=
m
t
j
m
t
j
n
p
k
jk
n
p
k
jk
a
c
ca )
(
,
R
c
∈
, (stałą można wyłączyć przed znak sumy),
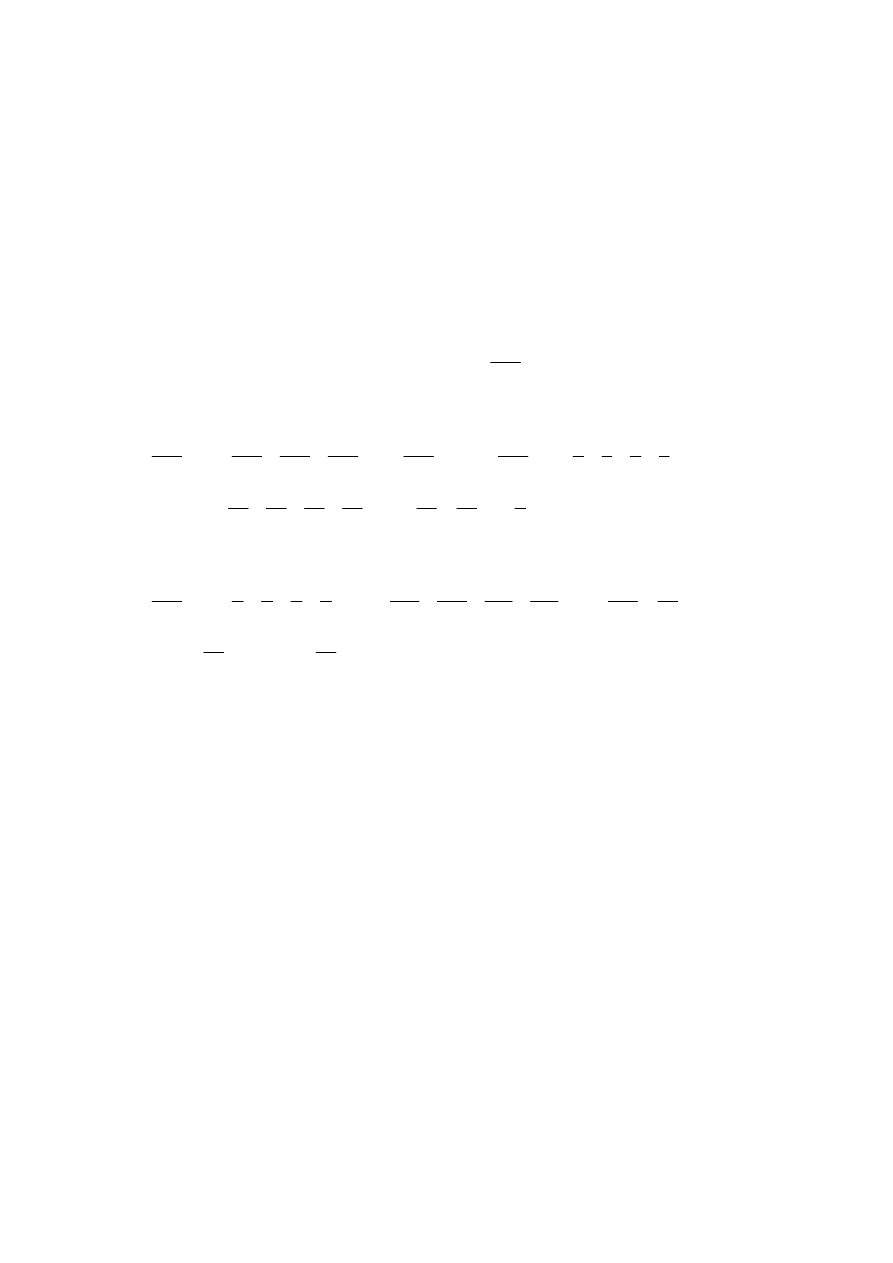
Wykłady z matematyki
Anna Witaszczyk
10
(3.8)
∑∑
=
=
+
−
+
−
=
m
t
j
n
p
k
c
p
n
t
m
c
)
1
)(
1
(
,
R
c
∈
,
(3.9)
∑
∑
∑
=
=
=
+
−
=
m
t
j
m
t
j
j
n
p
k
j
a
p
n
a
)
1
(
,
(3.10)
∑
∑
∑
=
=
=
+
−
=
m
t
j
n
p
k
k
n
p
k
k
a
t
m
a
)
1
(
,
(3.11)
∑
∑
∑
∑
=
=
=
=
=
m
t
j
n
p
k
k
m
t
j
j
n
p
k
k
j
b
a
b
a
)
(
.
Przykład 3.4. Obliczmy wartość sumy
∑∑
=
=
+
4
1
5
3
1
i
j
i
j
.
Sumę można rozwijać według dowolnej kolejności wskaźników. Zatem:
∑
∑
∑
∑∑
=
=
=
=
=
=
+
+
+
=
+
=
+
=
+
+
+
+
+
=
+
4
1
4
1
)
3
.
3
(
4
1
4
1
5
3
5
1
4
1
3
1
2
1
12
1
1
12
1
12
1
5
1
4
1
3
1
i
i
i
i
j
i
i
i
i
i
i
j
4
,
15
5
2
15
5
77
60
77
12
60
12
60
15
60
20
60
30
12
=
=
=
⋅
=
+
+
+
=
lub
∑
∑
∑
∑
∑∑
=
=
=
=
=
=
=
=
=
+
+
+
=
+
+
+
=
+
5
3
5
3
5
3
5
3
4
1
5
3
60
77
60
77
60
12
60
15
60
20
60
30
5
4
3
2
1
j
j
j
j
i
j
j
j
j
j
j
j
j
j
j
j
i
j
(
)
4
,
15
12
60
77
5
4
3
60
77
=
⋅
=
+
+
=
.
IV. CIĄGI LICZBOWE
1. DEFINICJA CIĄGU
Jeśli każdej liczbie ze zbioru liczb naturalnych N została przyporządkowana
jednoznacznie pewna liczba rzeczywista, to mówimy, że został określony
nieskończony ciąg
liczbowy. Inaczej: ciągiem nieskończonym nazywamy każdą funkcję, której dziedziną jest
zbiór N.
Jeżeli dziedziną ciągu jest skończony podzbiór {1, 2, ,…, k} zbioru N, to taki ciąg
nazywamy
skończonym..
Wartość f(n) funkcji f dla argumentu n nazywamy n-tym
wyrazem ciągu i oznaczamy
f(n)=a
n
. Ciąg a
1
, a
2
, a
3
,…, a
n
,... oznaczamy symbolem
{ }
n
a
.
Ciąg , podobnie jak funkcje można określać:
1. wymieniając kilka początkowych wyrazów, np.:
2, 4, 6,… - ciąg liczb parzystych,
0, 5, 10,… - ciąg liczb podzielnych przez 5,
3, 9, 27,… - ciąg potęg liczby 3 itd.
2. za pomocą wzoru na n-ty wyraz (w postaci jawnej), np.:
2
n
a
n
=
,
( )
n
n
b
1
−
=
,
2
3
−
=
n
c
n
itd.
Ten sposób definiowania ciągu jest najczęściej spotykany i zazwyczaj najbardziej przydatny.

Wykłady z matematyki
Anna Witaszczyk
11
3. za pomocą wyrażenia rekurencyjnego, tzn. wzoru pozwalającego obliczać n-ty wyraz na
podstawie jednego lub więcej wyrazów poprzednich (przekształcenie wyrażenia
rekurencyjnego do postaci jawnej może nie być łatwe), np.:
3a.
2
1
=
a
,
5
2
1
−
=
+
n
n
a
a
,
1
≥
n
(kilka kolejnych wyrazów tego ciągu:
2
1
=
a
,
1
5
2
2
2
−
=
−
⋅
=
a
,
( )
7
5
1
2
3
−
=
−
−
⋅
=
a
,
( )
19
5
7
2
4
−
=
−
−
⋅
=
a
,…),
3b.
3
1
=
a
,
n
n
a
a
3
1
=
+
,
1
≥
n
, ciąg ten składa się z liczb: 3, 9, 27,…, można więc
określić go przy pomocy wzoru ogólnego
n
n
a
3
=
.
Geometrycznie interpretujemy ciąg jako zbiór punktów leżących na płaszczyźnie, jest
to zbiór punktów
( )
1
,
1 a
,
(
)
2
,
2 a
,…,
(
)
n
a
n,
,… .
2.KLASYFIKACJA CIĄGÓW
Ciągi można podzielić na monotoniczne i niemonotoniczne, oraz ograniczone
nieograniczone. Wśród wszystkich ciągów można wyróżnić klasę ciągów arytmetycznych i
geometrycznych.
Ciąg nazywamy
rosnącym, jeśli każdy jego wyraz jest większy od poprzedniego, tzn.
n
n
N
n
a
a
>
∀
+
∈
1
lub
0
1
>
−
∀
+
∈
n
n
N
n
a
a
,
np. 1, 2, 3, 4, …
Ciąg nazywamy
malejącym, jeśli każdy wyraz ciągu jest mniejszy od wyrazu
poprzedniego, tzn.
n
n
N
n
a
a
<
∀
+
∈
1
lub
0
1
<
−
∀
+
∈
n
n
N
n
a
a
,
np. 0, -2, -4, -6, …
Ciąg nazywamy
niemalejącym, jeśli
n
n
N
n
a
a
≥
∀
+
∈
1
lub
0
1
≥
−
∀
+
∈
n
n
N
n
a
a
,
np. 1, 1, 2, 2, 3, 3, 4, 4, …
Ciąg nazywamy
nierosnącym, jeśli
n
n
N
n
a
a
≤
∀
+
∈
1
lub
0
1
≤
−
∀
+
∈
n
n
N
n
a
a
,
np. 1, 0, 0, 0, …
Ciągi spełniające warunki jednej z powyższych definicji nazywamy
ciągami
monotonicznymi, przy czym ciągi rosnące lub malejące nazywamy ciągami ściśle
monotonicznymi.
Ciąg nazywamy
stałym, jeżeli dla każdego
1
≥
n
zachodzi a
n
=const (constans – stały),
np. 1, 1, 1, …. Ciąg stały jest ciągiem monotonicznym.
Jeśli a
1
, a
2
, a
3
,…, a
n
,... jest ciągiem, wówczas ciąg
,...
,...,
,
,
3
2
1
k
n
n
n
n
a
a
a
a
, gdzie n
1
, n
2
,
n
3
,…, n
k
,… jest dowolnym ciągiem rosnącym liczb naturalnych, nazywamy
podciągiem
ciągu
{ }
n
a
.
Przykład 4.2.1 Ciąg określony wzorem
=
2
cos
π
n
a
n
ma początkowe wyrazy:
0
2
cos
1
=
=
π
a
,
1
cos
2
−
=
=
π
a
,
0
2
3
cos
3
=
=
π
a
,
1
2
cos
4
=
=
π
a
,
0
5
=
a
,
1
6
−
=
a
,…
Zauważmy, że w
{ }
n
a
można wyróżnić trzy podciągi stałe:
0
1
2
=
−
k
a
,
1
2
4
−
=
−
k
a
,
1
4
=
k
a
.

Wykłady z matematyki
Anna Witaszczyk
12
Przykład 4.2.2. Zbadajmy monotoniczność ciągu
1
3
2
−
+
=
n
n
a
n
.Wystarczy ustalić
znak różnicy między (n+1)-szym i n-tym wyrazem ciągu:
(
)
(
)
[
]
4
2
1
3
1
3
3
1
2
1
3
1
1
3
1
2
2
2
2
1
+
=
+
−
−
−
+
+
+
+
=
−
+
−
−
+
+
+
=
−
+
n
n
n
n
n
n
n
n
n
n
a
a
n
n
.
Ponieważ dla każdego n 2n+4>0, ciąg jest rosnący.
Jeżeli dla każdego
N
n
∈
a
n
>0, to wzory definiujące różne rodzaje monotoniczności
ciągu
{ }
n
a
są równoważne wzorom:
1
1
>
∀
+
∈
n
n
N
n
a
a
dla ciągu rosnącego,
1
1
<
∀
+
∈
n
n
N
n
a
a
dla ciągu
malejącego,
1
1
≥
∀
+
∈
n
n
N
n
a
a
dla ciągu niemalejącego,
1
1
≤
∀
+
∈
n
n
N
n
a
a
dla ciągu nierosnącego.
Ciąg nazywamy
przemiennym, jeśli
0
1
<
⋅
∀
+
∈
n
n
N
n
a
a
,
Np. 1, -2, 4, -8, 16, -32,…
Mówimy, że ciąg jest
ograniczony z góry (lub z dołu), gdy istnieje taka liczba M, że
M
a
n
N
n
≤
∀
∈
(lub
M
a
n
N
n
≥
∀
∈
).
Ciąg nazywamy
ograniczonym, jeżeli jest ograniczony z góry i z dołu lub inaczej:
jeżeli istnieje taka liczba M, że
M
a
n
N
n
≤
∀
∈
.
Przykład 4.2.3.
Ciąg
n
n
a
2
=
,
1
≥
n
(2, 4, 8, 16,…) jest ograniczony z dołu przez każdą liczbę mniejszą lub
równą 2.
Ciąg
1
+
−
=
n
b
n
,
1
≥
n
(0, -1, -2, -3,…) jest ograniczony z góry przez każdą liczbę większą
lub równą 0.
Ciąg
n
c
n
1
=
,
1
≥
n
,...
4
1
,
3
1
,
2
1
,
1
jest ograniczony. Jest ograniczony z dołu przez każdą
liczbę mniejszą lub równą 0, a z góry przez każdą liczbę większą lub równą 1.
Ciąg arytmetyczny i ciąg geometryczny
Zagadnienie
Ciąg arytmetyczny
Ciąg geometryczny
Definicja
Ciąg
{ }
n
a
, dla którego różnica
między dowolnym wyrazem i
wyrazem go poprzedzającym jest
stała:
r
a
a
n
n
N
n
=
−
∀
+
∈
1
.
Liczbę r nazywa się różnicą ciągu.
Ciąg
{ }
n
a
, dla którego
0
1
≠
a
, a
iloraz dowolnego wyrazu i
wyrazu go poprzedzającego jest
stały:
q
a
a
n
n
N
n
=
∀
+
∈
1
,
0
≠
n
a
.
Liczbę q nazywa się ilorazem
ciągu.
n-ty wyraz ciągu
r
n
a
a
n
)
1
(
1
−
+
=
,
1
≥
n
2
1
1
+
−
+
=
n
n
n
a
a
a
, n>1
1
1
−
=
n
n
q
a
a
,
1
≥
n
1
1
2
+
−
=
n
n
n
a
a
a
, n>1
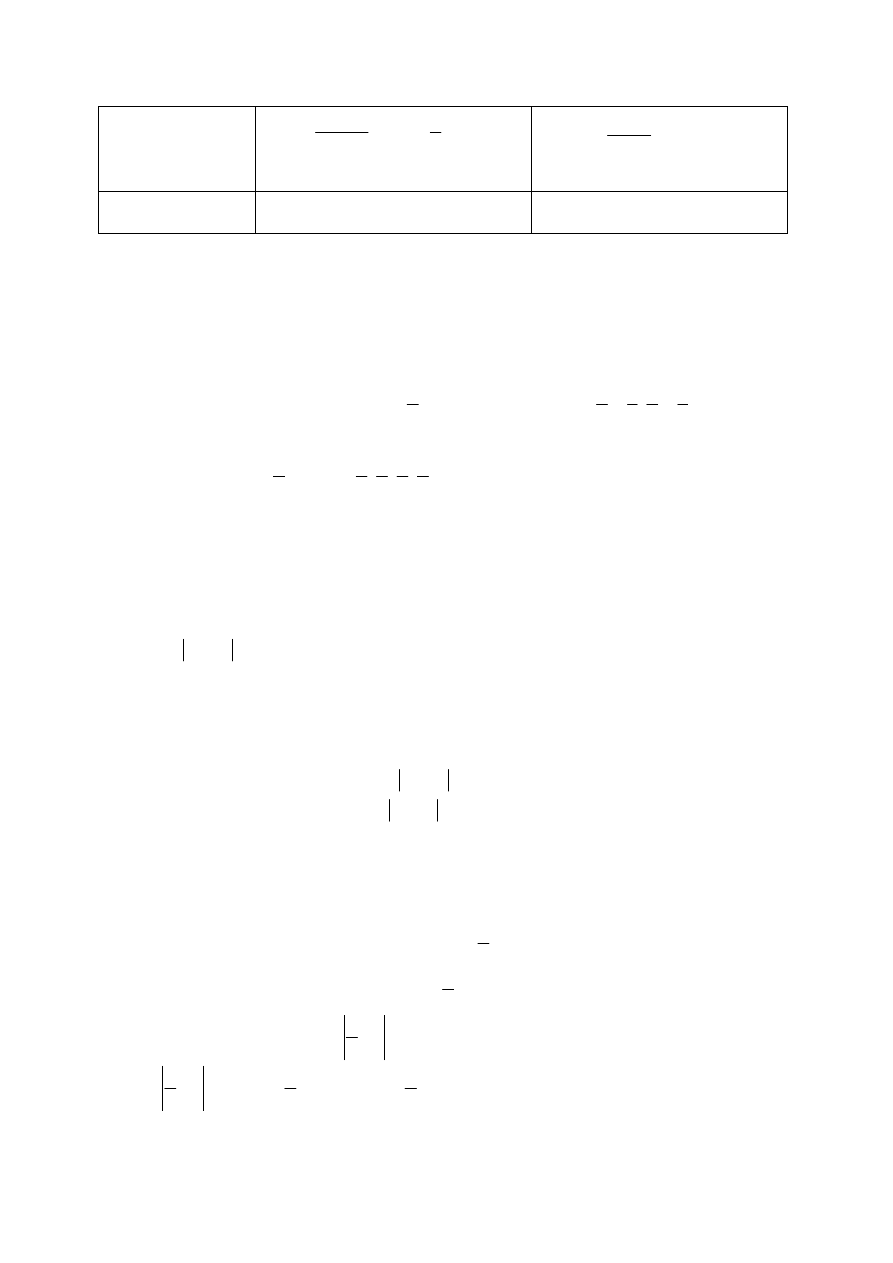
Wykłady z matematyki
Anna Witaszczyk
13
Suma n pierwszych
wyrazów ciągu
(
)
1
2
2
1
1
−
+
=
+
=
n
n
r
na
a
a
n
S
n
n
=
≠
−
−
=
1
1
1
1
1
1
q
dla
na
q
dla
q
q
a
S
n
n
Przykład
2, -1, -4, -7, -10, …
(a
1
=2, r=-3)
2, -6, 18, -54, 162, …
(a
1
=2, q=-3)
3. GRANICA CIĄGU
Pojęcie granicy ciągu jest jednym z fundamentalnych pojęć matematyki, leżących u
podstaw rachunku różniczkowego i całkowego (buduje się na nim pojęcie granicy funkcji,
pochodnej, całki).
Przykład 4.3.1. Ciąg
( )
n
a
n
n
1
1
−
=
składa się z liczb
−
−
−
,...
5
1
,
4
1
,
3
1
,
2
1
,
1
. Wyrazy
ciągu wraz ze wzrostem n „skupiają się” wokół liczby 1.
Wyrazy ciągu
n
a
n
1
1
−
=
, tzn.
,...
5
4
,
4
3
,
3
2
,
2
1
,
0
„dążą” do liczby 1.
„Skupianie się” wyrazów ciągu można opisać w sposób następujący: istnieje na osi
liczbowej taki punkt, że w dowolnie małym otoczeniu tego punktu leżą wyrazy o
wskaźnikach większych od pewnej liczby naturalnej N.
Jeśli liczba g ma tę własność, że w przedziale
(
)
ε
ε
+
−
g
g
,
o środku g i długości
ε
2
(
)
0
>
ε
leżą wszystkie wyrazy ciągu o indeksach n większych od pewnej liczby N, to
odległość
g
a
n
−
wyrazów ciągu o indeksach n>N od liczby g jest mniejsza od
ε
. Przedział
(
)
ε
ε
+
−
g
g
,
nazywa się
otoczeniem punktu g o promieniu
ε
.
Liczbę g nazywamy
granicą ciągu
{ }
n
a
wtedy i tylko wtedy, gdy dla każdej dowolnie
małej liczby dodatniej
ε
istnieje taka liczba naturalna N, że wszystkie wyrazy ciągu
{ }
n
a
o
wskaźnikach n>N spełniają nierówność
ε
<
−
g
a
n
.
(4.3.1)
ε
ε
<
−
∀
∃
∀
⇔
=
>
>
∞
→
g
a
g
a
n
N
n
N
n
n
0
lim
.
Inaczej: liczba g jest granicą ciągu liczbowego
{ }
n
a
wtedy i tylko wtedy, gdy do każdego
otoczenia liczby g należą prawie wszystkie wyrazy tego ciągu. Zwrot „prawie wszystkie
wyrazy” oznacza „wszystkie z wyjątkiem co najwyżej skończonej ich liczby”.
Przykład 4.3.1 Udowodnimy, że ciąg
n
a
n
1
=
ma granicę równą zeru. Niech
ε
będzie
dowolną liczbą dodatnią. Wykażemy, że
0
1
lim
=
∞
→
n
n
, jeśli wyznaczymy taką liczbę naturalną
N, zależną od
ε
, że nierówność
ε
<
−
0
1
n
jest spełniona dla n>N.
ε
ε
ε
1
1
0
1
>
→
<
→
<
−
n
n
n
.

Wykłady z matematyki
Anna Witaszczyk
14
Oznaczając przez N część całkowitą liczby
ε
1
, zauważamy, że dla wszystkich n>N
nierówność jest spełniona.
Ciąg mający granicę skończoną równą g nazywamy
ciągiem zbieżnym do liczby g.
Granicę zdefiniowaną równoważnością (4.3.1) nazywa się często
granicą właściwą.
Ponadto mamy poniższe definicje
granic niewłaściwych.
Ciąg ma
granicę niewłaściwą „plus nieskończoność” (jest rozbieżny do
∞
+
) wtedy
i tylko wtedy, gdy prawie wszystkie jego wyrazy są większe od dowolnej liczby rzeczywistej:
(4.3.2)
M
a
a
n
N
n
N
R
M
n
n
>
∀
∃
∀
⇔
+∞
=
>
∈
∞
→
lim
.
Ciąg ma
granicę niewłaściwą „minus nieskończoność” (jest rozbieżny do
∞
−
)
wtedy i tylko wtedy, gdy prawie wszystkie jego wyrazy są mniejsze od dowolnej liczby
rzeczywistej:
(4.3.3)
M
a
a
n
N
n
N
R
M
n
n
<
∀
∃
∀
⇔
+∞
=
>
∈
∞
→
lim
.
Podobnie jak w przykładzie 4.3.1. wykazuje się istnienie następujących granic:
(4.3.4)
c
c
n
=
∞
→
lim
,
R
c
∈
,
(ciąg stały),
(4.3.5)
1
lim
=
∞
→
n
n
n
,
(4.3.6)
1
lim
=
∀
∞
→
>
n
n
R
a
a
,
(4.3.7)
>
∞
+
=
<
<
−
=
∞
→
1
,
1
,
1
1
1
,
0
lim
q
q
q
q
n
n
,
(4.3.8)
1
1
sin
lim
=
∞
→
n
n
n
.
Ponadto istnieją ciągi, które nie mają granicy właściwej ani niewłaściwej. Przykładem
takiego ciągu jest ciąg o wyrazie ogólnym
( )
n
n
a
1
−
=
.
4. WŁASNOŚCI GRANICY
Badanie, czy dana liczba jest granicą ciągu, polegające na rozwiązaniu nierówności
ε
<
−
g
a
n
, nie ma na ogół zastosowania praktycznego. Ten sposób postępowania pozwala
jedynie stwierdzić, czy z góry zadana liczba jest, czy nie jest granicą ciągu. Przy badaniu
zbieżności ciągów będziemy opierać się na pewnych twierdzeniach dotyczących granic
ciągów.
Twierdzenie 4.4.1. Ciąg ma co najwyżej jedną granicę.
Twierdzenie 4.4.2. Ciąg zbieżny jest ograniczony.
Twierdzenie 4.4.3. Jeżeli ciąg jest zbieżny, to każdy podciąg tego ciągu jest zbieżny.

Wykłady z matematyki
Anna Witaszczyk
15
Twierdzenie 4.4.4. Iloczyn ciągu zbieżnego do zera przez ciąg ograniczony jest
ciągiem zbieżnym do zera.
Twierdzenie 4.4.5. Każdy ciąg monotoniczny i ograniczony jest zbieżny.
Twierdzenie 4.4.6. (TWIERDZENIE O TRZECH CIĄGACH) Jeśli dla dwóch
ciągów
{ }
n
a
i
{ }
n
c
zachodzi
g
c
a
n
n
n
n
=
=
∞
→
∞
→
lim
lim
, natomiast wyrazy ciągu
{ }
n
b
spełniają
(począwszy od pewnego n) warunek
n
n
n
c
b
a
≤
≤
, to również
g
b
n
n
=
∞
→
lim
.
Twierdzenie
4.4.7.
(O
DZIAŁANIACH
ARYTMETYCZNYCH
NA
GRANICACH WŁAŚCIWYCH) Jeżeli
a
a
n
n
=
∞
→
lim
i
b
b
n
n
=
∞
→
lim
, to
(
)
b
a
b
a
n
n
n
±
=
±
∞
→
lim
,
(
)
ab
b
a
n
n
n
=
∞
→
lim
,
b
a
b
a
n
n
n
=
∞
→
lim
jeśli
0
≠
b
oraz każde
0
≠
n
b
.
Twierdzenie 4.4.8. Jeżeli
a
a
n
n
=
∞
→
lim
i
0
≥
n
a
, to
α
α
a
a
n
n
=
∞
→
lim
, gdzie
{ }
0
\
R
∈
α
.
Twierdzenie 4.4.9. Jeżeli
0
>
n
a
i
0
lim
>
=
∞
→
a
a
n
n
, to
a
a
p
n
p
n
log
log
lim
=
∞
→
.
Twierdzenie 4.4.10. Jeżeli
a
a
n
n
=
∞
→
lim
, to
a
a
n
n
α
α
=
∞
→
lim
,
gdy
0
>
α
.
Przy wyznaczaniu granic ciągów rozbieżnych do
∞
+
lub
∞
−
granice występujące w
twierdzeniu 4.4.7 trzeba każdorazowo rozważać oddzielnie. Będziemy korzystać z twierdzeń,
które można zapisać symbolicznie w następujący sposób:
4.4.11.
( )
+∞
=
∞
+
+
∞
+
.
4.4.12.
( ) ( )
−∞
=
∞
−
+
∞
−
.
4.4.13.
( ) ( )
−∞
=
∞
+
−
∞
−
.
4.4.14.
( )( )
+∞
=
∞
+
∞
+
.
4.4.15.
( )( ) ( )( )
−∞
=
∞
+
∞
−
=
∞
−
∞
+
4.4.16.
( )( )
+∞
=
∞
−
∞
−
.
4.4.17.
+∞
=
+
+∞
=
∞
+
a
a
.
4.4.18.
−∞
=
+
−∞
=
∞
−
a
a
.
4.4.19.
Jeżeli a>0, to
( ) ( )
+∞
=
∞
+
=
∞
+
a
a
,
( ) ( )
−∞
=
∞
−
=
∞
−
a
a
,
+∞
=
∞
+
a
,
−∞
=
∞
−
a
.
4.4.20.
Jeżeli a<0, to
( ) ( )
−∞
=
∞
+
=
∞
+
a
a
,
( ) ( )
+∞
=
∞
−
=
∞
−
a
a
,
−∞
=
∞
+
a
,
+∞
=
∞
−
a
.

Wykłady z matematyki
Anna Witaszczyk
16
4.4.21.
0
=
∞
−
=
∞
+
a
a
.
4.4.22.
Jeżeli
0
lim
≠
=
∞
→
a
a
n
n
,
0
lim
=
∞
→
n
n
b
i
0
>
n
b
, to
<
∞
−
>
∞
+
=
=
+
∞
→
.
0
,
,
0
,
0
lim
a
gdy
a
gdy
a
b
a
n
n
n
4.4.23.
Jeżeli
0
lim
≠
=
∞
→
a
a
n
n
,
0
lim
=
∞
→
n
n
b
i
0
<
n
b
, to
>
∞
−
<
∞
+
=
=
−
∞
→
.
0
,
,
0
,
0
lim
a
gdy
a
gdy
a
b
a
n
n
n
Na przykład twierdzenie 4.4.15. czytamy: iloczyn ciągu rozbieżnego do
∞
+
i
rozbieżnego do
∞
−
jest ciągiem rozbieżnym do
∞
−
.
Wśród podanych twierdzeń nie ma twierdzenia, które orzekałoby o granicy ciągu
będącego różnicą ciągów rozbieżnych do
∞
+
. Otóż ciąg taki może być ciągiem zbieżnym
lub nie. Nie można tej kwestii rozstrzygnąć ogólnie. Trudność taka występuje nie tylko w
przypadku różnicy ciągów rozbieżnych do
∞
+
. Wszystkie tego rodzaju przypadki dadzą się
wyrazić symbolicznie i noszą one nazwę
wyrażeń nieoznaczonych. Są to wyrażenia typu:
0
0
,
∞
∞
,
( )
∞
+
−
∞
+
,
∞
⋅
0
,
∞
1 ,
0
0 ,
0
∞
.
5. LICZBA EULERA
Liczbą Eulera nazywa się granicę ciągu
n
n
n
a
+
=
1
1
. Granica ta jest liczbą
niewymierną, którą oznaczamy symbolem e:
(4.5.1)
72
,
2
...
7182818
,
2
1
1
lim
≈
=
+
=
∞
→
n
n
n
e
.
Liczba e jest podstawą
logarytmu naturalnego
x
x
y
e
log
ln
=
=
,
x>0,
często stosowanego, ze względu na proste własności, w analizie matematycznej. Równie
często spotykać się będziemy z funkcją wykładniczą
x
e
y
=
.
Zauważmy, że ciąg
n
n
n
a
+
=
1
1
jest ciągiem potęg naturalnych, których podstawy
tworzą ciąg dążący do liczby 1. Mamy tu do czynienia z nieoznaczonością typu
∞
1 .
Twierdzenie 4.5.1. Jeżeli
±∞
=
∞
→
n
n
b
lim
, to
(4.5.2)
e
b
n
b
n
n
=
+
∞
→
1
1
lim
.
Alternatywnie: jeżeli
0
lim
=
∞
→
n
n
b
, to
(4.5.3)
(
)
e
b
n
b
n
n
=
+
∞
→
1
1
lim
.

Wykłady z matematyki
Anna Witaszczyk
17
V. FUNKCJA JEDNEJ ZMIENNEJ
1. DEFINICJA FUNKCJI, WYKRES FUNKCJI
Funkcją określoną w zbiorze X nazywamy każde przyporządkowanie f elementom
zbioru X elementów zbioru Y. Zbiór X nazywamy dziedziną funkcji, zbiór Y – zbiorem
wartości funkcji. Jeżeli każdy element
Y
y
∈
został przyporządkowany pewnemu
elementowi
X
x
∈
, to mówimy, że przyporządkowanie f odwzorowuje zbiór X na zbiór Y.
Zapisujemy to symbolicznie:
( )
x
f
y
Y
X
f
X
x
Y
y
na
=
∃
∀
⇔
→
∈
∈
:
.
Wykresem funkcji
Y
X
f
→
:
nazywamy zbiór wszystkich punktów (x,y) przestrzeni
R
2
, których współrzędne spełniają warunki:
X
x
∈
i
( )
x
f
y
=
.
Punkt
(
)
0
0
0
,
y
x
P
jest punktem wykresu funkcji f wtedy i tylko wtedy, gdy
X
x
∈
0
i
( )
0
0
x
f
y
=
. Równanie
( )
x
f
y
=
nazywamy równaniem linii stanowiącej wykres funkcji f.
Cztery następujące funkcje:
1.
funkcję stałą
( )
c
x
f
=
, gdzie c oznacza dowolną liczbę rzeczywistą,
2.
funkcję liniową
( )
x
x
f
=
,
3.
funkcję wykładniczą
( )
x
a
x
f
=
, gdzie a jest dowolną liczbą rzeczywistą dodatnią
różną od jedności,
4.
funkcję trygonometryczną
( )
x
x
f
sin
=
,
będziemy nazywać
podstawowymi funkcjami elementarnymi.
Na funkcjach tych możemy wykonywać działania arytmetyczne i na tej drodze
otrzymywać „nowe” funkcje, z kolei na tych „nowych” funkcjach przez działania
arytmetyczne otrzymujemy jeszcze obszerniejszy zbiór funkcji.
Mnożąc
x
x
⋅
otrzymujemy funkcję
( )
2
x
x
f
=
. Mnożąc
x
x
⋅
2
otrzymujemy
( )
3
x
x
f
=
. W ten sposób można otrzymać dowolną
funkcję potęgową
( )
n
x
x
f
=
. Mnożąc
funkcję potęgową przez stałą c otrzymujemy zbiór
jednomianów postaci
( )
n
cx
x
f
=
. Przez
dodanie do siebie jednomianów
n
n
x
c
,
1
1
−
−
n
n
x
c
,
2
2
−
−
n
n
x
c
, …,
x
c
1
,
0
c otrzymujemy nowy typ
funkcji, tzw.
wielomian stopnia n
( )
0
1
1
1
...
c
x
c
x
c
x
c
x
f
n
n
n
n
+
+
+
+
=
−
−
,
0
≠
n
c
.
Zgodnie z wprowadzoną terminologią funkcja liniowa
( )
b
ax
x
f
+
=
,
0
≠
a
jest
wielomianem stopnia pierwszego, funkcja stała
( )
c
x
f
=
jest wielomianem stopnia zerowego.
Dzielenie wielomianów przez siebie prowadzi do nowego typu funkcji, tzw.
funkcji
wymiernych.
Przykład 5.1.1. Funkcja
( )
x
x
x
f
x
sin
4
2
3
2
−
⋅
=
należy do klasy funkcji elementarnych,
ponieważ powstała na drodze działań arytmetycznych na funkcjach podstawowych. Nie jest
to funkcja wymierna, bo nie jest ilorazem wielomianów.
Przez działania arytmetyczne na funkcjach podstawowych nie można wygenerować
wszystkich znanych nam funkcji. Do tego potrzebna jest jeszcze operacja składania funkcji
oraz możliwość tworzenia funkcji odwrotnych.

Wykłady z matematyki
Anna Witaszczyk
18
2. FUNKCJE ZŁOśONE
Niech dane będą funkcje
Y
X
f
na
→
:
i
Z
Y
g
→
:
. Funkcje f i g wyznaczają nową
funkcję
Z
X
h
→
:
, określoną następująco:
( )
( )
[ ]
x
f
g
x
h
z
=
=
dla każdego x.
Funkcja h nazywa się
superpozycją (złożeniem) f i g, przy czym f jest funkcją wewnętrzną,
g zaś –
zewnętrzną.
Przykład 5.2.1. Funkcja
( )
3
2
+
=
x
x
h
jest funkcją złożoną funkcji
( )
y
y
g
=
(zewnętrznej) i
( )
3
2
+
=
=
x
x
f
y
(wewnętrznej).
Przykład 5.2.2. Jeżeli
( )
x
x
f
sin
=
i
( )
1
2
+
=
x
x
g
, to możemy otrzymać z nich dwie
funkcje złożone:
( )
[ ]
(
)
1
sin
2
+
=
x
x
g
f
i
( )
[
]
1
sin
2
+
=
x
x
f
g
.
Przykład ten pokazuje, że składanie funkcji nie jest przemienne.
3. FUNKCJE ODWROTNE
Operację odwracania funkcji można stosować tylko dla funkcji różnowartościowych.
Funkcja
( )
x
f
określona na zbiorze X jest
funkcją różnowartościową, jeśli dla
każdych dwóch różnych elementów
1
x
i
2
x
spełniony jest warunek
( ) ( )
2
1
x
f
x
f
≠
, tzn.:
(5.3.1)
( ) ( )
2
1
2
1
,
2
1
x
f
x
f
x
x
X
x
x
≠
⇒
≠
∀
∈
.
Warunek (5.3.1) jest równoważny swojej kontrapozycji:
(5.3.2)
( ) ( )
2
1
2
1
,
2
1
x
x
x
f
x
f
X
x
x
=
⇒
=
∀
∈
.
Jeśli funkcja
( )
x
f
jest różnowartościowa, to jej wykres ma co najwyżej jeden punkt
wspólny z każdą prostą równoległą do osi OX.
Spośród podstawowych funkcji elementarnych jedynie funkcja liniowa i funkcja
wykładnicza są funkcjami różnowartościowymi.
Niech funkcja
( )
x
f
będzie określona na zbiorze X i różnowartościowa. Niech Y
będzie zbiorem wartości tej funkcji. Wtedy każdej wartości y ze zbioru Y odpowiada jedna i
tylko jedna wartość x ze zbioru X. Zatem przyporządkowanie elementom zbioru Y elementów
zbioru X jest także funkcją.
Niech
( )
x
f
będzie funkcją różnowartościową i niech
Y
X
f
na
→
:
. Funkcję
X
Y
g
→
:
nazywamy
funkcją odwrotną do
Y
X
f
→
:
, jeżeli dla każdego x zachodzi równość
(5.3.3)
( )
( )
[ ]
x
x
f
g
y
g
=
=
.
Najczęściej funkcję odwrotną do f oznaczamy symbolem
1
−
f
.
Ponieważ wykres funkcji f stanowi zbiór par uporządkowanych, to wykres funkcji
odwrotnej otrzymamy, gdy przestawimy w każdej parze kolejność elementów. Widać stąd, że
pojęcie funkcji odwrotnej jest symetryczne: jeśli g jest odwrotna do f, to f jest odwrotna do g.
Wykres funkcji odwrotnej znajdujemy przez odbicie symetryczne względem prostej y=x.

Wykłady z matematyki
Anna Witaszczyk
19
Przykład 5.3.1. Niech f(x)=2x+3. Jest to funkcja różnowartościowa
R
R
f
na
→
:
.
Istnieje więc dla niej funkcja odwrotna. Zgodnie z (5.3.3), z równania y=2x+3 należy
wyznaczyć x:
2
3
2
1
3
2
3
2
−
=
⇔
−
=
⇔
+
=
y
x
y
x
x
y
.
2
3
2
1
−
=
y
x
jest funkcją odwrotną do funkcji
3
2
+
=
x
y
. Ze względów tradycyjnych, a także
ze względu na interpretację geometryczną (wykres) funkcji odwrotnej, oznaczamy jej
argument także symbolem x. Zatem funkcją odwrotną do danej funkcji jest
( )
2
3
2
1
1
−
=
−
x
x
f
.
Przykład 5.3.2. Jeśli funkcja nie jest różnowartościowa, można znaleźć dla niej
funkcję odwrotną przy ograniczeniu do tej części dziedziny, w której ma ona tę własność.
Jeśli
2
x
y
=
, to dla
[
)
+∞
∈
,
0
x
jest to funkcja różnowartościowa i funkcją odwrotną do niej
jest
x
y
=
.
Przykład 5.3.3. Funkcja
x
e
y
=
jest różnowartościowa, istnieje więc dla niej funkcja
odwrotna. Ponieważ
x
y
y
e
x
=
⇔
=
ln
, funkcją odwrotną do
x
e
y
=
jest
x
y
ln
=
, x>0.
Jej wykres otrzymamy jako obraz krzywej
x
e
y
=
w symetrii względem prostej y=x.
Przykład 5.3.4. Funkcja
x
y
sin
=
jest różnowartościowa dla
−
∈
2
,
2
π
π
x
.
Definiujemy:
x
y
y
x
sin
arcsin
=
⇔
=
.
Symbol „arcsiny” czytamy „arkus sinus y”. Po zamianie zmiennych
x
y
arcsin
=
, gdzie
[ ]
1
,
1
−
∈
x
. Zbiorem wartości funkcji jest przedział
−
2
,
2
π
π
. Wykres tej funkcji otrzymamy
jako obraz wykresu funkcji
x
y
sin
=
określonej w przedziale
−
2
,
2
π
π
, w symetrii
względem prostej y=x. Funkcja
x
y
arcsin
=
jest jedną z funkcji cyklometrycznych –
odwrotnych do trygonometrycznych.
5. PODSTAWOWE WŁASNOŚCI FUNKCJI
Określeniem
funkcje monotoniczne obejmujemy funkcje rosnące, niemalejące,
malejące, nierosnące:
Y
X
f
→
:
jest
rosnąca w X
( ) ( )
2
1
2
1
,
2
1
x
f
x
f
x
x
X
x
x
<
⇒
<
∀
⇔
∈
,
Y
X
f
→
:
jest
niemalejąca w X
( ) ( )
2
1
2
1
,
2
1
x
f
x
f
x
x
X
x
x
≤
⇒
<
∀
⇔
∈
,
Y
X
f
→
:
jest
malejąca w X
( ) ( )
2
1
2
1
,
2
1
x
f
x
f
x
x
X
x
x
>
⇒
<
∀
⇔
∈
,
Y
X
f
→
:
jest
nierosnąca w X
( ) ( )
2
1
2
1
,
2
1
x
f
x
f
x
x
X
x
x
≥
⇒
<
∀
⇔
∈
.

Wykłady z matematyki
Anna Witaszczyk
20
Funkcje rosnące i malejące nazywamy ściśle monotonicznymi. Jeżeli zbiór X, w którym
określona jest funkcja, można przedstawić w postaci sumy przedziałów, w których funkcja
jest monotoniczna, to mówimy, że ta funkcja jest przedziałami monotoniczna.
Przykład 5.5.1. Funkcja
3
2
+
=
x
y
jest rosnąca w zbiorze liczb rzeczywistych R.
Jeśli bowiem
2
1
x
x
<
, to
2
1
2
2
x
x
<
i
3
2
3
2
2
1
+
<
+
x
x
, czyli
( ) ( )
2
1
x
f
x
f
<
.
Badanie monotoniczności najczęściej przeprowadza się wykorzystując twierdzenia
dotyczące pochodnej funkcji.
Funkcję
Y
X
f
→
:
nazywamy
parzystą, jeżeli:
( ) ( )
x
f
x
f
X
x
X
x
=
−
∧
∈
−
∀
∈
1
.
Wykres funkcji parzystej jest symetryczny względem osi OY. Parzyste są np. funkcje:
x
y
cos
=
,
2
x
y
=
,
x
y
=
.
Funkcję
Y
X
f
→
:
nazywamy
nieparzystą, jeżeli:
( )
( )
x
f
x
f
X
x
X
x
−
=
−
∧
∈
−
∀
∈
1
.
Wykres funkcji parzystej jest symetryczny względem początku układu współrzędnych.
Nieparzyste są np. funkcje:
x
y
sin
=
,
tgx
y
=
,
x
y
=
.
Funkcję
Y
X
f
→
:
nazywamy
okresową, jeżeli istnieje liczba
0
≠
T
taka, że:
(
)
(
)
(
) ( )
x
f
T
x
f
X
T
x
X
T
x
X
x
=
+
∧
∈
−
∧
∈
+
∀
∈
1
.
T nazywa się
okresem funkcji. Najmniejszy dodatni okres, o ile taki istnieje
nazywamy
okresem podstawowym. Przykładami funkcji okresowych są:
x
y
sin
=
,
x
y
cos
=
- okres podstawowy
π
2 ,
tgx
y
=
,
ctgx
y
=
- okres podstawowy
π
. Funkcja stała,
np. y=2 jest funkcją okresową, przy czym jej okresem jest każda liczba rzeczywista różna od
zera, a okres podstawowy nie istnieje.
VI. GRANICA I CIĄGŁOŚĆ FUNKCJI
1. DEFINICJA GRANICY FUNKCJI
Niech dany będzie punkt x
0
oraz dowolny ciąg x
1
, x
2
, …,x
n
, … punktów należących
do dziedziny D funkcji f(x), różnych od x
0
, zbieżny do x
0
. Każdemu takiemu ciągowi
odpowiada ciąg wartości funkcji: f(x
1
), f(x
2
), …,f(x
n
), …
Niezależnie od tego, czy funkcja f(x) jest określona w punkcie x
0
, czy nie, możemy
badać zachowanie się funkcji przy zbliżaniu się do punktu x
0
. Szczególnie ważne jest
stwierdzenie, czy funkcja w punkcie x
0
ma granicę.
Liczbę g nazywamy
granicą funkcji f(x) w punkcie x
0
, jeżeli dla każdego ciągu
{ }
n
x
argumentów funkcji f zbieżnego do x
0
o wyrazach różnych od x
0
, odpowiadający mu ciąg
( )
{
}
n
x
f
wartości funkcji f jest zbieżny do g:
( )
(
)
( )
(
)
g
x
f
x
x
g
x
f
n
n
x
x
D
x
x
x
n
n
→
⇒
→
∀
⇔
=
≠
∈
→
0
0
0
lim
.

Wykłady z matematyki
Anna Witaszczyk
21
Obliczanie granic funkcji sprowadza się więc do liczenia granic ciągów. Dlatego
twierdzenia dotyczące działań na granicach ciągów są prawdziwe także dla granic funkcji.
Przykład 6.1.1. Niech
( )
1
3
2
+
−
=
x
x
x
f
. Dziedziną tej funkcji jest zbiór liczb
rzeczywistych. Obliczymy granicę funkcji f w punkcie 2. Niech
{ }
n
x
będzie dowolnym
ciągiem liczb rzeczywistych różnych od 2, takim, że
2
lim
=
∞
→
n
n
x
.
( )
(
)
( )
(
)
( )
1
1
6
4
1
3
lim
lim
1
3
lim
1
3
lim
lim
2
2
2
2
2
−
=
+
−
=
+
+
=
+
−
=
+
−
=
∞
→
∞
→
∞
→
→
→
n
n
n
n
n
n
n
x
x
x
x
x
x
x
x
x
f
Liczbę g nazywamy
granicą lewostronną funkcji y=f(x) w punkcie x
0
, jeżeli dla
każdego ciągu
{ }
n
x
argumentów funkcji f zbieżnego do x
0
o wyrazach mniejszych od x
0
,
odpowiadający mu ciąg
( )
{
}
n
x
f
wartości funkcji f jest zbieżny do g:
( )
(
)
( )
(
)
g
x
f
x
x
g
x
f
n
n
x
x
D
x
x
x
n
n
→
⇒
→
∀
⇔
=
<
∈
→
−
0
0
0
lim
.
Analogicznie
definiuje
się
granicę
prawostronną.
Wyznaczanie
granic
jednostronnych polega więc na badaniu zachowania się funkcji na lewo i na prawo od punktu
x
0
. Ma to szczególne znaczenie wtedy, gdy w x
0
funkcja nie jest określona lub jest określona
innymi zależnościami na lewo i na prawo od tego punktu. Należy pamiętać, że granica funkcji
w danym punkcie istnieje, gdy granice lewostronna i prawostronna są równe.
Przykład 6.1.2. Rozpatrzmy funkcję
( )
≥
+
<
−
=
4
5
4
1
2
x
dla
x
x
dla
x
x
f
. Funkcja ta na lewo i
na prawo od x
0
=4 jest określona innym wzorem. Dla ciągów o wyrazach x
n
<4 i dążących do 4
( )
(
)
7
1
2
lim
lim
4
=
−
=
∞
→
→
−
n
n
x
x
x
f
, natomiast
( )
(
)
9
5
lim
lim
4
=
+
=
∞
→
→
+
n
n
x
x
x
f
. Zatem granica funkcji f w
punkcie 4 nie istnieje.
Liczbę g nazywamy
granicą funkcji w plus nieskończoności (analogicznie przy
−∞
→
x
), jeżeli dla każdego ciągu
{ }
n
x
rozbieżnego do
∞
+
(
∞
−
) odpowiadający mu ciąg
wartości funkcji
( )
{
}
n
x
f
dąży do g.
Nie wszystkie funkcje posiadają granicę w nieskończoności. Na przykład funkcje
trygonometryczne y=sinx, y=cos, y=tgx, y=ctg nie mają granicy w nieskończoności.
Mówimy, że w punkcie x
0
funkcja ma granicę niewłaściwą równą plus
nieskończoność (
( )
+∞
=
→
x
f
x
x
0
lim
), jeżeli dla każdego ciągu argumentów
{ }
n
x
dążącego do x
0
i
0
x
x
n
≠
ciąg wartości funkcji
( )
{
}
n
x
f
jest rozbieżny do
∞
+
.
Analogicznie określa się granicę f(x) równą
∞
−
, granice niewłaściwe jednostronne oraz
granice niewłaściwe funkcji przy x dążącym do plus lub minus nieskończoności.
2. CIĄGŁOŚĆ FUNKCJI
Funkcję y=f(x) nazywamy
ciągłą w punkcie x
0
wtedy i tylko wtedy, gdy spełnione są
warunki:
1)
f(x) jest określona w x
0
(
D
x
∈
0
),
2)
istnieje granica funkcji w punkcie x
0
,

Wykłady z matematyki
Anna Witaszczyk
22
3)
( ) ( )
0
0
lim
x
f
x
f
x
x
=
→
, tzn. granica funkcji w punkcie x
0
jest równa wartości funkcji w tym
punkcie.
Funkcja jest ciągła w przedziale [a,b], jeżeli jest ciągła w każdym punkcie tego
przedziału.
Intuicyjnie ciągłość funkcji pewnym przedziale oznacza, że krzywa będąca wykresem
funkcji jest linią ciągłą. Punkt nieciągłości natomiast to taki punkt, w którym występuje
„rozerwanie” wykresu.
Niech f będzie funkcją określoną w przedziale [a,b] i taką, że
( ) ( )
b
f
a
f
≠
. Niech y
oznacza dowolną liczbę leżącą między f(a) i f(b). Jeśli funkcja f jest ciągła w przedziale [a,b],
to istnieje w jego wnętrzu takie c, że f(c)=y. Jest to własność funkcji ciągłych, nazywana
własnością Darboux. Zwykle formułuje się ją następująco:
Funkcja f(x) ciągła w przedziale domkniętym przechodzi od jednej wartości do drugiej
przez wszystkie wartości pośrednie.
Zauważmy, że podstawowe funkcje elementarne, czyli y=c, y=x, y=a
x
, y=sinx są
funkcjami ciągłymi na całej osi OX. Każdą inną funkcję można otrzymać z wymienionych w
wyniku skończonej liczby działań (dodawania, odejmowania, mnożenia, dzielenia) i operacji
składania i odwracania. Jeżeli badana funkcja jest określona w punkcie x
0
, to jej ciągłość
można stwierdzić korzystając z następujących twierdzeń:
Twierdzenie 6.2.1. Suma, różnica i iloczyn funkcji ciągłych w danym punkcie są
funkcjami ciągłymi w tym punkcie. Iloraz funkcji f(x) i g(x) ciągłych w punkcie x
0
jest
funkcją ciągłą w tym punkcie, jeśli
( )
0
0
≠
x
g
.
Twierdzenie 6.2.2. Jeśli funkcja z=f(x) jest ciągła w punkcie x
0
i przyjmuje w nim
wartość z
0
=f(x
0
), a funkcja y =g(z) jest ciągła w punkcie z
0
, to funkcja złożona y=g[f(x)] jest
ciągła w x
0
.
Twierdzenie 6.2.3. Funkcja odwrotna względem funkcji ciągłej w pewnym przedziale jest
funkcją ciągłą w tym przedziale.
Przykład 6.2.1. Zbadamy ciągłość funkcji
( )
≥
+
<
=
2
2
3
2
3
x
dla
x
x
dla
x
x
f
.
W przedziale
(
)
2
,
∞
−
funkcja jest ciągła (wielomian), w przedziale
[
)
+∞
,
2
też jest ciągła jako
funkcja liniowa. Należy zbadać ciągłość w punkcie x
0
=2, w którym zmienia się sposób
określenia tej funkcji.
( )
8
lim
lim
3
2
2
=
=
−
−
→
→
x
x
f
x
x
,
( )
(
)
8
2
3
lim
lim
2
2
=
+
=
+
+
→
→
x
x
f
x
x
.
Granica funkcji zatem istnieje i równa się 8. Wartość funkcji f(2)=8. Funkcja jest więc ciągła
w całej dziedzinie.
Przykład 6.2.2. Dana jest funkcja
( )
>
+
≤
+
=
1
4
1
2
2
x
dla
ax
x
dla
x
x
f
.
Ustalimy wartość parametru a, dla którego funkcja jest ciągła.:
( )
(
)
3
2
lim
lim
1
1
=
+
=
+
+
→
→
x
x
f
x
x
,
( )
(
)
4
4
lim
lim
2
1
1
+
=
+
=
+
+
→
→
a
ax
x
f
x
x
.

Wykłady z matematyki
Anna Witaszczyk
23
Aby funkcja miała granicę w punkcie x=1, granice lewo- i prawostronna muszą być równe.
Więc a=-1. Wtedy f(1)=3 i f jest ciągła w tym punkcie. W pozostałych punktach dziedziny f
jest ciągła, ponieważ jest wielomianem.
Na zakończenie podamy jeszcze twierdzenie Cauchy’ego, będące wnioskiem z
własności Darboux.
Twierdzenie 6.2.4. Jeśli f(x) jest określona i ciągła w domkniętym przedziale [a,b] i
na końcach tego przedziału przyjmuje wartości przeciwnych znaków, to wewnątrz przedziału
istnieje taki punkt x
0
, że f(x
0
)=0.
Inaczej mówiąc, jeśli są spełnione założenia twierdzenia, to równanie f(x)=0 na pewno
ma pierwiastek wewnątrz przedziału [a,b].
Przykład 6.2.3. Zbadamy, czy równanie
1
3
2
2
+
=
x
x
x
ma pierwiastek rzeczywisty.
Zbadajmy znak wartości funkcji
( )
1
3
2
2
−
−
=
x
x
x
f
x
dla x=0 i x=1: f(0)=-1, f(1)=1. Zatem,
ponieważ funkcja jest ciągła, równanie ma pierwiastek w przedziale (0,1).
VII. FUNKCJE ELEMENTARNE
Poniżej przedstawiamy ważniejsze klasy funkcji elementarnych.
1. WIELOMIANY
Wielomianem n-tego stopnia (
N
n
∈
) nazywamy funkcję postaci
( )
0
1
1
1
...
a
x
a
x
a
x
a
x
f
n
n
n
n
+
+
+
+
=
−
−
,
gdzie
0
≠
n
a
.
Dziedziną wielomianu jest zbiór wszystkich liczb rzeczywistych. Wyraz wolny a
0
jest rzędną
przecięcia wykresu funkcji z osią OY. Wielomian stopnia pierwszego lub zerowego jest
funkcją liniową. Wykresem tych funkcji jest linia prosta. Wykresem wielomianu drugiego
stopnia, czyli funkcji kwadratowej jest parabola.
Dla n=0 f(x)=c. Wielomian stopnia zerowego jest funkcją stałą. Wykresem jest prosta
równoległa do osi OX, przecinająca oś OY w punkcie c. Gdy c=0 wykres pokrywa się z osią
OX.
Dla n=1 f(x)=ax+b,
0
≠
a
. Gdy współczynnik kierunkowy a jest dodatni, funkcja jest
rosnąca, gdy a<0 funkcja jest malejąca. Funkcja liniowa ma jedno miejsce zerowe
a
b
x
−
=
.
Dla n=2 f(x)=ax
2
+bx+c,
0
≠
a
. Wykres jest parabolą o ramionach skierowanych ku
górze (a>0) lub w dół (a<0) i wierzchołku w punkcie o współrzędnych
−
−
a
a
b
4
,
2
∆∆∆∆
, gdzie
ac
b
4
2
−
=
∆∆∆∆
- wyróżnik trójmianu kwadratowego. Jeżeli
0
<
∆∆∆∆
funkcja nie ma miejsc
zerowych, jeżeli
0
=
∆∆∆∆
funkcja ma jedno miejsce zerowe:
a
b
x
2
−
=
, jeżeli
0
>
∆∆∆∆
funkcja ma
dwa miejsca zerowe:
a
b
x
2
2
,
1
∆∆∆∆
±
−
=
.

Wykłady z matematyki
Anna Witaszczyk
24
2. FUNKCJE WYMIERNE
Funkcją wymierną nazywamy funkcję postaci
( )
( )
( )
x
Q
x
P
x
f
=
,
gdzie P(x) i Q(x) są wielomianami. Funkcja wymierna jest określona tylko dla tych x, dla
których mianownik jest różny od zera, czyli
( )
0
≠
x
Q
.
Przykładami funkcji wymiernych mogą być funkcje, których wykresy są krzywymi
typu
hiperbolicznego:
( )
n
x
a
x
f
=
(
)
0
,
,
0
≠
∈
≠
+
x
N
n
a
,
( )
d
cx
b
ax
x
f
+
+
=
-
funkcja
homograficzna
−
≠
≠
≠
c
d
x
bc
ad
c
,
,
0
.
3. FUNKCJA WYKŁADNICZA
Funkcją wykładniczą nazywamy funkcję postaci
( )
x
a
x
f
=
,
gdzie a>0,
R
x
∈
.
Funkcja wykładnicza nie ma miejsc zerowych, przyjmuje tylko wartości dodatnie
(
0
>
x
a
), dla x=0 przyjmuje wartość 1 (a
0
=1). Dla a>1 funkcja wykładnicza jest rosnąca, a
dla 0<a<1 jest malejąca, oś OX jest jednostronną asymptotą poziomą funkcji wykładniczej.
Jeśli
1
≠
a
, to dla funkcji wykładniczej
( )
x
a
x
f
=
istnieje funkcja odwrotna
+
−
→
R
R
f
:
1
dana zależnością
( )
x
x
f
a
log
1
=
−
.
Często rozważać będziemy funkcję wykładniczą
( )
x
e
x
f
=
, gdzie e oznacza liczbę
Eulera. Ponieważ e>1, więc funkcja ta jest rosnąca. Funkcją do niej odwrotną jest y=lnx.
Dla przypomnienia podajemy podstawowe własności ogólne:
y
x
y
x
a
a
a
+
=
⋅
,
y
x
y
x
a
a
a
−
=
,
x
x
a
a
1
=
−
,
( )
y
x
y
x
a
a
⋅
=
.
4. FUNKCJA LOGARYTMICZNA
Funkcją logarytmiczną nazywamy funkcję postaci
( )
x
x
f
a
log
=
,
gdzie a>0,
1
≠
a
, x>0.
Funkcja logarytmiczna ma jedno miejsce zerowe x=1. Dla a>1 funkcja logarytmiczna
jest rosnąca, a dla 0<a<1 jest malejąca, oś OY jest prawostronną asymptotą poziomą funkcji
logarytmicznej.
Definicja logarytmu:
b
a
c
b
c
a
=
⇔
=
log
, gdzie a>0,
1
≠
a
, b>0.
Podstawowe własności logarytmów:
0
1
log
=
a
1
log
=
a
a
( )
y
x
xy
a
a
a
log
log
log
+
=
y
x
y
x
a
a
a
log
log
log
−
=
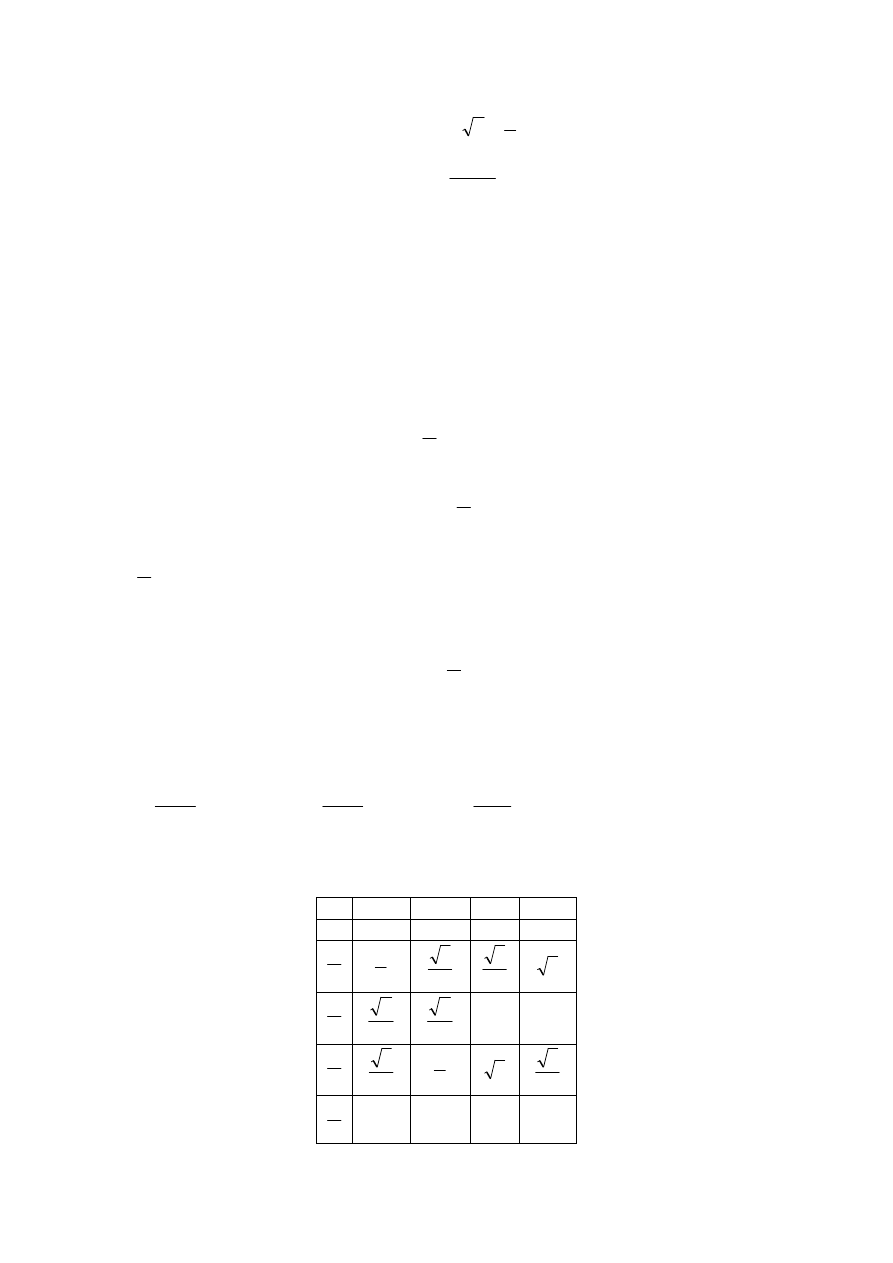
Wykłady z matematyki
Anna Witaszczyk
25
x
y
x
a
y
a
log
log
=
x
n
x
a
n
a
log
1
log
=
Zamiana podstawy logarytmu:
a
x
x
b
b
a
log
log
log
=
.
Logarytm dziesiętny:
x
x
10
log
log
=
.
Logarytm naturalny:
x
x
e
log
ln
=
(e=2,718…).
5. FUNKCJE TRYGONOMETRYCZNE
Funkcja y=sinx. Dziedzina:
R
x
∈
; zbiór wartości:
[ ]
1
.
1
−
∈
y
; okres podstawowy
π
2 ;
funkcja nieparzysta; miejsca zerowe:
π
k
x
=
,
C
k
∈
.
Funkcja y=cosx. Dziedzina:
R
x
∈
; zbiór wartości:
[ ]
1
.
1
−
∈
y
; okres podstawowy
π
2 ; funkcja parzysta; miejsca zerowe:
π
π
k
x
+
=
2
,
C
k
∈
.
Funkcja y=tgx. Dziedzina:
+
∈
π
π
k
R
x
2
\
; zbiór wartości:
R
y
∈
; okres
podstawowy
π
; funkcja nieparzysta; miejsca zerowe:
π
k
x
=
; asymptoty pionowe:
π
π
k
x
+
=
2
,
C
k
∈
; funkcja rośnie przedziałami w całej dziedzinie.
Funkcja y=ctgx. Dziedzina:
{ }
π
k
R
x
\
∈
; zbiór wartości:
R
y
∈
; okres podstawowy
π
; funkcja nieparzysta; miejsca zerowe:
π
π
k
x
+
=
2
; asymptoty pionowe:
π
k
x
=
,
C
k
∈
;
funkcja maleje przedziałami w całej dziedzinie.
Podstawowe wzory:
1
cos
sin
2
2
=
+
α
α
1
=
α
α
ctg
tg
α
α
α
cos
sin
=
tg
α
α
α
sin
cos
=
ctg
α
α
ctg
tg
1
=
α
α
α
cos
sin
2
2
sin
=
α
α
α
2
2
sin
cos
2
cos
−
=
Wybrane dokładne wartości funkcji trygonometrycznych
α
α
sin
α
cos
α
tg
α
ctg
0
0
1
0
-
6
π
2
1
2
3
3
3
3
4
π
2
2
2
2
1
1
3
π
2
3
2
1
3
3
3
2
π
1
0
-
0
Wykłady z matematyki
Anna Witaszczyk
26
6. FUNKCJE CYKLOMETRYCZNE (KOŁOWE)
Funkcje cyklometryczne to funkcje odwrotne do funkcji trygonometrycznych. Są one
określone
w
pewnych
przedziałach,
w
których
funkcje
trygonometryczne
są
różnowartościowe.
Funkcja y=arcsinx (czytamy: arkus sinus x). Jest to funkcja odwrotna do funkcji
y=sinx w przedziale
−
2
,
2
π
π
. Z określenia funkcji odwrotnej wynika, że arcsinx jest takim
kątem z przedziału
−
2
,
2
π
π
, którego sinus równa się x. Na przykład
2
1
arcsin
π
=
bo
1
2
sin
=
π
,
4
2
2
arcsin
π
=
bo
2
2
4
sin
=
π
,
4
)
2
2
arcsin(
π
−
=
−
bo
2
2
)
4
sin(
−
=
−
π
.
Dziedzina:
[ ]
1
.
1
−
∈
x
; zbiór wartości:
−
∈
2
,
2
π
π
y
; funkcja rosnąca, nieparzysta; miejsce
zerowe: x=0.
Funkcja y=arccosx (czytamy: arkus cosinus x). Jest to funkcja odwrotna do funkcji
y=cosx w przedziale
[ ]
π
,
0
. Wartością funkcji y=arccosx jest taki kąt z przedziału
[ ]
π
,
0
,
którego cosinus równa się x. Na przykład
2
0
arccos
π
=
bo
0
2
cos
=
π
,
3
2
1
arccos
π
=
bo
2
1
3
cos
=
π
,
0
1
arccos
=
bo
1
0
cos
=
,
π
=
−
)
1
arccos(
bo
1
cos
−
=
π
.
Dziedzina:
[ ]
1
.
1
−
∈
x
; zbiór wartości:
[ ]
π
.
0
∈
y
; funkcja malejąca; miejsce zerowe: x=1.
Funkcja y=arctgx. Jest to funkcja odwrotna do funkcji y=tgx w przedziale
−
2
,
2
π
π
.
Wartością funkcji y=arctgx jest taki kąt z przedziału
−
2
,
2
π
π
, którego tangens równa się x.
Na przykład
4
1
π
=
arctg
bo
1
4
=
π
tg
,
0
0
=
arctg
bo
0
0
=
tg
,
4
)
1
(
π
−
=
−
arctg
bo
1
)
4
(
−
=
−
π
tg
.

Wykłady z matematyki
Anna Witaszczyk
27
Dziedzina:
R
x
∈
; zbiór wartości:
−
∈
2
,
2
π
π
y
; funkcja rosnąca, nieparzysta; miejsce
zerowe: x=0; asymptoty poziome jednostronne:
2
π
−
=
y
(lewostronna),
2
π
=
y
(prawostronna).
Funkcja y=arcctgx. Jest to funkcja odwrotna do funkcji y=ctg w przedziale
( )
π
,
0
.
Wartością funkcji y=arcctgx jest taki kąt z przedziału
( )
π
,
0
, którego cotangens równa się x.
Na przykład
2
0
π
=
arcctg
bo
0
2
=
π
ctg
,
4
1
π
=
arcctg
bo
1
4
=
π
ctg
,
6
3
π
=
arcctg
bo
3
6
=
π
ctg
.
Dziedzina:
R
x
∈
; zbiór wartości:
( )
π
,
0
∈
y
; funkcja malejąca; brak miejsc zerowych;
asymptoty poziome jednostronne:
0
=
y
(lewostronna),
π
=
y
(prawostronna).
VIII. POCHODNA FUNKCJI
1. DEFINICJA POCHODNEJ FUNKCJI
Niech f będzie funkcją określoną w przedziale (a,b) i niech
( )
b
a
x
,
0
∈
. Nadajmy
argumentowi x
0
przyrost h dodatni lub ujemny tak, aby
( )
b
a
h
x
,
0
∈
+
. Przyrostowi h (inne
oznaczenie:
x
∆∆∆∆
) argumentu x
0
odpowiada przyrost wartości funkcji
(
) ( )
0
0
x
f
h
x
f
−
+
(ozn.
również:
f
∆∆∆∆
,
y
∆∆∆∆
).
Ilorazem różnicowym funkcji f w punkcie x
0
nazywamy stosunek
(
) ( )
h
x
f
h
x
f
0
0
−
+
.
Iloraz różnicowy nazywamy też
przeciętnym przyrostem funkcji w przedziale
[
]
h
x
x
+
0
0
,
,
tzn. przypadającym na jednostkę przyrostu zmiennej niezależnej.
Przykład 8.1.1. Przyrost przeciętny funkcji stałej f(x)=c jest równy zeru.
Przykład 8.1.2. Iloraz różnicowy funkcji liniowej f(x)=ax+b,
0
≠
a
jest równy:
(
) ( )
(
)
[
] [
]
a
h
ah
h
b
ax
b
ah
ax
h
b
ax
b
h
x
a
h
x
f
h
x
f
=
=
−
−
+
+
=
+
−
+
+
=
−
+
0
0
0
0
0
0
.
Przyrost przeciętny funkcji liniowej jest więc stały, niezależny od punktu x
0
i od przyrostu h
nadawanego zmiennej.
Pochodną funkcji f w punkcie x
0
nazywamy granicę ilorazu różnicowego przy h
dążącym do zera, tzn.
( )
(
) ( )
h
x
f
h
x
f
x
f
h
0
0
0
0
lim
'
−
+
=
→
,
jeśli ta granica istnieje.

Wykłady z matematyki
Anna Witaszczyk
28
Chcąc znaleźć pochodną
( )
0
' x
f
funkcji f(x) w punkcie x
0
, należy więc obliczyć jej
iloraz różnicowy, a następnie wyznaczyć jego granicę.
Przykład 8.1.3. Obliczmy pochodną funkcji
( )
x
x
x
f
3
2
2
+
=
w punkcie x
0
=1:
( )
(
) ( )
(
)
(
)
(
)
(
)
9
7
2
lim
7
2
lim
7
2
lim
5
1
3
1
2
lim
1
1
lim
1
'
0
0
2
0
2
0
0
=
+
=
+
=
=
+
=
−
+
+
+
=
−
+
=
→
→
→
→
→
h
h
h
h
h
h
h
h
h
h
h
f
h
f
f
h
h
h
h
h
Zauważmy, że skoro pochodna funkcji jest granicą ilorazu różnicowego, to pochodna
ta nie będzie istnieć wtedy, gdy ta granica nie będzie określona. Jak pamiętamy, granica w
punkcie istnieje wtedy, gdy granice lewo- i prawostronna w punkcie są równe. Jeśli nie
zachodzi równość granic jednostronnych ilorazów różnicowych funkcji w punkcie x
0,
można
zdefiniować pochodne jednostronne w tym punkcie według wzorów:
( )
( )
(
) ( )
h
x
f
h
x
f
x
f
h
0
0
0
0
lim
'
−
+
=
−
→
−
- pochodna lewostronna,
( )
( )
(
) ( )
h
x
f
h
x
f
x
f
h
0
0
0
0
lim
'
−
+
=
+
→
+
- pochodna prawostronna.
Przykład 8.1.4. Zbadamy istnienie pochodnej funkcji
( )
x
x
f
=
w punkcie x
0
=0.
Funkcję f(x) można oczywiście zapisać w następującej postaci:
( )
<
−
≥
=
0
0
x
gdy
x
x
gdy
x
x
f
.
Ponieważ na lewo i prawo od punktu x
0
=0 funkcja opisana jest innym wzorem, konieczne jest
tworzenie innych ilorazów różnicowych w zależności od tego, czy h jest większe czy
mniejsze od zera.
Dla h<0 mamy
( )
( )
( ) ( )
1
0
lim
0
lim
0
'
0
0
−
=
−
−
=
−
=
−
−
→
→
−
h
h
h
f
h
f
f
h
h
.
Dla h>0 otrzymamy
( )
( )
( ) ( )
1
0
lim
0
lim
0
'
0
0
=
−
=
−
=
−
+
→
→
+
h
h
h
f
h
f
f
h
h
.
Zatem dla tej funkcji pochodne jednostronne w punkcie x
0
=0 istnieją, a pochodna nie istnieje.
2. FUNKCJA POCHODNA
Niech funkcja f określona w przedziale (a,b) ma w każdym punkcie tego przedziału
pochodną f’(x). Funkcję, określoną w przedziale (a,b) w ten sposób, że jej wartościami są
liczby f’(x), nazywamy funkcją
pochodną funkcji f i oznaczamy symbolem f’(x). Symbol ten
ma więc podwójne znaczenie. Na ogół zamiast funkcja pochodna mówimy pochodna i z
kontekstu wynika, czy chodzi o pochodną w punkcie danej funkcji, czy o funkcję pochodną.
Dla oznaczenia pochodnej funkcji f(x) będziemy używać symbolu
f’(x) lub
( )
dx
x
df
,
a dla oznaczenia, że pochodna została obliczona w punkcie x
0
, symbolu

Wykłady z matematyki
Anna Witaszczyk
29
f’(x
0
) lub
( )
0
x
x
dx
x
df
=
.
Działanie
polegające
na
obliczaniu
pochodnej
danej
funkcji
nazywamy
różniczkowaniem. Zamiast mówić: znaleźć pochodną funkcji, mówi się: zróżniczkować
funkcję. O funkcji, która w każdym punkcie przedziału ma pochodną, mówimy, że jest w tym
przedziale różniczkowalna.
Nasuwa się pytanie, jakie funkcje są różniczkowalne. Różniczkowalne są funkcje
elementarne oraz funkcje otrzymane przez dodawanie, odejmowanie, mnożenie i dzielenie
oraz operacje składania i odwracania funkcji elementarnych. Ponadto:
8.2.1. jeśli funkcja f(x) nie jest ciągła w x
0
, to w punkcie x nie istnieje pochodna funkcji f;
8.2.2. z faktu, że funkcja jest ciągła w punkcie x
0
, nie wynika, że jest w tym punkcie
różniczkowalna (patrz przykład 8.1.4).
Zauważmy, że, jako kontrapozycja twierdzenia 8.2.1, prawdziwe jest następujące twierdzenie:
jeśli funkcja jest różniczkowalna w punkcie x
0
, to jest w tym punkcie ciągła.
Wzory podstawowych funkcji pochodnych
(8.2.1)
( )
0
'
=
c
,
(8.2.2)
( )
1
−
=
′
α
α
α
x
x
,
R
∈
α
.
Ze wzoru (8.2.2):
( )
x
x
2
1
=
′
=
2
1
α
,
2
1
1
x
x
−
=
′
(
)
1
−
=
α
.
(8.2.3)
( )
a
a
a
x
x
ln
=
′
,
a>0.
Ze wzoru (8.2.3):
( )
x
x
e
e
=
′
.
(8.2.4)
(
)
a
x
x
a
ln
1
log
=
′
,
( ) (
)
+∞
∪
∈
,
1
1
,
0
a
.
Ze wzoru (8.2.4):
( )
x
x
1
ln
=
′
.
(8.2.5)
(
)
x
x
cos
sin
=
′
,
(8.2.6)
(
)
x
x
sin
cos
−
=
′
,
(8.2.7)
( )
x
tgx
2
cos
1
=
′
,
(8.2.8)
( )
x
ctgx
2
sin
1
−
=
′
,
(8.2.9)
(
)
2
1
1
arcsin
x
x
−
=
′
,
(8.2.10)
(
)
2
1
1
arccos
x
x
−
−
=
′
,
Wykłady z matematyki
Anna Witaszczyk
30
(8.2.11)
(
)
2
1
1
x
arctgx
+
=
′
,
(8.2.12)
(
)
2
1
1
x
arcctgx
+
−
=
′
.
Uwaga! W powyższych wzorach pominięto założenia dotyczące zmiennej x.
Reguły różniczkowania
Niech funkcje f(x) i g(x) mają pochodne f’(x) i g’(x).
Twierdzenie 8.2.1. Pochodna iloczynu stałej c przez funkcję f(x) jest równa
iloczynowi stałej przez pochodną funkcji f(x):
(8.2.13)
( )
[
]
( )
x
cf
x
cf
'
=
′
.
Twierdzenie 8.2.2. Pochodna sumy (różnicy) funkcji f(x) i g(x) jest równa sumie
(różnicy pochodnych funkcji f(x) i g(x):
(8.2.14)
( ) ( )
[
]
( )
( )
x
g
x
f
x
g
x
f
'
'
±
=
′
±
.
Twierdzenie 8.2.3. Pochodna iloczynu funkcji f(x)g(x) wyraża się wzorem:
(8.2.15)
( ) ( )
[
]
( ) ( ) ( ) ( )
x
g
x
f
x
g
x
f
x
g
x
f
'
'
+
=
′
.
Twierdzenie 8.2.4. Jeśli
( )
0
≠
x
g
, to istnieje pochodna ilorazu
( )
( )
x
g
x
f
i wyraża się
wzorem:
(8.2.16)
( )
( )
( ) ( ) ( ) ( )
( )
x
g
x
g
x
f
x
g
x
f
x
g
x
f
2
'
'
−
=
′
.
O różniczkowaniu funkcji złożonej orzeka poniższe twierdzenie.
Twierdzenie 8.2.4. Jeżeli funkcja z=g(x) ma pochodną w punkcie x, a funkcja y=f(z)
ma pochodną w punkcie z=g(x), to funkcja złożona f[g(x)] ma w punkcie x pochodną
określoną wzorem:
(8.2.17)
( )
[ ]
{
}
( )
[ ]
( )
x
g
x
g
f
x
g
f
'
'
=
′
.
Przykład
8.2.1.
Wyznaczymy
pochodną
funkcji
( )
.
1
4
2
3
3
5
+
−
+
=
x
x
x
x
f
Skorzystamy z tw. 8.2.2, 8.2.1 i wzorów (8.2.2), (8.2.1).
( )
4
6
15
)'
(
4
)'
(
2
)'
(
3
)'
1
(
)'
4
(
)'
2
(
)'
3
(
'
2
4
)
2
.
2
.
8
(
3
5
)
1
.
2
.
8
(
),
13
.
2
.
8
(
3
5
)
14
.
2
.
8
(
−
+
=
−
+
=
+
−
+
=
x
x
x
x
x
x
x
x
x
f
.
Przykład 8.2.2. Pochodną funkcji
( )
x
x
f
x
sin
3
=
policzymy opierając się na tw.
8.2.3:
( )
x
x
x
x
x
f
x
x
x
x
cos
3
sin
3
ln
3
)'
(sin
3
sin
)'
3
(
'
)
5
.
2
.
8
(
),
3
.
2
.
8
(
)
15
.
2
.
8
(
+
=
+
=
.
Przykład 8.2.3. Pochodną
( )
3
x
x
f
=
otrzymujemy ze wzoru (8.2.2):

Wykłady z matematyki
Anna Witaszczyk
31
( )
3
2
3
2
3
2
1
3
1
)
2
.
2
.
8
(
3
1
3
1
3
1
3
1
3
1
)'
(
'
x
x
x
x
x
x
f
=
=
=
=
=
−
−
.
Przykład 8.2.4. Pochodną
( )
x
x
x
f
ln
1
ln
−
=
liczymy według tw. 8.2.4:
( )
2
2
2
)
16
.
2
.
8
(
)
ln
1
(
1
)
ln
1
(
)
1
(
ln
)
ln
1
(
1
)
ln
1
(
)'
ln
1
(
ln
)
ln
1
(
)'
(ln
'
x
x
x
x
x
x
x
x
x
x
x
x
x
f
−
=
−
−
−
−
=
−
−
−
−
=
.
Przykład 8.2.5. Pochodną funkcji złożonej
( )
x
e
x
f
cos
=
liczymy, zgodnie z tw. 8.2.4,
mnożąc pochodną funkcji zewnętrznej (e
x
) przez pochodną funkcji wewnętrznej (cosx):
( )
x
x
x
x
xe
x
e
x
e
e
x
f
cos
cos
cos
)
17
.
2
.
8
(
cos
sin
)
sin
(
)'
(cos
)'
(
'
−
=
−
=
=
=
.
Pochodna funkcji postaci y=f(x)
g(x)
. Ponieważ zmienia się zarówno podstawa potęgi,
jak i jej wykładnik, nie jest to ani funkcja wykładnicza, ani potęgowa. Chcąc policzyć
pochodną złożonej funkcji tej postaci, należy logarytmować obustronnie wyrażenie y=f(x)
g(x)
,
a następnie zapisać je w postaci funkcji wykładniczej o podstawie e:
(8.2.18)
( )
( )
( ) ( )
( )
( )
x
f
x
g
x
g
e
y
x
f
x
g
y
x
f
y
ln
ln
ln
ln
ln
=
⇒
=
⇒
=
,
a następnie skorzystać z tw. 8.2.4 i 8.2.3.
Przykład 8.2.6. Pochodna funkcji
( )
x
x
x
f
3
=
jest równa:
( )
[
]
)
1
(ln
3
)
1
(ln
3
)
3
ln
3
(
)
1
3
ln
3
(
)'
(ln
3
ln
)'
3
(
)'
ln
3
(
)'
(
)'
(
'
3
ln
3
ln
3
ln
3
ln
3
)
15
.
2
.
8
(
ln
3
)
17
.
2
.
8
(
ln
3
3
+
=
+
=
+
=
+
=
=
+
=
=
=
=
x
x
x
e
x
e
x
x
x
e
x
x
x
x
e
x
x
e
e
x
x
f
x
x
x
x
x
x
x
x
x
x
x
x
x
x
Przykład 8.2.7. Obliczmy pochodną funkcji
( ) (
)
x
x
x
f
3
cos
sin
=
. Ponieważ
( )
x
s
e
x
f
sin
ln
3
cos
=
, otrzymujemy:
( )
[
]
+
−
=
=
+
=
=
x
x
x
x
x
e
x
x
x
x
e
x
x
e
x
f
x
s
x
s
x
s
sin
cos
3
cos
sin
ln
3
sin
3
)'
sin
(ln
3
cos
sin
ln
)'
3
(cos
)'
sin
ln
3
(cos
'
sin
ln
3
cos
sin
ln
3
cos
sin
ln
3
cos
.
Przykład 8.2.8. Wyznaczyć pochodną funkcji
( ) ( )
( )
x
x
x
e
x
x
f
ln
ln
2
2
ln
=
=
w punkcie
x
0
=e.
( )
( )
( )
( )
( )
+
=
+
=
x
x
x
x
e
x
x
x
x
x
e
x
f
x
x
x
x
ln
ln
ln
2
ln
1
ln
ln
2
'
ln
ln
2
ln
ln
2
2
.
( )
( )
( )
e
e
e
e
e
e
e
f
e
e
=
+
=
ln
ln
ln
2
'
ln
ln
2
.
3. INTERPRETACJA GEOMETRYCZNA POCHODNEJ
Załóżmy, że dana jest funkcja y=f(x) określona i ciągła w pewnym przedziale i że
punkty x
0
oraz x
0
+h leżą wewnątrz tego przedziału. Oznaczmy przez A punkt o
Wykłady z matematyki
Anna Witaszczyk
32
współrzędnych
( )
(
)
0
0
,
x
f
x
, a przez B punkt o współrzędnych
(
)
(
)
h
x
f
h
x
+
+
0
0
,
. Prostą
przechodzącą przez punkty A i B nazywamy sieczną krzywej y=f(x). Iloraz różnicowy
(
) ( )
h
x
f
h
x
f
0
0
−
+
jest tangensem kąta
β
, który sieczna tworzy z dodatnim kierunkiem osi
OX. Gdy punkt B zbliża się do punktu A, czyli gdy h dąży do zera, to kąt
β
zmierza do kąta
α
, jaki tworzy styczna do krzywej w punkcie x
0
z dodatnim kierunkiem osi OX. Zatem
α
β
tg
tg
h
=
→
0
lim
.
Tangens kąta
α
jest współczynnikiem kierunkowym stycznej do krzywej w punkcie x
0
.
Ponieważ
(
) ( )
( )
0
0
0
0
0
'
lim
lim
x
f
h
x
f
h
x
f
tg
h
h
=
−
+
=
→
→
β
, więc
( )
α
tg
x
f
=
0
'
.
Interpretację geometryczną pochodnej funkcji w punkcie x
0
można zatem
sformułować w następujący sposób:
Jeśli funkcja f(x) ma w punkcie x
0
pochodną, to istnieje
styczna do wykresu funkcji f(x) w punkcie o odciętej x
0
, a współczynnik kierunkowy tej
stycznej jest równy wartości pochodnej funkcji w tym punkcie.
4. RÓśNICZKA FUNKCJI
Oznaczmy dowolnie mały (dodatni lub ujemny) przyrost zmiennej x symbolem dx
(tzn. dx=h).
Jeżeli funkcja f(x) ma w x
0
pochodną, to iloczyn pochodnej przez przyrost zmiennej
niezależnej x nazywamy
różniczką funkcji f w punkcie x
0
przy danym przyroście dx i
oznaczamy symbolem
( )
0
x
df
(8.4.1)
( )
( )
dx
x
f
x
df
0
0
'
=
.
Ponieważ
(
) ( )
( )
0
0
0
0
'
lim
x
f
h
x
f
h
x
f
h
=
−
+
→
, to różnica
(
) ( )
( )
0
0
0
'
x
f
h
x
f
h
x
f
−
−
+
wraz
z h dążącym do zera maleje do zera. Zatem dla dostatecznie małych przyrostów h można
przyjąć
(
) ( )
( )
0
'
0
0
0
≈
−
−
+
x
f
h
x
f
h
x
f
, skąd wynika, że
(8.4.2)
(
) ( )
( )
h
x
f
x
f
h
x
f
0
0
0
'
≈
−
+
.
Z zależności tej wynika, że przyrost wartości funkcji f w otoczeniu punktu x
0
jest
proporcjonalny do przyrostu h zmiennej x, a współczynnikiem proporcjonalności jest
pochodna funkcji w punkcie x
0
.
Z przekształcenia zależności (8.4.2) otrzymujemy praktyczny wzór:
(8.4.3)
(
) ( )
( )
h
x
f
x
f
h
x
f
0
0
0
'
+
≈
+
,
który oznacza, że wartość funkcji w punkcie z otoczenia x
0
można obliczyć, wykorzystując jej
wartość w punkcie x
0
i różniczkę funkcji w tym punkcie. A zatem, chcąc policzyć wartość dla
jednego argumentu, posługujemy się innym, dla którego wartość funkcji jest znana, jeśli
odległość między argumentami jest odpowiednio mała.
Przykład 8.4.1. Obliczymy przybliżoną wartość
01
,
4
.

Wykłady z matematyki
Anna Witaszczyk
33
Posłużymy się argumentem x
0
=4 i przyrostem argumentu h=0,01 dla
( )
x
x
f
=
. Ponieważ
( )
x
x
f
2
1
'
=
, na podstawie wzoru (8.4.3) otrzymujemy:
( ) (
) ( )
( ) ( )
( )
0025
,
2
400
1
2
01
,
0
4
2
1
4
01
,
0
4
'
4
4
4
01
,
0
4
01
,
4
=
+
=
+
=
+
=
+
≈
+
=
f
f
df
f
f
f
.
Porównując otrzymany wynik z uzyskanym za pomocą kalkulatora (2,0024984…)
stwierdzamy dokładność wyliczenia rzędu 10
-4
.
Przykład 8.4.2. Obliczmy wartość potęgi
(
)
20
99
,
0
. Niech
( )
20
x
x
f
=
, x
0
=1, h=-0,01.
Wówczas
( )
19
20
'
x
x
f
=
oraz, korzystając z (8.4.3):
(
) (
) ( )
( )
8
,
0
2
,
0
1
01
,
0
1
20
1
)
01
,
0
(
41
'
1
01
,
0
1
99
,
0
19
20
=
−
=
⋅
⋅
−
=
−
+
≈
−
=
f
f
f
f
.
Wykorzystując kalkulator otrzymujemy wartość 0,817906… Uzyskaliśmy zatem dokładność
rzędu 10
-1
.
5. POCHODNE WYśSZYCH RZĘDÓW
Jeżeli pochodna funkcji y=f(x) jest różniczkowalna w pewnym przedziale, to jej
pochodną nazywamy drugą pochodną lub pochodną drugiego rzędu funkcji y=f(x) i
oznaczamy jednym z symboli:
( )
x
f
′′
, y
′′
,
2
2
dx
y
d
.
Jeżeli druga pochodna funkcji y=f(x) jest także funkcją różniczkowalną, to pochodną
drugiej pochodnej nazywamy trzecią pochodną (pochodną trzeciego rzędu) funkcji y=f(x) i
oznaczamy jednym z symboli:
( )
x
f
′′′
, y
′′′
,
3
3
dx
y
d
.
Ogólnie pochodną n-tego rzędu funkcji y=f(x) nazywamy pochodną pochodnej rzędu
(n-1). Do jej oznaczenia używamy symboli:
( )
( )
x
f
n
,
( )
n
y
,
n
n
dx
y
d
. Tak więc:
( )
( )
( )
( )
[
]
′
=
−
x
f
x
f
n
n
1
.
Przykład 8.5.1. Wyznaczymy pierwsze trzy pochodne funkcji
( )
1
+
=
x
x
f
określonej w przedziale
[
)
+∞
−
,
1
i różniczkowalnej w przedziale
(
)
+∞
−
,
1
. Kolejne pochodne
wyrażają się wzorami:
( )
(
)
5
,
0
1
5
,
0
−
+
=
′
x
x
f
,
( )
(
)
5
,
1
1
25
,
0
−
+
−
=
′′
x
x
f
,
( )
(
)
5
,
2
1
375
,
0
−
+
=
′′′
x
x
f
.
Przykład 8.5.2. Obliczymy wszystkie pochodne funkcji potęgowej
( )
n
x
x
f
=
, gdzie n
jest liczbą naturalną. Kolejne pochodne wyrażają się wzorami:
( )
1
−
=
′
n
nx
x
f
,
( )
2
)
1
(
−
−
=
′′
n
x
n
n
x
f
,
( )
3
)
2
)(
1
(
−
−
−
=
′′′
n
x
n
n
n
x
f
,…
( )
( )
k
n
k
x
k
n
n
n
n
x
f
−
+
−
−
−
=
)
1
)...(
2
)(
1
(
,…,
( )
( )
!
1
)...
2
)(
1
(
n
n
n
n
x
f
n
=
−
−
=
,
( )
( )
(
)
( )
0
...
2
1
=
=
=
+
+
x
f
x
f
n
n
.
Przykład 8.5.3. Dla funkcji
( )
x
e
x
f
=
pochodne wszystkich rzędów są z nią
identyczne:
( )
( )
x
n
e
x
f
=
.
Wyszukiwarka
Podobne podstrony:
Matematyka LOGISTYKA wyklad cz2 Nieznany
Matematyka finansowa, Wyklad 9 F
Podstawy Logistyki Wykład I
Logistyka wykład, 9 01 2013
Matematyka Sem 2 Wykład Całki Powierzchniowe
Analiza i pomiar systemów logistycznych wykład 1( 24.02.2008)(1), Logistyka, Logistyka
logistykazaliczenie wykładów i, Logistyka
Logika matematyczna, ltm wyklad 02
Logistyka wykład magazyn zapasy definicje
WYKŁAD 5 CZ1
download Zarzadzanie Logistyka wykład na dzień 18.12.2004-[ www.potrzebujegotowki.pl ], Ściągi i wyp
logistyka wykłady, UE Katowice, II stopień sem2, LOGISTYKA
LOGISTYKA W12, LOGISTYKA - WYKŁAD 12
systemy logistyczne, wykład4, Przedmiot: SYSTEMY LOGISTYCZNE
do druku, UJK, zarzadzanie w sektorze publ i pryw 1 rok, logistyka wykłady
więcej podobnych podstron