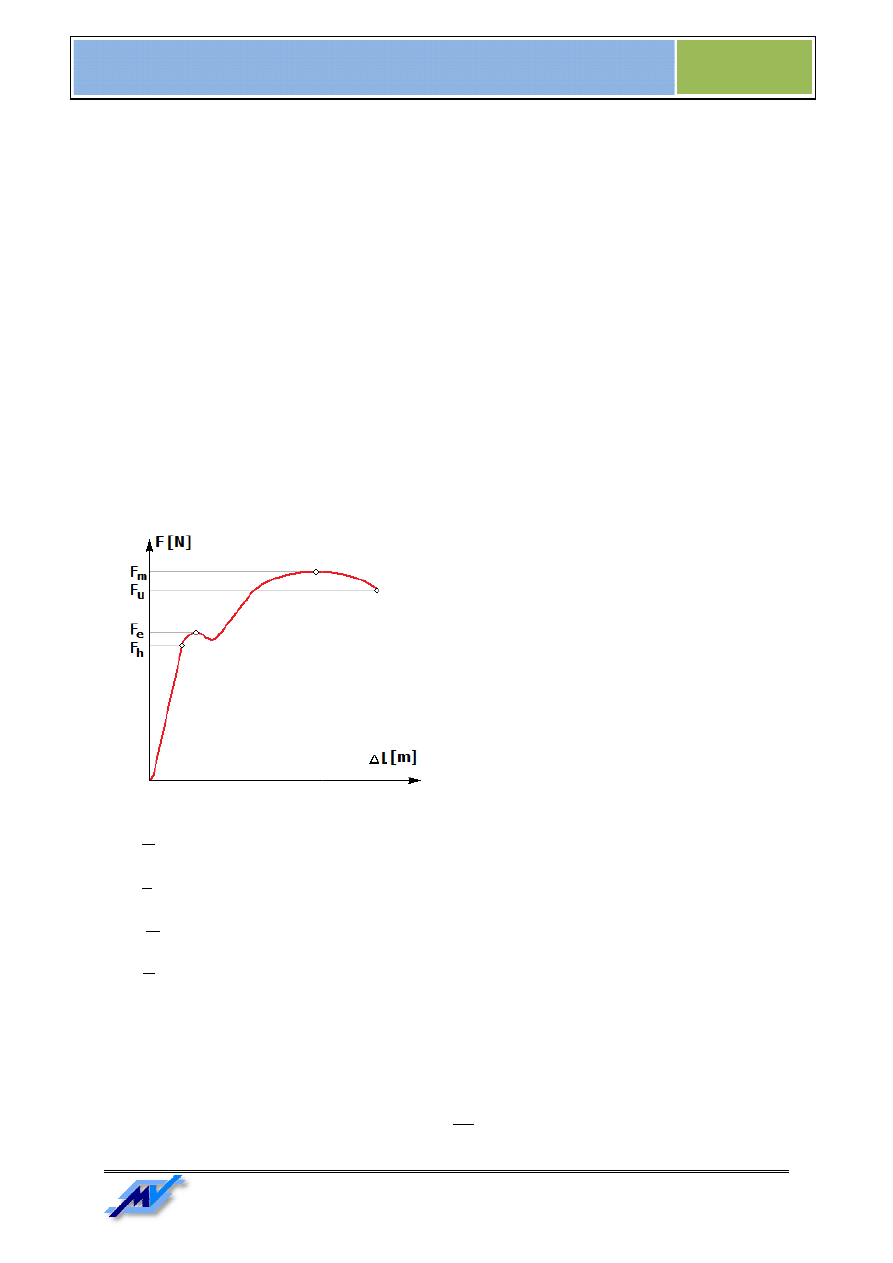
Rodzaje obciążeń, odkształceń i

Rodzaje obciążeń, odkształceń i

1.

Podział obciążeń i odkształceń

Oddziaływania na konstrukcję, w zależności od sposobu działania sił, mogą być statyczne lun dynamiczne.
Obciążenia statyczne występują wtedy, gdy układ sił działający na konstrukcję nie zmienia się w
wartość, zwrot, kierunek i punkt przyłożenia sił są stałe. W
działających na konstrukcję zmienia się w czasie. Jeżel
maksymalne i minimalne są tego samego znaku, to nazywamy je tętniącym. Jeżeli natomiast wartości graniczne
obciążeń są przeciwnego znaku, to takie obciążenie nazywamy wahającym.

Siły zewnętrzne działające na konstrukcje powodują w
mogą mieć charakter nietrwały, czyli inaczej mówiąc sprężysty lub charakter trwały, czyli plastyczny.

Odkształcenia powstają w wyniku sił powodujących rozciąganie, ściska

2.

Prawo Hooke’a

a.

Zależność wydłużenia od siły

Podczas działania sił na elementy konstrukcyjne występują odkształcenia, czyli

೓

- Granica proporcjonalności, czyli zakres obowiązywania prawa Hooke’a;

೐

- Granica plastyczności

೘

- Wytrzymałość mecha

ೠ

ೠ

- Naprężenie rozrywające

Prawo Hooke’a określa zależność wydłużenia materiału konstrukcyjnego w
można sformułować następująco: Wydłużenie jest wprost proporcjonalne do długości początkowej
i przyłożonej siły oraz odwrotnie proporcjonalne do przekroju i
opisuje poniższy wzór:

Rys. 1. Zależność wydłużenia od przyłożonej siły podczas

rozciągania

Rodzaje obciążeń, odkształceń i naprężeń

Rodzaje obciążeń, odkształceń i naprężeń

odkształceń

zależności od sposobu działania sił, mogą być statyczne lun dynamiczne.

statyczne występują wtedy, gdy układ sił działający na konstrukcję nie zmienia się w

punkt przyłożenia sił są stałe. W przypadku obciążeń dynamicznych układ sił

działających na konstrukcję zmienia się w czasie. Jeżeli obciążenie zmienia się w sposób okresowy tak, że siły

minimalne są tego samego znaku, to nazywamy je tętniącym. Jeżeli natomiast wartości graniczne

obciążeń są przeciwnego znaku, to takie obciążenie nazywamy wahającym.

jące na konstrukcje powodują w niej powstawanie różnych odkształceń. Odkształcenia te

mogą mieć charakter nietrwały, czyli inaczej mówiąc sprężysty lub charakter trwały, czyli plastyczny.

wyniku sił powodujących rozciąganie, ściskanie, ścinanie, zginanie i

Zależność wydłużenia od siły

Podczas działania sił na elementy konstrukcyjne występują odkształcenia, czyli zmiana wymiarów. Zależność

przyłożonej siły uzyskanego przyrostu długości
przedstawia poniższy wykres (Rys.
początku układu współrzędnych do
zakres sprężysty tzn. działająca siła i
siebie proporcjonalne. Po ustąpieniu siły wymiary
przedmiotu powracają do stanu pierwotnego. Dla sił
większych niż F

h

i mniejszych od

czynienia z zakresem plastycznym, czyli po
ustąpieniu siły rozciągającej przedmiot ulega
trwałemu odkształceniu. Dalszy wzrost siły powoduje
zmniejszanie się przekroju w sposób istotny. Po
osiągnięciu siły F

m

wydłużenie nadal się zwiększa aż

następuje zerwanie przedmiotu. Opisywanym siłom
odpowiadają naprężenia:

Granica proporcjonalności, czyli zakres obowiązywania prawa Hooke’a;

Granica plastyczności

Wytrzymałość mechaniczna

Naprężenie rozrywające

Prawo Hooke’a określa zależność wydłużenia materiału konstrukcyjnego w zależności od przyłożonej siły, które
można sformułować następująco: Wydłużenie jest wprost proporcjonalne do długości początkowej

proporcjonalne do przekroju i modułu sprężystości Younga. Prawo Hooke’a

∆

. Zależność wydłużenia od przyłożonej siły podczas

1

2010

naprężeń

zależności od sposobu działania sił, mogą być statyczne lun dynamiczne.

statyczne występują wtedy, gdy układ sił działający na konstrukcję nie zmienia się w czasie, tzn.

przypadku obciążeń dynamicznych układ sił

sposób okresowy tak, że siły

minimalne są tego samego znaku, to nazywamy je tętniącym. Jeżeli natomiast wartości graniczne

niej powstawanie różnych odkształceń. Odkształcenia te

mogą mieć charakter nietrwały, czyli inaczej mówiąc sprężysty lub charakter trwały, czyli plastyczny.

nie, ścinanie, zginanie i skręcanie.

zmiana wymiarów. Zależność

przyłożonej siły uzyskanego przyrostu długości

Rys. 1). W zakresie od

początku układu współrzędnych do F

h

występuje

zakres sprężysty tzn. działająca siła i przekrój są do
siebie proporcjonalne. Po ustąpieniu siły wymiary
przedmiotu powracają do stanu pierwotnego. Dla sił

mniejszych od F

e

mamy do

zakresem plastycznym, czyli po

iu siły rozciągającej przedmiot ulega

trwałemu odkształceniu. Dalszy wzrost siły powoduje

sposób istotny. Po

wydłużenie nadal się zwiększa aż

następuje zerwanie przedmiotu. Opisywanym siłom

Granica proporcjonalności, czyli zakres obowiązywania prawa Hooke’a;

zależności od przyłożonej siły, które

można sformułować następująco: Wydłużenie jest wprost proporcjonalne do długości początkowej

modułu sprężystości Younga. Prawo Hooke’a

Rodzaje obciążeń, odkształceń i

gdzie: ∆l – wydłużenie w [m]; F –
moduł sprężystości Younga w [Pa]. Po przekształceniach wzór można doprowadzić do postaci:

gdzie:

to naprężenie i

∆

b.

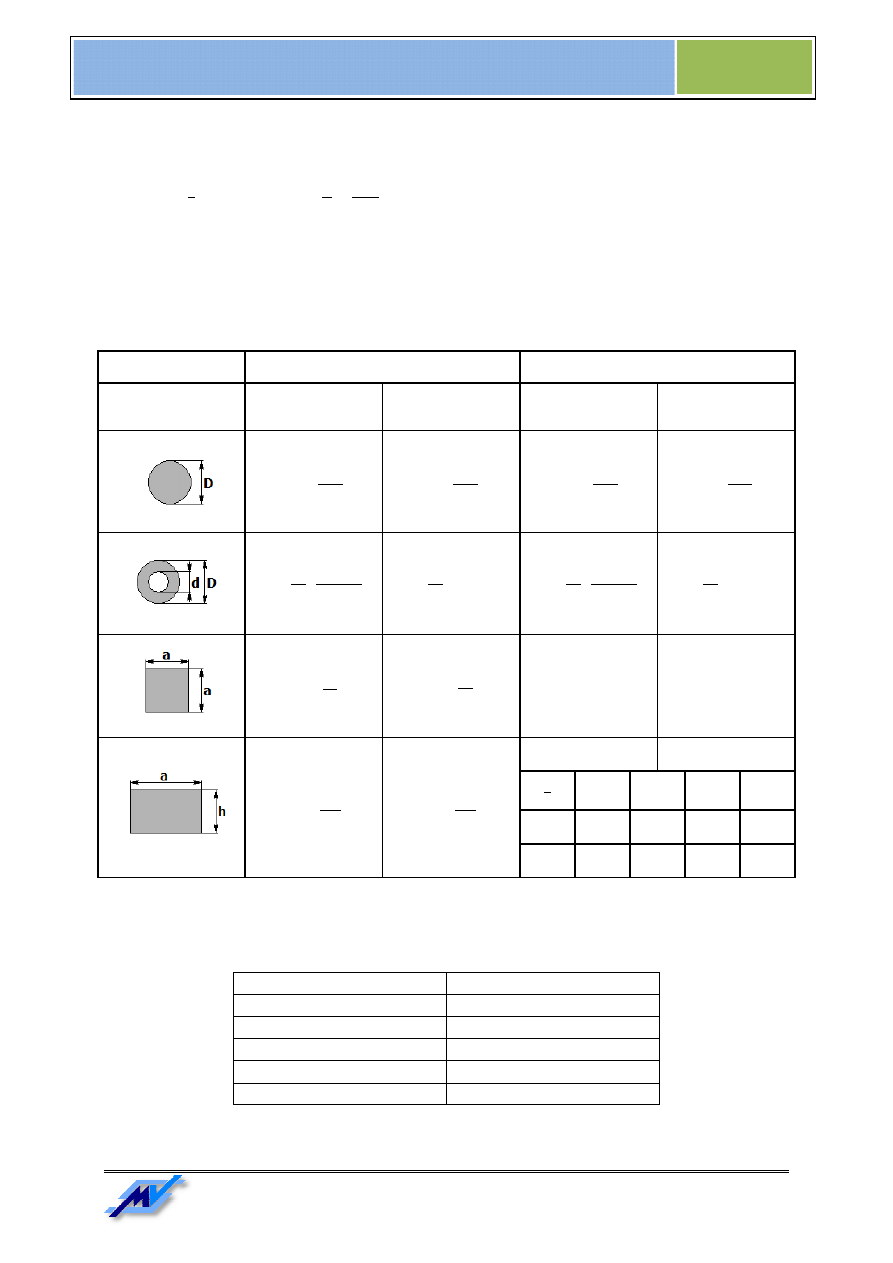
Moment bezwładności i wskaźnik przekroju

Podczas obliczeń odkształceń i naprężeń przy zginaniu i
kształtu przekroju elementu konstrukcyjnego. Są to moment bezwładności i
dla kilku najczęściej spotykanych kształtów przekrojów podaje poniższa tabel

Tabela 1. Wskaźniki przekroju i momenty bezwładności przekroju dla zginania i skręcania

Przekrój

Wskaźnik przekroju

w

x

[m

௫

௫

32

௫

௫

W celu obliczenia lub sprawdzenia poprawności doboru konstrukcji należy obliczać naprężenia występujące
w elementach konstrukcji i porównać je z
dopuszczalnych przedstawia poniższa tabelka.

Tabela

Rodzaj odkształcenia

Rozciąganie

Ściskanie

Zginanie

Ścinanie

Skręcanie

Rodzaje obciążeń, odkształceń i naprężeń

siła w [N]; l

0

– długość początkowa w [m]; S – pole przekroju w [

]. Po przekształceniach wzór można doprowadzić do postaci:

∆

೚

భ

೚

೚

to wydłużenie względne.

wskaźnik przekroju

ężeń przy zginaniu i skręcaniu należy korzystać z parametrów zależnych od

kształtu przekroju elementu konstrukcyjnego. Są to moment bezwładności i wskaźnik przekroju. Ich wartości
dla kilku najczęściej spotykanych kształtów przekrojów podaje poniższa tabelka.

Wskaźniki przekroju i momenty bezwładności przekroju dla zginania i skręcania

Zginanie

Skręcanie

Wskaźnik przekroju

m

3

]

Moment bezwładności

przekroju

J

x

[m

4

]

Wskaźnik przekroju

w

0

[m

3

]

ଷ

32

௫

ସ

64

଴

ଷ

16

ସ

ସ

௫

64

ସ

ସ

଴

16

ସ

ସ

ଷ

6

௫

ସ

12

଴

0,141

ଷ

ଶ

6

௫

ଷ

12

଴

ଵ

ଶ

݄

ܽ

1,5

k

1

0,196

0,229

k

2

0,231

0,246

celu obliczenia lub sprawdzenia poprawności doboru konstrukcji należy obliczać naprężenia występujące

porównać je z naprężeniami dopuszczalnymi. Przeciętne wartości naprężeń

dopuszczalnych przedstawia poniższa tabelka.

Tabela 2. Naprężenia dopuszczalne dla różnych odkształceń

Rodzaj odkształcenia

Naprężenie dopuszczalne

௥

0,48

௘

௖

௥

௚

0,53

௘

௧

0,27

௘

௦

௧

2

2010

pole przekroju w [m

2

]; E –

]. Po przekształceniach wzór można doprowadzić do postaci:

parametrów zależnych od

wskaźnik przekroju. Ich wartości

Skręcanie

Moment bezwładności

przekroju

J

0

[m

4

]

଴

ସ

32

଴

32

ସ

ସ

଴

0,208

ସ

଴

ଶ

ଷ

2

4

6

0,229

0,281

0,299

0,246

0,282

0,299

celu obliczenia lub sprawdzenia poprawności doboru konstrukcji należy obliczać naprężenia występujące

Przeciętne wartości naprężeń

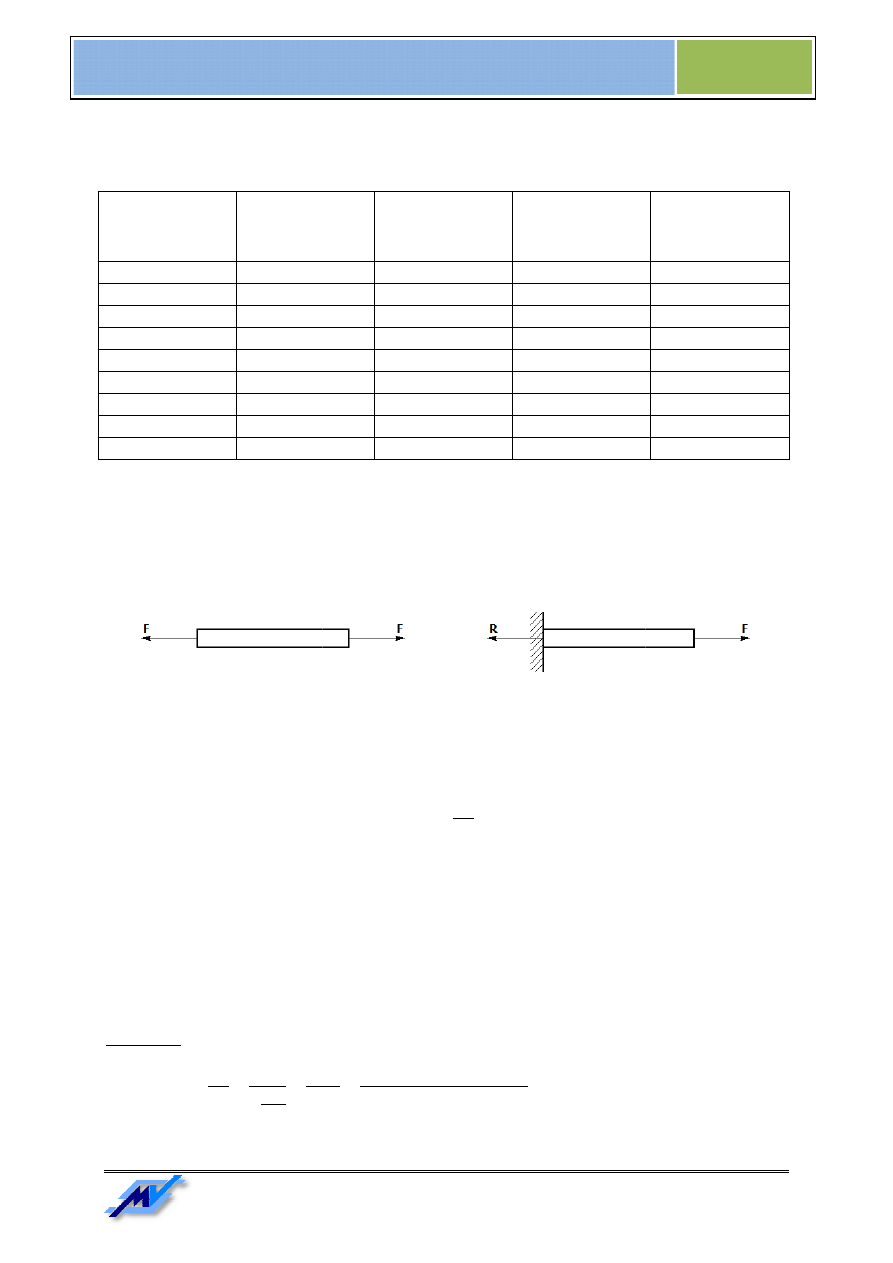
Rodzaje obciążeń, odkształceń i

Do obliczeń są również potrzebne są również stałe materiałowe. Dla kilku przykładowych materiałów w
są podane moduł sprężystości Younga
rozszerzalności cieplnej α.

Materiał

Moduł Younga

E

[

GPa

Diament

1200

Aluminium

70

Miedź

130

Srebro

74

Złoto

79

Stal

210

Szkło

80

Granit

30

Pleksi

3,2

3.

Rozciąganie

a.

Definicje i przykłady

Rozciąganie występuje, gdy dwie siły o
działają wzdłuż osi np. pręta. Powoduje to jego wydłużenie z

Rys. 2. Rozciąganie pręta swobodnego

Przykłady rozciągania pręta są pokazane na

b.

Obliczanie odkształceń i wytrzymałości

Wydłużenie rozciąganego pręta oblicza s

gdzie: ∆l – wydłużenie bezwzględne wyrażone w

l

0

– długość początkowa [m

F – siła powodująca rozciąganie [

E – Moduł Younga [MPa];

S – Przekrój pręta [m

2

].

Przykład 1:

Obliczyć, jakie wydłużenie spowoduje siła
i o długości l

0

=1,5 m. Przyjąć ż

P=0,293. Obliczyć również zmniejszenie średnicy pręta spowodowane wydłużeniem.

Rozwiązanie: W celu obliczenia wydłużenia należy skorzystać z

∆

4

4

Rodzaje obciążeń, odkształceń i naprężeń

Do obliczeń są również potrzebne są również stałe materiałowe. Dla kilku przykładowych materiałów w
są podane moduł sprężystości Younga E, Moduł skręcalności G, moduł Poissona P i współczynnik

Tabela 3. Wybrane parametry dla kilku materiałów

Moduł Younga

GPa

]

Moduł skręcalności

G

[

GPa

]

Moduł Poissona

P

480

0,25

26

0,345

48

0,343

27

0,367

28

0,420

85

0,293

23

0,270

12

0,300

1,14

0,400

Rozciąganie występuje, gdy dwie siły o równych wartościach i przeciwnych zwrotach (skierowane od siebie)
działają wzdłuż osi np. pręta. Powoduje to jego wydłużenie z jednoczesnym zmniejszeniem jego przekroju.

Rozciąganie pręta swobodnego

Rys. 3. Rozciąganie pręta utwierdzonego

Przykłady rozciągania pręta są pokazane na Rys. 2 i Rys. 3.

wytrzymałości

Wydłużenie rozciąganego pręta oblicza się z wzoru opisującego prawo Hooke’a:

∆

wydłużenie bezwzględne wyrażone w jednostkach długości [m];

m];

siła powodująca rozciąganie [N];

Obliczyć, jakie wydłużenie spowoduje siła F=30 kN obciążająca pręt stalowy o

. Przyjąć, że moduł Younga dla stali wynosi E=2,1

⋅

10

5

Obliczyć również zmniejszenie średnicy pręta spowodowane wydłużeniem.

celu obliczenia wydłużenia należy skorzystać z wzoru opisującego prawo Hooke’a:

4 · 30 · 10

· 1,5

210000 · 10

· 3,14 · 0,02

6,82 · 10

3

2010

Do obliczeń są również potrzebne są również stałe materiałowe. Dla kilku przykładowych materiałów w tabeli

współczynnik

Współczynnik

rozszerzalności

cieplnej

α

[

1/K

]

0,0118

⋅

10

4

0,224

⋅

10

4

0,162

⋅

10

4

0,195

⋅

10

4

0,142

⋅

10

4

0,12

⋅

10

4

0,005

⋅

10

4

0,083

⋅

10

4

0,8

⋅

10

4

przeciwnych zwrotach (skierowane od siebie)

jednoczesnym zmniejszeniem jego przekroju.

Rozciąganie pręta utwierdzonego

pręt stalowy o średnicy d=20 mm

MPa i Moduł Poissona

Obliczyć również zmniejszenie średnicy pręta spowodowane wydłużeniem.

wzoru opisującego prawo Hooke’a:

0,682

Rodzaje obciążeń, odkształceń i

∆

∆

Odpowiedź: Pręt ulegnie wydłużeniu o
w wyniku rozciągania ulegnie zmniejszeniu o

Przykład 2:

Drut stalowy o długości
sprawdzić naprężenie przyjmując naprężenie dopuszczalne

E=2,1

⋅

10

5

MPa = 2,1

⋅

10

Rozwiązanie: Ze względu na nieznaną siłę i
określającego prawo Hooke’a:

Stąd już łatwo można obliczyć wydłużenie względne

Odpowiedź: Naprężenie w drucie wynosi

Obliczanie wytrzymałości to między innymi dobór wymiarów konstrukcji takich jak długości i
elementów oraz sprawdzenie dopuszczalnych naprężeń w
W obliczeniach należy stosować współczynniki bezpieczeństwa dość znacznie łagod
konstrukcji. Punktem wyjścia jest naprężenie określone na granicy plastyczności
od rodzaju obciążenia. Przy rozciąganiu naprężenie dopuszczalne można przyjmować jako

Przykład 3:

Sprawdzić, czy pręt stalowy o
naprężenie dopuszczalne dla stali wynosi

Rozwiązanie: Aby sprawdzić obciążenie pręta, należy porównać naprężenie wywołane zadaną siłą
z naprężeniem dopuszczalnym. Podstaw

Odpowiedź: Obliczone naprężenie w

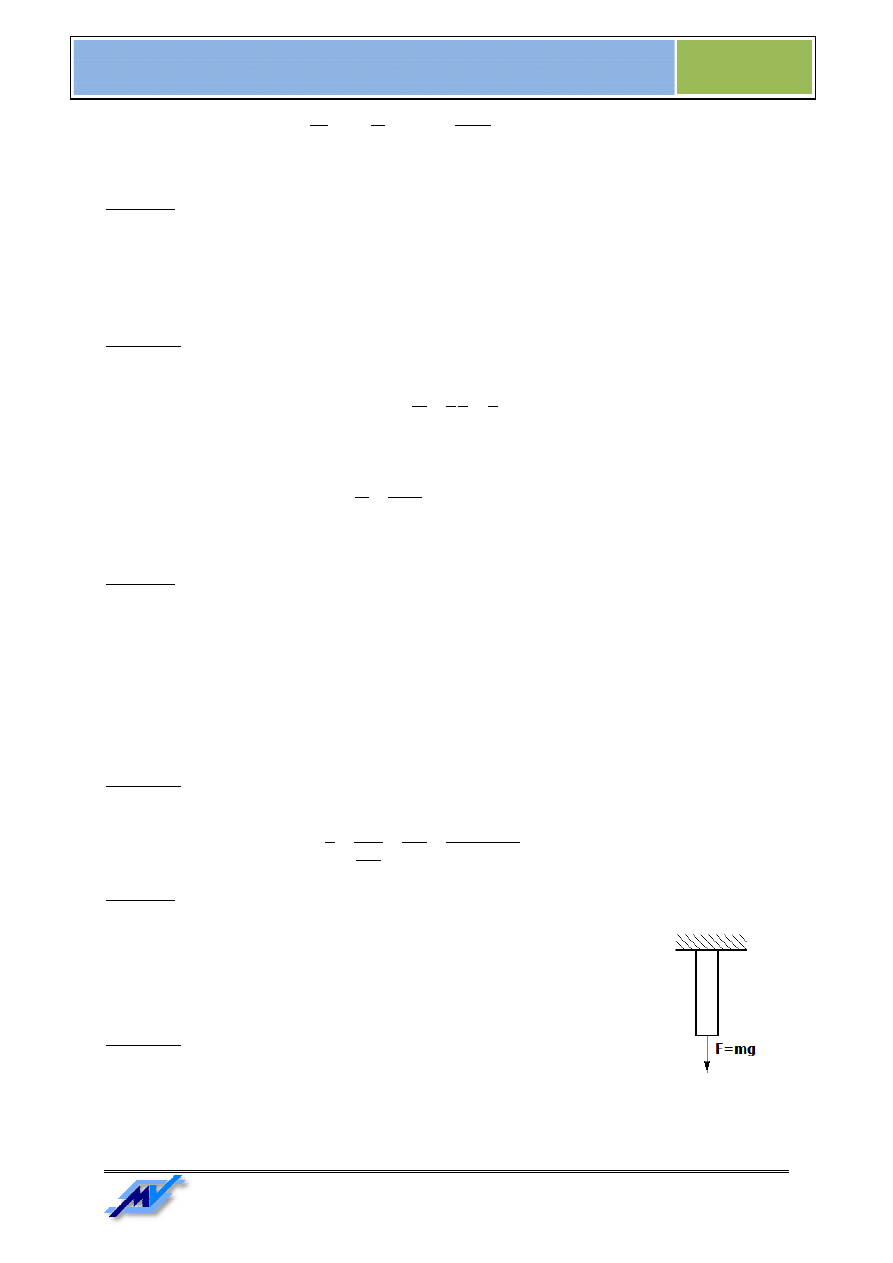
Przykład 4:

Obliczyć długość drutu stalowego o
zawieszonego jednym końcem
ciężarem nie zostanie przekroczone naprężenie dop
przyjąć, że naprężenie dopuszczalne dla stali wynosi
gęstość stali

γ

=7800 kg/m

Rozwiązanie: Największe naprężenie występuje oczywiście w
ponieważ jego obciążenie jest równe całemu ciężarowi drutu. Przyjmujemy, że nie może

być większe a co najwyżej równe naprężeniu dopuszczalnemu, czyli
kolejności obliczamy wielkość występującej tu siły:

Rodzaje obciążeń, odkształceń i naprężeń

∆

0,293

0,682

1500 0,000133

0,000133 · 0,02 2,66 · 10

2,66

: Pręt ulegnie wydłużeniu o ∆l=0,682 mm, czyli jego długość osiągnie l=1,500682

wyniku rozciągania ulegnie zmniejszeniu o ∆d=2,66

µ

m.

długości l

0

=6 m uległ wydłużeniu o ∆l=3 mm. Obliczyć wydłużenie względne oraz

sprawdzić naprężenie przyjmując naprężenie dopuszczalne k

r

=118 MPa i moduł Younga

10

11

Pa.

: Ze względu na nieznaną siłę i przekrój drutu musimy najpierw dokonać przekształcenia wzoru

∆

1

1

Stąd już łatwo można obliczyć wydłużenie względne α i naprężenie σ:

∆

3

6000 0,0005 0,5 · 10

0,5 · 10

· 2,1 · 10

105 · 10

105

drucie wynosi σ=105 MPa i jest mniejsze od dopuszczalnego k

trzymałości to między innymi dobór wymiarów konstrukcji takich jak długości i

elementów oraz sprawdzenie dopuszczalnych naprężeń w konstrukcjach o podanych wymiarach.

obliczeniach należy stosować współczynniki bezpieczeństwa dość znacznie łagodzące warunki pracy

konstrukcji. Punktem wyjścia jest naprężenie określone na granicy plastyczności R

E

oraz współczynnik zależny

od rodzaju obciążenia. Przy rozciąganiu naprężenie dopuszczalne można przyjmować jako

t stalowy o średnicy d=20 mm może być obciążony siłą F=30

naprężenie dopuszczalne dla stali wynosi k

r

=118 MPa.

: Aby sprawdzić obciążenie pręta, należy porównać naprężenie wywołane zadaną siłą

naprężeniem dopuszczalnym. Podstawiając dane do wzoru otrzymujemy:

4

4

4 · 30 · 10

3,14 · 0,02

95,5

: Obliczone naprężenie w pręcie jest mniejsze od dopuszczalnego, więc obciążenie jest prawidłowe.

długość drutu stalowego o przekroju S=1 mm

2

swobodnie

jednym końcem (Rys. 4), w którym pod jego własnym

ciężarem nie zostanie przekroczone naprężenie dopuszczalne. Do obliczeń
przyjąć, że naprężenie dopuszczalne dla stali wynosi k

r

=118 MPa oraz

kg/m

3

.

: Największe naprężenie występuje oczywiście w punkcie zawieszenia,

ponieważ jego obciążenie jest równe całemu ciężarowi drutu. Przyjmujemy, że nie może

być większe a co najwyżej równe naprężeniu dopuszczalnemu, czyli σ=k

r

. W pierwszej

wielkość występującej tu siły:

4

2010

=1,500682 m. Średnica pręta

. Obliczyć wydłużenie względne oraz

moduł Younga

przekrój drutu musimy najpierw dokonać przekształcenia wzoru

k

r

=118 MPa.

trzymałości to między innymi dobór wymiarów konstrukcji takich jak długości i przekroje

podanych wymiarach.

zące warunki pracy

oraz współczynnik zależny

od rodzaju obciążenia. Przy rozciąganiu naprężenie dopuszczalne można przyjmować jako k

r

=0,48 R

e

.

=30 kN? Przyjąć, że

: Aby sprawdzić obciążenie pręta, należy porównać naprężenie wywołane zadaną siłą

pręcie jest mniejsze od dopuszczalnego, więc obciążenie jest prawidłowe.

Rys. 4. Ilustracja

przykładu 4

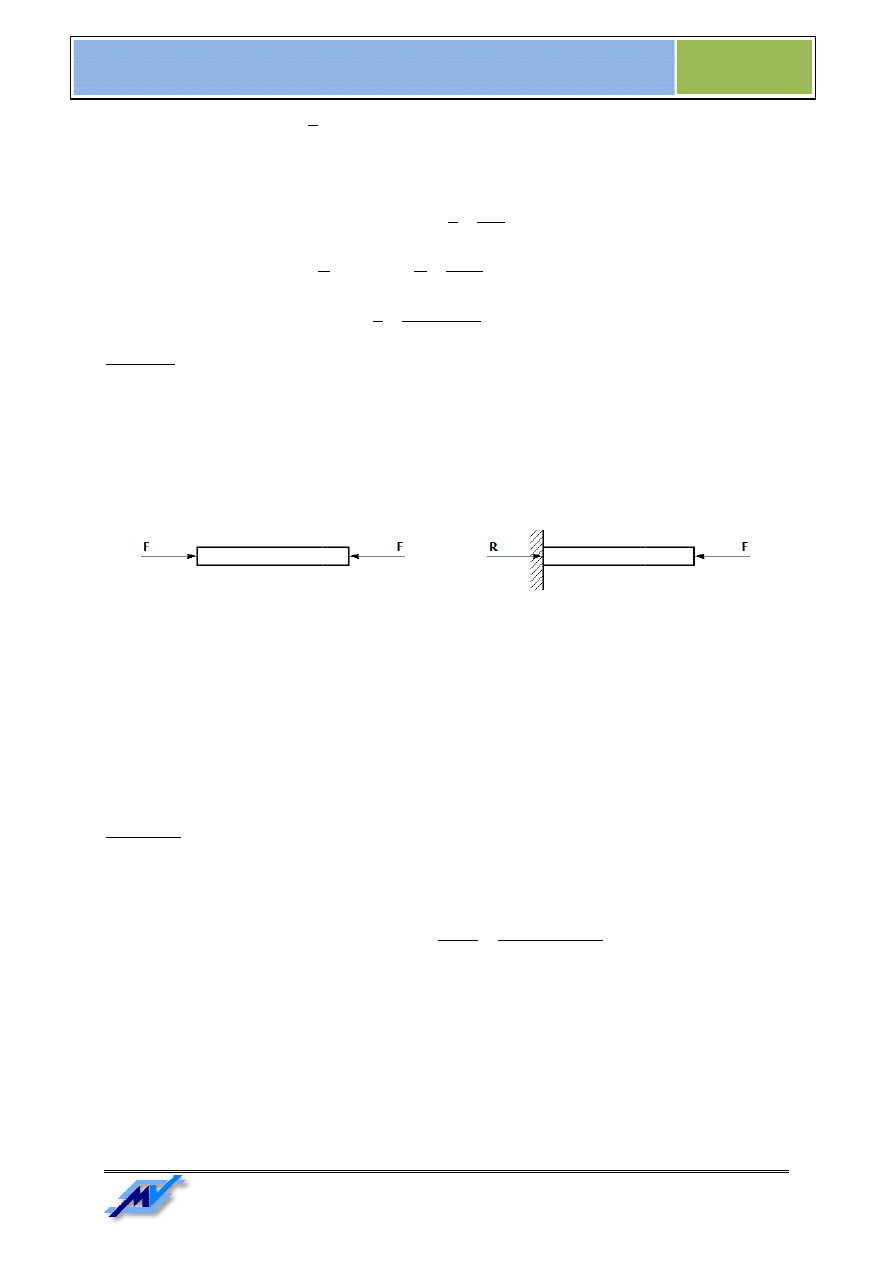
Rodzaje obciążeń, odkształceń i

Długość drutu obliczymy z jego objętości (objętość = przekrój
wyznaczając masę:

Odpowiedź: Długość drutu spełniającego warunki zadania wynosi

4.

Ściskanie

a.

Definicje i przykłady

Ściskanie występuje, gdy dwie siły o
działają wzdłuż osi np. pręta. Powoduje to jego skrócenie z

Rys. 5. Ściskanie pręta swobodnego

Przykłady rozciągania pręta są pokazane na

b.

Obliczanie odkształceń i wytrzymałości

Długość ściskanego pręta oblicza się

Przykład 5:

Pręt stalowy o długości
nieruchomymi ścianami odległymi od siebie o
po ogrzaniu go o ∆

υ

=100

α

υ

=0,12

⋅

10

-4

1/K, moduł Younga

Rozwiązanie: Rozwiązanie zostanie podzielone na dwie części. Najpierw zostanie obliczony przyrost
temperatury, który spowoduje wydłużenie pręta do dł
zostanie obliczony brakujący przyrost temperatury, który już wywoła naprężenia oraz samo naprężenie
i wywołującą je siłę. Z wzoru na rozszerzalność cieplną obliczamy przyrost temperatury

!1 "

∆#

Dalszy wzrost temperatury o

∆#

długości do l

2

. Oczywiście ten wzrost musi być ściśnięty do długości

obliczamy długość l

2

a następnie naprężenie

!1 "

Odpowiada to wydłużeniu względnemu:

Rodzaje obciążeń, odkształceń i naprężeń

118 · 10

· 1 · 10

118 $

Długość drutu obliczymy z jego objętości (objętość = przekrój

⋅

długość), natomiast objętość możemy obliczyć

%

%

118

9,81 12,03 &%

12,03

7800 1,542 · 10

1,542 · 10

1 · 10

1542,12 ( 1,54 &

: Długość drutu spełniającego warunki zadania wynosi l=1,54 km.

Ściskanie występuje, gdy dwie siły o równych wartościach i przeciwnych zwrotach (skierowane do siebie)
działają wzdłuż osi np. pręta. Powoduje to jego skrócenie z jednoczesnym zwiększeniem jego przekroju.

Ściskanie pręta swobodnego

Rys. 6. Ściskanie pręta utwierdzonego

Przykłady rozciągania pręta są pokazane na Rys. 5 i Rys. 6.

wytrzymałości

Długość ściskanego pręta oblicza się Parametry

długości l

0

=999 mm i o średnicy d=20 mm umieszczono między dwiema

nieruchomymi ścianami odległymi od siebie o l

1

=1 m. Obliczyć naprężenie występujące w

=100 K. Do obliczeń przyjąć współczynnik rozszerzalności cieplnej

, moduł Younga E=2,1

⋅

10

5

MPa.

: Rozwiązanie zostanie podzielone na dwie części. Najpierw zostanie obliczony przyrost

temperatury, który spowoduje wydłużenie pręta do długości l1, czyli nie spowoduje naprężeń. Następnie
zostanie obliczony brakujący przyrost temperatury, który już wywoła naprężenia oraz samo naprężenie

wzoru na rozszerzalność cieplną obliczamy przyrost temperatury ∆

#

) ∆#

1000 999

999 · 0,12 · 10

83,42

∆# ∆#

100 83,42 16,58 * spowodowałby dalszy wzrost

. Oczywiście ten wzrost musi być ściśnięty do długości l

1

wywołując siłę i naprężenie. Najpierw

a następnie naprężenie σ i siłę F:

∆#

) 1000!1 " 0,12 · 10

· 16,58) 1000,2

Odpowiada to wydłużeniu względnemu:

5

2010

długość), natomiast objętość możemy obliczyć

przeciwnych zwrotach (skierowane do siebie)

jednoczesnym zwiększeniem jego przekroju.

Ściskanie pręta utwierdzonego

umieszczono między dwiema

m. Obliczyć naprężenie występujące w pręcie

. Do obliczeń przyjąć współczynnik rozszerzalności cieplnej

: Rozwiązanie zostanie podzielone na dwie części. Najpierw zostanie obliczony przyrost

, czyli nie spowoduje naprężeń. Następnie

zostanie obliczony brakujący przyrost temperatury, który już wywoła naprężenia oraz samo naprężenie

∆

υ

1

.

42 *

spowodowałby dalszy wzrost

naprężenie. Najpierw

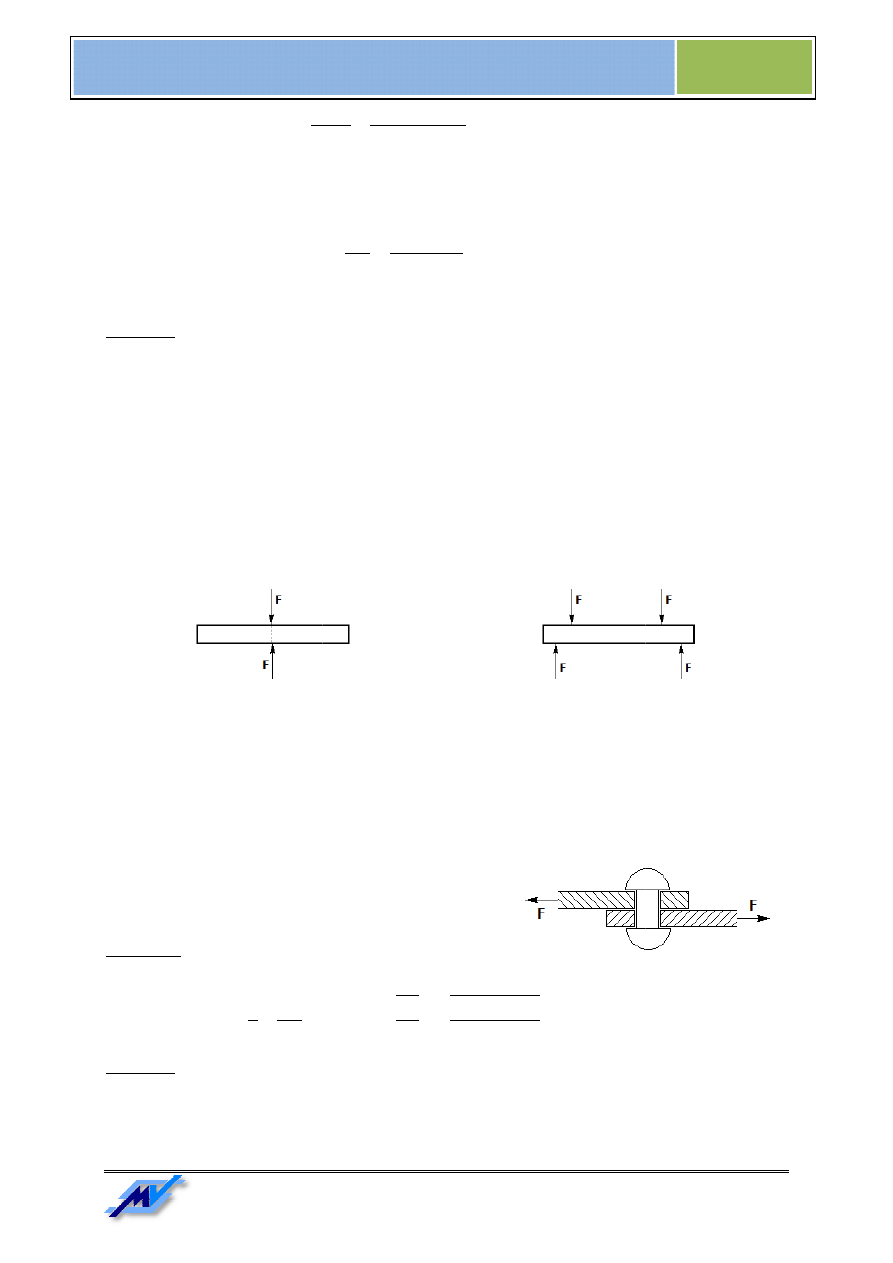
Rodzaje obciążeń, odkształceń i

Stąd naprężenie i siła są równe:

Odpowiedź: Podczas ogrzania pręta najpierw osiąga on długość równą odległości między ścianami, a
dalszemu wzrostowi długości towarzyszy mu ściskanie, w

5.

Ścinanie

a.

Definicje i przykłady

Ścinanie występuje wtedy, gdy para sił o
jednej części powodując jego przecięcie
Różnica polega na tym, że przy ścinaniu siły są nieco przesunięte względem siebie.
ścinania mogą być nożyce lub gilotyna, gdzie dąży się do rozcięcia materiału. W tym wypadku naprężenia tnące
muszą przekroczyć wytrzymałość ciętego materiału. Natomiast połączenia nitowane, gdzie również występują
siły tnące, musi być tak dobrane, aby siły styczne nie zerwały nitu.

Rys. 7. Ścinanie

Przykład ścinania pręta jest pokazany na

b.

Obliczanie odkształceń i wytrzymałości

Podczas ścinania siły działają poprzecznie na przekrój elementu konstrukcyjnego. Aby stwierdzić, czy siły
działające w układzie mechanicznym nie spowo
naprężenie ścinające, jak w poniższym przykładzie.

Przykład 6:

Obliczyć, jaka powinna być średnica nitu
aby nie doszło do zniszczenia pod wpływem ścięcia
jeżeli działa siła F= 40
naprężenie tnące wynosi

Rozwiązanie: Szukaną średnicę nitu obliczamy z
naprężenie wykonując proste przekształcenie.

+ , &

4

Odpowiedź: Minimalna średnica nitu wynosi

d=10 mm.

Rodzaje obciążeń, odkształceń i naprężeń

1000,2 1000

1000

0,0002 0,2 · 10

2,1 · 10

· 0,2 · 10

42

4

3,14 · 0,02

4

3,14 · 10

42 · 10

· 3,14 · 10

13188 $ ( 13,2 &$

: Podczas ogrzania pręta najpierw osiąga on długość równą odległości między ścianami, a

towarzyszy mu ściskanie, w wyniku, czego naprężenie osiąga wartość

Ścinanie występuje wtedy, gdy para sił o bardzo małym ramieniu działa na konstrukcję powodując przesunięcie

jego przecięcie. Ze względu na działanie sił jest to oddziaływanie podobne do ściskania.

Różnica polega na tym, że przy ścinaniu siły są nieco przesunięte względem siebie. Przykładem występowania
ścinania mogą być nożyce lub gilotyna, gdzie dąży się do rozcięcia materiału. W tym wypadku naprężenia tnące
muszą przekroczyć wytrzymałość ciętego materiału. Natomiast połączenia nitowane, gdzie również występują

być tak dobrane, aby siły styczne nie zerwały nitu.

Rys. 8. Zginanie pręta dwiema parami sił

Przykład ścinania pręta jest pokazany na Rys. 7.

wytrzymałości

Podczas ścinania siły działają poprzecznie na przekrój elementu konstrukcyjnego. Aby stwierdzić, czy siły

układzie mechanicznym nie spowodują ścięcia elementu konstrukcyjnego, należy sprawdzić

poniższym przykładzie.

Obliczyć, jaka powinna być średnica nitu d (Rys. 9),
aby nie doszło do zniszczenia pod wpływem ścięcia

= 4000 N i dopuszczalne

naprężenie tnące wynosi k

t

=55 MPa.

: Szukaną średnicę nitu obliczamy z wzoru na

naprężenie wykonując proste przekształcenie.

-

4

&

-

4 · 4000

3,14 · 55 · 10

0,00962

: Minimalna średnica nitu wynosi d=9,62 mm. Należy dobrać najbliższy większy znormalizowany np.

Rys. 9. Połączenie nitowane do przykładu 6

6

2010

: Podczas ogrzania pręta najpierw osiąga on długość równą odległości między ścianami, a następnie

wyniku, czego naprężenie osiąga wartość σ=42 Mpa.

bardzo małym ramieniu działa na konstrukcję powodując przesunięcie

. Ze względu na działanie sił jest to oddziaływanie podobne do ściskania.

Przykładem występowania

ścinania mogą być nożyce lub gilotyna, gdzie dąży się do rozcięcia materiału. W tym wypadku naprężenia tnące
muszą przekroczyć wytrzymałość ciętego materiału. Natomiast połączenia nitowane, gdzie również występują

Zginanie pręta dwiema parami sił

Podczas ścinania siły działają poprzecznie na przekrój elementu konstrukcyjnego. Aby stwierdzić, czy siły

dują ścięcia elementu konstrukcyjnego, należy sprawdzić

9,62

. Należy dobrać najbliższy większy znormalizowany np.

. Połączenie nitowane do przykładu 6

Rodzaje obciążeń, odkształceń i

6.

Zginanie

a.

Definicje i przykłady

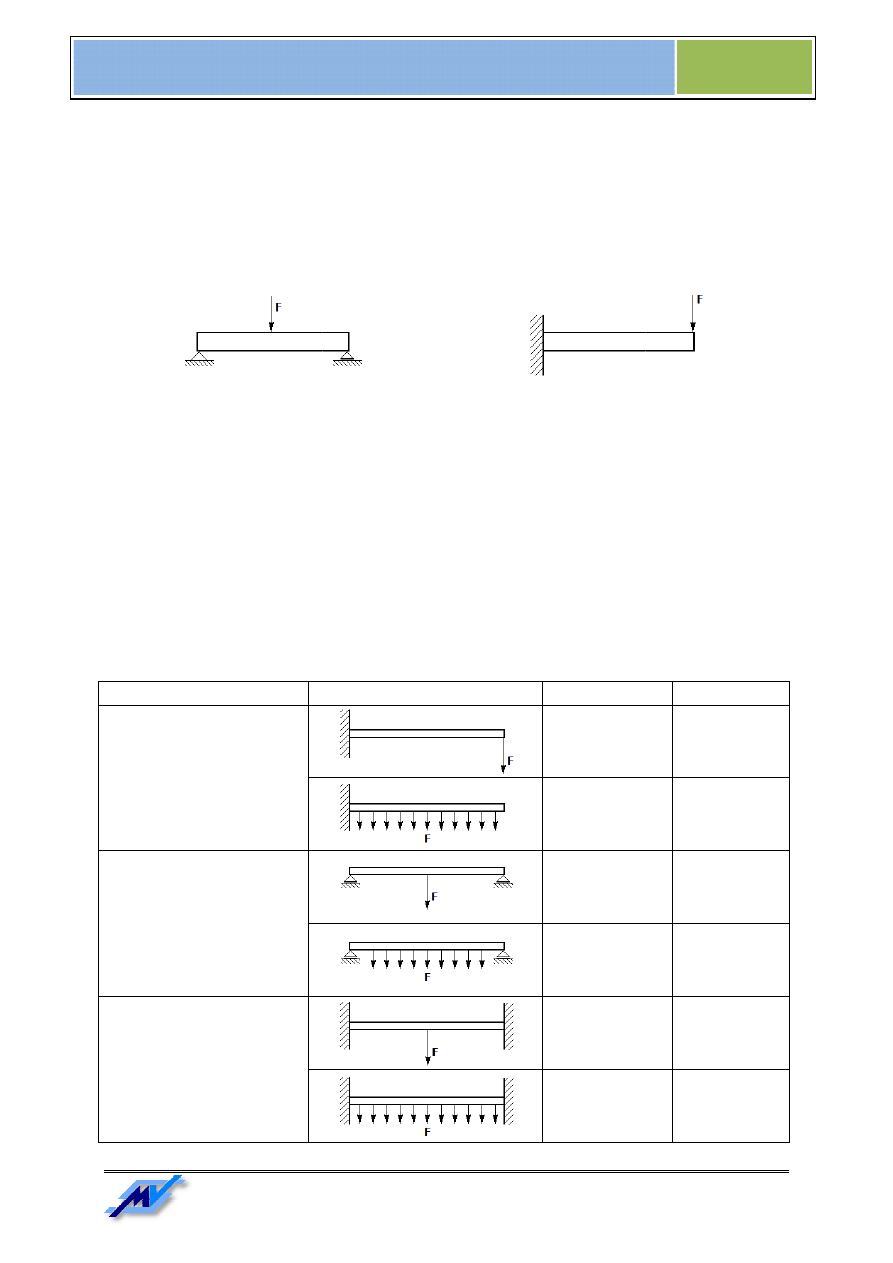
Zginanie pręta może wystąpić w następujących przypadkach. Pierwsza sytuacja dotyczy pręta, do którego
końców zostały przyłożone dwie pary sił (momenty zginające)
występuje również w przypadku pręta podpartego w
swobodna) obciążonego siłą przyłożoną między podporami. Do zginania dochodzi również w
utwierdzonego jednym końcem a do drugiego końca jest przyłożona siła zginająca.

Rys. 10. Zginanie pręta podpartego w dwóch punktach

Opisane sytuacje są przedstawione na

b.

Obliczanie odkształceń i wytrzymałości

Odkształcenia i wytrzymałość podczas zginania oblicza się nieco inaczej z
jednakowe w różnych miejscach przekroju. Wielkość naprężeń jest zależna również od kształtu
Dlatego też do obliczeń nie wystarczy jedynie powierzchnia tego przekroju, ale też współczynnik zależny od
kształtu. Mowa tu o wskaźniku przekroju oraz o
dla kilku różnych kształtów są podane w

Wielkość ugięcia jest zależne oczywiście od wielkości siły lub momentu gnącego, ale również od kształtu
przekroju i sposobu zamocowania pręta, belki, słupa itp. Współczynniki c
i obciążenia podaje tabela 4.

Tabela 4. Współczynniki do obliczania ugięcia w

Sposób mocowania

Jeden koniec zamocowany, drugi

swobodny

Oba końce podparte

Oba końce zamocowane

Rodzaje obciążeń, odkształceń i naprężeń

następujących przypadkach. Pierwsza sytuacja dotyczy pręta, do którego

końców zostały przyłożone dwie pary sił (momenty zginające) równych, lecz przeciwnie skierowanych. Zginanie

adku pręta podpartego w dwóch miejscach (przynajmniej jedna podpora jest

swobodna) obciążonego siłą przyłożoną między podporami. Do zginania dochodzi również w

do drugiego końca jest przyłożona siła zginająca.

dwóch punktach

Rys. 11. Zginanie pręta utwierdzonego

Opisane sytuacje są przedstawione na Rys. 8, Rys. 10 i Rys. 11.

wytrzymałości

wytrzymałość podczas zginania oblicza się nieco inaczej z tego powodu, że naprężenie nie jest

różnych miejscach przekroju. Wielkość naprężeń jest zależna również od kształtu

Dlatego też do obliczeń nie wystarczy jedynie powierzchnia tego przekroju, ale też współczynnik zależny od

wskaźniku przekroju oraz o momencie bezwładności przekroju. Wspomniane tu parametry

ane w tabeli 1.

Wielkość ugięcia jest zależne oczywiście od wielkości siły lub momentu gnącego, ale również od kształtu

sposobu zamocowania pręta, belki, słupa itp. Współczynniki c zależne od sposobu mocowania

. Współczynniki do obliczania ugięcia w zależności od zamocowania i sposobu obciążenia

Szkic

Sposób obciążenia

Na końcu

Równomierne

W środku

Równomierne

W środku

Równomierne

7

2010

następujących przypadkach. Pierwsza sytuacja dotyczy pręta, do którego

przeciwnie skierowanych. Zginanie

dwóch miejscach (przynajmniej jedna podpora jest

swobodna) obciążonego siłą przyłożoną między podporami. Do zginania dochodzi również w przypadku pręta

Zginanie pręta utwierdzonego

tego powodu, że naprężenie nie jest

różnych miejscach przekroju. Wielkość naprężeń jest zależna również od kształtu przekroju.

Dlatego też do obliczeń nie wystarczy jedynie powierzchnia tego przekroju, ale też współczynnik zależny od

momencie bezwładności przekroju. Wspomniane tu parametry

Wielkość ugięcia jest zależne oczywiście od wielkości siły lub momentu gnącego, ale również od kształtu

zależne od sposobu mocowania

sposobu obciążenia

Sposób obciążenia

Współczynnik c

1/3

Równomierne

1/8

1/48

Równomierne

5/384

1/192

Równomierne

1/384

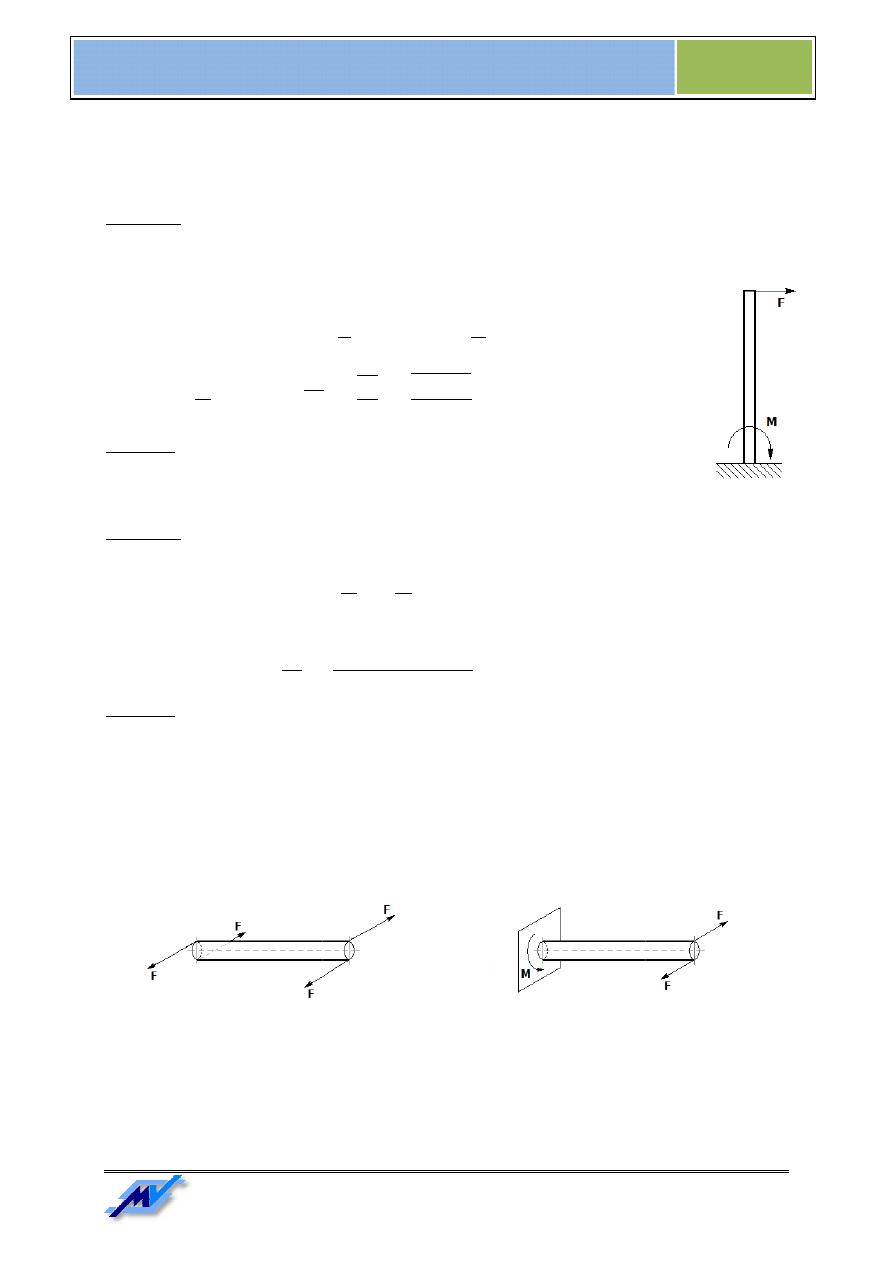
Rodzaje obciążeń, odkształceń i

Przykład 7:

Słup krańcowy o przekroju kwadratowym i
przewodów o sile F=450
dopuszczalne wynosi k

Rozwiązanie: W celu obliczenia wymiarów przekroju słupa należy obliczyć moment gnący, wskaźnik
wytrzymałości przekroju i ostatecznie wymiary poprzeczne słupa.

3. 3

Naprężenia mechaniczne w przekroju słupa powinny być mniejsze niż:

/

6 , √6/

య

Odpowiedź: Minimalne wymiary przekroju słupa wynoszą

Przykład 8:

Obliczyć wielkość ugięcia słupa z

moduł Younga E=150

Rozwiązanie: W celu obliczenia ugięcia słupa najpierw obliczamy moment bezwładności
przekroju:

1

Następnie korzystamy z następującego wzoru przyjmując współczynnik

∆2

3

1

Odpowiedź: Słup o długości h=12 m

7.

Skręcanie

a.

Definicje i przykłady

Gdy końce pręta są obciążone dwiema parami sił leżącymi w
i o momentach przeciwnie skierowanych występuje odkształcenie zwane skręcaniem. Skręcanie występuje
również w przypadku pręta utwierdzonego jednym kątem a
w płaszczyźnie prostopadłej do osi pręta.

Rys. 13. Skręcanie pręta swobodnego

Przykłady skręcania pręta są przedstawione na

b.

Obliczanie odkształceń i wytrzymałości

Rodzaje obciążeń, odkształceń i naprężeń

przekroju kwadratowym i o wysokości h=12 m jest obciążony naciągiem trzech

=450 N każdy. Dobrać wymiary przekroju słupa, jeżeli naprężenie

k

g

=15 MPa.

celu obliczenia wymiarów przekroju słupa należy obliczyć moment gnący, wskaźnik

ostatecznie wymiary poprzeczne słupa.

3 · 450 · 12 16200 $ 16,2 &$

przekroju słupa powinny być mniejsze niż:

/ 4 &

/ ,

&

/ -

6

&

య

-

6 · 16200

15 · 10

య

0,1864 18,64 3

: Minimalne wymiary przekroju słupa wynoszą a=16,64 cm.

Obliczyć wielkość ugięcia słupa z poprzedniego przykładu. Do obliczeń przyjąć

GPa.

: W celu obliczenia ugięcia słupa najpierw obliczamy moment bezwładności

1

12

1

12 0,1864

0,0001006

następującego wzoru przyjmując współczynnik c=0,333:

0,333 · 12

150 · 10

· 0,0001006 1350 0,155 15,53

ugnie się pod wpływem obciążenia przewodami o ∆x

Gdy końce pręta są obciążone dwiema parami sił leżącymi w płaszczyznach prostopadłych do osi pręta

ach przeciwnie skierowanych występuje odkształcenie zwane skręcaniem. Skręcanie występuje

przypadku pręta utwierdzonego jednym kątem a na drugi koniec działa siła lub para sił

płaszczyźnie prostopadłej do osi pręta.

Skręcanie pręta swobodnego

Rys. 14. Skręcanie pręta utwierdzonego

Przykłady skręcania pręta są przedstawione na Rys. 13 i Rys. 14.

wytrzymałości

8

2010

jest obciążony naciągiem trzech

każdy. Dobrać wymiary przekroju słupa, jeżeli naprężenie

celu obliczenia wymiarów przekroju słupa należy obliczyć moment gnący, wskaźnik

Do obliczeń przyjąć

3

∆

x=15,5 cm.

płaszczyznach prostopadłych do osi pręta

ach przeciwnie skierowanych występuje odkształcenie zwane skręcaniem. Skręcanie występuje

na drugi koniec działa siła lub para sił

Skręcanie pręta utwierdzonego

Rys. 12. Obciążenie

zginające do przykładu 7 i 8

Rodzaje obciążeń, odkształceń i

Skręcanie jest również obciążeniem, w
w różnych miejscach przekroju. Zależne są one od kształtu przekroju. Wynika z
że do obliczeń należy również stosować parametr zwany momentem bezwładności
przekroju. Zależności pozwalające go obliczyć są umieszczone w

Przykład 9:

Dobrać minimalną średnicę słupa przelotowego
dla najbardziej niekorzystnego przypadku, gdy zerwaniu ulegną dwa
skrajne, przeciwległe przewody. Siła naciągu pojedynczego przewodu
wynosi F=1000 N, długość poprzeczki słupa

Rozwiązanie: W pierwszej kolejności należy obliczyć m

22

Następnie z warunku wytrzymałości i

/

16

/

4 &

16

Odpowiedź: Minimalna średnica słupa wynosi

Przykład 10: Obliczyć skręcenie słupa z

G=70 GPa.

Rozwiązanie: W celu obliczenia kąta skręcenia słupa korzystamy z

∆5

2

67

32

6

Odpowiedź: Skręcenie słupa wyniesie

8.

Twardość materiałów

a.

Definicje i przykłady

Jednym ze sposobów pomiaru twardości jest metoda Brinella. Polega ona na
wywołaniu nacisku odpowiednią siłą na badany materiał głowicą
zakończoną kulką o średnicy D (stosowane średnice kulki są następujące: 10
– 5 – 2,5 – 2 – 1 mm). Następnie mierzy się średnicę odcisku
stopień twardości HR.

b.

Obliczanie odkształceń i stopnia twardości

Przykład 11: Obliczyć stopień twardości materiału, jeżeli średnica użytej

kulki wynosi D=10 mm

Rozwiązanie: W celu obliczenia twardości należy skorzyst

89

2

:;: √:

89 <

$

Odpowiedź: Twardość wynosi 168,8

Rodzaje obciążeń, odkształceń i naprężeń

Skręcanie jest również obciążeniem, w którym występują różne naprężenia

Zależne są one od kształtu przekroju. Wynika z tego,

że do obliczeń należy również stosować parametr zwany momentem bezwładności
przekroju. Zależności pozwalające go obliczyć są umieszczone w tabeli 1.

Dobrać minimalną średnicę słupa przelotowego o wysokości l=12 m
dla najbardziej niekorzystnego przypadku, gdy zerwaniu ulegną dwa
skrajne, przeciwległe przewody. Siła naciągu pojedynczego przewodu

, długość poprzeczki słupa x=0,5 m. Naprężenie dopuszczalne

pierwszej kolejności należy obliczyć moment skręcający:

2 · 1000 · 0,5 1000 $

warunku wytrzymałości i wzoru na wskaźnik przekroju obliczamy minimalną średnicę słupa:

16

4 &

, -

16

&

య

-

16 · 1000

3,14 · 5 · 10

య

0

: Minimalna średnica słupa wynosi d=10,1 cm.

skręcenie słupa z poprzedniego przykładu. Do obliczeń przyjąć moduł skręcalności

W celu obliczenia kąta skręcenia słupa korzystamy z poniższego wzoru:

6

32 · 1000 · 12

3,14 · 70 · 10

· 0,1006

0,017 7 0,163

: Skręcenie słupa wyniesie ∆

ϕ

=0,017 rad.

Twardość materiałów

Jednym ze sposobów pomiaru twardości jest metoda Brinella. Polega ona na
wywołaniu nacisku odpowiednią siłą na badany materiał głowicą

(stosowane średnice kulki są następujące: 10

Następnie mierzy się średnicę odcisku d i oblicza się

stopnia twardości

Obliczyć stopień twardości materiału, jeżeli średnica użytej

mm, średnica odcisku d=1,5 mm a siła nacisku F=3000 N

celu obliczenia twardości należy skorzystać z wzoru:

=

2 · 300

3,14 · 10 >10 ?10

1,5

@

168,8 89

$

10 · $

10

·

10

$

10

10 A

8 HB.

Rys.

Rys. 16. Metoda Brinella badania twardości

9

2010

. Naprężenie dopuszczalne k

s

=5 MPa.

wskaźnik przekroju obliczamy minimalną średnicę słupa:

0,1006 ( 10,1 3

moduł skręcalności

163 B%

N = 300 daN.

89 <

$

A

Rys. 15. Ilustracja przykładu 9 i 10

. Metoda Brinella badania twardości

materiałów

Rodzaje obciążeń, odkształceń i

Przykład 12: Obliczyć promień powierzchni styku kulki o

powierzchnię badaną. Do obliczeń przyjąć moduł sprężystości kuli
badanego E

2

=210 GPa

Rozwiązanie: Aby obliczyć promień powierzchni styku kulki
podstawić dane zawarte w treści zadania do wzoru:

7 -

2

3 C

1

"

య

Odpowiedź: Promień odcisku wyniesie

9.

Sprężyna

Wydłużenie sprężyny o N zwojach, o
wywołującej, co najwyżej naprężenie dopuszczalne w

Przykład 13: Obliczyć wydłużenie sprężyny o

o średnicy d=1 mm przyjmując naprężenie dopuszczalne
skręcalności G=85 GPa

Rozwiązanie: Do obliczeń korzystamy z

∆ 4$

6

Odpowiedź: Wydłużenie wyniesie 19

Rodzaje obciążeń, odkształceń i naprężeń

Obliczyć promień powierzchni styku kulki o promieniu R=5 mm naciskającej siłą
powierzchnię badaną. Do obliczeń przyjąć moduł sprężystości kuli E

1

=530 GPa

GPa.

: Aby obliczyć promień powierzchni styku kulki naciskającej na powierzchnię badaną należy

treści zadania do wzoru:

1

D -

2

3 · 3000 · 5 C

1

530 · 10

"

1

210 · 10

D

య

4,05

: Promień odcisku wyniesie r=4,05 mm.

zwojach, o średnicy D=2R wykonanej z drutu o średnicy d=2r pod wpływem siły

wołującej, co najwyżej naprężenie dopuszczalne w materiale sprężyny.

Obliczyć wydłużenie sprężyny o N=20 zwojach, o średnicy D=20 mm, wykonanej z

rzyjmując naprężenie dopuszczalne k

s

=50 MPa. Do obliczeń przyjąć moduł

GPa.

: Do obliczeń korzystamy z wzoru:

&

6 4 · 20

0,02

· 50 · 10

0,001 · 85 · 10

0,019 19

: Wydłużenie wyniesie 19 mm.

10

2010

naciskającej siłą F=3000 N na

GPa oraz materiału

na powierzchnię badaną należy

05

pod wpływem siły F

, wykonanej z drutu

. Do obliczeń przyjąć moduł