1

1

(T) TERMODYNAMIKA – Gaz doskonały

T. Równanie gazu doskonalego



robert.szczotka(at)gmail.com               

Fizyka i astronomia, I LO 2010

1

T: 

Równanie gazu doskonałego

(T) Termodynamika

•

I Liceum Ogólnokształcące

•

Im. Hugona Kołłątaja

•

ul. Kołłątaja 1

•

63-700 Krotoszyn

2

(T) TERMODYNAMIKA – Gaz doskonały

T. Równanie gazu doskonalego



robert.szczotka(at)gmail.com               

Fizyka i astronomia, I LO 2010

2

1. Model gazu doskonałego (zało

ż

enia)

• cząsteczki mają zaniedbywalne rozmiary - traktuje się 

je jako punkty materialne.

• cząsteczki nie oddziałują ze sobą - z  wyjątkiem 

krótkotrwałych zderzeń sprężystych.

• cząsteczki mają tylko energię kinetyczną ruchu 

postępowego.

2

3

(T) TERMODYNAMIKA – Gaz doskonały

T. Równanie gazu doskonalego



robert.szczotka(at)gmail.com               

Fizyka i astronomia, I LO 2010

3

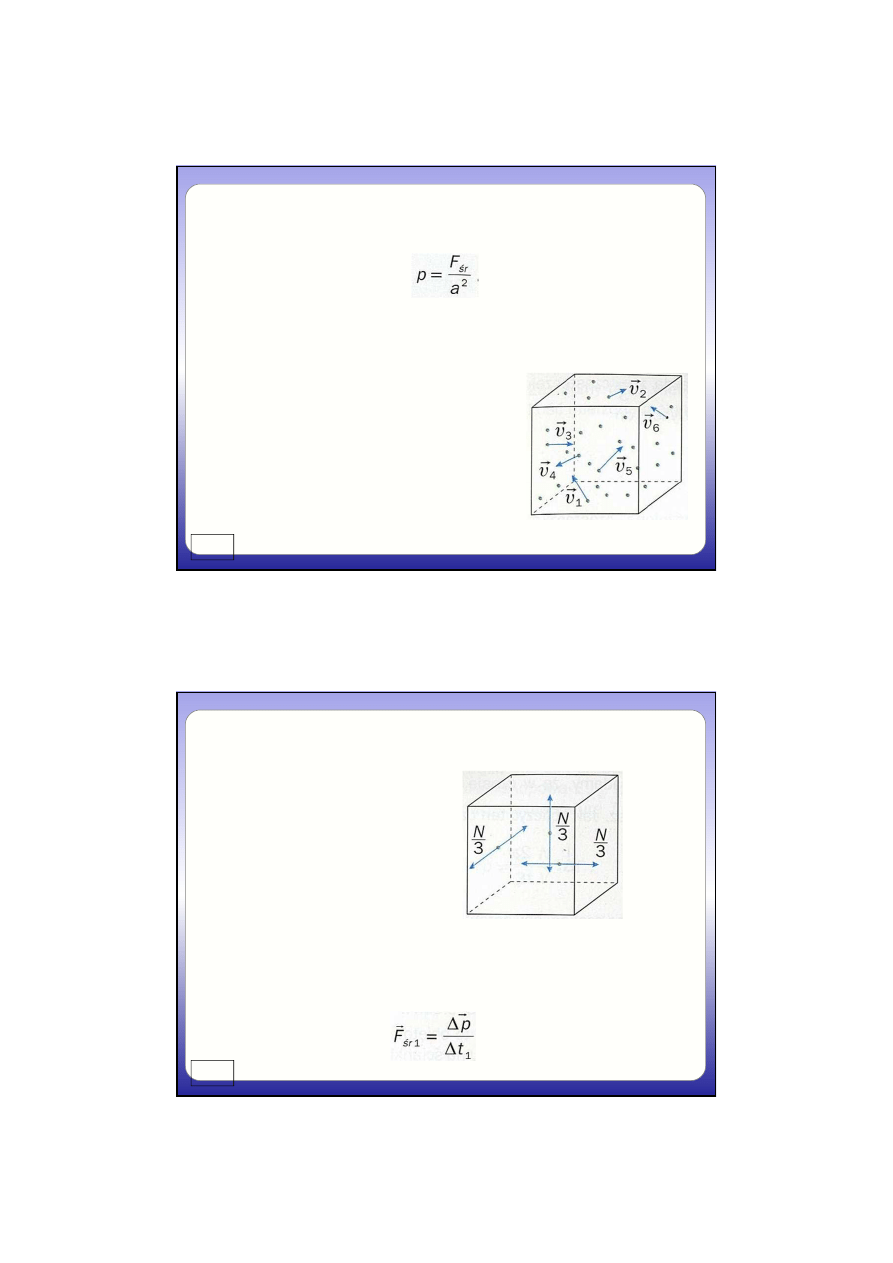
2. Ciśnienie gazu w zbiorniku zamkniętym

Ciśnienie w zbiorniku w kształcie sześcianu o 

boku a

2

Cz

ą

steczki w zbiorniku 

poruszaj

ą

 si

ę

 chaotycznie 

wi

ę

c 

ż

aden kierunek ruchu 

nie jest wyró

ż

niony

F

ś

r

– siła wywierana przez cz

ą

steczki na 

ś

cian

ę

 naczynia [N]

a

2

– powierzchnia jednej ze 

ś

cian zbiornika [m

2

]

4

(T) TERMODYNAMIKA – Gaz doskonały

T. Równanie gazu doskonalego



robert.szczotka(at)gmail.com               

Fizyka i astronomia, I LO 2010

4

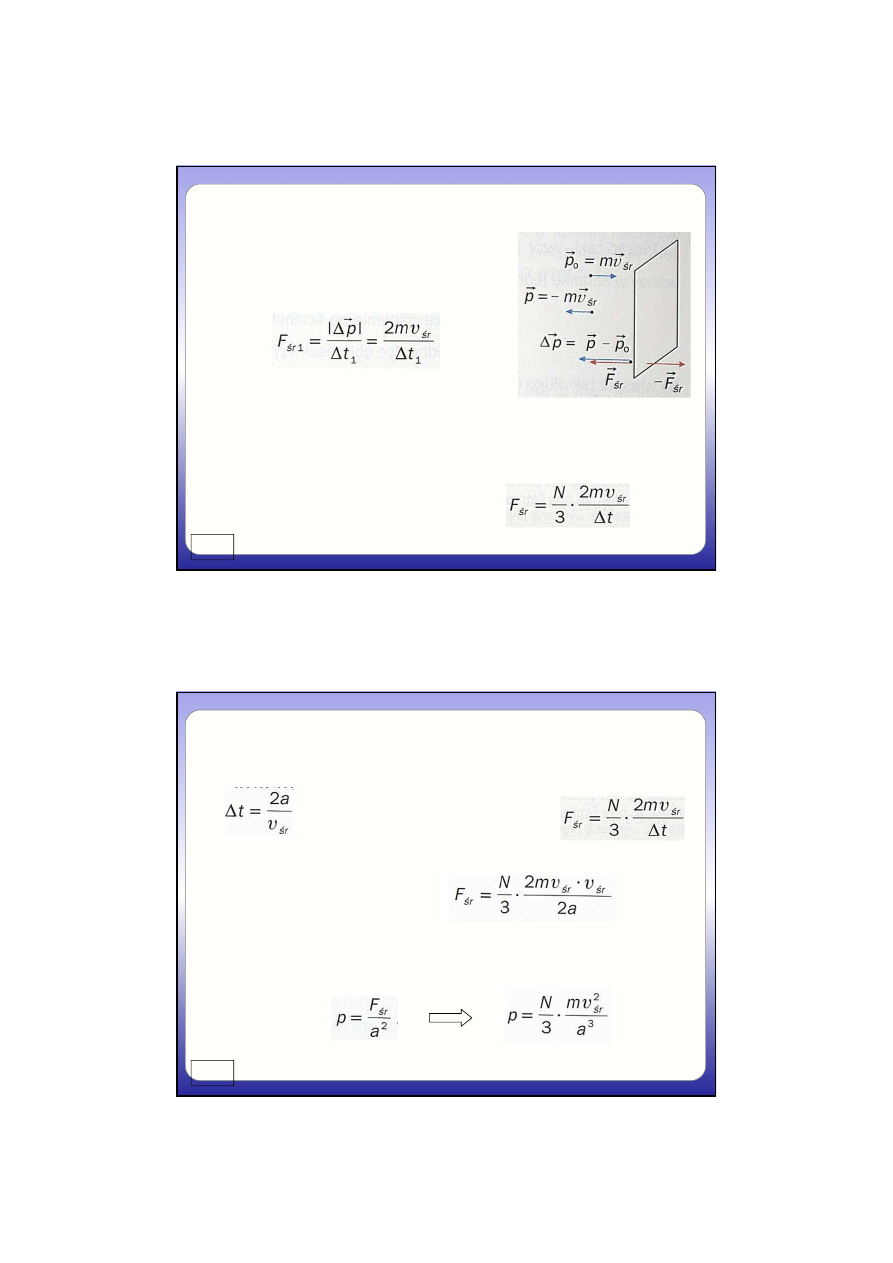
Dla uproszczenia możemy założyć, że w danej 

chwili każdym kierunku porusza się 1/3 
cząsteczek

Jedna cząsteczka poruszając się z prędkością V

ś

r

podczas zderzenia dozna działania siły

3

N – ilo

ść

 cz

ą

steczek w 

zbiorniku

3

5

(T) TERMODYNAMIKA – Gaz doskonały

T. Równanie gazu doskonalego



robert.szczotka(at)gmail.com               

Fizyka i astronomia, I LO 2010

5

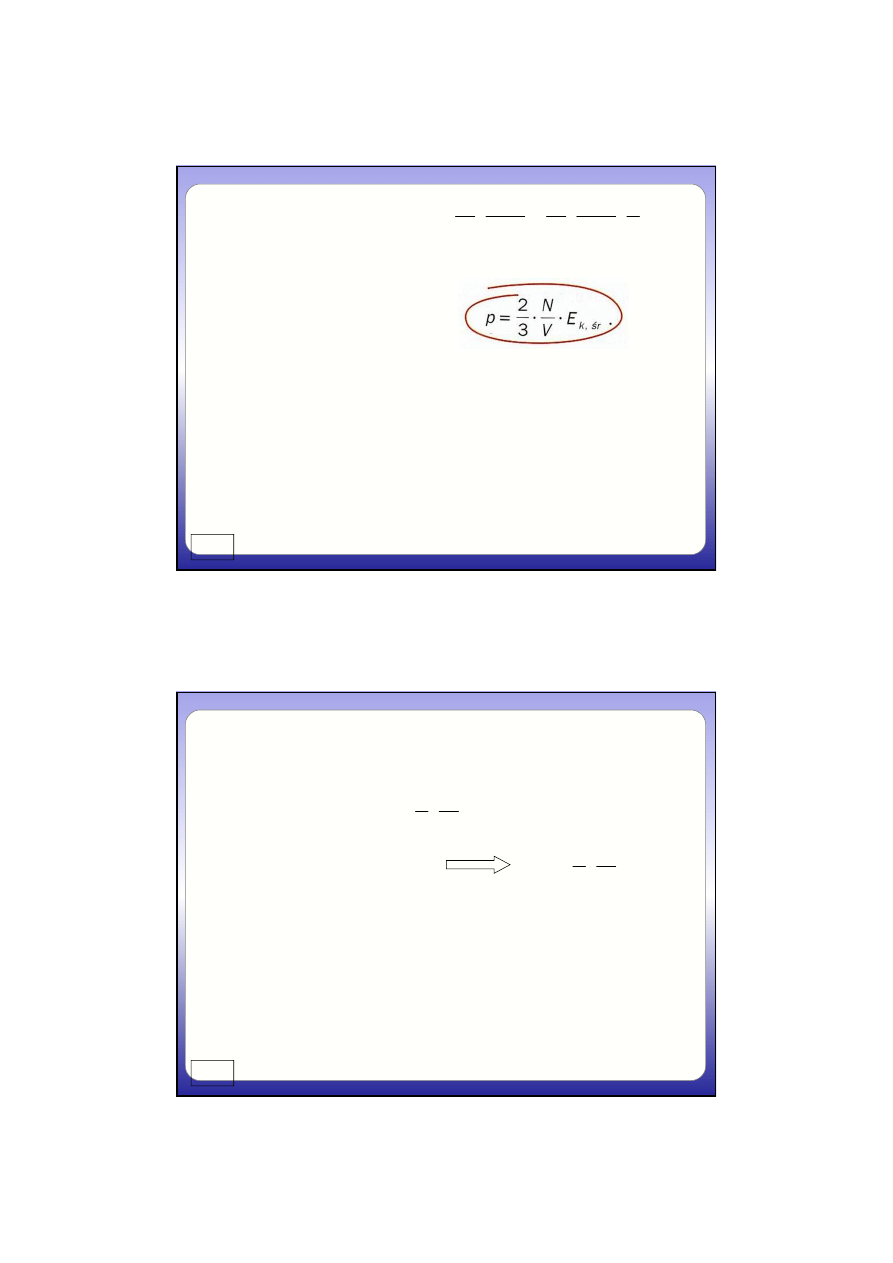
Siłą o takiej samej wartości 

ale przeciwnym zwrocie 
cząsteczka zadziała na 
ś

ciankę

4

Bior

ą

c pod uwag

ę

 wszystkie 

cz

ą

steczki poruszaj

ą

ce si

ę

 w 

tym samym kierunku

6

(T) TERMODYNAMIKA – Gaz doskonały

T. Równanie gazu doskonalego



robert.szczotka(at)gmail.com               

Fizyka i astronomia, I LO 2010

6

W czasie 

∆

t każda z cząsteczek uderzy w 

ś

cianę jeden raz a więc czas pomiędzy 

kolejnymi zderzeniami wynosi:

5

podstawiaj

ą

c do wzoru

Natomiast ci

ś

nienie gazu:

Otrzymujemy:

4

7

(T) TERMODYNAMIKA – Gaz doskonały

T. Równanie gazu doskonalego



robert.szczotka(at)gmail.com               

Fizyka i astronomia, I LO 2010

7

6

Ostatecznie:

V=a

3 

– obj

ę

to

ść

 naczynia [m

3

]

E

k,

ś

r

–

ś

rednia energia kinetyczna cz

ą

steczek gazu

2

2

3

3

3

2

3

2

⋅

⋅

=

⋅

=

a

mv

N

a

mv

N

p

ś

r

ś

r

Przekształcamy:

8

(T) TERMODYNAMIKA – Gaz doskonały

T. Równanie gazu doskonalego



robert.szczotka(at)gmail.com               

Fizyka i astronomia, I LO 2010

8

3. Równanie stanu gazu doskonałego

7

Ci

ś

nienie gazu w zbiorniku zamkni

ę

tym

ś

r

k

E

V

N

p

,

3

2

⋅

⋅

=

Je

ś

li zamiast

T

C

E

ś

r

k

⋅

=

,

T

C

V

N

p

⋅

⋅

⋅

=

3

2

Wielko

ś

ci: p, V i T charakteryzuj

ą

 gaz jako cało

ść

 

(s

ą

 to wi

ę

c wielko

ś

ci makroskopowe). Pozostałe 

wielko

ś

ci, dla danego gazu, s

ą

 niezmienne.

5

9

(T) TERMODYNAMIKA – Gaz doskonały

T. Równanie gazu doskonalego



robert.szczotka(at)gmail.com               

Fizyka i astronomia, I LO 2010

9

8

Przekształcaj

ą

c ostatni wzór otrzymujemy:

Jest to tzw. równanie stanu gazu doskonałego

NC

T

pV

3

2

=

const

T

pV

=

Tak wi

ę

c dla m=const mo

ż

emy zapisa

ć

lub

2

2

2

1

1

1

T

V

p

T

V

p

=