ROZWIĄZYWANIE BELEK

Zadanie S-1.

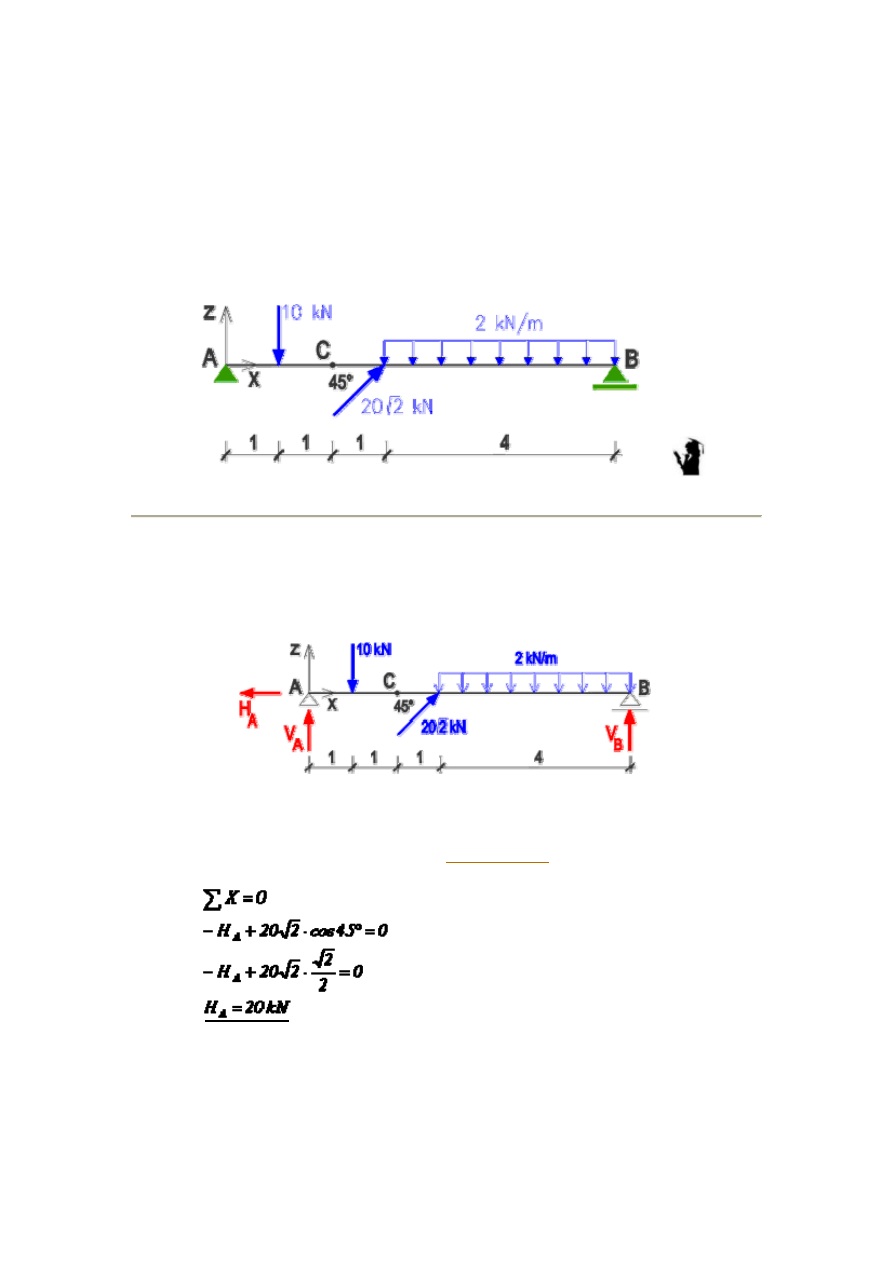
Znaleźć siły przekrojowe M, Q, N w punkcie C podanej belki.

Przykład 1.

Znaleźć siły przekrojowe M, Q, N w punkcie C podanej belki.

1. Obliczenie reakcji.

Obliczając reakcje, korzystamy z trzech

równań statyki

:

Układając równania statyki wygodnie jest stosować układ równań nie sprzężonych, tzn. z

każdego równania obliczamy tylko jedną niewiadomą. W przypadku jednego ciała

sztywnego (jedna tarcza, belka bez przegubów) zawsze jest to możliwe. Dzięki układowi

równań nie sprzężonych rozwiązanie jest szybsze a błąd popełniony w jednym równaniu

nie przenosi się na równania pozostałe.

Aby sprawdzić poprawność obliczenia reakcji postępujemy odwrotnie - układamy takie

równanie w którym wystąpią wszystkie reakcje. W naszym przykładzie może to być na

przykład równanie momentu względem punktu D o współrzędnych D(2,1).

Powyższa niedokładność jest dopuszczalna wynika bowiem z zaokrągleń poczynionych
przy obliczaniu reakcji.

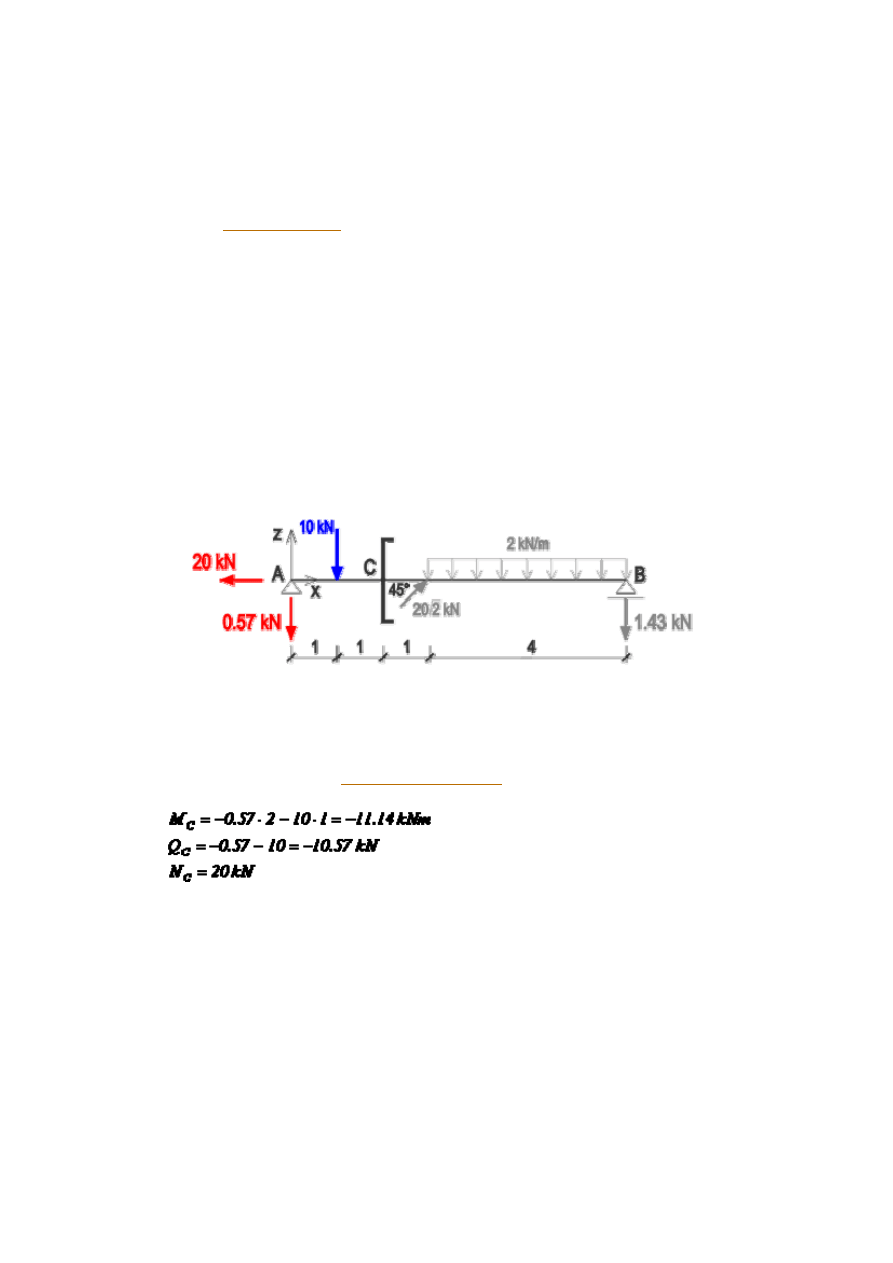
2. Obliczenie sił przekrojowych w punkcie C.

Aby znaleźć

siły przekrojowe

w punkcie C należy przez ten punkt poprowadzić przekrój,

dzielący belkę na dwie części i zredukować w punkcie C układ sił zewnętrznych
przyłożonych do jednej z tych części. Bez względu na to, którą część weźmiemy do
redukcji otrzymamy ten sam wynik (wartości sił przekrojowych w danym punkcie są
stałe). Praktycznie wybiera się tą część belki do której jest przyłożony mniej
skomplikowany układ sił, w celu uproszczenia obliczeń.
W naszym przykładzie, w celach dydaktycznych, dokonamy obliczeń redukując układ sił
zewnętrznych zarówno z lewej jak i z prawej strony punktu C.

2.1. Redukcja układu sił zewnętrznych przyłożonych do lewej części belki.

Przy obliczaniu wypadkowej zredukowanego układu sił będziemy od razu rozkładali ją
na siłę podłużną N (równoległą do osi belki) i siłę poprzeczną Q (prostopadłą do osi
belki). Pamiętając o przyjętej

konwencji znakowania

zapiszemy:

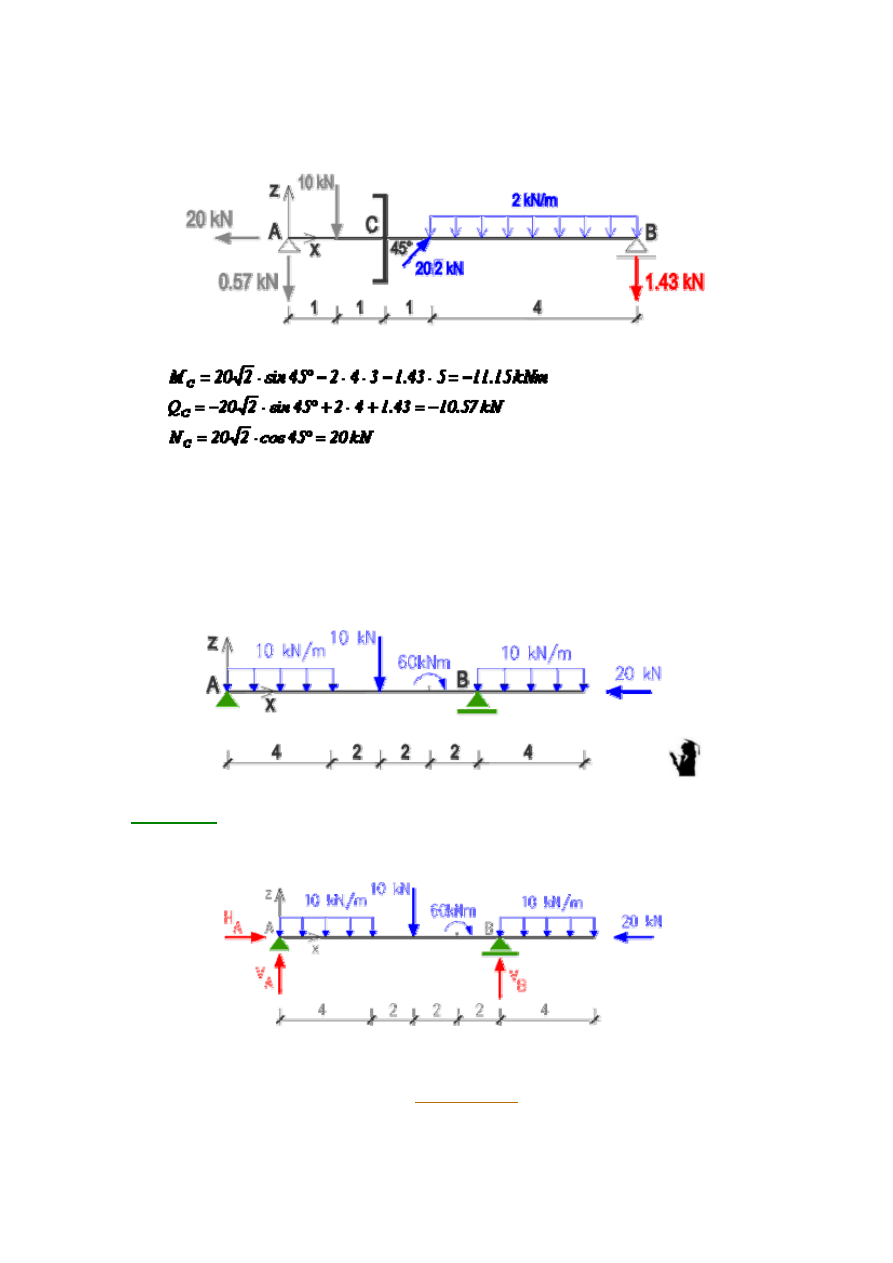
2.2. Redukcja układu sił zewnętrznych przyłożonych do prawej części belki.

Zadanie S-2.

Dla podanej belki napisać równania i sporządzić wykresy sił

przekrojowych M, Q, N.

Przykład 2.

Dla podanej belki napisać równania i sporządzić wykresy sił przekrojowych

M, Q, N.

1. Obliczenie reakcji.

Obliczając reakcje, korzystamy z trzech

równań statyki

:

Sprawdzenie:

2. Funkcje sił przekrojowych

Budując równania jakiejkolwiek funkcji, musimy przyjąć układ współrzędnych, w
którym te równania zapiszemy. Dla belek prostych najwygodniej jest przyjąć układ jak na
rysunku, tzn. na początku belki. Zdarza się jednak, że dla uproszczenia obliczeń,
przyjmuje się dwa układy współrzędnych (na obu końcach belki). Sposób przyjęcia
układu współrzędnych nie ma oczywiście żadnego wpływu na wykres siły przekrojowej
jaki otrzymamy na podstawie jej równania.

Przed przystąpieniem do układania funkcji

sił przekrojowych

, należy w belce wyznaczyć

tzw. punkty i przedziały charakterystyczne. Powodem jest inna postać funkcji sił
przekrojowych w każdym przedziale charakterystycznym. Dla każdego przedziału należy
napisać osobne równanie.

Punkty charakterystyczne są to:
- początek i koniec belki,
- punkty podparcia belki,

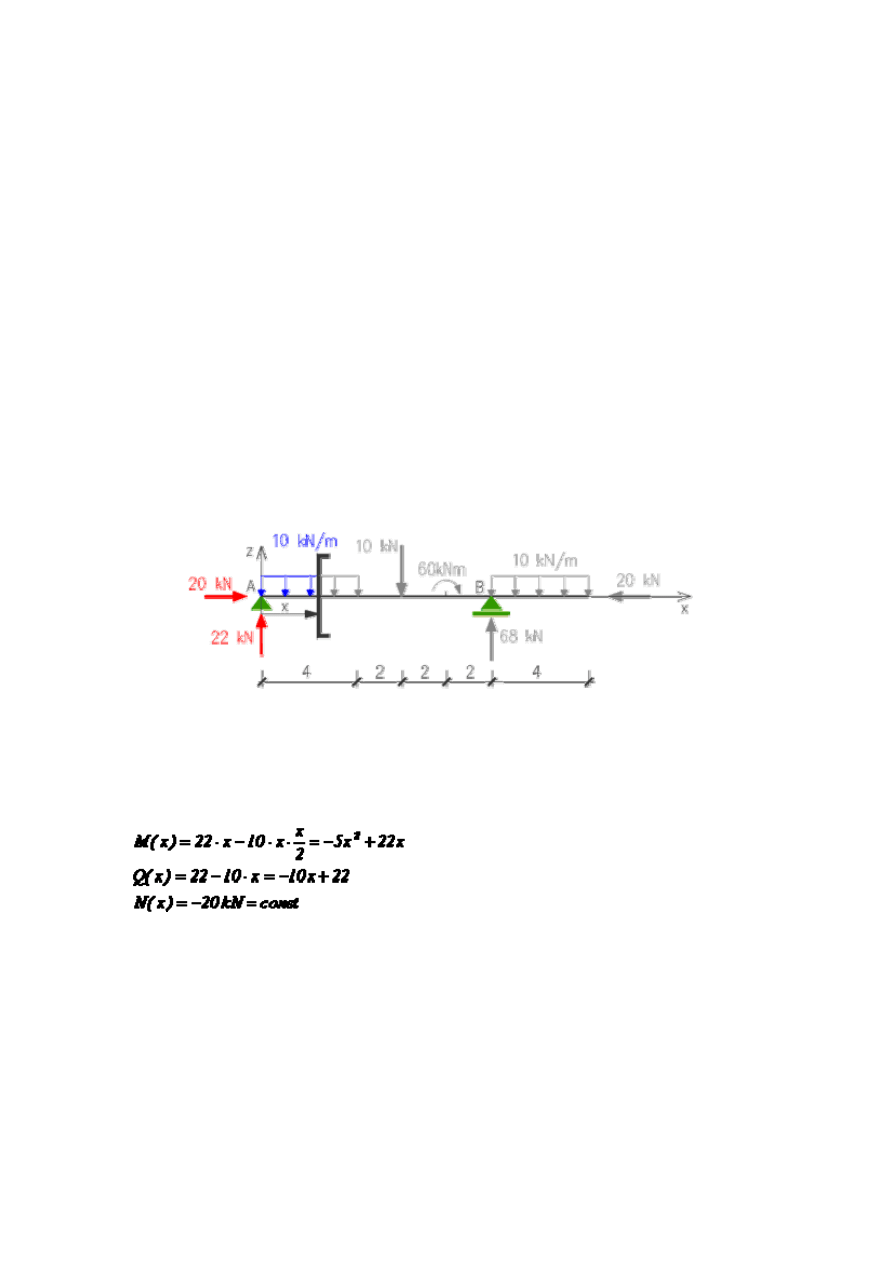
- miejsca przyłożenia sił i momentów skupionych,
- początek i koniec obciążenia ciągłego.

Przedziały charakterystyczne to odcinki belki pomiędzy punktami
charakterystycznymi.

W analizowanej belce występuje pięć przedziałów charakterystycznych.

Przedział: 0 < x < 4

Pisząc równania w pierwszym przedziale dokonujemy podziału belki przekrojem
przechodzącym przez ten przedział i redukujemy układ sił zewnętrznych położonych z
lewej części przekroju (można oczywiście redukować układ sił po prawej stronie ale jest
to bardziej pracochłonne).

Położenie przekroju nie jest ustalone w konkretnym punkcie, ale w odległość x od
początku układu współrzędnych. Zapisując wynik redukcji układu sił zewnętrznych w
miejscu o odciętej x otrzymujemy "automatycznie" funkcję danej wielkości.

Przedział: 4 < x < 6

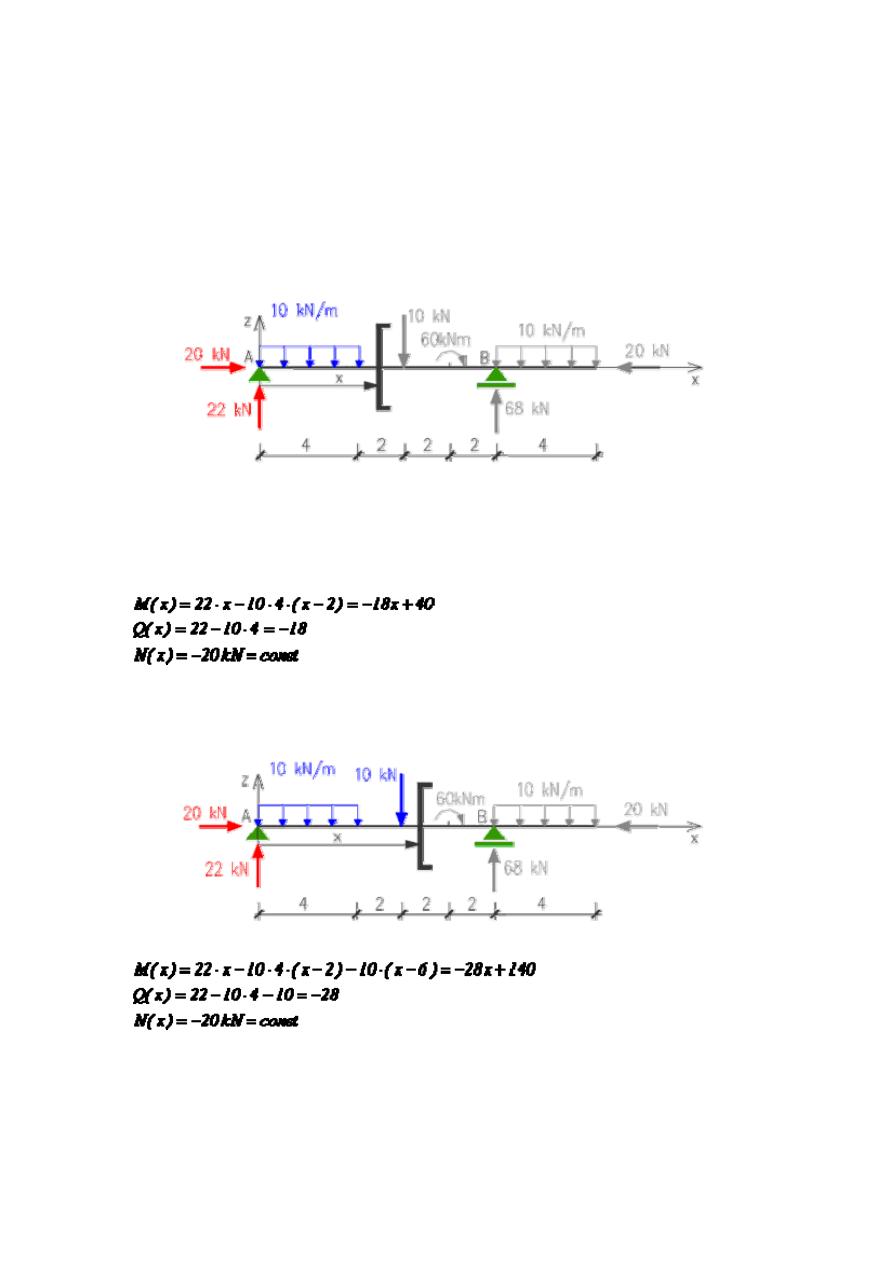
Analogicznie do poprzedniego przedziału dzielimy belkę przekrojem przechodzącym

przez analizowany przedział i redukujemy układ sił zewnętrznych położonych po jego

lewej stronie.

Należy zwrócić uwagę na fakt, że do redukcji należy wziąć teraz pełną wartość
obciążenia ciągłego i że położenie wypadkowej tego obciążenia jest już ustalone (x = 2).
W pierwszym przedziale położenie wypadkowej było zależne od położenia przekroju.

Przedział: 6 < x < 8

Przedział: 8 < x < 10

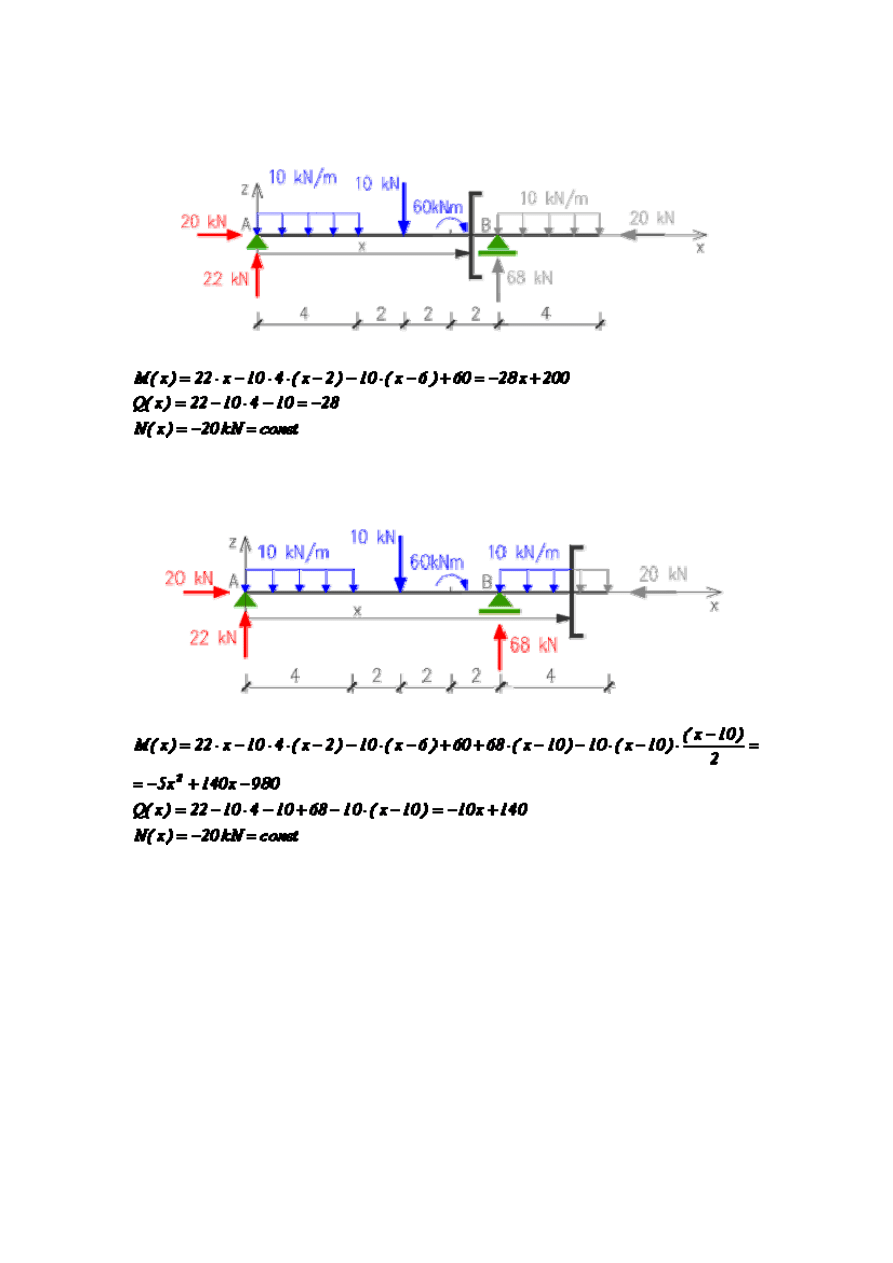
Przedział: 10 < x < 14

Wyznaczyliśmy funkcje sił przekrojowych w każdym przedziale możemy zatem przejść
do rysowania wykresów. Zanim to jednak zrobimy, zaznaczmy, że sposób tworzenia
równań w dwóch ostatnich przedziałach został tutaj zamieszczony tylko w celach
dydaktycznych. W praktyce, gdy belka ma więcej niż trzy, cztery przedziały
charakterystyczne, przyjmuje się nowy układ współrzędnych na drugim końcu belki, co
znacznie upraszcza obliczenia. Zaletę takiego podejścia pokażemy na przykładzie.
Przyjmiemy mianowicie układ współrzędnych (x

1

,z) jak na rysunku i wyznaczymy dla

porównania funkcje sił przekrojowych w dwóch ostatnich przedziałach belki.

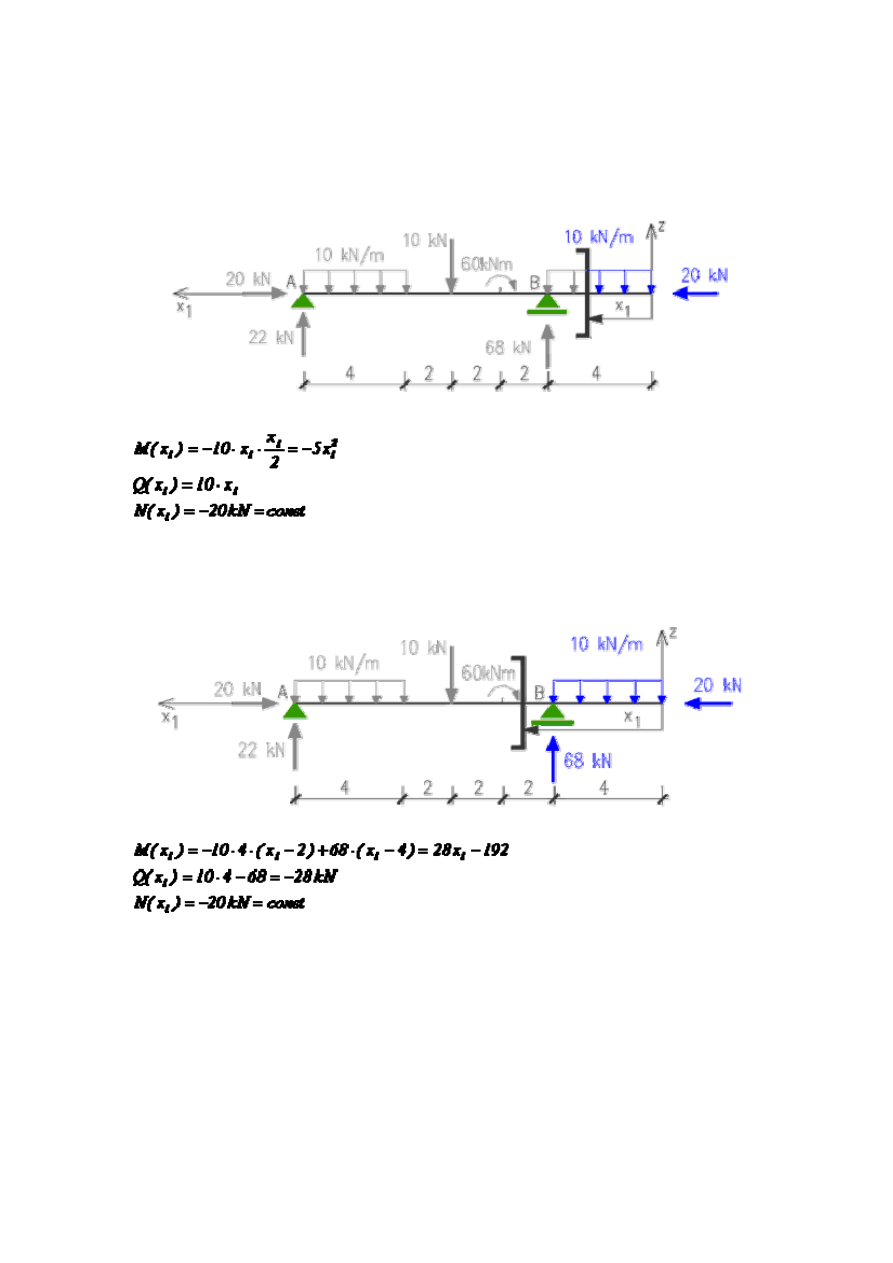
Przedział: 0 < x

1

< 4

Przedział: 4 <

x

1

< 6

W wyniku prostszych obliczeń otrzymaliśmy funkcje, które w przyjętym układzie

współrzędnych dadzą te same wykresy jak w układzie (x,z). Dla sprawdzenia można

porównać wartości sił przekrojowych w odpowiadających sobie punktach

charakterystycznych obliczone dla obu układów równań. Weźmy na przykład

przedostatni przedział:

8 < x < 10

2 < x

1

< 6

3. Wykresy sił przekrojowych

Po wyznaczeniu funkcji sił przekrojowych narysowanie ich wykresów nie przedstawia
żadnych trudności. Ponieważ jednak będzie się od studentów wymagać dużej biegłości w
rysowaniu tych wykresów, zwrócimy uwagę na kilka właściwości, których znajomość
znacznie uprości zadanie.

Gdy przyjrzymy się funkcjom momentu i siły poprzecznej w poszczególnych
przedziałach spostrzegamy, że siła poprzeczna jest pochodną momentu. Obciążenie
ciągłe q(x) jest pochodną siły poprzecznej pomnożoną przez (-1). Nie jest to przypadek,
zachodzą bowiem zależności:

zobacz dowód

W naszym przykładzie mamy:

0 < x < 4

4 < x < 6

Z zależności różniczkowych pomiędzy siłami przekrojowymi wynikają następujące
wnioski, wykorzystywane przy rysowaniu wykresów:

•

Jeżeli w przedziale charakterystycznym obciążenie ciągłe q(x) = 0, to wykres sił
poprzecznych w tym przedziale jest stały (aby narysować wykres wystarczy
wyznaczyć wartość siły poprzecznej w jednym punkcie), natomiast wykres
momentów zginających jest liniowy (do narysowania wykresu wystarczą dwie
wartości, policzone na przykład w punktach charakterystycznych na końcach
przedziału).

•

Jeżeli w przedziale charakterystycznym obciążenie ciągłe jest równomiernie
rozłożone q(x) = const, to wykres siły poprzecznej jest liniowy, a wykres
momentu zginającego parabolą drugiego stopnia, (itd. funkcja siły poprzecznej
zawsze o stopień wyższa od funkcji obciążenia q(x), a funkcja momentu o stopień
wyższa od funkcji siły poprzecznej).

•

Dana funkcja ma wartość ekstremalną w tym punkcie gdzie jej pochodna jest
równa zeru i jest to maksimum, gdy pochodna zmienia w tym punkcie znak z "+"
na "-" a minimum gdy zmienia znak z "-" na "+". Zatem ekstremalne wartości
na wykresie momentu zginającego występować będą wszędzie tam gdzie funkcja
siły poprzecznej zmienia znak.

•

Krzywoliniowy wykres momentu zginającego w każdym punkcie
charakterystycznym jest styczny do prostej, której współczynnik kierunkowy jest
równy wartości siły poprzecznej w tym punkcie. Liniowy wykres momentu jest
odchylony od osi belki o kąt, którego tangens jest równy wartości siły
poprzecznej w tym samym przedziale charakterystycznym. Powyższe zależności
wynikają z

interpretacji geometrycznej pochodnej

funkcji.

Widzimy zatem, że wykres siły poprzecznej należy narysować przed wykresem momentu
zginającego, aby właściwie wykorzystać powyższe właściwości.

Wykresy sił przekrojowych należy rysować w skali, która umożliwi dokładne pokazanie
wszystkich charakterystycznych elementów wykresu. Skala do każdego wykresu może
być inna.

Przed przystąpieniem do rysowania wykresów prowadzimy pod schematem belki linie
odnoszące przechodzące przez wszystkie punkty charakterystyczne. W każdym punkcie
charakterystycznym wyliczamy wartości poszczególnych sił przekrojowych, redukując
układ sił zewnętrznych z prawej lub z lewej strony tego punktu.

Siła podłużna N(x)

Wartości siły podłużnej są jednakowe we wszystkich przedziałach charakterystycznych:

N(x) = 20 kN = const.
Wykres siły podłużnej nie wymaga komentarza.

Siła poprzeczna Q(x)

Wyznaczamy wartości siły poprzecznej w każdym punkcie charakterystycznym,
pamiętając o tym że w punktach, w których jest przyłożona siła skupiona (czynna lub
bierna) te wartości musimy wyznaczyć z lewej i prawej strony każdego punktu.

Powstałe w ten sposób punkty łączymy linią prostą. Na odcinkach AC i BF wykres jest
liniowo zmienny, gdyż występuje tu obciążenie q = 10 kN/m. Na pozostałych odcinkach
wykres siły poprzecznej jest stały.
Dodatkowo spostrzegamy, że na odcinku AC funkcja Q(x) osiąga wartość zero, a więc w
tym punkcie moment zginający będzie miał wartość ekstremalną. Ponieważ siła
poprzeczna zmienia w tym punkcie znak z "+" na "-" będzie to maksimum.

Moment zginający M(x)

Tak jak w przypadku siły poprzecznej redukujemy odpowiednie układy sił zewnętrznych
w punktach charakterystycznych.

Należy jeszcze wrócić do przedziału AC celem wyliczenia momentu maksymalnego.
Punkt, w którym moment przyjmuje wartość maksymalną w tym przedziale
wyznaczymy, przyrównując do zera równanie funkcji siły poprzecznej w tym przedziale:

Współrzędną tego punktu można również wyznaczyć bezpośrednio z wykresu,
korzystając z twierdzenia Talesa:

Moment maksymalny:

We wszystkich przedziałach, gdzie obciążenie q = 0 wykres momentów jest liniowy.
Wartości w punktach charakterystycznych wystarczą zatem, aby narysować wykres w
tych przedziałach.
W przedziałach AC i BF wykres momentu jest parabolą drugiego stopnia. Do
narysowania wykresu w tych przedziałach wykorzystujemy następujące dane: wartości na
końcach przedziału, miejsca ekstremum i jego wartości oraz styczne do wykresu na
końcach przedziału.

Tak więc w przedziale AC:

•

na początku przedziału wykres styczny do prostej o współczynniku kierunkowym
m = 22

•

na końcu przedziału wykres styczny do prostej o współczynniku kierunkowym
m = - 18 (jednocześnie jest to wykres momentu w sąsiednim przedziale)

•

wartość ekstremalna w punkcie x

0

= 2.2 m, tutaj oczywiście wykres styczny do

linii poziomej.

W przedziale BF:

•

na początku przedziału wykres styczny do prostej o współczynniku kierunkowym
m = 40

•

na końcu przedziału wykres styczny do linii poziomej (w tym punkcie moment
osiąga wartość maksymalną bo siła poprzeczna jest równa zeru).

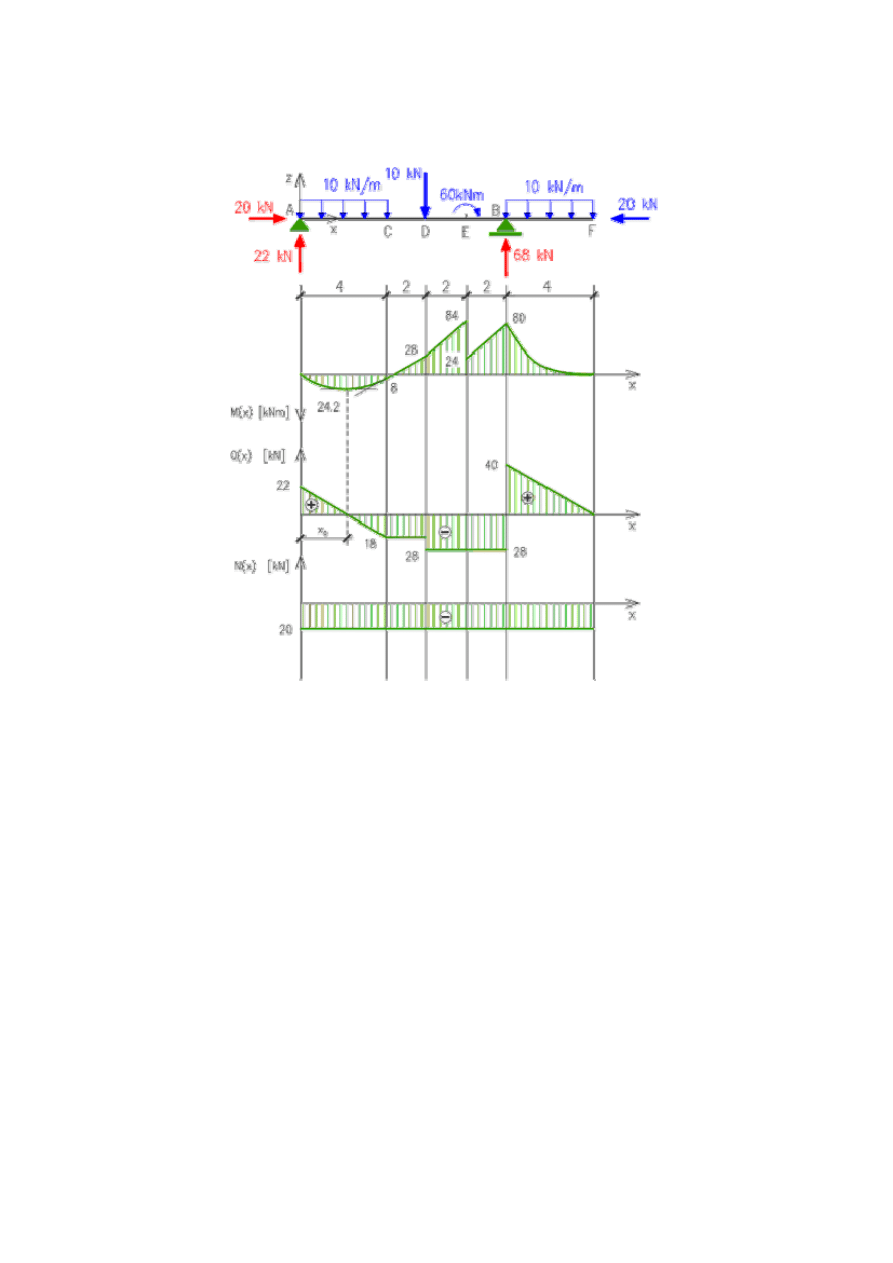
UWAGI:

Wypukłość wykresu momentu zginającego określa zwrot obciążenia ciągłego - wykres
jest zawsze wypukły w kierunku działania obciążenia.

Wykres momentów (albo styczna do części krzywoliniowej) ulega załamaniu w tych
punktach charakterystycznych, gdzie działa siła skupiona. W tych punktach bowiem na
wykresie siły poprzecznej występuje skok wartości.

W miejscu przyłożenia do belki momentu skupionego nie ma na wykresie załamania, jest
tylko skok o wartość przyłożonego momentu, natomiast sąsiednie fragmenty wykresu są
równoległe.

W naszym przykładzie odcinki DE i EB wykresu momentu są do siebie równoległe. Ich
kąt nachylenia spełnia zależność:

W przedziale CD:

Zadanie S-3.

Dla podanej belki napisać równania i sporządzić wykresy sił

przekrojowych M, Q, N.

Zadanie S-4.

Dla podanej belki napisać równania i sporządzić wykresy sił

przekrojowych M, Q, N.

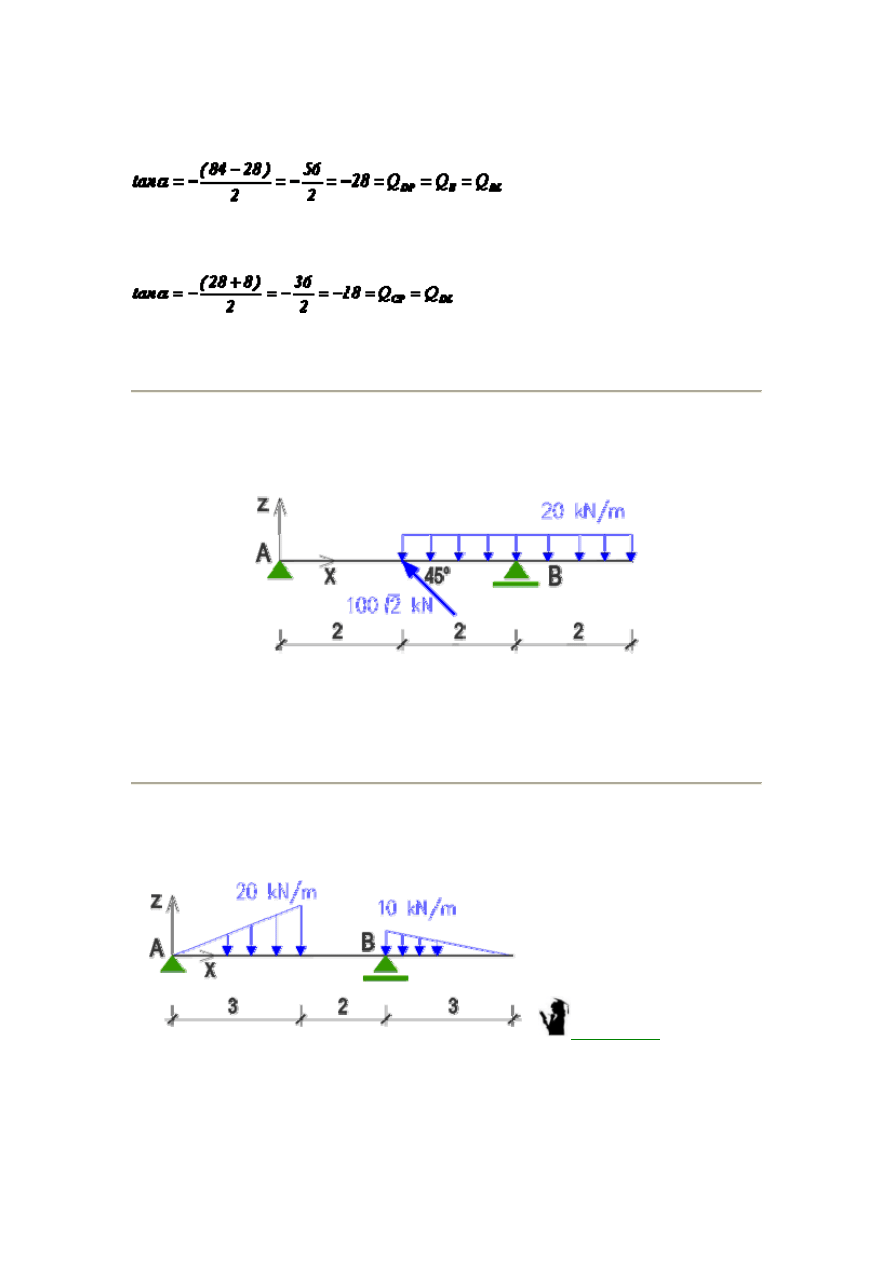
Przykład 4.

Dla podanej

belki napisać równania i sporządzić wykresy sił przekrojowych M, Q, N.

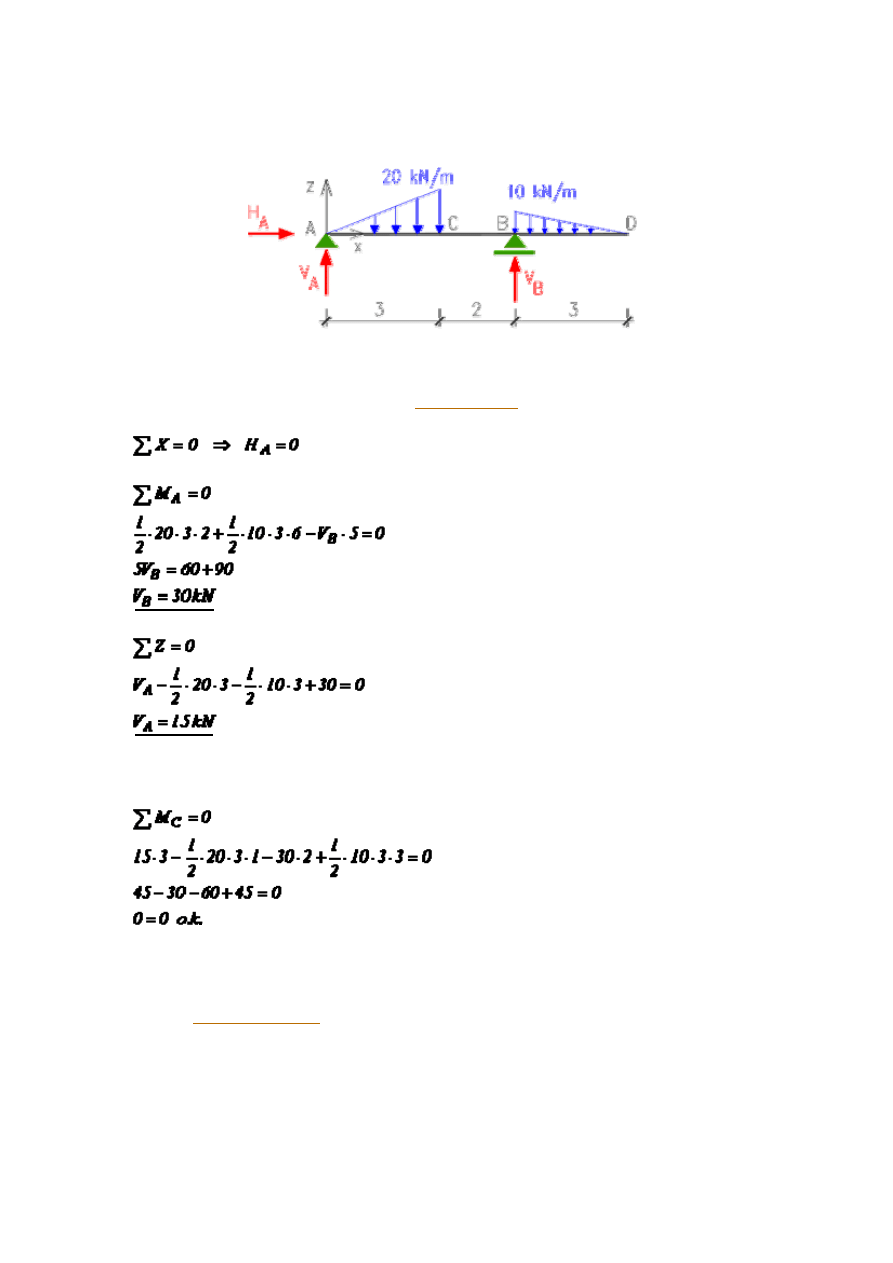
1. Obliczenie reakcji.

Obliczając reakcje, korzystamy z trzech

równań statyki

:

Sprawdzenie:

2. Funkcje sił przekrojowych

Funkcje

sił przekrojowych

zapiszemy w kolejnych przedziałach, przyjmując jeden układ

współrzędnych, a następnie pokażemy jak upraszają się obliczenia w ostatnim przedziale
charakterystycznym po zmianie układu.

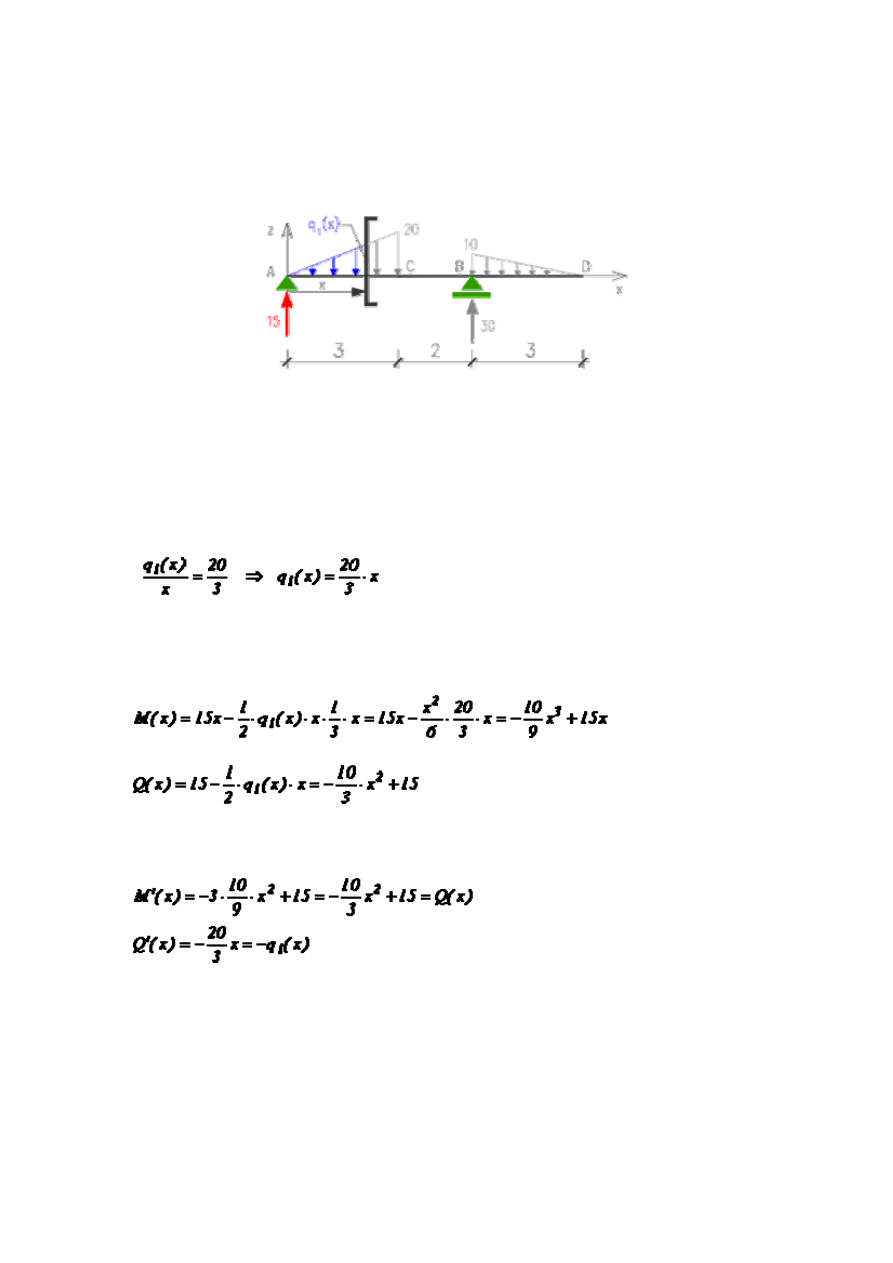
Przedział: 0 < x < 3

Obciążenie ciągłe jest rozłożone w sposób liniowo zmienny, zatem dla każdego przekroju
musimy określić jego wartość. Należy zatem w pierwszej kolejności wyznaczyć funkcję
obciążenia ciągłego. Możemy to zrobić pisząc jej równanie w przyjętym układzie
współrzędnych (prosta przechodząca przez punkty (0, 0) i (3, 20)) lub korzystając
z proporcji w trójkącie:

Teraz możemy napisać równania sił przekrojowych, redukując obciążenie trójkątne o
zmiennej rzędnej q

1

(x).

Spełnione są oczywiście zależności różniczkowe między siłami przekrojowymi:

Przedział: 3 < x < 5

W tym przedziale do redukcji będziemy brać całkowitą wartość wypadkowej obciążenia

ciągłego. Wypadkowa jest ustalona w punkcie x = 2.

Przedział: 5 < x < 8

Jak już powiedziano na wstępie, dużo szybciej otrzymamy równania sił przekrojowych w

tym przedziale, przyjmując układ współrzędnych na końcu belki. Teraz jednak w celach

dydaktycznych napiszemy te równania nie zmieniając na razie układu.

Widzimy, że obciążenie ciągłe w tym przedziale zmienia się liniowo - od wartości

największej do zerowej. W związku z tym do redukcji należy wziąć obciążenie w

kształcie trapezu. Wypadkową tego obciążenia jest oczywiście równa polu powierzchni

tego trapezu i położona jest w jego środku ciężkości. Unikniemy jednak wyznaczania tej

wypadkowej stosując

zasadę superpozycji

. Pozwala ona zastąpić dane obciążenie

trapezem, innym statycznie równoważnym obciążeniem, złożonym z prostokąta i

trójkąta.

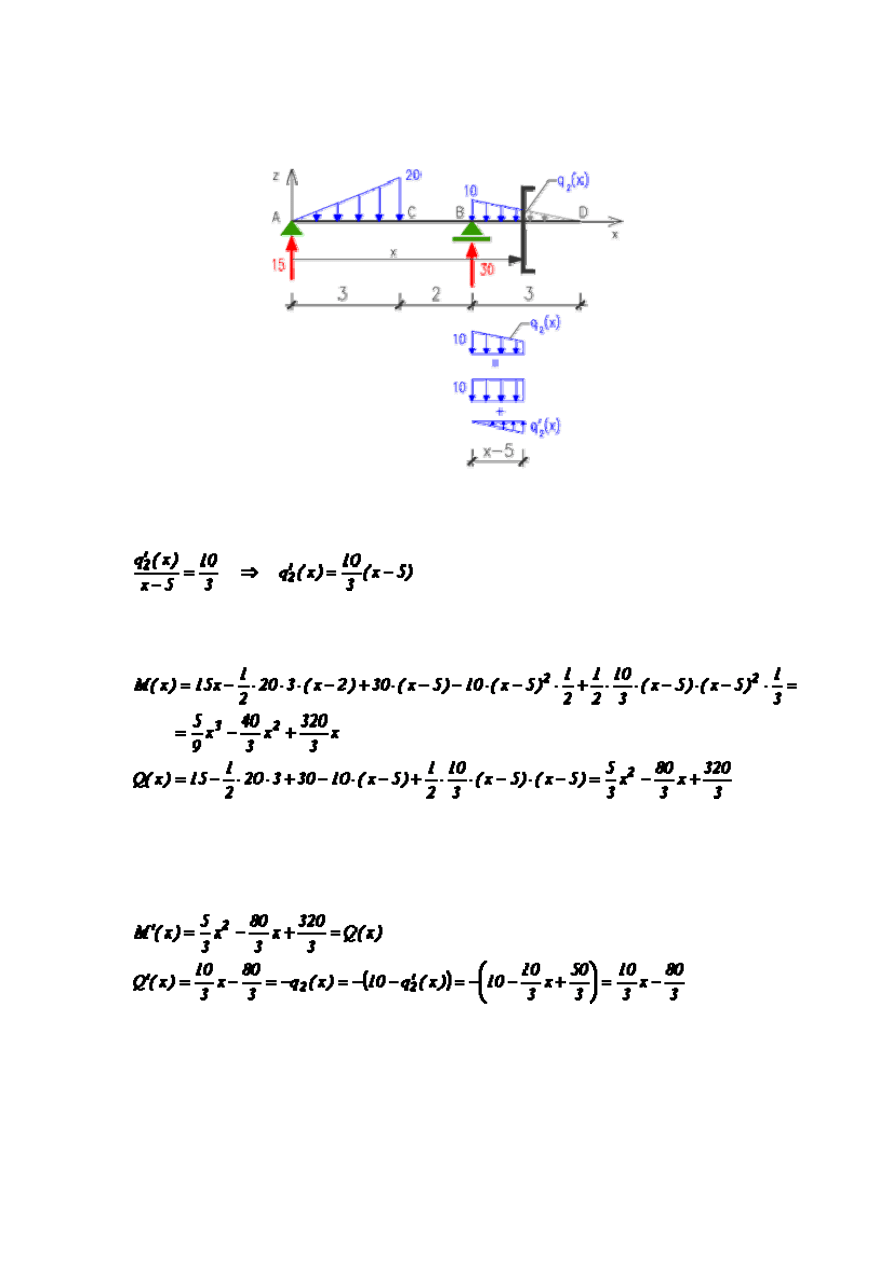
Funkcję obciążenia zmiennego q'

2

(x) korzystając z proporcji w trójkącie:

Funkcje sił przekrojowych możemy teraz zapisać następująco:

Sprawdzamy zależności różniczkowe:

Przedział: 0 < x

1

< 3

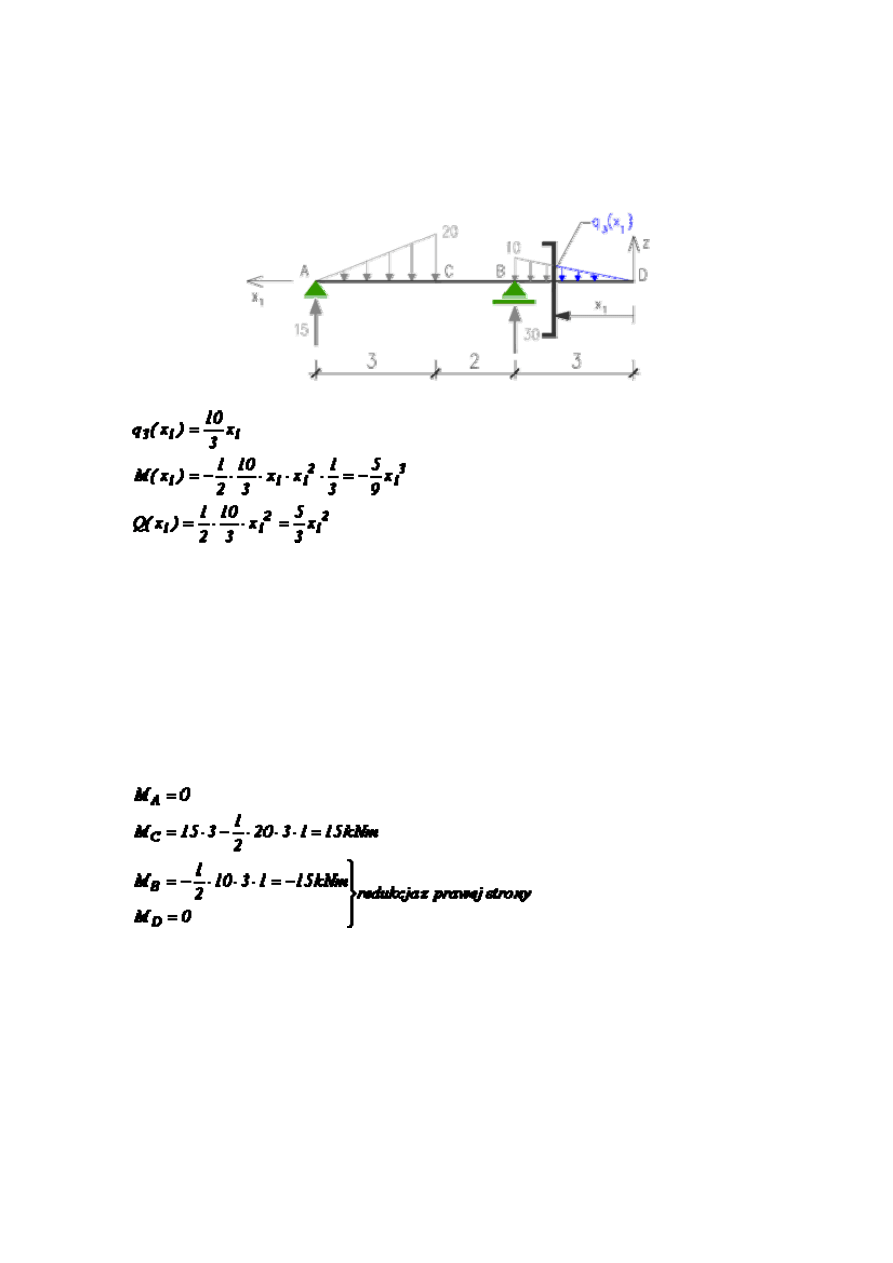
Po zmianie układu współrzędnych sposób tworzenia równań znacznie się upraszcza.

Podstawiając do powyższych równań wartości w punktach charakterystycznych , można

się przekonać, że wyniki są identyczne z otrzymanymi dla układu Oxz.

3. Wykresy sił przekrojowych

Przed narysowaniem wykresów momentu zginającego i siły poprzecznej, obliczymy
wartości tych sił w punktach charakterystycznych belki:

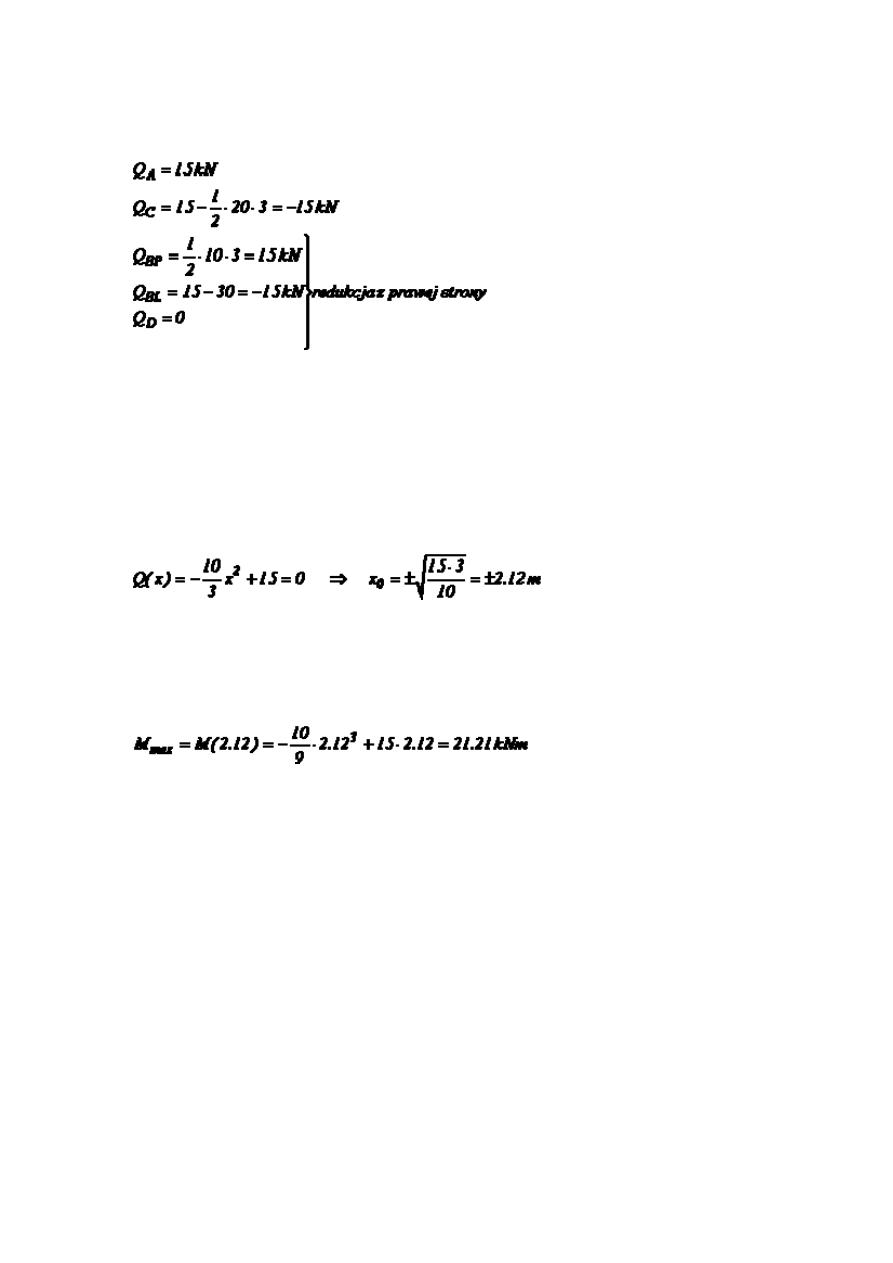
Spostrzegamy, że funkcja poprzeczna w przedziale AC zmienia znak (z +15 na -15),
musimy zatem określić jej miejsce zerowe, gdyż w tym punkcie moment ma wartość
maksymalną. Ponieważ wykres funkcji jest parabolą, nie możemy miejsca zerowego
obliczyć bezpośrednio z wykresu, jak to ma miejsce w przypadku wykresu liniowego,
czyli wtedy, gdy obciążenie ciągłe jest równomiernie rozłożone. Konieczne jest zatem
skorzystanie z równania siły poprzecznej w tym przedziale:

Wartość ujemna nie należy do dziedziny rozwiązania, ponieważ punkt o takiej
współrzędnej nie jest położony na belce. Wybieramy zatem punkt o współrzędnej x

0

=

2.12 m jako miejsce maksymalnego momentu.

Po obliczeniu wszystkich potrzebnych wartości możemy przystąpić do narysowania
wykresów.

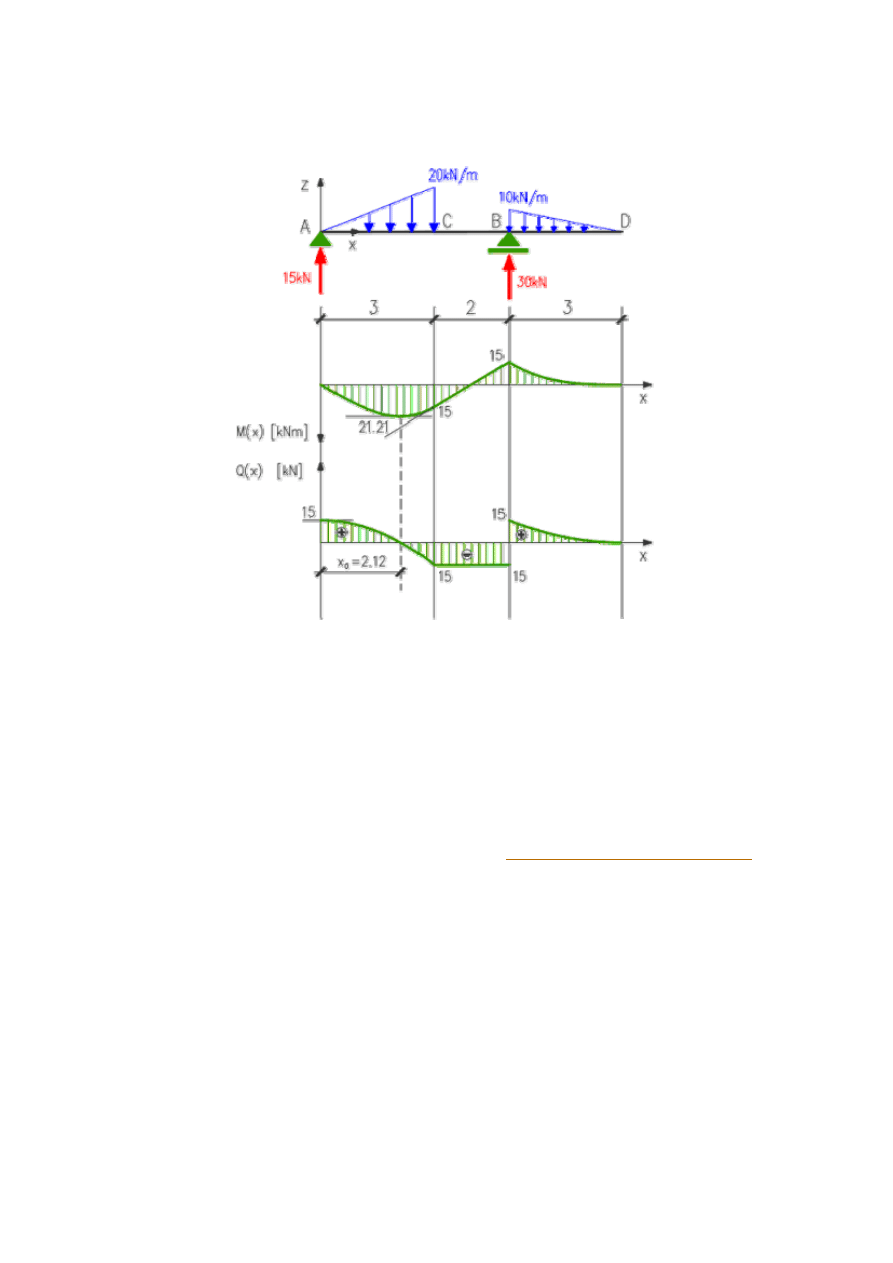
Rysunek rozpoczynamy od wykresu siły poprzecznej. W przedziale AC wykres jest
parabolą, przechodzącą na początku przedziału przez 15 na końcu przez -15 i w punkcie

x

0

= 2.12 przez zero. Dodatkowa informacja jaką mamy o tym wykresie wynika z

zależności różniczkowej między siłą poprzeczną a obciążeniem ciągłym.
Ponieważ obciążenie jest pochodną siły poprzecznej, wartość obciążenia q w danym
punkcie jest równa tangesowi kąta nachylenia stycznej do wykresu siły poprzecznej. Jest
to analogiczna zależność jak między wartością siły poprzecznej i nachyleniem stycznej
do wykresu momentów. (

Patrz przykład 2

).

Mamy zatem w punkcie A wartość obciążenia q = 0 więc wykres siły poprzecznej musi
być styczny do linii poziomej.
Ta informacja, plus wartości funkcji na końcach przedziału, wystarczają aby poprawnie
określić wypukłość wykresu.

UWAGA: Do określenia wypukłości wykresu siły poprzecznej nie ma ogólnej
zależności, jak w przypadku wykresu momentu zginającego, który jest zawsze wypukły
w kierunku działania obciążenia. Wypukłość wykresu siły poprzecznej określamy
każdorazowo, korzystając z zależności różniczkowych.

Na odcinku CB wykres siły poprzecznej jest stały. Na odcinku BD mamy znów funkcję
paraboliczną, o której wiemy, że na początku przedziału przechodzi przez 15, na końcu
przedziału przez zero, oraz że na końcu przedziału wykres musi być styczny do linii
poziomej (bo w tym punkcie obciążenie q = 0).

Wykres momentów w przedziale AC jest funkcją trzeciego stopnia, która osiąga wartość
maksymalną w punkcie x

0

= 2.12 oraz jest styczna do wykresu liniowego w przedziale

CB. Z kolei w przedziale BD funkcja trzeciego stopnia jest styczna w punkcie D do linii
poziomej, bo tutaj siła poprzeczna Q

D

= 0.

Wypukłość wykresu momentów zawsze w kierunku działania obciążenia.

Zadanie S-5.

Dla podanej belki przegubowej sporządzić wykresy sił przekrojowych M,

Q, N.

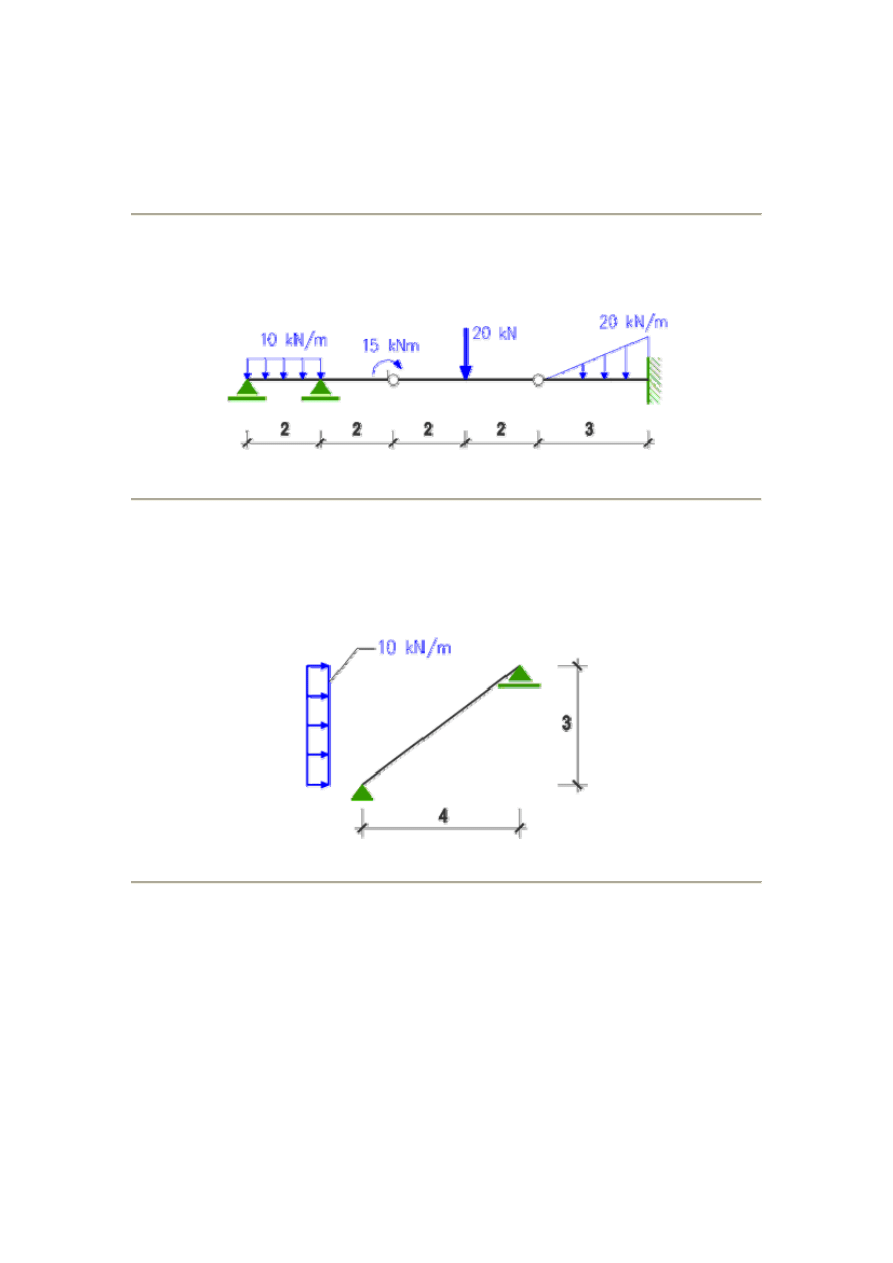
Przykład 5.

Dla podanej belki przegubowej sporządzić wykresy sił przekrojowych

M, Q, N.

1. Obliczenie reakcji.

Przed przystąpieniem do wyznaczenia reakcji należy zbadać

geometryczną niezmienność

i statyczną wyznaczalność konstrukcji. Podana belka składa się z czterech tarcz

połączonych ze sobą przegubami (dwa pręty) oraz z podłożem za pomocą podpór.
Podpory występujące w belce można zastąpić pojedynczymi prętami - zamocowanie
trzema, a podpory przegubowo-przesuwne jednym. Mamy zatem całkowitą liczbę prętów
łączących tarcze:

Liczba tarcz wynosi t = 4, zatem spełniony jest warunek konieczny geometrycznej
niezmienności:

Spostrzegamy też, że żadna z tarcz nie może poruszać się względem drugiej i względem
podłoża, zatem stwierdzamy, że układ jest geometrycznie niezmienny.
Spełnienie powyższego równania jest też warunkiem koniecznym i wystarczającym
statycznej niewyznaczalności, gdyby bowiem prawa strona równania była większa od
lewej, mielibyśmy za dużo niewiadomych (lub co na jedno wychodzi za mało równań)
aby móc wyliczyć reakcje.
W analizowanej belce do wyznaczenia jest sześć sił reakcji i taka sama jest liczba
niezależnych równań, które możemy ułożyć: trzy równania równowagi i trzy równania
przegubów. Te ostatnie wynikają z warunku, że aby konstrukcja była w równowadze, to
układ sił przyłożonych z każdej strony przegubu nie może powodować obrotu części
belki w tym przegubie. Brak obrotu oznacza zerowanie się momentu od wszystkich sił
przyłożonych po jednej stronie przegubu.
Wyznaczając reakcje musimy więc rozwiązać układ sześciu równań liniowych:

Po obliczeniu reakcji można przystąpić do rysowania wykresów sił przekrojowych,

zanim to jednak zrobimy, pokażemy inny sposób na obliczenie reakcji w belkach

przegubowych. Sposób podany powyżej, który można nazwać analitycznym, ma jedną

wadę, mianowicie rozwiązanie układu równań jest pracochłonne. Oczywiście jeżeli

dysponujemy programem komputerowym (lub dobrym kalkulatorem) kwestia

pracochłonności w ogóle nie ma znaczenia i wtedy lepsza wydaje się właśnie metoda

analityczna. Jednak nie zawsze możemy skorzystać z komputera (kolokwium) i wtedy

lepiej jest stosować metodę, polegającą na zastąpieniu belki przegubowej belkami

prostymi.

Procedura rozwiązywania belek przegubowych metodą rozkładu na belki proste jest
następująca:

1. Obliczenie reakcji poziomej dla całej belki. W statycznie wyznaczalnej belce reakcja
pozioma może być tylko jedna, możemy ją zatem policzyć z warunku zerowania się
sumy rzutów sił na kierunek osi belki. W przypadku, gdy na belkę nie działają siły
ukośne i poziome, liczba reakcji poziomych nie ma znaczenia - wszystkie muszą być
równe zero, co wynika z zasady akcji i reakcji. Jeżeli nie ma działania w danym kierunku
- nie pojawi się również przeciwdziałanie.
2. Wykluczenie w dalszej analizie sił poziomych.
3. Rozkład na belki proste poprzez rozcięcie w przegubach. Belka przegubowa składa
się z kilku tarcz połączonych ze sobą przegubami. Po rozcięciu w przegubach dostaniemy
pojedyncze tarcze, czyli belki proste. Należy teraz wyodrębnić te belki, które są
geometrycznie niezmienne, czyli posiadają podpory (jedno utwierdzenie lub dwie
podpory przegubowe lub utwierdzenie z pionowym przesuwem i podporę przegubową)
uniemożliwiające ruch belek. Nie analizujemy już ruchów poziomych. Belki
geometrycznie niezmienne rysuje się na samym dole a nad nimi belki pozostałe, w taki
sposób, że swobodny koniec zastępuje się podporą przegubową. Tak narysowane belki

górne, również muszą być geometrycznie niezmienne, z czego wynika, że belka która
miała na obu końcach przeguby musi być narysowana nad dwiema innymi belkami
(fizycznie oznacza to, że taka belka opiera się na belkach sąsiednich).
4. Obliczenie reakcji w belkach prostych. Obliczamy najpierw belki górne, stopniowo
schodząc w dół. Reakcje od belek górnych przekazujemy na belki dolne, pamiętając o
zmianie zwrotu reakcji.
5. Narysowanie wykresów. Wykresy sił przekrojowych można rysować dla każdej belki
prostej oddzielnie lub od razu dla całości. Sprawdzeniem poprawności rozwiązania mogą
być przeguby, w których moment musi być równy zeru, a na wykresie siły poprzecznej
nie powinno być skoku wartości (chyba że w przegubie jest przyłożona siła poprzeczna).

2. Rozkład na belki proste.

Przed rozkładem na belki proste obliczamy poziomą reakcję w utwierdzeniu. Ponieważ
do belki nie przyłożono żadnych sił poziomych więc ta reakcja jest równa zeru.
Rozcinamy belkę w przegubach i analizujemy powstałe w ten sposób belki proste. Idąc
od lewej strony spostrzegamy, że belka AB jest geometrycznie niezmienna (wspornik),
narysujemy ją zatem na samym dole. Następna belka nie posiada żadnej podpory, jest
chwiejna i musi się opierać na dwóch sąsiednich belkach. Taka belka zawsze będzie
narysowana na samej górze. Belka CE posiada jedną podporę przegubową może zatem
stanowić podparcie dla belki BC, sama jednak musi się opierać na innej belce. Tym
oparciem może być belka EG, która jest geometrycznie niezmienna (belka swobodnie
podparta). Powyższa analiza daje również odpowiedź co do geometrycznej
niezmienności całego układu. Gdyby belka EG miała tylko jedną podporę nie mogłaby
stanowić oparcia dla belki CE i cały układ byłby chwiejny.
Na rysunku poniżej przedstawiono rozkład na belki proste. Podpory i reakcje przyjęte w
miejscach przegubów zaznaczono innym kolorem niż podpory rzeczywiście przyłożone
do belki.

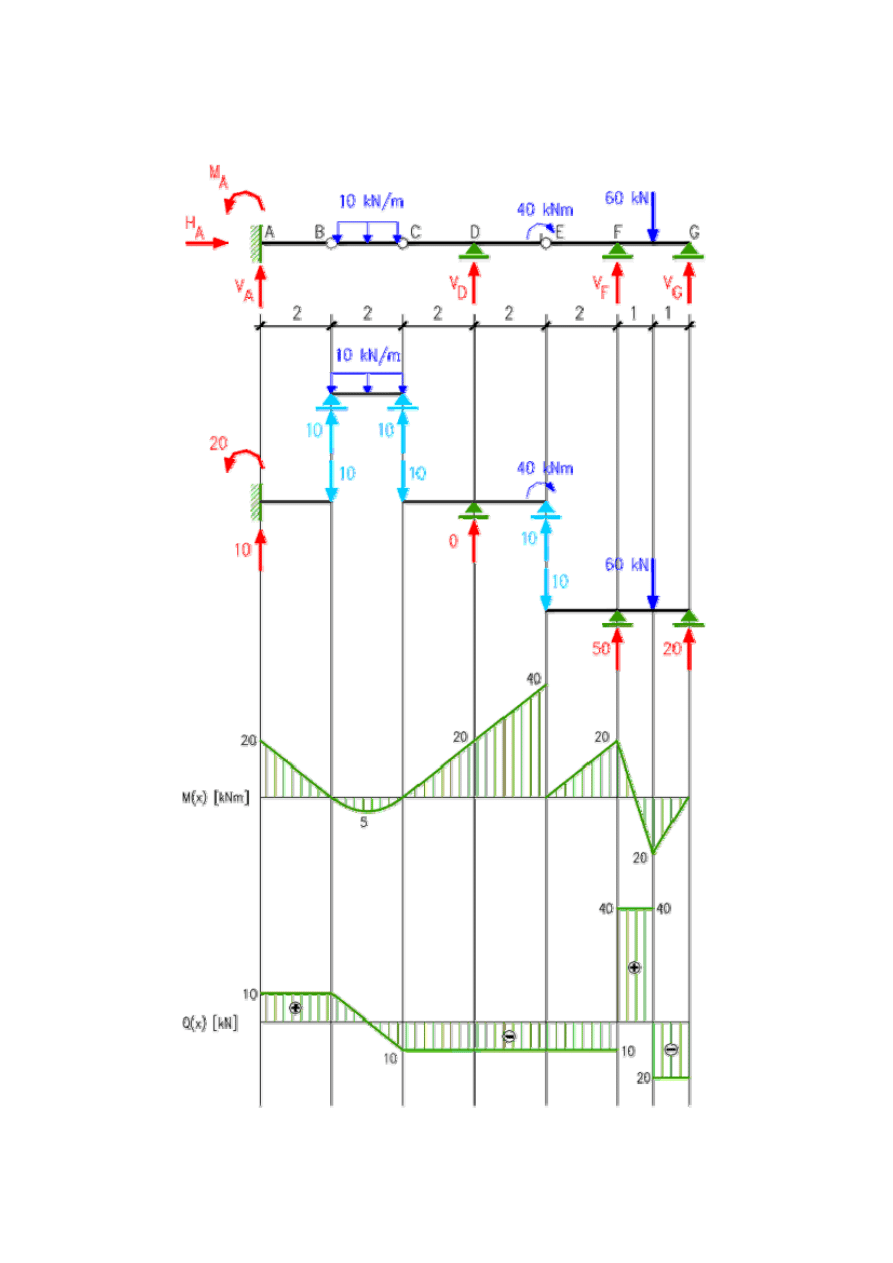
Zadanie S-6.

Dla podanej belki przegubowej sporządzić wykresy sił przekrojowych M,

Q, N.

ROZWIĄZYWANIE RAM

Zadanie S-7.

Dla podanej ramy napisać równania sił przekrojowych i narysować ich

wykresy.

Zadanie S-8.

Narysować wykresy sił przekrojowych w podanej ramie.

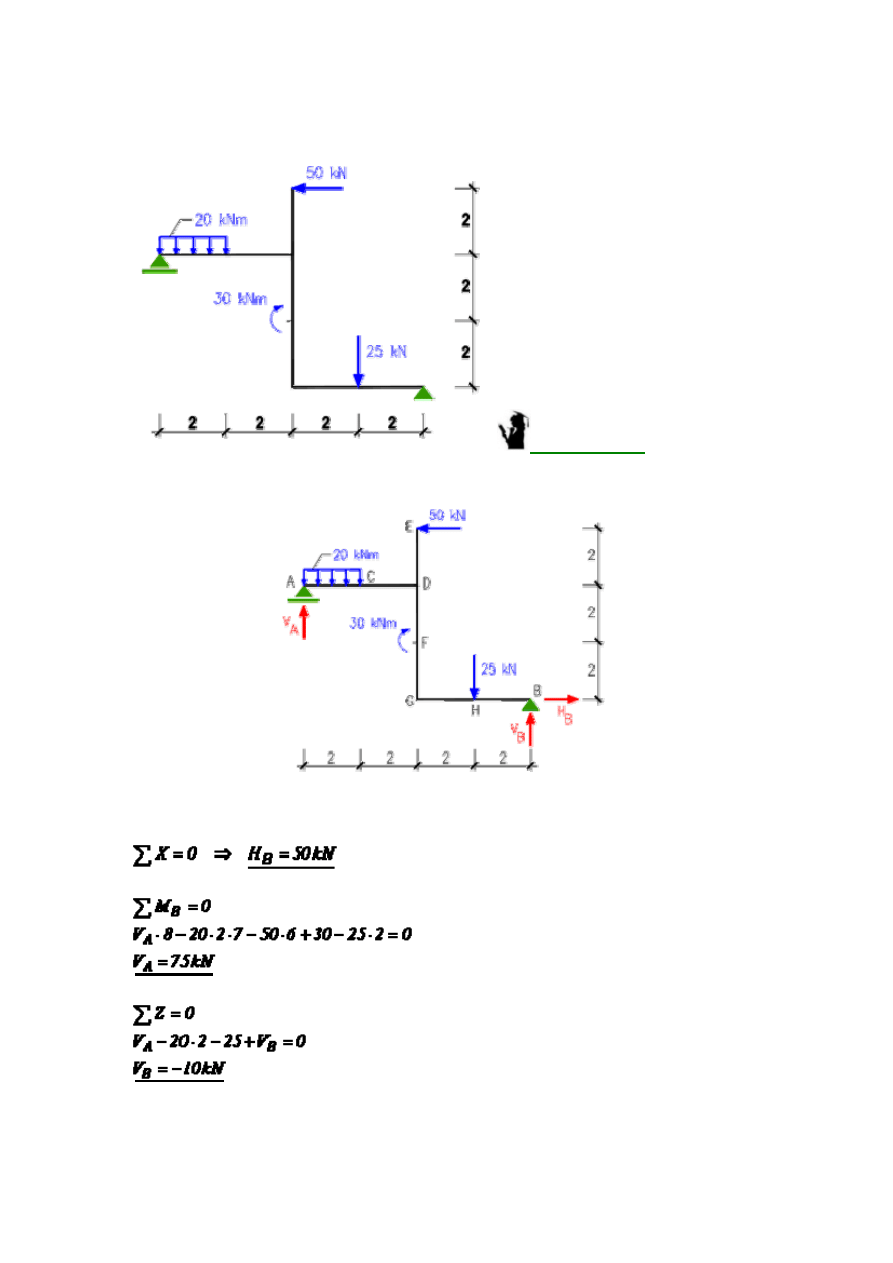
Przykład 8.

Narysować

wykresy sił przekrojowych w podanej ramie.

1. Obliczenie reakcji.

Sprawdzenie:

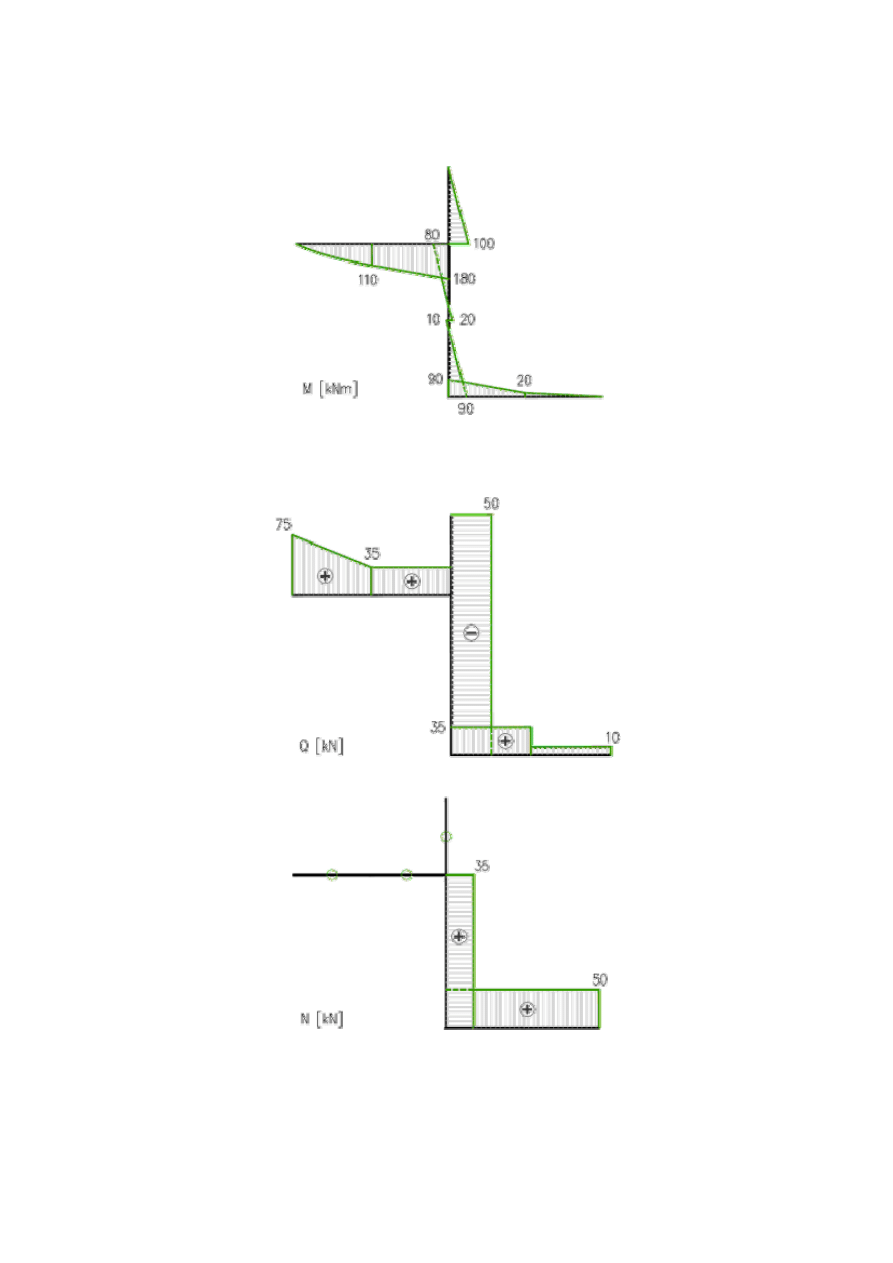
2. Wykresy sił przekrojowych.

Wykresy sił przekrojowych rysujemy na trzech rysunkach, oddzielnie moment

zginający, siła poprzeczna i siła podłużna. Zależności różniczkowe pomiędzy siłami

przekrojowymi są spełnione również w ramach i wszystkie wynikające stąd zasady

rysowania wykresów są takie same jak dla belek.

Stosujemy tą samą konwencję znakowania co w belkach, przy czym dla prętów

ukośnych, bądź słupów układ należy obrócić jak na rysunku poniżej.

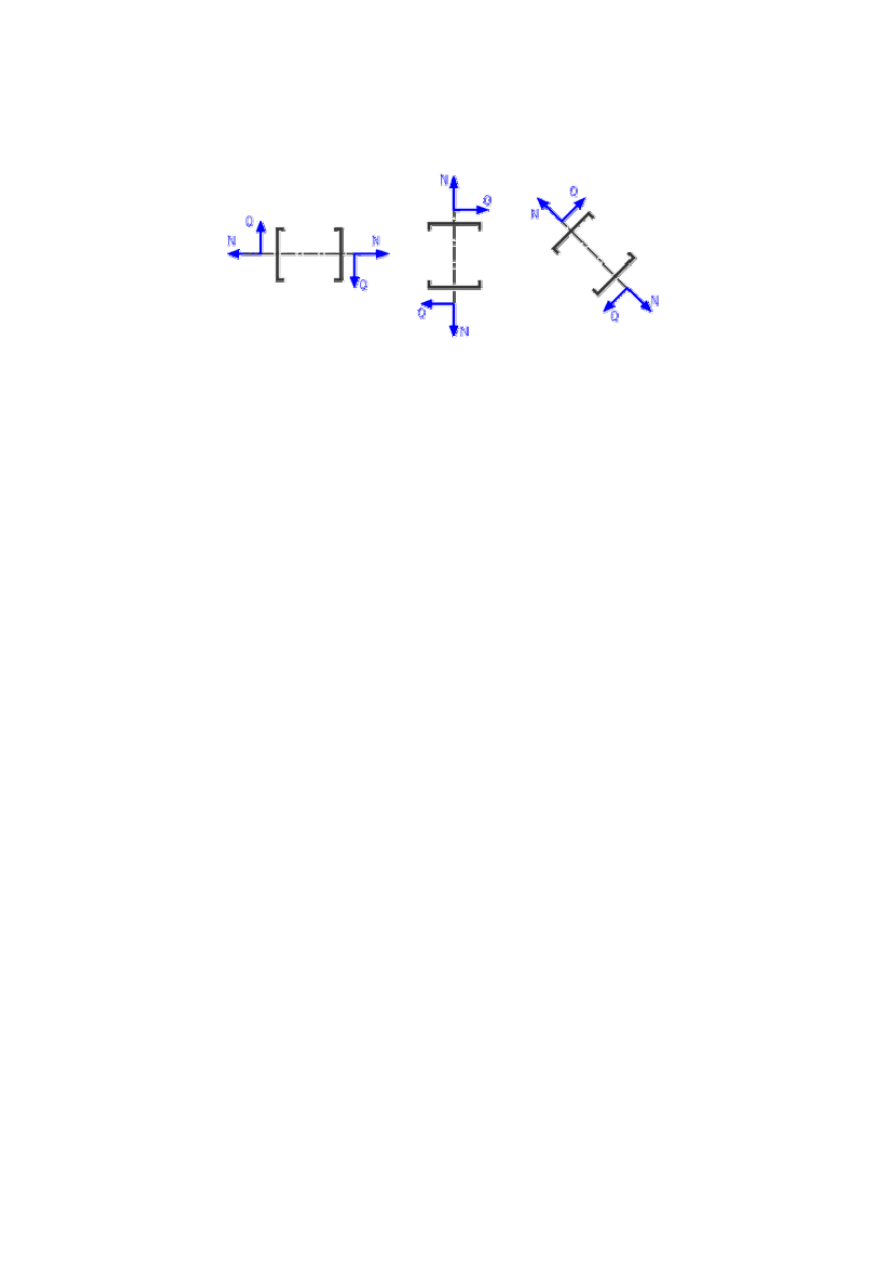
Aby przyjąć znak momentu zginającego należałoby wyróżnić pewne włókna i określić

moment rozciągający te włókna na przykład jako dodatni. Można jednak tego nie robić,

pamiętając tylko o tym, że wykres momentów zawsze musi być narysowany po stronie

włókien rozciąganych.

W punktach charakterystycznych każdego pręta obliczamy wartości poszczególnych sił

przekrojowych i zaznaczamy je na liniach odnoszących, prostopadłych do osi każdego

pręta. Jeżeli w danym przedziale nie występuje obciążenie ciągłe (w przypadku ram

obciążenie to może być pionowe i poziome, a także ukośne) to wykres siły poprzecznej

i podłużnej jest stały, a wykres momentu liniowy. Gdy występuje obciążenie ciągłe

równomiernie rozłożone, to wykresy siły poprzecznej i podłużnej są liniowo zmienne, a

wykres momentu jest parabolą. Dodatkowo w miejscu zerowania się siły poprzecznej

moment ma wartość ekstremalną.

Obliczając wartości sił w punktach charakterystycznych, redukujemy układ sił

przyłożonych do jednej z części belki podzielonej przekrojem. Oczywiście wygodniej jest

przyjąć do redukcji prostszy układ sił co upraszcza obliczenia i zmniejsza możliwość

wystąpienia pomyłki.

Dla sprawdzenia poprawności rozwiązania sprawdza się równowagę węzłów ramy. W

tym celu wycina się każdy węzeł i do ścianek przekroju przykłada się, odczytane z

wykresu, wartości sił przekrojowych. Jeżeli rozwiązanie jest poprawne, to każdy z

wyciętych węzłów powinien być w równowadze, czyli powinny być spełnione dla niego

równania statyki.

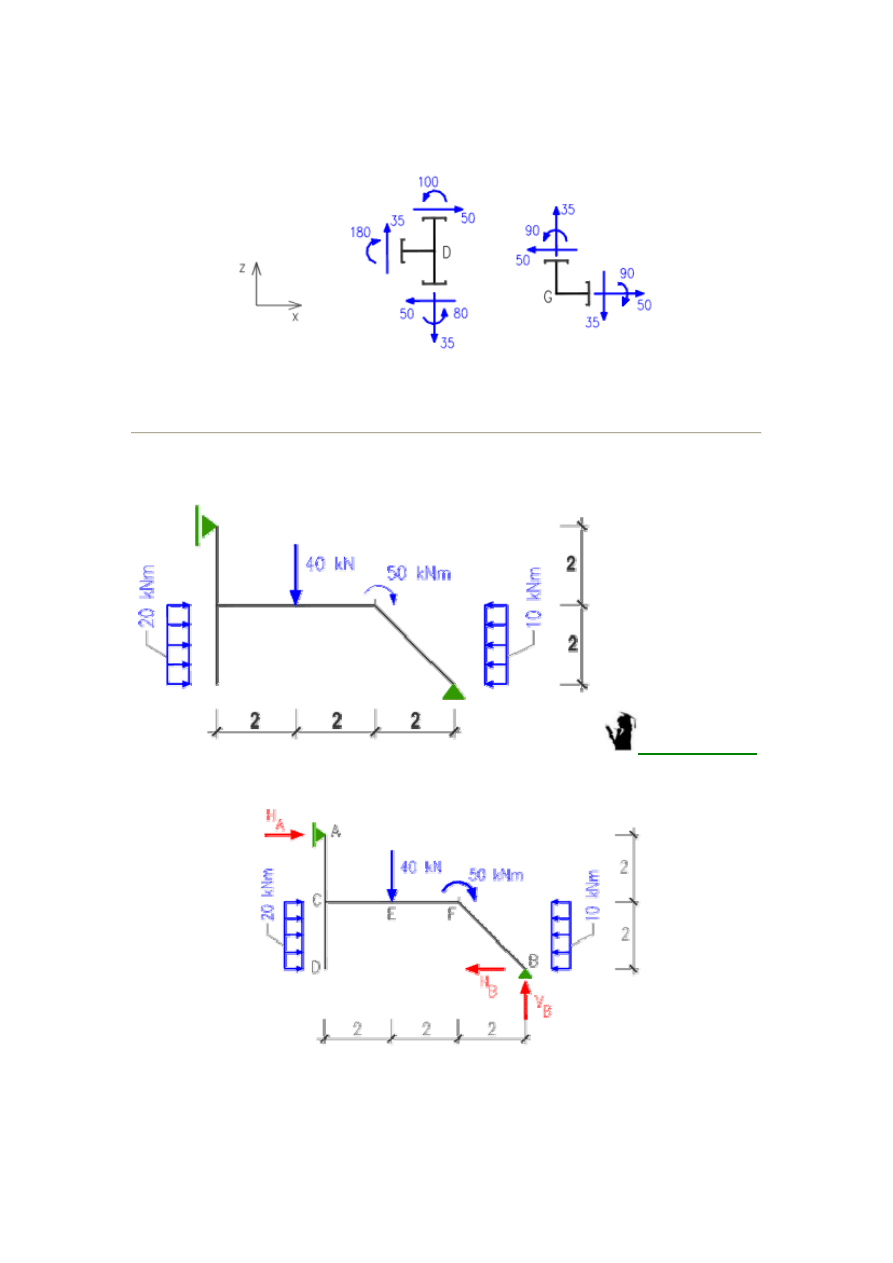
Sprawdzimy równowagę węzłów D i G. Siły przywęzłowe narysowano i opisano na

rysunku poniżej. Widzimy, że równania równowagi są spełnione:

dla węzła D dla węzła G

Zadanie S-9.

Narysować wykresy sił przekrojowych w podanej ramie.

Przykład 9.

Narysować wykresy sił przekrojowych w podanej ramie.

1. Obliczenie reakcji.

Sprawdzenie:

2. Wykresy sił przekrojowych.

Pręt BF

Siły przekrojowe są składowymi wypadkowej układu sił zewnętrznych zrzutowanymi na
kierunek osi pręta i na prostopadłą do osi. Należy zatem, w przypadku pręta ukośnego
BF, rozłożyć wypadkową redukowanego układu na te właśnie kierunki.
Do pręta BF jest przyłożone obciążenie ciągłe równomiernie rozłożone, zatem wykresy
siły podłużnej i poprzecznej będą liniowe. Wystarczy więc obliczyć wartości tych sił na
końcach pręta, aby narysować wykresy.
Jeżeli liczba sił do redukcji jest duża, można ułatwić sobie zadanie, rozkładając na
kierunek pręta wypadkową pionową i poziomą wszystkich sił. Jeżeli redukujemy układ
sił przyłożonych z prawej strony przekroju to siły podłużna i poprzeczna będą równe:

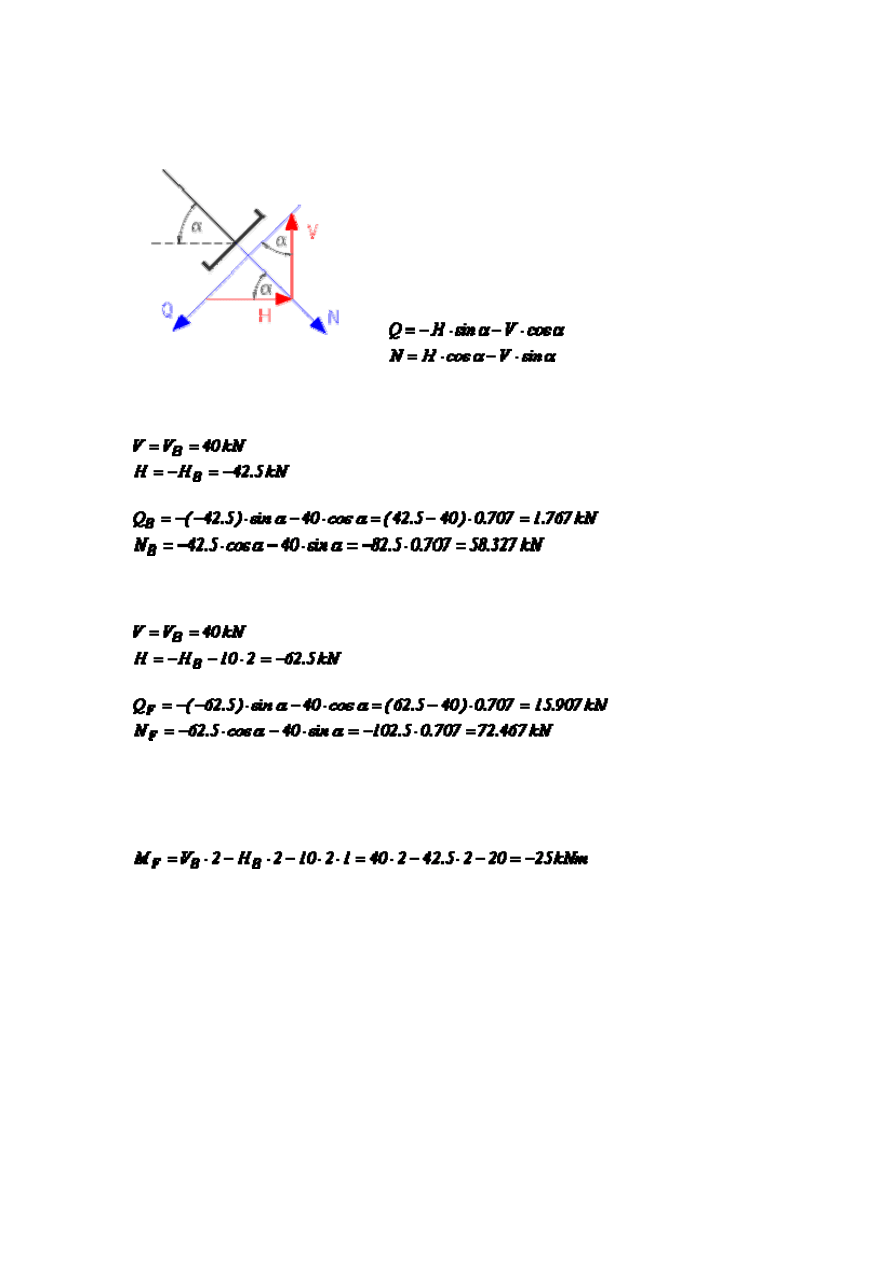
Obliczając wartości sił przekrojowych w punkcie B otrzymujemy:

Dla punktu F:

Wykres momentu zginającego na pręcie BF jest parabolą. Ponieważ siła poprzeczna nie
zmienia tutaj znaku, wykres momentu nie będzie miał ekstremum. Wartość momentu w
punkcie B jest oczywiście równa zeru a w punkcie F:

Przyjęliśmy tutaj znak minus dla momentu rozciągającego włókna górne.

Pręt CF

Poziomy pręt CF składa się z dwóch przedziałów charakterystycznych, na końcach
których musimy znać wartości sił przekrojowych.
Redukując układ sił zewnętrznych idąc z lewej strony otrzymujemy:

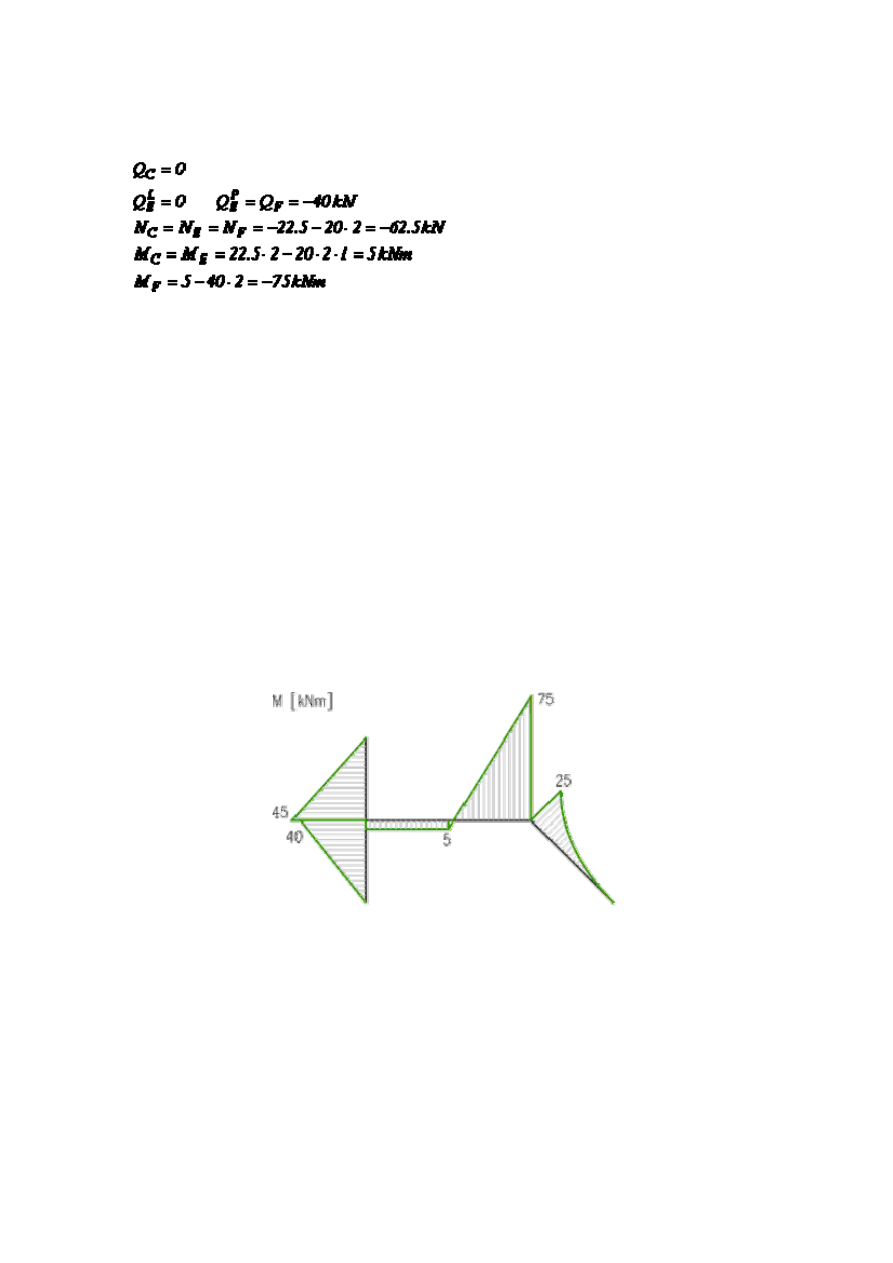
Dla momentu przyjęto znak plus jeżeli rozciąga włókna dolne pręta CF.

Pręt AC

Siła podłużna w tym pręcie jest równa zeru, redukując bowiem układ sił zewnętrznych
idąc od punktu A nie napotykamy sił równoległych do osi pręta. Siła poprzeczna jest w
całym przedziale stała i wynosi Q = 22.5 kN.
Moment zginający rozciąga włókna po lewej stronie pręta i zmienia się liniowo od zera
do M = 45 kNm.

Pręt DC

Również w tym pręcie siła podłużna jest równa zeru, natomiast siła poprzeczna zmienia
się liniowo (obciążenie równomiernie rozłożone) od zera w punkcie D do wartości Q

C

=

40 kN. Wykres momentu zginającego jest parabolą styczną w punkcie D do osi pręta.
Wartość w punkcie D jest równa zeru, natomiast w punkcie C 40 kNm. Moment rozciąga
włókna po lewej stronie pręta.

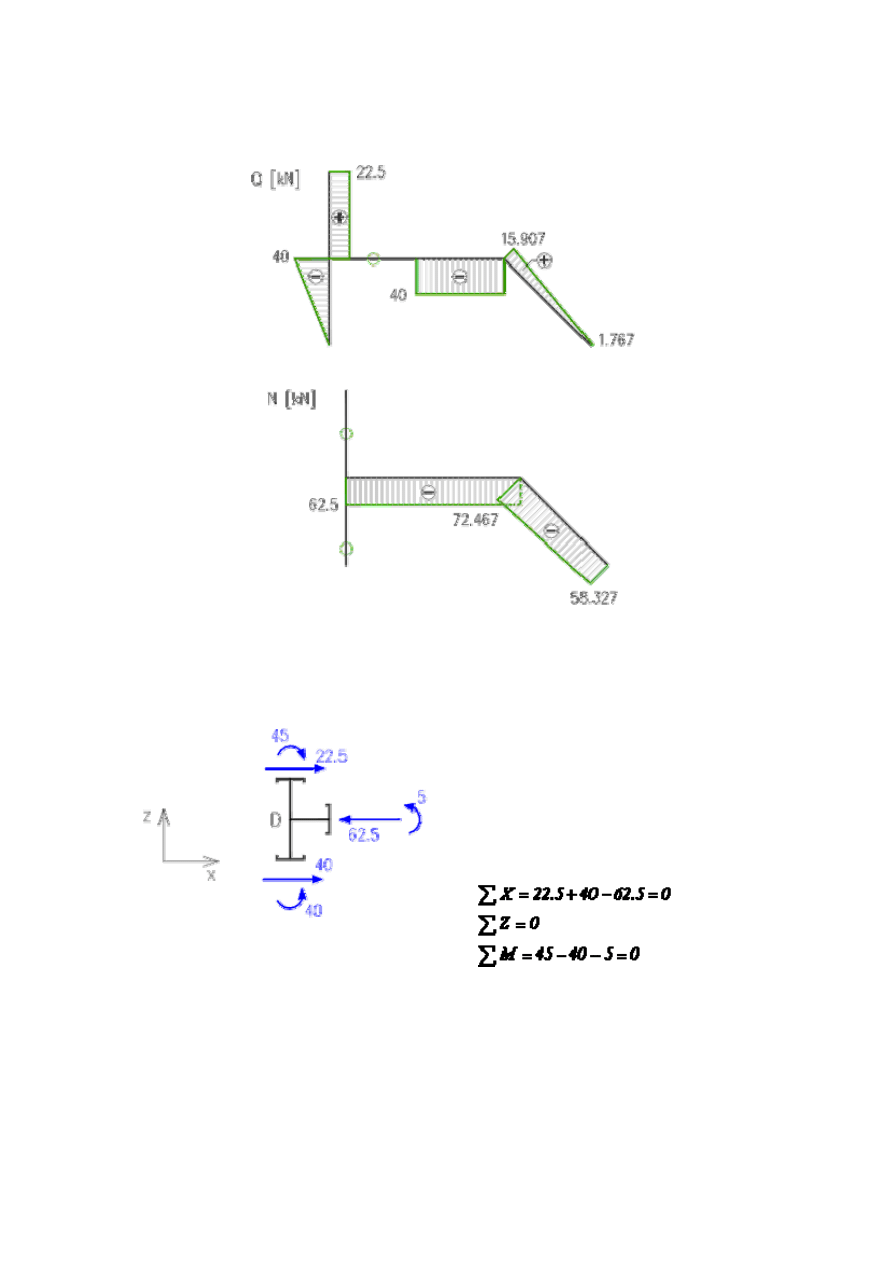
3. Sprawdzenie równowagi w węzłach.

Węzeł C

Węzeł F