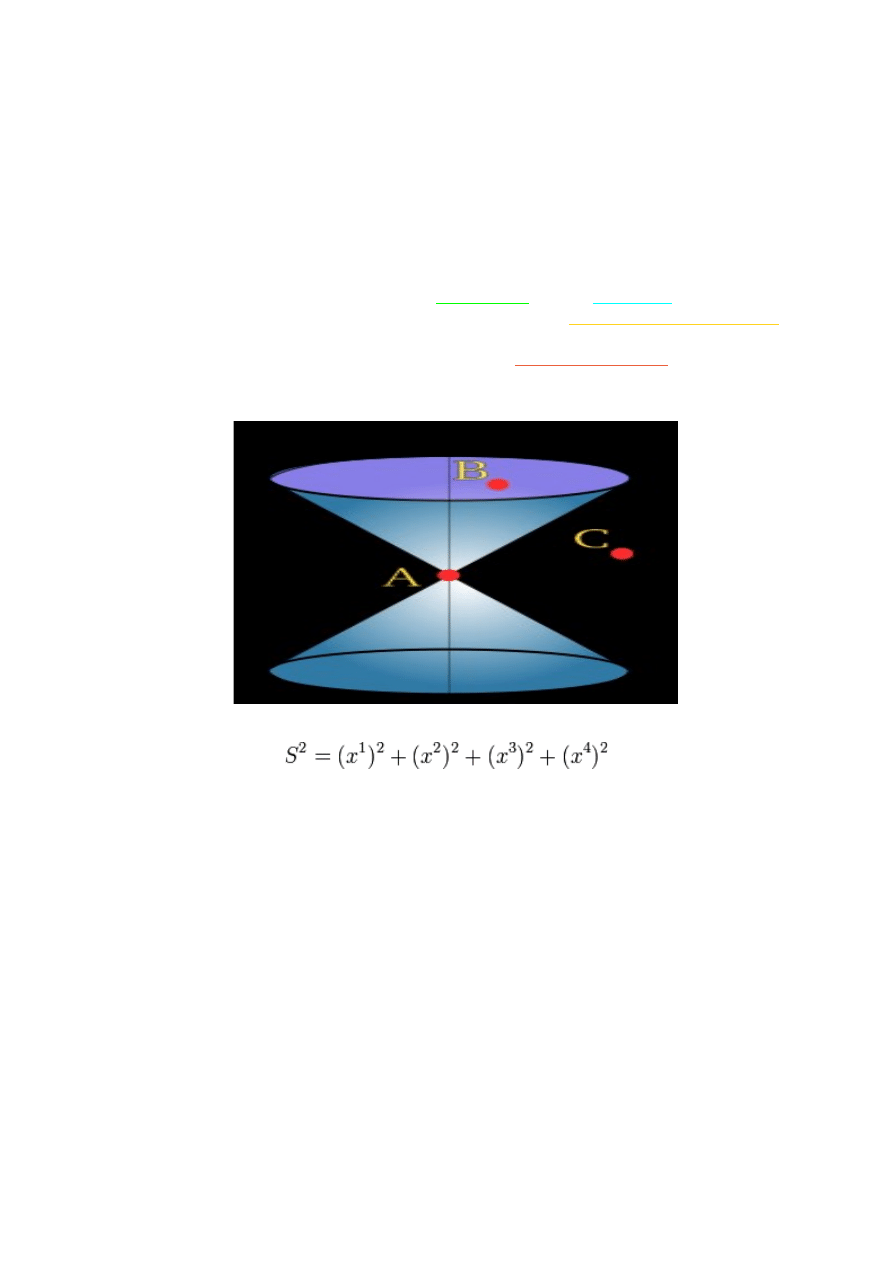
Idea ogólnej teorii względności

Ogólna teoria względności to popularna nazwa teorii grawitacji sformułowanej przez Alberta
Einsteina w 1915 roku, a opublikowanej w roku 1916. Zgodnie z ogólną teorią względności, siła
grawitacji wynika z lokalnej geometrii czasoprzestrzeni. Podłoże matematyczne tej teorii zostało
opracowane w pracach takich matematyków jak

János Bolyai

, a także

Carl Gauss

. Ogólnie

geometria nieeuklidesowa została rozwinięta przez ucznia Gaussa,

Georga Bernharda Riemanna

,

ale nieeuklidesowa geometria czasoprzestrzeni stała się znana szerzej dopiero po tym, jak w
opracowaną przez Einsteina szczególną teorię względności

Hermann Minkowski

wprowadził w

1907 roku Czasoprzestrzeń Minkowskiego.

Teoria Einsteina zawiera nietrywialne treści fizyczne dotyczące koncepcji czasu, przestrzeni,
geometrii czasoprzestrzeni, związków masy bezwładnej i ważkiej oraz spostrzeżenia dotyczące
równoważności grawitacji i sił bezwładności. Jest ona uogólnieniem

Szczególnej Teorii

Względności

obowiązującej dla inercjalnych układów odniesienia na dowolne, także nieinercjalne

układy odniesienia.

Anomalie orbitalne Merkurego a teoria względności

Świadectwem przeciw teorii Newtona i jednocześnie za teorią Einsteina była niezgodność ruchu
Merkurego. Ruch tej planety wykazywał niewielkie odchylenia znane od drugiej połowy XIX
stulecia, względem obliczeń wynikających z newtonowskich praw ruchu i grawitacji. Anomalia
orbity Merkurego jest bardzo niewielka, wynosi 43 sekundy kątowe na każde sto lat! Żadne z
proponowanych na gruncie teorii Newtona rozwiązań tego problemu nie okazało się skuteczne. W
roku 1916 Einstein wyjaśnił ową niezgodność przy pomocy praw grawitacji w ogólnej teorii
względności.

Szczególna Teoria względności

Szczególna teoria względności to teoria fizyczna, stworzona przez Alberta Einsteina w 1905 roku.
Zmieniła ona podstawy pojmowania czasu i przestrzeni opisane wcześniej w newtonowskiej
mechanice klasycznej, tak aby można było usunąć trudności interpretacyjne i sprzeczności
pojawiające się na styku mechaniki (zwanej obecnie klasyczną) i elektromagnetyzmu po ogłoszeniu
przez

Jamesa Clerka Maxwella

teorii elektromagnetyzmu.

W 1916 roku Albert Einstein opublikował ogólną teorię względności, będącą rozszerzeniem teorii
szczególnej o opis zjawisk zachodzących w obecności pola grawitacyjnego.

Albert Einstein oparł swe rozumowanie na dwóch postulatach:

•

Zasadzie względności

Zasada głosząca, że prawa fizyki są jednakowe we wszystkich układach inercjalnych — musi
obowiązywać dla wszystkich praw zarówno mechaniki jak i elektrodynamiki.

•

Niezmienność prędkości światła

Prędkość światła w próżni jest taka sama dla wszystkich obserwatorów, taka sama we
wszystkich kierunkach i nie zależy od prędkości źródła światła.

Z połączenia postulatów 1 i 2 dojdziemy do wniosku, że światło nie potrzebuje jakiegokolwiek

ośrodka (eteru) do rozchodzenia się.

Alternatywna forma założeń Szczególnej Teorii Względności, interesująca szczególnie z
teoretycznego punktu widzenia, jest oparta na następujących, prostszych założeniach:

•

Zasada względności Galileusza: "Wszystkie układy odniesienia poruszające się względem
siebie ze stałą prędkością są równoważne."

•

założenie że transformacja pomiędzy tak określonymi układami jest transformacją afiniczną
(liniową)

Einstein stwierdził, że wszystkie konsekwencje szczególnej teorii względności

mogą być znalezione, gdy zastosuje się transformację Lorentza.

Przekształcenia wynikające z transformacji Lorentza, a więc i szczególnej teorii względności,
prowadzą do różnych fizycznych wniosków w porównaniu do mechaniki Newtona przy
względnych prędkościach porównywalnych do prędkości światła. Prędkość światła jest
nieporównywalnie większa niż prędkości z którymi ludzie się spotkają na co dzień, dlatego też
niektóre wnioski szczególnej teorii względności są początkowo sprzeczne z intuicją:

•

Dylatacja czasu, czas jaki mija pomiędzy dwoma zdarzeniami nie jest jednoznacznie
określony, lecz zależy od obserwatora. Skutkiem interpretacji zjawiska w kontekście
zawracającego układu inercjalnego jest Paradoks bliźniąt, jakkolwiek bardziej poprawnie
tłumaczy to teoria ogólna. Czas trwania zjawiska, zachodzącego w punkcie przestrzeni,
obserwowany z punktów poruszających się względem tego punktu, jest dłuższy niż czas
trwania tego zjawiska w układzie odniesienia, w którym punkt ten spoczywa.

•

Względność jednoczesności, dwa zdarzenia określone przez jednego obserwatora, mogą
nie być jednoczesne dla innego obserwatora.

•

Kontrakcja przestrzeni, odległości między punktami zależą od układu. Wszystkie
poruszające się przedmioty obserwujemy jako krótsze. Zjawisko prowadzi do paradoksu
drabiny o długości większej niż długość stodoły, która zmieści się w niej w całości, jeżeli
będzie poruszała się odpowiednio szybko. Nie zmieściłaby się, gdyby okazało się, że
kontrakcja i dylatacja nie są równoczesne.

•

Wartości innych wielkości fizycznych takich jak siła, pęd, przyspieszenie, natężenie pola
elektrycznego zależą od obserwatora.

•

Nowa reguła składania prędkości, prędkości nie „dodają się”. Przykładowo: jeżeli rakieta
oddala się z prędkością 2/3 prędkości światła w stosunku do obserwatora i rakieta wysyła
pocisk z prędkością 2/3 prędkości światła w stosunku do rakiety, obserwator nie zanotuje
prędkości (2/3 + 2/3 = 4/3 prędkości światła) przewyższającej prędkość światła. W tym
przykładzie, obserwator widziałby pocisk poruszający się z szybkością 12/13 prędkości
światła. Podobnie, przy dwóch strumieniach cząstek poruszających się z prędkością bliską
światłu – jedne emitowane na lewo od źródła, drugie na prawo – z perspektywy jednych
cząstek drugie nie będą uciekały szybciej niż światło.

•

Masa jest równoważna energii a związek między tymi wielkościami opisuje wzór E = mc2.
Zwiększenie energii układu zwiększa jego masę, zmniejszenie energii powoduje
zmniejszenie masy. I odwrotnie ubytek masy oznacza ubytek energii układu (

Deficyt

masy

).

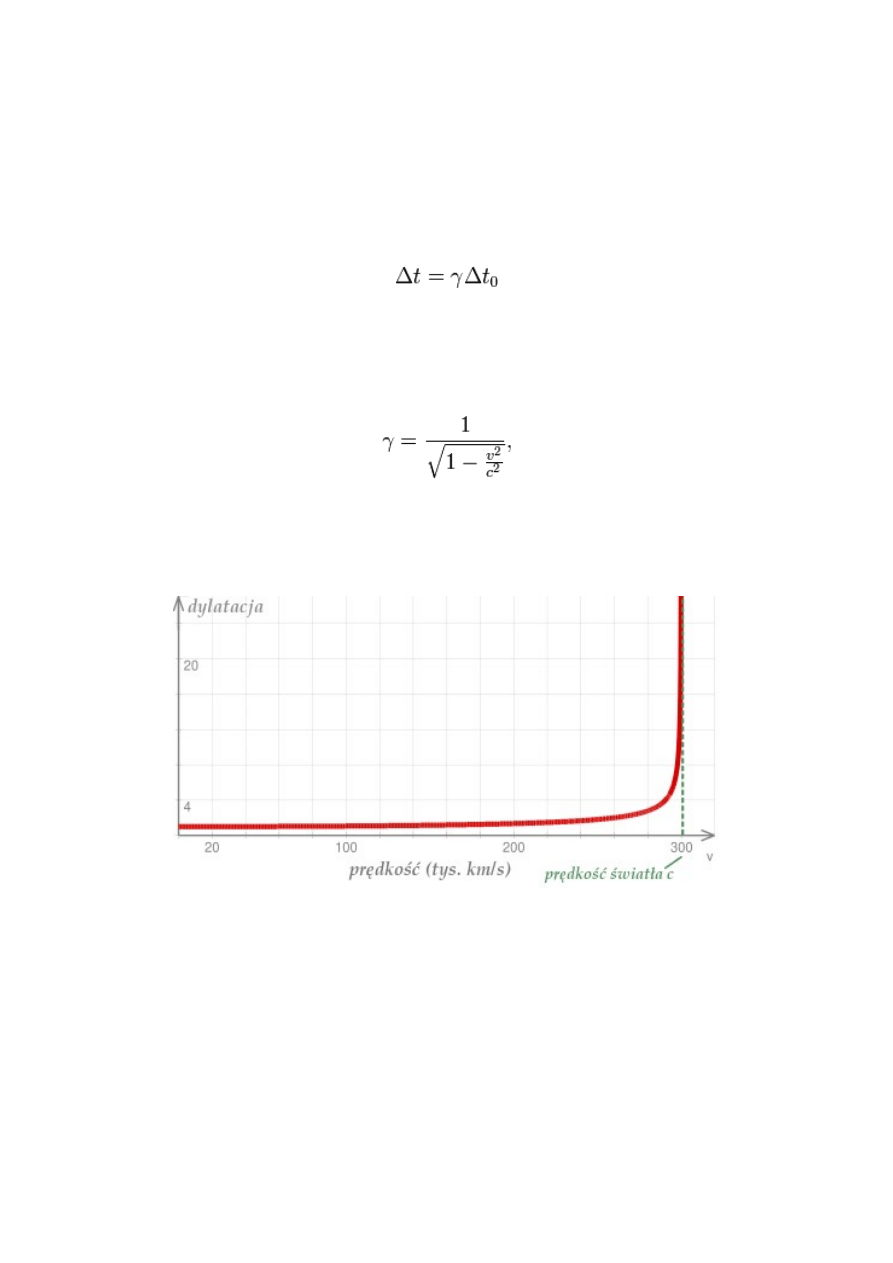
Dylatacja związana z prędkością

W szczególnej teorii względności czasy przebiegu tego samego zjawiska dla różnych
obserwatorów są powiązane zależnością:

Δt0 – czas trwania zjawiska zarejestrowany przez obserwatora spoczywającego względem
zjawiska,
Δt – czas trwania tego samego zjawiska zachodzącego w układzie odniesienia pierwszego
obserwatora rejestrowany przez obserwatora poruszającego się względem pierwszego z
prędkością v,

" Czynnik Lorentza "

v – względna prędkość obserwatorów,
c – prędkość światła w próżni.

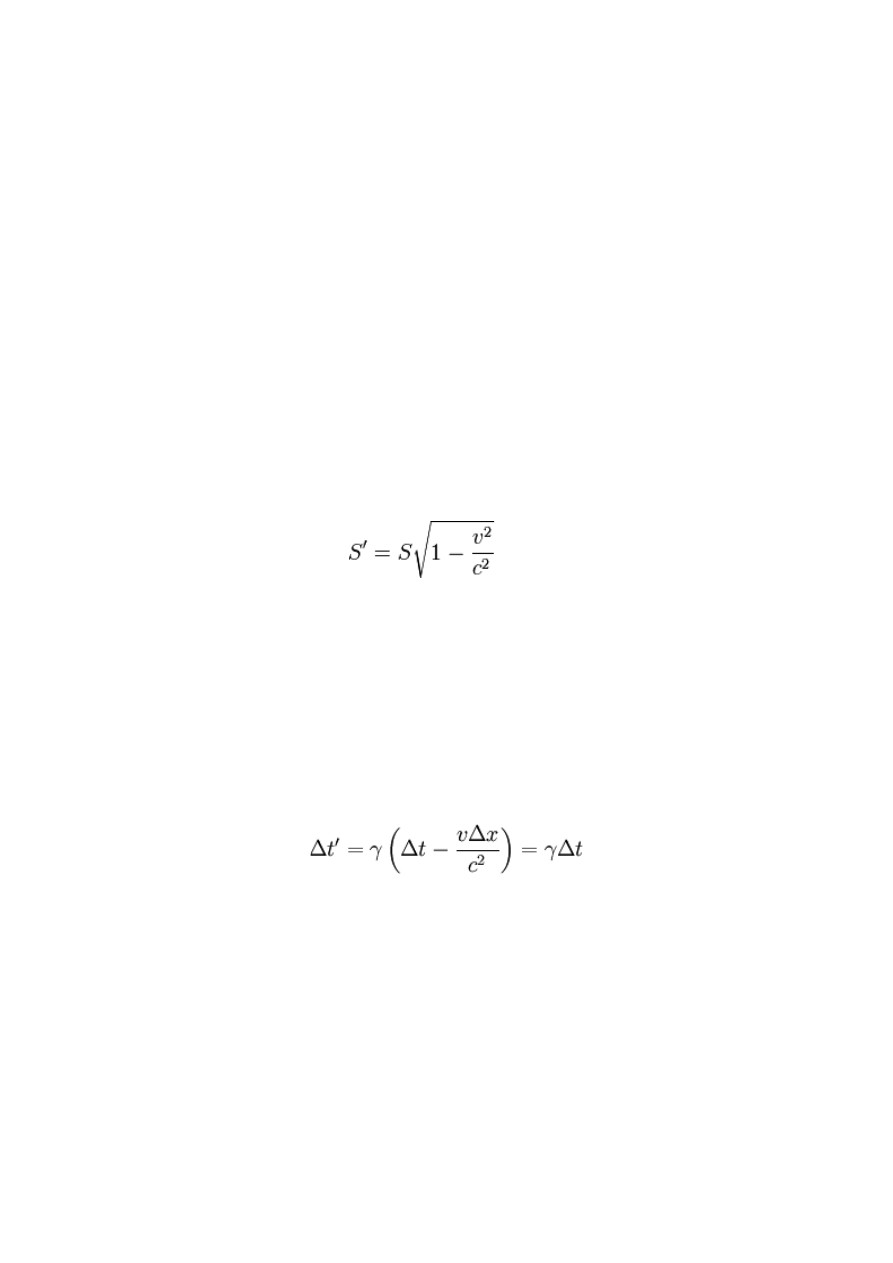
Transformacja Lorentza

Transformacja Lorentza to przekształcenie liniowe przestrzeni Minkowskiego zachowujące
odległości w metryce tej przestrzeni. W przeciwieństwie do transformacji Galileusza, gdzie
niezmiennikiem jest czas i odległość, w transformacji Lorentza niezmiennikami są np. interwał
(odległość zdarzeń w czasoprzestrzeni) i masa spoczynkowa, podczas gdy odległość i czas mogą
mieć różne wartości, zależne od prędkości układu odniesienia. Fundamentalną cechą transformacji
Lorentza jest niezależność prędkości światła od prędkości układu. W fizyce, transformacje Lorentza
opisują zależności między współrzędnymi i czasem tego samego zdarzenia w dwóch inercjalnych
układach odniesienia wg szczególnej teorii względności. Wg klasycznej mechaniki, zależność
między czasem i współrzędnymi opisują transformacje Galileusza.

Wzór Lorentza – wzór na skrócenie odległości (skrócenie Lorentza) mierzonej w kierunku
ruchu, w układzie odniesienia poruszającym się z prędkością relatywistyczną. Skrócenie to
wynika z transformacji Lorentza. Jeżeli układ porusza się z prędkością v względem układu
laboratoryjnego, wówczas odległość S mierzona w układzie laboratoryjnym, w układzie
poruszającym się będzie miała wartość S' :

Dylatacja czasu w transformacji

Czas własny układu mierzy się poprzez zdarzenia zachodzące w tym samym punkcie przestrzeni x
(np. przy pomocy zegara świetlnego; zegar świetlny mierzy wędrówkę promienia, prostopadłego do
dwóch ustawionych naprzeciw siebie luster). A zatem układ Ax,t mierzy swój czas własny przy
założeniu Δx=0. Przy przejściu do układu B zachowujemy to Δx=0, gdyż chodzi o te same
zdarzenia. Na podstawie transformacji Lorentza mamy: