
Jacek Kabziński
Automatyka i sterowanie
————————————————————————————————————————

2
Automatyka i sterowanie 12 Ruch w przestrzeni stanów
Układy czasu ciągłego i dyskretnego
Intuitively, the state may be regarded as a kind of information storage or memory or accumulation
of past causes. We must, of course, demand that the set of internal states x be sufficiently
rich to carry all information about the past history of x to predict the effect of the past upon
the future. We do not insist, however, that the state is the least such information although this
is often a convenient assumption.
R.E.Kalman, P.L. Falb and M.A.Arbib, Topics in Mathematical SystemTheory, 1969
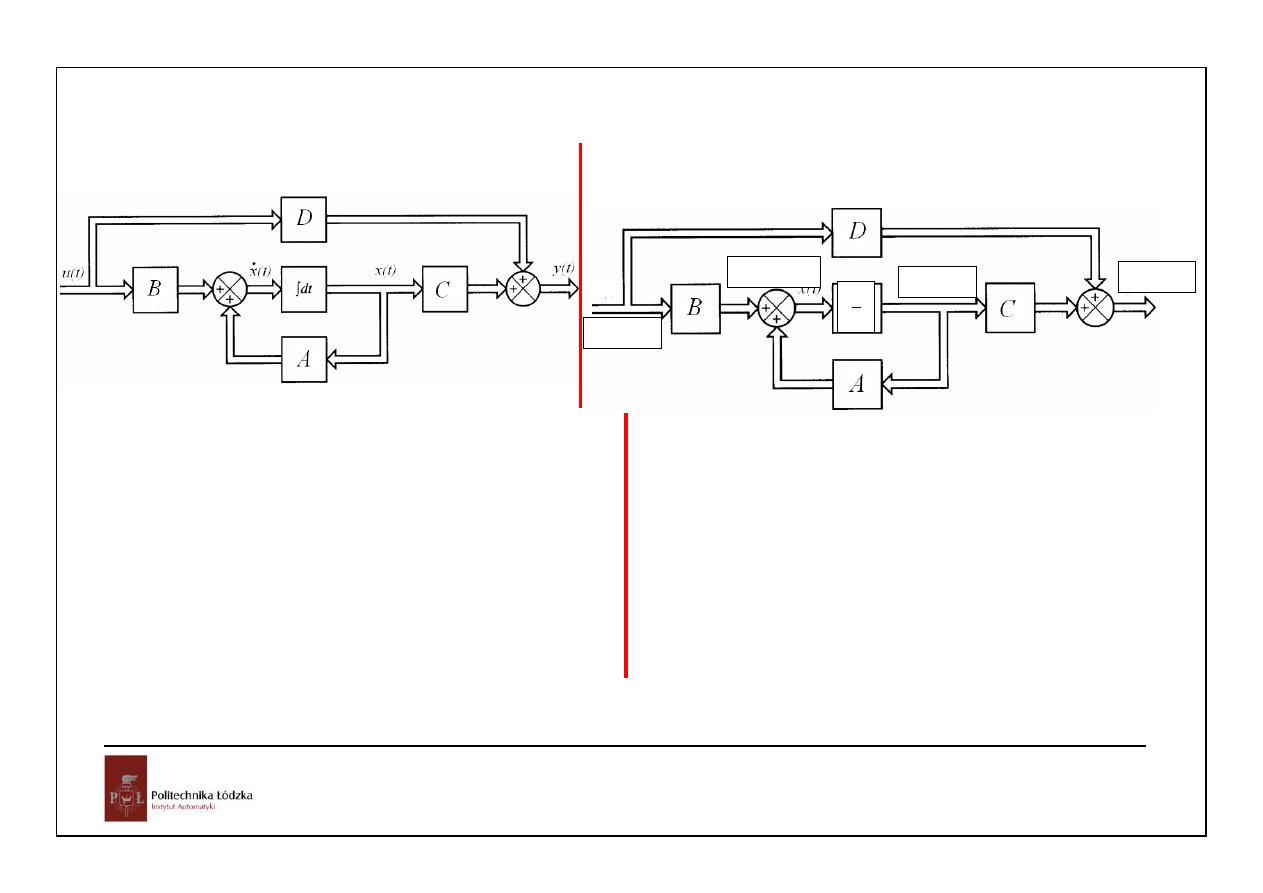
Rozważać będziemy opis układu w postaci:
równanie stanu
d
x( t ) Ax( t ) Bu( t )
dt
y( t ) Cx
równ
(
a
t )
ni
Du(
e wy ś
t )
j cia
=
+
=
+
)
(
)
(
)
(
)
(
)
(
)
)
1
((
kT
Du
kT
Cx
kT
y
kT
Bu
kT
Ax
T
k
x
+
=
+
=
+
x(t) – wektor zmiennych stanu o wymiarze nx1,
u(t) – wektor wejść/sterowań o wymiarze rx1
y(t) – wektor wyjść o wymiarze mx1
z warunkiem początkowym x(0)=x
0
lub bardziej ogólnie x(t
0
)=x
0
3
Automatyka i sterowanie 12 Ruch w przestrzeni stanów
Układy czasu ciągłego i dyskretnego
(
)
(
)
1
1
0
X ( s )
sI
A
x
sI
A
BU( s )
−
−
=
−
+
−
,
(
) (
)
)
(
)
0
(
)
(
1
z
Bu
zx
A
zI
z
X
+
−
=
−
0
0
t
x( t )
( t )x
( t
)Bu( )d
τ
τ τ
= Φ
+ Φ −
∫
)
(
)
0
(
)
(
1
0
1
i
Bu
A
x
A
kT
x
k
i
i
k
k
∑
−
=
−
−
+
=
=
=
)
)
((
)
0
(
1
1
T
i
k
Bu
A
x
A
k
i
i
k
−
+
∑
=
−
1
z
u(kT)
y(kT)
x(kT)
x((k+1)T
4
Automatyka i sterowanie 12 Ruch w przestrzeni stanów
Układy czasu ciągłego i dyskretnego
(
)
{
}
(
)
(
)
1
1
1
adj sI
A
( t ) L
sI
A
L
det sI
A
−
−
−
⎧
⎫
−
⎪
⎪
Φ
=
−
=
⎨
⎬
−
⎪
⎪
⎩
⎭
(
)
{
}
1
1
−
−
−
=
A
zI
z
Z
A
k
2 2
3 3
0
2
3
i i
i
A t
A t
A t
( t ) I
At
!
!
i!
∞
=
Φ
= +
+
+
+
=
∑
At
( t ) e
Φ
=
0
0
0
t
t
x( t )
( t t )x
( t
)Bu( )d
τ
τ τ
= Φ −
+ Φ −
∫
)
(
)
0
(
)
(
1
0
1
i
Bu
A
x
A
kT
x
k
i
i
k
k
∑
−
=
−
−
+
=
=
=
)
)
((
)
0
(
1
1
T
i
k
Bu
A
x
A
k
i
i
k
−
+
∑
=
−
5
Automatyka i sterowanie 12 Ruch w przestrzeni stanów
Układy czasu ciągłego i dyskretnego
Postać modalna rozwiązania:
( )
0
1
1
0
0
1
0
i
i
i
i
t
n
n
s t
s t
T
T
i
i
i
i
i
i
t
n
s t
s
T
i
i
i
x( t )
e v w x
e
v w Bu( )d
e v w
x
e
Bu( )d
τ
τ
τ τ
τ τ
−
=
=
−
=
=
+
=
⎡
⎤
=
+
⎢
⎥
⎣
⎦
∑
∑
∫
∑
∫
)
(kT
x
=
( )
)
0
(
1
x
w
v
z
T
i
i
n
i
k
i
∑
=
( )
)
)
((
1
0
1
T
i
k
Bu
z
w
v
i
j
k
i
n
j
T
j
j
−
+
−
=
=
∑
∑
(
)
1
Y ( s )
C sI
A
B D U( s ) G( s )U( s )
−
⎡
⎤
=
−
+
=
⎣
⎦
(
)
1
Y ( z )
C zI
A
B D u( z ) G( z )u( z )
−
⎡
⎤
=
−
+
=
⎣
⎦
(
)
(
)
(
)
1
adj sI
A
G( s ) C sI
A
B D C
B D
det sI
A
−
−
=
−
+ =
+
−
(
)
1
adj( zI
A)
G( z )
C zI
A
B D
C
B D
det( zI
A)
−
−
⎡
⎤
=
−
+
=
+
⎣
⎦
−
mogą wystąpić skrócenia – transmitancja może być niższego rzędu niż wymiar wektora stanu!!

6
Automatyka i sterowanie 12 Ruch w przestrzeni stanów
Układy czasu ciągłego i dyskretnego
Liniowe przekształcenie zmiennych stanu:
wprowadzamy nowe zmienne stanu:
0
Pq( t ) x( t ), det P
=
≠
0
Pq( kT ) x( kT ), det P
=
≠
równanie stanu
d
Pq( t ) APq( t ) Bu( t )
nowe
dt
y( t ) CPq( t ) Du( t )
now
równanie wyjś a
e
ci
=
+
=
+
1
Pq(( k
)T ) APq( kT ) Bu( kT )
y( kT ) CPq( kT ) Du( kT )
+
=
+
=
+
1
1
równanie st
d
q( t ) P APq( t ) P Bu( t )
nowe
dt
y( t ) CPq( t ) Du( t )
anu
równanie wyjścia
nowe
−
−
=
+
=
+
1
1
1
q(( k
)T ) P APq( kT ) P Bu( kT )
y( kT ) CPq( kT ) Du( kT )
−
−
+
=
+
=
+
1
1
d
q( t ) Aq( t ) Bu( t )
A P AP, B P B
dt
y( t ) Cq( t ) Du( t )
C CP
−
−
=
+
=
=
=
+
=
1
q(( k
)T ) Aq( kT ) Bu( kT )
y( kT ) Cq( kT ) Du( kT )
+
=
+
=
+
wartości własne nowej macierzy stanu są takie same jak starej!!
liniowe przekształcenie zmiennych stanu nie zmienia transmitancji!!

7
Automatyka i sterowanie 12 Ruch w przestrzeni stanów
Układy czasu ciągłego i dyskretnego
Układ ciągły:
)
(
)
(
)
(
)
(
)
(
)
(
t
u
D
t
x
C
t
y
t
u
B
t
x
A
t
x
dt
d
c
c
c
c
c
c
+
=
+
=
poprzedzony ekstrapolatorem zerowego rzędu
(odpowiedniego wymiaru) i impulsatorem:
∫
−
+
+
=
+
t
t
c
T
k
A
T
A
kT
u
B
d
e
kT
x
e
T
k
x
c
c
0
)
(
)
(
)
)
1
((
)
)
1
((
τ
τ
∫
∫
=
=
=
−
+
T
c
A
t
t
c
T
k
A
T
A
B
d
e
B
d
e
B
e
A
c
c
c
0
)
)
1
((
0
,
τ
τ
τ
τ
gdy
0
det
≠
c
A
[
]
c
T
A
c
T
c
A
B
I
e
A
B
d
e
B
c
c
−
=
=
−
∫
1
0
τ
τ
0
)
det(
)
det(
)
(
≠
=
=
⇒
=
T
A
tr
T
A
T
A
c
c
c
e
e
A
e
A

8
Automatyka i sterowanie 12 Ruch w przestrzeni stanów
Układy czasu ciągłego i dyskretnego
Diagonalizacja równania stanu
(
)(
)
(
)
(
) (
)
(
)
1
0
1
1
2
0
1
2
1
2
n
n
n
n
n
n
y( s )
b s
b s
b
c
c
c
G( s )
b
u( s )
s p
s p
s p
s p
s p
s p
−
+
+ +
=
=
=
+
+
+ +
+
+
+
+
+
+
(
)
1
i
i
i i
i
d
x ( s )
u( s )
x ( t )
p x ( t ) u( t )
s p
dt
=
⇒
= −
+
+
1
1
1
2
2
2
0
0
1
0
0
1
0
0
1
n
n
n
x ( t )
p
x ( t )
x ( t )
p
x ( t )
u( t )
x ( t )
p
x ( t )
−
⎡
⎤ ⎡
⎤ ⎡
⎤ ⎡ ⎤
⎢
⎥ ⎢
⎥ ⎢
⎥ ⎢ ⎥
−
⎢
⎥ ⎢
⎥ ⎢
⎥ ⎢ ⎥
=
+
⎢
⎥ ⎢
⎥ ⎢
⎥ ⎢ ⎥
⎢
⎥ ⎢
⎥ ⎢
⎥ ⎢ ⎥
−
⎣ ⎦
⎣
⎦ ⎣
⎦ ⎣
⎦
[
]
1
2
1
2
0
n
n
x ( t )
x ( t )
y( t )
c
c
c
b u( t )
x ( t )
⎡
⎤
⎢
⎥
⎢
⎥
=
+
⎢
⎥
⎢
⎥
⎣
⎦

9
Automatyka i sterowanie 12 Ruch w przestrzeni stanów
Układy czasu ciągłego i dyskretnego
Przypomnienie:
0
i
i
i i
v
, Av
s v
≠
=
definicja wartości wektorów własnych
(
)
0
i
i
s I
A v
−
=
(
)
0
i
det s I
A
−
=
(
)
det sI
A
−
wielomian charakterystyczny A
(
)
0
det sI
A
−
=
równanie charakterystyczne
czyli jest n wartości własnych A rzeczywistych lub zespolonych parami sprzężonych, jedno lub
wielokrotnych. Dalej zakładamy, że wartości własne są jednokrotne.
Równania definiujące wektory i wartości własne można zapisać łącznie:

10
Automatyka i sterowanie 12 Ruch w przestrzeni stanów
Układy czasu ciągłego i dyskretnego
[
] [
]
1
2
2
1
1
1
2
1
0
0
0
0
0
0
n
n
n
s
s
s
S
S
A
v
v
v
v
v
v
V V
V
V
V
,
V
A
S
A
A
−
−
⎡
⎤
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎦
=
=
=
⎥
⎣
=
Jeśli potrafimy wskazać n niezależnych liniowo wektorów własnych macierzy stanu, to równanie stanu
możemy przekształcić do postaci kanonicznej diagonalnej. Będzie tak zawsze w przypadku różnych
wartości własnych, ale nie tylko.

11
Automatyka i sterowanie 12 Ruch w przestrzeni stanów
Układy czasu ciągłego i dyskretnego
Co w przypadku wielokrotnych biegunów transmitancji:
(
) (
)
(
)
(
) (
) (
) (
)
1
0
1
1
2
3
4
0
3
3
2
1
4
1
4
1
1
n
n
n
n
y( s )
b s
b s
b
c
c
c
c
G( s )
b
u( s )
s p
s p
s p
s p
s p
s p
s p
−
+
+ +
=
=
=
+
+
+
+
+
+
+
+
+
+
+
+
3 4
i
, , ,n
=
…
:
(
)
1
i
i
i i
i
d
x ( s )
u( s )
x ( t )
p x ( t ) u( t )
s p
dt
=
⇒
= −
+
+
(
)
(
)
2
3
2
1 2
1
2
1
1
1
1
d
x ( s )
u( s )
x ( s )
x ( t )
p x ( t ) x ( t )
s p
dt
s p
=
=
⇒
= −
+
+
+
(
)
(
)
1
2
1
1 1
2
3
1
1
1
1
d
x ( s )
u( s )
x ( s )
x ( t )
p x ( t ) x ( t )
s p
dt
s p
=
=
⇒
= −
+
+
+

12
Automatyka i sterowanie 12 Ruch w przestrzeni stanów
Układy czasu ciągłego i dyskretnego
1
1
1
2
2
1
3
3
1
4
4
2
1
0
0
0
1
0
0
0
0
0
1
1
0
0
1
0
0
n
n
n
x ( t )
x ( t )
p
x ( t )
x ( t )
p
x ( t )
x ( t )
p
u( t )
x ( t )
x ( t )
p
x ( t )
x ( t )
p
⎡
⎤
−
⎡
⎤
⎡
⎤
⎡
⎤ ⎡ ⎤
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥ ⎢ ⎥
−
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥ ⎢ ⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥ ⎢ ⎥
−
⎣
⎦
=
+
⎢
⎥
⎢
⎥
⎢
⎥ ⎢ ⎥
−
⎢
⎥
⎢
⎥
⎢
⎥ ⎢ ⎥
⎢
⎥
⎢
⎥
⎢
⎥ ⎢ ⎥
⎢
⎥
⎢
⎥
⎢
⎥ ⎢ ⎥
−
⎢
⎥
⎣ ⎦
⎣
⎦
⎣
⎦
⎣
⎦
[
]
1
2
1
2
0
n
n
x ( t )
x ( t )
y( t )
c
c
c
b u( t )
x ( t )
⎡
⎤
⎢
⎥
⎢
⎥
=
+
⎢
⎥
⎢
⎥
⎣
⎦

13
Automatyka i sterowanie 12 Ruch w przestrzeni stanów
Układy czasu ciągłego i dyskretnego
Postać kanoniczna Jordana:
Klatką Jordana związaną z liczbą s
i
nazwiemy macierz postaci
1
0
0
0
1
0
0
0
0
1
0
0
0
i
i
ij
i
s
s
J
s
⎡
⎤
⎢
⎥
⎢
⎥
= ⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
…
…
…
…
a blokiem Jordana macierz blokową postaci
1
2
0
0
0
0
0
0
i
i
i
i
id
J
J
J
J
⎡
⎤
⎢
⎥
= ⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
…
…
…
gdzie J
i j
j=1,…,d
i
są klatkami Jordana związanymi z tą sama liczbą s
i
, a pozostałe elementy są zerami.
Jak widać każdy blok Jordana ma tylko jedna wartość własną s
i.
.

14
Automatyka i sterowanie 12 Ruch w przestrzeni stanów
Układy czasu ciągłego i dyskretnego
Każda macierz kwadratowa jest podobna do macierzy blokowej, która ma na głównej przekątnej bloki
Jordana, a poza nią bloki zerowe. Macierz tą
1
2
0
0
0
0
0
0
k
J
J
J
J
⎡
⎤
⎢
⎥
= ⎢
⎥
⎢
⎥
⎣
⎦
…
…
…
nazywamy postacią kanoniczną Jordana macierzy A.
Niech
1 2
n
T
t t
t
⎡
⎤
= ⎣
⎦
będzie macierzą przekształcenia do postaci kanonicznej Jordana składającej się z k
klatek Jordana o wartościach własnych
1
2
k
s ,s , s
…
i wymiarach (czyli krotnościach wartości własnych)
1
2
k
m ,m , m
…
.
15
Automatyka i sterowanie 12 Ruch w przestrzeni stanów
Układy czasu ciągłego i dyskretnego
1
2
0
0
0
0
0
0
k
J
J
AT T
J
⎡
⎤
⎢
⎥
= ⎢
⎥
⎢
⎥
⎣
⎦
…
…
…
1
1
1
2
1
0
0
0
0
0
1
0
0
0
0
0
0
k
s
s
s
AT T
J
J
⎡
⎤
⎡
⎤
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
=
⎣
⎦
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
…
…
…
1
1 11
2
11
1 1 2
1
1 1 1
1 1 1
,
,
,
m
,m
,m
At
s t
At
t
s t
At
t
s t
−
=
=
+
=
+
Jaka będzie macierz tranzycyjna, jeśli postacią kanoniczną macierzy stanu jest postać Jordana?
wektor własny związany z wartością własną s
1
wektory główne związane z wartością własną s
1

16
Automatyka i sterowanie 12 Ruch w przestrzeni stanów
Układy czasu ciągłego i dyskretnego
1
2
1
0
0
0
0
0
0
k
J t
J t
J t
e
e
( t ) T
T
e
−
⎡
⎤
⎢
⎥
⎢
⎥
Φ
=
⎢
⎥
⎢
⎥
⎣
⎦
(
)
1
1
1
0
0
0
i
i
i
i
i
i
i
i
s t
s t
m
s t
i
s t
J t
s t
s t
e
te
t
e
m
!
e
e
te
e
−
⎡
⎤
⎢
⎥
−
⎢
⎥
⎢
⎥
=
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
1
1
1
2
2
1
i
i
i
i
i
i
k
s t
s t
m
s t
T
T
T
i ,
i ,
i ,
i ,
i ,m
i ,m
i
( t )
e t
te t
t
e t
η
η
η
−
=
⎡
⎤
Φ
=
+
+ +
⎣
⎦
∑
1
1
2
T
T
T
n
T
:
η
η
η
−
⎡ ⎤
⎢ ⎥
⎢ ⎥
= Ν =
⎢ ⎥
⎢ ⎥
⎣ ⎦

17
Automatyka i sterowanie 12 Ruch w przestrzeni stanów
Układy czasu ciągłego i dyskretnego
Mody odpowiedzi swobodnej układu:
Jeśli postać kanoniczna macierzy stanu jest diagonalna:
V- nieosobliwa macierz wektorów własnych,
1
1
2
T
T
T
n
w
w
V
:W
w
−
⎡
⎤
⎢
⎥
⎢
⎥
=
=
⎢
⎥
⎢
⎥
⎣
⎦
1
2
1
0
0
0
0
0
0
n
s t
s t
s t
e
e
( t ) V
V
e
−
⎡
⎤
⎢
⎥
⎢
⎥
Φ
=
⎢
⎥
⎢
⎥
⎣
⎦
1
i
n
s t
T
i
i
i
( t )
e v w
=
Φ
=
∑

18
Automatyka i sterowanie 12 Ruch w przestrzeni stanów
Układy czasu ciągłego i dyskretnego
0
0
t
x( t )
( t )x
( t
)Bu( )d
τ
τ τ
= Φ
+ Φ −
∫
( )
0
0
1
1
1
0
0
i
i
i
i
t
t
n
n
n
s t
s t
s t
s
T
T
T
i
i
i
i
i
i
i
i
i
x( t )
e v w x
e
v w Bu( )d
e v w x
e
Bu( )d
τ
τ
τ τ
τ τ
−
−
=
=
=
⎡
⎤
=
+
=
+
⎢
⎥
⎣
⎦
∑
∑
∑
∫
∫
Bez wymuszenia:
0
1
i
n
s t
T
i
i
i
x( t )
e v w x
=
=
∑
Jeżeli wartość własna s
i
jest rzeczywista to odpowiadający jej wektor własny v
i
jest też rzeczywisty.
Składnik tej sumy – mod opisuje ruch rzutu rozwiązania na prostą wyznaczoną przez wektor v
i
.Jeżeli
0
i
x
v
α
=
, to
0
i
i
s t
s t
i
x( t )
e v
e x
α
=
=
, bo
1
0
T
T
i
i
j
i
w v
, w v
j i
=
=
≠
. Trajektoria rozpoczynająca się w x
0
będzie prostoliniowa, ekspotencjalnie dążąca do 0 lub nieskończoności zależnie od znaku s
i
. Jeżeli mod
związany z wartością własną s
i
ma nie wystąpić w rozwiązaniu, to warunek początkowy x
0
musi mieć
składową = zeru w kierunku wektora v
i
.
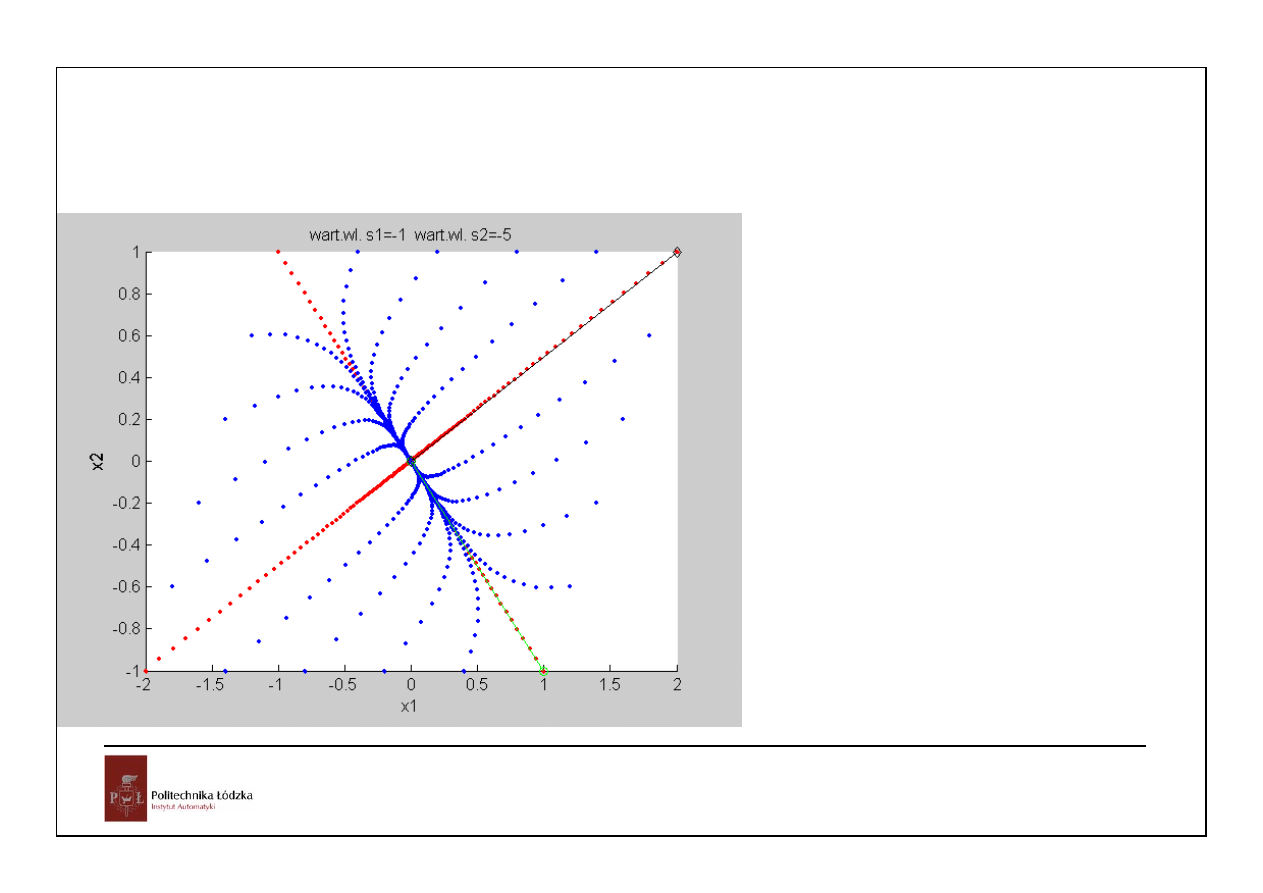
19
Automatyka i sterowanie 12 Ruch w przestrzeni stanów
Układy czasu ciągłego i dyskretnego
A =
-3.6667 -2.6667
-1.3333 -2.3333
S =
-1 0
0 -5
V =
1 2
-1 1
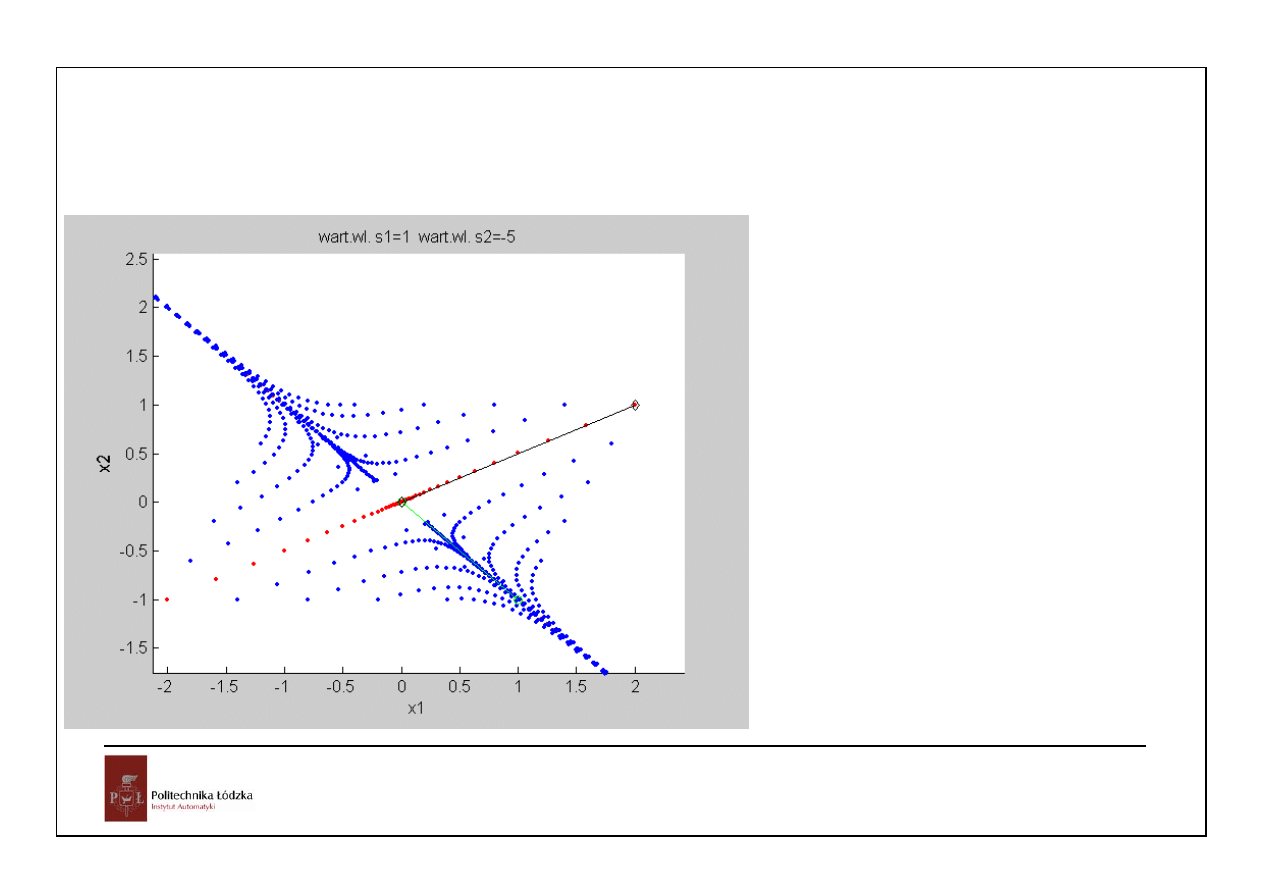
20
Automatyka i sterowanie 12 Ruch w przestrzeni stanów
Układy czasu ciągłego i dyskretnego
A =
-3.0000 -4.0000
-2.0000 -1.0000
S =
1 0
0 -5
V =
1 2
-1 1
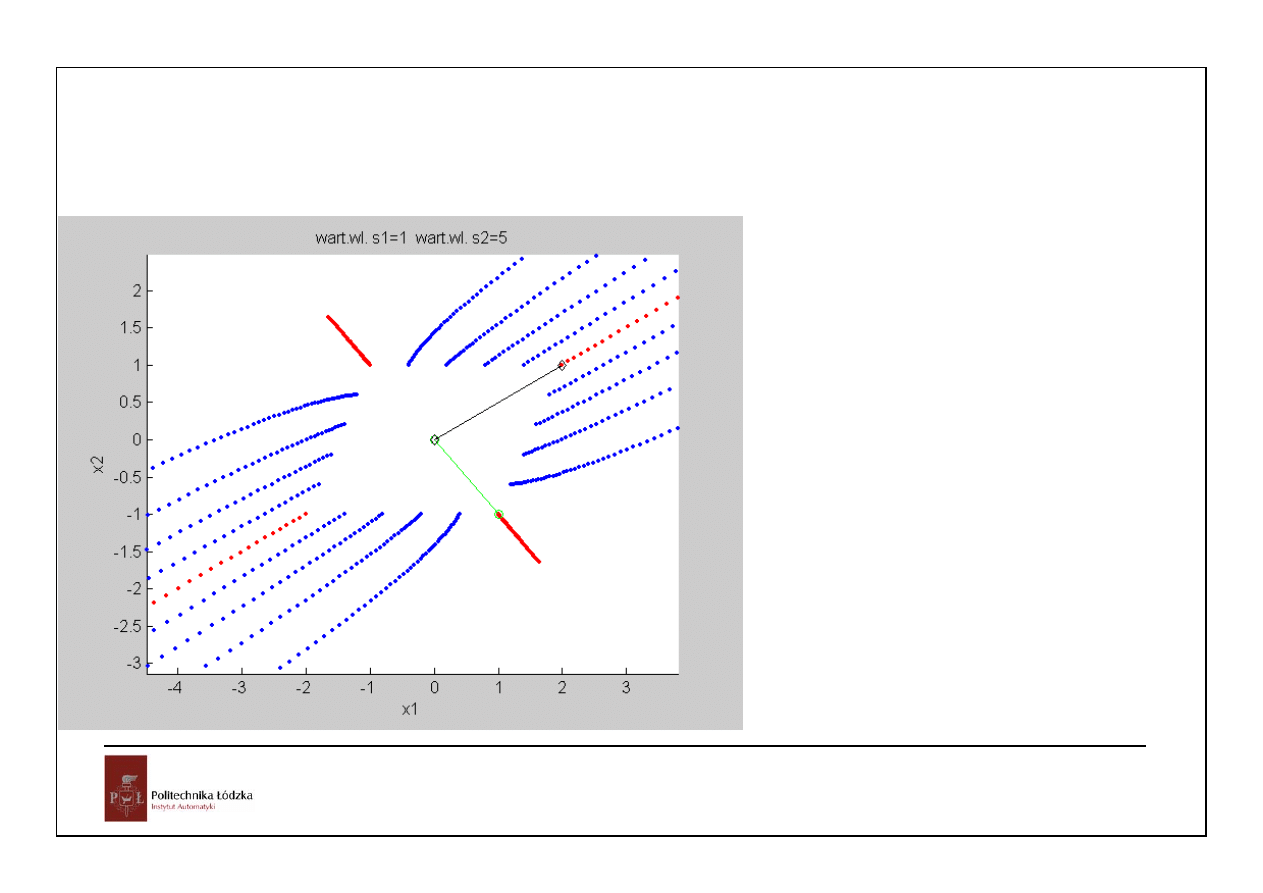
21
Automatyka i sterowanie 12 Ruch w przestrzeni stanów
Układy czasu ciągłego i dyskretnego
A =
-3.6667 -2.6667
-1.3333 -2.3333
S =
1 0
0 5
V =
1 2
-1 1
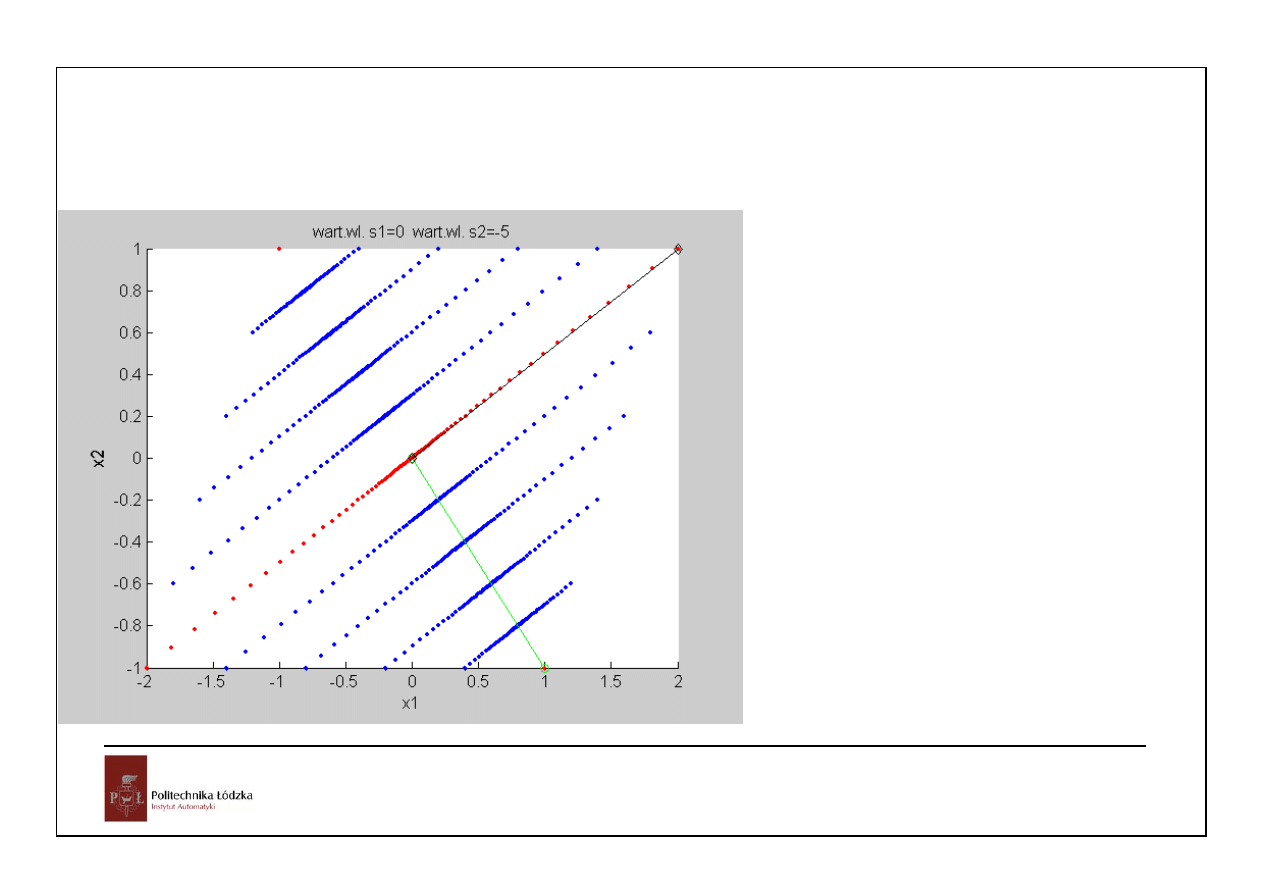
22
Automatyka i sterowanie 12 Ruch w przestrzeni stanów
Układy czasu ciągłego i dyskretnego
A =
-3.3333 -3.3333
-1.6667 -1.6667
S =
0 0
0 -5
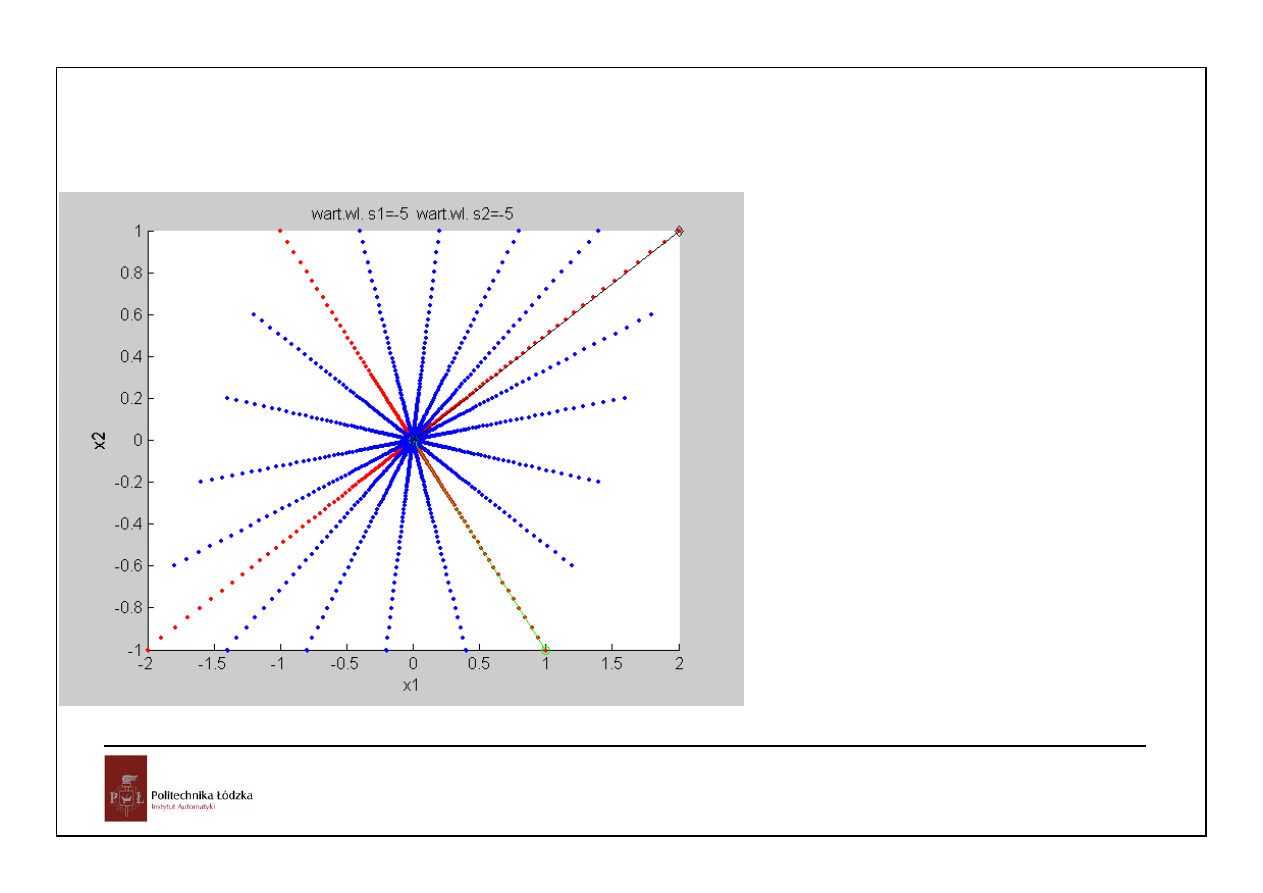
V =
1 2
-1 1
23
Automatyka i sterowanie 12 Ruch w przestrzeni stanów
Układy czasu ciągłego i dyskretnego
A =
-5.0000 0
0.0000 -5.0000
S =
-5 0
0 -5
wektorami własnymi mogą być dowolne
liniowo niezależne wektory

24
Automatyka i sterowanie 12 Ruch w przestrzeni stanów
Układy czasu ciągłego i dyskretnego
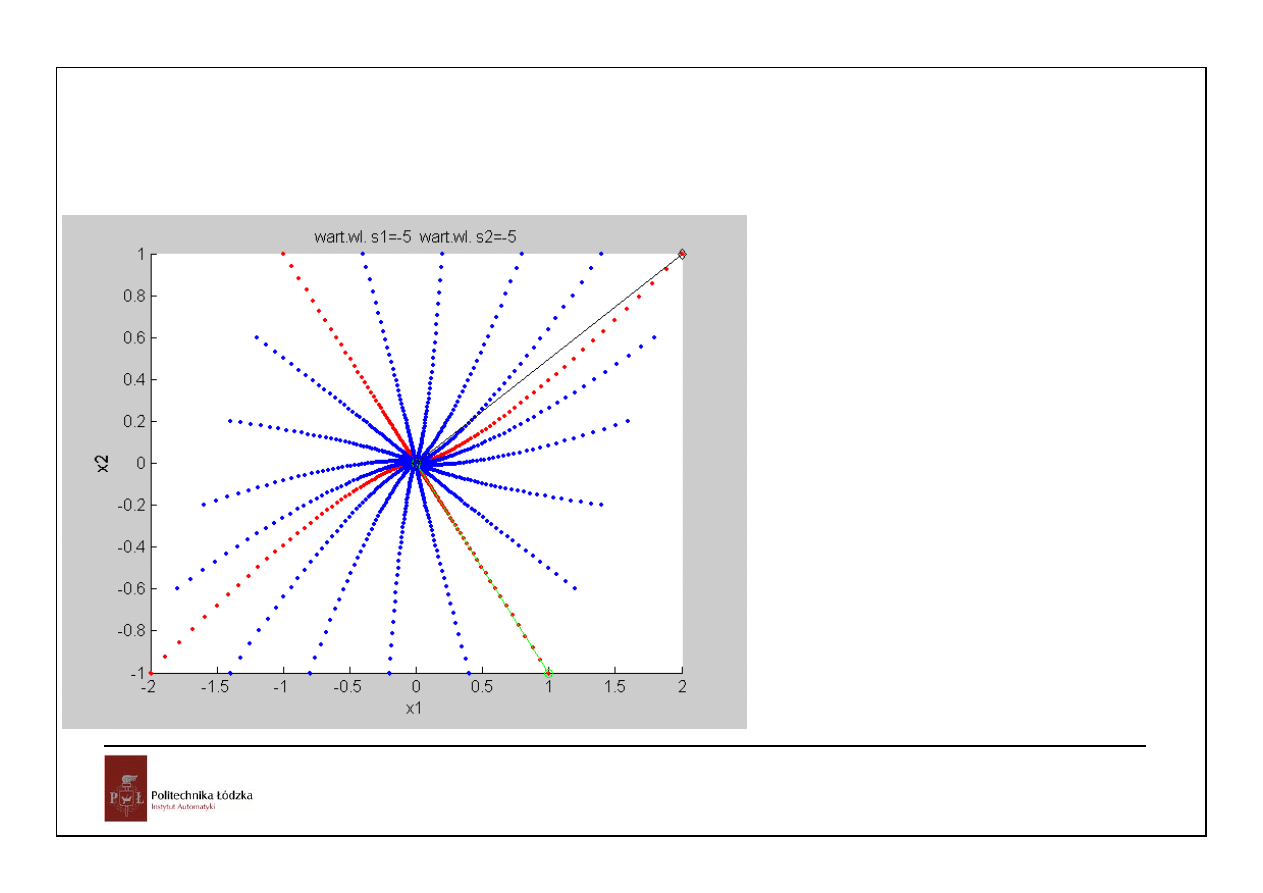
Jeżeli postać kanoniczna jest postacią Jordana (dalej rozważamy rzeczywiste wartości własne), to
trajektorie prostoliniowe będą wyznaczone tylko przez wektory własne (jest ich po jednym na klatkę
Jordana). Trajektorie zaczynające się na prostych wyznaczonych przez wektory główne nie są
prostoliniowe!
1
2
1
0
0
0
0
0
0
k
J t
J t
J t
e
e
( t ) T
T
e
−
⎡
⎤
⎢
⎥
⎢
⎥
Φ
=
⎢
⎥
⎢
⎥
⎣
⎦
(
)
1
1
1
0
0
0
i
i
i
i
i
i
i
i
s t
s t
m
s t
i
s t
J t
s t
s t
e
te
t
e
m
!
e
e
te
e
−
⎡
⎤
⎢
⎥
−
⎢
⎥
⎢
⎥
=
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
Trajektorie w przestrzeni stanów można rozłożyć na składowe odpowiadające rzutom na podprzestrzenie
rozpięte na wektorze własnym i wektorach głównych związanych z kolejnymi klatkami Jordana.
25
Automatyka i sterowanie 12 Ruch w przestrzeni stanów
Układy czasu ciągłego i dyskretnego
A =
-4.6667 0.3333
-0.3333 -5.3333
S =
-5 1
0 -5
T =
1 2
-1 1
26
Automatyka i sterowanie 12 Ruch w przestrzeni stanów
Układy czasu ciągłego i dyskretnego
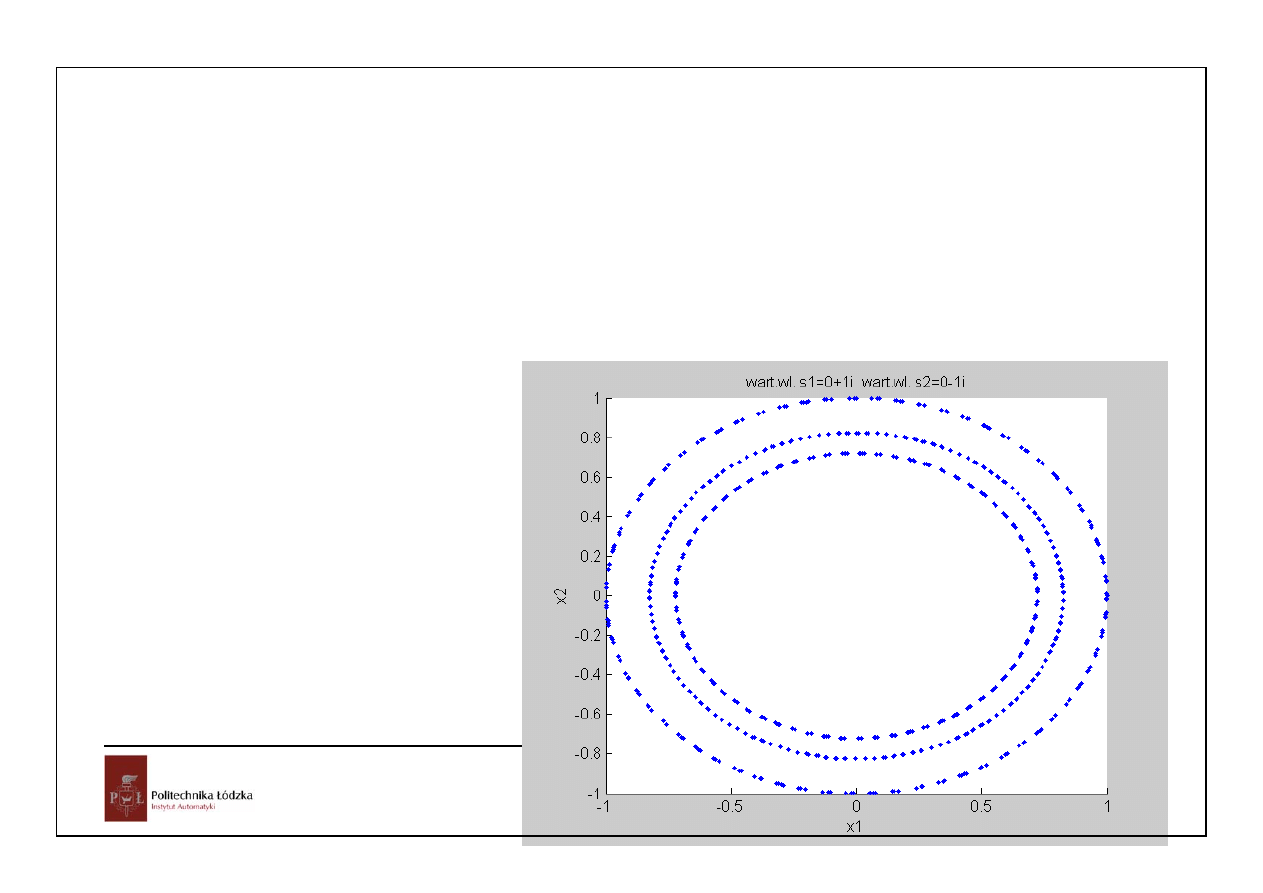
W przypadku zespolonej pojedynczej wartości własnej
i
s
j
σ
ω
= +
istnieje sprzężona do niej. Odpowiednie
wektory własne są też zespolone sprzężone. W sumie dwu modów zwianych ze sprzężonymi wartościami
własnymi nastąpi skrócenie części urojonych i pozostanie część rzeczywista w postaci drgań
harmonicznych o pulsacji równej modułowi części urojonej wartości własnej tłumiona (lub wzmacniana)
wykładniczo zgodnie z
t
e
σ
.
A =
0 1
-1 0
S =
0 + 1.0000i 0
0 0 - 1.0000i
V =
1.0000 + 1.0000i 1.0000 - 1.0000i
-1.0000 + 1.0000i -1.0000 - 1.0000i
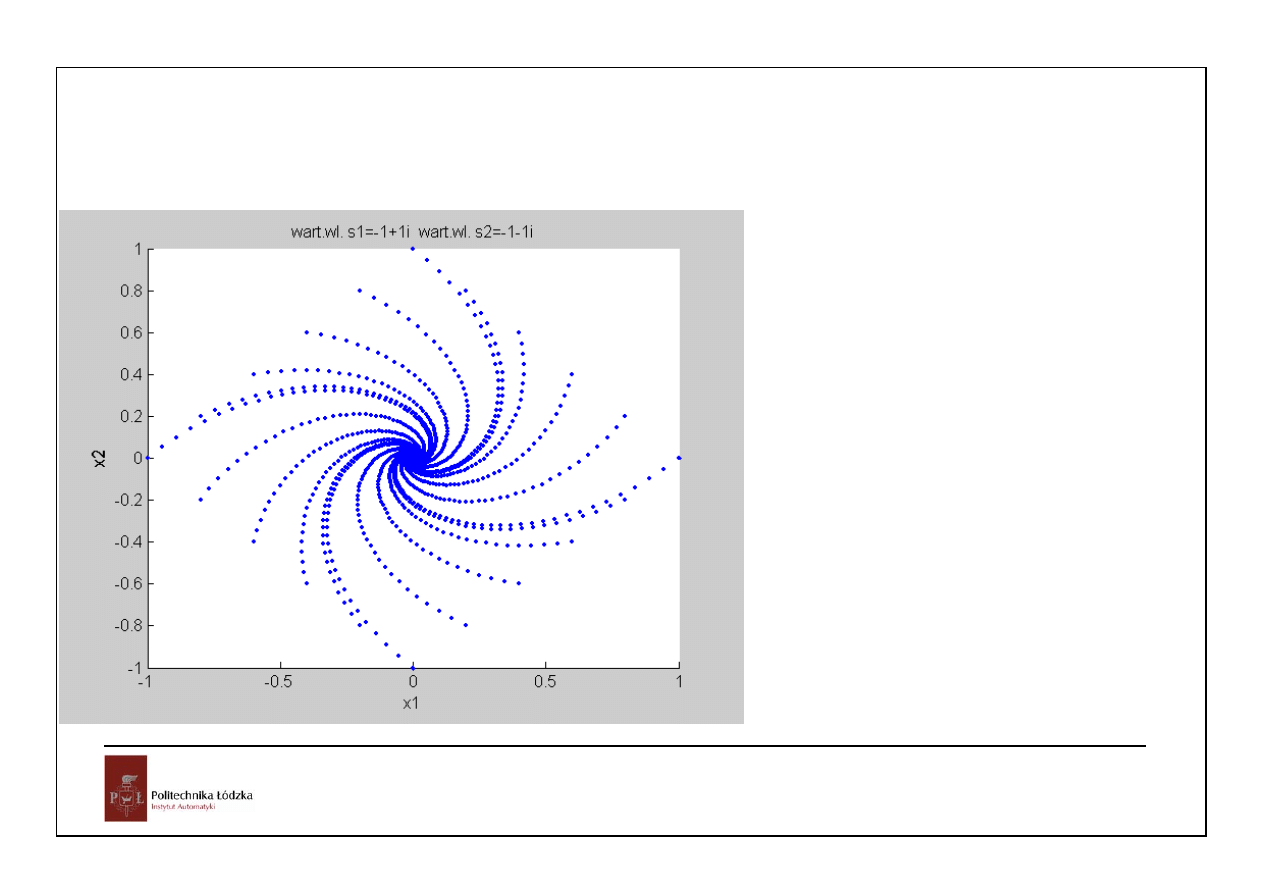
27
Automatyka i sterowanie 12 Ruch w przestrzeni stanów
Układy czasu ciągłego i dyskretnego
A =
-1 1
-1 -1
S =
-1.0000 + 1.0000i 0
0 -1.0000 - 1.0000i
V =
1.0000 + 1.0000i 1.0000 - 1.0000i
-1.0000 + 1.0000i -1.0000 - 1.0000i

28
Automatyka i sterowanie 12 Ruch w przestrzeni stanów
Układy czasu ciągłego i dyskretnego
Bardzo podobne rozważania można przeprowadzić dla układów dyskretnych w czasie korzystając z
zależności
)
(kT
x
=
( )
)
0
(
1
x
w
v
z
T
i
i
n
i
k
i
∑
=
.
Kosmita talerzowy łagodny porusza się w przestrzeni
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
3
2
1
x
x
x
skokami, zgodnie z równaniem
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
⋅
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
−
−
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
+
+
+
)
k
(
x
)
k
(
x
)
k
(
x
.
.
.
.
.
.
.
.
.
)
k
(
x
)
k
(
x
)
k
(
x
3
2
1
3
2
1
2
0
7
0
4
0
4
0
9
0
4
0
7
0
7
0
9
0
1
1
1
. Z którego punktu na kuli
10
3
2
1
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
x
x
x
musi wystartować kosmita by
trafić do początku układu współrzędnych po linii prostej. Narysuj wszystkie trajektorie prostoliniowe.
Po ilu skokach znajdzie się w odległości mniejszej niż zasięg szczypiec (0.1) od celu.

29
Automatyka i sterowanie 12 Ruch w przestrzeni stanów
Układy czasu ciągłego i dyskretnego
A =
0.9000 0.7000 -0.7000
0.4000 0.9000 -0.4000
0.4000 0.7000 -0.2000
>> [V S]=eig(A)
V =
0 -0.5774 0.7071
-0.7071 -0.5774 -0.0000
-0.7071 -0.5774 0.7071
S =
0.5000 0 0
0 0.9000 0
0 0 0.2000
Mamy 3 stabilne, rzeczywiste wartości własne, będą więc 3 proste wyznaczające trajektorie
prostoliniowe – kierunki 3 wektorów własnych. Dadzą one 6 punktów przecięcia ze sferą o promieniu 10.
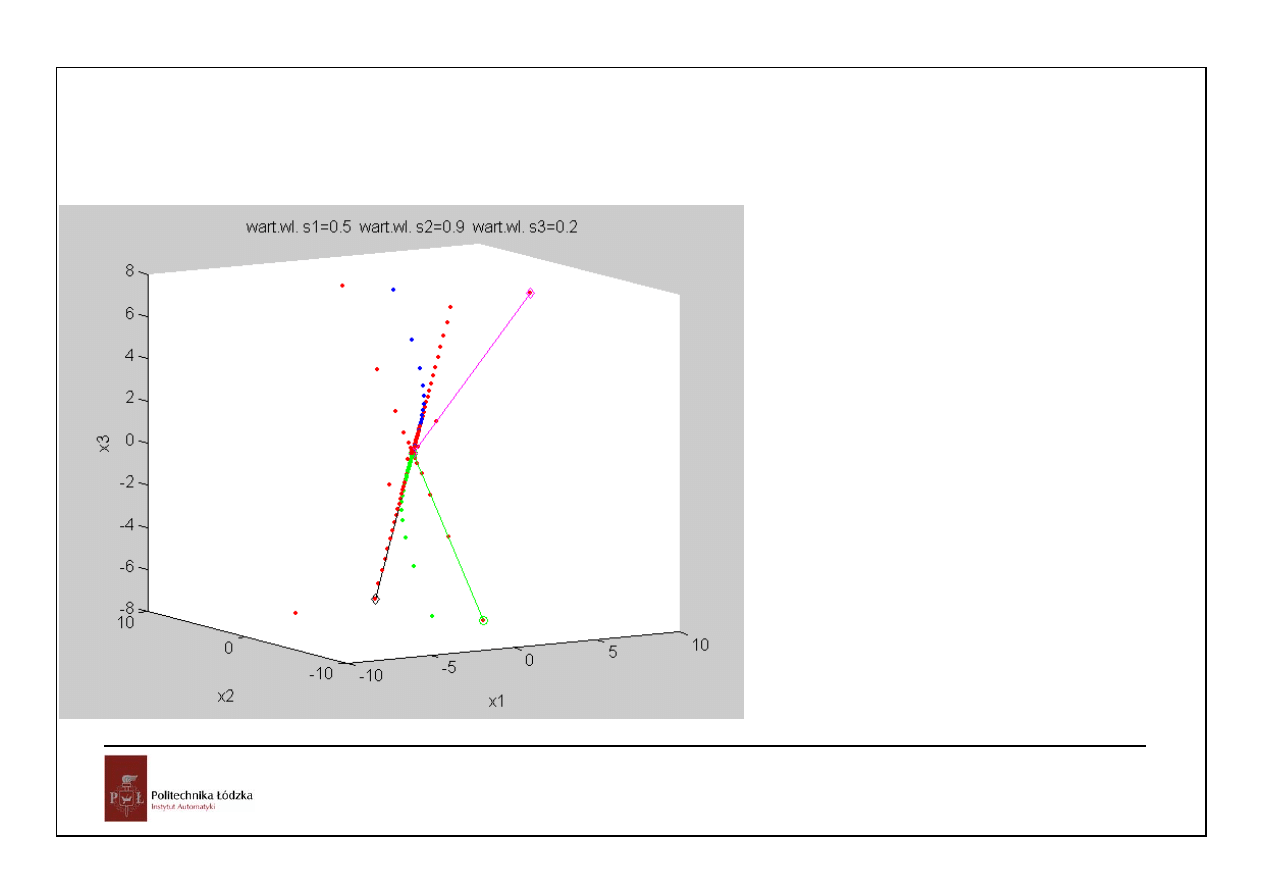
30
Automatyka i sterowanie 12 Ruch w przestrzeni stanów
Układy czasu ciągłego i dyskretnego
Najszybsza będzie trajektoria związana z
najmniejszą wartością własną 0.2. Ruch
po niej odpowiada mnożeniu położenia
w przestrzeni stanów przez 0.2 w
każdym kroku. Odległości od celu będą
więc wynosić kolejno 10, 2, 0.4, 0.08,
0.004 .......
Wyszukiwarka
Podobne podstrony:
automatyka i sterowanie wyklad Nieznany (12)
automatyka i sterowanie wyklad 15
automatyka i sterowanie wyklad Nieznany (8)
automatyka i sterowanie wyklad Nieznany (2)
automatyka i sterowanie wyklad 3
automatyka i sterowanie wyklad Nieznany (7)
automatyka i sterowanie wyklad Nieznany (14)
automatyka i sterowanie wyklad 16
automatyka i sterowanie wyklad Nieznany (16)
automatyka i sterowanie wyklad Nieznany (5)
automatyka i sterowanie wyklad 9
automatyka i sterowanie wyklad 11
automatyka i sterowanie wyklad 4
automatyka i sterowanie wyklad 5
automatyka i sterowanie wyklad Nieznany (10)
automatyka i sterowanie wyklad Nieznany (3)
automatyka i sterowanie wyklad 8
automatyka i sterowanie wyklad 2
automatyka i sterowanie wyklad 15
więcej podobnych podstron