P

o

dsta

wy

Chemii

K

w

an

to

w

ej

Molekuªy

π

-elektrono

w

e

i

mo

del

Hü

kla

orbita

l

i

molekular n

y

h

(mo

del

HMO)

Sform

uªo

w

anie

mo

delu

HMO:

Eri

h

Hü

k

el

(1932)

Rozwini

i

e

mo

delu

HMO:

C.

A.

Coulson

i

H.

C.

Longuet-Higgi

ns

(1947).

Przybli

»

eni

e

LCA

O

MO

(MO)

ψ

k

=

M

X

r

=1

χ

r

c

r,k

(LCA

O)

.

(1)

Charakteryst

yk

a

molekuªy

π

-elektrono

w

ej:

•

Molekuªa

zbudo

w

ana

jest

z

M

atomó

w

I

I

okresu

(B,C,N,O,F),

oraz

p

ewnej

lizb

y

atomó

w

H

(w

mo

delu

HMO

atom

y

H

s¡

p

omija

ne).

•

W

szystk

ie

atom

y

le»¡

w

jednej

pªaszzy¹

n

ie

(np.

XY

).

Pªaszzyz

n

a

ta

jest

zarazem

pªaszzyzn¡

symetrii

rozw

a»anej

molekuªy

.

•

Ze

wzgldu

na

ob

eno±¢

pªaszzyz

n

y

symetrii

rozró»niam

y

dw

a

t

yp

y

symetrii

or-

bitali

atomo

wy

h

(A

O)

i

molekular

n

y

h

(MO):

σ

A

O

i

σ

MO:

symetryzne

ze

wzgldu

na

o

dbiie

w

pªaszz.

XY

,

π

A

O

i

π

MO:

an

t

ysymetryzne

ze

wzgldu

na

o

dbiie

w

pªaszz.

XY

.

•

W

rama

h

k

onstruk

ji

LCA

O

MO

orbital

e

σ

MO

t

w

orzym

y

wyª¡znie

jak

o

k

om

binaje

lini

o

w

e

orbital

i

σ

A

O,

a

orbital

e

π

MO

wyª¡znie

jak

o

k

om

binaje

lini

o

w

e

orbital

i

π

A

O.

Uw

aga:

orbital

e

σ

A

O

i

π

A

O

s¡

funk

jami

rzezyw

ist

ymi,

ale

utrzymane

z

ni

h

orbital

e

molekular

ne

mog¡

b

y¢

funk

jmi

zesp

olon

ymi

(gdy»

wsp

óªzyn

n

iki

lini

o

w

e

c

r,k

mog¡

w

ogólno±i

b

y¢

lizbami

zesp

olon

ymi).

•

W

molekule

zbudo

w

anej

z

M

atomó

w

I

I

okresu

orbital

e

π

A

O

to

orbital

e

atomo

w

e

2

p

z

t

y

h

atomó

w.

Ka»dy

atom

dostarza

jednego

orbital

u

2

p

z

,

w

sumie

jest

wi

do

dysp

ozy

ji

M

t

y

h

orbital

i

.

Z

orbital

i

t

y

h

ut

w

orzy¢

wi

mo»na

dokªadnie

M

orbital

i

π

MO.

•

P

ary

atomó

w

p

oª¡zone

s¡

p

o

jedynzy

mi

wi¡zaniam

i

hemizn

ymi

t

ypu

σ

,

ut

w

orzo-

n

ymi

przez

orbital

e

zh

ybrydy

z

o

w

ane

sp

2

pary

s¡siaduj¡y

h

atomó

w.

Je±li

w

t

ym

szkieleie

wi¡za«

σ

nie

ma

napr»e«,

to

k

¡t

y

midzy

wi¡zaniam

i

s¡

bardzo

bliskie

120

o

.

Przybli

»

eni

e

π

-elektrono

w

e

W

rama

h

tego

przybli»enia

rozw

a»a

si

t

ylk

o

te

elektron

y

w

molekule,

które

s¡

opisane

orbital

a

m

i

t

ypu

π

.

P

osªugujem

y

si

zsto

skrótem

m

y±lo

wym,

nazyw

a

j¡

te

elektron

y

elektronami

π

.

Zakªada

si,

»e

elektron

y

π

p

orusza

j¡

si

w

p

ewn

ym

efekt

ywn

y

m

p

olu

wyt

w

orzon

ym

przez

j¡dra

atomo

w

e

oraz

elektron

y

opisane

orbital

a

m

i

σ

.

W

mo

delu

HMO

zakªada

si

do

datk

o

w

o,

»e

elektron

y

π

nie

o

dziaªuj¡

ze

sob¡,

zyli

za

ho

wuj¡

si

jak

z¡stki

niezale»ne.

1

Orbitale

atomo

w

e

ortogonalizo

w

ane

Orbital

e

atomo

w

e

nale»¡e

do

atomó

w

umieszzon

y

h

w

ró»n

y

h

punkta

h

przestrzen i

nie

s¡

ortogonalne.

Inazej:

maierz

aªek

nakryw

ania

w

bazie

A

O,

o

elemen

ta

h

hχ

r

|χ

s

i = s

r,s

,

(2)

jest

ró»na

o

d

maierzy

jednostk

o

w

ej.

Np.

w

molekule

b

enzen

u

orbital

e

t

ypu

2

p

z

s¡siedni

h

atomó

w

w

gla

(orbital

e

π

A

O)

ma

j¡

aªki

nakryw

ania

s

r,s

≈ 0.3

.

Zbiór

nieortogonal

n

y

h

orbital

i

atomo

wy

h

mo»na

jednak

p

o

dda¢

p

ewnej

transformaji,

zw

anej

symetryzn¡

ortogonalizaj¡

(Lö

wdin,

1950).

Przy

p

omo

y

tej

transformaji

M

nieortogonal

n

y

h

π

A

O

t

ypu

2

p

z

przeksz

taªa

si

w

M

tzw.

ortogonali

zow

an

y

h

orbital

i

atomo

wy

h

(

π

O

A

O):

{χ

1

, χ

2

, . . . , χ

M

} ,

(3)

które

sp

eªnia

j¡

w

arunki

ortonormal

no

±i

:

hχ

r

|χ

s

i = δ

r,s

.

(4)

Symetryzna

ortogonali

zaja

zap

ewnia,

»e

otrzymane

π

O

A

O

s¡

w

na

jwy»szy

m

mo»li

wym

stopniu

p

o

dobne

do

wyj±io

wy

h

π

A

O.

Uw

aga:

zaró

wno

π

A

O,

jak

i

π

O

A

O

s¡

funk

jami

rzezyw

ist

ymi:

χ

∗

r

= χ

r

.

Maierz

top

ologi

z

na

molekuªy

π

-elektrono

w

ej

Maierz

top

ologi

zna

t

(wymiaru

M

× M

):

t

r,s

= t

s,r

:=











0 ,

dla

r

= s ,

1 ,

dla

r

i

s

p

oª¡zon

y

h

wi¡z.

σ ,

0 ,

w

inn

y

h

wypadk

a

h

.

(5)

Jest

to

maierz

symetryzna:

t

= t

T

.

W

arunek

na

liz

b

na

jbli»szy

h

s¡siadó

w

danego

atom

u

r

:

1 ¬

M

X

s

t

r,s

¬ 3 .

(6)

Efekt

ywn

y

hamilt

oni

an

jedno

elektrono

wy

w

mo

delu

HMO

Efekt

ywn

y

hamil

t

o

ni

a

n

ˆh

eff

opisuj¡y

ukªad

elektronó

w

π

w

molekule

okre±lon

y

jest

w

mo

delu

HMO

w

sp

osób

nieja

wn

y

,

p

oprzez

k

onstruk

j

maierzy

op

eratora

ˆh

eff

w

bazie

orbital

i

π

O

A

O:

h

r,s

= h

s,r

:= hχ

r

|ˆh

eff

χ

s

i =

(

α

r

,

dla

r

= s ,

β

rs

,

dla

r

6= s .

(7)

Maierz

h

jest

maierz¡

symetryzn¡:

h

= h

T

.

Mo

del

HMO

jak

o

protot

yp

meto

d

p

óªemiryz

n

y

h

hemii

kw

an

to

w

ej

W

mo

delu

HMO

wpro

w

adza

si

parametry

empiryzne

:

aªki

kulom

b

o

wskie:

α

r

= α

[r]

,

(8)

aªki

rezonanso

w

e:

β

rs

= β

sr

= t

r,s

β

[rs]

.

(9)

gdzie:

[r]

oznaza

t

yp

atom

u

r

(np.

C,

N,

O),

[rs]

oznaza

t

yp

wi¡zania

rs

(np.

CC,

CN,

CO).

2

K

onstruk

ja

LCA

O

orbitali

molekularn

y

h

π

MO:

ψ

k

=

M

X

r

=1

χ

r

c

r,k

,

(10)

hψ

k

|ψ

l

i = δ

k,l

,

(11)

gdzie

k

= 1, 2, . . . , M

.

Energie

orbitalne

elektronó

w

π

deniujem

y

jak

o:

e

k

:= hψ

k

|ˆh

eff

ψ

k

i .

(12)

Numeraja

energii

orbital

n

y

h

(a

st¡d

π

MO)

zazwyz

a

j

stosujem

y

up

orz¡dk

o

w

anie

nie-

malej¡e:

e

1

¬ e

2

¬ . . . ¬ e

M

.

(13)

Lizb

y

obsadze«

π

MO:

n

π
k

= 2, 1, 0 .

(14)

W

arto±i

te

o

dp

o

wiada

j¡

sp

eªnieniu

zak

azu

P

auliego

.

Ró»ne

zbiory

w

arto±i

{n

π
k

}

ha-

rakteryzuj¡

ró»ne

stan

y

π

-elektrono

w

e

molekuªy

.

UW

A

GA:

w

mo

delu

HMO

zakªada

si,

»e

wszys

tk

ie

π

MO

dla

który

h

n

π
k

= 1

o

dp

o

wiada

j¡

obsadzon

ym

spinorbital

o

m

o

taki

h

sam

y

h

funk

ja

h

spino

wy

h

(np.

α

).

Oznaza

to,

»e

rozw

a»am

y

t

ylk

o

takie

(ot

w

artop

o

wªok

o

w

e)

stan

y

molekuªy

,

w

który

h

niesparo

w

ane

elek-

tron

y

ma

j¡

spin

y

ró

wnolegªe.

Caªk

o

wita

liz

ba

elektronó

w

π

w

dan

ym

stanie

molekuªy:

M

X

k

=1

n

π
k

= N

π

.

(15)

Caªk

o

wita

energia

elektronó

w

π

w

dan

ym

stanie

molekuªy:

E

π

:=

M

X

k

=1

n

π
k

e

k

.

(16)

W

a»n

y

przypadek

szzególn

y:

Stan

p

o

dsta

w

o

wy

molekuªy

zamknitop

o

wªok

o

w

ej,

gdzie

N

π

= 2m

i

mam

y

n

π
k

= 2

dla

k

= 1, 2. . . . , m ;

n

π
k

= 0

dla

k

= m + 1, . . . , M .

(17)

Wtedy

ró

wn.

(16)

zapisa¢

mo»na

w

p

ostai

E

π

= 2

m

X

k

=1

e

k

.

(18)

3

W

yznazanie

opt

ymaln

y

h

orbitali

molekularn

y

h:

meto

da

w

ariayjna

Ritza.

Rozw

a»am

y

k

onstruk

j

LCA

O

MO,

patrz

ró

wn.

(10),

i

zakªadam

y

sp

eªnienie

w

arun-

k

ó

w

ortonormal

no±i

(11).

Opt

ymali

zaja

orbital

i

molekularn

y

h

oparta

jest

na

w

arianie

meto

dy

wariayjnej

zw

anej

meto

d¡

Ritza.

Odp

o

wiednie

w

arunki

matemat

yzne:

dla

k

a»dego

k

= 1, 2, . . . , M

wyra»enie

hψ

k

|ˆh

eff

ψ

k

i − (hψ

k

|ψ

k

i − 1) e

k

,

(19)

osi¡

ga

warto±¢

ekstr

emaln¡

ze

wzgldu

na

dowolne

zmiany

wsp

ólzynnik

ó

w

LCA

O

c

r,k

i

parametru

e

k

.

Sens

opt

ymaliz

aji

orbitali

molekularn

y

h

w

meto

dzie

Ritza:

dla

na

jni»szego

p

oziom

u

energet

yz

n

e

go

sp

eªnion

y

jest

w

arunek

w

ariayjn

y

e

1

= minimum .

(20)

Wªasno±¢

ta

przenosi

si

tak»e

na

wy»sz

e

p

oziom

y

energet

yz n

e

:

e

2

osi¡

ga

w

arto±¢

mini

-

maln¡

dla

wszys

tk

i

h

stanó

w

p

ostai

(10),

ortogonaln

y

h

do

orbital

u

ψ

1

,

itd.

Naªo»enie

w

arunk

ó

w

(19)

pro

w

adzi

do

r

ówna«

maierzowyh

meto

dy

R

itza ,

zapisan

y

h

p

oni»ej

w

p

ostai

ogólnej:

hc

= sce ,

(21)

c

†

sc

= I ,

(22)

gdzie

wystpu j¡

maierze

kw

adrato

w

e

M

× M

:

h

= h

†

=









h

1,1

h

1,2

· · · h

1,M

h

2,1

h

2,2

· · · h

2,M

.

.

.

.

.

.

.

.

.

.

.

.

h

M,

1

h

M,

2

· · · h

M,M









,

s

= s

†

=









s

1,1

s

1,2

· · · s

1,M

s

2,1

s

2,2

· · · s

2,M

.

.

.

.

.

.

.

.

.

.

.

.

s

M,

1

s

M,

2

· · · s

M,M









,

(23)

c

=









c

1,1

c

1,2

· · · c

1,M

c

2,1

c

2,2

· · · c

2,M

.

.

.

.

.

.

.

.

.

.

.

.

c

M,

1

c

M,

2

· · · c

M,M









,

c

†

=









c

∗

1,1

c

∗

2,1

· · · c

∗

M,

1

c

∗

1,2

c

∗

2,2

· · · c

∗

M,

2

.

.

.

.

.

.

.

.

.

.

.

.

c

∗

1,M

c

∗

2,M

· · · c

∗

M,M









,

(24)

e

=









e

1

0

· · ·

0

0

e

2

· · ·

0

.

.

.

.

.

.

.

.

.

.

.

.

0

0

· · · e

M









,

I

=









1 0 · · · 0
0 1 · · · 0

.

.

.

.

.

.

.

.

.

.

.

.

0 0 · · · 1









.

(25)

Uw

aga:

W

mo

delu

HMO

p

o

ja

wia

j¡

sie

p

ewne

uproszzen

ia:

•

Maierz

hamil

t

o

ni

a

n

u

efekt

ywn e

go

h

jest

maierz¡

hermito

wsk

¡

i

rzezyw

ist¡,

patrz

ró

wn.

(7),

a

wi

jest

maierz¡

symetryzn¡:

h

= h

†

= h

T

.

•

K

orzystam

y

z

bazy

ortogonali

zo

w

an

y

h

orbital

i

atomo

wy

h,

π

O

A

O,

patrz

ró

wn.

(4),

a

wi

maierz

aªek

nakryw

ania

ró

wna

jest

maierzy

jednostk

o

w

ej:

s

= I

.

4

•

Maierz

wsp

óªzyn n

ik

ó

w

LCA

O

jest

wtedy

maierz¡

unitarn¡:

c

†

= c

−1

.

•

Co

wieej,

w

zastoso

w

aniu

do

sk

o«zon

y

h

molekuª

mo»na

zaªo»y¢,

»e

wsp

óªzyn

n

iki

LCA

O

s¡

lizbami

rzezyw

ist

ymi

(patrz

ni»ej);

wtedy

maierz

wsp

óªzyn n

ik

ó

w

LCA

O

jest

maierz¡

ortogonaln¡:

c

T

= c

−1

.

Ró

wnania

maierzo

w

e

meto

dy

Ritza

w

mo

delu

HMO

mo»na

wi

zapisa¢

w

p

ostai:

hc

= ce ,

(26)

c

T

c

= I .

(27)

Energie

orbitali

molekularn

y

h

(energie

orbitalne

HMO),

zdenio

w

ane

w

ró

wn.

(12)

i

up

orz¡dk

o

w

ane

w

edªug

s

hematu

(13),

wyznazy

¢

mo»na

jak

o

pierwiastki

tzw.

wielom

i

a-

n

u

harakteryst

yznego

(stopnia

M

)

zmiennej

rze

zywistej

e

:

W

(M )

(e) = det(h − eI) ,

(28)

gdy»

rozwi¡zania

ró

wn.

(26)

i

(27)

sp

eªnia¢

m

usz¡

w

arunek

W

(M )

(e

k

) = 0 .

(29)

Zna

j¡

w

arto±¢

energii

orbital

nej

e

k

,

z

ªat

w

o±i¡

zna

jdujem

y

wsp

óªzyn n

iki

LCA

O

c

r,k

o

dp

o

wiedniego

orbital

u

molekularnego

[t

w

orz¡

one

w

ektor

k

olumno

wy

c

k

b

d¡y

k

-t¡

k

o-

lumn¡

maierzy

maierzy

c

,

patrz

ró

wn.

(24)℄.

Rozwi¡zujem

y

w

t

ym

elu

ukªad

r

ówna«

liniowyh

je

dnor

o

dnyh

(h − e

k

I

)c

k

= 0 ,

(30)

gdzie

0

jest

w

ektorem

k

olumno

wym

zero

wym,

a

niewiadome

c

r,k

t

w

orz¡e

w

ektor

c

k

sp

eª-

nia¢

m

usz¡

w

arunek

unormo

w

ania

M

X

r

=1

c

2
k

= 1 ,

(31)

wynik

a

j¡y

z

ró

wnania

maierzo

w

ego

(27).

W

mo

delu

HMO

maierz

h

jest

rzezyw

ista,

patrz

deniaja

(7),

st¡d

rozwi¡zania

ró

wna«

lini

o

wy

h

(30)

tak»e

s¡

lizbami

rzezyw

i-

st

ymi

(a

wi

maierz

c

jest

maierz¡

rzezyw

ist¡).

Ukªad

ró

wna«

maierzo

wy

h

(26)

i

(27)

zapisa¢

mo»na

tak»e

w

ró

wno

w

a»nej

p

ostai:

c

T

hc

= e ,

(32)

c

T

c

= I .

(33)

Ozanaza

to,

»e

(diagonal

n¡

)

maierz

energi

orbital

n

y

h

e

otrzyma¢

mo»na

przepro

w

a-

dza

j¡

diagonalizaj

maierzy

hamil

t

o

ni

a

n

u

efekt

ywn e

go

h

przy

p

omo

y

maierzy

or-

togonalnej

c

.

T

o

sform

uªo

w

anie

jest

p

o

dsta

w

¡

algorytmó

w

k

omputero

wy

h

sªu»¡y

h

do

zna

jdo

w

ania

maierzy

e

i

c

.

P

o

dsumo

wuj¡:

w

wyniku

rozwi¡zania

ró

wna«

maierzo

wy

h

(26)

i

(27),

zy

ró

w-

no

w

a»n

y

h

im

ró

wna«

(32)

i

(33),

otrzym

ujem

y

wsp

óªzyn n

iki

lini

o

w

e

c

r,k

opt

ymaln

y

h

orbital

i

molekularn

y

h

przedsta

wion

y

h

w

p

ostai

(10).

Z

ró

wna«

maierzo

wy

h

(32)

wy-

nik

a,

»e

opt

ymalne

orbital

e

molekularne

sp

eªnia

j¡

w

arunki

hψ

k

|ˆh

eff

ψ

l

i =

(

0 ,

dla

k

6= l ,

e

k

,

dla

k

= l .

(34)

Natomia

st

ró

wnania

maierzo

w

e

(33)

o

dp

o

wiada

j¡

sp

eªnieniu

w

arunku

normali

zaji

(11)

orbital

i

molekularn

y

h:

hψ

k

|ψ

l

i = δ

k,l

.

dla

wszys

tk

i

h

par

wsk

a¹nik

ó

w

k, l

.

5

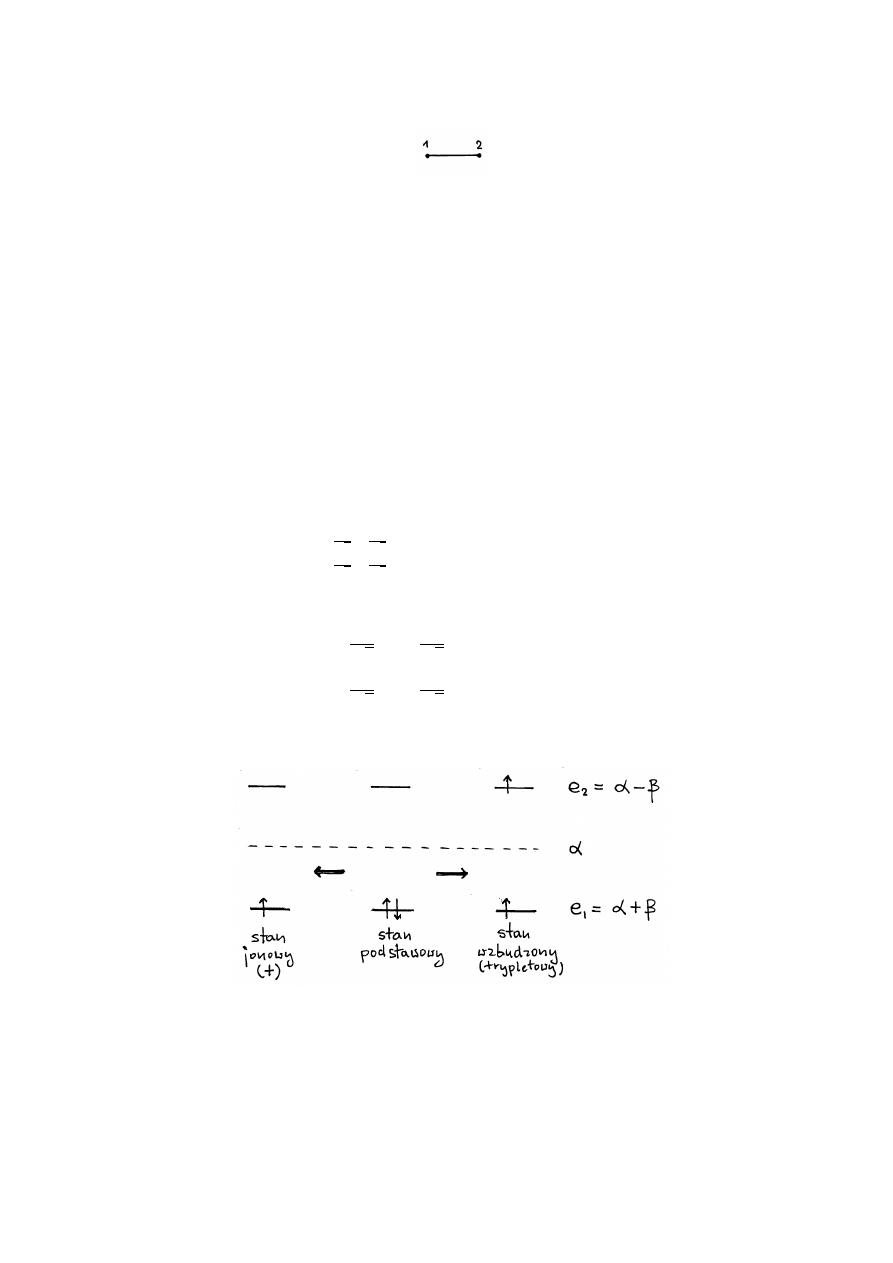
Przykªad:

molekuªa

et

ylen

u

,

C

2

H

4

.

Rysunek

1:

Et

ylen

szkielet

w

glo

wy

.

M

= 2

,

w

ob

o

jtnej

elektr.

molekule

N

π

= 2

.

Maierz

top

ologi

zna

i

maierz

hamil

t

o

ni

a

n

u

efekt

ywn e

go:

t

= t

T

=

0 1
1 0

!

,

h

= h

T

=

α β
β α

!

.

(35)

Wielom

i

a

n

harakteryst

y

z

n

y

W

(2)

(e) = det(h − eI) =







α

− e

β

β

α

− e







= (e − α)

2

− β

2

,

(36)

ma

pierwiastki

e

1

= α + β

i

e

2

= α − β

(za

ho

dzi

e

1

< e

2

).

Rozwi¡zanie

ró

wna«

maierzo

wy

h

(26),

przy

narzueniu

w

arunk

ó

w

ortonormal

no±i

(27),

da

je:

c

=

1

√

2

1

√

2

1

√

2

−1

√

2

!

,

e

=

α

+ β

0

0

α

− β

!

.

(37)

A

wi

opt

ymalne

π

MO

et

ylen

u

i

o

dp

o

wiada

j¡e

im

energie

orbital

ne

ma

j¡

p

osta¢:

ψ

1

=

1

√

2

χ

1

+

1

√

2

χ

2

,

e

1

= α + β ,

(38)

ψ

2

=

1

√

2

χ

1

−

1

√

2

χ

2

,

e

2

= α − β .

(39)

Ró»nia

energii

orbital

n

y

h:

e

2

− e

1

= −2β

Rysunek

2:

Et

ylen

stan

y

elektrono

w

e

w

mo

delu

HMO

6

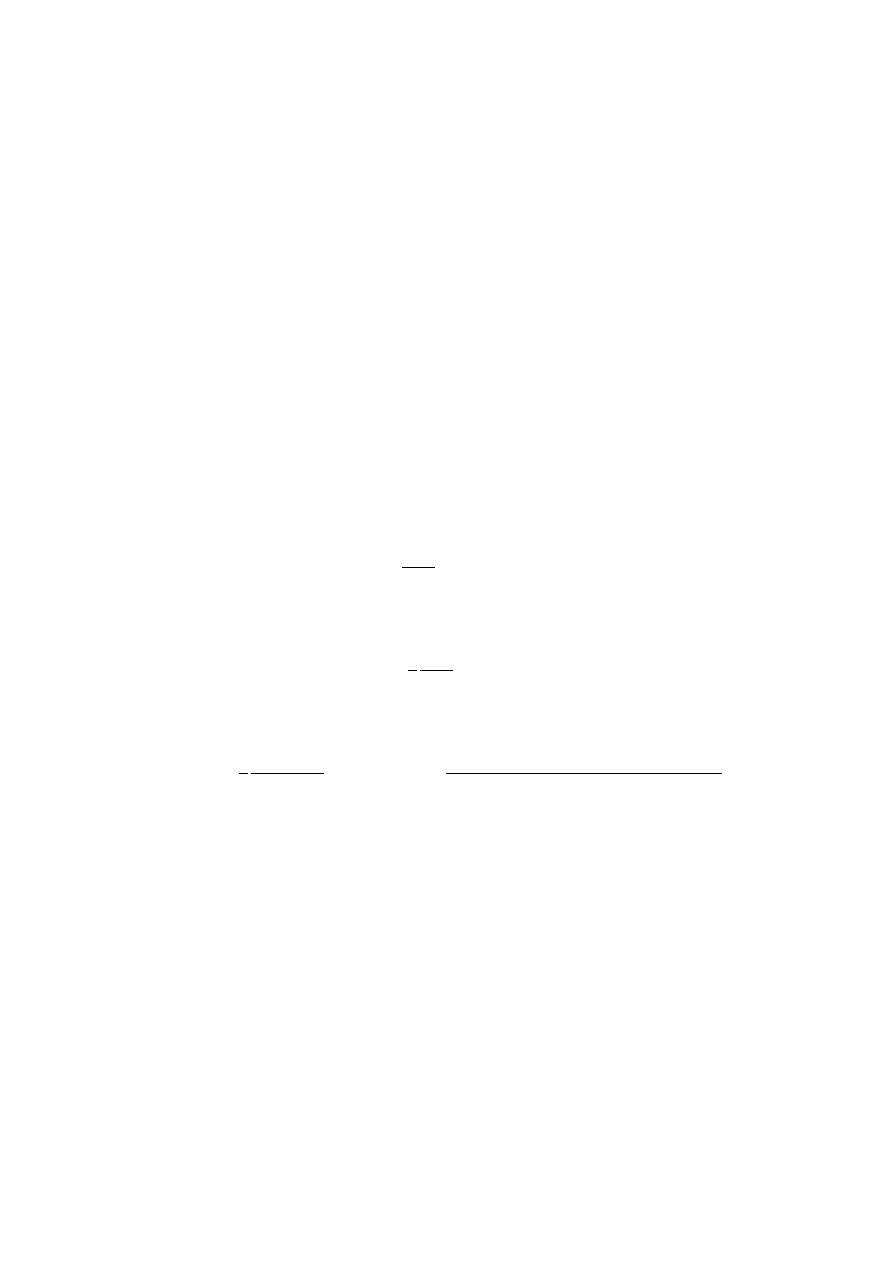
Dane

eksp

erymen

talne

dla

et

ylen

u:

Energia

jonizaji

I

= 10.5

e

V

(

≈ −e

1

).

Energia

wzbudze

n

ia

do

stan

u

trypleto

w

ego

∆E = 4.8

e

V

(

≈ e

2

− e

1

).

St¡d:

Prop

ono

w

ana

parametryzaja

mo

delu

HMO

dla

w

glo

w

o

doró

w

π

-elektrono

wy

h:

α

≡ α

C

= −8.00

e

V

,

(40)

β

≡ β

CC

= −2.50

e

V

.

(41)

Dla

et

ylen

u

otrzym

ujem

y:

Energia

jonizaji

−e

1

= 10.5

e

V

≈ I

.

Energia

wzbudze

n

ia

do

stan

u

trypleto

w

ego

e

2

− e

1

= 5.0

e

V

(

≈ ∆E

).

Energia

π

-elektrono

w

a

molekuªy

i

jej

p

o

ho

dne

Energia

π

-elektrono

w

a

molekuªy

w

mo

delu

HMO

zdenio

w

ana

jest

w

ró

wn.

(16).

P

o

ho

dne

energii

π

-elektrono

w

ej

p

o

parametra

h

mo

delu

HMO

p

ozw

ala

j¡

zdenio

w

a¢:

π

-elektrono

w

e

ªadunki

atomo

w

e:

q

r

=

∂E

π

∂α

r

=

M

X

k

=1

n

π
k

c

2
r,k

,

(42)

π

-elektrono

w

e

rzdy

wiaza«:

p

rs

= p

sr

=

1
2

∂E

π

∂β

rs

=

M

X

k

=1

n

π
k

c

r,k

c

s,k

,

(43)

π

-elektrono

w

e

p

olaryzo

w

alno±i

wi¡zanie-wi¡zani

e:

π

rs,vw

=

1
2

∂

2

E

π

∂β

rs

∂β

vw

=

M

X

k<l

(n

π
l

− n

π
k

)

(c

r,k

c

s,l

+ c

s,k

c

r,l

)(c

v,l

c

w,k

+ c

w,l

c

v,k

)

e

l

− e

k

.

(44)

Mo»na

wyk

aza¢,

»e

energia

π

-elektrono

w

a

molekuªy

w

mo

delu

HMO

mo»e

b

y¢

wyra»ona

przez

q

r

i

p

rs

:

E

π

=

M

X

r

=1

q

r

α

r

+ 2

M

X

r<s

p

rs

β

rs

.

(45)

Zmienno±

ró

wno

w

ago

wy

h

dªugo±i

wi¡za«

w

molekuªa

h

π

-elektrono

wy

h

W

zór

Coulsona-Goªbi

ewskiego:

R

e
rs

= R

o

[rs]

− x

[rs]

p

rs

,

(46)

gdzie:

R

o

[rs]

jest

dªugo±i¡

wi¡zania

p

o

jedynzego

(

p

rs

= 0

),

R

o

[rs]

− x

[rs]

jest

dªugo±i¡

wi¡zania

p

o

dw

ó

jnego

(

p

rs

= 1

)

w

ukªadzie

π

-elektrono

wym.

7

P

arametryzaja

dla

w

glo

w

o

doró

w

π

-elektrono

wy

h:

R

o

≡ R

o

[CC]

= 1.523

Å

,

(47)

x

≡ x

[CC]

= 0.189

Å

.

(48)

Wglo

w

o

dory

π

-elektrono

w

e

Wglo

w

o

dory

π

-elektrono

w

e

to

obszerna

i

zró»nio

w

ana

p

o

d

wzgldem

wªasno±i

grupa

zwi¡zk

ó

w:

o

d

et

ylen

u,

butadien

u,

itp.,

przez

b

enzen

i

p

oliykli

zne

w

glo

w

o

dory

aroma-

t

yzne

(p

oliyli

aromati

h

ydro

arb

ons

P

AH's),

p

o

fulleren

y

,

nanorurki

w

glo

w

e,

oraz

ukªady

rozi¡

gªe:

p

olia

et

ylen

(i

inne

p

olim

ery

π

-elektrono

w

e)

i

grafen

(zyli

pªaszzyz

n

grato

w

¡).

W

mo

delu

HMO

hamil

t

o

ni

a

n

efekt

ywn

y

w

glo

w

o

doru

π

-elektrono

w

ego

mo»na

zapisa

w

p

ostai

h

= αI + βt = αI − |β|t ,

(49)

gdzie

parametry

α

i

β

o

dp

o

wiada

j¡

ró

wn.

(40),

a

t

jest

maierz¡

top

ologi

zn¡

w

glo

w

o-

dru,

patrz

ró

wn.

(5).

Do

datnia

wielk

o±¢

|β|

mo»e

sªu»y¢

jak

o

je

dnostka

ener

gii

w

mo

delu

HMO

(gdy

nie

hem

y

deklaro

w

a¢

k

onkretnej

w

arto±i

tego

parametru).

W

ygo

dnie

jest

wpro

w

adzi¢

b

ezwymiar

owy

parametr

energii:

ε

:=

e

− α

|β|

,

(50)

p

ozw

ala

j¡y

wyrazi¢

do

w

oln¡

energi

orbital

n¡

e

w

p

ostai

e

= α + ε|β| .

(51)

Wielom

i

a

n

harakteryst

y

z

n

y

(28)

w

glo

w

o

doru

π

-elektrono

w

ego

mo»na

teraz

zapisa

w

p

ostai

W

(M )

(e) = det(h − eI) = det [(α − e)I − |β|t] = (−|β|)

M

det (εI + t) .

(52)

Otrzym

ujem

y

przeksztaª

ony

wielomian

har

akterystyzny

zmiennej

ε

,

w

(M )

(ε) := det (εI + t) ,

(53)

w

p

ostai

wyznaz n

ik

a

maierzy

o

bardzo

prostej

strukturze

(k

a»da

lizba

0

na

diagonal

i

maierzy

top

ologi

znej

zastapiona

zostaªa

przez

zmienn¡

ε

).

Energie

orbital

ne

HMO

w

-

glo

w

o

doru

π

-elektrono

w

ego

mo»na

teraz

oblizy¢

zna

jduj¡

pierwiastki

przeksz

taªone

go

wielomi

a

n

u

harakteryst

y

z

n

e

go:

w

(M )

(ε

k

) = 0 ,

(54)

k

= 1, 2, . . . , M

;

ze

wzoru

(51)

otrzym

ujem

y:

e

k

= α + ε

k

|β| .

(55)

Zna

j¡

w

arto±¢

energii

orbital

nej

e

k

,

z

ªat

w

o±i¡

zna

jdujem

y

wsp

óªzyn n

iki

LCA

O

c

r,k

o

dp

o

wiedniego

orbital

u

molekularnego,

patrz

ró

wn.

(30)

i

(31),

przy

zym

ukªad

ró

wna«

lini

o

wy

h

jednoro

dn

y

h

(30

mo»em

y

teraz,

k

orzysta

j¡

z

ró

wn.

(49)

i

(55),

przeksz

taªi¢

do

p

ostai

(t + ε

k

I

)c

k

= 0 .

(56)

8

Ró

wn.

(53-56)

ilustruj¡

in

teresuj¡¡

wªasno±¢

mo

delu

HMO

w

zastoso

w

aniu

do

w

glo

w

o-

doró

w

π

-elektrono

wy

h:

ukªad

energii

orbital

n

y

h

i

maierz

wsp

óªzyn

n

ik

ó

w

LCA

O

zale»¡

wyª¡znie

o

d

maierzy

top

ologi

znej

danego

w

glo

w

o

doru.

Mo

del

HMO

jest

wi

top

olo-

gizn

ym

mo

delem

orbitali

molekularn

y

h

w

glo

w

o

doró

w

π

-elektrono

wy

h .

Wglo

w

o

dory

π

-elektrono

w

e

naprzemienne

i

nienaprzemienne

W

w

glo

w

o

dorze

π

-elektrono

wym

atom

y

w

gla

próbujem

y

p

o

dzieli¢

na

dw

a

p

o

dzbio-

ry:

atom

y

gwiazdk

o

w

ane

i

atom

y

niegwiazdk

o

w

ane.

T

e

dw

a

p

o

dzbiory

ma

j¡

mie¢

na-

stpuj¡¡

wªasno±:

»aden

atom

danego

p

o

dzbioru

nie

jest

na

jbli»szym

s¡siadem

atom

u

z

tego

samego

p

o

dzbioru

(zyli

atom

y

gwiazdk

o

w

ane

mog¡

s¡siado

w

a¢

t

ylk

o

z

atoma-

mi

niegwiazdk

o

w

an

ymi

)

.

Je±li

tak

a

op

eraja

gwiazdk

o

w

ania

atomó

w

si

p

o

wiedzie,

to

rozw

a»an

y

w

glo

w

o

dór

π

-elektrono

wy

nazyw

am

y

w

glo

w

o

dorem

naprzemienn

ym;

w

przeiwn

ym

razie

mam

y

do

zynienia

z

w

glo

w

o

dorem

nienaprzemienn

ym.

Przykªady

obu

t

yp

ó

w

w

glo

w

o

doró

w

p

ok

azane

s¡

na

p

oni»szym

rysunku:

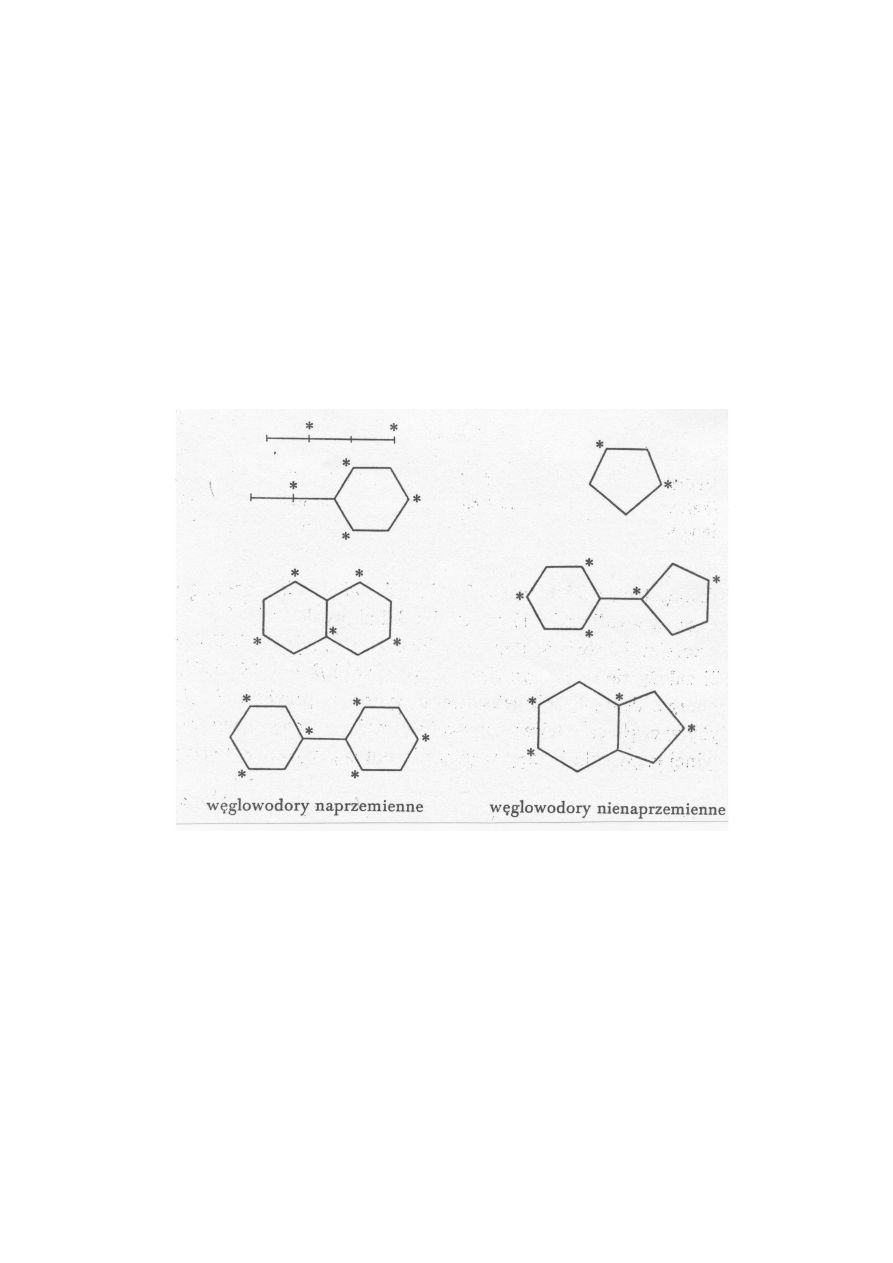
Rysunek

3:

Wglo

w

o

dory

π

-elektrono

w

e

naprzemienne

i

nienaprzemienne

Ok

azuje

si,

»e

w

arunkiem

wystarza

j¡ym,

b

y

dan

y

w

glo

w

o

dór

b

yª

naprzemienn

y

,

jest

brak

pier±ieni

o

nieparzystej

lizbie

atomó

w

w

gla

(w

glo

w

o

dory

b

ez

pier±ieni

s¡

wi

za

wsze

naprzemienne!).

Naprzemienno±¢

jest

wªasno±i¡

top

ologi

zn¡

wynik

a

z

wªasno±i

maierzy

top

ologi

znej

t

rozw

a»anego

w

glo

w

o

doru

(i

jest

niezale»na

o

d

symetrii

molekuªy

lub

jej

braku).

Lizb

y

atomó

w

gwiazdk

o

w

an

y

h

M

∗

i

niegwiazdk

o

w

an

y

h

M

o

sp

eªnia

j¡

zale»no±i

M

∗

+ M

o

= M ,

(57)

M

o

− M

∗

= ∆M

∗

­ 0 .

(58)

(przyjm

uje

si

tak

¡

zasad

gwiazdk

o

w

ania,

b

y

atomó

w

gwiazdk

o

w

an

y

h

b

yªo

nie

wieej

ni»

niegwiazdk

o

w

an

y

h).

9

Ok

azuje

si,

»e

w

glo

w

o

dory

naprzemienne

ma

j¡

p

ewne

harakteryst

y

z

n

e

wªasno±i:

•

Pierwiastki

wielomi

a

n

u

harakteryst

y

z

n

e

go

(53)

wystpuj¡

w

para

h:

ε

k

= −ε

M

−k

,

(59)

gdzie

zakªadam

y

up

orzadk

o

w

anie

takie

jak

w

s

hemaie

(13);

pierwiastki

zero

w

e

ε

k

=

0

mog¡

wystp

o

w

a¢

p

o

jedynzo.

Energie

orbital

ne

(55)

s¡

wi

uªo»one

symetryznie

wzgldem

energii

α

.

•

Je±li

lizb

y

atomó

w

gwiazdk

o

w

an

y

h

i

niegwiazdk

o

w

an

y

h

s¡

ró»ne,

zyli

w

ró

wn.

(58)

mam

y

∆N

∗

>

0

,

to

jest

nie

mniej

ni»

∆N

∗

zero

wy

h

w

arto±i

wielomi

a

n

u

harakte-

ryst

yzn

e

go

(53):

ε

k

= 0

dla

k

= M

∗

+ 1 , . . . , M

∗

+ ∆M

∗

,

(60)

którym

o

dp

o

wiada

j¡

w

arto±i

energii

orbital

n

y

h

e

k

= α

.

W

molekuªa

h

o

nieparzy-

stej

lizbie

atomó

w

w

gla

∆N

∗

­ 1

,

a

wi

wystpuje

o

na

jmniej

jeden

pierwiastek

zero

wy

.

•

W

stanie

p

o

dsta

w

o

wym

ob

o

jtnej

elektryznie

molekuªy

(

N

π

= M

)

atomo

w

e

ªadunki

π

-elektrono

w

e

na

wszys

tk

i

h

atoma

h

w

gla

s¡

iden

t

yzne

i

ró

wne

q

k

= 1 .

(61)

Nale»y

wi

o

zekiw

a¢,

ze

takie

molekuªy

,

na

w

et

gdy

symetria

na

to

p

ozw

ala,

b

d¡

prakt

yznie

p

ozba

wione

momen

tu

dip

olo

w

ego

(o

p

ot

wierdza

eksp

ery

men

t

i

oblize-

nia

zaa

w

anso

w

an

ymi

meto

dami

hemii

kw

an

to

w

ej).

10