
BAYESOWSKA TEORIA
BAYESOWSKA TEORIA
PODEJMOWANIA DECYZJI
PODEJMOWANIA DECYZJI
W WARUNKACH
W WARUNKACH
NIEPEWNOŚCI
MAREK NAWALANY
GRA TEXAŃSKA
(0)
GRA TEXAŃSKA
(0)
B
B
B
WZÓR BAYESA
WZÓR BAYESA
I
II
P(R|I)=2/3
P(R|I)=2/3
P(R|II)=1/3
)
(
*
)
|
(
I
P
I
R
P
)
(
*
)
|
(
)
(
*
)
|
(
)
(
*
)
|
(
)
|
(
II
P
II
R
P
I
P
I
R
P
I
P
I
R
P
R
I
P
++++
====
)
(
*
)
|
(
)
(
*
)
|
(
II
P
II
R
P
I
P
I
R
P
++++
Prawdopodobieństwo
wystąpienia danego stanu natury
wystąpienia danego stanu natury
I
II
P(R|I)=2/3
I
II
P(R|I)=2/3
P(R|II)=1/3
)
(
*
)
|
(
I
P
I
R
P
)
(
*
)
|
(
)
(
*
)
|
(
)
(
*
)
|
(
)
|
(
II
P
II
R
P
I
P
I
R
P
I
P
I
R
P
R
I
P
++++
====
)
(
*
)
|
(
)
(
*
)
|
(
II
P
II
R
P
I
P
I
R
P
++++
⇒
⇒
⇒
⇒
−−−−
====
⇒
⇒
⇒
⇒
≤≤≤≤
≤≤≤≤
====
αααα
αααα
αααα
1
)
(
1
0
,
)
(
II
P
I
P
Niech
⇒
⇒
⇒
⇒
−−−−
====
⇒
⇒
⇒
⇒
≤≤≤≤
≤≤≤≤
====
αααα
αααα
αααα
1
)
(
1
0
,
)
(
II
P
I
P
Niech
α
α
=
=
2
3
2
*
/
)
|
(
R
I
P
α
α
α
α
α
+
=
−
+
=
1
2
1
3
1
3
2
3
2
)
(
*
/
*
/
*
/
)
|
(
R
I
P
Prawdopodobieństwo
wystąpienia danego stanu natury
wystąpienia danego stanu natury
I
II
P(R|I)=2/3
I
II
P(R|I)=2/3
P(R|II)=1/3
)
(
*
)
|
(
II
P
II
R
P
)
(
*
)
|
(
)
(
*
)
|
(
)
(
*
)
|
(
)
|
(
II
P
II
R
P
I
P
I
R
P
II
P
II
R
P
R
II
P
++++
====
)
(
*
)
|
(
)
(
*
)
|
(
II
P
II
R
P
I
P
I
R
P
++++
α
α
−
−
1
1
3
1
)
(
*
/
α
α
α
α
α
+
−
=
−
+
−
=
1
1
1
3
1
3
2
1
3
1
)
(
*
/
*
/
)
(
*
/
)
|
(
R
II
P
α
α
α
+
−
+
1
1
3
1
3
2
)
(
*
/
*
/
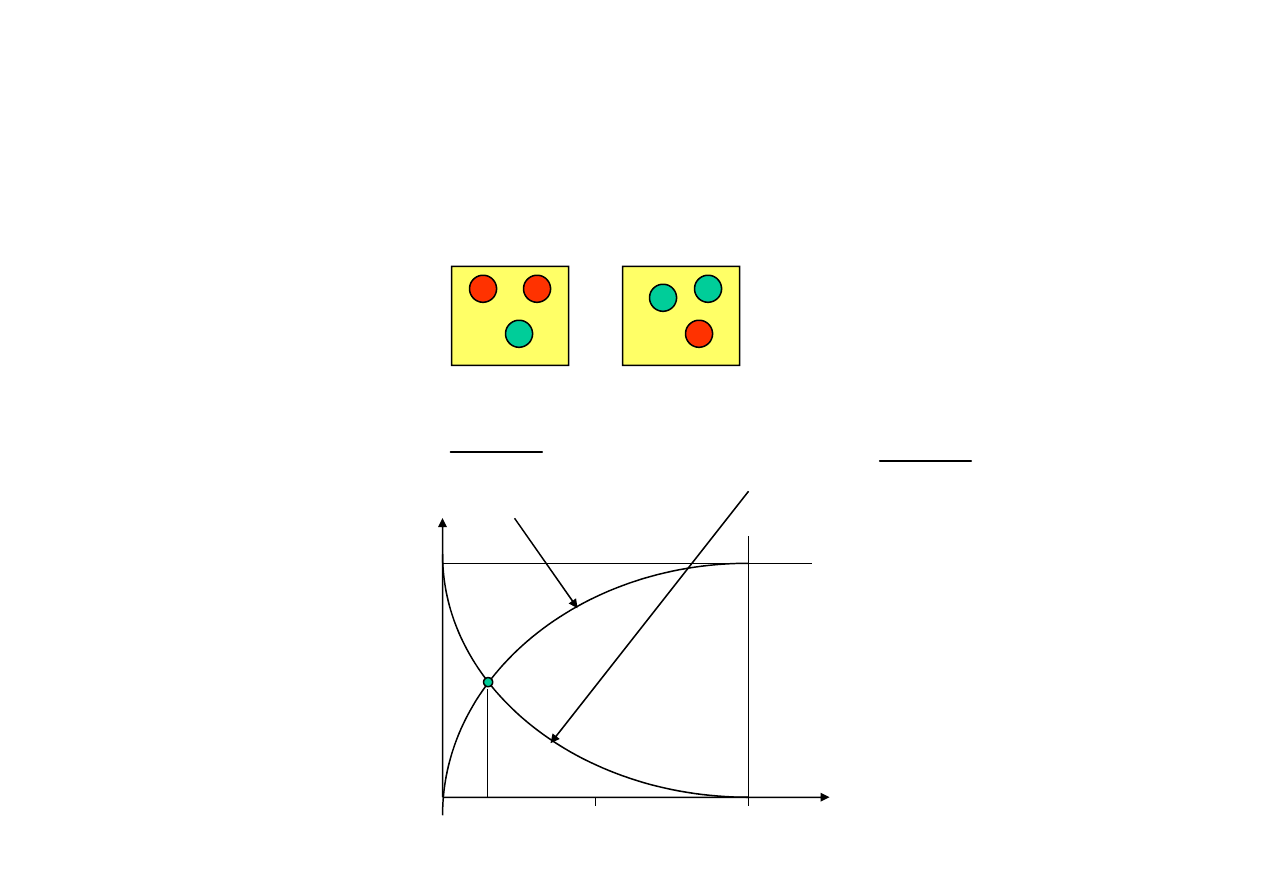
Prawdopodobieństwo
wystąpienia danego stanu natury
wystąpienia danego stanu natury
I
II
P(R|I)=2/3
I
II
P(R|I)=2/3
P(R|II)=1/3
α
−
=
1
)
|
(
R
II
P
α
=
2
)
|
(
R
I
P
α
α
+
−
=
1
1
)
|
(
R
II
P
α
+
=
1
)
|
(
R
I
P
1
1
α
1
0
1/3
HIV !!!
HIV !!!
1000
999
1000
1
=
¬
=
)
(
,
)
(
H
P
H
P
1000
1000
=
¬
=
)
(
,
)
(
H
P
H
P
5
99
=
¬
+
=
+
)
|
(
,
)
|
(
H
P
H
P
100
5
100
99
=
¬
+
=
+
)
|
(
,
)
|
(
H
P
H
P
)
(
*
)
|
(
)
|
(
H
P
H
P
H
P
+
=
+
)
(
*
)
|
(
)
(
*
)
|
(
)
(
*
)
|
(
)
|
(
H
P
H
P
H
P
H
P
H
P
H
P
H
P
¬
¬
+
+
+
+
=
+
HIV !!!
HIV !!!
)
(
*
)
|
(
)
|
(
H
P
H
P
H
P
+
=
+
)
(
*
)
|
(
)
(
*
)
|
(
)
(
*
)
|
(
)
|
(
H
P
H
P
H
P
H
P
H
P
H
P
H
P
¬
¬
+
+
+
+
=
+
*
100
99
1000
1
100
99
%
*
*
*
)
|
(
2
5000
100
4995
99
99
1000
999
100
5
1000
1
100
99
1000
100
=
≈
+
=
+
=
+
H
P
1000
100
1000
100
Do not worry (very much) !!
Do not worry (very much) !!
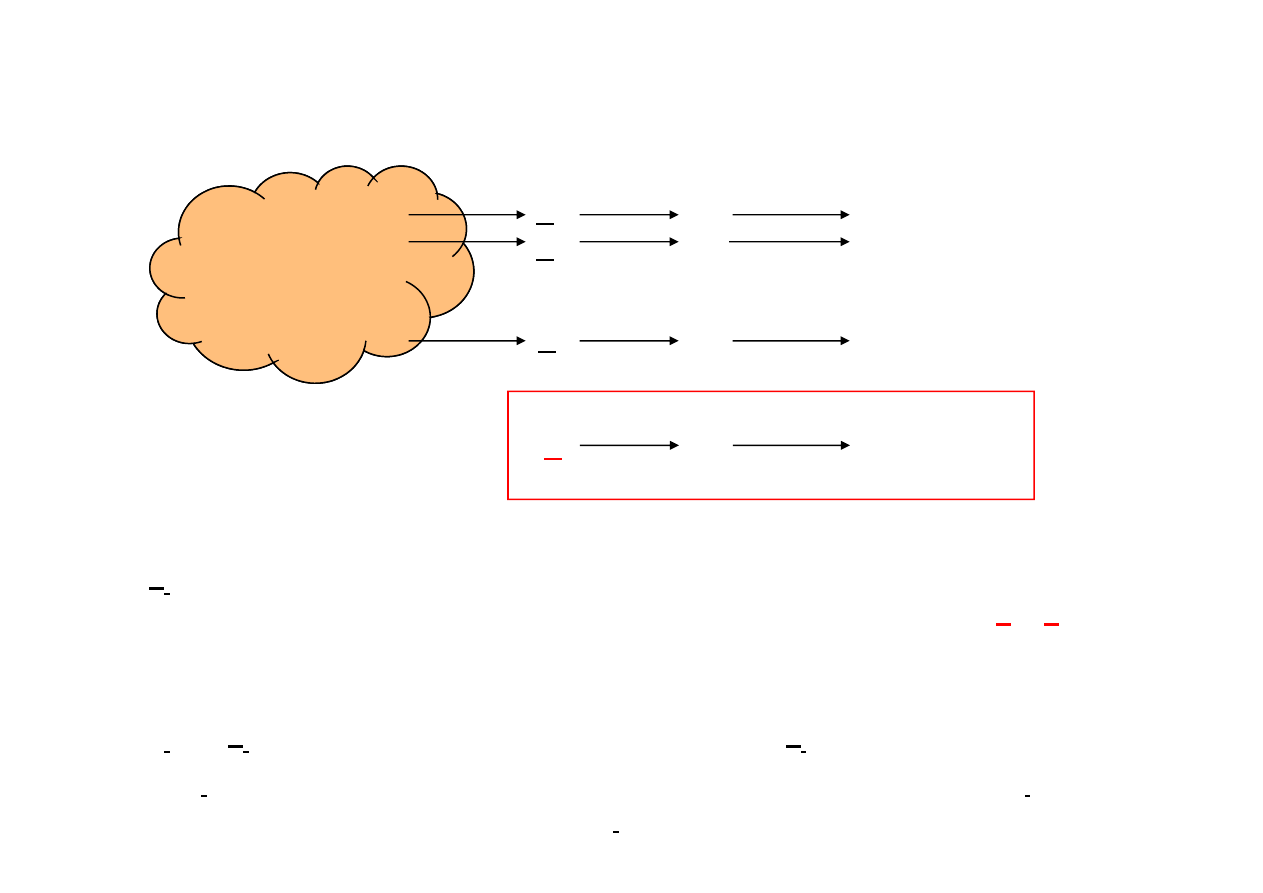
Losowa gra z Naturą (1)
Losowa gra z Naturą (1)
w (
w
)
x
1
x
2
.
a
1
a
2
.
k
1
= L(a
1
,w)
k
2
= L(a
2
,w)
d
w (
w
)
x
2
.
.
.
.
.
.
x
n
a
2
.
.
.
.
.
.
a
n
k
2
= L(a
2
,w)
k
n
= L(a
n
,w)
x
a
k
= L(
a,
w)
d
x
n
a
n
k
n
= L(a
n
,w)
w
– ustalony stan przyrody
x
a
k
= L(
a,
w)
x
i
,(i = 1,…,n) – zaobserwowane/pomierzone wartości wskaźnika stanu Natury dla
ustalonego stanu Natury w; wartości wskaźnika są realizacjami zm. l.
x = x(
w
)
d – (deterministyczna )
funkcja decyzyjna
odwzorowująca wyniki
d – (deterministyczna )
funkcja decyzyjna
odwzorowująca wyniki
obserwacji/pomiarów w decyzje
a
i
= d(
x
i
) – decyzja podjęta na podstawie obserwacji
x
i
i
i
i
L (a
i
, w) – deterministyczna
funkcja kosztów/strat
określająca koszty k
i
jakie
ponosi decydent podejmując decyzję a
i
gdy stan Natury jest równy w

Losowa gra z Naturą (2)
Losowa gra z Naturą (2)
d
x
a
L(
a
,w)
d
⇓
⇓
⇓
⇓
⇓
⇓
⇓
⇓
Koszty
k
= L(
a,
w
) są dla ustalonego stanu przyrody
w
i dla ustalonej funkcji decyzyjnej
d(.)
zmienną losową
Definicja :
Funkcja ryzyka
nazywamy
i dla ustalonej funkcji decyzyjnej
d(.)
zmienną losową
(bo
a
jest zm. losową)
⇓
⇓
⇓
⇓
Definicja :
Funkcja ryzyka
nazywamy
R(d,w
) =
E[
k
= L(
a,
w)]
⇓
⇓
⇓
⇓
R(d,w
) =
E[
k
= L(
a,
w)]
gdzie
E(.)
jest liczona z rozkładu warunkowego zm. l.
k
=
L
(. ,
w
) dla
ustalonego
w

Losowa gra z Naturą (3)
Losowa gra z Naturą (3)
Uwaga: Natura też realizuje swoje stany „
w”
z pewnym
prawdopodobieństwem g(
w
). Jeśli decyzje są podejmowane
⇓
⇓
⇓
⇓
prawdopodobieństwem g(
w
). Jeśli decyzje są podejmowane
przy zmieniającym się stanie Natury to funkcja ryzyka
R(d,
w
)
powinna być traktowana jako
zmienna losowa
o rozkładzie g(
w
)
Definicja :
Bayesowską Funkcją Ryzyka (BFR)
nazywamy
⇓
⇓
⇓
⇓
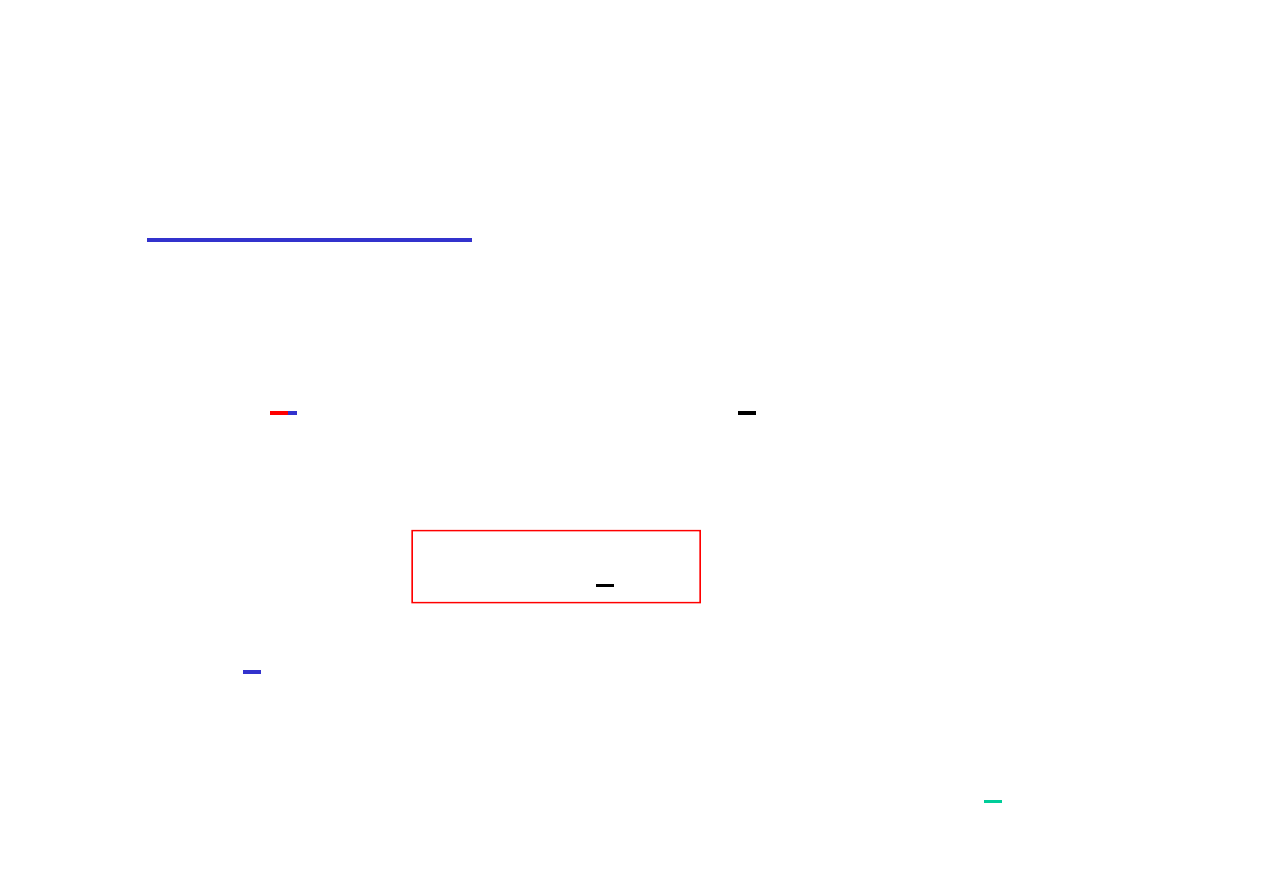
r(d) = E[R(d
,w)
]
=
∫
Ω
dw
w
g
w
d
R
)
(
)
,
(
Ω
Uwaga: Stosując w grze z Naturą różne funkcje decyzyjne
d(.)
otrzymujemy (dla stacjonarnej przyrody) różne wartości
BFR
Definicja :
Funkcję decyzyjną
d*
nazywamy
optymalną
jeśli
minimalizuje ona
BFR
w zbiorze wszystkich funkcji decyzyjnych, tj
r(d*)= min r(d)
r(d*)= min r(d)
Losowa gra z Naturą (4)
Losowa gra z Naturą (4)
B. ważne twierdzenie (bez dowodu)
Jeśli w grze statystycznej z Naturą decyzje podejmowane są
na podstawie wyniku obserwacji/pomiaru pewnej zmiennej
na podstawie wyniku obserwacji/pomiaru pewnej zmiennej
losowej
x
o rozkładzie warunkowym f(
x
|
w
) to optymalna
funkcja decyzyjna
d*
(względem danego rozkładu a priori
funkcja decyzyjna
d*
(względem danego rozkładu a priori
g(
w
) stanów Natury) jest zdefiniowana jako:
a* = d*(
x
)
gdzie x –
jest wynikiem obserwacji
gdzie x –
jest wynikiem obserwacji
a*
–
jest decyzją minimalizującą wartość oczekiwaną
funkcji strat/kosztów L(
a
,w) w warunkowym
funkcji strat/kosztów L(
a
,w) w warunkowym
rozkładzie
a-posteriori
stanów natury
g
1
(w|x).
Losowa gra z Naturą (5)
Losowa gra z Naturą (5)
Innymi słowy:
poszukiwaną optymalną funkcję decyzyjną
d*
można wyznaczyć
poszukiwaną optymalną funkcję decyzyjną
d*
można wyznaczyć
minimalizując straty
k
= L(
a,
w) względem rozkładu warunkowego
g
1
(w|x)
stanów natury pod warunkiem, że wynikiem obserwacji
jest
x.
jest
x.
Funkcję rozkładu p-stwa warunkowego a-posteriori
g
1
(w|
x
)
Funkcję rozkładu p-stwa warunkowego a-posteriori
g
1
(w|
x
)
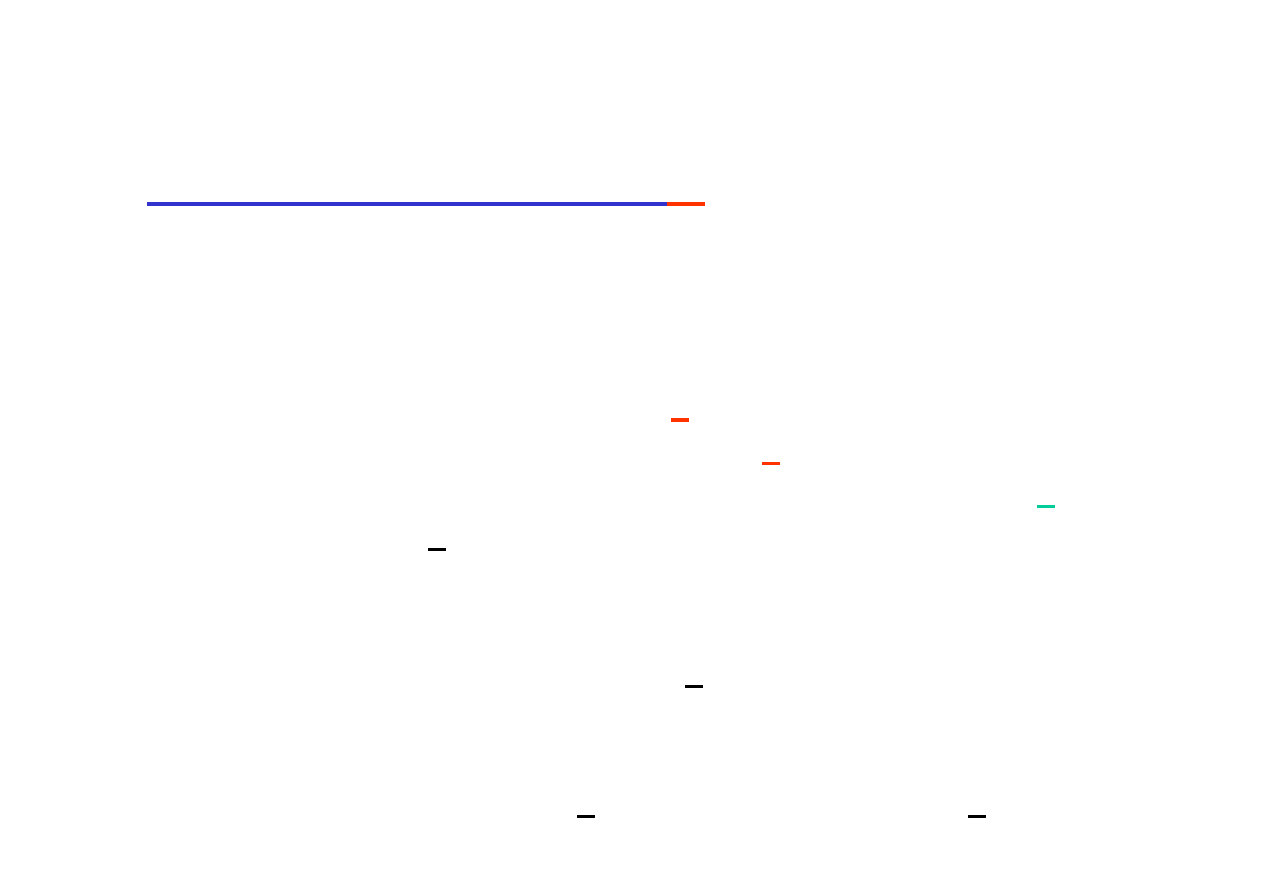
wyznacza się ze
wzoru Bayesa
:
)
,
(
)
(
)
|
(
w
x
f
w
g
w
x
f
(!)
)
(
)
,
(
)
(
)
(
)
|
(
)
|
(
1
x
f
w
x
f
x
f
w
g
w
x
f
x
w
g
====
====
gdzie f(x|w)-rozkład warunkowy wyników obserwacji/pomiaru
g(
w
) - rozkład a-priori stanów Natury
f(x) - rozkład brzegowy wyników obserwacji/pomiaru
f(x) - rozkład brzegowy wyników obserwacji/pomiaru
f(x,w) - rozkład dwuwymiarowy x oraz w
Losowa gra z Naturą (6)
Losowa gra z Naturą (6)
ALGORYTM WYZNACZANIA
d*
1. Określenie zbioru stanów Natury, zbioru (tzw. „czystych”)
1. Określenie zbioru stanów Natury, zbioru (tzw. „czystych”)
decyzji
{a
1
, a
2
, ...}
oraz funkcji strat
k = L(a,w)
2. Ustalenie rozkładu a-priori stanów Natury
g(w)
3. Wyznaczenie (na podst. obserwacji historycznych lub
3. Wyznaczenie (na podst. obserwacji historycznych lub
teoret. ) rozkładu warunkowego
f(x|w)
wyników pomiarów
4. Wyznaczenie rozkładu brzegowego
f(x)
4. Wyznaczenie rozkładu brzegowego
f(x)
5. Wyznaczenie rozkładu warunkowego a-posteriori
g
1
(w|x)
6. Dla ustalonego
x
:
6. Dla ustalonego
x
:
6.1 Dla każdej decyzji czystej
a
i
∈
∈
∈
∈
{a
1
, a
2
, ...}
wyznaczenie
wartości oczekiwanej funkcji strat
L(a
i
, w)
w
i
rozkładzie a posteriori
g
1
(w|
x
)
6.2. Wskazanie
a*
minimalizującej wartość oczekiwaną
funkcji strat.
funkcji strat.
6.3. Przypisanie danemu
x
→
→
→
→
a*
, tj. określenie
d*(
x
) =
a*

Przykład (1)
Przykład (1)
DECYDENT:
Producent komputerów
NATURA:
Dostawca podzespołów elektronicznych
ZAGADNIENIE DECYZYJNE:
ZAGADNIENIE DECYZYJNE:
a)
Podzespoły dostarczane są w paczkach (1 podzespół w paczce)
b)
Dostarczana partia zawiera tysiące paczek
c)
W każdej partii mogą się zdarzyć podzespoły wadliwe
d)
Decydent wybiera z partii losowo n = 5 paczek i dokonuje „szybkiej”
kontroli zawartych w nich podzespołów
kontroli zawartych w nich podzespołów
e)
w zależności od stwierdzonej liczby „braków” (wadliwie
funkcjonujących podzespołów) – x, (x = 0,1,…, n), Decydent podejmuje
jedną z dwóch decyzji - albo całą partię przyjmuje albo całą partię
jedną z dwóch decyzji - albo całą partię przyjmuje albo całą partię
odrzuca
PROBLEM DECYZYJNY: Jaka powinna być optymalna strategia
d*
przyjmowania/odrzucania partii podzespołów przez Decydenta by
przyjmowania/odrzucania partii podzespołów przez Decydenta by
zminimalizować (średnie długoterminowe) straty wynikające z
podejmowania nieprawidłowych decyzji, tj. z odrzucania partii, które nie
zawierały wielu ”braków” lub przyjmowania partii z dużą ilością
zawierały wielu ”braków” lub przyjmowania partii z dużą ilością
„braków”
Przykład (2)
Przykład (2)
Jak wyznaczyć
d*
dla przykładowego problemu ?
1. Określenie stanów Natury, zbioru (tzw. „czystych”) decyzji
{a
1
, a
2
, ...}
i
funkcji strat
L(a,w)
Stany Natury: w – wadliwość partii w %; dla uproszczenia przyjmuje się,
że Natura występuje w 3 stanach:
stan 1 ≡ {w = 0.01}, stan 2 ≡ {w = 0.05}, stan 3 ≡ {w = 0.1},
stan 1 ≡ {w = 0.01}, stan 2 ≡ {w = 0.05}, stan 3 ≡ {w = 0.1},
Zbiór „czystych” decyzji
A ={a
1
, a
2
}, gdzie
a
1
– „partię można przyjąć”
,
a
– ”partię należy odrzucić”
.
a
2
– ”partię należy odrzucić”
.
Funkcja strat/kosztów L(a,W) w postaci tabeli:
w = 0.01
w = 0.05
w = 0.1
a
1
0
0
50
a
1
0
0
50
a
2
30
30
0

Przykład (3)
Przykład (3)
2. Określenie/oszacowanie rozkładu a-priori stanów Natury
g(w)
g(w = 0.01)
= P{w = 0.01} =
0.3
g(w = 0.05)
= P{w = 0.05} =
0.5
g(w = 0.1)
= P{w = 0.1} =
0.2
3. Wyznaczenie (na podstawie obserwacji historycznych lub teoretycznie )
rozkładu warunkowego
f(x|w)
wyników pomiarów.
Niech w każdej partii badane jest n = 5 podzespołów. Jeśli wynik pomiaru
wynosi x wadliwych podzespołów (spośród n badanych) wtedy
)
5
,...,
1
,
0
(
,
)
1
(
5
}
|
{
5
====
−−−−
====
−−−−
x
w
w
x
w
x
P
x
x
x

Przykład (4)
Przykład (4)
4. Wyznaczenie rozkładu brzegowego
f(x)
4.1 Wyznaczenie rozkładu dwuwymiarowego
f(x,w)
f(x,w) = P{x|w}*g(w)
w = 0.01
w= 0.05
w = 0.1
x = 0
0.285
0.386
0.118
x = 1
0.014
0.101
0.065
x= 2
0.00029
0.0107
0.0145
x= 2
0.00029
0.0107
0.0145
x = 3
2.94e-06
5.64e-04
0.00162
x = 4
1.49e-08
1.48e-05
0.00009
x = 4
1.49e-08
1.48e-05
0.00009
x = 5
3.0e-11
1.56e-07
0.000002
4.2 Wyznaczenie rozkładu brzegowego
f(x)
– poprzez
4.2 Wyznaczenie rozkładu brzegowego
f(x)
– poprzez
sumowanie po wierszach rozkładu dwuwymiarowego
f(x,w):
f(x = 0) = 0.790, f(x = 1) = 0.181, f(x = 2) = 0.025,
f(x = 3) = 0.00218, f(x = 4) = 0.000104, f(x = 5) = 0.0000021
f(x = 3) = 0.00218, f(x = 4) = 0.000104, f(x = 5) = 0.0000021

Przykład (5)
Przykład (5)
5. Wyznaczenie rozkładu warunkowego a-posteriori
g
1
(w|x)
ze wzoru (!), tj. dzieląc
f(x,w)
przez
f(x)
w = 0.01
w= 0.05
w = 0.1
x = 0
0.361
0.486
0.1494
x = 0
0.361
0.486
0.1494
x = 1
0.0793
0.5599
0.3608
x = 2
0.045
0.4179
0.5706
x = 2
0.045
0.4179
0.5706
x = 3
0.0009
0.2581
0.7410
x = 4
0.000143
0.1412
0.8588
x = 4
0.000143
0.1412
0.8588
x = 5
0.0000014
0.0477
0.9543
Interpretacja:
g (w = 0.01|x = 1) =
0.0793,
Interpretacja:
g
1
(w = 0.01|x = 1) =
0.0793,
g
1
(w = 0.05|x = 1) =
0.5599
g
1
(w = 0.1 |x = 1) =
0.3608
g
1
(w = 0.1 |x = 1) =
0.3608

Przykład (6)
Przykład (6)
6. Dla ustalonego x, np.
dla x = 0
6.1
Dla decyzji czystej
a
1
wyznacza się
wartość oczekiwaną
strat
L(a
1
, w)
w rozkładzie a posteriori
g
1
(w|x=0)
strat
L(a
1
, w)
w rozkładzie a posteriori
g
1
(w|x=0)
L(a
1
,w = 0.01)*
g
1
(w = 0.01|x = 0) +
L(a
1
,w = 0.05)*
g
1
(w =
0.05|x = 0)
+
L(a ,w = 0.1)*
g (w = 0.1|x = 0) =
0*0.361+
0.05|x = 0)
+
L(a
1
,w = 0.1)*
g
1
(w = 0.1|x = 0) =
0*0.361+
+0*0.486+50*0.1494
=
7.47
Dla decyzji czystej
a
2
wyznacza się
wartość oczekiwaną
strat
L(a
2
, w)
w rozkładzie a posteriori
g
1
(w|x)
strat
L(a
2
, w)
w rozkładzie a posteriori
g
1
(w|x)
L(a
2
,w = 0.01)*
g
1
(w = 0.01|x = 0) +
L(a
2
,w = 0.05)*
g
1
(w =
2
1
2
1
0.05|x = 0)
+
L(a
2
,w = 0.1)*
g
1
(w = 0.1|x = 0) = 30
*0.361+
+30*0.486+0*0.1494
=
25.41

Przykład (7)
Przykład (7)
6. Dla ustalonego x, np.
dla x = 1
6.1
Dla decyzji czystej
a
1
wyznacza się
wartość oczekiwaną
strat
L(a
1
, w)
w rozkładzie a posteriori
g
1
(w|x=1)
strat
L(a
1
, w)
w rozkładzie a posteriori
g
1
(w|x=1)
L(a
1
,w = 0.01)*
g
1
(w = 0.01|x = 1) +
L(a
1
,w = 0.05)*
g
1
(w =
0.05|x = 1)
+
L(a ,w = 0.1)*
g (w = 0.1|x = 1) =
0*0.0793+
0.05|x = 1)
+
L(a
1
,w = 0.1)*
g
1
(w = 0.1|x = 1) =
0*0.0793+
+0*0.5599+50*0.3608
=
18.08
Dla decyzji czystej
a
2
wyznacza się
wartość oczekiwaną
strat
L(a
2
, w)
w rozkładzie a posteriori
g
1
(w|x)
strat
L(a
2
, w)
w rozkładzie a posteriori
g
1
(w|x)
L(a
2
,w = 0.01)*
g
1
(w = 0.01|x = 1) +
L(a
2
,w = 0.05)*
g
1
(w =
2
1
2
1
0.05|x = 1)
+
L(a
2
,w = 0.1)*
g
1
(w = 0.1|x = 1) = 30
*0.0793+
+30*0.5599+0*0.3608
=
19. 18

Przykład (8)
Przykład (8)
6. Dla ustalonego x, np.
dla x = 2
6.1
Dla decyzji czystej
a
1
wyznacza się
wartość oczekiwaną
strat
L(a
1
, w)
w rozkładzie a posteriori
g
1
(w|x=2)
strat
L(a
1
, w)
w rozkładzie a posteriori
g
1
(w|x=2)
L(a
1
,w = 0.01)*
g
1
(w = 0.01|x = 2) +
L(a
1
,w = 0.05)*
g
1
(w =
0.05|x = 2)
+
L(a ,w = 0.1)*
g (w = 0.1|x = 2) =
0*0.045+
0.05|x = 2)
+
L(a
1
,w = 0.1)*
g
1
(w = 0.1|x = 2) =
0*0.045+
+0*0.4179+50*0.5706
=
28.53
Dla decyzji czystej
a
2
wyznacza się
wartość oczekiwaną
strat
L(a
2
, w)
w rozkładzie a posteriori
g
1
(w|x)
strat
L(a
2
, w)
w rozkładzie a posteriori
g
1
(w|x)
L(a
2
,w = 0.01)*
g
1
(w = 0.01|x = 2) +
L(a
2
,w = 0.05)*
g
1
(w =
2
1
2
1
0.05|x = 2)
+
L(a
2
,w = 0.1)*
g
1
(w = 0.1|x = 2) = 30
*0.045+
+30*0.4179+0*0.5706
=
13.89

Przykład (9)
Przykład (9)
6. Dla ustalonego x, np.
dla x = 3
6.1
Dla decyzji czystej
a
1
wyznacza się
wartość oczekiwaną
strat
L(a
1
, w)
w rozkładzie a posteriori
g
1
(w|x=3)
strat
L(a
1
, w)
w rozkładzie a posteriori
g
1
(w|x=3)
L(a
1
,w = 0.01)*
g
1
(w = 0.01|x = 3) +
L(a
1
,w = 0.05)*
g
1
(w =
0.05|x = 3)
+
L(a ,w = 0.1)*
g (w = 0.1|x = 3) =
0*0.0009+
0.05|x = 3)
+
L(a
1
,w = 0.1)*
g
1
(w = 0.1|x = 3) =
0*0.0009+
+0*0.2581+50*0.7410
=
37.05
Dla decyzji czystej
a
2
wyznacza się
wartość oczekiwaną
strat
L(a
2
, w)
w rozkładzie a posteriori
g
1
(w|x)
strat
L(a
2
, w)
w rozkładzie a posteriori
g
1
(w|x)
L(a
2
,w = 0.01)*
g
1
(w = 0.01|x = 3) +
L(a
2
,w = 0.05)*
g
1
(w =
2
1
2
1
0.05|x = 3)
+
L(a
2
,w = 0.1)*
g
1
(w = 0.1|x = 3) = 30
*0.0009+
+30*0.2581+0*0.7410
=
7.77

Przykład (10)
Przykład (10)
6. Dla ustalonego x, np.
dla x = 4
6.1
Dla decyzji czystej
a
1
wyznacza się
wartość oczekiwaną
strat
L(a
1
, w)
w rozkładzie a posteriori
g
1
(w|x=4)
strat
L(a
1
, w)
w rozkładzie a posteriori
g
1
(w|x=4)
L(a
1
,w = 0.01)*
g
1
(w = 0.01|x = 4) +
L(a
1
,w = 0.05)*
g
1
(w =
0.05|x = 4)
+
L(a ,w = 0.1)*
g (w = 0.1|x = 4) =
0*0.0+
0.05|x = 4)
+
L(a
1
,w = 0.1)*
g
1
(w = 0.1|x = 4) =
0*0.0+
+0*0.1412+50*0.8588
=
42.94
Dla decyzji czystej
a
2
wyznacza się
wartość oczekiwaną
strat
L(a
2
, w)
w rozkładzie a posteriori
g
1
(w|x)
strat
L(a
2
, w)
w rozkładzie a posteriori
g
1
(w|x)
L(a
2
,w = 0.01)*
g
1
(w = 0.01|x = 4) +
L(a
2
,w = 0.05)*
g
1
(w =
2
1
2
1
0.05|x = 4)
+
L(a
2
,w = 0.1)*
g
1
(w = 0.1|x = 4) = 30
*0.0+
+30*0.1412+0*0.8588
=
4.24

Przykład (11)
Przykład (11)
6. Dla ustalonego x, np.
dla x = 5
6.1
Dla decyzji czystej
a
1
wyznacza się
wartość oczekiwaną
strat
L(a
1
, w)
w rozkładzie a posteriori
g
1
(w|x=5)
strat
L(a
1
, w)
w rozkładzie a posteriori
g
1
(w|x=5)
L(a
1
,w = 0.01)*
g
1
(w = 0.01|x = 5) +
L(a
1
,w = 0.05)*
g
1
(w =
0.05|x = 5)
+
L(a ,w = 0.1)*
g (w = 0.1|x = 5) =
0*0.0+
0.05|x = 5)
+
L(a
1
,w = 0.1)*
g
1
(w = 0.1|x = 5) =
0*0.0+
+0*0.0477+50*0.9543
=
47.72
Dla decyzji czystej
a
2
wyznacza się
wartość oczekiwaną
strat
L(a
2
, w)
w rozkładzie a posteriori
g
1
(w|x=5)
strat
L(a
2
, w)
w rozkładzie a posteriori
g
1
(w|x=5)
L(a
2
,w = 0.01)*
g
1
(w = 0.01|x = 5) +
L(a
2
,w = 0.05)*
g
1
(w =
2
1
2
1
0.05|x = 5)
+
L(a
2
,w = 0.1)*
g
1
(w = 0.1|x = 5) = 30
*0.0+
+30*0.0477+0*0.9543
=
1.243

Przykład (12)
Przykład (12)
6.2.
Wskazanie
a*
dla której średnia wartość funkcji
strat przyjmuje najmniejszą wartość gdy pomiar
wskazuje x -
tabela decyzyjna
d*(x) = a*
x
a*
x
a*
x = 0
a
1
x = 1
a
1
x = 2
a
2
x = 2
a
2
x = 3
a
2
x = 4
a
x = 4
a
2
x = 5
a
2

PODSUMOWANIE
Jeśli
GROMADZISZ INFORMACJE O STATYSTYKACH
POMIARÓW X PODCZAS GDY NATURA FLUKTUUJE
POMIARÓW X PODCZAS GDY NATURA FLUKTUUJE
oraz
MASZ DOBRE OSZACOWANIE ROZKŁADÓW STANÓW
NATURY
NATURY
to
TEORIA BAYESA DAJE CI NARZĘDZIE DO WYZNACZANIA
TEORIA BAYESA DAJE CI NARZĘDZIE DO WYZNACZANIA
OPTYMALNEJ STRATEGII (CZYLI STRATEGII, KTÓRA W
DŁUGIM HORYZONCIE CZASOWYMN MINIMALIZUJE TWOJE
KOSZTY/STRATY).
KOSZTY/STRATY).

GRA TEXAŃSKA ?
GRA TEXAŃSKA ?
SOLUTION
SOLUTION
GRA TEXAŃSKA
(STAY)
GRA TEXAŃSKA
(STAY)
B
B
B
GRA TEXAŃSKA
(MOVE)
GRA TEXAŃSKA
(MOVE)
B
B
B
B
B
B

DZIĘKUJĘ ZA UWAGĘ
DZIĘKUJĘ ZA UWAGĘ
Wyszukiwarka
Podobne podstrony:
Microsoft PowerPoint SYSTEMY I PROJEKTY W OCHRONIE SRODOWISKA tryb zgodno 234ci
Podejmowanie decyzji w warunkach niepewnosci
4 METODY PODEJMOWANIA DECYZJI W WARUNKACH NIEPEWNOŚCI
8. konspekt - Ekonomia menedżerska, Podejmowanie decyzji w warunkach niepewności
8 konspekt Ekonomia menedżerska Podejmowanie decyzji w warunkach niepewności
Podejmowanie decyzji w warunkach niepewnosci
004 Jak podejmujemy decyzje w przedsi biorstwie tryb zgodno ci
Microsoft PowerPoint Alergia na materiały protetyczne [tryb zgodności]
02z podejmowanie decyzji w warunkach niepewno ci i ryzyka (skrot)
Rozdział 8 Podejmowanie decyzji w warunkach niepewności
(Microsoft PowerPoint MR 6 zasady nauczania ppt [tryb zgodnosci])
(Microsoft PowerPoint MR 4 5 rozwoj czlowieka ppt [tryb zgodnosci])
(Microsoft PowerPoint Matematyka Farmacja [tryb zgodno 234ci])
Microsoft PowerPoint METODA MONTE CARLO tryb zgodno 234ci (1)
więcej podobnych podstron