Grawitacja

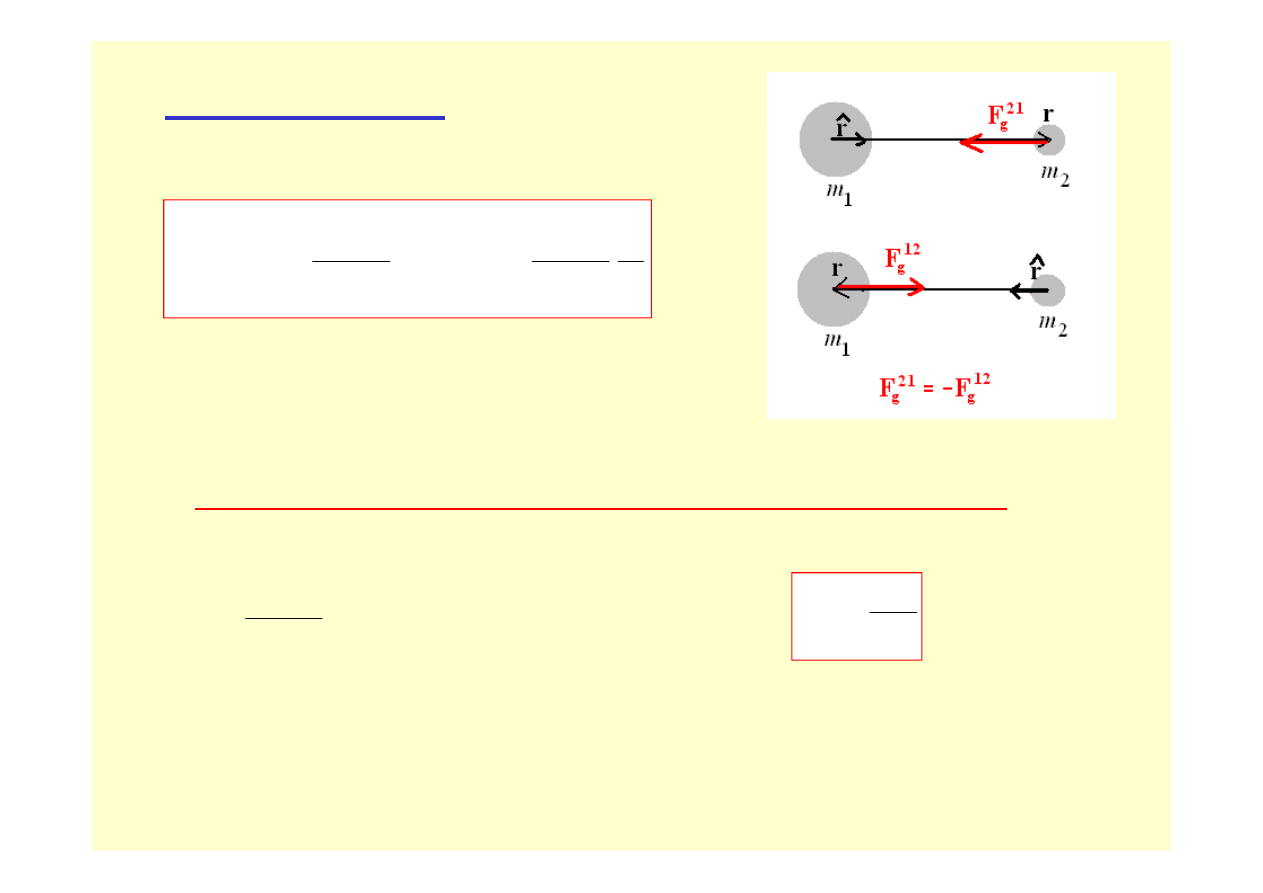
Siła grawitacji

Blisko powierzchni Ziemi:

r

r

Mm

G

r

Mm

G

r

r

F

2

2

ˆ

−

=

−

=

'

ale

'

2

m

m

g

m

R

M

m

G

z

Z

=

=

2

z

Z

R

M

G

g

=

Masa grawitacyjna (m) i bezwładna (m’) są sobie równe !!!

Jak zmierzy

ć

stał

ą

G ?

Pierwszy

ś

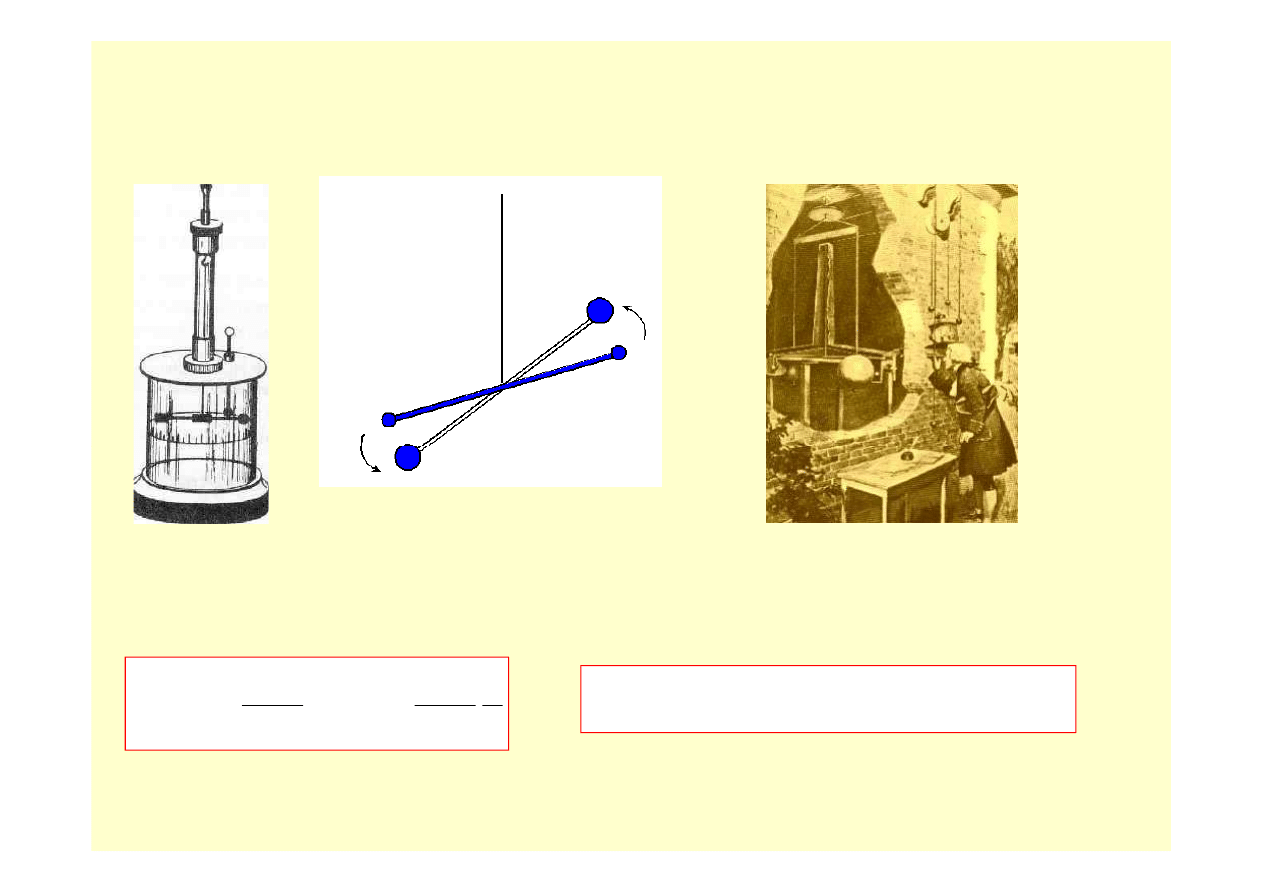
cisły pomiar stałej grawitacji został wykonany przez lorda Cavendisha

ok 1798 roku:

1798

Na dwóch cienkich pr

ę

tach umieszczone s

ą

parami znane masy. Jeden z pr

ę

tów mo

ż

e si

ę

obraca

ć

, skr

ę

caj

ą

c spr

ęż

yst

ą

nitk

ę

. Wskutek działania sił przyci

ą

gania grawitacyjnego pr

ę

t

ruchomy skr

ę

ci nitk

ę

o pewien k

ą

t, który odczytamy poprzez odbicie promienia

ś

wiatła od

lusterka przyklejonego do pr

ę

ta.

2

2

11

kg

Nm

10

6754

.

6

G

−

−

×

=

1798

r

r

Mm

G

r

Mm

G

r

r

F

2

2

ˆ

−

=

−

=

r

r

Mm

G

m

r

a

2

−

=

r

r

Mm

G

t

d

d

m

r

r

2

2

2

−

=

Równanie ruchu:

Rozwi

ą

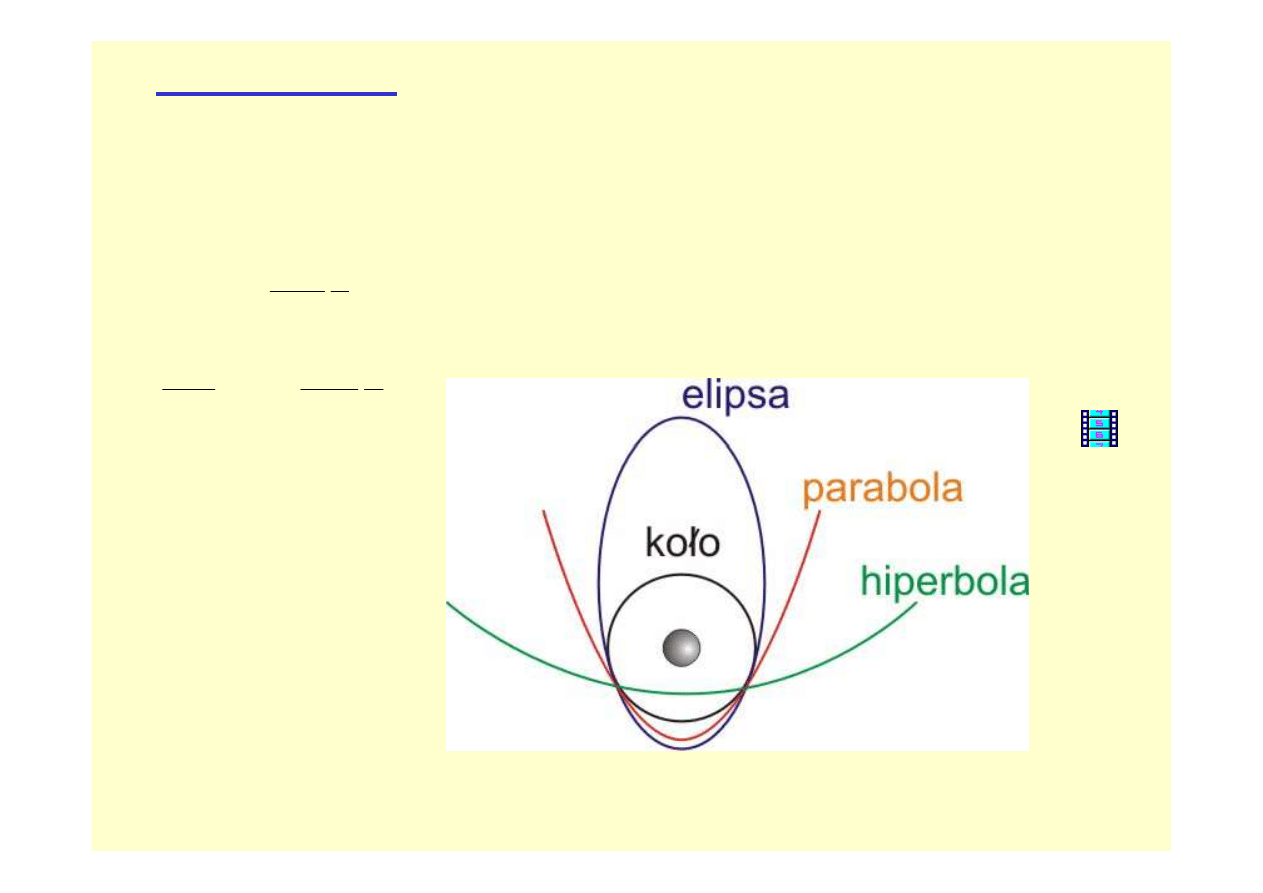
zania

krzywe sto

ż

kowe

Ruch planet

Mikołaj Kopernik (1473 – 1543), formułuje tzw. model heliocentryczny (opisany w jego dziele: „De
revolutionibus orbitum coelestium”, czyli „O obrotach sfer niebieskich” – wydanym w roku 1543).

Johannes Kepler (1571 - 1630) dokonał syntezy ówczesnej wiedzy na temat ruchu
planet wokół Słońca w postaci trzech prostych praw.

1.

Ka

ż

da planeta kr

ąż

y po orbicie eliptycznej, ze Sło

ń

cem w jednym z ognisk tej elipsy.

Ruch planet – prawa Keplera

2.

Linia ł

ą

cz

ą

ca Sło

ń

ce i planet

ę

zakre

ś

la równe pola w równych odst

ę

pach czasu (prawo

równych pól).

3.

Sze

ś

ciany półosi wielkich dla orbit dwóch dowolnych planet maj

ą

si

ę

do siebie jak

kwadraty ich okresów obiegu (póło

ś

wielka jest połow

ą

najdłu

ż

szej ci

ę

ciwy elipsy).

siła centralna:

r

r

Mm

G

r

F

2

−

=

0

)

(

3

2

=

×

−

=













−

×

=

×

=

r

r

r

r

F

r

M

r

Mm

G

r

r

Mm

G

moment siły centralnej:

L = const.

Moment p

ę

du jest zachowany w ruchu pod wpływem siły centralnej (np. siły grawitacji).

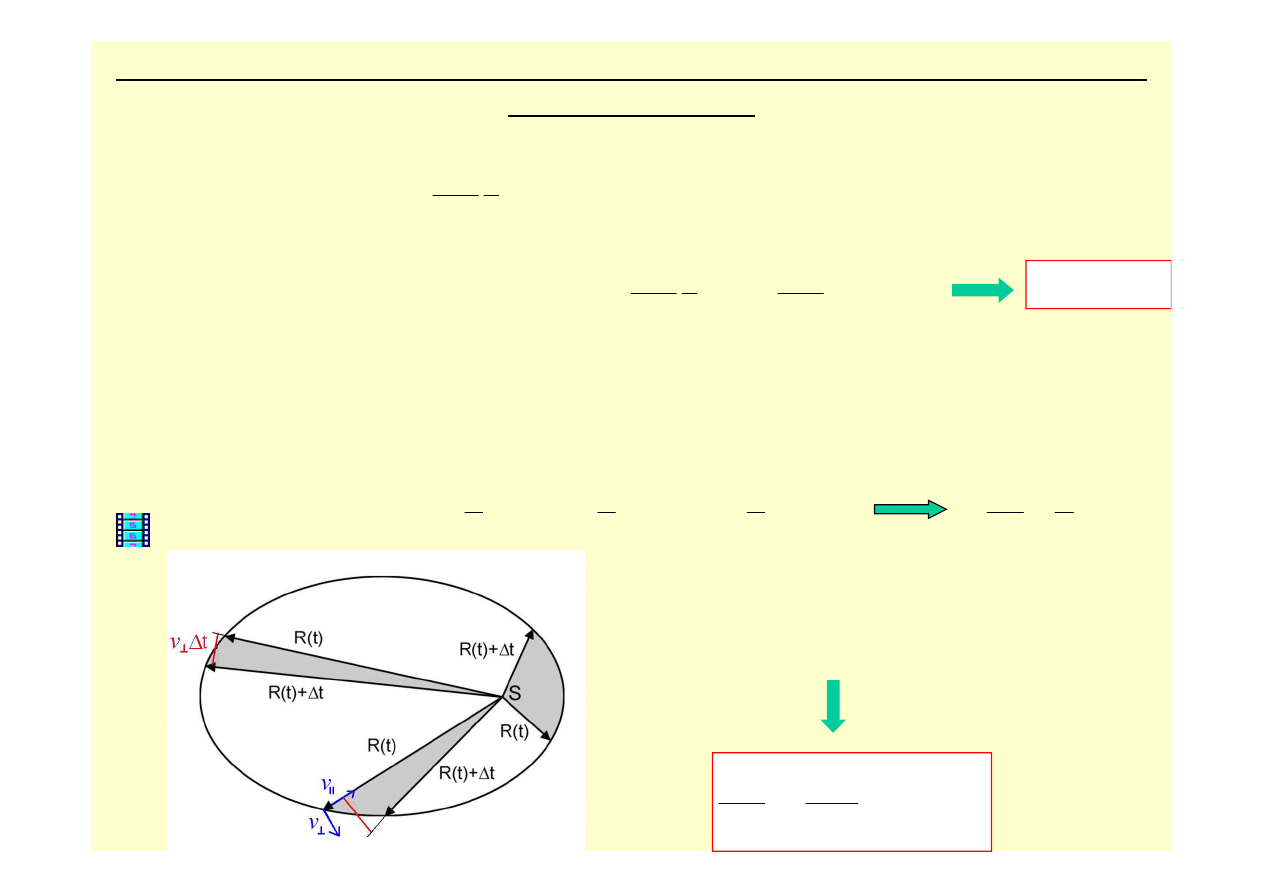
prawo 2: Linia łącząca Słońce i planetę zakreśla równe pola w równych odstępach czasu

(prawo równych pól).

dt

R

dt

R

R

dt

R

dS

ω

ω

2

2

1

2

1

2

1

=

=

=

⊥

v

2

2

1

R

dt

dS

ω

=

const.

R

m

R

m

L

=

=

=

⊥

2

ω

v

const.

m

L

t

d

S

d

=

=

2

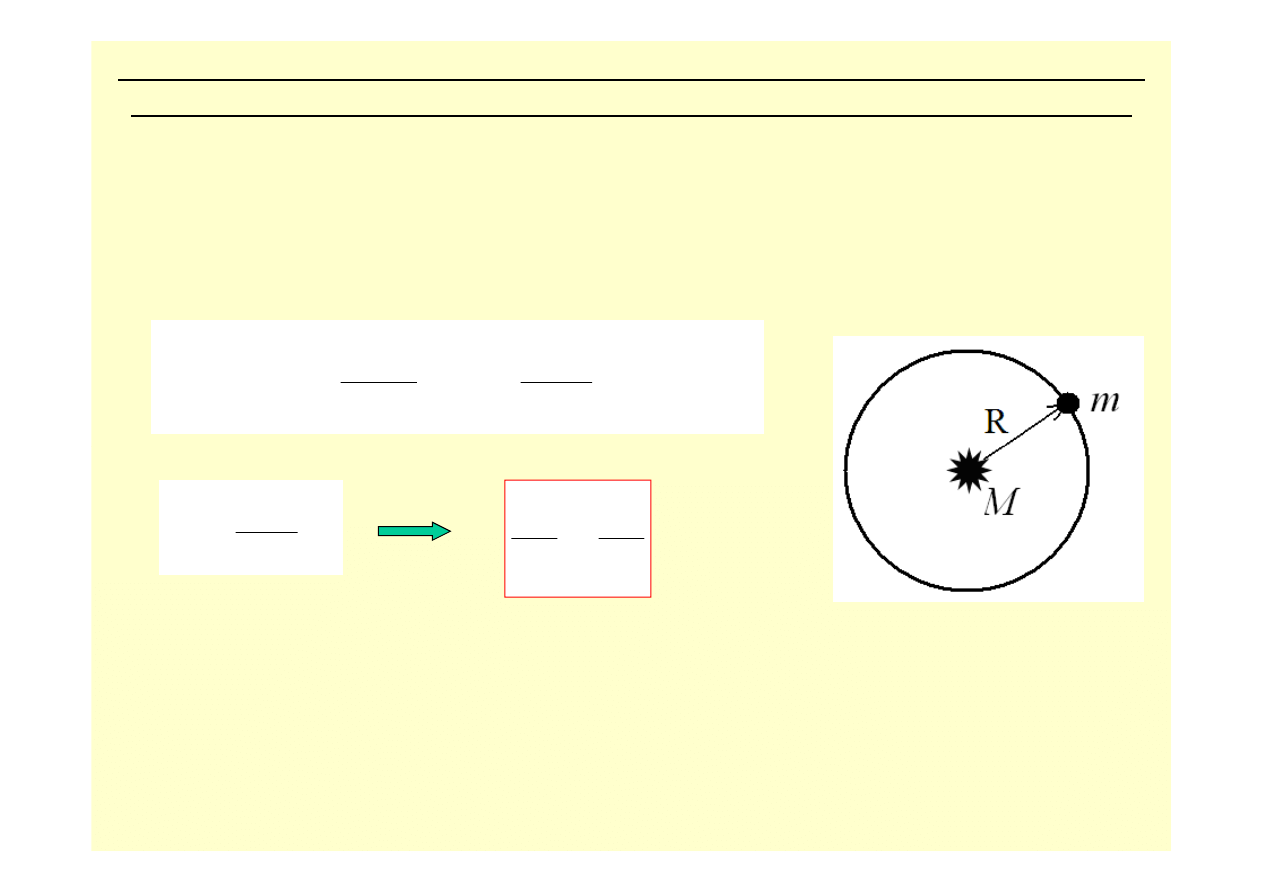
Załó

ż

my orbit

ę

kołow

ą

r=const. i

ω

=const.

GM

R

T

R

mM

G

R

m

=

=

3

2

2

2

2

4

;

π

ω

prawo 3: Sześciany półosi wielkich dla orbit dwóch dowolnych planet mają się do siebie

jak kwadraty ich okresów obiegu (półoś wielka jest połową najdłuższej cięciwy elipsy)

3

2

2

4

R

GM

T

π

=

2

2

2

1

3

2

3

1

T

T

R

R

=