1
Ruch bryły sztywnej,
dynamika ruchu obrotowego
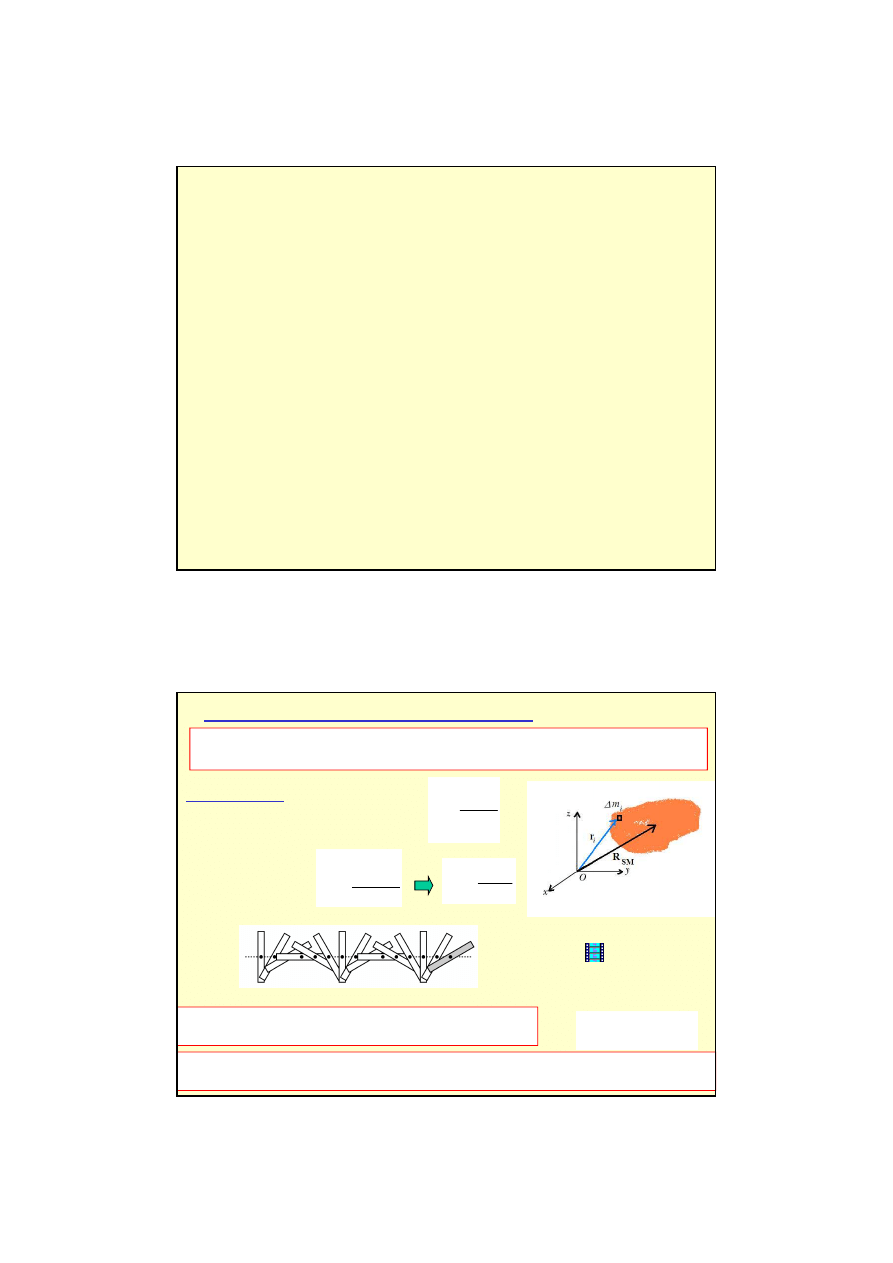
OPIS RUCHU BRYŁY SZTYWNEJ
Brył
ą
sztywna nazywamy zbiór punktów materialnych (niesko
ń
czenie wielu),
których wzajemne poło
ż
enie nie zmienia si
ę
pod wpływem działaj
ą
cych sił.
c
n
i
i
m
m
∑
=
∆
=
1
i
sm
r
R
c
m
dm
∫
=
r
R
sm
-dla układu punktów materialnych
-dla bryły sztywnej
m
m
=
i
N
=1
i
i
N
=1
i
∑
∑
r
R
i
sm
.
1
zewn
n
i
i
sm
M
F
F
a
=
=
∑
=
Ruch bryły sztywnej mo
ż
na rozło
ż
y
ć
na:
ruch post
ę
powy
ś
rodka masy i ruch obrotowy
Ś
rodek masy układu punktów materialnych porusza si
ę
w taki sposób, jakby cała masa
układu była skupiona w
ś
rodku masy i jakby wszystkie siły zewn
ę
trzne na
ń
działały.
Ruch post
ę
powy:
Ś
rodek masy:
2
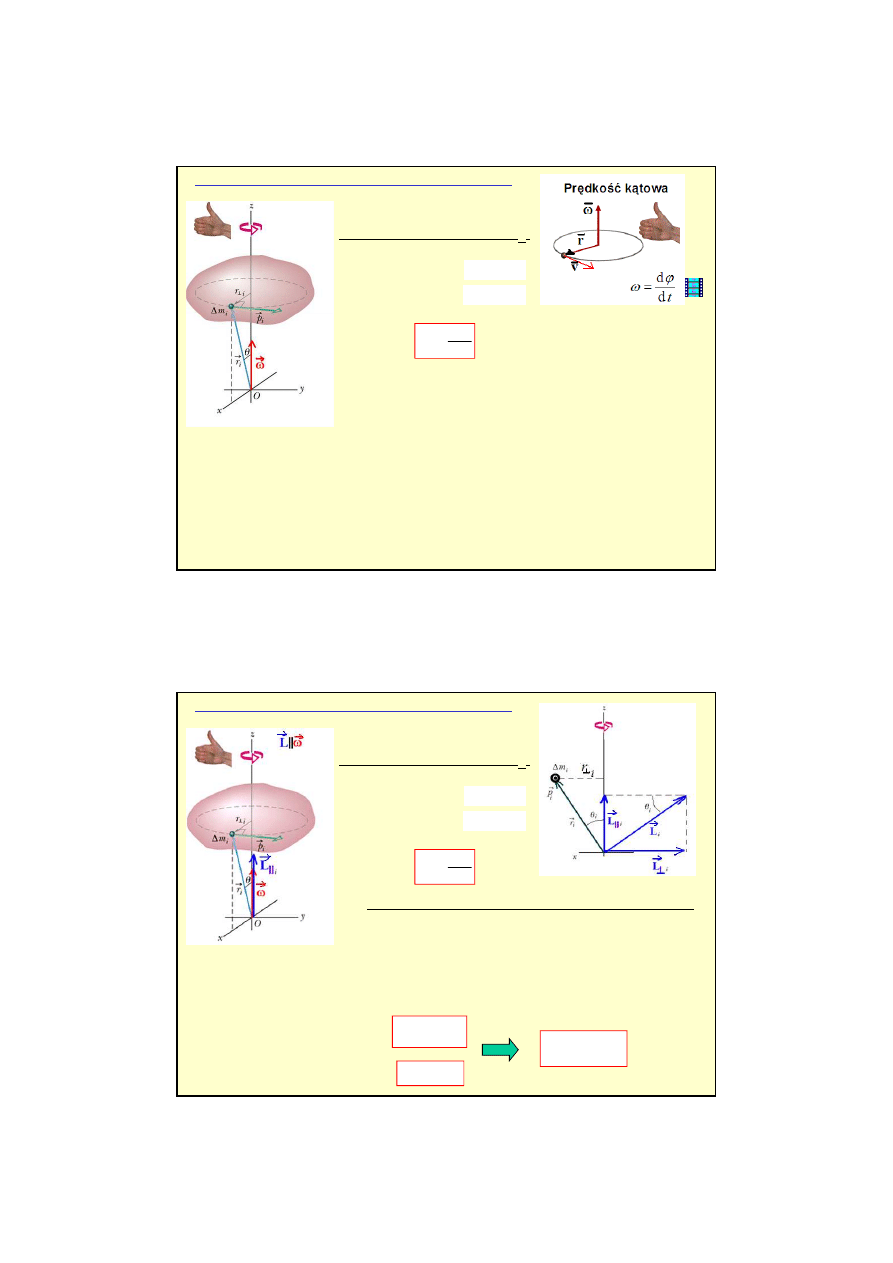
Ruch obrotowy (przypadek szczególny L||
ω
ω
ω
ω
)
Dla elementarnej masy
∆
m
i
:
i
i
i
F
r
M
×
=
i
i
i
p
r
L
×
=
- moment p
ę
du:
- moment siły:
t
i
i
d
d L
M
=
i
i
i
i
ω
r
ω
r
⊥
=
=
θ
sin
v
Ruch obrotowy (przypadek szczególny L||
ω
ω
ω
ω
)
Dla elementarnej masy
∆
m
i
:
i
i
i
F
r
M
×
=
i
i
i
p
r
L
×
=
- moment p
ę
du:
- moment siły:
t
i
i
d
d L
M
=
moment
bezwładno
ś
ci:
∑
∆
=
⊥
i
m
r
I
i
i
2
∫
=
m
r
I
d
2
ω
L
Ι
=
ω
ω
θ
θ
θ
∆
=
∆
=
∆
=
=
∆
=
=
=
=
∑
∑
∑
∑
∑
∑
⊥
⊥
⊥
⊥
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
m
r
r
r
m
r
m
r
m
p
r
L
L
L
2
||
)
(
sin
sin
sin
v
v
Dla całej bryły - obrót wokół osi (zakładaj
ą
c L||
ω
ω
ω
ω
):
i
i
ω
r
⊥
=
v
3
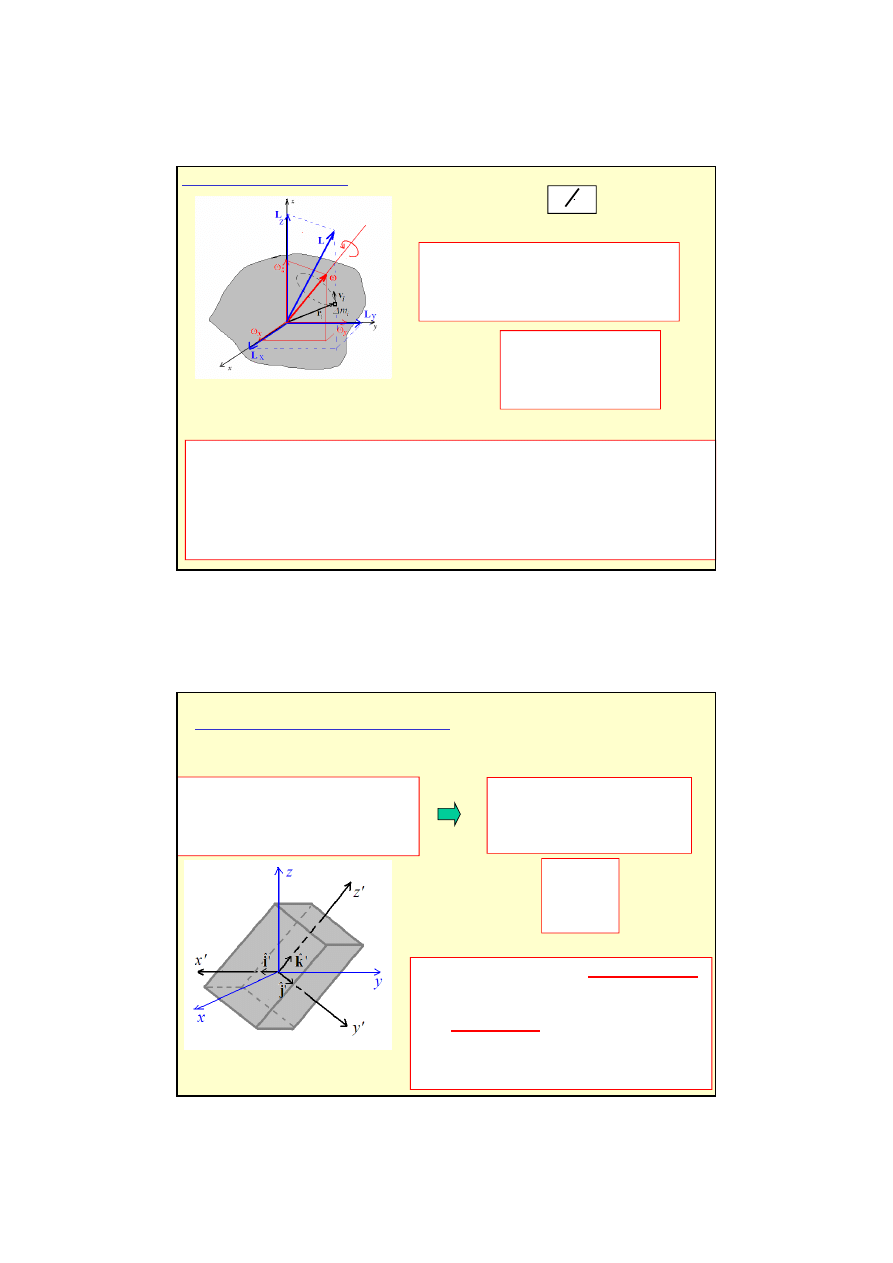
Ruch obrotowy ogólnie
Dla ka
ż
dej bryły sztywnej mo
ż
na zdefiniowa
ć
trzy prostopadłe osie, zwane głównymi
osiami bezwładno
ś
ci.
• Moment bezwładno
ś
ci ciała wzgl
ę
dem jednej z tych osi jest maksymalny, wzgl
ę
dem
drugiej jest minimalny, za
ś
wzgl
ę
dem trzeciej – ma warto
ść
po
ś
redni
ą
: I
I
≥
I
II
≥
I
III
,
• Je
ś
li ciało ma kształt symetryczny główne osie bezwładno
ś
ci s
ą
tak
ż
e osiami symetrii
ciała.
=
⇔
=
z
y
x
zz
zy
zx
yz
yy
yx
xz
xy
xx
z
y
x
I
I
I
I
I
I
I
I
I
L
L
L
ω
ω
ω
ω
I
L
ˆ
ω
L ||
ogólnie gdy:
z
zz
y
zy
x
zx
z
z
yz
y
yy
x
yx
y
z
xz
y
xy
x
xx
x
I
I
I
L
I
I
I
L
I
I
I
L
ω
ω
ω
ω
ω
ω
ω
ω
ω
+
+
=
+
+
=
+
+
=
Ruch obrotowy wokół osi głównych
1)
W ogólnym przypadku L nie jest równoległy
do
ω
ω
ω
ω
.
2) L jest równoległy do
ω
ω
ω
ω
wówczas, gdy osią
obrotu jest jedna z głównych osi
bezwładności (wtedy:
gdzie
I
jest
wartością skalarną).
ω
L
Ι
=
Kiedy L jest równoległy do
ω
ω
ω
ω
?
=
⇔
=
z
y
x
zz
zy
zx
yz
yy
yx
xz
xy
xx
z
y
x
I
I
I
I
I
I
I
I
I
L
L
L
ω
ω
ω
ω
I
L
ˆ
=
'
'
'
'
'
'
'
'
'
'
'
0
0
0
0
0
0
z
y
x
z
z
y
y
x
x
z
y
x
I
I
I
L
L
L
ω
ω
ω
Transformujemy tensor do układu, którego osie współrz
ę
dnych (x’,y’,z’) s
ą
równoległe
do osi głównych bezwładno
ś
ci:
Iˆ
'
'
'
'
'
'
'
'
'
'
'
'
z
z
z
z
y
y
y
y
x
x
x
x
I
L
I
L
I
L
ω
ω
ω
=
=
=
4
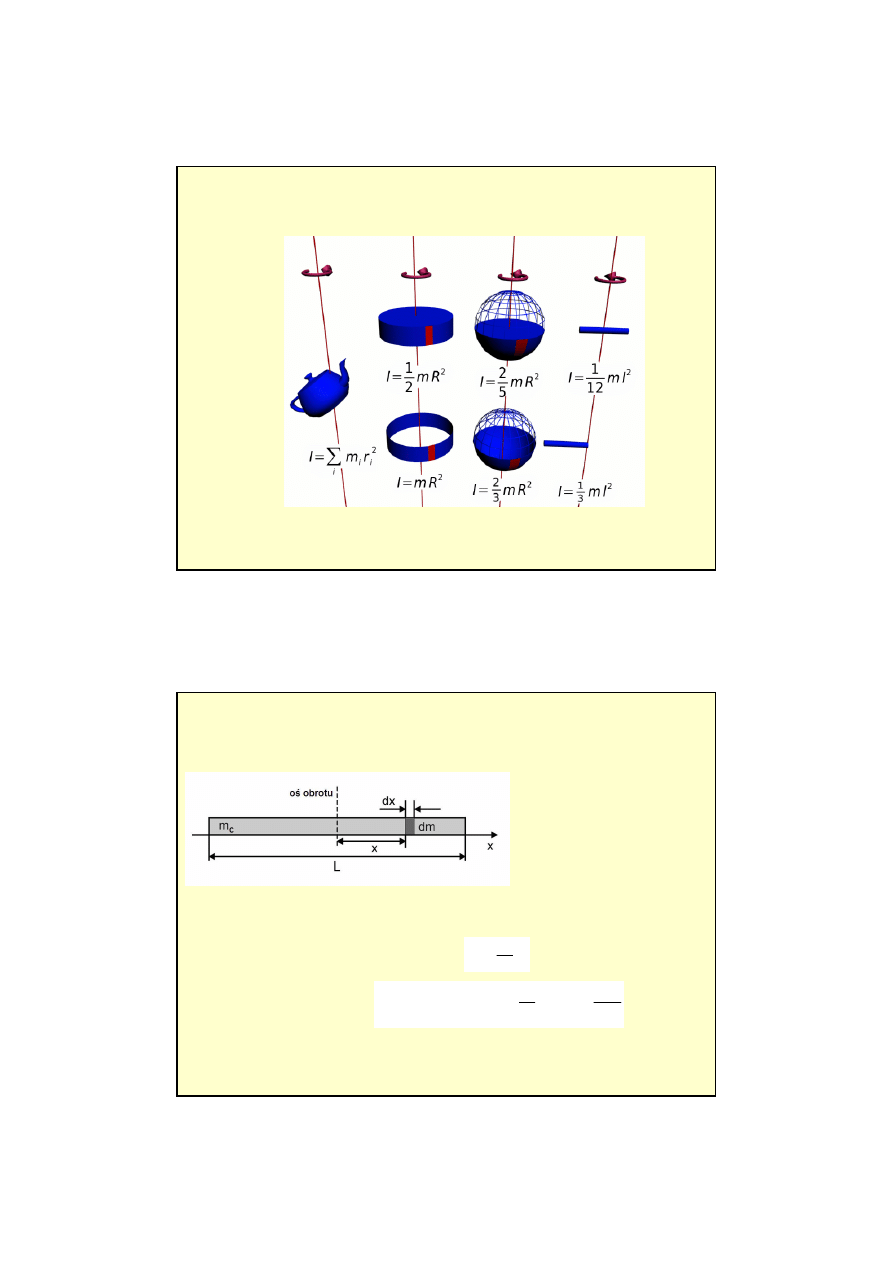
Przykład:
liczenie momentu bezwładno
ś
ci pr
ę
ta o masie M i długo
ś
ci L.
Moment bezwładno
ś
ci elementu
o masie dm wynosi x
2
dm
x
L
m
m
c
d
d
=
je
ż
eli pr
ę
t ma stał
ą
g
ę
sto
ść
:
12
d
d
d
2
2
/
2
/
2
2
/
2
/
2
2
L
m
x
x
L
m
m
x
m
x
I
c
L
L
c
L
L
i
i
i
∫
∫
∑
−
−
=
=
=
=
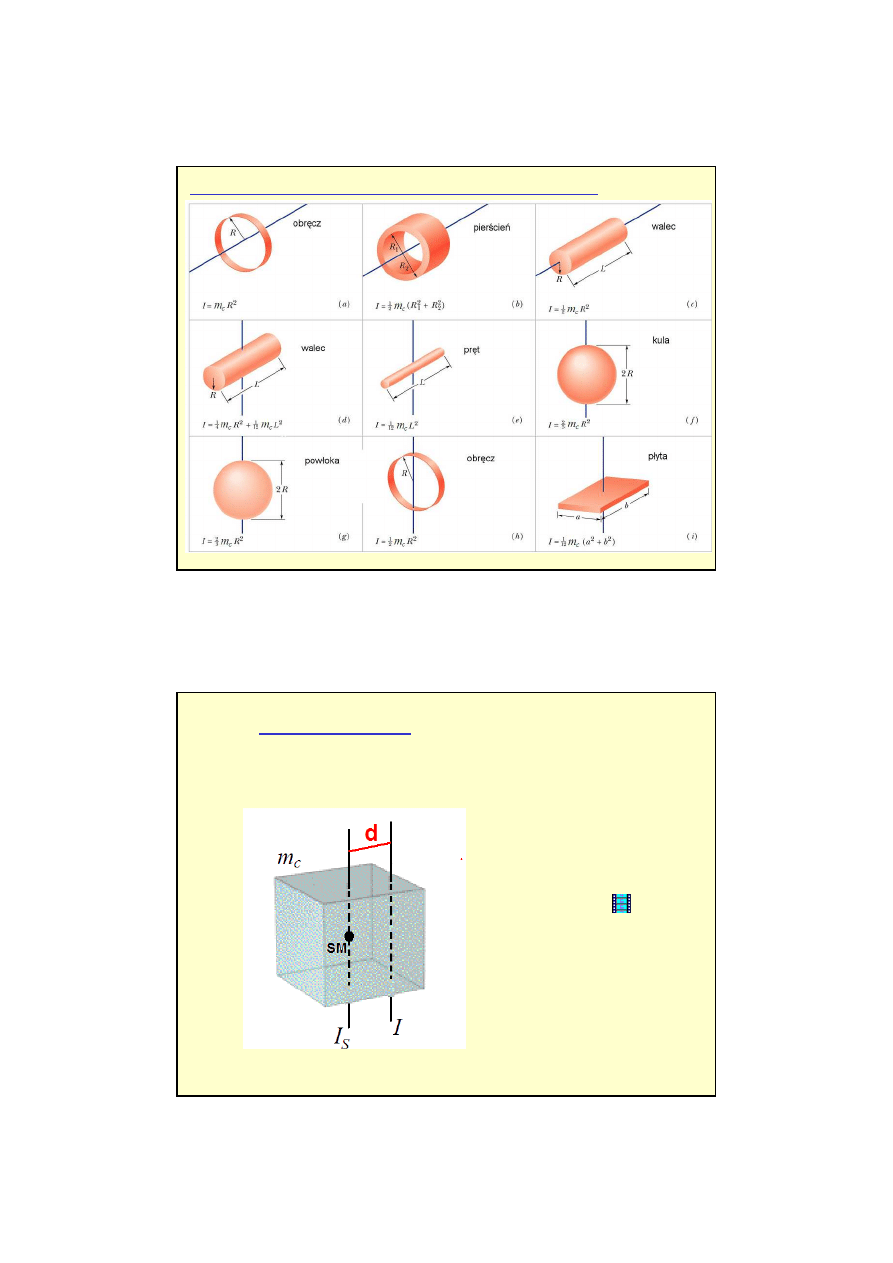
5
Przykładowe momenty bezwładno
ś
ci wokół osi głównych
2
d
m
Ι
Ι
c
S
+
=
Twierdzenie Steinera:
6
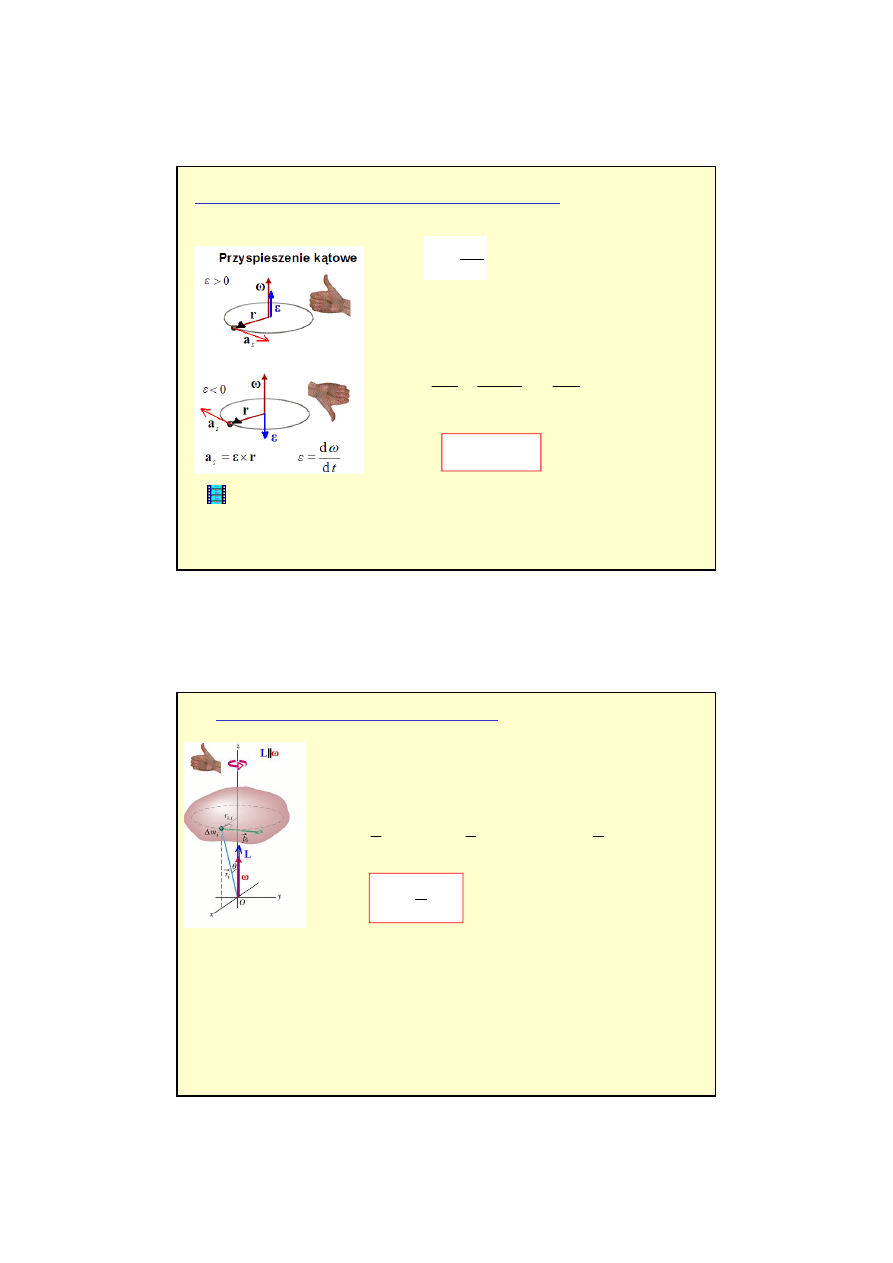
Ruch obrotowy (przypadek szczególny L||
ω
ω
ω
ω
i M||
ω
ω
ω
ω
)
t
d
d L
M
=
II zas. dynamiki Newtona dla
ruchu obrotowego ogólnie
spełniona
ε
ω
ω
L
M
I
t
I
t
I
t
=
=
=
=
d
d
d
)
d(
d
d
ε
M
I
=
Je
ś
li:
to:
ω
M ||
ω
L
Ι
=
oraz
Energia kinetyczna w ruchu obrotowym
2
2
2
2
2
1
)
(
2
1
2
1
ω
∆
ω
∆
∆
∑
∑
∑
=
=
=
⊥
⊥
i
i
i
i
i
i
i
i
i
k
r
m
r
m
m
E
v
2
2
1
ω
I
E
k
=
•przypadek szczególny, gdy wektor
ω
ω
ω
ω
jest równoległy do
jednej z osi głównych bezwładno
ś
ci (czyli
L
||
ω
ω
ω
ω
):
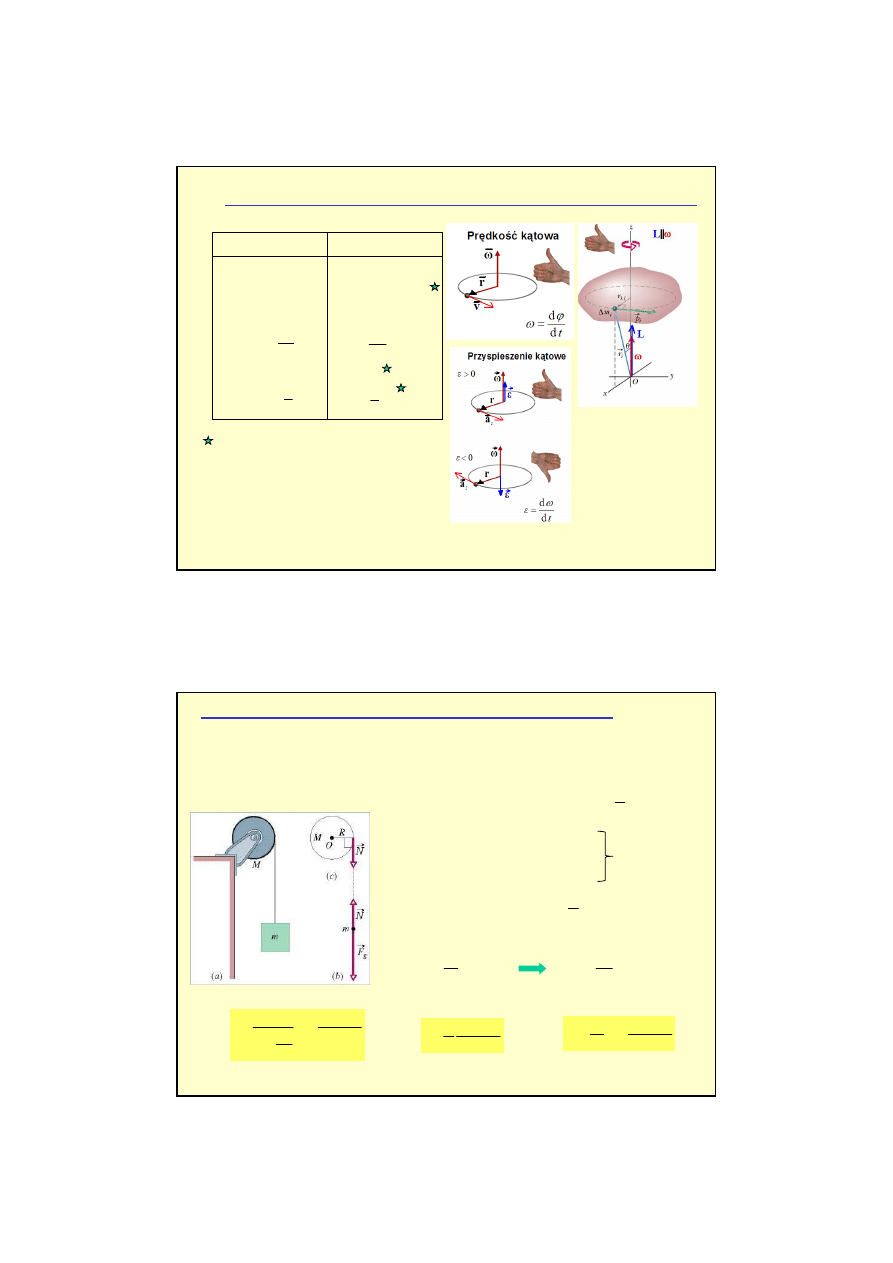
7
Ruch post
ę
powy
Ruch obrotowy
2
2
1
d
d
v
m
E
m
t
m
m
k
=
=
=
=
a
F
p
F
F
v
p
a,
v,
r,
2
2
1
d
d
,
Iω
E
I
t
Ι
I
k
=
=
=
×
=
=
×
=
ε
M
L
M
F
r
M
ω
L
p
r
L
ε,
ω,
,
ϕϕϕϕ
przypadek szczególny,
L
||
ω
ω
ω
ω
oraz
M
||
εεεε
Analogie ruchu obrotowego do ruchu post
ę
powego - uzupełnienie
Znajd
ź
przyspieszenie liniowe klocka o masie m, przyspieszenie k
ą
towe
bloczka oraz napr
ęż
enie nici. Dane s
ą
masa bloczka M i jego promie
ń
R. (Wszelkie
opory i tarcie pomijamy).
2
2
1
MR
Moment bezwładno
ś
ci bloczka wynosi
M
m
m
g
R
I
m
mg
a
+
=
+
=
2
2
2
M
m
mM
g
R
I
N
+
=
=
2
ε
M
m
m
R
g
+
=
2
2
ε
Ruch postępowy
Ruch obrotowy
ε
I
RN
M
wyp
=
=
ma
N
mg
F
wyp
=
−
=
R
a
=
ε
związek miedzy ruchem
postępowym i obrotowym
II zasada
dynamiki
Newtona
Przykład (1):
ma
R
I
mg
=
−
ε
ma
R
Ia
mg
=
−
2
PRZYKŁADY RUCHU BRYŁY SZTYWNEJ
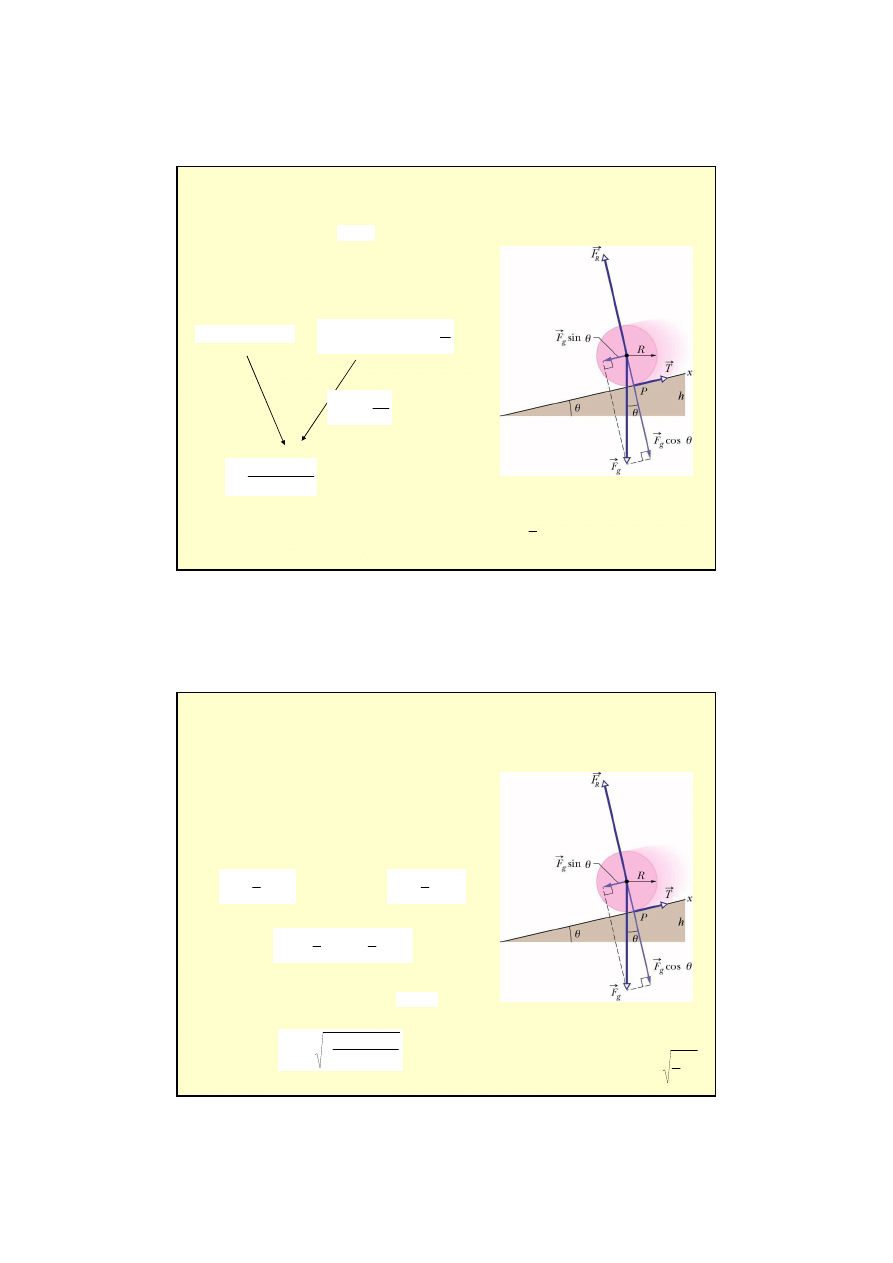
8
Przykład ruchu (3): Toczenie si
ę
(bez po
ś
lizgu) po równi pochyłej
– równania ruchu
Toczenie bez po
ś
lizgu:
R
a
ε
=
ma
T
mg
=
−
θ
sin
ruch post
ę
powy
ruch obrotowy
R
a
I
I
RT
M
SM
SM
=
=
=
ε
.
θ
sin
3
2
g
a
=
np. dla walca:
2
/
sin
R
I
m
mg
a
SM
+
=
θ
2
R
a
I
T
SM
=
Przykład ruchu (4): Toczenie si
ę
(bez po
ś
lizgu) po równi pochyłej
– zasada zachowania energii
ruch post
ę
powy
ruch obrotowy
2
2
1
SM
kp
m
E
v
=
R
ω
=
v
2
2
1
ω
I
E
SM
ko
=
2
2
2
1
2
1
ω
SM
SM
I
m
mgh
+
=
v
Toczenie bez po
ś
lizgu
np. dla walca
Z zasady zachowania energii
gh
SM
3
4
=
v
2
/
2
R
I
m
mgh
SM
SM
+
=
v
9
const.
0
d
d
=
⇒
=
=
L
L
M
t
const.
=
=
ω
ωω
ω
Ι
L
KONSEKWENCJE ZASADY ZACHOWANIA MOMENTU PĘDU I DRUGIEJ
ZASADY DYNAMIKI DLA RUCHU OBROTOWEGO
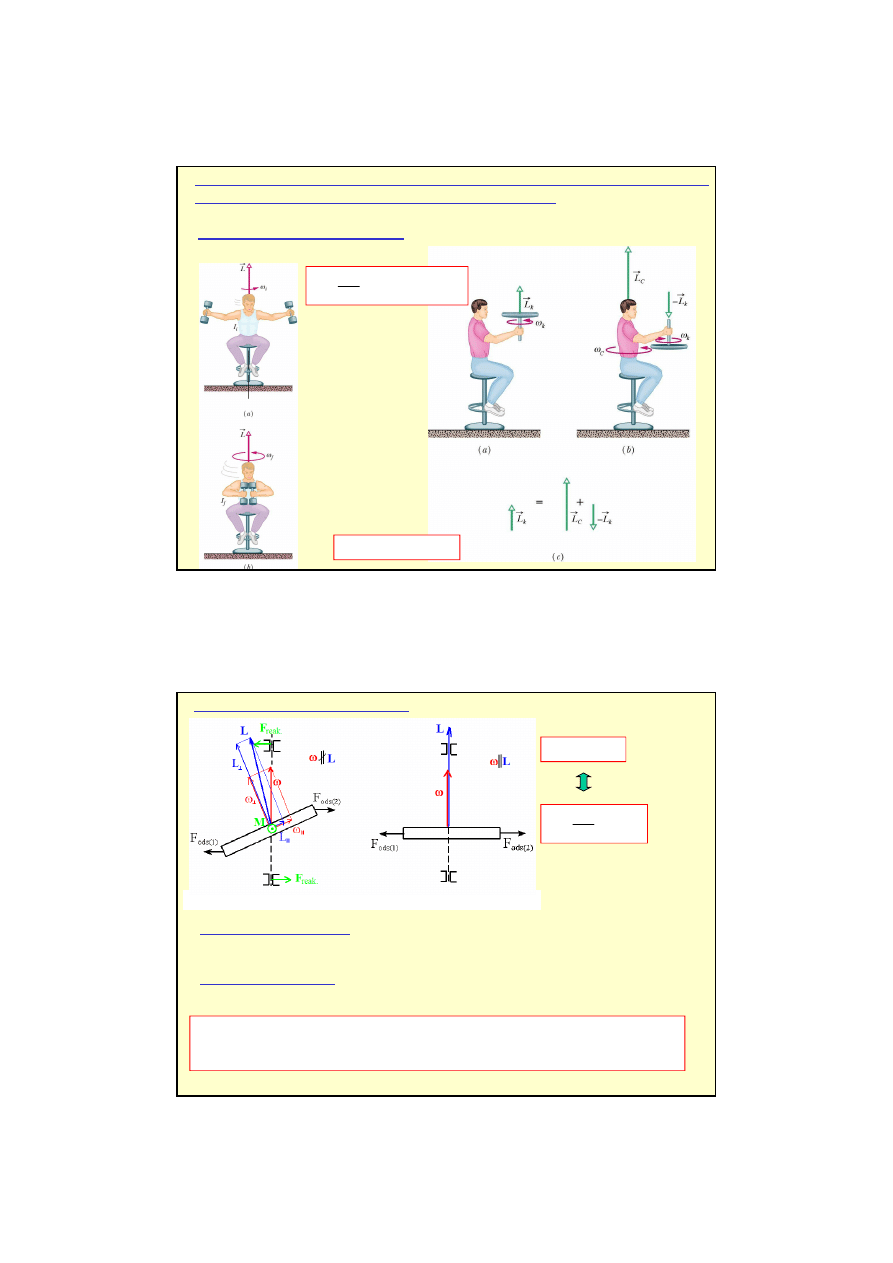
1. Przykład - stołek obrotowy
2. Stała wymuszona o
ś
obrotu
const.
≠
L
const.
d
d
≠
=
t
L
M
Obrót pręta wokół osi nieswobodnej (po lewej) i swobodnej (po prawej)
Obrót wokół osi nieswobodnej: Gdy za pomocą łożysk ustalimy w przestrzeni oś obrotu (narzucimy
na nią więzy), wektor momentu pędu będzie dążył do zmiany orientacji; spowoduje to powstanie sił
oddziaływania między osią a łożyskami. Momenty sił reakcji łożysk spowodują precesję wektora L.
Obrót wokół osi swobodnej: Nie potrzeba łożysk ponieważ momenty sił są zerowe.
W układzie obracającym się siła odśrodkowa dąży do rozmieszczenia masy jak najdalej od osi
obrotu (maksymalny moment bezwładności). Stabilny jest stan odpowiadający zerowemu
momentowi sił odśrodkowych, a tym samym zerowym siłom reakcji łożysk.
10
g
r
M
m
×
=
θ
θ
ϕ
ω
sin
1
sin
L
M
t
L
L
t
p
=
∆
∆
≅
∆
∆
=
∆
t
∆
L
M
=
θ
ω
sin
L
M
p
=
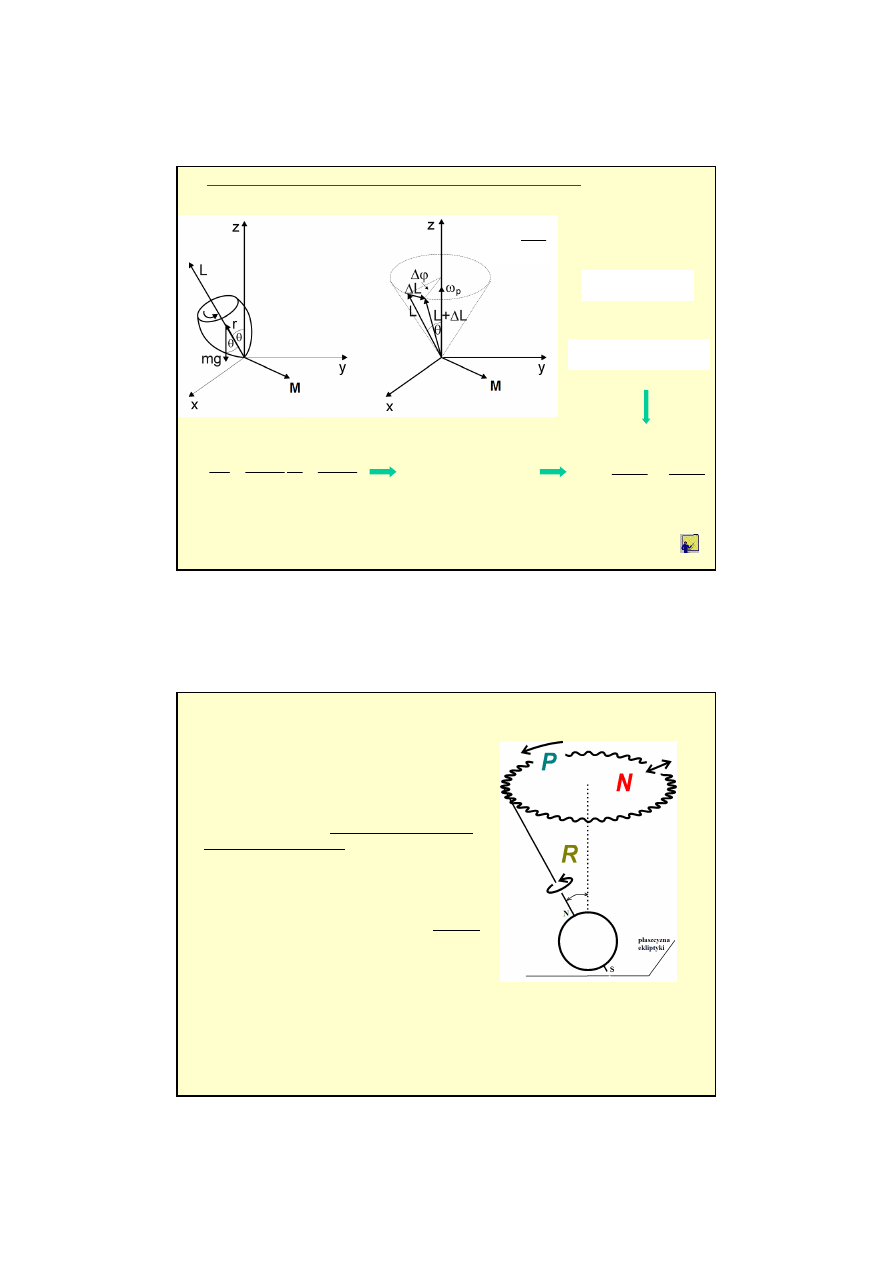
Precesja b
ą
ka pod wpływem siły ci
ęż
ko
ś
ci
3. Precesja pod wpływem działaj
ą
cego momentu siły
kolejka
ω
ω
I
mgr
L
mgr
p
=
=
θ
sin
mgr
M
=
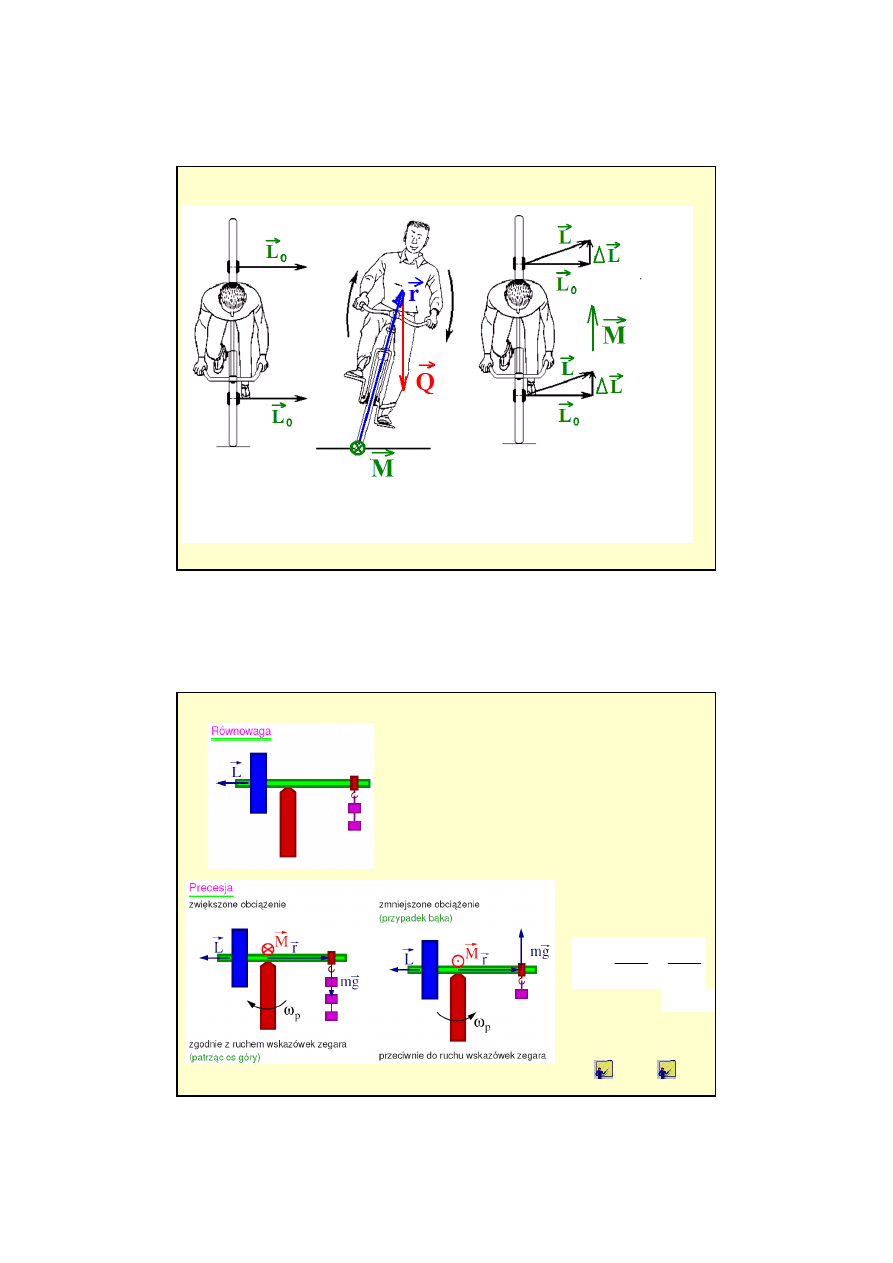
Precesja osi Ziemi spowodowana momentem siły grawitacyjnej
Ziemia nie jest b
ą
kiem swobodnym.
Niejednorodno
ś
ci pola grawitacyjnego w
którym si
ę
porusza (niezerowy moment sił
grawitacji) powoduj
ą
precesj
ę
astronomiczn
ą
wektora momentu p
ę
du (w przybli
ż
eniu
równoległ
ą
do osi obrotu Ziemi
*
). Okres
precesji wynosi ok. 26 000 lat.
Dodatkowo pole grawitacyjne zmienia si
ę
w
czasie (wpływ Ksi
ęż
yca) co powoduje nutacj
ę
.
11
Rower
Ż
yroskop
Je
ś
li
ż
yroskop jest w równowadze przy L = 0 to
b
ę
dzie tak
ż
e w równowadze dla L
≠
0.
Jak zachowa si
ę
ż
yroskop gdy zwi
ę
kszymy lub
zmniejszymy przeciwwag
ę
?
kompas
horyzont
Cz
ę
sto
ść
precesji
(podobnie jak dla
b
ą
ka):
o
90
=
θ
jest proporcjonalna do
odj
ę
tej/ dodanej masy m.
ω
ω
I
mgr
L
mgr
p
=
=

12
Żyroskop - sztuczny horyzont.
UZUPEŁNIENIE – WYJA
Ś
NIENIE DEMONSTRACJI
Wyszukiwarka
Podobne podstrony:
5 bryla sztywna [tryb zgodnosci Nieznany
(Fizyka ćwiczenia Bryła sztywna [tryb zgodności])
1 Bryła Sztywna Quizid 8461 ppt
2012 KU W5 tryb dzienny moodle tryb zgodnosci
(W7a Stale do kszta t na zimno cz I [tryb zgodno ci])
2 Sieci komputerowe 09 03 2013 [tryb zgodności]
Microsoft PowerPoint IP5 klasyfikacje tryb zgodnosci
Microsoft PowerPoint IP tryb zgodnosci
PA2 opis matematyczny [tryb zgodności]
ATMOSFERA [tryb zgodnosci]a id Nieznany
(Rachunkowosc podatkowa wyklad 4 5 [tryb zgodności])
Microsoft PowerPoint IP5 bazydanych tryb zgodnosci
OUN2009 [tryb zgodno
Bankowosc materialy 14 [tryb zgodnosci]
MikroI 9 [tryb zgodnosci]
(5 ja i samoocena (1 ) [tryb zgodności])id 1080
MT st w 06 [tryb zgodności]
cz 1c projektowanie systemow czasu rzeczywistego tryb zgodnosci
więcej podobnych podstron