
Politechnika Poznańska
Poznań, dnia 01.04.2004 r.
Instytut Konstrukcji Budowlanych
Zakład Mechaniki Budowli
Obliczanie ramy metodą przemieszczeń
przemieszczenia podpór
Konsultacje:
Wykonał:
dr inż.
P.
Litewka
Piotr
Siniecki
grupa
III
2003/2004
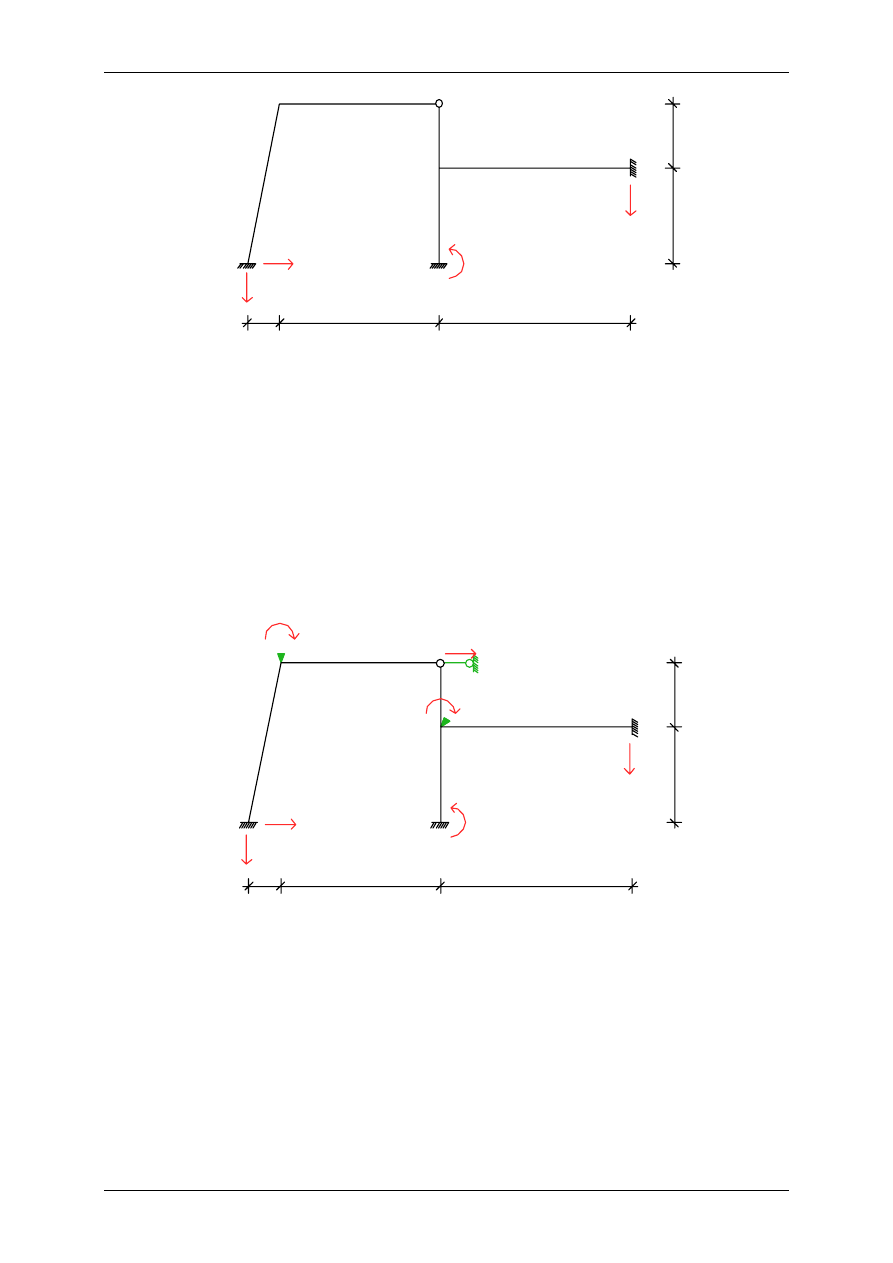
Obliczanie ramy metodą przemieszczeń – przemieszczenia podpór
- 2 -
Piotr Siniecki grupa III
2004-04-01
32
1
5
6
I
0,002
I
1
I
1
I
1
I
2
2
0,002
0,004
0,005
Przyjmuję układ podstawowy:
32
1
5
6
u
2
r
3
I
r
I
1
I
1
I
1
I
2
2
1
0,005
0,004
0,002
0,002
SGN = 3
=
+
⋅
+
⋅
+
⋅
=
+
⋅
+
⋅
+
⋅
=
+
⋅
+
⋅
+
⋅
∆
∆
∆
0
0
0
3
3
33
2
32
1
31
2
3
23
2
22
1
21
1
3
13
2
12
1
11
r
z
r
z
r
z
r
r
z
r
z
r
z
r
r
z
r
z
r
z
r
Ponieważ układ podstawowy jest identyczny jak dla ramy obliczonej od sił zewnętrznych reakcje
r
ik
pozostają takie same pozostaje tylko obliczyć r
i
∆
.
389
,
1
240
220
2
1
2
1
⋅
Ι
=
Ι
Ι
=
Ι
Ι
=
Ι
Ι
=
Ι
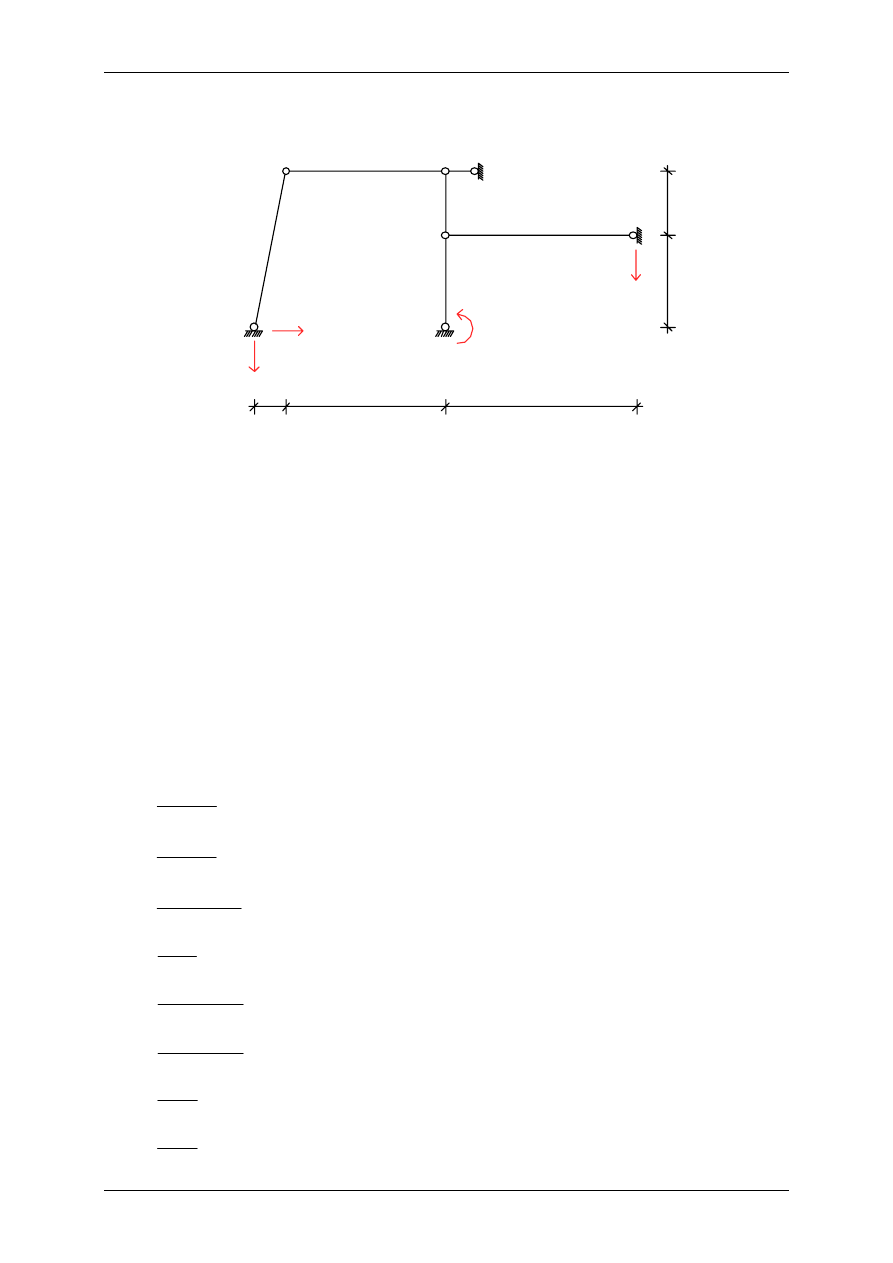
Obliczanie ramy metodą przemieszczeń – przemieszczenia podpór
- 3 -
Piotr Siniecki grupa III
2004-04-01
Łańcuch kinematyczny
1
5
6
32
0,005
Ψ
0,004
12
Ψ
23
Ψ
34
Ψ
35
0
1
2
3
4
5
Ψ
01
0,002
0,002
Kąty obrotu prętów
rad
004
,
0
5
002
,
0
012
)
(
01
)
(
01
−
=
Ψ
=
⋅
Ψ
+
→
∆
∆
0
0
3
534
)
(
35
)
(
35
=
Ψ
=
Ψ
⋅
→
∆
∆
rad
00083333
,
0
005
,
0
6
534
)
(
34
)
(
34
=
Ψ
=
Ψ
⋅
↓
∆
∆
0
0
2
3
532
)
(
23
)
(
23
)
(
35
=
Ψ
=
Ψ
⋅
+
Ψ
⋅
→
∆
∆
∆
rad
00072
,
0
0
5
004
,
0
01235
)
(
12
)
(
12
)
(
01
−
=
Ψ
=
Ψ
⋅
+
Ψ
+
↓
∆
∆
∆
Podstawiając do wzorów transformacyjnych otrzymujemy momenty w stanie
∆
]
[
26097
,
7
)
3
2
(
6
389
,
1
2
]
[
26097
,
7
)
3
2
(
6
389
,
1
2
0
)
(
2
3
]
[
76410
,
3
)
(
5
389
,
1
3
]
[
95257
,
2
)
3
2
(
09902
,
5
2
]
[
95257
,
2
)
3
2
(
09902
,
5
2
)
(
34
)
(
3
)
(
4
43
)
(
34
)
(
4
)
(
3
34
)
(
23
)
(
3
32
)
(
12
)
(
1
12
)
(
01
)
(
0
)
(
1
10
)
(
01
)
(
1
)
(
0
01
kNm
EI
M
kNm
EI
M
EI
M
kNm
EI
M
kNm
EI
M
kNm
EI
M
−
=
⋅
−
+
⋅
⋅
⋅
⋅
=
−
=
⋅
−
+
⋅
⋅
⋅
⋅
=
=
−
⋅
⋅
=
=
−
⋅
⋅
⋅
=
=
⋅
−
+
⋅
⋅
⋅
=
=
⋅
−
+
⋅
⋅
⋅
=
∆
∆
∆
∆
∆
∆
∆
∆
∆
∆
∆
∆
∆
∆
∆
∆
ψ
ϕ
ϕ
ψ
ϕ
ϕ
ψ
ϕ
ψ
ϕ
ψ
ϕ
ϕ
ψ
ϕ
ϕ
]
[
72800
,
16
)
3
2
(
3
2
]
[
36400
,
8
)
3
2
(
3
2
)
(
35
)
(
3
)
(
5
53
)
(
35
)
(
5
)
(
3
35
kNm
EI
M
kNm
EI
M
−
=
⋅
−
+
⋅
⋅
⋅
=
−
=
⋅
−
+
⋅
⋅
⋅
=
∆
∆
∆
∆
∆
∆
ψ
ϕ
ϕ
ψ
ϕ
ϕ
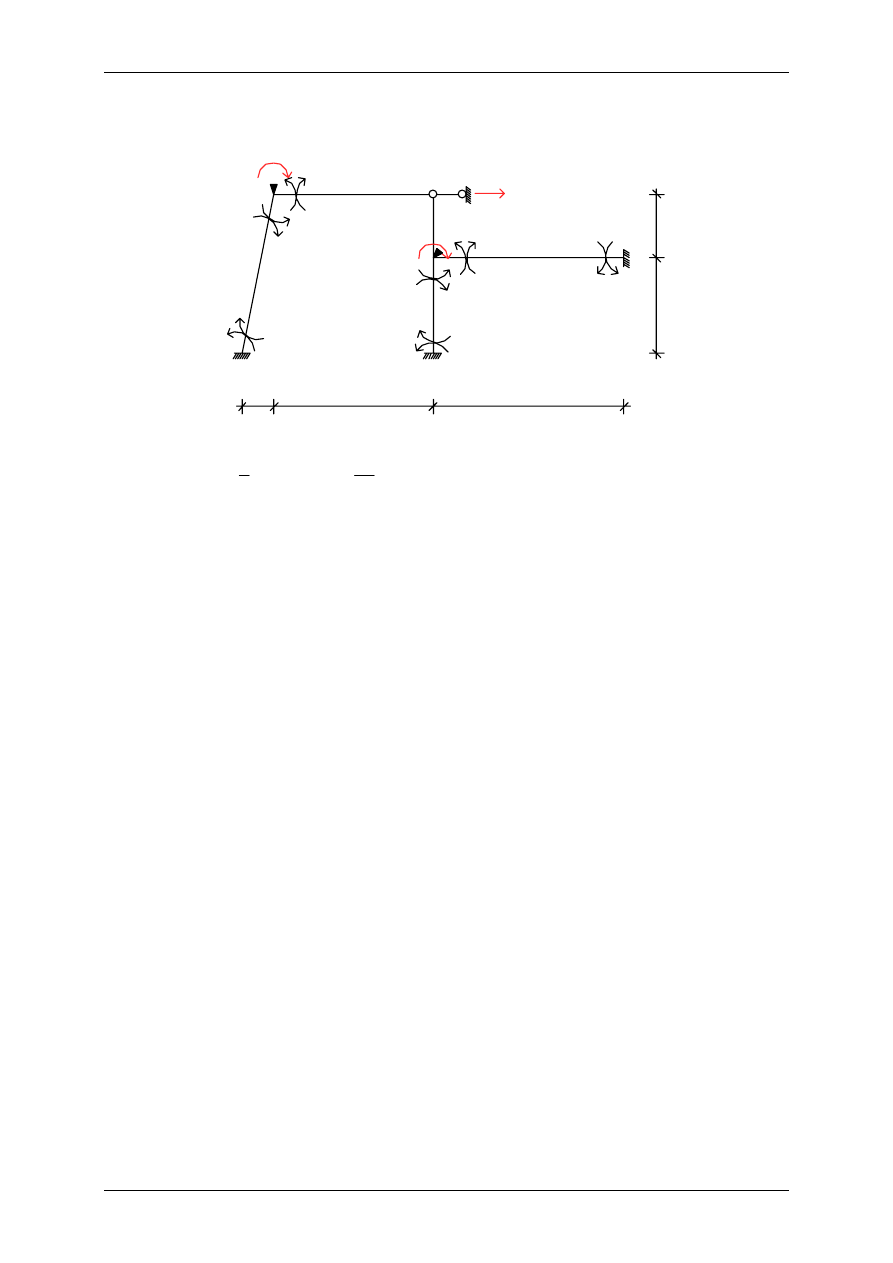
Obliczanie ramy metodą przemieszczeń – przemieszczenia podpór
- 4 -
Piotr Siniecki grupa III
2004-04-01
Stan
∆
32
1
5
6
1∆
2∆
-16,72800
-8,36400
3∆
2,95257
r
3,76410
-7,26097
-7,26097
r
r
2,95257
]
[
62497
,
15
0
)
36400
,
8
(
)
26097
,
7
(
]
[
17667
,
6
0
95257
,
2
76410
,
3
]
[
03046
,
1
0
25
1
76410
,
3
5
1
)
95257
,
2
(
1
3
3
1
1
2
2
kNm
r
r
kNm
r
r
kN
r
r
−
=
=
−
−
−
−
=
=
−
−
−
=
=
−
⋅
+
⋅
+
⋅
∆
∆
∆
∆
∆
−
−
−
∆
Korzystając z poprzednich obliczeń na r
ik
otrzymujemy układ równań:
=
−
⋅
⋅
+
⋅
⋅
−
=
−
⋅
⋅
−
⋅
⋅
+
⋅
⋅
−
=
+
+
⋅
⋅
−
⋅
⋅
0
62497
,
15
75930
,
3
75
,
0
0
0
03046
,
1
75
,
0
47047
,
0
20200
,
0
0
71667
,
6
0
20200
,
0
61786
,
1
3
2
3
2
1
2
1
z
EI
z
EI
z
EI
z
EI
z
EI
z
EI
z
EI
=
⋅
=
⋅
−
=
⋅
38949
,
6
19364
,
11
75398
,
2
3
2
1
z
EI
z
EI
z
EI
Podstawiając wartości do równań momentowych(wzory transformacyjne) z poprzedniej części
projektu oraz uwzględniając momenty od osiadań otrzymujemy.
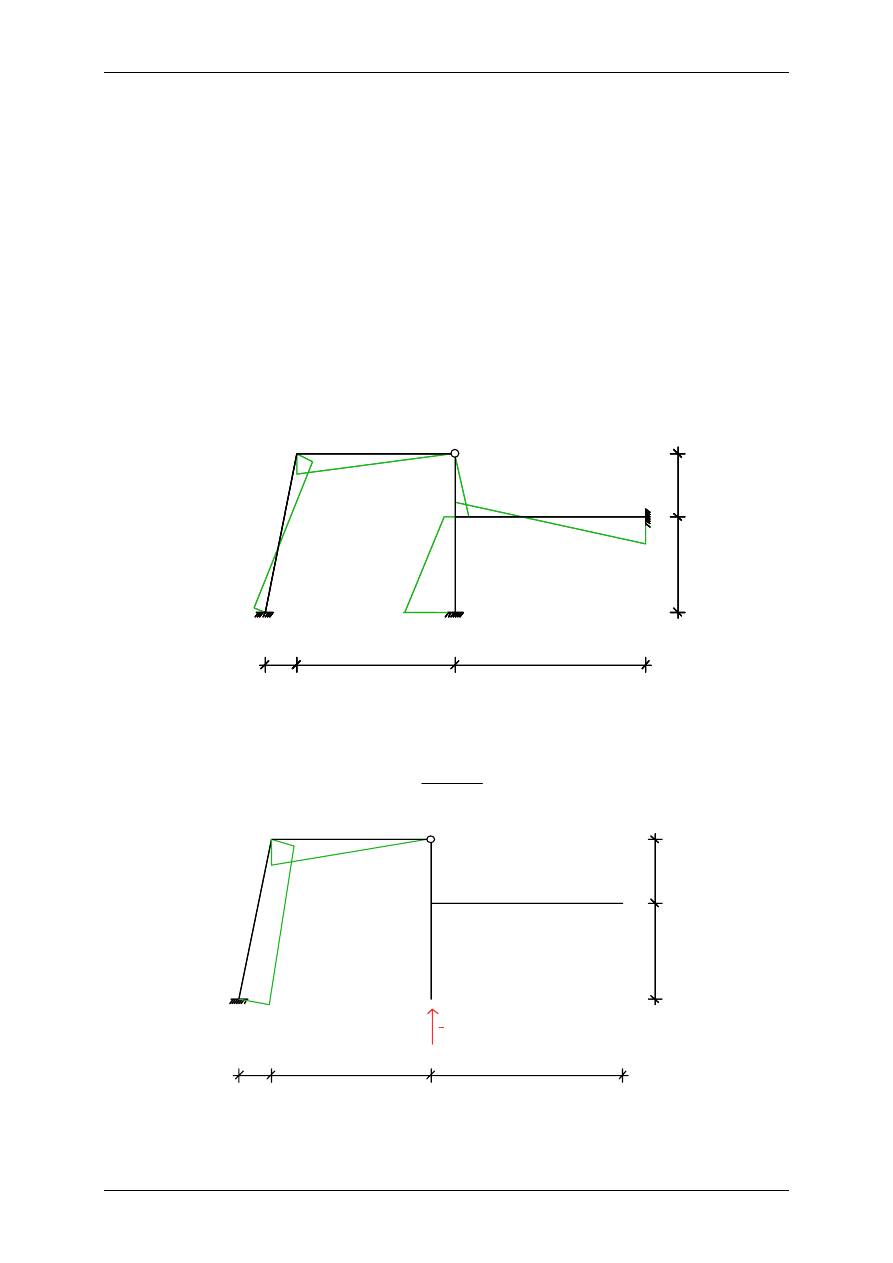
Obliczanie ramy metodą przemieszczeń – przemieszczenia podpór
- 5 -
Piotr Siniecki grupa III
2004-04-01
]
[
46834
,
12
72800
,
16
66667
,
0
]
[
15511
,
0
36400
,
8
33333
,
1
]
[
30264
,
4
26097
,
7
46300
,
0
]
[
34430
,
1
26097
,
7
92600
,
0
]
[
18901
,
1
75
,
0
5
,
1
]
[
84213
,
1
76410
,
3
03334
,
0
83340
,
0
]
[
84213
,
1
95257
,
2
23534
,
0
78446
,
0
]
[
76193
,
0
95257
,
2
23534
,
0
39223
,
0
3
53
3
35
3
43
3
34
2
3
32
2
1
12
2
1
10
2
1
01
kNm
z
EI
M
kNm
z
EI
M
kNm
z
EI
M
kNm
z
EI
M
kNm
z
EI
z
EI
M
kNm
z
EI
z
EI
M
kNm
z
EI
z
EI
M
kNm
z
EI
z
EI
M
−
=
−
⋅
⋅
=
=
−
⋅
⋅
=
−
=
−
⋅
⋅
=
−
=
−
⋅
⋅
=
=
⋅
⋅
−
⋅
⋅
=
=
+
⋅
⋅
+
⋅
⋅
=
−
=
+
⋅
⋅
−
⋅
⋅
=
−
=
+
⋅
⋅
−
⋅
⋅
=
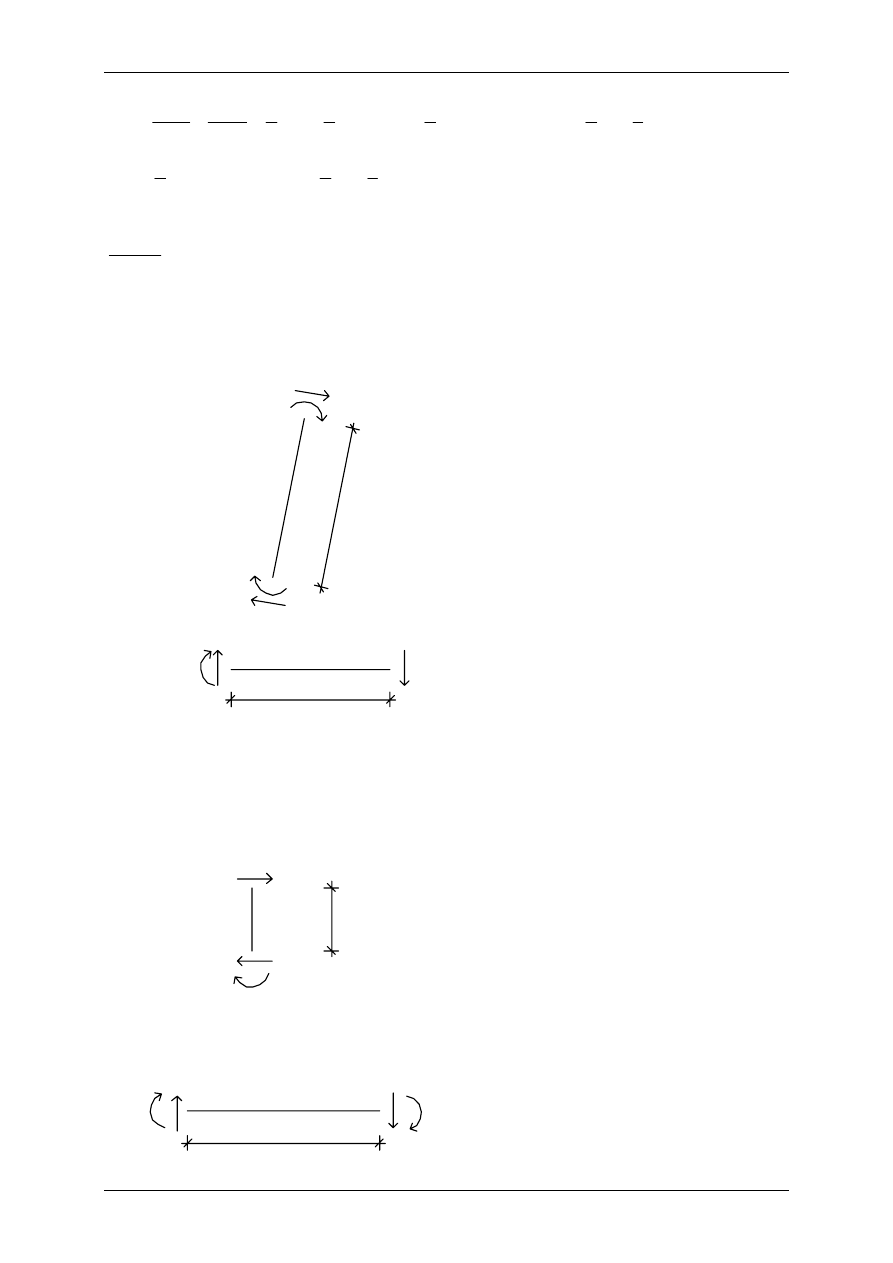
Wykres momentów [kNm]
32
1
5
6
32
1
5
6
32
1
5
6
32
1
5
6
1,18901
1,34430
0,15511
4,30264
12,46834
1,84213
0,76193
1,18901
1,34430
0,15511
4,30264
12,46834
1,84213
0,76193
Kontrola kinematyczna:
∆
⋅
−
⋅
=
⋅
∑∫
−
_
1
_
1
R
dx
EI
M
M
N
δ
3232
1
5
6
6
5
1
Obliczanie ramy metodą przemieszczeń – przemieszczenia podpór
- 6 -
Piotr Siniecki grupa III
2004-04-01
(
)
m
8
10
7
004
,
0
1
5
3
1
6
3
2
76192
,
0
09902
,
5
2
1
6
3
1
5
3
2
84213
,
1
09902
,
5
2
1
84213
,
1
3
2
5
5
2
1
389
,
1
1
6273
1
1
−
−
⋅
=
⋅
−
⋅
+
⋅
⋅
⋅
⋅
−
−
⋅
+
⋅
⋅
⋅
⋅
+
⋅
⋅
⋅
⋅
⋅
⋅
=
⋅
δ
Błąd procentowy:
%
002
,
0
%
100
004
,
0
10
7
8
=
⋅
⋅
−
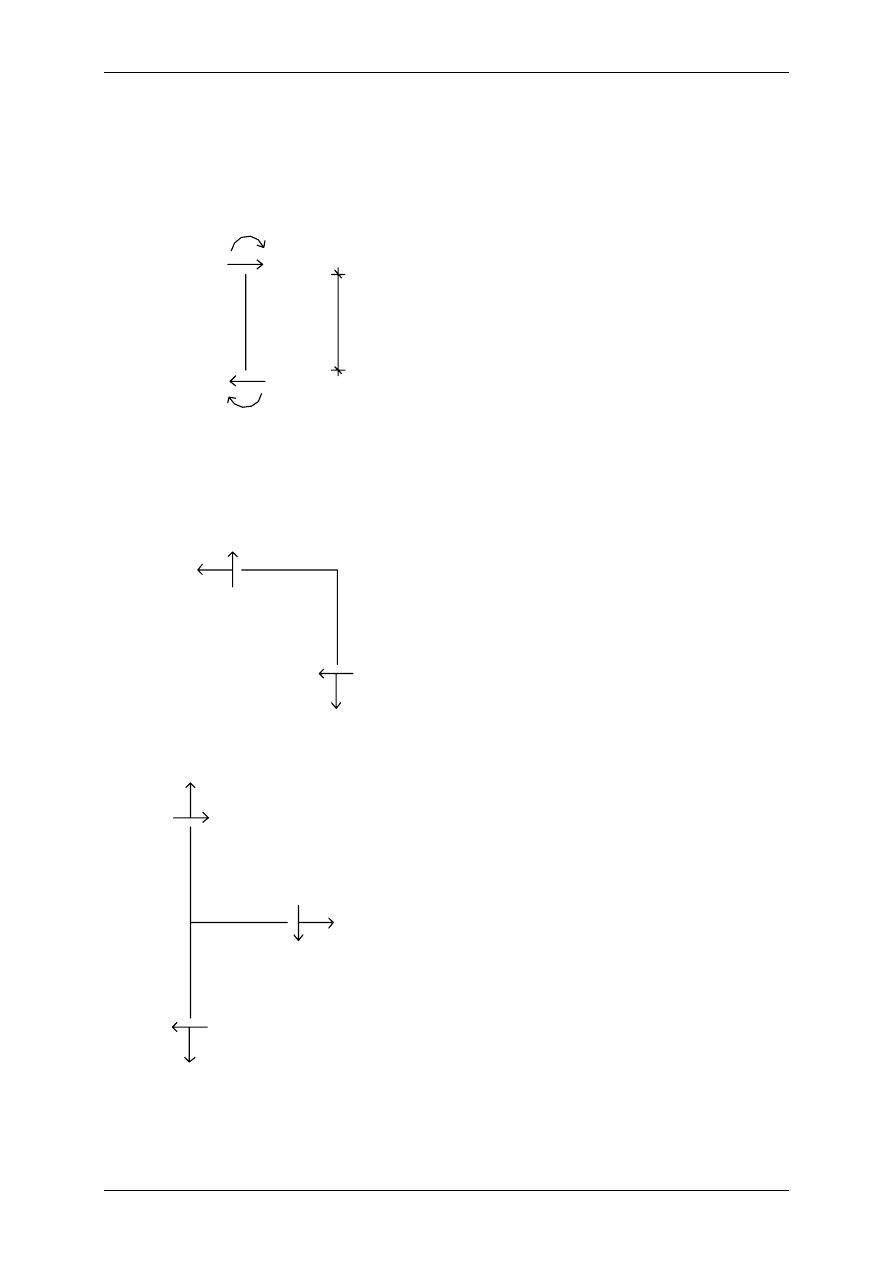
Obliczanie sił tnących:
5
,
0
9
9
0
2
-1,84123
-0,76193
T
10
T
01
]
[
51070
,
0
0
09902
,
5
76193
,
0
84213
,
1
0
10
10
0
kN
T
T
M
=
=
⋅
+
−
−
=
∑
]
[
51070
,
0
0
09902
,
5
84213
,
1
76193
,
0
0
01
01
1
kN
T
T
M
=
=
⋅
+
−
−
=
∑
5
1,842131
T
21
T
12
]
[
36843
,
0
0
5
84213
,
1
0
21
21
1
kN
T
T
M
−
=
=
⋅
+
=
∑
]
[
36843
,
0
0
5
84213
,
1
0
12
12
2
kN
T
T
M
−
=
=
⋅
+
=
∑
2
1,18901
T
32
23
T
]
[
59451
,
0
0
18901
,
1
2
0
23
23
3
kN
T
T
M
−
=
=
+
⋅
=
∑
]
[
59451
,
0
0
18901
,
1
2
0
32
32
2
kN
T
T
M
−
=
=
+
⋅
=
∑
6
T
T
34
43
-4,30264
-1,34430
]
[
94116
,
0
0
30264
,
4
34430
,
1
6
0
43
43
3
kN
T
T
M
=
=
−
−
⋅
=
∑
Obliczanie ramy metodą przemieszczeń – przemieszczenia podpór
- 7 -
Piotr Siniecki grupa III
2004-04-01
]
[
94116
,
0
0
30264
,
4
34430
,
1
6
0
34
34
4
kN
T
T
M
=
=
−
−
⋅
=
∑
3
-12,46834
0,15511
T
T
35
53
]
[
10441
,
4
0
469834
,
12
15511
,
0
3
0
53
53
3
kN
T
T
M
=
=
−
+
⋅
=
∑
]
[
10441
,
4
0
46834
,
12
15511
,
0
3
0
35
35
5
kN
T
T
M
=
=
−
+
⋅
=
∑
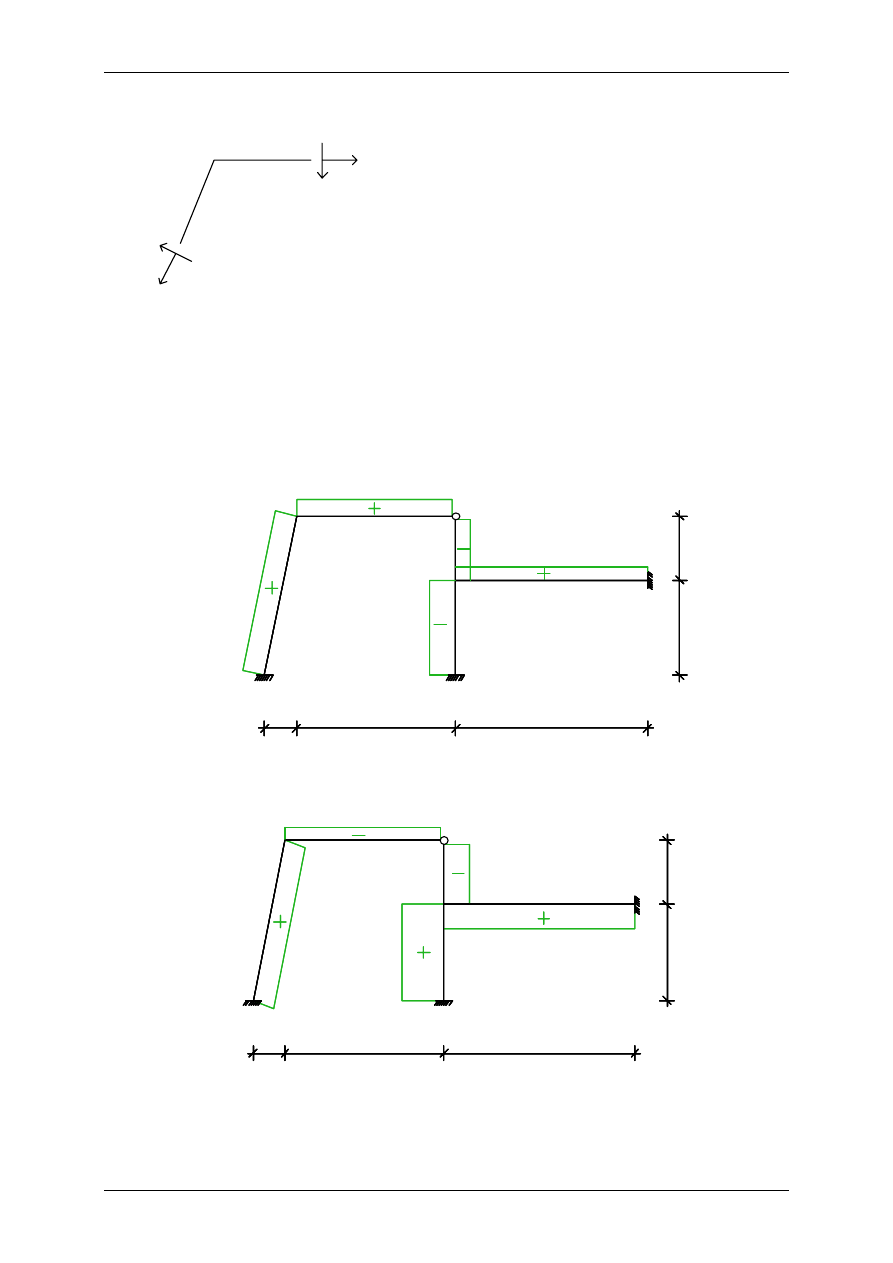
Obliczenie sił normalnych:
N
N
23
21
-0,59451
-0,36843
]
[
59451
,
0
0
)
59451
,
0
(
0
21
21
kN
N
N
X
=
=
−
−
−
=
∑
]
[
36843
,
0
0
)
36843
,
0
(
0
23
23
kN
N
N
Y
−
=
=
−
+
−
=
∑
N
N
N
32
34
35
-0,59451
0,94116
4,10441
]
[
69892
,
4
0
10441
,
4
59451
,
0
0
34
34
kN
N
N
X
=
=
−
−
=
∑
]
[
30959
,
1
0
36843
,
0
94116
,
0
0
35
35
kN
N
N
Y
−
=
=
−
−
−
=
∑
Obliczanie ramy metodą przemieszczeń – przemieszczenia podpór
- 8 -
Piotr Siniecki grupa III
2004-04-01
N
10
N
12
-0,36843
0,51070
]
[
47787
,
0
0
cos
51070
,
0
)
36843
,
0
(
sin
0
10
10
kN
N
N
Y
=
=
⋅
+
−
−
⋅
−
=
∑
α
α
]
[
59450
,
0
0
cos
47784
,
0
sin
51070
,
0
0
12
12
kN
N
N
X
=
=
⋅
−
⋅
−
=
∑
α
α
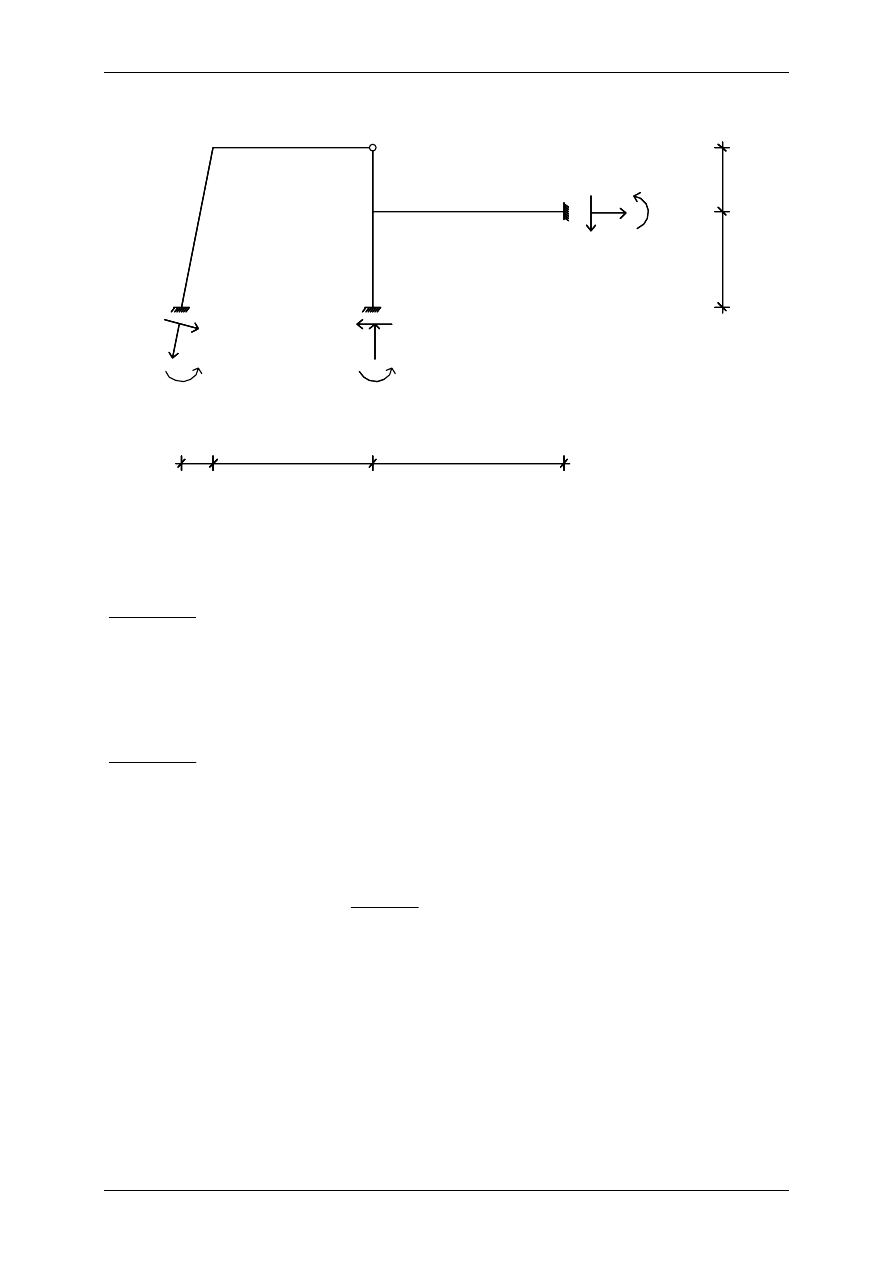
Wykres sił normalnych [kN]
32
1
5
6
32
1
5
6
32
1
5
6
32
1
5
6
-1,30959
4,69892
-0,36843
0,59450
0,47787
-1,30959
4,69892
-0,36843
0,59450
0,47787
Wykres sił tnących [kN]
32
1
5
6
32
1
5
6
32
1
5
6
32
1
5
6
0,51070
-0,36843
-0,59451
0,94116
4,10441
0,51070
-0,36843
-0,59451
0,94116
4,10441
Obliczanie ramy metodą przemieszczeń – przemieszczenia podpór
- 9 -
Piotr Siniecki grupa III
2004-04-01
Sprawdzenie statyczne:
1
5
6
32
1
5
6
32
1
5
6
32
1
5
6
32
I
I
1
I
1
I
1
I
2
2
0,51070
0,47787
0,76193
12,46834
4,10441
1,30959
0,94116
4,69892
4,30264
I
I
1
I
1
I
1
I
2
2
0,51070
0,47787
0,76193
12,46834
4,10441
1,30959
0,94116
4,69892
4,30264
I
I
1
I
1
I
1
I
2
2
0,51070
0,47787
0,76193
12,46834
4,10441
1,30959
0,94116
4,69892
4,30264
I
I
1
I
1
I
1
I
2
2
0,51070
0,47787
0,76193
12,46834
4,10441
1,30959
0,94116
4,69892
4,30264
kN
X
00000793
,
0
cos
47787
,
0
sin
51070
,
0
10441
,
4
69892
,
4
0
=
⋅
−
⋅
−
−
=
∑
α
α
%
0002
,
0
%
100
69892
,
4
00000793
,
0
=
⋅
kN
Y
00000128
,
0
sin
47787
,
0
cos
51070
,
0
30959
,
1
94116
,
0
0
−
=
⋅
−
⋅
+
+
−
=
∑
α
α
%
0001
,
0
%
100
30959
,
1
00000128
,
0
=
⋅
kNm
M
A
00023
,
0
3
69892
,
4
12
94116
,
0
30264
,
4
6
30959
,
1
46834
,
12
76193
,
0
0
=
⋅
+
⋅
+
−
⋅
−
−
−
=
∑
%
002
,
0
%
100
09676
,
14
00023
,
0
=
⋅
Wyszukiwarka
Podobne podstrony:
Obliczenia ramy Metodą przemieszczeń projekt38
OBLICZENIE RAMY METODĄ PRZEMIESZCZEŃOD TEMPERATURY projekt43
OBLICZENIE RAMY METODĄ PRZEMIESZCZEŃ OD OSIADANIA PODPÓR projekt42
Obliczenia ramy Metodą przemieszczeń temperatura projekt39
Obliczanie ramy metodą przemieszczeń obliczenie momentów oraz sił tnących korzystając z równania róż
Obliczenia ramy Metodą przemieszczeń temperatura projekt39
Obliczanie ramy metodą przemieszczeń
Metoda przemieszczen projekt4
Obliczanie ram metodą przemieszczeń wersja komputerowa
ROZWIĄZANIE RAMY METODĄ PRZEMIESZCZEŃ
szablon Obliczeniowy, Uczelnia, PKM, Sprawka i Projekty
Metoda przemieszczen projekt
Metoda przemieszczen projekt3 i Nieznany
OBLICZENIE WIĄZARA PŁATWIOWO KLESZCZOWEGO, Projekt domku
więcej podobnych podstron