Projekt „Informatyka – inwestycją w przyszłość”
współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego
Biuro Projektu:
Politechnika Radomska im. Kazimierza Pułaskiego
26-600 Radom, ul. Chrobrego 27, pok. nr 44, tel. 48 361 78 50, 48 361 70 81
www.zamawiane.pr.radom.pl; e-mail: informatyka@pr.radom.pl
Zajęcia wyrównawcze z fizyki -Zestaw 3
dr M.Gzik-Szumiata
Kinematyka,cz.2. Ruchy dwuwymiarowe: rzut poziomy, rzut ukośny, Prędkość, przyspieszenie, tor
ruchu, zasięg. Ruch po okręgu. Elementy szczególnej teorii względności.
Teoria.
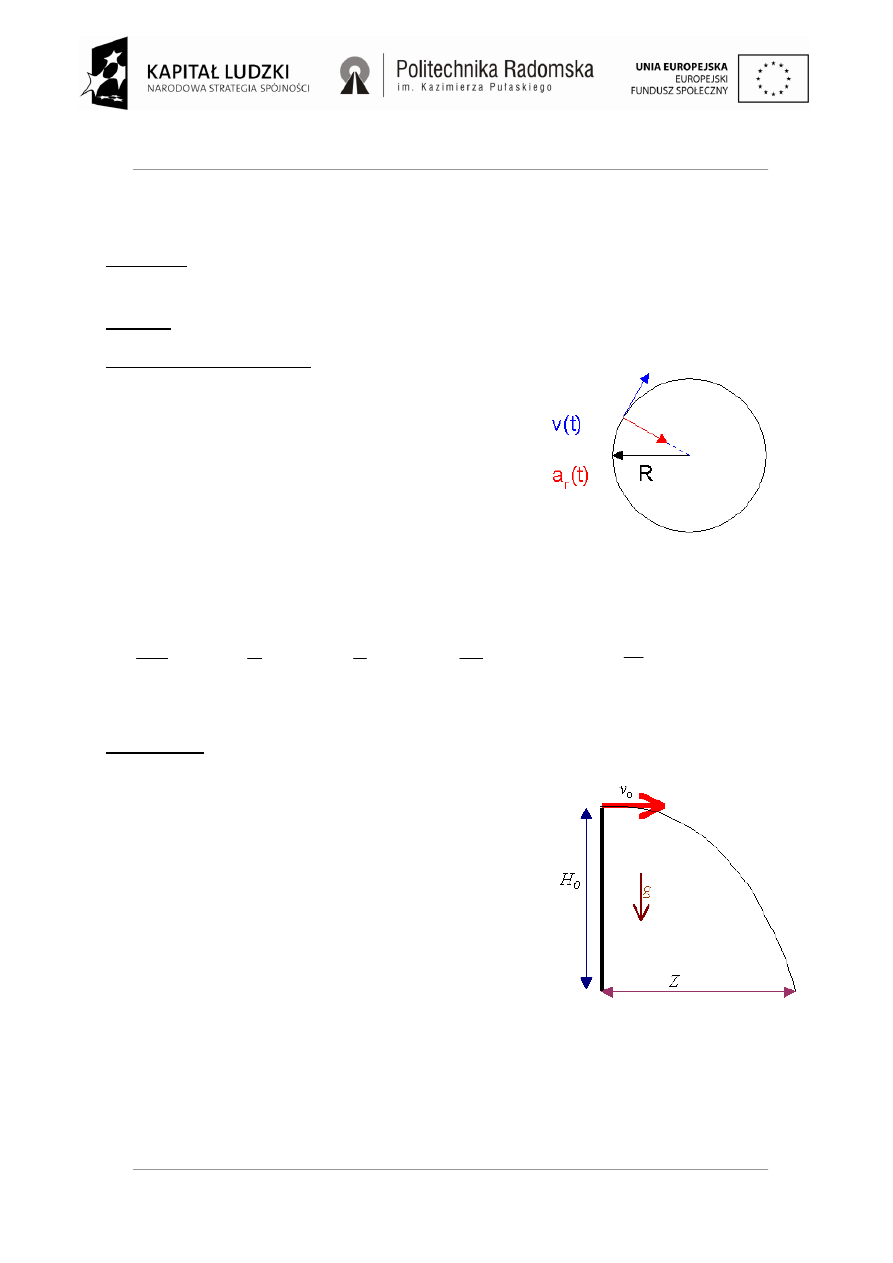
Ruch jednostajny po okręgu jest to ruch odbywający się po
torze w kształcie okręgu ze stałą wartością prędkości.
v
-prędkość
a
r
-przyspieszenie dośrodkowe
-prędkość kątowa
T
-okres ruchu po okręgu
f
-częstotliwość
T
R
v
2
R
v
T
f
1
f
T
2
2
R
v
a
r
2
Rzut poziomy
W rzucie poziomym mamy do czynienia z lotem ciała
wyrzuconego z pewnej wysokości H
0
nad poziomem zerowym.
Ciału jest nadawana pozioma prędkość początkowa o wartości v
0
.
Dzięki takiemu nadaniu prędkości przesuwa się ono cały czas w
poziomie. Jednocześnie jednak siła grawitacji zmienia pionowe
położenie ciała. W efekcie w pionie będzie ono opadać ruchem
jednostajnie przyspieszonym.
W efekcie złożeniu tych dwóch ruchów :
- poziomego: jednostajnego
- pionowego: jednostajnie przyspieszonego z przyspieszeniem
wynoszącym g
ciało porusza się po paraboli, (jeśli nie uwzględniamy oporu powietrza), by po pewnym czasie uderzyć
w ziemię.
Projekt „Informatyka – inwestycją w przyszłość”
współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego
Biuro Projektu:
Politechnika Radomska im. Kazimierza Pułaskiego
26-600 Radom, ul. Chrobrego 27, pok. nr 44, tel. 48 361 78 50, 48 361 70 81
www.zamawiane.pr.radom.pl; e-mail: informatyka@pr.radom.pl
Wysokość na jakiej znajduje się ciało po czasie t:
2
2
gt
H
h
o
Współrzędna x w funkcji czasu:
t
v
x
o
Prędkość w rzucie poziomym
Wartość prędkości poziomej
v
x
=
v
o
= const
Wartość prędkości pionowej
v
y
= -
g·t
Wartość prędkości całkowitej
Prędkość w momencie
uderzenia o ziemię:
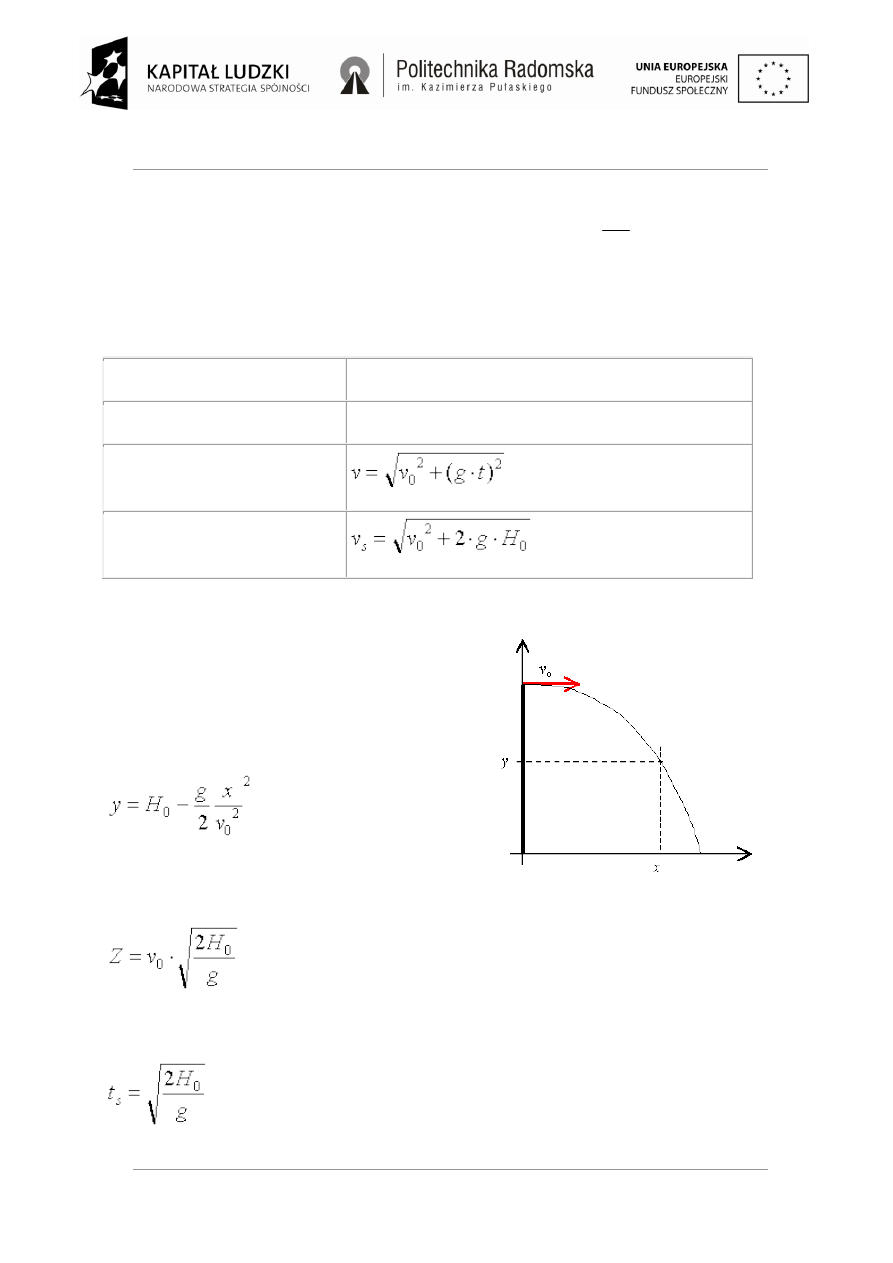
Tor rzutu poziomego
Tor rzutu poziomego ma kształt paraboli skierowanej
ramionami w dół.
Równanie toru rzutu poziomego:
Zasięg rzutu poziomego (odległość przebyta w
poziomie do momentu upadku)
Czas jaki upływa od momentu wyrzucenia do momentu upadku (uderzenia o ziemię):
Projekt „Informatyka – inwestycją w przyszłość”
współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego
Biuro Projektu:
Politechnika Radomska im. Kazimierza Pułaskiego
26-600 Radom, ul. Chrobrego 27, pok. nr 44, tel. 48 361 78 50, 48 361 70 81
www.zamawiane.pr.radom.pl; e-mail: informatyka@pr.radom.pl
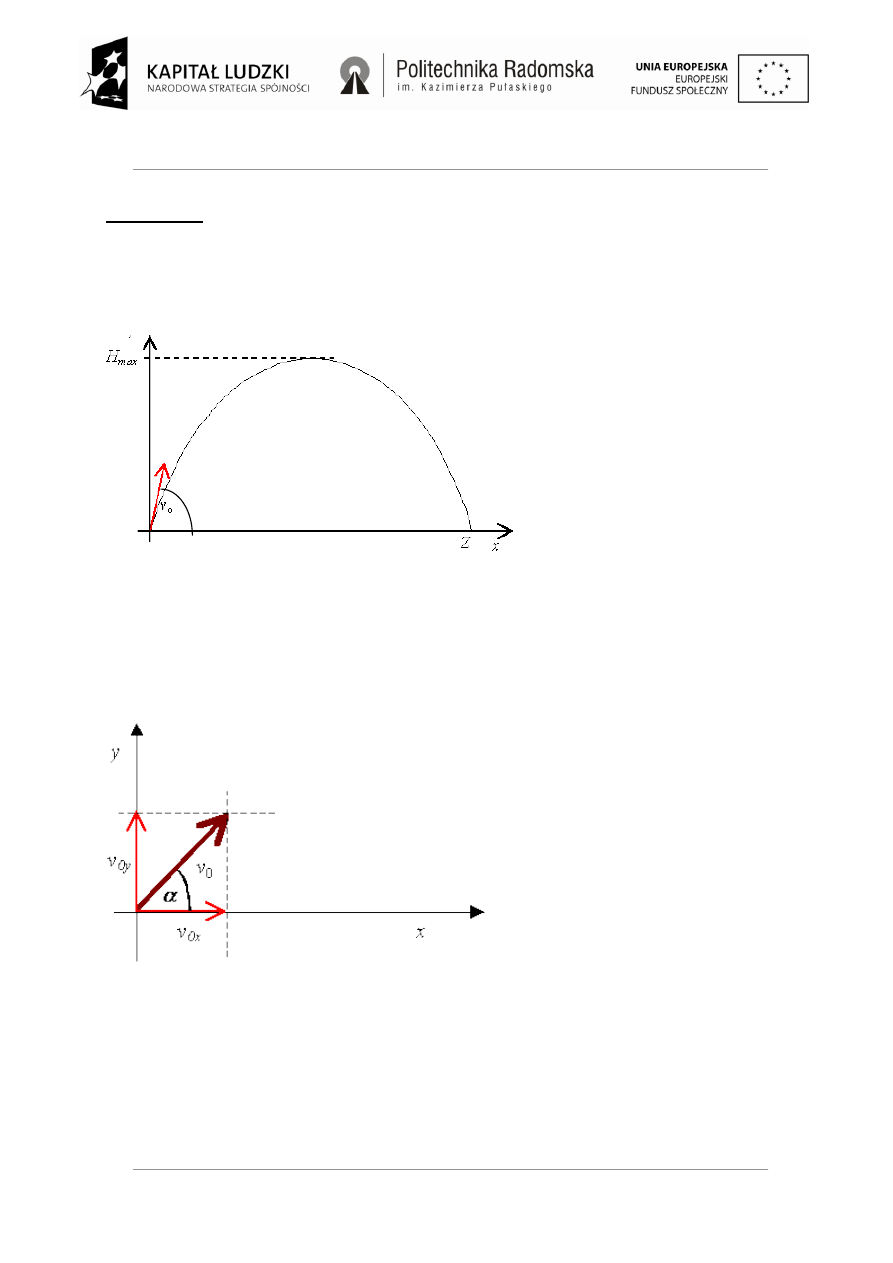
Rzut ukośny
W rzucie ukośnym mamy do czynienia z lotem ciała wyrzuconego z poziomu zerowego (y
0
= 0). Ciału
jest nadawana prędkość o wartości v
0
, skierowana pod kątem α do poziomu. Ciało porusza się po
łuku paraboli, by po pewnym czasie uderzyć w ziemię.
Odległość jaką przebywa ciało w
poziomie do momentu upadku na
poziom początkowy nazwiemy
zasięgiem (Z) rzutu ukośnego.
W przypadku gdy nie musimy uwzględniać oporu powietrza, torem ruchu ciała jest parabola. Ruch
ciała rozkłada się wtedy na dwa ruchy prostsze:
ruch w poziomie (współrzędna X-owa) – odbywa się ze stałą prędkością o wartości
składowej poziomej prędkości początkowej
v
0X
ruch w pionie (współrzędna Y-owa) – jest w istocie rzutem pionowym, czyli ruchem
jednostajnie zmiennym z prędkością początkową równą składowej pionowej
v
0Y
.
Wzory opisujące rzut ukośny
Prędkość pozioma v
x
(w dowolnej chwili czasu t):
v
x
= v
0x
= const
v
x
= v
0
·cos α
Projekt „Informatyka – inwestycją w przyszłość”
współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego
Biuro Projektu:
Politechnika Radomska im. Kazimierza Pułaskiego
26-600 Radom, ul. Chrobrego 27, pok. nr 44, tel. 48 361 78 50, 48 361 70 81
www.zamawiane.pr.radom.pl; e-mail: informatyka@pr.radom.pl
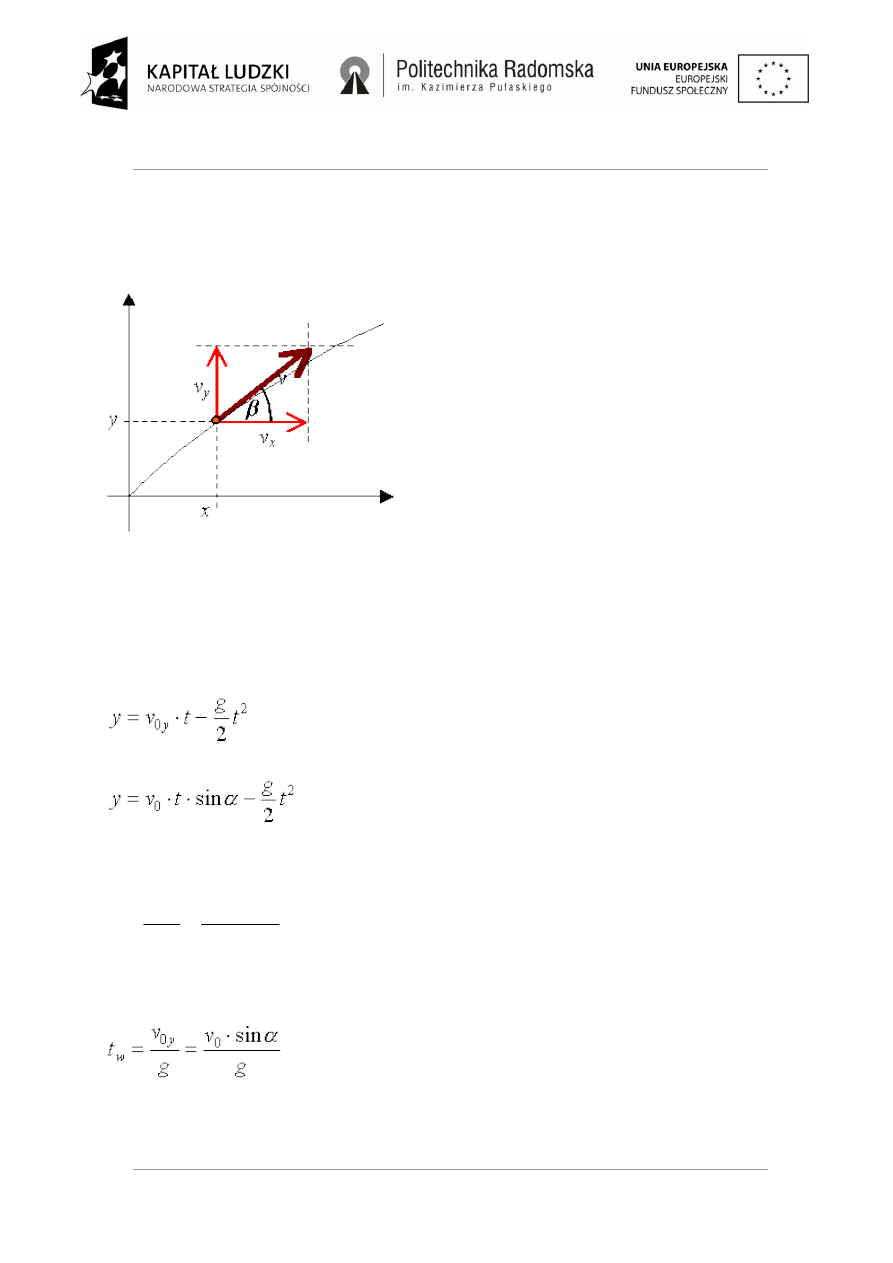
Prędkość pionowa v
y
po czasie t:
v
y
= v
0
·sin α - g·t
Odległość pozioma przebyta w poziomie po czasie t:
x = v
ox
·t = v
0
·t·cos α
Wysokość na jakiej znajduje się ciało po czasie t:
Czas lotu do momentu upadku na poziom początkowy:
g
v
g
v
t
y
c
sin
2
2
0
0
Czas wznoszenia do osiągnięcia maksymalnej wysokości:
t
w
= ½ t
c.
Projekt „Informatyka – inwestycją w przyszłość”
współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego
Biuro Projektu:
Politechnika Radomska im. Kazimierza Pułaskiego
26-600 Radom, ul. Chrobrego 27, pok. nr 44, tel. 48 361 78 50, 48 361 70 81
www.zamawiane.pr.radom.pl; e-mail: informatyka@pr.radom.pl
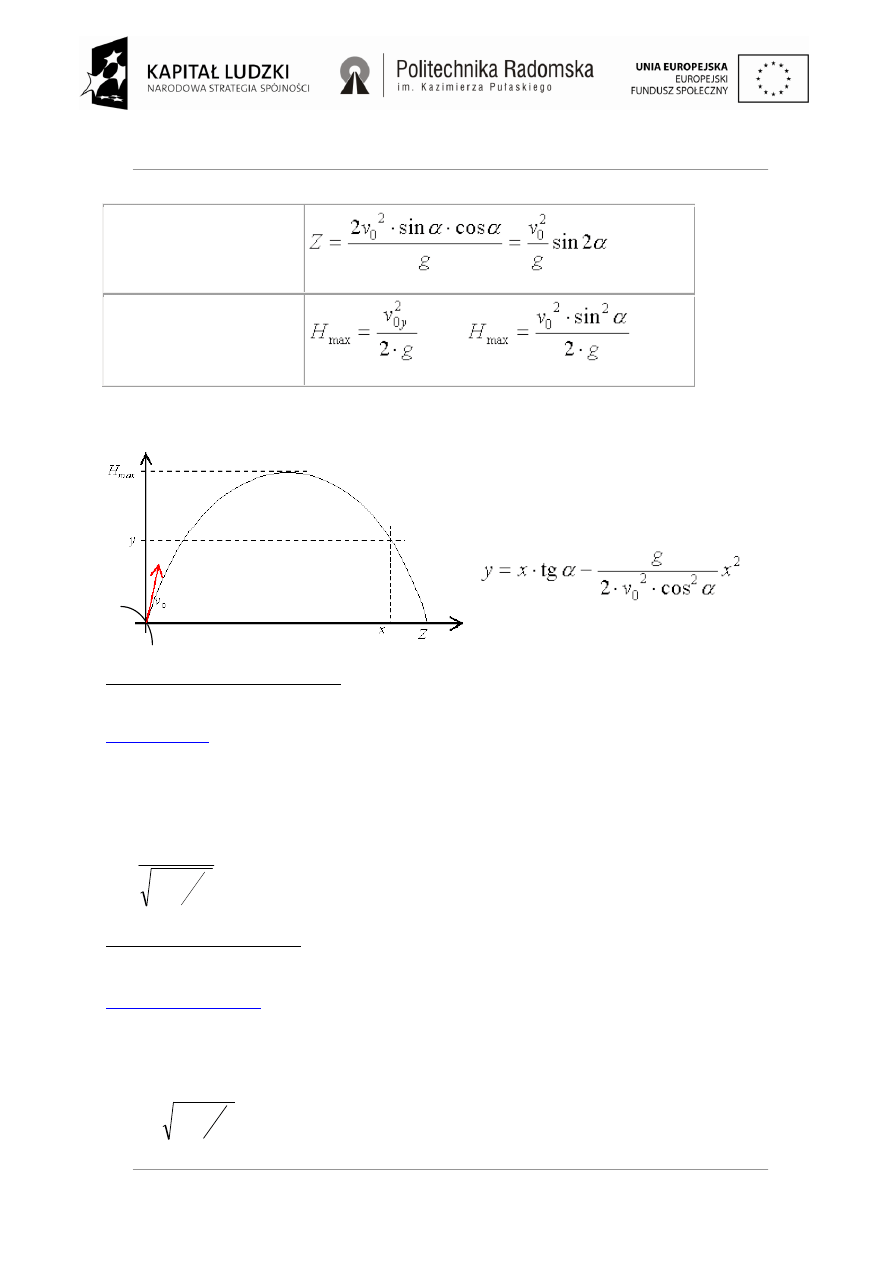
Zasięg rzutu ukośnego :
Maksymalna osiągnięta
wysokość:
Tor rzutu ukośnego ma kształt paraboli skierowanej ramionami w dół
Równanie toru rzutu ukośnego
Szczególna teoria względności –podstawowe wzory.
Dylatacja czasu
— czas jaki mija pomiędzy dwoma zdarzeniami nie jest jednoznacznie określony, lecz
zależy od obserwatora. Czas trwania zjawiska, zachodzącego w pewnym punkcie przestrzeni,
obserwowany z układu poruszającego się względem tego punktu, czyli
t
jest dłuższy niż czas trwania
tego zjawiska w układzie odniesienia, w którym punkt ten spoczywa, czyli
o
t
.
2
2
1
c
v
t
t
o
Względność jednoczesności — dwa zdarzenia określone przez jednego obserwatora jako
jednoczesne, mogą nie być jednoczesne dla innego obserwatora.
Kontrakcja przestrzeni
— odległości między punktami zależą od układu odniesienia. Wszystkie
poruszające się przedmioty obserwujemy jako krótsze. Zjawisko prowadzi do paradoksu drabiny o
długości większej niż długość stodoły, która zmieści się w niej w całości, jeżeli będzie poruszała się
odpowiednio szybko.
2
2
1
c
v
L
L
o
Projekt „Informatyka – inwestycją w przyszłość”
współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego
Biuro Projektu:
Politechnika Radomska im. Kazimierza Pułaskiego
26-600 Radom, ul. Chrobrego 27, pok. nr 44, tel. 48 361 78 50, 48 361 70 81
www.zamawiane.pr.radom.pl; e-mail: informatyka@pr.radom.pl
o
L
-długość przedmiotu zmierzona w układzie odniesienia, w którym ten przedmiot spoczywa
L
-długość przedmiotu zmierzona w układzie odniesienia, w którym ten przedmiot porusza się
Wartości innych wielkości fizycznych takich jak siła, pęd, przyspieszenie, natężenie pola elektrycznego
zależą od obserwatora.
Nowa reguła składania prędkości — prędkości o dużych wartościach, stanowiących zauważalny
ułamek prędkości światła nie „dodają się” w sposób, do którego jesteśmy przyzwyczajeni.
Przykładowo: jeżeli rakieta oddala się z prędkością 2/3 prędkości światła w stosunku do obserwatora
i rakieta wysyła pocisk z prędkością 2/3 prędkości światła w stosunku do rakiety, obserwator nie
zanotuje prędkości (2/3 + 2/3 = 4/3 prędkości światła) przewyższającej prędkość światła. W tym
przykładzie, obserwator widziałby pocisk poruszający się z szybkością 12/13 prędkości światła.
Podobnie, przy dwóch strumieniach cząstek poruszających się z prędkością bliską światłu – jedne
emitowane na lewo od źródła, drugie na prawo – z perspektywy jednych cząstek drugie nie będą
uciekały szybciej niż światło. Żaden obiekt nie może poruszać się bowiem z prędkością większą (ani
równą, dla obiektów materialnych) od prędkości światła.
Jeżeli obserwator S, widzi ciało poruszające się wzdłuż osi x, zgodnie z jej zwrotem, z
prędkością u , obserwator S' porusza się względem niego z prędkością v w tym samym
kierunku x, to prędkość u' tego ciała określona przez obserwatora S' wyniesie:
Prędkość tę dla obserwatora S można wyrazić wzorem
Z tego prawa dodawania prędkości wynika, że gdy w jednym układzie ciało porusza się z
prędkością u = c, to w drugim układzie poruszającym się z prędkością v ciało nadal poruszać
się będzie z prędkością c.
Masa jest równoważna energii
, a związek między tymi wielkościami opisuje wzór E = mc
2
.
Zwiększenie energii układu zwiększa jego masę, zmniejszenie energii powoduje zmniejszenie masy. I
odwrotnie ubytek masy oznacza ubytek energii układu (Deficyt masy).
2
mc
E
Zależność masy od prędkości:
o
m
-masa spoczynkowa, m-masa ciała w układzie, w którym ono się porusza.
2
2
1
c
v
m
m
o