WOJSKOWA AKADEMIA TECHNICZNA

im. Jarosława Dąbrowskiego

WYDZIAŁ CYBERNETYKI

Metody informatycznego wspomagania

decyzji

Autor pracy:
Łukasz Okła

Prowadzący:
dr Jarosław Olejniczak

1. Zadanie nr 2.

1.1. Treść zadania.

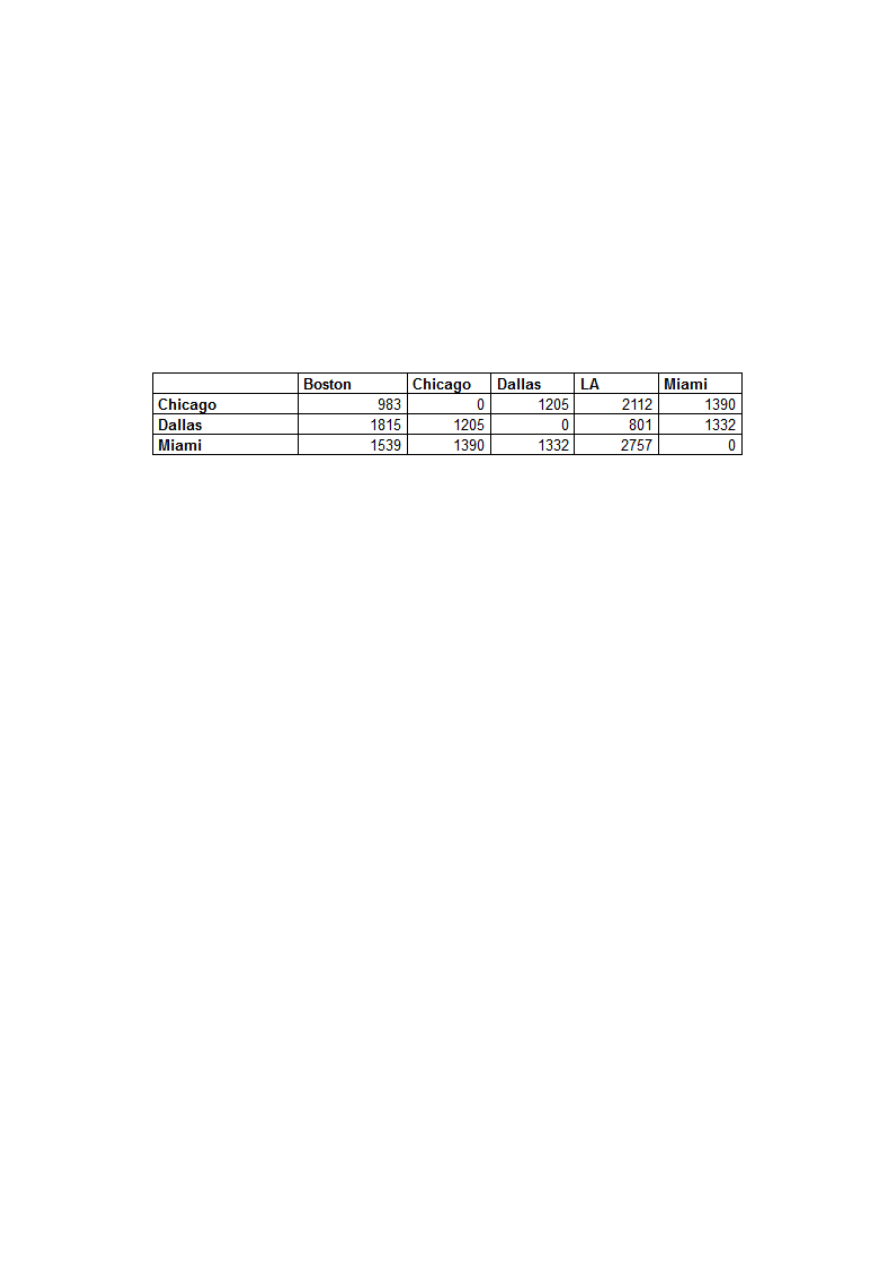
W zamieszczonej niżej tabeli podane są odległości między Bostonem, Chicago,

Dallas, Los Angeles i Miami. Każde z tych miast potrzebuje 40000 kilowatogodzin

(kwh) energii. Chicago, Dallas i Miami są w stanie wyprodukować 70000 kwh.

Załóżmy, przesłanie 1000 kwh na odległość 100 mil kosztuje 4,00 dolary. Skąd należy

wysłać energię, aby zminimalizować koszt zaspokojenia potrzeb każdego miasta?

1.2. Rozwiązanie zadania.

Podgląd konsoli:

library(lpSolve)

library(RODBC)

setwd("D:/")

dane <- odbcConnectExcel("koszty.xls")

koszty <- sqlQuery(dane, "select * from [Arkusz1$]")

koszty=as.matrix(koszty)

row.signs <- rep ("<=", 3)

row.rhs <- c(70000,70000,70000)

col.signs <- rep (">=", 5)

col.rhs <- c(40000,40000,40000,40000,40000)

lp.transport (koszty,"min",row.signs,row.rhs,col.signs,col.rhs)

lp.transport (koszty,"min",row.signs,row.rhs,col.signs,col.rhs)$solution

Dane, które znajdują się w pliku koszty.xls zostały zapisane w postaci kosztów dla

każdego z miast, jaki zostanie poniesiony podczas transportu energii (według tabelki
powyżej):

a1

a2

a3

a4

a5

393200

0

482000

844800

556000

726000

482000

0

320400

532800

615600

556000

532800 1102800

0

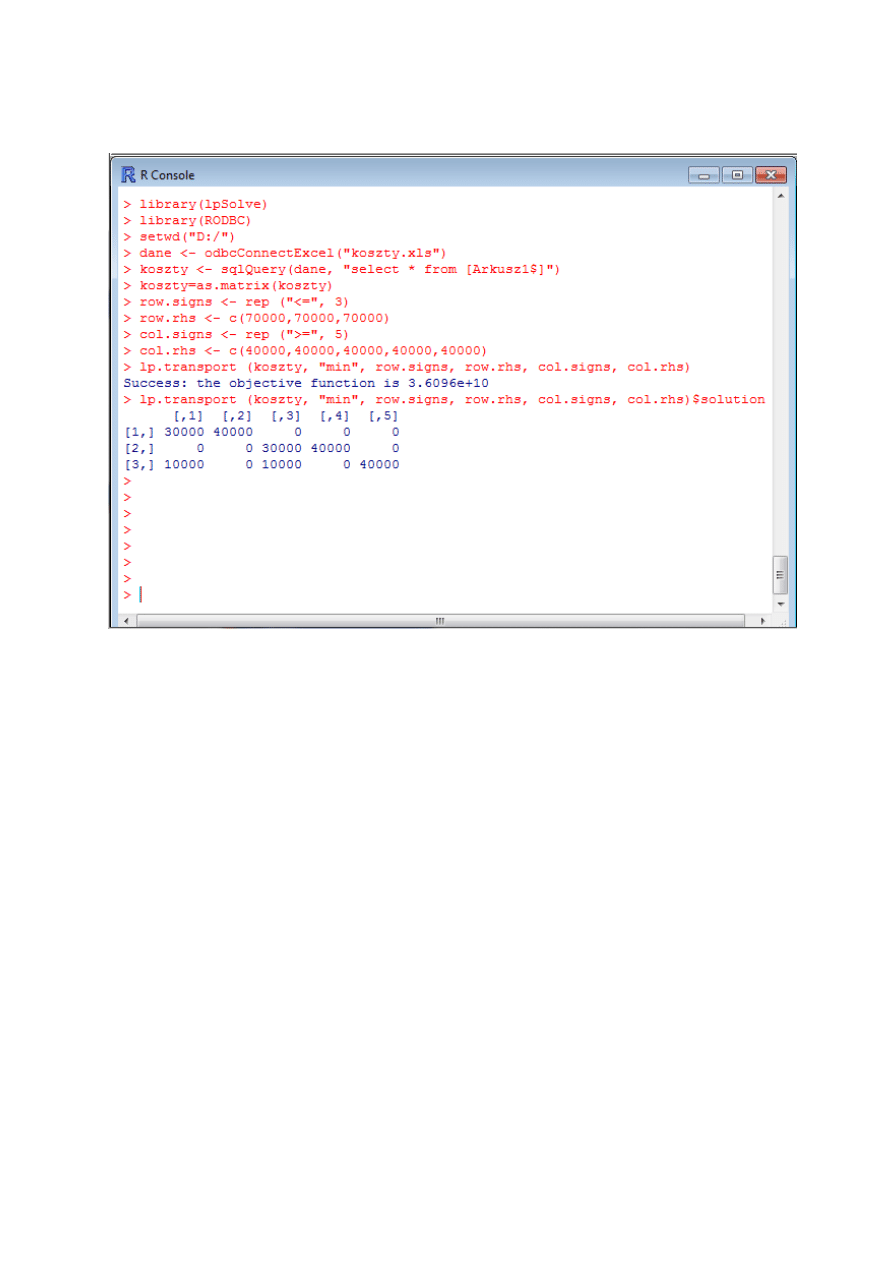
Zrzuty z konsoli przedstawiają się następująco:

1.3. Wnioski z zadania.

Aby koszty poniesione podczas transportu energii były najmniejsze, należy ją

przesyłać w następujący sposób:



Boston pobiera 30 tys. kwh energii od Chicago i 10 tys. kwh od Miami



Chicago całą energie bierze od siebie



Dallas 30 tys. kwh energii pobiera od siebie pozostałe 10 tys. kwh od Miami



LA całą energie ma od siebie



Miami także całą energie pobiera od siebie

2. Zadanie nr 3.

2.1. Treść zadania.

Przypuśćmy, że każdego dnia północna, centralna i południowa Kalifornia

zużywają 100 miliardów galonów wody. Załóżmy też, że północna i centralna Kalifornia

mają do dyspozycji 120 miliardów galonów wody, natomiast południowa Kalifornia ma do

dyspozycji 40 miliardów galonów wody. Koszt dostawy jednego miliarda galonów wody

między tymi regionami wygląda następująco:

Nie będziemy w stanie zaspokoić całego zapotrzebowania na wodę, zakładamy więc, że

każdy brakujący miliard galonów wody niesie za sobą następujące koszty niedoboru:

Jak należy rozdzielić wodę w Kalifornii, aby zminimalizować sumę kosztów

dostawy kosztów niedoboru?

2.2. Rozwiązanie zadania.

Polecenia wydane w konsoli:

library(lpSolve)

library(RODBC)

setwd("D:/")

dane <- odbcConnectExcel("koszty3.xls")

koszty <- sqlQuery(dane, "select * from [Arkusz1$]")

koszty=as.matrix(koszty)

row.signs <- rep ("<=", 4)

row.rhs <- c(120,120,40,280)

col.signs <- rep (">=", 3)

col.rhs <- c(100,100,100)

lp.transport (koszty,"min",row.signs,row.rhs,col.signs,col.rhs)

lp.transport (koszty,"min",row.signs,row.rhs,col.signs,col.rhs)$solution

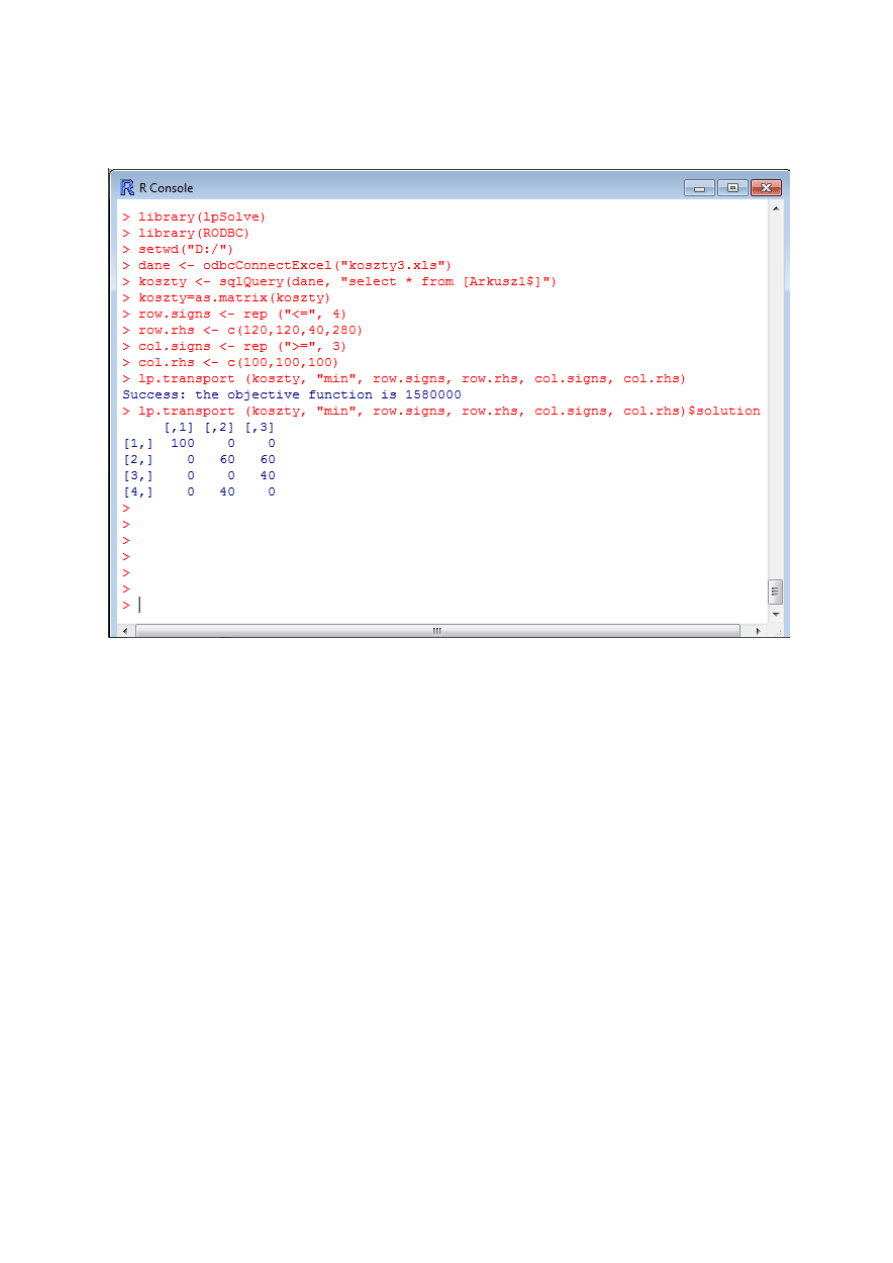
Zrzuty z konsoli wraz z wynikami:

2.3. Wnioski z zadania.

Aby koszty w transporcie wody były najmniejsze należy ją transportować tak:



Północna Kalifornia otrzymuje wodę ze swojego przydziału



Centralna Kalifornia otrzymuje 40 mld z deficytu, reszta stanowi własny przydział



Południowa Kalifornia otrzymuje 60 mld galonów Kalifornii centralnej, a reszta to jej
własny przydział

.