
2)
Przedział ufności dla wariancji
Najczęściej używanymi estymatorami wariancji σ
2
populacji generalnej są statystyki określone
wzorem:
∑
̅
̂
∑
̅
̂
W przypadku wyznaczania przedziału ufności dla wariancji, oba estymatory
̂
są
równoważne:
̂
∑
̅
MODEL I
Założenia:
- populacja generalna ma rozkład N(m,σ),
- wartość średnia m nieznana,
- odchylenie standardowe σ nieznane,
- próba losowana niezależnie,
- liczebność próby mała (n<30).
Wzór przedziału ufności dla wariancji σ
2
:
{
}
{
̂
̂
}
C
1
, c
2
– wartości zmiennej χ
2
wyznaczone z tablicy rozkładu χ
2
dla k = n – 1 stopni swobody oraz
współczynnika ufności 1 – α, tak aby:
(
)
(
)
Wartość c
1
odczytujemy z tablic rozkładu χ
2
dla prawdopodobieństwa 1 – ½ α, a c
2
dla ½ α.
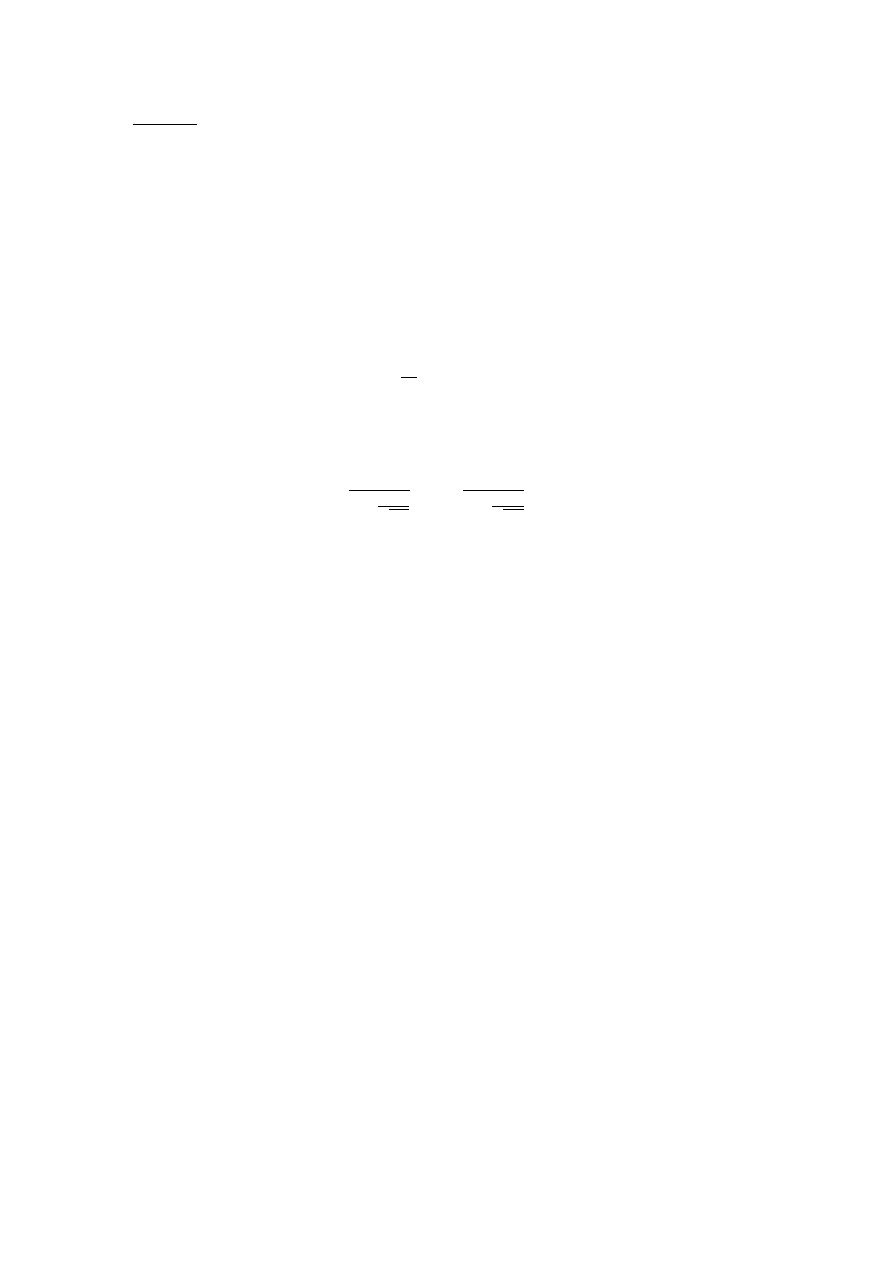
MODEL II
Założenia:
- populacja generalna ma rozkład N(m,σ),
- wartość średnia m nieznana,
- odchylenie standardowe σ nieznane,
- próba losowana niezależnie,
- liczebność grupy duża (n≥30).
Z próby wyznaczana jest wartość: √
Wzór przedziału ufności dla odchylenia standardowego populacji σ:
{
√
√
}
Wartość u
α
dla danego współczynnika ufności 1 – α, wyznaczana jest z tablicy dystrybuanty
rozkładu normalnego N(0,1), tak aby:
{
}
Wyszukiwarka
Podobne podstrony:
09 Przedział ufnosci dla sredniej i wariancji n małe
statystyka, Przedzial ufnosci dla m. Testowanie hipotezy dla m., PRZEDZIAŁ UFNOŚCI DLA WARTOŚCI OCZE
19 Przedziały ufności dla średniej
Zadanie przedzial ufnosci dla frakcji, TŻ, SEMI, SEM II, statystyka
3) Przedział ufności dla procentu (wskaźnika struktury)
1) Przedział ufności dla średniej
08 Przedz ufności dla średniej n duże (G 1 18)
Korelacja przedział ufności dla współczynnika (n duże)
25 xxx Korelacja przedział ufności dla współczynnika
Przedział ufności dla współczynnika korelacji (n duże)
7 4 Przedział ufności
10 przedzialy ufnosci zadaniaid Nieznany (2)
przedzialy ufnosci
5) Test dla wariancji populacji generalnej
05 Przedział ufnosci
więcej podobnych podstron