Przedziałowa

estymacja

parametryczna

Jerzy Neyman

lata 30 XX wieku

Warszawa

Berkeley

 

Wnioskowanie statystyczne - polega na uogólnianiu
wyników otrzymanych na podstawie próby losowej
na całą populację generalną, z której próba została
pobrana

Wnioskowanie statystyczne dzieli się na:

1.  

Estymację

–

szacowanie

wartości

parametrów lub postaci rozkładu zmiennej na
podstawie próby – na podstawie wyników próby
formułujemy wnioski dla całej populacji

2. Weryfikację hipotez statystycznych –
sprawdzanie określonych założeń sformułowanych
dla

parametrów

populacji

generalnej

na

podstawie wyników z próby – najpierw wysuwamy
założenie, które weryfikujemy na podstawie
wyników próby

Estymator – wielkość (charakterystyka, miara),
obliczona na podstawie próby, służąca do oceny
wartości nieznanych parametrów populacji
generalnej.

Najlepszym z pośród wszystkich estymatorów
parametru w populacji generalnej jest ten, który
spełnia wszystkie właściwości estymatorów
(jest

równocześnie

nieobciążony,

zgodny,

efektywny, dostateczny).

Estymacja przedziałowa

polega na budowie przedziału zwanego przedziałem
ufności, który z określonym prawdopodobieństwem
będzie zawierał nieznaną wartość szacowanego
parametru













1

)}

(

)

(

{

2

1

n

n

Z

g

Z

g

P

gdzie:



– nieznany parametr populacji generalnej,

końce przedziałów (dolna i górna
granica przedziału), będące funkcją
wylosowanej próby

)

(

1

n

Z

g

)

(

2

n

Z

g

1–α współczynnik ufności – prawdopodobieństwo
tego, że wyznaczając na podstawie n-elementowych

prób wartość funkcji g

1

i g

2

(dolną i górną granicę

przedziału) średnio w (1-α)·100% przypadkach
otrzymamy przedziały pokrywające nieznaną
wartość parametru Q – z prawdopodobieństwem (1-
α) przedział ufności pokrywa nieznaną wartość
szacowanego parametru

Im krótszy przedział (różnica między górną i dolną

granicą przedziału),

tym bardziej precyzyjna jest estymacja

przedziałowa.

Im wyższa jest wartość współczynnika ufności,

tym większa jest długość przedziału.

• Zadanie to nie jest jednoznaczne.
• Przykład: P=0,9=90%. a,b - ?
• P nazywamy poziomem ufności i

często zapisujemy w postaci ,
gdyż zwykle jest nieco mniejsze od
100% (najczęściej 95%, wtedy
)





1

%

5





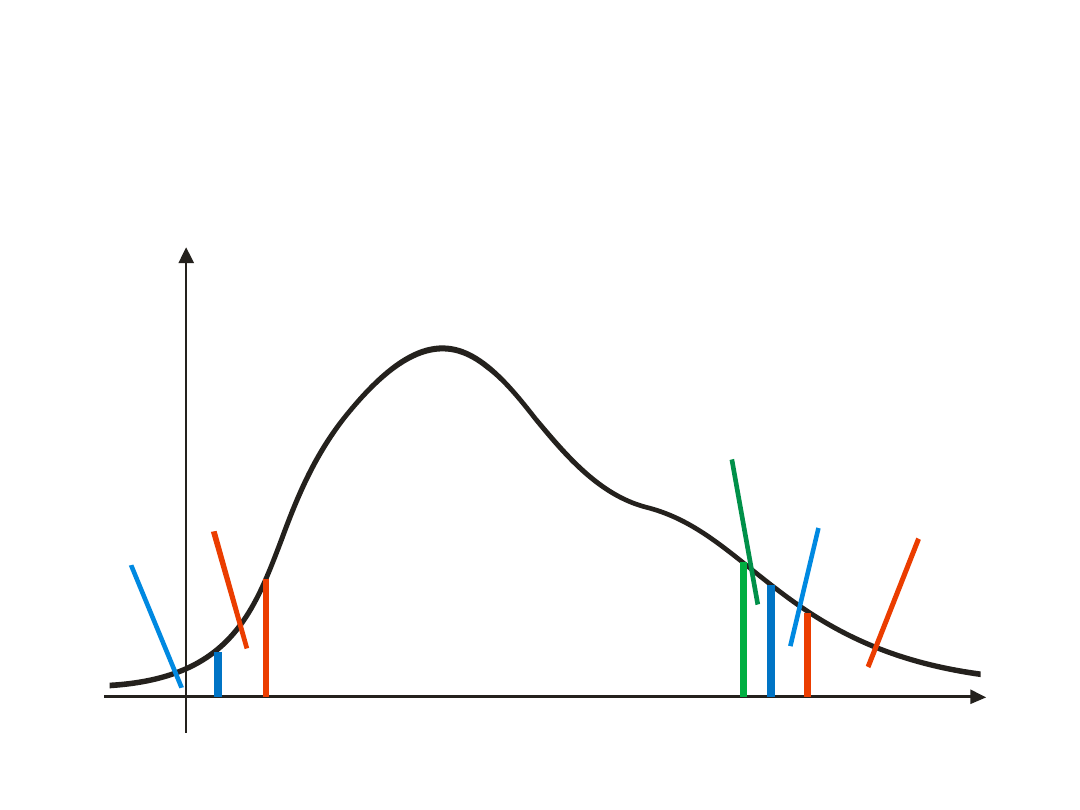
Wybór przedziału ufności

x

f x

( )

b

b

b

a

a

( =- )

a Ą

5%

5%

8%

10%

2%

Wybór przedziału ufności

• W praktyce stosujemy:

– symetryczny (dwustronny) wybór

przedziału (równe
prawdopodobieństwa po obu stronach)

– jednostronny wybór granicy przedziału

• prawostronny
• lewostronny

)

(





a

)

(





b

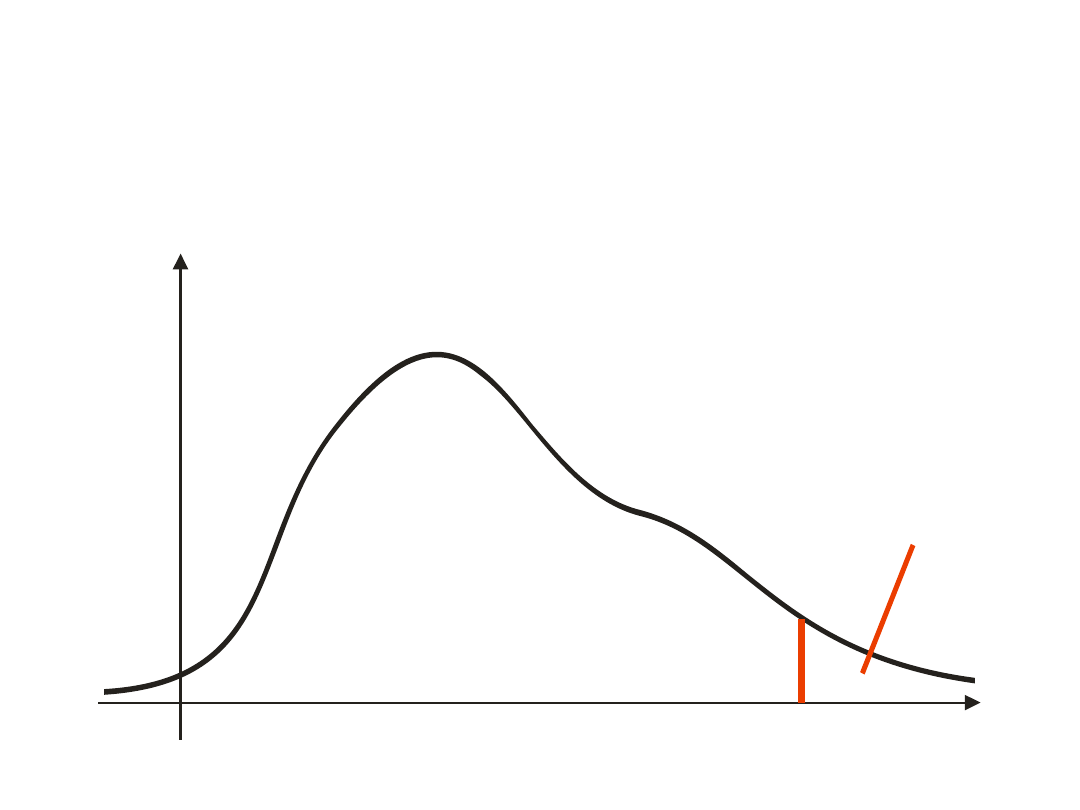
Niesymetryczne

x



f x

( )



 

1

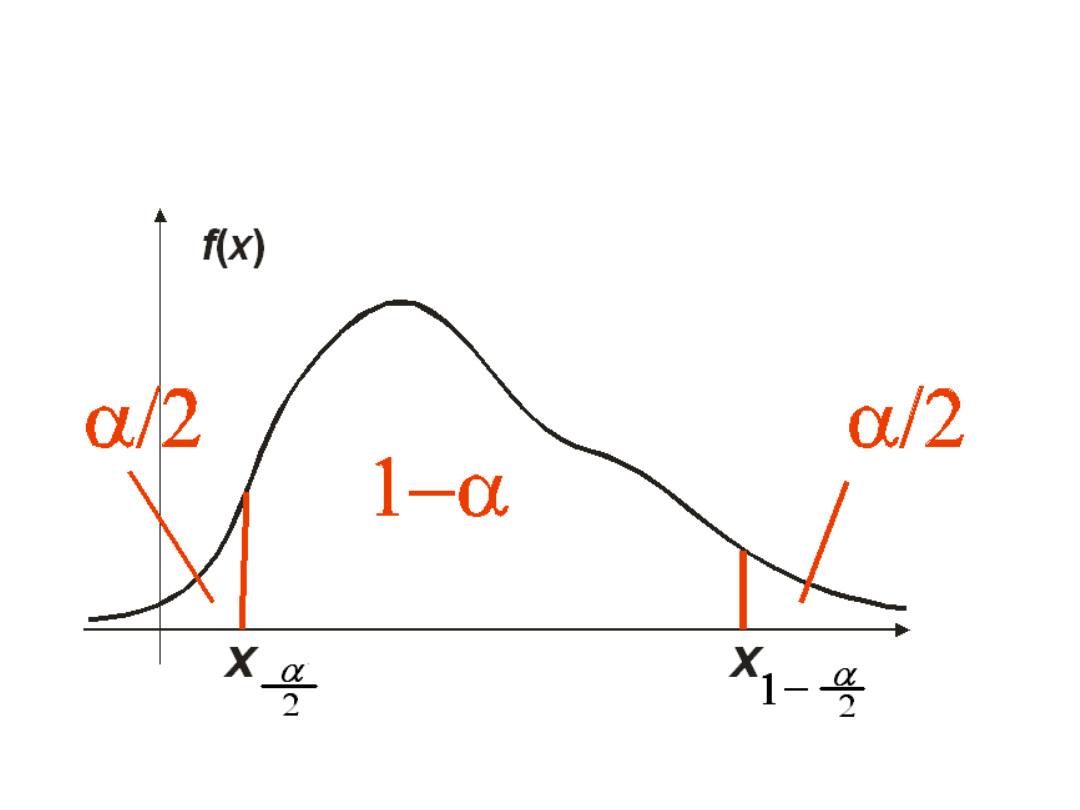
Symetryczny wybór

przedziału.

Symetryczny wybór

przedziału

• Przy symetrycznym wyborze

przedziału mamy .

• Jeśli funkcja gęstości jest parzysta

(symetryczna względem zera) to:

więc

• Rozkłady: standardowy normalny i t-

Studenta są parzyste.

2

1

2

,











x

b

x

a

2

2

,





x

b

x

a







2

1

2











x

x

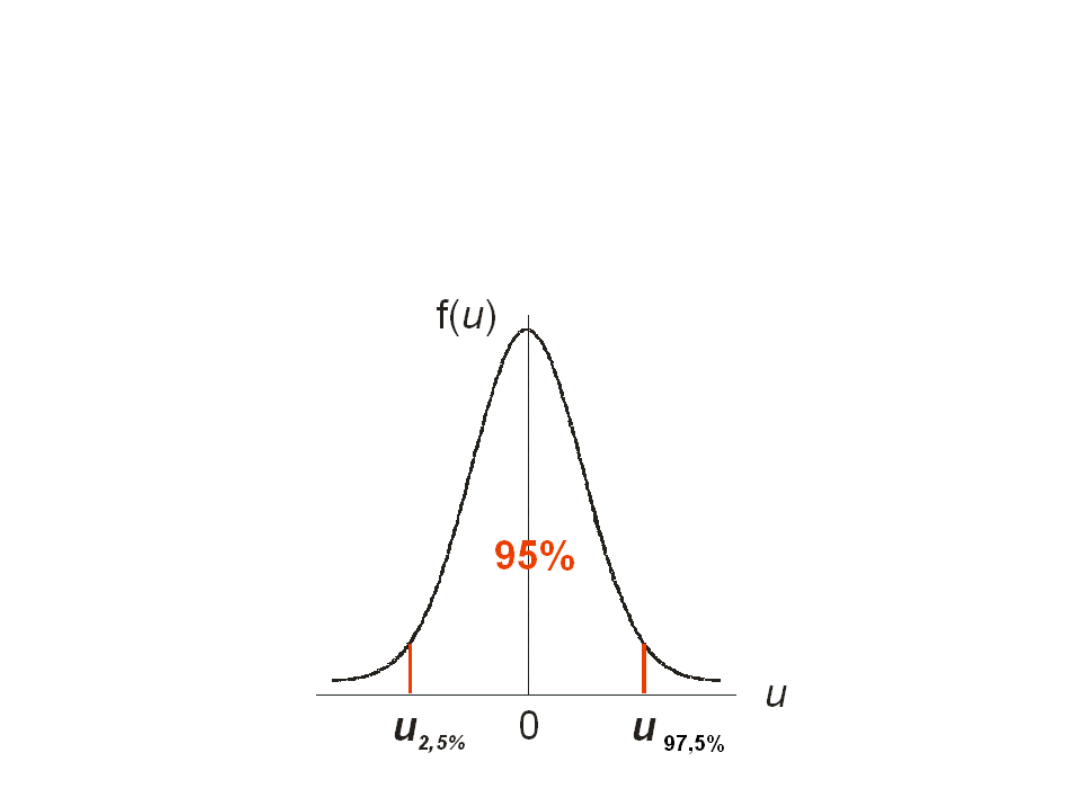
Symetryczny przedział dla

unorm. rozkładu

normalnego.

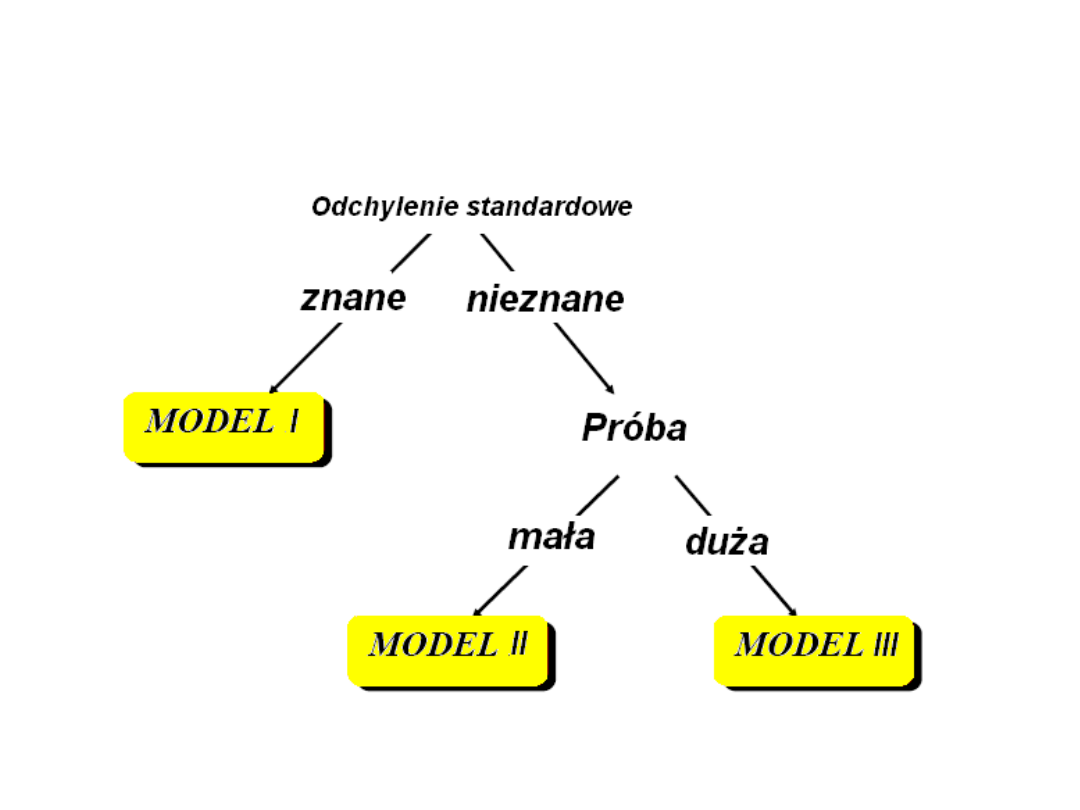
Przedział ufności dla wartości średniej

m populacji.

Przedział ufności

dla wartości średniej m

populacji.













n

m

N

X



,

~

Populacja ma rozkład

N(m, σ),

wartość przeciętna

wartość przeciętna

m – nieznany parametr,

odchylenie standardowe

odchylenie standardowe

σ – znany parametr.







n

1

i

i

X

n

1

X

wartość odczytaną z
tablicy rozkładu
N(0,1).

Model I

Model I



































1

)

(

1

)

(

)

(

u

U

u

P

u

U

P

u

U

P

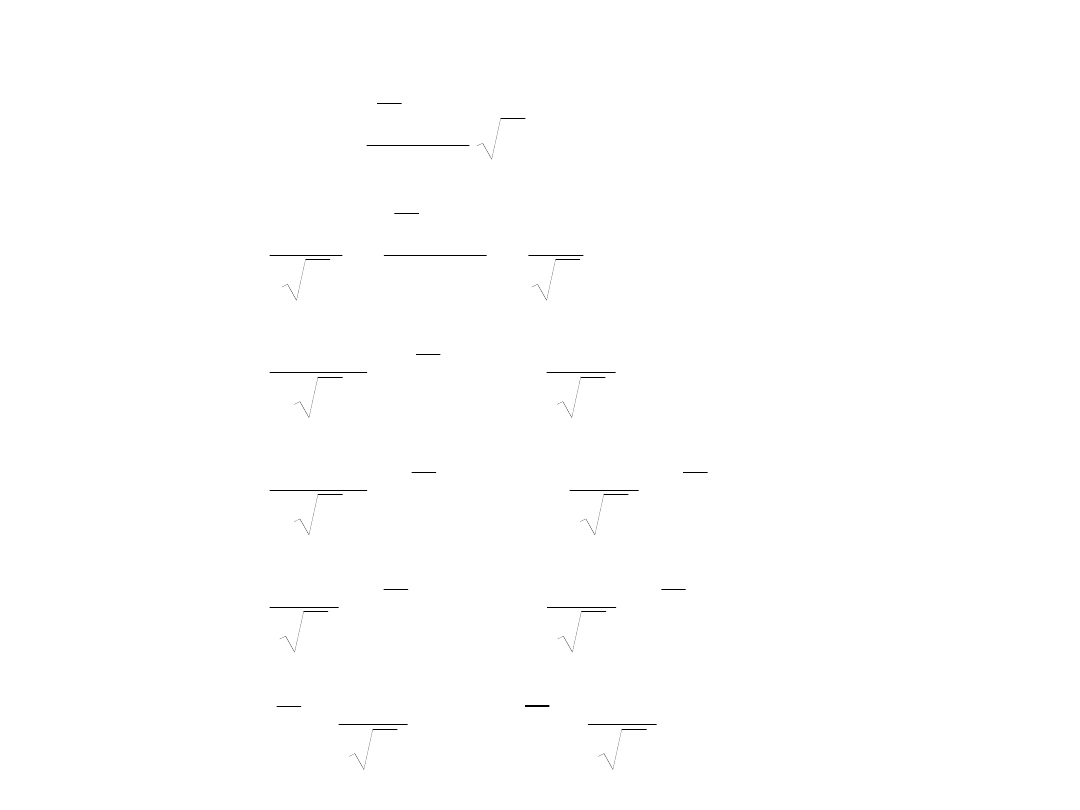
Ustalamy poziom
ufności 1-



 

1

,

0

~N

n

m

X

u

























































































































































































































1

1

1

1

1

1

)

(

1

)

(

n

u

X

m

n

u

X

P

X

n

u

m

X

n

u

P

X

n

u

m

X

n

u

P

n

u

m

X

n

u

P

n

u

m

X

n

u

P

u

n

m

X

u

P

u

U

u

P

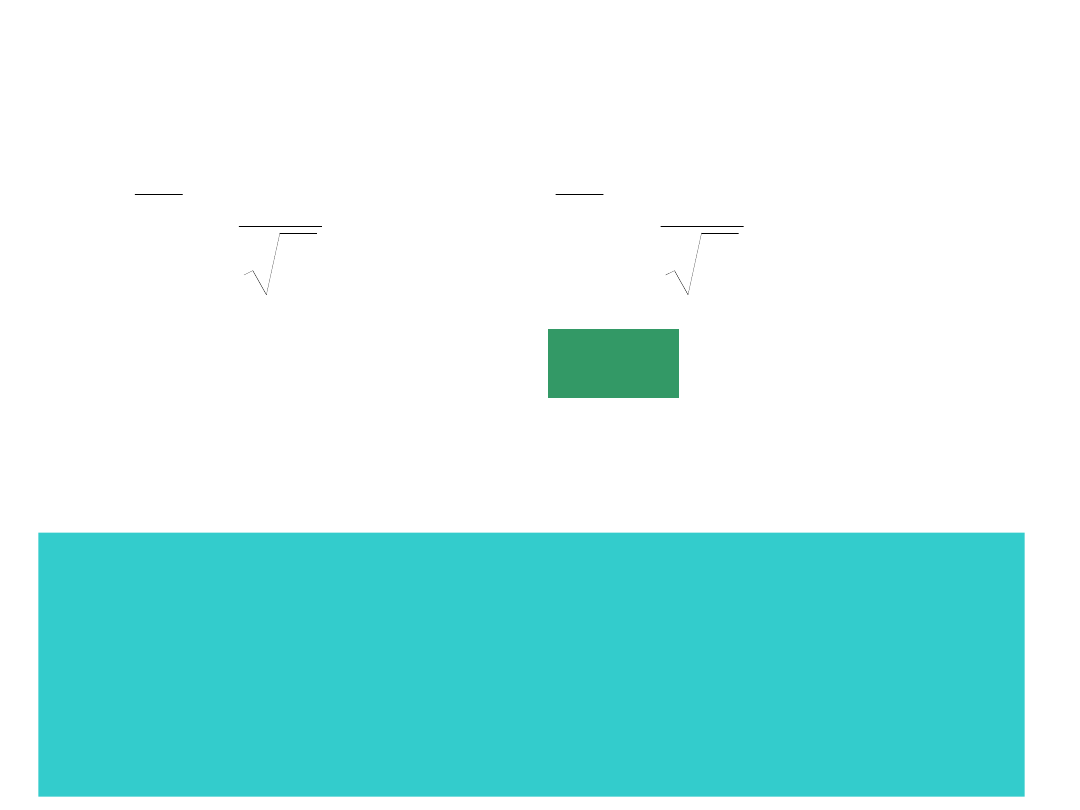
Przedziały ufności

Z prawdopodobieństwem (zwanym

poziomem ufności) wyznaczony przedział
zawiera wartość oczekiwaną m .



































1

u

n

X

m

u

n

X

P





1

Na przeszkodzie praktycznemu stosowaniu tego
wzoru stoi nieznajomość

σ

.

Czy popełnimy duży błąd zastępując σ jego estymatą
s ?

Przedział ufności dla wartości

średniej m populacji.



































1

1

1

n

S

t

X

m

n

S

t

X

P





























1

)

(

t

t

t

P

t

t

P

Populacja ma rozkład

N(m, σ),

m, σ – nieznane

parametry,

próba mała - n

 30 .







n

i

i

X

n

X

1

1

wartość odczytana z tablic
rozkładu

t-Studenta o n-1 stopniach
swobody

Model II

Model II













n

i

i

x

x

n

S

1

2

2

1

Ustalamy poziom ufności 1-



1







n

s

m

X

t





















































































































































































































1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

)

1

(

1

)

(

n

s

t

X

m

n

s

t

X

P

X

n

s

t

m

X

n

s

t

P

X

n

s

t

m

X

n

s

t

P

n

s

t

m

X

n

s

t

P

n

t

s

m

X

n

t

P

t

n

s

m

X

t

P

t

t

t

P

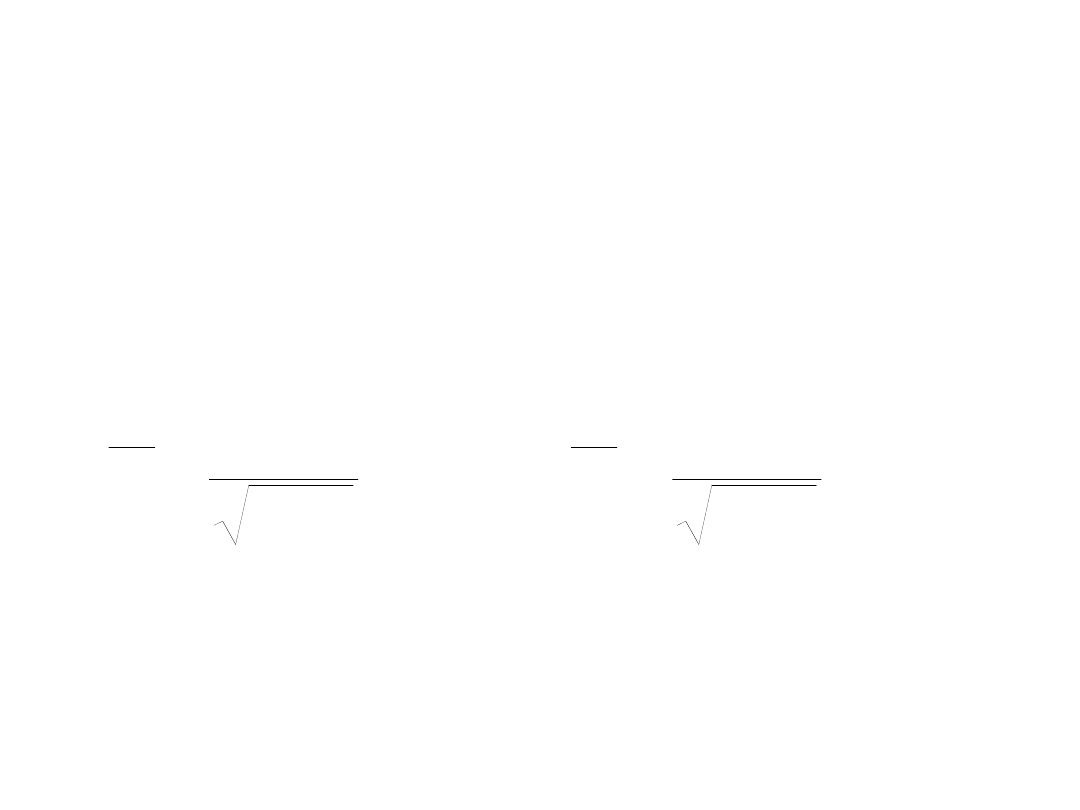
Przedziały ufności

• Rozumowanie bardzo podobne do

poprzedniego, prowadzi do wzoru:

• dla n > 30 różnica między t i u jest

znikoma



































1

1

1

t

n

s

X

m

t

n

s

X

P

Przedział ufności dla wartości

średniej m populacji.































1

ˆ

ˆ

n

s

u

X

m

n

s

u

X

P

Populacja ma rozkład

N(m, σ) bądź dowolny

inny o średniej m i o

wariancji skończonej

S

2

= σ

2

,

m, σ – nieznane

parametry,

próba duża - n > 30 .







n

i

i

X

n

X

1

1

wartość odczytaną z
tablicy rozkładu
N(0,1).

Model III

Model III



















n

i

i

x

x

n

s

n

n

s

1

2

2

2

1

1

1

ˆ

Ustalamy poziom ufności 1-





































1

)

(

1

)

(

)

(

u

U

u

P

u

U

P

u

U

P

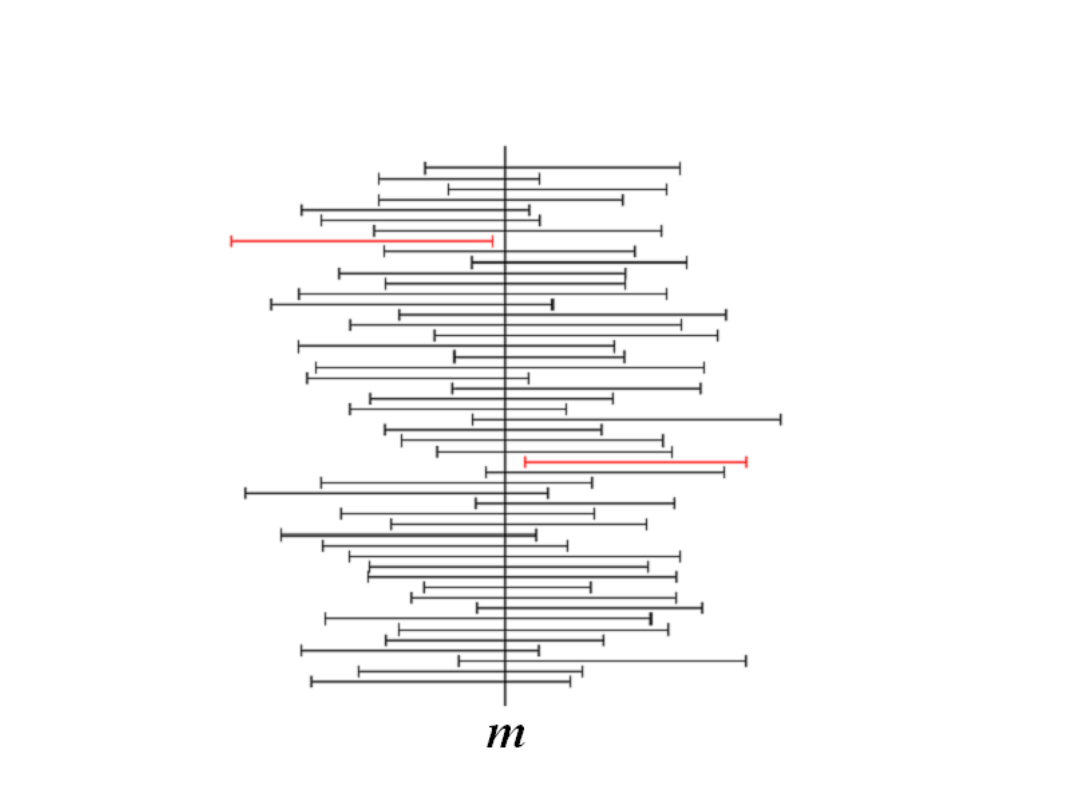
Przedział losowy i wartość m























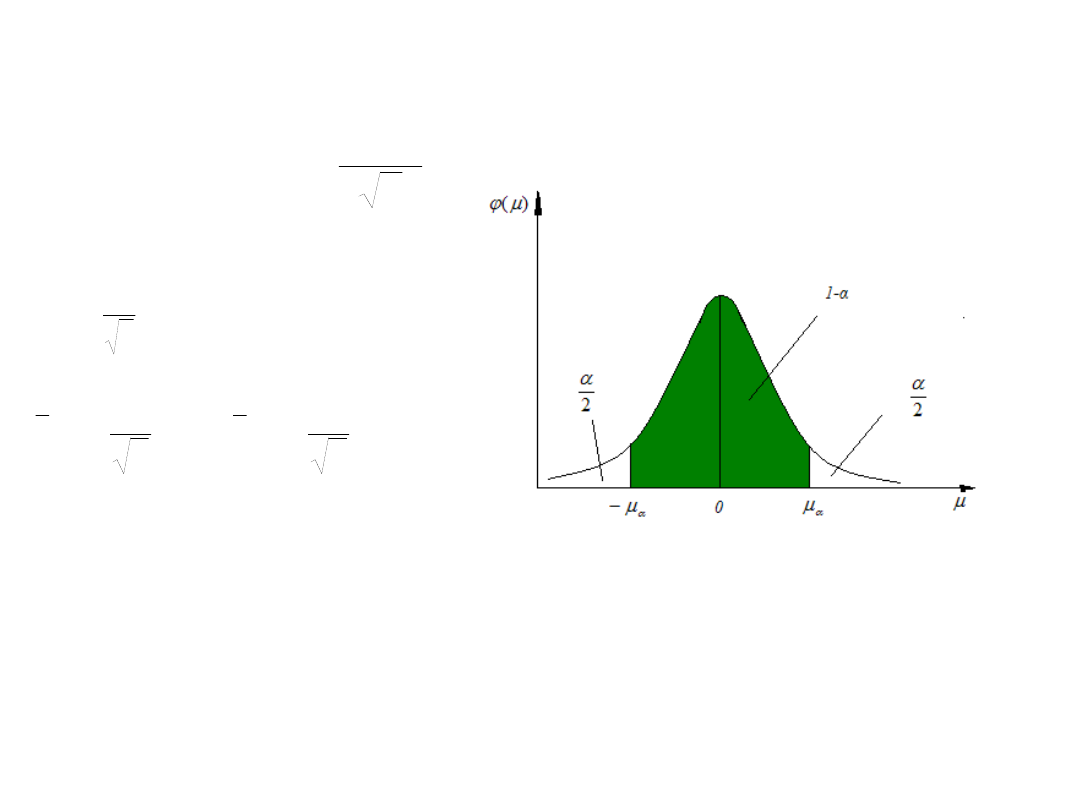
1

)

(

n

u

x

m

n

u

x

P

n

u 







- max. błąd oszacowania

Maksymalny błąd szacunku

Losowy przedział ufności ma dla wszystkich n-elementowych prób stałą
długość:

n

u





2

Jak znaleźć liczebność próby n , aby budowany przy
współczynniku ufności 1- przedział dla średniej m populacji

zapewniał maksymalny błąd szacunku nie przekraczający
ustalonej liczby d ?

Problem minimalnej liczebność

próby

Minimalna liczebność próby - taka liczebność

próby, która zapewni wymaganą dokładność

(precyzję oszacowania) przy danym poziomie

wiarygodności (prawdopodobieństwa).

Dla estymacji przedziałowej średniej m w
populacji przy znanym odchyleniu
standardowym σ w populacji

Poszukujemy takiej liczebność próby n, dla której
przy danym współczynniku ufności (1-α) połowa
długości przedziału ufności d – maksymalny błąd
szacunku – nie przekroczy ustalonej z góry
wartości.

2

2

2

d

u

n







2

2

2

d

u

n







stąd

Dla estymacji przedziałowej średniej m w
populacji przy nieznanym odchyleniu
standardowym σ w populacji

Losujemy próbę wstępną n

0

, obliczamy średnią i

wariancję z próby i na jej podstawie wyznaczamy
właściwą liczebność próby:

2

2

2

1

,

ˆ

0

d

S

t

n

n









t

α,n0-1

– wartość odczytana z tablic rozkładu Studenta

dla α i n

0

-1











n

i

i

n

X

X

S

1

1

1

2

)

(

ˆ

Jeżeli n ≤ n

0

to próbę wstępną traktujemy

jako właściwą. Jeżeli zaś n > n

0

to musimy

próbę powiększyć o n – n

0

.

Rozkład estymatora s

2

• Jeśli X ma rozkład normalny, to

ma rozkład zwany rozkładem

(chi-kwadrat) Pearsona.

• Kształt tego rozkładu zależy od liczby

stopni swobody r = n – 1. Dla dużych
n zbliża się on do rozkładu
normalnego.





1

2

2



n

s



2



Rozkład wariancji z próby













n

i

i

X

X

n

S

1

2

2

1





2

1

2

2

1

1

1

ˆ

S

n

n

X

X

n

S

n

i

i



























n

i

i

m

X

n

S

1

2

2

*

1

Twierdzenie

Rozkład tych statystyk zależy od rozkładów
populacji.

Jeżeli populacja generalna ma rozkład normalny N(m,

) i

wylosowano z niej

n-elementową próbę prostą, z której wyznaczamy statystykę S

*2

To liniowe jej przekształcenie , a mianowicie
statystyka

ma rozkład



2

o n stopniach swobody.

2

2

*



nS

2

1

2

2

2

2

ˆ

)

1

(









n

S

n

nS







Rozkład wariancji z
próby cd.

Dla statystyk

S

2

i

2

ˆ

S

Bardzo często korzysta się z szybkiej zbieżności
do rozkładu normalnego

1

2

2

2







k

U



2

2







1

,

1

2 

k

N

Dla k>30 zmienna
losowa

ma rozkład normalny
N(0,1)

Graniczne rozkłady samych statystyk S

2

i S, tzn. wariancji i

odchylenia standardowego z próby pochodzących z populacji
normalnych są też normalne





n































n

N

S

n

N

S

2

,

2

,

4

2

2









Gdy

Rozkład



2

Jeżeli U

1

, U

2

, ...,U

k

są niezależnymi zmiennymi

losowymi o standardowym rozkładzie normalnym
N(0,1) każda, to zmienna losowa będąca sumą ich
kwadratów:





k

i

i

U

1

2

ma rozkład



2

o k stopniach swobody.

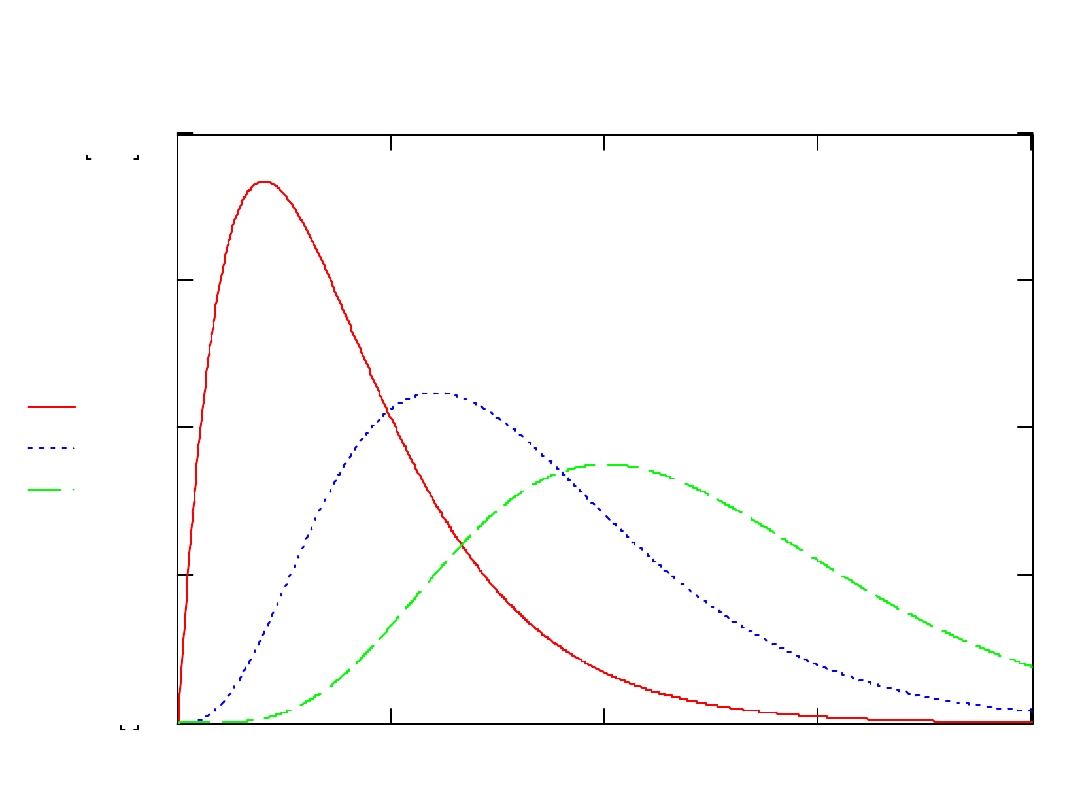
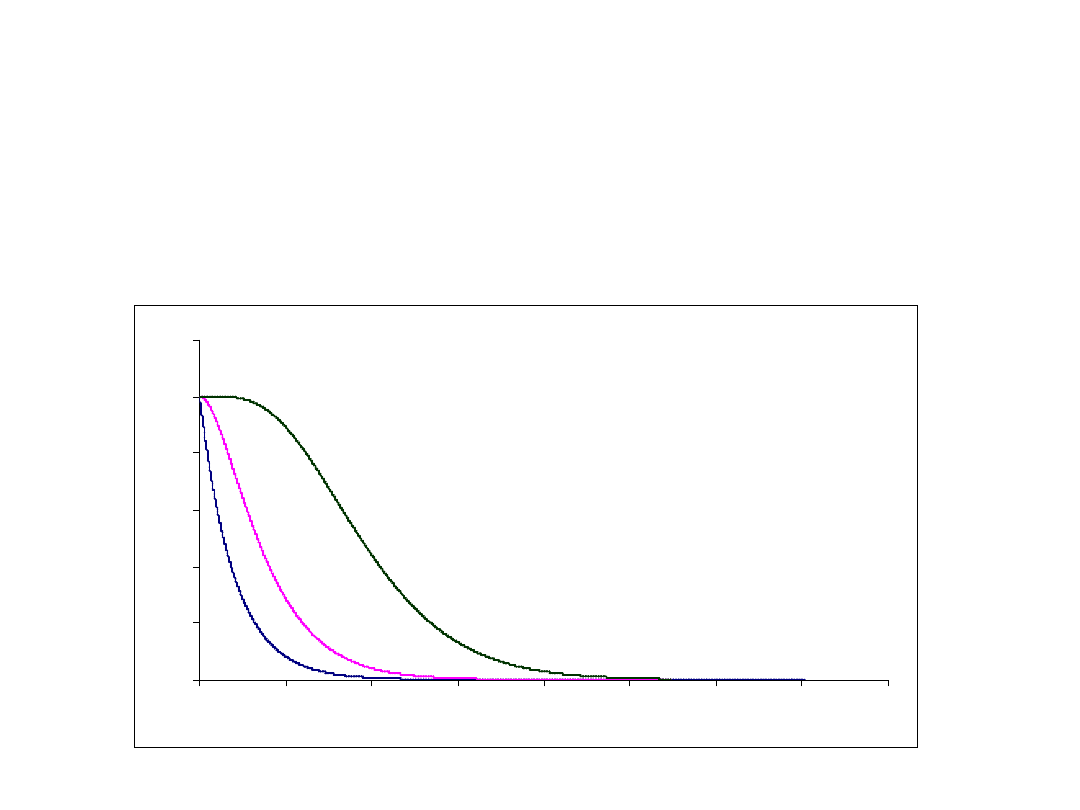
Gęstość rozkładu



2

0

5

10

15

20

0

0.05

0.1

0.15

0.2

0.184

0

dchisqx 4



(

)

dchisqx 8



(

)

dchisqx 12



(

)

20

0

x

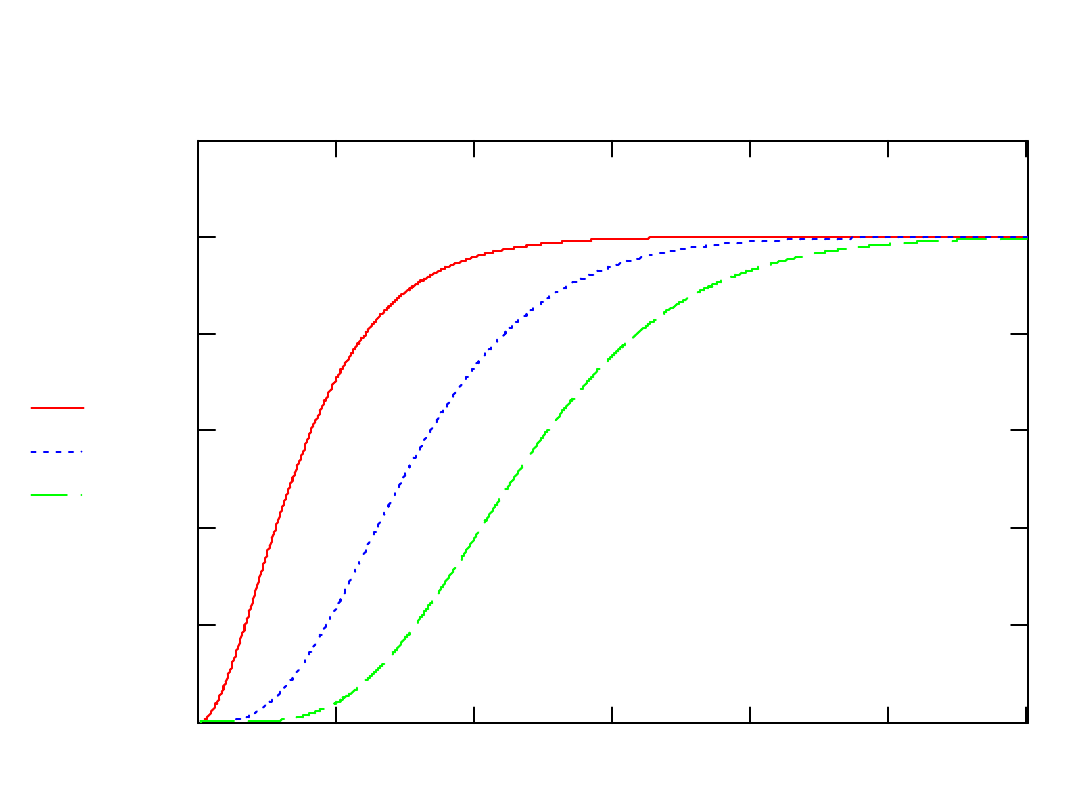
Dystrubuanta rozkładu



2

0

5

10

15

20

25

30

0

0.2

0.4

0.6

0.8

1

1.2

0

pchisqx 4



(

)

pchisqx 8



(

)

pchisqx 12



(

)

30

0

x x

 x



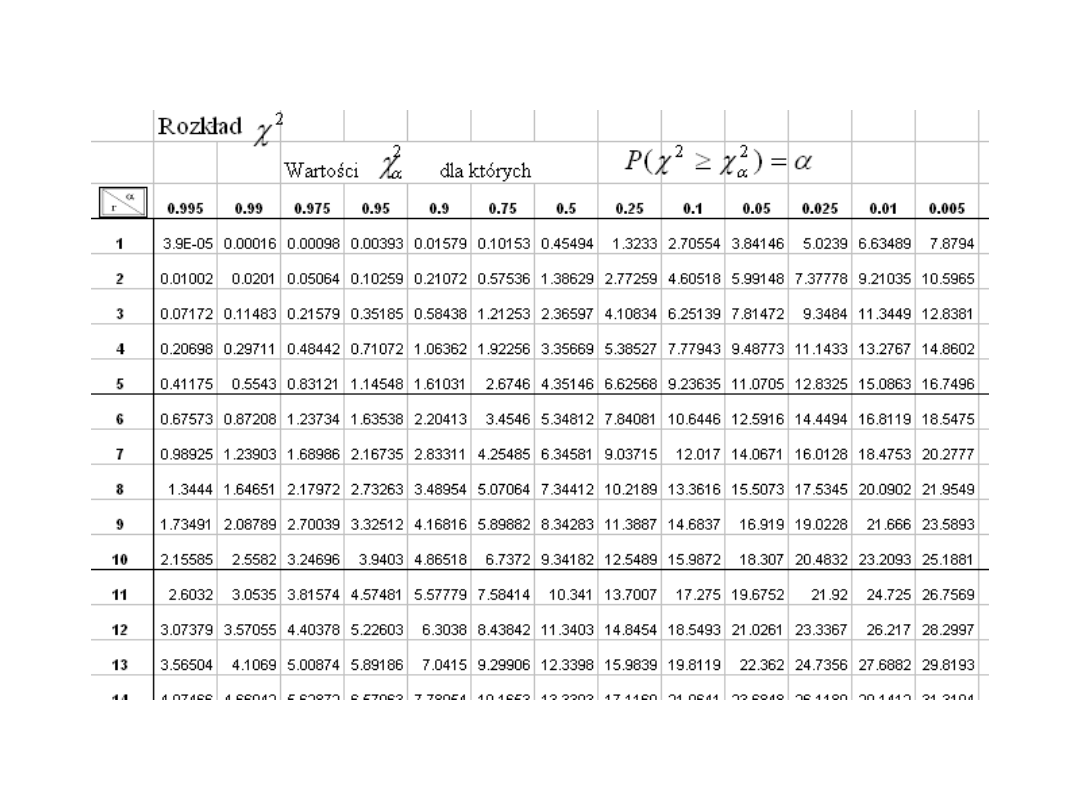
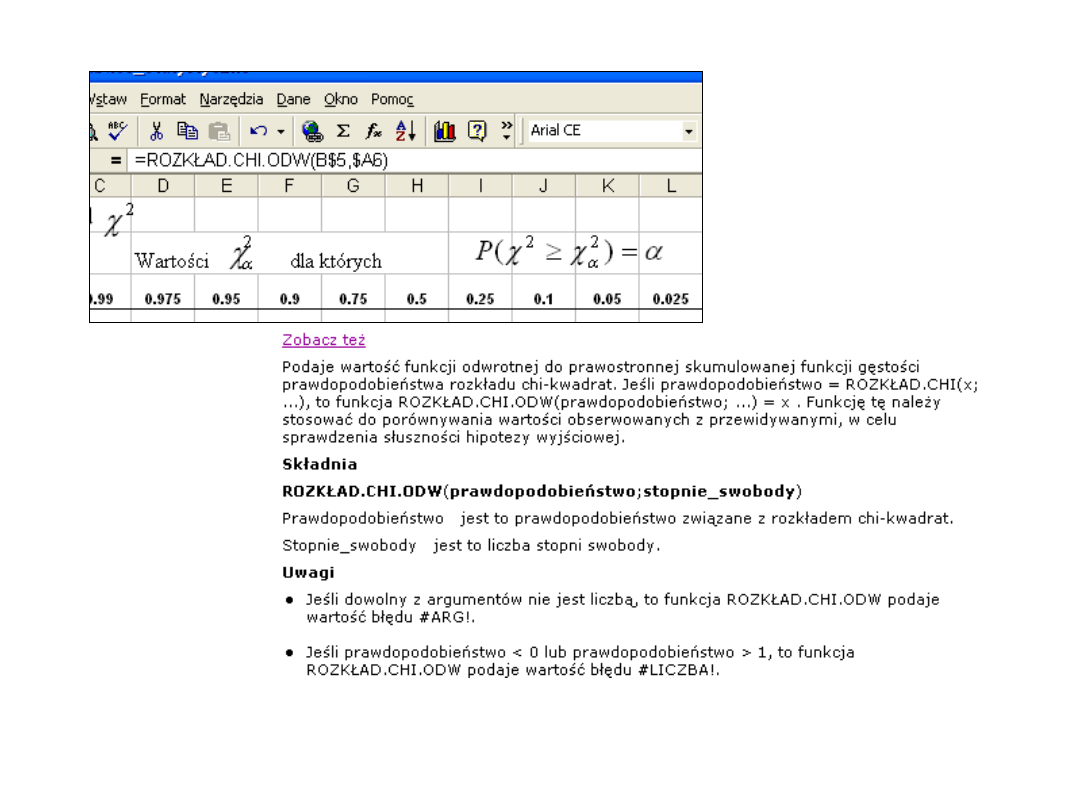
Rozkład



2

(Excel)

•Wartość funkcji ROZKŁAD.CHI wyznacza się
jako ROZKŁAD.CHI = P(X >x ), gdzie X jest zmienną losową χ

2

.

0

0.2

0.4

0.6

0.8

1

1.2

0

5

10

15

20

25

30

35

40

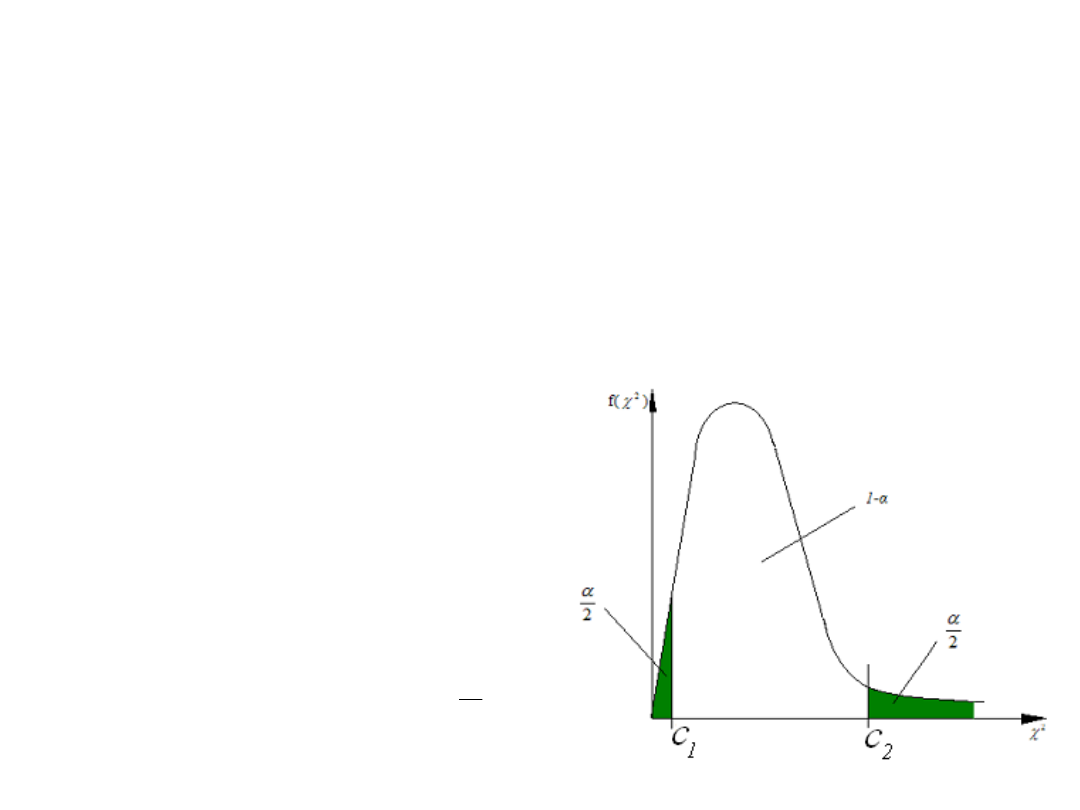
PRZEDZIAŁ UFNOŚCI DLA

WARIANCJI

-

wariancja z próby (estymator

obciążony)

-wariancja z próby (estymator

nieobciążony)

-wariancja z populacji

2

s

2

1

s

2



2

1

2

2

2

;

s

s















 













2

1

1

2

2

1

2

2

2

1

















c

P

c

P

c

c

P

n

n

n

Przedział ufności wariancji









1

ˆ

:

1

ˆ

2

2

2

2

1









n

s

c

n

s

c











1

ˆ

1

1

ˆ

2

2

2

2

1









n

s

c

n

s

c



Dla dodatnich a,b,c
a<b<c pociąga:

Np.









2

2

2

1

2

1

ˆ

1

ˆ

c

n

s

c

n

s











c

b

a

1

1

1





4

1

3

1

2

1

4

3

2











Przedział ufności wariancji.

• Z powyższego wynika, że przedział ufności

wariancji dany jest wzorem:

• Przedział ufności dla odchylenia standardowego

otrzymamy pierwiastkując wszystkie strony tej
nierówności.





































1

1

ˆ

1

ˆ

1

2

2

2

2

n

c

S

n

c

S

P

























1

1

2

2

2

2

n

c

S

n

c

S

P

























1

1

2

*

2

2

*

c

nS

c

nS

P

Przedział ufności odchylenia
standardowego dla dużych prób
n>30































n

N

S

n

N

S

2

,

2

,

4

2

2







































































1

2

1

2

u

n

S

u

P

u

U

u

P

n

S

U

n

u

S

n

u

S

n

u

S

n

u

n

u

S

n

u

n

u

S

n

u

2

1

2

1

2

1

1

2

1

1

2

1

2

1

2

1

2





































































































1

2

1

2

1

n

u

S

n

u

S

P

Zadanie 1.
Firma telefoniczna oszacowała przeciętną długość rozmów

lokalnych w czasie weekendu, których czas ma rozkład normalny

z odchyleniem standardowym 5,5 minuty. Z losowej próby 50

rozmów otrzymano średnią 14,5 minuty. Wyznacz z

prawdopodobieństwem 1- α =0,9 przedział ufności dla średniej

długości rozmów lokalnych.

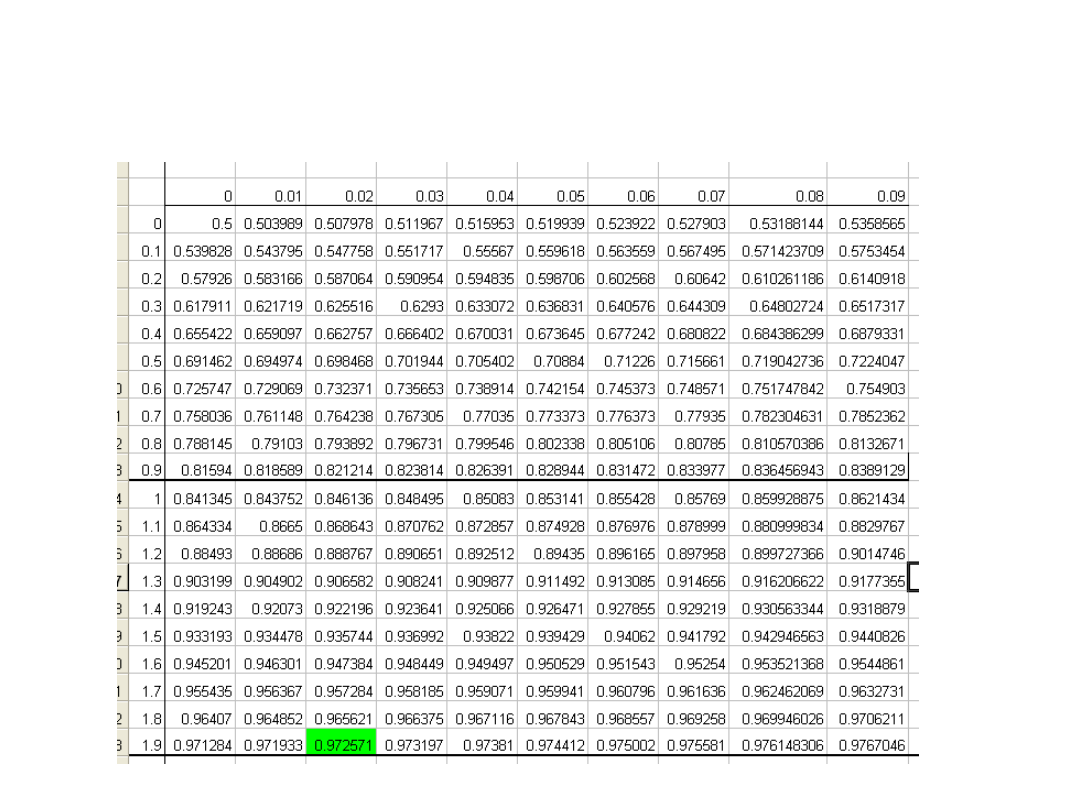
Zadanie 2. Wyznacz granice liczbowe krańców przedziału ufności

pomiaru odległości między dwoma wierzchołkami gór (w metrach)

przy poziomie ufności 1- =0.95 , jeśli wykonano 80 pomiarów ze

średnią równą 3000 m. Rozkład odległości jest rozkładem

normalnym z odchyleniem standardowym równym 10 m.

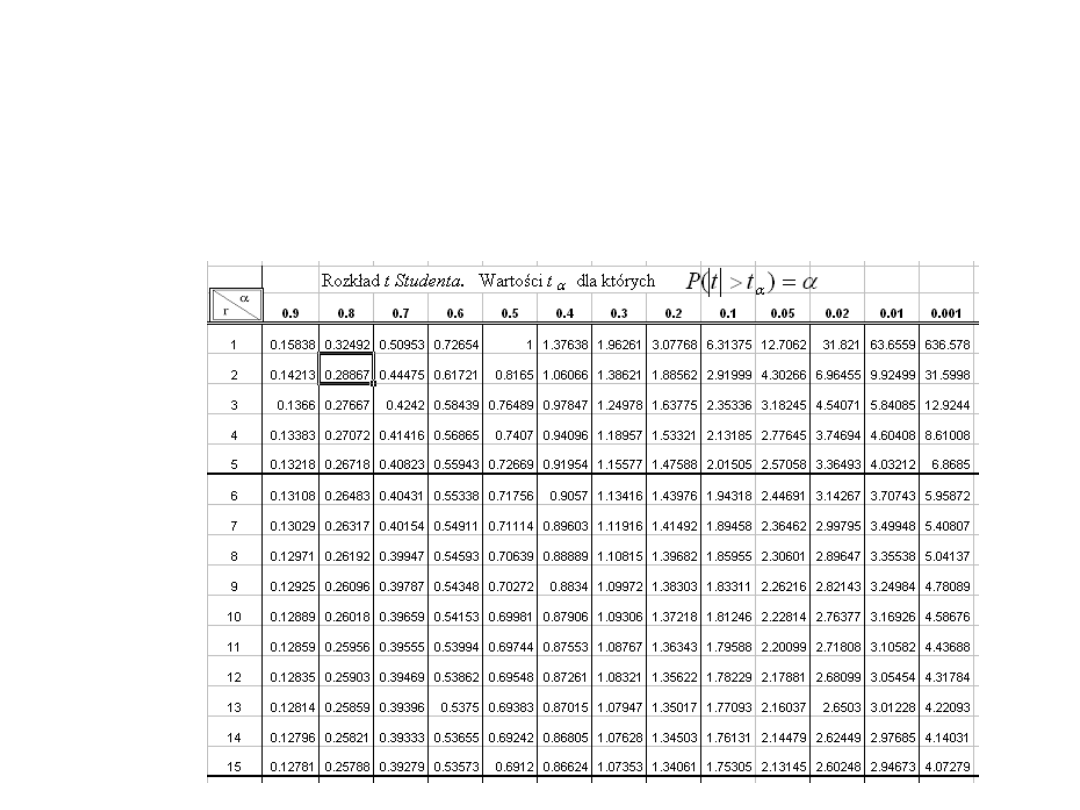
Zadanie 3.
W pewnej klasie wybrano losowo grupę 8 osobową, która

miała za zadanie rozwiązać zadanie z matematyki. Zmierzono
czas rozwiązania zadania przez każdego z uczniów: 25, 16,
12, 10, 12, 21, 25, 20. Oszacuj metodą przedziałową dla
współczynnika ufności średni czas niezbędny do rozwiązania
zadania w całej zbiorowości uczniów. Przyjmując poziom
istotności  = 0,05.

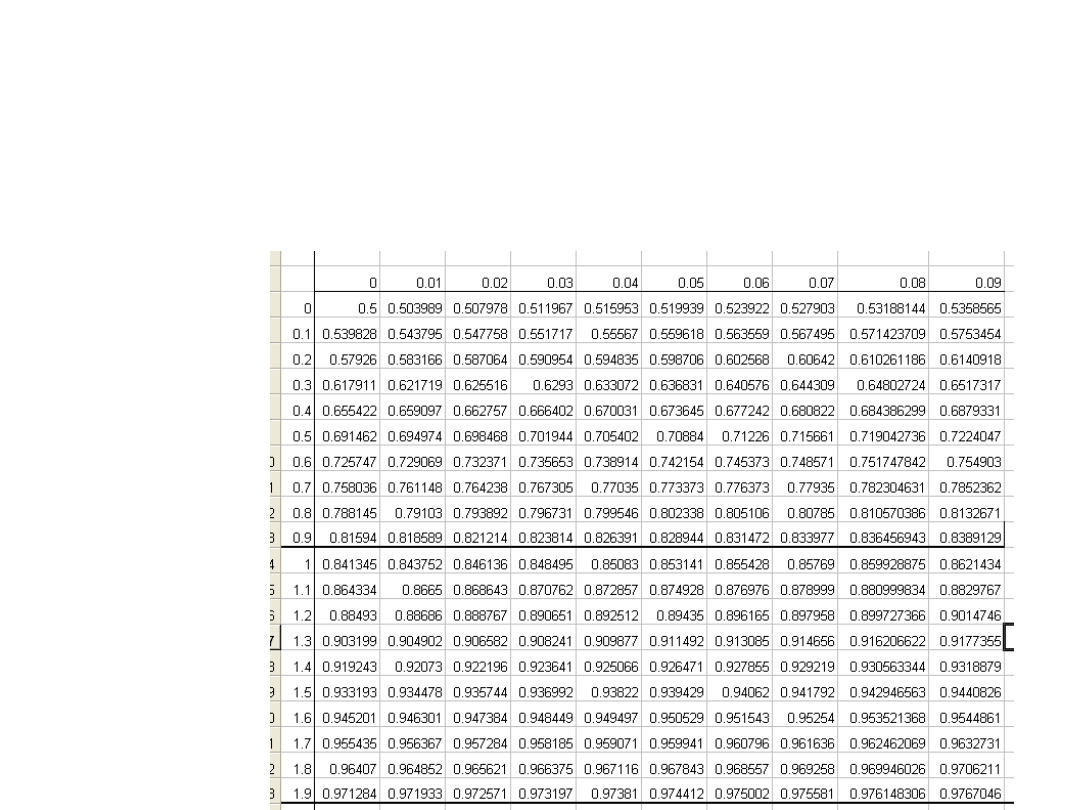
Zadanie 4.
W grupie losowo wybranych 625 pracowników w dużym
koncernie produkującym samochody osobowe, średnia liczba
dni nieobecności w pracy w badanym roku wynosiła 18,
natomiast odchylenie standardowe 3. Przyjmując poziom
ufności na poziomie 0,90 oszacować średni poziom
nieobecności pracowników w całym przedsiębiorstwie oraz
ocenić precyzję oszacowania.

Zadanie 5.

Firma zajmująca się wyszukiwaniem stanowisk dla personelu
kierowniczego chce oszacować średnią pensję, jaką może
uzyskać pracownik pełniący funkcję kierowniczą, z dokładnością
do 2000 $, przy poziomie ufności 95%. Wiadomo, że rozkład
pensji kierowniczych jest rozkładem normalnym o wariancji 40
mln. Jak liczna powinna być próba do oszacowania średniej
pensji kierowników?

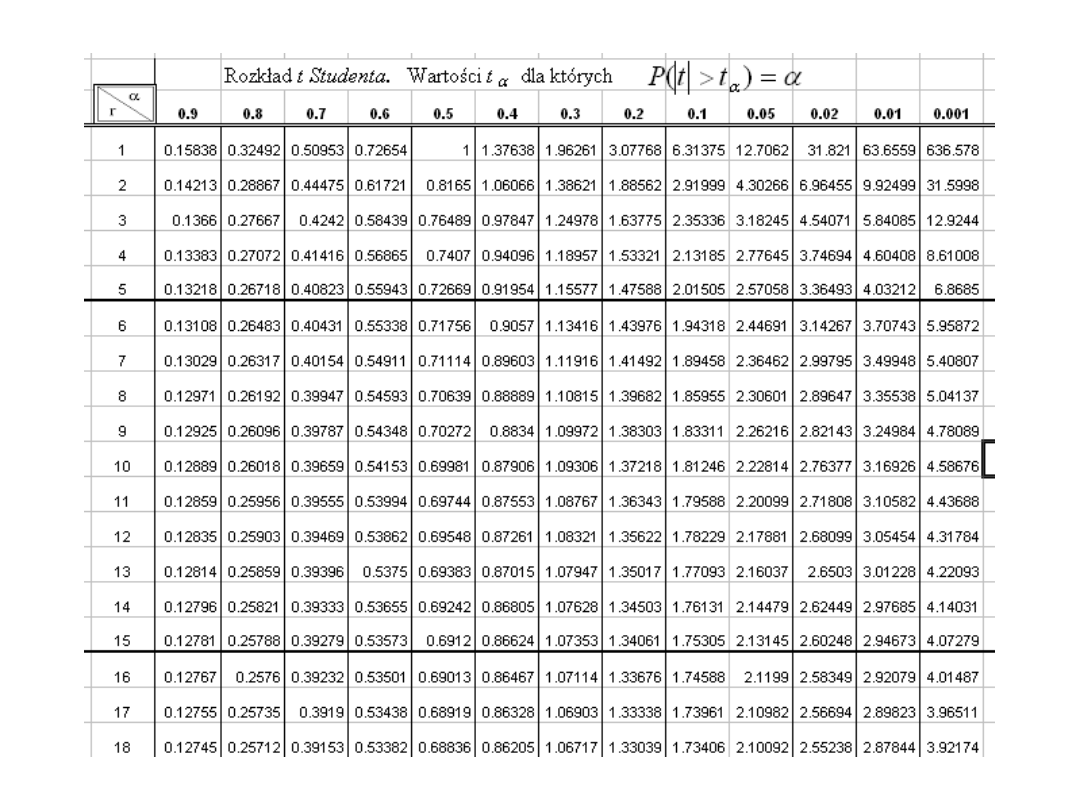
Zadanie 6.

W celu wyznaczenia przeciętnej długości drogi hamowania
samochodu na asfalcie, przeprowadzono przy prędkości 40
km/h 12 prób i otrzymano wyniki w metrach: 17,0; 19,0; 22,0;
20,5; 20,0; 21,0; 20,5; 20,0; 21,0; 18,0; 20,0; 21,0. Czy liczba
prób jest wystarczająca do wyznaczenia przedziału ufności
średniej o długości 0,5 m i dla 1- α = 0,95. Ewentualnie, jaką
liczbę prób należy jeszcze przeprowadzić?

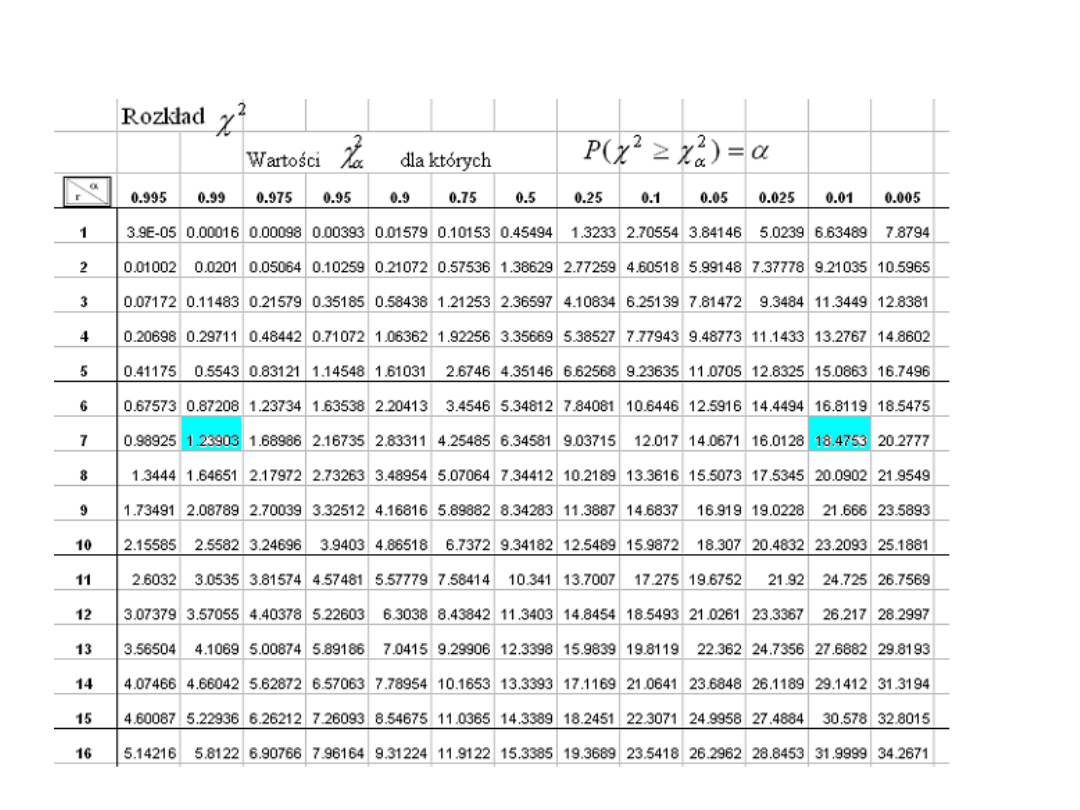
Zadanie 7. 

Z populacji rozkładzie normalnym N(m,σ)
wylosowano 8-elementową próbę prostą i
otrzymano wyniki:

1.2 1.0 0.7 1.4 1.1 0.9 1.2 1.3

W oparciu o te wyniki wyznaczyć przedział ufności
dla wariancji σ

2

przyjmując współczynnik ufności

1 – α = 0.98 .