200
300
400
500
600
700
0
0.5
1
p
i
dane_zred
i
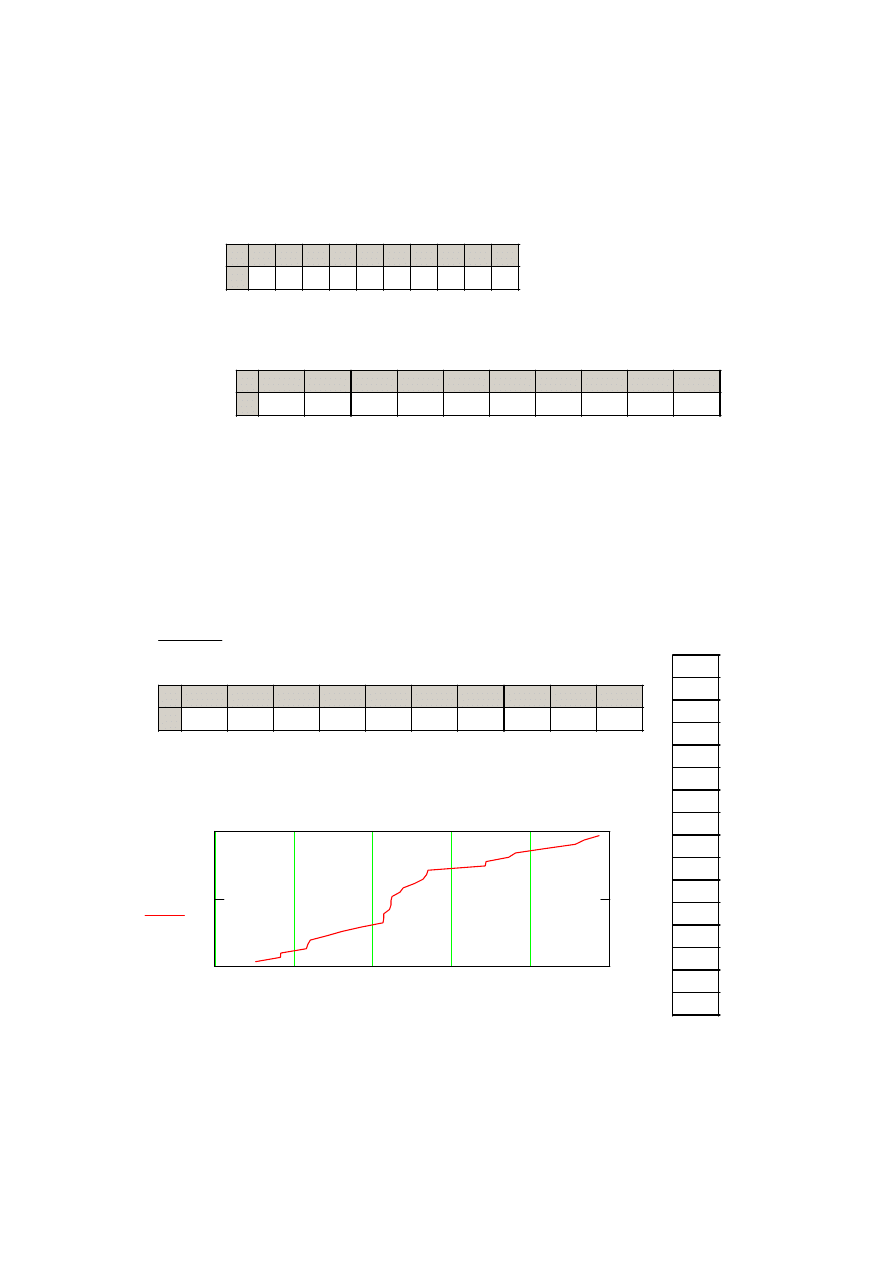
3. Rysujemy wykres
p
T
0
1
2
3
4
5
6
7
8
9
0 0.032 0.065 0.097 0.129 0.161 0.194 0.226 0.258
0.29 0.323
=
p
i
0.032
0.065
0.097
0.129
0.161
0.194
0.226
0.258
0.29
0.323
0.355
0.387
0.419
0.452
0.484
0.516
=
p
i
cz_wyst
i
M
:=
i
0 1
,
n 1
-
..
:=
M 31
=
M
cz_wyst
n 1
-
1
+
:=
n 30
=
n
rows cz_wyst
(
)
:=
2. Prawdopodobienstwo z proby
dane_zred
T
0
1
2
3
4
5
6
7
8
9
0 251.6 283.4 283.8 315.9
318 321.2 341.8 360.9 385.5
413
=
dane_zred
READPRN "D_ZRED.dat"
(
)
:=
Dane zredukowane
dane
cz_wyst
T
0
1
2
3
4
5
6
7
8
9
0
1
2
3
4
5
6
7
8
9 10
=
cz_wyst
READPRN "C_W.dat"
(
)
:=
Czestosc wystapienia
1. Odczyt danych (szereg kumulacyjny)
ROZKLAD LOGARYTMO-NORMALNY

Obliczanie wspóczynników prostej regresji y=a+b*x
a
intercept dane_zredl y
,
(
)
:=
a
20.771
-
=
b
slope dane_zredl y
,
(
)
:=
b 3.423
=
a
b
æ
ç
è
ö
÷
ø
line dane_zredl y
,
(
)
:=
a
20.771
-
=
b 3.423
=
OBLICZENIE PARAMETROW ROZKLADU
srednia_g
a
b
æ
ç
è
ö
÷
ø
-
:=
srednia_g 6.067
=
odch_std_g
1
b
:=
odch_std_g 0.292
=
sr
exp srednia_g 0.5
odch_std_g
(
)
2
×
+
éë
ùû
:=
sr 450.407
=
przelicz. sredniej na jedn.
zmiennej losowej
mean dane_zred
(
)
446.34
=
a to jest srednia danych
niezlogarytmowanych
odch
exp 2 srednia_g
×
odch_std_g
2
+
(
)
exp odch_std_g
2
(
)
1
-
(
)
×
:=
przeliczenie odchylenia na jednostki zmiennej losowej
odch 134.429
=
Stdev dane_zred
(
)
117.729
=
odchylenie std. danych niezlogarytmowanych (dane_zred)
Oszacowanie punktowe
dane_zredl
i
ln dane_zred
i
(
)
:=
srednial
mean dane_zredl
(
)
:=
srednial 6.067
=
srednia w jedn. ln
odch_stdl
Stdev dane_zredl
(
)
:=
odch_stdl
0.265
=
odch st. w jedn ln
sr
exp srednial 0.5
odch_stdl
(
)
2
×
+
éë
ùû
:=
sr 446.995
=
przeliczenie sredniej na jednostki
zmiennej losowej
mean dane_zred
(
)
446.34
=
dane niezlogarytmowane
(dane_zred)
odch
exp 2 srednial
×
odch_stdl
2
+
(
)
exp odch_stdl
2
(
)
1
-
(
)
×
:=
przeliczenie odchylenia na jednostki zmiennej losowej
odch 120.475
=
Stdev dane_zred
(
)
117.729
=
odchylenie std. danych niezlogarytmowanych (dane_zred)
Oszacowanie graficzne
alternatywnedo punktowego
(
)
tylko
-
igreki
os Y
y
i
qnorm p
i
0
,
1
,
(
)
:=
-To samo sie oblicza
wniosek "hipoteza nie jest odrzucona"
=
wniosek
if W2 W2_kryt
>
"hipoteza jest odrzucona"
,
"hipoteza nie jest odrzucona"
,
(
)
:=
Wniosek
H_w2 0.156
=
H_w2
W2
W2_kryt
:=
W2 0.388
=
W2_kryt
2.4933
:=
na poziomie istotnosci 0.05 wartosc krytyczna W2_kryt wynosi
W2 0.388
=
W2
n
-
1
n
æç
è
ö÷
ø
i
2
i
1
+
(
)
×
1
-
[
] ln prt
i
( )
×
2
n i
-
1
-
(
)
×
1
+
[
] ln 1
prt
i
-
(
)
×
+
éë
ùû
å
×
-
:=
prt
i
0.032
0.075
0.076
0.143
0.148
0.156
0.212
0.27
0.35
0.44
0.443
0.444
0.468
0.472
0.473
0.477
=
rownowaznie mozna zastosowac prti=cnorm(yti)
prt
i
pnorm yt
i
0
,
1
,
(
)
:=
wracamy do normalnej postaci
i
0
n 1
-
..
:=
n 30
=
yt
i
a
b dane_zredl
i
×
+
:=
wyznaczona z lini prostej
Test W kwadrat
TESTY ZGODNOSCI
5.4
5.6
5.8
6
6.2
6.4
6.6
2
0
2
y
i
pr x
( )
dane_zredl
i
x
,
pr x
( )
b x
×
a
+
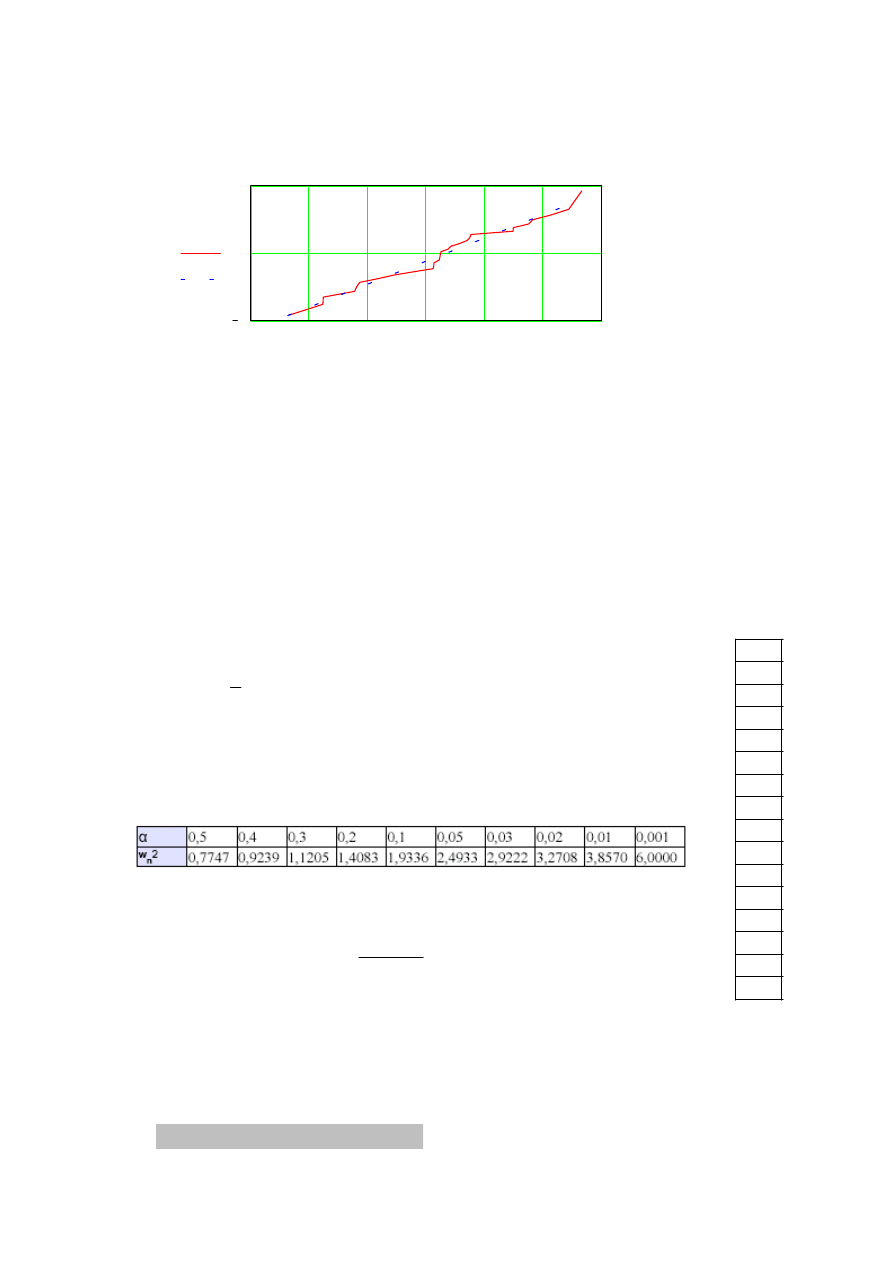
:=
x
min dane_zredl
(
) min dane_zredl
(
)
0.1
+
,
max dane_zredl
(
)
..
:=
Wykres

wniosek "hipoteza nie jest odrzucona"
=
wniosek
if w2 w2_kryt
>
"hipoteza jest odrzucona"
,
"hipoteza nie jest odrzucona"
,
(
)
:=
wniosek
H_w2
0.142
=
H_w2
w2
w2_kryt
:=
w2_kryt
0.4614
:=
na poziomie istotnosci 0,05 wartosc krytyczna
w2_kryt wynosi
w2 0.065
=
w2
1
12 n
×
i
dn
i
( )
2
å
+
:=
dn
i
p
i
prt
i
-
:=
test omega kwadrat
wniosek "hipoteza nie jest odrzucona"
=
wniosek
if max dn
(
) dn_kryt
>
"hipoteza jest odrzucona"
,
"hipoteza nie jest odrzucona"
,
(
)
:=
wniosek
H_ks
0.486
=
H_ks
max dn
(
)
dn_kryt
:=
dn_kryt
0.2417
:=
na poziomie istotnosci 0,05 wartosc krytyczna dn_kryt wynosi
max dn
(
)
0.118
=
dn
i
p
i
prt
i
-
:=
n 30
=
Test Kolmogorowa-Smirnowa
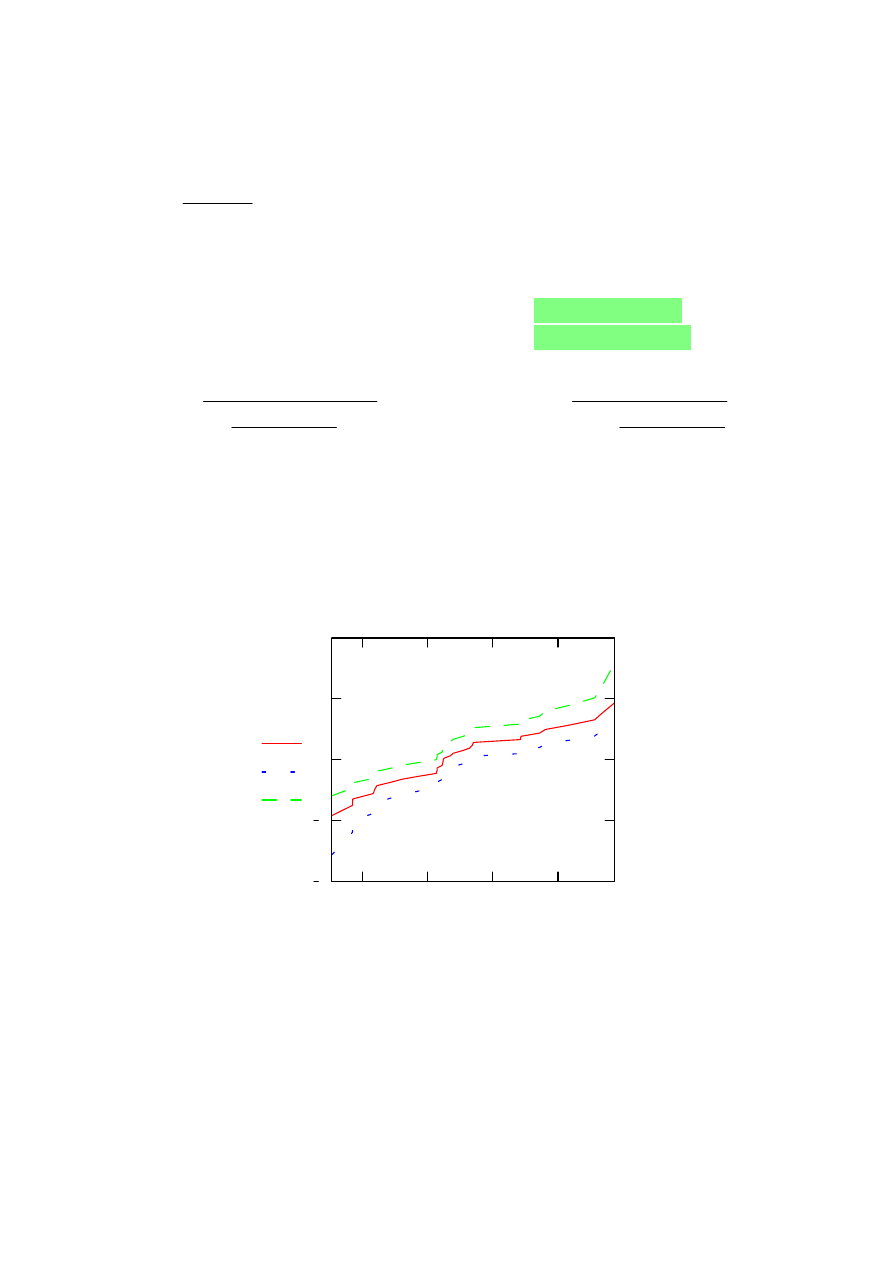
to byl rozklad logarytmo-normalny
300
400
500
600
4
2
0
2
4
y
i
y_d
i
y_g
i
dane_zred
i
Wykres
górny
y_g
i
qnorm F_g
i
0
,
1
,
(
)
:=
dolny
y_d
i
qnorm F_d
i
0
,
1
,
(
)
:=
F_g
i
f_g
i
f_g
i
M cz_wyst
i
-
(
)
cz_wyst
i
+
:=
F_d
i
1
1
M cz_wyst
i
-
(
)
cz_wyst
i
f_d
i
×
+
:=
Snedecora Fishera
-
kwantyle
-
rozkladu
f_g
i
qF b k2
i
,
k1
i
,
(
)
:=
f_d
i
qF b k1
i
,
k2
i
,
(
)
:=
k2
i
2 cz_wyst
i
×
:=
k1
i
2
M
cz_wyst
i
-
(
)
×
:=
b
0.975
=
b
1
0.95
+
(
)
2
:=
II. Obliczanie jednostronnych granic przedzialow ufnosci dla nieznanej dystrybuanty
na poziomie ufnosci b=0.95
OSZACOWANIE PRZEDZIALOWE

2
Wyszukiwarka
Podobne podstrony:
PF rozkład logarytmo normalny
J Ossowski Rozklad logarytmiczno normalny
J Ossowski Rozkład logarytmiczno normalny a względne i absolutne miary rozproszeń
PF rozkład normalny
PF rozkład Weibulla
PF rozkład Gumbela
Wyznaczanie rozkładu naprężeń normalnych i stycznych w przekroju belki zginanej, Budownictwo PCz, Wy
02b Rozkład normalnyid 4039 ppt
Tablica standaryzowanego rozkładu normalnego o wartości oczekiwanej równej zeru i wariancji równej j
T3 Rozkład normalny
sad-materialy-pomocnicze, Rozkład Normalny N, Rozkład Normalny N(0,1)
Prawdopodobieństwo Rozkład dwumianowy Rozkład normalny
Rozkład normalny, sql
rozklad normalny
więcej podobnych podstron