45

4. ZAGADNIENIA ŚCISKANIA I ROZCIĄGANIA OSIOWEGO

Ze stanem ściskania (lub rozciągania) mamy do czynienia wtedy, gdy na pręt działa jedynie

siła osiowa przyłożona w środku ciężkości pręta. Jeżeli pręt poddany działaniu siły osiowej

ma stały przekrój, to poszczególne przekroje poprzeczne pozostają płaskie po odkształceniu

(jeśli materiał jest izotropowy) i naprężenia normalne są stałe. Lokalne zmiany kształtu pręta

prowadzą do powstania koncentracji naprężeń. Stosując model materiału liniowo sprężystego

obliczamy naprężenia jako:

l

l

E

E

A

N

∆

⋅

=

⋅

=

=

ε

σ

.

Wydłużenie pręta obliczamy jako

EA

l

N

l

⋅

=

∆

. Odkształcenia w kierunkach poprzecznych do

osi pręta obliczamy jako:

z

z

x

y

νε

ε

νε

ε

−

=

−

=

,

. Dla materiałów o liczbie Poissona

0

>

ν

przy

rozciąganiu pręta otrzymujemy zwężenie części środkowej pręta. Oczywiście dla ciała

izotropowego mamy

>

∈<

2

1

,

0

ν

(materiał idealnie ściśliwy, materiał nieściśliwy).

N

N

W niektórych zastosowaniach praktycznych stosuje się model biliniowy określony jako











≥













−

+

⋅

≤

⋅

=

0

0

0

,

1

,

σ

σ

σ

ε

σ

σ

ε

σ

τ

τ

E

E

E

E

E

E

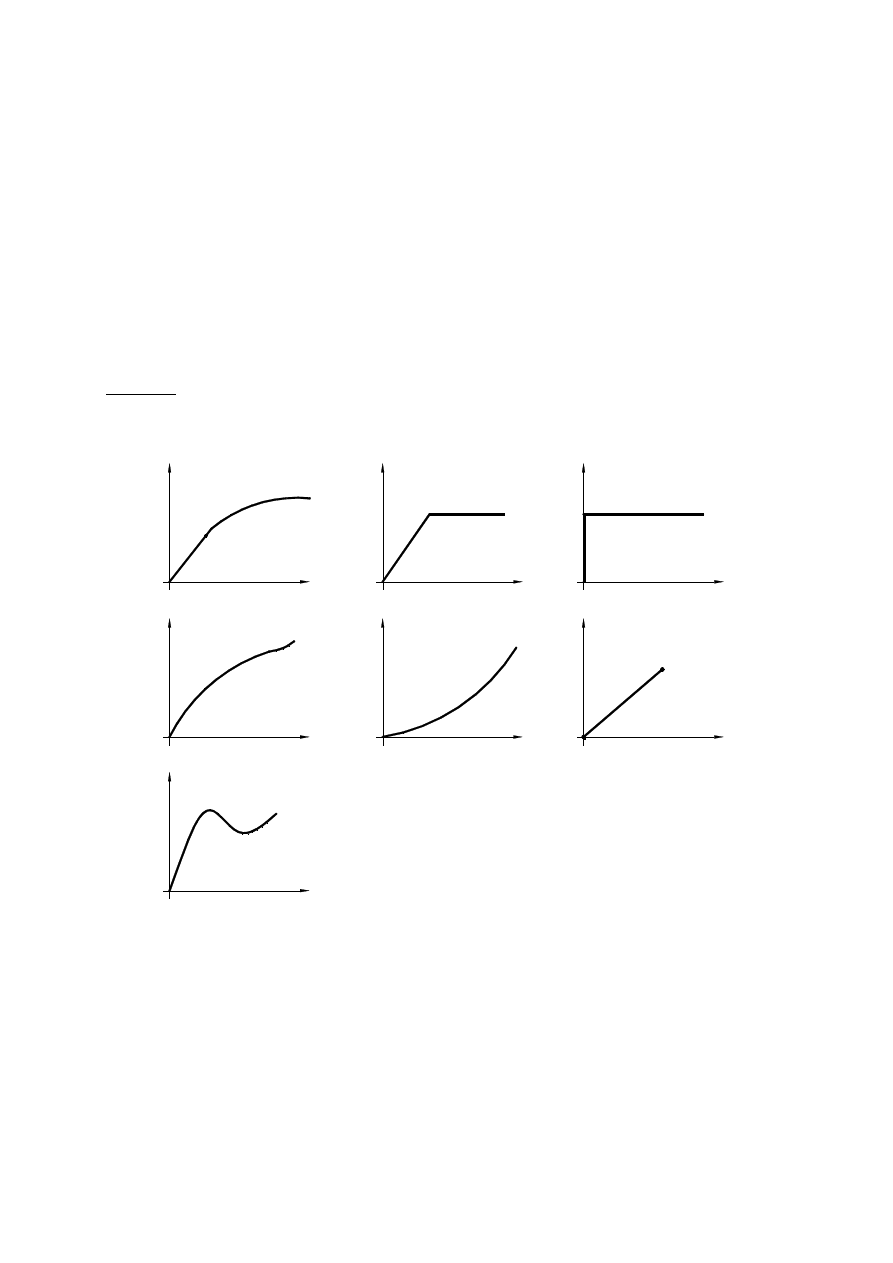
46

lub też modele hipo- lub hipersprężyste. Materiał w stanie sprężystym powraca do swojego

pierwotnego kształtu po usunięciu wszystkich obciążeń. W dalszej analizie będziemy

posługiwali się również modelami sprężysto-plastycznymi, w których występują odkształcenia

trwałe. Do analizy materiałów, których własności zmieniają się w czasie (z reguły maleją

wraz z upływem czasu) stosuje się modele lepko-sprężyste lub modele lepko-sprężysto-

plastyczne oraz lepko-plastyczne.

Polecenie. Na podstawie literatury dokonaj klasyfikacji materiału na podstawie wykresu

naprężenie-odkształcenie.

ε

σ

σ

ε

σ

ε

σ

ε

σ

ε

σ

ε

σ

ε

Bardzo często rozwiązując problemy z zakresu ściskania i rozciągania możemy uwzględniać

błędy montażowe,

jakie zdarzają się w rzeczywistych konstrukcjach; analizujemy

również wpływ temperatury na odkształcenia układu wywołany ogrzaniem lub schło-

dzeniem jednego z prętów. Błędy montażowe to odchyłki wymiarowe spowodowane

niedokładnym zestawieniem (połączeniem) odpowiednich elementów konstrukcji (wybrane

pręty są zbyt długie lub za krótkie w stosunku do pozostałych). Błędy te wywołują naprężenia

wstępne, które mogą pogorszyć wytrzymałość i niezawodność konstrukcji. Jak można się

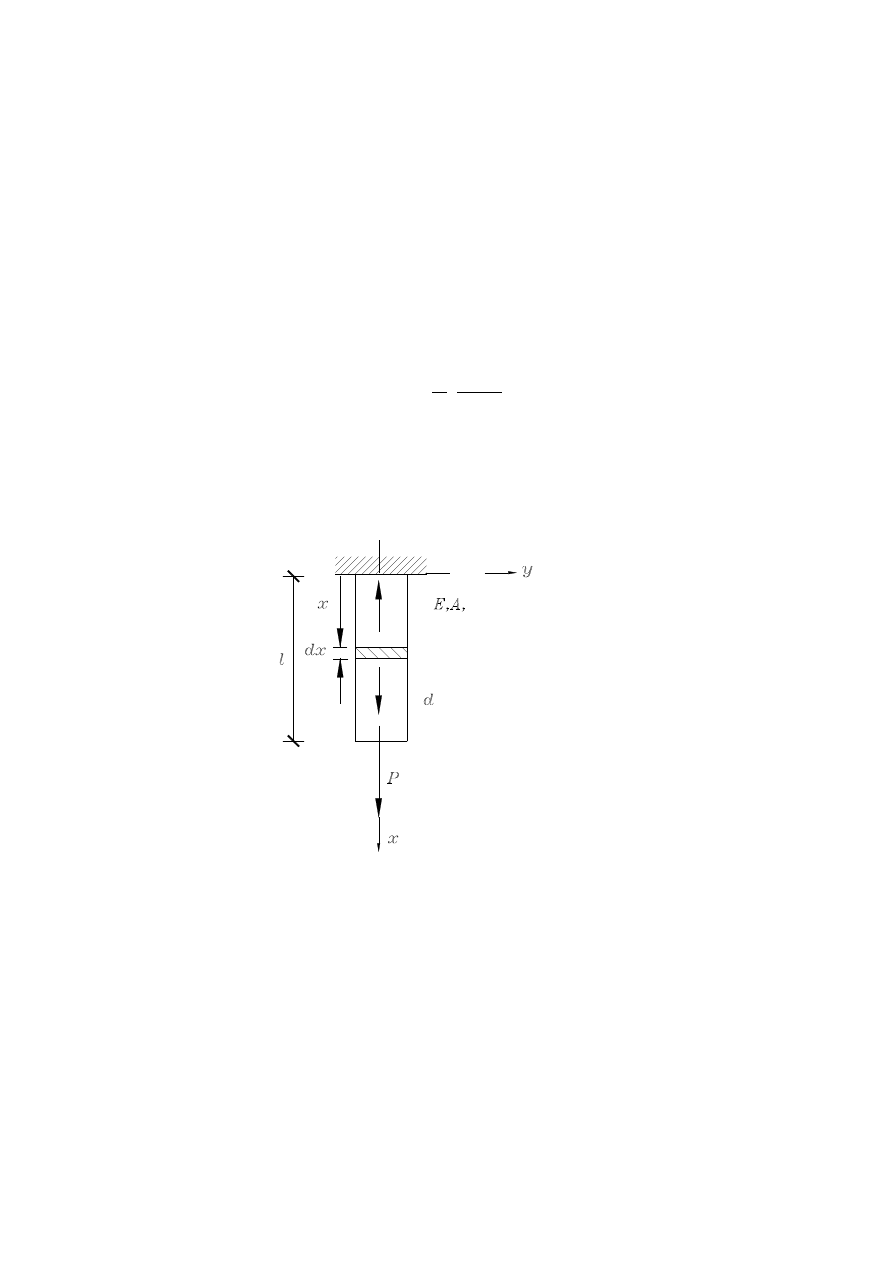
47

przekonać, w konstrukcjach statycznie niewyznaczalnych nawet nieznaczne błędy montażowe

mogą spowodować znaczne naprężenia i odkształcenia. Z drugiej strony w konstrukcjach

i elementach konstrukcyjnych o znacznych rozmiarach stosuje się świadomie tzw. dylatacje,

czyli otwory lub przerwy, które mają za zadanie zmniejszenie pojawiających się w nich

odkształceń termicznych.

Wpływ temperatury można pokazać na przykładzie pręta w temperaturze

o

0 o długości

0

l , przy

wzroście temperatury od

1

t

do

2

t

; jego długość zmienia się od

1

l

do

2

l

, a średnim

współczynnikiem rozszerzalności liniowej nazywamy iloraz

1

2

1

2

0

2

,

1

1

t

t

l

l

l

−

−

⋅

=

α

.

Oznaczając l

1

-l

2

=

∆

l , t

1

-t

2

=

∆

t ,

α

1,2

=

α

, otrzymujemy

∆

l = l

0

α∆

t,

ε

=

α∆

t.

Wyprowadźmy kolejno równania równowagi przy ściskaniu i/lub rozciąganiu dla pręta

obciążonego ciężarem własnym i siłą podłużną.

γ

σ

σ+ σ

Suma rzutów na oś x dla elementarnego odcinka jest następująca:

(

)

.

,

0

,

0

γ

σ

γ

σ

σ

γ

σ

σ

dx

d

Adx

Ad

A

Adx

d

A

−

=

=

+

=

−

+

+

Stałą C wyznaczamy z warunku brzegowego:

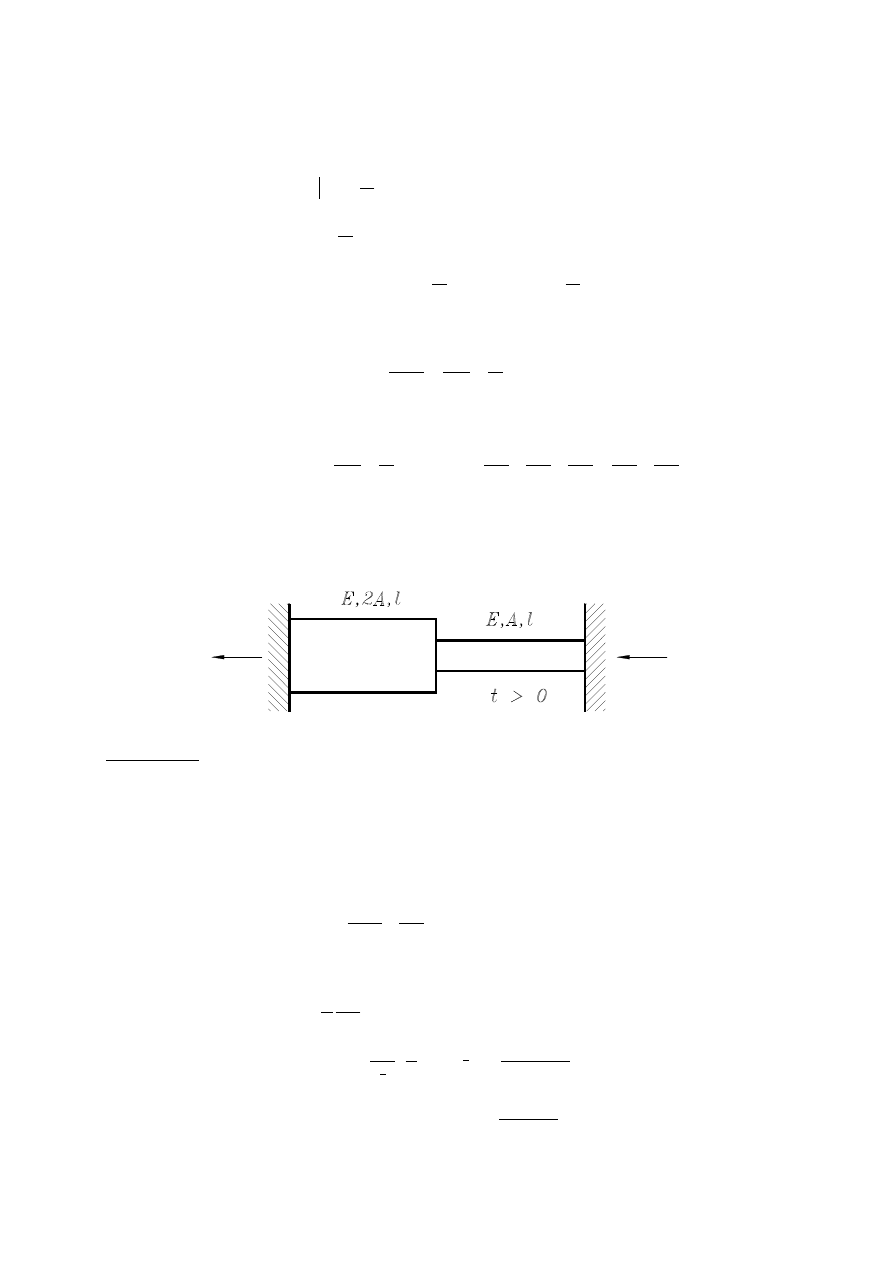
48

( )

(

)

.

,

,

,

0

A

P

x

l

l

A

P

x

x

l

A

P

C

C

l

A

P

C

x

dx

d

l

x

x

+

−

=

+

+

−

=

=

+

=

+

−

=

=

+

−

=

−

=

=

=

∫

∫

γ

γ

γ

σ

σ

γ

γ

σ

γ

γ

σ

σ

Odkształcenie natomiast wynosi

( )

( )

(

)

x

l

E

AE

P

E

x

x

−

+

=

=

γ

σ

ε

.

Całkowite wydłużenie pręta jest równe

( )

(

)

∫

∫

+

=

−

+

=













−

+

=

=

l

l

E

l

EA

Pl

E

l

E

l

EA

Pl

dx

x

l

E

AE

P

dx

x

0

2

2

2

0

2

2

γ

γ

γ

γ

ε

λ

.

Problem 4.1. Znaleźć reakcje w poniższym układzie statycznie-niewyznaczalnym.

∆

1

R

2

R

Rozwiązanie. Zapisujemy równanie równowagi sił podłużnych:

∑

=

+

=

0

;

0

2

1

R

R

P

y

oraz równanie geometryczne opisujące przyrosty długości poszczególnych prętów

( )

0

2

2

0

1

1

2

1

=

⋅

∆

+

+

=

+

⋅

∆

+

∆

+

∆

l

t

EA

l

R

EA

l

R

l

l

t

l

l

t

t

α

α

.

Obliczamy kolejno pierwszą reakcję

3

4

3

4

2

2

3

1

1

t

EA

l

t

l

EA

R

l

t

EA

l

R

t

t

t

∆

−

=

⋅

∆

⋅

−

=

⋅

∆

−

=

α

α

α

i obliczamy naprężenie normalne w tym pręcie

3

2

1

t

E

t

∆

−

=

α

σ

. Kolejno dla drugiego pręta

49

3

4

;

3

4

2

1

2

t

E

t

EA

R

R

t

t

∆

−

=

∆

=

−

=

α

σ

α

.

W obu częściach struktury prętowej mamy więc ściskanie.

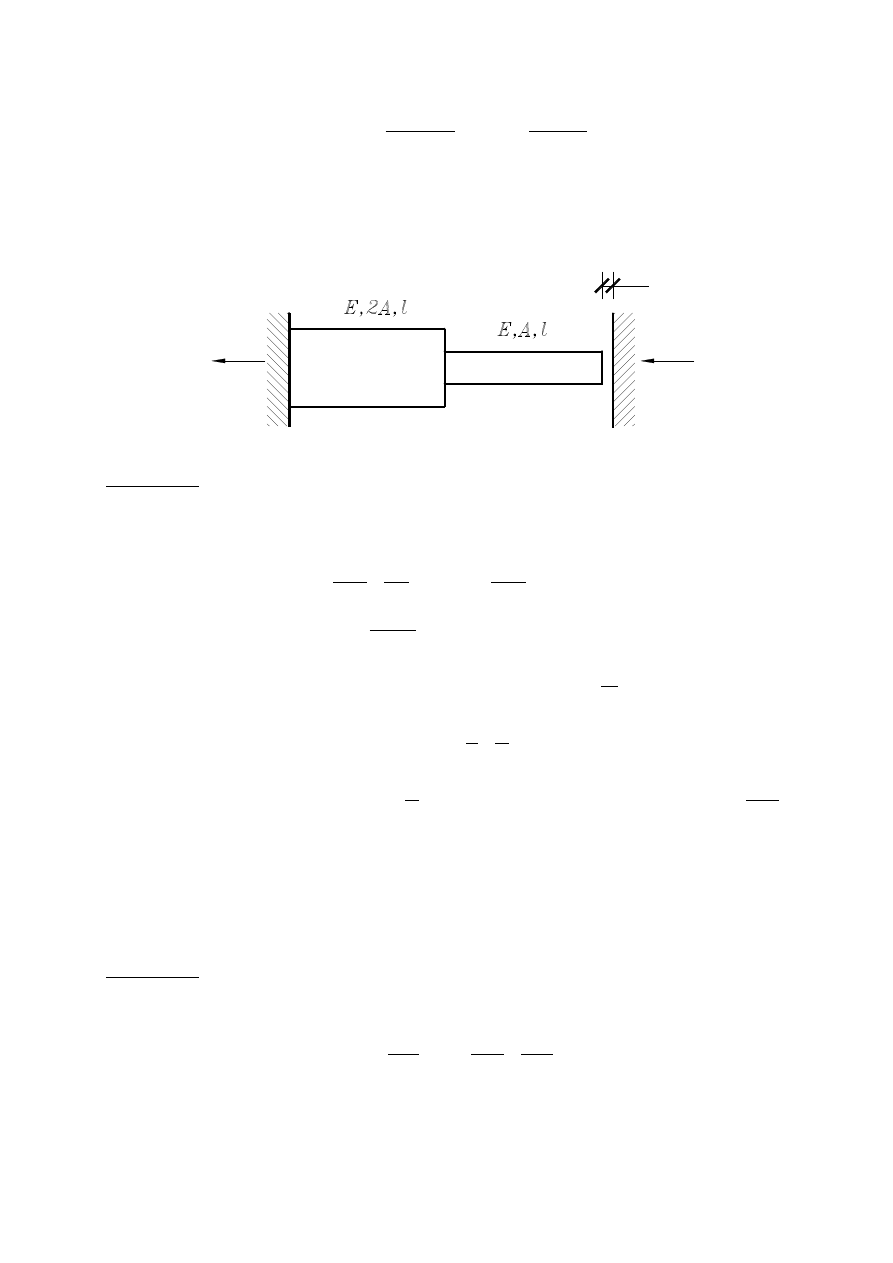
Problem 4.2. Znaleźć reakcje w następującym układzie statycznie niewyznaczalnym.

δ

1

R

2

R

Rozwiązanie. W pierwszej kolejności znajdujemy reakcje z następujących równań:

2

1

1

1

1

2

1

2

1

3

2

2

3

0

2

0

0

;

0

R

l

EA

R

EA

l

R

EA

l

R

EA

l

R

l

l

R

R

P

y

−

=

=

=

→

=

−

+

=

−

∆

+

∆

=

+

=

∑

δ

δ

δ

δ

.

W dalszej kolejności obliczamy naprężenia w prętach ze wzoru

A

N

=

σ

jako

l

E

δ

σ

σ

3

2

2

1

=

−

=

.

Dla wartości parametrów

3

10

,

210

−

=

=

l

GPa

E

δ

obliczamy

2

2

1

14

14

,

0

cm

kN

GPa

=

=

=

σ

σ

.

Jak widać zamontowanie zbyt krótkiego pręta powoduje powstanie rozciągających naprężeń

wstępnych w całym układzie prętowym.

Problem 4.3. Znaleźć reakcje dla następującego układu.

Rozwiązanie. Z równania równowagi mamy :

2

1

R

P

R

+

=

, natomiast z odkształceń wynika,

ż

e

0

2

1

=

∆

+

∆

l

l

, a więc

2

1

1

2

2

2

1

1

1

1

,

EA

l

R

EA

Pl

l

EA

l

R

l

−

=

∆

−

=

∆

.

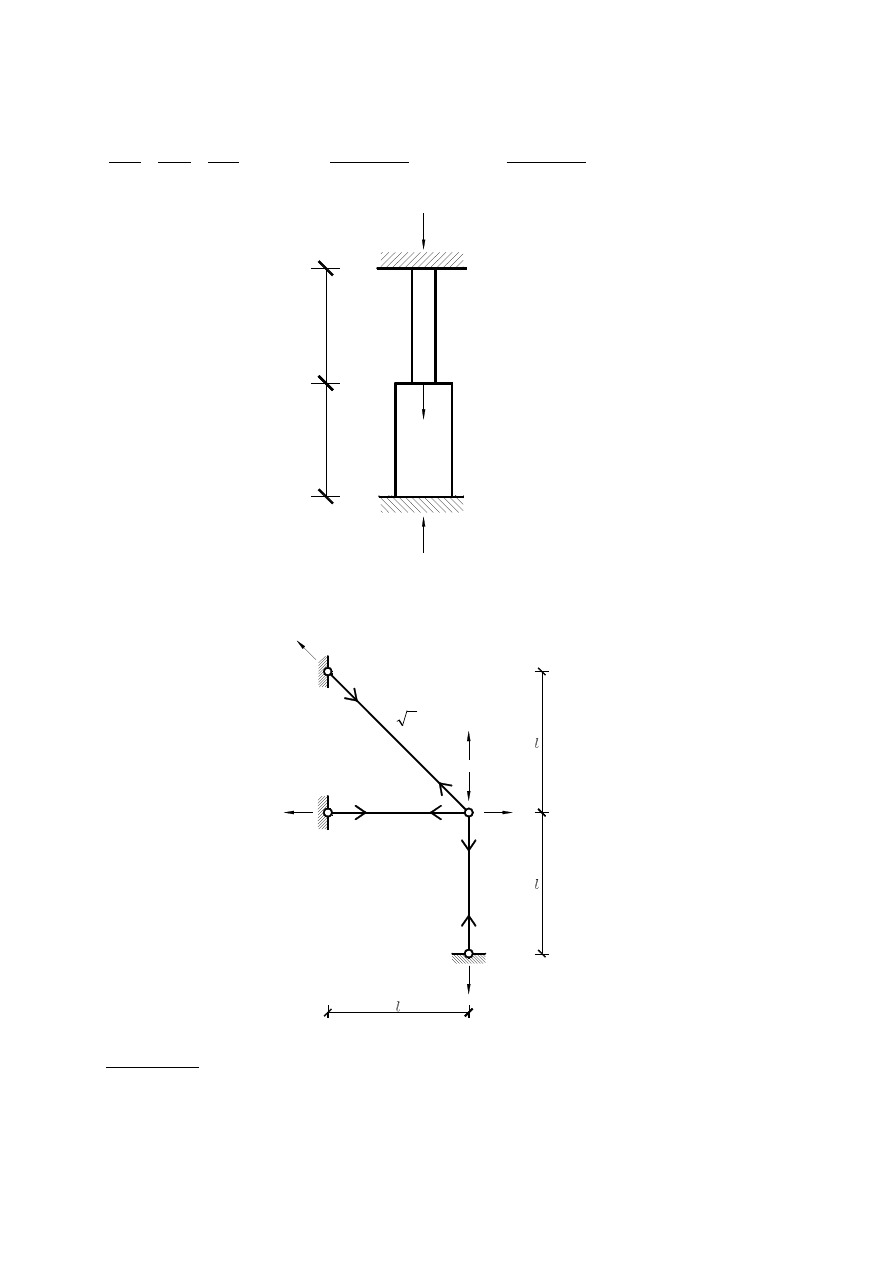
50

Sumując otrzymujemy

2

1

1

2

2

1

2

2

1

1

2

1

2

1

1

1

1

2

2

1

2

2

;

0

l

A

l

A

A

Pl

R

l

A

l

A

A

Pl

R

EA

l

R

EA

l

R

EA

Pl

+

−

=

+

=

⇒

=

−

−

.

2

l

1

l

2

R

1

R

P

1

EA

2

EA

Problem 4.4. Znaleźć siły wewnętrzne w następującym układzie statycznym.

1

S

1

S

2

S

2

S

3

S

3

S

A

E ,

A

E,

A

E ,

2

P

V

u

Rozwiązanie. Układ tak samo jak w poprzednich problemach jest statycznie niezwyzna-

czalny. W odróżnieniu jednak od poprzednich przykładów zawiera pręty niewspółliniowe,

więc równania geometryczne muszą zawierać stopnie swobody, jakie posiada węzeł

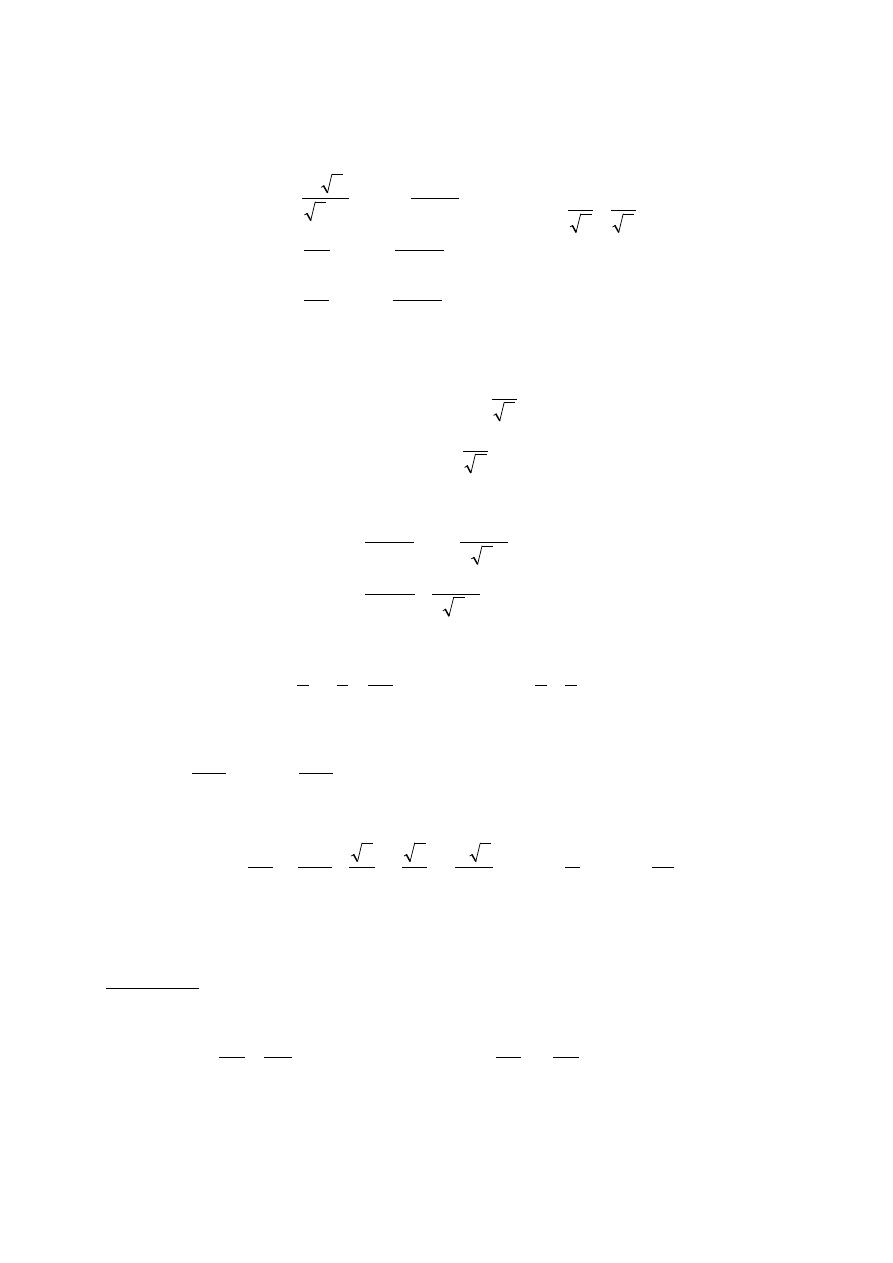
51

obciążony siłą P – niech będą to przemieszczenie poziome u oraz przemieszczenie pionowe v.

Zapisujemy kolejno związki fizyczne i geometryczne. Otrzymujemy





















∆

=

→

=

∆

∆

=

→

=

∆

∆

=

→

=

∆

l

l

EA

S

EA

l

S

l

l

l

EA

S

EA

l

S

l

l

l

EA

S

EA

l

S

l

3

3

3

3

2

2

2

2

1

1

1

1

2

2

,

















=

∆

=

∆

−

=

∆

v

l

u

l

v

u

l

3

2

1

2

2

.

Równania równowagi pozwalają obliczyć

0

2

;

0

0

2

;

0

1

2

1

3

=

−

−

=

=

+

−

−

=

∑

∑

S

S

Px

S

P

S

Py

,

co po podstawieniu daje

0

2

0

2

1

2

1

3

=

∆

−

∆

−

=

∆

+

−

∆

−

l

l

EA

l

l

EA

l

l

EA

P

l

l

EA

.

Wyrażając te równania przez przemieszczenia u i v otrzymujemy:

EA

Pl

u

v

=

+

−

2

2

3

;

0

2

2

=

+

−

−

v

u

u

.

Stąd wyznaczamy poszukiwane przemieszczenia:

EA

Pl

v

EA

Pl

u

4

3

,

4

−

=

−

=

oraz siły

4

3

,

4

,

4

2

2

2

3

2

2

4

3

2

1

P

S

P

S

P

EA

Pl

l

EA

S

−

=

−

=

=















−













−

=

.

Problem 4.5. Znaleźć siły wewnętrzne w podanym układzie statycznie niewyznaczalnym.

Rozwiązanie. Z geometrii układu wynika, że jedynym stopniem swobody jest obrót względem

podpory o kąt φ. A zatem z podobieństwa trójkątów obliczamy

2

1

2

1

2

2

l

l

l

l

l

l

∆

=

∆

→

∆

=

∆

;

EA

l

S

EA

l

S

2

1

2

−

=

bo

0

2

<

∆

l

.

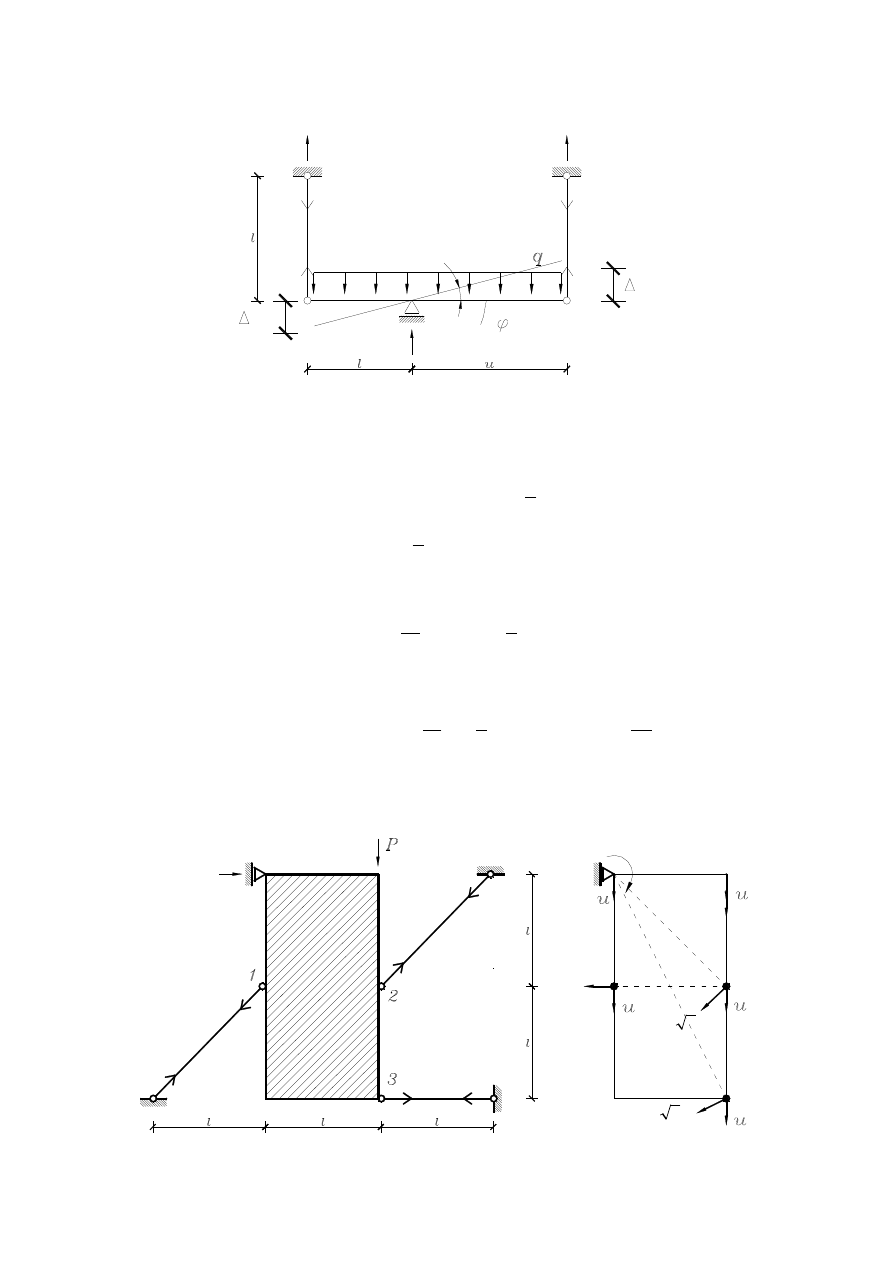
52

S

S

S

S

E,A

E,A

R

1

2

2

2

1

1

B

l

l

Stąd wynika, że

.

2

3

2

0

2

1

3

2

;

0

0

2

2

1

2

1

2

1

ql

S

S

l

ql

l

S

l

S

M

S

S

B

−

=

−

=

−

−

=

Σ

=

+

Rozwiązaniem tego zadania są następujące wielkości:

ql

S

ql

S

5

3

,

10

3

2

1

=

−

=

.

Z

∑

=

0

Py

obliczamy:

ql

R

ql

ql

ql

R

ql

S

S

R

10

27

0

3

5

3

10

3

0

3

2

1

=

⇒

=

−

+

−

⇒

=

−

+

+

.

Problem 4.6. Znaleźć siły w prętach dla następującego układu.

EA

EA

EA

1

S

2

S

3

S

A

H

ϕ

l

ϕ

l

ϕ

2

l

ϕ

5

l

ϕ

53

Rozwiązanie. Zapisujemy warunki równowagi:

.

0

2

2

2

2

;

0

,

0

2

2

2

2

;

0

,

0

2

2

2

2

;

0

3

2

1

2

1

3

2

1

∑

∑

∑

=

+

−

−

=

=

−

+

=

=

+

+

−

=

Pl

l

S

l

S

l

S

M

S

S

P

Py

S

S

S

H

Px

A

A

Warunki geometryczne otrzymujemy na podstawie następującego schematu:

l

l

l

l

l

l

u

l

l

u

l

ϕ

ϕ

ϕ

ϕ

2

5

2

5

;

2

2

2

;

2

2

2

2

3

2

1

=

⋅

=

∆

+

=

∆

−

−

=

∆

,

stąd

2

2

2

1

l

l

l

ϕ

=

∆

+

∆

i

l

l

ϕ

2

3

=

∆

,

zatem

4

2

3

2

1

l

l

l

∆

=

∆

+

∆

.

Związki fizyczne:

EA

l

S

A

E

l

S

l

EA

l

S

A

E

l

S

l

EA

l

S

A

E

l

S

l

3

3

3

3

3

3

2

2

2

2

2

2

1

1

1

1

1

1

;

2

;

2

=

=

∆

=

=

∆

=

=

∆

.

Podstawiając otrzymujemy:

4

2

2

2

3

2

1

EA

l

S

EA

l

S

EA

l

S

=

+

lub

0

4

3

2

1

=

−

+

S

S

S

.

Mamy:

.

0

4

1

,

2

2

2

2

,

3

2

1

3

2

1

2

1

=

−

+

−

=

−

−

−

=

−

S

S

S

P

S

S

S

P

S

S

.

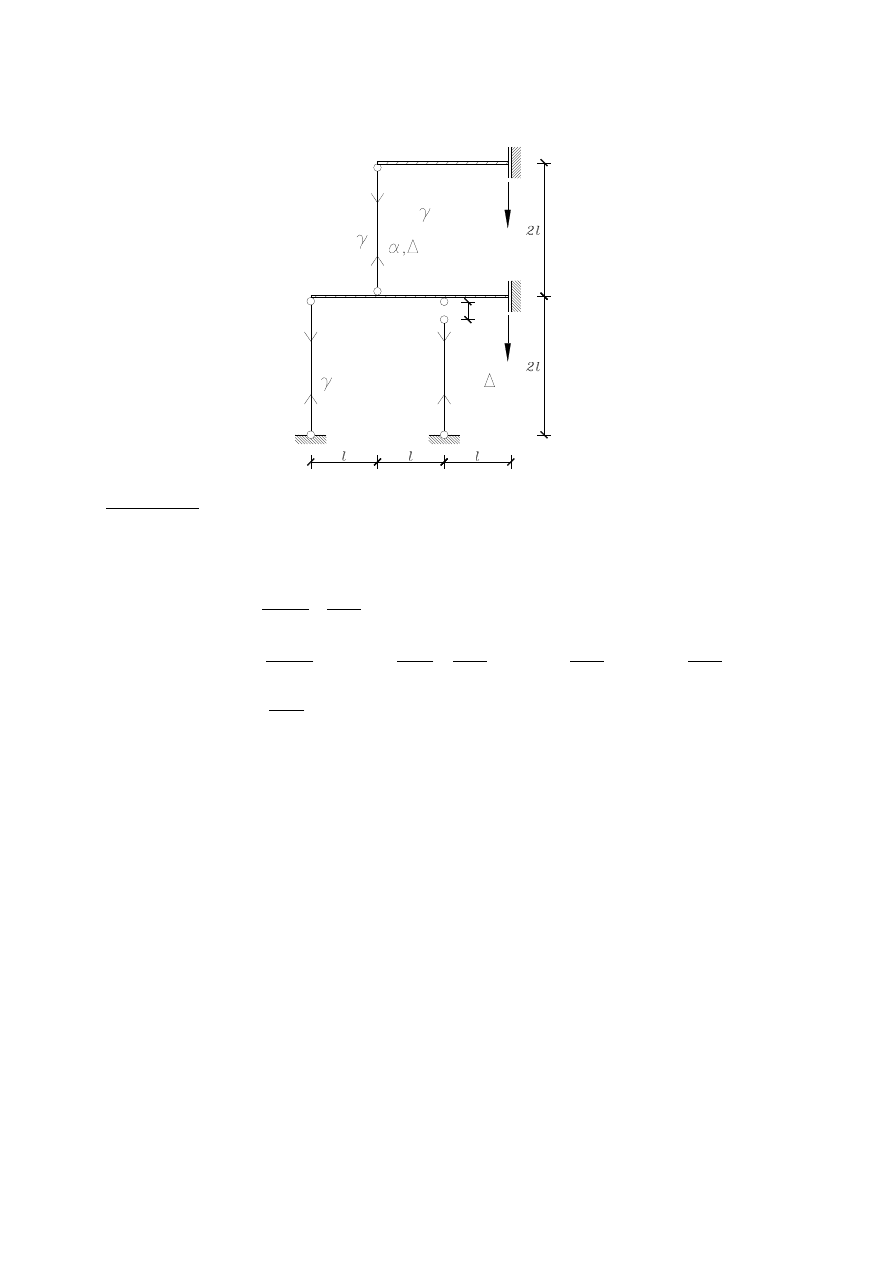
54

Problem 4.7. Obliczyć siły w prętach dla następującego układu.

∆

EA

EA

EA,

V

V

S

S

S

2

2

1

1

+ 2lA

t

t

t

Rozwiązanie. W rozwiązaniu ograniczymy się jedynie do podania podstawowych równań

pozostawiając czytelnikowi dokładne ich rozwiązanie. Otrzymujemy następujące związki

fizyczne:

( )

( )

.

2

,

2

2

,

2

2

4

2

2

2

2

2

2

,

2

2

2

2

3

1

3

2

2

2

2

2

1

2

1

2

1

1

A

l

S

l

t

EA

l

S

v

l

E

l

tl

E

l

l

t

E

l

EA

l

S

l

t

E

l

v

v

l

EA

l

S

E

l

v

l

t

t

t

t

⋅

⋅

−

=

∆

+

=

−

∆

=

∆

−

∆

=

−

∆

+

=

+

∆

+

=

−

=

∆

+

−

=

−

=

∆

γ

α

γ

α

γ

α

γ

α

γ

γ

Odpowiednie równanie równowagi ma następującą postać:

∑

=

−

+

−

=

0

;

0

3

2

1

S

S

S

Piy

.