Materiały pomocnicze do zajeć z ekonometrii SSW Chojnice 2012
Krzysztof Świetlik
Materiały pomocnicze do zajeć z ekonometrii SSW Chojnice 2012
Krzysztof Świetlik
1
1
1. SZACOWANIE LINIOWYCH I NIELINIOWYCH MODELI
TRENDU
Przykład 1.
Na podstawie danych przedstawionych w tabeli 1 oszacować liniowy model trendu spożycia pieczywa w
polskich gospodarstwach domowych.
Tabela 1. Przeciętne miesięczne spożycie pieczywa w polskich gospodarstwach domowych ogółem w latach 2007-2009 [kg
/ osobę] w układzie kwartalnym
2007 2008
2009
1 kwartał
7,14 6,94
6,67
2 kwartał
7,35 7,03
6,97
3 kwartał
7,36 7,15
6,86
4 kwartał
7,10 7,11
6,80
Naszym zadaniem jest oszacowanie MNK parametrów modelu o postaci ogólnej:
t
t
t
b
b
y
ε
+
⋅
+
=
1
0
Rolę zmiennej objaśnianej y
t
w naszym przykładzie gra zmienna miesięcznego spożycia pieczywa na
1 osobę. Z kolei rolę zmiennej objaśniającej x
1t
gra zmienna czasu t.
W celu wyznaczenia realizacji estymatora $
b musimy wyznaczyć macierz X’X. Ponadto musimy też
wyznaczyć wektor X’y. Dla tych działań pomocna okaże się tabela 2.
Tabela 2. Obliczenia pomocnicze do przykładu 1.
Numer
obserwacji
y
t
t t
2
y
t
*t
1 7,14 1 1 7,14
2 7,35 2 4 14,7
3 7,36 3 9 22,08
4 7,1 4 16 28,4
5 6,94 5 25 34,7
6 7,03 6 36 42,18
7 7,15 7 49 50,05
8 7,11 8 64 56,88
9 6,67 9 81 60,03
10 6,97 10 100 69,7
11 6,86 11 121 75,46
12 6,8 12 144 81,6
Suma (
Σ)
84,48 78 650 542,92
Macierz X’X będzie miała następującą postać:
′ =
=
∑
∑ ∑
X X
n
t
t
t
2
12
78
78 650
Wyznacznik macierzy X’X:
|X’X| = (12*650-78*78) = 1716
Macierz
dopełnień algebraicznych (X’X)
D
ma postać:
(
)
( )
( )
( )
( )
′
=
−
⋅
−
⋅
−
⋅
−
⋅
=
−
−
+
+
+
+
X X
D
1
650
1
78
1
78
1
12
650
78
78
12
1 1
1 2
2 1
2 2
Materiały pomocnicze do zajeć z ekonometrii SSW Chojnice 2012
Krzysztof Świetlik
Materiały pomocnicze do zajeć z ekonometrii SSW Chojnice 2012
Krzysztof Świetlik
2
2
Transponowana macierz dopełnień algebraicznych
(
)
[
]
′
X X
D /
jest identyczna z macierzą
(
)
′
X X
D
ze
względu na symetryczność tej ostatniej. Stąd operacja transponowania macierzy jest tutaj zbędna.
Macierz odwrotna do macierzy X’X jest określona następująco:
(
)
′
=
⋅
−
−
=
−
−
−
X X
1
1
1716
650
78
78
12
0 37878
0 04545
0 04545
0 00699
,
,
,
,
Teraz z kolei wyznaczmy wektor X’y. Skorzystamy tu z odpowiedniej formuły oraz wielkości obliczonych
w tabeli 2.
′ =
⋅
=
∑
∑
X y
y
y t
t
t
84 48
542 92
,
,
Korzystając z wyników powyższych obliczeń wyznaczymy wartość estymatora $b :
(
)
$
,
,
,
,
,
,
,
,
,
,
,
,
,
,
$
,
,
$
$
b
X X
X y
b
b
b
=
′
′ =
−
−
⋅
=
⋅
−
⋅
−
⋅
+
⋅
=
−
←
←
−1
0
1
0 37878
0 04545
0 04545
0 00699
84 48
542 92
0 37878 84 48 0 04545 542 92
0 04545 84 48 0 00699 542 92
7 3236
0 0446
Otrzymaliśmy zatem wektor ocen parametrów strukturalnych modelu. Górny element wektora to ocena
parametru b
0
, zaś dolny to ocena parametru b
1
. Model trendu możemy zatem zapisać w postaci analitycznej:
t
t
t
y
ε
ˆ
045
,
0
324
,
7
+
⋅
−
=
Po oszacowaniu modelu przystępujemy do jego interpretacji. Wyrazu wolnego $b
0
nie interpretujemy w
żadnym z modeli. Interpretujemy natomiast oceny parametrów przy zmiennych objasniających modelu.
Powiemy,
że w każdym kolejnym kwartale rozpatrywanych lat średnie miesięczne spożycie pieczywa w
przeliczeniu na 1 osobę w gospodarstwach domowych ogółem spadało przeciętnie o 0,045 kilograma. Stąd
wnioskujemy, że po czterech kwartałach, czyli roku analizowane spożycie pieczywa malało średnio o 4*0,045
kg, czyli 0,18 kg na osobę.
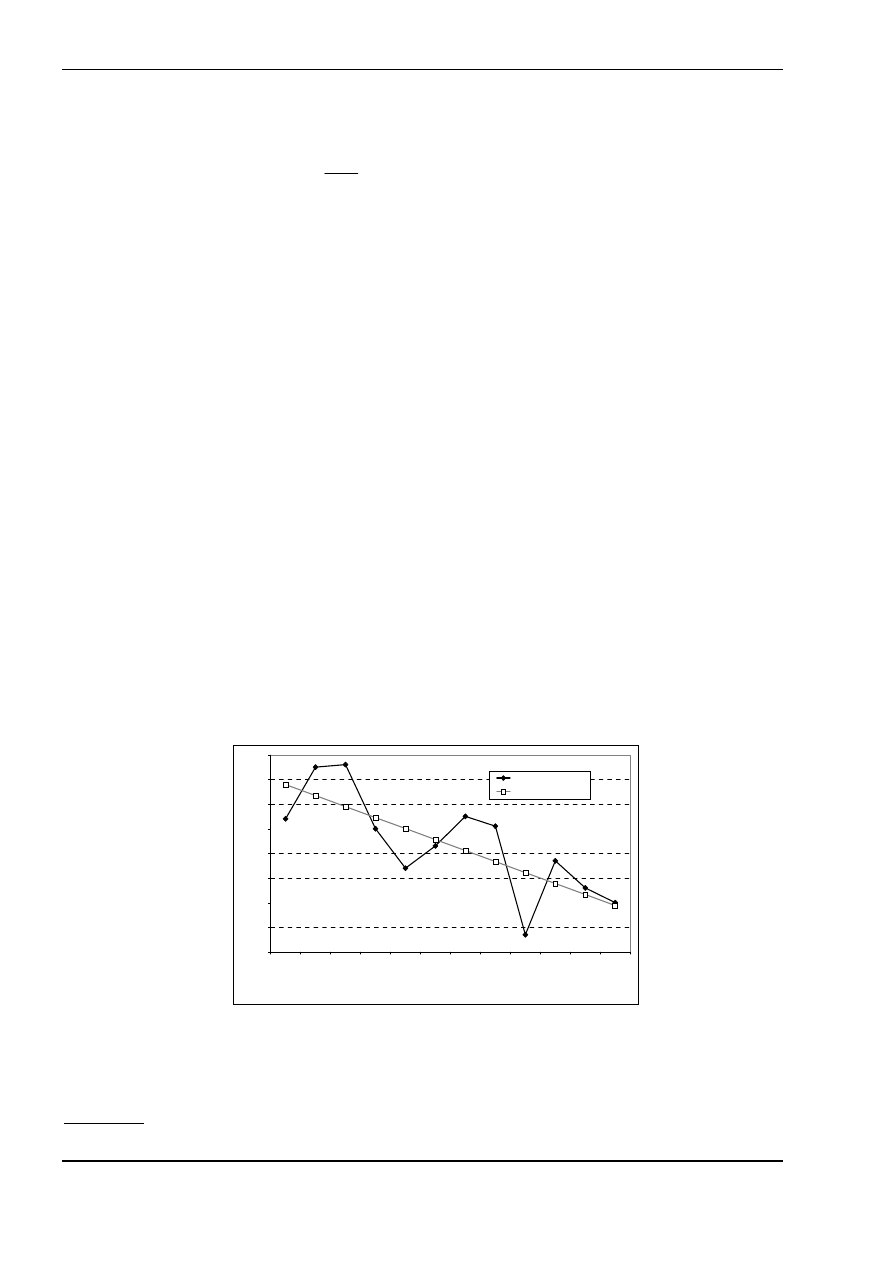
Na wykresie 2 przedstawiono graficzną reprezentację oszacowanego liniowego modelu trendu (prosta
opadająca) oraz wartości rzeczywistych.
Wykres 2. Wartości rzeczywiste i teoretyczne (oszacowane z modelu trendu ()) przeciętnego miesięcznego spożycia
pieczywa (do przykładu 1)
6,6
6,7
6,8
6,9
7
7,1
7,2
7,3
7,4
1 kw
97
2 kw
97
3 kw
97
4 kw
97
1 kw
98
2 kw
98
3 kw
98
4 kw
98
1 kw
99
2 kw
99
3 kw
99
4 kw
99
Wartości rzeczywiste
Wartości teoretyczne
okres
[kg /
mi
esi
ąc]
źródło: obliczenia własne na podstawie danych GUS
Jak
widać linia trendu nie przystaje do punktów oznaczających wartości zmiennej y
t
a jedynie przedstawia
tendencję rozwojową badanego zjawiska.
Przykład 2.
Na podstawie danych w tabeli 3 oszacować modele liniowy oraz wykładniczy trendu dla depozytów
Materiały pomocnicze do zajeć z ekonometrii SSW Chojnice 2012
Krzysztof Świetlik
Materiały pomocnicze do zajeć z ekonometrii SSW Chojnice 2012
Krzysztof Świetlik
3
3
złotowych gospodarstw domowych ogółem w latach 1993-1995.
Tabela 3. Depozyty złotowe gospodarstw domowych w Polsce na koniec kwartału w latach 1993-1995 [mln zł]
1993 1994
1995
1 kwartał
14225,2
17160,2
26779,4
2 kwartał
14577,9
18562,1
30670,3
3 kwartał
15295,2
19962,2
34771,8
4 kwartał
16265,5
22099,5
39672,6
A) Model liniowy
Model liniowy trendu opisany jest ogólnym wzorem:
t
t
t
b
b
y
ε
+
⋅
+
=
1
0
W naszym przykładzie rolę zmiennej objaśnianej y
t
gra zmienna depozytów gospodarstw domowych, zaś
zmienna opisująca jest t.
W celu wyznaczenia wartości estymatora $b musimy wyznaczyć macierz X’X. Ponadto musimy też
wyznaczyć wektor X’y. Dla tych działań pomocna okaże się tabela 4.
Tabela 4. Obliczenia pomocnicze do przykładu 2A.
Numer
obserwacji
y
t
t t
2
y
t
*t
1
14225,2
1 1
14225,2
2
14577,9
2 4
29155,8
3
15295,2
3 9
45885,6
4
16265,5
4 16
65062,0
5
17160,2
5 25
85801,0
6
18562,1
6 36
111372,6
7
19962,2
7 49
139735,4
8
22099,5
8 64
176796,0
9
26779,4
9 81
241014,6
10
30670,3
10 100
306703,0
11
34771,8
11 121
382489,8
12
39672,6
12 144
476071,2
Suma (
Σ)
270042 78 650
2074312,2
Macierz X’X będzie miała następującą postać:
′ =
=
∑
∑ ∑
X X
n
t
t
t
2
12
78
78 650
Wyznacznik macierzy X’X:
′ =
⋅
−
⋅
=
X X
12 650 78 78 1716
Macierz
dopełnień algebraicznych (X’X)
D
ma postać:
(
)
( )
( )
( )
( )
′
=
−
⋅
−
⋅
−
⋅
−
⋅
=
−
−
+
+
+
+
X X
D
1
650
1
78
1
78
1
12
650
78
78
12
1 1
1 2
2 1
2 2
Macierz odwrotna do macierzy X’X jest określona następująco:
(
)
′
=
⋅
−
−
=
−
−
−
X X
1
1
1716
650
78
78
12
0 37878
0 04545
0 04545
0 00699
,
,
,
,
Teraz z kolei wyznaczmy wektor X’y. Skorzystamy tu z wielkości obliczonych w tabeli 4.
=
⋅
=
′
∑
∑
2
,
2074312
270042
t
y
y
y
X
t
t
Korzystając z wyników powyższych obliczeń wyznaczymy wartość estymatora $b :
Materiały pomocnicze do zajeć z ekonometrii SSW Chojnice 2012
Krzysztof Świetlik
Materiały pomocnicze do zajeć z ekonometrii SSW Chojnice 2012
Krzysztof Świetlik
4
4
(
)
$
,
,
,
,
,
,
,
,
,
,
,
$
,
,
$
$
b
X X
X y
n
t
t
t
y
y t
b
b
b
t
t
=
′
′ =
⋅
⋅
=
−
−
⋅
=
=
⋅
−
⋅
−
⋅
+
⋅
=
←
←
−
∑
∑ ∑
∑
∑
1
2
0
1
0 37878
0 04545
0 04545
0 00699
270042
2074312 2
0 37878 270042 0 04545 2074312 2
0 04545 270042 0 00699 2074312 2
8009 02
2226 03
Otrzymaliśmy wektor ocen parametrów strukturalnych modelu. Górny element wektora to ocena parametru
b
0
, zaś dolny to ocena parametru b
1
. Szacowany model trendu możemy zatem zapisać w postaci analitycznej:
t
t
t
y
ε
ˆ
03
,
2226
02
,
8009
+
⋅
+
=
Interpretacja
modelu:
W
każdym kolejnym kwartale rozpatrywanych lat 1993-1995 wielkość depozytów złotowych ludności
wzrastała średnio o 2226,03 mln zł (2,22603 mld zł). Oznacza to, że średniorocznie wartość depozytów
przyrastała o 4*2226,03 = 8904,12 mln zł.
Przyjrzyjmy
się z kolei reprezentacji graficznej rozpatrywanego modelu.
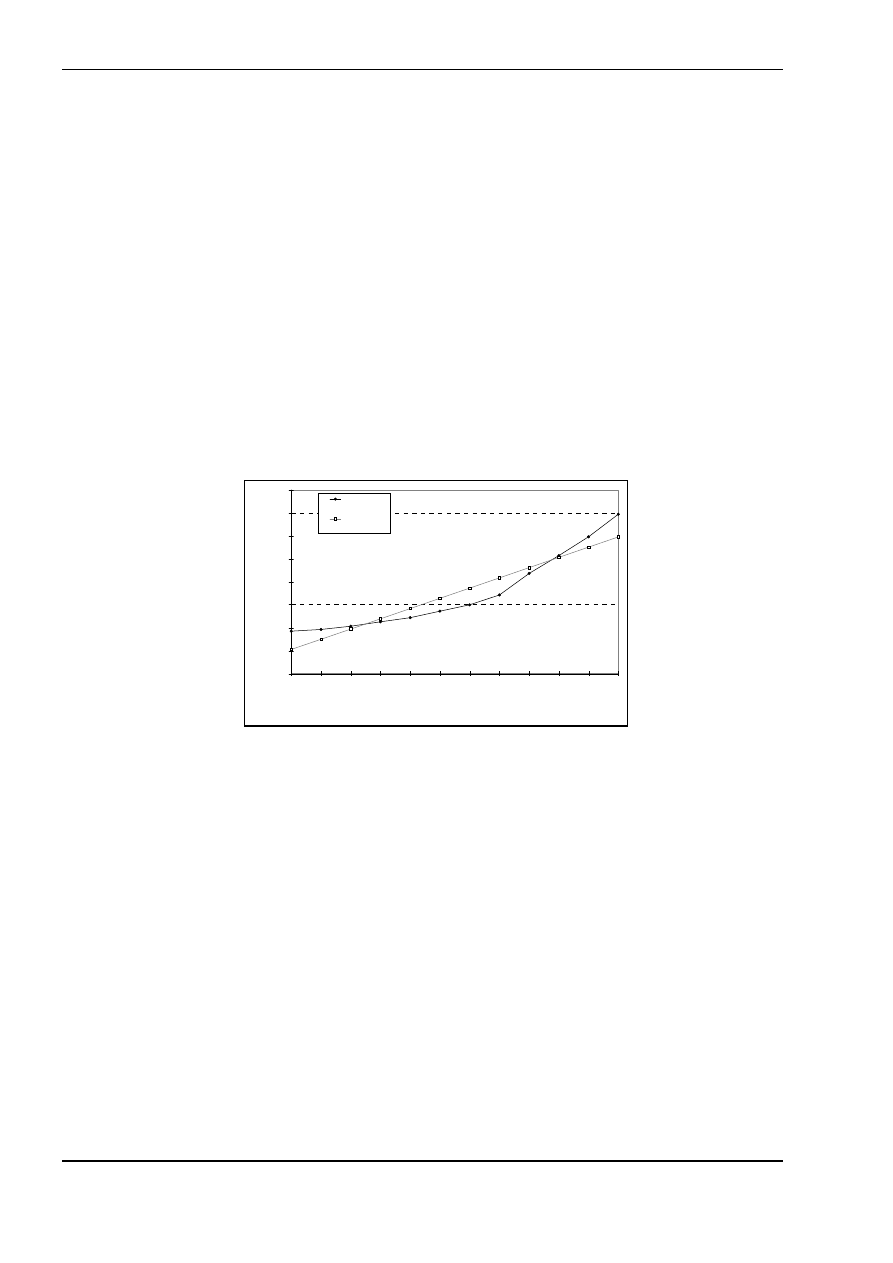
Wykres 3. Wartości teoretyczne (oszacowane z modelu liniowego trendu) i wartości rzeczywiste depozytów złotowych
ludności w latach 1993-1995 [mln zł] (do przykładu)
5000
10000
15000
20000
25000
30000
35000
40000
45000
1 kw
93
2 kw
93
3 kw
93
4 kw
93
1 kw
94
2 kw
94
3 kw
94
4 kw
94
1 kw
95
2 kw
95
3 kw
95
4 kw
95
wartości
rzeczywiste
wartości
teoretyczne
okres
[mln z
ł]
Jak
widać prosta linia trendu niezadowalająco wyjaśnia tendencję zmian depozytów gospodarstw
domowych w badanych latach. Sądząc po ułożeniu punktów wartości rzeczywistych tej zmiennej lepsze wyniki
powinniśmy uzyskać stosując wykładniczą funkcję trendu.
B) Model wykładniczy (nieliniowy)
Wykładniczy model trendu możemy zapisać w postaci:
t
e
e
y
t
b
b
t
ε
⋅
=
⋅
+
1
0
Pewna
niedogodność z modelami nieliniowymi polega na tym, że nie możemy bezposrednio uzyć
klasycznej metody najmniejszych kwadratów do ich oszacowania. KMNK jest metodą przeznaczoną do
szacowania parametrów modeli opisanych zależnościami liniowymi. Liniowość ta musi dotyczyć parametrów.
Pewne jednak rodzaje modeli nieliniowych można przekształcić tak, że mogą być szacowane KMNK, bowiem
stają się liniowe względem parametrów. Do tego typu modeli należy przedstawiony model wykładniczy.
Wspomniane
przekształcenie polega na obustronnym zlogarytmowaniu modelu:
t
e
e
y
t
b
b
t
ε
⋅
=
⋅
+
1
0
t
t
t
b
b
y
ε
+
⋅
+
=
1
0
ln
Jak
widać prawa strona uzyskanej zależności ma charakter addytywny; jest liniowa względem zmiennych
i parametrów. Po lewej jednak stronie znajduje się logarytm naturalny. Nie komplikuje to jednak naszych
przekształceń, bowiem są tu logarytmowane wartości zmiennej y
t
, które znamy. Podstawmy zamiast logarytmu
zmiennej y
t
nową zmienną Ly
t
:

Materiały pomocnicze do zajeć z ekonometrii SSW Chojnice 2012
Krzysztof Świetlik
Materiały pomocnicze do zajeć z ekonometrii SSW Chojnice 2012
Krzysztof Świetlik
5
5
Ly
y
t
t
= ln
Zmienna
Ly
t
jest wektorem zlogarytmowanych wartości zmiennej y
t
. Stąd nasz model możemy zapisać
w ostatecznej postaci:
t
t
t
b
b
Ly
ε
ˆ
1
0
+
⋅
+
=
Jak
widać uzyskaliśmy quasi-liniową postać modelu trendu, którą możemy szacować MNK. W celu
ułatwienia dalszych obliczeń posłużymy się tabelą 5.
Tabela 5. Obliczenia pomocnicze do przykładu 2B.
Numer
obserwacji
y
t
Ly
t
(ln y
t
)
t t
2
Ly
t
*t
1
14225,2 9,5628
1 1
9,5628
2
14577,9 9,5873
2 4
19,1745
3
15295,2 9,6353
3 9
28,9059
4
16265,5 9,6968
4 16
38,7872
5
17160,2 9,7503
5 25
48,7517
6
18562,1 9,8289
6 36
58,9733
7
19962,2 9,9016
7 49
69,3112
8
22099,5 10,0033
8 64
80,0265
9
26779,4 10,1954
9 81
91,7585
10
30670,3 10,3311
10 100
103,3105
11
34771,8 10,4566
11 121
115,0222
12
39672,6 10,5884
12 144
127,0610
Suma (
Σ)
270042 119,5377 78
650 790,6452
Jak wynika z postaci modelu rolę zmiennej objaśnianej yt w naszym przykładzie gra zmienna Lyt. Mając to
na uwadze wyznaczymy składniki estymatora $
b .
′ =
=
∑
∑ ∑
X X
n
t
t
t
2
12
78
78 650
|X’X| = (12*650-78*78) = 1716
(
)
( )
( )
( )
( )
′
=
−
⋅
−
⋅
−
⋅
−
⋅
=
−
−
+
+
+
+
X X
D
1
650
1
78
1
78
1
12
650
78
78
12
1 1
1 2
2 1
2 2
(
)
(
)
′
=
′
⋅
′
=
⋅
−
−
=
−
−
−
X X
X X
X X
D
1
1
1
1716
650
78
78
12
0 37878
0 04545
0 04545
0 00699
,
,
,
,
Wektor X’y ma w naszym przykładzie postać następującą:
′ =
⋅
=
∑
∑
X y
Ly
Ly t
t
t
119 5377
790 6452
,
,
Możemy przystąpić do oszacowania wartości parametrów b
0
i b
1
.
(
)
$
,
,
,
,
,
,
,
,
,
,
,
,
,
,
$
,
,
$
$
b
X X
X y
n
t
t
t
Ly
Ly t
b
b
b
t
t
=
′
′ =
⋅
⋅
=
−
−
⋅
=
=
⋅
−
⋅
−
⋅
+
⋅
=
←
←
−
∑
∑ ∑
∑
∑
1
2
0
1
0 37878
0 04545
0 04545
0 00699
119 5377
790 6452
0 37878 119 5377 0 04545 790 6452
0 04545 119 5377 0 00699 790 6452
9 3437
0 0936
Korzystając z wyników estymacji wykładniczy model trendu możemy zapisać w postaci:
Materiały pomocnicze do zajeć z ekonometrii SSW Chojnice 2012
Krzysztof Świetlik
Materiały pomocnicze do zajeć z ekonometrii SSW Chojnice 2012
Krzysztof Świetlik
6
6
t
e
e
y
t
t
ε
ˆ
0936
,
0
3437
,
9
⋅
=
⋅
+
Interpretacja
modelu:
W
każdym kolejnym kwartale rozpatrywanych lat 1993-1995 depozyty złotowe gospodarstw domowych
wzrastały przeciętnie o
(
)
e
0 0936
1 100 9 81
,
, %
− ⋅
=
. Oznacza to, że w ciągu jednego roku (czterech kwartałów)
średni przyrost depozytów wynosił
(
)
e
4 0 0936
1 100 45 41
⋅
− ⋅
=
,
, % .
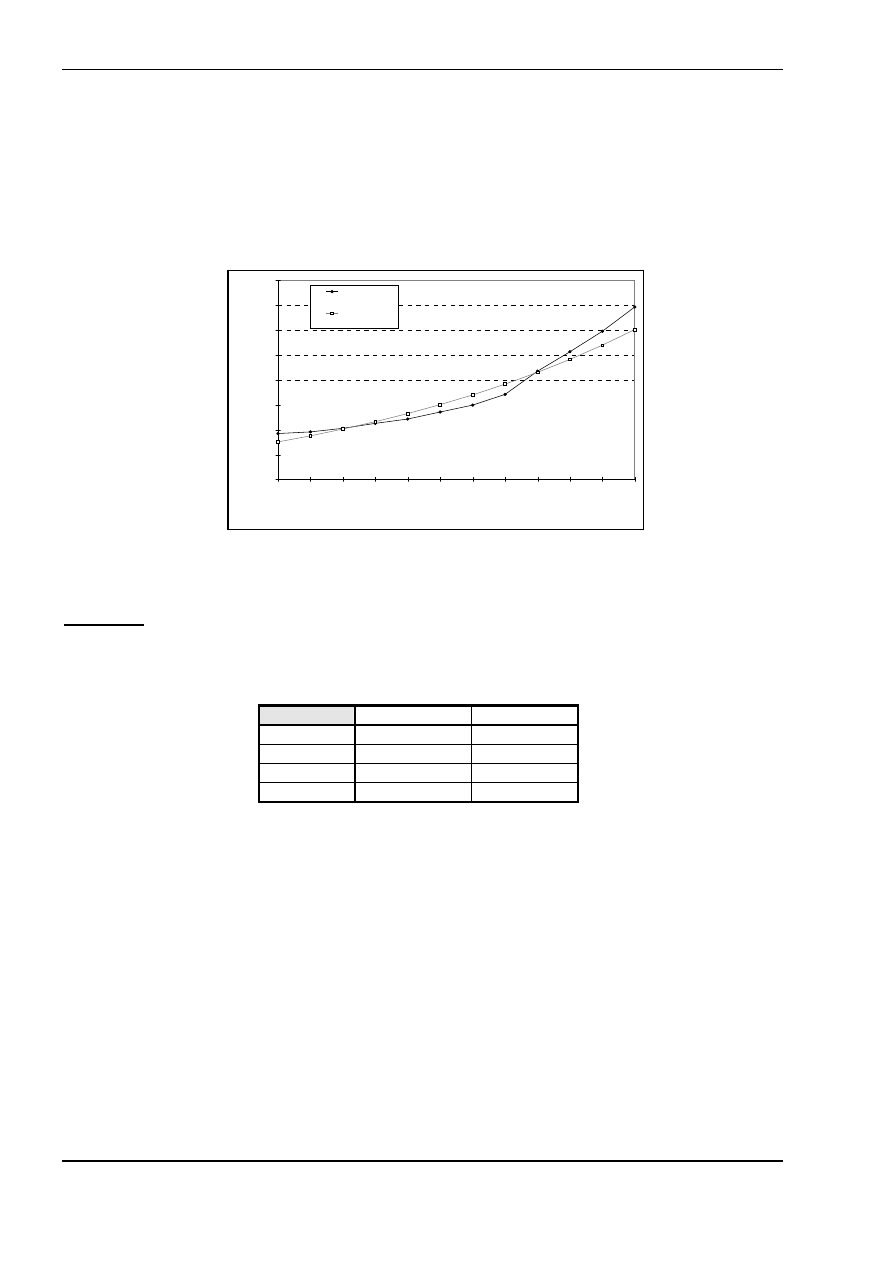
Przyjrzyjmy
się z kolei reprezentacji graficznej powyższego modelu.
Wykres 4.
5000
10000
15000
20000
25000
30000
35000
40000
45000
1 kw 93
2 kw 93
3 kw 93
4 kw 93
1 kw 94
2 kw 94
3 kw 94
4 kw 94
1 kw 95
2 kw 95
3 kw 95
4 kw 95
wartości
rzeczywiste
wartości
teoretyczne
[m
ln z
ł]
okres
Widzimy,
że model wykładniczy trendu lepiej niż model liniowy odwzorowuje zmienność rzeczywistą
depozytów gospodarstw domowych w badanych latach.
Przykład 3.
Oszacować wykładniczy model trendu kredytów gospodarstw domowych w Polsce w latach 2005-2006
według danych w tabeli 6.
Tabela 6. Kredyty gospodarstw domowych w Polsce w latach 2005-2006 [mld zł] w układzie kwartalnym
2005 2006
1 kwartał
3,5 6,4
2 kwartał
4,1 7,82
3 kwartał
4,7 9,39
4 kwartał
5,6 11,72
Przyjmujemy,
że szacowany model wykładniczy ma następującą postać analityczną:
t
t
t
b
b
y
ε
⋅
⋅
=
1
0
Aby
przekształcić model do postaci liniowej dokonujemy jego obustronnego logarytmowania:
( )
(
)
t
t
t
b
b
y
ε
⋅
⋅
=
1
0
ln
ln
t
t
t
b
b
y
ε
ln
ln
ln
ln
1
0
+
+
=
t
t
b
t
b
y
ε
ln
ln
ln
ln
1
0
+
⋅
+
=
Dokonując następujących podstawień:
Ly
y
t
t
= ln
Lb
b
0
0
= ln
Lb
b
1
1
= ln
t
t
L
ε
ε
ln
=
uzyskujemy model quasi-liniowy:
t
t
L
Lb
t
Lb
Ly
ε
+
⋅
+
=
0
0
Niestety, uzyskany model nie jest liniowy wzgledem parametru przy zmiennej t, stąd nie powinien byc
szacowany KMNK, która zakłada liniowość estymatorów parametrów. Z czysto arytmetycznego punktu
widzenia nie ma jednak problemów, aby dokonać oczasowania parametrów tego modelu.
W dalszych obliczeniach pomocna będzie tabela 7.

Materiały pomocnicze do zajeć z ekonometrii SSW Chojnice 2012
Krzysztof Świetlik
Materiały pomocnicze do zajeć z ekonometrii SSW Chojnice 2012
Krzysztof Świetlik
7
7
Tabela 7.
Numer
obserwacji
y
t
Ly
t
(ln y
t
)
t t
2
Ly
t
*t
1
3,5 1,25276 1
1 1,25276
2
4,1 1,41099 2
4 2,82198
3
4,7 1,54756 3
9 4,64268
4
5,6 1,72277 4
16 6,89108
5
6,4 1,8563 5
25 9,2815
6
7,82 2,05668 6
36 12,34008
7
9,397 2,24039 7
49 15,68273
8
11,721 2,46138 8
64 19,69104
Suma (
Σ)
53,238 14,54883 36
204 72,60385
Wyznaczmy
składniki estymatora
$b
=
=
′
∑
∑
∑
204
36
36
8
2
t
t
t
n
X
X
′ = ⋅
−
⋅
=
X X
8 204 36 36 336
(
)
( )
( )
( )
( )
−
−
=
⋅
−
⋅
−
⋅
−
⋅
−
=
′
+
+
+
+
8
36
36
204
8
1
36
1
36
1
204
1
2
2
1
2
2
1
1
1
D
X
X
(
)
−
−
=
−
−
⋅
=
′
−
02381
,
0
10714
,
0
10714
,
0
60714
,
0
8
36
36
204
336
1
1
X
X
X y
Ly
Ly t
t
t
'
,
,
=
⋅
=
∑
∑
14 54883
72 60388
$
,
,
,
,
,
,
,
,
,
,
,
,
,
,
b
=
−
−
⋅
=
⋅
−
⋅
−
⋅
+
⋅
0 60714
010714
010714
0 02381
14 54883
72 60388
0 60714 14 54883 010714 72 60388
010714 14 54883 0 02381 72 60388
$
,
,
$
$
b
Lb
Lb
=
←
←
1 0543
01699
0
1
Szacowany model w postaci quasi-liniowej możemy zatem zapisać następująco:
t
t
u
L
t
Ly
ˆ
1699
,
0
0543
,
1
+
⋅
+
=
Możemy teraz wyznaczyć oceny parametrów b
0
i b
1
.
Lb
b
b
e
Lb
b
b
e
$
ln $
,
$
,
$
ln $
,
$
,
,
,
0
0
0
1 0543
1
1
1
0 1699
1 0543
2 8699
01699
11852
=
=
⇒
=
=
=
=
⇒
=
=
Rozpatrywany
wykładniczy model trendu kredytów możemy ostatecznie zapisać w następującej postaci
analitycznej:
t
t
t
y
ε
ˆ
1852
,
1
8699
,
2
⋅
⋅
=
Parametr
b
1
w modelu jest stałym łańcuchowym indeksem zmiennej y w okresie t w odniesieniu do okresu
poprzedniego t-1. Oznacza to, że z okresu na okres zmienna y rosła średnio o 18,52 procenta.
Materiały pomocnicze do zajeć z ekonometrii SSW Chojnice 2012
Krzysztof Świetlik
Materiały pomocnicze do zajeć z ekonometrii SSW Chojnice 2012
Krzysztof Świetlik
8
8
Przykład 4.
Oszacować model liniowy trendu indeksu cen towarów i usług konsumpcyjnych (ICK) dla lat 1994-1995
w układzie kwartalnym według danych z tabeli 8.
Tabela 8. Indeks cen towarów i usług konsumpcyjnych (ICK) w Polsce w latach 1994-1995 [1 kwartał 94 = 100]
w układzie kwartalnym
1994 1995
1 kwartał
100,00 133,03
2 kwartał
106,70 140,61
3 kwartał
113,53 142,72
4 kwartał
123,18 150,28
Model trendu, który powinniśmy oszacować ma następująca postać ogólną:
t
t
t
b
b
y
ε
+
⋅
+
=
1
0
Rolę zmiennej objaśnianej y
t
w naszym przykładzie pełni zmienna ICK
t
. Zauważmy, że ICK
t
jest indeksem
jednopodstawowym (zmienną niemianowaną).
Indeks ICK przedstawia zmianę poziomu cen na koniec danego kwartału:
1. w stosunku do 1 kwartału 1994 roku - wyrażoną w procentach (np. na koniec 4 kwartału 1995 roku
inflacja wzrosła, w stosunku do 1 kwartału 1994 roku, o 50,28 procent)
2. w stosunku do innych kwartałów, jako różnica pomiędzy odpowiednimi indeksami - wyrażoną w
punktach procentowych
(np. na koniec 4 kwartału 1995 roku inflacja wzrosła, w stosunku do 4 kwartału
1994 roku, o 150,28 - 123,18 = 27,1 punkta procentowego).
Pamiętajmy, aby w rachunku indeksowym nie mylić pojęcia procentu i punktu procentowego
!
Dla
ułatwienia dalszych obliczeń posłużymy się tabelą 9.
Tabela 9.
Numer
obserwacji
y
t
(ICK
t
)
t t
2
y
t
*t
(ICK
t
*t)
1
100,00
1 1
100,00
2
106,70
2 4
213,39
3
113,53
3 9
340,59
4
123,18
4 16
492,72
5
133,03
5 25
665,14
6
140,61
6 36
843,66
7
142,72
7 49
999,07
8
150,28
8 64
1202,27
Suma (
Σ)
1010,05 36 204 4856,84
Wyznaczmy
składniki estymatora
$b
:
′ =
=
∑
∑ ∑
X X
n
t
t
t
2
8
36
36 204
′ = ⋅
−
⋅
=
X X
8 204 36 36 336
(
)
( )
( )
( )
( )
′
=
−
⋅
−
⋅
−
⋅
−
⋅
=
−
−
+
+
+
+
X X
D
1
204
1
36
1
36
1
8
204
36
36
8
1 1
1 2
2 1
2 2
(
)
′
=
⋅
−
−
=
−
−
−
X X
1
1
336
204
36
36
8
0 60714
0 10714
0 10714
0 02381
,
,
,
,

Materiały pomocnicze do zajeć z ekonometrii SSW Chojnice 2012
Krzysztof Świetlik
Materiały pomocnicze do zajeć z ekonometrii SSW Chojnice 2012
Krzysztof Świetlik
9
9
′ =
⋅
=
∑
∑
X y
y
y t
t
t
1010 05
4856 84
,
,
Wyznaczmy
wartość estymatora
$b
:
$
,
,
,
,
,
,
,
,
,
,
,
,
,
,
b
=
−
−
⋅
=
⋅
−
⋅
−
⋅
+
⋅
0 60714
0 10714
0 10714
0 02381
1010 05
4856 84
0 60714 1010 05 0 10714 4856 84
0 10714 1010 05 0 02381 4856 84
$
,
,
$
$
b
b
b
=
←
←
92 8799
7 4246
0
1
Uwzględniając wyniki powyższych obliczeń rozpatrywany model trendu możemy zapisać jako:
t
t
t
y
ε
ˆ
4246
,
7
8799
,
92
+
⋅
+
=
Interpretacja
modelu:
W
każdym kolejnym kwartale badanych lat (1994-1995) indeks cen towarów i usług konsumpcyjnych ICK
t
wzrastał średnio o 7,42 punkta procentowego. Średnioroczny wzrost ICK
t
w badanych latach wynosił 4*7,4246
= =29,69 punkta procentowego.
Wyszukiwarka
Podobne podstrony:
sprawko elementy liniowe i nieliniowe
Sprawozdanie obwody liniowe i nieliniowe
A6 Sprz enie zwrotne w uk?ach liniowych i nieliniowych
Sprawozdanie Badanie obwodów prądu stałego zawierającego elementy liniowe i nieliniowe (Moje)x
Elementy liniowe i nieliniowe obwodów elektrycznych, pomiar charakterystyk stałoprądowych (3)
Model z 1 zmienna liniowy i nieliniowy WZiE
A6 Sprz enie zwrotne w uk adach liniowych i nieliniowych
Modele tendencji rozwojowej z elementami sezonowymi
Sprawozdanie-Badanie obwodów prądu stałego zawierającego elementy liniowe i nieliniowe (3)
Cw 3 Liniowe i nieliniowe eleme Nieznany
ćw nr 4 Liniowe i nieliniowe elementy bierne obwodów elektrycznych
liniowy i nieliniowy model trendu
Ćw.4 Liniowe i nieliniowe elementy bierne obwodów elektrycznych, studia, semestr 3 (2011), Podstawy
Ekonometria modele, uczelnia, Programowanie Liniowe
UKLDYN-E, Dynamiczny układ liniowy (nieliniowy) - dowolny układ fizyczny rozpatrywany z punktu widze
Określenie jakości dopasowania równania regresji liniowej i nieliniowej 9
Elementy liniowe i nieliniowe obwodów elektrycznych , pomiar charakterystyk stałoprądowychx
Sprawozdanie Badanie obwodów prądu stałego zawierającego elementy liniowe i nieliniowe (2)
więcej podobnych podstron