8. Wyznaczanie częstości generatora na podstawie obserwacji dudnień

i krzywych Lissajous

Cel:

 Zapoznanie się ze zjawiskiem składania drgań harmonicznych prostych wzajemnie

równoległych i prostopadłych.

 Wyznaczenie częstości generatora w oparciu o bezpośrednią obserwację drgań oraz

na podstawie obserwacji dudnień i krzywych Lissajous.

Pytania kontrolne:



Równanie opisujące drganie harmoniczne proste.



Omówić zasadę pomiaru okresu i częstości napięcia zmiennego za pomocą
oscyloskopu.



Powstawanie i cechy charakterystyczne dudnień.



Zasada wyznaczania częstości generatora na podstawie obserwacji dudnień.



Powstawanie i cechy charakterystyczne krzywych Lissajous.



Zasada wyznaczania częstości generatora na podstawie obserwacji krzywych
Lissajous.

Opis ćwiczenia:

Do wyznaczenia częstości sygnału pochodzącego z badanego generatora używamy

oscyloskopu i drugiego, wzorcowego generatora. Nieznaną częstość generatora wyznaczamy
metodą pomiaru bezpośredniego, obserwacji krzywych Lissajous oraz obserwacji dudnień.

Bezpośredni pomiar

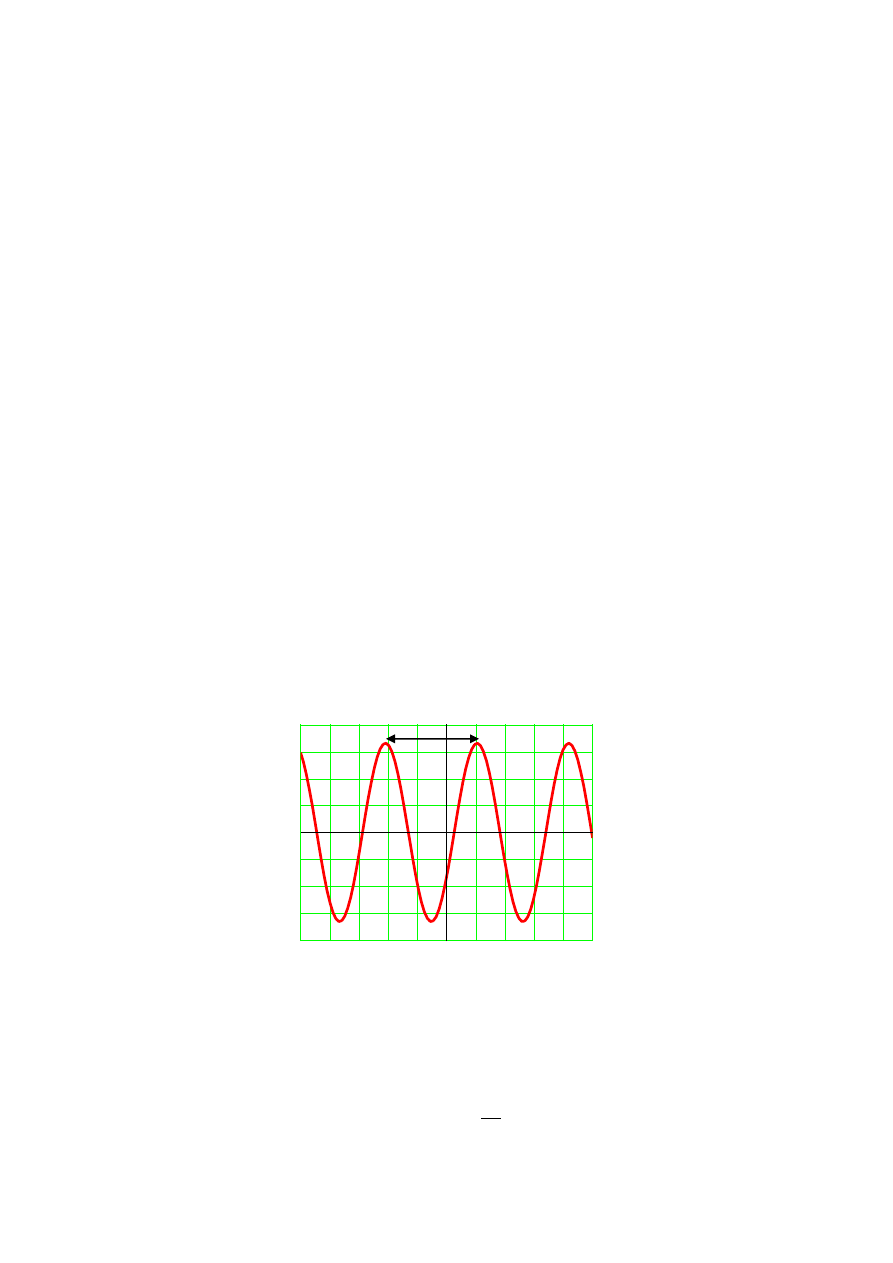
Rys. 8.1. Obraz zmian napięcia sinusoidalnie zmiennego

Sygnał z generatora o nieznanej częstości podłączamy do oscyloskopu. Po uzyskaniu na

ekranie stabilnego obrazu drgań harmonicznych wyznaczamy okres drgań

1

T . Częstość

kołową

1



sygnału obliczamy z relacji:

1

1

π

2

T





.

(8.1)

1

T

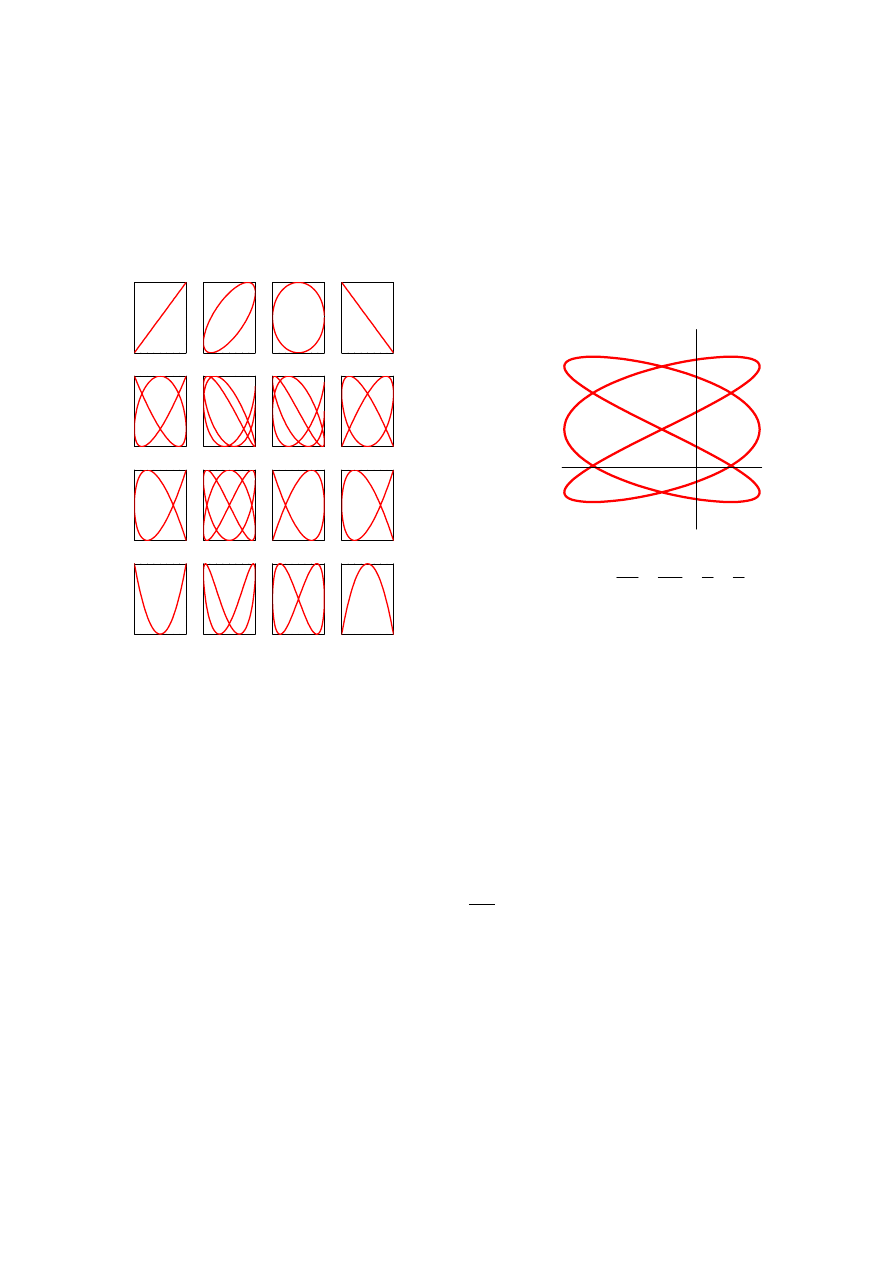
Krzywe Lissajous

Sygnał z badanego generatora podłączamy do wejścia

X oscyloskopu, a sygnał z

drugiego – wzorcowego generatora podłączamy do wejścia

Y . Wyłączamy podstawę czasu i

ustawiamy generator wzorcowy na częstość wyznaczoną w poprzednim punkcie. Regulując
częstość

2



tego generatora uzyskujemy na kranie obraz elipsy. Przerysowujemy obraz

powstałej krzywej Lissajous dla kilku różnych przesunięć fazowych.

Podobne pomiary wykonujemy dla innych częstości generatora wzorcowego, dla których na
ekranie powstaje stabilny obraz krzywej Lissajous.

Dla każdej zaobserwowanej krzywej wyznaczamy liczbę przecięć

x

N krzywej Lissajous

z osią poziomą oraz liczbę przecięć

y

N krzywej Lissajous z osią pionową. Wyznaczamy

częstość

1



sygnału badanego generatora:

2

1





x

y

N

N



.

(8.2)

Dudnienia

Włączamy podstawę czasu. Ustawiamy częstość generatora wzorcowego

2

 

poniżej

częstości

1



generatora badanego Częstość

2



regulujemy następnie tak, aby na ekranie uzy-

skać stabilny obraz dudnień.

y

N

x

N

2

3

4

6







x

y

y

x

N

N





Rys. 8.3. Określanie stosunku częstości dwóch

drgań tworzących krzywą Lissajous

Rys. 8.2. Przykłady krzywych Lissajous





0







45







90







180



y

x







2

y

x





2

3



y

x





3

4



y

x







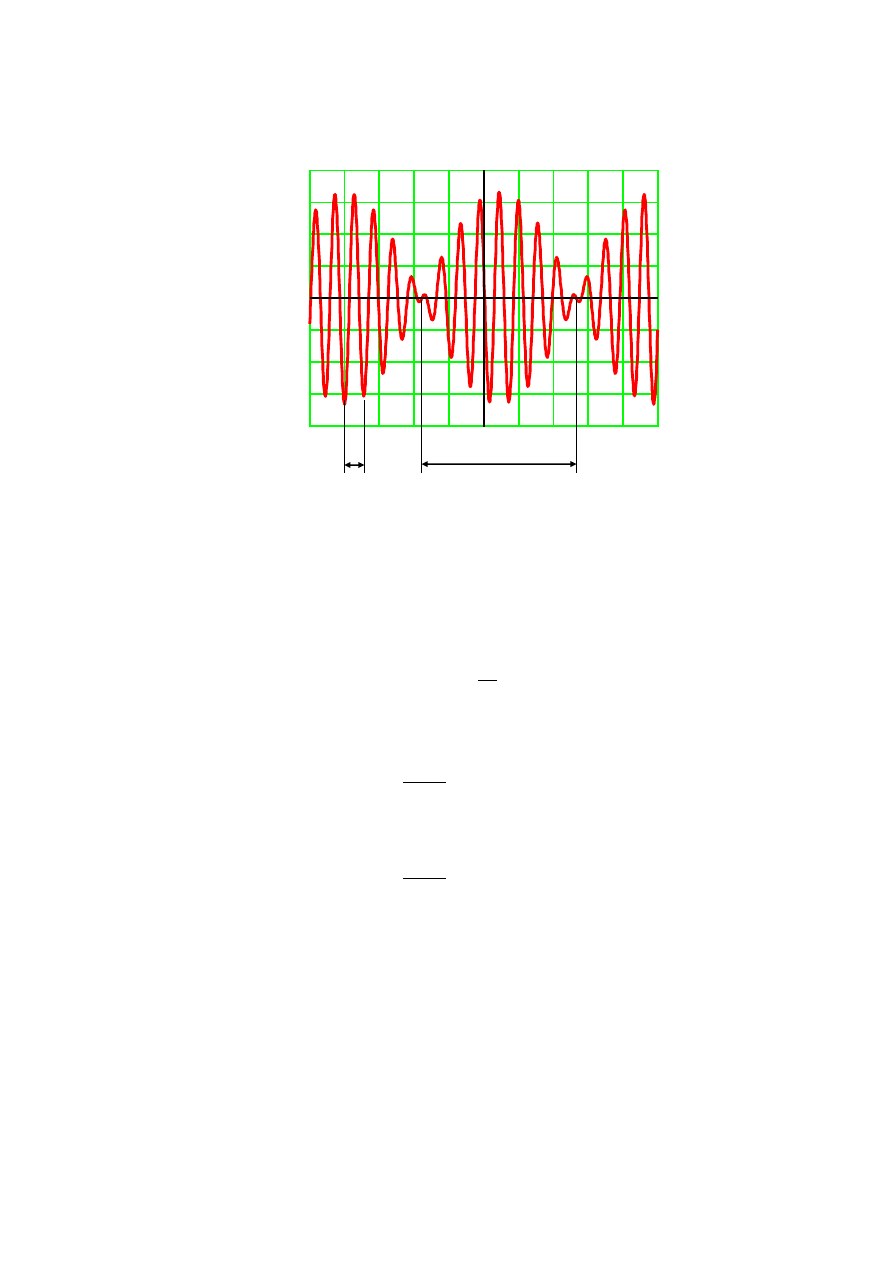
Rys. 8.1. Obraz dudnień

Mierzymy okres wypadkowy

w

T i okres dudnień

d

T . Powtarzamy pomiar dla kilku innych

wartości

2



poniżej i powyżej częstości

1

 

Przerysowujemy obraz dudnienia dla jednej,

wybranej częstości

2



.

Wyznaczamy liczbę n drgań fali wypadkowej przypadających na jeden okres dudnień

w

d

T

T

n



.

(8.3)

Z zależności

2

1

1

2

1

2











n

n

2

1

gdy







(8.4)

lub

2

1

1

2

1

2











n

n

2

1

gdy







(8.5)

wyznaczamy częstość

1



sygnału badanego generatora.

Porównujemy częstości

1



otrzymane trzema sposobami.

Literatura:

1. Daca T., Łukasiewicz M., Włodarski Z., Ćwiczenia laboratoryjne z fizyki. Skrypt dla

studentów I i II roku studiów stacjonarnych i zaocznych, WSM, Szczecin (dostępne
wydania).

w

T

d

T

2. Ćwiczenia laboratoryjne z fizyki. Cz. 2, praca zbiorowa pod red. J. Kirkiewicza, WSM,

Szczecin, 2003.

3. Szydłowski H., Pracownia fizyczna, PWN, Warszawa (dostępne wydania).
4. Ćwiczenia laboratoryjne z fizyki w politechnice, praca zbiorowa pod red. T. Rewaja,

PWN, Warszawa (dostępne wydania).

5. Ćwiczenia laboratoryjne z fizyki, praca zbiorowa pod red. T. Rewaja, Wydawnictwo

Politechniki Szczecińskiej, Szczecin (dostępne wydania).

6. Resnick R., Halliday D., Walker J., Podstawy fizyki T.1, PWN, Warszawa (dostępne

wydania).

7. Bobrowski C., Fizyka: krótki kurs, WNT, Warszawa (dostępne wydania).
8. Orear J., Fizyka T.1, WNT, Warszawa (dostępne wydania).