Rok akademicki 2008/2009

AKADEMIA GÓRNICZO – HUTNICZA im. STANISŁAWA STASZICA W

KRAKOWIE

WYDZIAŁ GEODEZJI GÓRNICZEJ I IN

ś

YNIERII

Ś

RODOWISKA

TEMAT 3

Wyznaczenie przebiegu lokalnej geoidy (quasi-geoidy).

Maria Gi

ż

a

Rok IV, Gr. 2 GIP

SKŁAD OPERATU:

1. Sprawozdanie techniczne.

2. Dane wyj

ś

ciowe.

3. Etapy oblicze

ń

.

4. Zestawienie wyników oblicze

ń

.

5. Wykres zale

ż

no

ś

ci odchylenia linii pionu od azymutu.

6. Mapa izolinii odst

ę

pów geoidy od elipsoidy w układzie 1992 w skali 1:50 000.

1. Sprawozdanie techniczne

Dane formalno-prawne:

Zleceniodawca: Akademia Górniczo-Hutnicza w Krakowie,
Wydział Geodezji Górniczej i In

ż

ynierii

Ś

rodowiska

Wykonawca: Maria Gi

ż

a

Przedmiot zlecenia: Wyznaczenie przebiegu lokalnej geoidy (quasi-geoidy).

Czas wykonania: 20.01.2009r.

2. Dane wyj

ś

ciowe:

2.1.

Zestaw nr 97.

2.2.

Punkt 97 traktujemy jako punkt testowy.

2.3.

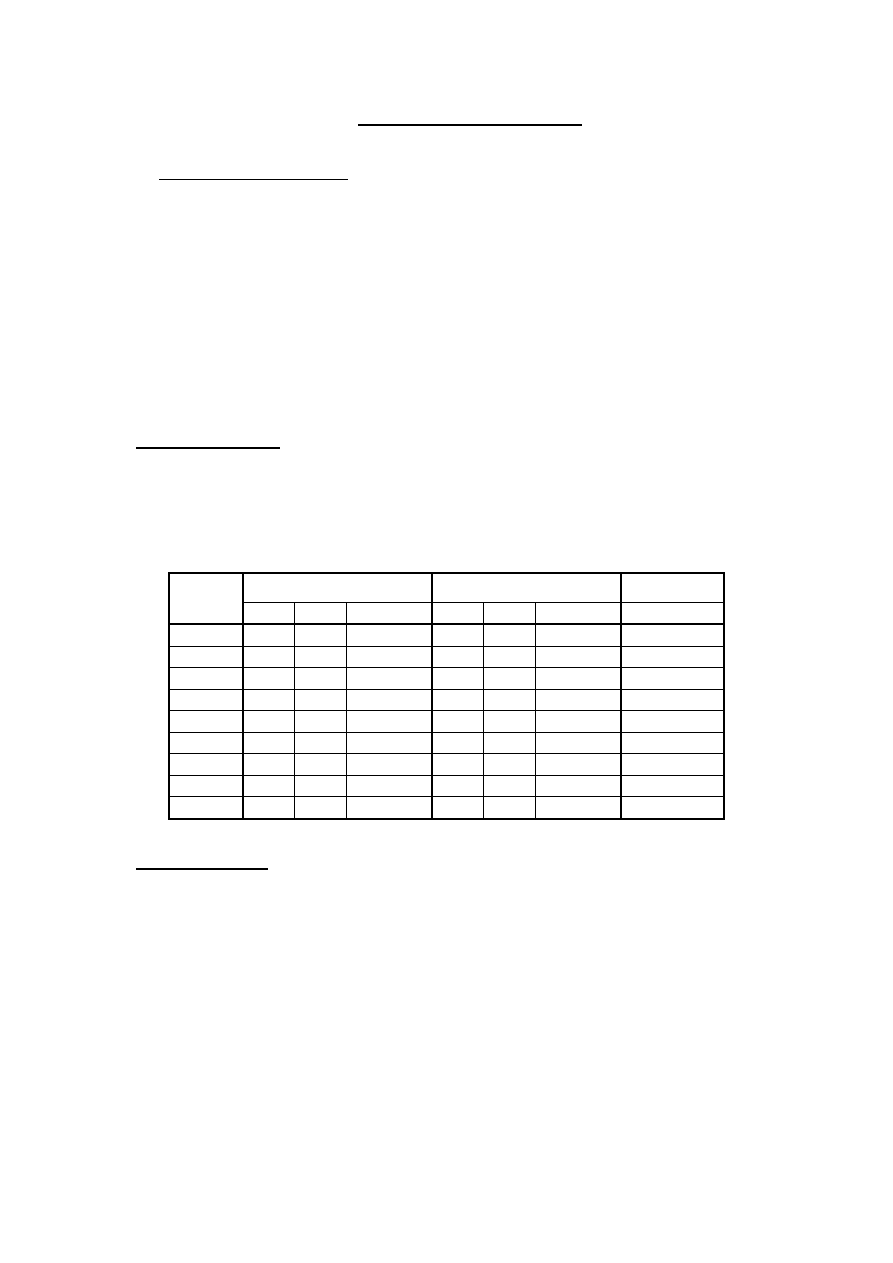
Dane dla punktów:

B

L

N

Nr Pkt

[ °]

[ ‘ ]

[ ‘’ ]

[ °]

[ ‘ ]

[ ‘’ ]

[m]

97

52

15

0.0000

20

30

0.0000

31.799

971

52

16

12.2687

20

30

11.4394

31.773

972

52

15

59.3248

20

32

22.2821

31.758

973

52

13

46.6801

20

32

2.4562

31.804

974

52

13

7.3973

20

32

1.7981

31.818

975

52

12

55.7034

20

27

58.6590

31.858

976

52

13

39.8234

20

26

23.8493

31.854

977

52

16

35.7440

20

27

9.0667

31.791

978

52

17

37.4014

20

30

4.0364

31.749

3. Etapy oblicze

ń

:

3.1.

Współrz

ę

dne elipsoidalne (B,L) 9 punktów wyj

ś

ciowych przetransformowano

do układu współrz

ę

dnych płaskich „1992” przy u

ż

yciu programu Transpol.

3.2.

Na podstawie obliczonych współrz

ę

dnych i odst

ę

pów 8 punktów (bez punktu

testowego) metod

ą

najmniejszych kwadratów wyznaczono dla dwóch

wariantów współczynniki (wraz z bł

ę

dami) wielomianu aproksymuj

ą

cego N o

postaci:

N

i

= ax

i

+ by

i

+ c – wariant 1

N

i

= ax

i

2

+by

i

2

+cx

i

y

i

+dx

i

+ey

i

+f – wariant 2

Gdzie:
x

i

, y

i

– współrz

ę

dne i-tego punktu w układzie 1992

a, b, c, d, e, f – parametry wielomianu aproksymuj

ą

cego

3.3.

Na podstawie wyznaczonego wielomianu obliczono warto

ść

N w punkcie

centralnym 97 i porównano j

ą

z warto

ś

ci

ą

podan

ą

.

3.4.

Wyznaczono składowe odchylenia linii pionu

ξ

i

η

wraz z ich bł

ę

dami w

punkcie centralnym na podstawie równa

ń

obserwacyjnych o postaci:

ε

ij

=

ξ

cosA

ij

+

η

sinA

ij

ε

ij

= -

∆

N

ij

/s

ij

Obliczenia wykonano dla wszystkich podanych punktów. Dla punktu
testowego wykorzystano warto

ść

N podan

ą

w danych wej

ś

ciowych.

3.5.

Obliczono maksymalne odchylenie pionu

ε

max

oraz jego azymut A

ε

max

a tak

ż

e

warto

ś

ci azymutu, dla których odchylenie pionu przyjmuje warto

ść

zerow

ą

.

3.6.

Na podstawie oblicze

ń

sporz

ą

dzono wykres zale

ż

no

ś

ci odchylenia linii pionu

od azymutu.

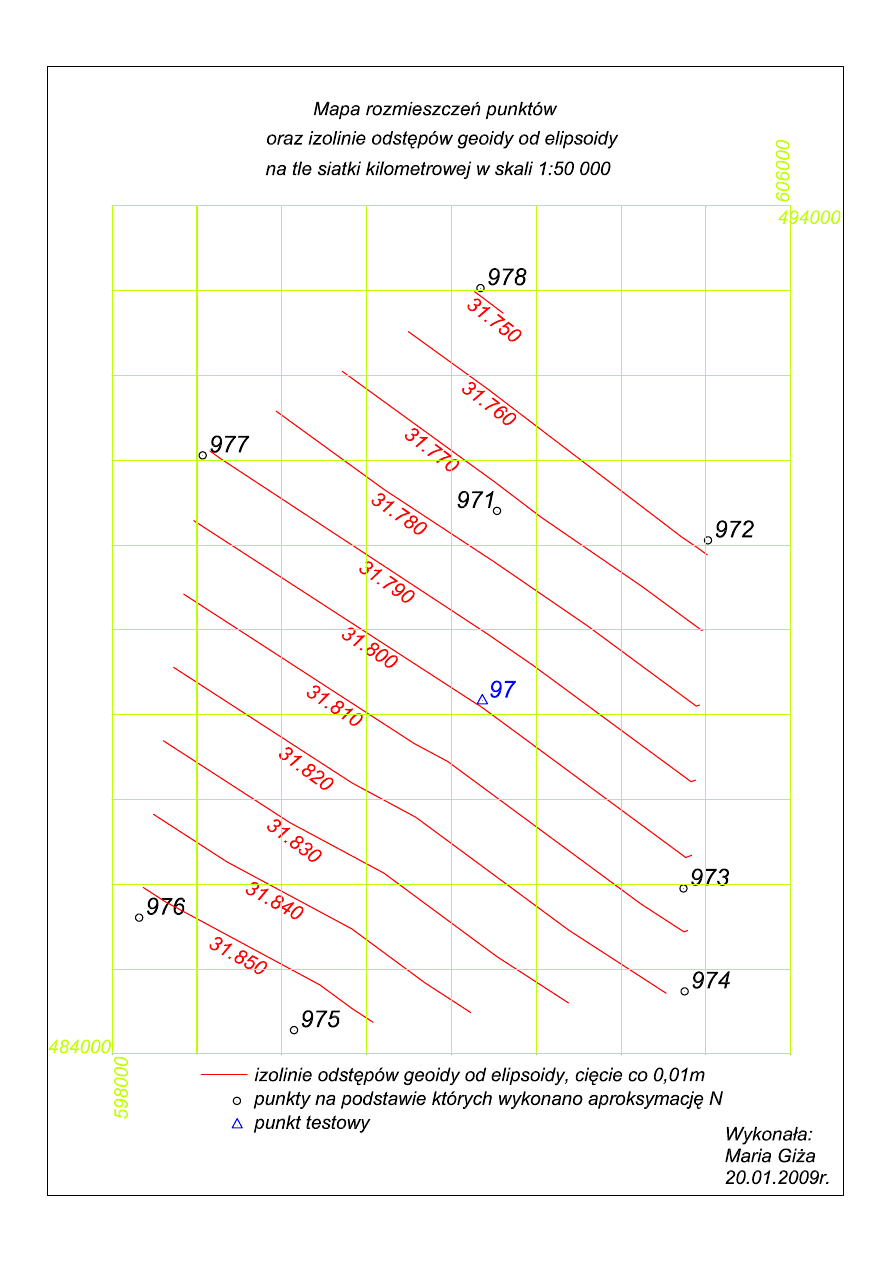
3.7.

Wykonano szkic sieci punktów w skali 1:50 000 na tle siatki kilometrowej
układu współrz

ę

dnych „1992” z zaznaczeniem punktów wykorzystanych do

aproksymacji N oraz map

ę

izolinii odst

ę

pów geoidy od elipsoidy na obszarze

ograniczonym danymi punktami.

Wykonała:

20.01.2009r.

Maria Gi

ż

a

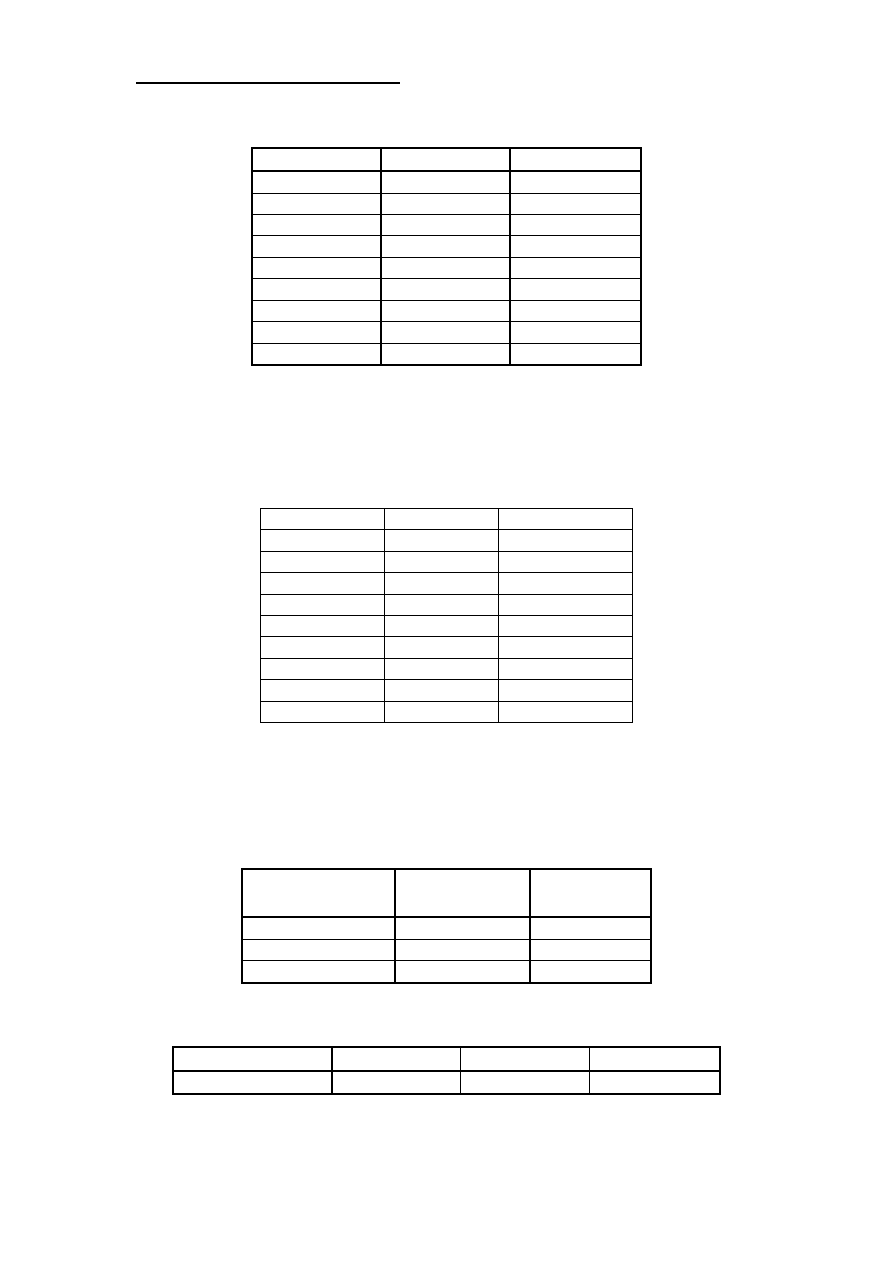
4. Zestawienie wyników oblicze

ń

.

4.1. Wykaz współrz

ę

dnych punktów w układzie 1992:

Nr

X[m]

Y[m]

97

488166.78971 602367.54447

971

490403.27958 602538.07065

972

490055.58752 605025.67916

973

485950.95046 604736.74627

974

484737.46092 604749.94340

975

484280.84145 600145.09411

976

485607.41568 598319.41557

977

491057.80466 599068.04899

978

493029.67599 602343.29993

W celu wyznaczenia współczynników wielomianu aproksymuj

ą

cego i ich bł

ę

dów

wykonuj

ę

transformacj

ę

współrz

ę

dnych o wektor:

x

0

= 488143.3118 y

0

= 602143.7603

Zestawienie otrzymanych współrz

ę

dnych:

Nr

X[m]

Y[m]

97

23.47794

223.78419

971

2259.96781

394.31037

972

1912.27575

2881.91888

973

-2192.36131

2592.98599

974

-3405.85085

2606.18312

975

-3862.47032

-1998.66617

976

-2535.89609

-3824.34471

977

2914.49289

-3075.71129

978

4886.36422

199.53965

4.2. Współczynniki wielomianu aproksymuj

ą

cego i ich bł

ę

dy dla wariantu 1.

N

i

= ax

i

+ by

i

+ c

Współczynnik

Warto

ść

[m]

Bł

ą

d [m]

a

-1.063*10

-5

1.765*10

-7

b

-7.301*10

-6

2.215*10

-7

c

31.800390

0.0006

Odst

ę

p N dla punktu testowego:

Pkt.

N

obl.

[m]

N

dane

[m]

∆

N [m]

97

31.7985

31.799

0.0005

4.3. Współczynniki wielomianu aproksymuj

ą

cego i ich bł

ę

dy dla wariantu 2.

N

i

= ax

i

2

+by

i

2

+cx

i

y

i

+dx

i

+ey

i

+f

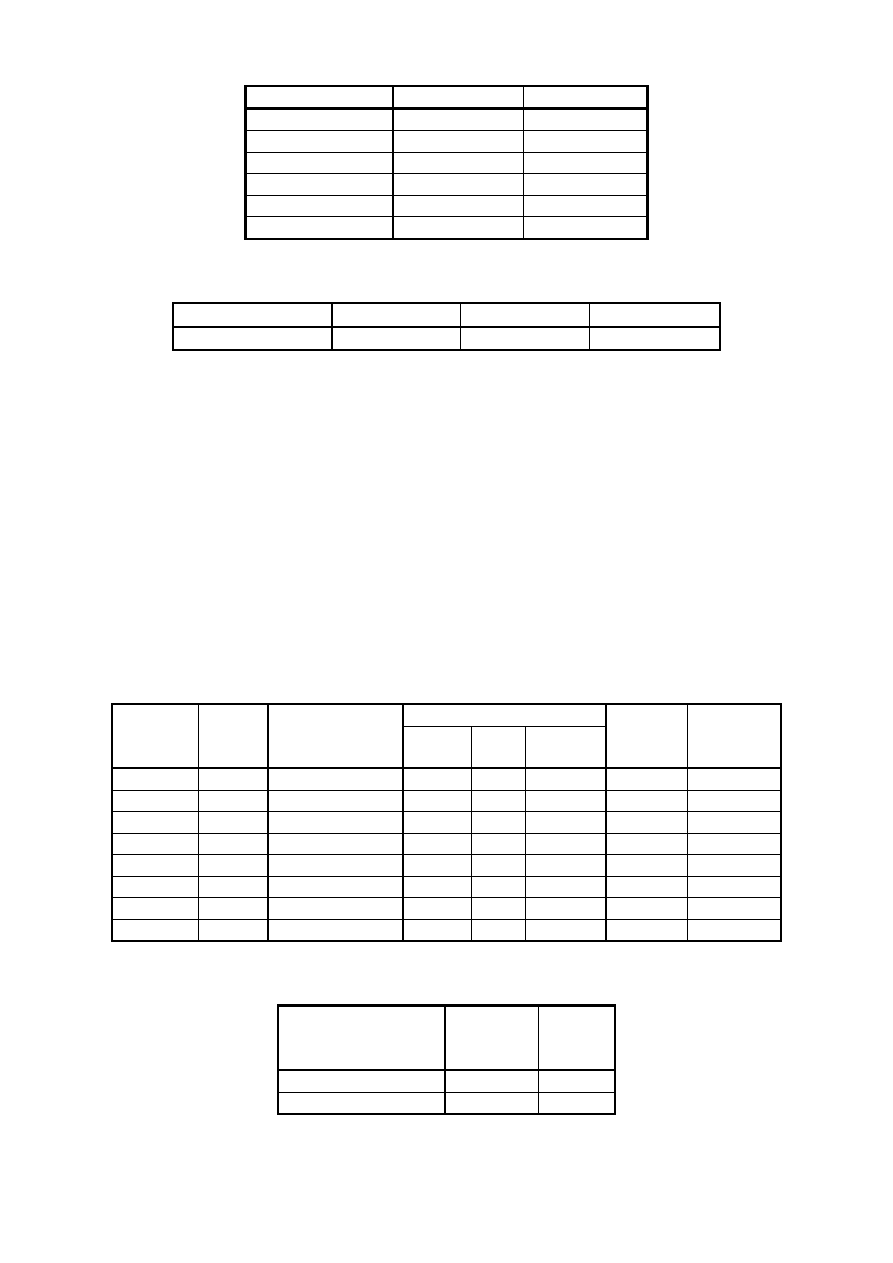
Współczynnik

Warto

ść

Bł

ą

d

a

1.487E-10

3.534E-11

b

-1.116E-10

5.644E-11

c

1.717E-11

2.789E-11

d

-1.076E-05

6.337E-08

e

-7.300E-06

8.907E-08

f

31.799619

0.0006

Odst

ę

p N dla punktu testowego:

Pkt.

N

obl.

[m]

N

dane

[m]

∆

N [m]

111

31.7977

31.799

0.0013

WNIOSKI:
Porównuj

ą

c warto

ś

ci undulacji N obliczonej na podstawie wielomianów

aproksymuj

ą

cych z warto

ś

ci

ą

podan

ą

zauwa

ż

amy,

ż

e oba wielomiany wystarczaj

ą

co

dokładnie przybli

ż

aj

ą

jej warto

ść

. Wielomian pierwszy (ni

ż

szego rz

ę

du) nieco

dokładniej przybli

ż

a warto

ść

odst

ę

pu, mimo i

ż

ma mniej skomplikowan

ą

posta

ć

ni

ż

wielomian drugi (N

i

= ax

i

2

+by

i

2

+cx

i

y

i

+dx

i

+ey

i

+f). W pierwszym wielomianie

współczynniki obarczone s

ą

mniejszymi bł

ę

dami ni

ż

współczynniki drugiego

wielomianu.
Dla obszarów o du

ż

ej powierzchni (gdy geoida traci swoj

ą

regularno

ść

) nale

ż

y

stosowa

ć

wielomian wy

ż

szego rz

ę

du, gdy

ż

lepiej przybli

ż

a on posta

ć

aproksymowanej powierzchni. Natomiast na małych powierzchniach (tak jak w
naszym temacie) gdy odst

ę

p geoidy od elipsoidy zmienia si

ę

jednostajnie w jednym

kierunku, aproksymacja wielomianem ni

ż

szego rz

ę

du daje lepszy wynik.

4.4. Warto

ś

ci s, A,

∆

N,

ε

dla ka

ż

dego kierunku.

Azymut

Pkt

pocz

ą

tk

Pkt

ko

ń

c

owy

Odległo

ść

[m]

[ °]

[ ‘ ]

[ ‘’ ]

∆

N

[m]

ε

[ ‘’ ]

97

971

2242.982

4

22

36.75

-0.026

2.39

97

972

3260.864

54

36

12.38

-0.041

2.59

97

973

3243.927

133

5

3.33

0.005

-0.32

97

974

4175.658

145

13

42.46

0.019

-0.94

97

975

4476.592

209

46

57.92

0.059

-2.72

97

976

4789.336

237

42

50.78

0.055

-2.37

97

977

4386.871

311

13

29.33

-0.008

0.38

97

978

4862.947

359

43

51.65

-0.050

2.12

4.5. Składowe odchylenia linii pionu w punkcie centralnym 97.

Składowa

odchylenia linii

pionu

Warto

ść

[ ‘’ ]

Bł

ą

d

[ ‘’ ]

ξ

2.21

0.0364

η

1.53

0.0463

4.6. Maksymalne odchylenie pionu

ε

max

dla punktu centralnego.

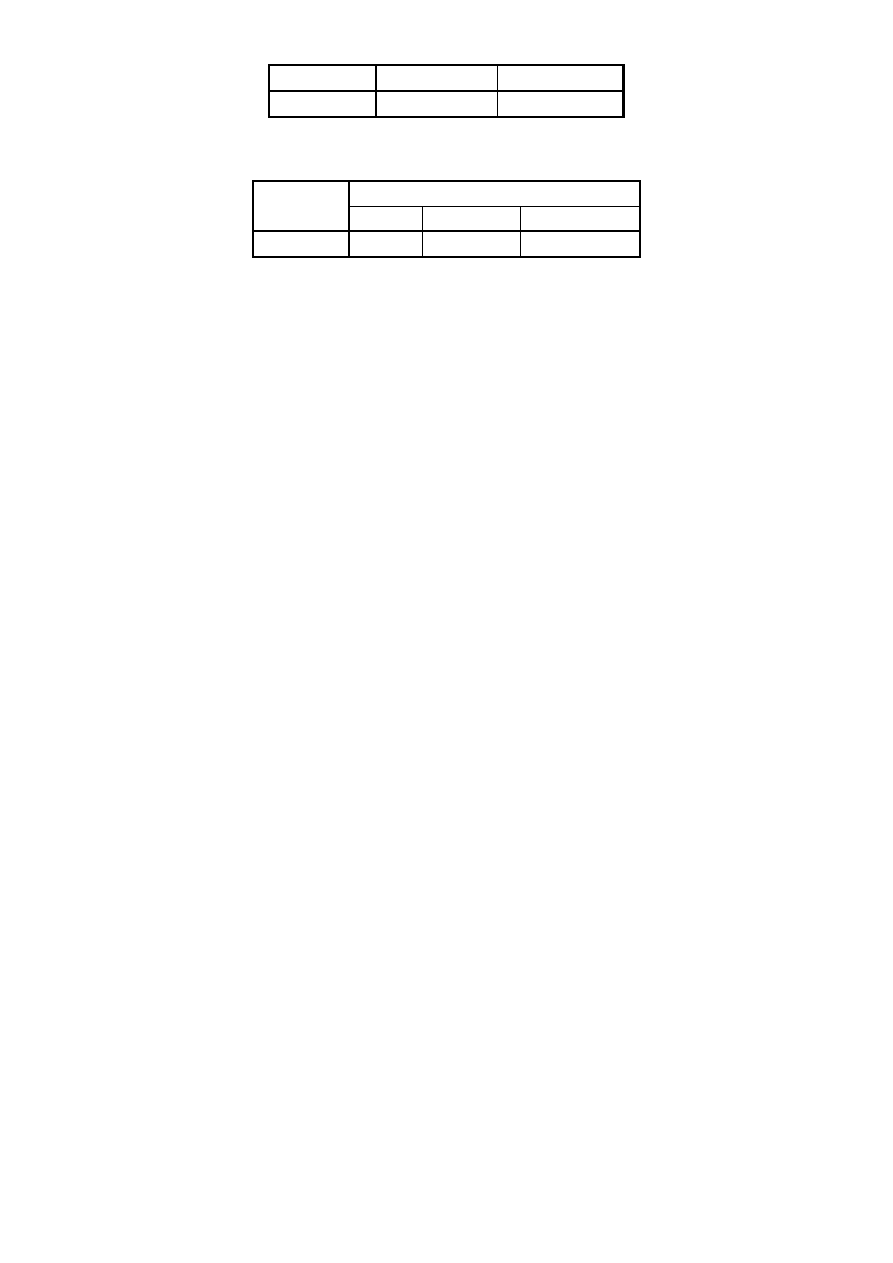
Pkt

ε

max

["]

ε

max

[cm/km]

97

2.69

1.303

4.7.Azymut maksymalnego odchylenia A

ε

max

dla punktu centralnego.

A

ε

max

Pkt

[

o

]

[ ‘ ]

[ ‘’ ]

97

34

39

43.40

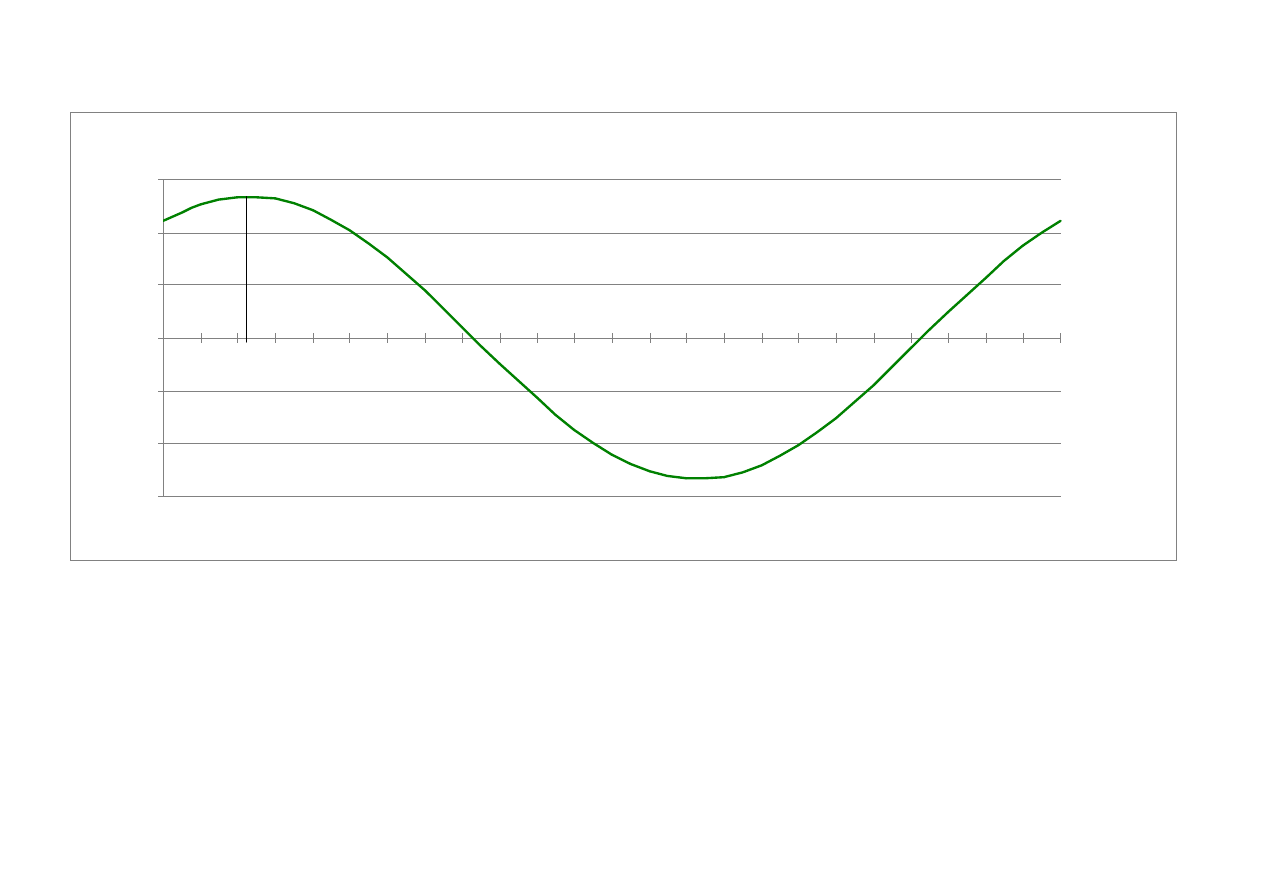
Wykres zale

ż

no

ś

ci odchylenia linii pionu od azymutu

-3.00

-2.00

-1.00

0.00

1.00

2.00

3.00

0

15

30

45

60

75

90

105 120 135 150 165 180 195 210 225 240 255 270 285 300 315 330 345 360

A [°]

ε

[

"

]

ε

max

= 2.69”

A

ε

=0

= 124° 39’ 43”

A

ε

=0

= 304° 39’ 43”

A

max

= 34° 39' 43”