Zapis i Podstawy Konstrukcji Mechanicznych Kinematyka mechanizmów

Temat: Wybrane zagadnienia kinematyki mechanizmów dźwigniowych

Ruch punktu:

•

prostoliniowy,

•

krzywoliniowy (np. po okręgu, elipsie, dowolnej krzywej)

Ruch bryły:

•

postępowy,

Liczbę niezależnych współrzędnych (współ-

rzędnych uogólnionych) potrzebnych do określenia
położenia punktu lub bryły w przestrzeni nazywamy
liczbą stopni swobody

•

obrotowy,

•

płaski,

•

kulisty,

•

śrubowy,

•

dowolny.

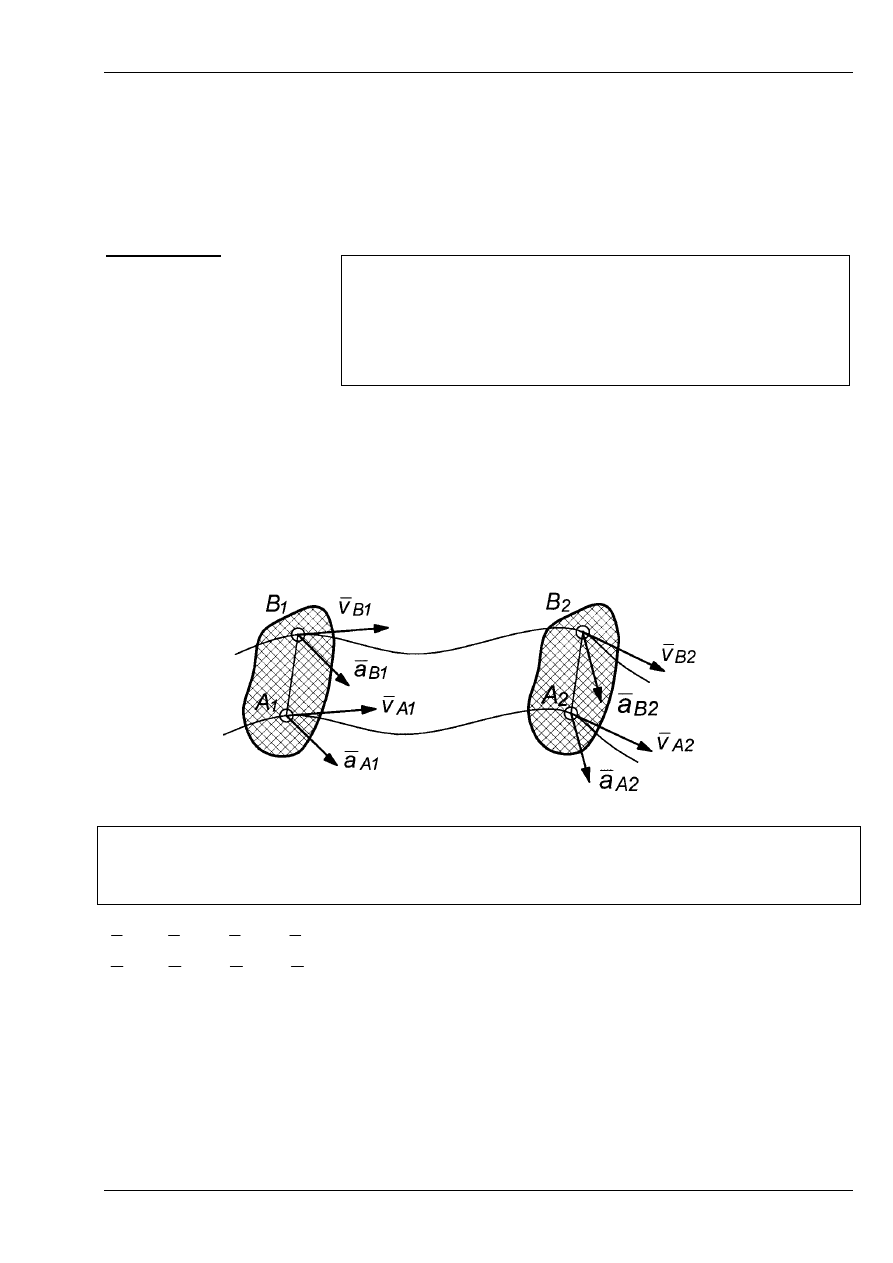
RUCH POSTĘPOWY BRYŁY

Ruch postępowy członu zachodzi wówczas, jeżeli dowolny odcinek AB zwią-
zany sztywno z członem zachowuje położenie równoległe w kolejnych położe-
niach mechanizmu: A

1

B

1

A

2

B

2

Rys. 1

Twierdzenie: Jeżeli bryła porusza się ruchem postępowym to wszystkie punkty
bryły poruszają się po torach przystających i w każdej chwili „t” mają te same
prędkości i przyspieszenia.

a

a

a

a

v

v

v

v

2

B

2

A

1

B

1

A

2

B

2

A

1

B

1

A

=

=

=

=

Równania ruchu postępowego:

)

t

(

z

z

),

t

(

y

y

),

t

(

x

x

=

=

=

x,y,z - współrzędne uogólnione

Opracował: J. Felis str. 1

Zapis i Podstawy Konstrukcji Mechanicznych Kinematyka mechanizmów

Przykład 1. Równoległobok przegubowy

Rozkład prędkości i przyspieszeń punk-
tów członu w ruchu postępowym.

Rys. 2

Tory punktów B, C, K, M są równoległe a ich prędkości i przyspieszenia równe.

M

K

C

B

a

a

a

a

=

=

=

M

K

C

B

v

v

v

v

=

=

=

0

2

=

ε

0

2

=

ω

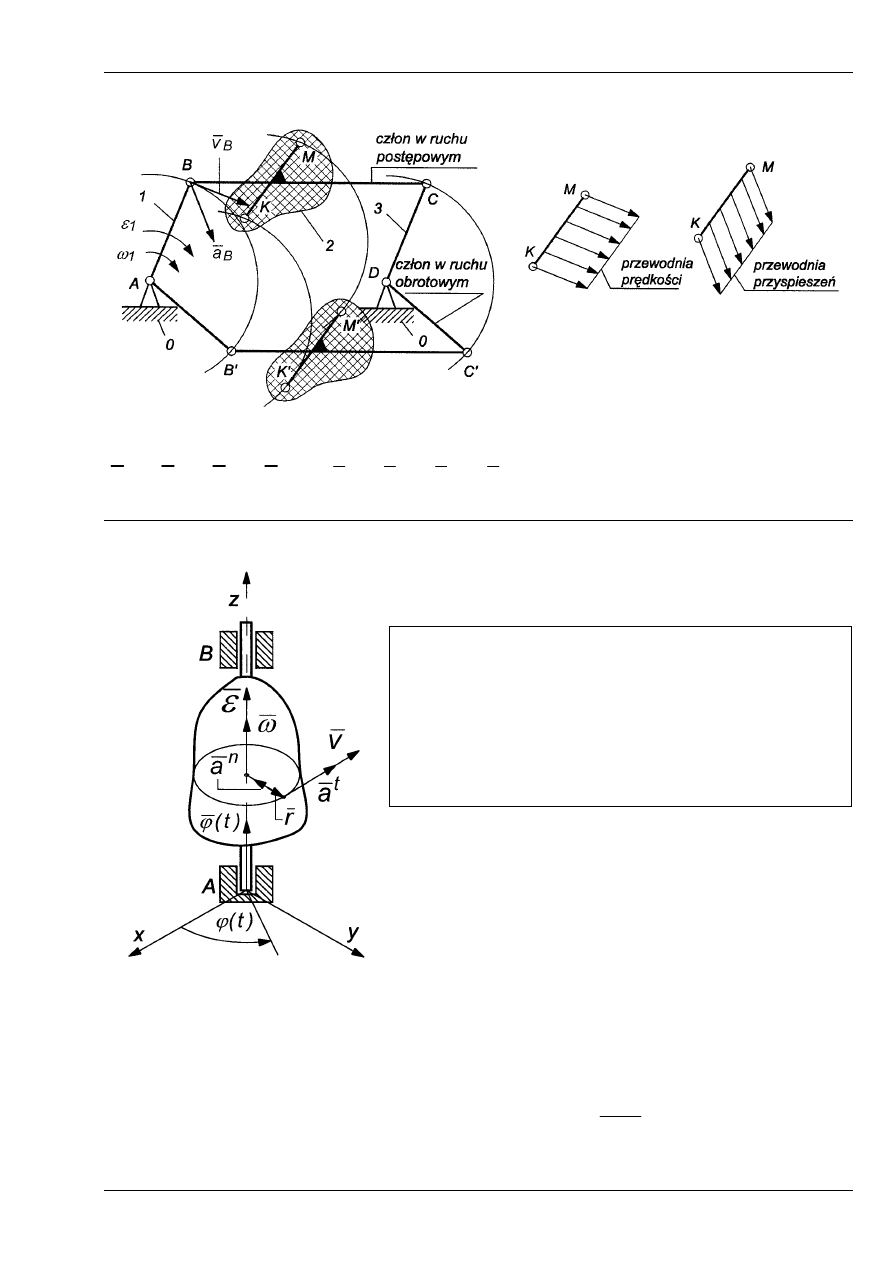
RUCH OBROTOWY BRYŁY

Bryła wykonuje ruch obrotowy, jeżeli wszyst-
kie punkty tej bryły poruszają się po torach ko-
łowych leżących w płaszczyznach do siebie
równoległych. Środki geometryczne torów
(okręgów) leżą na jednej prostej, która jest osią
obrotu bryły.

Rys. 3

Bryła w ruchu obrotowym ma jeden stopień swobody,

)

t

(

ϕ

ϕ

=

,

)

t

(

ϕ

- współrzędna uogólniona

Kąt obrotu bryły:

)

t

(

ϕ

ϕ

=

, Prędkość kątowa:

dt

d

ϕ

ω

=

Opracował: J. Felis str. 2

Zapis i Podstawy Konstrukcji Mechanicznych Kinematyka mechanizmów

Przyspieszenie kątowe:

dt

d

dt

d

2

2

ϕ

ω

ε

=

=

Prędkość liniowa dowolnego punktu bryły:

r

v

,

r

v

⋅

=

×

=

ω

ω

Przyspieszenie liniowe styczne dowolnego punktu bryły:

r

a

,

r

a

t

t

⋅

=

×

=

ε

ε

Przyspieszenie liniowe normalne dowolnego punktu bryły:

r

a

,

r

v

a

2

n

n

⋅

=

×

×

=

×

=

ω

ω

ω

ω

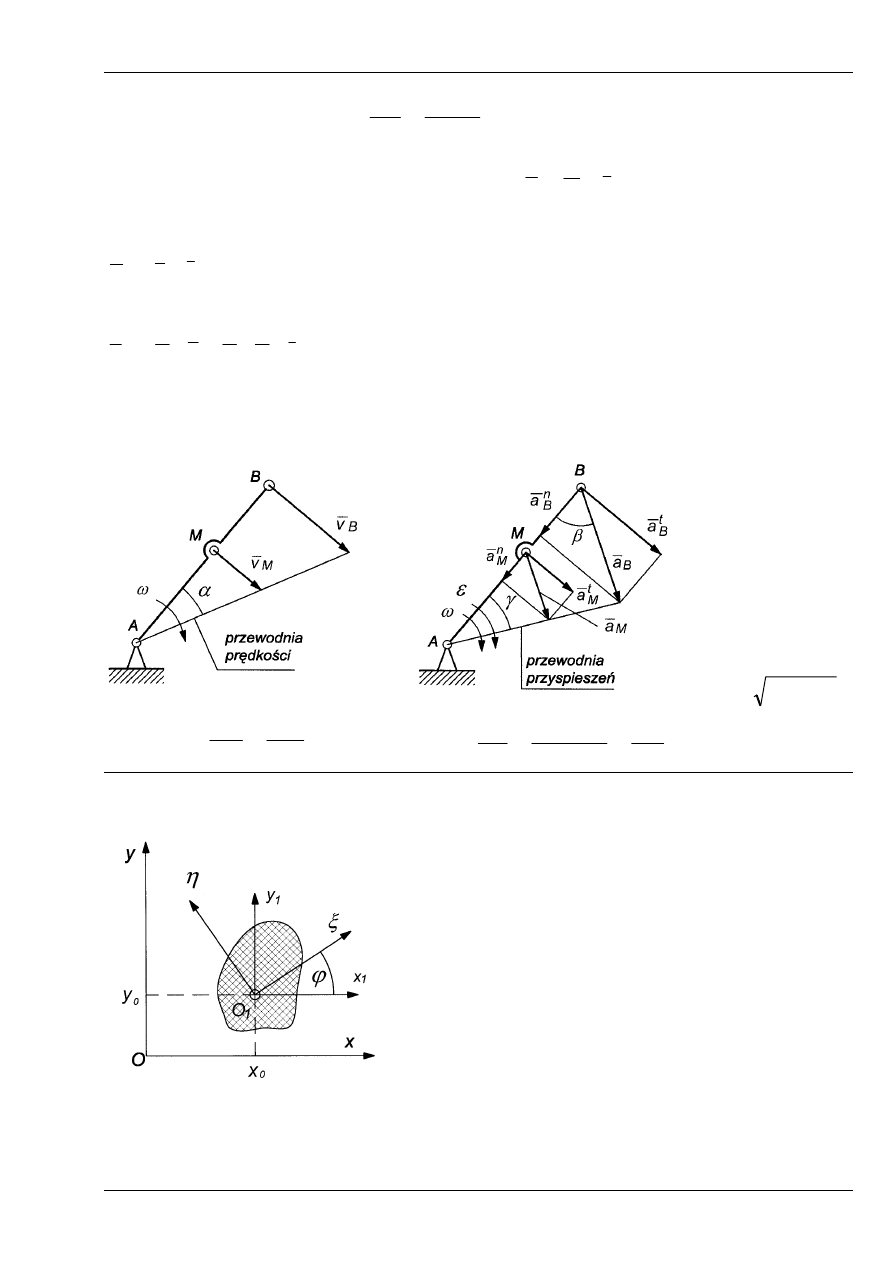
Przykład 2. Człon mechanizmu płaskiego w ruchu obrotowym

Rys. 4

AB

v

⋅

=

ω

B

AB

a

,

AB

a

t

B

2

n

B

⋅

=

⋅

=

ε

ω

2

4

B

AB

a

ε

ω

+

=

2

2

n

B

t

B

AB

AB

a

a

tg

ω

ε

ω

ε

β

=

⋅

⋅

=

=

AM

v

AB

v

tg

M

B

=

=

=

ω

α

RUCH PŁASKI BRYŁY

Rys. 5

Bryła wykonuje ruch płaski, jeżeli
wszystkie punkty bryły poruszają się w
płaszczyznach równoległych do pewnej
płaszczyzny nieruchomej.

Równania ruchu płaskiego:

)

t

(

),

t

(

y

y

),

t

(

x

x

0

0

0

0

ϕ

ϕ

=

=

=

.

Opracował: J. Felis str. 3

Zapis i Podstawy Konstrukcji Mechanicznych Kinematyka mechanizmów

Twierdzenie: Jeżeli figura płaska porusza się w swej płaszczyźnie to z każde-
go położenia daje się przesunąć w inne położenie poprzez obrót dookoła punk-
tu leżącego w płaszczyźnie, zwanego chwilowym środkiem obrotu.

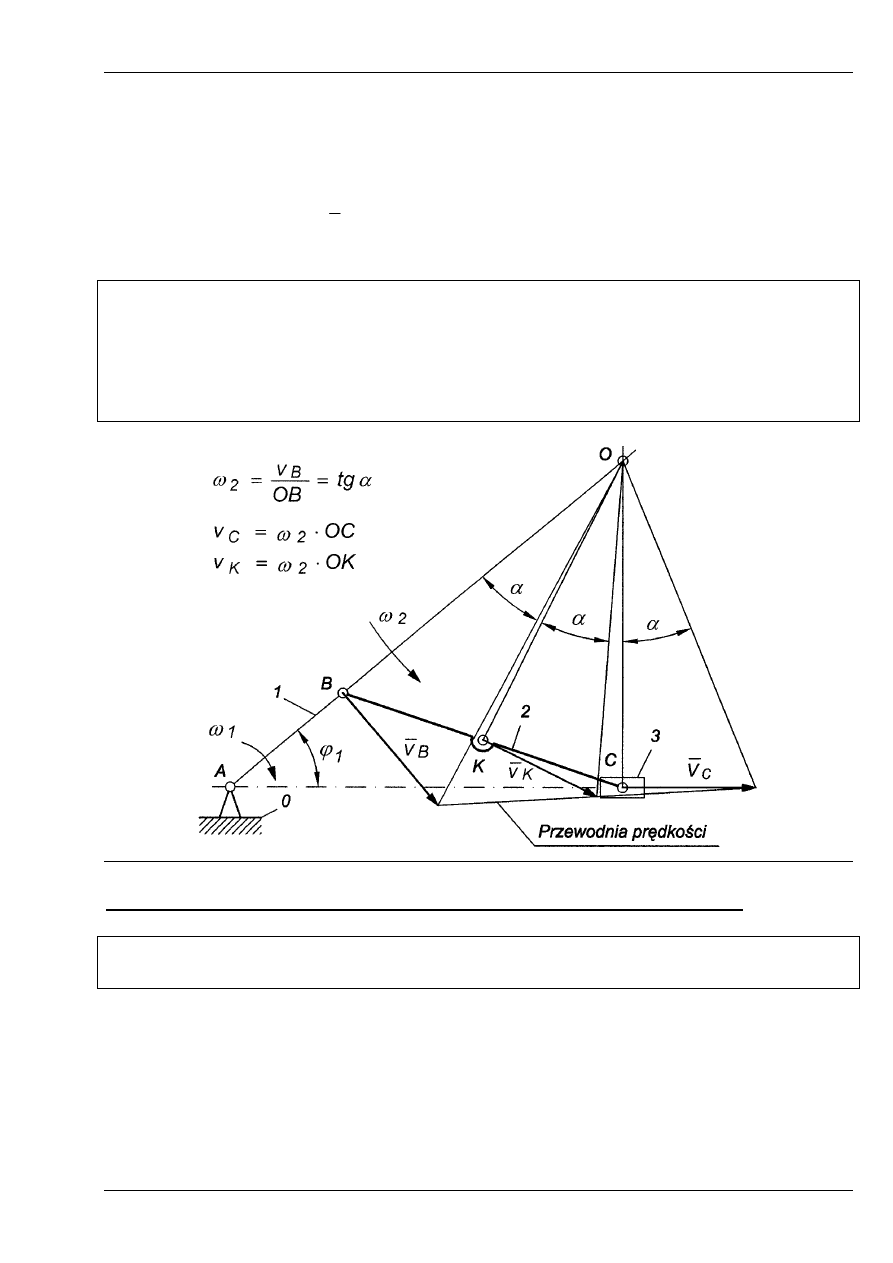
Przykład 3.

Dane: prędkość punktu B -

B

v

, oraz kierunek prędkości punktu C.

Należy wyznaczyć wartość prędkości punktu C należącego członu 2, który wykonuje ruch
płaski.
W celu wyznaczenia chwilowego środka obrotu członu 2 rysujemy prostą prostopadłą
do wektora prędkości punktu B w jego początku oraz analogicznie rysujemy prostą
prostopadłą do wektora prędkości punktu C. Na przecięciu obydwu prostych znajdu-
jemy punkt O stanowiący chwilowy środek obrotu członu 2. Następnie obliczamy
prędkość kątową

2

ω

. Znając prędkość kątową

2

ω

obliczamy prędkość dowolnego

punktu tego członu, np. punktu C i K.

v

AB

1

B

ω

=

Rys. 6



Wyznaczanie prędkości i przyspieszeń metodą grafoanalityczną nazywanej
również metodą planów prędkości i przyspieszeń lub metodą superpozycji

Prędkości i przyspieszenia punktów członów mechanizmów są

wyznaczane na podstawie składania ruchu unoszenia i ruchu względnego

Metoda planów prędkości i przyspieszeń jest metodą grafoanalityczną, co

oznacza, że niektóre wielkości (prędkości i przyspieszenia liniowe i oraz pręd-
kości i przyspieszenia kątowe) obliczamy z równań algebraicznych a pozostałe
prędkości i przyspieszenia liniowe wyznaczamy z równań wektorowych.

Opracował: J. Felis str. 4

Zapis i Podstawy Konstrukcji Mechanicznych Kinematyka mechanizmów

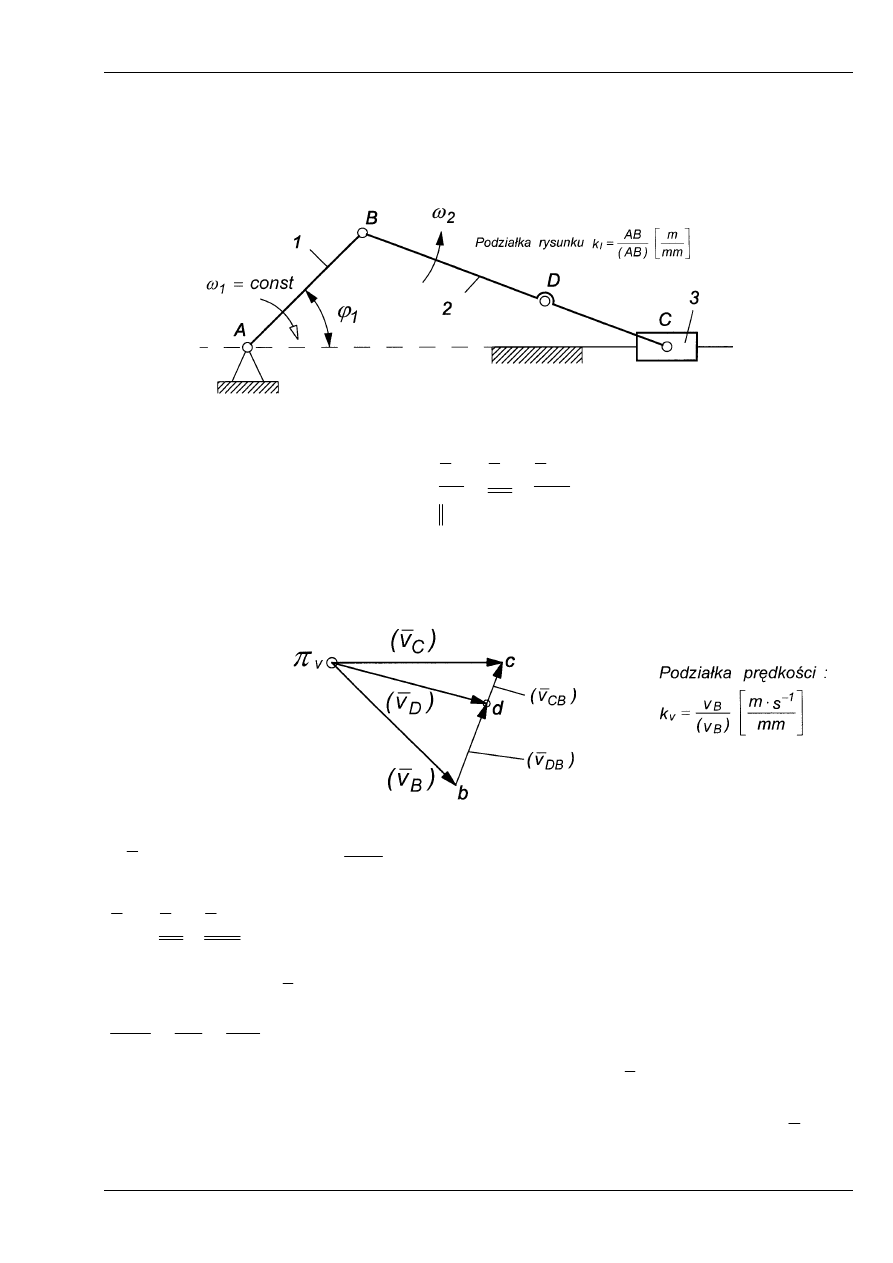
Przykład 4

Wyznaczyć prędkość i przyspieszenie punktów B, C, D mechanizmu korbowo-suwakowego
grafoanalityczną metodą planów.
Dane:

, wymiary mechanizmu AB, BC, BD.

const

1

=

ω

Zadanie rozwiązać dla zadanego położenia kątowego członu napędzającego

ϕ

1.

Rys. 7

Równania planu prędkości

Obliczamy:

,

AB

v

1

B

⋅

=

ω

następnie piszemy równanie wektorowe:

BC

AB

AC

CB

B

C

v

v

v

⊥

⊥

+

=

(P4.1)

Przyjmujemy punkt biegunowy

π

v

i rozwiązujemy wykreślnie w podziałce równanie (1), ry-

sując tzw. plan prędkości, (rys. 8). Z planu prędkości otrzymamy wartość prędkości:

v

,

v

B

C

C

Rys. 8

Prędkość kątową dźwigni 2 obliczymy po odczytaniu z planu prędkości wartości wekto-

ra

v

(odcinek bc

) :

CB

CB

v

CB

2

=

ω

;

W celu wyznaczenia prędkości punktu D napiszemy równania:

DB

v

v

v

v

2

DB

DB

B

D

⋅

=

+

=

ω

(P4.2)

Prędkość względną - v

DB

można również wyznaczyć korzystając z proporcji:

DB

CB

db

cb

v

v

DB

CB

=

=

następnie należy zaznaczyć na planie punkt „d” (koniec wektora v

DB

).

Po połączeniu bieguna

π

v

z punktem ”d” z otrzymamy wektor prędkości punktu D tj.

v

D

Opracował: J. Felis str. 5

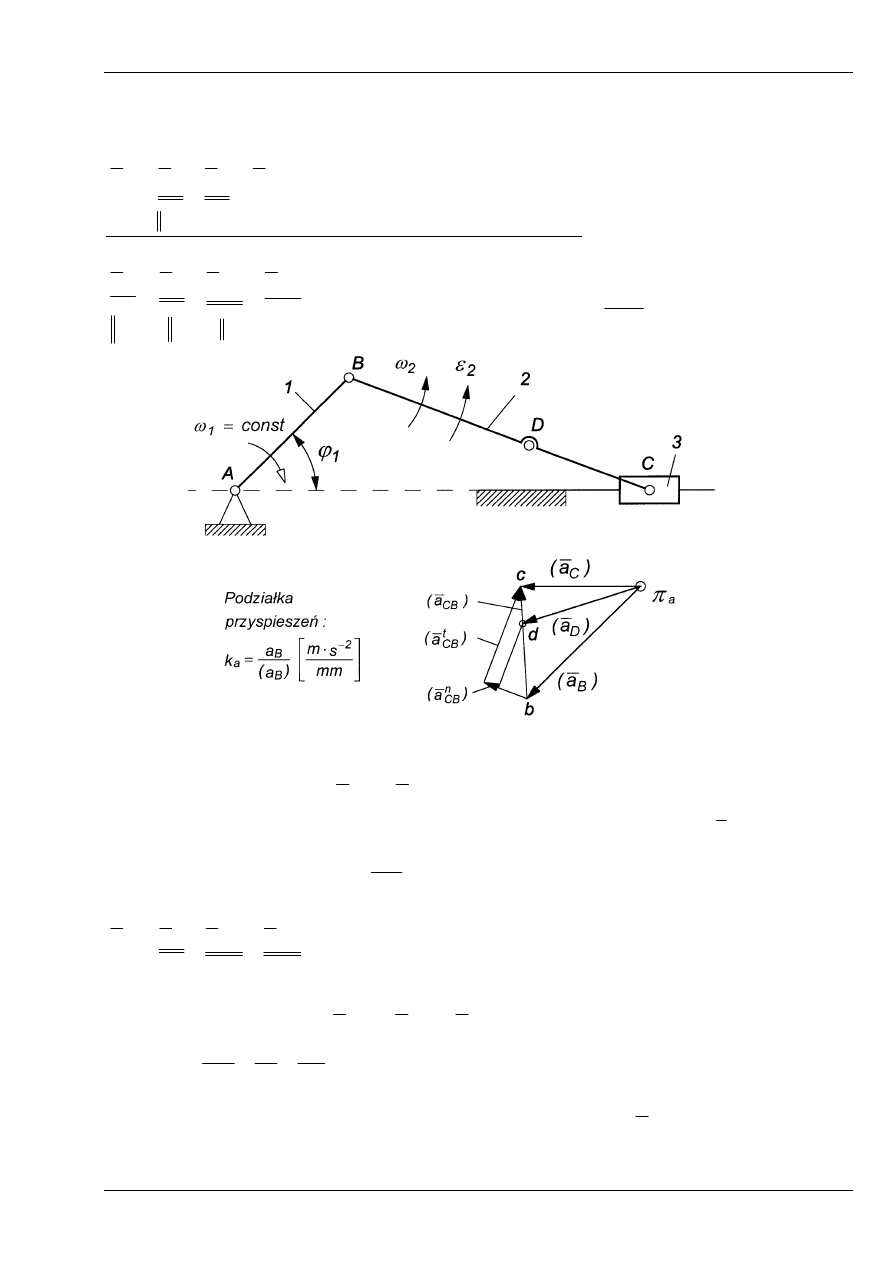
Zapis i Podstawy Konstrukcji Mechanicznych Kinematyka mechanizmów

Równania planu przyspieszeń:

Równania przyspieszeń piszemy podobnie jak równania prędkości.

AB

1

t

B

n

B

t

B

n

B

B

0

ponieważ

0

a

a

a

a

a

=

=

=

+

=

ε

CB

CB

AB

AC

t

CB

n

CB

B

C

a

a

a

a

⊥

+

+

=

(P4.3)

gdzie:

CB

CB

v

a

2

2

2

CB

n

CB

⋅

=

=

ω

Rys. 9

Rozwiązujemy wykreślnie w podziałce równanie (3), rysując tzw. plan przyspieszeń
z dowolnie przyjętego bieguna

π

a

(rys. 9),

Otrzymamy przyspieszenia:

a

i

a

t

CB

C

Przyspieszenie kątowe dźwigni 2 obliczymy po odczytaniu wartości wektora

a

z planu

przyspieszeń (odcinek bc):

t

CB

CB

a

t

CB

2

=

ε

.

Następnie znajdziemy przyspieszenie punktu D na podstawie równań:

DB

a

oraz

,

DB

a

:

gdzie

a

a

a

a

2

2

n

DB

2

t

DB

t

DB

n

DB

B

D

⋅

=

⋅

=

+

+

=

ω

ε

(P4.4)

Przyspieszenie względne -

a

a

a

t

DB

n

DB

DB

+

=

, można też wyznaczyć korzystając

z proporcji:

DB

CB

db

cb

a

a

DB

CB

=

=

.

Wyznaczając w ten sposób położenie punktu „d” na planie przyspieszeń i łącząc następnie
biegun

π

a

z tym punktem znajdziemy wykreślnie przyspieszenie

a

D .

Opracował: J. Felis str. 6

Zapis i Podstawy Konstrukcji Mechanicznych Kinematyka mechanizmów

Analiza kinematyczna mechanizmów dźwigniowych metodą wieloboku
wektorowego

W opisywanej metodzie łańcuch kinematyczny dowolnego płaskiego me-

chanizmu dźwigniowego przedstawia się w postaci zamkniętego wieloboku
wektorowego (Rys. 10), który określa chwilowe położenie członów.

Każdy z wektorów

i

I tego wieloboku zdefiniowany jest we współrzędnych

biegunowych przez dwa parametry: długość wektora

i

i

I

I

=

oraz kąt

i

ϕ

okre-

ślający jego kierunek.

Rys. 10. Mechanizm dźwigniowy Rys. 11. Określanie kątów w metodzie
jako wielobok wektorowy wieloboku wektorowego

Dodatni kąt

i

ϕ

jest to taki kąt o jaki należy obrócić oś

x układu współrzęd-

nych

Oxy w kierunku przeciwnym do ruchu wskazówek zegara w prawoskręt-

nym układzie współrzędnych aby jej dodatni zwrot pokrył się z dodatnim zwro-
tem wektora

i

I

co przedstawiono na Rys. 11.

Przy takiej umowie współrzędne wektora

)

I

,

I

(

I

iy

ix

i

wynoszą zawsze:

i

i

iy

i

i

ix

sin

I

I

,

cos

I

I

ϕ

ϕ

=

=

(1)

a znaki współrzędnych są określone poprzez znaki funkcji

i

.

ϕ

i

sin

ϕ

i

cos

Mechanizm płaski zdefiniowany jest przez zamknięty wielobok składający się

z n wektorów, co zapisujemy następująco:

0

I

n

1

i

i

=

∑

=

(2)

Opracował: J. Felis str. 7

Zapis i Podstawy Konstrukcji Mechanicznych Kinematyka mechanizmów

Wielobok wektorowy zbudowany na
członach mechanizmu posiada
2

⋅

n parametrów.

0

I

n

1

i

i

=

∑

=

(2)

Rys. 10 powtórzony. Mechanizm dźwigniowy jako wielobok wektorowy

Wielobok wektorowy opisany równaniem (2) po zrzutowaniu go na osie pła-
skiego układu współrzędnych odpowiada dwóm równaniom skalarnym:

0

cos

l

,

0

l

i

n

1

i

i

n

1

i

ix

=

∑

⇒

=

∑

=

=

ϕ

(3)

0

sin

l

,

0

l

i

n

1

i

i

n

1

i

iy

=

∑

⇒

=

∑

=

=

ϕ

(4)

Ponieważ układ równań (3), (4) musi być oznaczony, na jego podstawie
można wyznaczyć dwa szukane parametry geometryczne np. dwie długo-
ści, długość i kąt lub dwa kąty. Pozostałe 2n - 2 parametry muszą być zatem
znane i należy je przyjąć jako dane w momencie definiowania mechanizmu.

Po zróżniczkowaniu równań (3), (4) względem czasu otrzymujemy układy
równań:

0

dt

dl

,

0

dt

dl

n

1

i

iy

n

1

i

ix

=

∑

=

∑

=

=

(5)

oraz

0

dt

l

d

,

0

dt

l

d

n

1

i

2

iy

2

n

1

i

2

ix

2

=

∑

=

∑

=

=

(6)

Z układu równań (5) wyznacza się dwie szukane prędkości liniowe lub kątowe

a na podstawie (6) dwa szukane przyspieszenia liniowe lub kątowe.

Opracował: J. Felis str. 8

Zapis i Podstawy Konstrukcji Mechanicznych Kinematyka mechanizmów

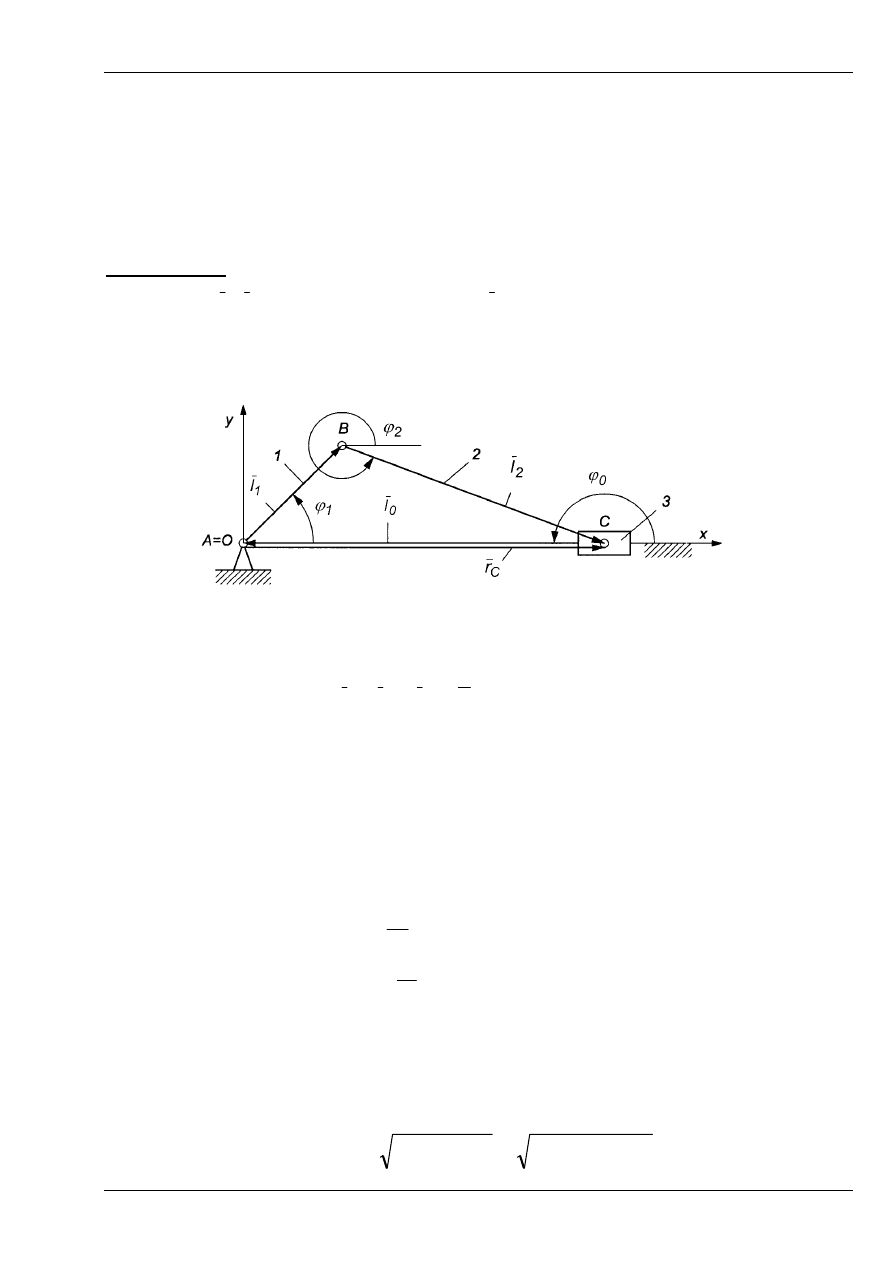
Przykład 5. Mechanizm korbowo-suwakowy

Mechanizm można zapisać trzema wektorami w sposób pokazany na Rys. 3. Należy zatem
przyjąć

2

⋅

3 – 2 = 4 parametry.

Dane:

π

ϕ

ϕ

ϕ

=

=

0

1

1

),

t

(

,

2

1

l

BC

,

l

AB

=

=

Szukane:

, v

)

t

(

),

t

(

x

x

2

2

C

C

ϕ

ϕ

=

=

)

t

(

),

t

(

v

2

2

C

C

ω

ω

=

=

,

)

t

(

),

t

(

a

a

2

2

C

C

ε

ε

=

=

Rozwiązanie

Dwa wektory

2

1

l

,

l

mają stałą długość. Wektor

0

l

zmienia swoją długość w czasie ruchu

mechanizmu. Wpisujemy wielobok wektorowy w kontur mechanizmu i oznaczamy położenia
kątowe poszczególnych wektorów względem osi

Ox za pomocą kątów skierowanych.

Rys. 12

Opisujemy wielobok wektorowy równaniem wektorowym:

0

l

l

l

0

2

1

=

+

+

(P5.1)

Następnie piszemy odpowiednie równania skalarne:

(P5.2)

0

l

cos

l

cos

l

0

2

2

1

1

=

−

+

ϕ

ϕ

(P5.3)

0

sin

l

sin

l

2

2

1

1

=

+

ϕ

ϕ

l

Przyjmując oznaczenie mamy z (P5.3) mamy:

l

=

λ

ϕ

λ

ϕ

ϕ

1

1

2

1

2

sin

sin

l

l

sin

−

=

−

=

P5.4)

2

1

i stąd

)

sin

sin(

arc

1

2

ϕ

λ

ϕ

−

=

(P5.5)

Dalej oznaczymy:

1

2

2

2

2

2

sin

1

sin

1

cos

A

ϕ

λ

ϕ

ϕ

−

=

−

=

=

(P5.6)

Opracował: J. Felis str. 9

Zapis i Podstawy Konstrukcji Mechanicznych Kinematyka mechanizmów

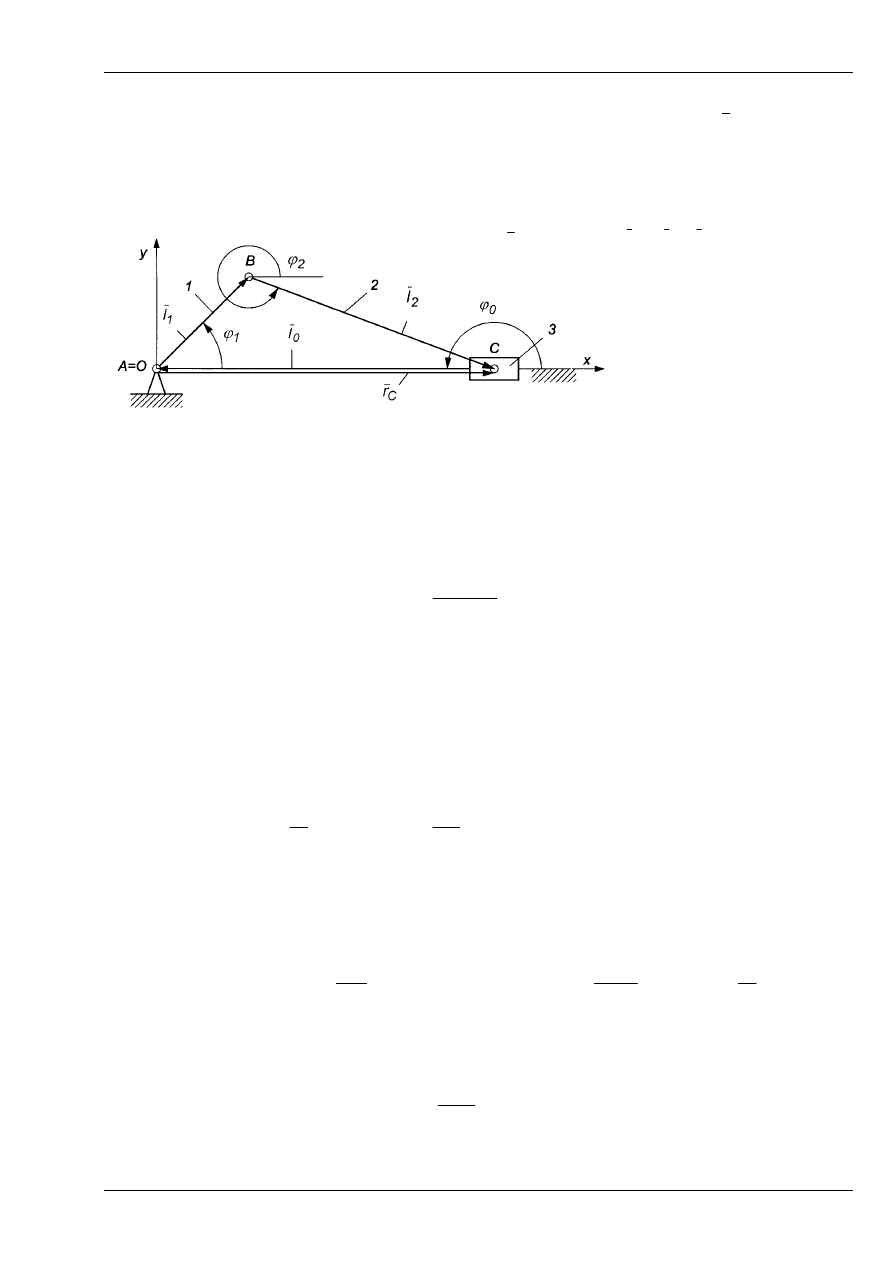
W celu wyznaczenia prędkości liniowej oraz przyspieszenia liniowego punktu C ko-
nieczne jest wprowadzenie wektora promienia wodzącego tego punktu

C

r

.

Wektor promień wodzący dowolnego mechanizmu płaskiego lub przestrzen-

nego prowadzony jest zawsze od początku układu współrzędnych do danego
punktu, którego prędkość lub przyspieszenie chcemy obliczyć.

2

1

0

C

C

l

l

l

)

0

,

x

(

r

+

=

−

=

(P5.7)

Rys. 12 powtórzony

Współrzędna wektora promienia wodzącego określająca położenie

suwaka wynosi:

A

l

cos

l

cos

l

cos

l

l

l

x

2

1

1

2

2

1

1

x

2

x

1

C

⋅

+

=

+

=

+

=

ϕ

ϕ

ϕ

P5.8)

W celu obliczenia prędkości kątowej różniczkujemy (P5.5) względem czasu:

1

1

1

2

1

1

2

2

1

1

2

2

cos

A

cos

cos

cos

cos

ϕ

ϕ

λ

ϕ

ϕ

ϕ

λ

ϕ

ω

ϕ

ϕ

λ

ϕ

ϕ

−

−

=

−

=

=

−

=

&

&

&

&

&

(

P5.9)

Następnie różniczkując (P1.8) względem czasu obliczymy prędkość liniową punktu

C:

(P5.10)

)

2

sin

A

5

,

0

(sin

l

x

v

1

1

1

1

1

C

C

ϕ

λ

ϕ

ϕ

−

+

−

=

=

&

&

W celu obliczenia przyspieszenia kątowego różniczkujemy (P5.9) względem czasu:

















−













−

=

=

1

1

1

1

2

1

2

1

2

2

cos

2

sin

cos

A

sin

A

ϕ

ϕ

ϕ

ϕ

λ

ϕ

ϕ

λ

ϕ

ε

&&

&

&&

(P5.11)

Następnie różniczkujemy (P5.10) i otrzymamy przyspieszenie liniowe punktu

C: (P5.12)















+

+

−













+

−

=

=

1

1

2

3

3

1

2

1

1

1

1

1

1

C

C

2

cos

A

2

sin

A

4

cos

l

2

sin

A

2

sin

l

x

a

ϕ

λ

ϕ

λ

ϕ

ϕ

ϕ

λ

ϕ

ϕ

&

&&

&&

Jeżeli korba

obraca się ze stałą prędkością kątową, wtedy jej przyspieszenie

kątowe jest równe zero czyli

1

I

AB

=

0

dt

d

1

1

1

=

=

=

ω

ε

ϕ

&&

, co należy uwzględnić w równaniach.

Opracował: J. Felis str. 10

Zapis i Podstawy Konstrukcji Mechanicznych Kinematyka mechanizmów

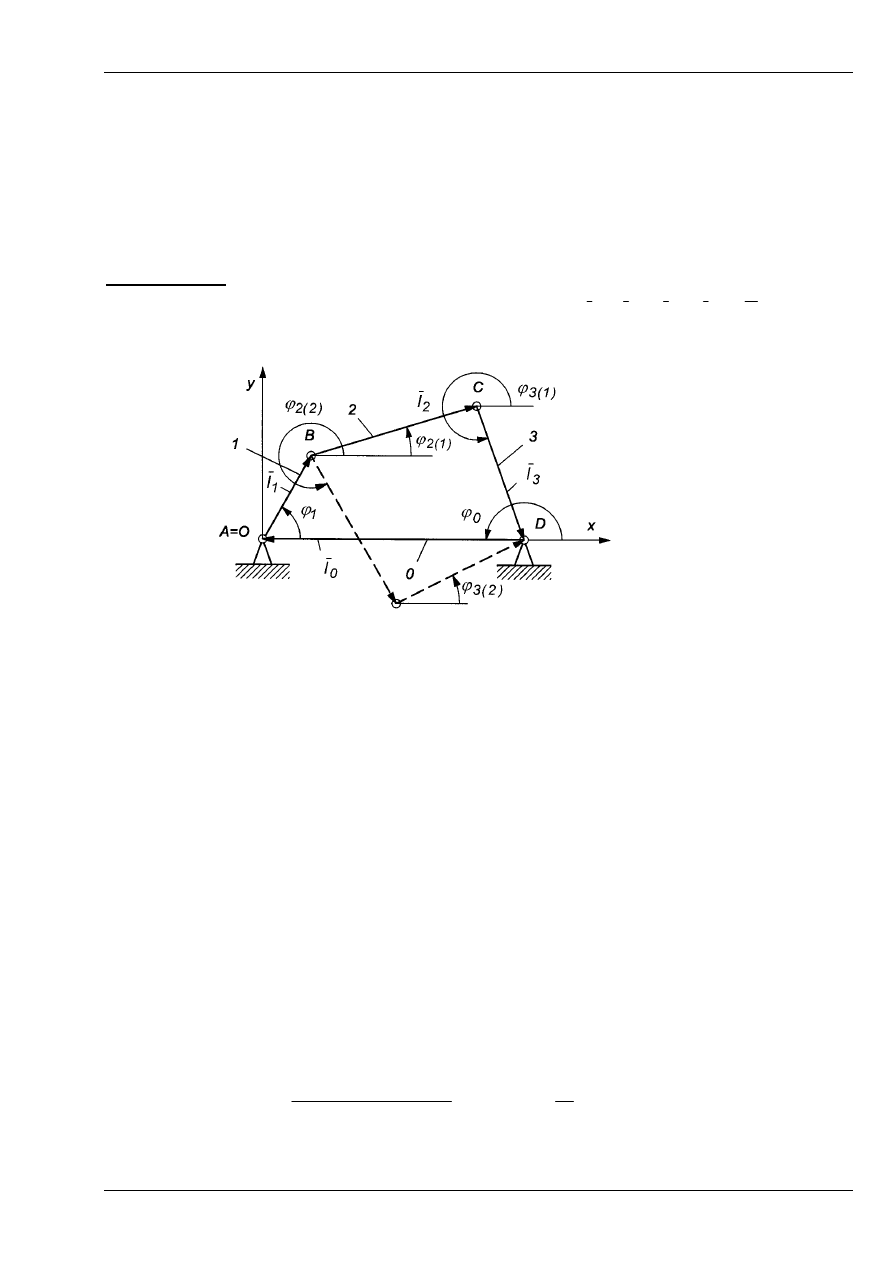
Przykład 6. Mechanizm czworoboku przegubowego

W ten mechanizm wpisujemy cztery wektory (Rys. 13). Należy zatem przyjąć

2

⋅

4 – 2 = 6

parametrów. Wszystkie wektory w przypadku tego mechanizmu mają stałą długość.

Dane:

π

ϕ

ϕ

=

0

0

3

2

1

1

,

l

,

l

,

l

,

l

,

Szukane:

3

2

3

2

3

2

,

,

,

,

,

ε

ε

ω

ω

ϕ

ϕ

.

Rozwiązanie

Mechanizm zapisujemy wielobokiem wektorowym:

0

l

l

l

l

0

3

2

1

=

+

+

+

(P6.1)

Rys. 13

Po rzutowaniu równania (P2.1) na osie układu współrzędnych otrzymamy:

(P6.2)

0

sin

l

sin

l

sin

l

0

l

cos

l

cos

l

cos

l

3

3

2

2

1

1

0

3

3

2

2

1

1

=

+

+

=

−

+

+

ϕ

ϕ

ϕ

ϕ

ϕ

ϕ

Przekształcamy układ równań (P2.2) do postaci:

(P6.3)

3

3

2

2

1

1

3

3

0

2

2

1

1

sin

l

sin

l

sin

l

cos

l

l

cos

l

cos

l

ϕ

ϕ

ϕ

ϕ

ϕ

ϕ

−

=

+

−

=

−

+

Po wprowadzeniu oznaczeń:

,

sin

l

B

,

l

cos

l

A

1

1

0

1

1

ϕ

ϕ

=

−

=

otrzymamy:

(P6.4)

3

3

2

2

3

3

2

2

sin

l

sin

l

B

cos

l

cos

l

A

ϕ

ϕ

ϕ

ϕ

−

=

+

−

=

+

Równania (P6.4) podnosimy do kwadratu i dodajemy stronami

(P6.5)

0

l

l

sin

Bl

2

B

cos

Al

2

A

2

3

2

2

2

2

2

2

2

2

=

−

+

+

+

+

ϕ

ϕ

Równanie (P6.5) dzielimy przez

2

Al

2

0

sin

A

B

cos

Al

2

l

l

B

A

2

2

2

2

3

2

2

2

2

=

+

+

−

+

+

ϕ

ϕ

(P6.6)

Opracował: J. Felis str. 11

Zapis i Podstawy Konstrukcji Mechanicznych Kinematyka mechanizmów

Przyjmiemy oznaczenia:

2

2

3

2

2

2

2

Al

2

l

l

B

A

C

−

+

+

=

,

A

B

D

=

0

2

=

,

zatem (P2.6) przyjmie postać:

C

sin

D

cos

2

+

+

ϕ

ϕ

(P6.7)

Po podniesieniu (P2.6) stronami do kwadratu otrzymujemy:

(P6.8)

0

)

D

C

(

cos

C

2

cos

)

D

1

(

2

2

2

2

2

2

=

−

+

+

+

ϕ

ϕ

Po podstawieniu

2

cos

w

ϕ

=

otrzymamy równanie kwadratowe w postaci:

(P6.9)

0

)

D

C

(

Cw

2

w

)

D

1

(

2

2

2

2

=

−

+

+

+

z którego wyznaczymy dwa pierwiastki

a następnie dwie wartości

kąta

,

w

,

w

2

1

2

ϕ

, tj. kąty

)

2

(

2

)

1

(

2

,

ϕ

ϕ

.

Dwa rozwiązania równania kwadratowego (P6.9) odpowiadają dwóm warian-

tom położenia członów mechanizmu czworoboku przegubowego przy ustalo-
nym położeniu członu napędzającego

1

ϕ

co pokazano na Rys. 13. Kąt

3

ϕ

znajdziemy z równania (P6.4). Otrzymamy odpowiednio:

)

2

(

3

)

1

(

3

,

ϕ

ϕ

.

W celu wyznaczenia prędkości kątowej członów

2 i 3 różniczkujemy pierwsze

z równań (P6.2) i otrzymujemy:

0

sin

l

sin

l

sin

l

3

3

3

2

2

2

1

1

1

=

+

+

ϕ

ω

ϕ

ω

ϕ

ω

(P6.10)

gdzie:

,

dt

d

,

dt

d

,

dt

d

3

3

2

2

1

1

ϕ

ω

ϕ

ω

ϕ

ω

=

=

=

- pochodne kątów,

W celu wyznaczenia prędkości kątowej

3

ω

obracamy układ współrzęd-

nych o kąt

2

ϕ

. Równanie (P6.10) przyjmie postać:

0

)

sin(

l

)

sin(

l

)

sin(

l

2

3

3

3

2

2

2

2

2

1

1

1

=

−

+

−

+

−

ϕ

ϕ

ω

ϕ

ϕ

ω

ϕ

ϕ

ω

(P6.11)

a ponieważ wyrażenie

0

)

sin(

l

2

2

2

2

=

−

ϕ

ϕ

ω

to otrzymamy:

)

sin(

l

)

sin(

l

2

3

3

2

1

1

1

3

ϕ

ϕ

ϕ

ϕ

ω

ω

−

−

−

=

(P6.12)

Opracował: J. Felis str. 12

Zapis i Podstawy Konstrukcji Mechanicznych Kinematyka mechanizmów

Analogicznie obracając układ współrzędnych o kąt

mamy:

ϕ

3

0

)

sin(

l

)

sin(

l

)

sin(

l

3

3

3

3

3

2

2

2

3

1

1

1

=

−

+

−

+

−

ϕ

ϕ

ω

ϕ

ϕ

ω

ϕ

ϕ

ω

(P6.13)

Ponieważ

0

)

sin(

3

3

=

−

ϕ

ϕ

to prędkość kątowa członu 2:

1

3

2

2

3

1

1

2

)

sin(

l

)

sin(

l

ω

ϕ

ϕ

ϕ

ϕ

ω

⋅

−

−

−

=

(P6.14)

W celu obliczenia przyspieszeń kątowych różniczkujemy równanie (P6.10)

0

sin

l

cos

l

sin

l

cos

l

sin

l

cos

l

3

3

3

3

3

2

3

2

2

2

2

2

2

2

1

1

1

1

1

2

1

=

+

+

+

+

+

ϕ

ε

ϕ

ω

ϕ

ε

ϕ

ω

ϕ

ε

ϕ

ω

(P6.15)

Przyspieszenie kątowe członu

3 -

3

ε

otrzymamy obracając układ współrzęd-

nych o kąt

ϕ

2

)

sin(

l

)

cos(

l

l

)

sin(

l

)

cos(

l

2

3

3

2

3

3

2

3

2

2

2

2

1

1

1

2

1

1

2

1

3

ϕ

ϕ

ϕ

ϕ

ω

ω

ϕ

ϕ

ε

ϕ

ϕ

ω

ε

−

−

+

+

−

+

−

−

=

(

P6.16)

Przyspieszenie kątowe członu 2 -

2

ε

otrzymamy obracając układ w

rzędnych o kąt

ϕ

3

spół-

)

sin(

l

l

)

cos(

l

)

sin(

l

)

cos(

l

3

2

2

3

2

3

3

2

2

2

2

3

1

1

1

3

1

1

2

1

2

ϕ

ϕ

ω

ϕ

ϕ

ω

ϕ

ϕ

ε

ϕ

ϕ

ω

ε

−

+

−

+

−

+

−

−

=

(P6.17)

Równania (P6.15), (P6.16) i (P6.17) ulegną uproszczeniu jeżeli prędkość
kątowa

const

1

=

ω

, wówczas przyspieszenie

0

1

=

ε

.

Opracował: J. Felis str. 13

Zapis i Podstawy Konstrukcji Mechanicznych Kinematyka mechanizmów

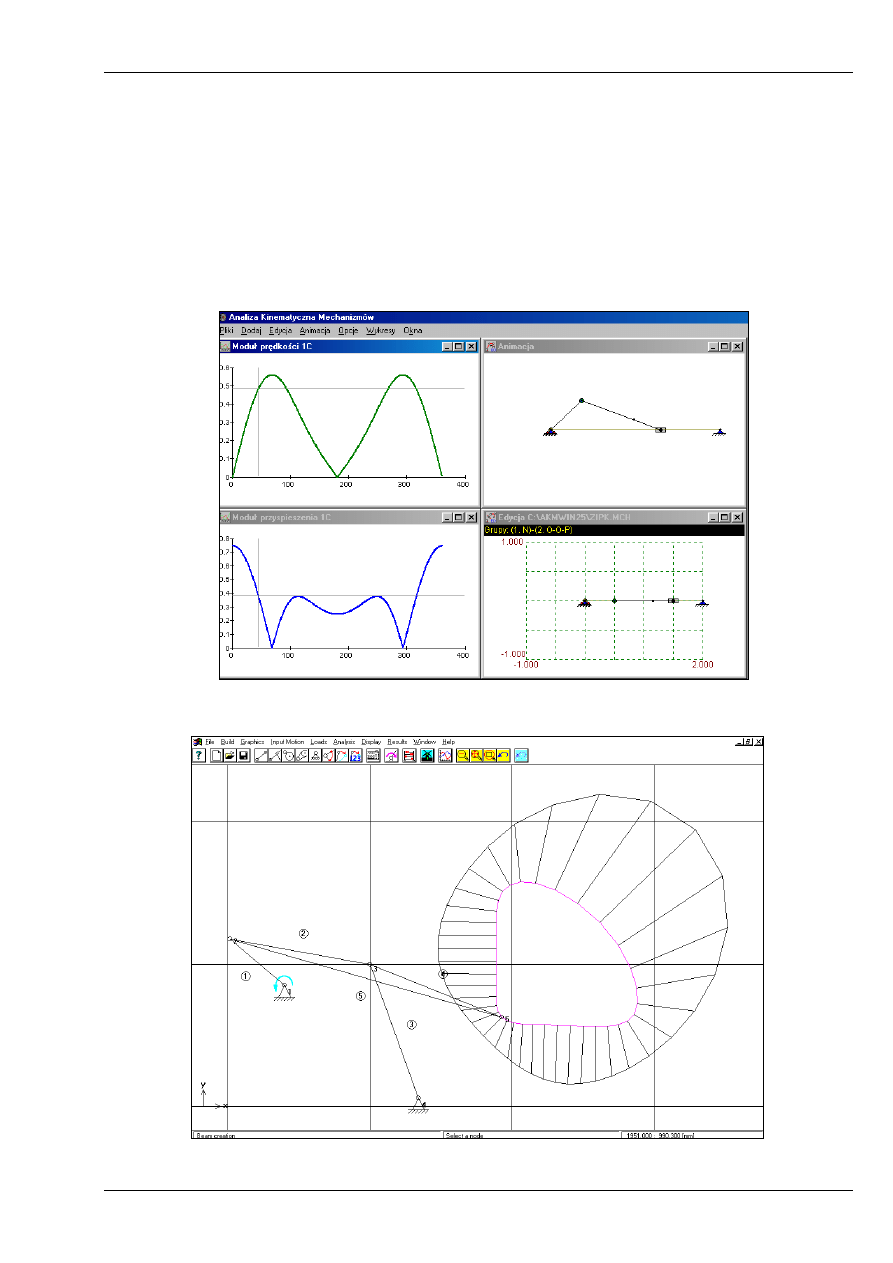
Wspomaganie komputerowe analizy kinematycznej mechanizmów
Programy:

1. Analiza kinematyczna mechanizmów – AKM WIN 2,53 (ga-

laxy.uci.agh.edu.pl\~kmtmipa)

2. Simulation and Analysis of Mechanisms – SAM 4.2 (www.artas.nl)
3. Working Model

AKM WIN 2,53: analiza kinematyczną płaskich mechanizmów dźwigniowych
i krzywkowych

SAM: Analiza kinematyczna i kinetostatyczna (siłowa) mechanizmów płaskich

Opracował: J. Felis str. 14

Zapis i Podstawy Konstrukcji Mechanicznych Kinematyka mechanizmów

Opracował: J. Felis str. 15

ZADANIA DO ROZWIĄZANIA NA ĆWICZENIACH

Mechanizm można również

zamodelować w programie SAM