
Matematyczne podstawy opracowania pomiarów
statystyczne metody analizy danych eksperymentalnych (przedziały ufności, zagadnienia
regresji, wybrane testy statystyczne), rachunek błędu
1 godzina wykładu (zaliczenie na podstawie wyniku kolokwium)
1 godzina laboratorium (zajęcia komputerowe grupowane po 3 godziny – zaliczenie na podstawie wyniku
kolokwium) (pendrive, tablice dystrybuanty rozkładu normalnego i rozkładu t-Studenta)
Literatura:
1. J. B. Czermiński, A. Iwasiewicz, Z.
Paszek, A. Sikorski
Metody statystyczne dla chemików
PWN, Warszawa 1992
4. J. R. Taylor
Wstęp do analizy błędu
pomiarowego
PWN, Warszawa 1995
2. J. Greń
Statystyka matematyczna
PWN, Warszawa 1987
5. W. Klonecki
Statystyka dla inżynierów
PWN, Warszawa 1995
3. J. Greń
Statystyka matematyczna. Modele i
zadania
PWN, Warszawa 1978
6. W. Ufnalski, K. Mądry
Excel dla chemików i nie tylko
WNT, Warszawa 2000
WYKŁADY
Ćwiczenia
1. Histogram, średnia, odchylenie stand.
Zapisy
2. Rozkłady ciągłe, rozkład normalny
3. Rozkład t-Studenta, przedziały ufności
4. Testy parametryczne, test chi-kwadrat
5.Korelacja, regresja
6. Błędy, ANOVA, Excel
7. Wielomian, regresja wieloraka
8. Regresja nieliniowa linearyzowalna
9. Regresja nieliniowa
10.Rachunek błędu
11. Rachunek błędu, funkcje
Kolokwium
12. Kolokwium wykładowe
13. Podsumowanie (błędy, wykresy, prezentacja)
14. Oceny
Ramowy program zajęć
Matematyczne podstawy opracowania pomiarów

Pomiar -
czynności doświadczalne mające na celu wyznaczenie wartości
wielkości mierzonej. Pomiary wykonujemy za pomocą przyrządów (narzędzi)
pomiarowych i
wzorców miar. Przyrządy: np. wagi, mierniki elektryczne,
spektrometry, liczniki cząstek promieniowania. Przykładami wzorców miar są:
odważniki, pojemniki miarowe (cylindry, pipety), przymiary (linijka, suwmiarka).
Wynikiem pomiaru jest
wartość wielkości (liczba mianowana). Jest to
iloczyn
wartości liczbowej (liczby) i jednostki, wskazujący ile razy
zmierzona
wartość jest większa od jednostki. Niektóre wielkości są
bezwymiarowe, np. ułamek molowy. Tę samą wartość wielkości można wyrazić
za pomocą iloczynów różnych liczb i odpowiadających im jednostek. Na
przykład zmierzoną szybkość można podać następująco:
v = 72 km/h = 72/60 km/min = 1,2 km/min = 1 200 m/min = 20 m/s
Symbole
wielkości drukujemy czcionką pochyłą (italiką, kursywą), również ich
indeksy
górne i dolne, jeżeli są symbolami wielkości. Natomiast liczby i jednostki,
a
także symbole pierwiastków i cząstek elementarnych, piszemy czcionką prostą
(
antykwą). Do nielicznych wyjątków należy symbol pH.

Wartości różnych wielkości uzyskuje się z pomiarów bezpośrednich bądź
pomiarów pośrednich. W pomiarze bezpośrednim często odczytuje się wynik
wprost ze wskazania
przyrządu, przeważnie wyskalowanego w jednostkach
mierzonej
wielkości. W pomiarze pośrednim wartość określonej wielkości jest
oznaczana na podstawie
bezpośrednich pomiarów innych wielkości. Wynik
pomiaru oblicza
się używając wzoru. Pomiar pośredni często nazywa się
oznaczaniem.
Sposób wykonania pomiaru jest oparty na określonej podstawie naukowej, którą
nazywamy
zasadą pomiaru. Na przykład pomiar prędkości może być oparty na
zjawisku Dopplera, a temperaturę można mierzyć na podstawie zjawiska
termoelektrycznego.
Metodą pomiarową nazywamy logiczny ciąg operacji
wykonywanych podczas pomiaru. Szczegółowy opis tych operacji nazywa się
procedurą pomiarową. Nauka o pomiarach, metrologia, rozróżnia wiele metod
pomiarowych. Wśród nich szczególne znaczenie mają metody bezwzględne i
bezpośrednie, oparte na prawach fizycznych dających się wyrazić przez
podstawowe stałe (c, G, h, k, F, N
A
...) i podstawowe wielkości (długość l, masa
m, czas t
, prąd elektryczny I, temperatura T, ilość substancji n, światłość I
v
).
Takich metod pomiarowych rzadko używamy w zwykłych laboratoriach
chemicznych. Przeważnie stosujemy metody porównawcze.

Zmierzone wartości wszystkich wielkości są obarczone błędami pomiarowymi,
nazywanymi także niepewnościami pomiarowymi. Błąd pomiaru e
x
jest różnicą
między zmierzoną wartością x oraz wartością prawdziwą (ang. true value),
nazywaną też wartością rzeczywistą, oznaczaną symbolem
:
e
x
= x -
Wartość prawdziwa jest pojęciem idealnym. Wartości tej nie można poznać, jednak
można ją ocenić (oszacować, estymować). Ocenę tę w warunkach i w momencie
pomiaru nazywa się wartością umownie prawdziwą, wartością poprawną lub
uznaną i oznacza symbolem
(w dalszej części wykładu również m). Powinna ona
być tak bliska wartości prawdziwej, aby różnica
między nimi:
=
-
była pomijalnie mała z punktu widzenia celu wykorzystania wartości poprawnej.
Różnica
jest błędem systematycznym
.
.
Błędy pomiarów podaje się jako bezwzględne lub względne. Błąd bezwzględny jest
różnicą wartości zamierzonej i wartości poprawnej:
x = x -
Błąd bezwzględny może być dodatni lub ujemny. Błąd względny jest stosunkiem
modułu (bezwzględnej wartości) błędu bezwzględnego do wartości poprawnej:
x
/
.
Przeważnie jest wyrażany w procentach.
d
x =
x
/

Rozróżniamy błędy systematyczne,
x
syst.
, przypadkowe,
x, i grube,
x
gr.
.
Błędy grube
x
gr.
pochodzą z pomyłek eksperymentatora, niezauważonych
przez niego
niesprawności przyrządów i niewłaściwych warunków pomiaru.
Błędy grube pojawiają się gdy eksperymentator pomyli odczynniki lub roztwory,
nieprawidłowo odczyta wskazania przyrządu, źle zanotuje liczby lub jednostki,
pomyli
się w obliczeniach, wykorzysta niewłaściwe dane literaturowe itp. Jedną z
przyczyn
błędów grubych u początkujących eksperymentatorów jest przesadne
zaufanie do sprawnego
działania przyrządów i niestaranne prowadzenie notatek
laboratoryjnych.
Rażąco duże błędy grube dają się łatwo wykryć i usunąć.
Niektóre można odróżnić od błędów przypadkowych za pomocą testów
statystycznych.

Błędy systematyczne pochodzą z niepoprawności przyrządów pomiarowych,
niepoprawnej ich kalibracji (skalowania
), nieidentyczności warunków pomiaru
(temperatury, ciśnienia, wilgotności, zasilania przyrządu itp.) z warunkami
kalibracji przyrządów, a także indywidualnych cech eksperymentatora i
nieścisłości wzorów obliczeniowych. Błędów systematycznych nie można
zauważyć podczas pomiaru. Aby wykryć błędy pochodzące z niepoprawności
przyrządu należy daną wielkość zmierzyć lepszym przyrządem.
Każdy eksperymentator ma indywidualny sposób wykonywania pomiaru, np.
odczytu
wskazań przyrządów, zauważania zmiany barwy, przez co wpływa na
powstanie
błędu systematycznego. Błąd ten nie wynika natomiast z
niestaranności eksperymentatora, która może być przyczyną błędów grubych.
Umiejętności manualne i doświadczenie eksperymentatora wpływają na
zmniejszenie
błędów systematycznych poprzez zapewnienie właściwych
warunków pomiaru. Ocena wartości błędów systematycznych wymaga analizy
wszystkich
czynników aparaturowych i osobowych wpływających na wynik
pomiaru.
Analizę taką utrudnia nieznana prawdziwa wartość wielkości mierzonej.
Błędy systematyczne można zmniejszyć wykonując pomiary metodą
pomiarową porównawczą, często stosowaną w laboratoriach chemicznych. W
metodzie tej
używa się wzorców miar o znanych wartościach poprawnych albo
materiałów wzorcowych (materiałów odniesienia).

Błędy przypadkowe
x
charakteryzują się tym, że w serii pozornie identycznych
powtórzeń pomiaru tej samej wartości mierzonej błędy te mogą być dodatnie,
x > 0, i ujemne,
x < 0, a
także małe i duże. Powstają pod wpływem wielu
czynników, których praktycznie nie daje się przewidzieć. Przyczyną błędów
przypadkowych
są niewielkie fluktuacje (wahania wokół wartości przeciętnej)
temperatury,
ciśnienia, wilgotności i innych parametrów zarówno w przyrządach
pomiarowych i ich
częściach, jak i w badanych obiektach, gdyż próbki użyte do
kolejnych
powtórzeń pomiaru mogą mieć przypadkowo nieznacznie różne
własności fizyczne i chemiczne. Również chwilowe zmiany przyzwyczajeń
eksperymentatora,
wynikające nawet z jego nastroju, mogą być przyczyną błędów
przypadkowych.
Błędy przypadkowe
x
podlegają prawom statystyki matematycznej i dlatego
bywają także nazwane błędami statystycznymi lub losowymi. Konsekwencją
przypadkowości tych błędów jest możliwość opisania, a także przewidywania, ich
wartości za pomocą funkcji nazywanych rozkładami prawdopodobieństwa.

Z
błędami przypadkowymi i systematycznymi są związane trzy pojęcia:
dokładność, poprawność, precyzja.
Dokładność odnosi się zarówno do wyniku pomiaru – wartości zmierzonej, jak
i do
przyrządu lub metody pomiarowej. Wartość zmierzona jest dokładna, jeżeli
jest zgodna z
wartością prawdziwą mierzonej wielkości, a więc wartość
dokładna nie jest obarczona błędem systematycznym i błędem
przypadkowym. Jest to
oczywiście nieosiągalny ideał, ponieważ wszystkie
zmierzone
wartości są bardziej lub mniej niedokładne. Jednakże analiza
błędów pomiarowych kilku wartości zmierzonych może wykazać, że jedne
wartości są dokładniejsze od innych. Podobnie charakteryzujemy przyrządy i
metody pomiarowe jako bardziej lub mniej
dokładne. Niektórym przyrządom
przypisuje
się umowne klasy dokładności.
Pojęcie poprawności jest związane z błędami systematycznymi i odnosi się
tylko do
przyrządów lub metod pomiarowych. Poprawny przyrząd daje wyniki
pomiaru pozbawione
błędu systematycznego, natomiast przyrząd niepoprawny
ma
określony, często nieznany, błąd systematyczny (ang. bias). Oczywiście
wszystkie
przyrządy i metody pomiarowe są bardziej lub mniej niepoprawne.
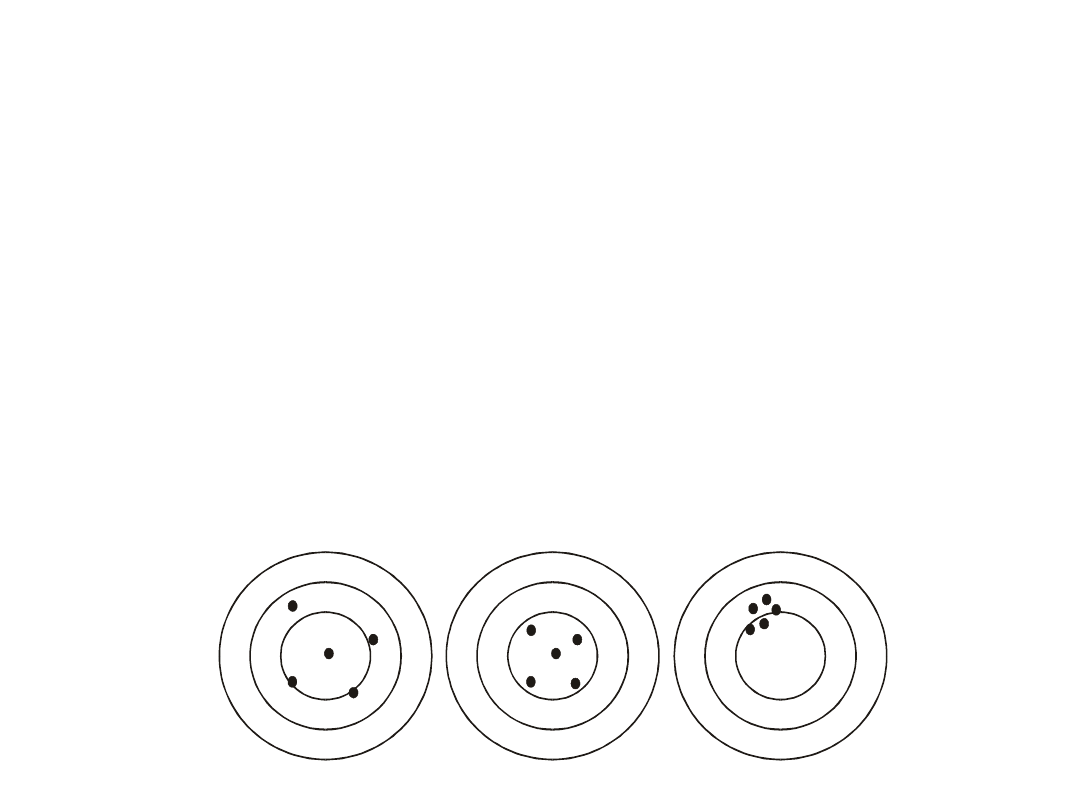
Pojęcie precyzji jest związane tylko z błędami przypadkowymi i odnosi się
zarówno do wartości zmierzonych, jak i do przyrządów lub metod
pomiarowych. Precyzja
przyrządu lub metody pomiarowej zależy od
pewnej
przeciętnej wartości błędu przypadkowego, którym jest obarczony
każdy wynik pomiaru. Wynik pomiaru otrzymany metodą bardzo
precyzyjną ma mały błąd przypadkowy, zaś otrzymany metodą mniej
precyzyjną ma większy błąd przypadkowy. Aby uzyskać odpowiednio
precyzyjny wynik pomiaru
metodą o dużej precyzji wystarczy pomiar
powtórzyć na ogół kilka razy, podczas gdy otrzymanie tak samo
precyzyjnego wyniku
metodą mniej precyzyjną wymaga wykonania
znacznie
większej liczby powtórzeń. Pomiary wykonywane metodami
bardziej precyzyjnymi
są więc oszczędniejsze i mniej pracochłonne.
Zwiększenie liczby powtórzeń pomiaru nie zmienia natomiast błędu
systematycznego zmierzonych
wartości, jeśli otrzymano je za pomocą
przyrządu niepoprawnego.
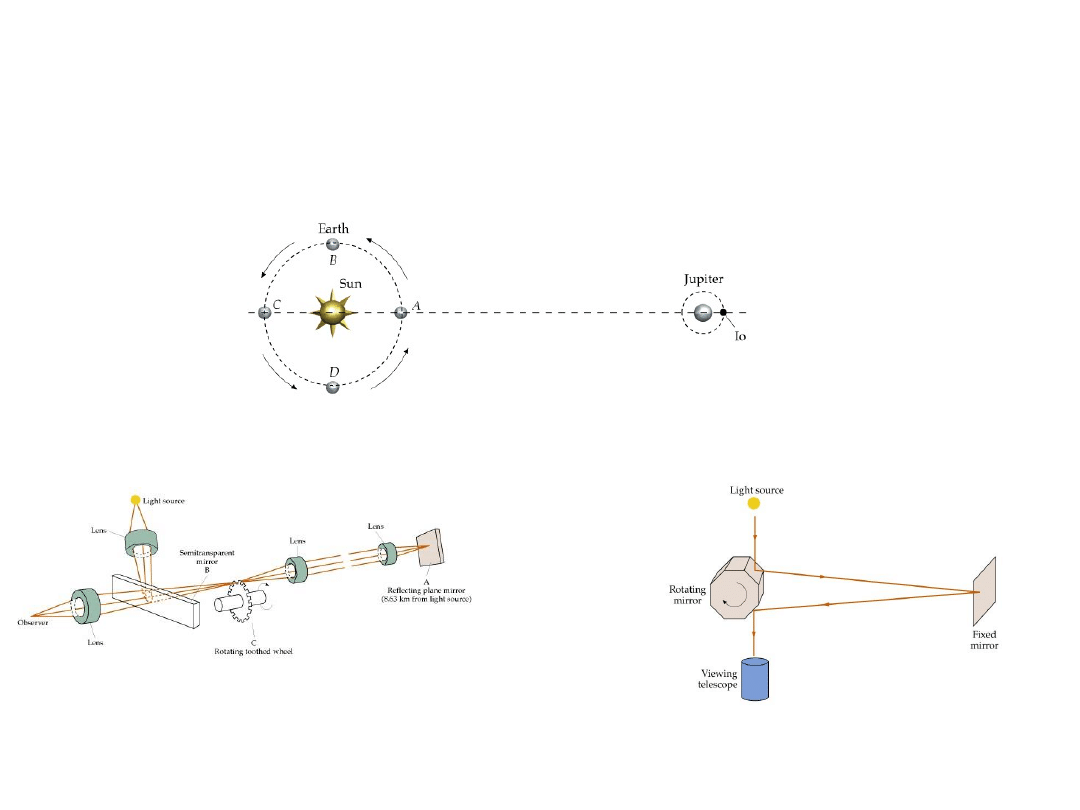
Prędkość światła
Galileusz
Ole R mer (1675 r.) - zaćmienie Io księżyca Jowisza
w pkt C 16.6 min później niż w pkt A
c = x/ t = 3 10 m/16.6 min = 3.01 10 m/s
ø
11
8
Fizeau (1849)
Foucault (1850) c
> c
powietrze
woda
Michelson (1880-1930)
c =299 792 458 m/s

Sekunda (
– następna, najbliższa) –
większości
np.
– obecnie
oznaczana s.
Jest to czas równy 9 192 631 770 okresom promieniowania odpowiadającego
przejściu między dwoma poziomami F = 3 i F = 4 struktury nadsubtelnej stanu
podstawowego
2
S
1/2
atomu cezu
133
(powyższa definicja odnosi się do atomu
cezu w spoczynku w temperaturze 0
K). Definicja ta, obowiązująca od
została ustalona przez
XIII Generalną Konferencję Miar
. Poprzednio sekundę
definiowano jako 1/31 556
925,9747 część
Generalna Konferencja Miar z
r.) lub 1/86400 część
•
Metr
–
w układach:
oznaczenie m
. Metr został zdefiniowany
w celu
ujednolicenia jednostek odległości. W myśl definicji zatwierdzonej przez
w
jest to odległość, jaką pokonuje
w
1/299 792 458
•
Poprzednio metr zdefiniowany był jako:
•
) długość równa 10
-7
długości mierzonej wzdłuż
. Na podstawie tej definicji wykonano
wzorzec metra. W trakcie powtórnych pomiarów stwierdzono
różnice między wzorcem a definicją. Wzorzec przechowywany jest w
Międzynarodowym Biurze Miar i Wag w
koło
.
•
) I Generalna Konferencja Miar (1889) określiła metr jako
odległość między odpowiednimi kreskami na wzorcu, równą 0,999914 · 10
-7
połowy
•
) XI Generalna Konferencja Miar (1960) zdefiniowała metr jako
długość równą 1 650 763,73 długości fali promieniowania w próżni
odpowiadającego przejściu między poziomami 2p
10
a 5d
5
atomu
86
Kr (
86).

Sposób przestawienia wyniku pomiaru
Liczba cyfr w rozwinięciu dziesiętnym liczby, wyniku pomiaru bezpośredniego,
ograniczona jest dokładnością pomiaru (klasą używanego przyrządu) lub
niepewnością pomiarową. Zawarte w takim wyniku cyfry możemy podzielić na
cyfry znaczące, czyli określające dokładność oznaczenia i zera służące do
wyznaczenia pozycji dziesiętnych cyfr znaczących. Cyframi znaczącymi są
więc wszystkie cyfry różne od zera, zera zawarte pomiędzy tymi cyframi oraz te
zera na końcu liczby, których znaczenie wynika z dokładności pomiaru, np.
(cyfry znaczące zaznaczone pogrubieniem):
0,0234
0,0002; 120,50
0,01; 560700
300; 789
40
Liczba 300 może mieć jedną (300), dwie (300) lub 3 cyfry znaczące (300)
Nie znając dokładności pomiarowej nie możemy tego jednoznacznie stwierdzić.
By uniknąć niejednoznaczności:
560700
300, (56070
30
)∙10
1
, (5607
3
)∙10
2
x
± Δx = x(1 ± Δx/|x|) = x(1 ± δx)

Zasady zaokrąglania liczb
•
Jeżeli pierwsza z odrzucanych cyfr jest mniejsza od 5, to cyfry
zaokrąglonej liczby pozostają bez zmian
12,34
≈ 12,3; 1,253789∙10
3
≈ 1,25 ∙10
3
•
Jeżeli pierwsza z odrzucanych cyfr jest większa od 5, to ostatnia cyfra
zaokrąglonej liczby zwiększa się o 1
12,36
≈ 12,4; 1,258789∙10
3
≈ 1,26 ∙10
3
•
Jeżeli pierwsza z odrzucanych cyfr jest równa 5, i następują po niej
liczby niezerowe to ostatnia cyfra zaokrąglonej liczby zwiększa się o 1
12,351
≈ 12,4; 1,255789∙10
3
≈ 1,26 ∙10
3
, 1,255000001
∙10
3
≈ 1,26 ∙10
3
•
Jeżeli pierwsza z odrzucanych cyfr jest równa 5, i następują po niej
tylko zera to ostatnia cyfra zaokrąglonej liczby:
-
zostaje bez zmian, gdy jest parzysta lub zero
-
zwiększa się o 1, gdy jest nieparzysta
12,45
≈ 12,4; 12,35 ≈ 12,4; 1,2550∙10
3
≈ 1,26 ∙10
3
, 1,22500
∙10
3
≈ 1,22 ∙10
3

Reguły zaokrąglania wyników pomiarów
•
Niepewność pomiarową przedstawia się liczbą z 2 cyframi znaczącymi
36,234
± 0,058; 16234 ± 15;
(2,62
± 0,25)∙10
2
Dla przyrządów wskazówkowych o niepewności pomiarowej decyduje
rozdzielczość pomiaru, czyli najmniejsza zmiana wielkości mierzonej. W
zależności od klasy przyrządu odpowiada ona najczęściej 0,5 działki elementarnej
(klasa techniczna), choć może przyjmować wartości 0,1 lub 0,2 działki elementarnej
(klasa laboratoryjna).
•
Niepewność przedstawiona jedną cyfrą znaczącą powinna być zaokrąglona
w górę (wyjątek stanowią zmiany poniżej 10%)
Δx = 2,35 ≈ 3;
Δx = 3,25 ≈ 3
(jeżeli pierwszą cyfrą znaczącą jest 1, to dążymy do pozostawienia dwóch cyfr
znaczących, by uniknąć dużego błędu względnego zaokrąglenia)
Δx = 1,35 ≈ 1,4
•
Ostatnia cyfra znacząca wartości zmierzonej powinna występować na
pozycji dziesiętnej ostatniej cyfry znaczącej niepewności pomiarowej
36,234
± 0,058; 16234 ± 15;
(2,62
± 0,25)∙10
2

Niepewność sumy i różnicy
q = x + y
q =
x +
y
q = x - y
q =
x +
y
Rachunek błędu maksymalnego
x
x, y
y
q = f(x,y); q
q
błąd względny
d
x =
x/
x
Suma, różnica
q = x + y
Min. (x -
x) + (y -
y) = (x + y) - (
x +
y)
Max. (x +
x) + (y +
y) = (x + y) + (
x +
y)
q = x - y
Min. (x -
x) - (y +
y) = (x - y) - (
x +
y)
Max. (x +
x) - (y -
y) = (x - y) + (
x +
y)
Rachunek błędu maksymalnego
Niepewność iloczynu i ilorazu
q = x
y
d
q =
d
x +
d
y
q = x/y
d
q =
d
x +
d
y
Iloczyn, iloraz
x
x = x(1
x/x) = x(1
d
x)
y
y = y(1
d
y)
q = x
y
Min. x(1 -
d
x)
y(1 -
d
y) = x
y(1 -
d
x -
d
y +
d
x
d
y)
x
y[1-(
d
x+
d
y)]
Max. x(1 +
d
x)
y(1 +
d
y) = x
y(1 +
d
x +
d
y +
d
x
d
y)
x
y[1+ (
d
x+
d
y)]
Ponieważ
d
x i
d
y jako błędy pomiarowe są małe ( na ogół < 0,1) to
d
x
d
y
jest pomijalnie małe.

Mnożenie przez stałą
q = B
x(1
d
x)
(
d
q =
d
B +
d
x =
d
x)
q =
d
q
q
=
d
x
B
x
=
B
x
q
q = Bx
B
x
Potęgowanie
q = x
n
= x
x
...
x
d
q =
d
x +
d
x + ... +
d
x = n
d
x
q =
d
q
q
= n
d
x
x
n
= n
x
n
x/
x
= n
x
n-1
x

Zostawiając odpowiednią liczbę cyfr znaczących wykonaj
następnie działania:
x = 2,0487
10
-4
1
10
-5
x = (2,0
0,1)
10
-4
d
x=0,05
y = 1,24999
10
3
3
10
2
y = (1200
300)
d
y=0,25
z = (1,804
1)
10
3
z = (2000
1000)
y+z = ?; 3
z = ?; 3
z = ?
y+z = 3200
1300
3
z = 6000
3000
y
x = 0,24(1
0,3)=0,240
0,072
x = (2,0
0,1)
10
-4
= 2,0(1
0,1/2,0)
10
-4
= 2,0
10
-4
(1
0,05)
y = (1200
300) = 1200(1
300/1200) = 1200(1
0,25)
y
x = 2,0
10
-4
1200(1
[0,05 + 0,25])
x
y
2
2
y
x
q
Porównanie rachunku błędu maksymalnego z metodami
statystycznymi
q = x + y
q =
x +
y
N(m
x
,
x
) + N(m
y
,
y
) = N(m
q
,
q
)
m
q
=m
x
+ m
y
;
2
2
y
x
q
Funkcje jednej zmiennej
q(x)
x
x
q
q
y=[df(x)/dx] x+C
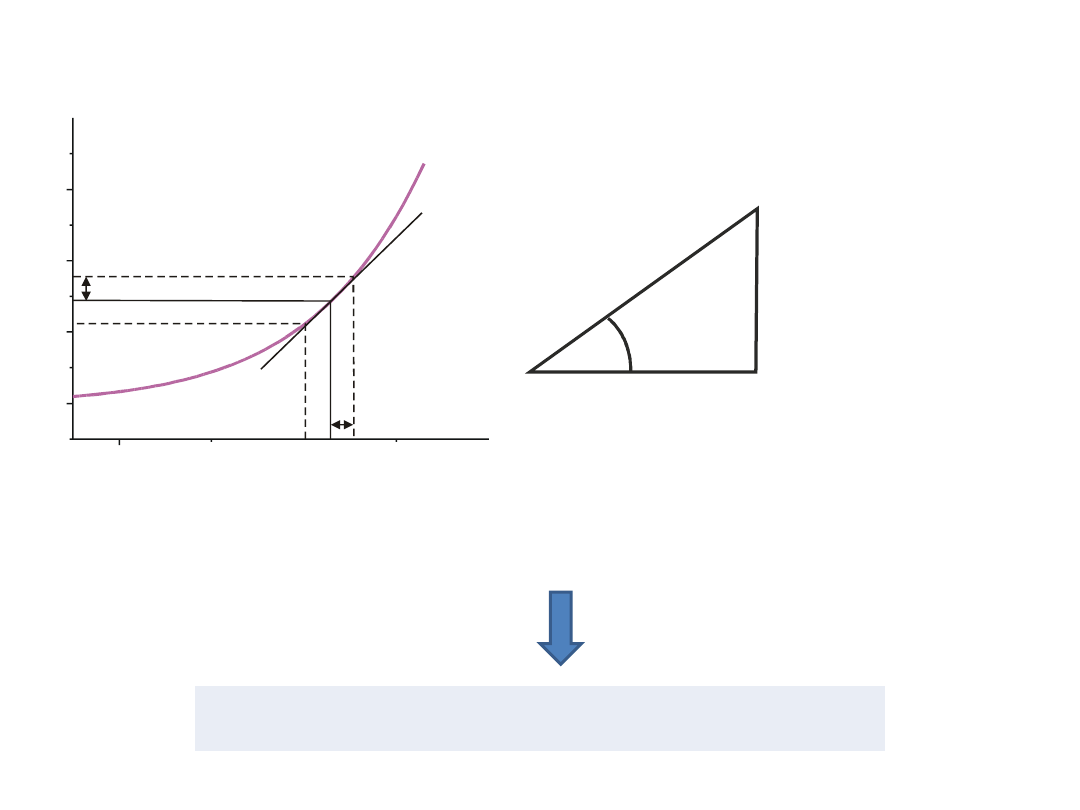
Niepewność wartości funkcji jednej zmiennej
q =
dq/dx
x
q = q(x) = f(x)
q = q(x +
x) - q(x)
Ponieważ dla dostatecznie małego przedziału f(x+u)-f(x) = df/dx
u
x
q
x
= tg
|df/dx|
x =

x = 2,00
± 0,03
q = f(x) = x
n
np. q = f(x) = x
3
= 8; q = f(x) = 2/x
2
= 2x
-2
= 0,5
q = |df(x)/dx)|
x
∙
x = | nx
n-1
|
2
∙
x
np.
q = | 3x
2
|
2
∙ 0,03 = 0,36 q = 8,00 ± 0,036
q = | -4x
-3
|
2
∙ 0,03 = 0,015 q = 0,500 ± 0,015
x = 1,00
± 0,01
q = f(x) = e
x
= exp(x) = e
1
= 2,71828
q = |df(x)/dx)|
x
∙
x = |e
x
|
1
∙
x = e
1
∙ 0,01 = 0,027
q = 2,718
± 0,027
Podstawa
(inaczej liczba Eulera lub liczba
Nepera
) w przybliżeniu wynosi 2,7182818, oznacza się ją literą e.
x = 2,00
± 0,01
q = f(x) = lnx = ln(1) = 0,69314
q = |df(x)/dx)|
x
∙
x = |1/x|
2
∙
x
= 0,5∙0,01 = 0,005
q = 0,693
± 0,005

α = 30º ± 2º
q = f(
α) = sinα = sin 30º = 0,5
q = |df(
α)/dα)|
α
∙
α = |cos 30º|∙???
360º (deg.) = 2π (rad.)
2º (deg.) = 4π/360 (rad.) = 0,035 =
α
q = |df(
α)/dα)|
α
∙
α = |cos 30º|∙0,035 = 0,0303109

q = x + y
q =
q/
x
x +
q/
y
y
q =
1
x +
1
y =
x +
y
q = x - y
q =
q/
x
x +
q/
y
y
q =
1
x +
-1
y =
x +
y
q = x
y
q =
q/
x
x +
q/
y
y
q =
y
x +
x
y =
x +
y |:q=|xy|
δq = |y/xy|
x + |x/xy|
y =
δx + δy

Przykład 1:
Pojemność cieplna kalorymetru: K = i
2
R
t/
T gdzie:
i -
natężenie prądu = 12
0,225A
R -
opór spirali grzejnej = 57
3
t -
czas przepływu prądu = 600
2 s
T - przyrost temperatury kalorymetru = 30
1
K
K =
K/
i
i +
K/
R
R +
K/
t
t +
K/
(
T)
(
T)
K =
2iRt/
T
i +
i
2
t/
T
R +
i
2
R/
T
t + |i
2
Rt/(
T)
2
(
T)
Przykład 2
z
x
y
x
q
Policzyć
q dla x=20
1, y = 2, z = 0
q =
q/
x
x +
q/
y
y +
q/
z
z =
=
2
)
(
1
)
(
)
(
1
z
x
y
x
z
x
x = 2/400
1=0,005
1
20
1
22
1,1(1
(1/22+1/20) =1,1
0,1
Wyszukiwarka
Podobne podstrony:
IM wykład 1
Technologie informacyjne - wykład 2-4, AM SZCZECIN, Informatyka - Wykłady
Bezpieczeństwo nawigacji - Wykład 1, AM SZCZECIN, Bezpieczeństwo nawigacji
Bezpieczeństwo nawigacji - Wykład 9, AM SZCZECIN, Bezpieczeństwo nawigacji
EgzaminMikrobPytania2008, chemia organiczna, biologia ewolucyjna-wykłady, genetyka, biologia komórki
2012 AMI wyklad print cz1
Fizjologia zwierząt wszystkie opracowania, chemia organiczna, biologia ewolucyjna-wykłady, genetyka,
Bezpieczeństwo nawigacji - Wykład 6, AM SZCZECIN, Bezpieczeństwo nawigacji
Bezpieczeństwo statku - Wykład 3, AM SZCZECIN, BEZPIECZEŃSTWO STATKU, Bezpieczeństwo Statku - Wykład
Bezpieczeństwo statku - Wykład 2, AM SZCZECIN, BEZPIECZEŃSTWO STATKU, Bezpieczeństwo Statku - Wykład
im wyklad id 210863 Nieznany
Bezpieczeństwo nawigacji - Wykład 5, AM SZCZECIN, Bezpieczeństwo nawigacji
Bezpieczeństwo statku - Wykład 8, AM SZCZECIN, BEZPIECZEŃSTWO STATKU, Bezpieczeństwo Statku - Wykład
wykład 3 i 4, AM, rozne, genetyka, genetyka
Bezpieczeństwo statku - Wykład 4, AM SZCZECIN, BEZPIECZEŃSTWO STATKU, Bezpieczeństwo Statku - Wykład
IM wykład 5 przemiany w HSS podczas obróbki cieplnej vA
więcej podobnych podstron