Fizyka Ciała Stałego II
opracowanie zagadnień
1. Ciepło właściwe wg Debye’a.
Ciepło właściwe, powtórka:
Gaz doskonały, jednoatomowy:
ciepło właściwe przy stałej objętości
R
c
V
2
3
=
ciepło właściwe przy stałym ciśnieniu
R
c
p
2
5
=
- wyniki, które chcemy wyprowadzić.
Dla 1 mola gazu:
R
T
pV
=
Rozważmy gaz w sześciennym pudle o krawędzi l . Możemy rozpatrywać oddzielnie każdą cząstkę.
Jeśli prędkość danej cząstki w jednym kierunku, np. w kierunku y , wynosi
y
v
, to
czas między kolejnymi uderzeniami o ściankę:
y
v
l
t
2
=
.
Zmiana pędu w jednorazowym akcie zderzenia:
y
mv
p
2
=
∆
Siła:
dt
p
d
dt
v
d
m
a
m
F
=
=
=
, stąd siła działająca na ścianki:
l
mv
v
l
mv
t
p
F
y
y
y
2
2
2
=
=
∆
=
Ciśnienie, jakie wywiera jedna cząsteczka na ścianki naczynia:
V
mv
l
mv
l
F
p
y
y
2
3
2
2
=
=
=
Gdy weźmiemy dużo cząstek:
ś
rednia prędkość:
2
2
2
2
z
y
x
ś
r
v
v
v
v
+
+
=
z
y
x
v
v
v
=
=
→
2
2
2
2
3
1
ś
r
z
y
x
v
v
v
v
=
=
=
Ciśnienie całkowite jednego mola:
V
mv
N
p
A
cał
3
2
=
2
3
1
mv
N
V
p
A
cał
=
1
2
2
k
E
mv
=
- energia kinetyczna 1 cząsteczki
U
E
E
N
V
p
cał
k
k
A
cał
3
2
3
2
3
2
,
1
=
=
=
Ze wzoru
R
T
pV
=
→
RT
pV
=
RT
U
=
3
2
→
RT
U
2
3
=
Ciepło właściwe to ilość energii, jaką musimy dostarczyć, aby ogrzać ciało o 1°C:
R
T
U
V
2
3
=
∂
∂
A co będzie, jeśli zmienimy objętość, np. przesuwając tłok o powierzchni S o x
∆
?
Praca wykonana podczas przesuwania tłoka:
V
p
x
S
p
x
F
W
∆
⋅
=
∆
⋅
⋅
=
∆
⋅
=
p
RT
V
=
p
RT
V
1
1
=
p
RT
V
2
2
=
→
(
)
T
R
T
T
p
R
p
V
p
W
∆
⋅
=
−
=
∆
⋅
=
1
2
Stąd dodatkowa praca wykonana kosztem dostarczonego ciepła na rozprężenie gazu:
R
T
W
=
∆
∆
R
R
R
T
U
p
2
5
2
3
=
+
=
∂
∂
Ciepło właściwe dla ciał stałych (prawo Doulonge’a – Petitte’a) :
R
T
U
V
3
=
∂
∂
Zależność ciepła właściwego od temperatury jest jak
3
T . Próbował to wyjaśnić najpierw Einstein, który
założył, że drgania sieci są skwantowane. Jego teoria dobrze sprawdzała się w pewnym zakresie
temperatur, jednak uwzględniała tylko drgania optyczne, podczas gdy w niskich temperaturach
dominują drgania akustyczne.
W pełni wyjaśnił tą zależność Debye, który założył liniową zależność częstości od wektora falowego.
Rozważmy wielkość zależną od temperatury. Temperatura wynika z drgań fononów o częstości
ω
od 0 do
max
ω
:
ω
ω
ω
ω
ω
d
Z
f
A
T
A
⋅
⋅
⋅
=
∫
)
(
)
(
)
(
)
(
| |
prawdopodobieństwo gęstość
obsadzenia stanu
o danej częstości
N
d
Z
3
)
(
max
0
=
⋅
∫
ω
ω
ω
- ilość drgań zależnych od wektora falowego dla fononów
Oznaczenie wektora falowego: elektrony -
k
, fonony - q
π
π
8
1
)
2
(
1
)
(
3
=
=
q
Z
- podobnie jak dla elektronów, tylko 2 razy mniej, bo bez spinów (dla
1
=
V
)
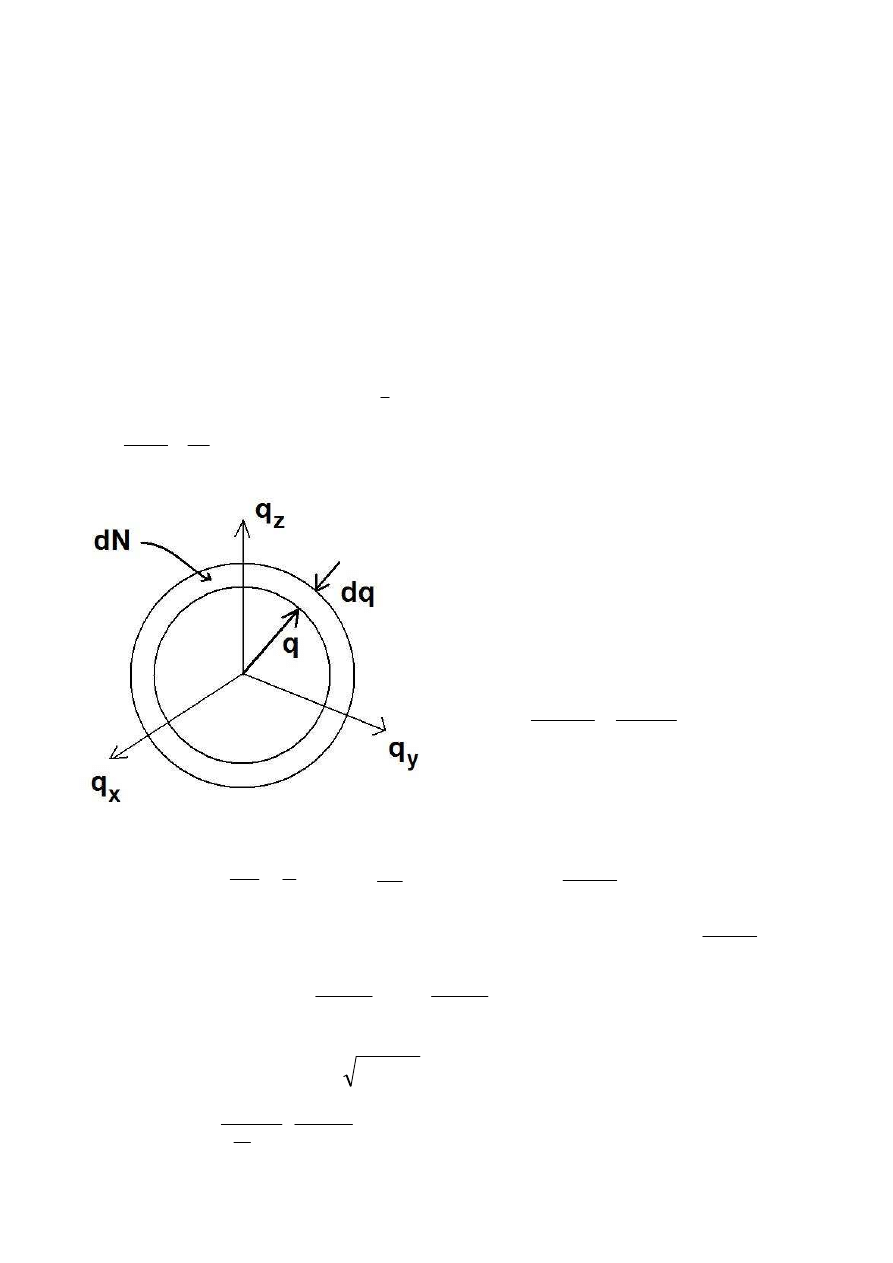
Fala stojąca w ciele stałym jest skwantowana
(mamy skończoną ilość możliwych długości fali)
– długość fali jest ograniczona od góry przez
rozmiary kryształu, a od dołu przez odległość
między atomami.
ω
ω
π
d
Z
dq
q
q
Z
dN
⋅
=
⋅
=
)
(
4
)
(
1
2
1
(dla jednej gałęzi drgań)
ω
π
ω
π
π
ω
d
dq
q
d
dq
q
Z
2
2
3
2
1
2
8
4
)
(
=
=
Debye założył, że częstość jest zależna liniowo od
wektora falowego, a współczynnikiem
proporcjonalności jest prędkość dźwięku.
q
u
⋅
=
ω
→
u
d
dq
1
=
ω
,
2
2
2
u
q
ω
=
, stąd:
3
2
2
1
2
)
(
u
Z
π
ω
ω
=
Powyższy wynik dotyczy jednej gałęzi. A więc całkowita gęstość:
3
2
2
1
2
3
)
(
3
)
(
u
Z
Z
π
ω
ω
ω
=
⋅
=
N
d
Z
3
)
(
max
0
=
⋅
∫
ω
ω
ω
→
A
N
u
d
u
3
2
2
3
3
2
3
max
0
3
2
2
max
=
=
⋅
∫
π
ω
ω
π
ω
ω
- wstawiamy tu liczbę Avogadro
(liczymy ciepło molowe)
A
N
u
3
2
3
max
6
π
ω
=
→
u
N
A
⋅
=
3
2
max
6
π
ω
∫
⋅
−
⋅
=
max
0
3
2
2
2
3
1
1
)
(
)
(
ω
ω
ω
π
ω
ω
d
u
e
A
T
A
kT
h
|
statystyka Bosego-Einsteina (fonony są bozonami)
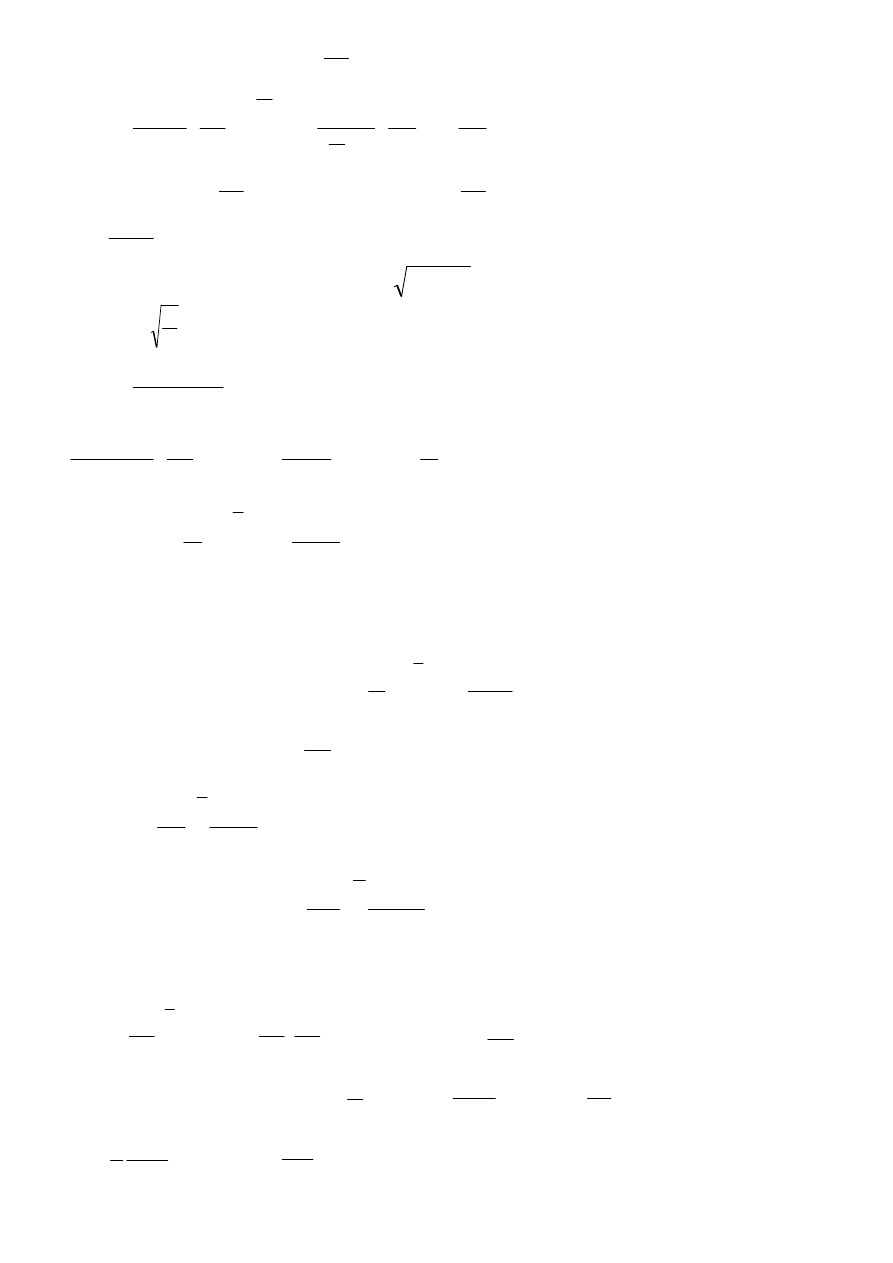
Bierzemy zmienną do całkowania:
kT
ω
h
−
⋅
=
∫
kT
d
kT
e
A
kT
u
T
A
kT
kT
ω
ω
ω
π
ω
ω
h
h
h
h
h
0
2
3
3
2
1
1
)
(
2
3
)
(
Debye zauważył, że
k
ω
h
ma wymiar temperatury (bo
kT
ω
h
jest bezwymiarowe)
stąd:
Θ
=
k
max
ω
h
- tzw. temperatura Debye’a
max
ω
zależy od prędkości dźwięku:
u
N
A
⋅
=
3
2
max
6
π
ω
z kolei
m
u
α
~
, gdzie
α
- stała sprężystości
A
N
u
2
3
max
3
6
π
ω
=
- wstawiamy to do wyrażenia przed całką:
3
3
max
3
3
max
2
2
9
9
2
6
3
Θ
=
=
⋅
T
N
kT
N
kT
N
A
A
A
h
h
ω
ω
π
π
, a stąd:
x
d
e
x
A
T
N
T
A
T
x
A
∫
Θ
−
⋅
Θ
=
0
2
3
1
)
(
9
)
(
ω
- jest to wzór odnoszący się do wszystkich materiałów
Możemy policzyć średnią energię:
energia 1 fononu:
ω
ω
h
=
)
(
A
ś
rednia energia:
x
d
e
x
A
T
N
U
T
A
T
x
A
∫
Θ
−
⋅
Θ
=
=
0
2
3
1
)
(
9
)
(
ω
ω
h
zauważamy, że:
kTx
kT
kT
=
=
ω
ω
h
h
x
d
e
x
T
kN
U
T
x
A
∫
Θ
−
⋅
Θ
=
0
3
3
4
1
9
,
R
kN
A
=
Ostatecznie:
x
d
e
x
T
R
U
T
x
∫
Θ
−
⋅
Θ
=
0
3
3
4
1
9
Rozwiązanie analityczne:
1° wysokie temperatury:
Θ
>>
T
,
1
<<
x
,
1
max
<<
x
,
x
x
e
x
=
−
+
≈
−
1
1
1
RT
T
T
R
x
d
x
T
R
U
T
3
9
9
3
3
3
4
0
2
3
4
=
Θ
⋅
Θ
=
⋅
Θ
=
∫
Θ
,
R
T
U
c
V
3
=
∂
∂
=
2° niskie temperatury:
Θ
<<
T
→
∞
→
Θ
T
,
const
x
d
e
x
x
=
=
−
∫
∞
15
chyba
1
2
0
3
π
Θ
≅
4
5
3 RT
U
,
3
~ T
T
U
c
V
∂
∂
=
- pojawia się zależność, którą wcześniej otrzymano
Dla elektronów w metalach:
T
c
V
~
.
2. Równanie kinetyczne Boltzmanna i czas relaksacji.
Rozwiązując równanie Schrödingera, Boltzmann uwzględnił oddziaływania z defektami. Stworzył
klasyczne równanie transportu.
Rozład równowagowy z poziomem Fermiego:
1
1
)
(
0
−
=
−
kT
E
E
F
e
E
f
Modyfikujemy funkcję rozkładu:
)
(
)
(
)
(
1
0
E
f
E
f
E
f
+
=
, gdzie
)
(
)
(
1
0
E
f
E
f
>>
Zakłada się, że ta nowa funkcja będzie stacjonarna.
Energia w zależności od wektora falowego:
(
)
*
2
2
2
2
*
2
2
2
2
m
k
k
k
m
k
E
z
y
x
+
+
=
=
h
h
Po przyłożeniu zewnętrznego pola elektr. zmienia się rozkład – następuje przesunięcie kuli Fermiego.
Zmiana funkcji rozkładu w czasie:
zd
dryf
dt
df
dt
df
dt
df
+
=
|
|
człon dryfowy człon zderzeniowy
Aby opisać klasycznie cząstkę, trzeba podać jej położenia i prędkości:
z
y
x
k
k
k
z
y
x
,
,
,
,
,
- współrzędne
w 6-wymiarowej przestrzeni fazowej. Dryf odbywa się w przestrzeni fazowej. Możemy z niej wydzielić
jedną komórkę i rozważyć przepływ cząstek. Po czasie t
∆
do komórki wpłyną cząstki, które były przed
nią, stąd przed wyrażeniem
t
v
∆
⋅
stawiamy minus:
(
)
z
y
x
z
z
y
y
x
x
z
y
x
k
k
k
z
y
x
f
t
k
k
t
k
k
t
k
k
t
v
z
t
v
y
t
v
x
f
f
,
,
,
,
,
,
,
,
,
,
−
∆
−
∆
−
∆
−
∆
−
∆
−
∆
−
=
∆
•
•
•
wartość funkcji w czasie
t
t
∆
+
Obliczamy pochodną z definicji:
dryf
k
r
t
dt
df
f
k
f
r
dt
dx
x
f
t
f
dt
df
=
∇
−
∇
−
=
+
∂
∂
−
=
∆
∆
=
•
•
→
∆
....
lim
0
To był człon dryfowy, teraz człon zderzeniowy:
(
) (
)
'
'
k
k
b
k
k
a
dt
df
zd
→
−
→
=
,
gdzie
b
a,
- całki zderzeniowe
|
|
zderzenia, które przejścia
ze stanów
'
k
w odwrotnym
przeprowadzają kierunku
do stanów
k
Stąd:
b
a
dt
df
dt
df
dryf
−
+
=
Boltzmann założył, że zmiany są wolne w czasie – ustala się stan stacjonarny: człon dryfowy zrównuje
się ze zderzeniowym i pochodna się zeruje.
Stąd równanie Boltzmanna ma postać:
b
a
f
k
f
r
k
r
−
+
∇
−
∇
−
=
•
•
0
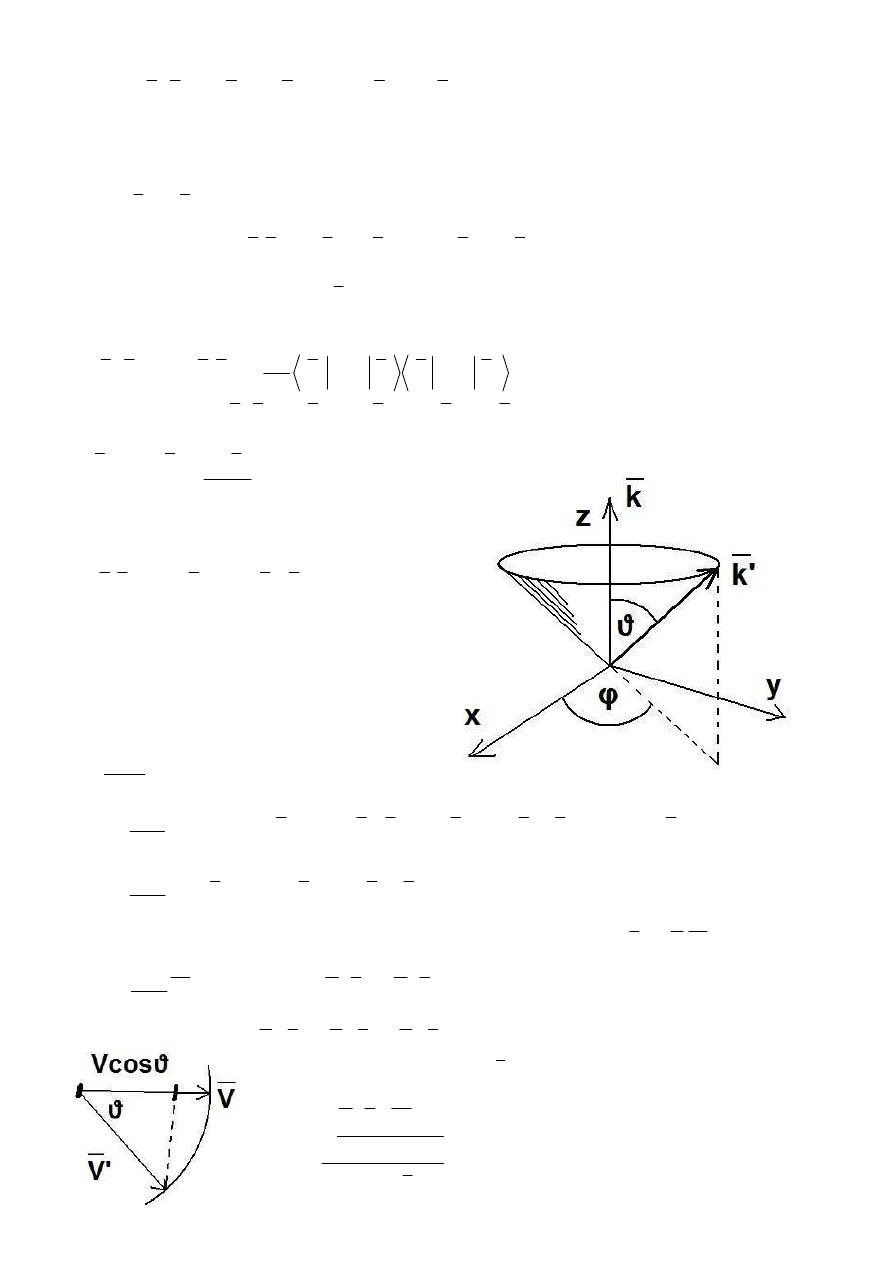
Przybliżenie czasu relaksacji:
( ) ( ) ( )
( )
(
)
∫
−
=
SB
k
d
k
f
k
f
k
k
k
w
a
'
'
1
'
'
,
'
3
ρ
|
|
|
|
prawdopodobień- gęstość stan stan
stwo przejścia stanów zajęty wolny
ze stanu
'
k
do
k
Podobnie:
( ) ( ) ( )
( )
(
)
∫
−
=
SB
k
d
k
f
k
f
k
k
k
w
b
3
1
'
,
ρ
Całka
a
zwiększa obsadzenie stanu
k
, z kolei całka b zmniejsza. SB – strefa Brillouina.
W mechanice kwantowej prawdopodobieństwo przejścia w jedną stronę jest równe
prawdopodobieństwu przejścia w drugą stronę:
(
) ( )
'
ˆ
ˆ
'
2
~
'
,
,
'
k
H
k
k
H
k
k
k
w
k
k
w
zb
zb
h
π
=
Stąd:
( ) ( ) ( ) ( )
(
)
∫
−
=
−
SB
k
d
k
f
k
f
k
k
k
w
b
a
'
'
'
,
'
3
ρ
( ) ( ) ( )
k
f
k
f
k
f
1
0
+
=
↑ wpływ sił zewnętrznych
Przybliżenie:
( ) ( ) (
)
'
,
'
,
k
k
k
k
k
w
−
Θ
=
δ
ϑ
,
gdzie
ϑ
- kąt między osią a tworzącą stożka
Zakładamy, że prawdopodobieństwo nie zależy
od energii (przy pojedyńczym procesie przejścia
energia zmienia się tak nieznacznie, że możemy
tą zmianę zaniedbać).
*
2
2
2m
k
E
h
=
(
) (
) ( ) ( )
(
)
∫ ∫
∫
∞
→
−
−
Θ
=
−
π
π
ϑ
ϑ
δ
ϑ
ϕ
π
0
0
2
2
0
3
sin
'
'
'
,
'
4
1
k
k
d
d
k
k
f
k
f
k
k
k
d
b
a
(
) ( ) ( )
(
)
∫
−
Θ
=
−
π
ϑ
ϑ
ϑ
π
0
2
2
sin
'
'
,
'
2
1
d
k
k
f
k
f
k
b
a
Rozbijamy funkcję w szereg Maclaurina i bierzemy pierwszy wyraz:
( )
)
(
1
E
V
k
f
χ
=
(
)
( ) ( )
(
)
∫
−
Θ
=
−
π
ϑ
ϑ
ϑ
χ
π
0
2
2
sin
'
,
)
(
2
1
d
k
k
V
k
V
k
E
b
a
( ) ( ) ( )
(
)
1
cos
'
−
=
−
ϑ
k
V
k
V
k
V
- zostają tylko rzuty na kierunek
k
(po wycałkowaniu znikną prędkości
prostopadłe)
( )
(
)(
)
∫
−
Θ
−
=
−
π
ϑ
ϑ
ϑ
ϑ
π
χ
0
2
2
sin
cos
1
,
2
)
(
d
k
k
E
k
V
b
a
↑
( )
k
f
1

Możemy powyższe równanie zapisać w postaci:
( )
τ
k
f
b
a
1
−
=
−
, gdzie
(
)(
)
∫
−
Θ
=
π
ϑ
ϑ
ϑ
ϑ
π
τ
0
2
2
sin
cos
1
,
2
1
1
d
k
k
τ
jest czasem relaksacji.
Rówanie Boltzmanna przyjmuje postać:
( )
0
1
=
−
∇
−
∇
−
•
•
τ
k
f
f
k
f
r
k
r
, gdzie
1
0
f
f
f
+
=
Gdy wyłączamy pole zewnętrzne, pozostaje nam tylko człon zderzeniowy:
τ
1
f
dt
df
−
=
→
τ
1
1
f
dt
df
−
=
→
τ
dt
f
df
−
=
1
1
→
τ
t
e
f
t
f
−
⋅
=
0
1
1
)
(
Czas relaksacji zależy od energii (liczonej od dna pasma):
2
1
)
(
−
⋅
=
p
E
A
E
τ
- fonony akustyczne:
0
=
p
- fonony optyczne:
1
=
p
- domieszki neutralne:
2
1
=
p
- domieszki zjonizowane:
2
=
p
Ś
rednia droga swobodna między zderzeniami:
v
l
τ
=
;
2
1
~ E
v
→
p
AE
l
=
Widać, że dla fononów akustycznych średnia droga między zderzeniami nie zależy od energii.
Ruchliwość:
ε
µ
v
=
, gdzie
v
- prędkość unoszenia,
ε
- pole elektryczne
Istnieją materiały, które w temperaturach ciekłego helu mają
V
cm
10
3
7
=
µ
. W metalach
µ
jest rzędu
V
cm
10
3
1
- to dlatego, że metale są substancjami polikrystalicznymi – występuje rozpraszanie na
granicach krystalitów. Z kolei półprzewodniki można wytworzyć w postaci dużych monokryształów.
W pomiarach bardzo często uzyskuje się czas relaksacji rzędu
7
10
−
, co oznacza, że między zderzeniami
elektron pokonuje tysiące stałych sieciowych. Wynika to z niepoprawności klasycznego opisu kryształu.
3.
Prawo Ohma.
Klasyczne prawo Ohma: stosunek napięcia do natężenia prądu jest stały i równy oporowi elektrycznemu
I
U
R
=
gęstość prądu:
S
I
j
=
=
ε
σ
l
U
⋅
=
ε
→
S
I
l
U
=
σ
R
I
U
S
l
=
=
σ
1
→
S
l
R
ρ
=
, gdzie
σ
ρ
1
=
- opór właściwy
Prawo Ohma półkwantowo:
wychodzimy od
( )
0
1
=
−
∇
−
∇
−
•
•
τ
k
f
f
k
f
r
k
r
Zakładamy, że nie ma gradientu przestrzennego:
0
=
∇
r
;
0
=
∇
−
•
f
r
r
h
h
h
F
k
k
=
=
•
•
1
0
1
=
+
∇
τ
f
f
F
k
h
E
E
f
E
E
f
E
E
f
f
k
k
k
k
∇
∂
∂
+
∇
∂
∂
=
∇
∂
∂
=
∇
1
0
robimy pierwsze przybliżenie:
0
1
=
∇
∂
∂
E
E
f
k
V
E
f
E
E
f
E
E
f
f
k
k
k
∂
∂
=
∇
∂
∂
=
∇
∂
∂
=
∇
0
0
0
1
h
h
h
Wstawiamy to do
0
1
=
+
∇
τ
f
f
F
k
h
:
0
1
0
=
+
∂
∂
τ
f
V
E
f
F
ε
q
F
=
(siła elektrostatyczna)
0
1
0
=
+
∂
∂
τ
ε
f
V
E
f
q
Podobnie jak poprzednio:
( )
)
(
1
E
V
k
f
χ
=
0
)
(
0
=
+
∂
∂
V
E
E
f
q
τ
χ
ε
Stąd:
ε
τ
χ
∂
∂
−
=
E
f
q
E
0
)
(
ε
τ
V
E
f
q
f
∂
∂
−
=
0
1
- znaleźliśmy funkcję określającą odchylenie od położenia równowagi
Funkcja ta zależy od czasu relaksacji.
Gęstość prądu: suma po wszystkich nośnikach:
(
)
=
+
=
=
=
∫
∫
∑
=
SB
SB
N
i
k
d
f
f
V
q
k
d
k
f
k
q
V
q
V
q
j
3
1
0
3
3
1
4
1
)
(
)
(
π
∫
∫
+
=
SB
SB
k
d
f
V
q
k
d
f
V
q
3
1
3
3
0
3
4
1
4
1
π
π
0
4
1
3
0
3
=
∫
SB
k
d
f
V
q
π
(równowaga termodynamiczna – prąd nie płynie)
Pozostaje tylko całka
∫
SB
k
d
f
V
q
3
1
3
4
1
π
, do której
wstawiamy
ε
τ
V
E
f
q
f
∂
∂
−
=
0
1
:
∫
∂
∂
−
=
SB
k
d
V
E
f
q
j
3
2
0
3
2
4
ε
τ
π
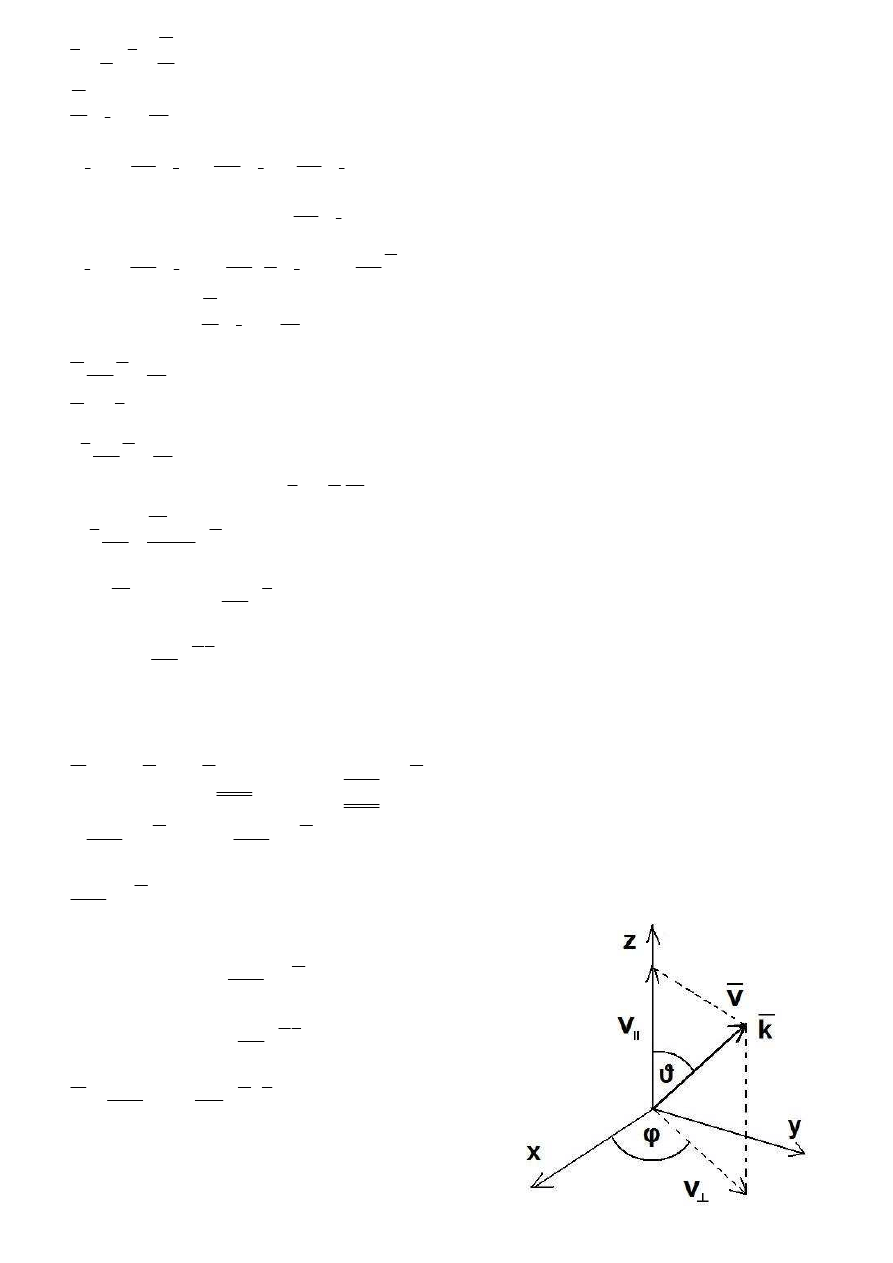
Przyjmujemy kierunek pola elektrycznego z i rzutujemy
wektor prędkości na dwa kierunki – równoległy i
prostopadły.
(
)
∫ ∫∫
∞
⊥
∂
∂
−
+
=
π π
ϑ
ϕ
ϑ
ϑ
ε
τ
π
2
0 0 0
3
2
0
||
3
2
sin
cos
4
k
d
d
d
k
v
E
f
v
v
e
j
⊥
v
- zmiana prędkości niezależna od pola (równe prawdopodobieństwo skierowania się w obie strony,
stąd całka = 0)
||
v
- zmiana prędkości wymuszona polem,
ϑ
cos
||
v
v
=
∫∫
∞
∂
∂
−
=
π
ϑ
ϑ
ϑ
τ
π
ε
0 0
3
2
2
2
0
2
2
sin
cos
2
k
d
d
k
v
E
f
e
j
3
2
sin
cos
0
2
=
∫
π
ϑ
ϑ
ϑ
d
(podstawienie:
dx
d
x
=
−
=
ϑ
ϑ
ϑ
sin
cos
,...)
∫
∞
∂
∂
−
=
0
3
2
2
0
2
2
3
k
d
k
v
E
f
e
j
τ
π
ε
k
v
m
h
=
*
→
*
m
k
v
h
=
;
( )
dk
k
m
dk
k
v
4
2
*
2
2
2
h
=
Chcemy całkować po
dE
:
*
2
2
2m
k
E
h
=
→
*
2
m
k
dk
dE
h
=
→
dE
k
m
dk
2
*
h
=
( )
( )
dE
m
k
dE
k
m
k
m
dk
k
m
*
3
2
*
4
2
*
2
4
2
*
2
=
=
h
h
h
∫
∞
∂
∂
−
=
0
3
0
*
2
2
3
dE
k
E
f
m
e
j
τ
ε
π
Niech
∫
∞
∂
∂
−
=
0
3
0
2
)
(
3
1
dE
k
E
f
E
X
X
π
będzie średnią statystyczną z pewną wagą
Podstawiamy 1:
=
+
=
+
−
=
∂
∂
−
=
∫
∫
∫
∞
∞
+∞
∞
0
2
2
0
0
2
0
2
0
2
3
0
0
3
0
2
0
3
3
1
3
3
1
1
dk
k
f
dE
dE
dk
k
f
k
f
dE
k
E
f
π
π
π
π
n
k
d
k
f
dk
k
f
=
=
=
∫
∫
∞
∞
0
3
0
0
3
2
0
)
(
4
4
ρ
π
π
- liczba wszystkich nośników
| |
prawdopodobieństwo gęstość
obsadzenia (z poziomem
Fermiego)
dE
E
k
E
f
E
)
(
)
(
3
1
0
3
0
2
∫
∞
∂
∂
−
=
τ
π
τ
(wstawiając
1
=
τ
otrzymamy liczbę nośników)
Stąd:
ε
τ
*
2
m
e
j
=
Jednocześnie
ε
σ
=
j
A więc przewodność właściwa:
*
2
m
e
τ
σ
=
Na podstawie pomiarów można wyciągnąć wnioski co do zmian czasu relaksacji.
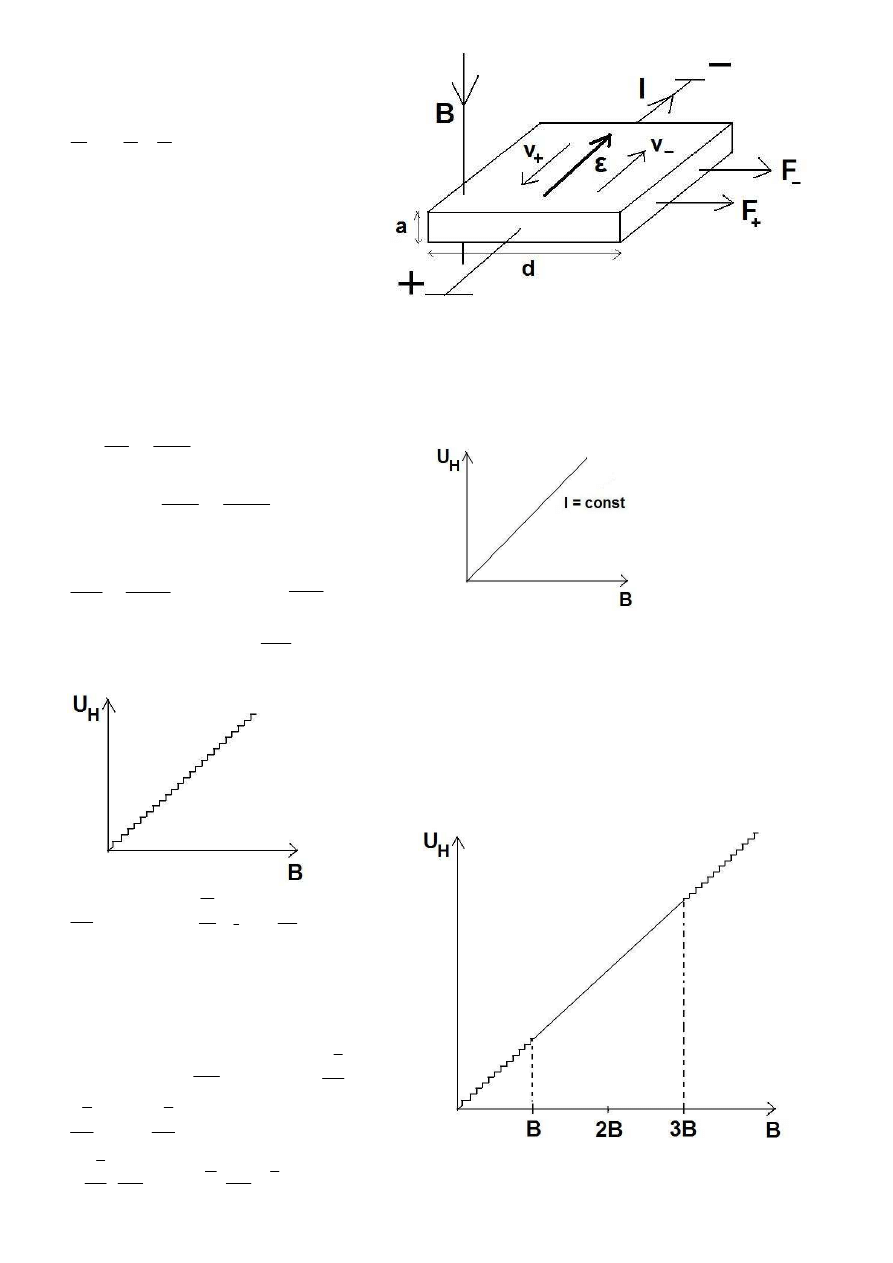
4. Efekt Holla.
Na poruszający się ładunek w polu
magnetycznym działa siła Lorenza:
B
V
q
F
×
=
Nośniki ładunku, zarówno dodatnie, jak
i ujemne, są odchylane w tą samą stronę
(bo wędrują w przeciwnych kierunkach).
Na podstawie ładunku, jaki zgromadzi
się na boku płytki można
wywnioskować, jakie cząstki przewodzą
prąd.
siła pola magnetycznego:
evB
F
B
±
=
siła pola elektrycznego, powstającego w wyniku efektu Holla:
H
e
F
H
ε
ε
=
Korzystamy ze wzoru
nev
j
=
, gdzie
u
v
v
≡
- prędkość unoszenia
neS
I
ne
j
v
=
=
,
gdzie
ad
S
=
Stąd:
neda
IB
neS
IB
H
=
=
ε
Napięcie hollowskie:
d
U
H
H
ε
=
neda
IB
d
U
H
=
→
nea
IB
U
H
=
(często pisze się:
IB
nea
U
H
1
±
=
- znak zależy od ładunku nośników)
Okazuje się, że w pewnych strukturach zachodzi tzw. kwantowy
efekt Holla (QHE).
Później dostrzeżono również ułamkowy kwantowy efekt Holla
(FQHE) – kwantowanie pojawiało się w niskich temperaturach
dla trzykrotnie wyższych B:
0
=
dt
df
0
1
=
+
∇
τ
f
f
F
k
h
1
0
f
f
f
+
=
1
0
f
f
f
k
k
k
∇
+
∇
=
∇
Jeżeli weźmiemy tylko pole elektryczne,
możemy dla tego przypadku pominąć
1
f
k
∇
:
E
E
f
f
f
k
k
k
∇
∂
∂
=
∇
≈
∇
0
0
/
h
ε
q
⋅
=
∇
≈
∇
0
f
q
f
q
k
k
h
h
ε
ε
ε
ε
q
E
f
V
E
E
f
q
k
∂
∂
=
∇
∂
∂
=
0
0
h
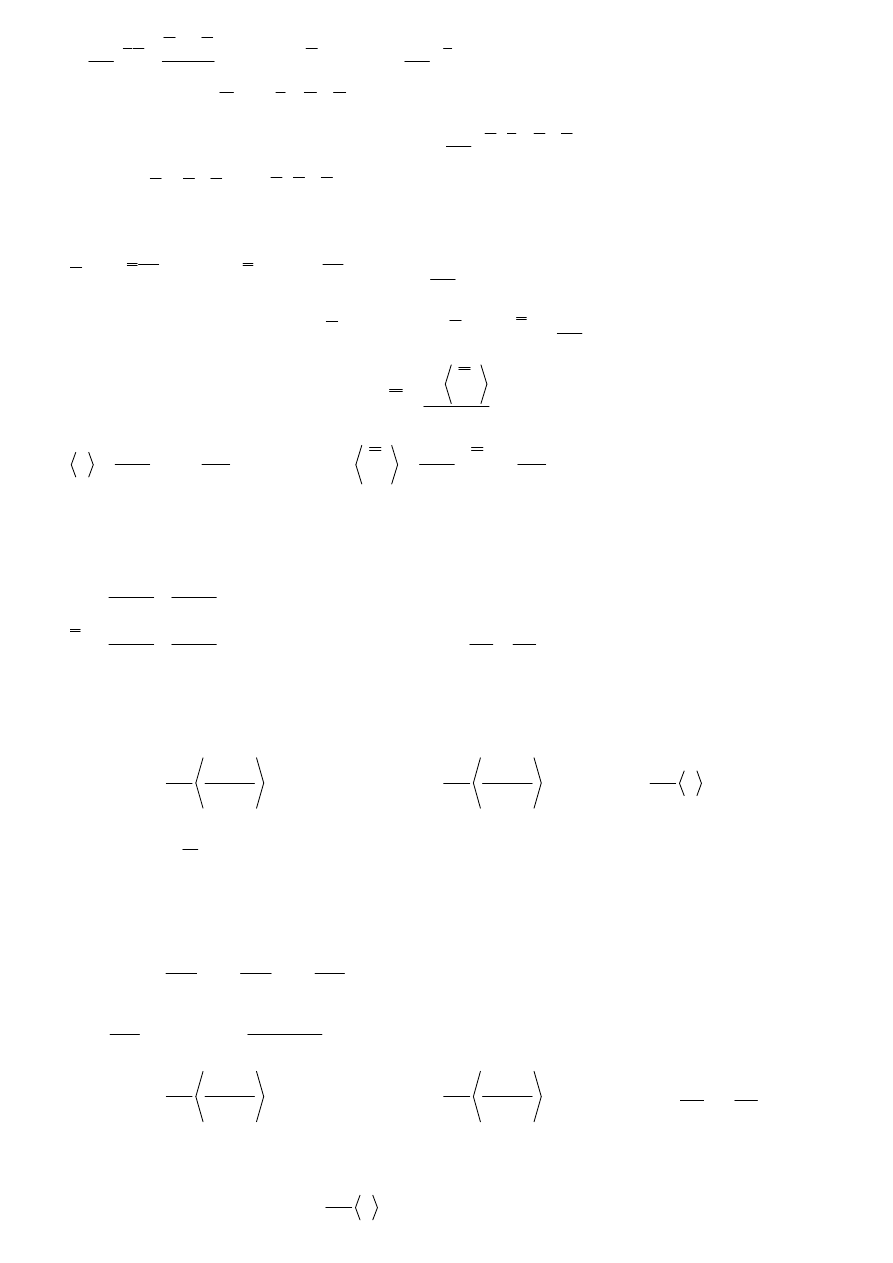
0
)
(
0
=
+
∂
∂
τ
χ
ε
V
E
V
E
f
q
, gdzie
ε
τ
χ
∂
∂
−
=
E
f
q
E
0
)
(
Wprowadzamy siłę:
(
)
B
V
q
F
×
+
=
ε
Korzystając z
0
f
f
k
k
∇
≈
∇
dostaniemy:
(
)
B
V
V
E
f
q
f
×
+
∂
∂
−
=
ε
τ
0
1
Z definicji
,
B
V
V
×
⊥
stąd
0
=
×
⋅
B
V
V
, co oznacza, że nie możemy sobie pozwolić na to przybliżenie
i musimy uwzględnić całość:
1
0
f
f
f
k
k
k
∇
+
∇
=
∇
Jest to skomplikowane i w ogólnym przypadku nie da się tego rozwiązać. Stosujemy inne przybliżenie:
)
(
)
(
0
E
S
E
χ
χ
=
, gdzie S - tensor,
ε
τ
χ
∂
∂
−
=
E
f
q
E
0
0
)
(
Pole magnetyczne zmienia funkcję
)
(E
χ
w tensor:
ε
τ
χ
∂
∂
−
=
E
f
S
q
E
0
)
(
Również przewodnictwo będzie tensorem:
*
2
m
S
e
τ
σ
=
dE
k
E
f
m
k
∫
∂
∂
−
=
0
3
0
2
3
1
τ
π
τ
, stąd:
dE
k
E
f
S
S
m
k
∫
∂
∂
−
=
0
3
0
2
3
1
τ
π
τ
Dokładna postać tensora nie jest znana, wiemy tylko co nieco o pewnych wyróżnionych kierunkach, np.
(
)
0
,
0
,
x
x
ε
ε
ε
=
=
;
(
)
z
z
B
B
B
,
0
,
0
=
=
Wówczas po skomplikowanych wyprowadzeniach:
+
+
−
+
+
=
1
0
0
0
1
1
1
0
1
1
1
2
2
2
2
S
S
S
S
S
S
S
;
τ
ω
C
S
=
, gdzie
Τ
=
=
π
ω
2
*
m
eB
C
- częstość ruchu po okręgu elektronów
Przechodzimy do współrzędnych tensora:
ij
σ
σ
→
2
*
2
22
11
1 S
m
e
+
=
=
τ
σ
σ
;
2
*
2
21
12
1 S
S
m
e
+
=
−
=
τ
σ
σ
;
τ
σ
*
2
33
m
e
=
Pozostałe:
0
=
ij
σ
Gęstość prądu:
j
ij
i
j
ε
σ
=
y
x
x
j
ε
σ
ε
σ
12
11
+
=
0
22
21
=
+
=
y
x
y
j
ε
σ
ε
σ
- w kierunku y prąd nie płynie
Stąd:
y
y
y
x
ε
σ
σ
ε
σ
σ
ε
σ
σ
ε
12
11
12
22
21
22
=
=
−
=
y
y
y
x
j
ε
σ
σ
σ
ε
σ
ε
σ
σ
12
2
12
2
11
12
12
2
11
+
=
+
=
2
*
2
22
11
1
S
m
e
+
=
=
τ
σ
σ
;
2
*
2
21
12
1
S
S
m
e
+
=
−
=
τ
σ
σ
;
τ
π
τ
τ
ω
Τ
=
=
=
2
*
m
eB
S
C
τ
- czas rozpraszania (krótki, rzędu
10
10
~
−
s)
Im wyższe pole tym większa
C
ω
i tym krótszy okres T. W słabych polach T
τ
>>
i wówczas
1
<<
S
-
możemy je pominąć i wtedy
τ
σ
*
2
11
m
e
≈
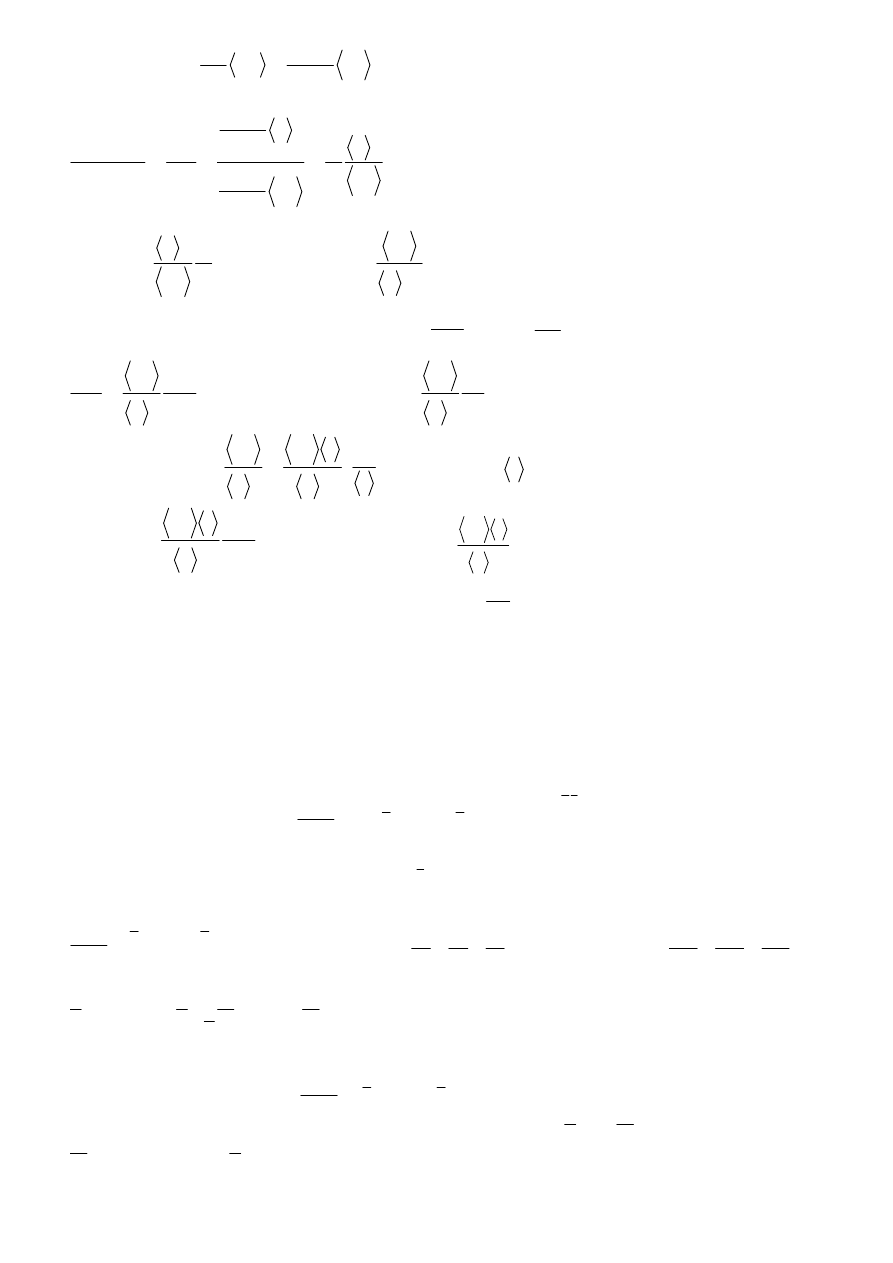
Podobnie:
( )
2
2
*
3
*
2
12
τ
τ
σ
m
B
e
S
m
e
=
≈
( )
( )
2
2
2
2
*
3
2
2
*
4
12
2
11
12
2
12
2
11
τ
τ
τ
τ
σ
σ
σ
σ
σ
B
e
m
B
e
m
e
=
=
≈
+
Stąd:
y
x
B
e
j
ε
τ
τ
2
2
=
→
B
j
e
x
y
2
2
τ
τ
ε
=
Napięcie hollowskie:
y
y
H
d
U
U
ε
=
=
;
d
U
H
y
=
ε
;
ad
I
j
x
x
=
- wstawiamy to do wzoru:
B
I
ade
d
U
x
H
1
2
2
τ
τ
=
,
ostatecznie:
B
I
ae
U
x
H
1
2
2
τ
τ
=
Stosujemy przejście:
1
1
1
2
2
2
2
⋅
=
τ
τ
τ
τ
, pamiętając, że
n
=
1
to koncentracja nośników
Stąd:
B
I
nae
U
x
H
1
1
2
2
τ
τ
=
,
gdzie wyrażenie
r
=
2
2
1
τ
τ
to tzw. współczynnik hollowski
Przewodnictwo typu n i p:
(
)
2
2
p
e
p
n
c
µ
µ
σ
+
=
, gdzie
τ
µ
~
*
m
e
=
- ruchliwość
Mierząc napięcie hollowskie nie możemy od razu obliczyć koncentracji nośników, bo jest zafałszowana
przez czynnik hollowski, który na ogół 1
≠
. Dodatkowo, gdy przewodzą nośniki dwojakiego rodzaju,
należy uwzględnić powyższy wzór. Wówczas współczynnik hollowski może zmianiać znak ze względu
na różną ruchliwość elektronów i dziur (dziury mają większą bezwładność).
5.
Poziomy Landaua.
Metoda masy efektywnej:
( )
( )
r
E
r
m
ψ
ψ
=
∇
−
2
*
2
h
;
r
k
i
e
=
ψ
Bez potencjału elektron w krysztale porusza się jak elektron swobodny z masą efektywną. W masie
efektywnej zawarta jest informacja o funkcji
( )
r
u
k
.
Landau zapisał równanie Schrödingera w postaci:
( )
( )
r
E
r
m
p
ψ
ψ
=
*
2
2
ˆ
, gdzie
∂
∂
+
∂
∂
+
∂
∂
−
=
∇
−
=
z
y
x
i
i
p
h
h
ˆ
;
∂
∂
+
∂
∂
+
∂
∂
−
=
⋅
=
2
2
2
2
2
2
2
ˆ
ˆ
ˆ
z
y
x
p
p
p
h
Mechanika klasyczna wprowadza pęd uogólniony:
p
→
A
c
e
p
+
, gdzie
A - potencjał wektorowy dla pola elektromagnetycznego
Potencjał wektorowy jest tylko zabiegiem matematycznym, nie istnieje jako wielkość fizyczna.
Wstawiamy pęd uogólniony do
( )
( )
r
E
r
m
p
ψ
ψ
=
*
2
2
ˆ
Pole magnetyczne traktujemy jako rotację potencjału wektorowego:
A
B
rot
=
(
)
0
,
0
,
yB
A
−
=
(
)
B
B
,
0
,
0
=
(skalowanie landauowskie)
( )
( )
r
E
r
A
c
e
p
m
ψ
ψ
=
+
2
*
ˆ
ˆ
2
1
( )
( )
r
E
r
z
y
By
c
e
x
i
m
ψ
ψ
=
∂
∂
−
∂
∂
−
−
∂
∂
−
2
2
2
2
2
2
2
*
2
1
h
h
h
Rozwiązanie:
( ) ( )
z
ik
x
ik
z
x
e
r
r
+
=
ϕ
ψ
Rozpisujemy i wstawiamy:
( )
( )
z
ik
x
ik
z
ik
x
ik
z
x
z
x
e
r
E
e
r
z
y
y
B
c
e
x
By
c
e
i
x
m
+
+
=
∂
∂
−
∂
∂
−
+
∂
∂
+
∂
∂
−
ϕ
ϕ
2
2
2
2
2
2
2
2
2
2
2
2
2
*
2
2
1
h
h
h
h
( )
( )
y
E
y
m
k
y
y
B
c
m
e
By
cm
e
k
m
k
z
x
x
ϕ
ϕ
=
+
∂
∂
−
+
−
−
*
2
2
2
2
2
2
2
2
*
2
*
*
2
2
2
2
2
h
h
h
h
Częstość cyklotronowa:
w układzie SI:
*
m
eB
C
=
ω
;
w układzie jednostek Gaussa:
c
m
eB
C
*
=
ω
( )
( )
r
E
r
m
x
m
ψ
ψ
ω
=
+
∂
∂
2
2
2
*
2
1
2
1
- równanie Schrödingera dla oscylatora harmonicznego
Energia drgań jest skwantowana:
+
=
2
1
n
E
ω
h
Wyłączamy przed nawias:
2
*
2
2
2
2
*
2
2
*
2
*
2
2
2
1
c
m
B
e
c
m
B
e
m
m
C
=
=
ω
( )
( )
y
m
k
E
y
m
k
B
e
c
m
By
cm
e
k
B
e
c
m
y
c
m
B
e
y
m
z
x
x
ϕ
ϕ
−
=
+
−
+
∂
∂
−
*
2
2
*
2
2
2
2
*
*
2
2
2
*
2
2
*
2
2
2
2
*
2
2
2
2
2
2
2
h
h
h
h
( )
( )
y
m
k
E
y
eB
c
k
y
eB
c
k
y
m
y
m
z
x
x
C
ϕ
ϕ
ω
−
=
+
−
+
∂
∂
−
*
2
2
2
2
2
*
2
2
*
2
2
2
2
1
2
h
h
h
h
Podstawiamy:
eB
c
k
y
x
h
−
=
η
;
y
∂
∂
=
∂
∂
η
Ostatecznie:
( )
( )
η
ϕ
η
ϕ
η
ω
η
−
=
+
∂
∂
−
*
2
2
2
2
*
2
2
*
2
2
2
1
2
m
k
E
m
m
z
C
h
h
Interpretacja:
elektron swobodny miał energię:
(
)
*
2
2
2
2
2m
k
k
k
E
z
y
x
+
+
=
h
Gdy wprowadzamy pole magnetyczne, energia ulega
skwantowaniu w płaszczyźnie prostopadłej do kierunku tego
pola.
+
→
+
2
1
2
2
n
k
k
y
x
ω
h
*
2
2
2
2
1
m
k
n
E
z
C
h
h
+
+
=
ω
W kierunku równoległym do kierunku pola nie ma
kwantowania.
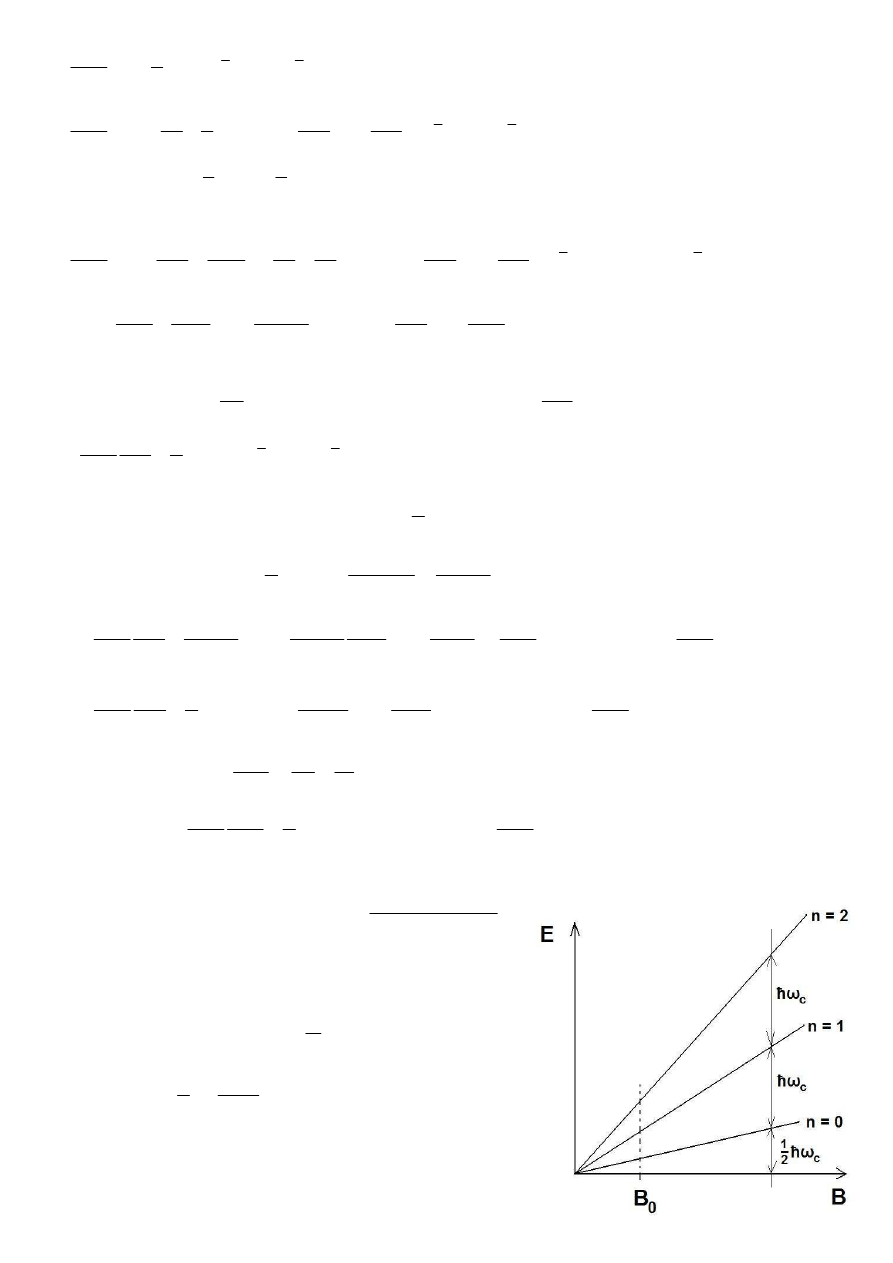
Efekty kwantowe w polu magnetycznym:
Metodą epitaksji uzyskuje się bardzo cienkie
warstwy półprzewodnika o zadanym składzie, np:
Ga
1-x
Al
x
As | GaAs | Ga
1-x
Al
x
As | GaAs ...
W ten sposób otrzymuje się studnię kwantową.
Przerwa energetyczna pomiędzy Ga
1-x
Al
x
As a
GaAs rozkłada się równo między pasmo
przewodnictwa a pasmo walencyjne.
Możemy ten układ potraktować jako
nieskończoną studnię potencjału o szerokości L
i rozwiązać równanie Schrödingera dla jednego
kierunku:
)
(
)
(
2
2
2
2
x
E
x
dx
d
m
ψ
ψ
=
−
h
m
k
E
2
2
2
h
=
Z warunków brzegowych:
π
n
kL
kL
=
→
=
0
sin
;
L
n
k
n
π
=
;
2
2
2
2
2
n
mL
E
n
π
h
=
W studni potencjału elektron zachowuje się jak fala stojąca. Jego energia jest skwantowana. W realnym
przypadku mamy studnię w paśmie przewodnictwa i paśmie walencyjnym, ale tylko w kierunku wzrostu
kryształu ( z ). Energia elektronu w rzeczywistej studni:
(
)
*
2
2
2
2m
k
k
E
E
y
x
n
+
+
=
h
Wprowadzając domieszkę (domieszkowanie modulacyjne) uzyskujemy dodatkowy elektron, który
wpada do studni i uzyskuje ogromną ruchliwość
V
cm
10
7
≈
µ
. Niestety utrzymuje się ona tylko w
niskich temperaturach (w wysokich fonony utrudniają ruch).
Zamiast tego dostajemy półprzewodnik o ściśle określonej liczbie nośników prądu.
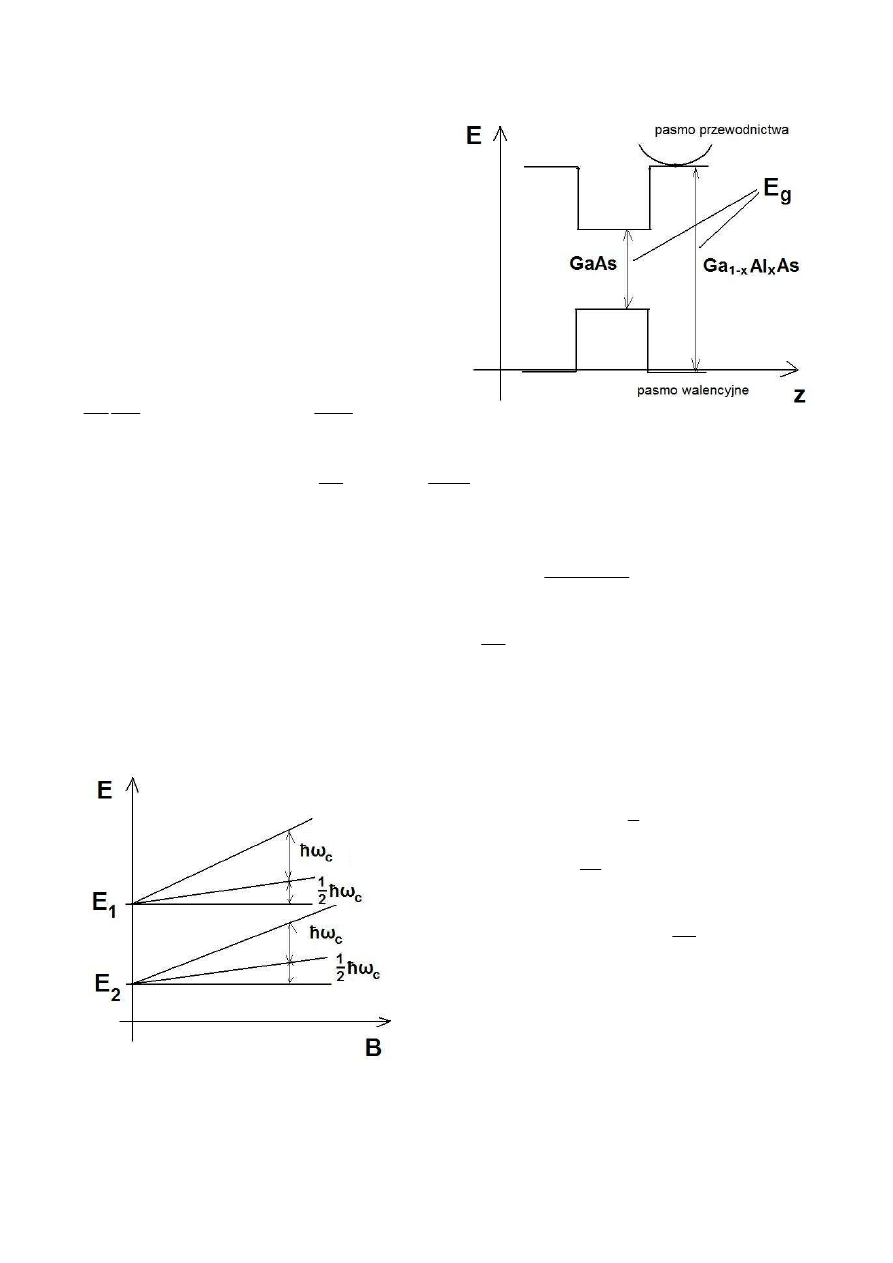
Gdy wprowadzimy układ w pole magnetyczne, kwantowanie pojawi się również na kierunkach
x
i y .
A więc energia elektronu zostanie całkowicie
skwantowana:
+
+
=
2
1
)
,
(
B
C
n
B
z
n
E
n
n
E
z
ω
h
;
gęstość stanów:
h
eB
B
=
ρ
- rośnie wraz z polem magnetycznym
Poziomy są dosyć oddalone:
*
m
eB
C
=
ω
, i na każdym
poziomie, jeśli B jest duże, pojawia się dużo stanów.
W wysokich B wszystkie elektrony siedzą na
najniższym poziomie Landaua. Gdy zmniejszamy pole,
część elektronów będzie mogła wskoczyć na wyższe
poziomy. Stąd kwantowy efekt Holla. Warto zauważyć,
ż
e jest on w zasadzie kwantowaniem oporu elektr.

6. Zespolony współczynnik załamania / zespolone przewodnictwo, częstość plazmowa.
Pole elektromagnetyczne należy traktować jako szybko zmienne pole elektryczne.
W polu wolnozmiennym dryf i zderzenia się równoważą:
const
f
f
f
=
+
=
1
0
;
0
1
=
−
=
+
=
τ
f
dt
df
dt
df
dt
df
dt
df
dryf
zd
dryf
→
τ
1
f
dt
df
dryf
=
W polu szybkozmiennym jest zupełnie inaczej:
Weźmy równanie fali EM, np.
(
)
r
k
t
i
e
t
±
=
ω
ε
ε
0
)
(
, wówczas:
t
i
e
f
f
ω
0
1
1
=
0
1
≠
−
=
τ
f
dt
df
dt
df
dryf
;
dt
df
f
dt
df
dryf
+
=
τ
1
dt
df
dt
df
dt
df
1
0
+
=
;
const
f
=
0
;
0
0
=
dt
df
→
1
0
1
1
f
i
e
f
i
dt
df
dt
df
t
i
ω
ω
ω
=
=
=
+
=
ω
τ
i
f
dt
df
dryf
1
1
Dla pola wolnozmiennego wyprowadziliśmy:
*
2
m
e
τ
σ
=
W polu EM zamiast
τ
mamy
ωτ
τ
ω
τ
i
i
+
=
+
−
1
1
1
2
1
2
2
*
2
2
2
*
2
*
2
1
1
1
*
σ
σ
τ
ω
τ
ω
τ
ω
τ
ωτ
τ
σ
i
m
e
i
m
e
i
m
e
+
=
+
−
+
=
+
=
- zespolone przewodnictwo
__________________________
równania Maxwella:
- prawo Faraday’a:
t
B
E
c
∂
∂
−
=
rot
- prawo Gaussa:
ρ
=
D
div
- prawo, które mówi, że nie ma monopoli magnetycznych:
0
div
=
B
- prawo Ampera:
j
t
D
H
c
π
4
rot
−
∂
∂
=
|
|
prąd przesunięcia normalny prąd
_____________________________
Korzystając z czwartego równania Maxwella możemy dokonać interpretacji wyniku:
ε
πα
ε
ε
4
+
=
+
=
p
D
(układ jednostek Gaussa)
|
|
pole elektr.
polaryzowalność
H
B
µ
=
;
ε
σ
=
j
Podstawiamy to do
j
t
D
H
c
π
4
rot
−
∂
∂
=
:
ε
πσ
ε
πα
ε
4
4
rot
+
∂
∂
+
∂
∂
=
t
t
H
c
;
t
i
e
ω
ε
ε
0
=
Stąd:
(
)
ωα
σ
π
ε
i
t
H
c
+
+
∂
∂
=
4
rot
gdzie
2
2
*
2
1
*
τ
ω
τ
σ
+
=
m
e
- to co mierzymy eksperymentalnie jako przewodnictwo
2
2
2
*
2
1
τ
ω
τ
α
+
−
=
m
e
- część urojona, opisuje nam polaryzowalność ośrodka
Jeśli
12
10
~
−
τ
s, a
50
~
ω
Hz, możemy przyjąć, że
τ
σ
*
2
m
e
≈
, jednak dla fal EM (już od
podczerwieni) musimy uwzględnić
1
1
2
2
≠
+
τ
ω
.
Wyprowadzenie równania falowego:
H
B
µ
=
;
1
=
µ
→
H
B
=
+
∂
∂
∂
∂
=
∂
∂
j
t
D
t
H
c
t
π
4
rot
;
ε
πα
ε
4
+
=
D
t
t
t
c
∂
∂
+
∂
∂
+
∂
∂
=
−
ε
πσ
ε
πα
ε
ε
4
4
rot
rot
2
2
2
2
2
t
t
t
c
∂
∂
+
∂
∂
+
∂
∂
=
∇
ε
πσ
ε
πα
ε
ε
4
4
2
2
2
2
2
2
- równanie falowe Maxwella
Rozwiązując to równanie całkiem klasycznie odkrywamy, że pole elektromagnetyczne może być falą
(przypomina falę mechaniczną).
Najprostsza fala:
(
)
r
k
t
i
e
−
=
ω
ε
ε
0
;
Τ
=
π
ω
2
;
λ
π
2
=
k
(
)
−
=
−
ω
ω
ω
r
k
t
i
r
k
t
i
;
V
k
1
=
Τ
=
λ
ω
, gdzie
n
c
V
=
- prędkość fali w ośrodku
n
- współczynnik załamania;
u
N
n
=
, u - wektor jednostkowy
−
=
−
c
r
u
N
t
i
r
k
t
i
ω
ω
ω
−
=
c
r
u
N
t
i
e
ω
ε
ε
0
1) w próżni:
0
=
α
,
0
=
σ
:
2
2
2
2
2
ω
ω
−
=
−
c
c
N
;
1
2
=
N
;
1
=
N
;
1
=
n
2) w ośrodkach nieprzewodzących (dielektrykach, np. szkłach):
0
≠
α
,
0
=
σ
:
2
2
2
2
2
2
4
παω
ω
ω
−
−
=
−
c
c
N
;
πα
4
1
2
+
=
N
;
0
4
1
ε
πα
=
+
=
N
- stała dielektryczna
3) w ośrodkach przewodzących:
0
≠
α
,
0
≠
σ
:
ω
πσ
παω
ω
ω
i
c
c
N
4
4
2
2
2
2
2
2
+
−
−
=
−
;
σ
ω
π
πα
i
N
4
4
1
2
−
+
=
ik
n
N
−
=
*
- zespolony współczynnik załamania ( k - tzw. współczynnik ekstynkcji)
( )
nik
k
n
N
2
*
2
2
2
−
−
=
Ostatecznie mamy więc:
0
2
2
ε
=
−
k
n
ω
πσ
4
2
=
nk
Natężenie promieniowania jest proporcjonalne do kwadratu natężenia pola EM:
2
~
ε
I
Przechodzimy na jedną współrzędną:
z
r
→
( )
−
−
=
z
c
ik
n
t
i
e
z
ω
ε
ε
2
2
0
2
;
( )
z
c
k
z
c
n
t
i
e
e
z
ω
ω
ε
ε
2
2
2
0
2
−
=
Stąd znane prawo:
z
e
I
I
η
−
=
0
,
gdzie
η
- współczynnik absorbcji
c
k
ω
η
2
=
;
Τ
=
π
ω
2
→
λ
π
η
k
4
=
Część urojona współczynnika załamania światła jest odpowiedzialna za pochłanianie energii wiązki
ś
wiatła, czyli za absorpcję.

Jeśli
1
≈
k
i weźmiemy
6
10
−
=
λ
m ( = 1µm, światło widzialne: 0,4–0,8µm), to
η
będzie rzędu
6
10
m
1
−
W ciałach stałych przy przejściach prostych
k
rzeczywiście jest rzędu
n
. Widzimy, że
σ
~
k
- stąd w
materiałach przewodzących mamy bardzo silne pochłanianie.
Przy dużych częstościach (
∞
→
ω
) wartość
nk
dąży do 0. Są dwie możliwości:
I.
0
→
k
, wówczas
0
2
2
2
ε
=
≈
−
n
k
n
;
0
ε
=
n
II.
0
→
n
, wtedy
0
2
ε
=
−
k
;
0
ε
−
=
k
- to oznacza, że stała dielektryczna musi być ujemna
Czy taki przypadek jest możliwy?
Mamy:
πα
ε
4
1
0
2
2
+
=
=
−
k
n
Jeśli uwzględnimy polaryzowalność sieciową, za 1 musimy wstawić
S
ε
:
πα
ε
4
2
2
+
=
−
S
k
n
;
ω
πσ
2
=
nk
Wstawiamy:
2
2
*
2
1
*
τ
ω
τ
σ
+
=
m
e
;
2
2
2
*
2
1
τ
ω
τ
α
+
−
=
m
e
;
2
2
2
*
2
2
2
1
4
τ
ω
τ
π
ε
+
−
=
−
m
e
k
n
S
;
2
2
*
2
1
2
τ
ω
ω
τ
π
+
=
m
e
nk
k
może być dużo większe niż
n
- stała dielektryczna może być ujemna. Elektrony przeciwdziałają
przyłożonej zmianie pola (reguła samoindukcji Lenza).
Przyjmijmy, że mamy
e
N nośników, np. elektronów w metalu:
2
2
2
*
2
2
2
2
*
2
2
2
1
4
1
4
τ
ω
τ
π
ε
τ
ω
τ
π
ε
+
⋅
−
=
+
−
=
−
e
S
S
N
m
e
m
e
k
n
2
2
*
2
2
2
*
2
1
2
1
2
τ
ω
ω
τ
π
τ
ω
ω
τ
π
+
⋅
=
+
=
e
N
m
e
m
e
nk
ponieważ
S
p
m
e
ε
π
ω
*
2
2
4
=
, otrzymujemy:
+
−
=
−
2
2
2
2
2
2
1
1
τ
ω
τ
ω
ε
p
S
k
n
;
+
=
2
2
2
1
2
τ
ω
ω
τ
ω
ε
p
S
nk
;
gdzie
p
ω
- częstość plazmowa
Wzory te są dobre, jeśli ciało stałe może być opisane statystyką Boltzmanna.
τ
- czas relaksacji, rzędu
12
10
−
s (jest to czas pomiędzy zderzeniami elektronów z siecią)
γ
τ
=
1
- współczynnik tłumienia (opór stawiany elektronom podczas ich wędrówki przez sieć)
Częstość plazmowa: w metalach o
3
23
cm
1
10
≈
e
N
jest rzędu
s
1
10
16
, a więc
γ
ω
>>
p
.
Gdy
γ
ω
ω
>>
>>
p
(np. dla światła widzialnego
s
1
10
14
≈
ω
), rozważajac oddziaływanie
promieniowania z nośnikami ładunku możemy uprościć wcześniejsze wyrażenia:
−
≈
+
−
=
−
2
2
2
2
2
2
2
1
1
ω
ω
ε
ω
γ
ω
ε
p
S
p
S
k
n
;
3
2
2
2
2
2
ω
γ
ω
ε
ω
γ
γ
ω
ω
ε
p
S
p
S
nk
≈
+
⋅
=
Wynika z tego tzw. metaliczne odbicie.
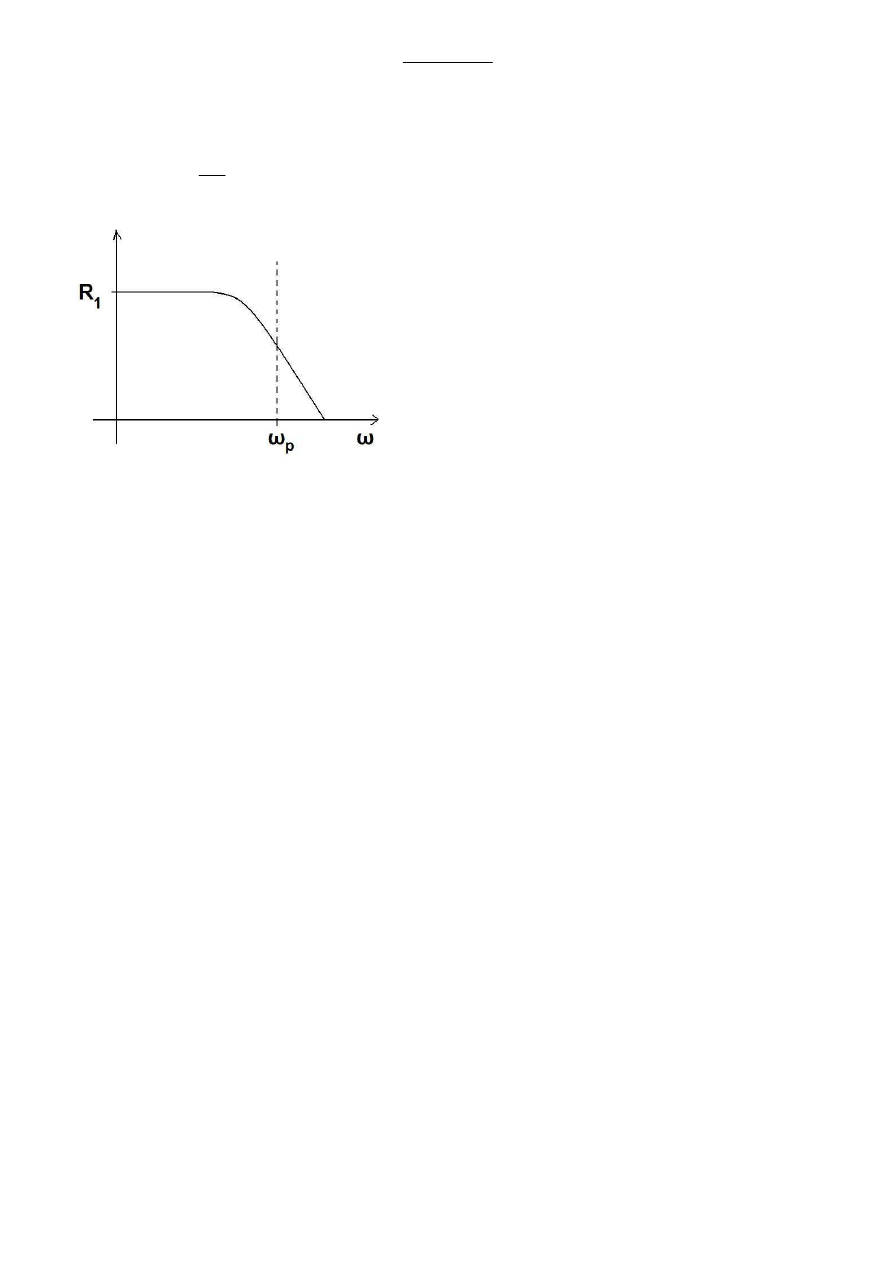
Wzory Frenera na współczynnik odbicia:
(
)
(
)
2
2
2
2
1
1
k
n
k
n
R
+
+
+
−
=
,
gdzie:
k
- współczynnik ekstynkcji;
n
- zwykły współczynnik odbicia
Jeśli
0
2
→
nk
, to albo
0
→
k
,
0
→
n
. Widzimy, że to
0
→
n
, bo
ω
ω
>>
p
, stąd
0
2
2
<<
−
k
n
.
A zatem
2
2
2
ω
ω
ε
p
S
k
=
, i dostajemy
1
=
R
(
%
100
=
R
) – odbicie metaliczne (czysty metal odbija 100%
ś
wiatła widzialnego).
Częstość plazmowa to częstość promieniowania, przy
której wszystkie nośniki ładunku drgają w takt pola fali
elektromagnetycznej. W pobliżu częstości plazmowej
metal nie odbija już 100% . Dla aluminium
odpowiadająca tej częstości długość fali wynosi
200
=
p
λ
nm. Z kolei półprzewodniki odbijają 100%
w obszarze bardzo dalekiej podczerwieni, natomiast
słabo odbijają światło widzialne. Można to zmienić
poprzez domieszkowanie, jednak to nie zmienia faktu,
ż
e GaAs może odbić maksymalnie 30% światła
widzialnego.
opracował: Radek Kołkowski
Wyszukiwarka
Podobne podstrony:
bryja, fizyka ciała stałego II, Ciepło właściwe wg Debye’a
bryja, fizyka ciała stałego II, Ciepło właściwe wg Debye’a
Fizyka Ciala Stalego II id 1766 Nieznany
bryja, fizyka ciała stałego II, efekt holla, Poziomy Landaua
bryja, fizyka ciała stałego II, Równanie kinetyczne Boltzmanna i czas relaksacji, prawo ohma (1)
bryja, fizyka ciała stałego II, Zespolony współczynnik załamania zespolone przewodnictwo, częstość p
II 14 Fizyka ciala stalego
TEORIA fizyka rok 1, Studia, Mibm, semestr II, Fizyka Ciała Stałego, Fizyka
ZESTAW 2 G, Studia, Mibm, semestr II, Fizyka Ciała Stałego, Fizyka, Zestawy
ZESTAW 1 G, Studia, Mibm, semestr II, Fizyka Ciała Stałego, Fizyka, Zestawy
II 14 Fizyka ciala stalego
Ciżman, fizyka ciała stałego L, sprawozdanie dwójłomność spontaniczna
bryja, fizyka ciała stałego, Równanie kp
bryja, fizyka ciała stałego, Model ciasnego wiązania
fizyka ciala stalego
bryja, fizyka ciała stałego, Równanie kp
więcej podobnych podstron