
1
lista - funkcje wielu zmiennych
2
lista - pochodne cząstkowe
3
lista - ekstrema funkcji wielu zmiennych
4
lista - całki podwójne 1
5
lista - całki podwójne 2
6
lista - całki potrójne
7
lista - zastosowawnie całek wielokrotnych
8
lista - zbieżność szeregów 1
8.1
sumy częsciowe
dane: a
n
, n
0
, gdzie
∞
P
n=n
0
a
n
=?
rozwiązanie:
• obliczyć S
n
=
n
P
k=n
0
a
k
• obliczyć
∞
P
n=n
0
a
n
= lim
n→∞
S
n
• sprawdzić czy
∞
P
n=n
0
a
n
∈ R
• na podstawie obliczeń określić zbieżność szeregu
a)
a
n
=
5
6
n
, n
0
= 0
S
n
=
n
X
k=n
0
a
k
=
n
X
k=0
5
6
k
=
1 −
5
6
n+1
1 −
5
6
= 6
"
1 −
5
6
n+1
#
∞
X
n=n
0
a
n
= lim
n→∞
S
n
= lim
n→∞
(
6
"
1 −
5
6
n+1
#)
= 6
badany szereg jest zbieżny i ma sumę 6.
b)
a
n
=
n−1
n!
, n
0
= 2
S
n
=
n
X
k=n
0
a
k
=
n
X
k=2
k − 1
k!
=
n
X
k=2
1
(k − 1)!
−
n
X
k=2
1
k!
= 1 +
n
X
k=3
1
(k − 1)!
−
n
X
k=2
1
k!
= 1 +
1
2
+
1
3
+ ... +
1
n
−
1
2
+
1
3
+ ... +
1
n
= 1
∞
X
n=n
0
a
n
= lim
n→∞
S
n
= lim
n→∞
1 = 1
badany szereg jest zbieżny i ma sumę 1.
1

c)
a
n
=
1
(2n−1)(2n+1)
, n
0
= 1
S
n
=
n
X
k=n
0
a
k
=
n
X
k=1
1
(2k − 1) (2k + 1)
=
n
X
k=1
1
2 (2k − 1)
−
n
X
k=1
1
2 (2k + 1)
=
1
2
"
1 +
n
X
k=2
1
2 (2k − 1)
−
n−1
X
k=1
1
2 (2k + 1)
−
1
2 (2n + 1)
#
=
1
2
−
1
4 (2n + 1)
∞
X
n=1
a
n
= lim
n→∞
S
n
= lim
n→∞
1
2
−
1
4 (2n + 1)
=
1
2
badany szereg jest zbieżny i ma sumę
1
2
.
d)
a
n
=
1
√
n+1+
√
n
, n
0
= 1
a
n
=
1
√
n + 1 +
√
n
=
1
√
n + 1 +
√
n
·
√
n + 1 −
√
n
√
n + 1 −
√
n
=
√
n + 1 −
√
n
n + 1 − n
=
√
n + 1 −
√
n
S
n
=
n
X
k=n
0
a
k
=
n
X
k=1
√
n + 1 −
√
n =
√
2 −
√
1 +
√
3 −
√
2 + ... +
√
n −
√
n − 1 +
√
n + 1 −
√
n
= −1 +
√
n + 1
∞
X
n=1
a
n
= lim
n→∞
S
n
= lim
n→∞
−1 +
√
n + 1
= ∞
badany szereg nie jest zbieżny.
8.2
kryterium całkowe
dane: a
n
, n
0
, gdzie
∞
P
n=n
0
a
n
=?
rozwiązanie:
• znaleźć f (x) ∼ a
n
• obliczyć
∞
R
n
0
f (x)dx = lim
T →∞
T
R
n
0
f (x)dx
• sprawdzić, czy
∞
R
n
0
f (x)dx ∈ R
• na podstawie kryterium całkowego określić zbieżność szeregu
a)
a
n
=
1
n
2
+n
, n
0
= 1
f (x) =
1
x
2
+ x
T
Z
n
0
f (x)dx =
T
Z
1
1
x
2
+ x
dx =
T
Z
1
1
x
−
1
x + 1
dx
=
[ln x]
x=T
x=1
− [ln (x + 1)]
x=T
x=1
= ln T − ln (T + 1) + ln 2
lim
T →∞
T
Z
n
0
f (x)dx = lim
T →∞
{ln T − ln (T + 1) + ln 2)} = ln 2 + lim
T →∞
ln
T
T + 1
= ln 2
z kryterium całkowego wynika, że dany szereg jest zbieżny.
2
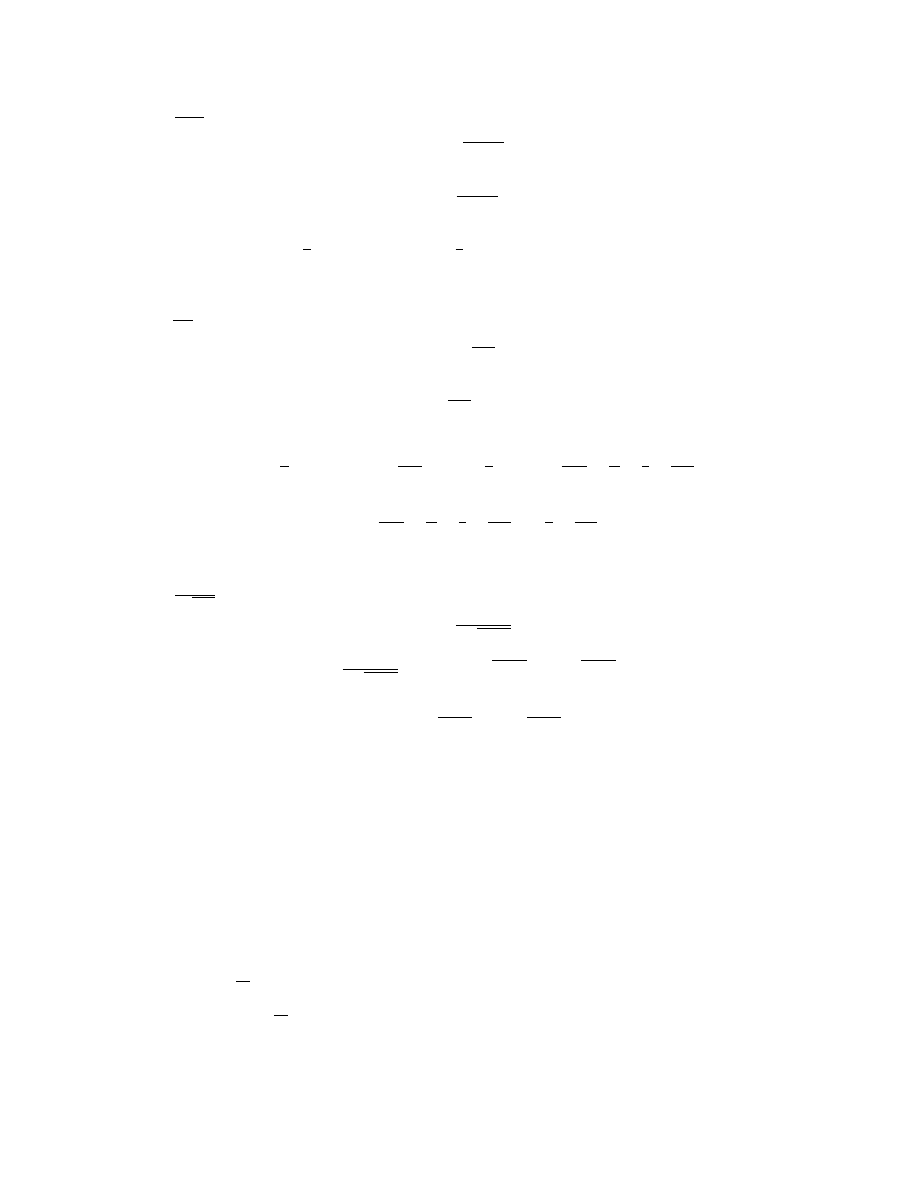
b)
a
n
=
n
n
2
+4
, n
0
= 1
f (x) =
x
x
2
+ 4
lim
T →∞
T
Z
1
x
x
2
+ 4
dx
= lim
T →∞
1
2
ln x
2
+ 4
x=T
x=1
= −
1
2
ln 5 + lim
T →∞
ln T
2
+ 4
= ∞
z kryterium całkowego wynika, że dany szereg jest rozbieżny.
c)
a
n
=
ln n
n
2
, n
0
= 2
f (x) =
ln x
x
2
T
Z
2
ln x
x
2
dx
=
T
Z
2
−
1
x
0
ln(x)dx =
−
ln x
x
x=T
x=2
−
1
x
x=T
x=2
= −
ln T
T
−
1
T
+
1
2
+
ln 2
2
lim
T →∞
−
ln T
T
−
1
T
+
1
2
+
ln 2
2
=
1
2
+
ln 2
2
z kryterium całkowego wynika, że dany szereg jest zbieżny.
d)
a
n
=
1
n
√
n+1
, n
0
= 1
f (x) =
1
x
√
x + 1
Z
f (x)dx =
Z
1
x
√
x + 1
dx = ln(1 −
√
x + 1) − ln(
√
x + 1 + 1) + C
lim
T →∞
T
Z
n
0
f (x)dx = lim
T →∞
ln(1 −
√
x + 1) − ln(
√
x + 1 + 1)
x=T
x=n
0
= ... = iπ
i cały żart tkwi w tym, że jest to zespolone. ha! cóż rzec teraz?
8.3
kryterium ilorazowe
dane: a
n
, n
0
, gdzie
∞
P
n=n
0
a
n
=?
rozwiązanie:
• znaleźć b
n
∼ a
n
• sprawdzić czy
∞
P
n=n
0
b
n
∈ R
• obliczyć lim
n→∞
a
n
b
n
• sprawdzić czy lim
n→∞
a
n
b
n
∈ R
+
• na podstawie kryterium ilorazowego określić zbieżność szeregu
3

a)
a
n
=
n
2
+n+1
2n
3
−1
, n
0
= 1
b
n
=
1
n
∞
X
n=n
0
b
n
= ∞
lim
n→∞
a
n
b
n
= lim
n→∞
n
3
+ n
2
+ n
2n
3
− 1
=
1
2
z kryterium ilorazowego wynika, że dany szereg jest rozbieżny.
b)
a
n
=
n+1
√
n
3
+1
, n
0
= 1
b
n
=
n
n
3
2
=
1
√
n
∞
X
n=n
0
b
n
= ∞
lim
n→∞
a
n
b
n
= lim
n→∞
(n + 1)
√
n
√
n
3
+ 1
= lim
n→∞
r
(n + 1)
2
n
n
3
+ 1
= lim
n→∞
r
n
3
+ 2n
2
+ n
n
3
+ 1
= 1
z kryterium ilorazowego wynika, że dany szereg jest rozbieżny.
c)
a
n
=
2
n
−1
3
n
−1
, n
0
= 1
b =
2
3
n
∞
X
n=n
0
b
n
= 0
lim
n→∞
n
X
k=1
b
k
= lim
n→∞
1 −
2
3
n+1
1 −
2
3
=
3
2
lim
n→∞
(
1 −
2
3
n+1
)
=
3
2
lim
n→∞
a
n
b
n
= lim
n→∞
2
n
− 1
3
n
− 1
·
3
n
2
n
= lim
n→∞
3
n
2
n
·
2
n
3
n
·
1 −
1
2
n
1 −
1
3
n
= 1
z kryterium ilorazowego wynika, że dany szereg jest zbieżny.
d)
a
n
=
sin
π
3n
sin
π
2n
, n
0
= 1
b
n
=
π
3
n
π
2
n
=
2
3
n
∞
X
n=n
0
b
n
= 0
lim
n→∞
n
X
k=1
b
k
= lim
n→∞
1 −
2
3
n+1
1 −
2
3
=
3
2
lim
n→∞
(
1 −
2
3
n+1
)
=
3
2
lim
n→∞
a
n
b
n
= lim
n→∞
sin
π
3n
π
3n
sin
π
2n
π
2n
=
1
1
= 1
z kryterium ilorazowego wynika, że dany szereg jest zbieżny.
4

8.4
kryterium porównawcze
dane: a
n
, n
0
, gdzie
∞
P
n=n
0
a
n
=?
rozwiązanie:
• znaleźć b
n
∼ a
n
• sprawdzić czy
∞
P
n=n
0
b
n
∈ R
• sprawdzić czy 0 ¬ a
n
¬ b
n
lub 0 ¬ b
n
¬ a
n
• na podstawie kryterium ilorazowego określić zbieżność szeregu
a)
a
n
=
3
n
2
+2
, n
0
= 1
0 ¬
3
n
2
+ 2
¬ 3
1
n
2
z kryterium porównawczego wynika, że dany szereg jest zbieżny.
b)
a
n
=
n+1
n
2
, n
0
= 1
n + 1
n
2
+ 1
n + 1
n
2
=
1
n
+
1
n
2
z kryterium porównawczego wynika, że dany szereg jest rozbieżny.
c)
a
n
= sin
π
2
n
, n
0
= 1
0 ¬ sin
π
2
n
¬
π
2
n
= π
1
2
n
z kryterium porównawczego wynika, że dany szereg jest zbieżny.
d)
a
n
=
2
n
+sin n!
3
n
, n
0
= 0
0 ¬
2
n
+ sin n!
3
n
¬
2
n
+ 1
3
n
=
2
3
n
+
1
3
n
z kryterium porównawczego wynika, że dany szereg jest zbieżny.
e)
a
n
=
3−2 cos n
2
√
n
, n
0
= 1
3 − 2 cos n
2
√
n
1
√
n
z kryterium porównawczego wynika, że dany szereg jest rozbieżny.
f )
a
n
=
3
n
+1
n3
n
+2
n
, n
0
= 1
3
n
+ 1
n3
n
+ 2
n
3
n
n3
n
+ 3
n
=
3
n
3
n
(n + 1)
=
1
n + 1
0
z kryterium porównawczego wynika, że dany szereg jest rozbieżny.
8.5
kryterium d’alemberta
dane: a
n
, gdzie
∞
P
n=1
a
n
=?
rozwiązanie:
• obliczyć lim
n→∞
|
a
n+1
a
n
|
• sprawdzić czy lim
n→∞
|
a
n+1
a
n
| < 1 lub lim
n→∞
|
a
n+1
a
n
| > 1
• na podstawie kryterium d’alemberta określić zbieżność szeregu
5

a)
a
n
=
100
n
n!
lim
n→∞
a
n+1
a
n
= lim
n→∞
100
n+1
(n + 1)!
·
n!
100
n
= lim
n→∞
100
n + 1
= 0 < 1
z kryterium d’alemberta wynika, że dany szereg jest zbieżny.
b)
a
n
= n
2
sin
π
2
n
lim
n→∞
a
n+1
a
n
= lim
n→∞
(n + 1)
2
sin
π
2·2
n
n
2
sin
π
2
n
= lim
n→∞
n + 1
n
2
·
1
2
sin
π
2·2n
π
2·2n
sin
π
2n
π
2n
=
1
2
< 1
z kryterium d’alemberta wynika, że dany szereg jest zbieżny.
c)
a
n
=
n!
n
n
lim
n→∞
a
n+1
a
n
= lim
n→∞
n!(n + 1)
(n + 1)
n
(n + 1)
·
n
n
n!
= lim
n→∞
n
n + 1
n
= lim
n→∞
1 +
1
n
−n
=
1
e
< 1
z kryterium d’alemberta wynika, że dany szereg jest zbieżny.
d)
a
n
=
(n!)
2
(2n)!
lim
n→∞
a
n+1
a
n
= lim
n→∞
(n!)
2
(n + 1)
2
(2n + 2)!
·
(2n)!
(n!)
2
= lim
n→∞
(n + 1)
2
(2n)!
(2n)!(2n + 1)(2n + 2)
= lim
n→∞
n
2
+ 2n + 1
4n
2
+ 6n + 2
=
1
4
< 1
z kryterium d’alemberta wynika, że dany szereg jest zbieżny.
e)
a
n
=
n
n
3n!
lim
n→∞
a
n+1
a
n
= lim
n→∞
(n + 1)
n
(n + 1)
3 · 3
n
· n!(n + 1)
·
3
n
n!
n
n
= lim
n→∞
(n + 1)
n
3n
n
=
1
3
lim
n→∞
1 +
1
n
n
=
e
3
< 1
z kryterium d’alemberta wynika, że dany szereg jest zbieżny.
f )
a
n
=
2
n
+1
n
5
+1
lim
n→∞
a
n+1
a
n
= lim
n→∞
2 · 2
n
+ 1
(n + 1)
5
+ 1
·
n
5
+ 1
2
n
+ 1
= lim
n→∞
2
n
(n
5
· 2 +
n
5
2
n
+ 2 +
1
2
n
)
2
n
((n + 1)
5
+
(n+1)
5
2
n
+ 1 +
1
2
n
)
= lim
n→∞
2n
5
+
n
5
2
n
+ 2 +
1
2
n
(n + 1)
5
+
(n+1)
5
2
n
+ 1 +
1
2
n
= 2 > 1
z kryterium d’alemberta wynika, że dany szereg jest rozbieżny.
9
lista - zbieżność szeregów 2
9.1
kryterium cauchy’ego
dane: a
n
, gdzie
∞
P
n=1
a
n
=?
rozwiązanie:
• obliczyć lim
n→∞
n
p|a
n
|
• sprawdzić czy lim
n→∞
n
p|a
n
| < 1 lub lim
n→∞
n
p|a
n
| > 1
• na podstawie kryterium cauchy’ego określić zbieżność szeregu
6

a)
a
n
=
(n+1)
2n
(2n
2
+1)
n
lim
n→∞
n
p|a
n
| = lim
n→∞
(n + 1)
2
2n
2
+ 1
= lim
n→∞
1 +
2
n
+
1
n
2
2 +
1
n
2
=
1
2
< 1
z kryterium cauchy’ego wynika, że dany szereg jest zbieżny.
b)
a
n
=
2
n
+3
n
3
n
+4
n
lim
n→∞
n
p|a
n
| = lim
n→∞
n
s
3
n
2
3
n
+ 1
4
n
3
4
n
+ 1
=
3
4
lim
n→∞
n
s
2
3
n
+ 1
3
4
n
+ 1
=
3
4
< 1
z kryterium cauchy’ego wynika, że dany szereg jest zbieżny.
c)
a
n
=
3
n
n
n2
(n+1)
n2
lim
n→∞
n
p|a
n
| = lim
n→∞
n
s
3
n
n
n·n
(n + 1)
n·n
= lim
n→∞
3 · n
n
(n + 1)
n
= 3 lim
n→∞
n
n + 1
n
= 3 lim
n→∞
1 +
1
n
n
−1
=
3
e
> 1
z kryterium cauchy’ego wynika, że dany szereg jest rozbieżny.
d)
a
n
= arc cos
n 1
n
2
lim
n→∞
n
p|a
n
| = lim
n→∞
n
r
arc cos
n
1
n
2
= lim
n→∞
arc cos
1
n
2
= arc cos(0) =
π
2
> 1
z kryterium cauchy’ego wynika, że dany szereg jest rozbieżny.
9.2
warunek konieczny zbieżności
dane: a
n
, gdzie lim
n→∞
a
n
=?
rozwiązanie:
• znaleźć b
n
, gdzie
∞
P
n=1
b
n
=
∞
P
n=1
a
n
∨
∞
P
n=1
b
n
=
∞
P
n=1
a
n
−1
• sprawdzić czy
∞
P
n=1
b
n
∈ R [z dowolnego kryterium; tutaj kryterium d’alemberta]
• na podstawie warunku koniecznego zbieżności uzasadnić równość
a)
a
n
=
7
n
n
5
∞
X
n=n
0
b
n
=
∞
X
n=1
n
5
7
n
lim
n→∞
a
n+1
a
n
= lim
n→∞
(n + 1)
5
7
n+1
·
7
n
n
5
=
1
7
lim
n→∞
n + 1
n
5
=
1
7
< 1
z kryterium d’alemberta wynika, że dany szereg jest zbieżny.
zatem wobec warunku koniecznego zbieżności szeregów mamy:
lim
n→∞
n
5
7
n
= 0
+
⇔ lim
n→∞
7
n
n
5
=
1
0
+
= ∞
7

b)
a
n
=
n
n
(n!)
2
∞
X
n=1
n
n
(n!)
2
lim
n→∞
a
n+1
a
n
= lim
n→∞
(n + 1)
n+1
((n + 1)!)
2
·
(n!)
2
n
n
= lim
n→∞
(n + 1)
n
· (n + 1)
n! · (n + 1) · n! · (n + 1)
·
n! · n!
n
n
= lim
n→∞
n + 1
n
n
·
1
n + 1
= 0 < 1
z kryterium d’alemberta wynika, że dany szereg jest zbieżny.
zatem wobec warunku koniecznego zbieżności szeregów mamy:
lim
n→∞
n
n
(n!)
2
= 0
c)
a
n
=
n!
n
n
∞
X
n=1
n!
n
n
lim
n→∞
a
n+1
a
n
= lim
n→∞
(n + 1)!
(n + 1)
n+1
·
n
n
n!
= lim
n→∞
n!(n + 1)
(n + 1)
n
(n + 1)
·
n
n
n!
= lim
n→∞
n
n + 1
n
=
1
e
< 1
z kryterium d’alemberta wynika, że dany szereg jest zbieżny.
zatem wobec warunku koniecznego zbieżności szeregów mamy:
lim
n→∞
n!
n
n
= 0
d)
9.3
szeregi naprzemienne
dane: a
n
, gdzie
∞
P
n=1
a
n
=?
rozwiązanie:
• znaleźć b
n
, gdzie a
n
= (−1)
n
b
n
∨ a
n
= (−1)
n+1
b
n
• sprawdzić czy lim
n→∞
b
n
= 0
• sprawdzić czy ∃n
0
∈ N takie, że dla n > n
0
: ¬(b
n
%)
• na podstawie twierdzenia liebniza określić zbieżność szeregu
a)
a
n
= (−1)
n n−1
n
2
+5
b
n
=
n − 1
n
2
+ 5
lim
n→∞
b
n
= lim
n→∞
n − 1
n
2
+ 5
= lim
n→∞
1 −
1
n
n +
5
n
= 0
dla n > 3 : b
n
=
n − 1
n
2
+ 5
&
z twierdzenia leibniz’a wynika, że dany szereg naprzemienny jest zbieżny
8

b)
c)
a
n
= (−1)
n
ln n
n ln ln n
b
n
=
ln n
n ln ln n
lim
n→∞
b
n
= lim
n→∞
ln n
n ln ln n
= 0
dla n > 3 : b
n
=
ln n
n ln ln n
&
z twierdzenia leibniz’a wynika, że dany szereg naprzemienny jest zbieżny
d)
a
n
= (−1)
n
e − 1 +
1
n
n
b
n
=
e −
1 +
1
n
n
lim
n→∞
b
n
= lim
n→∞
e −
1 +
1
n
n
= 0
dla n ∈ N :
1 +
1
n
n
%⇒ b
n
=
e −
1 +
1
n
n
&
z twierdzenia leibniz’a wynika, że dany szereg naprzemienny jest zbieżny
9.4
sumy przybliżone
9.5
zbieżność bezwzględna
dane: a
n
, n
0
, gdzie
∞
P
n=1
a
n
=?
rozwiązanie:
• znaleźć b
n
, gdzie a
n
= (−1)
n
b
n
∨ a
n
= (−1)
n+1
b
n
⇒
∞
P
n=1
|a
n
| =
∞
P
n=1
b
n
• sprawdzić czy
∞
P
n=1
b
n
∈ R
• na podstawie twierdzenia o zbieżności bezwzględnej określić zbieżność szeregu
• jeśli szereg nie jest zbieżny bezwzględnie:
– sprawdzić czy lim
n→∞
b
n
= 0
– sprawdzić czy ∃n
0
∈ N takie, że dla n > n
0
: ¬(b
n
%)
– na podstawie twierdzenia liebniza określić zbieżność warunkową szeregu
a)
a
n
=
(−1)
n+1
2
n
+1
b
n
=
1
2
n
+ 1
0 ¬
1
2
n
+ 1
¬
1
2
n
n
z kryterium porównawczego wynika, że szereg
∞
P
n=1
b
n
jest zbieżny.
zatem twierdzenia twierdzenia o zbieżności bezwzględnej wynika, że dany szereg naprzemienny
∞
P
n=1
a
n
jest
bezwzględnie zbieżny.
9
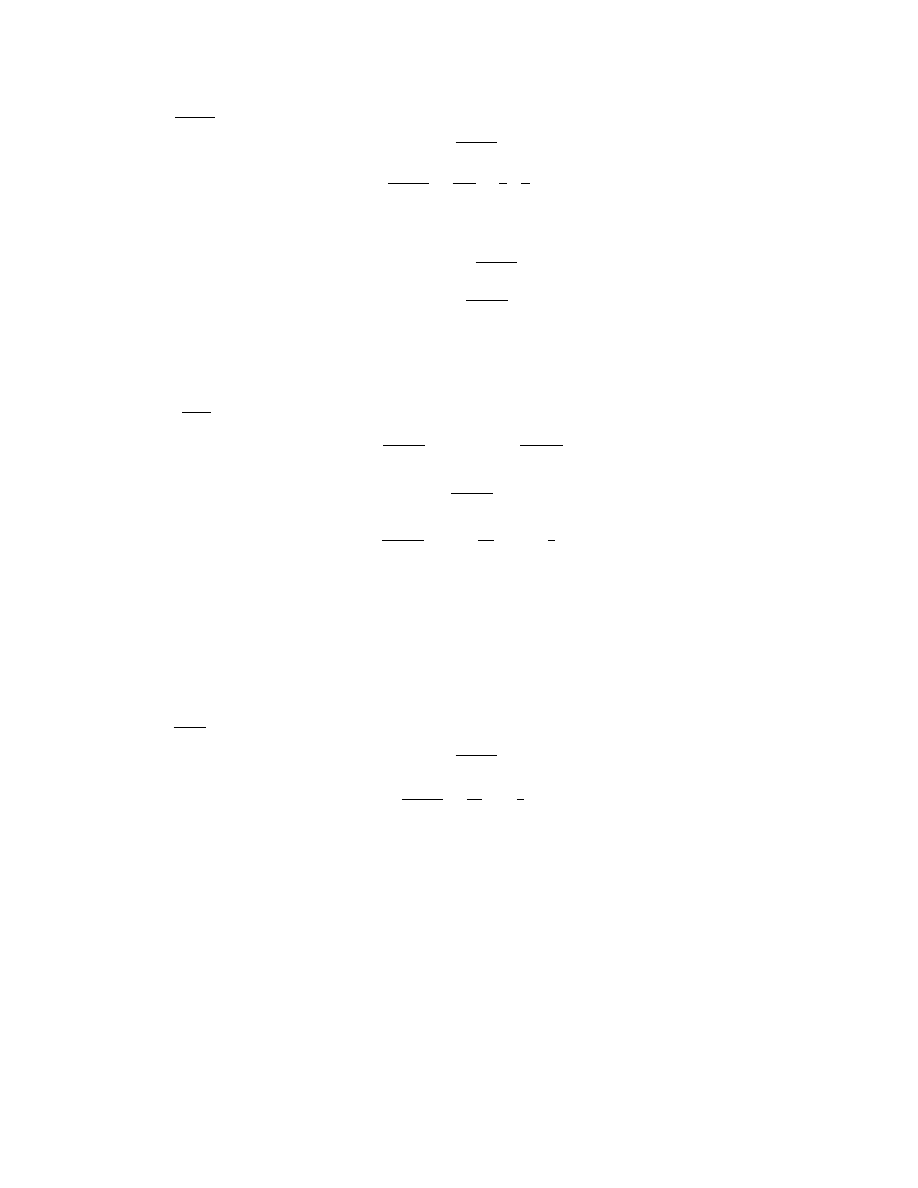
b)
a
n
=
(−1)
n
n
n
2
+1
b
n
=
n
n
2
+ 1
n
n
2
+ 1
n
2n
2
=
1
2
·
1
n
z kryterium porównawczego wynika, że szereg
∞
P
n=1
b
n
jest rozbieżny.
lim
n→∞
b
n
= lim
n→∞
n
n
2
+ 1
= 0
dla n ∈ N :
n
n
2
+ 1
&
zatem twierdzenia twierdzenia o zbieżności bezwzględnej wynika, że dany szereg naprzemienny
∞
P
n=1
a
n
jest
zbieżny warunkowo.
c)
a
n
=
−2n
3n+5
n
a
n
=
−2n
3n + 5
n
= (−1)
n
2n
3n + 5
n
b
n
=
2n
3n + 5
n
0 ¬
2n
3n + 5
n
¬
2n
3n
n
=
2
3
n
z kryterium porównawczego wynika, że szereg
∞
P
n=1
b
n
jest zbieżny.
zatem twierdzenia twierdzenia o zbieżności bezwzględnej wynika, że dany szereg naprzemienny
∞
P
n=1
a
n
jest
bezwzględnie zbieżny.
d)
e)
a
n
=
(−2)
n
3
n
+1
b
n
=
2
n
3
n
+ 1
0 ¬
2
n
3
n
+ 1
¬
2
n
3
n
=
2
3
n
z kryterium porównawczego wynika, że szereg
∞
P
n=1
b
n
jest zbieżny.
zatem twierdzenia twierdzenia o zbieżności bezwzględnej wynika, że dany szereg naprzemienny
∞
P
n=1
a
n
jest
bezwzględnie zbieżny.
f )
10
10
lista - szeregi potęgowe, szereg maclaurina
dane: c
n
, x
0
, gdzie
∞
P
n=1
c
n
(x − x
0
)
n
=?
rozwiązanie:
• znaleźć c
n
• obliczyć R = lim
n→∞
|
c
n
c
n+1
|
• znaleźć x
0
• sprawdzić zbieżność
∞
P
n=1
c
n
(x
0
− R)
n
oraz
∞
P
n=1
c
n
(x
0
+ R)
n
• na podstawie obliczeń określić przedział zbieżności szeregu
10.1
przedziały zbieżności szeregów potęgowych
a)
∞
P
n=1
x
n
n2
n
c
n
=
1
n2
n
R = lim
n→∞
|
c
n
c
n+1
| = lim
n→∞
1
n2
n
·
(n + 1)2
n+1
1
= lim
n→∞
2 ·
n + 1
n
= 2
x
0
= 0
x ∈ (x
0
− R, x
0
+ R) = (−2, 2)
∞
X
n=1
(x
0
− R)
n
n2
n
=
∞
X
n=1
(−2)
n
n2
n
=
∞
X
n=1
(−1)
n
1
n
= − ln 2
zbieżny
∞
X
n=1
(x
0
+ R)
n
n2
n
=
∞
X
n=1
2
n
n2
n
=
∞
X
n=1
1
n
rozbieżny
x ∈ [−2, 2)
b)
∞
P
n=1
n(x − 2)
n
c
n
= n
R = lim
n→∞
|
c
n
c
n+1
| = lim
n→∞
n
n + 1
= 1
x
0
= 2
x ∈ (x
0
− R, x
0
+ R) = (1, 3)
∞
X
n=1
n(x
0
− R − 2)
n
=
∞
X
n=1
n(−1)
n
=
∞
X
n=1
(−1)
n
1
n
= − ln 2
zbieżny
∞
X
n=1
n(x
0
− R + 2)
n
=
∞
X
n=1
n1
n
=
∞
X
n=1
n = ∞
rozbieżny
x ∈ [1, 3)
11

c)
∞
P
n=1
(x+3)
n
n
3
c
n
=
1
n
3
R = lim
n→∞
|
c
n
c
n+1
| = lim
n→∞
1
n
3
·
n
3
+ 3n
2
+ 3n + 1
1
= 1
x
0
= −3
x ∈ (x
0
− R, x
0
+ R) = (−4, 2)
∞
X
n=1
(x
0
− R + 3)
n
n
3
=
∞
X
n=1
(−1)
n
n
3
=
∞
X
n=1
(−1)
n
1
n
3
zbieżny
∞
X
n=1
(x
0
+ R + 3)
n
n2
n
=
∞
X
n=1
1
n
n
3
=
∞
X
n=1
1
n
3
zbieżny
x ∈ [−4, 2]
d)
∞
P
n=1
x
n
2
n
+3
n
c
n
=
1
2
n
+ 3
n
R = lim
n→∞
|
c
n
c
n+1
| = lim
n→∞
2 · 2
n
+ 3 · 3
n
2
n
+ 3
n
= lim
n→∞
2 · (
2
3
)
n
+ 3 · 1
(
2
3
)
n
+ 1
= 3
x
0
= 0
x ∈ (x
0
− R, x
0
+ R) = (−3, 3)
∞
X
n=1
(x
0
− R)
n
2
n
+ 3
n
=
∞
X
n=1
(−3)
n
2
n
+ 3
n
=
∞
X
n=1
(−1)
n
3
n
2
n
+ 3
n
zbieżny
∞
X
n=1
(x
0
+ R)
n
2
n
+ 3
n
=
∞
X
n=1
3
n
2
n
+ 3
n
rozbieżny
x ∈ [−3, 3)
e)
∞
P
n=1
n
n
2
+1
(x + 1)
n
c
n
=
n
n
2
+ 1
R = lim
n→∞
|
c
n
c
n+1
| = lim
n→∞
n + 1
(n + 1)
2
+ 1
·
n
1
+ 1
n
= lim
n→∞
n
3
+ n
2
+ n + 1
n
3
+ 2n
2
+ 2n
= 1
x
0
= −1
x ∈ (x
0
− R, x
0
+ R) = (−2, 0)
∞
X
n=1
n
n
2
+ 1
(x
0
− R − 1)
n
=
∞
X
n=1
n
n
2
+ 1
(−1)
n
zbieżny
∞
X
n=1
n
n
2
+ 1
(x
0
+ R + 1)
n
=
∞
X
n=1
n
n
2
+ 1
rozbieżny
x ∈ [−2, 0]
12
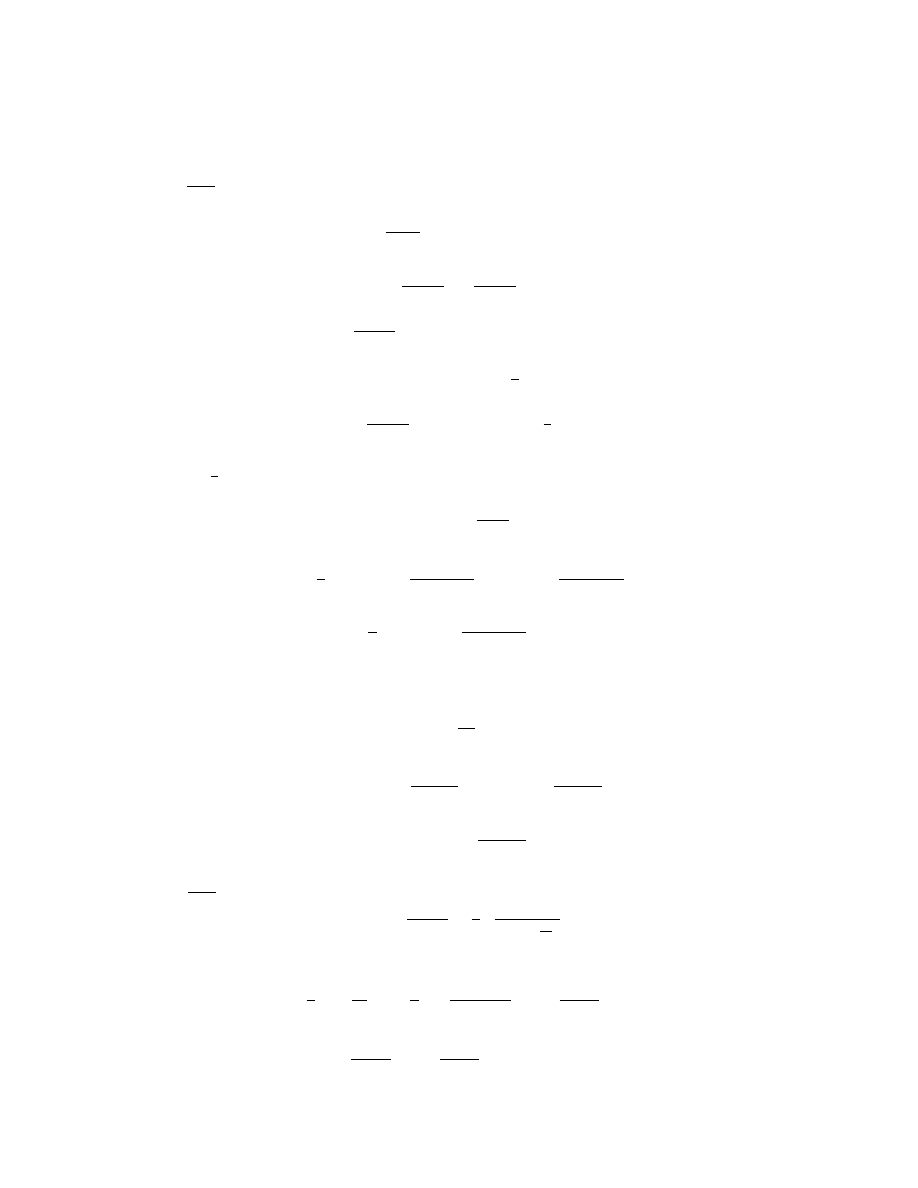
f )
10.2
szeregi maclaurina
a)
f (x) =
2
1−3x
skorzystamy ze wzoru:
1
1 − x
=
∞
X
n=0
x
n
, |x| < 1
2
1 − 3x
= 2
1
1 − 3x
2
1
1 − 3x
= 2
∞
X
n=0
(3x)
n
=
∞
X
n=0
2(3x)
n
|3x| < 1 ⇒ |x| <
1
3
2
1 − 3x
=
∞
X
n=0
2(3x)
n
, |x| <
1
3
b)
f (x) = cos
x
2
skorzystamy ze wzoru:
cos x =
∞
X
n=0
(−1)
n
x
2n
(2n)!
, x ∈ R
cos
x
2
=
∞
X
n=0
(−1)
n
x
2n
· 2
−2n
(2n)!
=
∞
X
n=0
(−1)
n
x
2n
(2n)! · 2
2n
cos
x
2
=
∞
X
n=0
(−1)
n
x
2n
(2n)! · 2
2n
, x ∈ R
c)
f (x) = xe
−2x
skorzystamy ze wzoru:
e
x
=
∞
X
n=0
x
n
n!
, x ∈ R
xe
−2x
= x
∞
X
n=0
(−2x)
n
n!
= x
∞
X
n=0
(−1)
n
2
n
x
n+1
n!
xe
−2x
= x
∞
X
n=0
(−1)
n
2
n
x
n+1
n!
, x ∈ R
d)
f (x) =
x
9+x
2
f (x) =
x
9 + x
2
=
x
9
·
1
1 − (−
x
2
9
)
skorzystamy ze wzoru: ? [szereg geometryczny]
∞
X
n=0
x
9
·
−
x
2
9
n
=
x
9
∞
X
n=0
(−1)
n
x
2n
9
n
=
∞
X
n=0
(−1)
n
9
n+1
x
2n+1
x
9 + x
2
=
∞
X
n=0
(−1)
n
9
n+1
x
2n+1
, |x| < 3
13

e)
f )
10.3
liczenie pochodnych z rozwinięć maclaurina
a)
f (x) = x sin x
skorzystamy ze wzoru:
sin x =
∞
X
n=0
(−1)
n
x
2n+1
(2n + 1)!
, x ∈ R
x sin x = x
∞
X
n=0
(−1)
n
x
2n+1
(2n + 1)!
=
∞
X
n=0
(−1)
n
x
2n+2
(2n + 1)!
c
n
=
1
(2n + 1)!
f
(50)
(0) = 50! · c
50
= 50!
1
(2 · 50 + 1)!
=
50!
101!
b)
c)
d)
10.4
szeregi potęgowe
10.5
sumy szeregów potęgowych
10.6
przybliżona wartość całki oznaczonej
11
lista - szereg fouriera
11.1
wyznaczanie szeregów fouriera
11.2
rozwijanie funkcji w szereg fouriera
11.3
szereg fouriera sinusów
11.4
szereg fouriera cosinusów
11.5
rozwijanie funkcji okresowych w szereg fouriera
11.6
współczynniki fouriera
11.7
wzór całkowy fouriera
12
lista - transformata fouriera
13
lista - transformata laplace’a
14
Wyszukiwarka
Podobne podstrony:
print 2011 06 02 analiza finansowa i ocena ryzyka
organizacja uslug w gastronomii wyklad 3 06.02.2011, GWSH, organizacja usług w gastronomii
dokonczenie wykladu org.usług.w.gastr.z 06.02.2011, GWSH, organizacja usług w gastronomii
Egzamin zima 2011 2012 02 06 poprawkowy
2011 06 20 matematyka finansowaid 27373
06 02 LWULAZB6F74J7VWU3XTCSTK2T2GBNYFUD7ZRHXY
06-02 PAM - Połączenie z Waszą Radą Światła, CAŁE MNÓSTWO TEKSTU
06 02 18 21
2011 06 20 Dec nr 230 MON Gosp mieniem Skarbu Państwa
egz CC 2011 06 25(SdS)
2001 06 02 matematyka finansowaid 21606
GIge zal 06 02 03 Przekroj geo inz
GIge zal 06 02 07 Przekroj geo inz
Makroekonomia I 11 Cykl koniunkturalny (2009 06 02)
2011 12 02
2011 06 10 LZPN test okregowka 07062011 odp a (2)
(20120404 124320) sb 2011 06
więcej podobnych podstron