Rachunek prawdopodobienstwa i statystyka Wojciech Kordecki skrypt 66str

ojciech

rdecki

Rachunek prawdopodobie«stwa

i statystyka matematyczna

cª

1998

Spis tre±ci

Wst¦p

1. Prawdopodobie«stwo

1.1. Aksjomaty prawdopodobie«stwa

1.1.1. Przestrze« zdarze«

1.1.2. Aksjomaty Koªmogorowa

1.1.3. Geometryczna i klasyczna denicja prawdopodobie«stwa 5

1.1.4. Zadania

1.2. Prawa wielkich liczb i symulacja

1.2.1. Mocne i sªabe prawo wielkich liczb

1.2.2. Pierwsze przykªady symulacji

1.2.3. Zadania

1.3. Prawdopodobie«stwo warunkowe

1.3.1. Denicja i podstawowe wªasno±ci

1.3.2. Wzór Bayesa

1.3.3. Zadania

2. Zmienne losowe

2.1. Rozkªady zmiennych losowych

2.1.1. Denicja zmiennej losowej

2.1.2. Dystrybuanta zmiennej losowej

2.1.3. G¦sto±¢

2.1.4. Zadania

2.2. Momenty zmiennych losowych

2.2.1. Caªka Stieltjesa

2.2.2. Warto±¢ oczekiwana

2.2.3. Momenty wy»szych rz¦dów

2.2.4. Zadania

2.3. Rozkªady dyskretne

2.3.1. Rozkªad dwupunktowy i dwumianowy

2.3.2. Rozkªad Poissona

2.3.3. Zadania

2.4. Rozkªady ci¡gªe

2.4.1. Rozkªad jednostajny

2.4.2. Rozkªad wykªadniczy

2.4.3. Rozkªad normalny

2.4.4. Zadania

3. Twierdzenia graniczne

3.1. Nierówno±¢ Czebyszewa i prawa wielkich liczb

3.1.1. Nierówno±ci Markowa i Czebyszewa

3.1.2. Prawa wielkich liczb

3.1.3. Zadania

3.2. Funkcje charakterystyczne

3.2.1. Denicje i wªasno±ci

3.2.2. Rozkªad gamma

3.2.3. Zadania

3.3. Centralne twierdzenie graniczne

3.3.1. Twierdzenie Lindeberga-Levy'ego

3.3.2. Rozkªady chi-kwadrat i t-Studenta

3.3.3. Zadania

4. Podstawowe poj¦cia statystyki

4.1. Denicje

4.1.1. Sªownik poj¦¢ statycznych

4.1.2. Najwa»niejsze statystyki

4.1.3. Zadania

4.2. Dystrybuanta empiryczna i histogramy

4.2.1. Dystrybuanta empiryczna

4.2.2. Histogramy

4.2.3. Zadania

5. Estymacja

5.1. Estymacja punktowa

5.1.1. Metoda momentów

5.1.2. Metoda najwi¦kszej wiarogodno±ci

5.1.3. Zadania

5.2. Estymacja przedziaªowa

5.2.1. Przedziaªy ufno±ci

5.2.2. Przedziaªy ufno±ci dla ±redniej

5.2.3. Przedziaªy ufno±ci dla wariancji

5.2.4. Zadania

6. Testowanie hipotez

6.1. Testy parametryczne

6.1.1. Testy dla ±redniej

6.1.2. Testy dla wariancji

6.1.3. Testy dla dwóch ±rednich

6.1.4. Zadania

6.2. Testy nieparametryczne

6.2.1. Testy zgodno±ci

6.2.2. Testy niezale»no±ci

6.2.3. Zadania

Literatura

Wst¦p

Materiaª zawarty w konspekcie wykªadu jest podzielony na dwie zasadnicze

cz¦±ci { rachunek prawdopodobie«stwa i statystyk¦ matematyczn¡. Przezna-

czony on jest na jednosemestralny wykªad w wymiarze 4 godzin tygodniowo.

Caªy wykªad rachunku prawdopodobie«stwa jest oparty na aksjomatyce Koª-

mogorowa, w tym na ±cisªym zdeniowaniu zdarze« jako podzbiorów prze-

strzeni zdarze« elementarnych , tworz¡cych

-algebr¦ zdarze«. Z tego po-

wodu eksponowana jest raczej ÿgeometryczna denicja prawdopodobie«stwa"

zamiast ÿkombinatorycznej denicji prawdopodobie«stwa". Z drugiej strony,

na samym pocz¡tku wykªadu podaje si¦ prawo wielkich liczb w najprostszej

postaci, aby mo»na byªo wprowadzi¢ intuicje cz¦sto±ciowe, (autor ±wiadomie

unika terminu ÿcz¦sto±ciowa denicja prawdopodobie«stwa", obawiaj¡c si¦

jego nieco baªamutnego wyd¹wi¦ku), co pozwala na ilustracj¦ wykªadu symula-

cjami komputerowymi. Z tego wzgl¦du, nieco na marginesie wykªadu pojawia

si¦ te» metoda Monte Carlo i generatory liczb losowych.

Druga poªowa semestru po±wi¦cona jest na statystyk¦ matematyczn¡. Nacisk

jest poªo»ony przede wszystkim na podanie ogólnych metod i ich zrozumienie,

a nie na podanie szczegóªowych rozwi¡za«, które mo»na znale¹¢ w licznych,

a cz¦stokro¢ bardzo dobrych podr¦cznikach i poradnikach. Ta cz¦±¢ wykªadu

jest uzupeªniona o procedury uªatwiaj¡ce obliczanie warto±ci niektórych staty-

styk. Procedury te, napisane gªównie w Pascalu, tylko cz¦±ciowo umieszczone

s¡ w tym konspekcie. Wszystkie procedury s¡ dost¦pne w internecie pod ad-

Adres

internetowy

resem

http://neyman.im.pwr.wroc.pl/~kordecki

Przy opracowaniu tego konspektu, autor korzystaª z wielu podr¦czników.

Przede wszystkim z nieco przestarzaªego ju», ale dobrego podr¦cznika M. Fi-

sza [2] oraz z ksi¡»ek W. Fellera [5] i [6]. S¡ to jednak ksi¡»ki trudne, prze-

znaczone raczej dla matematyków i studentów matematyki, ni» dla studentów

politechnik. Zbiory zada«, to przede wszystkim skrypt T. Inglota, T. Ledwiny

i Z. awniczak [4] oraz podr¦cznik J. Grenia [3].

Obecnie na rynku ksi¦garskim i bibliotekach mo»na spotka¢ wielk¡ liczb¦ ty-

tuªów, po±wi¦conych zagadnieniom rachunku prawdopodobie«stwa i statystyki

matematycznej.Ich przegl¡dowi b¦dzie po±wi¦cony ostatni rozdziaª konspektu.

1. Prawdopodobie«stwo

1.1. Aksjomaty prawdopodobie«stwa

1.1.1. Przestrze« zdarze«

Niech b¦dzie dowolnym zbiorem, zwanym przestrzeni¡ zdarze« elementar-

Zdarzenia

elementarne

nych. Elementy tej przestrzeni

nazywamy zdarzeniami elementarnymi.

Przykªad.

Rzut monet¡: =

;

, gdzie

jest stron¡ monety z orªem,

jest stron¡ monety z reszk¡.

Rzut kostk¡ do gry: =

[1]

;[2];[3];[4];[5];[6]

, gdzie [

i] jest t¡ ±ciank¡ kostki,

na której jest

i oczek.

Strzelanie do tarczy: jest ±cian¡, na której wyznaczono koªo o danej ±rednicy.

Traenie jest punktemz tej ±ciany { zakªadamy tu, »e zawsze w ±cian¦ traamy,

cho¢ niekoniecznie w tarcz¦.

Zdarzeniami b¦dziemy nazywa¢ podzbiory przestrzeni zdarze« elementarnych

. Jednak»e nie wszystkie takie podzbiory musz¡ by¢ zdarzeniami. Musz¡

one jednak speªnia¢ pewne warunki. Aby na przykªad okre±li¢ zdarzenie

jako ÿwyrzucono co najmniej 5 oczek lub co najwy»ej 2 oczka" warto mie¢

sum¦ zdarze«

A = A

[

, gdzie

oznacza wyrzucenie co najwy»ej

2 oczek, a

oznacza wyrzucenie co najmniej 5 oczek. Podobnie, je±li

b¦dzie zdarzeniem polegaj¡cym na traeniu w tarcz¦, warto okre±li¢ zdarzenie

przeciwne

A polegaj¡ce na nietraeniu w tarcz¦. Rozwa»ania te

prowadz¡ nas do nast¦puj¡cej denicji.

Denicja.

Niech b¦dzie ustalon¡ przestrzeni¡ zdarze« elementarnych.Zda-

rzeniami nazywamy podzbiory przestrzeni , które tworz¡ rodzin¦ (czyli zbiór

-algebra

zdarze«

zbiorów)

tak¡, »e

(i)

;

(ii) je»eli

(iii) je»eli dla dowolnego ci¡gu

, to

[

;

gdzie

A =

;

nazywamy zdarzeniem niemo»liwym, a

A nazywamy

zdarzeniem przeciwnym do

A. Rodzin¦

nazywamy

-algebr¡ zdarze«.

Wyst¦puj¡ca w denicji suma mo»e by¢ sko«czona lub niesko«czona. Stosuje

si¦ cz¦sto skrótowy zapis, podobny do zapisu sumy liczb:

[

;

[

::: :

Bezpo±rednio z denicji wynikaj¡ dalsze wªasno±ci

-algebry zdarze«.

1.1 Aksjomaty prawdopodobie«stwa

Fakt 1.1.1.

Je»eli jest przestrzeni¡ zdarze« elementarnych, a

jest

-al-

gebr¡ zdarze«, to

(1.1.1)

Dowód.

Poniewa»

;

oraz =

;

, to z (i) i (ii) wynika, »e

Zdarzenie

A = nazywamy zdarzeniem pewnym. Podobnie jak dla sumy,

stosuje si¦ dla iloczynu zbiorów zapis, podobny do zapisu iloczynu liczb:

;

::: :

Fakt 1.1.2.

Je»eli dla dowolnego ci¡gu

, to

Dowód.

Powy»sz¡ równo±¢ otrzymuje si¦ z prawa de Morgana oraz z wªasno±ci

(ii) i (iii). Poniewa»

A =

[

;

oraz

. to równie»

A = (A

)

Wyst¦puj¡ca w powy»szym wzorze suma mo»e by¢ sko«czona lub niesko«-

czona.

1.1.2. Aksjomaty Koªmogorowa

Podana ni»ej denicja prawdopodobie«stwa zwana aksjomatyczn¡ denicj¡

prawdopodobie«stwa, pochodzi od A. N. Koªmogorowa. Byªa opublikowana

w roku 1933 roku

i staªa si¦ podstaw¡ wspóªczesnej teorii prawdopodobie«-

stwa.

Denicja. Aksjomaty Koªmogorowa.

Je»eli jest przestrzeni¡ zdarze«

elementarnych, a

jest

-algebr¡ zdarze«, to prawdopodobie«stwem nazy-

wamy funkcj¦ Pr :

, czyli funkcj¦ przypisuj¡c¡ liczby zdarzeniom tak¡,

»e

Denicja

prawdopodo-

bie«stwa

Pr(

;

(1.1.2)

Pr() = 1

;

(1.1.3)

A. N. Koªmogorow (1903 { 1987), miaª wtedy zaledwie 30 lat!

1.1 Aksjomaty prawdopodobie«stwa

je»eli dla dowolnych

j jest A

;

, to

[

Pr(

)

(1.1.4)

Je»eli

B =

;

to mówimy, »e

A i B s¡ wykluczaj¡ce si¦. Warunek 1.1.4

oznacza, »e dla ci¡gu parami wykluczaj¡cych si¦ zdarze«, prawdopodobie«stwo

sumy jest równe sumie prawdopodobie«stw.

Uwaga.

Dla iloczynów zdarze« nie ma podobnej wªasno±ci.

Z aksjomatów Koªmogorowa wynikaj¡ dalsze wªasno±ci.

Twierdzenie 1.1.1.

Je»eli

to Pr(

) = 1

Pr(

A).

Dowód.

Poniewa»

;

, to z równo±ci (1.1.3) i (1.1.4) wynika, »e Pr(

A)+

Pr(

) = 1.

Podobnie dowodzi si¦ nast¦puj¡cego wyniku.

Twierdzenie 1.1.2.

Je»eli

A, to Pr(A

B) = Pr(A)

Pr(

B).

Kilka nast¦pnych u»ytecznych wzorów, pozostawimy do samodzielnego udo-

wodnienia jako zadania.

Trójk¦ (

;

;Pr) nazywa si¦ przestrzeni¡ probabilistyczn¡. W nast¦pnym

Przestrze«

probabili-

styczna

punkcie rozpatrzymy dwa specjalne przypadki przestrzeni probabilistycznych.

Teraz tylko jeden bardzo prosty (najprostszy nietrywialny) przykªad.

Przykªad.

Rzucamy jeden raz monet¡. Wtedy =

;

fO g

;

fRg

;

oraz Pr(

) = Pr(

) = 1

=2. Wten sposób zostaªa okre±lona caªa przestrze«

probabilistyczna (

;

;Pr).

Niezale»no±¢ zdarze« jest wªasno±ci¡ nie tylko samych zdarze« jako zbiorów,

Niezale»no±¢

zdarze«

ale zale»y od okre±lonego na nich prawdopodobie«stwa.

Denicja.

Ci¡g zdarze«

;::: (sko«czony lub niesko«czony) jest nieza-

le»ny, gdy dla dowolnego jego sko«czonego podci¡gu

;:::A

zachodzi

równo±¢

Pr(

) = Pr(

)Pr(

)

Pr(

)

(1.1.5)

Je»eli o pewnych zdarzeniach wiemy, »e s¡ niezale»ne, to znaj¡c ich prawdo-

podobie«stwa mo»emy obliczy¢ prawdopodobie«stwa ich iloczynów.

Przykªad.

Rzucamy dwoma monetami. Je»eli wiemy, »e rzuty s¡ niezale»ne

i prawdopodobie«stwa wyrzucenia zarówno orªa jak i reszki s¡ równe, to praw-

dopodobie«stwo wyrzucenia dwóch orªów jest (jak dobrze zreszt¡ wiadomo)

równe Pr(

)

Pr(

) = (1

=2)(1=2) = 1=4.

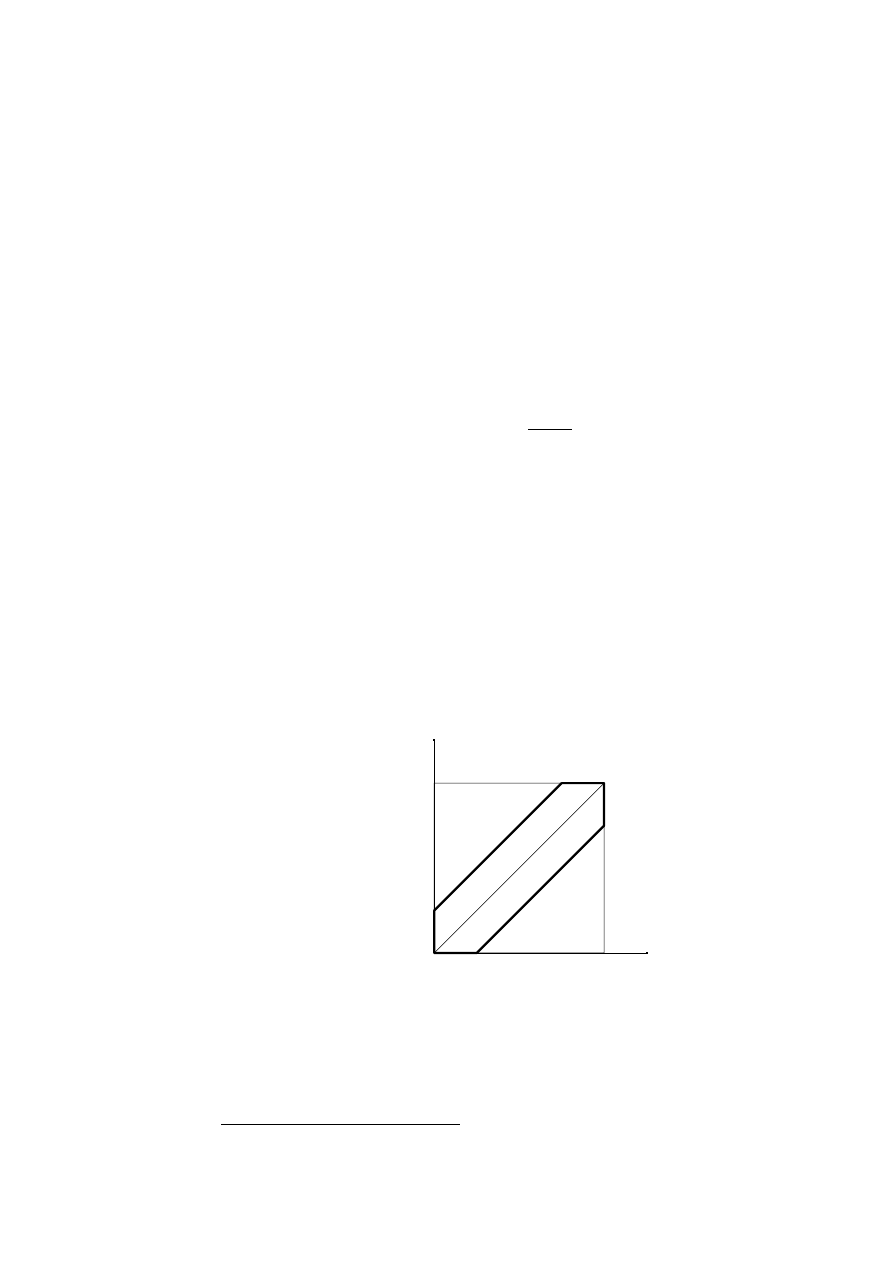
1.1 Aksjomaty prawdopodobie«stwa

1.1.3. Geometryczna i klasyczna denicja prawdopodobie«stwa

Rozpatrzymy teraz dwa szczególne przypadki. Jako pierwszy okre±limy tzw.

geometryczn¡ denicj¦ prawdopodobie«stwa. Nazwa denicja jest tu myl¡ca,

bo tak naprawd¦, jest to tylko szczególny przypadek ogólnej, aksjomatycznej

denicji prawdopodobie«stwa.

Niech b¦dzie pewnym podzbiorem

, gdzie

k = 1;2;3, tzn. jest podzbio-

Geometryczna

denicja

prawdopodo-

bie«stwa

rem prostej, (najcz¦±ciej odcinkiem), pªaszczyzny lub przestrzeni trójwymia-

rowej. Zdarzeniami z

b¦d¡ podzbiory z maj¡ce miar¦

m(A) { dªugo±¢,

powierzchni¦ lub obj¦to±¢. Prawdopodobie«stwo zdarzenia

A okre±limy wzo-

rem

Pr(

A) = m(A)

m() :

(1.1.6)

Tak okre±lone prawdopodobie«stwo nazywamy geometrycznym.

Przykªad.

Na odcinku [0

;1] umieszczamy losowo, tzn. zgodnie z prawdopo-

dobie«stwem geometrycznym oraz niezale»nie, dwa punkty

x i y. Przestrze«

mo»emy wobec tego okre±li¢ jako kwadrat o wierzchoªkach w punktach (0

;0),

;1), (1;0) oraz (1;1). Teraz zdarzeniami elementarnymi s¡ punkty z tego

kwadratu:

! = (x;y)

. Dla jednego punktu

x zgodnie ze wzorem (1.1.6)

mamy Pr(

! : x

[

a;b]; b > a

) =

a. To samo mamy dla punktu y. Po-

niewa» punkty s¡ umieszczane niezale»nie, to

Pr(

! : !

[

a;b]

[

c;d]; b > a; d > c

) = (

a)(d

c):

Iloczyn kartezja«ski odcinków [

a;b]

[

c;d] jest oczywi±cie prostok¡tem we-

wn¡trz kwadratu .

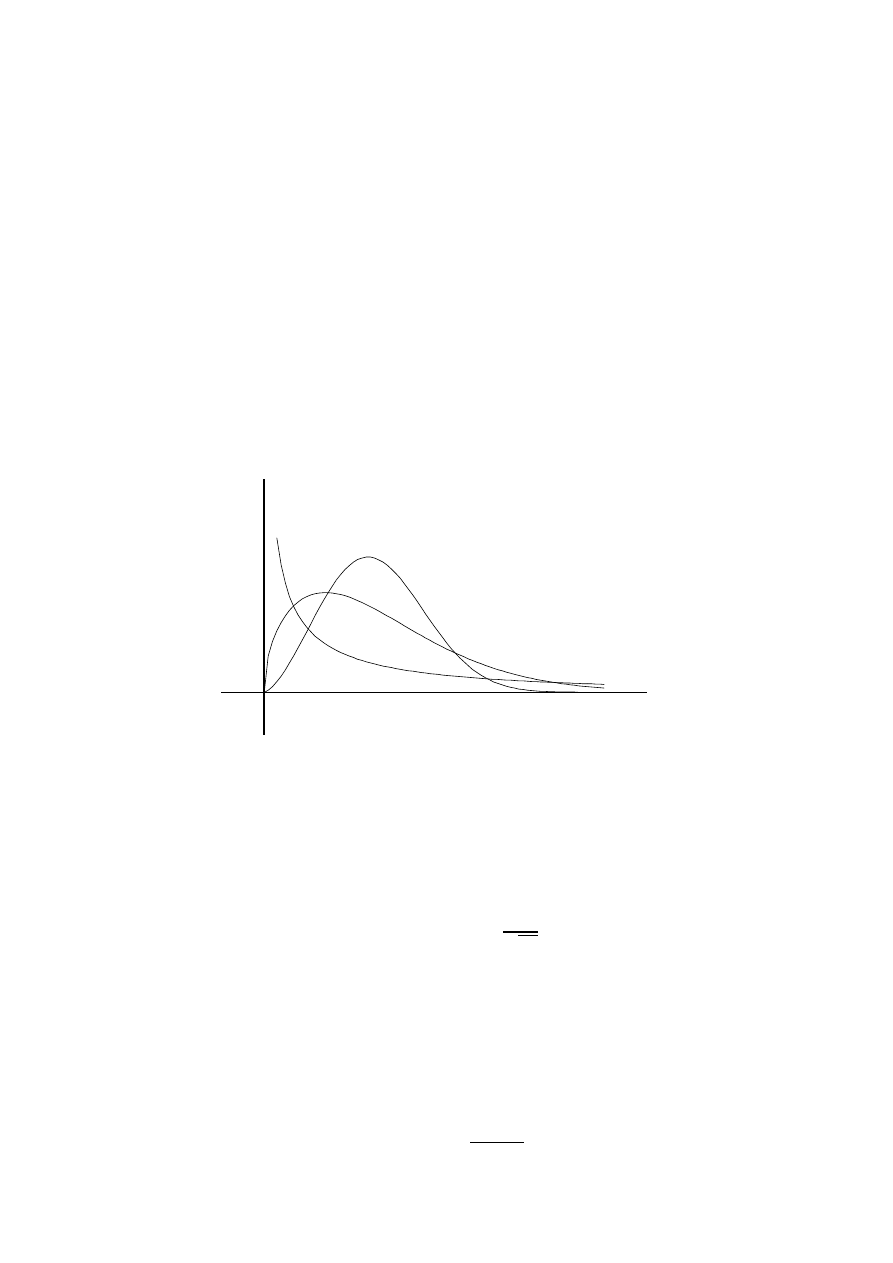
Rysunek 1: Prawdopodobie«stwo, »e

< d.

Niech

b¦dzie zdarzeniem polegaj¡cy na tym, »e

< d, tzn.

! :

< d

Nie na wszystkich zbiorach z

da si¦ okre±li¢ miar¦, ale tym zagadnieniem nie b¦dziemy

si¦ zajmowa¢

1.1 Aksjomaty prawdopodobie«stwa

Zbiór punktów le»y wewn¡trz obszaru obwiedzionego grubsz¡ lini¡ na rysun-

ku 1. Pole tego obszaru jest równe

Pr(

) = 1

Zaªó»my teraz, »e =

[

oraz wszystkie

i =

Klasyczna

denicja

prawdopodo-

bie«stwa

;2;:::;n s¡ wykluczaj¡ce si¦ i maj¡ to samo prawdopodobie«stwo, a wi¦c

Pr(

) = 1

=n. Wtedy dla dowolnego zdarzenie A b¦d¡cego sum¡ k zdarze«

postaci

, czyli dla

A = A

[

ma pradopodobie«stwo Pr(

A) = k=n.

Zdarzenia

A nazywa si¦ wtedy zdarzeniami sprzyjaj¡cymi zdarzeniu A, a

jego prawdopodobie«stwo jest równe stosunkowi liczby zdarze« sprzyjaj¡cych

do wszystkich

n zdarze«. Tak okre±lone prawdopodobie«stwo nosi tradycyjn¡

nazw¦ ÿklasycznej denicji prawdopodobie«stwa", cho¢ nie jest denicj¡, ale

pewnym bardzo szczególnym przypadkiem.

Zauwa»my, »e w tym wªa±nie przypadku

-algebr¦

wystarczy ograniczy¢ do

zdarze«

i ich wszystkich sum. Taka

-algebra jest rodzin¡ 2

zdarze«.

Przykªad.

Rzucamy

n razy monet¡. Niech A b¦dzie zdarzeniem polegaj¡cym

na wyrzuceniu

m orªów. Przestrzeni¡ zdarze« elementarnych mo»e tu by¢

zbiór wszystkich ci¡gów zero-jedynkowych dªugo±ci

n, gdzie jedynka to wyrzu-

cenie orªa, a zero to wyrzucenie reszki. Zdarzenia

= (

:::x

gdzie

i = (x

)

jest liczb¡ w postaci binarnej odpowiadaj¡cej takiemu

ci¡gowi, s¡ wzajemnie wykluczaj¡ce si¦ i maj¡ te same prawdopodobie«stwa.

Jest ich 2

. Zdarze« sprzyjaj¡cych zdarzeniu

A jest

. St¡d

Pr(

A) =

1.1.4. Zadania

Do±wiadczenie polega na rzucaniu kostk¡ do gry, a» do wyrzucenia po raz

pierwszy sze±ciu oczek. Okre±li¢ przestrze« probabilistyczn¡.

Uogólni¢ zadanie 1 na przypadek rzucania

n kostkami, a» do wyrzucenia po

raz pierwszy co najmniej

k szóstek w jednym rzucie, k

W zadaniach 1 i 2 obliczy¢ prawdopodobie«stwo, »e liczba rzutów b¦dzie

równa

m, m = 1;2;::: .

Drut o dªugo±ci

l zgi¦to w dwóch niezale»nie wybranych punktach. Obliczy¢

prawdopodobie«stwo, »e mo»na w ten sposób utworzy¢ trójk¡t.

Z odcinka [0

;1] wybieramy losowo dwie liczby p i q. Jakie jest prawdo-

podobie«stwo tego, »e równanie

px + q = 0 b¦dzie miaªo dwa sprz¦»one

pierwiastki zespolone? Jakie jest prawdopodobie«stwo tego, »e b¦dzie miaªo

dwa ró»ne pierwiastki rzeczywiste?

Dla jakich zdarze«

A i B zachodzi wzór

Pr(

[

B) = Pr(A) + Pr(B)

Pr(

B)?

1.1 Aksjomaty prawdopodobie«stwa

Udowodni¢, »e Pr(

[

B) = Pr(A) + Pr(B)

Pr(

B).

Wzoruj¡c si¦ na zadaniu 7, sformuªowa¢ wzór na Pr(

[

C) i spróbowa¢

go uogólni¢ na przypadek sumy

n zdarze«, tzn. znale¹¢ wzór na obliczenie

[

Udowodni¢, »e

;

nie wykonuj¡c rachunków.

10.

W urnie jest

3 biaªych i

3 czarnych kul. Obliczy¢ prawdopodo-

bie«stwo wylosowania trzech czarnych kul, gdy kule losujemy

a) bez zwracania,

b) ze zwracaniem.

1.2 Prawa wielkich liczb i symulacja

1.2. Prawa wielkich liczb i symulacja

1.2.1. Mocne i sªabe prawo wielkich liczb

Wedªug potocznych opinii, je»eli przeprowadzaj¡c

n obserwacji, zaobserwu-

jemy interesuj¡ce nas zjawisko

k razy, to prawdopodobie«stwo zaj±cia tego

zjawiska powinno wynosi¢

k=n. Iloraz ten jest cz¦sto przyjmowany za tzw.

ÿstatystyczn¡ denicj¦ prawdopodobie«stwa". Okre±lenie to nie jest caªkiem

poprawne, ale intuicyjnieuzasadnione, a poni»sze twierdzenia nadaj¡ mu ±cisªy

matematycznie charakter.

Twierdzenie 1.2.1.

Niech (

;

;Pr) b¦dzie przestrzeni¡ probabilistyczn¡, a

Mocne prawo

wielkich liczb

b¦dzie niesko«czonym ci¡giem zdarze« niezale»nych o tym samym

prawdopodobie«stwie Pr(

) =

p. Niech !

b¦dzie dowolnym, ale ustalo-

nym zdarzeniem elementarnym. Oznaczmy przez

N(n;!) liczb¦ tych zdarze«

, dla których

, gdy

i = 1;2;:::;n. Wtedy

! : lim

N(n;!)

n = p

= 1

(1.2.1)

Twierdzenie 1.2.2.

Przy oznaczeniach z twierdzenia 1.2.1 dla ka»dego

" > 0

Sªabe prawo

wielkich liczb

zachodzi równo±¢

lim

! :

N(n;!)

> "

= 0

(1.2.2)

Twierdzenie 1.2.1 nosi nazw¦ mocnego prawa wielkich liczb, a twierdzenie 1.2.2

{ sªabego prawa wielkich liczb. Tak te» jest. Z mocnego prawa wielkich liczb

ªatwo jest wyprowadzi¢ sªabe prawo wielkichliczb. Dowodów tych nie b¦dziemy

tu przeprowadza¢, a sªabe prawo wielkich liczb udowodnimy po¹niej, w innej,

ªatwiejszej i ogólniejszej postaci. W tym momencie zajmiemy si¦ interpretacj¡

tych twierdze«.

W twierdzeniu 1.2.1 zdarzenie elementarne

! jest ustalonym do±wiadczeniem,

polegaj¡cym na niesko«czonymci¡gu obserwacji. W ka»dej obserwacji badamy,

czy zaszªo interesuj¡ce nas zjawisko, tzn. czy w

i-tej obserwacji byªo !

Tak wi¦c

N(n;!) jest liczb¡ zaobserwowanych zjawisk w pierwszych n obser-

wacjach, w ustalonym do±wiadczeniu

!. Równo±¢ (1.2.1) mówi, »e stosunek

liczby zjawisk zaobserwowanych w

n obserwacjach do liczby obserwacji równej

n, d¡»y do prawdopodobie«stwa zaobserwowania zjawiska przy jednej obser-

wacji dla prawie wszystkich do±wiadcze«, tzn. mog¡ si¦ zdarzy¢ do±wiadczenia,

w których nie zajdzie równo±¢ (1.2.1), ale stanie si¦ to z zerowym prawdopo-

dobie«stwem.

Podobny charakter ma twierdzenie 1.2.2. Mówi ono, »e stosunek liczby zjawisk

zaobserwowanych w

n obserwacjach do liczby obserwacji ró»ni si¦ niewiele

od prawdopodobie«stwa zaobserwowania zjawiska przy jednej obserwacji, tzn.

prawdopodobie«stwo, »e ró»ni si¦ wi¦cej ni» dowolnie maªa liczba

", d¡»y do

zera, a wi¦c jest dowolnie maªe, je±li tylko we¹miemy dostatecznie du»e

1.2 Prawa wielkich liczb i symulacja

Przykªad.

Rzucamy

n razy kostk¡ do gry, a n jest ÿbardzo du»e". Je»eli liczba

wyrzuconych szóstek

N(n) daje nam N(n)=n znacznie ró»ni¡ce si¦ od 1/6, to

w my±l twiedzenia 1.2.2 albo zabserwowali±my zjawisko rzadkie, które powinno

zdarzy¢ si¦ z maªym prawdopodobie«stwem (dokªadniej, z prawdopodobie«-

stwem d¡»¡cym do zera) albo kostka jest faªszywa, tzn. prawdopodobie«stwo

wyrzucenia szóstki jest ró»ne od 1/6. Twierdzenie 1.2.1 mówi za± wi¦cej { za-

obserwowali±my zjawisko, które zdarzy¢ si¦ w ogóle nie powinno, bo mo»e zaj±¢

z prawdopodobie«stwem zero, cho¢ oczywi±cie tylko w granicy, przy

1.2.2. Pierwsze przykªady symulacji

Przedstawimy tu dwa przykªady wykorzystania praw wielkich liczb do symu-

lacji, zwanej metod¡ Monte-Carlo.

Przykªad.

Na pªaszczyzn¦ poliniowan¡ liniami równolegªymi, odlegªymi od

Igªa Buona

siebie o 1, rzucamy losowo igª¦ o dªugo±ci 1. Jakie jest prawdopodobie«stwo,

»e igªa przetnie lini¦?

Aby rozwi¡za¢ ten przykªad, musimy sprecyzowa¢, co rozumiemy przez okre-

±lenie ÿna poliniowan¡ pªaszczyzn¦ rzucamy losowo igª¦ o danej dªugo±ci". W

tym celu zaªó»my, »e linie na pªaszczyznie s¡ uªo»one poziomo oraz wpro-

wad¹my oznaczenia:

x { odlegªo±¢ dolnego ko«ca igªy od najbli»szej linii pod

igª¡,

{ k¡t mi¦dzy ligª¡ a lini¡, 0

< . Poªo»enie igªy jest teraz okre-

±lone przez par¦ liczb (

x;). Losowo±¢ rzutu na pªaszczyzn¦ rozumiemy w tym

przykªadzie jako umieszczenie punktu (

x;) w prostok¡cie [0;1]

;], zgod-

nie z geometryczn¡ denicj¡ prawdopodobie«stwa. Niech

A b¦dzie zdarzeniem

polegaj¡cym na tym, »e igªa przetnie lini¦.

Igªa przecina lini¦ wtedy, gdy sin

> 1

x. Poniewa» pole obszaru speªniaj¡-

cego ten warunek jest równe

sin

d = 2;

a pole prostok¡ta jest równe

, to Pr(A) = 2=. Je»eli teraz r

;::: b¦-

dzie niezale»nym ci¡giem punktów, ka»dy z odcinka [0

;1] wybranym zgodnie z

geometryczn¡ denicj¡ prawdopodobie«stwa, to ci¡g (

)

;(r

)

;::: b¦-

dzie niezale»nym ci¡giem punktów, ka»dy z prostok¡ta [0

;1]

;] wybranym

zgodnie z geometryczn¡ denicj¡ prawdopodobie«stwa. Niech teraz

b¦dzie

zdarzeniem polegaj¡cym na tym, »e w

i-tym rzucie igªa przetnie lini¦. Zgodnie

z twierdzeniem 1.2.1 i przyj¦tymi w nim oznaczeniami, ze wzoru (1.2.1) wy-

nika, »e dokonuj¡c coraz to wi¦kszej liczby rzutów, stosunek ich liczby

n do

liczby tych rzutów

k w których igªa przeci¦ªa lini¦, n=k, b¦dzie d¡»yª prawie

zawsze do

=2. Dla n sko«czonego, n=k b¦dzie tylko przybl»eniem liczby , o

losowym bª¦dzie. Oszacowaniem tego bª¦du zajmiemy si¦ po¹niej.

Symulacja polega na dokonaniu takiego eksperymentu i obliczeniu

n=k. Gdy

punkty

s¡ otrzymywane nie z zycznego eksperymentu, a generowane s¡ na

1.2 Prawa wielkich liczb i symulacja

drodze programowej, to taki komputerowy eksperyment daje wygodn¡ i ta-

ni¡ metod¦ otrzymywania przybli»e« { w wielu przypadkach wygodniejsz¡ od

czysto numerycznych oblicze«.

Pzykªad ten nie ma praktycznego znaczenia. Warto±¢ liczby

jest znana z wy-

starczaj¡c¡ dokªadno±ci¡, lepsz¡ od mo»liwej do otrzymania metod¡ symulacji.

Nast¦pny przykªad mo»e mie¢ ju» znaczenie nieco bardziej praktyczne.

Przykªad.

Obliczy¢ caªk¦

Caªka

obliczona

metod¡ Monte

Carlo

sin

1 +

dx;

(wykres funkcji podcaªkowej na rysunku 2).

Rysunek 2: Wykres funkcji z przykªadu

Caªki tej nie da si¦ obliczy¢ analitycznie. Metoda Monte Carlo polega na otrzy-

maniu ci¡gu

n niezale»nych punktów (x

) z prostok¡ta [0

;1]

;1], a na-

st¦pnie obliczeniu liczby

k tych punktów, które speªniaj¡ nierówno±¢

< e

sin

1 +

Wtedy na podstawie prawa wielkich liczb (twierdzenia 1.2.1 i 1.2.2) mo»na

przyj¡¢, »e

k=n

sin

1 +

dx;

gdy» maksimum funkcji podcaªkowej wynosi 1.

1.2 Prawa wielkich liczb i symulacja

Procedura

Symulacja

w Turbo

Pascalu

const n=1000;
var i,k:integer;

x,y:double;

begin

randomize;
k:=0;
for i:=1 to n do
begin

x:=random;
y:=random;
if y<exp(-sqr(sin(pi*x)))/(1+sqr(x)) then inc(k);

end;
writeln('Caªka=',k/n:0:4);

end;

daªa dla 5 kolejnych przebiegów

liczby:

0.5320, 0.4870 0.5340 0.4610 0.5160,

a ta sama procedura, ale dla

n = 10000 daªa

0.5045, 0.5011, 0.5046, 0.5006, 0.5045,

podczas gdy prawdziwa warto±¢ caªki (obliczona numerycznie przy pomocy

programu

Mathematica

) jest równa 0.503498.

1.2.3. Zadania

1*.

Niech b¦dzie kwadratem o boku 2

R oraz A b¦dzie koªem wpisanym w

ten kwadrat. Poda¢ metod¦ obliczania liczby

metod¡ Monte Carlo i napisa¢

odpowiedni¡ procedur¦ obliczaj¡c¡.

2*.

Obliczy¢ caªk¦

arctg(

sin

(1 + (

x) dx

metod¡ Monte Carlo.

3*.

Hipocykloida jest krzyw¡ zakre±lon¡ przez punkt okr¦gu koªa o promieniu

r tocz¡cego si¦ bez po±lizgu po wewn¦trznej stronie okr¦gu staªego koªa o

promieniu

R. Je»eli m = R=r > 2 jest liczb¡ caªkowit¡, to krzywa ta nie

przecina si¦ i ogranicza obszar wewn¡trz koªa. Dla

m = 4 krzywa taka jest

znana jako

asteroida

Napisa¢ procedury obliczaj¡ce metod¡ Monte Carlo pole ograniczone takimi

krzywymi dla

m > 2. Porówna¢ te wyniki z wynikami dokªadnymi. Dla m = 3

pole wynosi

S = 2r

, a dla

m = 4 pole wynosi S =

Dla nast¦pnych 5 przebiegów dostanie si¦ zapewne inne liczby

1.3 Prawdopodobie«stwo warunkowe

1.3. Prawdopodobie«stwo warunkowe

1.3.1. Denicja i podstawowe wªasno±ci

Prawdopodobie«stwem warunkowym zdarzenia

A jest prawdopodobie«stwo

tego samego zdarzenia

zwanego skutkiem, ale maj¡ce inn¡ warto±¢, zmody-

kowan¡ na podstawie informacji o innym zdarzeniu, zwanym przyczyn¡ lub

warunkiem. Nie ma natomiast poj¦cia zdarzenia warunkowego.

Denicja.

Prawdopodobie«stwo warunkowe zdarzenia

A pod warunkiem zda-

rzenia

B okre±lonwe jest wzorem

Pr(

B) = Pr(A

Pr(

B) ;

(1.3.1)

przy zaªo»eniu Pr(

B) > 0.

Bezpo±rednio z denicji otrzymuje si¦ nast¦puj¡cy

Fakt 1.3.1.

Pr(

B) = Pr(A

B)Pr(B);

(1.3.2)

dla Pr(

B) > 0.

Wªasno±¢ wyra»ona wzorem (1.3.2) jest bardzo u»yteczna w sytuacji, gdy

prawdopobie«stwa warunkowe s¡ znane w sposób naturalny, a nieznane s¡

prawdopodobie«stw iloczynów.

Przykªad.

W ciemnym pokoju mamy dwie urny: du»¡, do której traamy z

pradopodobie«stwem 3/4 i maª¡ do której traamy z prawdopodobie«stwem

1/4. W maªej urnie mamy 2 czarne i 1 biaª¡ kul¦, a du»ej 2 biaªe i 1 czarn¡

kul¦. Jakie jest prawdopobie«stwo, »e tramy na du»¡ urn¦ i równocze±nie

wyci¡gni¦ta z urny kula b¦dzie biaªa.

Rozwi¡zanie. Niech

A b¦dzie zdarzeniem polegaj¡cym na traeniu do du-

»ej urny,

B zdarzenie polegaj¡ce na wylosowaniu kuli biaªej. Jest jasne, »e

Pr(

A) = 2=3, a poniewa» Pr(A) = 3=4, to zgodnie ze wzorem (1.3.2) otrzy-

mujemy

Pr(

B) = 23

4 =

2 :

Prawdopodobie«stwo warunkowe ma wszystkie wªasno±ci ÿzwykªego" prawdo-

podobie«stwa, tzn. zachodzi nast¦puj¡ce twierdzenie.

Twierdzenie 1.3.1.

Dla dowolnej przestrzeni probabilistycznej (

;

;Pr)

i ustalonego

takiego, »e Pr(

B) > 0, prawdopodobie«stwo warun-

kowe Pr

(

) = Pr(

B) speªnia postulaty Koªmogorowa (1.1.2) { (1.1.4), tzn.

(

;

;Pr

) jest przestrzeni¡ probabilistyczn¡.

Intuicje dotycz¡ce prawdopodobie«stwa warunkowego zgodne s¡ z nast¦puj¡-

cym rezultatem.

Twierdzenie 1.3.2.

Je»eli zdarzenia

A i B s¡ niezale»ne i Pr(B) > 0, to

Pr(

B) = Pr(A):

1.3 Prawdopodobie«stwo warunkowe

1.3.2. Wzór Bayesa

Twierdzenia przedstawione w tym punkcie znane s¡ pod tradycyjn¡ nazw¡

wzorów. Trzeba jednak zwróci¢ uwag¦, »e wzory te s¡ prawdziwe tylko przy

speªnionych zaªo»eniach, wspólnych dla obydwóch twierdze«.

Twierdzenie 1.3.3.

(prawdopodobie«stwo caªkowite). Niech

b¦dzie ci¡-

Wzór na

prawdopodo-

bie«stwo

caªkowite

giem zdarze« takim, »e

;

dla

j oraz

Pr(

) = 1. Wtedy

Pr(

B) =

Pr(

)

P(A

)

(1.3.3)

Dowód.

Twierdzenie udowodnimy w szczególnym przypadku, gdy zaªo»enie

Pr(

) = 1 zast¡pimy mocniejszym:

= . Ze wzoru (1.3.2) otrzy-

mujemy zale»no±¢ Pr(

)

P(A

) = Pr(

B). Poniewa» A

s¡ rozª¡czne, to

równie» rozª¡czne s¡

oraz

B = B

. St¡d

Pr(

B) = Pr

[

= Pr

[

(

)

Pr(

)

P(A

)

Bezpo±rednio ze wzorów (1.3.1) i (1.3.2) otrzymuje si¦ nast¦puj¡ce

Twierdzenie 1.3.4.

(Bayesa

). Przy zaªo»eniach z twierdzenia 1.3.3 oraz

Wzór Bayesa

dla Pr(

B) > 0:

Pr(

B) = Pr(B

)Pr(

)

Pr(

;

(1.3.4)

gdzie Pr(

B) wyznaczone jest ze wzoru (1.3.3).

Przykªad.

Dwóch strzelców strzela do tarczy. Strzelec 1 traa z prawdopo-

dobie«stwem 2/3, a strzelec 2 z prawdopodobie«stwem 1/2. Po oddaniu po

jednym strzale okazaªo si¦, »e tarcza zostaªa traona dokªadnie raz. Jakie jest

prawdopodobie«stwo, »e traª strzelec 1?

Oznaczmy przez

fakt traenia w tarcz¦ przez obydwóch strzeleców,

{

przez pierwszego,

{ przez drugiego, a przez

przez »adnego. Poniewa»

strzelcy strzelaj¡ niezale»nie (to trzeba zaªo»y¢), to Pr(

) = 1

=3, Pr(A

) =

=3, Pr(A

) = 1

=6, Pr(A

) = 1

=6. Wszystkie te zdarzenia s¡ rozª¡czne, wi¦c

s¡ speªnione zaªo»enia twierdzenia 1.3.4. Przez

B oznaczmy fakt traenia w

tarcz¦ dokªadnie raz. Szukanym prawdopodobie«stwem jest

Pr(

[

B) = Pr(A

B);

gdy» Pr(

B) = 0. Wiadomo te», »e Pr(B

)Pr(

) = 1

=3 oraz

Pr(

)Pr(

) = 1

=6, pozostaªe prawdopodobie«stwa warunkowe s¡ równe

Thomas Bayes

1763

1.3 Prawdopodobie«stwo warunkowe

zeru. Tak wi¦c ze wzoru (1.3.3) otrzymujemy Pr(

B) = 1=2. Ze wzoru Bayesa

(1.3.4) wynika, »e

Pr(

B) = 1=3

=2 ;

co jest szukanym prawdopodobie«stwem.

Wyst¦puj¡ce w nast¦pnym punkcie zadania 1 i 2 równie» s¡ typowymi zasto-

sowaniami wzoru na prawdopodobie«stwo caªkowite i wzoru Bayesa.

1.3.3. Zadania

W ka»dej z trzech urn s¡ po cztery kule { w urnie

i-tej jest i kul biaªych,

a reszta czarnych. Z urny pierwszej losujemy jedn¡ kul¦ i przekªadamy do

drugiej, z drugiej losujemy jedn¡ kul¦ i przekªadamy do trzeciej, a w ko«cu z

trzeciej urny losujemy jedn¡ kul¦. Jakie jest prawdopodobie«stwo, »e b¦dzie

to kula biaªa?

W urnie pierwszej s¡ 2 dwie biaªe i dwie czarne kule, a w drugiej jedna

biaªa i trzy czarne kule. Z ka»dej urny losujemy po jednej kuli i nast¦pnie

losujemy z nich jedn¡ kul¦. Okazaªo si¦, »e wylosowali±my kul¦ biaª¡. Jakie

jest prawdopodobie«stwo, »e kula ta pochodziªa z pierwszej urny.

Udowodni¢, »e je±li Pr(

B) = Pr(A

), to zdarzenia

A i B s¡ niezale»ne.

Przy szeregowej transmisji danych do ka»dego bajtu dodawany jest jeden bit

tak, aby liczba jedynek byªa parzysta. Prawdopodobie«stwo przekªamania dla

ka»dego bitu wynosi

p. Obliczy¢ prawdopodobie«stwo niewykrycia przekªama-

nia { dokªadne dla dowolnego

p oraz przybli»one, gdy p jest bardzo maªe.

2. Zmienne losowe

2.1. Rozkªady zmiennych losowych

2.1.1. Denicja zmiennej losowej

Formuªowanie problemów wyª¡cznie w terminach przestrzeni zdarze« elemen-

tarnych,

-algebry zdarze« i prawdopodobie«stwa okre±lanego bezpo±rednio

na zdarzeniach, nie jest zbyt wygodne. Cz¦sto bowiem zamiast okre±lenia ca-

ªej przestrzeni probabilistycznej (

;

;Pr), wystarczy okre±li¢ charakterystyki

liczbowe zdarze« elementarnych, bez opisywania samych zdarze«. Na przykªad

je±li przy rzutach monet¡ interesuje nas tylko liczba wyrzuconych orªów, to

zamiast opisywa¢ rzut monet¡ w terminach orªów i reszek, mo»na zast¡pi¢

je zerami i jedynkami i dodawa¢ tylko te ÿlosowe" liczby. Co to wi¦c s¡ te

ÿlosowe" liczby? Potrzebna jest tutaj nast¦puj¡ca denicja.

Denicja.

Zmienn¡ losow¡ nazywamy funkcj¦ okre±lon¡ na przestrzeni zda-

Zmienna

losowa

rze« elementarnych i przyjmuj¡c¡ warto±ci rzeczywiste:

X :

;

tak¡, »e

! : X(!) < x

;

(2.1.1)

dla ka»dego

Zamiast pisa¢

A =

! : X(!) < x

b¦dzie pisa¢ w skrócie

A =

X < x

Denicja powy»sza zapewnia nam, »e mo»na powiedzie¢: ÿzdarzenie polegaj¡ce

na tym, »e

X < x".

Bezpo±redno z denicji wynika równie», »e zdarzeniami s¡ równie» zbiory:

! : X(!)

;

! : X(!) > x

;

! : X(!)

;

! : X(!) = x

;

! : X(!)

[

a;b]

;

! : X(!)

[

a;b)

;

! : X(!)

(

a;b]

;

! : X(!)

(

a;b)

Równie» w tych przypadkach najcz¦±ciej stosowa¢ b¦dziemy skrótowy zapis,

np.

;1]

zamiast peªnego

! : X(!)

;1]

, pami¦taj¡c jednak

zawsze, »e

X = X(!), czyli »e zmienna losowa jest funkcj¡ zdarze« elementar-

nych.

B¦dziemy równie» równie» pisa¢ Pr(

X < x) zamiast

! : X(!) < x

. Podob-

nie we wszystkich dalszych przypadkach.

2.1 Rozkªady zmiennych losowych

Na zmiennych losowych mo»na dokonywa¢ rozmaitych operacji, co precyzuje

nast¦puj¡ce twierdzenie.

Twierdzenie 2.1.1.

Je»eli

X(!) jest zmienn¡ losow¡, a h(x) jest funkcj¡ prze-

dziaªami ci¡gª¡, której dziedzina zawiera zbiór warto±ci

X, to Y (!) = h(X(!))

jest te» zmienn¡ losow¡ okre±lon¡ na tej samej przestrzeni probabilistycznej co

2.1.2. Dystrybuanta zmiennej losowej

Denicja zmiennej losowej zapewnia nam poprawno±¢ denicji podanej ni»ej.

Denicja.

Dystrybuant¡ nazywamy funkcj¦ rzeczywist¡ zmiennej rzeczywi-

Dystrybuanta

stej, okre±lon¡ wzorem

F(x) = Pr(

! : X(!) < x

) = Pr(

X < x):

(2.1.2)

Twierdzenie 2.1.2.

Funkcja

F jest dystrybuant¡ pewnej zmiennej losowej

Warunki

konieczne

i dostateczne

wtedy i tylko wtedy, gdy

(a) jest niemalej¡ca,

(b) lim

!,1

= 0, lim

= 1,

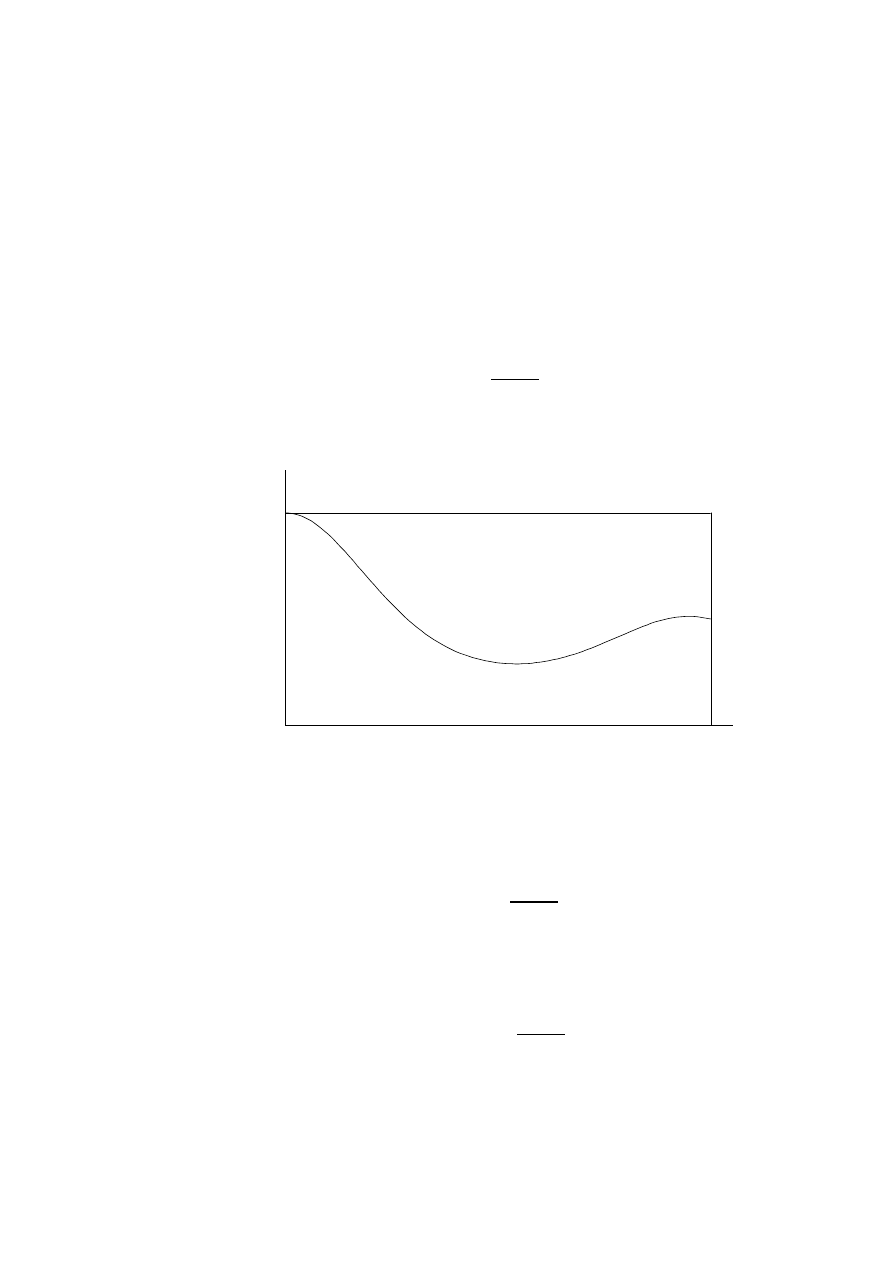
Przykªad.

Nale»y dobra¢ staªe

A, B, C, D, E i F tak, aby funkcja

F(x) =

dla

x <

C dla

Dx + E dla 0 < x

dla

x > 1

byªa dystrybuant¡ pewnej zmiennej losowej. Trzeba wi¦c staªe dobra¢ tak, aby

byªy speªnione warunki (a) { (c) w twierdzeniu 2.1.2. Najpierw sprawdzimy

warunek (b). Wynika z niego, »e musi by¢

A = 0 oraz F = 1. Na to, aby dla

x =

1 byª speªniony warunek (c),

F(x) musi by¢ lewostronnie ci¡gªa w tym

punkcie, a wi¦c musiby¢ równie» ci¡gªa, (bo inaczej byªaby tylko prawostronnie

ci¡gªa) co oznacza, »e

B +C = 0. Dla speªnienia warunku (a) na odcinku [0;1]

trzeba przyj¡¢, »e

0, a wi¦c równie»

0. Dalej, w punktach

x = 0

x = 1 funkcja F(x) jest zawsze lewostronnie ci¡gªa, wystarczy wi¦c sprawdzi¢

warunek (a). Oznacza to, »e

0 oraz

E. Tak wi¦c tylko

dwa parametry s¡ wyznaczone jednoznacznie, (

A = 0 i F = 1), a pozostaªe s¡

okre±lone przy pomocy ukªadu nierówno±ci i równo±ci. Na rysunku 3 pokazany

jest wykres takiej dystrybuanty dla

B =

:25, C =

B = 0:25, D = 0:25,

E = 0:5.

Przy pomocy dystrybuanty mo»na okre±li¢ prawdopodobie«stwa zdarze«, o

2.1 Rozkªady zmiennych losowych

-1

0.25

0.5

0.75

Rysunek 3: Wykres dystrybuanty z przykªadu

których byªa mowa punkcie 2.1.1.

Pr(

x) = lim

F(t) = F(x

)

;

Pr(

X < x

) =

F(x

)

F(x

)

;

Pr(

X = x) = F(x

)

F(x);

Pr(

X > x) = 1

F(x

)

i tak dalej.

W±ród zmiennych losowych mo»na, ze wzgl¦du na posta¢ dystrybuanty, wy-

ró»ni¢ dwa typy:

zmiennelosowe typu skokowego (zmiennelosowe dyskretne),których dys-

trybuanta jest przedziaªami staªa, a ponadto ma tylko skoki w punktach

{ taka zmienna losowa mo»e przyjmowa¢ (z prawdopodobie«stwem 1)

tylko warto±ci

zmienne losowe typu ci¡gªego, których dystrybuant¦

F(x) mo»na przed-

stawi¢ w postaci

F(x) =

f(t)dt:

(2.1.3)

Funkcj¦

f(x) okre±lon¡ wzorem (2.1.3) nazywa si¦ g¦sto±ci¡.

Uwaga.

Nie ma zmiennych losowych ci¡gªych, bo nie s¡ one funkcjami zmien-

nej rzeczywistej, a mog¡ by¢ okre±lone na zbiorach dowolnej natury. S¡ tylko

zmienne losowe

typu ci¡gªego

, tzn. takie, które maj¡ g¦sto±¢.

Wªasno±ci g¦sto±ci omówimy dokªadniej w nast¦pnym punkcie.

Rozkªadem zmiennej losowej okre±lamy jej dystrybuant¦ lub inne funkcje w

peªni j¡ chakteryzuj¡ce, np. g¦sto±¢ dla zmiennej losowej typu ci¡gªego lub

prawdopodobie«stwa

= Pr(

X = x

) dla zmiennej losowej dyskretnej.

2.1 Rozkªady zmiennych losowych

W dwóch nast¦pnych punktach omówimy najwa»niejsze rozkªady dyskretne

i rozkªady typu ci¡gªego.

Niezale»no±¢ zmiennych losowych deniuje si¦ przy pomocy niezale»no±ci zda-

Niezale»no±¢

rze« lub przy pomocy dystrybuant. Tutaj podamy tylko denicj¦ niezale»no±ci

dwóch zmiennych losowych, cz¦±ciowo w terminach dystrybuant. Ogólna de-

nicja zostanie podana pó¹niej, przy okazji rozpatrywania wektorów losowych

i ich dystrybuant.

Denicja.

Zmienne losowe

X i Y s¡ niezale»ne, gdy

Pr(

X < x;Y < y) = F(x)G(y);

gdzie

F jest dystrybuant¡ zmiennej losowej X, a G { zmiennej losowej Y .

2.1.3. G¦sto±¢

Wzór (2.1.3) deniuje g¦sto±¢ rozkªadu. Mówi si¦ te» w przypadku, gdy

F(x)

jest dystrybuant¡ zmiennej losowej

X, »e f(x) jest g¦sto±ci¡ zmiennej losowej

X mimo, »e X nie wyst¦puje jawnie w denicji g¦sto±ci.

Podobnie jak twierdzenie 2.1.2 podaje warunki konieczne i dostateczne na

Warunki

konieczne

i dostateczne

to, aby dana funkcja byªa dystrybuant¡, poni»sze twierdzenie podaje warunki

konieczne i dostateczne na to, aby funkcja byªa g¦sto±ci¡.

Twierdzenie 2.1.3.

Funkcja

f(x) jest g¦sto±ci¡ pewnej zmiennej losowej

wtedy i tylko wtedy, gdy

(A)

f(x)

(B)

f(x)dx = 1.

Nale»y zwróci¢ uwag¦, »e g¦sto±¢ nie musi by¢ okre±lona jednoznacznie, ponie-

wa» mo»na w dowolny sposób ustali¢ jej warto±¢ w sko«czonej liczbie punktów.

Dzieje si¦ tak, gdy» zarówno we wzorze (2.1.3) deniuj¡cym g¦sto±¢ jak i w wa-

runku (B) w twierdzeniu 2.1.3, warto±ci caªek nie zmieniaj¡ si¦ przy zmianie

warto±ci funkcji podcaªkowej w sko«czonej liczbie punktów. Przyjmuje si¦ jed-

nak zawsze, »e speªniony jest warunek (A) w twierdzeniu 2.1.3.

Bezpo±rednim wnioskiem ze wzoru (2.1.3) jest

Wzór na

g¦sto±¢

2.1 Rozkªady zmiennych losowych

byªa g¦sto±ci¡ pewnej zmiennej losowej. Trzeba wi¦c dobra¢ staªe tak, aby byª

speªniony warunek (A) w twierdzeniu 2.1.3, sk¡d wynika

0 oraz

=2.

Dla speªnienia warunku (B) w tym twierdzeniu, musi by¢ speªniona równo±¢

cos

xdx = 1:

St¡d po obliczeniu caªki otrzymujemy warunek

asinb = 1, przy czym a > 0.

Za pomoc¡ g¦sto±ci mo»na ªatwo wyznaczy¢ prawdopodobie«stwo nale»enia

warto±ci zmiennej losowej do zbioru.

Twierdzenie 2.1.4.

Je»eli zmienna losowa

X ma g¦sto±¢ f(x), to

Pr(

[

a;b]) = Pr(X

[

a;b))

= Pr(

(

a;b]) = Pr(X

(

a;b)) =

f(x)dx:

(2.1.5)

2.1.4. Zadania

Dla jakich parametrów

a i b funkcja F(x) = aarctgx+b jest dystrybuant¡

pewnej zmiennej losowej?

Niech

F(x) =

(

; dla x

;

dla

x < 0,

b¦dzie dystrybuant¡ zmiennej losowej

X, (sprawdzi¢, »e jest to dystrybuanta).

Wyznaczy¢ Pr(

X > 1), Pr(1 < X

2), Pr(

X = 3).

Dla jakich warto±ci

a i b funkcja f(x) =

1 + (

bx)

jest g¦sto±ci¡ pewnej

zmiennej losowej? Wyznaczy¢ dystrybuant¦.

Niech dystrybuanta

F(x) zmiennej losowej X b¦dzie funkcj¡ ±ci±le rosn¡c¡ i

ci¡gª¡, a funkcja

h(x) b¦dzie ró»nowarto±ciowa. Znale¹¢ dystrybuant¦ zmiennej

losowej

h(X).

Niech

f(x) =

(

a dla x

;],

0 dla

x =

;]

b¦dzie g¦sto±ci¡ zmiennej losowej

X. Wyznaczy¢ a, znale¹¢ dystrybuant¦

zmiennej losowej

X oraz korzystaj¡c z zadania 4 znale¹¢ dystrybuant¦ i g¦sto±¢

zmiennej losowej

Y = sinX.

2.2 Momenty zmiennych losowych

2.2. Momenty zmiennych losowych

2.2.1. Caªka Stieltjesa

Podana w tym punkcie denicja caªki Stieltjesa

jest uogólnieniem zwykªej

caªki. Jej u»ycie umo»liwia podanie jednolitej denicji momentów zmiennych

losowych, zarówno dla typu ci¡gªego, jak i skokowego.

Denicja.

Zaªó»my, »e dystrybuanta

F(x) jest przedziaªami ci¡gªa i ró»nicz-

kowalna. Caªk¡ Stieltjesa z funkcji

g(x) wzgl¦dem dystrybuanty F(x) nazy-

wamy liczb¦, okre±lon¡ wzorem

Caªka

Stieltjesa

g(x)dF(x) =

g(x)dF(x)

dx dx +

g(x

)

F(x

)

F(x

)

; (2.2.1)

gdzie

s¡ punktami skoków dystrybuanty

F(x), pomi¦dzy którymi jest ona

ci¡gªa i ró»niczkowalna.

Je»eli dystrybuanta

F(x) ma g¦sto±¢, to we wzorze (2.2.1) znika suma, (bo

Przypadki

szczególne

caªki Stieltjesa

dystrybuanta jest ci¡gªa, wi¦c skoki s¡ równe zeru), a caªka Stieltjesa sprowa-

dza si¦ do zwykªej caªki Riemanna. Je±li natomiast zmienna losowa jest typu

skokowego, to pochodna pomi¦dzy skokami jest równa zeru, (bo dystrybuanta

jest tam staªa), a caªka Stieltjesa redukuje si¦ we wzorze (2.2.1) do sumy.

Przykªad.

Okre±lmy dystrybuant¦

F(x) wzorem

F(x) =

(

dla

=2 dla x > 0.

Wtedy skok w zerze

F(0

)

F(0) = 1=2, caªka w przedziale (

;0) jest

równa zeru, a wi¦c

(

x + 1)dF(x) = 12

(

x + 1)e

dx + 12 =

2 :

2.2.2. Warto±¢ oczekiwana

Warto±¢ oczekiwana zmiennej losowej, zwana te» nadziej¡ matematyczn¡, war-

to±ci¡ ±redni¡ lub przeci¦tn¡, nale»y do podstawowych poj¦¢ rachunku praw-

dopodobie«stwa.

Denicja.

Warto±ci¡ oczekiwan¡ zmiennej losowej

g(X) o dystrybuancie

F(x) = Pr(X < x) jest liczba oznaczana jako Eg(X) i okre±lona wzorem

g(X) =

g(x)dF(x);

(2.2.2)

Thomas Stieltjes, (1856-1895), matematyk holenderski.

2.2 Momenty zmiennych losowych

o ile caªka we wzorze (2.2.2) jest bezwzgl¦dnie zbie»na, to znaczy je»eli istnieje

caªka

g(x)

dF(x):

(2.2.3)

Je»eli zmienna losowa jest typu ci¡gªego o g¦sto±ci

f(x), to warto±¢ oczekiwana

Warto±¢

oczekiwana {

przypadki

szczególne

zamiast wzorem (2.2.2), wyra»a si¦ wzorem

g(X) =

g(x)f(x)dx;

a je±li jest dyskretna, to wzorem

g(X) =

g(x

)

;

gdzie

= Pr(

X = x

). Oczywi±cie w obydwóch tych przypadkach, suma lub

caªka musi by¢ bezwzgl¦dnie zbie»na.

Je»eli caªka (2.2.2) nie istnieje lub je±li istnieje, ale nie jest bezwzgl¦dnie

zbie»na, a wi¦c nie istnieje caªka (2.2.3), to mówimy, »e warto±¢ oczekiwana

nie istnieje. W przypadku, gdy

g(x)

0 i nie istnieje warto±¢ oczekiwana, to

mówi si¦ te», warto±¢ oczekiwana jest niesko«czona.

W pewnych przypadkach mo»na ªatwo stwierdzi¢, »e warto±¢ oczekiwana ist-

nieje. Przykªadem s¡ tu dwa, ªatwe do udowodnienia fakty.

Fakt 2.2.1.

Je±li zmienna losowa

X ma g¦sto±¢ f(x), która jest równa zeru

poza pewnym ograniczonym zbiorem na prostej rzeczywistej, (tzn. istnieje od-

cinek (

a;b) taki, »e je±li x =

(

a;b), to f(x) = 0) oraz je±li g(x) jest ograniczona

na tym zbiorze, to istnieje E

g(X).

Fakt 2.2.2.

Je±li zmiennalosowa dyskretna

X przybiera tylkosko«czon¡ liczb¦

warto±ci

, to warto±¢ oczekiwana E

g(X) istnieje.

Poni»ej przedstawione zostan¡ dwa najprostsze, ale bardzo wa»ne przykªady.

Przykªad.

Rozkªad zero-jedynkowy: Pr(

X = 1) = p, Pr(X = 0) = q = 1

a wi¦c zmienna losowa

X nie przyjmuje innych warto±ci ni» 0 i 1.

X = 0

q + 1

p = p:

Przykªad.

Rozkªad jednostajny na odcinku [0

;1]:

f(x) =

(

1 dla

;1],

0 dla

x =

;1].

Warto±¢ oczekiwana istnieje (patrz fakt 2.2.2) i wyra»a si¦ wzorem

X =

xdx = 12 :

2.2 Momenty zmiennych losowych

Dla warto±ci oczekiwanych prawdziwa jest wªasno±¢ taka jak dla caªek, któr¡

mo»na sªownie sformuªowa¢ nast¦puj¡co:

warto±¢ oczekiwana sumy jest równa sumie warto±ci oczekiwanych, (o ile

warto±ci oczekiwane istniej¡),

staª¡ mo»na wyci¡gn¡¢ przed znak warto±ci oczekiwanej.

Formalnie sformuªujemy to w postaci twierdzenia.

Operator

liniowy

Twierdzenie 2.2.1.

Je»eli istniej¡ E

X i EY , to istnieje E(aX + bY ) oraz

aX + bY ) = aEX + bEY ;

(2.2.4)

czyli warto±¢ oczekiwana jest

operatorem liniowym

Podobnie jak dla caªek, nie ma ogólnej reguªy, jak oblicza¢ warto±¢ oczeki-

Warto±¢

oczekiwana

iloczynu

wan¡ iloczynu zmiennych losowych. Reguªa taka istnieje tylko dla niezale»nych

zmiennych losowych.

Twierdzenie 2.2.2.

Je»eli zmienne losowe

X i Y s¡ niezale»ne, to

XY ) = (EX)(EY ):

(2.2.5)

Warto±¢ oczekiwana zmiennej losowej

X, nazywa si¦ momentem rz¦du pierw-

szego i oznaczana jest bardzo cz¦sto symbolem

m = m

= E

2.2.3. Momenty wy»szych rz¦dów

Momentem rz¦du

k, czyli momentem k-tego rz¦du lub krótko, k-tym momen-

Moment

zwykªy

tem zmiennej losowej

X jest warto±¢ oczekiwana jej k-tej pot¦gi, czyli EX

Moment rz¦du

k jest cz¦sto oznaczany symbolem m

. Moment ten nazywany

jest momentem zwykªym, dla odró»nienia od innego rodzaju momentów oma-

wianych dalej.

Przykªad.

Dla zmiennej losowej zero-jedynkowej

= E

= 0

p + 1

q = p:

Przykªad.

Dla zmiennej losowej rozkªadzie jednostajnym na [0

;1]

= E

dx = 1

k + 1 :

Dalej deniuje si¦ moment centralny rz¦du

k, (k-ty moment centralny), wzo-

Wariancja

rem

= E(

. Przypadek

k = 2 ma szczególn¡ rol¦ w rachunku

prawdopodobie«stwa. Moment centralny drugiego rz¦du nazywa si¦ wariancj¡

i jest oznaczany symbolem D

2.2 Momenty zmiennych losowych

X = E(X

(2.2.6)

Ze denicji wariancji wynika w szczególno±ci, »e D

0. Na oznaczenie

Wariancja jest

nieujemna!

wariancji u»ywany jest te» symbol Var

X. Z wariancj¡ zwi¡zana jest wa»na

charakterystyka, zwana ±rednim odchyleniem standardowym lub dyspersj¡,

oznaczona symbolem

i okre±lana jako pierwiastek z wariancji: =

Z istnienia momentów wy»szych rz¦dów wynika istnienie momentów ni»szych

rz¦dów.

Twierdzenie 2.2.3.

Je»eli istnieje E

oraz

l < k, to istnieje EX

Dla wariancji nie jest prawdziwy bez dodatkowych zaªo»e« odpowiednik twier-

dzenia 2.2.1. Mo»na jednak sformuªowa¢ twierdzenie nast¦puj¡ce.

Twierdzenie 2.2.4.

(

aX) = a

X ;

(2.2.7)

a je»eli zmienne losowe

X i Y s¡ niezale»ne, to

(

X + Y ) = D

X + D

(2.2.8)

lub oznaczaj¡c

X i

Y ,

Wariancja zmienne losowej

X, a zwªaszcza jej dyspersja, jest miar¡ odchylenia

si¦ zmiennej od jej ±redniej warto±ci, czyli miar¡ rozrzutu. Interpretacja taka

wynika bezpo±rednio ze wzoru (2.2.6). Wariancj¦ ªatwiej ni» ze wzoru (2.2.6),

mo»na obliczy¢ korzystaj¡c z nast¦puj¡cej wªasno±ci.

Fakt 2.2.3.

X = EX

(2.2.9)

albo równowa»nie

Dowód.

Ze wzoru (2.2.6) wynika, »e

X = E

XEX + (EX)

= E

X + m

Nast¦pnie z twierdzenia 2.2.1 wynika, »e

X = EX

X + m

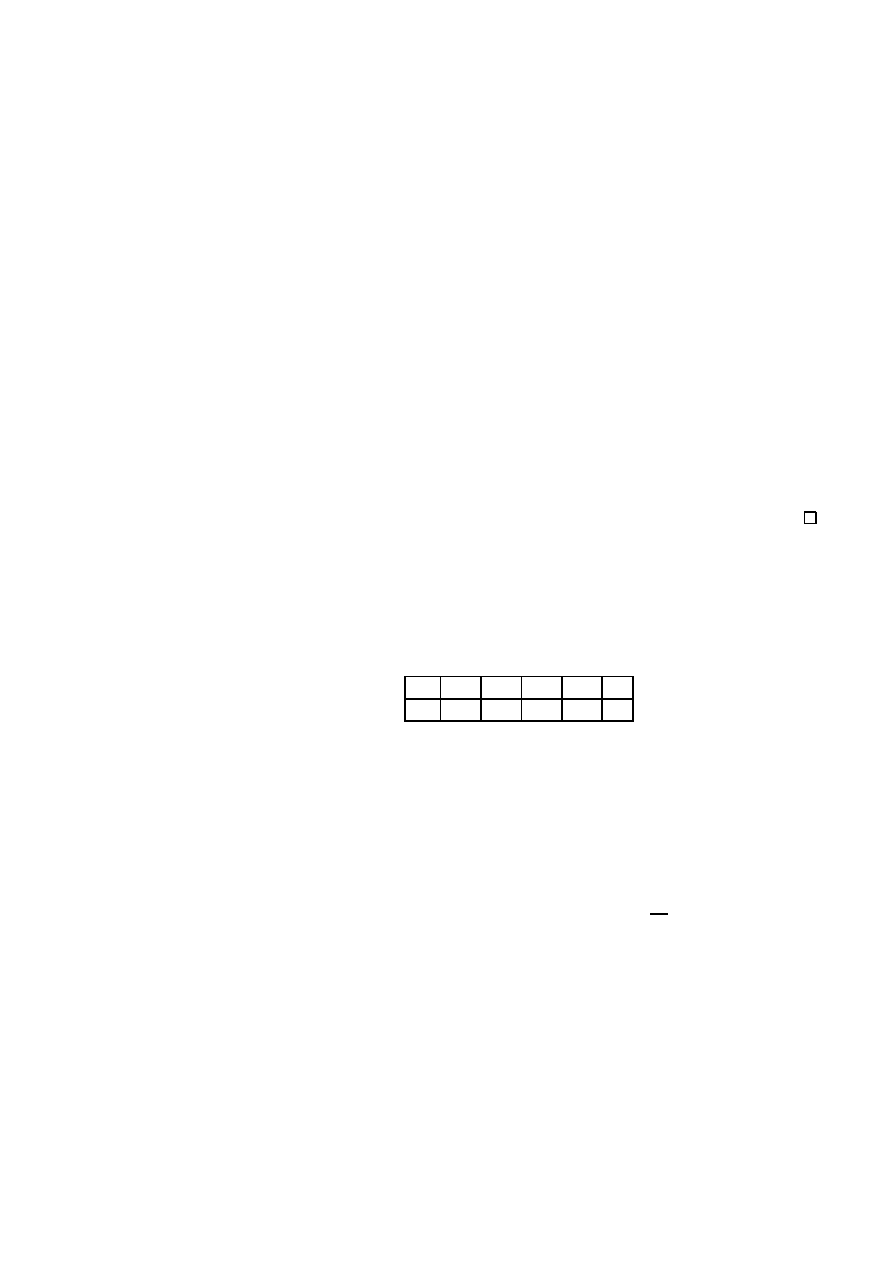
2.2 Momenty zmiennych losowych

Ponadto mamy nast¦puj¡cy

Fakt 2.2.4.

X = 0 wtedy i tylko wtedy, gdy zmienna losowa X przyjmuje

warto±¢ staª¡ z prawdopodobie«swem 1, to znaczy, gdy Pr(

X = x

) = 1 dla

pewnej warto±ci

Dowód.

Je»eli Pr(

X = x

) = 1, to

oraz

, a wi¦c D

X = 0.

Z drugiej strony, je±li D

= 0, to oczywi±cie D

X > 0. Przypu±¢my, »e

X = 0, a równocze±nie Pr(X = x

)

< 1. Ze wzoru (2.2.6) otrzymujemy

= D

X =

(

dF(x)

;

gdy» (

0, przy czym

= 0 tylko wtedy, gdy funkcja podcaªkowa jest

to»samo±ciowo równa zeru, (co nie jest prawd¡) albo gdy w dokªadnie jednym

punkcie

m dystrybuanta F(x) ma skok równy 1, czyli F(x

)

F(x

) =

2.2.4. Zadania

Niech

R b¦dzie zmienn¡ losow¡ o rozkªadzie jednostajnym na odcinku [0;1].

Obliczy¢ momenty zwykªe i centralne

k-tego rz¦du.

Zmienna losowa

X ma rozkªad dany tabel¡:

0 1 2 3 4

:2 0:1 0:1 0:3 A

Znale¹¢ staª¡

A, a nast¦pnie warto±¢ oczekiwan¡ oraz wariancj¦ zmiennych X

Y = sin(X=2).

Rzucamy trzy razy monet¡. Niech

X b¦dzie liczb¡ wyrzuconych orªów.

Obliczy¢ E

X i D

Zmiennalosowa

X przyjmujetylko warto±ci 2

dla

k = 1;2;::: oraz Pr(X =

) = 4

. Znale¹¢ E

X oraz D

X. Czy istnieje trzeci moment zmiennej X?

Zmienna losowa

X przyjmuje tylko warto±ci 3

dla

k = 1;2;::: oraz

Pr(

X = 3

) = 2

. Czy istnieje E

X? Obliczy¢ E

Rzucamy dwoma kostkami. Obliczy¢ warto±¢ oczekiwan¡ i wariancj¦ sumy

oczek.

2.3 Rozkªady dyskretne

2.3. Rozkªady dyskretne

2.3.1. Rozkªad dwupunktowy i dwumianowy

Zmienna losowa

X ma rozkªad dwupunktowy, gdy z prawdopodobie«stwem 1

przyjmuje tylko dwie warto±ci, tzn. je±li Pr(

X = x

) =

p i Pr(X = x

) =

p + q = 1. atwo policzy¢ momenty: EX = x

p + x

q, co w przypadku

p = q = 1=2 daje m = x

2 , czyli ±redni¡ arytmetyczn¡. Moment zwykªy

rz¦du

k wynosi m

p + x

Szczególnym przypadkiem rozkªadu dwupunktowego jest rozkªad zero-jedyn-

kowy, rozwa»any ju» w punkcie 2.2.2. Zajmiemy si¦ tym przypadkiem dokªad-

niej, bo mimo swej prostoty, (a mo»e wªa±nie dzi¦ki swej prostocie), jest on

podstaw¡ wielu dalszych rozwa»a«.

Niech

i = 1;2:::;n b¦dzie ci¡giemniezale»nychzmiennychlosowych o tym

Rozkªad zero-

jedynkowy

samym rozkªadzie zero-jedynkowym, Pr(

= 1) =

p, Pr(X

= 0) =

q = 1

Oznaczmy przez

X sum¦ n takich zmiennych losowych:

X = X

(2.3.1)

Z twierdze« 2.2.1 i 2.2.4 otrzymujemy równo±ci: E

X = np i D

X = npq, sk¡d

te»

npq.

Zbadajmy rozkªad zmiennej losowej

X, to znaczy obliczmy prawdopodobie«-

stwa Pr(

X = k) = p

. Przede wszystkim zauwa»my, »e

k mo»e zmienia¢ si¦

tylko od 0 do

n. Poniewa» zdarzenie

X = k

zachodzi wtedy i tylko wtedy,

gdy na dokªadnie

k pozycjach w sumie pojawi si¦ jedynka { prawdopodo-

bie«stwo tego wynosi

, a mo»liwych takich ukªadów

k jedynek w ci¡gu

n-elementowym jest

, to

Rozkªad

dwumianowy

Pr(

X = k) =

(2.3.2)

Wzór (2.3.2) okre±la rozkªad, znany jako rozkªad dwumianowy (gªównie w lite-

raturze anglosaskiej) lub rozkªad Bernoulliego

. Zmienn¡ losow¡

X okre±lon¡

wzorem (2.3.1) mo»na interpretowa¢ jako liczb¦ sukcesów (jedynek) w ci¡gu

niezale»nych do±wiadcze«, zwanych próbami Bernoulliego, gdzie prawdopodo-

bie«stwo sukcesu wynosi

p, a pora»ki (zera) wynosi q = 1

Przykªad.

Wykonujemy ci¡g

n = 10 do±wiadcze« Bernoulliego. W ka»dym

z nich odnosimy sukces z prawdopodobie«stwem

p = 0:9. Jakie jest prawdo-

podobie«stwo, »e w w dokªadnie jednej próbie lub w nie wi¦cej ni» 10% prób

odniesiemy sukces. W tym przypadku rozwi¡zanie jest proste. Zarówno w jed-

nym jak i w drugim przypadku obliczamy

Pr(

X = 1) =

= 9

Jakub Bernoulli (1654 { 1705), matematyk szwajcarski, jeden z licznej rodziny Berno-

ullich, autor

onje

ctandi

, pierwszego dzieªa po±wi¦conego rachunkowi prawdopodobie«-

stwa.

2.3 Rozkªady dyskretne

Co jednak b¦dzie, gdy przy tym samym

n b¦dzie p = 0:09? Obliczenie liczby

:09

:91

jest ju» kªopotliwe, a obliczenie prawdopodobie«stwa, »e uda si¦ nie

wi¦cej ni» 10% do±wiadcze« z 1000 prób jest ju» praktycznie bardzo trudne.

Spróbujmy bowiem bezpo±rednio i dokªadnie obliczy¢

Pr(

100) =

100

1000

1000,

Napisanie procedur (np. w Pascalu lub C) wykorzystuj¡cych wprost wzory

(2.3.2) i obliczaj¡cy wspóªczynniki Newtona ze wzoru rekurencyjnego

nie daje zadowalaj¡cych efektów dla wi¦kszych

n i k.

Dla wygody przyjmiemy oznaczenie

Wzór

rekurencyjny

b(n;k;p) =

Wtedy ªatwo jest udowodni¢ wzór rekurencyjny

b(n;0;p) = q

;

(2.3.3)

b(n;k + 1;p) = n

k + 1

q b(n;k;p):

(2.3.4)

Wzór ten do bezpo±redniego zaprogramowania nadaje si¦ w równie maªym

stopniu jak i wzór (2.3.2), ale stanowi¢ b¦dzie podstaw¦ dla efektywnych przy-

bli»e« rozpatrywanych w nast¦pnym punkcie.

2.3.2. Rozkªad Poissona

Zmienna losowa

X przyjmuj¡ca tylko waro±ci caªkowite nieujemne ma rozkªad

Poissona

z parametrem

, gdy

Pr(

X = k) = e

k! :

(2.3.5)

Denicja tego rozkªadu jest poprawna, to znaczy wszystkie prawdopodobie«-

stwa s¡ nieujemne i sumuj¡ si¦ do jedynki, gdy» jak wiadomo z rozwini¦cia

funkcji

w szereg Maclaurina,

k! = e

= 1

Podobnie jak dla rozkªadu dwumianowego, równie» dla rozkªadu Poissona

przyjmiemy oznaczenie

p(k;) = e

k! :

2.3 Rozkªady dyskretne

Twierdzenie 2.3.1.

(Poissona) Je»eli

np = np

dla n

, to dla

Przybli»enie

rozkªadem

Poissona

ka»dego

lim

b(n;k;p) = p(;k):

(2.3.6)

Dowód.

Dla uproszczenia przyjmiemy

np = , zamiast granicy np

. Dowód

przeprowadzimy przez indukcj¦.

n;0; n

;

n;k + 1;

n;k;

q =

k + 1

k + 1 =

p(k + 1;)

p(k;) ;

co daje wzór (2.3.5)

Uwaga.

Twierdzenie 2.3.1 daje dobre przybli»enie rozkªadu dwumianowego

Przybli»enie

dla ±rednich

rozkªadem Poissona, gdy

n jest du»e, (n

100),

p jest maªe, a ±rednie.

Wtedy zamiast (2.3.6) mo»na przyj¡¢

b(n;k;p)

p(;k):

(2.3.7)

Przykªad.

n = 100 próbach Bernoulliego prawdopodobie«stwo sukcesu

wynosi

p = 0:98. Niech X b¦dzie liczb¡ pora»ek. Prawdopodobie«stwo pora»ki

wynosi

q = 0:02. Szukamy prawdopodobie«stwa, »e poniesiemy co najwy»ej

jedn¡ pora»k¦. Poniewa»

= nq = 2, to mo»na zastosowa¢ przybli»enie wzo-

rem (2.3.7):

Pr(

1) = Pr(

X = 0) + Pr(X = 1)

0! +

= 3

Przykªad.

Prawdopodobie«stwo przesªania bª¦dnego bitu wynosi 2

niezale»nie od pozostaªych. Przesyªamy 10

bitów i na ko«cu dodajemy bit pa-

rzysto±ci. Bª¦dny ci¡g odbierzemy jako prawdziwy, gdy przekªamaniu ulegnie

parzysta liczba bitów. Prawdopodobie«stwo odebrania bª¦dnego ci¡gu jako

prawdziwego, wynosi w przybli»eniu

=2, gdzie = 0:25, gdy» prawdo-

podobie«stwo przekªamania czterech bitów wynosi

=24 i mo»e by¢ po-

mini¦te, tak jak i dalsze parzyste liczby przekªama«. Tak wi¦c prawdopodo-

bie«stwo odebrania bª¦dnego ci¡gu jako prawdziwego wynosi w przybli»eniu

=2! = 2:5

=2 = 0:2565.

Na koniec obliczmy parametry w rozkªadzie Poissona { warto±¢ oczekiwan¡

i wariancj¦.

Twierdzenie 2.3.2.

Je»eli zmienna losowa

X ma rozkªad Poissona z parame-

trem

, to EX = i D

X = .

Simeon Denis Poisson (1781 { 1840), francuski mechanik, zyk i matematyk

2.3 Rozkªady dyskretne

Dowód.

Korzystaj¡c z twierdzenia 2.3.1 mo»na zauwa»y¢, »e przyjmuj¡c

np otrzymujemy

X = lim

np =

oraz

X = lim

np(1

p) = lim

2.3.3. Zadania

Prawdopobie«stwo sukcesu w jednej próbie wynosi 0

:01. Niech X

b¦dzie

liczb¡ sukcesów w

n niezale»nych próbach. Znale¹¢ Pr(X

1), gdy a)

n = 3,

n = 100.

Ksi¡»ka o 500 stronicach zawiera 50 bª¦dów drukarskich. Obliczy¢ prawdo-

podobie«stwo tego, »e na przypadkowo wybranej stronicy znajd¡ si¦ co naj-

mniej 3 bª¦dy.

3*.

Pokaza¢, »e je±li

X ma rozkªad dwumianowy przy ustalonym n i p, to

b(n;k;p) ma tylko jedn¡ lub dwie równe warto±ci najwi¦ksze. Znale¹¢ takie k

przy których te warto±ci s¡ przyjmowane.

4*.

Pokaza¢, »e analogiczn¡ wªasno±¢ maj¡ prawdopodobie«stwa w rozkªadzie

Poissona.

Bity przekazywane szeregowo s¡ przekªamywane niezale»nie od siebie, ka»dy

z prawdopodobie«stwem

p = 10

. Na ko«cu ka»dego bloku bitów dodajemy bit

parzysto±ci. Jaka jest najwi¦ksza dªugo±¢ bloku, przy której prawdopodobie«-

stwo niewykrycia bª¦du jest mniejsze od 0.001?

2.4 Rozkªady ci¡gªe

2.4. Rozkªady ci¡gªe

2.4.1. Rozkªad jednostajny

Rozkªad jednostajny na odcinku [

a;b] ma g¦sto±¢ okre±lon¡ wzorem

f(x) =

a dla x

[

a;b],

dla

x =

[

a;b].

Momenty zwykªe

= 1

dx = 1

k + 1

= b

(

a)(k + 1)

maj¡ dla

a = 0 i b = 1 szczególnie prost¡ posta¢ (patrz zadanie 1 do roz-

dziaªu 2.2):

= 1

=(k + 1). St¡d obliczamy wariancj¦

= a

ab + b

+ 2

ab + b

= (b

12 :

Dla rozkªadu jednostajnego momenty centralne nieparzystego rz¦du s¡ równe

zeru. atwo jest te» obliczy¢ momenty rz¦du parzystego, co jednak pozosta-

wimy jako zadania 6 i 7 do tego rozdziaªu. Zauwa»my tu jednak, (co b¦dzie

pomocne przy rozwi¡zywaniu tych zada«), »e je±li zmienna losowa

X ma roz-

kªad jednostajny na odcinku [0

;1], to zmienna losowa Y = (b

a)X + a ma

rozkªad jednostajny na odcinku [

a;b].

2.4.2. Rozkªad wykªadniczy

Rozkªad wykªadniczy z parametrem

> 0 ma g¦sto±¢ okre±lon¡ wzorem

f(x) =

(

dla

x < 0,

(2.4.1)

której wykres jest przedstawiony na rysunku 4. Ze wzoru (2.4.1) otrzymujemy

wzór na dystrybuant¦

F(x) =

(

dla

x < 0.

(2.4.2)

Obliczmy dwa pierwsze momenty i wariancj¦.

dx;

sk¡d obliczaj¡c caªk¦ przez cz¦±ci, (

), otrzymujemy

Warto±¢

oczekiwana

2.4 Rozkªady ci¡gªe

f(x)

= 1
= 0:5

= 2

Rysunek 4: Wykres g¦sto±ci rozkªadu wykªadniczego

+ 1

= 1 :

Podobnie, ale dwukrotnie caªkuj¡c przez cz¦±ci, obliczamy

dx = 2

;

sk¡d

Wariancja

= 1

Rozkªad wykªadniczy jest cz¦sto u»ywany w teorii niezawodno±ci, gdzie dobrze

opisuje czas pracy elementów niestarzej¡cych si¦. Je»eli zmienna losowa

T jest

czasem pracy elementu, to

= 1= jest ±rednim czasem pracy, a parametr

= 1= jest nazywany intensywno±ci¡ uszkodze«. Niestarzenie si¦ elementu

oznacza, »e prawdopodobie«stwo uszkodzenia si¦ elementu w czasie

t od chwili

obecnej, nie zale»y od dotychczas przepracowanego czasu

. Wªasno±¢ ta nazy-

wana jest brakiem pami¦ci rokªadu wykªadniczego. Sformuªujemy j¡ w postaci

twierdzenia.

Twierdzenie 2.4.1.

Je»eli

T jest zmienn¡ losow¡ o rozkªadzie wykªadniczym,

Pr(

T > t + t

T > t

) = Pr(

T > t):

(2.4.3)

Dowód.

Poniewa»

T > t+t

T > t

oraz Pr(

T > t) = 1

F(x) = e

Pr(

T > t + t

T > t

) = Pr(T > t + t

)

Pr(

T > t

)

(

)

= Pr(

T > t):

2.4 Rozkªady ci¡gªe

Mo»na te» pokaza¢, czego jednak nie b¦dziemy robi¢, »e tylko rozkªad wykªad-

niczy ma wªasno±¢ braku pami¦ci, to znaczy speªnia równanie (2.4.3).

Uogólnieniem rozkªadu wykªadniczego jest rozkªad Weibulla, którego dystry-

Rozkªad

Weibulla

buanta jest modykacj¡ dystrybuanty danej równaniem (2.4.2)

F(x) =

(

dla

x < 0.

(2.4.4)

G¦sto±¢ tego rozkªadu wyra»a si¦ wzorem

f(x) =

(

dla

x < 0,

(2.4.5)

której wykres dla

= 1 i = 0:5, = 1:5, = 2:5 jest przedstawiony na

rysunku 5. Przypadek

= 1 daje rozkªad wykªadniczy. Rozkªad Weibulla jest

f(x)

= 0:5

= 1:5

= 2:5

Rysunek 5: Wykres g¦sto±ci rozkªadu Weibulla

stosowany w teorii niezawodno±ci.

2.4.3. Rozkªad normalny

Rozkªad normalny N(0

;1) ma g¦sto±¢ dan¡ wzorem

f(x) = 1

;

(2.4.6)

której wykres jest przedstawiony na rysunku 6. Je±li zmienna losowa

Y ma

rozkªad normalny N(0

;1), to zmienna losowa

Rozkªad

normalny

)

X = Y + m

(2.4.7)

ma rozkªad normalny N(

m;). W ten sposób deniuje si¦ rozkªad normalny o

parametrach

m i . Z drugiej strony, je±li X ma rozkªad normalny N(m;), co

oznaczamy symbolicznie jako

m;), to jak ªatwo sprawdzi¢

X = X

N(0

;1):

(2.4.8)

2.4 Rozkªady ci¡gªe

Operacj¦ dan¡ równaniem (2.4.8), (odwrotn¡ do (2.4.7)), nazywa si¦ standa-

ryzacj¡ zmiennej losowej

Poniewa» g¦sto±¢ zmiennej losowej

Y = aX +b, a > 0, gdy X ma g¦sto±¢ f(x),

wyra»a si¦ wzorem (patrz zadanie 9),

f(x)

= 1af

;

to g¦sto±¢ rozkªadu normalnego N(

m;) wyra»a si¦ wzorem

G¦sto±¢

rozkªadu

)

f(x) = 1

)

(2.4.9)

Wzór (2.4.9) jest bezpo±rednim wnioskiem ze wzorów (2.4.7) i (2.4.6). Ponie-

wa» g¦sto±¢

f(x) rozkªadu N(0;1) jest funkcj¡ parzyst¡, to xf(x) jest funkcj¡

nieparzyst¡, a wi¦c dla

m;) otrzymujemy E

X = 0, sk¡d ze wzorów

(2.4.7) i (2.4.8): E

X = m. Nieco wi¦cej zachodu wymaga obliczenie D

Wystarczy jednak obliczy¢, »e D

X = 1, (zadanie 10), sk¡d od razu, ze wzoru

(2.4.7) otrzymujemy, »e D

X =

Dystrybuant¦ zmiennej losowej

N(0

;1) oznacza si¦ tradycyjnie symbolem

(

x). Dystrybuanta rozkªadu normalnego nie jest funkcj¡ elementarn¡, dlatego

jej warto±ci trzeba odczytywa¢ z tablic rozkªadu normalnego lub korzysta¢ z

programów komputerowych. Bez »adnych oblicze« mamy jednak (0) = 0

:5.

Ze wzgl¦du na (2.4.7), warto±ci dystrybuanty rozkªadu N(

m;) mo»na otrzy-

ma¢ z warto±ci dystrybuanty rozkªadu N(0

;1). Czasem w tablicach zamiast

warto±ci dystrybuanty (

x) podaje si¦ warto±ci funkcji

(

x) = 1

dt = (x)

:5:

Dla

x >

2.4 Rozkªady ci¡gªe

Dla rozkªadu normalnego mo»na z tablic odczyta¢ nast¦puj¡c¡ wªasno±¢,

Reguªa

3-sigmowa

znan¡ jako reguªa trzy-sigmowa.

Fakt 2.4.1.

Je»eli zmienna losowa

X ma rozkªad normalny N(m;), to

Pr(

> 3) < 0:01:

(2.4.10)

Dowód.

Poniewa» Pr(

X > x) = 1

(

x) = (

x), to

Pr(

> 3) = Pr

> 3

= 2(1

(

x))

= 2

:00135 = 0:0027 < 0:01:

Dla rozkªadów innych ni» normalny, nierówno±¢ (2.4.10) nie musi by¢ praw-

dziwa.

Przykªad.

Dla zmiennej losowej

X o g¦sto±ci

f(x) = 2e

;

jest E

X = 0, gdy» f(x) jest funkcj¡ parzyst¡, a caªka

xf(x)dx = 2

xf(x)dx

jest bezwzgl¦dnie zbie»na (i równa 1

=, b¦d¡c warto±ci¡ oczekiwan¡ w rozkªa-

dzie wykªadniczym). Wariancja

X = 2

dx =

dx = 2

jest drugim momentem zwykªym rozkªadu wykªadniczego, sk¡d

Obliczamy

Pr(

> 3) = 2Pr

X > 3

:1199;

a wi¦c nierówno±¢ (2.4.10) jest dla tego rozkªadu nieprawdziwa.

2.4 Rozkªady ci¡gªe

2.4.4. Zadania

Niech

R b¦dzie zmienn¡ losow¡ o rozkªadzie jednostajnym na odcinku [0;1],

tzn.

f(x) = 1 dla x

;1] oraz f(x) = 0 dla x =

;1]. Niech F(x) b¦dzie

ci¡gª¡ i ró»nowarto±ciow¡ dystrybuant¡ pewnej zmiennej losowej. Pokaza¢, »e

X = F

(

R) ma dystrybuant¦ F(x).

W oparciu o zadanie 1 poda¢ algorytm generowania zmiennej losowej o

rozkªadzie wykªadniczym z parametrem

, maj¡c do dyspozycji generator liczb

losowych o rozkªadzie jednostajnym na odcinku [0

;1].

Korzystaj¡c z tablic rozkªadu normalnego obliczy¢

Pr(

X < 0:5), Pr(X >

1), Pr(1

:5 < X

dla zmiennych losowych

N(1

;1), X

;0:5), X

N(1

:5;1) i X

N(1

:5;0:1).

Korzystaj¡c z tablic rozkªadu normalnego obliczy¢ parametr

speªniaj¡cy

równanie Pr(

X > x

) =

dla warto±ci = 0:1 oraz warto±ci = 0:05 dla

zmiennej losowej

N(0

;1) oraz X

:5;2).

Przez analogi¦ do reguªy 3{sigmowej sformuªowa¢ ÿreguª¦

n{sigmow¡" je-

±li termin ÿbardzo maªy" chcemy rozumie¢ jako ÿmniejszy od 0.0001". Jak

nale»aªoby rozumie¢ termin ÿbardzo maªy" chc¡c mie¢ ÿreguª¦ 2{sigmow¡"?

Pokaza¢, »e w rozkªadzie jednostajnym momenty centralne rz¦du nieparzy-

stego s¡ równe zeru.

Obliczy¢ momenty centralne parzystego rz¦du dla zmiennych losowych o

rozkªadzie jednostajnym na odcinku [

a;b].

8**.

Niech

X i S b¦d¡ niezale»nymi zmiennymi losowymi takim, »e X b¦dzie

miaªa rozkªad wykªadniczy oraz Pr(

S = 1) = Pr(S =

1) = 1

=2. Znale¹¢

rozkªad zmiennej losowej

Z = SX.

Niech

Y = aX + b, a > 0 oraz niech X ma dystrybuant¦ F(x) i g¦sto±¢

f(x). Znale¹¢ dystrybuant¦ i g¦sto±¢ zmiennej losowej X.

10.

Niech

X ma rozkªad normalny N(0;1). Obliczy¢ D

11*.

Korzytaj¡c z rozwini¦cia g¦sto±ci rozkªadu normalnego w szereg Maclau-

rina, znale¹¢ rozwini¦cie dystrybuanty. Korzystaj¡c z niego napisa¢ procedur¦

obliczania warto±ci dystrybuanty rozkªadu N(

m;).

3. Twierdzenia graniczne

3.1. Nierówno±¢ Czebyszewa i prawa wielkich-72B5p4--249k7znBf7 0 0 -0.24 532.8 5

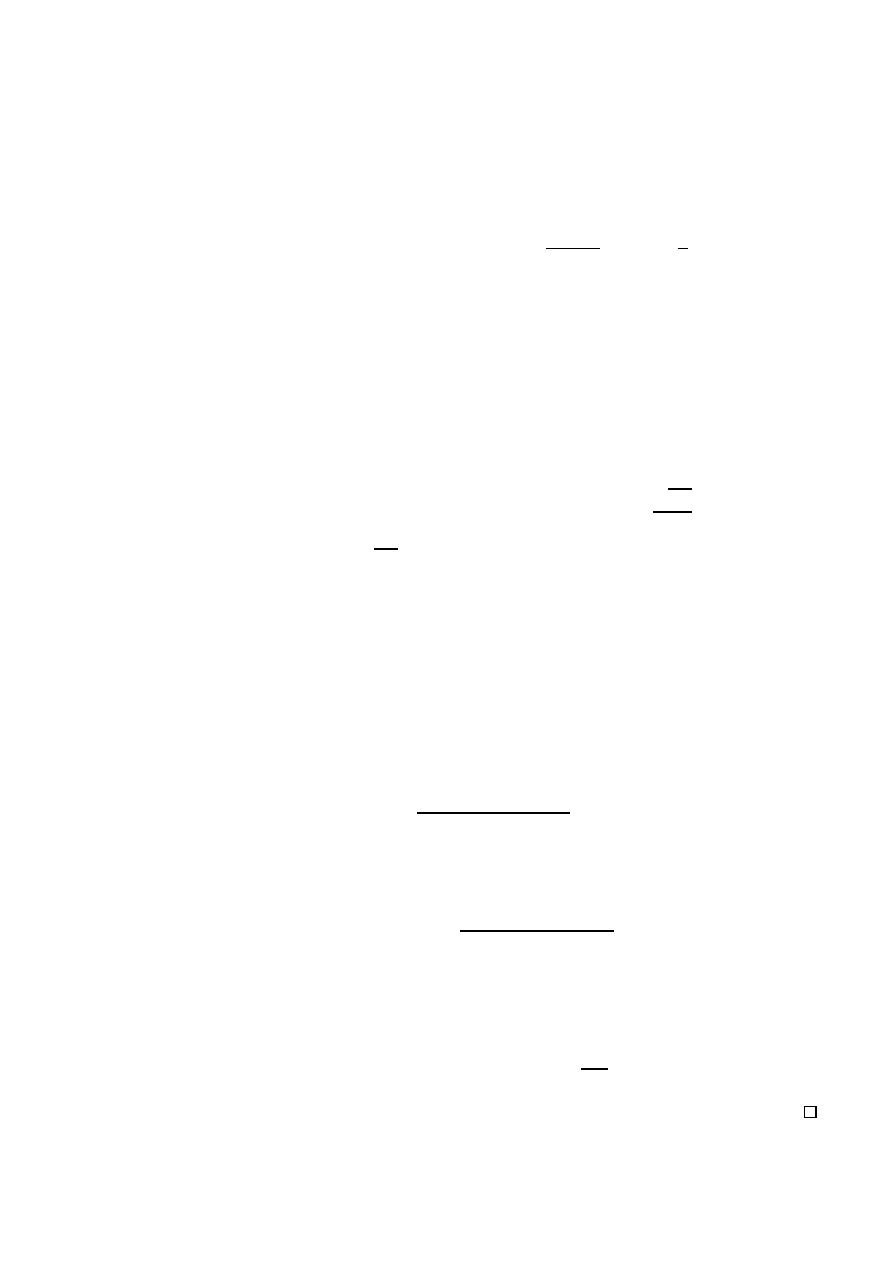
3.1 Nierówno±¢ Czebyszewa i prawa wielkich liczb

Przykªad.

Niech

X ma dowolny rozkªad speªniaj¡cy zaªo»enia twierdze-

nia 3.1.2. Wtedy z (3.1.2) mamy

Pr(

) = Pr

9 :

Je»eli za±

m;), (X speªnia równie» zaªo»enia twierdzenia 3.1.2), to z

(2.4.10) wynika oszacowania lepsze o rz¡d, to znaczy ponad dziesi¦ciokrotnie

lepsze.

Przykªad.

Niech

X b¦dzie liczb¡ sukcesów w 20 próbach, gdzie prawdopo-

dobie«stwo sukcesu w jednej próbie wynosi

p = 0:4. Oszacujmy z doªu praw-

dopodobie«stwo, »e liczba sukcesów b¦dzie zawarta mi¦dzy 4 i 12.

Poniewa»

m = EX = 20

:4 = 8 oraz

= D

X = 20

:6 = 4:8 to

Pr(4

12) = Pr(

4 = 1

Pr(

> 4)

Pr(

16 = 0:7;

przyjmuj¡c

t = 4=

:8 we wzorze (3.1.2).

3.1.2. Prawa wielkich liczb

Z nierówno±ci Czebyszewa mo»na wyprowadzi¢ sªabe prawo wielkich liczb dla

zmiennychlosowych. Takie sformuªowanie prawa wielkichliczb jest ogólniejsze,

ni» sformuªowanie tylko dla zdarze«, jak to zrobiono w punkcie 1.2.1.

Twierdzenie 3.1.3.

Niech

;::: b¦d¡ ci¡giem niezale»nych zmiennych

Sªabe prawo

wielkich liczb

losowych o tym samym rozkªadzie, o warto±ci oczekiwanej

m i wariancji

. Wtedy dla ka»dego

" > 0

lim

< "

= 1

(3.1.3)

Dowód.

Dla skrócenia zapisu oznaczmy

= X

Z niezale»no±ci zmiennych losowych

wynika, »e D

=n, a tak»e

m. Z nierówno±ci Czebyszewa (3.1.2) mo»na przyjmuj¡c " = t na-

pisa¢

Pr(

;

co daje tez¦ twierdzenia dla

3.2 Funkcje charakterystyczne

3.2. Funkcje charakterystyczne

3.2.1. Denicje i wªasno±ci

Zmienn¡ losow¡ zespolon¡ nazywamy funkcj¦

Z :

tak¡, »e

Zmienna

losowa

zespolona

Z(!) = X(!) + iY (!);

gdzie

X(!) i Y (!) s¡ rzeczywistymi zmiennymi losowymi zdeniowanym w

rozdziale 2.1.1.

Funkcj¡ charakterystyczn¡ nazywamy funkcj¦ zmiennej rzeczywistej

'(t) okre-

Funkcja cha-

rakterystyczna

±lon¡ wzorem

'(t) = Ee

itX

itx

dF(x):

(3.2.1)

Funkcja charakterystyczna ma nast¦puj¡ce wªasno±ci, które w wielu przypad-

kach pomagaj¡ oblicza¢ i bada¢ ró»ne charakterystyki zmiennych losowych i

ich rozkªadów.

Twierdzenie 3.2.1.

Funkcja charakterystyczna

'(t) okre±lona wzorem (3.2.1)

(i) jest jednostajnie ci¡gªa,

(ii)

'(0) = 1,

(iii)

'(t)

(iv)

t) =

'(t).

Poni»sze twierdzenie pomaga oblicza¢ rozkªady i funkcje charakterystyczne

Niezale»ne

zmienne

losowe

sum zmiennych losowych.

Twierdzenie 3.2.2.

Je»eli zmienne losowe

X i Y s¡ niezale»ne, to

(

t) = '

(

t)'

(

t);

gdzie

(

t) i '

(

t) s¡ funkcjami charakterystycznymi zmiennych losowych X

Y .

Równie» obliczanie momentów zmiennych losowych mo»e by¢ znacznie prost-

Momenty

sze, gdy znamy ich funkcje charakterystyczne.

Twierdzenie 3.2.3.

Istnienie

k-tego momentu zmiennej losowej jest równo-

wa»ne istnieniu

k-tej pochodnej jej funkcji charakterystycznej, przy czym

= '

(

)

(0)

Bezpo±rednio ze wzoru (3.2.1) wynika wzór, analogiczny do znanych wzorów

w przeksztaªceniu Laplace'a:

(

t) = '

(

at):

3.2 Funkcje charakterystyczne

Z kolei z twierdzenia 3.2.2 wynika, »e

(

t) = e

ita

(

t);

gdy» staª¡

a mo»na traktowa¢ jako zmienn¡ losow¡ przyjmuj¡c¡ tylko jedn¡

warto±¢

a, a taka zmienna losowa jest niezale»na od dowolnych zmiennych

losowych i ma funkcj¦ charakterystyczn¡ (co ªatwo sprawdzi¢) równ¡

ita

Omówimyteraz funkcje charakterystyczne rozkªadów typu ci¡gªego, które byªy

przedstawione w rozdziale 2.4. Obliczenie funkcji charakterystycznej rozkªadu

jednostajnego pozostawimy jako zadania 1 i 3, policzmy natomiast funkcje cha-

rakterystyczne rozkªadu wykªadniczego (strona 29) i normalnego (strona 31).

Przykªad.

Dla rozkªadu wykªadniczego z parametrem

funkcj¦ charaktery-

Rozkªad

wykªadniczy

styczn¡ obliczamy ze wzoru (3.2.1)

'(t) =

itx

dx = 1

(3.2.2)

Przykªad.

Dla rozkªadu normalnego:

Rozkªad

normalny

'(t) = 1

)

dx = e

3.2.2. Rozkªad gamma

Rozkªad gamma deniujemy jako rozkªad, którego funkcja charakterystyczna

Rozkªad

gamma

ma posta¢

'(t) =

;

(3.2.3)

gdzie

b > 0 i p > 0.

Z porównania wzorów (3.2.2) i (3.2.3) wynika, »e rozkªad wykªadniczy jest

szczególnymprzykªadem rozkªadu gamma.Ponadto z Twierdzenia 3.2.2 otrzy-

Rozkªad

Erlanga

mujemy, »e je±li

p = n jest liczb¡ naturaln¡, to zmienna losowa o takim roz-

kªadzie gamma jest sum¡

n zmiennych losowych niezale»nych, o tym samym

rozkªadzie wykªadniczym. Taki szczególny przypadek rozkªadu gamma nazywa

si¦ rozkªadem Erlanga o

n stopniach swobody.

Dla rozkªadu gamma mo»na wyznaczy¢ g¦sto±¢. Wyra»a si¦ ona wzorem

f(x) =

,(p)x

dla

x < 0,

3.2 Funkcje charakterystyczne

gdzie

,(p) =

jest funkcj¡ specjaln¡ zwan¡ funkcj¡ Gamma. Funkcja ta ma ciekaw¡ wªasno±¢,

,(p + 1) = p,(p), która pozwala ograniczy¢ si¦ jedynie do znajomo±ci jej

warto±ci dla 0

< p

1. Proste obliczenia pokazuj¡ te», »e

,(1) = 1, sk¡d

ªatwo ju» otrzyma¢ równo±¢:

,(n) = (n

1)!.

3.2.3. Zadania

Obliczy¢ funkcj¦ charakterystyczn¡ rozkªadu jednostajnego na odcinku

;1].

Obliczy¢ funkcj¦ charakterystyczn¡ rozkªadu o g¦sto±ci

f(x) = e

=2.

Korzystaj¡c z wyniku zadania 1 i wªasno±ci funkcji charakterystycznych,

znale¹¢ funkcj¦ charakterystyczn¡ rozkªadu jednostajnego na odcinku [

a;b].

Korzystaj¡c z funkcji charakterystycznej rozkªadu N(0

;1), obliczy¢ mo-

menty

k-tego rz¦du tego rozkªadu.

5*.

Pokaza¢, »e

,(p)x

dx = 1

dla

b > 0 i p > 0.

Korzystaj¡c z funkcji charakterystycznej rozkªadu gamma obliczy¢ warto±¢

oczekiwan¡ i wariancj¦ w tym rozkªadzie.

Niech

X i Y b¦d¡ niezale»ne o rozkªadzie jednostajnym na odcinku

[

:5;0:5]. Udowodni¢, »e ich suma ma rozkªad o g¦sto±ci

f(x) =

x + 1 dla x

[

;0),

x + 1 dla x

;1],

dla

x =

[

;1].

3.3 Centralne twierdzenie graniczne

3.3. Centralne twierdzenie graniczne

3.3.1. Twierdzenie Lindeberga-Levy'ego

Dystrybuant¦ rozkªadu normalnego N(0

;1) oznaczamy jak zwykle jako (x).

Twierdzenie 3.3.1.

(Lindeberga-Levy'ego) Niech

;:::;X

b¦d¡ nieza-

X <

istnieje

wariancja

le»nymi zmiennymi losowymi o tym samym rozkªadzie, warto±ci oczekiwanej

m = EX i wariancji 0 <

= D

X <

. Wtedy

lim

< x

= (

x):

(3.3.1)

Dowód.

Funkcja charakterystyczna rozkªadu normalnego N(0

;1) jest równa

'(t) = e

. Oznaczmy przez

(

t) funkcj¦ charakterystyczn¡ zmiennej lo-

sowej

m, a przez '

(

t) funkcj¦ charakterystyczn¡ zmiennej losowej

= X

wyst¦puj¡cej po lewej stronie wzoru (3.3.1). Uwzgl¦dniaj¡c znane ju» wªasno±ci

(paragraf 3.2.1) funkcji charakterystycznej otrzymujemy, »e

(

t) =

(3.3.2)

Rozwiniemy teraz funkcj¦

(

t) w szereg Maclaurina. Poniewa» '

(0) = 1,

(0) =

m oraz '

(0) =

, to

(

t) = 1

(

)

;

gdzie

(

)

0 dla

0. Ze wzoru (3.3.2) otrzymujemy z kolei

(

t) =

n + R

(

=n)

oraz

lim

(

=n) = 0:

Podstawiaj¡c

u = t

=2n + R

(

=n) otrzymujemy

(

t) = nln(1

u) = n

=2n + R

(

=n)

=2 + nR

(

=n);

sk¡d

lim

(

t) =

=2;

czyli

lim

(

t) = e

3.3 Centralne twierdzenie graniczne

Bezpo±rednio z twierdzenia 3.3.1 wynika

Twierdzenie 3.3.2.

(Moivre'a-Laplace'a) Niech Pr(

k) = b(n;k;p),

(patrz strona 26), czyli

ma rozkªad dwumianowy z parametrami

n i p.

Wtedy

lim

npq < x

= (

x):

Wªasno±¢ wyra»on¡ w twierdzeniu 3.3.2 mo»na interpretowa¢ tak, »e

ma dla

Asymptotycz-

normalno±¢

du»ych

n rozkªad w przybli»eniunormalny N(0;1) albo »e Y

ma w przybli»eniu

rozkªad normalny N(

np;

npq). Mówimy te», »e Y

ma rozkªad asymptotycznie

normalny z parametrami

np i

npq.

3.3.2. Rozkªady chi-kwadrat i t-Studenta

Niech

i = 1;2;:::;n b¦d¡ niezale»nymi zmiennymi losowymi o rozkªadzie

Rozkªad

chi-kwadrat

normalnym N(0

;1). Zmienn¡ losow¡

okre±la si¦ wzorem:

(3.3.3)

Mówimy, »e zmienna losowa

okre±lona wzorem (3.3.3) ma rozkªad chi-

kwadrat Pearsona

n stopniach swobody. Poniewa» E

= E

oraz

= D

= 2 to z twierdzenia 3.3.1 wynika asymptotyczna normalno±¢

rozkªadu zmiennej losowej

n stopniach swobody, przy czym ten rozkªad

normalny ma parametry

n i

n, czyli

Asymptotycz-

na normalno±¢

lim

n < x

= (

x):

Asymptotyczn¡ normalno±¢ rozkªadu chi kwadrat mo»na okre±li¢ te» przez

zdeniowanie zmiennej

, która te» ma rozkªad asymptotycznie normalny,

ale N(

;1).

Zbie»no±¢ rozkªadu chi-kwadrat do rozkªadu normalnego jest tak szybka, »e

dla

n > 30 dystrybuanta (x) przybli»a dystrybuant¦ rozkªadu chi-kwadrat

wystarczaj¡co dobrze. Z tego powodu dla

n >

3.3 Centralne twierdzenie graniczne

Studenta okre±lony jako rozkªad zmiennej losowej

t danej wzorem

t = t

= X

=n ;

(3.3.4)

gdzie

N(0

;1), a

ma rozkªad chi-kwadrat o

n stopniach swobody oraz X

s¡ niezale»ne. Rozkªad

t-Studenta jest równie» asymptotycznie normalny

N(0

;1), przy czym podobnie jak dla rozkªadu chi-kwadrat, przybli»enie jest

dobre ju» dla

n > 30.

3.3.3. Zadania

Korzystaj¡c z twierdzenia Lindeberga-Levy'ego pokaza¢, »e rozkªad chi-

kwadrat o

n stopniach swobody jest asymptotycznie normalny N(n;

n).

Niezale»ne zmienne losowe

;:::;X

maj¡ rozkªad jednostajny na

odcinku [1

;3]. Niech

X =

Obliczy¢ przybli»on¡ warto±¢ wyra»e« Pr(

X > 130), Pr(X < 115) oraz

Pr(118

< X < 123). Które z tych przybli»e« mo»na otrzyma¢ równie» z nie-

równo±ci Markowa lub Czebyszewa? Porówna¢ dokªadno±¢ tych oszacowa«.

Niezale»ne zmienne losowe

;:::;X

100

maj¡ rozkªad Poissona o para-

metrze

= 2:5. Obliczy¢ przybli»on¡ warto±¢ wyra»enia

100

> 220

Korzystaj¡c z tablic znale¹¢

takie, »e Pr(

dla = 0:1,

= 0:05 i = 0:01, gdy zmienna losowa

ma rozkªad chi-kwadrat Pearsona

n = 2, n = 5, n = 15 i n > 30 stopni swobody.

To samo co w zadaniu 4, ale dla zmiennej losowej

, gdy

t ma rozkªad

t-Studenta.

Korzystaj¡c z tablic znale¹¢ Pr(

< x) dla zmiennej losowej o rozkªadzie

chi-kwadrat Pearsona o

n = 2, n = 5, n = 15 i n > 30 stopniach swobody oraz

x = 0:5 i x = 5.

To samo co w zadaniu 6, ale dla zmiennej losowej

t, o rozkªadzie t-Studenta.

4. Podstawowe poj¦cia statystyki

4.1. Denicje

W rozdziale tym podane s¡ najwa»niejsze poj¦cia statystyczne oraz najcz¦±ciej

spotykane funkcje, którymi posªuguje si¦ statystyka. W tym i w nast¦pnych

rozdziaªach skupiono si¦ na matematycznych tre±ciach statytystyki, pozosta-

wiaj¡c zagadnienia zastosowa« do samodzielnej lektury. Popularne podej±cie

do zagadnie« statystyki zawiera przyst¦pnie napisana ksi¡»ka F. Clegga [1].

Podr¦cznik J. Grenia [3] podaje najpotrzebniejsze denicje i wiele gotowych

wzorów potrzebnych do rozwi¡zywania problemów statystycznych, tak»e wiele

zada« oraz niezb¦dnie tablice statystyczne.

4.1.1. Sªownik poj¦¢ statycznych

Statystyka posªuguje si¦ specycznym j¦zykiem, dlatego najpierw podamy jej

podstawowe poj¦cia w postaci sªownika.

Populacja generalna { zbiorowo±¢ statystyczna, tzn. zbiór dowolnych elemen-

tów, nieidentycznych z punktu widzenia badanej cechy

Próba { cz¦±¢ populacji, dost¦pnej bezpo±redniej obserwacji ze wzgl¦du na

ustalon¡ cech¦,

i-ty element populacji ma cech¦ X

, czyli prób¦ mo»na

traktowa¢ jako ci¡g zmiennych losowych (

;:::;X

Próba prosta { próba, w której cechy elementów

s¡ niezale»ne i o tym

samym rozkªadzie co cecha

X w populacji generalnej.

Statystyka { zmienna losowa b¦d¡ca dowoln¡ funkcj¡ wyników próby losowej,

tzn. dowoln¡ funkcj¡

Z = f(X

;:::;X

Estymator { dowolna statystyka

Z sªu»¡ca do oszacowania nieznanej warto±ci

parametru

populacji generalnej.

Hipoteza statystyczna { dowolne przypuszczenie dotycz¡ce rozkªadu populacji

generalnej.

Test statystyczny { reguªa post¦powania, która na podstawie wyników próby

ma doprowadzi¢ do decyzji przyj¦cialub odrzucenia postawionej hipotezy

statystycznej.

Podane powy»ej hasªa b¦d¡ dalej uzupeªniane o nowe poj¦cia.

4.1.2. Najwa»niejsze statystyki

Momenty zmiennych losowych, zwykªe

= E

i centralne

= E(

)

zwane s¡ w statystyce momentami teoretycznymi. Momenty empi-

ryczne b¦dziemy dla odró»nienia oznacza¢ du»ymi literami

. Niech

(

;:::;X

) b¦dzie

n-elementow¡ prób¡ prost¡. Okre±limy k-ty moment

empiryczny (zwykªy) wzorem

= 1n

;

4.1 Denicje

k-ty empiryczny moment centralny wzorem

= 1n

(

)

Moment

k-ty nazywany jest te» momentem rz¦du k.

Podobnie jak dla momentów teoretycznych, dla momentu pierwszego i dla

drugiego momentu centralnego istniej¡ specjalne oznaczenia i nazwy. S¡ to

rednia

empiryczna

±rednia empiryczna

X = 1n

;

(4.1.1)

zwana potocznie statystyk¡ ÿ

X z kresk¡" oraz wariancja empiryczna

Wariancja

empiryczna

= 1n

(

)

;

(4.1.2)

zwana statystyk¡ ÿ

S kwadrat". Ponadto wprowadza si¦ jeszcze wariancj¦ em-

piryczn¡ poprawion¡

= 1

(

)

;

(4.1.3)

zwan¡ statystyk¡ ÿ

S kwadrat daszkiem".

Jest ªatwe do sprawdzenia, »e E

X = EX, gdy X jest cech¡ w populacji

generalnej, (

;:::;X

) jest prób¡ prost¡ z tej populacji oraz warto±¢

oczekiwana istnieje. Trudniej ju» sprawdzi¢, »e E ^

= D

X, co oznacza te»,

»e

= n

n D

X :

Niech

b¦dzie pewnym parametrem rozkªadu cechy X w populacji generalnej.

Przez

oznaczymy estymator tego parametru, czyli jego statystyczne

oszacowanie. B¦dziemy mówi¢, »e statystyka

jest estymatorem nieobci¡»o-

Wªasno±ci

estymatorów

nym parametru

, gdy EZ

. Estymator jest zgodny, gdy

lim

Pr(

< ") = 1

dla ka»dego

" > 0. Estymator jest asymptotycznie nieobci¡»ony, gdy

lim

Z powy»szych okre±le« wynika, »e

X jest estymatorem nieobci¡»onym war-

to±ci oczekiwanej, a ze sªabego prawa wielkich liczb wynika, »e jest równie»

estymatorem zgodnym.

4.1 Denicje

Przykªad.

Proste obliczenia pokazuj¡, »e je»eli

X jest cech¡ w populacji o

rozkªadzie normalnym N(

m;), to X

m;=

n).

Trudniej jest dowie±¢ nast¦puj¡ce wa»nego wyniku.

Twierdzenie 4.1.1.

Je»eli

X jest cech¡ w populacji o rozkªadzie normal-

nym N(

m;), to statystyka n^S

ma rozkªad chi-kwadrat o

1 stopniach

swobody.

Zaskakuj¡cy jest natomiast wynik nast¦puj¡cy.

Twierdzenie 4.1.2.

Je»eli cecha

X w populacji generalnej ma rozkªad nor-

malny, to statystyki

X i S

s¡ niezale»ne.

Nale»y tu zwróci¢ uwag¦, »e

X i S

o których mowa w twierdzeniu 4.1.2 po-

chodz¡

z tej samej

próby.

4.1.3. Zadania

Dokonano 20 niezale»nych prób, otrzymuj¡c nast¦puj¡e wyniki: 0.50 0.93

0.75 0.89 0.15 0.94 0.16 0.00 0.63 0.57 0.33 0.10 0.14 0.21 0.05 0.15 0.37 0.51

0.09 0.25. Obliczy¢

X, S

i ^

Dokonano 30 niezale»nych prób, otrzymuj¡c nast¦puj¡e wyniki: 1.05 1.13

0.41 0.12 0.12 0.19 3.02 0.08 3.87 0.54 2.63 0.40 1.15 0.24 0.46 1.07 0.58 0.29

0.56 2.11 0.40 0.04 0.74 1.41 0.18 3.14 0.40 0.64 0.29 2.47. Obliczy¢

X, S

i ^

Przeprowadzi¢ nast¦puj¡cy eksperyment: rzuci¢ 50 razy monet¡, obliczy¢

X, S

i ^

oraz porówna¢ z E

X, D

4**.

Niech

;:::X

b¦d¡ niezale»nymi zmiennymi losowymi o jednako-

wych rozkªadach normalnych N(

m;). Dla jakiej warto±ci k estymator

W = k

jest nieobci¡»onym estymatorem parameru

5**.

Niech

;:::X

b¦d¡ niezale»nymi zmiennymi losowymi o jednako-

wych rozkªadach normalnych N(

m;). Dobra¢ staª¡ k tak, aby funkcja

(

)

byªa nieobci¡»onym estymatorem wariancji.

Zmienna losowa

X ma rozkªad jednostajny na [a;a + 1]. Otrzymano n

niezale»nych obserwacji tej zmiennej losowej. Sprawdzi¢, »e

= 1n

jest estymatorem zgodnym i nieobci¡»onym parametru

4.2 Dystrybuanta empiryczna i histogramy

4.2. Dystrybuanta empiryczna i histogramy

4.2.1. Dystrybuanta empiryczna

Podobnie jak dla momentów, istnieje empiryczny odpowiednik dystrybuanty,

zwanej ju» dalej teoretyczn¡. Niech (

;:::;X

) b¦dzie prób¡ prost¡. Dys-

trybuanta empiryczna jest funkcj¡ okre±lon¡ wzorem:

(

x) = 1n

i : X

< x

Poniewa» wszystkie

(

!) s¡ funkcjami okre±lonymi na przestrzeni zda-

rze« elementarnych , to dystrybuanta empiryczna

(

x) jest zmienn¡ losow¡

dla ka»dego ustalonego

x. Je»eli natomiast ustalimy zdarzenie elementarne !,

(

x) jest funkcj¡ zmiennej rzeczywistej, która speªnia wszytkie wn-7 TD[())-140To121 cb

5. Estymacja

5.1. Estymacja punktowa

5.1.1. Metoda momentów

Metoda momentów jest jedn¡ z wielu metod konstruowania estymatorów para-

metrów rozkªadu cechy w populacji generalnej. Przyjmijmy, »e parametr

jest

jednoznacznie okre±lony przez warto±ci pierwszych

k momentów teoretycznych

cechy. Oznacza to, »e

= f(m

:::;m

)

Estymator ^

parametru okre±la si¦ wzorem

^= f(^m

:::; ^m

)

gdzie ^

s¡ momentamiempirycznymi.W szczególno±ci parametr

mo»e

by¢ funkcj¡ tylko pierwszego momentu teoretycznego

m, wtedy estymator jest

funkcj¡ tylko statystyki

Przykªad.

Niech

X ma rozkªad jednostajny na odcinku [a;b]. Przyjmijmy,

»e

a = 0 oraz = b jest nieznanym parametrem tego rozkªadu. Poniewa»

X = a + b

2 D

X = (b

12 ;

(5.1.1)

= 2m, a wi¦c ^ = 2x. Nie jest to estymator najlepszy, gdy» mo»na spotka¢

takie dane, »e niektóre z nich wyjd¡ poza prawy koniec tak oszacowanego

przedziaªu. Je»eli chcemy oszacowa¢ oba ko«ce

a i b, które nie s¡ znane, to

najpierw trzeba rozwi¡za¢ ukªad dwóch równa« (5.1.1) obliczaj¡c

a i b w funkcji

m i .

Przykªad.

Dla rozkªadu wykªadniczego, którego g¦sto±¢ jest okre±lona wzo-

rem (2.4.1), E

X = 1=. St¡d ^ = 1=^x.

5.1.2. Metoda najwi¦kszej wiarogodno±ci

Idea metody najwi¦kszej wiarogodno±ci polega oszacowaniu nieznanych pa-

rametrów tak, aby empiryczne dane byªy przy tym oszacowaniu najbardziej

prawdopodobne. Dla znalezieniatakiego estymatora konstruuje si¦ funkcj¦ wia-

rogodno±ci

L. Jest ona ró»na dla przypadku ci¡gªego i dyskretnego.

Najpierw omówimy przypadek dyskretny. Niech Pr(

X = x

(

)

) =

p(x

(

)

;),

gdzie

= (

;:::;

) jest wektoremparametrów lub w szczególnymprzypadku

{ parametrem. Funkcj¦ wiarogodno±ci okre±la si¦ wzorem

Funkcja

wiarogodno±ci

L() = L(x

;:::;x

;) = p(x

;)p(x

;):::p(x

;):

(5.1.2)

5.1 Estymacja punktowa

Zwró¢my tu uwag¦, »e

(

)

jest ci¡giem warto±ci, które dyskretna zmienna

losowa mo»e przyj¡¢, a

s¡ danymi, czyli warto±ciami, otrzymanymi w rze-

czywisto±ci, na przykªad z eksperymentu.

Dla cechy typu ci¡gªego o g¦sto±ci

f(x;), funkcja wiarogodno±ci okre±lona

jest wzorem

L() = L(x

;:::;x

;) = f(x

;)f(x

;):::f(x

;):

(5.1.3)

Estymatorem parametru

jest ta jego warto±¢, przy której funkcja wiaro-

MNW

godno±ci osi¡ga warto±¢ najwi¦ksz¡. Jest to estymator otrzymany metod¡ naj-

wi¦kszej wiarogodno±ci { MNW. Je»eli funkcja

L okre±lona wzorami (5.1.2)

lub (5.1.3) jest ró»niczkowalna, jej maksimum mo»na znale¹¢ szukaj¡c miejsca

zerowania si¦ pochodnej. Ze wzgl¦du na to, »e

L jest iloczynem funkcji, to

wygodnie jest bada¢ pochodn¡ nie

L, a pochodn¡ lnL.

Przykªad.

Niech

X ma rozkªad Poissona z parametrem okre±lonym wzo-

rem (2.3.5). Wtedy dla danych (

;:::;k

)

L() = e

:::k

! ;

sk¡d

L() =

n + (k

)ln

ln(

:::k

Po obliczeniu pochodnej otrzymujemy dla znalezienia maksimum równanie

n + k

= 0

;

a wi¦c ^

= x.

Przykªad.

Dla rozkªadu wykªadniczego z parametrem

okre±lonego wzorem

(2.4.1),

L() =

(

)

Po zlogarytmowaniu i zró»niczkowaniu otrzymujemy równanie

= 0

;

a wi¦c ^

= 1=x.

Je»eli

L nie jest funkcj¡ ró»niczkowaln¡, to jej maksimum nie mo»e by¢ znale-

zione w ten sposób.

Przykªad.

Niech

X ma rozkªad jednostajny na odcinku [0;]. Wtedy

L() =

(

dla

< ,

dla

< max

Taka funkcja

L osi¡ga swoje maksimum w punkcie max

, w którym nie ma

pochodnej. St¡d ^

= max

5.1 Estymacja punktowa

5.1.3. Zadania

Skonstruowa¢ metod¡ momentów estymatory parametrów

p i n w rozkªadzie

dwumianowym.

G¦sto±¢ wyra»a si¦ wzorem

f(x) =

(

;

dla

x < ,

; dla x

gdzie

> 0. Obliczy¢ i nast¦pnie wyznaczy¢ metod¡ najwi¦kszej wiarogod-

no±ci estymator parametru

Niech g¦sto±¢ wyra»a si¦ wzorem

f(x) = 2e

Wyznaczy¢ metod¡ najwi¦kszej wiarogodno±ci estymator parametru

Niech g¦sto±¢ wyra»a si¦ wzorem

f(x) =

(

x + ; dla 0

;

poza tym.

Wyznaczy¢ metod¡ momentów estymatory parametrów

i .

5.2 Estymacja przedziaªowa

5.2. Estymacja przedziaªowa

5.2.1. Przedziaªy ufno±ci

Idea estymacji przedziaªowej polega na tym, aby zamiast szacowania para-

metru

za pomoc¡ jednej liczby, znale¹¢ przedziaª, w którym nieznany nam

parametr znajdzie si¦ z zadowalaj¡cym nas prawdopodobie«stwem. Ko«ce tego

przedziaªu musz¡ by¢ wobec tego zmiennymi losowymi { statystykami b¦d¡-

cymi funkcjami próby

(

;:::;X

) i

(

;:::;X

)

takimi, aby Pr(

(

)) byªo bliskie 1. Blisko±¢ jedynki okre±la si¦ liczb¡

Poziom

ufno±ci

i nazywa poziomem ufno±ci. atwo jest zauwa»y¢, »e im mniejsze ,

tym dªu»szy jest przedziaª ufno±ci. Zazwyczaj

przybiera jedn¡ z warto±ci

0.1, 0.05, 0.01, przy czy warto±¢

= 0:05 jest najcz¦±ciej u»ywana { mówimy

wtedy o 95 procentowym przedziale ufno±ci.

Sposób okre±lenia przedziaªu ufno±ci zale»y od rozkªadu w którym wyst¦puje

nieznany parametr, od tego czy znamy pozostaªe parametry w tym rozkªadzie

i od liczebno±ci próby. W nast¦pnych punktach omówimy szerzej dwa typowe

przypadki: przedziaªy ufno±ci dla parametru

m = EX i =

X. Wiele

innych u»ytecznych wzorów mo»na znale¹¢ w ksi¡»ce [3]. Wszystkie te wzory

opieraj¡ si¦ na tej samej zasadzie, omówionej bardziej szczegóªowo w nast¦p-

nym punkcie.

5.2.2. Przedziaªy ufno±ci dla ±redniej

Rozpatrywane s¡ trzy przypadki, w zale»no±ci od przyj¦tych zaªo»e«. We

wszystkich jednak przypadkach, przedziaª ufno±ci jest symetryczny wzgl¦dem

±redniej empirycznej

X okre±lonej wzorem (4.1.1).

Model I

. Populacja generalna ma rozkªad N(

m;), odchylenie standardowe

Rozkªad

normalny,

znane

jest znane. Nieznany jest parametr

m, dla którego szukamy przedziaªu ufno±ci.

Dla próby o liczebno±ci

m, ko«ce przedziaªu ufno±ci wyra»aj¡ si¦ wzorami

n ;

X + u

n ;

gdzie

jest takie, »e Pr(

> u

) =

oraz U

m;). Wtedy

n < m <

X + u

= 1

(5.2.1)

Aby dla otrzymanychju» danych, a wi¦c ustalonego zdarzenia elementarnego

wyznaczy¢ przedziaª ufno±ci, nale»e w miejsce

X we wzorze (5.2.1) podstawi¢

5.2 Estymacja przedziaªowa

Model II

. Populacja generalna ma rozkªad N(

m;), odchylenie standardowe

Rozkªad

normalny,

nieznane

jest nieznane. Nieznany jest te» parametr

m, dla którego szukamy przedziaªu

ufno±ci. Dla próby o liczebno±ci

m ko«ce przedziaªu ufno±ci wyra»aj¡ si¦ wzo-

rami

1 ;

X + t

1 ;

gdzie

jest takie, »e Pr(

> t

) =

oraz t ma rozkªad t-Studenta o n

stopniach swobody. Statystyka

S =

okre±lona jest wzorem (4.1.2). Wtedy

1 < m <

X + t

= 1

(5.2.2)

lub równowa»nie przy pomocy statystyki ^

S =

n < m <

X + u

= 1

(5.2.3)

Poniewa» we wzorach (5.2.1), (5.2.2) i (5.2.2) znamy dokªadne rozkªady staty-

styk, to mo»na je stosowa¢ nawet przy maªych próbach.

Model III

. Rozkªad dowolny, ale

n musi by¢ du»e, (co najmniej kila dzie-

Rozkªad

dowolny, du»a

próba

si¡tków) oraz istnieje wariancja,

= D

X <

. Wtedy przedziaªy ufno±ci

wyznaczane s¡ ze wzoru (5.2.1), przy czym zamiast

podstawiamy S lub ^S,

(dla du»ego

n ró»nica mi¦dzy S i ^S jest nieznaczna).

Przykªad.

Przyjmijmy poziom ufno±ci 1

= 0:95. Poniewa»

Pr(

> u

) = 2Pr(

U > u

) = 2(1

(

)) =

= 0:05

czyli (

) = 1

=2 = 0:975. Z tablic rozkªadu normalnego odczytujemy, »e

= 1

:96. Z n = 100 danych o rozkªadzie normalnym obliczono x = 2:0031 i

s = 0:1967.

Ze wzoru (5.2.2) po podstawieniu

= ^s otrzymujemy przedziaª ufno±ci dla

±redniej

:0031

:960:1967

10 ;2:0031 + 1:96

:1967

10 );

a wi¦c przedziaª (1

:965;2:042).

Gdyby do oblicze« dost¦pne byªy tylko pocz¡tkowe cztery dane: 2.17, 1.85,

1.87, 1.97, to

x = 1:9650 oraz ^s = 0:1464. Wtedy korzystaj¡c z rozkªadu t-

Studenta o trzech stopniach swobody, (model II), otrzymujemy

= 3

:182. Ze

wzoru (5.2.2) otrzymujemy przedziaª ufno±ci (1

:918;2:011).

5.2 Estymacja przedziaªowa

Je»eli wiadomo byªoby, »e

= 0:2, to z modelu I, wzór (5.2.1) mamy jak

na pocz¡tku

= 1

:96, sk¡d przedziaª ufno±ci (1:926;2:004). Dane do tego

przykªadu zostaªy wzi¦te z populacji o rozkªadzie N(2

;0:2):

2.17

1.85

1.87

1.97

2.27

2.15

1.74

2.06

1.98

1.94

2.01

1.94

2.27

1.71

2.01

1.59

1.73

2.32

1.83

2.07

1.76

1.97

1.85

1.90

2.30

2.03

1.80

2.12

2.09

1.88

2.03

1.95

1.76

1.88

2.04

1.94

2.24

2.11

1.80

2.03

2.30

2.06

1.89

1.87

2.10

2.06

2.09

2.13

1.79

1.67

1.82

1.88

2.17

2.60

2.12

1.65

2.18

2.02

2.07

2.12

1.86

2.40

2.14

1.86

2.07

2.05

1.99

2.03

2.02

2.01

2.19

1.96

2.18

1.99

2.27

2.06

1.59

2.27

1.91

2.36

1.72

1.77

1.80

2.42

2.36

1.74

2.05

1.85

2.10

1.92

2.04

2.13

2.01

1.88

1.82

1.94

2.37

1.72.

Na zako«czenie zwró¢my uwag¦ na istotn¡ rol¦ zaªo»enia o rozkªadzie normal-

nym populacji. Tylko przy tym zaªo»eniu próba mo»e by¢ maªa. Je»eli to za-

ªo»enie nie jest speªnione, to musi by¢ du»a próba. To ostatnie zaªo»enie ozna-

cza asymptototyczn¡ normalno±¢ na mocy twierdzenia Lindeberga-Levy'ego,

(Twierdzenie 3.3.1).

5.2.3. Przedziaªy ufno±ci dla wariancji

Przedziaª ufno±ci dla wariancji nie zale»y od warto±ci oczekiwanej

m = EX.

St¡d tylko dwa rozwa»ane przypadki.

Model I

. Populacja generalna ma rozkªad normalny. Nieznany jest parametr

Rozkªad

normalny,

maªa próba

, dla którego szukamy przedziaªu ufno±ci. Próba jest maªa (n < 30). Przedziaª

ufno±ci okre±lony jest wzorem

< nS

= 1

(5.2.4)

lub równowa»nie wzorem

(

1)^

< (n

1)^

= 1

;

(5.2.5)

gdzie

speªniaj¡ równania

Pr(

< c

) = Pr(

> c

) =

dla zmiennej losowej

o rozkªadzie chi-kwadrat o

1 stopniach swobody.

Zwró¢my uwag¦, »e tak otrzymany przedziaª ufno±ci nie jest symetryczny

wzgl¦dem

Zaªo»enie, »e próba jest maªa ma charakter czysto rachunkowy { dla

n > 30

rozkªad chi-kwadrat jest na tyle zbli»ony do normalnego, »e tablice zawieraj¡

na ogóª warto±ci tylko do

n = 30.

Model II

. Populacja generalna ma rozkªad normalny i

30 lub zbli»ony

Rozkªad

normalny,

du»a próba

do normalnego i próba jest du»a. Wtedy przybli»ony przedziaª ufno±ci wyra»a

si¦ wzorem

1 +

< s

;

(5.2.6)

gdzie

jest takie, »e Pr(

> u

) =

oraz U

m;).

5.2 Estymacja przedziaªowa

5.2.4. Zadania

Dla danych -0.23, 0.61, -0.85, -0.72, -0.39, 0.73, oszacowa¢ na poziomie ufno-

±ci 0.9 warto±¢ oczekiwan¡ i wariancj¦, przyjmuj¡c, »e rozkªad jest normalny.

Dla danych -1.09, 0.26, 1.09, 0.56, -1.35, 0.65, oszacowa¢ na poziomie ufno±ci

0.9 warto±¢ oczekiwan¡ i wariancj¦, przyjmuj¡c, »e rozkªad jest normalny.

3*.

Napisa¢ procedur¦ generuj¡c¡

n niezale»nych zmiennych losowych X

f(R

), gdzie

maj¡ rozkªady jednostajne na odcinku [0

;1], a f(x) jest dowol-

nie wybran¡ funkcj¡, której dziedzin¡ jest odcinek [0

;1]. Obliczy¢ m = EX

= D

, a nast¦pnie z wygenerowanej próby znale¹¢ przedziaªy ufno±ci dla

m i

dla poziomów ufno±ci 1

= 0:90, 1

= 0:95 i 1

= 0:99.

6. Testowanie hipotez

6.1. Testy parametryczne

Testy statystyczne maj¡ za zadanie werykacj¦ pewnej hipotezy, na podsta-

Intuicje testów

wie danych statystycznych. Testy parametryczne sªu»¡ do werykacji hipotez o

warto±ciach parametrów w rozkªadach zmiennych losowych. Testy nieparame-

tryczne, o których b¦dzie mowa w nast¦pnym rozdziale, b¦d¡ sprawdza¢ praw-

dziwo±¢ hipotez, w których nie s¡ b¡d¹ nie musz¡ by¢ sprecyzowane warto±ci

parametrów. Testowanie hipotez statystycznych ma (w ka»dym razie w zakre-

sie tego wykªadu) charakterystyczn¡ posta¢ { hipoteza ma posta¢ równo±ci

, gdzie

jest prawdziw¡, a nam nieznan¡ warto±ci¡ parametru rozkªadu,

natomiast

jest warto±ci¡ hipotetyczn¡. Oznacza to, »e taka równo±¢ jest

sprawdzan¡ (werykowan¡) hipotez¡, któr¡ mo»na przyj¡¢ (cho¢ tego raczej

si¦ nie robi) albo odrzuci¢ i w zamian przyj¡¢ inn¡, (na przykªad

) albo

postanowi¢, »e nie ma podstaw do jej odrzucenia, cho¢ nie oznacza to jej przy-

j¦cia, a mo»e oznacza¢ konieczno±¢ przeprowadzenia dalszych bada«. Kiedy

jeste±my skªonni hipotez¦ odrzuci¢? Intuicyjnie zrobimy tak, gdyby przyj¦cie

hipotezy oznaczaªoby, »e zaszªo zadarzenie bardzo maªo prawdopodobne, na

przykªad zdarzenie, którego prawdopodobie«stwo byªoby mniejszeod

= 0:05,

czyli takie, które zadarzaªoby si¦ ±rednio 5 razy na 100.

Rozumowanie to sprecyzujemy nast¦puj¡co. Niech

b¦dzie parametrem w

Formalizacja

testów

pewnym rozkªadzie o dystrybuancie

F(x;). Niech

oznacza, »e stawiamy hipotez¦

zwan¡ hipotez¡ zerow¡ któr¡ mo-

»emy odrzuci¢ na korzy±¢ hipotezy

zwanej hipotez¡ alternatywn¡,

któr¡ przyjmujemy. Znak

oznacza tu jeden z trzech operatorów: =,

< lub

>. Z rozkªadem F(x;) i parametrem zwi¡zujemy statystyk¦

Z = Z(X

;:::;X

)

oraz obszar

sªu»¡ce do werykacji hipotezy

w ten sposób, aby przy

zaªo»eniu prawdziwo±ci

byªa speªniona równo±¢

Pr(

Q) = :

(6.1.1)

Wtedy odrzucamy

i przyjmujemy

o ile istotnie zdarzy si¦, »e

z = Z(!)

Q, czyli gdy zajdzie zdarzenie maªo prawdopodobne. W praktyce statystycznej

przyjmuje si¦ zwykle, »e

= 0:05 albo czasem = 0:01 lub ewentualnie

= 0:1.

Obszar

Q nazywa si¦ obszarem krytycznym, a liczb¦ nazywa si¦ poziomem

Obszar

krytyczny i

poziom

istotno±ci

istotno±ci. A wi¦c hipotez¦ zerow¡ odrzucamy na korzy±¢ alternatywnej, gdy

warto±¢ zwi¡zanej z hipotez¡ statystyki znajdzie si¦ w obszarze krytycznym.

Mo»e si¦ oczywi±cie zdarzy¢, »e

Q mimo, »e hipoteza H

jest prawdziwa.

Zdarzy si¦ to jednak z maªym prawdopodobie«stwem

. Popeªniamy wtedy

6.1 Testy parametryczne

bª¡d polegaj¡cy na odrzuceniu hipotezy prawdziwej, zwany bª¦dem pierw-

szego rodzaju. Przyj¦cie hipotezy

faªszywej stanowi bª¡d drugiego rodzaju.

W przyj¦tej tutaj procedurze nie ma jednak przyjmowania

, co najwy»ej

stanowi si¦, »e nie ma podstaw do jej przyj¦cia. Tak¡ procedur¦ post¦powa-

nia przyj¦to, gdy» nie precyzuje si¦ tu prawdopodobie«stwa popeªnienia bª¦du

drugiego rodzaju. W nast¦pnych dwóch punktach omówimy dwa przykªadu

testów statycznych, gdzie nieznanymi parametrami próby b¦d¡ warto±¢ ocze-

kiwana i wariancja. Liczne przykªady innych testów mo»na znale¹¢ w ksi¡»ce

[3].

6.1.1. Testy dla ±redniej

Podobnie jak dla przedziaªów ufno±ci, rozpatrujemy trzy modele: rozkªad nor-

malny i znana wariancja, rozkªad normalny i nieznana wariancja, rozkªad do-

wolny ze sko«czon¡ wariancj¡ i du»a próba. We wszystkich modelach

n oznacza

liczebno±¢ próby.

Model I

. Populacja generalna ma rozkªad N(

m;), odchylenie standardowe

Rozkªad

normalny,

znane

jest znane. Nieznany jest parametr

m, dla którego stawiamy hipotez¦ H : m =

przeciwko jednej z trzech hipotez:

;

m > m

;

m < m

Statystyka sªu»¡ca do werykacji hipotezy dana jest wzorem

U =

(6.1.2)

która przy zaªo»eniu prawdziwo±ci hipotezy

ma rozkªad N(0

;1).

W przypadku hipotezy alternatywnej

obszar krytyczny jest

dwustronny, symetryczny i dla poziomu istotno±ci

okre±lony jest wzorem

Q = (

;

)

[

(

;

), gdzie

wyznaczone jest z zale»no±ci Pr(

) =

. Dla hipotezy alternatywnej H

m < m

obszar krytyczny jest

lewostronny i okre±lony jest wzorem

Q = (

), a dla

m > m

obszar

krytyczny jest prawostronny i okre±lony jest wzorem

Q = (u

;

) gdzie

wyznaczone jest z zale»no±ci Pr(

U > u

) =

. Zmienna losowa U ma tutaj

rozkªad normalny N(

m;).

Model II

. Populacja generalna ma rozkªad N(

m;), odchylenie standardowe

Rozkªad

normalny,

nieznane

jest nieznane. Hipoteza zerowa i hipotezy alternatywne s¡ takie same jak w

poprzednim modelu. Poniewa» jednak

nie jest znane, to statystyka sªu»¡ca

do werykacji hipotezy dana jest wzorem

t = X

1 =

(6.1.3)

która przy zaªo»eniu prawdziwo±ci hipotezy

ma rozkªad

t-Studenta o n

stopniach swobody. Wobec tego

jest zast¡pione przez

wyznaczone ze

wzorów Pr(

> t

) =

lub Pr(t > t

) =

6.1 Testy parametryczne

Poniewa» dost¦pne tablice statyczne podaj¡ warto±¢

dla danych

i n, to

przy jednostronnych (lewo i prawostronnych) obszarach krytycznych trzeba

skorzysta¢ z zale»no±ci 2Pr(

t > t

) = Pr(

> t

Model III

. Populacja generalna ma rozkªad N(

m;), parametr mo»e, ale

Rozkªad

normalny,

du»a próba

musi by¢ znany, natomiast próba jest du»a, (

n conajmniejkilkadziesi¡t).Wzory

takie same jak w modelu I lub II, to znaczy (6.1.2) lub (6.1.3), gdzie

jest

zast¡pione przez

lub ^

Przykªad.

Posªó»my si¦ danymi ze strony 53. Dla takich danych mamy

x = 2:0031 i ^s = 0:1967. Je»eli postawimy hipotez¦ H

m = 2 przeciw

hipotezie

= 2 na poziomie istotno±ci

= 0:05, to obliczona ze wzoru

(6.1.2) statystyka

= 0

:16 < u

= 1

6.1 Testy parametryczne

Obliczaj¡c otrzymujemy ^

= 0

:004779 oraz ^s = 0:06913. St¡d i ze wzoru

(6.1.4) mamy

= 17

:20. Poniewa» dla 9 stopni swobody

= 16

:919, to

odrzucamy hipotez¦ zerow¡ na korzy±¢ alternatywnej czyli przyjmujemy, »e

dokªadno±¢ jest gorsza ni» 0

:05 jednostki. Je»eli jednak zadowala nas dokªad-

no±¢ 0

:1 jednostki, to wtedy

= 4

:30 i stwierdzamy, »e nie ma podstaw do

odrzucenia takiej hipotezy.

6.1.3. Testy dla dwóch ±rednich
6.1.4. Zadania

Cecha w populacji generalnej ma rozkªad normalny. Z pomiarów otrzymano

4 wyniki: 121, 120, 133, 122. Na poziomie istotno±ci

= 0:05 zwerykowa¢

hipotez¦, »e

m = 125 oraz hipotez¦, »e = 5. Na poziomie ufno±ci 1

oszacowa¢ metod¡ przedziaªow¡ parametry

m i . Powtórzy¢ obliczenia dla

= 0:01 i = 0:02.

Cecha w populacji generalnej ma rozkªad normalny N(

m;1:2). Z pomiarów

otrzymano 5 wyników: 2.3922, 3.9655, 5.2769, 2.2171, 1.9742. Na poziomie

istotno±ci

= 0:05 zwerykowa¢ hipotez¦, »e m = 3. Na poziomie ufno±ci

oszacowa¢ metod¡ przedziaªow¡ parametr m. Powtórzy¢ obliczenia dla

= 0:01 i = 0:02.

Z próby 100 elementowej obliczono

x = 1:28 i s

= 0

:21. Czy na poziomie

istotno±ci

= 0:01 mo»na zwerykowa¢ hipotez¦, »e m = 1:25 oraz hipotez¦, »e

= 0

:2? Na poziomie ufno±ci 1

oszacowa¢ metod¡ przedziaªow¡ parametr

4*.

Dla danych z zadania 3 zwerykowa¢ hipotez¦, »e

m i maj¡ warto±ci

obliczone jako parametry teoretyczne. Przyj¡¢ poziom istotno±ci

= 0:1, =

:05 i = 0:01.

6.2 Testy nieparametryczne

6.2. Testy nieparametryczne

6.2.1. Testy zgodno±ci

Testy zgodno±ci sªu»¡ do werykacji hipotez o postaci rozkªadów, a dokªadniej

o postaci dystrybuant rozkªadów. Hipoteza zerowa, któr¡ b¦dziemy weryko-

wa¢ b¦dzie miaªa posta¢

F(x) = F

(

x) lub H

F(x;) = F

(

x;), prze-

ciw hipotezie alternatywnej

F(x)

(

x) lub H

F(x;)

(

x;),

gdzie

jest parametrem rozkªadu, które warto±¢ te» mo»e by¢ werykowana.

Przykªad.

Hipotez¡ mo»e by¢

F(x)

m;), gdzie m i s¡ pew-

nymi, nie interesuj¡cymi nas parametrami. Hipoteza mo»e te» by¢ postaci

F(x)

N(0

;) albo te» H

F(x)

N(0

;1).

Test sªu»¡cy do werykacji hipotezy o postaci dystrybuanty rozkªadu, powinien

mierzy¢ rozbie»no±ci pomi¦dzy dytrybuant¡ hipotetyczn¡

(

x) a wynikami

otrzymanymiz próby. Pierwszym takim testemjest test chi-kwadrat Pearsona.

Test zgodno±ci

Pearsona

Polega on na tym, »e o± liczbow¡ dzielimyna rozª¡czne przedziaªy

punktami

i = 1;2;:::;r

1. Otrzymujemy w ten sposób

n przedziaªów,

= (

)

;

= [

)

; :::;

= [

;

)

Oznaczmy przez

liczb¦ wyników w przedziale

n = n

. Niech

= Pr(

, gdzie

X jest zmienn¡ losow¡ (cech¡ w populacji generalnej),

F(x) jej dystrybuant¡ (hipotetyczn¡). Statystyka

(

)

(6.2.1)

mierzy tak¡ wªa±nie rozbie»no±¢ mi¦dzy wynikami otrzymanymi a dystrybu-

ant¡ hipotetyczn¡. Nale»y jednak zwróci¢ uwag¦, »e dla efektywnego obliczenia

prawdopodobie«stw

nale»y zna¢ równie» wszystkie parametry wyst¦puj¡ce

w dystrybunancie

F(x). Je»eli nie s¡ one jednak znane, to trzeba je estymowa¢.

Twierdzenie 6.2.1.

Je»eli nieznane parametry dystrybuanty

F(x) s¡ oszaco-

wane metod¡ najwi¦kszej wiarogodno±ci, to dystrybuanta statystyki okre±lonej

wzorem (6.2.1) jest zbie»na dla

do dystrybunaty rozkªadu chi-kwadrat

Pearsona o

1 stopniach swobody, gdzie

k jest liczb¡ nieznanych para-

metrów.

Je»eli

n jest dostatecznie du»a (n równe kilkadziesi¡t, na przykªad n = 60)

oraz w ka»dej klasie

jest conajmniej 8 wyników,

8, to mo»na na pod-

stawie twierdzenia 6.2.1 przyj¡¢, »e statystyka okre±lona wzorem (6.2.1) ma w

przybli»eniu rozkªad chi-kwadrat. Je»eli w jakiej± klasie jest mniej ni» 8 wyni-

ków, to tak¡ klas¦ nale»y poª¡czy¢ z s¡siedni¡. Obszar krytyczny jest postaci

przedziaªu (

;

), a wi¦c hipoteza zerowa zostanie odrzucona na poziomie

istotno±ci

, gdy

, a

jest wyznaczone ze wzoru (i odczytane z

tablic) Pr(

) =

Innym testem zgodno±ci jest test Koªmogorowa. W porównaniu z testem

Test zgodno±ci

Koªmogorowa

Pearsona ma on liczne ograniczenia. Wymaga on wyników dokªadnych, nie

6.2 Testy nieparametryczne

pogrupowanych w klasy, du»ej próby i mo»na nim sprawdza¢ tylko hipotezy

dotycz¡ce rozkªadów ci¡gªych, w których sprecyzowano warto±ci parametrów.

Idea testu Koªmogorowa polega na mierzeniu odchylenia dystrybuanty teore-

tycznej od empirycznej. Stawiamy hipotez¦

F(x) = F

(

x), gdzie F

(

jest dystrybuant¡ typu ci¡gªego, z wszystkimi sprecyzowanymi parametrami.

Niech

(

x) b¦dzie dystrybuan¡ empiryczn¡. Oznaczmy

nsup

(

F(x)

(6.2.2)

Twierdzenie 6.2.2.

Statystyka okre±lona wzorem (6.2.2) ma w granicy przy

zaªo»eniu prawdziwo±ci hipotezy

oraz dla

, rozkªad niezale»ny od

postaci

F(x).

Rozkªad graniczny statystyki

okre±lonej wzorem (6.2.2) nazywa si¦ rozkªa-

dem Koªmogorowa. Jest on stablicowany, przy czym najcz¦±ciej podaje si¦

warto±ci

, przy których Pr(

) =

. Obszar krytyczny tworzy przedziaª

(

;

), czyli hipotez¦

odrzucamy, gdy

6.2.2. Testy niezale»no±ci

Populacj¦ generaln¡ badamy ze wzgl¦du na dwie cechy,

X i Y . Testujemy

hipotez¦ zerow¡

X i Y s¡ niezale»ne, czyli H

F(x;y) = F

(

x)F

(

przeciwko hipotezie alternatywnej

F(x;y)

(

x)F

(

y).

Oznaczmy przez

n liczebno±¢ próby. Warto±ci cechy X dzielimy na r klas, a

warto±ci cechy

Y na s klas. W ten sposób wszytkie elementy dzielimy na rs

klas. Przez

oznaczmy liczb¦ elementów, które ze wzgl¦du na cech¦

X s¡

w klasie

i-tej, a ze wzgl¦du na cech¦ Y s¡ w klasie j-tej. Okre±lmy ponadto

liczebno±ci brzegowe

; n

i = 1

Wtedy

n =

Z liczebno±ci brzegowych szacuje si¦ prawdopodobie«stwa brzegowe

= n

n ; p

= n

n :

Zakªadaj¡c prawdziwo±¢

, to znaczy niezale»no±¢ cech

X i Y , oblicza si¦

prawdopodobie«stwa hipotetyczne

6.2 Testy nieparametryczne

St¡d podobnie jak we wzorze (6.2.1) konstruuje si¦ statystyk¦

(

)

(6.2.3)

Twierdzenie 6.2.3.

Dystrybuanta statystyki okre±lonej wzorem (6.2.3) jest

zbie»na dla

do dystrybunaty rozkªadu chi-kwadrat Pearsona o (

1)(

1) stopniach swobody.

Obszar krytycznyjest okre±lony tak samo jak dla statystyki (6.2.1). Ze wzgl¦du

na to, »e statytystyka (6.2.3) ma rozkªad chi-kwadrat tylko przy

, to

musi by¢ bardzo du»e, a wszystkie

Je»eli

r = s = 2, to tablica [n

] nazywa si¦ tablic¡ czteropolow¡. W tym

przypadku mamy jeden stopie« swobody statystyki

6.2.3. Zadania

Przy pomocy testu chi-kwadrat Pearsona sprawdzi¢, czy cecha w populacji

generalnej ma rozkªad jednostajny, gdy z próby uzyskano nast¦puj¡ce wyniki:

2.07, 2.35, 1.52, 2.73, 2.30, 2.56, 1.46, 2.61, 2.86, 1.82, 1.81, 2.56, 1.97, 1.21,

2.16, 1.66, 2.62, 2.07, 1.29, 2.32. Czy mo»na odrzuci¢ hipotez¦, »e rozkªad jest

jednostajny na odcinku [1

;3] lub [1:2;2:2]? Przyj¡¢ poziom istotno±ci = 0:05.

Dane z próby

n-elementowej zostaªy pogrupowane w tabeli, gdzie

Przedziaª Liczba wyników

Na poziomie istotno±ci

= 0:02

zwerykowa¢ hipotez¦, »e rozkªad

jest a) wykªadniczy, b) wykªadni-

czy z parametrem

= 0:5.

3*.

Wygenerowa¢ w dowolny sposób 100 liczb o rozkªadzie normalnym z pa-

rametrami N(

m;), a nast¦pnie zwerykowa¢ przy pomocy testu chi-kwadrat

Pearsona, »e jest to a) rozkªad normalny, b) rozkªad normalny z parametrem

m, c) rozkªad normalny z parametrem , d) rozkªad normalny z parametrami

m i .

4*.

Dla danych z zadania 3 zwerykowa¢ przy pomocy testu Koªmogorowa

hipotez¦, »e s¡ to dane z rozkªadu normalnego z parametrami

m i .

Niech

b¦dzie liczb¡ rzutów kostk¡, w których wyrzucono

i oczek. W 180

rzutach otrzymano

= 25,

= 31,

= 24,

= 32,

= 28. Czy taki

wynik mo»na na poziomie istotno±ci

= 0:05 usprawiedliwi¢ przypadkiem?

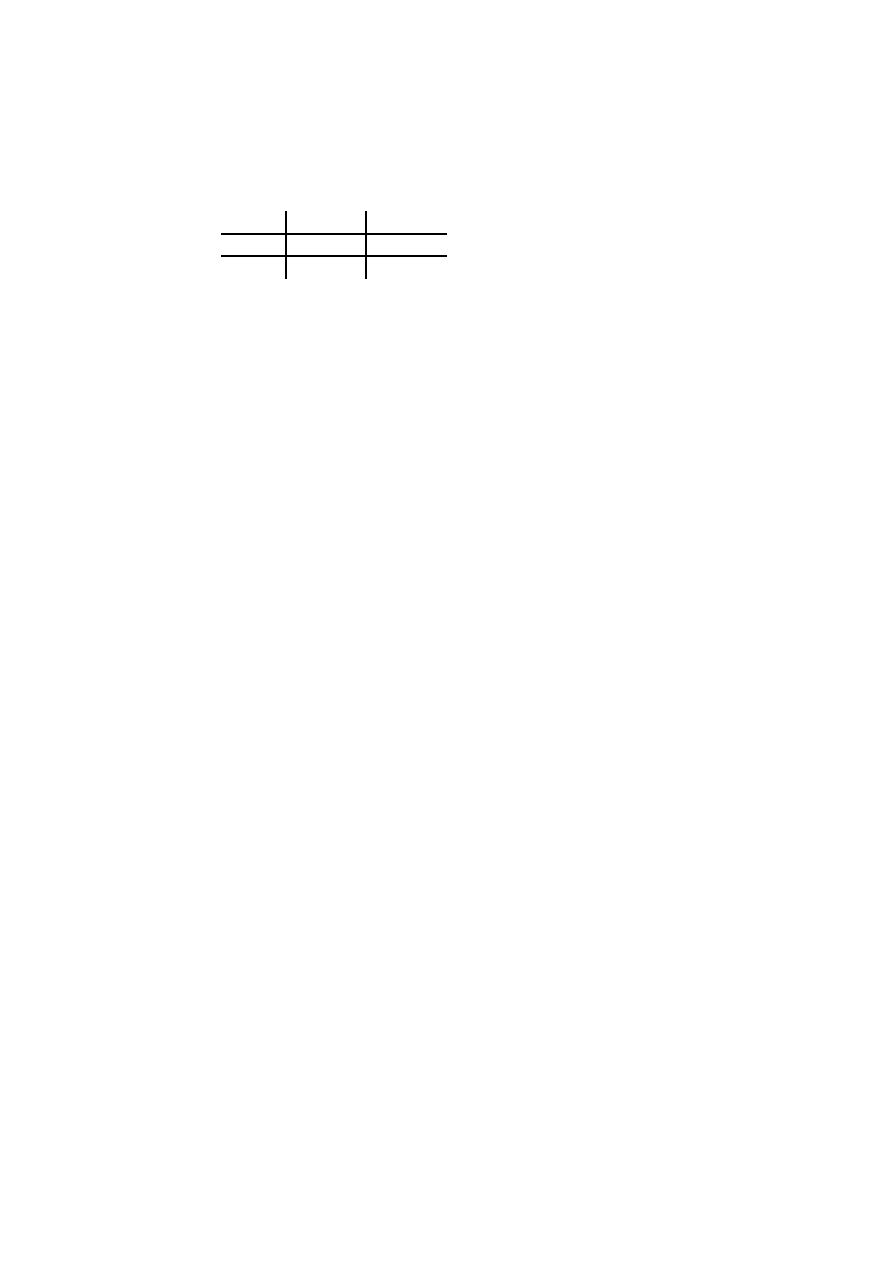
6.2 Testy nieparametryczne

Ka»dy element ma dwie cechy, cech¦

;1) oraz cech¦ Y przyjmuj¡c¡

tylko warto±ci 0 i 1. Czteropolowa tablica wygl¡da nast¦puj¡co:

X < 0:5 X

Y = 0

Y = 1

Na poziomie istotno±ci

= 0:05 zwerykowa¢ hipotez¦ o niezale»no±ci cech X

Y .

Literatura

[1] F. Clegg, Po prostu statystyka, Wyd. Szk. i Pedag., Warszawa 1994.

[2] M. Fisz, Rachunek prawdopodobie«stwa, PWN, (wiele wyda«).

[3] J. Gre«, Statystyka matematyczna, modele i zadania, PWN, (wiele wy-

da«)

[4] T. Inglot, T. Ledwina, Z. awniczak, Materiaªy do ¢wicze« z rachunku

prawdopodobie«stwa i statystyki matematycznej, skrypt P. Wr., 1979.

[5] W. Feller, Wst¦p do rachunku prawdopodobie«stwa, t. I, PWN, 1966.

[6] W. Feller, Wst¦p do rachunku prawdopodobie«stwa, t. II, PWN, 1969.