
WYDZIAŁ MECHANICZNY ENERGETYKI I LOTNICTWA
POLITECHNIKI WARSZAWSKIEJ
Zakład Teorii Maszyn i Robotów
Laboratorium Podstaw Automatyki i Sterowania IV
Instrukcja do ćwiczenie nr 5
Dobór nastaw regulatora w komputerowym
modelu układu regulacji
1. Cel ćwiczenia
Celem ćwiczenia jest dobór nastaw regulatora, znajdującego się w układzie
sterowania pewnym obiektem dynamicznym. Znana jest transmitancja obiektu, zatem re-
gulator można dobrać, budując, a następnie badając komputerowy model układu regulacji.
Warunki techniczne narzucają konieczność uzyskania zerowego uchybu ustalonego,
dlatego zdecydowano się na zastosowanie regulatora PI. Układ sterowania musi ponadto
charakteryzować się czasem regulacji poniżej 5 s, przeregulowaniem mniejszym niż 35%,
zapasem modułu co najmniej 16 dB, zapasem fazy nie mniejszym niż 45° i pasmem
przenoszenia o pulsacji granicznej co najmniej 1 rad/s.
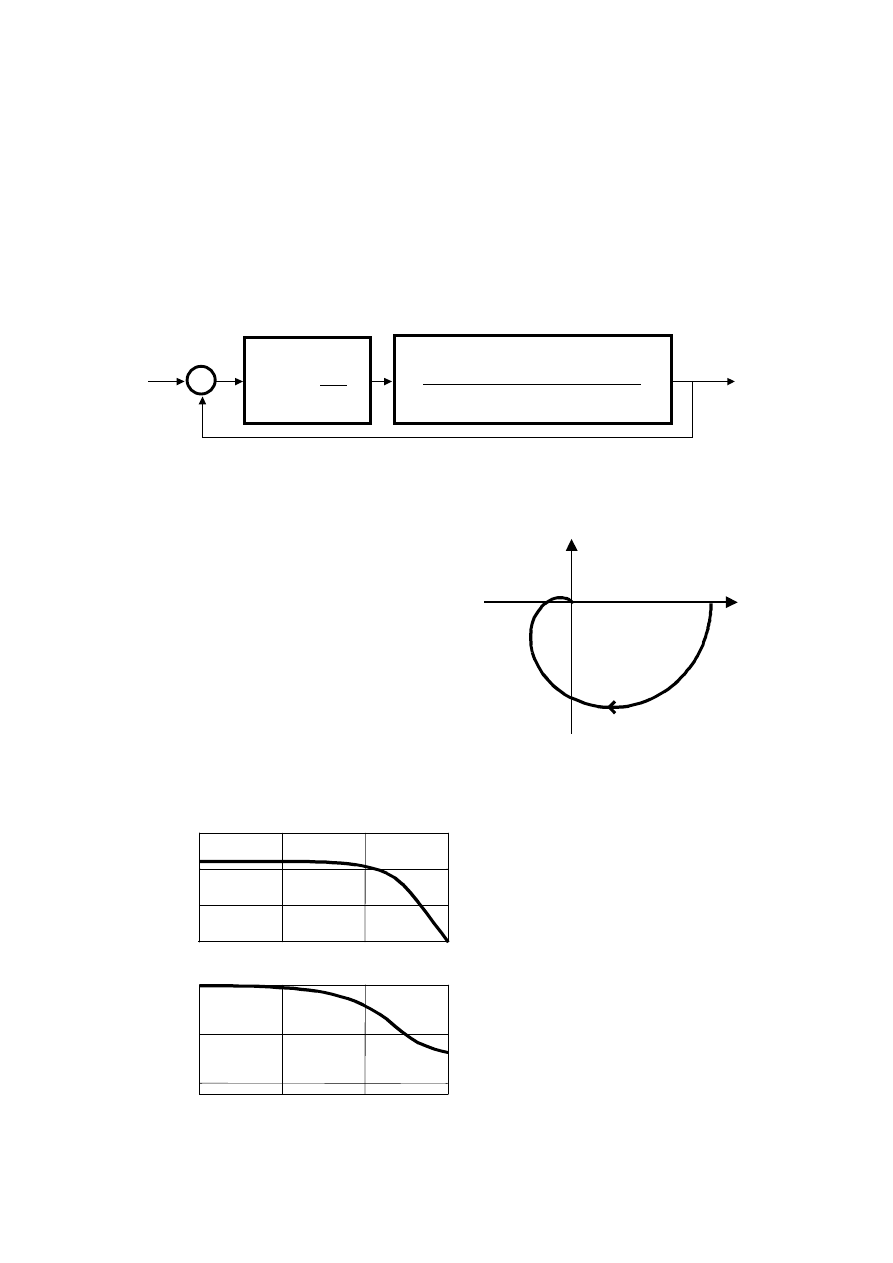
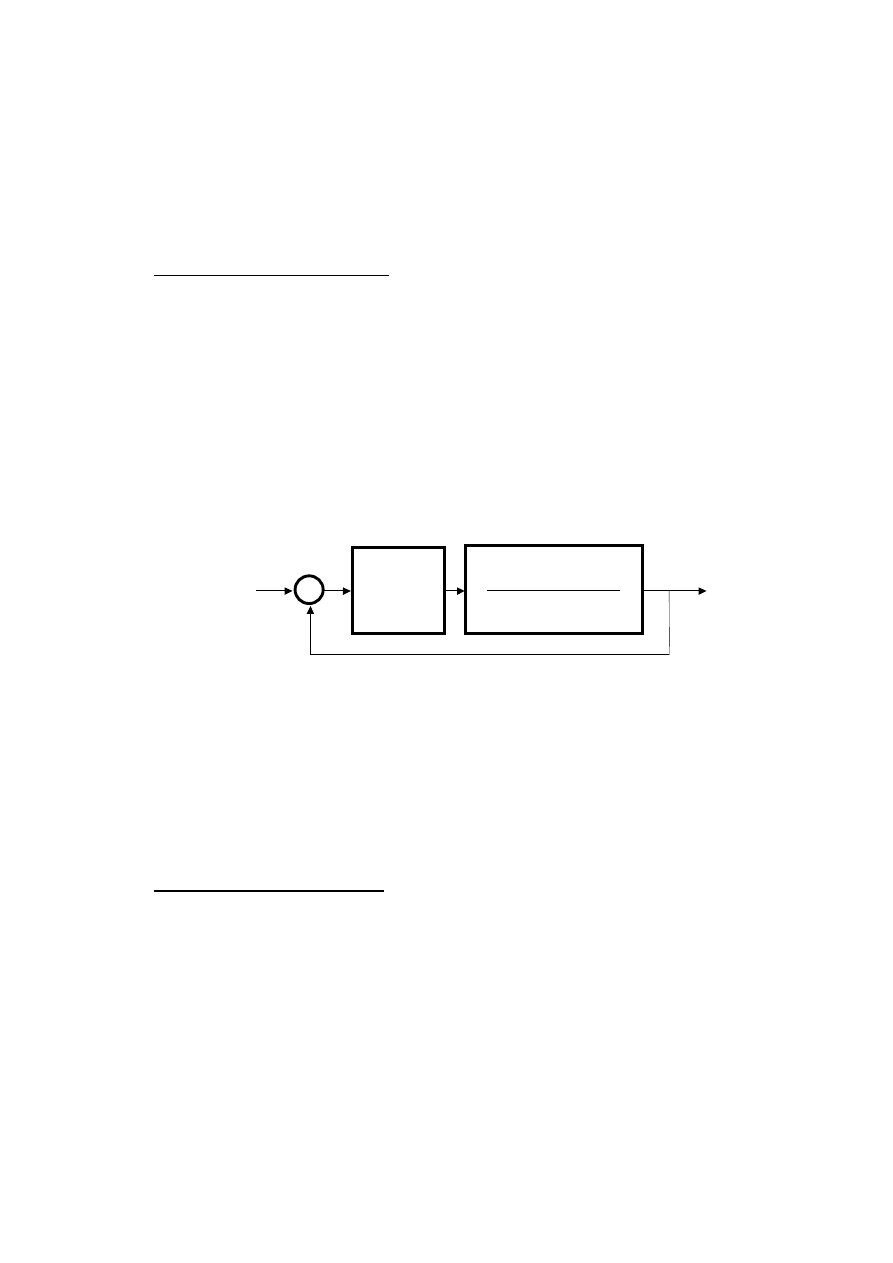
Schemat blokowy układu automatycznej regulacji przedstawiony jest na rysunku.
Obiekt regulacji
(
)
(
)
(
)(
)
1
+
0.01s
1
+
s
+
5s
+
s
1
+
s
0.05
2
2
B
A
Regulator PI
k 1 +
1
T s
p
i
+ –
Wielkość
zadana
Wielkość
regulowana
Rys. 1
. Schemat blokowy układu regulacji
2. Przypomnienie niezbędnych wiadomości
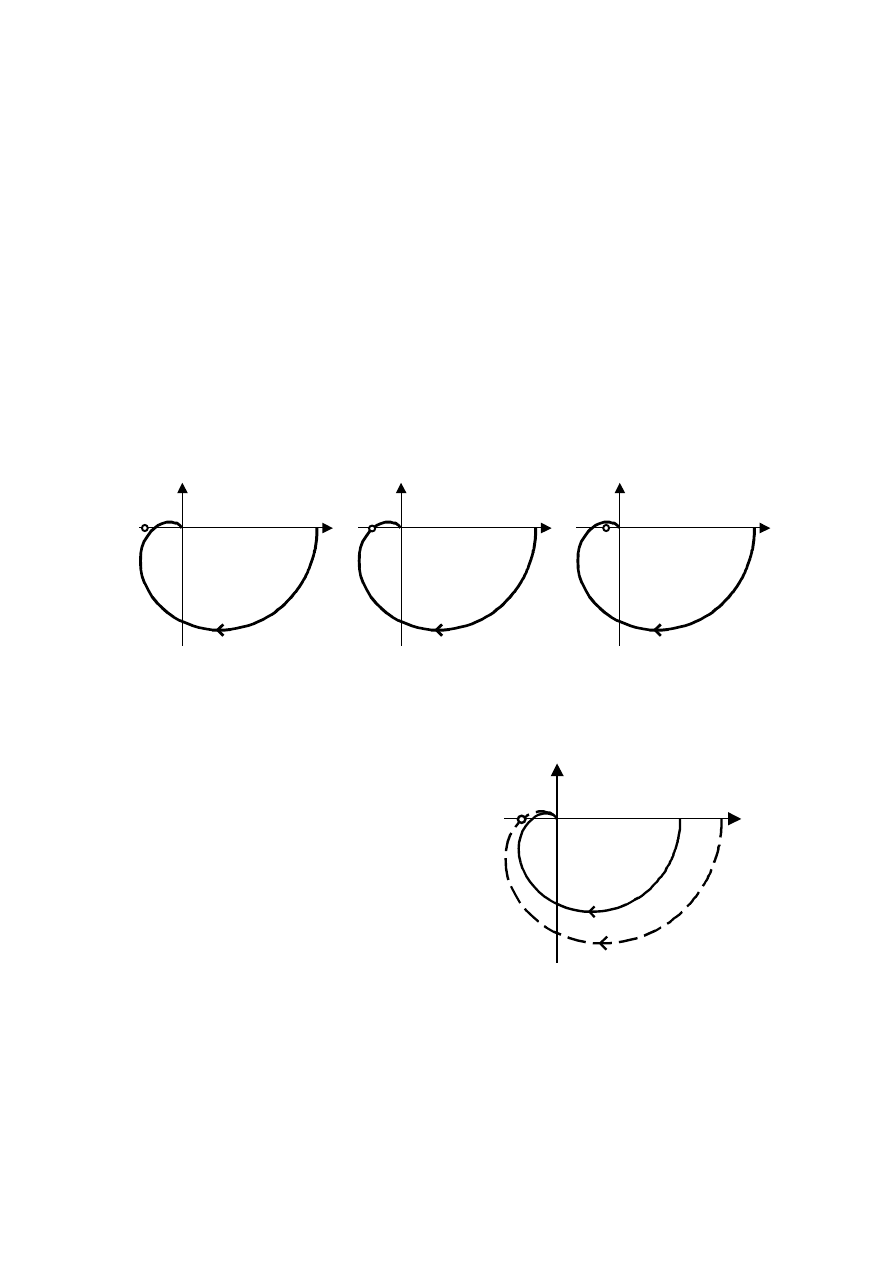
O własnościach dynamicznych układu
świadczy jego transmitancja widmowa G(jω)
(zob. rozdz. 3.3. z [1]). Wykres transmitancji
widmowej na płaszczyźnie zespolonej nazy-
wany jest
charakterystyką amplitudowo-fa-
zową (charakterystyką Nyquista). Każdy
punkt tego wykresu odpowiada innej czę-
stotliwości ω i reprezentuje liczbę zespoloną,
której moduł |G(jω)| oznacza stosunek
amplitudy odpowiedzi ustalonej do amplitudy
wymuszenia harmonicznego, a argument
arg
G(j
ω
) przesunięcie fazowe między odpo-
wiedzią a wymuszeniem.
Często stosowane są charakte-
rystyki Bodego:
- logarytmiczna charakterystyka ampli-
tudowa M(
ω) = 20 log |G(jω)| (M(ω) to
wzmocnienie wyrażone w decybelach);
- logarytmiczna charakterystyka fazowa
ϕ(ω) = arg G(jω).
Na wykresach Bodego podziałka częs-
totliwości jest logarytmiczna dekadowa,
tzn. każdej dekadzie (stosunkowi
częstotliwości równemu 10) odpowiada
odcinek jednakowej długości, a podziałki
M(
ω) i ϕ(ω
) są liniowe.
Wykreślanie charakterystyk Bo-
dego i charakterystyki amplitudowo-fa-
zo
wej to dwa różne sposoby graficznego
Im
Re
Rys. 2. Charakterystyka amplitudowo-fazowa
20
-180
-360
0
-40
-20
0
Częstość [rad/s]
10
1
10
0
10
-1
10
-2
Częstość [rad/s]
10
1
10
0
10
-1
10
-2
[dB]
W
z
m
o
c
n
i
e
n
i
e
[deg]
F
a
z
a
Rys. 3. Charakterystyki Bodego
1
przedstawienia tych samych informacji o
układzie dynamicznym. Charakterystyki Bodego
bywają jednak wygodniejsze w użyciu, gdyż informację o częstości sygnału można odczytać
wprost z wykresu, razem z odpowia
dającym jej wzmocnieniem i przesunięciem fazowym.
Podawanie wzmocnienia w decy
belach (20 logarytmów dziesiętnych z ilorazu amplitud
sygnału wyjściowego i wejściowego) ułatwia zapoznanie się z własnościami układu przy
wysokich częstościach sygnału, kiedy wzmocnienie osiąga małe wartości.
Układem regulacji nazywa się układ ze sprzężeniem zwrotnym, składający się
z regulatora i obiektu regulacji
. Regulator dobiera się tak, aby układ regulacji po
zamknięciu pętli sprzężenia zwrotnego był stabilny. Układy stabilne charakteryzowane są
przez zapas modułu i zapas fazy (zob. rozdz. 6.3.3 z [1]).
Pojęcia zapasu fazy i zapasu modułu związane są z twierdzeniem Nyquista
o
stabilności. Głosi ono, że jeżeli pewien układ otwarty jest stabilny, a jego charakterystyka
amplitudowo-fazowa nie obejmuje punktu (–1,0), to po z
amknięciu pętli sprzężenia
zwrotnego układ pozostanie stabilny; jeśli charakterystyka układu otwartego przechodzi
przez punkt (–
1,0), to po zamknięciu pętli sprzężenia zwrotnego znajdzie się on na granicy
stabilności; jeżeli natomiast charakterystyka obejmuje punkt (–1,0), to po zamknięciu pętli
sprzężenia zwrotnego będzie on niestabilny.
(–1,0)
Im
Re
(–1,0)
Im
Re
(–1,0)
Im
Re
a)
b)
c)
Rys. 4. Charakterystyki Nyquista układu otwartego.
Po zamknięciu pętli sprzężenia zwrotnego układ będzie:
a) stabilny, b) na granicy stabilności, c) niestabilny
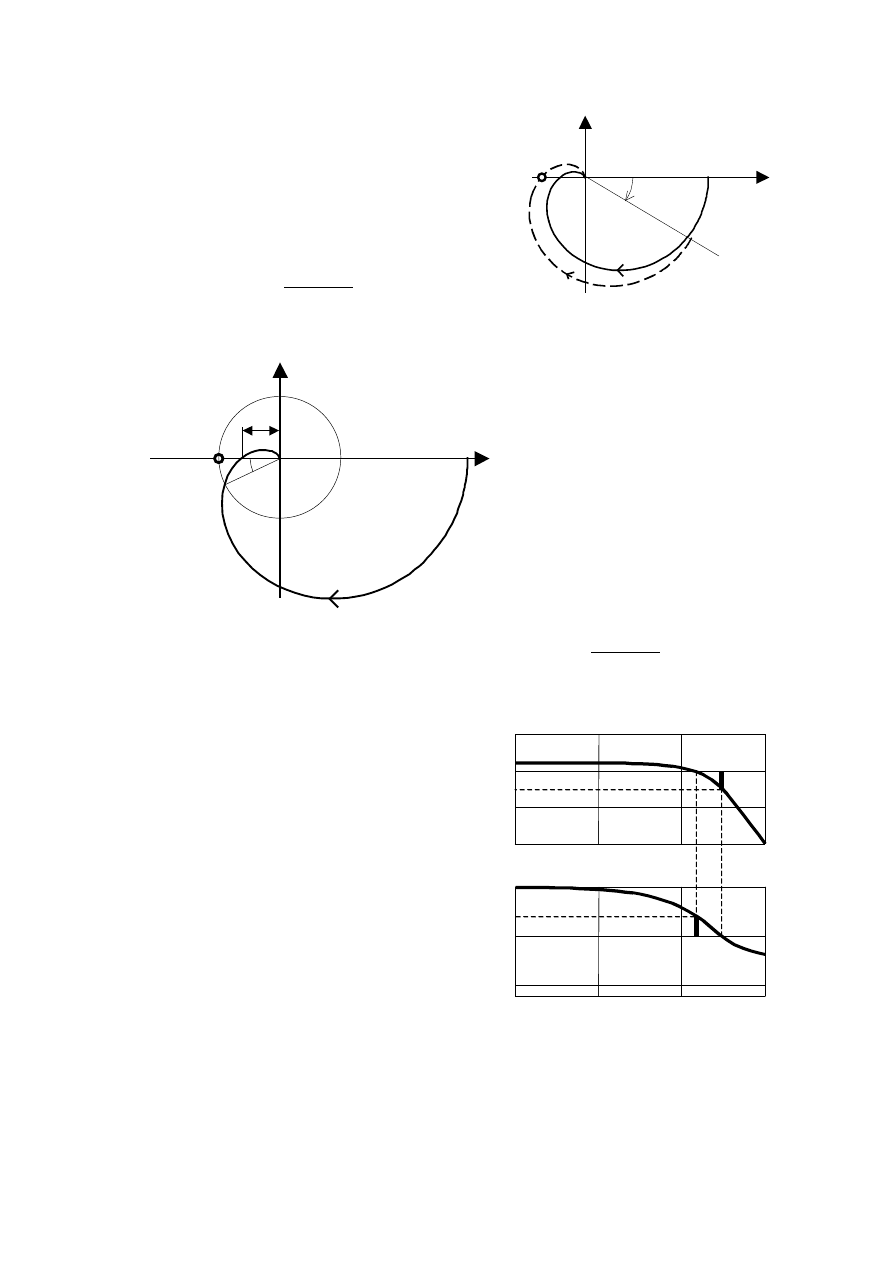
Gdyby
zwiększyć
wzmocnienie
w
układzie otwartym i pozostawić przesunię-
cie fazo
we bez zmian, to po zamknięciu pętli
sprzężenia zwrotnego układ znalazłby się na
granicy stabilności. Współczynnik, przez jaki
należałoby pomnożyć wzmocnienie, stanowi
miarę oddalenia układu od granicy stabilności;
jest on nazywany zapasem modułu i definio-
wany następująco:
Zapas modułu jest współczynnikiem
α
, przez jaki należy pomnożyć wzmoc-
nienie układu otwartego przy niezmie-
nionym argumencie transmitancji
widmowej, aby układ regulacji po
zamknięciu pętli sprzężenia zwrotnego znalazł się na granicy stabilności. Zapas
modułu wyraża się zwykle w decybelach, wynosi on wtedy 20 log α.
Gdyby zmienić przesunięcie fazowe w układzie otwartym i pozostawić wzmocnienie
bez zmian, to po zamknięciu pętli sprzężenia zwrotnego układ znalazłby się na granicy
stabilności. Kąt zmiany fazy jest miarą oddalenia układu od granicy stabilności; jest on
nazywany zapasem fazy i
definiowany następująco:
(–1,0)
Im
Re
Rys. 5. Doprowadzanie układu do granicy
stabilności poprzez zwiększanie wzmocnienia
2
Zapas fazy
określa wartość zmiany
argumentu transmitancji widmowej układu
otwartego przy niezmienionym wzmoc-
nieniu, która spowo
duje, że układ po
zamknięciu pętli sprzężenia zwrotnego
z
najdzie się na granicy stabilności. Zapas
fazy wyrażany jest w stopniach.
Zapas fazy
∆ϕ
odczytuje się z wykresu
Nyquista dla układu otwartego
Zapas modułu można także
odczytać z wykresów Bodego dla
uk
ładu
, wykre
ślając okrąg
o
środku w punkcie (0,0) i promieniu 1, a następnie
znajdując punkt jego przecięcia
z charaktery
styką
amplitudowo-
fazową. Różnica pomiędzy położe-
niem kątowym punktu przecięcia
a
kątem –180° to poszukiwany
zapas fazy. Zapas modu
łu ∆M
oblicza się, znajdując punkt prze-
cięcia charakterystyki z osią rzeczy-
wis
tą, odczytując wzmocnienie k
w tym punkcie, a
następnie wyraża-
jąc je w decybelach i zmieniając
znak.
otwartego
(należy tylko
pamiętać, że punkt (–1,0) na
wykresie Nyquista odpowiada wzmocnieniu 0 dB i
przesunięciu fazowemu –180°). Z wy-
kresu fazy od
czytuje się częstość ω
f
Podobnie z wykresów Bodego dla
układu otwartego odczytać można zapas fazy.
Z
wykresu modułu odczytuje się częstość ω
, dla której
prze
sunięcie fazowe wynosi –180°. Jeżeli
wzmoc
nienie dla tej częstości wynosi m dB
(m
<0), to układ znajdzie się na granicy sta-
bilności dopiero po zwiększeniu wzmocnienia
o –m
dB, zapas modułu wynosi zatem –m dB.
m
,
przy której wzmocnienie wynosi 0 dB. Jeżeli
przesunięcie fazowe dla tej częstości wynosi
f
° (f
<0), to układ znajdzie się na granicy
stabilności dopiero po zmianie przesunięcia
fazowego o (
f
°
– (–180°)
(–1,0)
Im
Re
), zapas fazy wynosi
zatem f °+180°.
Rys. 6. Doprowadza
nie układu do
granicy stabilności poprzez zmianę fazy
Im
Re
∆ϕ
k
∆M = 20 log α = 20 log(1/k) = –20 log k
(
–1,0)
Rys. 7. Odczytywanie zapasu fazy i modułu
z wykresu Nyquista
20
-180
-360
0
-40
-20
0
10
1
10
-1
10
-2
10
1
10
0
10
-1
10
-2
ω [rad/s]
ω
f
ω
m
∆M
∆ϕ
m
f
ϕ(ω) [deg]
M(
ω) [dB]
Rys. 8. Odczytywanie zapasu fazy i modułu
z wykresów Bodego
3
Sposób odczytania zapasu modułu i zapasu fazy z wykresów Bodego można opisać
jednym zdaniem: je
żeli charakterystyka amplitudowa ma wartość 0 dB przy częstości ω
m
,
a cha
rakterystyka fazowa wartość –180° przy częstości ω
f
, to zapas modułu wynosi –M(ω
f
),
a zapas fazy 180°+
ϕ(ω
m
).
O własnościach dynamicznych układu regulacji świadczy także jego pasmo
przenoszenia oraz przeregulowanie i czas regulacji (zob. rozdz. 7.3.2 z [1]).
Pasmem przenoszenia
układu nazywa się zakres częstotliwości, przy którym
charakterystyka amplitudowa M(
ω
) układu zamkniętego jest płaska (zmienia się o nie
więcej niż 3 dB). Częstość ω
g
ograniczająca to pasmo nazywana jest pulsacją graniczną
układu. Pulsacja graniczna równa jest w przybliżeniu częstości ω
m
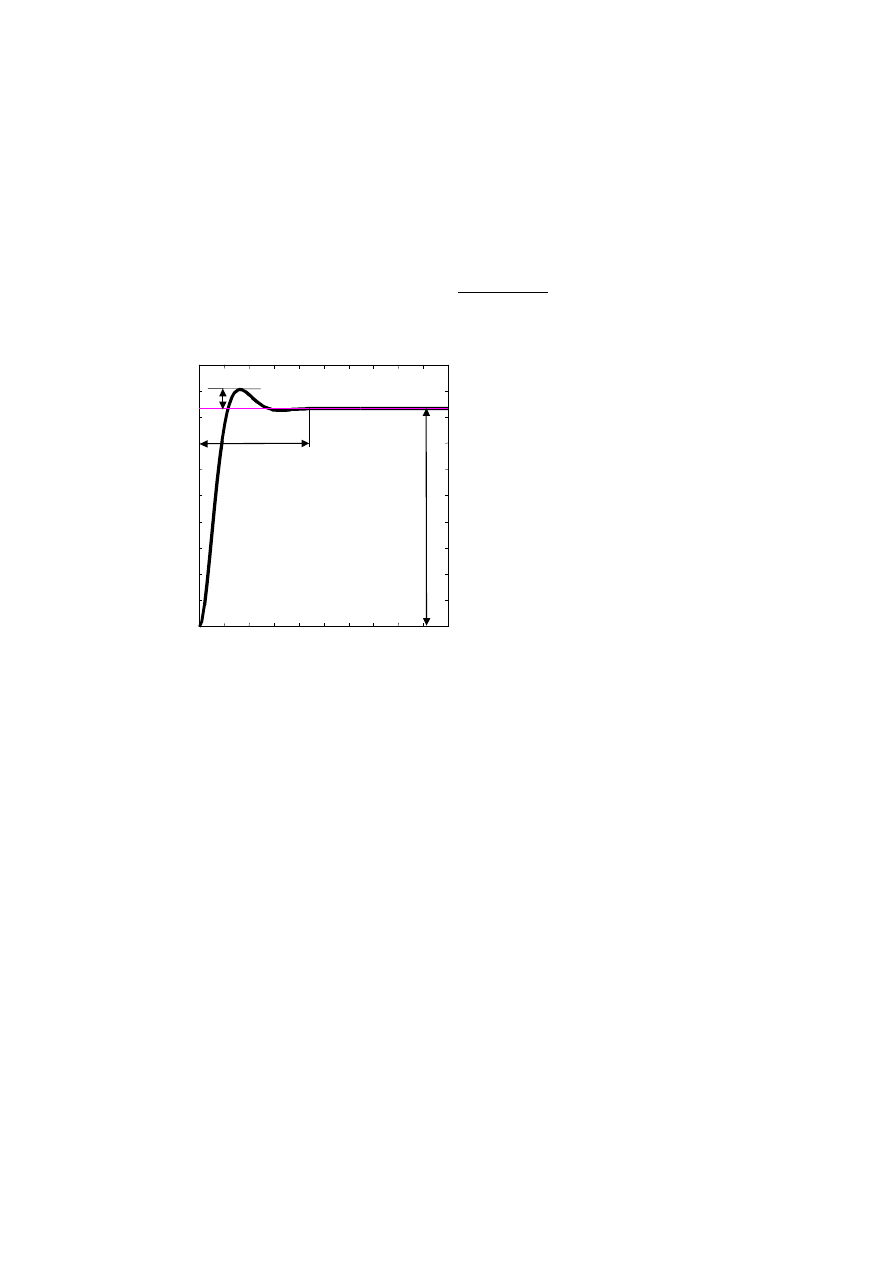
Typową charakterystyką układu
regulacji jes
t jego odpowiedź na
wymuszenie skokiem jednostkowym. Na
podstawie odpowiedzi układu na skok
jednostkowy określa się czas regulacji t
dla układu otwartego.
r
Czas regulacji jest to czas liczony
od chwili wystąpienia wymuszenia
skokowego do chwili, po której wiel
kość
regulowana różni się od wielkości
ustalonej mniej niż o założoną wartość
(zwykle 1% ÷
5% wartości ustalonej).
i przeregulowanie
κ.
Przeregulowanie
to różnica mak-
sy
malnej wartości chwilowej odpowiedzi
i
wartości ustalonej podzielona przez war-
tość ustaloną (jeśli wartość ustalona jest
niezerowa).
Jednym ze sposobów wstępnego
doboru nastaw regulatora jest posłużenie się metodą Zieglera-Nicholsa. Docelowy regulator
zastępuje się regulatorem proporcjonalnym, następnie uruchamia się układ regulacji
i
zwiększa wzmocnienie aż do wystąpienia niegasnących oscylacji sygnału wyjściowego
(innymi słowy doprowadza się układ regulacji do granicy stabilności). Notuje się
wzmocnienie k
osc
, przy którym wystąpiły niegasnące oscylacje oraz ich okres T
osc
. Nastawy
docelowego reg
ulatora dobiera się, wykorzystując uzyskane doświadczalnie wartości k
osc
i T
osc
oraz tabelę podającą orientacyjne nastawy w zależności od wybranego typu regulatora.
Np. dla regulatora PI wstępne nastawy wynoszą: k
p
= 0.45 k
osc
oraz T
i
= 0.85 T
osc
Jeżeli znany jest matematyczny opis badanego obiektu regulacji (np. jego
transmitancja operatorowa), to doświadczenie Zieglera-Nicholsa można przeprowadzić
metodą symulacji komputerowej.
.
t
r
y
u
d
10
2
1
0
Czas [s]
A
m
p
l
i
t
u
d
a
κ = d/y
u
Rys. 9. Charakterystyka skokowa
4
3. Użyteczne procedury programu „Matlab”
Komputerowy model układu regulacji wygodnie jest zbudować, posługując się
programem „Matlab”, gdyż jest on przeznaczony m.in. do symulacji układów sterowania.
Poniżej zamieszczono skrótowy opis procedur programu, które ułatwią wykonanie
ćwiczenia. Szczegółowy opis procedur można znaleźć, wpisując w „Matlabie” polecenie
help wraz z
nazwą procedury.
•
⇒ Licznik i
mianownik transmitancji zapisuje się osobno, w postaci wektorów zawiera-
jących współczynniki wielomianów stojące przy kolejnych (uporządkowanych malejąco)
potęgach zmiennej s. Wektor wpisuje się w nawiasach kwadratowych, oddzielając kolejne
elementy przecinkami lub odstępami (np. L=[1 2 1]; ).
Zapis transmitancji w „Matlabie”
⇒
Program wypisuje na ekranie wynik wykonanej operacji, jeśli polecenie nie zostało
zakończone średnikiem.
⇒
Dwa wielomiany można pomnożyć przez siebie, używając dwuargumentowej procedury
conv(),
mnożąc więcej wielomianów należy wywołać tę procedurę wielokrotnie
(np. ABC=conv(A,conv(B,C)); ).
Przykład:
Obiekt regulacji
(
)
(
)
1
2s
s
1
5s
3
s
2
+
+
+
+
Regulator P
5
k
p
=
+ –
Model matematyczny obiektu o
transmitancji danej na rysunku można zapisać
w
„Matlabie” następująco:
>> L=[1 3]
Wynik:
L =
1 3
>> M=conv([5 1],[1 2 1])
Wynik:
M =
5 11 7 1
•
⇒
Wielomian można pomnożyć przez skalar (np. N=5*L , albo N=5*[1 5] ).
Obliczanie zapasu modułu i fazy
⇒ Procedura bode(L,M)
służy do wykreślania charakterystyk Bodego (L jest wektorem
zawierającym współczynniki wielomianu w liczniku, M – w mianowniku transmitancji).
⇒ Procedura margin(L,M)
działa identycznie jak procedura bode(), stosuje się ją dla układu
otwartego, uzyskując dodatkową informację o zapasie modułu i fazy oraz o częstościach
przecięcia
ω
m
i
ω
f
Przykład:
.
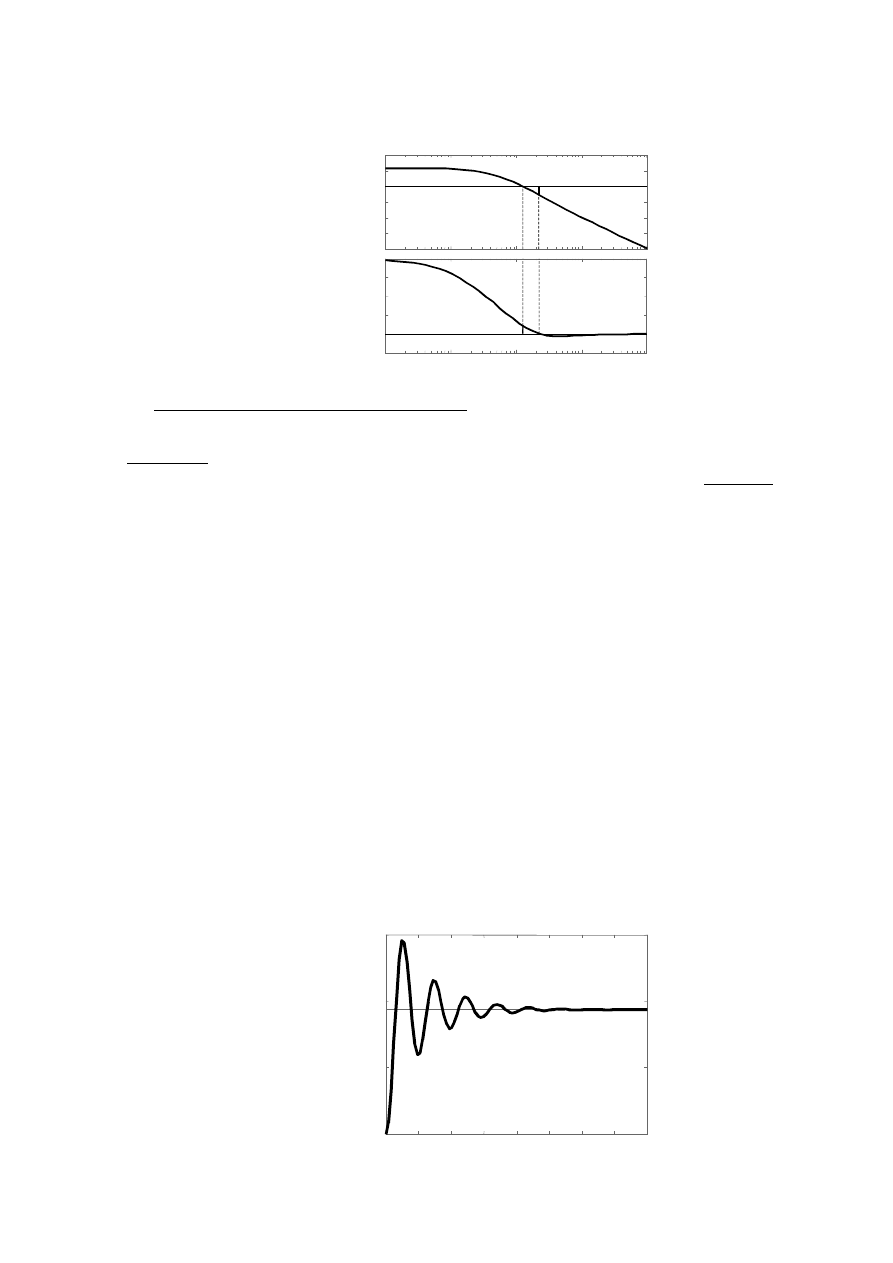
Zapas modułu i fazy przykładowego obiektu regulacji wraz z regulatorem P o wzmoc-
nieniu k
p
>> N=5*L;
=5 można obliczyć następująco:
5
>> margin(N,M)
Wynik:
-80
-60
-40
-20
0
20
40
Gm = 11.146 dB (at 2.2383 rad/sec), Pm = 18.989 deg (at 1.2512 rad/sec)
10
-2
10
-1
10
0
10
1
10
2
-225
-180
-135
-90
-45
0
•
⇒ Procedura cloop()
służy do obliczenia licznika Lz i mianownika Mz układu po
Obliczanie odpowiedzi na skok jednostkowy
zamknięciu pętli ujemnego sprzężenia zwrotnego (L jest wektorem zawierającym
wspó
łczynniki wielomianu w liczniku, M – w mianowniku transmitancji układu otwartego
⇒ Procedura step(Lz,Mz)
służy do obliczenia i wykreślenia odpowiedzi układu na skok
jednostkowy (Lz
jest wektorem zawierającym współczynniki wielomianu w liczniku, Mz –
w
mianowniku transmitancji układu, na którego wejście podawany jest skok jednostkowy).
;
jeśli trzeci argument będzie równy +1, to sprzężenie zwrotne będzie dodatnie). Procedurę
wywołuje się tak: [Lz,Mz]=cloop(L,M,-1).
⇒ Procedura linspace(a,b) generuje 50-elementowy wektor o
wartościach od a do b,
którego kolejne elementy są od siebie równo oddalone w podziałce liniowej. Procedurę tę
wykorzystuje się, aby określić dla jakiego przedziału czasu ma być wykreślana odpowiedź
skokowa (np. » step(Lz,Mz, linspace(0,40)) ).
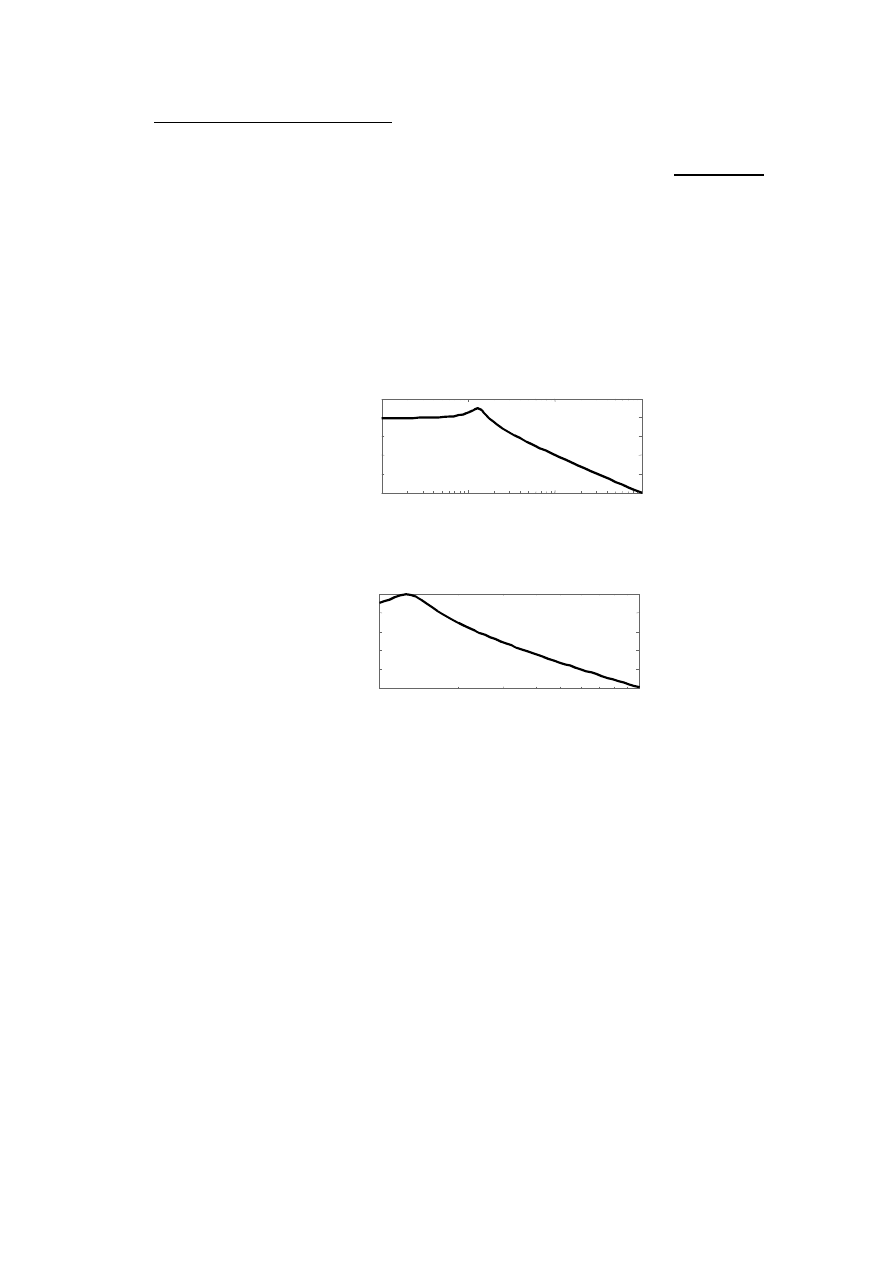
Przykład:
Odpowiedź przykładowego układu regulacji (z zamkniętą pętlą sprzężenia zwrotnego) na
skok jednostkowy można obliczyć następująco:
>> [Lz,Mz]=cloop(N,M,-1)
Wynik:
Lz =
0 0 5 15
Mz =
5 11 12 16
>>
step(Lz,Mz,linspace(0,40))
Wynik:
0
5
10
15
20
25
30
35
40
0
0.5
1
1.5
6
•
⇒
Charakterystykę amplitudową układu regulacji można wyznaczyć, używając procedury
bode()
(wstawiając jako argumenty licznik i mianownik transmitancji układu
Wyznaczanie pasma przenoszenia
zamkniętego
⇒ Procedura logspace(a,b) generuje 50-elementowy wektor o
wartościach od 10
).
a
do 10
b
Przykład:
,
którego kolejne elementy są od siebie równo oddalone w podziałce logarytmicznej. Pocedurę
tę wykorzystuje się do określenia dla jakich częstości mają być wykreślane charakterystyki
Bodego(np. » bode(Lz,Mz,logspace(-1,3)) ).
Pasmo przenoszenia przykładowego układu regulacji można oszacować na podstawie
charakterystyki amplitudowej:
>> bode(Lz,Mz)
Wynik (górny wykres):
-80
-60
-40
-20
0
20
Zwiększenie dokładności odczytu pulsacji granicznej jest możliwe dzięki zawężeniu
przedziału częstości obserwowanej charakterystyki amplitudowej:
>> bode(Lz,Mz,logspace(0,1))
Wynik (górny wykres):
-40
-30
-20
-10
0
10
4. Przebieg ćwiczenia
1.
Obliczyć licznik L i mianownik M transmitancji obiektu regulacji, dla
współczynników A i B zadanych przez prowadzącego.
2.
Sprawdzić, czy zamykając pętlę sprzężenia zwrotnego, uzyska się układ regulacji
o
wymaganych parametrach (zob. cel ćwiczenia), czy też konieczne jest zastosowanie
regulatora
. Należy zatem:
a)
Wykreślić charakterystyki Bodego dla obiektu regulacji i określić zapas modułu
i fazy.
b)
Obliczyć licznik Lz i mianownik Mz transmitancji układu zamkniętego (bez
regulatora).
c)
Uzyskać odpowiedź układu zamkniętego na skok jednostkowy, a następnie
określić czas regulacji i przeregulowanie.
d)
Wyznaczyć pasmo przenoszenia układu.
3.
Przeprowadzić doświadczenie Zieglera-Nicholsa i określić wstępne wartości nastaw
regulatora, wykonując następujące czynności:
a)
Na podstawie zapasu modułu (wyznaczonego w punkcie 2a) obliczyć, jak duże
powinno być wzmocnienie k
osc
regulatora proporcjonalnego, aby układ po
zamknięciu pętli sprzężenia zwrotnego znajdował się na granicy stabilności.

7
b)
Obliczyć licznik Lz i mianownik Mz transmitancji układu zamkniętego
(z regulatorem proporcjonalnym o wzmocnieniu k
osc
c)
Uzyskać wykres odpowiedzi układu regulacji z zamkniętą pętlą sprzężenia
zwrotnego na skok jednostkowy i
wyznaczyć okres oscylacji sygnału
wyjściowego T
).
osc
d)
Dobrać nastawy k
.
p
i T
i
regulatora PI zgodnie z
regułą Zieglera-Nicholsa, tzn.
przyjąć k
p
= 0.45 k
osc
oraz T
i
= 0.85 T
osc
4.
Sprawdzić, czy wstępnie dobrane nastawy regulatora PI pozwalają na osiągnięcie
zakładanego zapasu modułu i fazy, jeśli nie, to skorygować nastawy regulatora:
.
a)
Obliczyć licznik Lr i mianownik Mr regulatora PI o nastawach k
p
i T
i
b)
Obliczyć licznik Lc i mianownik Mc transmitancji układu otwartego (obiektu
regulacji wraz z regulatorem PI).
.
c)
Wykreślić charakterystyki Bodego dla układu otwartego oraz określić zapas
modułu i fazy.
d)
Jeżeli zapas modułu jest mniejszy niż wymagany, to obliczyć nową wartość k
p
e)
Jeżeli uzyskany zapas fazy nie jest satysfakcjonujący, to zmieniając wartość
nastawy T
,
przy której osiągnięta zostanie żądana wartość zapasu, a następnie powtórzyć
obliczenia z punktów a, b i c.
i
, zbad
ać jej wpływ na zapas modułu i fazy. Metodą prób i błędów,
powtarzając obliczenia z punktów a, b, c oraz d, dobrać nastawy k
p
i T
i
5.
Sprawdzić, czy dobrane nastawy regulatora pozwalają na osiągnięcie zakładanego
przeregulowania, czasu regulacji i
pasma przenoszenia, jeśli nie, to skorygować
nastawy regulatora:
, przy
których układ regulacji spełnia narzucone warunki.
a)
Obliczyć licznik Lz i mianownik Mz transmitancji układu zamkniętego.
b)
Uzyskać wykres odpowiedzi układu zamkniętego na skok jednostkowy
i
określić czas regulacji t
r
dla y(t
r
) = (1±0.05) y
u
c)
Wyznaczyć pasmo przenoszenia układu.
oraz przeregulowanie
κ
.
d)
Jeśli pulsacja graniczna jest mniejsza od żądanej lub czas regulacji większy od
żądanego, to należy zbadać ich zależność od nastaw regulatora i dobrać nowe
nastawy (pamiętając o utrzymaniu niezbędnego zapasu stabilności).
W sprawozdaniu należy umieścić:
•
Zwięzły opis zadania i zastosowanej metody doboru nastaw regulatora.
•
Obliczoną transmitancję obiektu regulacji.
•
Wyznaczone wartości k
osc
i T
osc
• Dobrane nastawy k
.
p
i T
i
•
Obliczoną transmitancję obiektu regulacji wraz z regulatorem (układ otwarty).
regulatora.
• Charakterystyki Bodego obiektu regulacji wraz z
regulatorem, obliczony zapas modułu
i zapas fazy.
•
Obliczoną transmitancję układu regulacji (układ zamknięty).
•
Wykres odpowiedzi układu regulacji na skok jednostkowy, odczytany czas regulacji t
r
•
Charakterystykę amplitudową układu regulacji z zaznaczonym pasmem przenoszenia.
i przeregulowanie
κ
.
• Wnioski.
5. Piśmiennictwo
[1]
Zarys dynamiki i automatyki uk
ładów – pr. zb. pod red. A. Olędzkiego, 1991.
Document Outline
Wyszukiwarka
Podobne podstrony:
05 Dobor nastaw regulatora w ko Nieznany (2)
Banas Chrabaszcz zaoczne Dobor nastaw regulatorów
DOBÓR NASTAW REGULATORA PID
DOBÓR NASTAW REGULATORÓW TYPU PID METODĄ CHARAKTERYSTYK SKOKOWYCH
DOBÓR NASTAW REGULATORÓW W MODELOWYM UKŁADZIE AUTOMATYCZNEJ REGULACJI, SGGW Technika Rolnicza i Leśn
Dobór nastaw regulatorów
Dobór nastaw regulatorów
Dobór nastaw regulatora
syposz,podstawy automatyki, DOBÓR NASTAW REGULATORÓW
15 dobor nastaw regulatoraid 16127 ppt
888 banas chrabaszcz zaoczne dobor nastaw regulatorow, szkoła PŚK, Automatyzacja
6 Dobór nastaw regulatorów
6b dobor nastaw regulatora
DOBÓR NASTAW REGULATORÓW TYPU PID METODĄ ZIEGLERA NICHOLSA
PA9 dobor nastaw regulat
więcej podobnych podstron