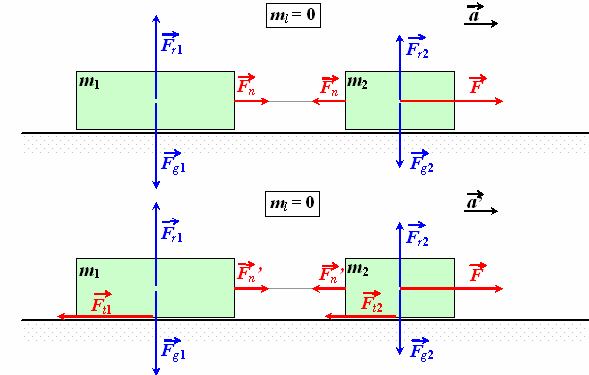
Przykład zastosowania II zasady dynamiki Newtona dla ruchu postępowego

a)

b)

ciała m 1 i m 2 połączone linką założenia:

• masa linki pomijalnie mała ( ml = 0)

• linka nierozciągliwa

cały układ ciał m 1 + m 2 porusza się ze wspólnym przyspieszeniem siła naprężenia linki jednakowa w każdym punkcie rozkładamy działające siły na równoległe i prostopadłe do kierunku ruchu a) przypadek bez uwzględnienia tarcia ciało m 1:

F || = F

w 1

n

|

→

m a

1

=

(1a)

| :

n

F

F || = m a

w 1

1

F ⊥ = F

− F = 0

⊥

w 1

g 1

r 1

:

F

= F = m g

g 1

r 1

1

ciało m 2:

F || = F − F

w 2

n

|

→

m a

2

= F −

(2a)

| :

n

F

F || = m a

w 2

2

F ⊥ = F

− F = 0

⊥

w 2

g 2

r 2

:

F

= F = m g

g 2

r 2

2

(1a) + (2a):

1

( m

a =

1 + m ) a

2

= F →

F

m + m

1

2

m 1

(1a):

m a

F =

1

= n

F

→

F

n

m + m

1

2

b) przypadek z uwzględnieniem tarcia zakładamy jednakowe współczynniki tarcia dla obu ciał: µ 1 + µ 2 = µ

modyfikacji ulegają równania (1a) i (2a) ciało m 1:

F || ' = F ' − F =

w 1

n

t 1

= F ' − F

µ

=

|

n

r 1

→

m '

a = F ' − µ m g (1b)

| :

= F ' − µ m g

1

n

1

n

1

F || ' = m '

a

w 1

1

ciało m 2:

F || ' = F − F ' − F =

w 2

n

t 2

= F − F ' − F

µ

=

|

n

r 2

→

m '

a = F − F ' − µ m g (2b)

| :

= F − F ' − µ m g 2

n

2

n

2

F || ' = m '

a

w 2

2

(1b) + (2b):

1

( m + m ) '

a = F − µ ( m + m ) g

'

a =

F − µ

1

2

1

2

→

g

m 1 + m 2

a’ < a

(1b):

m '

a = F ' − µ m g 1

n

1

F '

1(

µ

n = m

'

a + g) =

m 1



1



=

=

→

F '

F

m

n

+

1

F − µ g + µ g 

m

m



1

2

m 1 + m 2



Fn’ = Fn

w przypadku ciał wykonanych z tego samego materiału (o jednakowych współczynnikach tarcia o podłoże) obecność tarcia wpływa na przyspieszenie układu, ale nie wpływa na siłę naprężenia linki