RACHUNEK CAŁKOWY FUNKCJI WIELU ZMIENYCH

(w sensie Riemana)

Całka podwójna w prostokącie.

Niech

 





d

y

c

b

x

a

y

x

P











,

:

,

R



P

f :

f – funkcja ograniczona

a

b

P

c

d

P

2

P

3

P

1

P

k

P

n

y

x

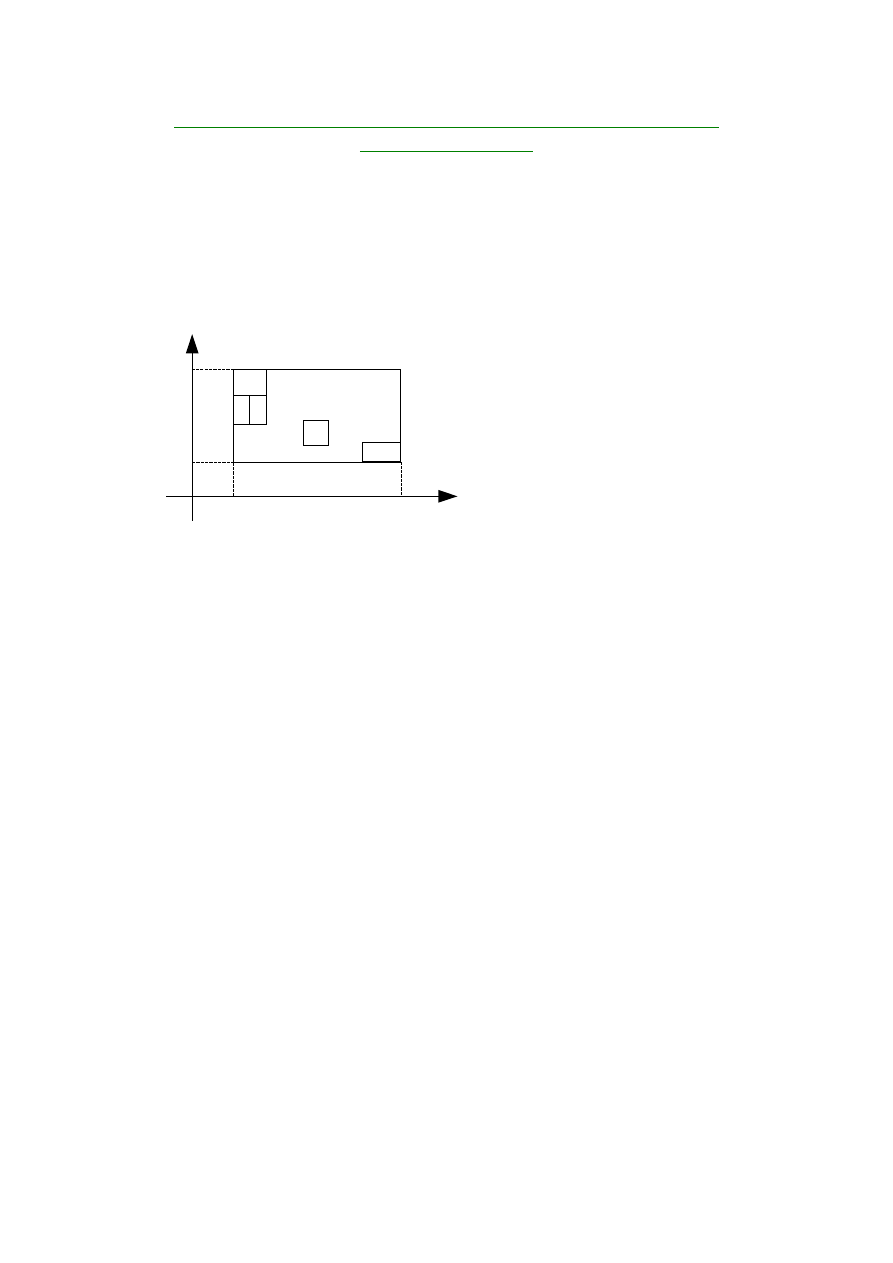
Tworzymy następujący podział prostokąta P i oznaczamy

n



.

•

prostokąt P dzielimy na n prostokatów

k

P

o polach

n

k

k

,...,

1

,





•

w każdym z prostokatów

k

P

wybieramy punkt





k

k

k

k

P

y

x

A



,

•

następnie tworzymy sumę całkową





k

n

k

k

k

n

y

x

f

S











1

,

Wprowadzamy oznaczenia
d

k

– długość przekątnej prostokąta P

k

k

 – średnica podziału

n

 , gdzie

k

 jest największą długością przekątnej;

k

n

k

n

d







1

max

:



Tworzymy ciąg podziałów

 

N





n

n

prostokąta P.

Definicja

Ciąg

 

N





n

n

nazywamy

ciągiem normalnym podziałów

, jeśli odpowiadający mu ciąg średnic

dąży do 0, tzn.

0



 







n

n



Definicja

(całki podwójnej)

Jeśli dla każdego ciągu normalnego podziałów prostokąta P ciąg sum całkowych

 

N

n

n

S



jest

zbieżny do tej samej granicy właściwej, niezależnej od wyboru punktów A

k

, to granicę tę

nazywamy

całką podwójną

funkcji

 

y

x

f ,

w prostokącie P i oznaczamy

 



P

d

y

x

f



,

Zatem

 

n

P

S

d

y

x

f

n

0

lim

:

,











.

Uwaga

Ograniczoność funkcji

 

y

x

f ,

jest warunkiem koniecznym istnienia całki, lecz nie jest to

warunek wystarczający.

Twierdzenie

(

o całkowalności funkcji dwóch zmiennych

)

Z:

)

,

( y

x

f

– funkcja ograniczona w prostokącie P oraz ciągła poza zbiorem miary 0,

tzn. poza zbiorem punktów, który można pokryć skończoną liczbą prostokątów
o dowolnie małej sumie pól (mniejszej niż ε).

T: f jest całkowalna w prostokącie P.

Wniosek

Z twierdzenia wynika:



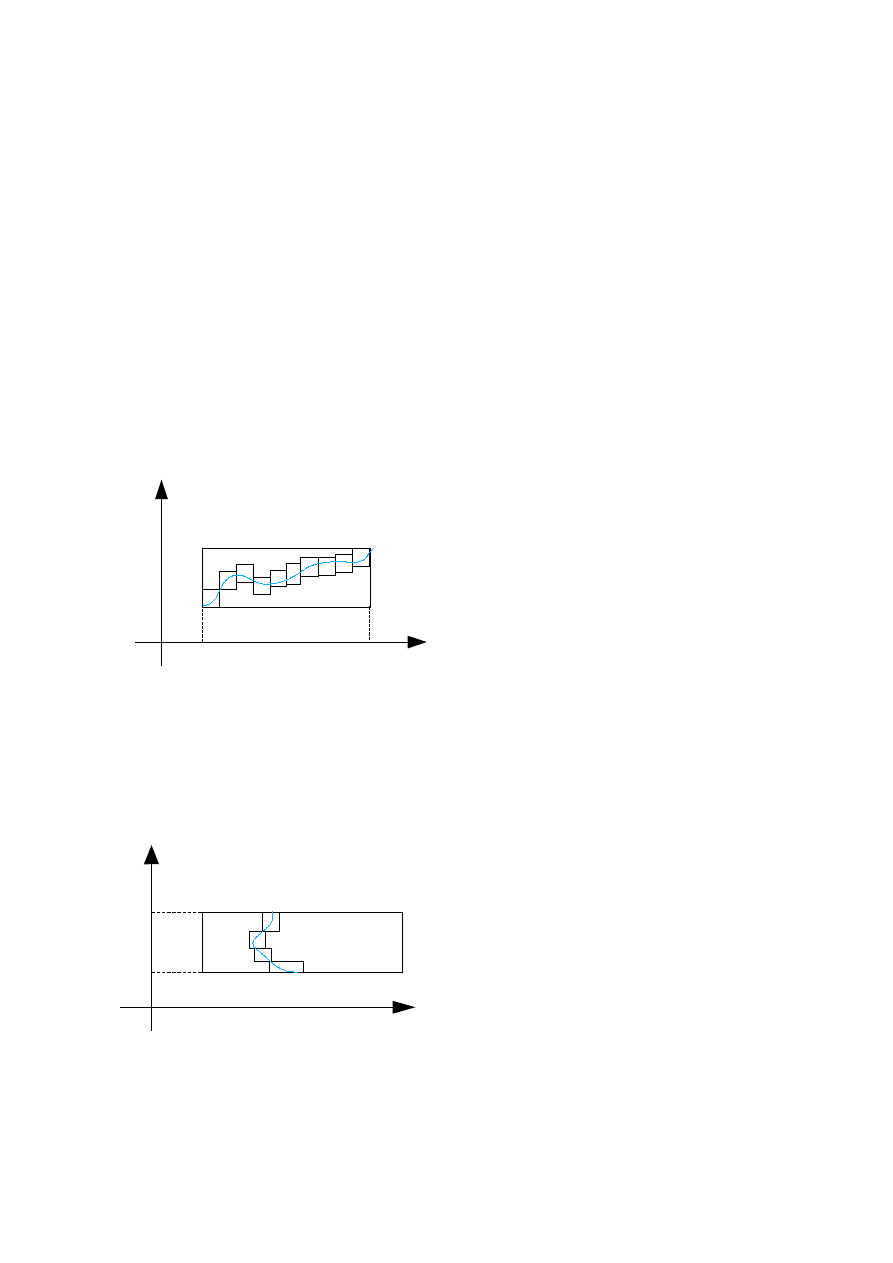
1 f – ciągła w P z wyjątkiem punktów położonych na krzywej, będącej wykresem

funkcji

 











b

a

C

x

y

,

gdzie

),

(





f – całkowalna w P

Uzasadnienie:
zbiór

 





 





b

a

x

x

x

,

:

,





jest zbiorem miary

zero (można go pokryć skończoną liczbą
prostokątów o dowolnie małych polach)



2 f – ciągła w P z wyjątkiem punktów położonych na krzywej, będącej wykresem

funkcji

 











d

c

C

y

x

,

gdzie

),

(





f – całkowalna w P

c

d

x=ψ(y)

P

x

y

Wniosek

Funkcja może nie być ciągła na brzegu prostokąta, a mimo to będzie całkowalna.

a

b

y=φ(x)

P

x

y