
Wykład 36
Promieniowanie atomów
W stanie podstawowym atom zajmuje poziom o najniższej energii. Jeżeli nie ma
zewnętrznych zaburzeń, to atom przebywa w stanie podstawowym nieskończenie długo. Atom
przechodzi do stanu wzbudzonego kosztem energii doprowadzonej z zewnątrz
(promieniowanie albo zderzenie).
Absorpcja i emisja promieniowania
Absorpcja promieniowania polega na tym, że atom znajdujący się w stanie
a
E , dzięki
pochłonięciu fotonu o energii
a
b
ba
E
E
h
−
=
ν
przechodzi do wyższego stanu energetycznego
b
E . Liczba przejść atomów ze stanu
a
E do stanu
b
E pod wpływem absorpcji światła
zachodzących w ciągu 1 sekundy
abs
dt
dN
)
/
(
, jest proporcjonalna do liczby atomów
a
N
znajdujących się w stanie
a
E oraz do gęstości energii promieniowania
ρ
. Wprowadzając
współczynnik proporcjonalności
ab
B możemy zapisać
ρ
ab
a
abs
B
N
dt
dN
=
. (36.1)
W mechanice kwantowej udowodniono, że promieniowanie o częstości
h
E
E
a
b
ba
/
)
(
−
=
ν
wywołuje nie tylko przejście atomu ze stanu
a
E do stanu
b
E . Pod wpływem tego
promieniowania możliwe jest przejście odwrotne - ze stanu
b
E do stanu
a
E . Takie przejście
nie jest związane z pochłonięciem fotonu, a odwrotnie jest związane z emisją fotonu o
częstości
ba
ν
. Proces emisji fotonu atomem pod wpływem promieniowania nazywa się emisją
wymuszoną.
b
E . Liczba przejść atomów ze stanu
b
E do stanu
a
E pod wpływem padającego
światła zachodzących w ciągu 1 sekundy
.
.
)
/
(
wym
em
dt
dN
, jest proporcjonalna do liczby atomów
b
N znajdujących się w stanie
b
E oraz do gęstości energii promieniowania
ρ
. Wprowadzając
współczynnik proporcjonalności
ba
B możemy zapisać
ρ
ba
b
wym
em
B
N
dt
dN
=
.
.
. (36.2)
464
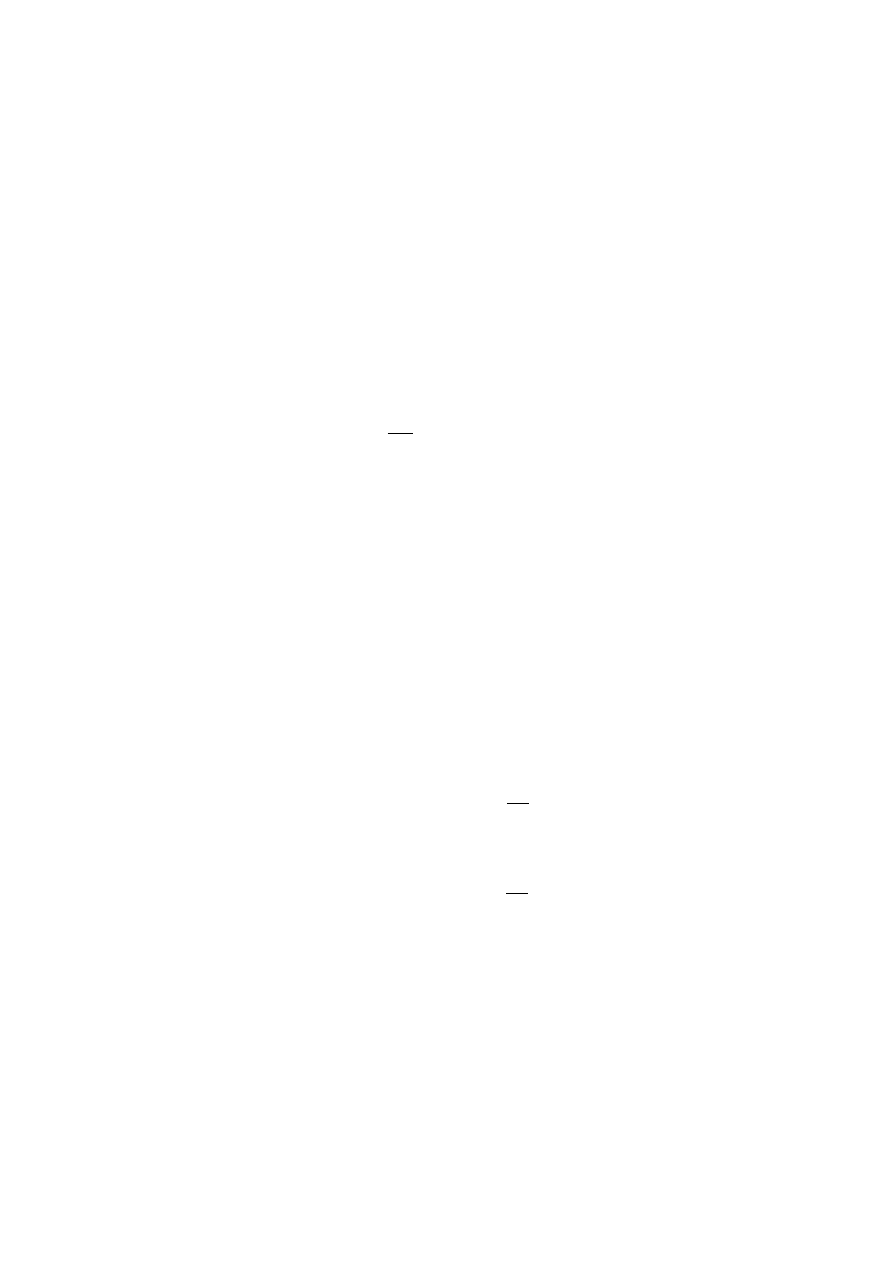
Atom w stanie wzbudzonym
b
E jest układem nietrwałym i zawsze po pewnym czasie
przechodzi samorzutnie do stanów o mniejszej energii. Ten proces emisji nazywa się emisją
spontaniczną. (Emisja spontaniczna jest związana z istnieniem próżni fizycznej, jednak
omówienie tego pojęcia przekracza poziom niniejszego wykładu). Emisja spontaniczna nie
wymaga istnienia padającego fotonu, a zatem liczba przejść spontanicznych atomów ze stanu
b
E do stanu
a
E zachodzących w ciągu 1 sekundy
.
.
)
/
(
spont
em
dt
dN
, jest proporcjonalna tylko
do liczby atomów
b
N znajdujących się w stanie
b
E . Wprowadzając współczynnik
proporcjonalności
ba
A możemy zapisać
ba
b
spont
em
A
N
dt
dN
=
.
.
. (36.3)
Współczynniki
ba
ab
A
B ,
i
ba
B po raz pierwszy wprowadził Einstein. Z tego powodu te
współczynniki nazywają się współczynnikami Einsteina.
Współczynniki Einsteina są związane ze sobą. Związek pomiędzy nimi można znaleźć
rozważając zachowanie układu złożonego z
N
identycznych atomów, pozostającego w
równowadze termodynamicznej z promieniowaniem. Rozkład obsadzeń poziomów
energetycznych atomów takiego układu w temperaturze
T
określa prawo Boltzmanna.
Zgodnie z tym prawem obsadzenia
a
N i
b
N w stanie równowagi termicznej są odpowiednio
równe
−
⋅
=
kT
E
C
N
a
a
exp
, (36.4)
−
⋅
=
kT
E
C
N
b
b
exp
, (36.5)
gdzie
∑
−
=
)
/
exp(
/
kT
E
N
C
i
jest stała.
Zwykle energia wzbudzonych poziomów atomowych jest rzędu kilku eV. A zatem,
żeby współczynnik
kT
E
a
/
był rzędu jedynki
kT
musi być rzędu kilku eV. Dla temperatur
1000
<
T
K iloczyn
kT
<0,1 eV, a zatem
5
10
5
)
10
exp(
)
/
exp(
−
⋅
≈
−
≈
−
kT
E
a
. Oznacza to, że
w tych warunkach tylko nieznaczna część atomów znajduje się w stanach wzbudzonych.
465

W stanie równowagi, liczba przejść do stanów wyższych musi być równa liczbie przejść
do stanów niższych. A zatem ze wzorów (36.1)-(36.3) znajdujemy
ba
b
ba
b
ab
a
A
N
B
N
B
N
+
=
ρ
ρ
. (36.6)
Skąd
(
)
1
/
1
−
⋅
=
−
=
ba
b
ab
a
ba
ba
ba
b
ab
a
ba
b
B
N
B
N
B
A
B
N
B
N
A
N
ρ
. (36.7)
Ze wzorów (36.4) i (36.5) wynika, że
)
/
exp(
]
/
)
exp[(
/
kT
h
kT
E
E
N
N
ba
a
b
b
a
ν
=
−
=
,
a zatem wzór (36.7) możemy przepisać w postaci
(
)
1
)
/
exp(
/
1
−
⋅
=
−
=
kT
h
B
B
B
A
B
N
B
N
A
N
ab
ba
ab
ba
ba
ba
b
ab
a
ba
b
ν
ρ
. (36.8)
Skorzystamy teraz z oczywistego postulatu mówiącego, że gdy temperatura dąży do
nieskończoności gęstość promieniowania musi też dążyć do nieskończoności. Przy
∞
→
T
ze
wzoru (36.8) otrzymujemy
∞
→
−
=
∞
→
ba
ab
ba
B
B
A
T
)
(
ρ
. (36.9)
Równanie (36.9) będzie spełnione tylko wtedy, gdy
ab
ab
B
B
=
. (36.10)
A zatem współczynniki Einsteina, określające absorpcję i emisję wymuszoną atomu są równe
siebie.
Związek między współczynnikami Einsteina dla emisji spontanicznej i wymuszonej
znajdziemy zakładając, że promieniowanie które pada na układ atomów jest promieniowaniem
doskonale czarnego ciała. Dla doskonale czarnego ciała gęstość energii promieniowania dla
częstości
ba
ν
jest wyrażona wzorem Plancka
1
)
/
exp(
8
)
,
(
2
2
−
=
kT
h
h
c
T
ba
ba
ba
ba
ν
ν
πν
ν
ρ
. (36.11)
466

Biorąc pod uwagę (36.10) oraz porównując wzory (36.8) i (36.11) otrzymujemy
=
−
1
)
/
exp(
8
2
2
kT
h
h
c
ba
ba
ba
ν
ν
πν
1
)
/
exp(
1
−
⋅
kT
h
B
A
ba
ba
ba
ν
.
Skąd mamy
ba
ba
ba
B
c
h
A
2
3
8
ν
π
=
. (36.12)
Korzystając ze wzoru (36.12) znajdziemy stosunek mocy promieniowania emisji spontanicznej
spont
W
do mocy promieniowania wymuszonego
wym
W
dla układu promieniującego w
równowadze termodynamicznej. Zgodnie ze wzorem (36.3) moc promieniowania emisji
spontanicznej wynosi
ba
ba
b
spont
h
A
N
W
ν
⋅
=
. (36.13)
Moc promieniowania wymuszonego, zgodnie ze wzorem (36.2) jest równa
ba
ba
b
wym
h
B
N
W
ν
ρ ⋅
=
.
. (36.14)
Biorąc pod uwagę wzory (36.11), (36.12) otrzymujemy
1
exp
−
=
=
kT
h
B
A
W
W
ba
ba
ba
wym
spont
ν
ρ
. (36.15)
Ze wzoru (36.15) wynika, że ze wzrostem temperatury, jak też długości fali (
ba
ba
c
ν
λ
/
=
)
udział promieniowania wymuszonego w stosunku do promieniowania spontanicznego rośnie.
Promieniowanie elektryczne i magnetyczne różnej multipolowości
Atom stanowi układ cząstek naładowanych elektryczne. Elektryczne i magnetyczne
właściwości takiego układu możemy traktować za pomocą momentów atomu: momentu
dipolowego atomu, momentu kwadrupolowego atomu oraz momentów
m
Q elektrycznych i
magnetycznych wyższej multipolowości. Oddziaływanie tych momentów z polem
elektromagnetycznym i powoduje przejścia spektroskopowe atomu z jednego poziomu do
drugiego.
467

W mechanice kwantowej udowodniono, że prawdopodobieństwo przejścia między
poziomami
b
E i
a
E jest wprost proporcjonalne do elementu macierzowego
dV
Q
B
a
m
b
m
ba
∫
ψ
ψ
*
)
(
~
, (36.16)
gdzie
a
ψ
jest funkcją falową stanu
a
E ;
b
ψ
jest funkcją falową stanu
b
E ;
m
Q -
m
- ty
multipolowy moment atomu.
W zależności od tego z jakim momentem multipolowym atomu jest związane przejście
spektroskopowe między poziomami
b
E i
a
E rozróżniamy: przejście elektryczne dipolowe
1
E
(przejście to jest związane z oddziaływaniem elektrycznego momentu dipolowego atomu z
elektrycznym polem fali -
1
=
m
); przejście magnetyczne dipolowe
1
M
(przejście to jest
związane z oddziaływaniem magnetycznego momentu dipolowego atomu z magnetycznym
polem fali -
1
=
m
); przejście elektryczne kwadrupolowe
2
E
(przejście to jest związane z
oddziaływaniem elektrycznego momentu kwadrupolowego atomu z elektrycznym polem fali -
2
=
m
) oraz przejścia wyższej multipolowości, które jednak ze względu ma ich niezmiernie
małe prawdopodobieństwa można zawsze zaniedbać. Dla atomów większe
prawdopodobieństwo ma przejście elektryczne dipolowe
1
E
.
Dynamika przejścia spektroskopowego
Dotychczas nic nie mówiliśmy jak zachodzą przejścia atomu między poziomami
(termami) atomu. Jednak przed tym jak rozważyć dynamikę przejść spektroskopowych w
fizyce atomowej, przypomnimy siebie jak w fizyce klasycznej zachodzi promieniowanie fal
elektromagnetycznych wskutek drgań dipolu elektrycznego.
Promieniowanie dipolu w fizyce klasycznej
Z określenia dipolowy moment elektryczny układu, składającego się z
N
ładunków
elektrycznych, jest równy
∑
=
=
N
i
i
i
r
q
p
1
, (36.17)
gdzie
i
q jest wartość
i
-tego ładunku znajdującego się w punkcie określonym wektorem
wodzącym
i
r
.
468

W klasycznej elektrodynamice udowodniono, że jeżeli dipol elektryczny wykonuje
drgania, to układ ładunków zaczyna promieniować fali elektromagnetyczne i wartość energii
wypromieniowanej układem w jednostce czasu we wszystkich kierunkach wynosi
3
0
2
6
c
p
W
prom
πε
=
, (36.18)
gdzie
2
2
/ dt
p
d
p
=
. Wzór (36.18) nazywa się wzorem Hertza.
Dla uproszczenia będziemy rozważać dalej układ składający się z dwóch ładunków:
e
q
+
=
1
i
e
q
−
=
2
. W tym przypadku dipolowy moment elektryczny takiego układu wynosi
r
e
p
=
, (36.19)
gdzie
r
jest wektorem łączącym ładunek
e
q
−
=
2
z ładunkiem
e
q
+
=
1
.
Załóżmy teraz, że wskutek drgań ładunków wektor
r
zmienia się w czasie zgodnie ze
wzorem
t
t
r
t
r
0
0
cos
)
(
)
(
ω
=
. (36.20)
W tym wzorze zapisaliśmy amplitudę drgań dipolu jako funkcję czasu. Ta zależność od czasu
)
(
0
t
r
powstaję wskutek straty energii dipolem na promieniowanie. Będziemy zakładali, że
tłumienie drgań dipolu zachodzą w czasie znacznie większym niż okres drgań dipolu
0
/
2
ω
π
=
T
, czyli będziemy zakładali, że
1
<<
T
γ
, tu
γ
jest charakterystyczna stała,
określająca tłumienie drgań dipolu.
Jeżeli będziemy rozważali czas t znacznie mniejszy niż
1
−
γ
, to we wzorze (36.20)
możemy na chwili zaniedbać zależność amplitudy drgań dipolu od czasu i rozważać zamiast
(36.20) wzór
t
r
t
r
0
0
cos
)
(
ω
=
. (36.21)
Tu
0
r
nie zależy od czasu.
Biorąc pod uwagę (36.21) ze wzoru (36.19) znajdujemy
t
r
e
p
0
2
0
0
cos
ω
ω
−
=
. (36.22)
Po podstawieniu (36.22) do wzoru (36.18) otrzymujemy
469
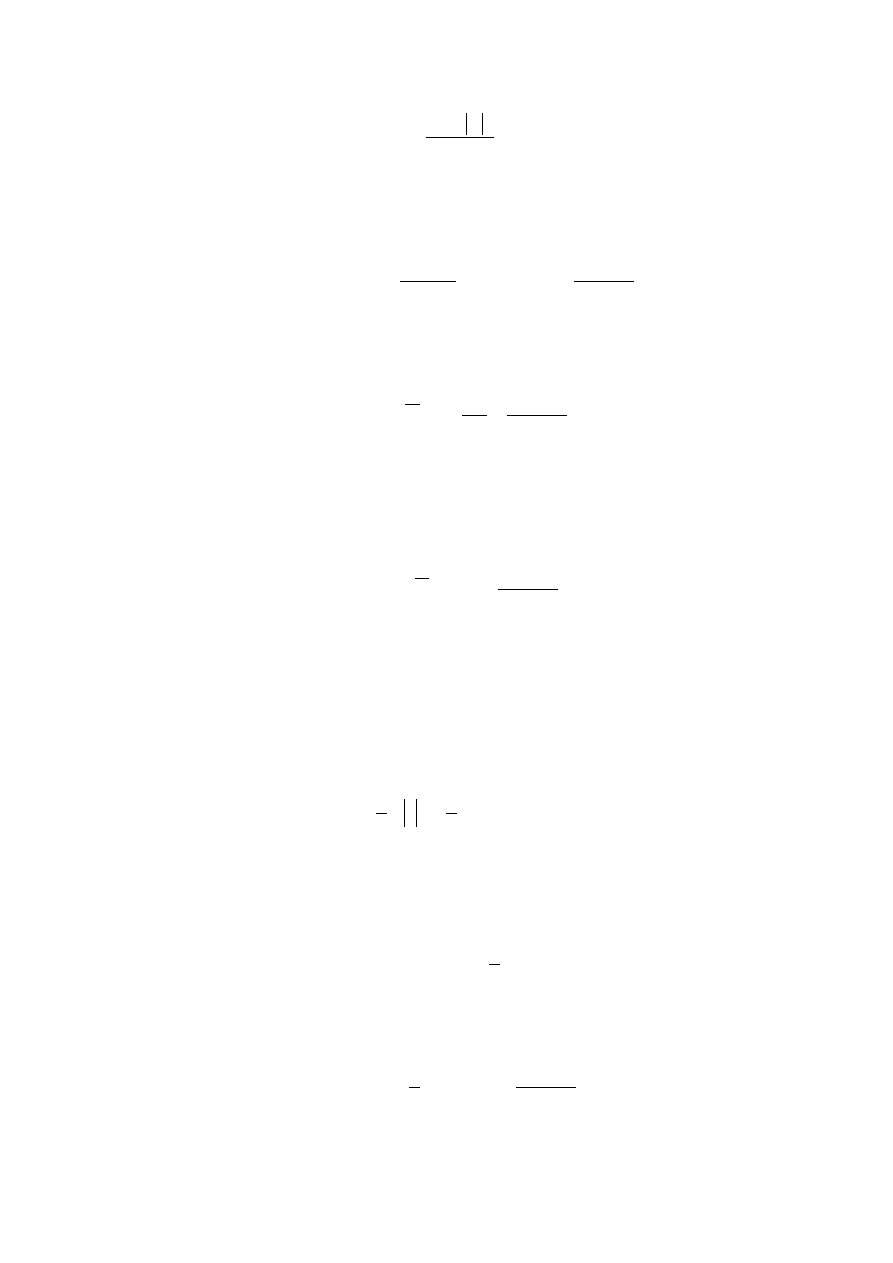
)
(
cos
6
0
2
3
0
2
0
4
0
2
t
c
r
e
W
prom
ω
πε
ω
=
. (36.23)
Za okres drgań dipolu
0
/
2
ω
π
=
T
zostaje wypromieniowana energia
T
c
r
e
dt
t
c
r
e
dt
W
W
T
T
prom
T
⋅
=
=
=
∫
∫
3
0
2
0
4
0
2
0
0
0
2
3
0
2
0
4
0
2
12
)
(
cos
6
πε
ω
ω
πε
ω
. (36.24)
Ze wzoru (36.24) wynika, że za jednostkę czasu dipol elektryczny promieniuje średnią energię
3
0
2
0
4
0
2
12
c
r
e
T
W
W
T
prom
πε
ω
=
=
. (36.25)
Uwzględniając (36.25) dla energii, którą traci dipol za czas
dt
(przypomnimy, że rozważamy
czas znacznie mniejszy niż
1
−
γ
) otrzymujemy
dt
c
r
e
dt
W
dW
prom
prom
3
0
2
0
4
0
2
12
πε
ω
−
=
−
=
. (36.26)
Znak minus oznacza, że energia dipolu zmniejsza się.
Energia drgającego dipolu składa się z kinetycznej i potencjalnej energii drgających
ładunków. Przy czym wiemy z mechaniki, że w ciągu drgań energia potencjalna przechodzi w
energię kinetyczną i na odwrót. Kinetyczna energia drgającego dipolu jest równa
)
(
sin
2
1
2
1
0
2
2
0
2
0
2
t
r
m
r
m
T
ω
ω
⋅
=
=
. (36.27)
Ze wzoru (36.27) wynika, że energia zmagazynowana w dipolu na początku jego drgań (ta
energia pokrywa się z maksymalną energią kinetyczną), jest równa
2
0
2
0
max
2
1
r
m
T
W
prom
ω
=
=
. (36.28)
Po podstawieniu (36.28) do wzoru (36.26) znajdujemy
dt
c
r
e
dr
m
dW
prom
3
0
2
0
4
0
2
2
0
2
0
12
2
1
πε
ω
ω
−
=
=
. (36.29)
470

Wprowadzając oznaczenie
3
0
2
0
2
6
mc
e
πε
ω
γ ≡
, (36.30)
zapiszmy wzór (36.29) w postaci
dt
r
dr
2
0
2
0
⋅
−
=
γ
. (36.31)
Otrzymaliśmy, równanie, które określa tłumienie amplitudy drgań dipolu. Rozwiązanie
równania (36.31) ma postać
t
e
r
t
r
γ
−
⋅
=
)
0
(
)
(
2
0
2
0
. (36.32)
A zatem wskutek promieniowania amplituda drgań dipolu elektrycznego zmniejsza się i wynosi
2
/
0
0
)
0
(
)
(
t
e
r
t
r
γ
−
⋅
=
. (36.33)
Po podstawieniu (36.33) do wzoru (36.20) znajdujemy
)
cos(
)
0
(
)
(
0
2
/
0
t
e
r
t
r
t
ω
γ
−
⋅
=
. (36.34)
Po podstawieniu (36.34) do wzoru (36.23) znajdujemy
3
0
2
4
0
2
6
)
(
c
t
r
e
W
prom
πε
ω
=
=
)
(
cos
)
0
(
0
2
t
e
W
t
prom
ω
γ
−
⋅
=
, (36.35)
gdzie
3
0
2
0
4
0
2
6
)
0
(
)
0
(
c
r
e
W
prom
πε
ω
=
.
Ponieważ energia fali elektromagnetycznej jest wprost proporcjonalna
2
E ze wzoru
(36.35) otrzymujemy, że
)
cos(
)
(
0
2
/
0
t
e
E
t
E
t
ω
γ
−
⋅
=
. (36.36)
Ze wzoru (36.36) wynika, że dipol Hertza nie promieniuje fale monochromatyczną (fale jednej
częstości).
471
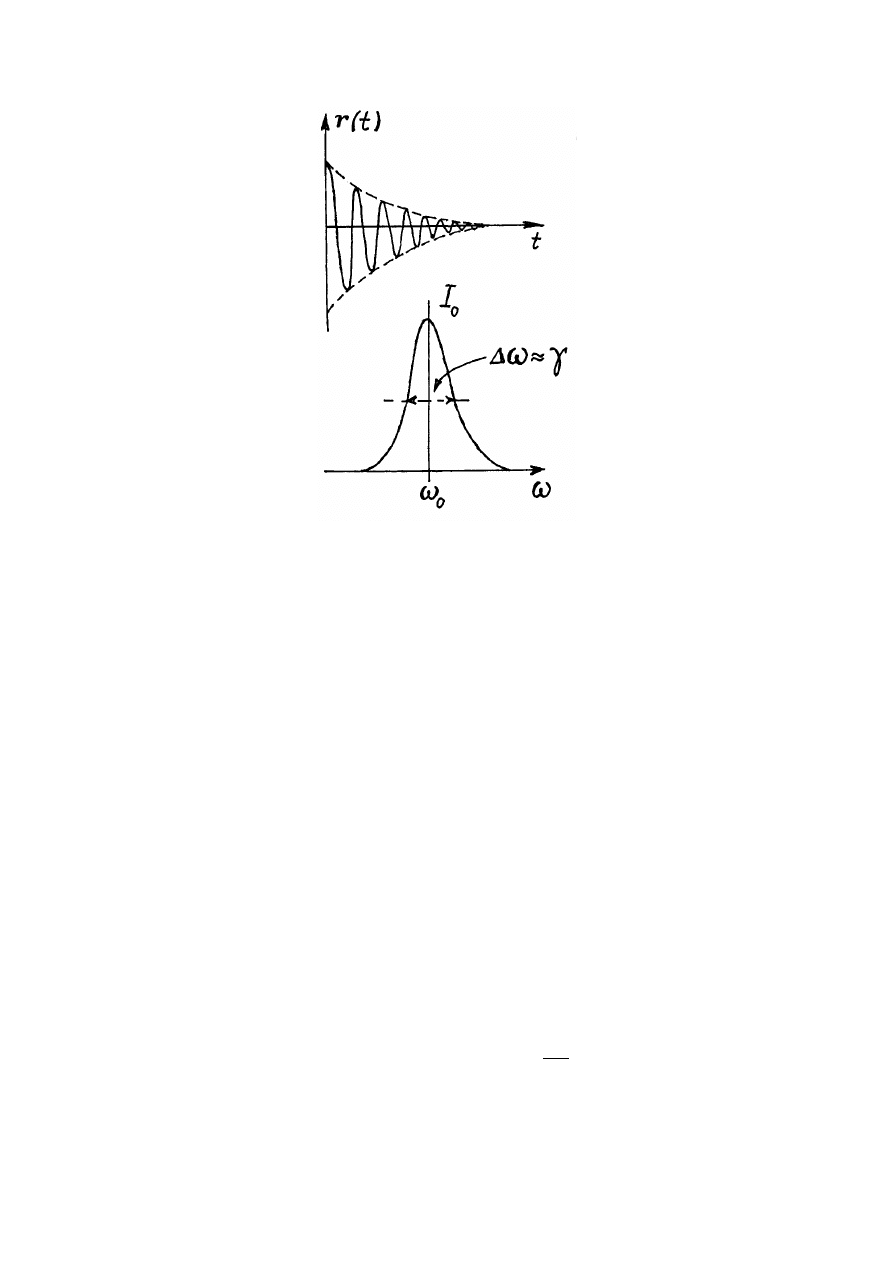
Przekształcenie Fouriera wzoru (36.36) daje widmo promieniowania. To widmo
pokazano jest na rysunku wyżej. Łatwo udowodnić, że szerokość tego widma jest wprost
proporcjonalna do współczynnika tłumienia
γ
.
Promieniowanie dipolu w fizyce atomowej
Zgodnie z jednym z postulatów N. Bohra atom w stanie stacjonarnym, pomimo, że
elektron doznaje przyspieszenia, nie wypromieniowuje energię. Okazuje się, że ten postulat nie
jest sprzeczny z fizyką klasyczną i mechanika kwantowa tłumaczy ten postulat w sposób
następujący. W stanie stacjonarnym
nl
E funkcja falowa, zgodnie z (33.23) ma postać
−
⋅
=
Ψ
t
E
i
r
t
r
nl
nlm
nlm
l
l
exp
)
(
)
,
(
ψ
. (36.37)
472

Korzystając ze wzoru (36.37) łatwo udowodnić, że moment dipolowy elektryczny atomu (a
również i inne momenty multipolowe) w stanie stacjonarnym atomu
nl
E
∫
∫
≡
Ψ
Ψ
=
dV
r
r
e
r
dV
t
r
r
e
t
r
p
l
l
l
l
nlm
nlm
nlm
nlm
)
(
)
)(
(
)
,
(
)
)(
,
(
*
*
ψ
ψ
(36.38)
nie zależy od czasu. Zgodnie z fizyką klasyczna jeżeli moment dipolowy układu ładunków nie
zależy od czasu, to taki układ nie promieniuje fal elektromagnetycznych. A zatem postulat N.
Bohra jest związany z tym, że w stacjonarnych stanach
nl
E momenty multipolowe atomu nie
zależą od czasu a więc atom nie może promieniować.
Rozważmy teraz co się dzieje z atomem, gdy na atom pada fala elektromagnetyczna.
Jeżeli rozważmy układ atom + fala, to w takim układzie, w odróżnieniu od izolowanego
atomu, powstaje wyróżniony kierunek związany z kierunkiem rozchodzenia się fali. W tym
przypadku funkcje falowe (36.37) już nie określają stan układu atom + fala. Jednak w
mechanice kwantowej udowodniono, że dowolny niestacjonarny stan atomu możemy opisać
jako superpozycję (sumę) funkcji stacjonarnych (36.37)
∑
Ψ
=
Ψ
)
,
(
)
(
)
(
t
r
t
c
t
i
i
, (36.39)
gdzie
)
,
(
)
,
(
t
r
t
r
l
nlm
i
Ψ
≡
Ψ
.
W stanie superpozycyjnym (36.39) w atomie może powstać zależny od czasu moment
elektryczny dipolowy, istnienie którego i powoduje, że atom zaczyna promieniować albo
absorbować fali elektromagnetyczne.
Zilustrujemy to na przykładzie stanu superpozycyjnego atomu wodoru, które składa się
z funkcji falowych stanów 1s i 2p
z
atomu
t
i
t
i
e
r
c
e
r
c
t
2
1
)
(
)
(
)
(
210
2
100
1
ω
ω
ψ
ψ
−
−
+
=
Ψ
. (36.40)
Tu
/
1
1
E
=
ω
,
/
2
2
E
=
ω
;
1
E - energia atomu w stanie 1s;
2
E - energia atomu w stanie 2p
z
.
Znajdziemy teraz moment dipolowy elektryczny atomu w stanie (36.40).
∫
∫
∫
∫
∫
−
−
−
+
+
+
+
=
=
Ψ
Ψ
=
dV
r
e
e
c
c
dV
r
e
e
c
c
dV
r
e
c
c
dV
r
e
c
c
dV
t
r
e
t
p
t
i
t
i
210
*
100
)
(
2
*
1
100
*
210
)
(
*
2
1
210
*
210
*
2
2
100
*
100
*
1
1
*
)
(
)
(
)
(
)
(
)
(
)
)(
(
1
2
1
2
ψ
ψ
ψ
ψ
ψ
ψ
ψ
ψ
ω
ω
ω
ω
. (36.41)
473
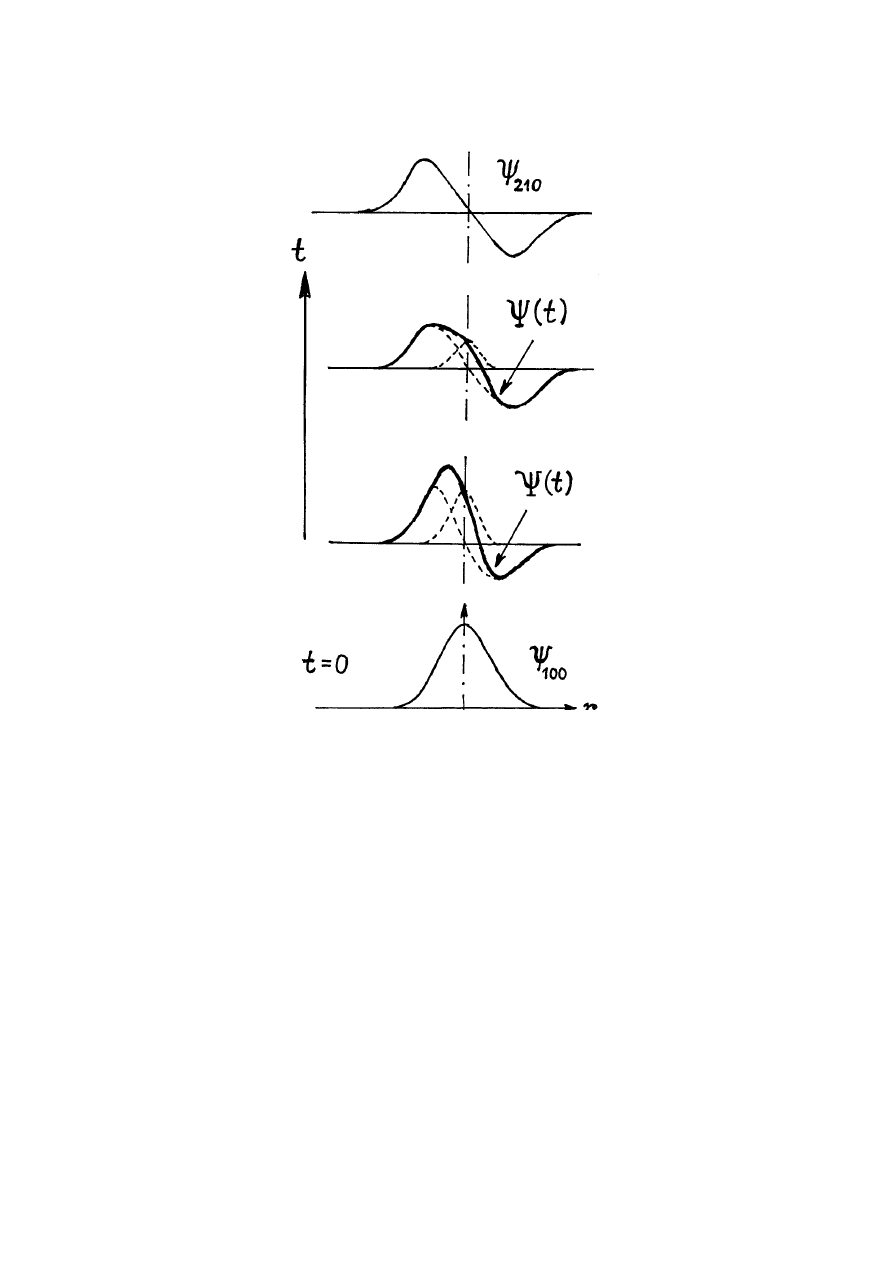
Pierwsze dwa wyrazy w (36.41) nie zależą od czasu i określają momenty dipolowe elektryczne
atomu w stanach stacjonarnych 1s i 2p. Pomijając te stacjonarne wyrazy zapiszmy wzór
(36.41) w postaci
474

(
)
t
p
t
E
E
p
t
p
21
0
1
2
0
cos
cos
)
(
ω
≡
−
⋅
=
. (36.42)
Tu
/
)
(
1
2
21
E
E
−
=
ω
i
0
p
jest rzeczywistą częścią wyrazu
}
)
(
Re{
2
100
*
210
)
(
*
2
1
0
1
2
∫
−
⋅
=
dV
r
e
e
c
c
p
t
i
ψ
ψ
ω
ω
. (36.43)
A więc udowodniliśmy, że w stanie superpozycyjnym atom uzyskuje zależny od czasu moment
dipolowy. Częstość drgań takiego momentu dipolowego pokrywa się, jak widać ze wzoru
(36.42), z częstością przejścia spektroskopowego
21
ω
.
Ścisłe rozważanie tego problemu, które wymaga rozwiązania niestacjonarnego
równania Schrödingera, wykazuje, że współczynniki
1
c i
2
c we wzorze (36.40) są funkcjami
czasu. A mianowicie, jeżeli w chwili
0
=
t
, czyli w chwili gdy atom znajdował się w stanie 1s i
1
)
0
(
1
=
c
i
0
)
0
(
2
=
c
, na atom pada fala elektromagnetyczna, to atom przechodzi w stan
superpozycyjny (36.40). W stanie superpozycyjnym współczynnik
2
c zaczyna rosnąć, a
współczynnik
1
c zaczyna maleć. (
1
2
2
2
1
=
+
c
c
). Po upływie określonego czasu, który zależy
od funkcji falowych stanów między którymi zachodzi przejście, współczynnik
2
c staje się
równym jedynce i atom okazuje się w stanie 2p.
Warto podkreślić, że w stanie superpozycyjnym energia atomu nie jest określona. Tylko
w tak zwanych stanach stacjonarnych (czystych) 1s, 2p itd. energia atomu ma wartości
określone. Nie oznacza to jednak, że stan superpozycyjny - "przejściowy" nie jest
obserwowany, ponieważ energia, którą pochłania albo promieniuje atom jest wielkością
mierzalną.
475
Wyszukiwarka
Podobne podstrony:
PATOMORFOLOGIA wykład 36 10, PATOMORFOLOGIA wykład 10 (36) (14 XII 01)
wyklad 36- prostata, wykłady K6 PATOMORFA
wyklad 36
wyklad 36 Którą z wymienionych przez Pawła kobiet można utożsamiać z przyjaciółką Tekli
Wykłady 36
36-42, Wykłady rachunkowość bankowość
36 Wykłady z Zarządzania Strategicznego
MSRy2,16,18,36,37 wykład (1)
36 Wyklad 3 Atrakcyjnosc
Logistyka i Zarządzanie Łańcuchem dostaw Wykłady str 36
36-40, EIT, FPGA, Opracowane pytania do zaliczenia wykładu
wyklady WSNSiD DTP 36
36 Wykłady z Zarządzania Strategicznego
Napęd Elektryczny wykład
wykład5
Psychologia wykład 1 Stres i radzenie sobie z nim zjazd B
więcej podobnych podstron