1
1
Agata Nawrocka
Agata Nawrocka
Katedra Automatyzacji Proces
Katedra Automatyzacji Proces
ó
ó
w
w
Akademia G
Akademia G
ó
ó
rniczo
rniczo
-
-
Hutnicza
Hutnicza
Automatyka i Robotyka
Automatyka i Robotyka
2
2
Plan wyk
Plan wyk
ł
ł
adu:
adu:
9
Sterowanie proporcjonalne
9
Sterowanie całkowe
9
Sterowanie proporcjonalno - całkowe
9
Sterowanie proporcjonalno - różniczkowe
9
Sterowanie proporcjonalno - całkowo - różniczkowe
Automatyka i Robotyka
Wykład nr 11
3
3
W regulatorze z
proporcjonalnym
proporcjonalnym algorytmem sterowania
(typu
P
P), związek pomiędzy sygnałem
wyjściowym
regulatora u(t), a sygnałem uchybu e(t) jest następujący:
)
(
)
(
t
e
K
t
u
p
=
S
S
terowani
terowani
e
e
proporcjonalne
proporcjonalne
gdzie: K
p
jest nazwane wzmocnieniem proporcjonalnym
(współczynnikiem wzmocnienia)
Automatyka i Robotyka
Wykład nr 11
4
4
Regulator proporcjonalny jest wzmacniaczem
z
nastawianym wzmocnieniem.
Po zastosowaniu transformaty Laplace’a transmitancja
regulatora ma postać:
p
K
s
E
s
U
=
)
(
)
(
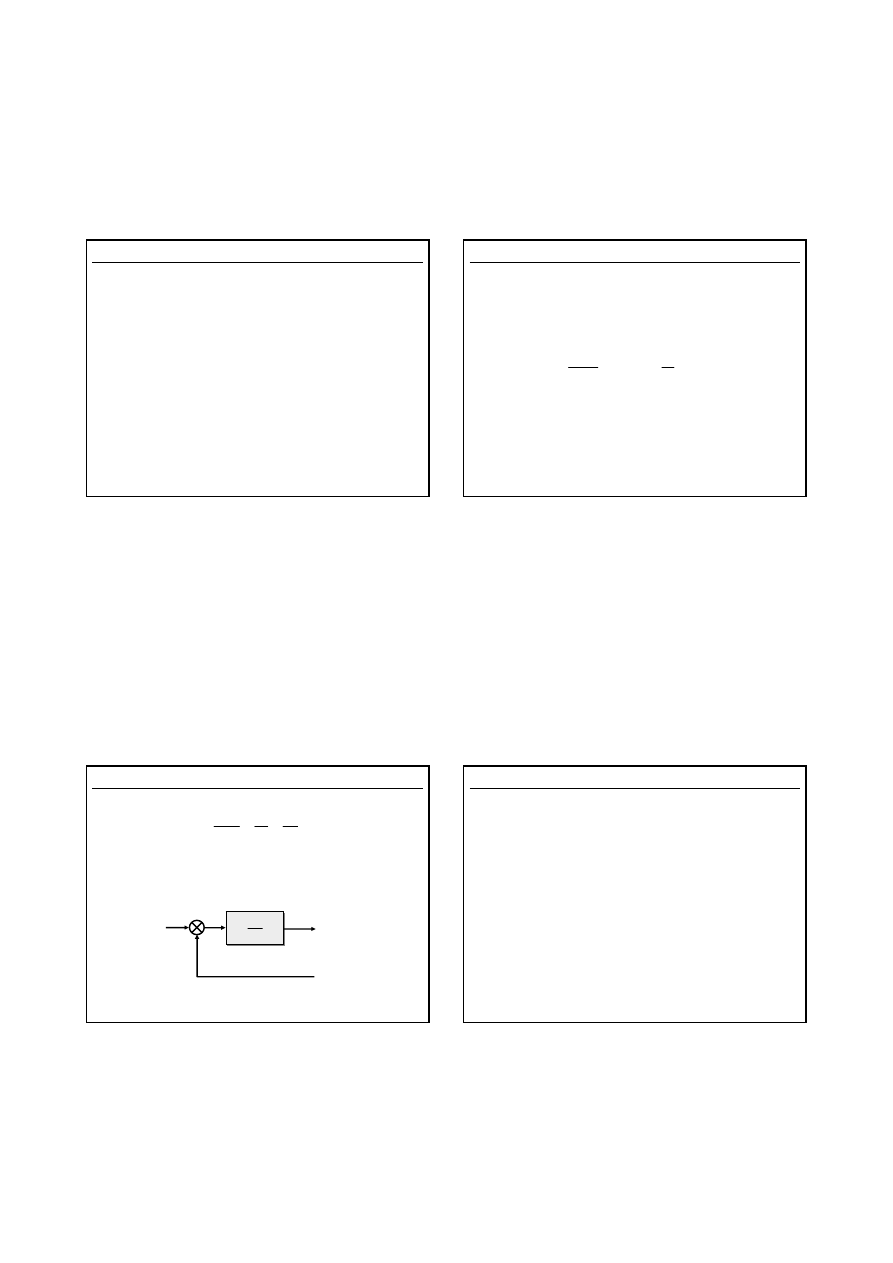
Schemat blokowy regulatora typu P
K
p
–
E
E
(s)
(s)
U(s)
U(s)
Automatyka i Robotyka
Wykład nr 11
5
5
Automatyka i Robotyka
Wykład nr 11
Regulatory proporcjonalne są stosowane:
9
do obiektów o niskim rzędzie inercji i krótkich czasach
opóźnienia, pracujących w obecności stałych zakłóceń i w
układach dopuszczających błąd w stanie ustalonym.
9
stosuje się je również w układach regulacji kaskadowej
jako regulatory pomocnicze.
Zastosowanie s
Zastosowanie s
terowani
terowani
a
a
proporcjonalne
proporcjonalne
go
go
6
6
S
S
terowani
terowani
e
e
c
c
a
a
ł
ł
kow
kow
e
e
W regulatorze z
ca
ca
ł
ł
kowym
kowym algorytmem sterowania, w
skrócie typu
I
I, przyrost wartości sygnału wyjściowego u(t)
zmienia się proporcjonalnie do sygnału uchybu e(t), czyli:
)
(
1
)
(
)
(
t
e
T
t
e
K
dt
t
du
i
i
=
=
lub można powiedzieć, że sygnał wyjściowy u(t) jest
proporcjonalny do całki sygnału wejściowego e(t):
∫
=
t
o
i
dt
t
e
K
t
u
)
(
)
(
gdzie: K
i
– stała nastawna, T
i
– czas całkowania (czas zdwojenia)
Automatyka i Robotyka
Wykład nr 11
7
7
Transmitancja regulatora całkowego ma postać:
U s
E s
K
s
T s
i
i
( )
( )
=
=
1
Jeśli wartość e(t) jest stała przez okres czasu T
i
, to wartość
u
(t) podwoi się po upływie tego czasu. Dla wartości uchybu
e
(t) równego zero wartość u(t) pozostaje niezmienna.
Schemat blokowy regulatora typu I
E
E
(s)
(s)
U(s)
U(s)
–
s
K
i
Automatyka i Robotyka
Wykład nr 11
8
8
Automatyka i Robotyka
Wykład nr 11
Regulatory całkujące są stosowane:
9
do regulacji obiektów inercyjnych przy powolnych
zmianach zakłóceń,
9
w układach regulacji poziomów, przepływów, ciśnień,
temperatur,
9
dla obiektów, w których opóźnienie
τ zawarte jest w
granicach 2÷40 sec.
Zastosowanie s
Zastosowanie s
terowani
terowani
a
a
ca
ca
ł
ł
kowego
kowego
9
9
Przykład 1.
Sterowanie proporcjonalne układu poziomowania cieczy, przy
skokowym sygnale wejściowym, da
uchyb w stanie
uchyb w stanie
ustalonym
ustalonym. Uchyb może być wyeliminowany, jeśli regulator
będzie zawierał
algorytm sterowania ca
algorytm sterowania ca
ł
ł
kowego
kowego.
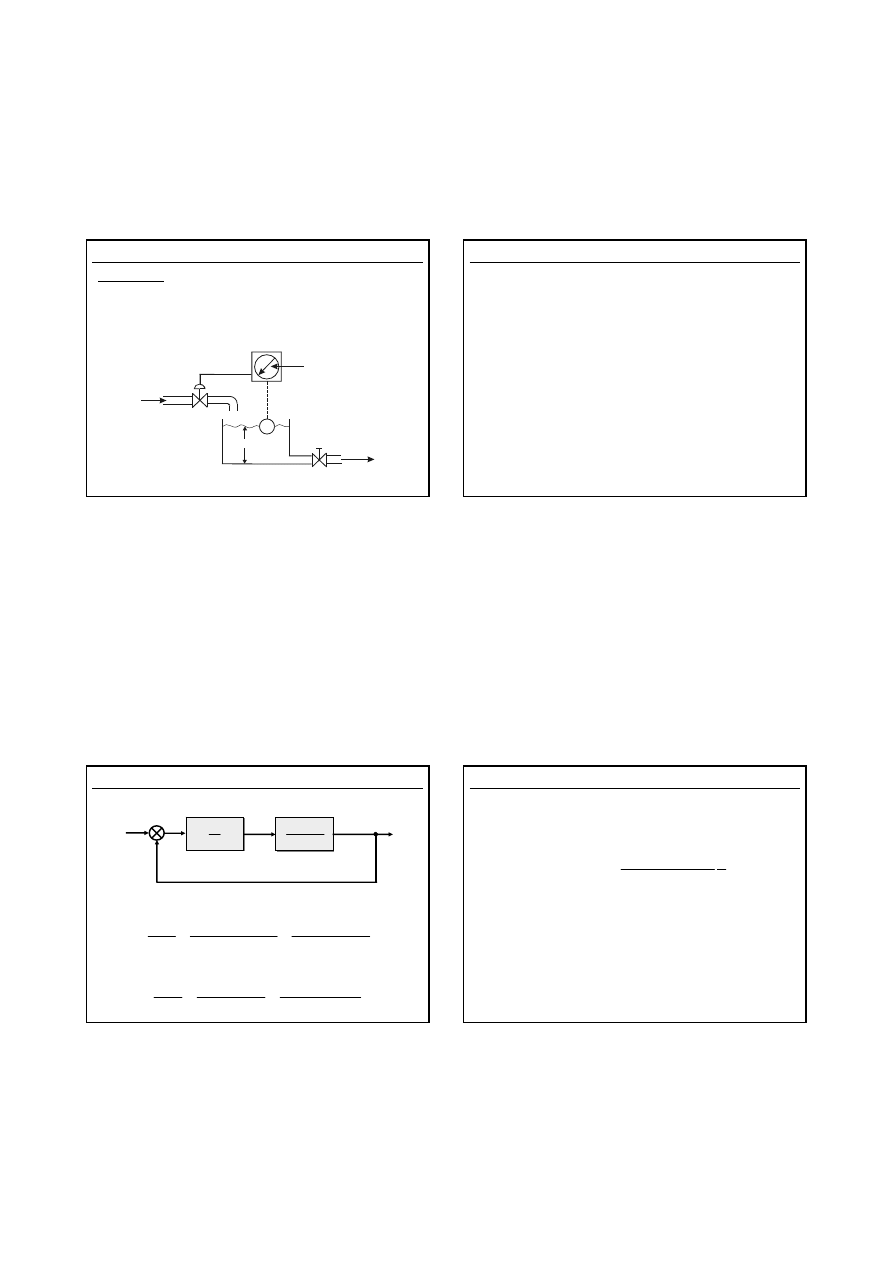
Układ regulacji poziomu cieczy w zbiorniku
R
0
q
Q
+
x
X
+
i
q
Q
+
C
h
H
+
Automatyka i Robotyka
Wykład nr 11
10
10
9
Regulator jest regulatorem całkującym
9
Nie jest znany model układu - (może on być nieliniowy)
- dokonujemy jego linearyzacji wokół punktu pracy,
zakładając małe odchylenia x, q
i
, h
i q
o
od ich wartości
w stanie ustalonym
9
Początek układu współrzędnych ustawiamy w punkcie
pracy, wtedy układ można traktować jako stabilny
Założenia:
Automatyka i Robotyka
Wykład nr 11
11
11
Schemat blokowy układu
X(s)
X(s)
E
E
(s)
(s)
H(s)
H(s)
–
s
K
1
+
RCs
R
Transmitancja układu zamkniętego ma postać:
KR
s
RCs
KR
s
G
s
G
s
G
s
G
s
X
s
H
O
R
O
R
+
+
=
⋅
+
⋅
=
2
)
(
)
(
1
)
(
)
(
)
(
)
(
Stąd:
KR
s
RCs
s
RCs
s
X
s
H
s
X
s
X
s
E
+
+
+
=
−
=
2
2
)
(
)
(
)
(
)
(
)
(
Automatyka i Robotyka
Wykład nr 11
12
12
Uchyb statyczny
0
1
)
(
)
(
lim
2
2
0
=
+
+
+
=
=
→
s
KR
s
RCs
s
RCs
s
s
sE
e
s
u
9
Wynika stąd, że sterowanie całkowe układem
poziomowania cieczy, eliminuje uchyb statyczny w
odpowiedzi na skokowy sygnał wejściowy.
Automatyka i Robotyka
Wykład nr 11
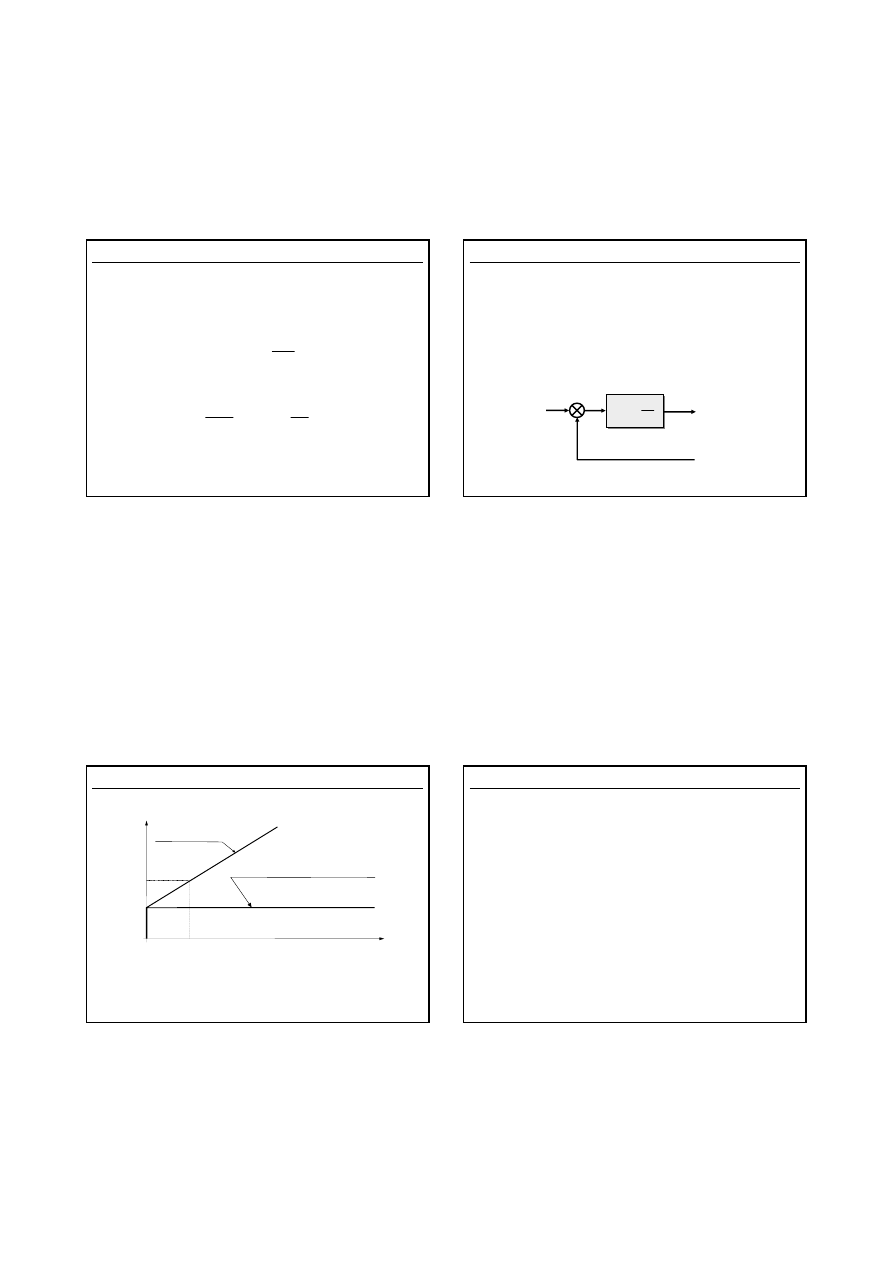
13
13
S
S
terowani
terowani
e
e
proporcjonalno
proporcjonalno
-
-
c
c
a
a
ł
ł
kowe
kowe
Algorytm pracy regulatora
proporcjonalno
proporcjonalno
-
-
ca
ca
ł
ł
kowego
kowego, w
skrócie typu
PI
PI, zdefiniowany jest wzorem:
∫
+
=
t
o
i
p
p
dt
t
e
T
K
t
e
K
t
u
)
(
)
(
)
(
a transmitancja regulatora ma postać:
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
=
s
T
K
s
E
s
U
i
p
1
1
)
(
)
(
gdzie:
K
p
- wzmocnienie proporcjonalne,
T
i
- czas całkujący (czas zdwojenia).
Automatyka i Robotyka
Wykład nr 11
14
14
9
Stała czasowa całkowania
T
i
umożliwia
zmianę
parametrów algorytmu całkowego
9
Zmiana wartości K
p
wpływa zarówno na część
proporcjonalną, jak i na część całkową algorytmu
sterowania.
9
Odwrotność stałej czasowej T
i
jest nazywana szybkością
działania całkującego.
Schemat blokowy regulatora typu PI
E
E
(s)
(s)
U(s)
U(s)
–
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
s
T
K
i
p
1
1
Automatyka i Robotyka
Wykład nr 11
15
15
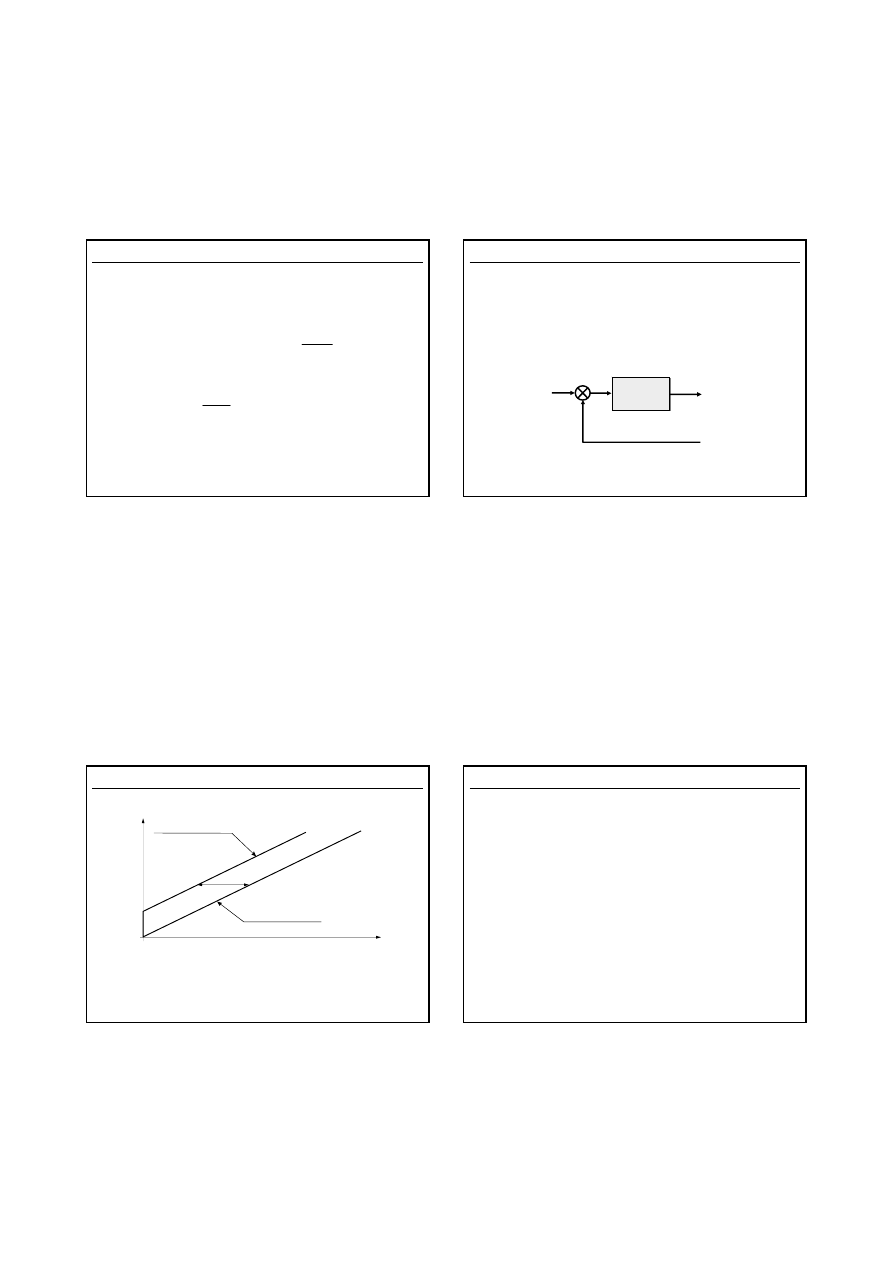
Sterowanie PI
Odpowiedź skokowa regulatora typu PI
p
K
0
u(t)
t
i
T
p
K
2
e(t)
Sygnał wejściowy
Automatyka i Robotyka
Wykład nr 11
16
16
Automatyka i Robotyka
Wykład nr 11
Zastosowanie s
Zastosowanie s
terowani
terowani
a
a
proporcjonalno
proporcjonalno
-
-
ca
ca
ł
ł
kowego
kowego
Regulatory PI są stosowane:
9
w układach regulacji, w których można wykorzystać
zarówno zalety regulacji statycznej i astatycznej,
9
działanie proporcjonalne jest szybkie ale niedokładne
(e≠0),
9
całkowanie działa wolno, ale dokładnie (e=0),
9
regulatory PI zapewniają dobrą regulację przy
zakłóceniach o niskich częstotliwościach.
17
17
S
S
terowani
terowani
e
e
proporcjonalno
proporcjonalno
-
-
r
r
ó
ó
ż
ż
niczkowe
niczkowe
Algorytm pracy regulatora
proporcjonalno
proporcjonalno
-
-
r
r
ó
ó
ż
ż
niczkowego
niczkowego,
w skrócie typu
PD
PD, zdefiniowany jest wzorem:
dt
t
de
T
K
t
e
K
t
u
d
p
p
)
(
)
(
)
(
+
=
a transmitancja regulatora ma postać:
)
1
(
)
(
)
(
s
T
K
s
E
s
U
d
p
+
=
gdzie:
K
p
- wzmocnienie proporcjonalne,
T
d
- stała nazywana czasem różniczkującym
lub czasem wyprzedzenia
Automatyka i Robotyka
Wykład nr 11
18
18
9
Z algorytmem sterowania różniczkowego mamy do
czynienia, gdy wartość sygnału wyjściowego regulatora
jest proporcjonalna do szybkości zmiany sygnału uchybu.
Czas różniczkujący T
d
jest miarą, na ile sterowanie PD
wyprzedza sterowanie z regulatorem proporcjonalnym P.
Schemat blokowy regulatora typu PD
E
E
(s)
(s)
U(s)
U(s)
–
(
)
s
T
K
d
p
+
1
Automatyka i Robotyka
Wykład nr 11
19
19
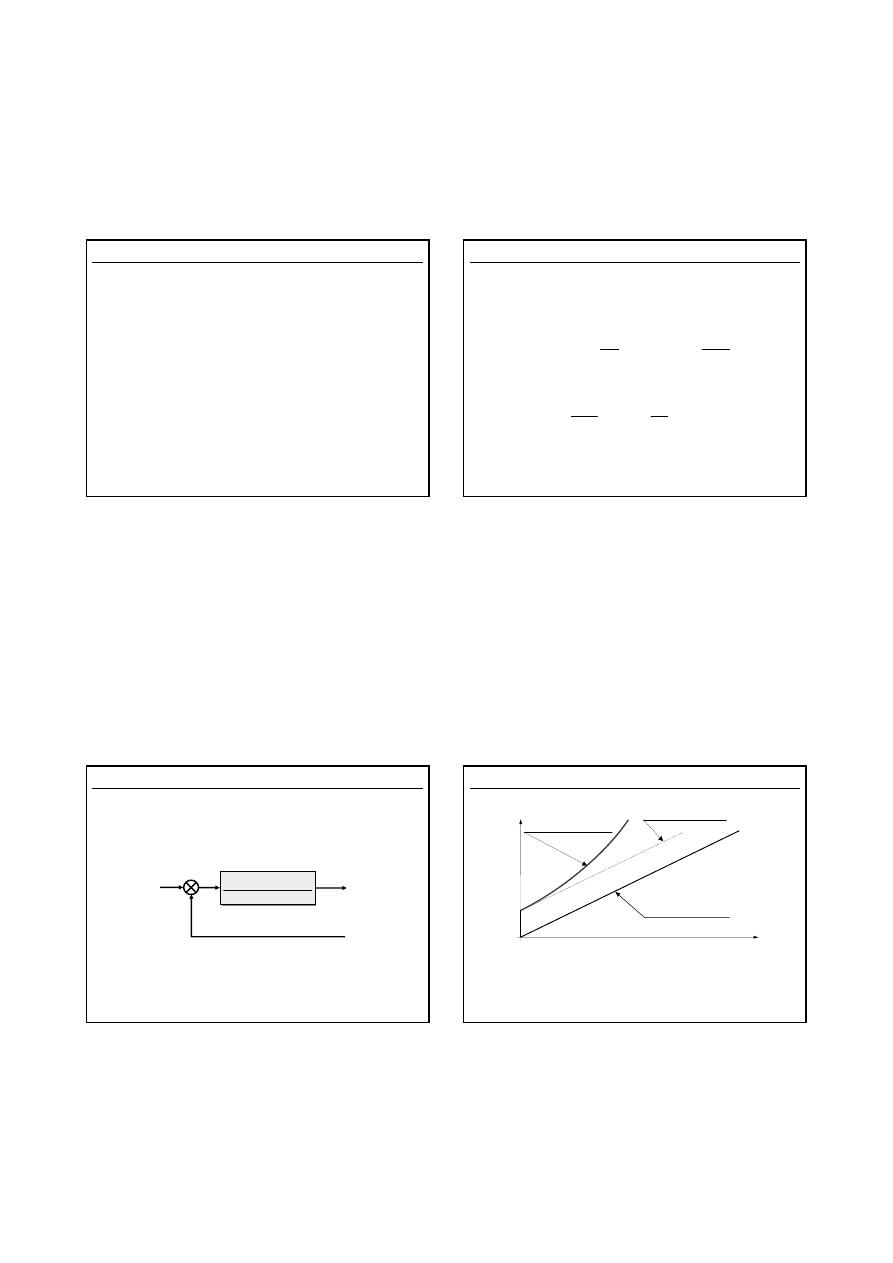
Sygnał wejściowy
Sterowanie PD
d
T
Odpowiedź liniowa regulatora typu PD
0
u(t)
t
e(t)
Automatyka i Robotyka
Wykład nr 11
20
20
9
Różniczkowy algorytm sterowania
ma charakter
wyprzedzający. „Podbija” on sygnał wyjściowy
9
Wada: wzmacnia sygnały szumów i może powodować
efekt nasycenia w urządzeniu wykonawczym
9
Algorytm ten stabilizuje
układ, nie pogarszając
właściwości dynamicznych, uchyb ustalony jest znacznie
większy niż
przy algorytmie
całkowym,
przy
równoczesnym zwiększeniu zapasu stabilności
Automatyka i Robotyka
Wykład nr 11
21
21
Automatyka i Robotyka
Wykład nr 11
Zastosowanie s
Zastosowanie s
terowani
terowani
a
a
proporcjonalno
proporcjonalno
-
-
r
r
ó
ó
ż
ż
niczkowego
niczkowego
9
Regulatory PD są stosowane w układach pracujących
przy małych i szybkich zakłóceniach,
9
W układach z regulatorem PD otrzymuje się krótsze
czasy regulacji niż z regulatorem P,
9
Przy zastosowaniu regulatora PD można uzyskać
szybszą likwidację błędu dynamicznego podczas zmian
sygnału zadającego oraz uzyskać złagodzenie skutków
zmian zakłóceń.
22
22
Równanie regulatora
PID
PID ma postać:
dt
t
de
T
K
dt
t
e
T
K
t
e
K
t
u
t
o
d
p
i
p
p
)
(
)
(
)
(
)
(
∫
+
+
=
a transmitancja regulatora ma postać:
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
+
=
s
T
s
T
K
s
E
s
U
d
i
r
1
1
)
(
)
(
gdzie:
K
p
- wzmocnienie proporcjonalne,
T
i
- czas całkującym,
T
d
- czas różniczkujący.
S
S
terowani
terowani
e
e
proporcjonalno
proporcjonalno
-
-
r
r
ó
ó
ż
ż
niczko
niczko
wo
wo
-
-
ca
ca
ł
ł
kowe
kowe
Automatyka i Robotyka
Wykład nr 11
23
23
Schemat blokowy regulatora typu PID
E
E
(s)
(s)
U(s)
U(s)
–
(
)
s
T
s
T
T
s
T
K
i
d
i
i
p
2
1
+
+
Ten połączony algorytm ma zalety każdego z trzech
wcześniej wspomnianych algorytmów.
Automatyka i Robotyka
Wykład nr 11
24
24
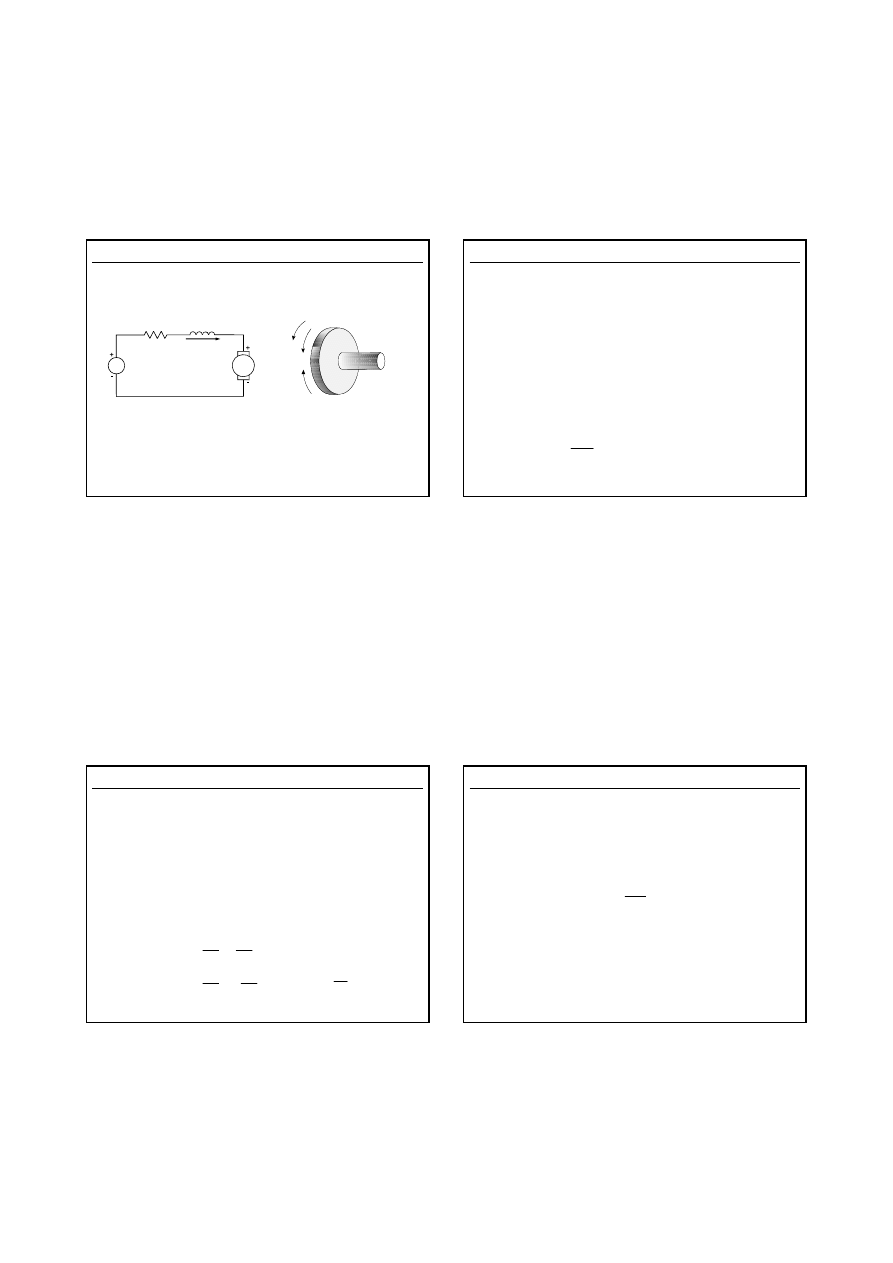
Odpowiedź liniowa regulatora typu PID
0
u(t)
t
Sygnał wejściowy
e(t)
Sterowanie PID
Sterowanie PD
Automatyka i Robotyka
Wykład nr 11
25
25
Regulacja pr
Regulacja pr
ę
ę
dko
dko
ś
ś
ci
ci
silnika pr
silnika pr
ą
ą
du sta
du sta
ł
ł
ego
ego
a
R
a
L
a
v
Θ
=
.
e
K
e
a
i
∼
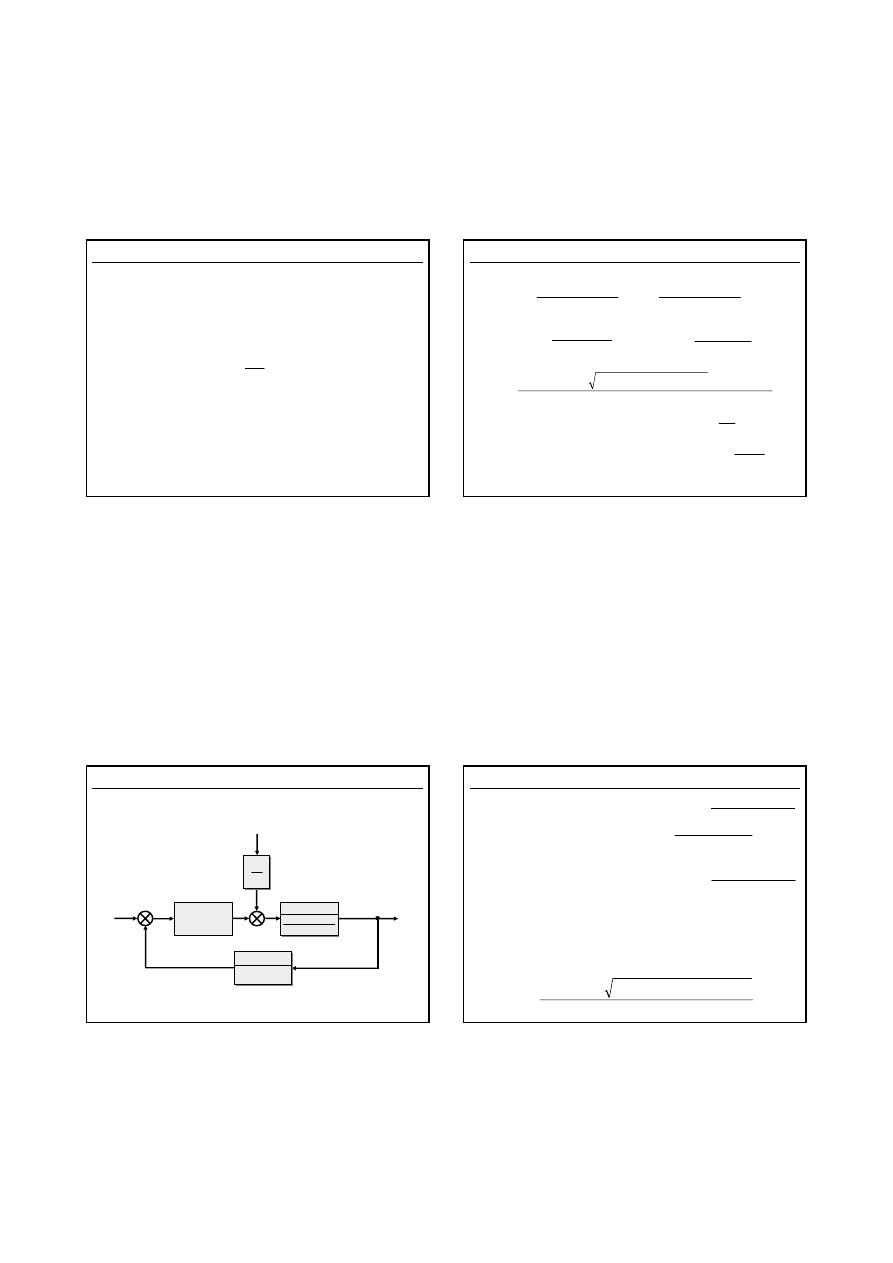
a) obwód elektryczny silnika
prądu stałego
T
m
Θ
m
b
Θ
.
m
J
b) model mechaniczny wirnika
silnika prądu stałego
Automatyka i Robotyka
Wykład nr 11
26
26
Moment bezwładności wirnika wynosi J
m
, opory ruchu
reprezentuje współczynnik b, a moment czynny M = K
t
i
a
Równanie dynamiczne ruchu układu ma postać:
z
a
t
m
m
m
M
i
K
b
J
+
=
+
θ
θ
&
&&
Równanie obwodu elektrycznego:
m
e
a
a
a
a
a
K
v
i
R
dt
di
L
θ
&
−
=
+
Automatyka i Robotyka
Wykład nr 11
27
27
Jeżeli zdefiniujemy wektor stanu układu jako:
[
]
T
m
m
i
,
,
x
a
θ
θ
&
=
to macierze układu i sterowania mają postać:
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
−
−
−
=
a
a
a
e
m
t
m
L
R
L
K
J
K
J
b
0
0
0
1
0
A
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
=
a
L
1
0
0
B
Automatyka i Robotyka
Wykład nr 11
28
28
Równania układu zapiszemy w postaci:
⎪⎩
⎪
⎨
⎧
=
+
+
+
=
+
a
a
a
a
a
e
z
a
t
m
v
i
R
dt
di
L
K
M
i
K
b
J
m
m
m
θ
θ
θ
&
&
&&
gdzie: M
z
jest momentem zakłócającym
Automatyka i Robotyka
Wykład nr 11
29
29
⎪⎩
⎪
⎨
⎧
=
+
+
+
=
+
a
a
a
a
a
e
a
t
m
v
i
R
dt
di
L
y
K
z
i
K
by
y
J
&
Stosując
przekształcenie Laplace’a, przy zerowych
warunkach początkowych otrzymamy równania algebraiczne:
⎩
⎨
⎧
=
+
+
+
=
+
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
sJ
m
s
V
s
I
R
s
I
sL
s
Y
K
s
Z
s
I
K
s
bY
s
Y
a
a
a
a
a
e
a
t
Definiując sygnał wyjściowy
m
θ
&
Δ
=
y
i zakłócający
z
M
z
Δ
=
otrzymamy:
Automatyka i Robotyka
Wykład nr 11
30
30
Obliczamy Y(s):
gdzie:
e
t
a
t
K
K
bR
K
A
+
=
e
t
a
K
K
bR
B
+
=
1
)
(
)
1
)(
1
(
)
(
)
1
)(
1
(
)
(
2
1
2
1
s
Z
s
s
B
s
V
s
s
A
s
Y
a
+
+
+
+
+
=
τ
τ
τ
τ
a
m
e
t
a
a
m
a
a
m
a
a
m
L
J
K
K
bR
L
J
bL
R
J
bL
R
J
2
)
(
4
)
(
)
(
2
1
2
,
1
+
−
+
+
=
+
−
−
τ
9
Jeżeli b=0 i L
a
jest małe, wtedy stała nazywana
jest elektryczną stałą czasową zaś stała
nazywana jest elektromechaniczną stałą czasową.
a
a
R
L
=
2
τ
e
t
m
a
K
K
J
R
=
1
τ
Automatyka i Robotyka
Wykład nr 11
31
31
W(s)
W(s)
E
E
(s)
(s)
Y(s)
Y(s)
Y(s)
Y(s)
Z(s)
Z(s)
–
A
B
Regulator
(
)(
)
1
1
2
1
+
+
s
s
A
τ
τ
Silnik
Czujnik
1
V
V
a
a
Schemat blokowy uk
Schemat blokowy uk
ł
ł
adu regulacji pr
adu regulacji pr
ę
ę
dko
dko
ś
ś
ci
ci
Automatyka i Robotyka
Wykład nr 11
32
32
Zakładając, że w układzie zastosowany będzie regulator typu P,
dla którego:
G
R
(s) = K,
)
1
)(
1
(
)
(
2
1
+
+
=
s
s
A
s
G
O
τ
τ
Równanie charakterystyczne pętli zamkniętej:
)
(
)
(
1
1
s
G
s
G
O
R
+
ma postać:
0
1
)
(
2
1
2
2
1
=
+
+
+
+
AK
s
s
τ
τ
τ
τ
Bieguny układu w pętli zamkniętej są funkcją wzmocnienia K:
2
1
2
1
2
2
2
1
2
,
1
2
)
1
(
4
)
(
)
(
τ
τ
τ
τ
τ
τ
τ
τ
AK
s
+
−
+
+
−
=
+
−
Automatyka i Robotyka
Wykład nr 11
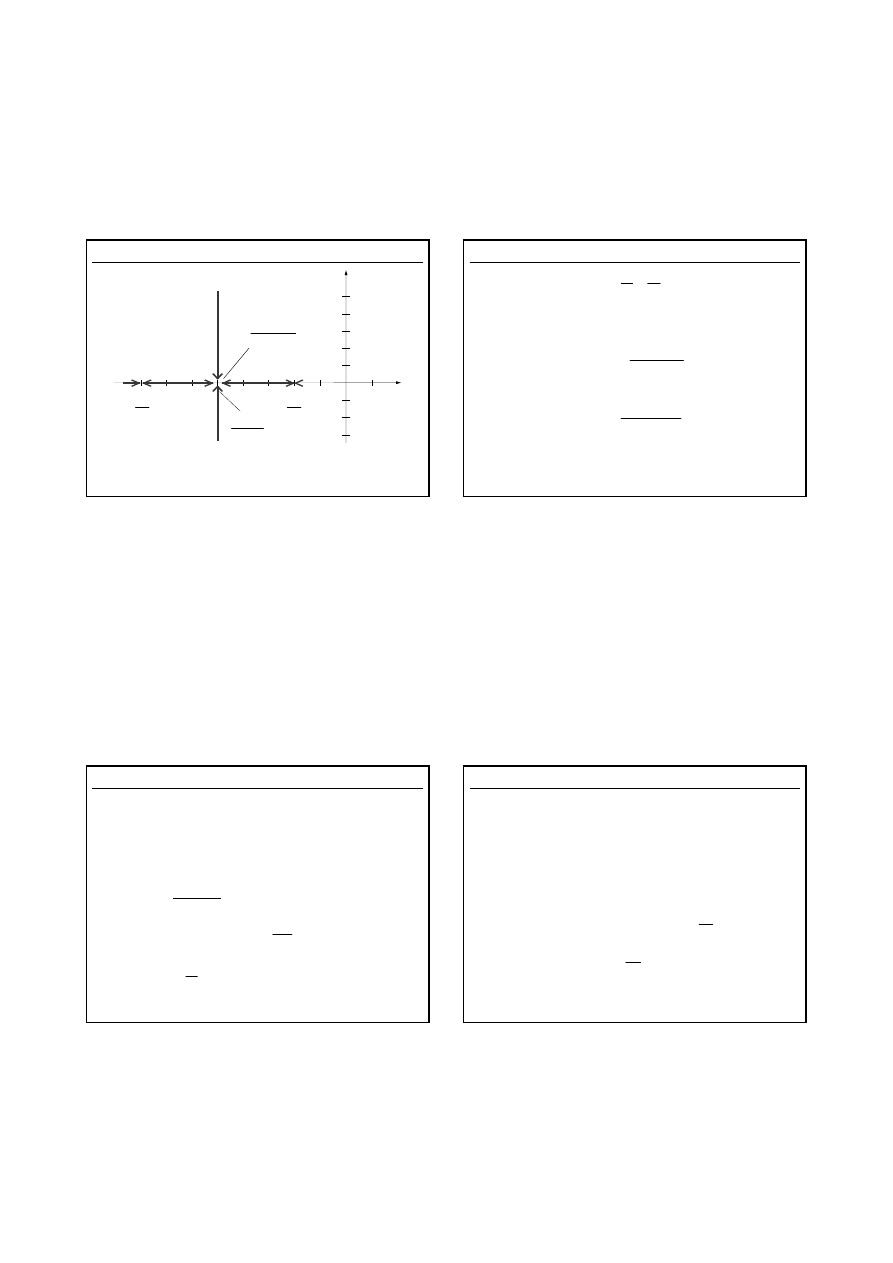
33
33
Lokalizacja biegunów na płaszczyźnie zmiennej zespolonej dla
zmieniającej się wartości K
K=0
Im(s)
Re(s)
K=0
2
1
τ
−
2
1
τ
−
(
)
A
K
2
1
2
2
1
4
τ
τ
τ
τ
−
=
2
1
2
1
2
τ
τ
τ
τ
+
−
0
Automatyka i Robotyka
Wykład nr 11
34
34
Pierwiastki lokują się w:
2
1
1
,
1
τ
τ
−
−
dla otwartej pętli (K = 0) i zaczynają się do siebie zbliżać
wraz ze wzrostem wartości K poza przedział:
,
4
)
(
0
2
1
2
2
1
A
K
τ
τ
τ
τ
−
<
<
co oznacza zmniejszenie stałej czasowej układu.
A
K
2
1
2
2
1
4
)
(
τ
τ
τ
τ
−
>
składowa rzeczywista pierwiastków nie zależy od K,
natomiast składowa urojona rośnie i w ten sposób czas
odpowiedzi układu maleje.
Dla wartości:
Automatyka i Robotyka
Wykład nr 11
35
35
9
Lepsze sterowanie w stanach
ustalonych, bez
konieczności stosowania dużych wzmocnień można
uzyskać wprowadzając regulator całkujący.
9
Zakładając, że w układzie wprowadzimy dodatkowo
regulację całkującą, transmitancja regulatora przyjmie
postać:
s
T
K
s
G
i
R
=
)
(
gdzie:
i
T
1
jest miarą szybkości odpowiedzi
Automatyka i Robotyka
Wykład nr 11
36
36
Najistotniejszym zadaniem regulatora całkującego jest
zmniejszenie lub wyeliminowanie błędu w stanie ustalonym,
lecz jest to okupione pogorszeniem odpowiedzi stanu
przejściowego.
Równanie charakterystyczne dla układu z regulatorem
całkującym:
0
)
(
2
2
1
3
2
1
=
+
+
+
+
i
T
K
A
s
s
s
τ
τ
τ
τ
Zwiększanie wzmocnienia
i
T
K
do nieznacznego przesunięcia pierwiastków dla danych
wartości K.
takiego układu doprowadzi
Automatyka i Robotyka
Wykład nr 11
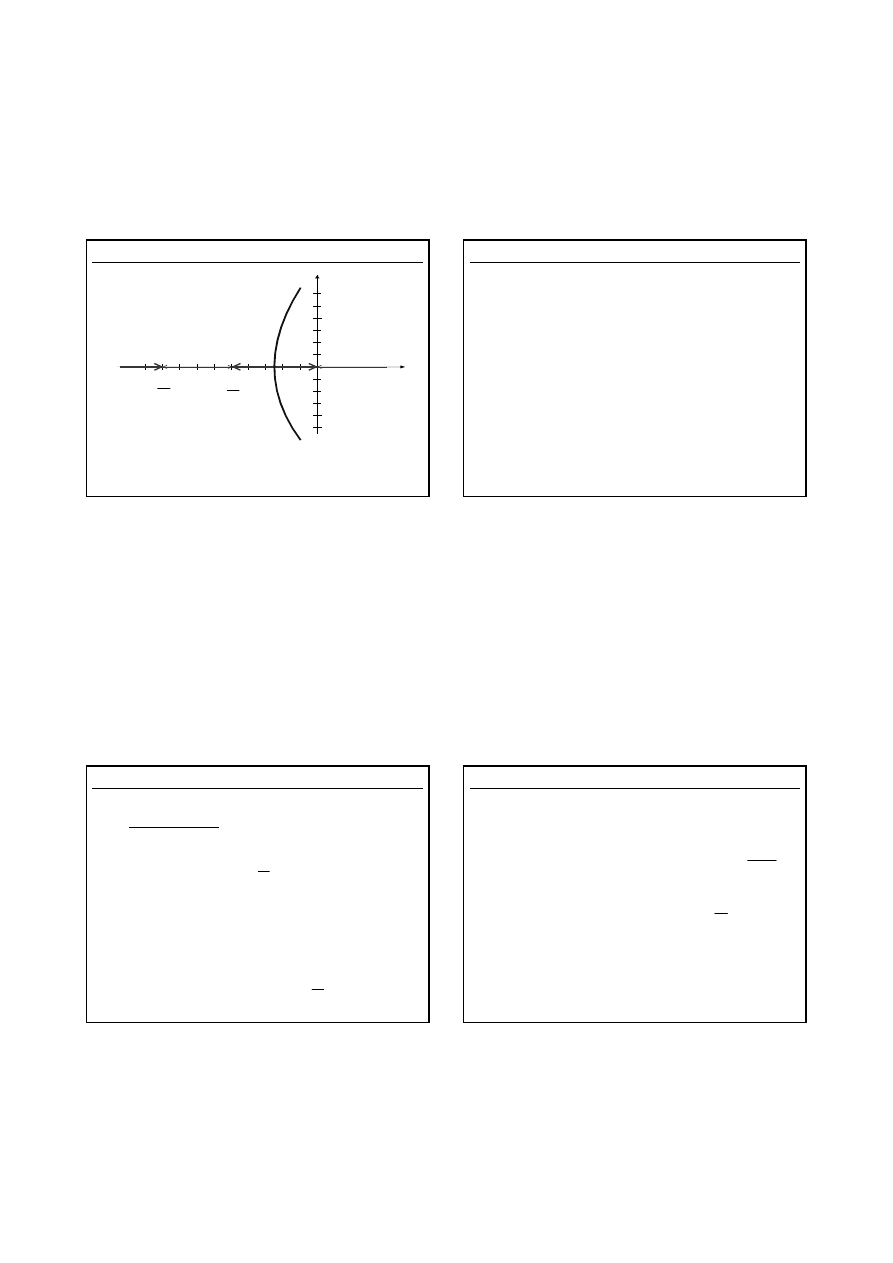
37
37
Lokalizacja pierwiastków równania charakterystycznego
K=0
K=0
K=0
2
1
τ
−
1
1
τ
−
0
Im(s)
Re(s)
Automatyka i Robotyka
Wykład nr 11
38
38
9
Jeśli zwiększymy dynamikę odpowiedzi przy dużym
całkowitym wzmocnieniu, to odpowiedź będzie miała
charakter oscylacyjny.
9
Sposobem uniknięcia takiej niekorzystnej cechy dla
niektórych przypadków jest jednoczesne zastosowanie
sterowania proporcjonalnego i całkującego.
9
Pomimo tego, że regulacja całkowa polepsza śledzenie
odpowiedzi w stanach ustalonych, spowalnia jednak czas
odpowiedzi przy niezmiennym przeregulowaniu.
Automatyka i Robotyka
Wykład nr 11
39
39
Przy równoczesnym zastosowaniu regulacji proporcjonalnej,
czyli regulatora typu PI, napięcie sterujące dla rozważanego
przypadku przyjmie postać:
⎥
⎦
⎤
⎢
⎣
⎡
−
+
−
=
∫
t
o
i
a
d
y
w
T
y
w
K
η
ϑ
)
(
1
gdzie:
K
- wzmocnienie proporcjonalne
Równanie ruchu układu możemy zapisać jako:
[
]
z
B
y
w
T
K
y
w
K
A
y
y
y
i
&
&
&
&
&&
&&
&
+
⎥
⎦
⎤
⎢
⎣
⎡
−
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
−
=
+
+
+
)
(
)
(
2
1
2
1
τ
τ
τ
τ
Automatyka i Robotyka
Wykład nr 11
40
40
Tak jak w przypadku regulacji całkowej, gdy zakłócenie
(moment) i prędkość zadana są stałe, więc:
0
=
z
&
0
=
w
&
i
Wtedy równanie charakterystyczne układu
)
(
)
(
)
(
s
W
s
Y
s
G
=
zapiszemy następująco:
0
)
1
(
)
(
2
2
1
3
2
1
=
+
+
+
+
+
i
T
K
A
s
AK
s
s
τ
τ
τ
τ
Dobierając odpowiednio K i T
i
, można niezależnie ustawić
wartości współczynników przy s i wartości stałe, i w ten
sposób niezależnie
regulować
dwa
spośród trzech
parametrów w równaniu charakterystycznym.
Automatyka i Robotyka
Wykład nr 11
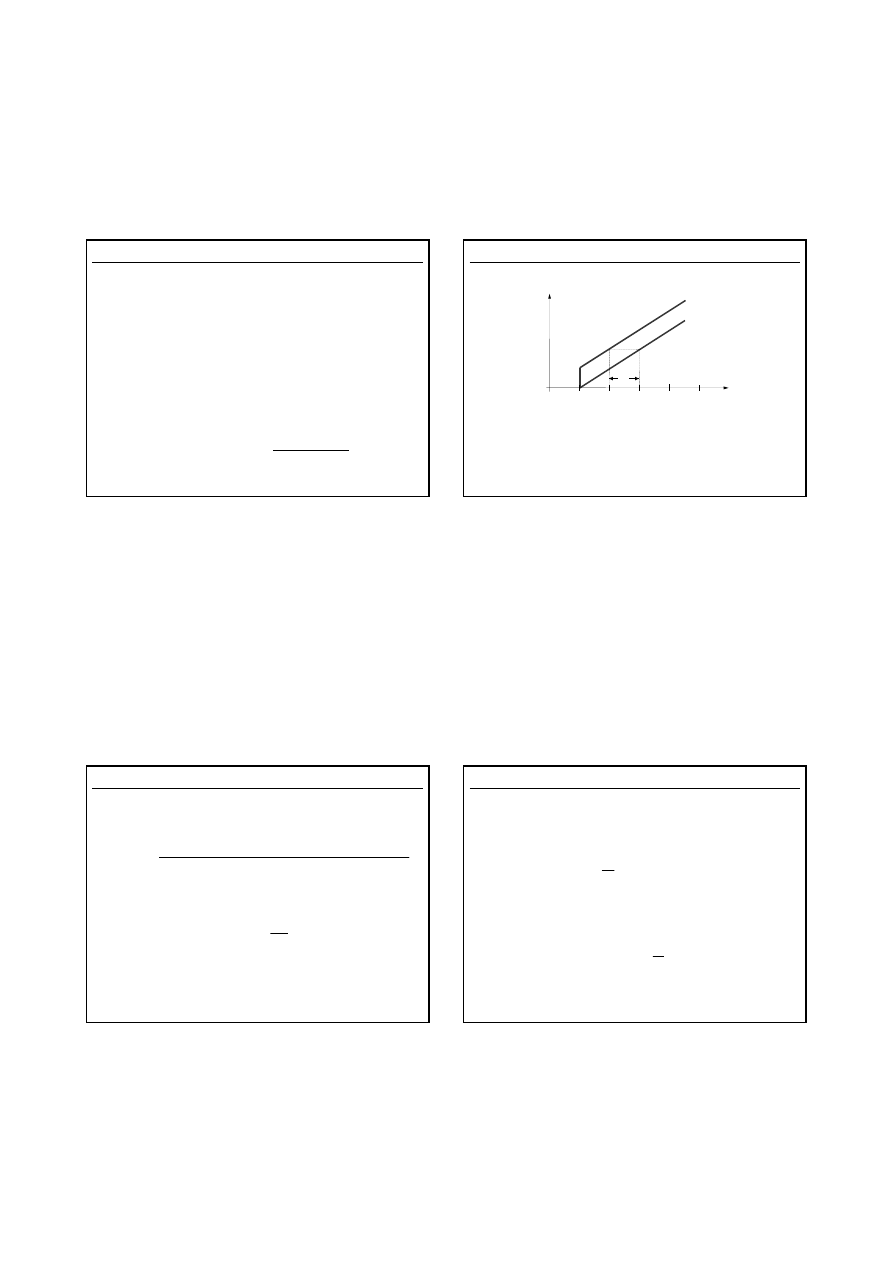
41
41
W przypadku zastosowania regulacji różniczkującej
transmitancja regulatora:
s
KT
s
G
d
R
=
)
(
W praktyce czysty element różniczkujący nie występuje.
Stosuje się go w połączeniu z proporcjonalnym i całkującym
by zwiększyć tłumienie i poprawić stabilność układu.
Regulator z elementem różniczkującym generuje odpowiedź
z wyprzedzeniem. Odpowiedź regulatora PD wyprzedza
odpowiedź regulatora P o T
D
– sekund.
Automatyka i Robotyka
Wykład nr 11
42
42
Charakterystyka czasowa regulatora PD dla wzrastającego
błędu e(t)
u(t)
t
0
2
3
4
1
5
T
D
Automatyka i Robotyka
Wykład nr 11
43
43
Celem zmniejszenia błędów stanów ustalonych i przej-
ściowych przy zachowaniu stabilności i odpowiedniego
tłumienia możemy połączyć wszystkie trzy rodzaje regulacji
i otrzymać
regulacj
regulacj
ę
ę
proporcjonalno
proporcjonalno
-
-
ca
ca
ł
ł
kowo
kowo
-
-
r
r
ó
ó
ż
ż
niczkow
niczkow
ą
ą:
Regulatory
PID
PID są powszechnie stosowane w przemyśle.
Ogólnie transmitancja regulatora PID przyjmuje postać:
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
+
=
s
T
s
T
K
s
G
D
i
R
1
1
)
(
By zaprojektować konkretny układ regulacji należy dobrać
stałe K, T
i
i T
D
by osiągnąć zamierzony rezultat.
Automatyka i Robotyka
Wykład nr 11
44
44
Dla rozważanego przykładu regulacji prędkości silnika z
regulatorem PID, napięcie sterujące przyjmuje postać:
⎥
⎦
⎤
⎢
⎣
⎡
−
+
−
+
−
=
∫
t
o
D
i
a
y
w
T
d
y
w
T
y
w
K
v
)
(
)
(
1
&
&
η
Różniczkując równanie układu w pętli zamkniętej otrzymujemy:
z
B
y
w
KT
y
w
T
K
y
w
K
A
y
y
y
D
i
&
&&
&&
&
&
&
&&
&&
&
+
⎥
⎦
⎤
⎢
⎣
⎡
−
+
−
+
−
=
+
+
+
)
(
)
(
]
[
)
(
2
1
2
1
τ
τ
τ
τ
Automatyka i Robotyka
Wykład nr 11
45
45
Równanie charakterystyczne zapiszemy jako:
[
]
0
)
1
(
)
(
2
2
1
3
2
1
=
+
+
+
+
+
AK
s
AK
T
s
AKT
T
s
T
i
D
i
i
τ
τ
τ
τ
9
Jeśli równanie to podzielimy przez
τ
1
τ
2
T
i
, otrzymujemy
trzy współczynniki i trzy parametry (K, T
i
i T
D
).
9
Dołączenie działania różniczkującego do takiego układu
pozwala na pełniejsze kształtowanie jego dynamiki.
9
Rozważmy omawiany silnik prądu stałego i przyjmijmy:
K
= 5, T
D
= 0,0004 i T
i
= 0,01.
Automatyka i Robotyka
Wykład nr 11
46
46
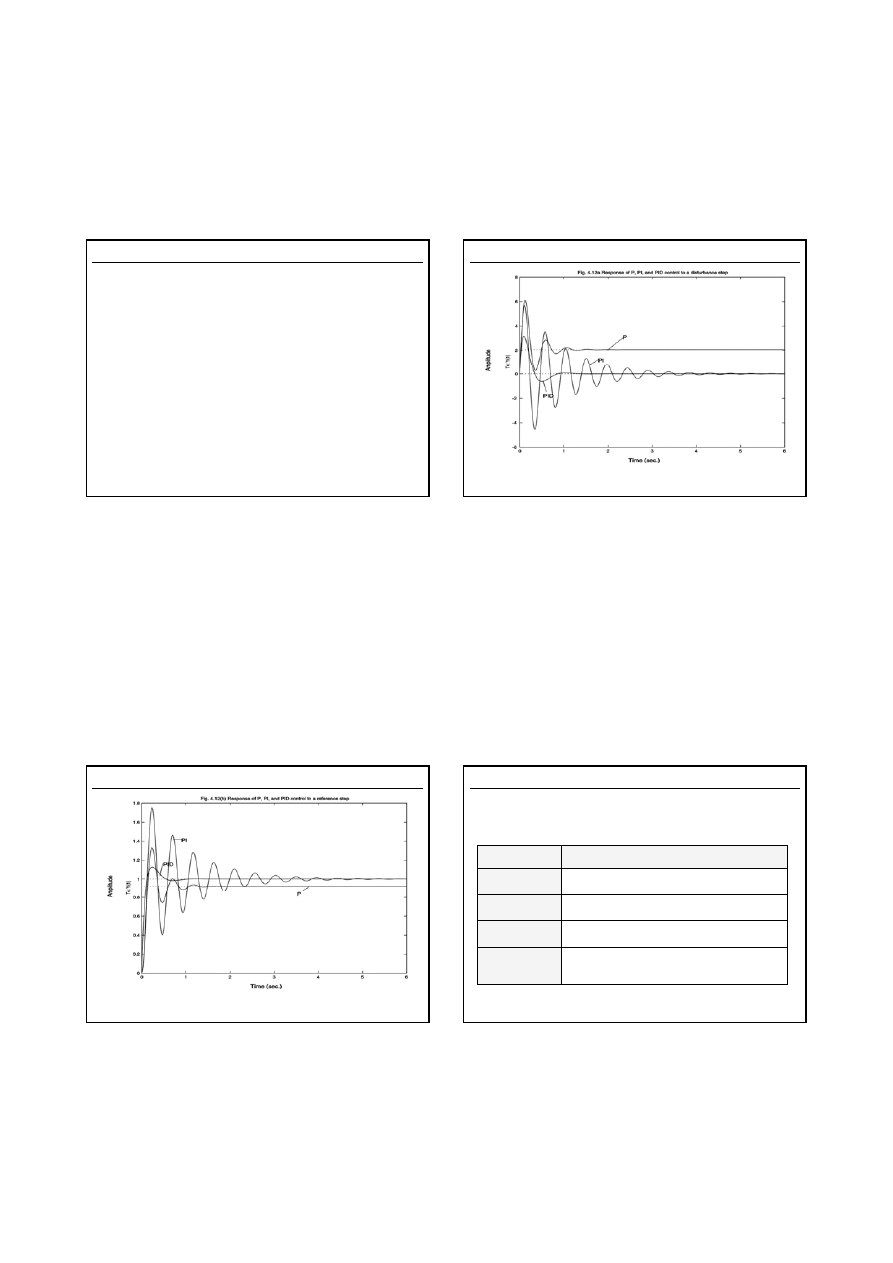
Odpowiedzi układu na skokową zmianę zakłócenia
dla różnych regulatorów
Automatyka i Robotyka
Wykład nr 11
47
47
Odpowiedzi układu na skokową zmianę wartości zadanej
dla różnych regulatorów
Automatyka i Robotyka
Wykład nr 11
48
48
Automatyka i Robotyka
Wykład nr 11
Zasady doboru funkcji przej
Zasady doboru funkcji przej
ś
ś
cia typowych
cia typowych
regulator
regulator
ó
ó
w liniowych
w liniowych
Przewidywane działanie regulatora
Regulator
Likwidacja lub zmiana uchybu statycznego, zmiana
przeregulowania, nieduża zmiana lub skrócenie
czasu regulacji
PID
Likwidacja lub zmiana uchybu statycznego, zmiana
przeregulowania, wydłużenie czasu regulacji
PI
Skrócenie czasu regulacji, zmiana uchybu
statycznego, zmiana przeregulowania
PD
Zmiana uchybu statycznego, zmiana
przeregulowania i czasu regulacji
P
49
49
Automatyka i Robotyka
Wykład nr 11
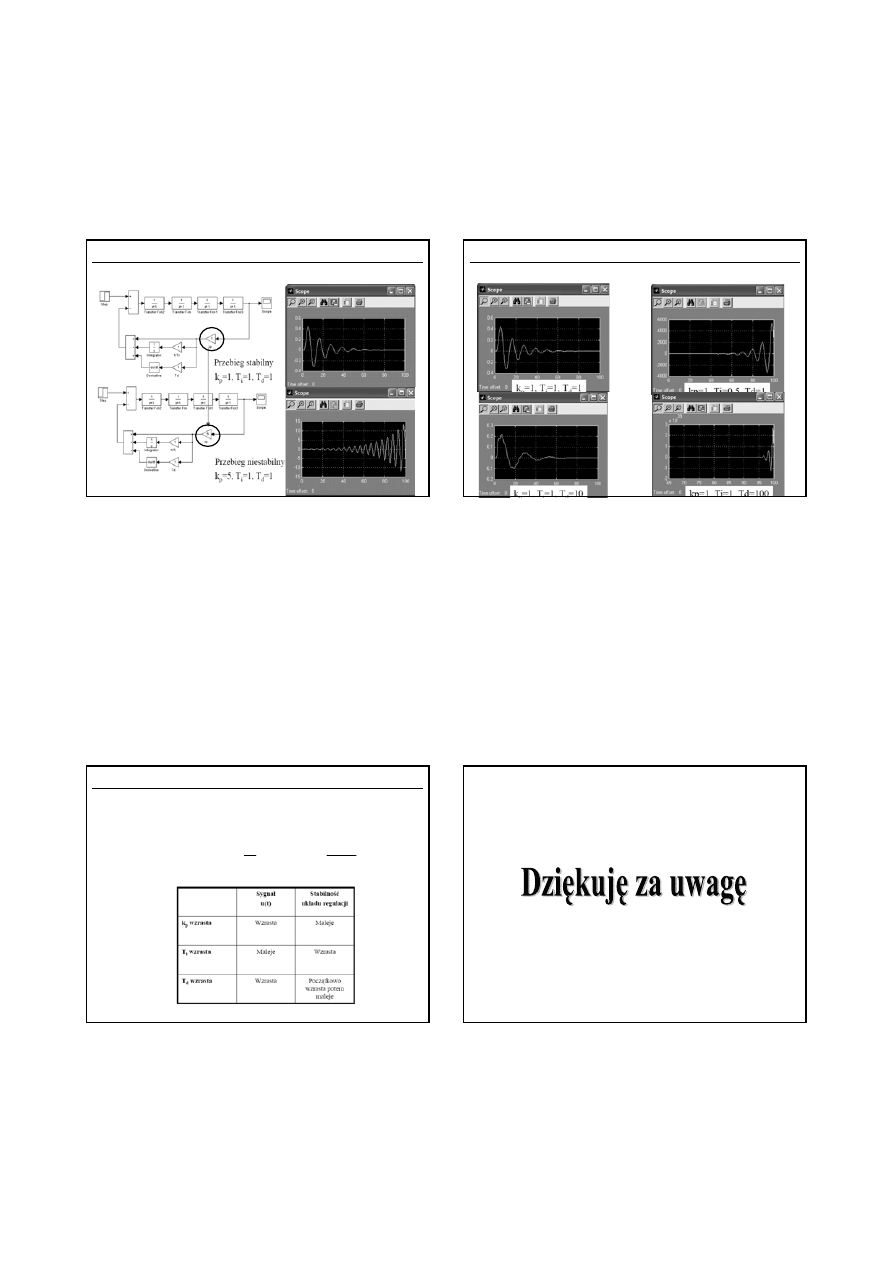
Wp
Wp
ł
ł
yw nastaw regulatora na przebieg przej
yw nastaw regulatora na przebieg przej
ś
ś
ciowy
ciowy
50
50
Automatyka i Robotyka
Wykład nr 11
Wp
Wp
ł
ł
yw nastaw regulatora na przebieg przej
yw nastaw regulatora na przebieg przej
ś
ś
ciowy
ciowy
51
51
Automatyka i Robotyka
Wykład nr 11
Wp
Wp
ł
ł
yw nastaw regulatora na przebieg
yw nastaw regulatora na przebieg
przej
przej
ś
ś
ciowy
ciowy
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
+
=
∫
dt
t
de
T
dt
t
e
T
t
e
K
t
u
t
o
d
i
p
)
(
)
(
1
)
(
)
(
52
52
Wyszukiwarka
Podobne podstrony:
9 podstawowe algorytmy sterowania nowy
9 podstawowe algorytmy sterowania nowy
10 Podstawowe algorytmy sterowania
Układy Napędowe oraz algorytmy sterowania w bioprotezach
nieodporny sprawozdanie, Pwr, Metody i algorytmy sterowania cyfrowego, sprawka
Implementacja i badania algorytmów sterowania robotem dwukołowym
Przegląd podstawowych algorytmów
Podstawowym urządzeniem sterowanym w przemyśle przez?lowniki są klatkowe silniki indukcyjne prądu zm
Podstawy algorytmów ewolucyjnych2013
Podstawy programowania sterowników PLC (2)
Implementacja algorytmów sterowania osi robota
Metody i algorytmy sterowania cyfrowego spr2, Pwr, Metody i algorytmy sterowania cyfrowego, Metody p
CHRAPEK,podstawy robotyki, Sterowanie robotów przemys owych
sprawozdanie filtr Noi, Pwr, Metody i algorytmy sterowania cyfrowego, sprawka
Metody i algorytmy sterowania cyfrowego spr3, Pwr, Metody i algorytmy sterowania cyfrowego, Metody p
Cw8LPCPS, Edukacja, studia, Semestr IV, Podstawy i Algorytmy Przetwarzania Sygnałów, Ćwiczenia, Cwic
cps tablica transformat, Edukacja, studia, Semestr IV, Podstawy i Algorytmy Przetwarzania Sygnałów
teoretyczne podstawy wychowania sylabus nowy
więcej podobnych podstron