
Teoria produkcji
• Zajmuje się wyznacznikami zmian
wielkości produkcji oraz
związkami między nakładami a
rozmiarami wytwarzanego
produktu

Produkcja oznacza:
• Dostosowywanie i przekształcanie
dóbr przyrody w produkty użyteczne
dla człowieka – zaspakajające jego
potrzeby
• Wykorzystywanie zasobów, które
przekształca jedne dobra w inne, w
czasie i przestrzeni (wytwarzanie,
transport, przechowywanie)
• Przekształcanie nakładów w produkty
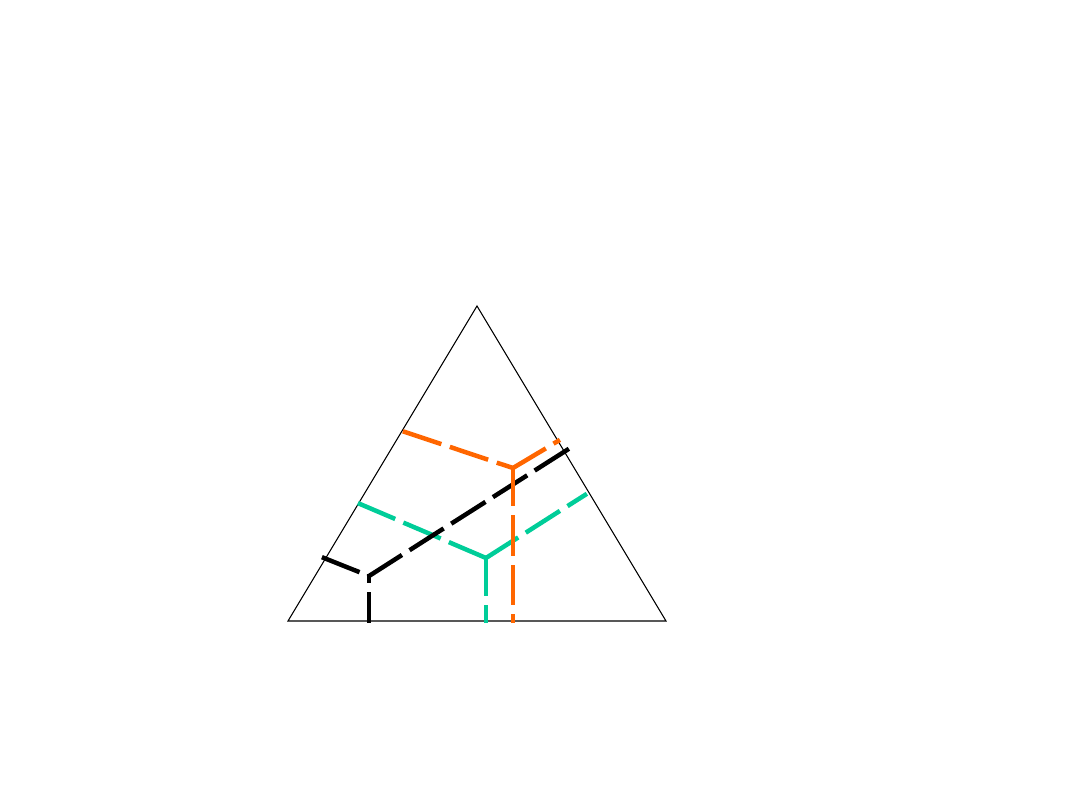
Trójkąt Herllemana
Trójkąt równoboczny obrazuje
ograniczoność zasobów czynników
produkcji
ziemia
pr
ac
a
ka
pi
ta
ł

Funkcja produkcji
• Podstawowa kategoria teorii
produkcji
Q = (A, B, C...N)
Q – ilość
A, B, C...N – nakłady czynników
produkcji

Uproszczony zapis
Q = f (K, L)
L – nakłady pracy
K – nakłady kapitału
Zmiany wielkości produkcji
wynikają z łącznego zastosowania
nakładów czynników produkcji

Produkcję można mierzyć
• Produkt całkowitym TP – wielkość
produkcji przy danym kapitale,
którą dają kolejne jednostki
zatrudnienia pracy
• Q - ilość produkcji np. sztuki, tony,
litry
• L – praca w osobach zatrudnionych
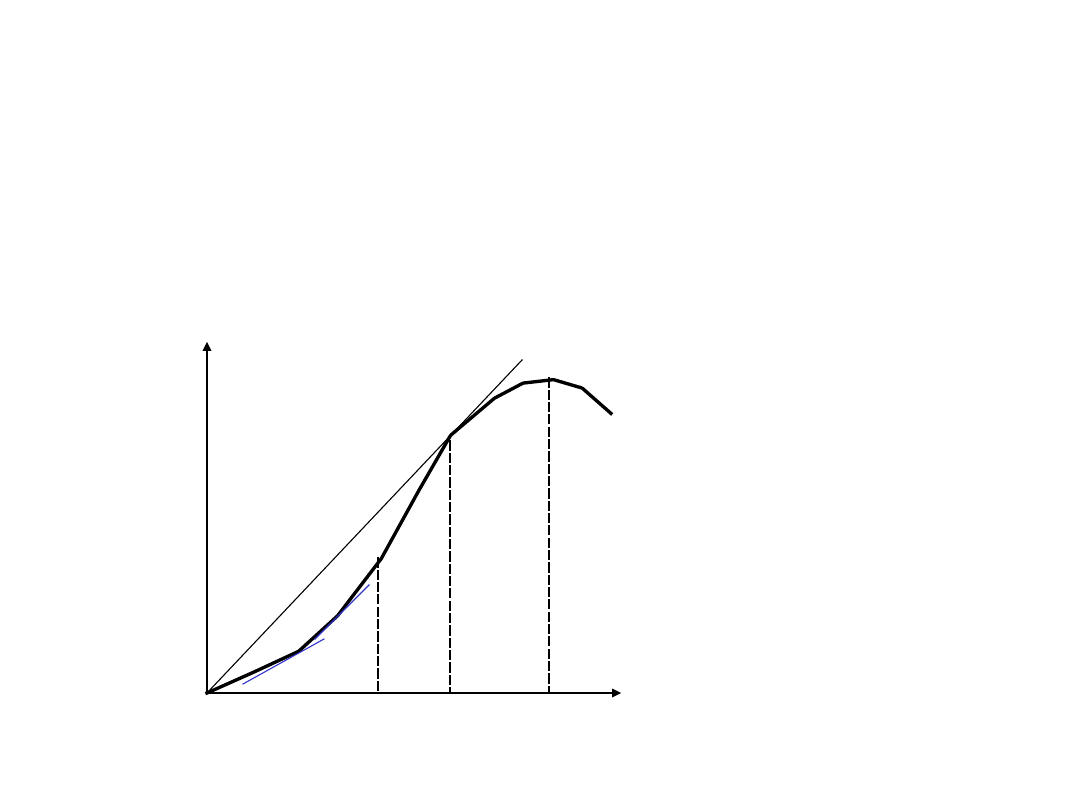
Krzywa produktu
całkowitego
• Graficzny obraz funkcji produkcji
0
L
Q
TP
B
.
g
A
.
.
C
m
n
K = const

Produkcję można mierzyć
• Produktem przeciętnym AP
AP = TP/ L
ilość produktu całkowitego na 1
jednostkę pracy (wydajność
pracy)
Produkcję można mierzyć
• Produktem krańcowym MP
MP =
TP
L
MP jest zmianą wielkości produktu
całkowitego wynikającego ze zmiany
nakładu zmiennego czynnika produkcji o 1
jednostkę
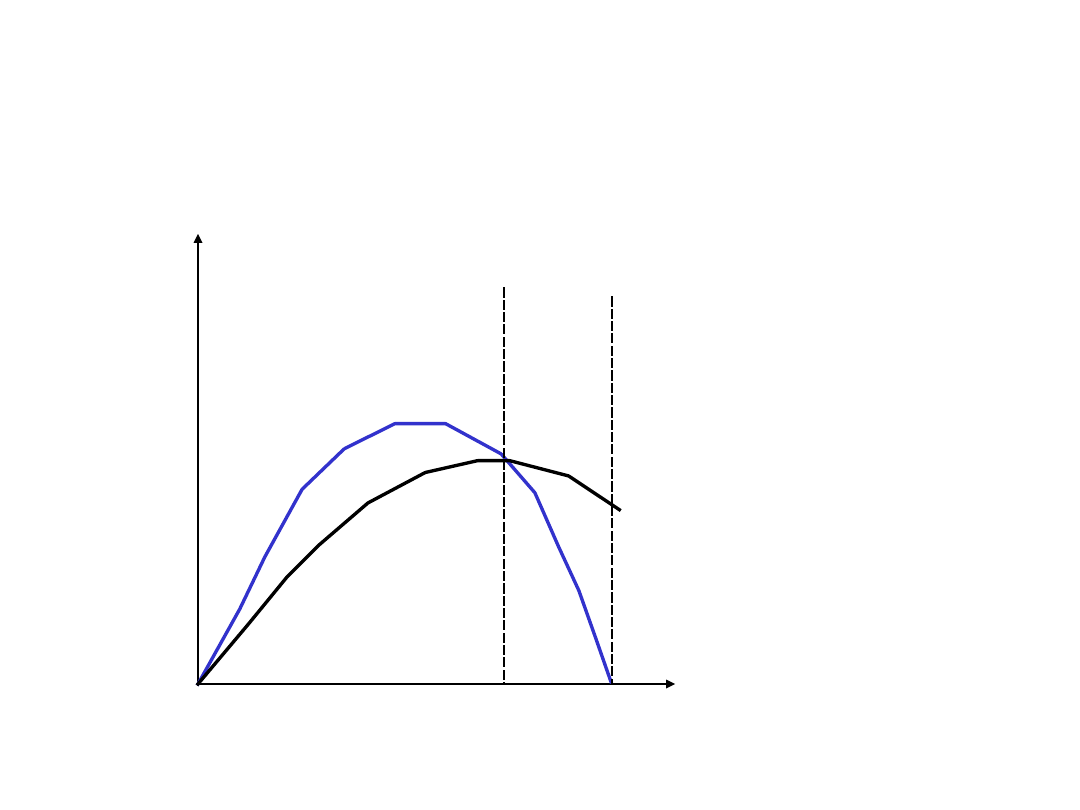
Krzywe AP i MP
0
Q
L
MP
AP
I
II
II
I
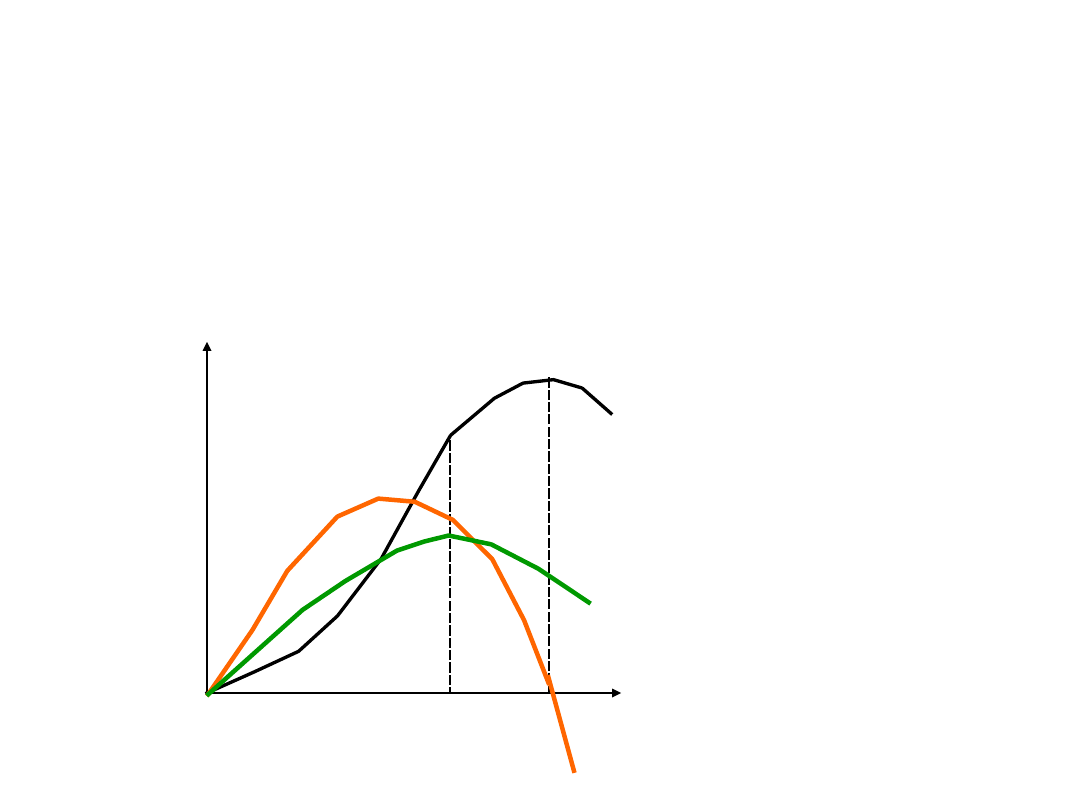
Krzywe TP, AP, MP
0
L
Q
TP
B
.
A
.
.
C
K = const
MP
AP

Prawo malejących
przychodów krańcowych
Utrzymując technologie i wszystkie
nakłady, z wyjątkiem jednego, na stałym
poziomie, gdy dodawane są równe
kolejne zwiększenia zmiennego nakładu,
od pewnego punktu wynikające stąd
zwiększenia produktu będą malejące.
Od pewnego punktu będzie maleć
krańcowy produkt nakładu czynnika
zmiennego.
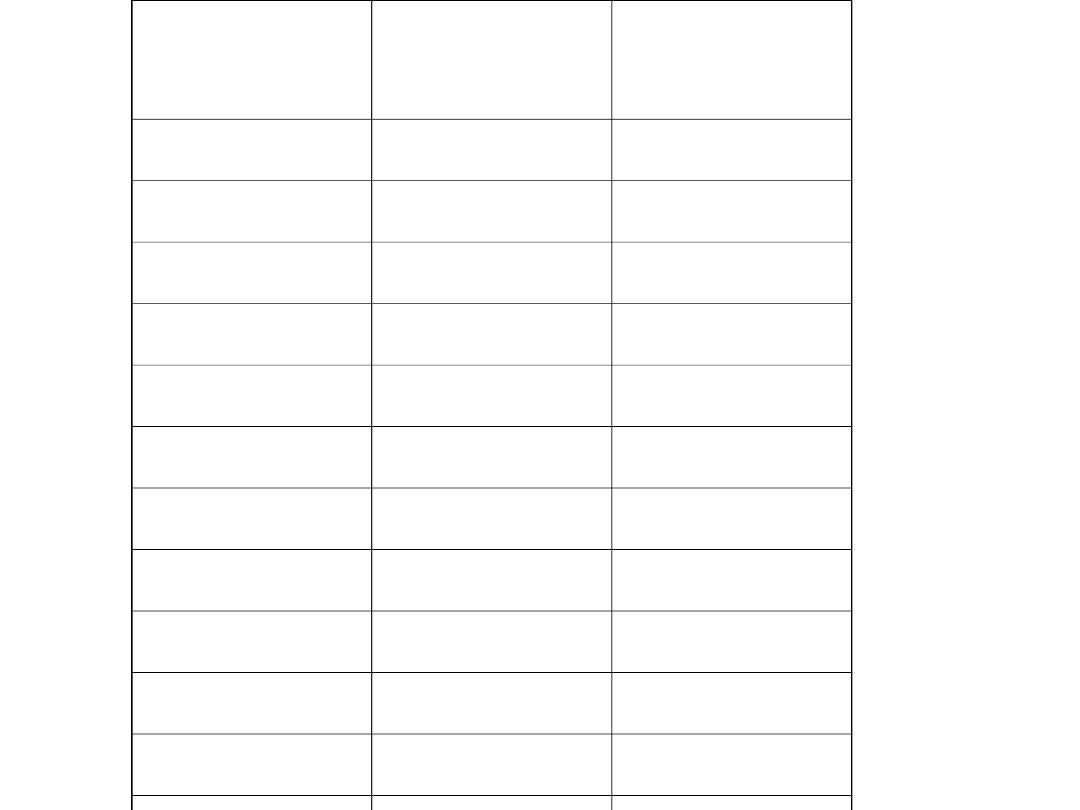
Ilość L
zatrudnionyc
h
TP
MP
1
10
10
2
22
12
3
36
14
4
50
14
5
62
12
6
72
10
7
80
8
8
86
6
9
90
4
10
92
2
11
92
0
12
90
-2

Czy działa prawo
malejących przychodów ?
• Jego autorem jest Robert Malthus, w
swojej teorii ludnościowej( Prawo
ludności,1798) twierdzi, że liczba ludności
rośnie w postępie geometrycznym (2, 4, 8,
16, 32...), a produkcja żywności w
postępie arytmetycznym (2, 4, 6, 8, 10...).
• Za dużo ludzi, za mało żywności – głód,
epidemie, katastroficzna wizja przyszłości.

W długim okresie
wszystkie czynniki
produkcji są zmienne
• Nie działa więc prawo malejących
przychodów krańcowych
• Zmieniają się technologie.
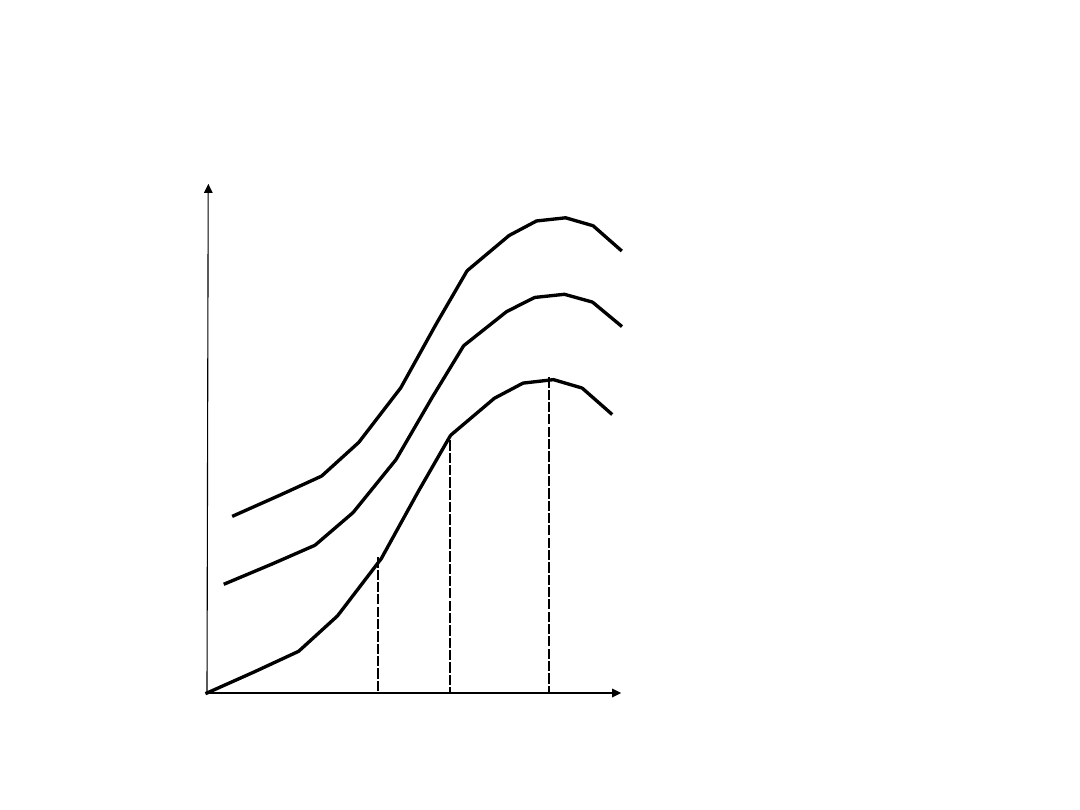
Długi okres
0
L
Q
TP t
1
B
.
A
.
.
C
TP t
2
TP t
3

Kiedy działa prawo
malejących przychodów
• W specyficznie określonych warunkach:
- przynajmniej jeden czynnik jest stały (K)
- Nie zmienia się technologia
- Jest ono empirycznym uogólnieniem:
Dodatkowe nakłady zmiennego czynnika
produkcji współpracują z coraz mniejszymi
ilościami czynnika stałego. Przekroczenie
pewnych granicznych kombinacji czynników
produkcji prowadzi do zmniejszenia
produktywności dodawanego czynnika.
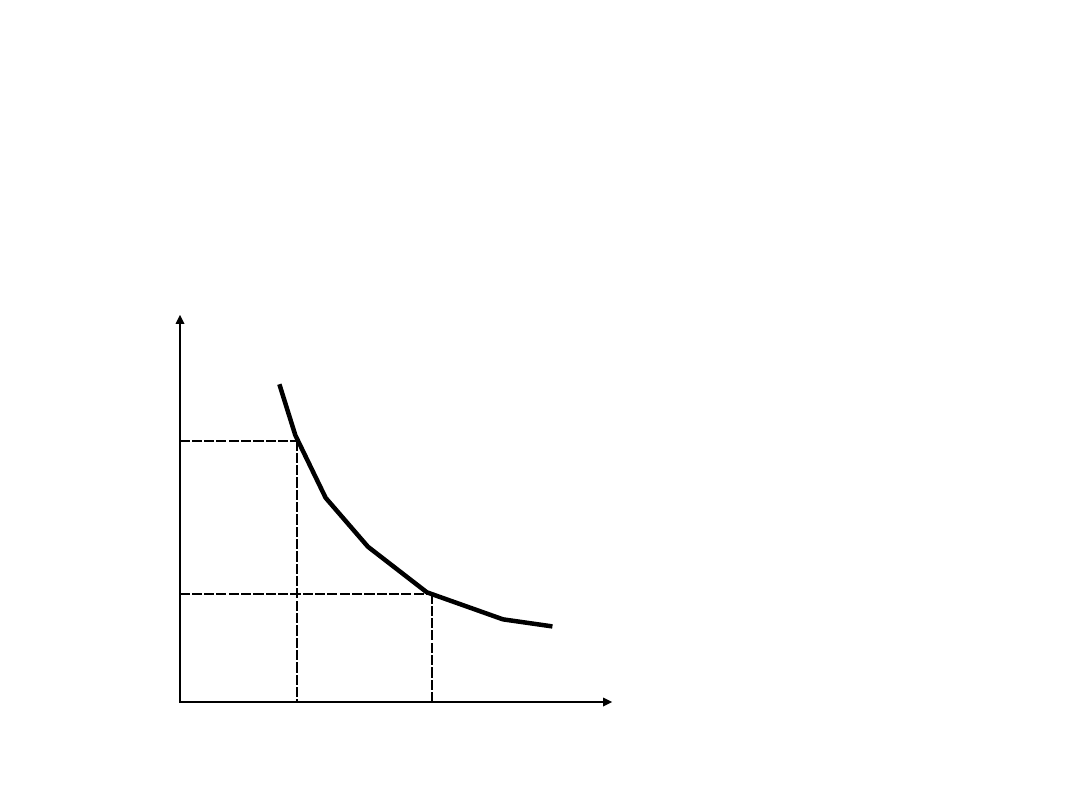
Izokwanta – krzywa
jednakowego produktu
Jakie kombinacje pracy i kapitału można
zastosować dla uzyskania danej
wielkości produkcji
0
K
L
Q
Krańcowa stopa
technicznej substytucji
MRST
LK
• Nachylenie izokwanty jest miarą
MRST
LK
• Oznacza ona ilość, o którą może
być zmniejszony kapitał, bez
zmiany wielkości produkcji, gdy
zwiększa się o jednostkę ilość
pracy.
MRST
LK
=
- K
L
=
MP
L
MP
K
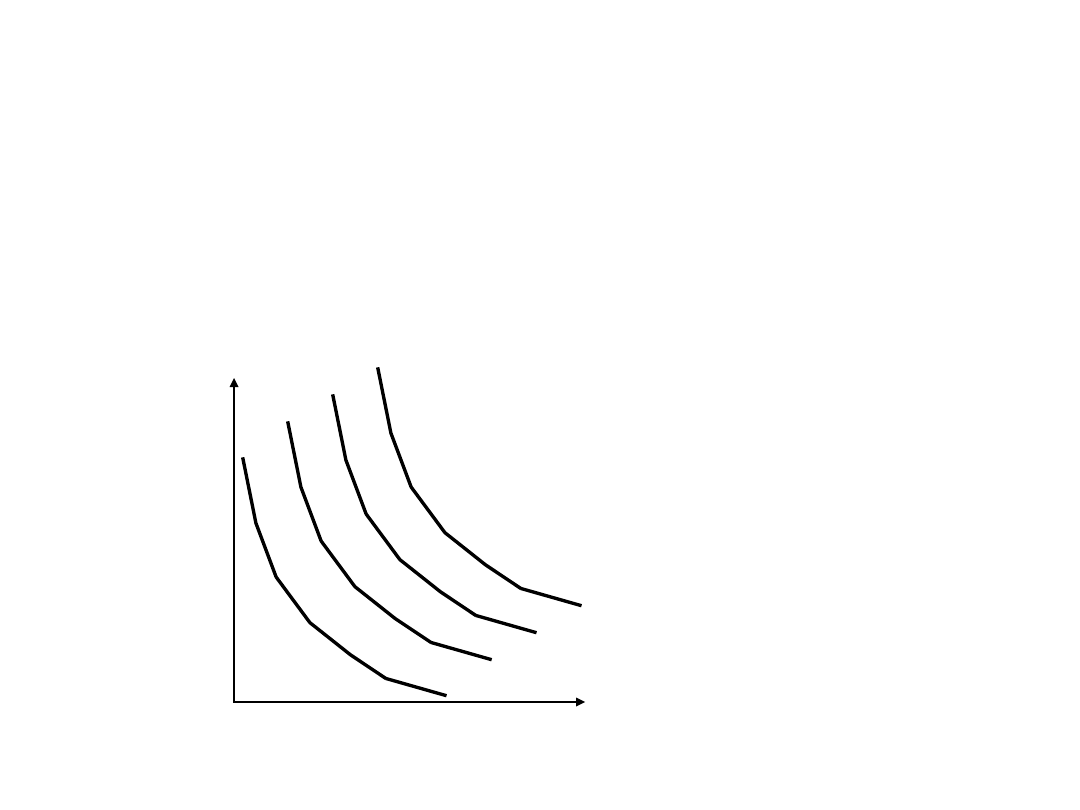
Mapa izokwant
Zakładając, że ilości czynników produkcji
mogą być zmienione można wykreślić
mapę izokwant
0
K
L
J
1
J
4
J
3
J
2

Podsumowując
• Funkcja produkcji opisuje, jak
zmienia się wielkość produkcji w
miarę zwiększania ilości
zmiennego czynnika produkcji.
• Izokwanty pozwalają badać różne
kombinacje dwóch czynników dla
uzyskania danych rozmiarów
produkcji.

Koszty produkcji
(wartościowe ujęcie
produkcji)
• Użycie zasobów na dany efekt
gospodarczy kosztuje (
nakłady mnożymy
przez cenę jednostki nakładu, wartość =
ilość czynnika produkcji x jego cena Np.
liczba godzin pracy x stawka godzinowa –
4 PLN).
• Koszty zawsze określamy w jednostkach
pieniężnych
• Firmę interesują dwie grupy kosztów:
- koszty okazji
- koszty własne produkcji

Koszty okazji
• Kosztem użycia zasobów w dany sposób
jest wartość tego, co te zasoby mogłyby
wytworzyć, gdyby zostały użyte w
najlepszy alternatywny sposób.
• Kosztem wyprodukowania danego
towaru jest wartość tego czego trzeba
się wyrzec, aby ten towar wytworzyć
• Te tracone korzyści to koszty okazji
(koszty alternatywne, koszty traconych
korzyści)

Przykład kosztów okazji
• Koszty okazji zastosowania nakładów pracy
• Mamy małą firmę, której właściciel sam pracuje.
Firma przynosi mu roczny zysk w wysokości 40.000
PLN (przychody minus koszty księgowe). Właściciel
jest wybitnym specjalistą i otrzymał ofertę pracy w
innej dużej firmie za 60.000 PLN rocznie.
• Ta alternatywna roczna pensja to koszt okazji
zastosowania jego pracy, wartość dostępnej
najlepszej alternatywy czy wielkość traconych
korzyściW naszym przykładzie księgowa/y obliczyła
zysk na 40.000 PLN, odejmując od przychodów
poniesione koszty (100.000 minus 60.000)
• W naszym przykładzie księgowa/y obliczyła zysk na
40.000 PLN, odejmując od przychodów poniesione
koszty (100.000 minus 60.000)

Koszt księgowy a koszt
ekonomiczny
• 100.000 – 60.000(koszty księgowe)
= 40.000 zysk księgowy
• 100.000 – 60.000 – 60.000
(utracona pensja – koszty okazji
jego pracy)= -20.000

Koszt okazji zastosowania
kapitału
• Mając 200.000 PLN właściciel podejmuje się
produkcji określonych dóbr (np. kostki
brukowej). Rocznie produkcja ta przynosi
mu zysk 20.000 PLN.
• Alternatywą będzie tu lokata pieniędzy w
banku np. na 10% rocznie (koszty okazji
zastosowania kapitału)
• Uwzględnienie do kosztów produkcji
dodatkowo 20.000 PLN kosztów okazji
powoduje, że rzeczywisty zysk
wynosi............

Amortyzacja - przykład
• Firma „OK. spółka z o.o.” produkująca
okna i drzwi kupuje samochód
dostawczy za 73.200 PLN (brutto),
VAT 13.200 PLN, netto 60.000 PLN.
Data faktury to 03.11.2006 r.
• Czy firma może zaliczyć do kosztów
produkcji w listopadzie kwotę wydaną
na zakup samochodu?

Amortyzacja – przykład
cd.
• NIE
• Zakup samochodu to powiększenie majątku
trwałego firmy (
czyli inwestycja
), 60.000
PLN nie będzie więc kosztem tylko
inwestycją.Według obowiązujących stawek
odpisów amortyzacyjnych samochód
księgowo zużywać się będzie w ciągu 5 lat
(20% rocznie – to przewidziana przez
Ministra Finansów stawka amortyzacyjna
dla środków transportu)

Amortyzacja- przykład cd.
• Księgowi zakładają, że zakupiony
samochód będą zaliczać w koszty
następująco:
• 60.000PLN/ 5 lat = 12.000 PLN
rocznie
• 12.000 PLN / 12 miesięcy = 1.000
PLN miesięcznie

Plan amortyzacji -
przykład
• Pierwsza kwota (rata) amortyzacji
zostanie
zaliczona w koszty dopiero w grudniu 2006
r. (w miesiącu zakupu nie ma zużycia środka
trwałego).
• 12.2006 r. – 1.000 PLN
• 1-12.2007 r. – 12.000 PLN
• 1-12.2008 r. – 12.000 PLN
• 1-12.2009 r. – 12.000 PLN
• 1-12.2010 r. – 12.000 PLN
• 1-11.2011r. – 11.000 PLN
( listopad 2011 r.
ostatnia rata)
• razem 60 rat – 60.000 PLN

Iloś
ć
Q
koszt
y
TFC
stałe
całkowit
e
koszt
y
TVC
zmienne
całkowit
e
koszt
y
TC
całkowit
e
koszt
y
MC
krańcow
e
koszt
y
AC
przeciętn
e
całkowit
e
koszt
y
AVC
przecięt
ne
zmienne
koszt
y
AFC
przecięt
ne stałe
0
45 -
45 -
-
-
-
1
45 65
110 65
110
65
45
2
45 105 150 40 75
52,5
22,5
3
45 130 175 25
58,3
43,3
15
4
45 175 220 45 55
43,7
11,2
5
45 240 285 65 57
48
9
6
45 340 385 100
64,2
56,7
7,5
7
45
485 530 145
75,7
69,3
6,4
8
45 690 735 205
91,9
86,3
5,6
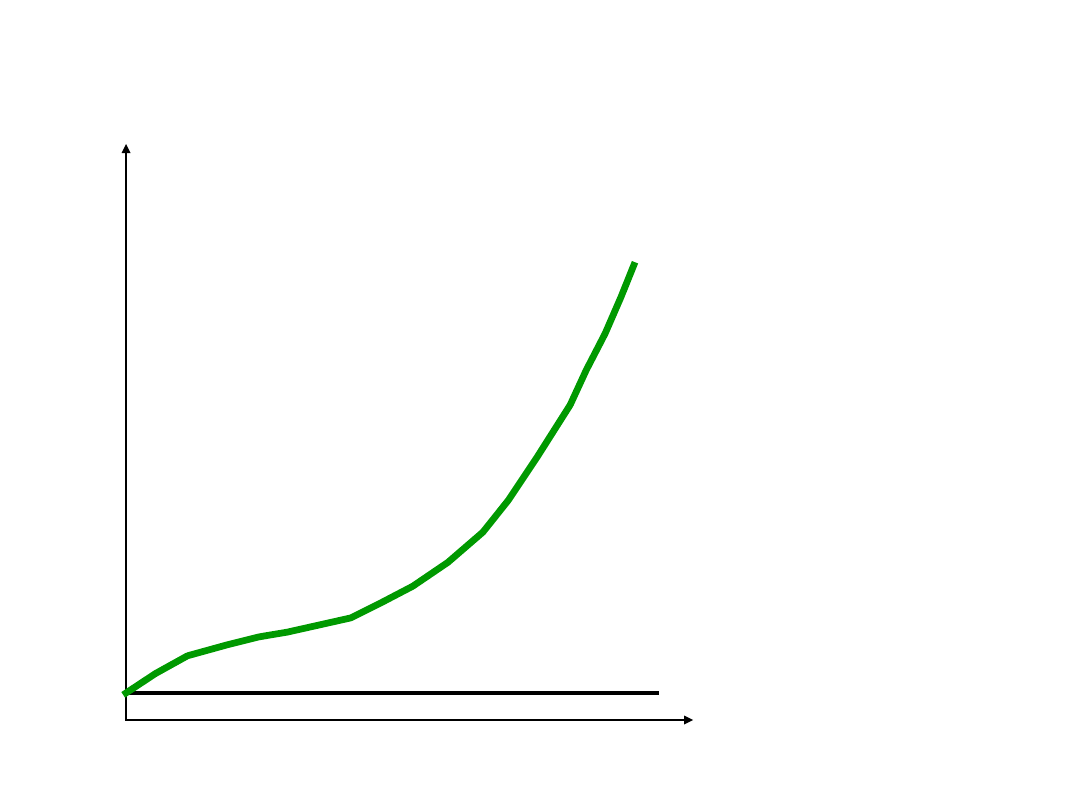
Krzywa kosztu
całkowitego
0
C
Q
80
0
70
0
60
0
50
0
40
0
30
0
20
0
10
0
1 2 3 4 5 6
7 8
TFC
TC (TVC)
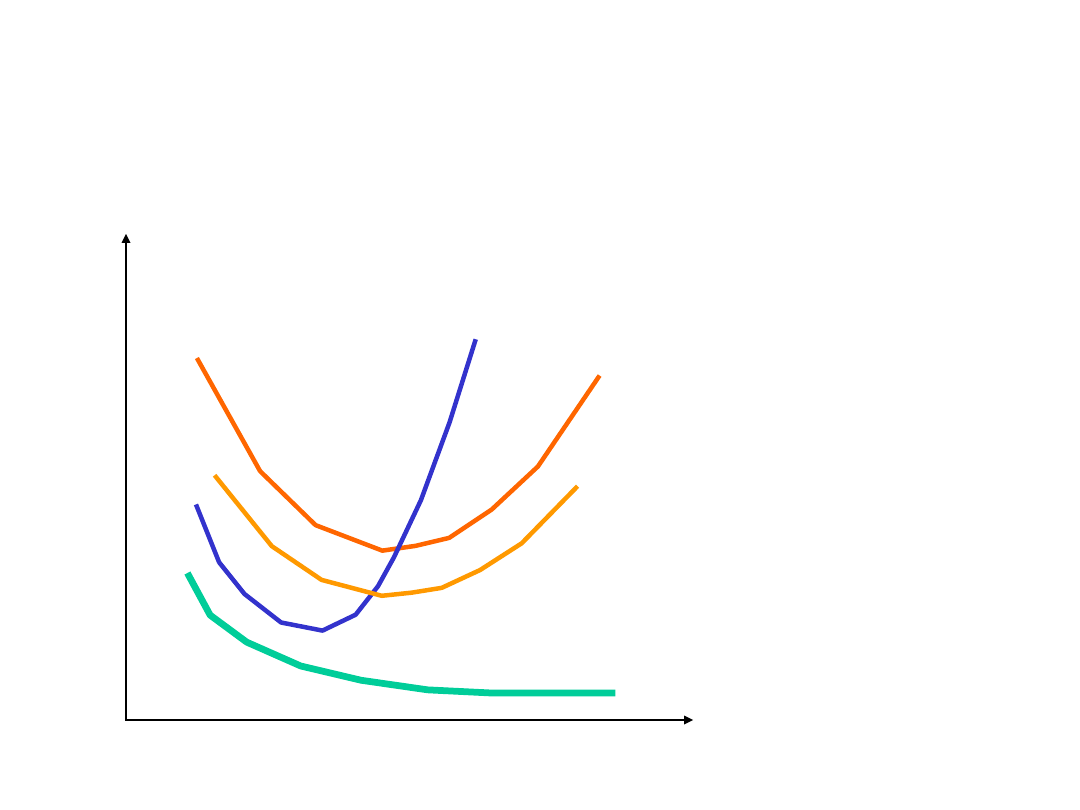
Krzywe kosztu przeciętnego i
krańcowego
0
C
Q
11
0
10
0
90
80
70
60
50
40
30
20
10
1 2 3 4 5 6
7 8
AC
MC
AVC
AFC
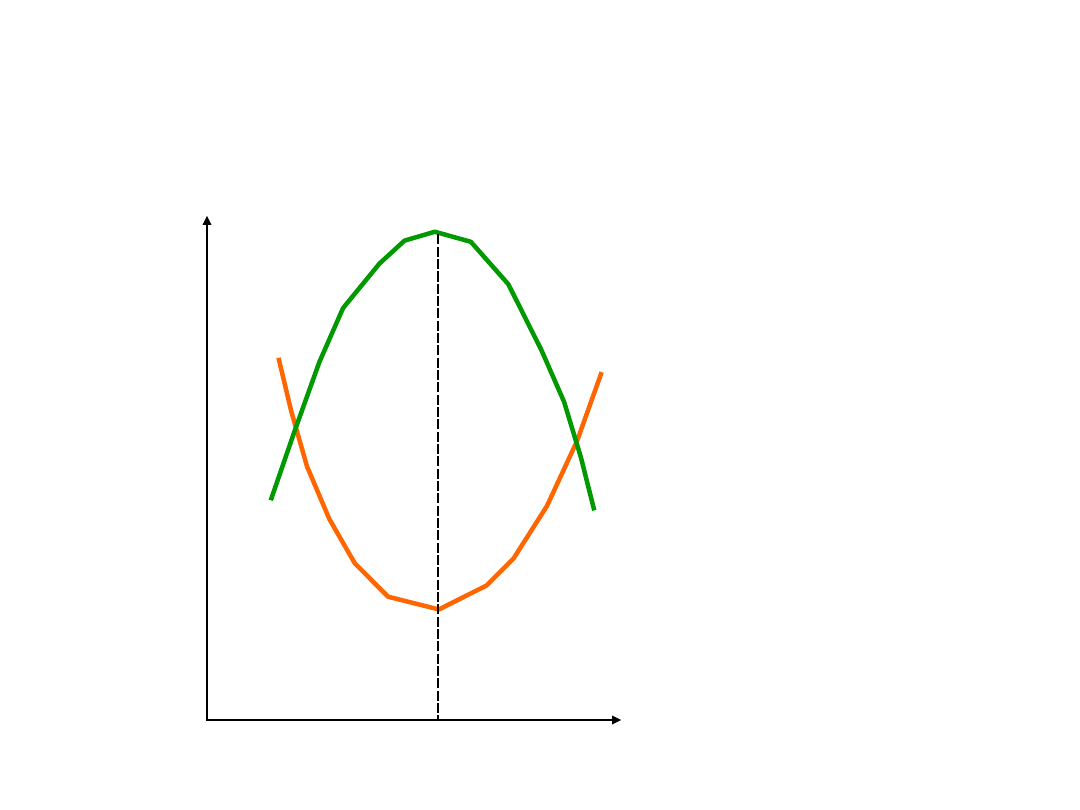
Krzywe kosztów a krzywe
produktów
Q
0
C, P
MC
MP
Min kosztów
Max produktu
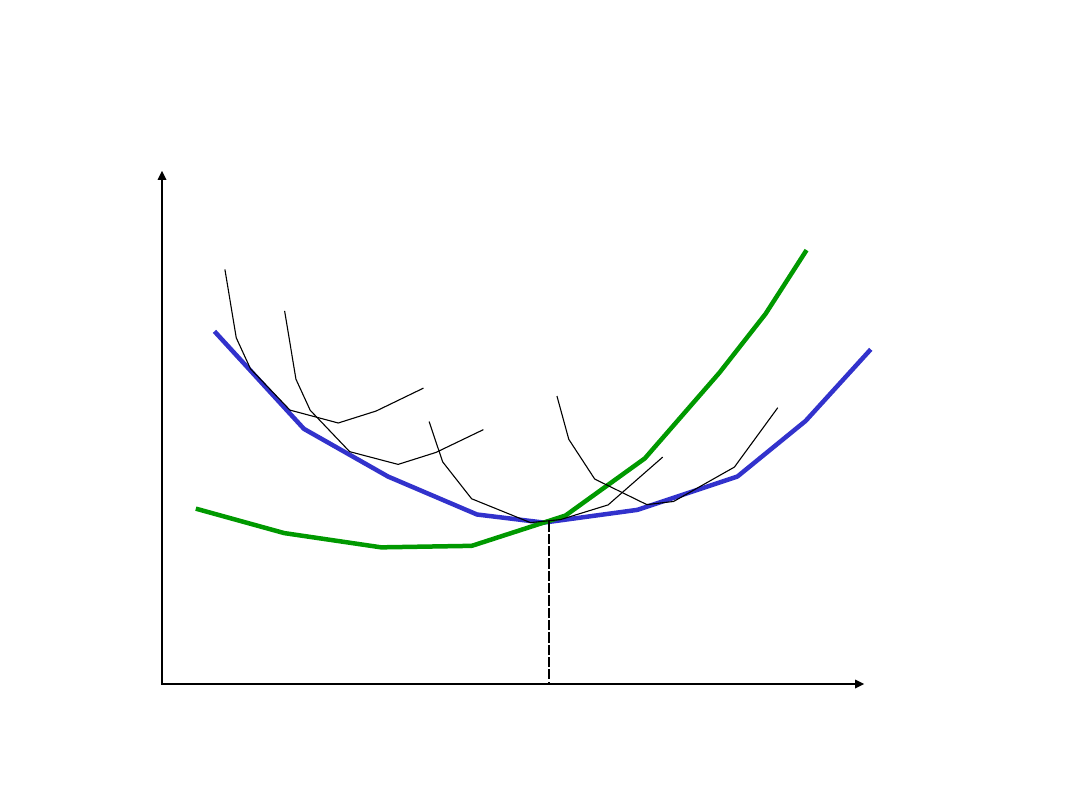
Długookresowe krzywe
kosztów
C
Q
0
LAC
LMC
AC
1
AC
3
AC
2
AC
4
q
0

Rzeczywiste krzywe
kosztów
Mają kształt odwróconej litery L
C
Q
0
ATC
AVC i MC
Zasada najniższego kosztu
Krańcowy produkt L
=
Krańcowy produkt K
Cena
L
Cena K
Krańcowy wkład do produktu wnoszony
przez każdą złotówkę wartości pracy,
kapitału, materiałów itd.. musi być taki
sam.
Zasada substytucji
Jeśli zmienia się cena któregoś z czynników
produkcji, kiedy inne pozostają stałe, firma
skorzysta zastępując droższe czynnikami
tańszymi.
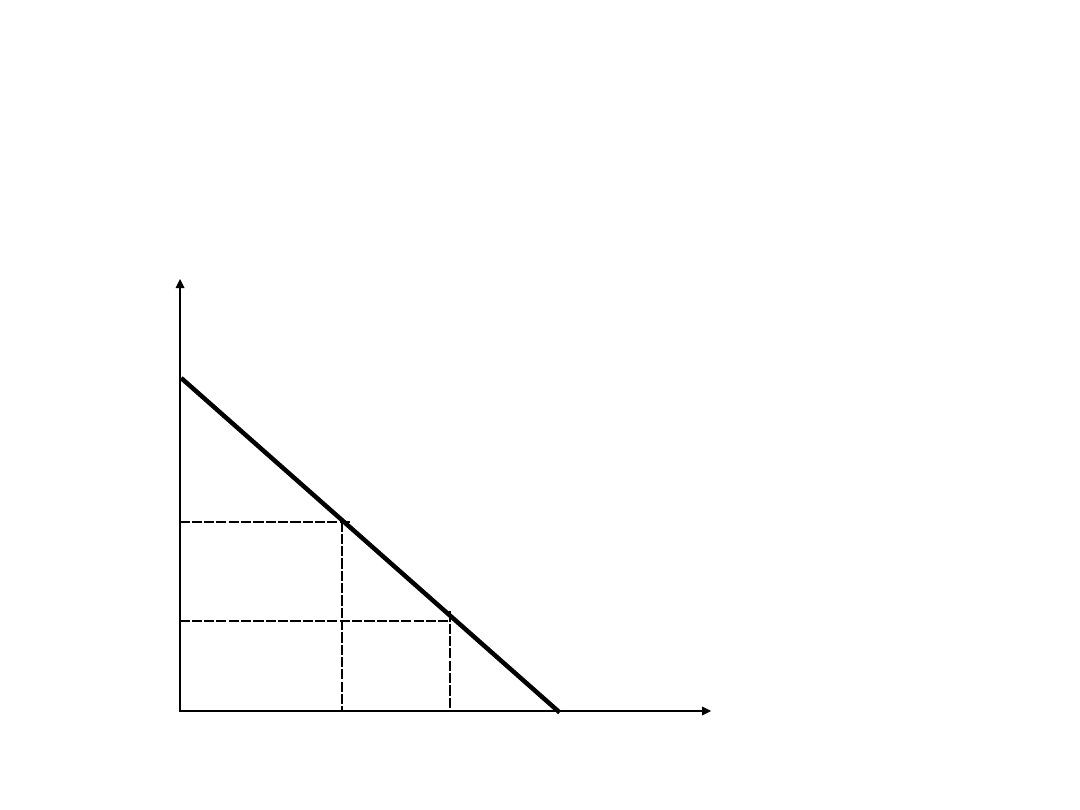
Krzywa jednakowych kosztów -
izokoszta
Krzywa izokosztów wyznacza możliwe kombinacje
kapitału K i pracy L w ramach posiadanych środków.
Prosta K`L` nazywa się krzywą izokosztów – równe
koszty różnych kombinacji nakładów.
0
K
L
K`
b
a
K
b
K
a
L
b
L
a
L`
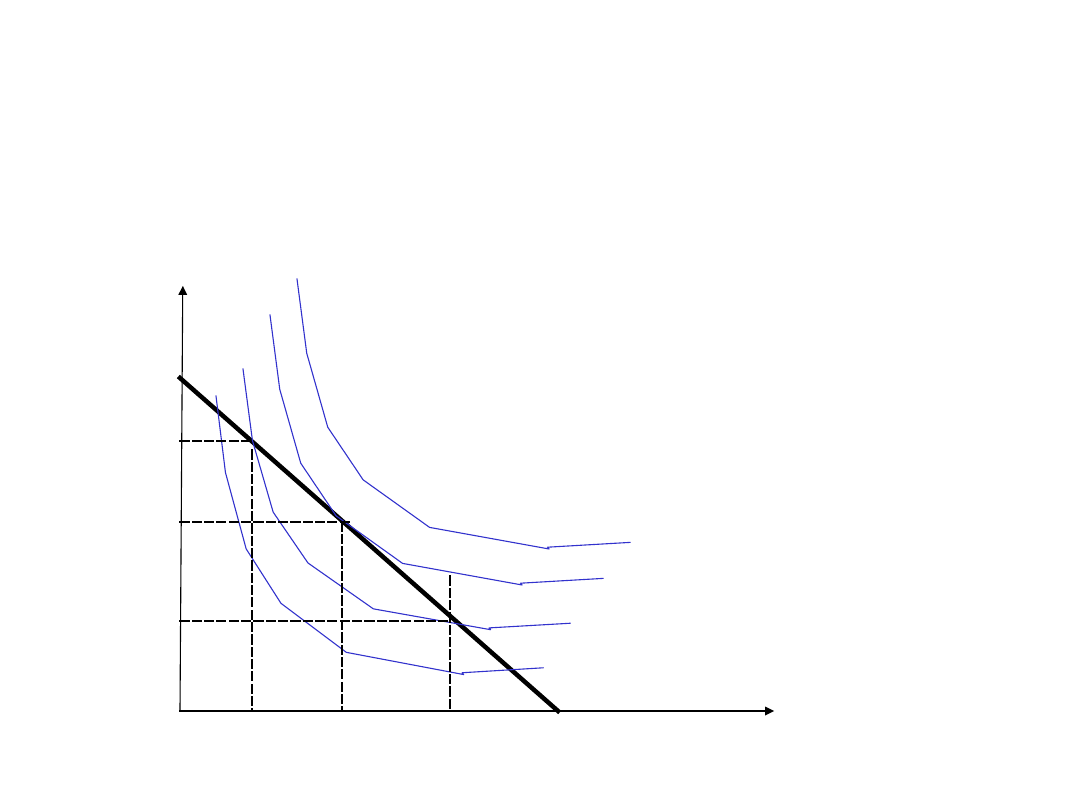
Krzywe izokosztów i
izokwant
Krzywe izokwant x
1
– x
4
pokazują co firma może
technologicznie zrobić, jak kombinować nakłady Ki L
dla równych wielkości produkcji. Nakładając izokosztę
można wskazać co firma będzie rzeczywiście robić.
0
K
L
K`
L
`
x
1
x
2
x
3
x
4
S
B
T
K
1
K
2
K
3
L
1
L
2
L
3
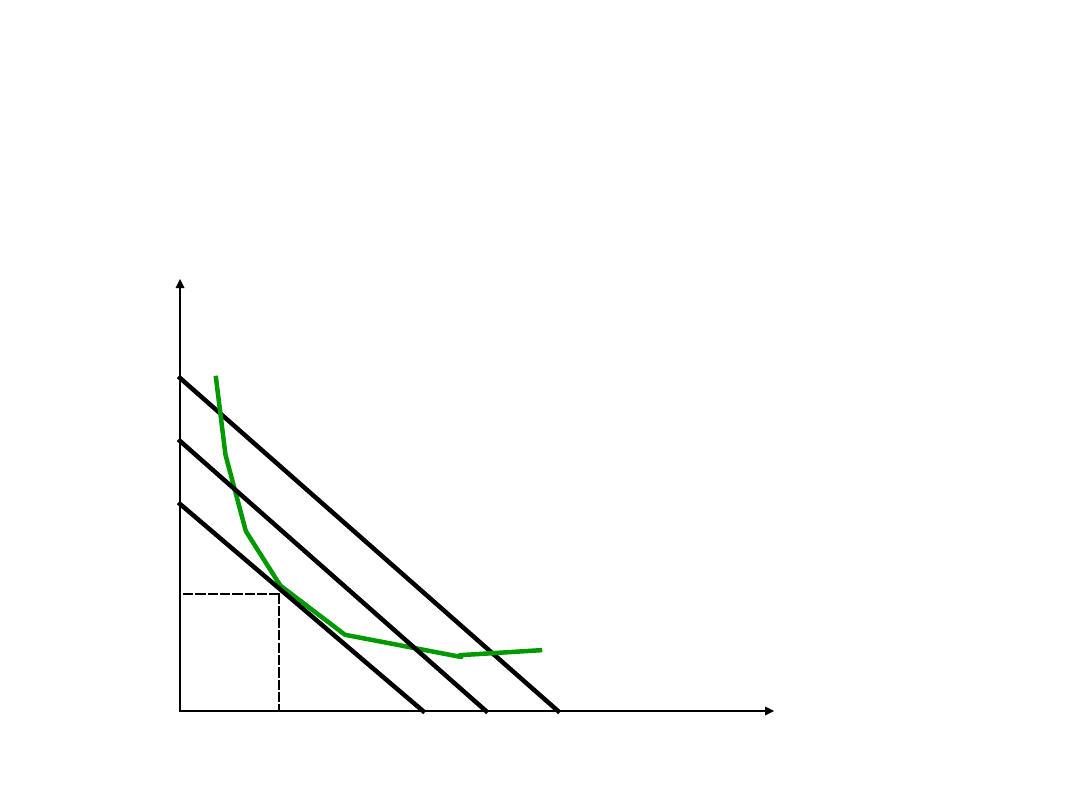
Optimum produkcji
0
K
L
x
0
K
3
K
2
K
1
L
0
L
3
L
2
T
L
1
MRST
LK
= K / L = P
L
/
P
K
MRST
LK
= MP
L
/ MP
K
MP
L
/ MP
K
= P
L
/ P
K
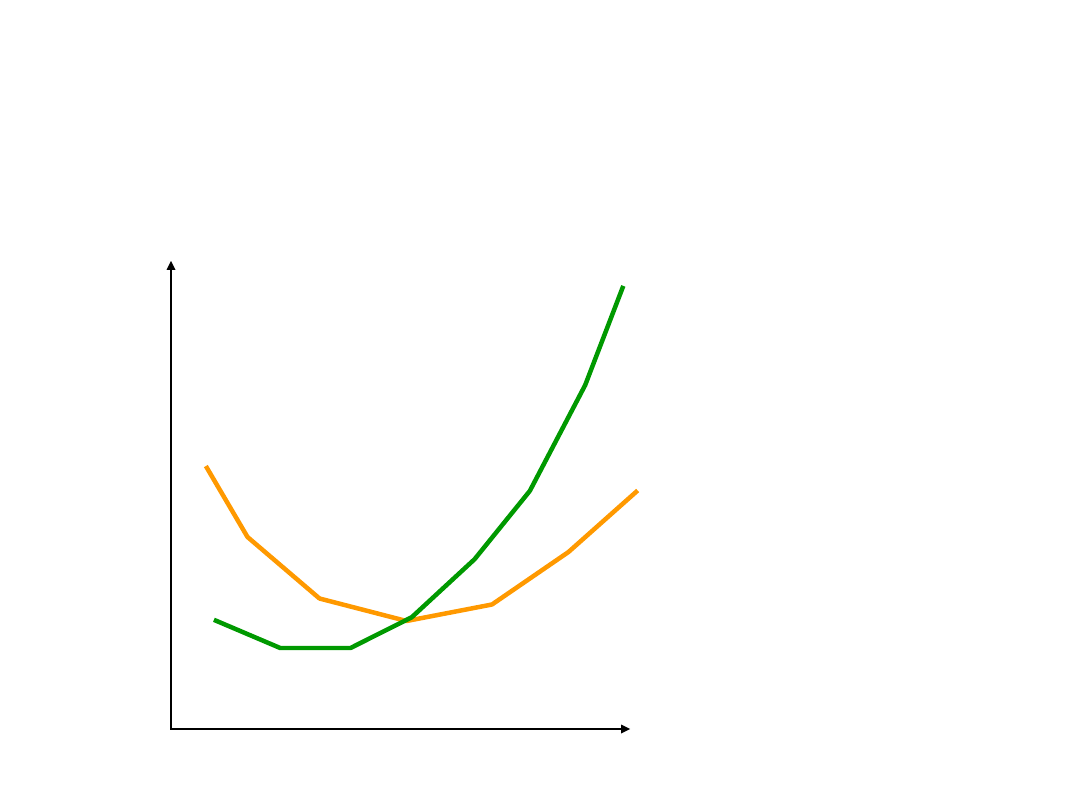
Korzyści i niekorzyści
skali
0
C
Q
LMC
LAC
.
E
ko
rzy
ści
nie
ko
rz
yś
ci
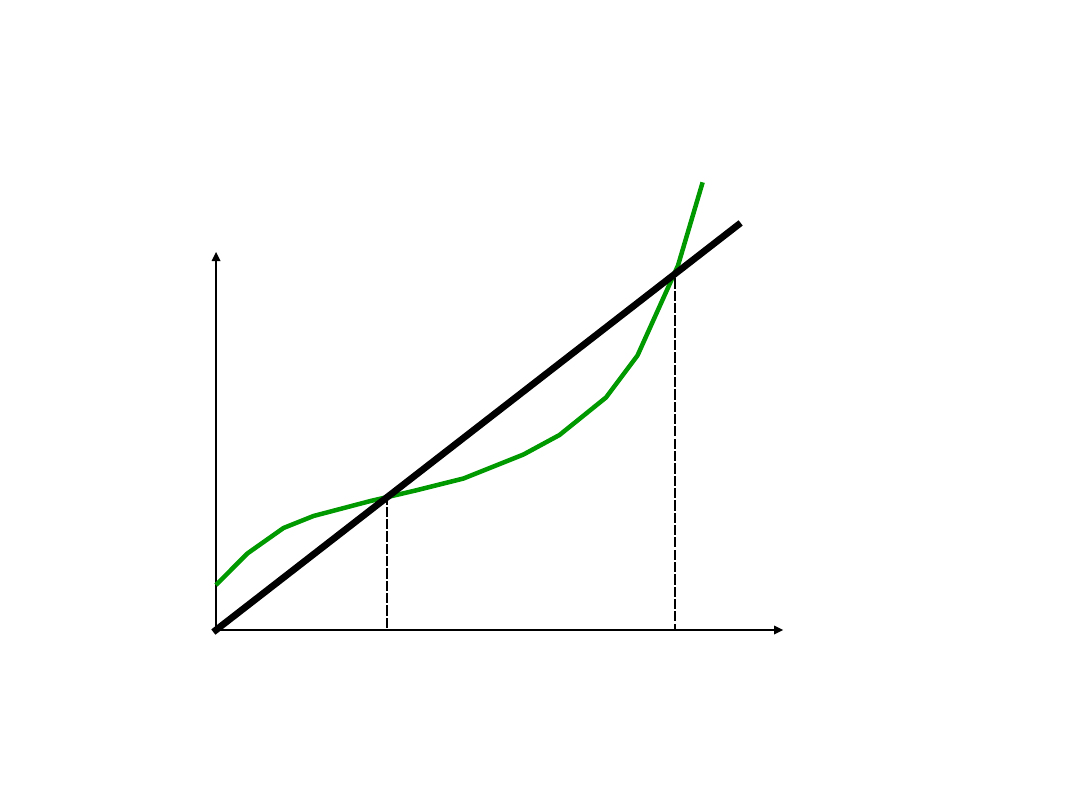
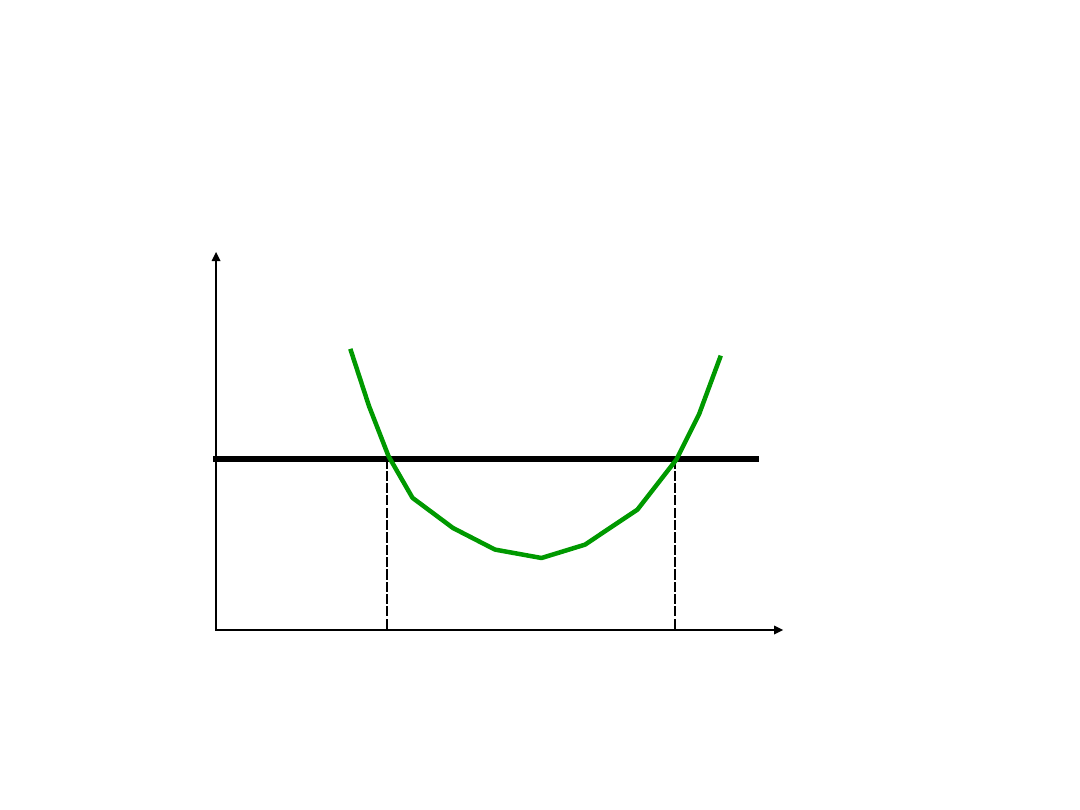
Próg rentowności -
wartości
całkowite
C
R
Q
0
TC
TR
q
1
q
2
B
1
B
2

Próg rentowności
– praktyczne
zastosowanie analizy kosztów
• Przy sprzedaży mniejszej niż q
1
firma nie
pokrywa kosztów produkcji (TC) i ponosi straty.
Sprzedaż q
1
zrównuje koszty z osiąganym
utargiem TR = p x q (TC = TR). Dalsze
zwiększanie sprzedaży powoduje, że krzywa TR
przecina TC w punkcie B
1
i firma zaczyna
osiągać zyski – staje się rentowna. Punkt B
1
jest
pierwszym progiem rentowności. Dalsze
zwiększanie sprzedaży
powoduje początkowo
przyrost zysków, a następnie ich zmniejszanie
się aż do punktu B
2
-
drugi próg rentowności.
Przy produkcji większej od q
2
firma zaczyna
ponosić straty. Przedział rentowności mieści się
zatem między wielkością sprzedaży q
1
a q
2
.
Próg rentowności -
wartości
przeciętne
C
R
Q
0
q
1
q
2
B
2
MR = P
AC
B
1
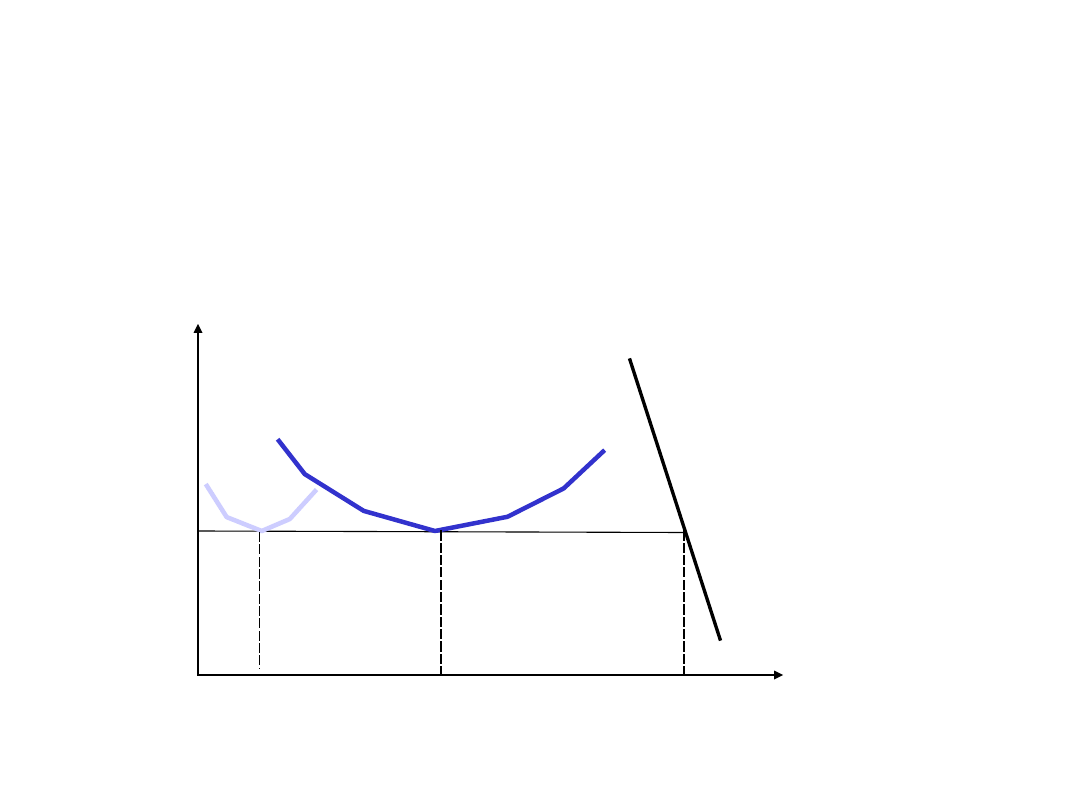
Dłogookresowe krzywe kosztów a
struktura rynku
Przy krzywej LAC
1
na rynku zmieści się 20 firm.
Przy krzywej LAC
2
na rynku jest miejsce dla 2
firm.
Technologia przesądza o strukturze
danego rynku.
0
X
C
D
0,5
X
LAC
2
LAC
1
D
0,05X
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26
- Slide 27
- Slide 28
- Slide 29
- Slide 30
- Slide 31
- Slide 32
- Slide 33
- Slide 34
- Slide 35
- Slide 36
- Slide 37
- Slide 38
- Slide 39
- Slide 40
- Slide 41
- Slide 42
- Slide 43
- Slide 44
- Slide 45
Wyszukiwarka
Podobne podstrony:
Teoria produkcji i koszty
teoria produkcji i koszty produkcji
teoria produkcji, Ekonomia
Notatki do prezentacji teoria produkcji i kosztow
Teoria produkcji 3
Teoria produkcji 2
Teoria produkcji slajdy
5 teoria produkcji ujecie neoklasyczne
Prezentacja = Produkcja i koszty w przedsiębiorstwie
Ściągi mikro, Ściąga wykład 9, Teoria produkcji- zajmuje się rzeczową stroną procesów wytwórczych, a
002 12 Produkcja i koszty w okresie krótkim, SZKOLNY, ekonomika
Teoria produkcji
4 Teoria przedsiębiorstwa i teoria produkcji notatki, ekonomia
mikroekonomia4-Teoria produkcji, Administracja, I ROK, Mikroekonomia
więcej podobnych podstron