XII PRODUKCJA I KOSZTY W OKRESIE KRÓTKIM

Mechanizm rynkowy działa przez siły popytu i podaży. O popycie wiemy już dużo, pora zatem zająć się teorią podaży. Podaż powstaje w przedsiębiorstwach, czyli organizacjach gospodarczych, które decydują o wielkości i strukturze produkcji, zatrudnieniu określonych czynników wytwórczych, o sposobach wytwarza­nia swoich produktów i o wszelkich aspektach prowadzonej działalności.

Firmy prowadzą swoją działalność podlegając dwom rodzajom ograniczeń. Pierwsze to ograniczenie rynkowe, na które składają się warunki, w jakich zakupywane są czynniki wytwórcze i sprzedawane są produkty. Drugim jest ograniczenie technologiczne tworzone przez dostępne metody produkcyjne. Oznacza to, że ten sam produkt może być wytwarzany z wykorzystaniem nowoczesnych metod lub metod tradycyjnych, metod pracochłonnych lub metod kapitałochłonnych itp.

W analizie zjawisko podaży najważniejszą rolę odgrywa pojecie kosztu we wszystkich jego różnorod­nych aspektach.

Przedsiębiorstwa przywiązują wagę do kosztów bo celem ich właścicieli jest maksymalizacji korzyści z działalności gospodarczej , czego pieniężnym wyrazem jest zysku, będący różnicą między całkowitymi przychodami ze sprzedaży i całkowitymi kosztami poniesionymi na produkcję. Firmy muszą dbać o koszty, gdyż każde ich zwiększenie przy pozostałych warunkach niezmienionych, zmniejsza ich zyski.

Jednakże dla ekonomisty koszty są ważne z innej, dużo głębszej, przyczyny. Ilości, jakie firmy skłonne są wytwarzać i sprzedawać, czyli ich podaż, zależne są bowiem z jednej strony od przychodu, jaki przynosi sprzedaż każdej dodatkowej jednostki wytwarzanego w firmie dobra, czyli od tzw. utargu krańcowego. Z drugiej zaś od kosztu wytworzenia ostatniej wyprodukowanej jednostki, czyli tzw. od kosztu krańcowego. Zwiększenie produkcji i podaży o dodatkową jednostkę jest opłacalne tylko wtedy, gdy przychód ze sprzedaży tej dodatkowej jednostki (czyli przychód krańcowy) jest większy lub, co najwyżej równy kosztowi wyprodukowanie tej jednostki czyli kosztowi krańcowemu.

Ta zależność decyzji podażowej od kosztu obowią­zuje w odniesieniu do przedsiębiorstw działających we wszystkich możliwych strukturach rynkowych. Ma ona miejsce w warunkach konkurencji doskonałej, w odniesieniu do monopolu, oligopolu oraz konkurencji monopolistycznej. Ze względu na jej uniwersalny charakter, teorii kosztów poświęcimy dużo uwagi. Poddamy analizie różnorodne koncepcje kosztu w ujęciu ekonomicznym. Ale nie koniec na tym

Wiemy już, że koszty pieniężne, to ilość używanych do produkcji czynników przemnożona przez rynkowe ceny, jakie firmy płacą za ich używanie. Aby zatem wiedzieć ile wynoszą koszty danej wielkości produkcji i jak zmieniają się ze zmianami wielkości produkcji musimy wiedzieć, jakie ilości czynników są niezbędne, do wytworzenie danej wielkości oraz jaka jest ich rynkowa cena. Jeśli chwilowo zapomnimy o cenach i przyjmiemy że są one niezależne od ilości użytego czynnika, wówczas ustalenie zależności między produkcją, kosztami wymagać będzie gruntownego przebadania zależności miedzy nakładami czyli ilością użytych czynników, a osiąganą z nich produkcją.

Związki miedzy fizycznymi ilościami nakładów czynników, a wielkością uzyskiwanej z nich produkcji wyjaśnia teoria produkcji. Bez niej nie da się zbudować żadnej rozsądnej teorii kosztów, dlatego właśnie nasz wykład zaczniemy od wyjaśnienia zależności ilościowych, jakie zachodzą miedzy nakładami a produkcją.

W części wstępnej zapoznamy się z narzędziem zwanym funkcją produkcji dla przedsiębiorstwa. Z niej wyprowadzimy wszystkie interesujące nas kategorie kosztów, które przedstawimy różnego rodzaju funkcji .

Kiedy już będziemy mieć za sobą analizę pojęć kosztu, będziemy w stanie w kolejnym wykładzie podjąć analizę podaży przedsiębiorstwa i gałęzi w warun­kach konkurencji doskonałej. Wtedy pokażemy, że krzywą podaży indywidualnej firmy i podaży rynkowej można utożsamić z krzywymi kosztów krańcowych, a to oznacza, że na rynku doskonale konkurencyjnym teoria kosztów jest fundamentem teorii podaży?

Dla analizy produkcji i kosztów szczególne znaczenie ma czas, dla którego przeprowadza się analizę. Aby dokładniej przyjrzeć się działalności firmy, należy wprowadzić tu rozróżnienie na okres krótki i długi. Są to pojęcia oczywiste, ale dość nieprecyzyjne.

W ekonomii przyjmuje się, że o okresie krótkim mówimy wtedy, gdy zatrudnienie niektórych czynników wytwórczych nie zmienia się wraz ze zmianami wielkości produkcji, natomiast zużycie innych czynników zależy od wielkości produkcji.Pierwsze z tych czynników nazywamy stałymi czynnikami produkcyjnymi i zaliczamy do nich na przykład hale fabryczne czy biurowce, drugie z czynników określamy mianem zmiennych a ich przykładem może być praca czy surowce. Okresem długim nazywamy czas, w którym nakłady wszystkich czynników mogą ulegać zmianie i dlatego w okresie tym mamy do czynienia tylko ze zmiennymi czynnikami produkcyjnymi.

W tym wykładzie przeprowadzimy analizę produkcji i kosztów dla okresu krótkiego, w którym część nakładów jest niezależna od wielkości produkcji, zatem część kosztów też jest stała, a część zmienna. W następnym przejdziemy do analizy długookresowej, w której nakłady wszystkich czynników są zmienne, zatem siłą rzeczy wszystkie koszty też są zmienne.

Teoria produkcji dla okresu krótkiego

Prezentując teorię produkcji zaczynimy od przypomnienia, że pod pojęciem produkcji rozumiemy świadomą, celową i zorganizowana działalność ludzi, polegającą na łączeniu czynników wytwórczych, w celu wytwarzania dóbr materialnych i świadczenia usług zaspokajających bezpośrednio lub pośrednio ludzkie potrzeby. Aby wytworzyć jakiekolwiek dobra czy usługi konieczne są czynniki wytwórcze. Produkcja jest procesem, w którym czynniki wytwórcze przekształcane są w określone ilości produktów.

Czynniki wytwórcze

Do wytwarzania używane są różne czynniki wytwórcze. Tradycyjne czynniki to siła robocza, ziemia, surowce, materiały i kapitał rzeczowy. Każdy z tych nakładów możemy dalej dzielić na różne rodzaje siły roboczej, ziemi i kapitału. Gdybyśmy chcieli, to moglibyśmy wyróżnić 50, 100 a może i 1000 róż­nych czynników.

Aby zbytnio nie komplikować analizy najczęściej przyjmujemy, że mamy do czynienia z kategoriami zagregowanymi. W ujęciu syntetycznym wyróżnia się: pracę (L), kapitał (K) surowce (S) i ziemię (Z).

Te rzeczowe składniki procesu produkcyjnego współpracując ze sobą w ramach stosowanych przez firmy technologii umożliwiają wytwarzanie założonych rozmiarów produkcji. Natomiast pojedynczo nie są na ogół w stanie wytworzyć niczego. Ale nie koniec na tym. By powstała produkcja potrzebny jest przedsiębiorca, którego wola jest czynnikiem sprawczym produkcji. To on na własne ryzyko podejmuje i realizuje decyzje, do jakich zastosowań i w jakich ilościach powinny być one używane. Dlatego technologię i przedsiębiorczość traktuje się obecnie jako czynniki produkcji na równi z tradycyjnymi. Oba te czynniki działają z różną siłą w zależności od istniejącego w danym społeczeństwie systemu gospodarczego. Niestety są one niewymierne, dlatego je pominiemy.

Nakłady (inputs) oraz wyniki (outputs) procesu produkcji
Nakłady	Firmy	Wyniki
Siła robocza Kapitał rzeczowy Surowce, półfabrykaty, maszyny, urządzenia Ziemia Usługi innych czynników produkcji	=> Proces produkcji	Dobra pośrednie Dobra finalne: Dobra inwestycyjne Dobra konsumpcyjne - trwałe - jednorazowe Usługi produkcyjne Usługi konsumpcyjne

Nakłady i wyniki

Zużywane w procesie produkcyjnym zasoby (materiały, maszyny, urządzenia, budynki, energia, siła robocza) nazywamy nakładami. W przeciwieństwie do liczonych w postaci pieniężnej kosztów, nakłady wyrażamy w jednostkach fizycznych (np. sztuki, litry kilogramy, osoby, roboczogodziny, maszynogodziny itp.). Nakładami są zatem fizyczne ilości czynników wytwórczych niezbędne do uzyskania danej wielkości produkcji.

Ilościową miarą produkcji jest fizyczna wielkość produktu (tzw. produktu całkowitego) osiągana w danej jednostce czasu z użytych przez firmę ilości wszystkich czynników. Miarą wartościową jest ilość produktów przemnożona przez przyjęte do agregacji ceny.

Komplementarność czynników

Aby wytworzyć określoną ilość danego dobra czy usługi przedsiębiorstwa muszą zastosować odpowiednie ilości połączonych ze sobą czynników wytwórczych. Czynniki są komplementarne i pojedynczo nie wytwarzają zazwyczaj niczego. Wszystkie one, są bowiem ściśle ze sobą powiązane. Po co mi łopata, jeśli nie ma ogrodu. Po co mi ogrodnik, jeśli nie ma on łopaty. Dopiero ogrodnik z łopatą staje się użyteczny - jeśli, rzecz jasna, jest i ogród, czyli ziemia.

Jeżeli dys­ponujemy pewną ilością pracy, ziemi i odpowiednią ilością innych czynników, takich jak surowce i narzędzia, oraz wiemy jak je ze sobą łączyć, to ile można za ich pomocą maksymalnie wyprodukować? O ile zmieni się produkcja, gdy wzrośnie lub spadnie ilość stosownych czynników?

Analizą zależności pomiędzy nakładami czynników i osiąganym z nich rozmiarami produkcji zajmuje się teoria produkcji. Pokazuje ona, że przyczyną procesu produkcji są nakłady czynników (lub ich zmiany), natomiast skutkiem tego jest określona wielkość produkcji (lub jej zmiany). Związki między nakładami a fizyczną ilością otrzymywanych w procesie produkcji dóbr są na tyle widoczne i ważne, że ekonomiści podnieśli do rangi ekonomicznego prawa przyczynowo - skutkowego. Podstawowym narzędziem analitycznym tego związku jest tzw. funkcja produkcji.

Funkcja produkcji - prawo technologii uzależniające wyniki od nakładów

Funkcja produkcji jest zestawem kombinacji różnych ilości czynników wytwórczych (nakładów) i maksymalnej, jaką można z nich otrzymać wielkości produkcji. Znaczy to, że produkt „zależy" od nakładów, lub że jest wynikiem" użytych do produkcji nakła­dów.

Funkcja produkcji pokazuje o ile zmieni się wielkość produkcji, gdy zostanie zwiększona ilość stosowanych przez firmę czynników? O jej przebiegu decydują normy technologiczne, które jednej strony określają, ile jednostek czynników niezbędne jest do wytworzenia jednostki danego dobra, z drugiej zaś wyznaczają, maksymalne ilości dóbr, jakie można uzyskać z każdej możliwej kombinacji czynników. To one decydują o kształcie i przebiegu funkcji produkcji.

W analizach ekonomicznych w zależności od czasu analizy będziemy posługujemy się funkcjami wieloczynnikowymi lub jednoczynnikowymi..

Wieloczynnikowa funkcja produkcji

Jeżeli przyjmiemy, że na zmiany wielkości produkcji wpływają jednocześnie zmiany wszystkich czynników produkcji, wówczas funkcyjny związek między wielkością produkcji Q a ilością stosowanych nakładów pracy (L), kapitału (K), ziemi (Z) i surowców (S) w najogólniejszej postaci zapiszemy jak poniżej:

Q= f(K, L, Z, S)

Tego typu zapis ten nie obrazuje ścisłych funkcyjnych zależności. Stwierdza jedynie, że maksymalna ilość możliwych do wyprodukowania dóbr zależy od ilości używanych w procesie produkcji czynników: pracy, kapitału, ziemi i surowców. Ponieważ w zapisie tym produkcja uzależniona jest jednocześnie od zmian wielu czynników nazywamy ją wieloczynnikową funkcję produkcji.

Ale taka bardzo rozbudowana funkcja nie będzie nam potrzebna (w dodatku trudno jest ją przedstawić graficznie). Dla naszych dalszych analiz wystarczy funkcja uproszczona do dwóch czynników: pracy L i kapitału K

Q=f(K, L)

Tabelaryczna dwuczynnikowa funkcja produkcji

Gdy w modelu uwzględniamy tylko dwa czynniki pracę L i kapitał K, to dla każdej kombinacji K i L znaleźć można maksymalną, z technicznego punktu widzenia, fizyczną wielkość produkcji Q. Hipotetyczne zależności pomiędzy ilością stosowanych czynników a wielkością uzyskanej produkcji przedstawić można posługując się liczbami zawartymi w poniższej tabeli.

K
6	48	70	84	94	102	108
5	46	64	78	88	96	102
4	40	56	70	80	88	94
3	34	48	60	70	78	84
2	28	38	48	56	64	70
1	10	24	36	42	46	48
0	1	2	3	4	5	6	L
Tabelaryczna funkcja produkcji

Tabela jest skonstruowana w ten sposób, że na osiach współrzędnych odłożono liczone w roboczogodzinach ilości czynnika pracy L (oś pozioma) oraz liczone w maszynogodzinach ilości kapitału K (oś pionowa). Każdej kombinacji czynnika pracy i kapitału odpowiada, znajdująca się wewnątrz tabeli możliwa do wytworzenia przy ich pomocy maksymalna z technicznego punktu widzenia wielkość produkcji (Q).

Przyglądając się zawartym w tabeli liczbom możemy stwierdzić, że między ilościami nakładów a uzyskiwaną z nich wielkością produkcji występują pewne prawidłowości, które matematycznie można przedstawić w postaci równań, a geometrycznie w postaci wykresu funkcji.

Izokwanta, czyli funkcja jednakowego produktu

Zacznijmy od przypomnienia, że miedzy czynnikami występuje zjawisko substytucji. Tę samą wielkość produkcji można wytwarzać przy pomocy różnych kombinacji obu czynników wytwórczych. Obrazuje to ciąg liczb czerwonych. Gdy nakład jednego czynnika np. kapitału maleje o ΔK<0, to aby utrzymać fizyczną wielkość produkcji, na niezmienionym poziomie np. Q=48, należy ubywający kapitał zastąpić dodatkową ilością czynnika drugiego, czyli pracy, zatem ΔL>0.

Linia łącząca wszystkie zaznaczone na czerwono punkty przedstawiające tę samą wielkość produkcji, to krzywa jednakowego produktu, czyli izokwanta.

K
6	48	70	84	94	102	108
5	46	64	78	88	96	102
4	40	56	70	80	88	94
3	34	48	60	70	78	84
2	28	38	48	56	64	70
1	10	24	36	42	46	48
0	1	2	3	4	5	6	L
Tabelaryczna funkcja produkcji

Zauważmy ,że gwarantująca utrzymanie produkcji na stałym poziomie stopa zamiany jednego czynnika na drugi, czyli tzw. krańcowa techniczna stopa substytucji ΔK/ΔL nie jest stała, tylko najczęściej malejąca, oznacza to, że aby utrzymać niezmienioną produkcję ubywającą jednostkę jednego z czynników musi być zastąpiona coraz większymi ilościami drugiego.

Nakłady K/L = const	6/1	3/2	2/3	1/6
Produkcja Q	48	48	48	48
ΔK/ΔL	-	-3/+1	-1/+1	-1/+3

W efekcie nasza izokwatna jest krzywą ta jest wypukłą w kierunku początku układu.

Dwuczynnikowa funkcja produkcji

Z tabelarycznej funkcji produkcji wynika, że ilość wytwarzanej przez firmę produkcji uzależniona jest od ilości używanych przez firmę czynników.

Aby trwale zwiększyć możliwości produkcyjne, firma musi powiększyć swoje rozmiary, czyli inaczej mówiąc skalę produkcji. Musi zatem jednocześnie powiększyć nakłady obu czynników. Funkcję tę symbolicznie zapisujemy.

Q= f (L, K )

Ścieżka ekspansji

Gdy nakłady rosną proporcjonalnie to ilustrujący te kombinacje w układzie współrzędnych K L zbiór punktów tworzy tzw ścieżkę ekspansji firmy.

Nakłady K/L = const	1/1	2/2	3/3	4/4	5/5	6/6
Produkcja Q	10	38	60	80	96	108
ΔQ/ΔK lub ΔQ/ΔL	-	28	22	20	16	12

Zamieszczona powyżej tabela przedstawia sytuacją, gdy nakłady obu czynników rosną o ΔK=+1 i ΔL=+1, czyli proporcjonalnie, a to oznacza, że utrzymuje się stały stosunek K/L=1

Każdej kombinacji czynników na ścieżce odpowiada zaznaczona na niebiesko wielkość produkcji. Im więcej obu czynników firma używa, tym produkcja ta jest większa.

Z zawartych w tabeli danych wynika, iż z kombinacji czynników (K=1,L=1) firma może maksymalnie uzyskać Q=10 jednostek produktu, jeżeli natomiast zwiększy ilości stosowanych nakładów do (K=2, L=2), czyli o ΔK=1 i ΔL=1, wówczas możliwa do uzyskania produkcja wzrośnie do poziomu Q=38, czyli o ΔQ=28 Dalsze powiększenie nakładów obu czynników o jednostkę do ilości (K=3,L=3) spowoduje kolejny wzrost produkcji do poziomu Q=60 , czyli o ΔQ=32.

Wykres dwuczynnikowej funkcji

Nad każdym punktem ścieżki ekspansji wisi w przestrzeni oznaczony na niebiesko punkt, który przedstawia maksymalną do uzyskania z tej kombinacji fizyczną wielkość produkcji Q. Mierzy ją wysokość położenia tego punktu.

Każda z przedstawionych kombinacji K i L daje jeden punkt na płaszczyźnie ograniczonej osiami K i L. Np. kombinacji czynników L1 i K1 odpowiada w przestrzeni punkt o współrzędnych (Q1 ,L1 ,K2) , natomiast kombinacji czynników (K2 i L2 ) odpowiada punkt o współrzędnych (Q2, L2 ,K2 ) itd. Zbiór punktów Q wyznaczający maksymalny dla każdej leżącej na ścieżce ekspansji kombinacji K/L poziom produkcji, tworzy trójwymiarowy wykres dwuczynnikowej funkcji produkcji.

Rys Dwuczynnikowa trójwymiarowa funkcja produkcji

Q

Q2 * Q=f(K,L)

Q1 * L

L2

L1 *

*

K1 K2 K

Analogiczną funkcję produkcji możemy wyznaczyć dla ścieżki ekspansji K/L=1/2, czy 2/1 i wiele innych.

Nakłady K/L = const	1/2	2/4	4/6
Produkcja Q	Q1 = 24	Q2 = 56	Q3 = 94

Nakłady K/L = const	2/1	4/2	6/4
Produkcja Q	Q1 = 28	Q2 = 56	Q3 = 94

Im więcej możliwych ścieżek ekspansji, tym więcej wiszących na nimi funkcji produkcji. Natomiast, gdyby czynniki wytwórcze były doskonale podzielne, to ilość kombinacji K i L była nieskończenie duża, wtedy wiszące nad układem współrzędnych punkty zlałyby się w jedną płaszczyznę. Każdy punkt na niej przedstawiałby technicznie możliwą maksymalną produkcję z danej kombinacji czynników.

Jeśli płaszczyznę tę przetniemy przechodzącą przez początek układu płaszczyzną pionową do układu współrzędnych K. L to jej górna krawędź ilustruje dwuczynnikową funkcję produkcji leżącą nad zaznaczoną w układzie współrzędnych K L ścieżką ekspansji firmy.

Wprowadzenie trzeciego czynnika produkcji np. ziemi czy czwartego np. surowców oznacza, że do naszego modelu musimy wprowadzić dodatkowo czwarty i piąty wymiar. W tych warunkach nie będziemy już mogli posługiwać się tradycyjnymi wykresami. Z tego miedzy innymi względu w naszych dalszych analizach będziemy uwzględniać maksymalnie dwa czynniki produkcji. Panuje powszechne przekonanie, że powinna to być praca L i kapitał K.

Jednoczynnikowa funkcja produkcji

Z zamieszczonej poniżej tabelarycznej funkcji produkcji wynika, że produkcja zmienia się również wtedy gdy zmienia się jeden czynnika podczas gdy drugi pozostaje niezmieniony.

K
6	48	70	84	94	102	108
5	46	64	78	88	96	102
4	40	56	70	80	88	94
3	34	48	60	70	78	84
2	28	38	48	56	64	70
1	10	24	36	42	46	48
0	1	2	3	4	5	6	L
Tabelaryczna funkcja produkcji

Tak wygląda sytuacja gdy czynnikiem zmiennym jest praca a czynnikiem stałym kapitał

Nakłady = K const	1	1	1	1		1
Nakłady L	1	2	3	4	5	6
Produkcja	10	28	34	42	46	48
ΔQ/ΔL	-	18	12	6	4	2

Można sobie również wyobrazić sytuację , gdy czynnikiem stały jest praca a zmiennym kapitał.

Nakłady = L const	1	1	1	1		1
Nakłady K	1	2	3	4	5	6
Produkcja	10	24	36	42	46	48
ΔQ/ΔK	-	14	12	6	4	2

W obu przypadkach mamy do czynienia z jednoczynnikowymi funkcjami produkcji .Ich cechą charakterystyczną jest to że w miarę wzrostu nakładu czynnika produkcja całkowita rośnie. Zauważmy, że ale kolejne przyrosty ΔQ/ΔL i ΔQ/ΔK są w naszym przykładzie coraz mniejsze

Okres analizy

Rozszerzenie lub zwiększenie produkcji zawsze wymaga powiększenie nakładów czynników (np. na zakup dodatkowych budynków, maszyn, surowców, zatrudnienie dodatkowych pracowników lub wydłużenie ich czasu pracy). Zdobycie dodatkowych czynników wymaga czasu. Czas ten kształtuje się różnie w zależności od rodzaju potrzebnego do wzrostu produkcji czynnika.

W wykładzie poświeconym rynkowi analizowaliśmy zjawisko podaży w zależności od hory­zontu czasowego. Oddzielnie dla okresu ultrakrótkiego, krótkiego i długiego. W naszej analizie produkcji i kosztów nawiążemy do tego podziału.

Okres ultrakrótki

W okresie bardzo krótkim, firma nie jest w stanie zdobyć żadnego z wymienionych powyżej czynników. Wszystkie czynniki są stałe, a to znaczy, że produkcja jest również stała, zatem analizując funkcję produkcji przypadek ten możemy pominąć.

Okres krótki (rynkowy)

Okres ten charakteryzuje się tym, że niektóre czynniki produkcji są firmie niedostępne, czynniki te będziemy uznawać za stałe, natomiast te które w tym okresie są dostępne traktujemy jako zmienne. Zatrudniając ich więcej lub mniej firma może zmieniać wielkość produkcji w przeciągu dni lub tygodni.

Czynniki zmienne

Jakie czynniki może firma zdobyć, gdy chce szybko zwiększyć rozmiary produkcji? W krótkim okresie firma może dowolnie zmieniać wielkość nakła­dów takich czynników jak:

- ilość siły roboczej. Może zmieniać ilość zatrudnionych pracowników zatrudnionych przy produkcji produkcyjnych lub ilość roboczogodzin. Firma może wydłużyć czas pracy aktualnie pracującej załogi, wprowadzić pracę w nadgodzinach czy zwiększyć ilość pracujących osób.

- Ilość użytych do produkcji surowców materiałów, półfabrykatów, paliwa energia narzędzia ręczne itp.

- Ilość kapitału obrotowego.

W tym samym czasie niektóre czynniki są niedostępne. Ich ilość pozostaje bez względu na wielkość produkcji niezmienna. Te niedostępne w krótkim okresie czynniki nazywamy stałymi.

Czynniki stałe

Typowym przykładem stałego czynnika produkcji jest trwały kapitał rzeczowy (budynki fabryczne i ciężkie wyspecjalizowane maszyny itp.). Zmiana jego zasobu wymaga, bowiem czasu. Rozbudowa istniejącej fabryki lub budowa nowej może trwać kilka lat. Równie trudne lub niemożliwe w krótkim okresie może być także zmniejszenie zasobu kapitału przedsiębiorstwa. Jeżeli nawet producent benzyny w pewnym momencie zorientuje się, iż dysponuje znaczną nadwyżką zdolności rafinacji ropy (w stosunku do popytu), to może się okazać, że w dającej się przewidzieć przyszłości sprzedaż czy inny sposób zagospodarowania tych nie wykorzystanych mocy wytwórczych są niemożliwe.

Jeżeli z kolei przedsiębiorstwo działa w warunkach, w których swobodę jego działania ograniczają długookresowe umowy o pracę, to jego możliwości zmiany stanu zatrud­nienia mogą być ograniczone w czasie obowiązywania umowy, czyli nawet w ciągu trzech lat. W takim przypadku praca będzie w krótkim okresie czynnikiem stałym.

Długi okres.

Długi okres to czas wystarczająco długi do tego, aby zmieniać nakłady wszystkich czynników. Jest to czas wystarczająco długi, aby przedsiębiorstwo zbudo­wało drugą fabrykę, zainstalowało nowe maszyny, czy zmieniło technologię produkcji.

Zmiana skali produkcji

Przykładowo, jeśli firma zauważy, że popyt na jej produkty przez cały czas się zwiększa, to może zdecydować się na powiększenie swojego majątku i zain­stalowanie nowych urządzeń. Może dokupić nowe maszyny, zbudować hale fabryczne, powierzchnie magazynowe. Może również powiększyć ilości wszystkich pozostałych czynników produkcji. Inaczej mówiąc jest to czas niezbędny by firma mogła zmienić swoje rozmiary lub jak to się również mówi zmienić skalę swojej działalności.

Zmiana technologii produkcji

Może też pod wpływem postępu technicznego zmienić stosowaną technologię. Jednakże wprowadzenie nowej technologii, podobnie jak powiększenie zasobu kapitału rzeczowego czy zasobu ziemi, wymaga nakładów inwestycyjnych na nowe urządzenia, maszyny, instalacje, itp. Będzie to, zatem zmiana długookresowa, a w długim okresie podział czynników na stałe i zmienne nie ma sensu. Powstaje zatem pytanie, jak długo trwa okres krótki, kiedy się kończy i zaczyna okres długi? Odpowiedz jest prosta, nie istnieje żadna uniwersalna reguła pozwalająca wyznaczyć granicę między krótkim i długim okresem.

Jak długo trwa okres krótki?

Nie da się jednoznacznie określić krótkiego okresu liczbą dni czy tygodni, czy miesięcy. Z analizą krótkookresową mamy do czynienia, gdy przedsiębiorstwo wytwarza dany produkt przy pomocy tej samej ilości maszyn, na tej samej powierzchni hal produkcyjnych oraz za pomocą samej technologii. Nie jest ważne czy stan ten trwa miesiąc, rok, czy może nawet też kilka lat.

Dokładne i jednoznaczne określenie krótkiego i długiego okresu nie jest możliwe, zależy to bowiem od specyfiki branży, w jakiej działa firma, długości życia produktu, cyklu inwestycyjnego i wielu innych czynników. Faktyczna długość krótkiego okresu różni się w poszczególnych przedsiębiorst­wach.

Przykładowo, w niektórych gałęziach przemysłu, zatrud­niających względnie proste urządzenia i niewykwalifikowaną lub przyuczoną siłę roboczą, krótki okres może oznaczać tylko kilka miesięcy. W innych gałęziach przemysłu, jak produkcja stali, rafinacja ropy naftowej czy wytwarzanie energii elektrycznej, czy górnictwo krótki okres rozciąga się od kilku do kilkunastu lat, gdyż tyle czasu potrzeba na wybudowanie nowych zakładów. Linia podziału musi raczej być określona w każdym przypadku z osobna, gdyż zależy on od rodzaju przemysłu.

Związku z tym przyjmujemy umownie, że okres długi, to taki, w którym wszystkie czynniki są dostępne, czyli traktujemy je jako zmienne. Natomiast okres krótki jest to czas, w którym firma nie jest w stanie zmienić posiadanego zasobu kapitału rzeczowego, ziemi, dana jest również technologia produkcji. Stałymi czynnikami produkcji w krótkim okresie są, zatem: ziemia, kapitał oraz wiedza technologiczna.

Po tych wyjaśnieniach możemy przystąpić do analizy krótkookresowej jednoczynnikowej funkcji produkcji

Krótkookresowa jednoczynnikowa funkcja produkcji

W każdej gospodarce istnieje tysiące różnych funkcji produkcji, po jednej przynajmniej dla niezliczonych firm i najrozmaitszych produktów. Precyzyjnie przedstawienie krótkookresowych zależności pomiędzy ilościami stosowanych czynników a maksymalną wielkością produkcji, kiedy firma wykorzystuje tylko jeden zmienny czynnik produkcji, pozostałe zaś są stałe, wymaga przyjęcia kilku założeń upraszczających.

Po pierwsze zakładamy, że analizowana przez nas funkcja produkcji odnosi się do sytuacji, gdy wytwa­rzany jest jeden określony produkt. Inaczej mówiąc produkowany towar jest jednorodny (homogeniczny). Wytwarzanie innych produktów charakteryzuje się innymi kombinacjami czynników, czyli innymi funkcjami produkcji.

Po drugie, przyjmujemy, że w krótkim okresie czynnikiem zmiennym jest praca, zaś czynniki stałe ograniczymy wyłącznie do kapitału. Taki podział wynika z przyjętej konwencji, choć ma swoje uzasad­nienie praktyczne, jako że w krótkim okresie firma nie może zmienić posiadanego zasobu kapitału rzeczowego ,natomiast względnie łatwo może zatrudnić dodatkowych pracowników.

Po trzecie, przyjmujemy, że praca ludzka jest jednorodna. Oznacza to, że każdy pracownik posiada jednakowe kwalifikacje i jednakową chęć do pracy.

Przy tych założeniach wielkość produkcji uzależniona jest wyłącznie od ilości użytych do produkcji ilości jednostek nakładów prac, zatem przyrost produkcji na­stępuje wyłącznie wskutek zmian ilości czynnika pracy. Krótkookresową funkcję produkcji można zatem uznać za funkcję jednoczynnikową, której najogólniejsza postać zapisujemy jak poniżej:

Q=f(L) ; K=const

Z zapisu wynika ,że jeżeli więc firma uzna za celowe, może w krótkim okresie zwiększyć swoją produkcję, może to zrobić tylko w zakresie, wyznaczonym możliwościami pozyskania dodatkowych pracowników.

Analizując zależności pomiędzy wielkością nakładów czynnika pracy a rozmiarami wytworzonej produkcji, w pierwszej kolejności musimy określić kształt funkcji produkcji. Inaczej mówiąc, musimy ustalić, jaki wzrost produkcji towarzyszy stałym wzrostom nakładów pracy o ΔL=1. Mówiąc inaczej musimy ustalić jak zachowuje się produkt krańcowy ΔQ/ΔL. Od jego wartości zależy bowiem, czy produkcja rośnie proporcjonalnie do poniesionych nakładów (ΔQ/Q=ΔL/L), szybciej niż nakłady (ΔQ/Q>ΔL/L), czy wolniej od nakładów (ΔQ/Q<ΔL/L).

Gdy produkt krańcowy rośnie, produkcja rośnie szybciej od nakładu czynnika, czyli rośnie bardziej niż proporcjonalnie, gdy produkt krańcowy jest słały wzrost produkcji jest proporcjonalny do wzrostu nakładów, natomiast gdy produkt krańcowy maleje, produkcja rośnie wolniej od nakładu czynnika zmiennego, czyli mamy do czynienia ze wzrostem mniej niż proporcjonalnym.

Na pierwszy rzut oka można by sądzić, że wzrost liczby pracowników lub ilości przepracowanych godzin powinien zawsze prowadzić do proporcjonalnego wzrostu produkcji. Okazuje się jednak, że problem ten jest bardziej skomplikowany, bo produkcją w okresie krótkim rządzi prawo nieproporcjonalnych przychodów.

Prawo nieproporcjonalnych przychodów.

Analizując prawa rządzące produkcją rolną francuski uczony J. Turgot żyjący w latach (1727-81) zauważył, że gdy na danym i niezmienionym areale uprawy (w tym przypadku czynnikiem stałym jest ziemia) rozpoczynamy produkcję od zera, wówczas każda dodatkowo zatrudniona jednostka czynnika zmiennego (czyli pracy), przynosi najpierw coraz to większe przyrosty produkcji, czyli występuje zjawisko rosnącego produktu krańcowego pracy ludzkiej. Jednakże po przekroczeniu pewnego poziomu zatrudnienia kolejne stałe przyrosty pracy zaczynają przynosić coraz mniejszy przyrost produkcji, czyli produkt krańcowy pracy zaczyna spadać. Wreszcie po osiągnięciu pewnego krytycznego poziomu zatrudnienia, produkt krańcowy będzie zerowy, a po jego przekroczeniu może być nawet ujemny.

Dziś uważa się , że prawo to dotyczy każdego krótkookresowego procesu produkcyjnego i że każde zwiększanie zatrudnienia (powiększanie nakładów czynnika zmiennego) przy stałej ilości aparatu wytwórczego, np. w postaci maszyn, urządzeń, hal produkcyjnych itd. przyczynia się do wzrostu produkcji, najpierw w coraz większym, a od pewnego poziomu zatrudnienia i produkcji w coraz mniejszym stopniu. W skrajnych przypadkach przyrost ten może być zerowy, a nawet ujemny , co oznacza ,że zatrudnienie dodatkowego pracownika powodować będzie nie wzrost, lecz spadek ogólnej wielkości produkcji.

Krzywa Knight`a

Opisane powyżej zależności można zilustrować przy pomocy zamieszczonej poniżej tabeli. Zawiera ona różne wielkości zatrudnienia oraz odpowiadające im zgodnie z prawem nieproporcjonalnych przychodów wielkości produktu całkowitego i krańcowego. Wyobraźmy sobie firmę produkującą owocowe napoje orzeźwiające w puszkach. Dysponuje ona lokalem posiada wszystkie niezbędne maszyny. Teraz trzeba zdecydować ilu pracowników zatrudnić i ile puszek napojów produkować, aby osiągnąć maksymalny zysk.

Krótkookresowa funkcja produkcji pokazuje, jak zmienia się wielkość produkcji, czyli ilość wyprodukowa­nych puszek, w zależności od ilości zatrudnionej pracy. Jasne jest, że im więcej zatrudni pracowników, tym większa będzie produkcja, ale żeby bliżej przyjrzeć się tej zależności, posłużymy się pojęciami: produktu całkowitego, krańcowego i przeciętnego. W naszej firmie zmiennym czynnikiem produkcyjnym jest praca, zatem produkt j całkowity jest jej funkcją. Zależności tę przedstawić można w postaci poniższej tabeli

Zatrudnienie ( L)	Produkt całkowity ( Q )	Produkt krańcowy ΔQ/ΔL
0	0	-
1	10 rośnie	10 rosnący
2	24 rośnie	14 rosnący
3	39 rośnie	15 maksymalny
4	52 rośnie	13 malejący
5	60 rośnie	8 malejący
6	66rośnie	6 malejący
7	66 bez zmian	0 zerowy
8	63 maleje	-3 ujemny

Z zawartych w niej danych możemy odczytać, jak zmienia się w ciągu dnia liczba wyprodukowanych puszek napoju wraz ze zmianą oznaczonej przez L ilości pracy, czyli liczbą zatrudnionych pracowników. Jeśli nie jest zatrudniony żaden pracownik, to produkcja wynosi zero. Wraz ze wzrostem zatrudnienia zwiększa się całkowita wielkość wytworzonej produkcji zwana produktem całkowitym (ang. total produkt TP). Kolejnym potrzebnym do dalszych analiz pojęciem jest produkt krańcowy czynnika produk­cyjnego (ang. marginal produkt MP). Jest to przyrost produkcji spowodowany wzrostem zatrudnienia tego czynnika o jednostkę. W naszym przypadku wyraża go stosunek ΔQ/ΔL.

Q

Qc=66 C

Rys. A Krzywa Knight`a

Qa=39

A

L

ΔQ/ΔL La=3 Lc=7

ΔQ/ΔL=15

Rys. B. Krzywa produktu krańcowego

L

La=3 Lc=7

Produkt ten najpierw rośnie przy pewnej wielkości zatrudnienia osiąga maksimum , następnie maleje do zera

Zawarte w tabeli dane możemy nanieść na układ współrzędnych i wykreślić jako to pokazano wyżej funkcję produktu całkowitego Q=f(L) znaną nam jako „krzywą Knight`a” oraz jej pochodną, czyli funkcję produktu krańcowego ΔQ/ΔL.

Krótkookresowa funkcja produkcji pokazuje zależność między czynnikami produkcyjnymi wykorzystanymi w procesie produkcyjnym a produktami otrzymanymi jako wynik tego procesu. W naszym przykładzie produkcja rośnie najpierw bardziej, potem mniej niż proporcjonalnie, następnie zaczyna spadać. Jest tak, bo decydujący o przyrostach produkt krańcowy pracy jest najpierw rosnący, potem malejący, przy pewnej wielkości zatrudnienia osiąga zero, a nawet może przyjąć wartości ujemne

Dlaczego produkt krańcowy jest zmienny?

Co może być przyczyną nieproporcjonalności przyrostów produkcji? Czy nie jest ona przypadkiem skutkiem niejednorodności pracy ludzkiej? Można sądzić, że gdy zatrudniamy kolejno pracowników o coraz wyższych kwalifikacjach, to spowodowany tym przyrost produkcji powinien być przynajmniej z teoretycznego punktu widzenia coraz wyższy, czyli uzyskiwany z ich pracy produkt krańcowy powinien rosnąć. Można również przypuszczać, że gdy sięgamy po ludzi o coraz niższych kwalifikacjach, czy słabszej motywacji, przynoszony przez nich produkt będzie coraz mniejszy.

Tego rodzaju tłumaczenie nie wytrzymuje jednak konfrontacji z rzeczywistością. Nieproporcjonalne przychody wystąpią również wówczas, gdy praca będzie jednorodna, czyli gdy wszyscy kolejno zatrudnieni będą mieli takie same umiejętności i chęć do pracy. Muszą zatem istnieć jeszcze inne uniwersalne przyczyny tego zjawiska. Zastanówmy się, czy u podstaw nieproporcjonalnych przychodów nie leżą przypadkiem przyczyny techniczne?

Bryłowatość urządzeń technologicznych

Zwróćmy w pierwszej kolejności uwagę na fakt, że używane w procesach produkcji urządzenia technologiczne są z natury swojej bryłowate, nie podlegają miniaturyzacji, czyli inaczej mówiąc są niepodzielne. Nie da się zmniejszyć maszyny o połowę, gdy chcemy produkować o połowę mniej. Ponadto wszystkie uczestniczące w procesie produkcyjnym urządzenia tworzą tzw. ciągi technologiczne, polegające na tym, że wytwarzany produkt przechodzi w poszczególnych fazach przetwórstwa z jednego stanowiska do drugiego. Również z tego względu nie da się zmniejszyć ilości maszyn o połowę.

Z drugiej strony, aby procesy produkcji przebiegały sprawnie z technicznego punktu widzenia, potrzebny jest pewna ilość ludzi, którzy nie tylko obsługuje poszczególne maszyny, ale muszą ze sobą współpracować, ludzi ci pracują zespołowo tworząc tzw. załogę.

Jeżeli przedsiębiorstwo nie zatrudni żadnego pracownika, aparat wytwórczy nie będzie wykorzystany, a produkcja wyniesie zero. Jeżeli do stojących do dyspozycji urządzeń zatrudnimy tylko jednego pracownika, to będzie on musiał sam zorganizować proces produkcyjny, pobrać surowce z magazynu, dostarczyć je na stanowisko pracy, przygotować dokumentację techniczną, ustawić maszyny, usuwać odpady produkcyjne, wreszcie odtransportować gotowe produkty do magazynu. Ponadto, robotnik ten musi przechodzić w kolejnych fazach przetwórstwa od jednego do drugiego, trzeciego itd. stanowiska pracy. Jego efektywny czas pracy będzie, zatem bardzo krótki, gdyż większość wykonywanych przez niego czynności będzie jedynie pośrednio związana z wytwarzaniem konkretnych dóbr. Stąd też wytworzony przez pierwszego zatrudnionego produkt krańcowy jest niewspółmiernie niski w stosunku do technicznych możliwości firmy.

Jaki wpływ na wielkość produkcji będzie mieć zatrudnienie kolejnego robotnika, o identycznych kwalifikacjach i motywacji do pracy? Możemy przypuszczać, że drugi pracownik w jakiś sposób ułatwi pracę pierwszemu. Jeżeli jego zatrudnienie umożliwi wyeliminowanie części przynajmniej pośrednich czynności, wówczas efektywny czas pracy pierwszego zatrudnionego wydłuży się wytwarzany przez niego produkt wzrośnie. Ponadto, w efekcie współpracy na dwóch stanowiskach pracy, będzie on w stanie wytworzyć większą ilość produktów w jednostce czasu (np. w czasie jednej godziny). W takiej sytuacji produkt krańcowy z tytułu zatrudnienia drugiego pracownika będzie większy od produktu pierwszego pracownika. Czy jednak produkt krańcowy będzie wzrastał w nieskończoność? Otóż nie.

Okazuje się, że może on rosnąć tylko do określonego poziomu zatrudnienia, a następnie zaczyna maleć. Na przeszkodzie dalszemu jego wzrostowi stanie, bowiem ograniczony zasób czynnika stałego np. kapitału trwałego. W każdej firmie przy danej ilością maszyn i innych urządzeń, istnieje pewien poziom zatrudnienia mierzony ilością pracowników, przy którym wszystkie urządzenia produkcyjne są obsadzone, maszyny w pełni wykorzystane, a współpraca pomiędzy poszczególnymi stanowiskami pracy jest najpełniejsza. Przy tym poziomie zatrudnienia produkt krańcowy osiąga maksymalną wielkość. Po jego przekroczeniu zaczyna spadać.

Optymalne wykorzystania czynnika zmiennego

Jeżeli przyjmiemy, że produkt krańcowy jest miara efektywności wykorzystania czynnika zmiennego, to analizując dane ilustrujące przebieg funkcji produktu całkowitego i krańcowego, dochodzimy do wniosku, że optymalne wykorzystanie czynnika zmiennego ma miejsce przy tym poziomie produkcji i zatrudnienia, przy której produkt krańcowy jest największy. Ponieważ w punkcie tym produkt krańcowy osiąga wartość maksymalną, ma zatem miejsce optymalne z technicznego punktu widzenia wykorzystanie czynnika zmiennego.

Dolna i górna granica zatrudnienia

Gdy ilość pracowników jest niższa od La, to każdy dodatkowy pracownik przynosić będzie rosnący produkt krańcowy, stąd dla firmy będzie korzystne zwiększanie zatrudnienia przynajmniej do poziomu La=4. Z punktu widzenia technicznej racjonalności produkcji nie powinna nigdy spadać poniżej tego poziomu.

Dalszy wzrost zatrudnienia przynosić będzie firmie dodatkową produkcję, ale produkt krańcowy każdego kolejno zatrudnianego będzie już ze względów czysto technicznych coraz mniejszy. Z przebiegu funkcji wynika, że przy zatrudnieniu Lc nasycenie kapitału pracą może stać się tak duże, że efekt zatrudnienia dodatkowych pracowników będzie zerowy ΔQ/ΔL=0).Wreszcie zatrudnienia dalszych pracowników doprowadzi najprawdopodobniej do spadu produkcji, czego wyrazem będzie ujemna wartość produktu krańcowego ΔQ/ΔL< 0 i zmiana nachylenia funkcji produkcji.

Ponieważ firmie na pewno nie będzie opłacało się zatrudniać pracowników, którzy przynoszą zerowy a tym bardziej ujemny przyrost produkcji, możemy uznać, ze zatrudnienie na poziomie Lc=7 wyznacza górne, techniczne możliwości produkcyjne przedsiębiorstwa.

W świetle tych ustaleń możemy przyjąć, że techniczne warunki produkcji wyznaczają poziom zatrudnienia w przedziale <La, Lc>, a produkcji w przedziale <Qa,Qc> Oznacza to, że gdyby firma kierowała się tylko czysto technicznymi kryteriami to będzie działać w warunkach prawa malejących przychodów (krańcowych. Musi się zatem liczyć się z faktem, że przy danej ilości czynnika stałego (kapitału), każda dodatkowa jednostka czynnika zmiennego czyli pracy będzie dawać coraz mniejszy przyrost produkcji.

Produkt krańcowy i przeciętny

Granice opłacalnej z technicznego punktu widzenia produkcji można skorygować, gdy do naszej analizy wprowadzimy dodatkowe narzędzie zwane produktem przeciętnym.

Wielkość tę obliczamy jako stosunek produktu całkowitego Q do ilości użytego, dostępnego czynnika zmiennego, czyli w danym przypadku pracy L.

Zatrudnienie L	Produkcja Q	Krańcowy produkt pracy ΔQ/ΔL	Przeciętny produkt pracy Q/L
0	0	-	-
1	10	10	10
2	24	14	12
3	39	15	13
4	52	13	13
5	60	8	12
6	66	6	11
7	66	0	9,4

Niech podstawą dla nich będą dane zawarte w powyższej tabeli. Z przedstawionego w tabeli rozkładu funkcji produktu krańcowego i przeciętnego wynika, że pomiędzy oboma kategoriami istnieje swojego rodzaju korelacja. Zależności, w jakich pozostają względem siebie wielkości przeciętne i krańcowe mają charakter czysto arytmetyczny i znaleźć je można, np. w statystykach meczów piłkarskich. Aby ją wyjaśnić posłużymy się przykładem zaczerpnięto z książki D. Begg i inni: „ Ekonomia „ t 1. PWE)

Zawodnik, który w trzech meczach uzyskał 3 bramki zdobył przeciętnie 1 gola w meczu. Jeżeli w czwartym (krańcowym) spotkaniu zdobędzie 2 bramki, to jego krańcowy wynik przewyższa dotychczasową średnią z trzech meczy. Podnosi to średnią w czterech meczach do (3+2):(3+1)=5/4=1,25 Jeżeli w kolejnym meczu strzeli on 5 bramek, to jego średnia wyniesie (5+5):(4+1)=10/5=2.

Jeżeli teraz, w następnym (krańcowym) szóstym meczu zdobędzie dodatkowo 2 gole, czyli tyle, ile wynosi jego dotychczasowa średnia, wówczas jego średnia ze wszystkich spotkań pozostanie niezmieniona (10+2)/(5+1)=12/6=2.

Jeżeli w następnym (siódmym) meczu zdobędzie tylko jedną bramkę, czyli mniej niż wynosi dotychczasowa średnia, jego średnia ze wszystkich spotkaniach spadnie do (12+1)/(6+1)=13/7=1,8

Podobną analizę można przeprowadzić dla zachowania się produktu przeciętnego i krańcowego. Generalna zasada jest tak. Gdy do danego produktu przeciętnego dodajemy większy do niego produkt krańcowy, to produkt przeciętny wzrośnie. Jeżeli do danego produktu przeciętnego dodamy równy mu produkt krańcowy, to produkt przeciętny nie zmieni się. W przypadku natomiast, gdy do danego produktu przeciętnego dodamy niższy od niego produkt krańcowy, to produkt przeciętny spadnie.

Z algebraicznych zasad liczenia wielkości przeciętnych wynika, że w warunkach działania prawa nieproporcjonalnych przychodów produkt przeciętny rośnie wraz ze wzrostem produktu krańcowego. Rośnie w dalszym ciągu gdy produkt krańcowy spada ale jest od przeciętnego większy Produkt przeciętny osiąga maksimum dla tej wielkości zatrudnienia i produkcji, przy których już spadający produkt krańcowy zrównuje się z nim (L=4, Q=52), następnie wraz z dalszym wzrostem zatrudnienia i produkcji zaczyna spadać przewyższając jednak poziom produktu krańcowego.

Produkt całkowity przeciętny i krańcowy (Analiza trygonometryczna)***

Trygometryczną miarą produktu krańcowego jak to przedstawiono na rysunku poniżej jest tangens linii prostej przecinającej funkcję produkcji w dwóch interesujących nas punktach tgα=ΔQ/ΔL. Rys Trygonometryczne sposoby pomiaru produktu krańcowego

Rys A Rys B

Q b Q

Qb

Qa a α ΔQ B

ΔL

α

A

α

α

La Lb L

W przypadku natomiast zmian nieskończenie małych jak to przedstawia rys B jest to tangens linii prostej stycznej do krzywej produktu całkowitego w interesującym nas punkcie tg α =δQ/δL.

W miarę wzrostu zatrudnienia, funkcja produkcji zmienia swoje nachylenie, a zatem zmienia się wartość mierzącego produkt przeciętny tangens siecznej na rysunku A lub tangens stycznej na rysunku B

Trygonometrycznie można również wyznaczyć wielkość produktu przeciętnego (Q/L) Jego miarą jest tangens linii łączącej początek układu współrzędnych z interesującym nas punktem na krzywej produktu całkowitego.

Rys Mierzenie produktu przeciętnego

Q

Qb

b

Qa a

α

La Lb L

Współzależność produktu krańcowego i przecieranego

Analizując wykres krzywej produktu całkowitego, przeciętnego i krańcowego podkreślenia wymagają pewne charakterystyczne zależności między tymi kategoriami. Przedstawia je rysunek poniżej.

Rys Współzależność produktu krańcowego i przeciętnego

Q

Qc C

Qb B

tg α = Qa/La

Qa tg α = Qb/Lb

A

α

La Lb Lc L

La=3 Lb=4 Lc=7 L

Początkowo (przy stosunkowo małym poziomie zatrudnienia) nachylenie krzywej produktu całkowitego rośnie, gdyż produkt krańcowy również wzrasta a wraz z nim rośnie produkt przeciętny.

W punkcie A (Qa, La) nachylenie krzywej zmienia się z rosnącego na malejące, z matematycznego punktu widzenia. Jest to punkt przegięcia funkcji produkcji. W punkcie tym produkt krańcowy osiąga maksimum. Oznacza to, że przy dalszym wzroście zatrudnienia każdy kolejny pracownik będzie wprawdzie zwiększał produkcję, ale już w coraz mniejszym stopniu. Przy dalszym wzroście produkcji produkt krańcowy maleje, ale w dalszym ciągu rośnie produkt przeciętny. Dzieje się tak do momentu osiągnięcia punktu B

Optymalne wykorzystanie czynnika stałego i zmiennego

Styczna punkcie B (Qb, Lb) wychodzi z początku układu co oznacza, że produkt równy jest produktowi krańcowemu. Jednocześnie zgodnie z prawami algebry w punkcie tym produkt przeciętny osiąga maksimum. Jest to zatem wielkość produkcji optymalna z punktu widzenia wykorzystania czynnika stałego i zmiennego dlatego punkt ten zwany jest również optimum technologicznym.

W punkcie C (Qc, Lc) krzywa produktu całkowitego osiąga swoje maksimum jednocześnie zmienia nachylenie z dodatniego na ujemny. W punkcie tym produkt krańcowy wynosi zero.

Wreszcie po przekroczeniu punktu C, produkt całkowity spada, krzywa zmienia nachylenie z dodatniego na ujemne; produkt krańcowy jest ujemny a produkcja pomimo wzrostu zatrudnienia spada.

Sformułowane przez nas pojęcie optimum technologicznego przesuwa do góry dolną granicę wyboru wielkości zatrudnienia w przedsiębiorstwie. Zwiększenie zatrudnienia do poziomu Lb i powiększenie produkcji do poziomu Qb będzie dla firmy opłacalne. Trudno bowiem przypuszczać, by firma dobrowolnie zrezygnowała z pracowników, którzy przynoszą jej wprawdzie malejący ale cały czas większy od przeciętnego produkt krańcowy. Zwróćmy uwagę na fakt, że wzrost produktu przeciętnego jest efektem coraz lepszego wykorzystania wszystkich czynników produkcji.

Niestety, na podstawie znajomości produktu całkowitego, krańcowego i przeciętnego nie możemy dowiedzieć się wszystkiego o funkcjonowaniu firmy. Narzędzia te nie wystarczają, by precyzyjnie ustalić, ilu ludzi zatrudniać będzie firma ani określić najkorzystniejszej wielkości produkcji. Tak więc pytanie o optymalną wielkość produkcji i zatrudnienia, przy których osiągany jest maksymalny zysk, pozostaje w dalszym ciągu bez odpowiedzi.

Aby rozstrzygnąć ten problem, obok kryterium technologicznego, musimy wprowadzić dodatkowo kryterium ekonomiczne a jest nim opłacalności produkcji. Kierując się nimi firma powinna określić wielkość produkcji i zatrudnienia na takim poziomie, przy którym firma osiąga najlepszy wynik finansowy liczony jako różnica między możliwymi do otrzymania przychodami a ponoszonymi na ich uzyskanie kosztami produkcji. Aby móc to uczynić firma musi orientować się jak w zależności od poziomu produkcji kształtują się utargi i koszty produkcji. W dalszej części wykładu pokażemy między teorią produkcji i kosztów istnieje ścisły związek. Można by powiedzieć ,że są to dwie strony tego samego medalu.

Podsumowania

1 W tej części wykładu tym zapoznaliśmy się z teorią produkcji.

2 Do wytwarzania używane są różne czynniki produkcji. Ilości stosowane do produkcji to nakłady. Nakładem jest siła robocza, ziemia i kapitał. Możemy je dalej dzielić na różne rodzaje siły roboczej, ziemi i kapitału.

3. Produkt przedsiębiorstwa jest „funkcją" nakła­dów. Znaczy to, że produkt „zależy" od nakładów lub, że, jest wynikiem" nakładów.

4. Zależności między wielkością produkcji a rozmiarem nakładu czynników można przedstawić w formie funkcji produkcji. Funkcja produkcji jest zestawem kombinacji ilości wielu różnych czynników wytwórczych (nakładów) i maksymalną wielkość produkcji, jaką z nich można otrzymać. Funkcje produkcji mogą być jednoczynnikowe i wieloczynnikowe. Rozróżniliśmy krótkookresowe i długo­okresowe decyzje produkcyjne.

5. W krótkim okresie czasu wielkość firmy i technologia produkcji są dane. Nie zmieniają się nakłady na budynki, ziemia, maszyny i urządzenia, itp. Mogą się natomiast zmieniać nakłady niektórych czynników jak np. siła robocza, surowce, półfabrykaty, energia itp.). Krótki okres to okres, w którym przedsiębior­stwo może zmieniać wielkość nakładów tylko niektórych czynników produk­cji - tzw. czynników zmiennych.

6.Długi okres to okres, w którym przedsiębior­stwo może zmieniać nakłady wszystkich czynników produkcji oraz stosowaną techniką produkcji. W okresie tym wszystkie czynniki produkcji są zmienne.

7. W analizie krótkookresowej konsekwencją tego jest podział czynników na zmienne i stałe.

8. Produkcyjność krańcowa czynnika zmiennego, to przyrost produkcji uzyskiwany dzięki zwiększeniu o jednostkę jego nakładu (przy założeniu, że nakłady pozostałych czynników nie ulegają zmianie).

9. W krótkim okresie czasu produkcja podlega działaniu prawa nieproporcjonalnych przychodów. Zwiększając, ceteris paribus, nakład czynnika zmiennego jego produkt krańcowy najpierw rośnie. Istniej taka wielkość produkcji, po przekroczeniu, której każda dodatkowa jednostka czynnika zmiennego przynosi coraz mniejsze przyrosty produkcji. Produkt mar­ginalny czynnika produkcji jest malejący a to znaczy, że produkcja rośnie coraz wolniej.

10. Prawo malejących przychodów działa, obowiązuje w danym czasie, w danych warunkach technicz­nych przy danej kombinacji czynników stałych i zmiennych produkcji.

11. Biorąc pod uwagę kształtowanie się produktu przeciętnego i produktu krańcowego, można wyróżnić trzy fazy funkcji produkcji.

W pierwszej fazie produkt krańcowy rośnie, aż do osiągnięcia wielkości maksymalnej, wraz z nim rośnie produkt przeciętny.

Druga faza etap produkt krańcowy spada, ale jak długo jest on większy od przeciętnego zgodnie z prawami algebry produkt przeciętny rośnie.

W fazie tej produkt przeciętny osiągnie wielkość maksymalną, gdy zrówna się z malejącym produktem krańcowym. Faza trzecia dodatni produkt krańcowy spada i wraz z nim spada wyższy od niego produkt przeciętny. Faza czwarta produkt krańcowy z dodatniego zmienia się na ujemny. Funkcja produkcji zmienia nachylenia z dodatniego na ujemne.

12. Trudno przecenić znaczenie funkcji produkcji w teorii ekonomii już w drugiej części wykładu pokażemy, w jaki sposób funkcje produkcji dla przedsiębiorstwa generują jego krzywe kosztów.

13. Teoria produkcji jest fundamentem teorii kosztów ważnego elementu rachunku ekonomicznego w przedsiębiorstwie.

Koszty produkcji w okresie krótkim

Dla podejmowania decyzji optymalnych konieczna jest znajomość poziomu każdej z poznanych kategorii kosztu odpowiadająca każdemu poziomowi produkcji. Wiedzy na ten temat dostarcza nam teoria kosztów. W zależności od okresu analizy może to być teoria krótkookresowa bądź długookresowa. W tej części wykładu zajmiemy się okresem krótkim

Koszty własne produkcji to wyrażone w formie pieniężnej wydatki poniesione na wytworzenie określonej ilości dobra lub usługi. Jest to suma iloczynów stosowanych do produkcji ilości czynników przemnożonych przez ich ceny.

Ich poziom zależy zatem od ilość użytych do produkcji czynników wytwórczych, czyli nakładów oraz cen, jakie trzeba za nie płacić.

W krótkim okresie nakłady niektórych czynników są stałe. Ich ilości np. maszyn budynków w badanym okresie powiększyć się nie da. W tym samym okresie nakłady innych czynników można bez problemu powiększyć, np. surowce, robocizna energia itp. Uwzględniając tę klasyfikację możemy mówić o nakładach stałych i zmiennych. W związku z tym w analizach krótkookresowych rozróżniamy koszty stałe KS i zmienne KZ.

Koszty stałe (ang. fixed costs - FC)

W krótkim okresie - inaczej niż w długim - nakłady niektórych czynników produkcji pozostaję niezależnie od wielkości produkcji. Opłaty za ich użytkowanie są takie same zarówno przy produkcji zerowej, jak i przy pełnym wykorzystaniu zdolności produkcyjnych przedsiębiorstwa. Są to więc koszty stale

Zaliczymy do nich koszt zużycia środków trwałych, dzięki którym firma odzyskuje poniesione w przeszłości wydatki na wyposa­żenie przedsiębiorstwa w środki trwałe, czyli amortyzację. Do koszów stałych zaliczamy również wynagro­dzenie kadry kierowniczej i pracowników administracyjnych, wydatki na ubezpieczenia majątku przedsiębiorstwa itp., koszty spłat kredytu, koszty opłacanych abonamentów, niektóre podatki. Osobną pozycję stanowią czynsze, czyli opłaty za wynajęcie na pewien okres lokalu lub za wypożyczenie maszyny.

Koszty zmienne (ang. variable costs -VC)

Jeżeli firma zaczyna cokolwiek produkować, to czekają ją pewne dodatkowe wydatki na zakup zmiennych czynników produkcji (np. praca, surowce, energia, itp.) Wszystkie te dodatkowe wydatki tworzą zależne od wielkości produkcji koszty zmienne. Dla naszej dalszej analizy ważny jest podział na koszty zmienne rzeczowe i osobowe.

Zmienne koszty osobowe

Wydatki związane z nakładami czynnika ludzkiego, generują osobowe koszty zmienne. W ich skład wchodzą m.in. ustawowe wynagrodzenia pracowników, wynagrodzenia, pozaustawowe (np. praca w wolne dni, wynagradzanie pracowników sezonowych, itp.).

Zmienne koszty rzeczowe

Wydatki związane z nakładami rzeczowych czynników określane są jako rzeczowe koszty zmienne. W ich skład wchodzą m.in. ponoszone przez firmy wydatki na surowce, materiały, komponenty, paliwo i energię, wydatki na transport, komunikację o podobne usługi.

Koszty zmienne obliczamy jako iloczyn ilość stosowanych do jej wytworzenia nakładów zmiennych czynników produkcji przemnożonych przez ich ceny rynkowe. Gdy produkcja jest równa zero, koszty zmienne są również równe, zero. Ale skoro zaczynamy cokolwiek produkować, zaczynamy ponosić koszty zmienne.

Będzie nas kosztować każda kolejna wyprodukowana jednostka. Aby ją wytworzyć trzeba używać dodatkowe ilości czynników (nakłady) i ponosić dodatkowe koszty ich zakupu. Im większa produkcja, tym większe ilości zmiennych czynników (pracy, surowców, energii itp.) musisz kupować, tym wyższe będą koszty zmienne i rzecz oczywista koszty całkowite, które są sumą kosztów stałych i kosztów zmiennych.

Koszty produkcji w krótkim okresie czasu
Koszty zmienne	Koszty stałe
• koszt wynagrodzenia pracowników produkcyjnych • koszty surowców, materiałów i półproduktów • koszty energii, wody	• wynagrodzenie pracowników administracji i obsługi • koszty zużywania się budynków; maszyn, urządzeń • koszty użytkowania ziemi, • koszty wynajmu lokali • koszty kredytów • niektóre podatki • abonamenty • koszt ubezpieczenia majątku • koszt składek
Zob. M Rekowski cyt. wyd. s.

Koszty całkowite (ang. total costs TC)

Gdy nie produkujemy nic, kosztami całkowitymi są koszty stałe, ale gdy zaczynamy produkować cokolwiek oprócz kosztów stałych ponosimy koszty zmienne. Całkowity krótkookresowy koszt produkcji KC składa się, zatem z kosztów stałych KS, które nie ulegają zmianie wraz ze wzrostem wielkość produkcji oraz zmiennych KZ, które rosną wraz ze wzrostem produkcji.

KC=KS+KZ,

Powyższa tabela pozwoli na się zorientować, jakie pozycje kosztów księgowych zaliczamy do poszczególnych kategorii.

Inne stosowane w analizie kategorie kosztów

Inne ważne dla analizy teoretycznej teorii kategorie kosztów to: koszty przypadające na jednostkę produkcji, czyli przeciętne Kp. W ramach koszów przeciętnych rozróżniamy: przeciętny (jednostkowy) koszt stały (Kps=KS/Q), przeciętny koszt zmienny liczony jako (Kpz=KZ/Q) i przeciętny całkowity obliczany jako (Kpc=KC/Q).

Szczególne znaczenie mieć będzie dla nas koszt wytworzenia dodatkowej jednostki produkcji, czyli tzw. koszt krańcowy lub inaczej marginalny (ang marginal cost-M.C.). Przedstawia go stosunek przyrostu kosztu całkowitego ΔKC do przyrostu produkcji ΔQ, zatem Kk=ΔKC/ΔQ.

Koszty zmienne to suma kosztów krańcowych

Znając wielkości kosztów krańcowych dla różnych poziomów produkcji, możemy bez trudu ustalić przebieg funkcji kosztów zmiennych. Aby ustalić ich poziom dla danej wielkości produkcji wystarczy zsumować koszty krańcowe.

KZ=ΣKk

Teoria kosztów krótkookresowych

Nie ulega wątpliwości, że każda z wyżej wymienionych kategorii kosztów związana jest z rozmiarami produkcji. Aby opisać syntetycznie charakter i siłę tych związków idziemy na daleko idące uproszczenia.

* Po pierwsze zakładamy, że mamy do czynienia z produktem jednorodnym.

* Po drugie ograniczamy ilość czynników do dwóch: pracy i kapitału rzeczowego, a to oznacza, że w naszych analizach posługujemy się dwuczynnikową funkcją produkcji:

Q=f(K, L)

Przy tych założeniach upraszczających koszt całkowity, to łączny koszt użycia nakładów pracy i kapitału. W gospodarce rynkowej obliczamy go jako sumę iloczynów ilości użytych czynników i ich rynkowej ceny. Formułę kosztu całkowitego możemy zatem bardzo ogólnie zapisać jak poniżej:

KC=K*R+L*W

Gdzie:

K -ilość kapitału; R- cena kapitału, L - ilość czynnika pracy; W-cena pracy.

W analizie krótkookresowej rozróżniamy czynniki stałe i zmienne. Jeśli przyjmiemy, że kapitał jest czynnikiem stałym, to koszt stały zostaje sprowadzony do kosztu użycia kapitału, co zapisujemy jako:

KS=K*R=const

Kosztem zmiennym KZ jest koszt zatrudnienia czynnika pracy, co zapisujemy jako:

KZ=L*W

Koszty całkowite składają się zatem z dwóch elementów:

KC=KS+KZ=K*R+L*W

Z formuły wynika, że całkowity koszt produkt zależy od ilości użytych do jej wytworzenia nakładów poszczególnych czynników produkcji oraz ich cen Jeśli przyjmijmy, że ceny czynników wytwórczych pracy - W i kapitału- R, które producent nabywa na rynku są niezależne od rozmiarów jego zakupów, to wielkość poszczególnych kategorii kosztów zależą tylko i wyłącznie od ilości użytych czynników, czyli od nakładów.

W rachunku księgowego do tak obliczonych kosztów należy dodać tę części kosztów ogólnych, która nie reprezentuje zużycia żadnych czynników wytwórczych - np. podatki itp.

Kształt i przebieg funkcji kosztów stałych

Załóżmy, że suma kosztów stałych w skali roku wynosi 100 zł niezależnie od tego czy wartość produkcji w tym samym przedziale czasu wynosi10 zł, czy też 20 sztuk. Ponieważ koszty stałe pozostają niezależnie od wielkości produkcji, ich ilustracją graficzną jest linią prosta pozioma.

Rys Koszty stałe

Q KS0 KS1

KS 0 100 120

KS1 10 100 120

KS0 20 100 120

30 100 120

0 10 20 30 Q

Zauważmy jednak, że gdy np. rynkowa cena kapitału, czynsz, czy wynagrodzenie kadry kierowniczej wzrosną, wraz z nimi wzrośnie koszt stały, ale wzrost ten odbywa się niezależnie od wielkości produkcji Jego graficzną ilustracją jest zatem przesuniecie krzywej do góry.

Kształt i przebieg funkcji kosztów całkowitych

Koszty całkowite które są sumą kosztów stałych i zmiennych rosną wraz ze wzrostem produkcji. Jeżeli rosną proporcjonalnie do wzrostu produkcji, to wykresem funkcji kosztów jest linią prosta ze stałym przyrostem - o stałym nachyleniu. Jeśli rosną bardziej niż proporcjonalnie, to wykresem jest krzywa z rosnącym przyrostem, czyli coraz bardziej stroma. Jeżeli natomiast rosną one wolniej od wzrostu produkcji, to funkcja koszów zmiennych jest krzywą z malejącym przyrostem, czyli coraz bardziej płaska.

Jak z tego wynika o przebiegu i kształcie funkcji kosztów całkowitych decyduje przyrost kosztu całkowitego ΔKC, a dokładniej koszt wytworzenie dodatkowej produkcji ΔQ, czyli koszt krańcowy Kk=ΔKC/ΔQ.

Jeśli koszt krańcowy rośnie wówczas funkcja kosztu całkowitego staje się coraz bardziej stroma, i koszt rośnie bardziej niż proporcjonalnie w stosunku do produkcji. Gdy koszt krańcowy jest stały, funkcja kosztów całkowitych ma stałe nachylenie i koszt rośnie proporcjonalnie w stosunku do produkcji. Gdy natomiast koszt krańcowy maleje, funkcja kosztu całkowitego ma nachylenie malejące a koszt całkowity rośnie mniej niż proporcjonalnie w stosunku do wzrostu produkcji. Powstaje zatem pytanie od czego zależy dynamika kosztu krańcowego Aby na nie odpowiedzieć, musimy dokładniej zdefiniować pojecie kosztu krańcowego, a następnie odwołać się to teorii produkcji i prawa nieproporcjonalnych przychodów z czynnika zmiennego.

Koszt krańcowy (ang. marginal cost - MC)

W krótkim okresie koszt krańcowy liczymy jako stosunek przyrost kosztu zmiennego do przyrostu produkcji. Kk=ΔKZ/ΔQ. Jest tak, bo koszt krańcowy:

Ponieważ ΔKC=ΔKS+ΔKZ, zaś KS=const, zatem ΔKS=0, to znaczy, że:

Dynamika kosztu krańcowego

Każdy wzrost produkcji o wielkość ΔQ wymaga użycia dodatkowych ilości zmiennych czynników wytwórczych. Jeżeli ilości te przemnażamy przez ceny rynkowe ich zakupu, to otrzymamy wywołany przez wzrost produkcji, przyrost absolutny kosztu zmiennego ΔKZ. Jeśli przyrost ten odniesiemy do wzrostu produkcji o ΔQ to otrzymamy wielkość kosztu krańcowego, który zdefiniowaliśmy jako Kk=ΔKZ/ΔQ.

W naszej analizie koszt zmienny sprowadzamy do kosztu pracy, zatem jego poziom uzależniony jest od ilości użytej pracy (L-ang. labour) oraz od poziomu stawki płace (W- ang. wagę). Koszt zmienny wyraża wówczas iloczyn:

KZ=L*W

Natomiast wynikający ze wzrostu produkcji o wielkość ΔQ przyrost kosztu zmiennego ΔKZ to :

ΔKZ=ΔL*W+ΔW*L+ΔL*ΔW

Jeśli W=const, to ΔW=0 , zatem:

ΔKZ=ΔL*W

Koszt krańcowy Kk otrzymujemy dzieląc obie strony równania przez ΔQ.

ΔL*Wo ΔL

Kk = ----------- = ------ * W

ΔQ ΔQ

Na tym etapie analizy przyjmujemy, że stawka płac nie jest zależna od ilości zużytego czynnika pracy, czyli od wielkości produkcji. Jeśli W=const., to ΔW=0, zatem absolutny przyrost kosztu zmiennego zależy tylko i wyłącznie od wartości wyrażenia:

ΔL/ΔQ

które informuje, ile dodatkowej pracy trzeba zatrudnić, by wyprodukować dodatkowo ΔQ ilości produkcji. Jest to krańcowa pracochłonność która nic innego odwrotnością znanej nam z teorii produkcji krańcowej produktywności czynnika pracy.

1

ΔL/ΔQ = ----------

ΔQ/ΔL

Formułę określającą poziom kosztu krańcowego można zatem zapisać w nieco innej zmodyfikowanej postaci jako:

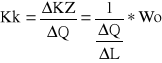
Jeżeli przedsiębiorstwo nabywa stałe i zmienne czynniki produkcji po ustalonych na rynku cenach, bez względu na wielkość swej produkcji i zapotrzebowania, to z przekształconej do powyżej formuły kosztu krańcowego możemy wyciągnąć dwa bardzo istotne dla teorii kosztów wnioski.

Po pierwsze wielkość kosztów krańcowych pozostaje w ścisłym związku z produktywności krańcową czynnika pracy.

- gdy produktywność krańcowa rośnie, pracochłonność krańcowa maleje, dodatkowa produkcja wymaga coraz mniejszej ilości nakładu pracy, co oznacza że koszt krańcowy wyprodukowania dodatkowej jednostki ΔQ maleje

- gdy produktywność krańcowa maleje, krańcowa pracochłonność rośnie, zatem koszt krańcowy rośnie.

Po drugie gdy produktywność krańcowa osiąga maksimum, to koszt krańcowy osiąga minimum.

Funkcja kosztu krańcowego a funkcja produktu krańcowego

Sformułowane powyżej zależności między produktywnością krańcową pracy a kosztem krańcowym można przedstawić postaci wykresu poniżej.

Rys Współzależność produkcji i kosztów krańcowych

Q

ΔQ/ΔL

Kk=ΔL/ΔQ*W La L

Z wykresu wynika, że funkcja kosztów krańcowych jest zwierciadlanym odbiciem funkcji produktu krańcowego, która jest pochodną funkcji produktu całkowitego.

Funkcja kosztów zmiennych

Wiemy już, że koszty zmienne możemy obliczyć sumując koszty krańcowe. KZ=ΣKk Znajomość przebiegu funkcji kosztów krańcowych pozwala zatem prześledzić przebieg funkcji kosztów zmiennych. W lepszym zrozumieniu tych zależności pomogą nam hipotetyczne liczby zawarte w tabeli poniżej

Q	ΔQ/ΔL	ΔQ/ΔL	ΔL/ΔQ	Wo=const	Kk = ΔL/ΔQ*Wo	KZ=ΣKk
0	-	-	-	10	-	-
1	0,33	1/3	3	10	30	30
2	0,5	1/2	2	10	20	50
3	1,0	1,0	1	10	10	60
4	2,0	1/0,5	0,5	10	5	65
5	1,0	1,0	1	10	10	75
6	0,6	1/1,5	1,5	10	15	90
7	0,5	1/2	2	10	20	110
8	0,33	1/3	3	10	30	140
9	0,25	1/4	4	10	40	180
10	0,2	1/5	5	10	50	230

Przedstawione w tabeli zależności można zilustrowane graficznie w postaci wykresów odpowiednich funkcji.

Rys. Koszt krańcowy a koszt zmienny

KZ=65 KZ

Q

Q=4

• 
  

Kk Kk

Kk=5 Q

Q=4

Z ich przebiegu na rysunku A wynika, że kształt krzywej kosztu krańcowego, a co za tym krzywych kosztu zmiennego i całkowitego podporządkowane są działaniu prawa nieproporcjonalnych przychodów

Rys Funkcja kosztów zmiennych a funkcja produkcji

KZ Q

KZ= L*W La L

Gdy produkt krańcowy rośnie, koszt krańcowy maleje, a koszty zmienne rosną mniej niż proporcjonalnie. Gdy natomiast produkt krańcowy maleje, koszt krańcowy rośnie a koszt zmienny rośnie bardziej niż proporcjonalnie.

Funkcja kosztów zmiennych, co ilustruje zamieszczony powyżej rysunek jest zwierciadlanym odbiciem funkcji produkcji. Tam gdzie produkcja rośnie bardziej niż proporcjonalnie koszty zmienne rosną mniej niż proporcjonalnie a tam gdzie rośnie wolniej niż produkcja koszty zmienne rosną szybciej.

Funkcja kosztów całkowitych

Znając przebieg funkcji kosztów zmiennych możemy z łatwością ustalić przebieg funkcji kosztów całkowitych. Wystarczy do kosztów zmiennych dla dowolnej wielkości produkcji dodać koszty stałe. KC=Σ(Kk+KS ).

Q	Kk	KZ=ΣKk	KS	KC=ΣKk+KS
0	-	-	100	100
1	30	30	100	130
2	20	50	100	150
3	10	60	100	160
4	5	65	100	165
5	10	75	100	175
6	15	90	100	190
7	20	110	100	210
8	30	140	100	240
9	40	180	100	280
10	50	230	100	330

Zawarte w tabeli dane liczbowe możemy przedstawić w postaci wykresu:

KC KZ

KC

KZ

KS

KS KS

KS = 100

• 
  Produkcja ( Q )

Kk

Kk

5

0 Q=4 Q

Ponieważ koszty całkowite dla danej wielkości produkcji to koszty zmienne powiększone o koszt stały, zatem jest to krzywa o identycznym kształcie tylko przesunięta do góry o wartość kosztu zmiennego. Jej punkt przegięcia wystąpi zatem przy tej samej wielkości produkcji, co na funkcji kosztu zmiennego.

Koszty przeciętne

Omówione powyżej koszty całkowite, zmienne i krańcowe będą wykorzystywane w analizie zachowania firmy na rynku. Są to narzędzia potrzebne i użyteczne, ale nie zawsze wystarczające. W niektórych sytuacjach, będziemy musieli dodatkowo posługiwać się pojęciem kosztu przeciętnego. Ten rodzaj kosztu możemy utworzyć od każdego kosztu całkowitego po podzieleniu go przez wielkość produkcji. W dalszych analizach będziemy zatem posługiwać się kosztem przeciętnym całkowitym (KC/Q), kosztem przeciętnym zmiennym (KZ/Q) oraz kosztem przeciętnym stałych (KS/Q).

Q	KS	KZ	KC	Kk	Kps	Kpz	Kpc
0	100	-	100	-	-	-	-
1	100	30	130	30	100	30	130
2	100	50	150	20	50	25	75
3	100	60	160	10	33,3	20	53,33
4	100	65	165	5	25,0	16,25	41,25
5	100	75	175	10	20,0	15,00	35,00
6	100	90	190	15	16,6	15,00	31,62
7	100	110	210	20	14,29	15,71	30,00
8	100	140	240	30	12,5	17,50	30,00
9	100	180	280	40	11,1	20,00	31,11
10	100	230	330	50	10,0	23,00	33,00

Powyższa tabela przedstawia znane nam już wielkości kosztów całkowitych, towarzyszących różnym rozmiarom produkcji oraz wyliczone dla każdej wielkości produkcji koszty przeciętne (jednostkowe). Zamieszczone w niej dane umożliwiają nam dokładniejszą analizę przebiegu poszczególnych funkcji kosztów oraz pozwolą nam wychwycić i wyjaśnić zachodzące między nimi podobieństwa różnice i zależności.

Przeciętne (jednostkowe) koszty stałe

Przeciętne (jednostkowe) koszty stałe Kps obliczamy dzieląc całkowity koszt stały przez produkcję (Q).Ilustracją graficzną przeciętnych kosztów stałych jest krzywa opadająca na prawo do dołu.

Rys Przeciętne koszty stałe

Kps= KS/Q

Q	KS	Kps = KS/Q
0	100	-
1	100	100
2	100	50
3	100	33,3
4	100	25,0
5	100	20,0
6	100	16,6
7	100	14,29
8	100	12,5
9	100	11,1
10	100	10,0

Q

Z jej przebiegu wynika, że w miarę wzrostu produkcji koszt ten nieustannie maleje. Jest to spowodowane tym, że w miarę jak produkcja rośnie, koszt stały rozkłada się na coraz większą liczbę produkowanych jednostek. Z matematycznego punktu widzenia koszt ten dąży asymptotycznie do zera, gdy ilość produkowanych jednostek zmierza od nieskończoności. Jeżeli z kolei dopuścimy możliwość coraz mniejszej, ułamkowej produkcji, wówczas przy nieskończonej małej produkcji (ΔQ→0), krzywa Kps rozpoczyna swój bieg na poziomie nieskończenie wysokim.

Przeciętne (jednostkowe) koszty zmienne

Przeciętny koszt zmienny Kpz dla danej wielkości produkcji Q obliczamy, dzieląc całkowity koszt zmienny wykonania danej wielkości produkcji przez wytworzoną ilość.

Rys Przeciętne koszty zmienne Kpz=KZ/Q

Q	KZ	Kpz	Kk
0	-	-	-
1	30	30	30
2	50	25	20
3	60	20	10
4	65	16,25	5
5	75	15,00	10
6	90	15,00	15
7	110	15,71	20
8	140	17,50	30
9	180	20,00	40
10	230	23,00	50

4 6 Q

Z przedstawionej tabeli i wykresu widać, że mamy do czynienia z pewnymi prawidłowościami.

Przy niewielkiej produkcji Kpz spada (podobnie jak Kps) wraz ze wzrostem produkcji. Jednocześnie koszty przeciętne zmienne przewyższają koszt krańcowy Kpz >Kk.

Od pewnego poziomu produkcji (w naszym przykładzie dla Q=6), przy którym zrównuje się z rosnącym już kosztem krańcowym, koszt przeciętny zmienny osiąga minimalny poziom

Dalszemu wzrostowi produkcji towarzyszy wzrost kosztu przeciętnego zmiennego, który już obecnie jest niższy od kosztu krańcowego (Kpz<Kk).

Żadna z opisanych powyżej prawidłowości nie jest przypadkowa. Wiemy już, że zachowaniem kosztów krańcowych „rządzi ” prawo nieproporcjonalnych przychodów. Z kolei zależności miedzy wielkościami przeciętnymi i krańcowymi mają, jak pamiętamy z analizy funkcji produktu przeciętnego i krańcowego, charakter czysto arytmetyczny.

Aby to wyjaśnić odwołajmy się do twoich ocen z egzaminów. Kolejne oceny wpisywane do indeksu może­my potraktować jako oceny krańcowe (Kk) i obserwować, jak pod ich wpływem kształtuje się przeciętna ze wszystkich uzyskanych ocen (Kpz). Przypuśćmy, że startujemy z wysoka 5, lecz stopniowo obniżamy lot: i otrzymujemy 4, 3, 2. Każda dodatkowa (krańcowa) nota obniża nam średnią; niemniej jednak średnia wciąż kształtuje się powyżej ostatniej uzyskanej oceny. Ostatnia ocena wynosi 2, ale średnia ocena jest wyższa i wynosi (5+4+3+2):4=3,5. Jest to właśnie przypadek, gdy Kpz maleje pod wpływem spadku Kk, ale są od nich wyższe Kk<Kpz.

Teraz odbijamy się od dna i zaczynamy uzyskiwać coraz wyższe oceny 2,5,3.( Koszty krańcowe rosną). Ponieważ w momencie odbicia nasza średnia wynosiła 3,5 to zwyżka od 2 do 2,5 nie poprawia nam średniej, lecz nadal ją obniża. (3,5+2,5):2 = 3. Jeśli do średniej wielkości większej dodamy mniejszą, to kolejna średnia będzie mniejsza. Zatem w punkcie odwrócenia spadkowej tendencji kosztów krańcowych Kk, są one większe Kk<Kpz, zatem przeciętny koszt zmienny Kpz będzie malał.

Tendencja spadkowa Kpz utrzyma się tak długo jak długo rosnący koszt krańcowy wytworzenia dodatkowej jednostki produkcji jest mniejszy od przeciętnego kosztu wszystkich wytworzonych do tej pory jednostek.

Gdy rosnący koszt wytworzenia dodatkowej jednostki produkcji zrówna się z dotychczasowym kosztem przeciętnym, Kk=Kpz, zwiększenie produkcji o jednostkę nie zmieni wielkości przeciętnego kosztu wytworzenia wszystkich, dotychczasowych jednostek. Od tego punktu dalszy wzrost kosztu krańcowego będzie podnosił przeciętny koszt zmienny, ale będzie on od kosztu krańcowego mniejszy.

Przy krzywej kosztu krańcowego w kształcie litery „U”, krzywa przeciętnego kosztu zmiennego też ma kształt litery „U”. Przy takim ułożeniu krzywych kosztów, koszt krańcowy znajduje się poniżej przeciętnego kosztu zmiennego na lewo od punktu odpowiadającego minimum Kpz, natomiast na prawo od minimum Kpz, koszt krańcowy jest wyższy od przeciętnych kosztów zmiennych. Krzywa kosztów krańcowych przecina zatem krzywą przeciętnych kosztów zmiennych w najniższym jej punkcie.

Produkt przeciętny a przeciętny koszt zmienny

Pamiętamy, że koszt krańcowy pozostaje w bezpośredniej współzależności z produktem krańcowym. Wynika z tego, że przeciętny koszt zmienny (Kpz = KZ/Q) powinien być powiązany z produktem przeciętnym (Q/L). Aby udowodnić, że tak jest w rzeczywistości, przedstawiamy przeciętny koszt zmienny w nieco innej postaci:

Lub trochę inaczej, jako:

Wyrażenie L/Q to nic innego, jak odwrotność przeciętnej produktywności czynnika pracy

1

L/Q= ------

Q/L

W sytuacji, gdy stawka płac pozostaje niezmieniona, czyli gdy W=const, przeciętny koszt zmienny spada, gdy przeciętna produktywność pracy rośnie i na odwrót. Wreszcie przeciętny koszt zmienny osiąga swoje minimum dla wielkości zatrudnienia i produkcji, dla której produkt przeciętny osiąga wielkość maksymalną.

Trygonometryczna miara kosztu krańcowego i przeciętnego kosztu zmiennego

Trygonometryczną miarą kosztu krańcowego dla dowolnej wielkości produkcji jest wartość tangensa linii prostej, stycznej do krzywej kosztów zmiennych.

KZ

Q

Kk=tg α=ΔKZ/ΔQ

Natomiast trygonometryczną miarą kosztu przeciętnego zmiennego (Kpz=KZ/Q) jest wartość tangensa linii prostej łączącej dany punkt na krzywej

Gdy obie wielkości są sobie równe są sobie równe, styczna i sieczna wychodząca z początku układy są nachylone pod tym samym kątem, zatem muszą się one na siebie nakładać.

Współzależność wielkości przeciętnych i krańcowych

Poniższy rysunek przedstawia współzależność wielkości przeciętnych i krańcowych

Koszt przeciętny i krańcowy Funkcja produkcji

Q

Kpz

Kk

B

A

Kk, Kpz Kpz=min 0 La Lb L

ΔQ/ΔL

Q/L

0 La Lb L

Produkt przeciętny i krańcowy

Z przedstawionych na rysunku zależności wynika, że gdy produkt krańcowy rośnie ,koszt krańcowy maleje W punkcie A na funkcji produktu całkowitego produkt krańcowy osiąga maksimum, natomiast koszt krańcowy minimum Dalszemu wzrostowi produkcji towarzyszy malejący produkt krańcowy i rosnący koszt krańcowy.

Produktywność przeciętna (Q/L) rośnie na całym odcinku OB, zatem przeciętny koszt zmienny musi na całej długości tego odcinka spadać. W punkcie B, produkt przeciętny osiąga swoje maksimum, zatem koszt przeciętny zmienny osiąga minimum. Jednocześnie punkcie tym produktywność krańcowa zrównuje się z przeciętną, zatem koszt krańcowy zrównuje się z przeciętnym kosztem, który osiąga wówczas swoje minimum. Dalszy wzrost produkcji i zatrudnienia powodować będzie spadek przeciętnego produktu a zatem przeciętny koszt zmienny będzie rósł.

Rys Koszty zmienne krańcowe i przeciętne

KZ KZ

KZ1

KZ0

α

Q₀ Q₁ Q

Kk Kk Kpz

Kpz

Q

Zwróćmy uwagę na fakt, że wielkość produkcji, przy której firma wytwarza po najniższych przeciętnych kosztach zmiennych, możemy uznać za optymalne z punktu widzenia wykorzystania czynnika zmiennego, gdyż zapewnia ono najniższy jednostkowy koszt użycia czynnika pracy.

Przeciętny (jednostkowy) koszt całkowity

W analizach rynkowego zachowania firmy szczególną rolę odgrywają przeciętne koszty całkowite, obliczane od funkcji kosztów całkowitych.

Przeciętny koszt całkowity obliczamy dzieląc koszt całkowity KC= KS+ KZ przez wielkość produkcji (Q)

Kpc= KC/Q Kpc =KS/Q+KZ/Q

Oznacza to ze

Kpc=Kpz+Kps

Z formuły kosztu całkowitego wynika, że:

* Jest on dla każdej wielkości produkcji większy od przeciętnego kosztu zmiennego.

* Różnica pomiędzy przeciętnym kosztem całkowitym a przeciętnym kosztem zmiennym zmniejsza się w miarę wzrostu produkcji, co jest wynikiem spadku przeciętnego kosztu stałego.

* Dla wielkości produkcji Q
∞,

KS

Kps=------ =>0

∞

a więc Kpc= Kps+Kpz dąży do zrównania z Kpz

Jeśli koszt krańcowy ma kształt litery u to wpływa on na przebieg funkcji przeciętnych kosztów całkowitych w sposób identyczny, jak w przypadku przeciętnych kosztów zmiennych.

Rys Koszt całkowity krańcowy i przeciętny

Kk, Kpc Kk Kpc

Kpz

Q

Q₁ Q₂

KC

KC

Q

Koszt średni a koszt krańcowy

Jeżeli twoje koszty podniosą się o 50 złotych, to twój koszt krańcowy wynosi te 50 złotych. Jeżeli te 50 złotych przewyższają średnie koszty na jednostkę, to spowodują podwyższenie twoich średnich kosztów. Jeżeli te 50 złotych są mniejsze niż twoje średnie (jednostkowe) koszty wówczas koszty się obniżą. Wyższy „dodatkowy koszt na jednostkę" popycha „średnie koszty na jed­nostkę" w górę, niższy „dodatkowy koszt na jednost­kę" ściąga „średnie koszty na jednostkę" w dół. To oczywiste!

Gdy koszt krańcowy jest niższy od kosztów śred­nich, to ściąga te średnie w dół. Gdy koszt krańco­wy jest wyższy od kosztów średnich, to podnosi je w górę. Dlaczego? Dlatego, że krańcowym jest ten dodatek! Jeżeli „dodatek" jest większy od średniej, to ta średnia podnosi się. Oto przykład.

Przypuśćmy, że w turnieju wiedzy ekonomicz­nej uzyskałeś średnią ocenę 80, po czym zrobiłeś dodatkowy test oceniony na 90. Średnia podniosła się w górę, ponieważ ten krańcowy wynik był wy­ższy od średniej. Gdybyś w tym krańcowym teście otrzymał ocenę 70, to co by się stało z twoją śred­nią? Obniżyłaby się. To samo dzieje się z kosztem krańcowym.

Gdy koszt wyprodukowania dodatkowej jednostki jest mniejszy od osiągniętego już koszty przeciętnego, ten ostatni będzie spadać, nawet wówczas, gdy dodatkowej produkcji towarzyszy rosnący koszt krańcowy. Będzie się tak dziać, jak długo koszt krańcowy jest od przeciętnego niższy.

Przy pewnym poziomie produkcji przeciętny koszt całkowity osiąga najniższy z możliwych poziom. W punkcie tym zrównuje się on z rosnącym kosztem krańcowym. Dalszy wzrost produkcji i kosztu krańcowego pociąga za sobą wzrost przeciętnego kosztu całkowitego.

Trygonometryczną miarą przeciętnego kosztu całkowitego dla dowolnej wielkości produkcji jest tangens nachylenia linii prostej, łączącej początek układu współrzędnych z dowolnym punktem na krzywej kosztów całkowitych.

Trygonometryczną miarą kosztu krańcowego jest tangens stycznej do funkcji koszt w całkowitych. Zwróćmy uwagę, że dla wielkości produkcji, dla której koszty krańcowe równe są kosztom przeciętnym styczna i sieczna pokrywają się ze sobą.

A zatem, dla wielkości produkcji, dla której przeciętne koszty całkowite osiągają swój najniższy poziom (Qb) zrównują się one z kosztem krańcowym.

Współzależność wszystkich rodzajów kosztów

Wszystkie te krzywe kosztów reprezentują różne sposoby patrzenia na tę samą rzecz. Przypuśćmy, że wiedziałeś, jakie będą twoje koszty całkowite dla każdej wielkości produkcji. Czy mógłbyś wykreślić twoją krzywą kosztów całkowitych? Na pewno tak. Ale co z innymi krzywymi? Czy mógłbyś wyliczyć twoje całkowite koszty stałe, albo średnie koszty stałe? Albo twoje całkowite lub średnie koszty zmienne? Na pewno bez problemu! Pomyśl o tym przez chwilę, a zobaczysz, że:

1. Twoja krzywa całkowitych kosztów mówi ile wynoszą twoje koszty stałe. Gdy twoja produkcja równa się zero, to twoje koszty stałe są twoimi kosztami całkowitymi.

2. Krzywa kosztów całkowitych mówi ci ile wynoszą twoje koszty zmienne. Jeżeli odejmiesz twoje koszty stałe od kosztów całkowity dla każdego poziomu produkcji, to ta otrzymana różnica jest twoimi kosztami zmiennymi.

3. Twoje koszty całkowite mówią ci również ile wynosi twój koszt krańcowy. Wystarczy od kosztu całkowitego produkcji X jednostek odjąć koszt całkowity produkcji ilości x-1 jednostek. Otrzymana różnica to nic innego tylko twój koszt krańcowy.

Łatwo jest dowiedzieć się, jakie są koszty zmienne i koszty krańcowe, gdy znane są koszty całkowite. A co z kosztami przeciętnymi? To również jest łatwe.

Żeby przełożyć koszty całkowite na średnie, wystarczy podzielić wielkość dowolnego kosztu przez liczbę jednostek produktu. Jeżeli produkt wynosi 10 jednostek a całkowite koszty równają się 900 zł, to średnie koszty całkowite wyniosą 90 zł jeśli koszty stałe wynoszą 150 zł to średnie koszty stałe wyniosą 15 zł natomiast średnie koszty zmienne wyniosą (900-150): 10 = 75 zł.

Przypuśćmy, że wiesz, ile wynoszą koszty stałe, jak też ile wyniósłby koszt krańcowy przy powiększeniu produkcji od zera do jednej jednostki z jednej do dwóch z dwóch do trzech itp. Czy mógłbyś wtedy wyliczyć koszty całkowite i zmienne i koszty przeciętne?

Oczywiście! Koszty zmienne na każdym etapie produkcji równałyby się sumie wszystkich kosztów krańcowych aż do obecnego poziomu produktu. Po dodaniu do nich kosztów stałych, otrzymałbyś całkowity koszty produkcji na obecnym poziomie!

Wynika z tego ze wszystkie te krzywe kosztów muszą być ze sobą w jakiś sposób powiązane a my przez cały czas oglądamy ten sam obraz tylko przedstawiany na coraz to inny sposób

Mapa kosztów

Po zapoznaniu się z różnymi rodzajami kosztów produkcji, możemy zadać sobie dwa zasadnicze pytania:

• Czy ktokolwiek jest w stanie zapamiętać te wszystkie krzywe?

• Czy krzywe te są nam do czegokolwiek potrzebne?

Szczegółowe odpowiedzi na drugie pytanie znajdziemy w dalszych wykładach. W odpowiedzi na pierwsze pytanie pomoże nam zamieszczony powyżej rysunek zwany mapą kosztów, przedstawiający trzy podstawowe rodzaje kosztów: przeciętne, całkowite i krańcowe. Mapa kosztów jest syntetycznym obrazem związków pomiędzy różnymi kategoriami kosztów. Ilustruje ona wszystkie, poznane przez nas dotychczas zależności.

Rys Mapa kosztów

KC KC

KZ

KS c

a KZ

b

a

KS

Produkcja

Kk Kpc

Kk Kpz

Kpc =min

Kpz=min

Kk=min

Qa Qb Qc Q

Na przedstawionej powyżej mapie kosztów mamy zaznaczony kształt i przebieg wszystkich interesujących nas funkcji kosztów. W górnej części przedstawiono koszty całkowite, zaś w dolnej odpowiadające im koszty przeciętne. Wszystkiemu „przodują” określające kształt pozostałych funkcji, wyprowadzone z prawa malejących przychodów, koszty krańcowe.

Dla dalszych analiz szczególne znaczenie mieć będą wielkości produkcji Q, przy których w dolnej części mapy, koszty krańcowe oraz przeciętne koszty zmienne i całkowite (z wyjątkiem Kps) osiągają minimum.

Na naszej mapie kosztów, mamy trzy takie, leżącej na jednej wspólnej linii kosztu krańcowego punkty A, B i C, którym odpowiada rosnąca wielkość produkcji Q_A < Q_B < Q_C.

Nie ulega wątpliwości, że w każdym z leżących punktów przyjmujemy inne kryterium optymalizacji.

W punkcie A, produkcja Q_A zapewnia firmie najmniejszy koszt krańcowy Kk=min . Przy tej wielkości produkcji, produkt krańcowy ΔQ/ΔL=max - ma, zatem miejsce najlepsze wykorzystanie czynnika zmiennego (pracy). W górnej części mapy punktowi temu odpowiadają punkty przegięcia funkcji kosztów zmiennych i całkowitych.

W punkcie B, przy wielkości produkcji Q_B, firma osiąga największy produkt przeciętny Q/L=max, a jednocześnie wytwarza po najniższych przeciętnych kosztach zmiennych. Przy tych rozmiarach produkcji, koszt krańcowy i minimalny koszt przeciętny zmienny, przedstawione w dolnej części rysunku, są sobie równe Kk=Kpz=min. Przy tym poziomie produkcji w górnej części rysunku, styczna w tym punkcie do krzywej kosztu zmiennego i sieczna mają to samo nachylenie a więc pokrywają się ze sobą.

Produkcja, jak pamiętamy polega na łączeniu ze sobą czynników wytwórczych w oparciu o znane, dostępne sposoby technologiczne. Koszt zmienny to koszt stosowania tylko czynnika pracy, tymczasem firma ponosi także koszt posiadania i użytkowania czynnika kapitału rzeczowego nie mówiąc o kosztach związanych z utrzymanie firmy w ruchu i dobrej kondycji ( w praktyce: raty kredytowe, koszty administracyjne).Wszystkie te pozycje zawarte są w kategorii kosztów stałych i dopiero, uwzględniający je koszt całkowity przedstawia kompletny obraz kosztu stosowania obu czynników jednocześnie w powiązaniu z wiedzą technologiczną.

W punkcie C przy wielkości produkcji Q_C, firma wytwarza po najniższych przeciętnych kosztach całkowitych Przy tych rozmiarach produkcji, koszt krańcowy i minimalny przeciętny koszt całkowity, przedstawione w dolnej części rysunku, są sobie równe Kk=Kpz=min. Na górnym rysunku w punkcie tym linia wychodząc z początku układu jest styczna do funkcji kosztów całkowitych. Przy tym poziomie produkcji ma miejsce najmniejsze zużycie czynnika pracy i czynnika kapitału.

Zapewniające to wielkości produkcji nazywamy optymalnymi a stan taki nazywamy optimum technologiczne (najlepszy ze wszystkich), gdyż każde zwiększenie bądź zmniejszenie rozmiarów produkcji prowadzić będą do wzrostu kosztów.

Zmiany kosztów pod wpływem czynników zewnętrznych

Dotychczasowa analiza kosztów przedsiębiorstwa opierała się na założeniu ceteris paribus, obejmującym stałość czynników niezależnych od przedsiębiorstwa. Wpływ na koszty ma jednak wiele różnych czynników zewnętrznych.

W krótkim okresie przebieg krzywych kosztów zależy ceteris paribus - od prawa nieproporcjonalnych przychodów, a w długim okresie od efektów skali produkcji. Natomiast zmiana ich położenie tych krzywych, a więc zmiana ich poziom dla danej ilości produkcji, zależy od następujących czynników zewnętrznych:

- cen czynników produkcji, a więc cen dóbr produkcyjnych, płac czynszów odsetek od kredytów itd.;

- rozliczeń przedsiębiorstwa z budżetu państwa, jak podatki, cła, dotacje.

Wpływ cen czynników na poziom kosztów krótkookresowych przedsiębiorstwa zależy od tego, czy dotyczą one czynników stałych czy zmiennych

Koszty Kk1 Kk0 Kpc1

Kpc0

Kpz11

Kpz0

Q

Jest rzeczą oczywistą, że zmiany cen, które musimy płacić za zmienne czynniki produkcji, zmieni koszt krańcowy i przeciętny

1. Jeżeli zmienne czynniki produkcji drożeją (lub stają się mniej produktywne), to krzywa kosztów krańcowych przesuwa się do góry wraz z nią przesuwa się krzywa przeciętnych kosztów zmiennych.

2. Jeżeli czynniki tanieją (lub stają się bardziej produktywne), to koszt krańcowy się obni­ży, wraz z nim obniży się przeciętny koszt zmienny.

Natomiast pionowa odległość pomiędzy kosztami całkowitymi i zmiennymi pozostanie taka sama.

Jeżeli natomiast rośnie cena jednego z stałych czynników (np. odsetki, czynsz itp., to w góry przesunie się krzywa kosztu stałego i kosztu przeciętnego, natomiast krzywe kosztu, krańcowego zmiennego i przeciętnego kosztu zmiennego nie zmienią położenia.

Rys Mapa kosztów w warunkach zmiany kosztu stałego

Kk Kk0 Kpc1

Kpc Kpc0

Kpz

Kpz0

Q

Które z krzywych są najbardziej użyteczne?

W związku z tym powstaje pytanie, do czego te wszystkie krzywe mogą się nam przydać no i które z nich są dla nas są najbardziej uży­teczne? Na pytania te nie ma jednoznacznej odpowiedzi. Wszystko zależy od tego, co chcemy się dowiedzieć?

Krzywe całkowite powiedzą natychmiast, jakie będą koszty całkowite na każdym poziomie produkcji. O kosztach jednostkowych poinformują krzywe kosztów przeciętnych. Z nich dowiemy się, jaki koszt stały i zmienny zawarty jest w każdej jednostce na każdym poziomie produkcji, przy jakiej wielkości produkcji są one najniższe,

Jeśli chcemy dowiedzieć się o ile wzrośnie koszt, gdy powiększmy dzienną produkcję o jedną jednostkę, to poinformuje nas o tym koszt krańcowy. Jest bardzo ważna informacja, bo jest ona niezbędna do ustalenie najbardziej opłacalną, czyli optymalną wielkość produkcji, to znaczy taka, która pozwoli firmie osiągnąć maksymalny zysk lub zminimalizować stratę.

Same koszty nie wystarczą do jej wyznaczenie, bo nie wiemy, jakie będą osiągane z każdej dodatkowej sprzedanej jednostki przychody.

Gdy krańcowy przychód jest większy od kosztu krańcowego każda dodatkowo sprzedana jednostka poprzynosi firmie nadwyżkę, a zatem zwiększanie produkcji jest opłacalne, pod warunkiem, że całkowite przychody pokrywają w całości całkowite koszty. Jeśli są one od nich niższe, to kierownictwo firmy ma do wyboru albo przestawić się na produkcję cze­goś innego, co pozwalałoby je w całości, albo pracować ze stratą licząc na poprawę sytuacji, albo zawiesić nas jakiś czas działalność i ponosić koszty stałe Wreszcie może ono podjąć decyzję o całkowitej likwidacji działalność. Wszystkie podejmowane w oparciu o koszty decyzje rzutować będą na wielkość podaży firmy i gałęzi.

Zanim jednak będziemy mogli posunąć się dalej ze zro­zumieniem teorii podaży rynkowej oferowanej przez pojedyncze przedsiębiorstwo i cała gałąź, musimy dowiedzieć się więcej o przychodach tworzonych przez wynikające z popytu rynkowego na twój produkt ilości i ceny.

Przeczytasz o tym w następnych wykładach, ale zanim to nastąpi musisz jeszcze zapoznać się teorią kosztów w długim okresie. To ona właśnie będzie przedmiotem następnego wykładu.

Podsumowanie i synteza

1. Mikroekonomia zajmuje się przeważnie wyjaśnianiem jak działa mechanizm proces rynkowy: Wymaga to zrozumienie zjawiska podaży i popytu opartego o ceny mechanizmu alokacji.

2 Koszty produkcji stanowią istotny składnik optymalizacji decyzji podejmowa­nych przez producenta. Znajomość kształtowania się kosztów pozwala okre­ślić rozmiary produkcji maksymalizujące wynik finansowy producenta.

3. Rozumienie podaży oznacza rozumienie kosztów produkcji, ponieważ podaż produktu, (czyli ilości, które będą oferowane do sprzedaż po różnych cenach proponowanych za produkt na rynku) jest wyznaczana przez koszt produkcji danego wyrobu. Im wyższe są koszty, tym ceteris paribus mniejsza jest podaż.

4 Koszt ekonomiczny obejmuje: koszty księgowe (udokumentowane wydatki) oraz koszty alternatywne (własnego kapitału i pracy właściciela)i ryzyka.

5 Szczególne znaczenie ma analiza kształtowania się kosztów produkcji w krótkim i w długim okresie czasu. Z tego punktu widzenia w krótkim okresie koszty dzieli się na stałe i zmiennie całkowite i krańcowe.

6 Koszt czynników zmiennych wzrasta ze wzrostem produkcji, ponieważ wiąże się to ze zwiększeniem ich zużycia.

7. W krótkim okresie, z definicji, przedsiębiorstwo nie może zmienić nakładów kapitału i ziemi, lecz może zmienić wielkość zatrudnienia. Koszt zatrudnienia jest, zatem w krótkim okresie kosztem zmiennym, koszt pozostałych czynników jest kosztem stałym.

8. Koszty całkowite przedsiębiorstw a składają się z kosztów stałych (ogólnych), które należy płacić nawet wów­czas, gdy się nic nie produkuje oraz z kosztów, zmien­nych, które rosną, gdy wzrasta wielkość produkcji. Koszty stałe plus koszty zmienne to koszty całkowite produkcji w krótkim okresie.

9. Koszty całkowite są najniższe, gdy nic się nie produkuje. Koszty te w stosunku do wzrostu produkcji rosną początkowo wolno, potem coraz szybciej.

10. W krótkim okresie oprócz kosztów stałych i zmiennych i całkowitych w analizie ekonomicznej się ponadto następujące kategorie kosztów koszt krańcowy, czyli przyrost kosztu całkowitego wynikająca ze zwiększenia rozmiarów produkcji o jednostkę. Koszty przeciętne, które otrzymujemy dzieląc koszty stałe, zmienne i całkowite przez wielkość produkcji. Analiza wszystkich kategorii kosztów służy do wyjaśnienia, czym kierują się firmy przy ustaleniu optymalnych to znaczy przynoszących najkorzystniejsze wynik finansowy rozmiarów produkcji.

11. Istniej funkcyjny związek pomiędzy wielkością produkcji a poziomej kosztów całkowitych. Związek ten nie jest wprost proporcjonalny. Przy niewielkim poziomie produkcji koszty rosną mniej niż proporcjonalnie do rozmiarów produkcji, ale gdy produkcja przekroczy pewien poziom zaczynają rosnąć więcej niż proporcjonalnie.

12. Całkowity koszt zmienny przy niewielkim poziomie produkcji wzrasta mniej niż proporcjonalnie do wzrostu produk­cji, lecz po przekroczeniu pewnego poziomu rośnie bardziej niż proporcjonalnie

13. Dynamika kosztów całkowitych uzależnia jest od dynamiki kosztów zmiennych, a te zależą od dynamiki kosztów krańcowych. Gdy koszty krańcowe rosną koszty całkowite rosną bardziej niż proporcjonalnie, gdy koszty krańcowe maleją koszty całkowite rosną mniej niż proporcjonalnie.

14. Koszt krańcowy to koszt wytworzenia dodatkowej jednostki produkcji. Jest to przyrost kosztów związany ze zwiększeniem produk­cji o jednostkę. Dynamika kosztów krańcowych pozostaje pod wpły­wem prawa nieproporcjonalnych przychodów.

15. W krótkim okresie, przy stałej ilości niektórych czynników produkcji, działa prawo nieproporcjonalnych przychodów. Początkowo produkcja rośnie szybciej w porównaniu ze wzrostem nakładów - występuje efekt rosnących przychodów (produkcyjność krańcowa zmiennych czynników wytwórczych rośnie). Od pewnego punktu produkcja rośnie coraz wolniej ze wzrostem nakładów - występuje zjawisko malejących przychodów (produkcyjność krańcowa zmiennych czynników wytwórczych maleje).

16. Koszty krańcowe kształtują się pod wpływem działania prawa nieproporcjonalnych przychodów. Gdy produkt krańcowy rośnie, koszty krańcowe maleją, gdy od pewnego poziomu pro­dukcji produkt krańcowy zaczyna maleć koszt krańcowy zaczyna rosnąć. Powyższe efekty sprawiają, że krótkookresowa krzywa kosztów krańcowych, przyjmują kształt litery U.

17. Oprócz kosztów stałych zmiennych i krańcowych w analizach ekonomicznych posługujemy się również pojęciem kosztów przeciętnych. Koszt przeciętny to koszt całkowity podzielony przez wielkość produ­kcji.

18. Koszt przeciętny, podobnie jak koszt całkowity, możemy podzielić na koszt stały i koszt zmienny i całkowity. W związku z tym rozróżniamy przeciętne koszty stałe Kps przeciętne koszty zmienne, Kpz, oraz przeciętne koszty całkowite Kpz.

19. Przeciętny koszt stały zmniejsza się wraz ze wzrostem wielkości produkcji i spadają asymptotycznie do zera. Powodem tego jest fakt, iż przypada on na coraz większą liczbę wytworzonych jednostek produkcji.

20. Krzywe przeciętnych kosztów zmiennych przyjmują kształt litery U. Ich dynamika jest zależna od wielkości kosztu krańcowego. Gdy koszt krańcowy maleje wraz z nim maleje przeciętny koszt zmienny. Gdy koszt krańcowy zaczyna rosnąć, ale jest mniejszy od przeciętnego ten ostatni jeszcze maleje. Gdy rosnący koszt krańcowy zrównuje się ze spadającym kosztem przeciętnym, ten ostatni osiąga swoje minimum. Dalszemu wzrostowi kosztu krańcowego towarzyszy rosnący, ale mniejszy od niego przeciętny koszt zmienny koszt. Cechą charakterystyczną funkcji przeciętnego kosztu zmiennego jest to, że w punkcie minimum jest on równy rosnącemu kosztowi krańcowemu.

21. Funkcja przeciętnego kosztu całkowitego ma podobny kształt i przebieg. Jest to, bowiem funkcja kosztu zmiennego przesunięta do góry o wielkość przeciętnego kosztu stałego Przeciętne koszty całkowite spadają wraz ze spadkiem kosztu krańcowego. Spadają również na odcinku rosnącego kosztu krańcowego do momentu, w którym nie nastąpi zrównanie rosnącego kosztu krańcowego z malejącym kosztem przeciętnym. W punkcie tym osiągają swoje minimum. Dalszemu wzrostowi produkcji towarzyszyć będą rosnące, ale niższe krańcowych przeciętne koszty całkowite. Wzrost przeciętnych kosztów całkowitych ma miejsce przy produkcji większej niż w przypadku kosztów zmiennych.

22. Współzależności między zmianami kosztów są takie, że Kps spada, natomiast krzywa Kk przecina krzywe Kpz i Kpc w punktach, w których te ostatnie osiągają minimum.

23. Ponieważ przeciętny koszt stały maleje coraz bardziej odległość między funkcją przeciętnych kosztów całkowitych i zmiennych zmniejsza się wraz ze wzrostem produkcji.

24. Znając przebieg krzywych funkcji kosztów całkowitych i zmiennych możemy dla każdego poziomu produkcji trygonometrycznie wyznaczyć wartość kosztów przeciętnych i marginalnych dla dowolnej wielkości produkcji.

25. Koszt przeciętny to tangens nachylenie linii (siecznej) łączącej początek układu z wybranym punktem na krzywej kosztu całkowitego. Koszt marginalny to wartość tangensa nachylenie linii stycznej do wybranego punktu na krzywej kosztu całkowitego.

26. Między przeciętnym kosztem zmienny i produktem przeciętny­m, a także między kosztem krańcowym i produktem marginalny istnieje zależność odwrotna.

27. Wraz ze wzrostem wielkości produkcji koszty kształtują się następująco: - Kk początkowo zmniejsza się a następnie zaczyna wzrastać KZ, które są sumą kosztów krańcowych począt­kowo rosną wolniej od wzrostu produkcji a następnie zaczynają wzrastać szybciej aniżeli produkcja. Podobnie zachowują się koszty całkowite, jako że są to koszt zmienne przesunięte do góry wielkość kosztów stałych ­KS, które nie ulegają zmianie -Kps nieustannie zmniejsza się. Kpz początkowo spada, a później zaczynają wzrastać podobnie zachowują się Kpc .

28. Charakterystyczny kształt litery, U jaki przybierają krzywe kosztów przeciętnych oraz kosztów marginalnych w krótkim okresie czasu odzwierciedleniem prawa malejących przychodów w produkcji.

29. W okresie długim można zmienić nakłady wszystkich czynników produkcji. Rozróżnianie kosztów stałych i zmiennych traci wtedy sens.

WYKORZYSTANA LITERATURA

1 Begg D. i inni :Ekonomia PWE 1993 1992 t.1 roz. 6 , 7

2. Bowden E Bowden J Ekonomia Fundacja Innowacja Warszawa, 2002 roz.23

3. Czarny B. i inni:Podstawy ekonomii. PWE1998 roz. 5

4. Czarny E. Nojszewska E.: Mikroekonomia PWE1997 roz. 2

5. Dębniewski G i inni: Mikroekonomia.Wybrane problemy do wykładów i ćwiczeń ART. Olsztyn 1997 roz. 9

6. Encyklopedia Internetowa „Wiem ” Portal ONET

7. Encyklopedia Internetowa „Internautica ” Portal INTERIA

8. Encyklopedia Internetowa PWN Portal W.P

9. Encyklopedia Marketingu Portal ONET

10. Ekonomia Portal ODEON

11. Kamerschen D .i inni :Ekonomia . Fundacja Gospodarcza NSZZ ”Solidarność „ Gdańsk 1991 roz. 20, 21

12. Leksykon Buisnessu Portal ONET

13 Marks S.G Samuelson W.H :Ekonomia menedżerska PWE 1998 roz. 6 , 7

14. Matkowski Z. Podstawy ekonomii. Mikroekonomia.WSZiP im. B.Jańskiego 1999 roz.

15. Niemczycki K.: Ekonomia Wyższa Szkoła Zarządzania PRET S.A. Warszawa 1996

15. Nojszewska E .Podstawy ekonomii W.S.P 1995 roz. 5

16. Nojszewska E.Szamrej Z. Mikroekonomia kurs podstawowy. Fundacja naukowa Taylora SGH Zeszyt nr 14

16. Piasecki B. :Ekonomika i zarządzanie małą firmą PWN 1998 roz.

17. Podstawy Ekonomii (red.. R.Milewski). PWN1998 roz. 6

18. Portal Onet Bizes „ Firma ”

29 Portal Odeon

20.Próchnicki L. Zrozumieć gospodarkę Makroekonomia Zachodniopomorska Szkoła Biznes Szczecin 1999 roz. 1

21. Rekowski M.:Wprowadzenie do mikroekonomii Polsoft-Akademia Poznań 1993 ss.133-138; 171174

22. Samuelson P. Nordhaus W.Ekonomia PWE 1995 rozdz.20

23. Stanlake G. F. Podstawy ekonomii W.S. i P. 1992 roz. 7

24. Varian H. Mikroekonomia Kurs średni. Ujęcie nowoczesne PWN.1999 roz. 17, 19,20

25. Wisznewski Z. Mikroekonomia współczesna. Syntetyczne ujęcie Olympus 1994 roz.

ĆWICZENIA, ZADANIA, TEST

Funkcja produkcji przedstawia:

a) maksymalną wielkość produkcji, którą można uzyskać z danej ilości czynników produkcji,

b) zależność funkcjonalną między czynnikami produkcji i wielkością produkcji,

c) minimum produkcji, jaka winna być uzyskana z dostępnych czynników produkcji,

d) żadna z powyższych możliwości.

e) wszystkie prawidłowe

Produkt marginalny jest:

a) dodatkową jednostką produktu całkowitego,

b) jednostką produkcji uzyskaną w czasie ponadnormatywnym pracy,

c) zmianą wielkości produktu całkowitego wynikającą z zastosowania dodatkowej jednostki czynnika zmiennego nakładów,

d) żadnym z powyższych stwierdzeń.

e) wszystkie

Produkt marginalny jest:

a) zmianą wielkości produktu całkowitego wynikającą z zastosowania dodat­kowej jednostki czynnika zmiennego nakładu;

b) dodatkową jednostką produktu całkowitego;

c) jednostką produkcji uzyskaną w dodatkowym czasie pracy;

d) żadne z powyższych stwierdzeń.

e) wszystkie

Jeżeli krzywa produktu całkowitego stale rośnie to:

a) produkt przeciętny także rośnie,

b) produkt marginalny rośnie,

c) produkt marginalny ma wartość dodatnią,

d) nie zachodzi żadna z wymienionych zależności.

e wszystkie

Jeżeli krzywa produktu całkowitego stale rośnie, to:

a) produkt marginalny ma wartość dodatnią;

b) produkt marginalny rośnie;

c) produkt przeciętny także rośnie;

d) nie zachodzi żadna z wymienionych zależności.

e) wszystkie

Produkt przeciętny jest maksymalny wówczas, gdy:

a) produkt marginalny jest maksymalny,

b) produkt marginalny równa się produktowi przeciętnemu,

c) produkt całkowity jest maksymalny,

d) produkt marginalny ma wartość zero.

e) żadna

Produkt przeciętny jest maksymalny, gdy:

a) produkt marginalny wynosi zero;

b) produkt całkowity jest maksymalny;

c) produkt marginalny jest maksymalny;

d) produkt marginalny jest równy produktowi przeciętnemu.

e) żadna

Działanie prawa malejących przychodów jest widoczne wówczas, gdy:

a) przyrost produktu całkowitego jest ujemny ;

b) produkt przeciętny nie zmienia się;

c) produkt marginalny zaczyna maleć;

d) produkt marginalny ma wartość ujemną.

e) żadna

Jeżeli krzywa produktu całkowitego stale rośnie, to:

a) produkt marginalny ma wartość dodatnią;

b) produkt marginalny rośnie;

c) produkt przeciętny także rośnie;

d produkt krańcowy maleje a przeciętnyrośn8ie

e nie zachodzi żadna z wymienionych zależności.

Jeżeli produkt marginalny jest większy od zera, a produkt przeciętny spada, to:

a) produkt marginalny jest mniejszy od produktu przeciętnego;

b) produkt marginalny jest większy od produktu przeciętnego;

c) Produkt marginalny jest równy przeciętnemu

d) produkt całkowity maleje;

e) żadna

Jeżeli produkt marginalny jest większy od zera a produkt przeciętny rośnie, wówczas:

a) występuje II etap produkcji,

1. Produkt marginalny jest większy od produktu przeciętnego,

2. Produkt marginalny jest mniejszy od produktu przeciętnego,

3. Produkt całkowity maleje.

4. żadna

e) wszystkie

W punkcie, w którym produkt marginalny zmienia się z rosnącego w malejący, występuje:

a) punkt przegięcia krzywej produktu całkowitego;

b) maksymalny poziom produktu całkowitego;

c) maksymalny poziom produktu przeciętnego;

d) maksymalny poziom produktu krańcowego i przeciętnego

e) żadne z wymienionych zjawisk.

W punkcie, w którym produkt marginalny zmienia się z malejącego w ujemny występuje:

a) maksymalny poziom produktu przeciętnego,

b) maksymalny poziom produktu całkowitego,

3. punkt przegięcia krzywej produktu całkowitego,

4. maksymalny poziom produktu krańcowego

5. żadne z wymienionych zjawisk.

Produkt przeciętny jest maksymalny, gdy:

a) produkt marginalny wynosi zero;

b) produkt całkowity jest maksymalny;

c) produkt marginalny jest maksymalny;

d) produkt marginalny jest równy produktowi przeciętnemu.

e) żadna

Prawo malejących przychodów działa:

a) w przemyśle;

b) w rolnictwie;

c) w całej gospodarce niezależnie od okresu;

d) w całej gospodarce w kresie krótkim.

e) żadna

Działanie malejących przychodów jest widoczne wówczas, gdy:

a) przyrost produktu całkowitego maleje;

b) produkt przeciętny nie zmienia się;

c) produkt przeciętny zaczyna maleć;

d) produkt marginalny ma wartość ujemną. e) żadna

Korzystając z danych w tabeli poniżej oblicz

Nakłady czynnika pracy	Produkt całkowity
0	0
1	20
2	50
3	90
4	100
5	110
6	105

1. Produkt marginalny trzeciej jednostki czynnika pracy wynosi:

a) 90 b) 100, c) 20, d) 40, e) żadna

2. Produkt marginalny ma wartość ujemną dla czynnika pracy:

a) czwartego, b) piątego, c) szóstego, d) żadnego z wymienionych.

3 Produkt przeciętny czterech czynników pracy ma wartość:

a) 20, b) 25, c) 30, d) trudno odpowiedzieć, bez znajomości ceny produktu całkowitego.

Prawo malejących przychodów krańcowych mówi, że gdy nakłady co najmniej jednego czynnika wytwórczego są stałe, a coraz większe ilości zmiennego czynnika wytwórczego są :

1. Dodawane w procesie produkcji, wówczas poczynając od pewnego punktu, przyrosty poziomu produkcji zaczną się zwiększać

2. Dodawane w procesie produkcji, wówczas poczynając od pewnego punktu, przyrosty produkcji zaczną się zmniejszać

3. Wyłączane z udziału w procesie produkcji, wówczas poczynając od pewnego punktu, wielkość obniżek poziomu produkcji zacznie się zwiększać

4. Wyłączne z udziału w procesie produkcji, wówczas, poczynając od pewnego punktu, wielkość obniżek poziomu produkcji zacznie się zmniejszać

5. żadne z powyższych nie jest prawdziwe

Koszty

1. Przedstaw różne klasyfikacje kosztów.

2. Jakie rodzaje kosztów ponosi przedsiębiorstwo w krótkim okresie? Jakie jest kryterium ich wyodrębnienia?

3. Od czego zależy nieliniowy przebieg krzywej kosztu całkowitego?

4. Jakie czynniki powodują zmianę kosztów w krótkim okresie i przesunięcie krzywych kosztów Kk , Kpc , Kpz,

5. Wyjaśnij, dlaczego krótkookresowy koszt przeciętny ma kształt litery U?

Zadanie 3 Wiedząc, że w firmie „ bajer „ przy wielkości produkcji = Q, zatrudnienie ( L ) i koszty całkowite ( KC ) wynoszą odpowiednio tyle, ile podano w tablicy,

Q	0	40	80	110	130
L	0	15	30	50	65
KC	100	380	700	970	1 170

Oblicz :

1. Koszty stałe

2. Koszty zmienne

3. koszty krańcowe

4. Przeciętne koszty całkowite

Zadanie Poniższe dane charakteryzują sytuację firmy i warunki jej działania.

Wielkość sprzedaży wyrobu A	2000
Wielkość sprzedaży wyrobu B	250
Cena wyrobu A	3
Cena wyrobu B	10
Wynagrodzenie za pracę	3000
Składka ZUS	45%
Amortyzacja	700
Opłata za wieczyste użytkowanie gruntu	50
Dzierżawa budynku	650
Surowce do produkcji	2750
Stopa procentowa	8%
Rynkowa wartość majątku firmy	45 00
Podatek od zysku	40%

Oblicz :

1. Utarg

2. Koszty stałe

3. Koszty zmienne

4. Koszty alternatywne

5. Zysk ekonomiczny

6. Zysk księgowy brutto

7. Zysk księgowy netto

8. Jaką strategię powinni przyjąć właściciele tej firmy? W odpowiedzi postaraj się abstrahować od innych wielkości niż podane w tabeli.

Uzupełnij następującą tabelę i przedstaw graficznie krzywe kosztów.

Q KS KZ KC Kk Kps Kpz Kpc

0 45 0

1 45 48

2 45 80

3 45 120

4 45 170

5 45 230

6 45 310

7 45 420

8 45 590

Zadanie Wskaż, jak zmiana poszczególnych rodzajów kosztów wpłynie na położenie każdej z krzywych kosztów (całkowitych, stałych, zmiennych). Czy krzywe te przesuną się do góry, w dół, czy nie zmienią położenia?:

a. Wzrost kosztów stałych:

b krzywa kosztów całkowitych

c. krzywa kosztów zmiennych

d.. krzywa kosztów stałych

Zadania Zastanów się, jak poniższe sytuacje wpłyną na zmianę kosztów i określ, jak w związku z tym zmieni się położenie krzywych kosztów: czy przesuną się one do góry, czy w dół, czy też ich położenie się nie zmieni?

1. Wzrost godzinowych stawek dla pracowników:

1. krzywa kosztów przeciętnych całkowitych

2. krzywa kosztów przeciętnych zmiennych

3. krzywa kosztów przeciętnych stałych

Dwu absolwentów Akademii Ekonomicznej postanowiło uruchomić firmę, w której byłby wytwarzany wyrób X. W związku z tym wykonali kalkulację kosztów dla różnych wariantów rozmiarów produkcji w ciągu miesiąca. Koszty te ilustruje poniższa tablica.

Wielkość produkcji	Koszty
		Najem hali i terenu	Amortyzacja maszyn i urządzeń	Surowce materiały energia	Wydatki ·finansowe	Płace i ubezpieczenia pracowników	Ubezpieczenie firmy
0	100	95	-	20		5
10	100	95	30	20	55	5
20	100	95	60	20	75	5
30_	100	95	90	20	90	5
40_	100	95	120	20	100	5
50	100	95	160	20	130	5
60	100	95	200	20	260	5

1. Dokonaj pogrupowania kosztów na stałe i zmienne i całkowite Oblicz koszt przeciętny zmienny, koszt przeciętny całkowity oraz koszt marginalny.

2. Wykreśl kształtowania się kosztów zmiennych przeciętnych, kosztów całkowitych przeciętnych i kosztów marginalnych.

3. Określ punkt optimum technologicznego firmy.

TEST WYBORU KOSZTY PRODUKCJI

W krótkim okresie wzrost kosztów przeciętnych całkowitych produkcji jest spowodowany przez:

a) wzrost cen czynników produkcji;

b) przesunięcie się krzywej podaży produktu na lewo;

c) brak możliwości poszerzenia wielkości zakładu i jego wyposażenia tech­nicznego;

d) żadna z wymienionych przyczyn.

e) wszystkie

Jeżeli koszt marginalny jest mniejszy niż koszt całkowity przeciętny, to krzywa kosztu całkowitego przeciętnego jest:

a) opadająca;

b) rosnąca;

c) trudno stwierdzić bez dodatkowych informacji..

d) żadna

e) wszystkie

Dla jakiego rodzaju kosztów spośród wymienionych krzywa kosztu prze­ciętnego stale maleje pod wpływem wzrostu produkcji:

a) koszty zmienne; b) koszty marginalne; c) koszty stałe; d) koszty całkowite. e) żadna

Która z wymienionych krzywych kosztów musi opadać pod wpływem wzrostu produkcji, jeśli koszt marginalny znajduje się poniżej ich wartości?

a) krzywa kosztu stałego przeciętnego;

b) krzywa kosztu zmiennego przeciętnego;

c) krzywa kosztu całkowitego przeciętnego;

d) wszystkie przytoczone.

e. żadna ­

Które z wymienionych zdarzeń obniży przeciętny koszt stały?

a) obniżka stopy procentowej kredytów;

b) wzrost produkcji;

c) spadek kosztów surowca;

d) podwyżka cen wytworzonego produktu; e) obniżka czynszu dzierżawnego;

e) obniżka cen opakowań.

Które z podanych stwierdzeń jest prawdziwe?

a) jeżeli działa prawo malejących przychodów, koszt marginalny zaczyna rosnąć;

b) gdy produkt marginalny jest rosnący, koszt marginalny maleje;

c) jeżeli produkt marginalny jest malejący, koszt marginalny rośnie;

d) wszystkie przytoczone powyżej.

e) żadna

Jeśli koszty stałe rosną to

a. Przeciętne koszty zmienne maleją

b. krzywa kosztów krańcowych, przeciętnych zmiennych i całkowitych przesuwają się w górę,

c. Krzywa całkowitych kosztów przeciętnych przesuwa się w górę,

d. Koszt krańcowy rośnie

e. Krzywa kosztu przeciętnego całkowitego przesuwa się w dół

W procesie produkcji minimum kosztu marginalnego występuje wówczas, gdy produkt marginalny znajduje się w punkcie:

a) zerowym;

b) minimalnym;

c) maksymalnym;

d) o wartości ujemnej

e) żadna

Którą z wymienionych krzywych krótkookresowa krzywa kosztu krańcowego przecina w punkcie minimum?

a. krzywą kosztu przeciętnego zmiennego

b. krzywą kosztu stałego

c. krzywą kosztu przeciętnego całkowitego

d. krzywą kosztu całkowitego

e. żadną

Które z poniższych twierdzeń jest prawdziwe?

a. przeciętny koszt całkowity równa się sumie kosztu zmiennego i stałego podzielonej przez wielkość produkcji

b. koszt krańcowy równy jest sumie mianie kosztów zmiennych , podzielonej przez zmianę poziomu produkcji

c. przeciętny koszt stały równa się zmianie kosztów stałych, podzielonych przez zmianę wielkość produkcji

d. przeciętny koszt zmienny równy jest sumie kosztów zmiennych, podzielonej przez zmianę poziomu produkcji.

e. wszystkie odpowiedzi są prawidłowe

Jeżeli wyprodukowanie Q = 1,2, 3 jednostek produktu zwiększa koszty o wielkość 0 2, 4, 6 zł, wtedy koszty krańcowe:

a. są stałe b. rosną c. spadają. wynoszą odpowiednio : 2, 4, 6 zł e. Nie można ich obliczyć na podstawie tych danych

Jeżeli krzywa kosztów krańcowych leży pod krzywą całkowitych kosztów przeciętnych, oznacza to, że

a. koszty krańcowe musza spadać

b. koszty krańcowe musza rosnąć

c. przeciętne koszty całkowite muszą spadać

d. przeciętne koszty całkowite musza rosnąć

e. żadna

W krótkim okresie, gdy produkcja rośnie

a. koszty całkowite zawsze krosna

b. koszty krańcowe zawsze rosną

c. koszty krańcowe zawsze maleją

d. gdy koszty przeciętne rosną, koszty krańcowe maleją

e. gdy koszty krańcowe maleją koszty przeciętne rosną

Przy produkcji, dla której przeciętne koszty całkowite są minimalne:

a. przeciętne koszty zmienne są równe przeciętnym kosztom całkowitym

b. koszty krańcowe są równe przeciętnym kosztom stałym

c. koszty krańcowe sa równe przeciętnym kosztom całkowitym

d. koszty stałe są równe zero

e. żadna odpowiedź nie jest dobra

.

Które z poniższych zdarzeń spowoduje spadek przeciętnych kosztów stałych?

a. obniżka cen energii elektrycznej

b. wzrost produkcji

c. podwyżka cen wytwarzanego produktu

d. spadek kosztów surowców

e. żadna odpowiedź nie jest prawidłowa

Które z poniższych zdarzeń spowoduje wzrost przeciętnych kosztów stałych?

a. obniżka cen energii elektrycznej

b. Spadek produkcji

c. podwyżka cen wytwarzanego produktu

d. spadek kosztów surowców

e. żadna odpowiedź nie jest prawidłowa

Którą z wymienionych krzywych krótkookresowa krzywa kosztu krańcowego przecina w punkcie minimum:

1. Krzywą kosztu przeciętnego zmiennego

2. Krzywą kosztu przeciętnego stałego

3. Krzywą kosztu przeciętnego całkowitego

4. Krzywą kosztu całkowitego

5. Krzywe a i c

Koszt krańcowy może się różnić, w zależności od wielkości produkcji, ze względu na :

1. Działanie prawa malejącej użyteczności krańcowej

2. Możliwość wzrostu kosztu alternatywnego czasu producenta

3. Możliwość wzrostu kosztu alternatywnego czasu konsumenta

4. Koszty utopione

5. Działanie prawa nieproporcjonalnych przychodów krańcowych

Przy produkcji, dla której przeciętne koszty całkowite są minimalne:

1. Przeciętne koszty zmienne są równe przeciętnym kosztom całkowitym

2. Koszty krańcowe są równe przeciętnym kosztom stałym

3. Koszty krańcowe są równe przeciętnym kosztom całkowitym

4. Koszty stałe są równe zero

5. Żadna odpowiedź nie jest dobra

Optimum techniczne to wielkość produkcji, przy której:

1. Koszt krańcowy równy jest kosztowi całkowitemu

2. Koszt krańcowy równy jest przeciętnemu kosztowi stałemu

3. Koszt krańcowy równy jest kosztowi całkowitemu

4. Koszt krańcowy równy jest kosztowi przeciętnemu zmiennemu

5. Koszt krańcowy równy jest kosztowi przeciętnemu całkowitemu

Przy produkcji, dla której przeciętne koszty całkowite są minimalne:

a. przeciętne koszty zmienne są równe przeciętnym kosztom całkowitym

b. koszty krańcowe są równe przeciętnym kosztom stałym

c. koszty krańcowe sa równe przeciętnym kosztom całkowitym

d. koszty stałe są równe zero

e. żadna odpowiedź nie jest dobra

.

Jeżeli krzywa kosztów krańcowych leży pod krzywą całkowitych kosztów przeciętnych, oznacza to, że

1. Koszty krańcowe musza spadać

2. Koszty krańcowe musza rosnąć

3. Przeciętne koszty całkowite muszą spadać

4. Przeciętne koszty całkowite musza rosnąć

5. Przeciętne koszty całkowite mogą rosnąć lub spadać, w zależności od tego, czy koszty krańcowe rosną czy spadają

Przy produkcji, dla której przeciętne koszty całkowite są minimalne:

a. Przeciętne koszty zmienne są równe przeciętnym kosztom całkowitym

b. Koszty krańcowe są równe przeciętnym kosztom stałym

c. Koszty krańcowe są równe przeciętnym kosztom całkowitym

d Koszty stałe są równe zero

e. Żadna odpowiedź nie jest dobra

Pionowa odległość pomiędzy krzywą kosztu całkowitego i krzywą kosztu stałego jest graficznym wyrazem:

1. Kosztu krańcowego

2. Przeciętnego kosztu stałego

3. Przeciętnego kosztu zmiennego

4. Przeciętnego kosztu całkowitego

5. Żadna

W krótkim okresie, gdy produkcja rośnie:

1. Koszty całkowite zawsze rosną

2. Koszty krańcowe zawsze rosną

3. Koszty krańcowe zawsze maleją

4. Gdy koszty przeciętne rosną, koszty krańcowe maleją

5. Gdy koszty krańcowe maleją koszty przeciętne rosną

Za okres krótki uważa się taki okres, w którym:

a. ceny są niezmienne

b. ceny i wielkość produkcji są stałe

c. nakład przynajmniej jednego czynnika produkcji jest stały

d. nakłady wszystkich czynników produkcji są zmienne

e. wszystkie

Krańcowy produkt czynnika jest to:

a. jego cena

b. przyrost utargu wywołany jednostkowym przyrostem nakładów wszystkich czynników

c. przyrost produkcji wywołany jednostkowym przyrostem wszystkich czynników produkcji

d. przyrost wielkości produkcji wywołany przyrostem jednego czynnika produkcji

e. żadna

Krzywa kosztów krańcowych (MC):

a. nigdy nie przecina krzywej przeciętnych kosztów zmiennych (Kpz)

b. przecina krzywą przeciętnych kosztów całkowitych (Kpc) w punkcie minimum Kpc

c . przecina krzywą przeciętnych kosztów zmiennych (Kpz) w punkcie maksimum Kpz

4. przecina krzywą przeciętnych kosztów całkowitych (ATC) w punkcie maksimum ATC

5. żadna

Krzywa kosztów krańcowych przedsiębiorstwa to Kk=2q. Całkowite koszty zmienne wytworzenia 10 jednostek produktu wynoszą:

a. 100

b. 245

c. 50

d. 200

e.żadna

ENCYKLOPEDIA INTERNETOWA

Amortyzacji stopa, procentowy wskaźnik zużycia majątku trwałego w procesie produkcji w danym okresie, w stosunku do jego wartości początkowej. Stopa amortyzacji może mieć charakter liniowy, proporcjonalny do normatywnego okresu użytkowania (jest wówczas jednakowa w całym okresie użytkowania) lub degresywny, malejący (spada w miarę upływu czasu).

Analiza długookresowa - dotyczy okresu, w którym mogą się zmieniać wszyst­kie nakłady (wszystkie czynniki produkcji są zmienne, przedsiębiorstwo może inwestować i zmieniać stosowaną technikę produkcji).

Analiza krótkookresowa - zakłada, że niektóre warunki działania firmy są niezmienne. Konsekwencją jest występowanie stałych i zmiennych czynników produkcji.

Czas pracy(work time) przewidziany ustawowo czas, w którym pracownik pozostaje w zakładzie pracy lub poza nim do dyspozycji pracodawcy w celu świadczenia pracy na podstawie umowy o pracę.

Czas ten występuje przede wszystkim jako stanowiona przez prawo norma trwania pracy i w tej też postaci jest on powszechnie stosowany w rozliczeniach między pracownikiem a pracodawcą oraz oceniany jako miara świadczonej pracy.

Czas pracy jest złożoną kategorią ekonomiczną formującą się w gospodarce rynkowej nie tylko według praw rynku, ale także pod wpływem osiągnięć w zakresie produktywności pracy i nacisków ze strony potrzeb społecznych wynikających z cywilizacyjnego i materialnego awansu danego kraju. Jak każda kategoria ekonomiczna wyraża on realne stosunki ekonomiczne, tj. stosunki nawiązujące się między ludźmi w procesie gospodarowania i jako taka kategoria kształtuje czas pracy jako termin prawny.

Czas pracy spełnia w gospodarce różnorodne funkcje. Występuje on jako:

• miara nakładu pracy: postęp techniczny i organizacyjny oraz wysoka intensywność pracy sprawiają, że miara ta staje się coraz bardziej pojemna, co oznacza, że społeczeństwa potrzebują coraz mniej czasu na wytworzenie jednostki produktu;

• miara udziału pracownika w tworzeniu produktu społecznego: w takim rozumieniu czas pracy określa ekstensywną normę trwania pracy, tj. długość jej trwania, która w zależności od poziomu technicznego uzbrojenia pracy i jej intensywności określa wielkość pracy;

• czynnik tworzenia wartości; w takim ujęciu czas pracy stanowi ramy, w których w wyniku zespolenia czynników produkcji powstaje wartość. Toteż jako element warunkujący wykorzystanie tych czynników ma on swoją wartość i cenę, które stale rosną;

• czynnik regulujący rytm życia człowieka: rozkład czasu pracy, jego wymiar i usytuowanie w okresie doby (i czasu kalendarzowego) determinuje rytm życia społecznego, rodzinnego i osobistego pracującego człowieka, określa strukturę jego czasu po pracy i sposoby wykorzystania czasu wolnego;

element układu człowiek-praca: w takim ujęciu określa on czas wystawienia pracownika na działanie procesu pracy i warunków jej środowiska, co ma bardzo ważne znaczenie dla zachowania przez niego potencjału zdrowia i sił do pracy.

Czynnik produkcji - dobro używane do wytwarzania innego dobra.

Czynniki produkcji, czynniki wytwórcze, materialne i niematerialne środki niezbędne do prowadzenia procesu produkcji. Materialnymi czynnikami produkcji są ziemia i jej zasoby naturalne oraz kapitał (budynki, maszyny, urządzenia, surowce, materiały itp.). Czynnikami niematerialnymi są praca (siła robocza) i wiedza (know-how).

Funkcja produkcji - określa maksymalną wielkość produkcji przy danych nakładach czynników produkcji.

Funkcja produkcji (function of the production) Zależność między nakładami a wynikami. Ogólny obraz równania funkcji produkcji jest następujący: Q = f(L,K), gdzie: Q symbolizuje wielkość wyników, L symbolizuje nakłady pracy, K - nakłady kapitałowe, a f stanowi wyraz funkcyjnej zależności między nakładami a wynikami produkcji.

Granica możliwości produkcyjnych - linia pokazująca największą produkcję możliwą do uzyskania przy użyciu danego zasobu czynnika zmiennego i czyn­ników stałych.

KNIGHT FRANK HYNEMAN (1885-1972), ekonomista amer.; 1927-55 prof. uniw. w Chicago; przedstawiciel ekonomii neoklasycznej, zajmował się gł. teorią kapitału oraz teorią zysku przedsiębiorcy (Risk, Uncertainty and Profit 1921); wprowadził zróżnicowanie między ryzykiem, które uważał za wielkość mierzalną, i niepewnością — niemierzalną; gł. praca Freedom and Reform: Essays in Economics and Social Philosophy (1982).

Know-how, angielski termin (brak polskiego odpowiednika), oznacza dosłownie "wiedzieć, jak (robić)". Jest to w istocie znajomość tajników produkcji. Jako jedna z form międzynarodowego transferu wiedzy technicznej umowy know-how są kontraktami dotyczącymi innowacji technicznych, zwłaszcza technologi produkcji, nie opatentowanych z różnych powodów.

Umowy know-how są częstokroć połączone z zakupami patentów, które uzupełniają o rozwiązania technologiczne.

Koszty alternatywne (alternative costs, opportunity costs) Termin zapożyczony z ekonomii anglosaskiej. W języku polskim występują jego synonimy, takie jak "koszty utraconych korzyści" czy "koszt poświęconej alternatywy użytkowej". Dotyczy to sytuacji, w której wykorzystując pewien środek w jednym procesie produkcji (lub zakupu) nie jesteśmy w stanie użyć go w innym procesie, w jakim wykorzystanie mogłoby nam przynieść większą korzyść gospodarczą (dochód). Zawsze mamy bowiem do czynienia z wyborem (alternatywą) sposobu wykorzystania określonych środków. W rolnictwie na przykład alternatywnym kosztem pszenicy mogą być buraki cukrowe czy rzepak możliwe do uzyskania z tej samej ziemi, przy tym samym nawożeniu i tej samej obsłudze technicznej. Koszty alternatywne są więc kosztem najlepszego zastosowania w wyniku rezygnacji z jednego rozwiązania na rzecz wyboru innego rozwiązania lub prościej: wartością najbardziej cennej nie wykorzystanej alternatywy - koszt zaniechanych możliwości.

Uwzględnienie kosztów alternatywnych jest nieodzowne przy analizie efektywności alokacyjnej każdego przedsięwzięcia inwestycyjnego, gdyż w przeciwnym razie nie byłoby wiadomo, czy wybrany wariant jest najbardziej opłacalny.

Koszty pracy (labour costs) Koszty osobowe; suma wynagrodzeń wypłacanych zatrudnionym za rzeczywiście wykonaną pracę i kosztów (korzyści) nie związanych bezpośrednio z wykonywaną pracą, poniesionych przez pracodawcę na rzecz pracobiorcy w formie pieniężnej i niepieniężnej. Wynagrodzenia za wykonaną pracę obejmują: płacę według ustalonej stawki za jednostkę obowiązującego czasu pracy, wynagrodzenie za pracę w godzinach nadliczbowych i za przepracowane dni wolne od pracy zgodnie z ustawą o pracy, premie i dodatki wypracowane periodycznie oraz dodatki wyrównawcze. Dodatkowe koszty pracy stanowią zaś bardzo obszerną pozycję zależną od ustawodawstwa pracy, ustawodawstwa socjalnego i obciążeń podatkowych pracodawcy. Zawierają one wiele pozycji, jak np.: wynagrodzenia za dni urlopowe, dni nie przepracowane z powodu choroby czy opieki nad chorym członkiem rodziny, gratyfikacje, nagrody jubileuszowe, dodatki stażowe itp.
W krajach o niedużych świadczeniach socjalnych dodatkowe elementy kosztów pracy stanowią około 30% całości kosztów pracy, a w krajach o rozbudowanych świadczeniach socjalnych udział ten wynosi nawet 50%.

Koszty produkcji (production costs) wyrażone w formie pieniężnej zużycie środków produkcji i zasobów pracy niezbędne w celu pozyskania dobra (produktu) lub usługi. Koszty produkcji obejmują więc wartość pracy uprzedmiotowionej i tę część wartości pracy żywej, która jest bezpośrednio opłacana. Koszty produkcji powiększone o sumę nakładów finansowych (podatek od płac, składki ZUS itp.) stanowią koszty własne przedsiębiorstwa. W skład kosztów własnych wchodzą:

koszty osobowe - przede wszystkim płace i wynagrodzenia, odpisy na zakładowy fundusz socjalny;

koszty rzeczowe (materiałowe) obejmujące głównie koszty amortyzacji, materiałów, paliwa, energii, konserwacji i remontów,

koszty finansowe - wliczane w ciężar kosztów własnych, jak składki ubezpieczeniowe, podatki i opłaty, oprocentowanie kredytów i inne.

Koszty własne są to więc ponoszone przez firmę koszty produkowanego przez nią dobra lub usługi. Koszt własny związany z wytworzeniem wszystkich produktów (usług) nazywa się kosztem całkowitym (pełnym) (total cost). Jest on iloczynem kosztu średniego i ilości wytworzonej produkcji i obejmuje koszty stałe oraz koszty zmienne.

Koszty stałe (fixed costs) to część obciążeń finansowych przedsiębiorstwa, która jest związana z samym faktem jego istnienia oraz z utworzeniem zaplecza przemysłowo-handlowego. Koszty te często określa się mianem kosztów strukturalnych, gdyż zależą one od rozmiarów i struktury firmy. Są one ponoszone niezależnie od wielkości produkcji.

Koszty zmienne (variable costs) są ściśle związane z poziomem i przebiegiem operacji produkcyjnych i handlowych danego przedsiębiorstwa (koszty płac, surowców, energii itd.). Koszty te zależą od poziomu i rytmu przedsiębiorstwa i często też są nazywane kosztami proporcjonalnymi (zmieniają się wraz ze zmianami rozmiarów produkcji).

Koszty bezpośrednie (direct costs) - pozycje kosztów, które można przypisać do produktu za pośrednictwem dokumentów księgowych, a więc dające się dokładnie obliczyć dla danej jednostki kalkulacyjnej. Są to głównie materiały bezpośrednie, robocizna bezpośrednia oraz inne koszty bezpośrednie (np. poniesione na przygotowanie nowej produkcji).

Koszty pośrednie (indirect costs) - pozycje kosztów, które na podstawie dokumentów pierwotnych nie mogą być wprost odniesione na określone jednostki kalkulacyjne. Są one rejestrowane łącznie dla wszystkich wyrobów, a następnie rozliczane na poszczególne wyroby za pomocą narzutu przeciętnego, proporcjonalnego do przyjętego klucza podziałowego tych kosztów. Takim kluczem podziałowym jest najczęściej robocizna bezpośrednia. Koszty pośrednie obejmują koszty wydziałowe i ogólnozakładowe. Są to takie koszty jak: zużycie energii, czynsze, podatki, oświetlenie i ogrzewanie, materiały biurowe, płace nadzoru i administracji, amortyzacja urządzeń, delegacje służbowe itp.

Koszty społeczne (social costs) Szkodliwe następstwa i straty, które ponoszą osoby trzecie lub społeczeństwo w rezultacie działalności gospodarczej poszczególnych producentów i konsumentów (przedsiębiorstw i gospodarstw domowych). Są to straty i przykrości ponoszone przez ludzi nie uczestniczących bezpośrednio w produkcji, konsumpcji lub wymianie danego dobra czy usługi. Te straty i przykrości (uciążliwości) mogą wyrażać się w uszczerbku na zdrowiu fizycznym i psychicznym ludzi, w zniszczeniu lub zmniejszeniu wartości majątku i przedwczesnym wyczerpaniu bogactw naturalnych, deformacji krajobrazu, zmianach klimatu, zakłóceniu środowiska akustycznego itp.

Do kosztów tych zalicza się także koszty utraconych możliwości, tj. te elementy kosztów, które przybierają formę różnego rodzaju marnotrawstwa i braku sprawności (np. wielkie nierentowne inwestycje, sprzedaż zakładów produkcyjnych za "bezcen" itp.). Koszty społeczne w ekonomii noszą nazwę kosztów zewnętrznych, które oznaczają szkodliwe efekty zewnętrzne procesów gospodarowania.

Koszty utopione (utracone) (sunk costs) Koszty poniesione przed przystąpieniem do rozpatrywania danego projektu inwestycyjnego, nawet gdyby w całości lub części służyły temu projektowi. Koszty utracone są nieistotne z punktu widzenia podejmowanych decyzji.

Koszt całkowity - suma wydatków pieniężnych związanych z zatrudnieniem czynników produkcji. Jest on opisany wzorem KC= KS+KZ Koszty całkowite obliczamy sumując iloczyny ilości używanych przez firmę czynników produkcji i ich cen rynkowych

Koszt krańcowy - przyrost kosztów przypadający na jednostkowy przyrost produkcji. Analitycznie oblicza się go za pomocą pierwszej pochodnej funkcji kosztu całkowitego;

Koszty krańcowe (marginal costs) Przyrost kosztów całkowitych konieczny do wytworzenia jednej dodatkowej jednostki produkcji; wzrost kosztów zmiennych związany z ostatnią lub kolejną wyprodukowaną jednostką. Koszty krańcowe dzielą się na malejące, stałe lub wzrastające. Z reguły na początku produkcji koszty te zmniejszają się a następnie rosną powodując wzrost kosztu przeciętnego, tj. średniego kosztu wytworzenia jednostki produkcji (koszt całkowity podzielony przez ilość wytworzonych produktów). Koszty krańcowe wykorzystuje się do obliczania stosunku przyrostu kosztów lub wzrostu czynników oddziałujących na wielkość produkcji.

Koszty krańcowe oblicza się według wzoru:
Kk = ΔKC / Δ Q = Δ KS/ Δ Q + Δ KZ/ Δ Q a ponieważ ΔKS = 0 zatem Kk= Δ KZ/ Δ Q
gdzie:
Kk - koszt krańcowy;
KS - koszt stały
KZ - koszt zmienny;
KC - koszt całkowity;
ΔQ - przyrost ilości produkcji.

Koszty produkcji (production costs) wyrażone w formie pieniężnej zużycie środków produkcji i zasobów pracy niezbędne w celu pozyskania dobra (produktu) lub usługi. Koszty produkcji obejmują więc wartość pracy uprzedmiotowionej i tę część wartości pracy żywej, która jest bezpośrednio opłacana. Koszty produkcji powiększone o sumę nakładów finansowych (podatek od płac, składki ZUS itp.) stanowią koszty własne przedsiębiorstwa. W skład kosztów własnych wchodzą:

1.koszty osobowe - przede wszystkim płace i wynagrodzenia, odpisy na zakładowy fundusz socjalny;

2.koszty rzeczowe (materiałowe) obejmujące głównie koszty amortyzacji, materiałów, paliwa, energii, konserwacji i remontów,

3.koszty finansowe - wliczane w ciężar kosztów własnych, jak składki ubezpieczeniowe, podatki i opłaty, oprocentowanie kredytów i inne.

Koszty własne są to więc ponoszone przez firmę koszty produkowanego przez nią dobra lub usługi. Koszt własny związany z wytworzeniem wszystkich produktów (usług) nazywa się kosztem całkowitym (pełnym) (total cost). Jest on iloczynem kosztu średniego i ilości wytworzonej produkcji i obejmuje koszty stałe oraz koszty zmienne.

Koszt przeciętny - średni koszt wytworzenia jednostki produktu. Rozróżniamy przeciętne koszt stałe, zmienne i całkowite

Koszty stałe (fixed costs) to część obciążeń finansowych przedsiębiorstwa, która jest związana z samym faktem jego istnienia oraz z utworzeniem zaplecza przemysłowo-handlowego. Koszty te często określa się mianem kosztów strukturalnych, gdyż zależą one od rozmiarów i struktury firmy. Są one ponoszone niezależnie od wielkości produkcji.

Koszty zmienne (variable costs) są ściśle związane z poziomem i przebiegiem operacji produkcyjnych i handlowych danego przedsiębiorstwa (koszty płac, surowców, energii itd.). Koszty te zależą od poziomu i rytmu przedsiębiorstwa inaczej mówiąc zmieniają się one wraz ze zmianami rozmiarów produkcji). Kosazt zmienne obliczamy jako sumę kosztów krańcowych

Koszty bezpośrednie (direct costs) - pozycje kosztów, które można przypisać do produktu za pośrednictwem dokumentów księgowych, a więc dające się dokładnie obliczyć dla danej jednostki kalkulacyjnej. Są to głównie materiały bezpośrednie, robocizna bezpośrednia oraz inne koszty bezpośrednie (np. poniesione na przygotowanie nowej produkcji).

Koszty pośrednie (indirect costs) - pozycje kosztów, które na podstawie dokumentów pierwotnych nie mogą być wprost odniesione na określone jednostki kalkulacyjne. Są one rejestrowane łącznie dla wszystkich wyrobów, a następnie rozliczane na poszczególne wyroby za pomocą narzutu przeciętnego, proporcjonalnego do przyjętego klucza podziałowego tych kosztów. Takim kluczem podziałowym jest najczęściej robocizna bezpośrednia. Koszty pośrednie obejmują koszty wydziałowe i ogólnozakładowe. Są to takie koszty jak: zużycie energii, czynsze, podatki, oświetlenie i ogrzewanie, materiały biurowe, płace nadzoru i administracji, amortyzacja urządzeń, delegacje służbowe itp.

Koszty utopione (utracone) (sunk costs) Koszty poniesione przed przystąpieniem do rozpatrywania danego projektu inwestycyjnego, nawet gdyby w całości lub części służyły temu projektowi. Koszty utracone są nieistotne z punktu widzenia podejmowanych decyzji.

Nakłady (expenses, input, outlay) Wszelkiego rodzaju dobra i usługi wykorzystywane w procesie produkcji; rzeczywiste lub potencjalne wydatki związane z działalnością przedsiębiorstwa lub jego strukturą finansową; rzeczy lub czynniki używane w procesie przekształcania (w modelu wkład - zysk): na przykład produkty są wkładem do procesu konsumpcji, którego zyskiem jest użyteczność.

W przedsiębiorstwie wyróżnia się nakłady pracy uprzedmiotowionej i nakłady pracy żywej. Nakłady mogą różnić się od kosztów zakresem czasowym, zasięgiem przedmiotowym oraz podstawą wyceny.

Ogólna produktywność czynników produkcji (total productivity factors) Produktywność wytwarzania nie przypisana jakiemuś czynnikowi z osobna, ale wszystkim łącznie. Wzrost ogólnej produktywności mierzony jest często jako średnia ważona wzrostu przeciętnej produktywności wszystkich zastosowanych czynników wytwórczych.

Okres długi (long period) Czas niezbędny do dostosowania się nabywców do zmian cen, a producentów do zmian warunków działania wymagających zastosowania nowych urządzeń produkcyjnych lub wprowadzenia nowocześniejszych technologii. W makroekonomii termin ten jest używany do określenia czasu, w którym wszystkie ceny, umowy o pracę, stawki podatkowe oraz oczekiwania dostosują się do nowych warunków.
Przeciwstawieniem tego okresu jest okres krótki (short period). Jest to czas, w którym nie jest możliwe pełne dostosowanie się czynników produkcji do zmienionych warunków rynkowych; wielkość zużycia jednego lub kilku rodzajów zasobów nie może ulec zmianie, wskutek czego krótkookresowe koszty mogą być względnie stałe.

Okres krótki (short period). Jest to czas, w którym nie jest możliwe pełne dostosowanie się czynników produkcji do zmienionych warunków rynkowych; wielkość zużycia jednego lub kilku rodzajów zasobów nie może ulec zmianie, wskutek czego krótkookresowe koszty mogą być względnie stałe.

Okres rynkowy (market period) Okres czasu, zwykle bardzo krótki, w którym sprzedający nie są w stanie zmienić ilości produktu lub ilości środka produkcji na rynku. Podaż występująca w tym okresie jest więc zupełnie nieelastyczna.

Płaca (wage) Wynagrodzenie za każdy rodzaj wykonywanej pracy, przyznawane pracownikowi związanemu z pracodawcą umową o najem usług (płaca nominalna). Umowa ta może być wyraźnie sformułowana albo wynikać ze związku podporządkowania lub uzależnienia ekonomicznego. W zależności od charakteru pracobiorcy lub rodzaju wynagradzanych usług, w języku potocznym płaca może przybierać różne nazwy: pensja, pobory, gaża itp.

Rozróżnia się płacę brutto, która stanowi ogólną kwotę płacy i płacę netto, która oznacza płacę brutto pomniejszoną o podatek i składkę ubezpieczeniową oraz inne potrącenia.

Płaca jest dla każdego pracobiorcy decydującym kryterium standardu życia, gdyż pokrywa z niej koszty swego utrzymania. Płaca, którą otrzymuje on od pracodawcy nie zawsze zapewnia mu ten standard. Zależy to od tzw. realnej wartości płacy, czyli od jej siły nabywczej. Dlatego odróżnia się płace nominalne (wyrażone w pieniądzu) od płac realnych (wartość dóbr i usług, które można nabyć za płacę nominalną). Wzrost płac prowadzi do wzrostu siły nabywczej poszczególnego pracobiorcy wówczas, gdy wzrost cen jest niższy od wzrostu płac.

Prawo malejących przychodów (law of diminishing revenues (returns)) Prawo głoszące, że po przekroczeniu pewnego poziomu czynnika zmiennego dalsze zwiększanie jego zużycia przynosi coraz mniejsze przyrosty produkcji (czyli spada jego produktywność krańcowa). Oznacza to, że krańcowy przyrost czynnika zmiennego zmniejsza się po przekroczeniu pewnego punktu. Prawo to działa przy założeniu, że nakłady wszystkich pozostałych czynników produkcji nie ulegają zmianie.

PRAWO MALEJĄCYCH PRZYCHODÓW KRAŃCOWYCH, ekon. prawo proporcji czynników zmiennych, w ekonomii neoklas. określa związek między nakładami czynników produkcji (ziemią, kapitałem i pracą) a wielkością produktu, wyrażoną we właściwych dla niego jednostkach naturalnych (sztukach, tonach, metrach itp.). Przy założeniu, iż ilość jednego czynnika produkcji (np. kapitału) jest stała, a drugiego (np. pracy) jest zmienna, zależność między przyrostem produkcji a przyrostem zatrudnienia, przy danych zasobach kapitału, jest następująca: zwiększenie zatrudnienia początkowo powoduje rosnące przyrosty produkcji (gdyż uzyskiwane są efekty specjalizacji pracy); przy pewnym poziomie zatrudnienia przyrosty produkcji spowodowane wzrostem zatrudnienia osiągają maksimum, a dalsze jego zwiększanie powoduje malejące przyrosty produkcji — wtedy właśnie ujawnia się prawo malejących przychodów krańcowych. Jego działanie jest tłumaczone malejącą ilością czynnika stałego (kapitału), przypadającą na kolejne jednostki czynnika zmiennego (pracy): każdy kolejny zatrudniony ma do dyspozycji coraz mniejszą część kapitału i dlatego jego efekty produkcyjne są coraz mniejsze; nadmierne zatrudnienie może prowadzić nawet do ujemnych przyrostów produkcji. Prawo malejących przychodów krańcowych działa tylko w krótkim okresie, gdy nie można zmienić ilości jednego z czynników produkcji; przestaje działać w długim okresie, gdy przedsiębiorcy mogą dokonywać zmian wielkości nakładów wszystkich czynników produkcji.

Produkcja, pierwsza i najważniejsza faza procesu gospodarowania. Świadoma, celowa i zorganizowana działalność ludzi, polegająca na wytwarzaniu dóbr materialnych i świadczeniu usług dla zaspokojenia ich potrzeb.

Warunkiem prowadzenia produkcji jest połączenie w jednym miejscu i czasie trzech tradycyjnych czynników produkcji: pracy (zatrudnienia), ziemi i kapitału oraz dwóch nowoczesnych - techniki i technologii oraz przedsiębiorczości. Rozmiary produkcji uzależnione są od: nakładów czynników produkcji, możliwości ich powiększania w czasie oraz od możliwości substytucji jednych czynników przez inne (głównie pracy przez kapitał).

W przedsiębiorstwie w krótkim okresie (kilkunastu tygodni) istnieje możliwość powiększania nakładów tylko niektórych czynników produkcji (zatrudnienia i obrotowej części kapitału), w tych warunkach wielkość produkcji rośnie najpierw szybciej, a później wolniej od nakładów tych czynników, po czym osiąga maksimum.

W długim okresie, gdy wszystkie czynniki mogą zostać powiększone, wielkość produkcji rośnie proporcjonalnie (bez zmiany techniki i technologii) lub bardziej niż proporcjonalnie (wraz z postępem technicznym) w stosunku do nakładów czynników produkcji.

Produkt (product) wyrób, usługa lub informacja składająca się z wiązki materialnych i niematerialnych atrybutów, które zaspokajają potrzeby konsumenta i są wymieniane na pieniądze lub inne jednostki wartości. Atrybuty te, to właściwości fizyko-chemiczne, estetyczne, ergonomiczne, prestiżowe, opakowanie, usługi posprzedażne, gwarancje, finansowe warunki sprzedaży itp. Są one jako całość przedmiotem oceny materialnej i źródłem decyzji o zakupie towaru.

Produkt jest głównym elementem marketing-mix. Wszystkie inne elementy kompozycji marketingowej są pochodnymi strategii produktu firmy.

W zależności od wpływu wywieranego na konsumenta produkty można podzielić na (wg Ph. Kotlera):

• produkty pożądane (desirable products) - wpływają one na wysoki stopień satysfakcji konsumenta zarówno w krótkim, jak i długim okresie (np. dobre książki, sprawny samochód, wygodne i estetyczne meble itp.);

• produkty wadliwe (defective products) - ich spożycie daje konsumentowi niską satysfakcję zarówno bieżącą jak i długookresową (np. niesolidnie wykonany ubiór);

• produkty konsumowane dla przyjemności (pleasure products) - dają one wysoki poziom satysfakcji, ale nie zawsze wpływają korzystnie na "dobrobyt" konsumenta (np. papierosy, używki, lody itp.);

• produkty zdrowotne (salutary products) - przynoszą one relatywnie niskie zadowolenie z ich bieżącej konsumpcji, ale pozytywnie wpływają na rozwój człowieka w dłuższym okresie (np. benzyna o niskiej zawartości ołowiu, której użycie zmniejsza sprawność silnika, ale zmniejsza zatrucie środowiska).

Produktywność (productivity) stosunek ilościowy między rozmiarem produkcji i rozmiarem jednego lub kilku czynników zaangażowanych w jej uzyskanie; stosunek ilości wyjść (produktów) systemu do ilości zasobów wejściowych zużytych do ich wytworzenia.

Wyróżnia się produktywność cząstkową i całkowitą. Produktywność cząstkowa jest to stosunek całkowitej liczby produktów (lub liczby produktów poszczególnych rodzajów) do ilości poszczególnych rodzajów zasobów użytych do ich wytworzenia. Produktywność ta dotyczy więc różnych czynników wytwórczych, i tak można mówić o produktywności pracy, produktywności kapitału, produktywności ziemi, produktywności energii, produktywności materiałów itp. Produktywność całkowita jest to stosunek całkowitej liczby produktów do łącznej ilości zasobów zużytych do ich uzyskania. Obserwacja, ocena i analiza produktywności w przedsiębiorstwie jest narzędziem skutecznego zarządzania. Zdaniem A. Kosieradzkiej umożliwia ona:

• ocenę wyników osiąganych przez przedsiębiorstwo w porównaniu z innymi przedsiębiorstwami w ramach tej samej branży;

• identyfikację "słabych miejsc", tzn. obszarów działania, które są przyczyną niskiej produktywności i które wymagają usprawnienia;

• formułowanie programów poprawy produktywności;

• formułowanie planów strategicznych przedsiębiorstwa;

• obserwację trendów zmian wskaźników produktywności całkowitej i cząstkowych;

• powiązanie polityki płacowej przedsiębiorstwa z jego produktywnością.

Wymagania rynku zmuszają przedsiębiorstwa do ciągłego podnoszenia produktywności i poszukiwania sposobów jej wzrostu. W wielu krajach, a zwłaszcza Japonii, podnoszenie produktywności traktuje się jako rodzaj filozofii działania firmy i tworzy specjalny ruch produktywności.

Produktywność krańcowa ( margianl productivity) przyrost wielkości produkcji, odpowiadający zatrudnieniu dodatkowej jednostki czynnika zmiennego.

Produktywność przeciętna - średnia produkcyjność jednostki zatrudnionego czynnika produkcji.

Produktywny (productive) Dający dobre wyniki, efekty w produkcji, w wytwarzaniu czegoś, tworzący dobre rezultaty, dużo wytwarzający, wydajny, efektywny. Pojęcie produktywny nie jest tożsame z pojęciem produkcyjny. Pojęcie "produktywny" wiąże się z osobą, działaniem przynoszącym korzyści, osiąganiem dobrych rezultatów w działaniu, zaś pojęcie "produkcyjny" dotyczy produkcji, produkowania, przystosowania czy przeznaczenia czegoś do produkowania, tzn. wdrażania czegoś, brania udziału w produkcji itp. Tak więc mówi się o systemie produkcyjnym, potencjale produkcyjnym, czynnikach produkcyjnych, zdolności produkcyjnej. itp.
Niekiedy też pojęcie produkcyjny odnosi się do człowieka. Mówi się na przykład o wieku produkcyjnym, który oznacza okres życia, w którym człowiek, dysponując pełnią sił fizycznych i intelektualnych, jest zdolny do wydajnej pracy.

Quasi-stały czynnik produkcji - czynnik, którego wielkości zatrudnienia nie można dowolnie zmieniać nawet w długim okresie: może być ona zmieniana tak długo, jak długo firma nie zdecyduje, jaka ma być realizowana wielkość produkcji, do niej bowiem jest dostosowana ilość tego czynnika.

Siła robocza, ogół ludzi pracujących i poszukujących pracy (bezrobotnych). W tym znaczeniu siła robocza jest jednym z zasobowych, tradycyjnych czynników produkcji.

Stałe korzyści skali - występują, jeśli a-krotnemu (a> 1) zwiększeniu ilości czynników wytwórczych towarzyszy a-krotny przyrost produkcji.

Stały czynnik produkcji - czynnik, którego ilości producent nie może zmienić, nawet, jeśli zrezygnuje z podjęcia produkcji. Ze stałymi czynnikami wytwór­czymi mamy do czynienia w krótkim okresie.

System produkcyjny (production system) celowo zaprojektowany i zorganizowany układ osobowy, materialny, energetyczny i informacyjny eksploatowany przez człowieka i służący wytwarzaniu określonych produktów (wyrobów i usług) w celu zaspokajania potrzeb konsumentów. Według I. Durlika system produkcyjny składa się z pięciu podstawowych elementów:

• wektora wejścia, w skład którego wchodzą wszystkie czynniki produkcji;

• wektora wyjścia, w skład którego wchodzą wyroby, usługi, a także szkodliwe odpady produkcyjne zanieczyszczające środowisko;

• procesów przetwarzania wektora wejścia w wektor wyjścia nazywanych zazwyczaj procesem produkcyjnym;

• sprzężenia materialnego, energetycznego i informacyjnego pomiędzy wyżej wymienionymi elementami systemu produkcyjnego.

Turgot Anne Robert Jacques de l'Aulne (1727-1781), francuski ekonomista, polityk, prawnik.1752 radca parlamentu paryskiego. Od 1774 generalny kontroler finansów Francji (minister finansów, handlu i robót publicznych). Rozpoczął reformy gospodarki, mające zlikwidować pozostałości merkantylistycznej reglamentacji i doprowadzić do liberalizacji życia gospodarczego. Ustąpił ze stanowiska w 1776 ze względu na niepopularność reform, odsunął się od polityki.

Autor licznych prac teoretycznych: Discours sur l'histoire universelle (1750), Réflexions sur la formation et la distribution des richesses (1766), pisał artykuły dla Wielkiej Encyklopedii Francuskiej.

TURGOT ANNE ROBERT JACQUES de l'Aulne (1727-81), ekonomista franc.; Zwolennik fizjokratyzmu; 1774-76 generalny kontroler finansów Francji (min. finansów, handlu i robót publ.); Przeprowadził reformy gosp. we Francji, które likwidowały pozostałości merkantylistycznej reglamentacji i liberalizowały życie gosp. (wprowadzały m.in. wolny handel zbożem i znosiły przywileje cechowe); autor tezy, że postęp społ. jest uwarunkowany rozwojem nauki i techniki, te zaś są wyrazem stopniowych postępów umysłu ludzkiego (rozprawa Discours sur l'histoire universelle 1750). W teorii ekonomii oparł się na koncepcji fizjokratów, dotyczącej czystego produktu rolnego, oraz na ich podziale społeczeństwa na klasy; wiele uwagi poświęcił koncepcji zysku i stopy procentowej; twórcze rozwinięcie idei fizjokratów polegało na sformułowaniu tezy, że zysk i procent (dochód od kapitału) muszą powstawać również w pozaroln. gałęziach gospodarki; zwolennik wolnej konkurencji w gospodarce; przyczynił się także do wzbogacenia teorii pieniądza; gł. praca: Réflexions sur la formation et la distribution des richesses (1766); artykuły w Wielkiej encyklopedii francuskiej.

Wydajność pracy (productivity of work) Wielkość (wartość) produkcji przypadająca na jednego zatrudnionego; stosunek produkcji do czasu pracy niezbędnego do jej wykonania. W przeszłości w naszej teorii ekonomicznej wydajność pracy odnoszono głównie do pracy żywej i definiowano jako "stosunek produkcji wartości użytkowych do czasu pracy żywej". Obecnie coraz bardziej utożsamia się wydajność z produktywnością i rozumie się przez to pojęcie stosunek wartości produkcji wykonanej w danym systemie za dany okres czasu do wartości środków potrzebnych do wykonania tej produkcji; czyli stosunek stworzonych wartości do całkowitych udziałów pracy.

Zmienny czynnik produkcji - czynnik, którego zatrudnioną ilość można zmienić w krótkim okresie.

Przedsiębiorstwa mogą być zorganizowane na różne sposoby, mogą różnić się wielkością, gdyż tak samo działalność gospodarczą prowadzi firma jednoosobowa, jak i przedsiębiorstwo zatrudniające dziesiątki tysięcy pracowników. Firma może być własnością jednej osoby, która może pracować w niej samodzielnie lub może zatrudniać innych ludzi. Przedsiębiorstwami są również wszelkie spółki osobowe i kapitałowe. Ponadto działal­ność gospodarczą prowadzą spółdzielnie, w których pracują ich właściciele, czyli członkowie tych spółdzielni. Oprócz tego działają jeszcze przedsiębiorstwa publiczne , które są własnością rządu (państwowe) lub samorządu (komunalne)

Należy tu zwrócić uwagę na różnicę między przedsiębiorstwem a zakładem produkcyjnym, który stanowi tylko jeden z jego elementów.

Rozróżnienie na okres krótki i długi, a więc na czynniki stałe zmienne, zależy od rodzaju przemysłu. Jeśli na przykład zapadnie decyzja budowie nowej elektrowni, to zanim nowy zakład zacznie produkcję, minie kilka lat i tyle właśnie wynosi okres krótki w tym przemyśle. Oczywiście inne rodzaje przemysłu mają ten okres o wiele krótszy.

W tym miejscu przypomnimy, że pojecie kapitału może być interpretowane dwojako, mówiąc o kapitale mamy z jednej strony na myśli dobra kapitałowe, czyli dobra, które same są wytworzone z przeznaczeniem do ich wykorzystania w dalszej produkcji. Dobra kapitałowe to różnego rodzaju surowce, energia maszyny, np. traktory, budynki, komputery itp. Dla określenia tych czynników produkcji będziemy używać pojęcia kapitał rzeczowy. Z drugiej strony pojęcie kapitału jest używane do określenia pieniędzy wykorzystywanych do rozpoczęcia i utrzymania działalności gospodarczej. W stosunku do tego czynnika będziemy używali terminu kapitał finansowy (pieniężny).W tej c części analizy interesuje nas kapitał rzeczowy

Przykładowo, wydawnictwo drukujące podręczniki może zwiększyć swoją produkcję w krót­kim okresie, zatrudniając więcej pracowników, i wprowadzić dodatkowe zmiany, zużywając więcej papieru, farby, elektryczności, itd. Czyli będzie bardziej intensywnie wykorzys­tać istniejące moce wytwórcze, czyli czynniki stałe. Podobnie jeśli przedsiębiorstwo żeglugi pasażerskiej zechce przewozić więcej pasażerów, bo wzrasta popyt na jego usługi, to w krótkim okresie może zabrać więcej pasażerów na pokład posiadanych statków (w miarę wolnych miejsc). Może też zwiększyć liczbę rejsów, zatrudniając dodatkowe załogi i zużywając więcej paliwa. W krótkim okresie nie może jednak zakupić większej liczby statków, gdyż ich i zbudowanie zajmuje dużo więcej czasu.

Dla kopalni okres krótki może sięgać nawet kilkunastu lat, (czas niezbędny do wybudowania nowej kopalni), dla rafinerii okres może wynosi około pięciu lat. Dla sieci barów szybkiej obsługi będzie to okres 6 miesięcy; tyle na ogół trwa zdobycie niezbędnych pozwoleń i budowa nowej restauracji. I tak, jeżeli rolnik potrzebuje całego roku, aby zakupić dodatkową ziemię, budynki czy urządzenia, to krótkim okresem dla niego będzie czas nie dłuższy niż rok, a długim okresem - czas dłuższy niż rok. Z kolei, jeżeli przedsiębiorstwo żeglugowe potrzebuje około trzech lat, aby zakupić nowy prom czy statek, to krótkim okresem będzie dla niego okres do trzech lat, a okresem długim - okres powyżej trzech lat.

W ten sposób upraszczamy problem różnych indywidualnych cech pracowników takich jak: doświadczenie, kwalifikacje, zdolności, chęć do pracy, wiek, płeć itp., które w praktyce mają wpływ na wydajność i ogólną „jakość” pracownika.

Anne Robert Jacques Turgot (1727-178) - główny kontroler finansów, w państwie Ludwika XVI próbował naprawić sytuację finansową ówczesnej Francji, m.in poprzez próbę nałożenia podatków na szlachtę i duchowieństwo, ograniczenie wydatków dworskich, oraz przeprowadzenie reform takich jak: swoboda handlu zbożem, zniesienie ograniczeń cechowych, zamiana szarwarków chłopskich na specjalny podatek itd. Popierał doktrynę fizjokratyzmu i był jednym z jej najwybitniejszych przedstawicieli. Był również jednym z autorów Wielkiej Encyklopedii Francuskiej

W naszej analizie okresu krótkiego rozpatrujemy wyłącznie zmiany czynnika pracy, ale musimy sobie zdawać sprawę z faktu, że prawo nieproporcjonalnych przychodów obowiązuje zawsze, gdy mamy do czynienia przynajmniej z jednym jakimkolwiek czynnikiem stałym.

Frank Hyneman Knight (1985-1972) amerykański ekonomista, przedstawiciel szkoły chicagowskiej Urodził się w małej wiosce w stanie Illinois , w głęboko wierzącej chrześcijańskiej rodzinie. Nigdy nie ukończył szkoły średniej, ale mimo to został dopuszczony na studia w 1905 roku na American University w Teeessee . Jego najbardziej znaną pracą jest książka Risk Uncertainity and Profit wyd 1921

”

Kk

Kpz

---