TWIERDZENIE

PITAGORASA

Spis treści:

Kim był Pitagoras?

•

Co to jest twierdzenie?

•

Układanka wprowadzająca do twierdzenia Pitagorasa.

•

Twierdzenie Pitagorasa

•

Dowód I

•Dowód II
•Twierdzenie odwrotne do tw. Pitagorasa
•Trójkąt egipski i pitagorejski.
•Zastosowanie w zadaniach:
Obliczanie długości przeciwprostokątnej
Obliczanie długości przyprostokątnej
Obliczanie odległości punktów
Sprawdzanie czy trójkąt jest prostokątny
Obliczanie długości przekątnej: prostokąta i kwadratu
Obliczanie długości wysokości w trójkącie
Obliczanie długości promienia okręgu wpisanego i
opisanego
Konstrukcja odcinków o długościach wymiernych
Dyplom dla najlepszego ucznia

OGÓLNE WIADOMOŚCI O TWIERDZENIU.

W matematyce często formułujemy zdania, wyrażające pewną

prawdę matematyczną. Zdania te nazywamy

twierdzeniami

twierdzeniami.

Najczęściej twierdzenie ma postać zdania warunkowego.

Na przykład w twierdzeniu: Jeżeli czworokąt jest
równoległobokiem, to ma przeciwległe kąty równe. – pierwsza
część zdania, zaczynająca się po słowie „jeżeli”, nazywa się
założeniem , druga, następująca po słowie „to” nazywa się
tezą.

W założeniu twierdzenia podajemy warunki, przy których
ma być spełniona teza, tzn. podajemy informacje, które są nam
znane.

W tezie twierdzenia formułujemy własność, która ma być
spełniona tzn. to co mamy udowodnić.

W dowodzie twierdzenia korzystamy z tego, co jest dane w
założeniu i przeprowadzamy rozumowanie, które doprowadza
do wykazania tezy.

W matematyce spotykamy się także z takim pojęciem jak
aksjomat-jest to twierdzenie, które przyjmuje się bez
dowodu.

Pitagoras – to grecki matematyk i filozof. Żył w VI wieku

p.n.e.Położył wielkie zasługi dla rozwoju matematyki,
astronomii i fizyki. W mieście Krotonie założył na wpół tajemny
związek znany pod nazwa pitagorejskiego. Związek przetrwał
swego twórcę i działał przez następne 100 lat.

Twierdzenie Pitagorasa to jedno z najstarszych twierdzeń
matematycznych. Znane było w starożytnym Babilonie, w
Chinach, w Egipcie na długo przed Pitagorasem. Pierwsze
dowody tego twierdzenia przypisuje się jednak
pitagorejczykom.

Ta układanka jest stara jak świat.

Na pierwszym rysunku widać cztery
jednakowe trójkąty prostokątne o
bokach a, b i c ułożone w taki sposób,
że wewnątrz powstał kwadrat o boku
c.Na dolnym rysunku te same trójkąty
zostały ułożone inaczej, tak że pojawiły
się dwa mniejsze kwadraty. Te dwa
mniejsze kwadraty mają taki samo
pole, jak wewnętrzny kwadrat na
górnym rysunku.



Jakie jest pole wewnętrznego

kwadratu na górnym rysunku?



Zapisz wyrażenie, opisujące pola

kwadratów na dolnym rysunku.



Czy dostrzegasz jakąś regułę?

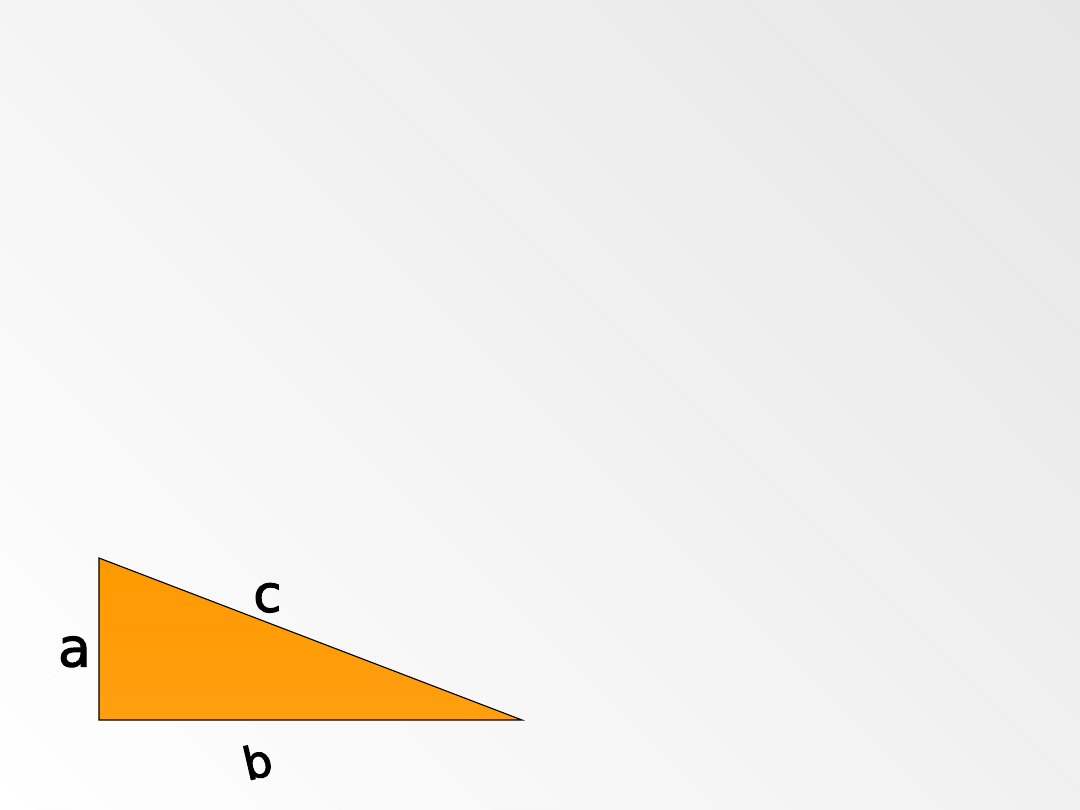
TWIERDZENIE PITAGORASA

TWIERDZENIE PITAGORASA

Jeżeli trójkąt jest prostokątny, to kwadrat zbudowany na
przeciwprostokatnej ma takie samo pole jak suma pól
kwadratów zbudowanych na przyprostokątnych.

Lub inaczej:

W trójkącie prostokątnym o bokach a, b i c, zachodzi równość

c

2

=a

2

+b

2

Dowód I

Dalej

ADC i ABC (ponieważ kąt A jest wspólny i
trójkąty mają po jednym kącie prostym ). Stąd:

BCD i ABC (kąt B jest wspólny i trójkąty mają
po jednym kącie prostym). Stąd:

AB

AC

AC

AD



AB

BC

BC

DB



C

A

B

D

Obliczając proporcje otrzymamy:

2

2

BC

AB

DB

AC

AB

AD









Dowód I

– ciąg

dalszy

Ponieważ:

AC = b,

BC = a,

AB = c

Stąd:

a

2

+ b

2

= c

2

Co należało udowodnić.

Przez dodanie stronami równań otrzymujemy:





2

2

2

2

2

2

2

2

2

AB

BC

AC

AB

AB

BC

AC

BD

AD

AB

BC

AC

AB

DB

AB

AD

BC

AC





























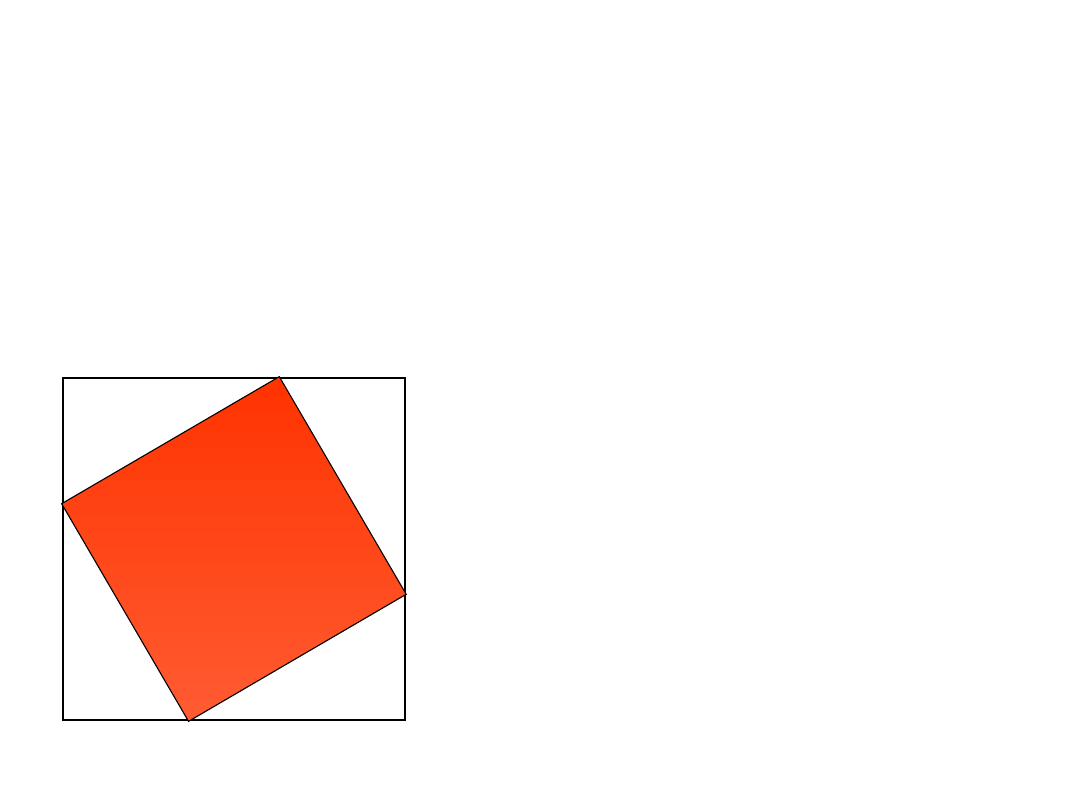
Dowód II

Dowód – Przyjmijmy, że a, b są długościami
przyprostokątnych rozważanego trójkąta, c –długością
przeciwprostokątnej.

Należy wykazać, że

c

2

= a

2

+ b

2

.

Rozważmy kwadrat o boku a+b, na każdym zaznaczmy
odcinki a i b.

b

b

a

b

b

a

a

a

c

c

c

c

Dalej

Pole kwadratu o boku a+b
jest sumą pola kwadratu o
boku c oraz pól czterech
trójkątów prostokątnych o
przyprostokątnych a i b. Pole
każdego takiego trójkąta
prostokątnego wynosi:
½*a*b,

zatem:

Dowód II

– ciąg dalszy

( a + b )

2

= c

2

+ 4 *1/2* ab,

a

2

+ 2ab + b

2

= c

2

+ 2ab,

a

2

+ b

2

=c

2

Co należało dowieść.

Znając długości dwóch

boków trójkąta

prostokątnego możemy na

podstawie twierdzenia

Pitagorasa wyznaczyć

długość trzeciego boku

tego trójkąta.

Twierdzenie odwrotne do Twierdzenia

Pitagorasa

Jeżeli w trójkącie długości

boków: a, b, c są takie, że

c

2

=a

2

+b

2

to

trójkąt jest

prostokątny

oraz a i b są

przyprostokątnymi, a bok

c jest

przeciwprostokątną.

Trójkąt prostokątny, którego

długości boków są liczbami

naturalnymi nazywamy

trójkątem pitagorejskim.

Trójkąt o bokach 3, 4, 5

nazywamy trójkątem

egipskim.

ZADANIE 1

Znając długości przyprostokątnych trójkąta,
oblicz długość przeciwprostokątnej.

a

b

c

a=3cm, b=4cm

c=?

c

2

=

a

2

+b

2

c

2

=3

2

+4

2

c

2

=9+16

c

2

=25

c=5

Rozwiązanie:

Odpowiedź

:Długość przeciwprostokątnej wynosi

5cm.

ZADANIE 2

Oblicz długość przyprostokątnej, wiedząc że
druga przyprostokątna wynosi 8cm, a
przeciwprostokątna jest równa 10cm.

b

c

a

c

2

=

a

2

+b

2

10

2

=8

2

+b

2

b

2

=100-64

b

2=

16

b=4

Odpowiedź

: Długość

przyprostokątnej wynosi
4cm.

ROZWIĄZANIE

a=8cm,
c=10cm

b=?

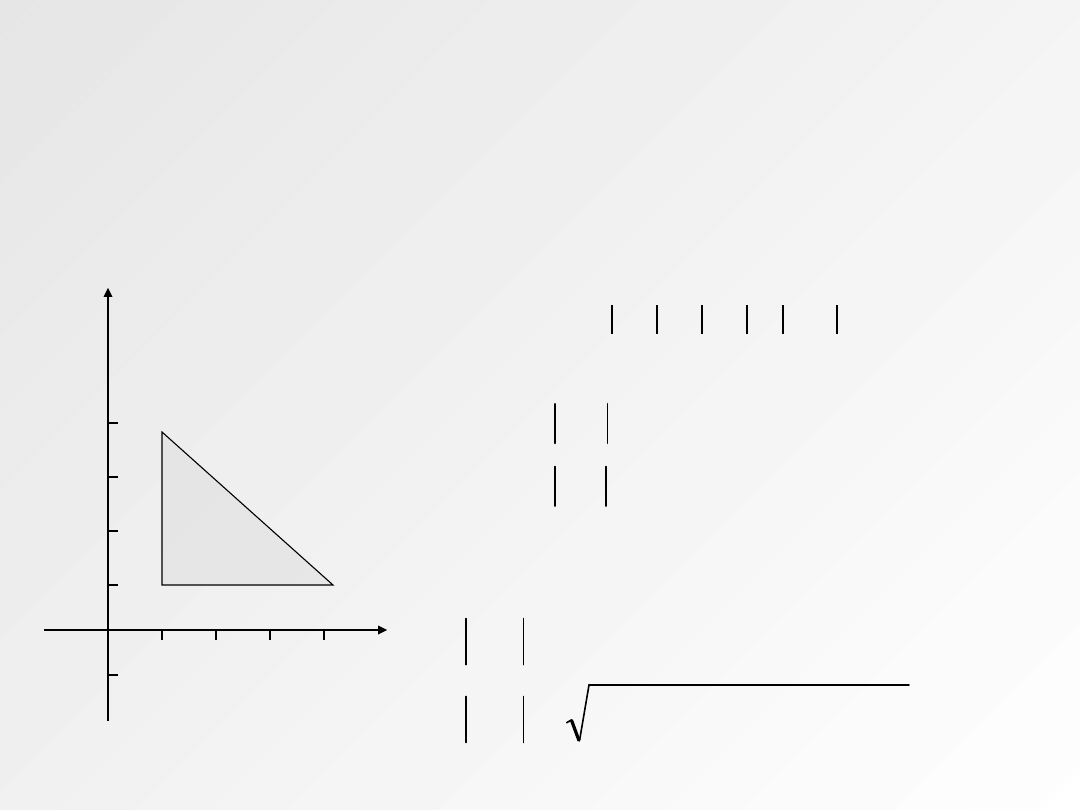
ZADANIE 3

Oblicz odległość punktów A=(x

1

,y

2

),B=(x

1

,y

2

)

X

Y

x

1

x

2

Y

1

y

2

A

B

C

ROZWIĄZANIE:

Rzutując punkty A i B na osie układu
otrzymujemy trójkąt prostokątny, więc z
tw. Pitagorasa : AB

2

= AC

2

+ BC

2

Z rysunku wynika, że:

podstawiając do pierwszego wzoru
otrzymamy:









2

1

2

2

2

2

1

2

x

x

BC

y

y

AC











 





 



2

1

2

2

2

1

2

1

2

2

2

1

2

x

x

y

y

AB

x

x

y

y

AB

















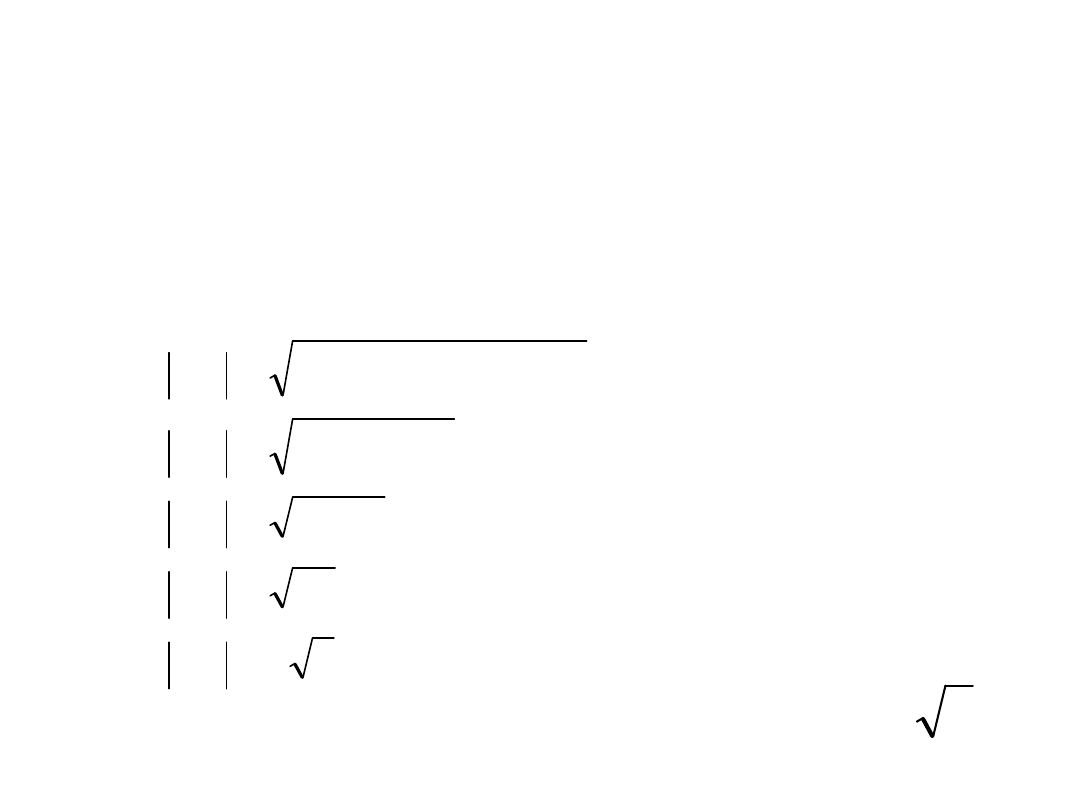
ZADANIE 3a

Oblicz odległość punktów A=(1,3), B=(3,-1).

ROZWIĄZANIE:

Korzystając ze wzoru obliczonego w
poprzednim zadaniu i po podstawieniu do
niego danych otrzymamy:





 





 

5

2

20

16

4

4

2

1

3

3

1

2

2

2

2

























AB

AB

AB

AB

AB

5

2

Odpowiedź

: Odległość między punktami A i B wynosi

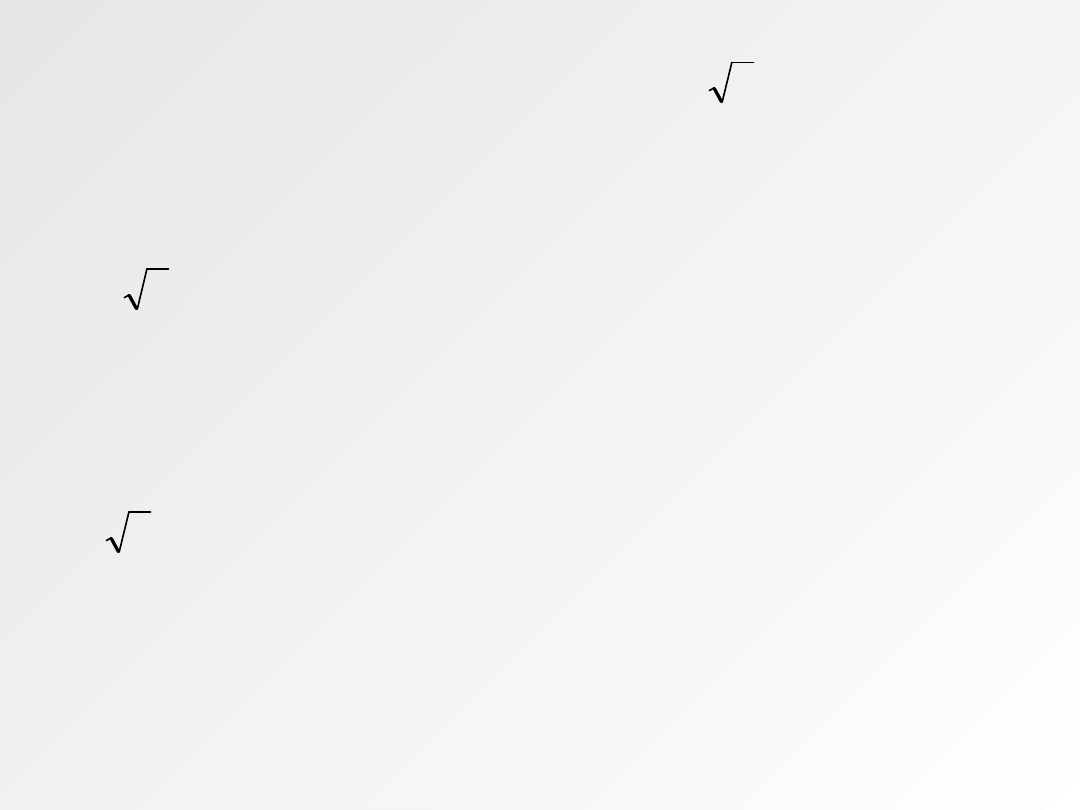
ZADANIE 4

Sprawdź, czy trójkąt o bokach: 2, 4, 3 jest
prostokątny?

5

Przeciwprostokątna w trójkącie prostokątnym to bok
najdłuższy, więc oznaczmy

c=3 , b=4, a=2

Podstawiamy dane do twierdzenia Pitagorasa i zgodnie z
tw. odwrotnym do tw. Pitagorasa, jeżeli będzie zachodziła
równość to trójkąt będzie prostokątny.

c

2

=a

2

+b

2

(3 )

2

=2

2

+4

2

45=4+16

45=20

5

5

ROZWIĄZANIE:

Odpowiedź

:Ponieważ lewa strona nie równa się stronie

prawej, to znaczy, że trójkąt o podanych bokach nie jest

prostokątny

ZADANIE 4 a

Sprawdź, czy trójkąt o bokach: 25, 20, 15, jest
prostokątny?

ROZWIĄZANIE:

c=25

b=20

a=15

Podstawiamy do wzoru Pitagorasa: c

2

=a

2

+b

2

25

2

=15

2

+20

2

625=225+400

625=625

Odpowiedź:

Ponieważ zachodzi równość, więc

trójkąt o bokach 25, 20 i 15 jest prostokątny.

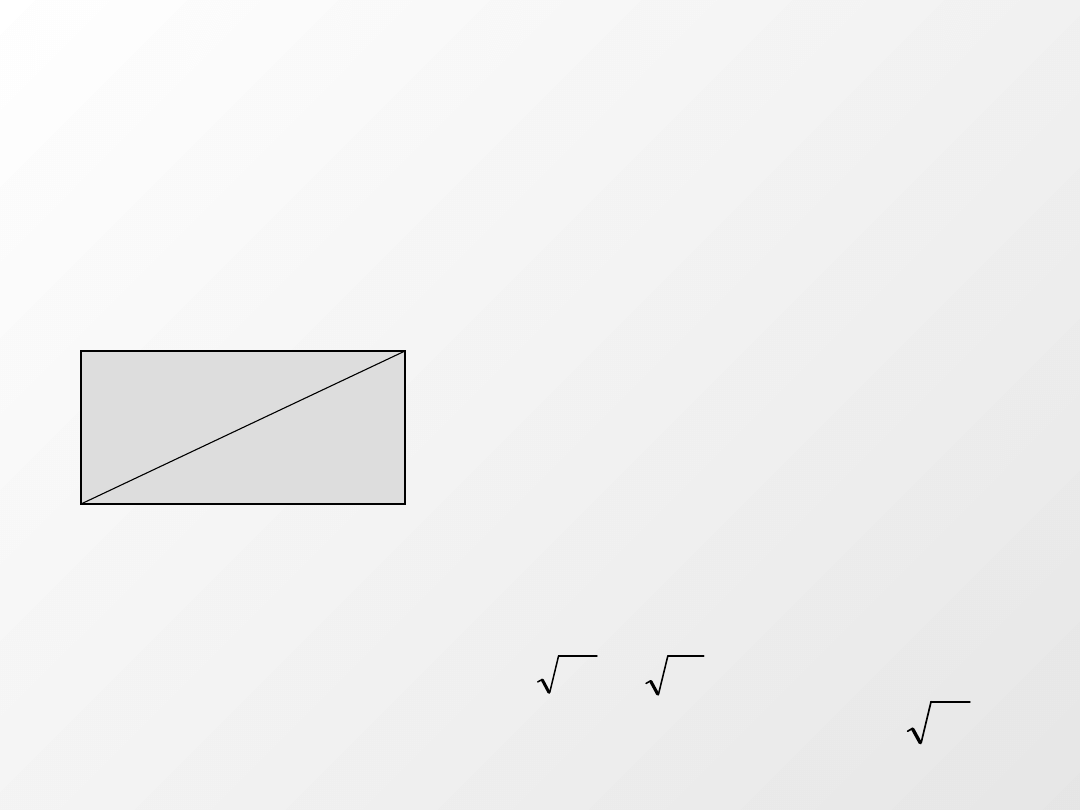
ZADANIE 5

Oblicz długość przekątnej prostokąta o
bokach

a=4cm, b=6cm.

ROZWIĄZANIE:

b

a

d

Odpowiedź

:Długość przekątnej prostokąta wynosi 2

cm.

13

Przekątna w prostokącie dzieli go
na dwa trójkąty prostokątne, więc
możemy zastosować twierdzenie
Pitagorasa do policzenia długości
przekątnej d.

d

2

=a

2

+b

2

d

2

=4

2

+6

2

d

2

=16+36

d

2

=52

d= =2

52

13

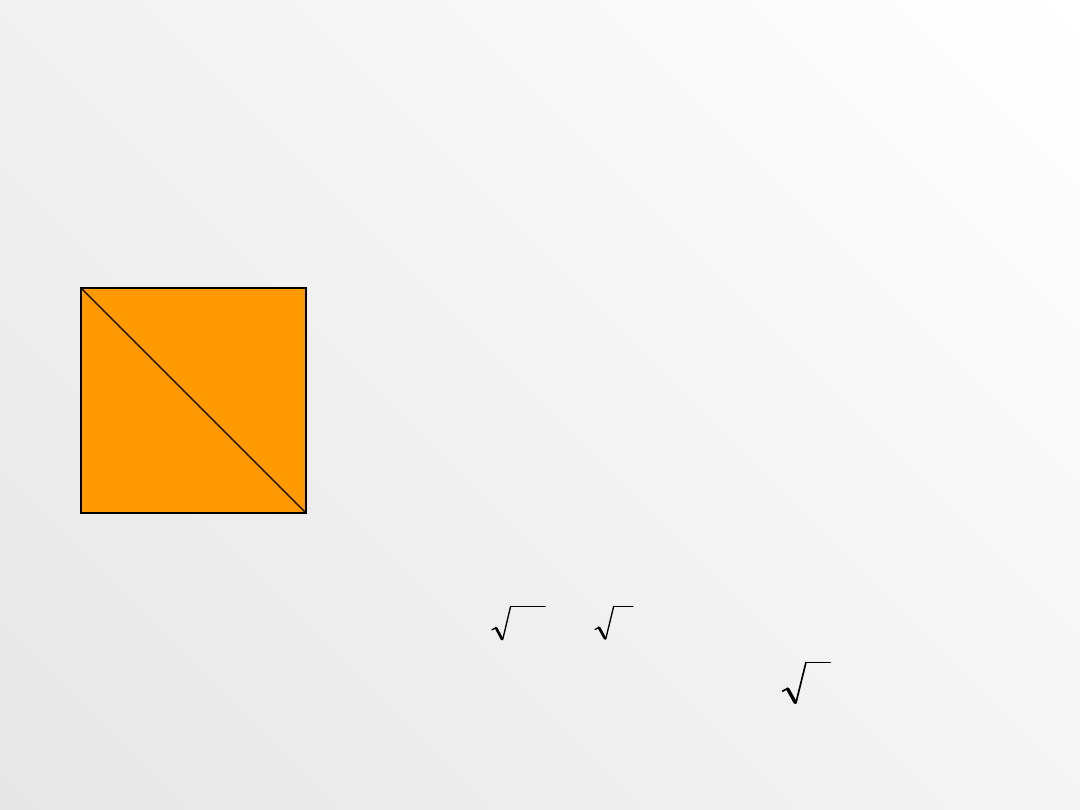
ZADANIE 6

Oblicz długość przekątnej kwadratu o boku 5cm.

ROZWIĄZANIE:

a

a

d

a

Przekątna dzieli kwadrat na dwa
równoramienne trójkąty prostokątne,
więc możemy zastosować tw.
Pitagorasa do obliczenia długości
przekątnej.

d

2

=a

2

+a

2

d

2

=2a

2

d

2

=2*5

2

d

2

=2*25

d=

2

5

50

ODPOWIEDŹ

: Przekątna kwadratu wynosi cm.

2

5

Spis treści

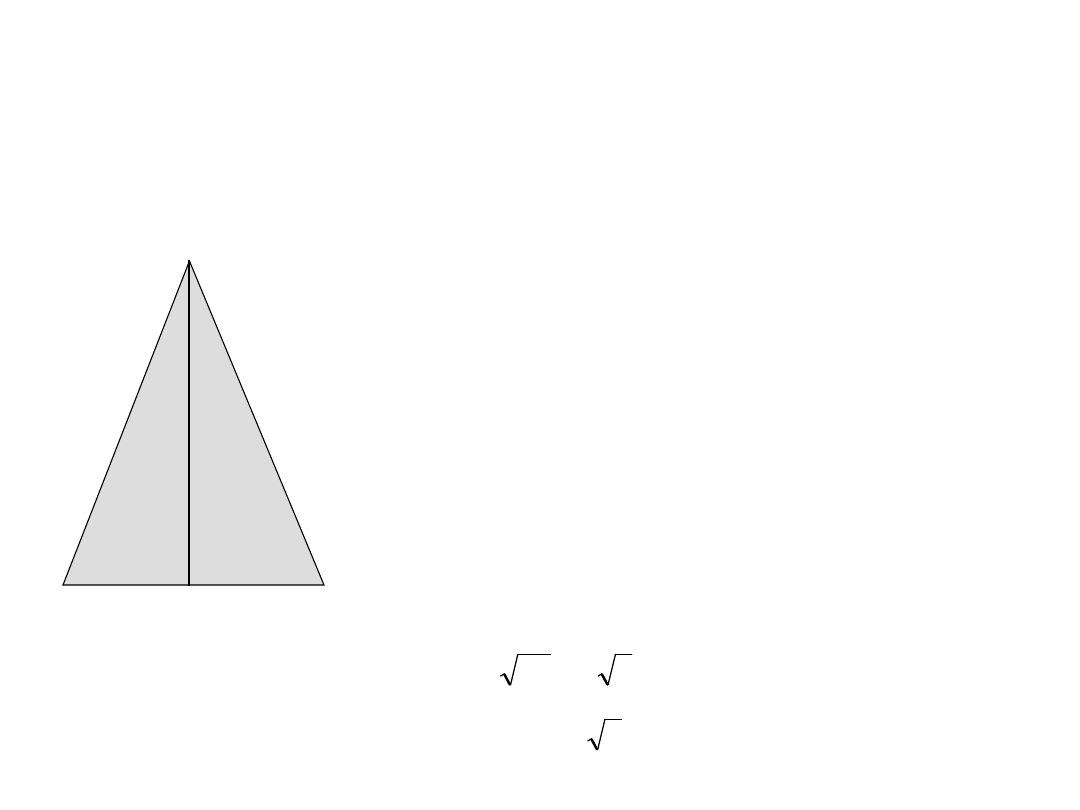
ZADANIE 7

W trójkącie równoramiennym długość ramienia ma
6 cm, a podstawa 8 cm. Oblicz jego wysokość.

ROZWIĄZANIE:

a

b

h

a=6cm, b=8cm

h=?

Wysokość podzieliła trójkąt na dwa
trójkąty prostokątne, podstawa
została podzielona na połowę. Do
policzenia wysokości tego trójkąta
zastosujemy tw. Pitagorasa.

a

2

=h

2

+(1/2b)

2

6

2

=h

2

+4

2

h

2

=36-16

h=

5

2

20

Odpowiedź

:Wysokość trójkąta wynosi cm.

5

2

Spis treści

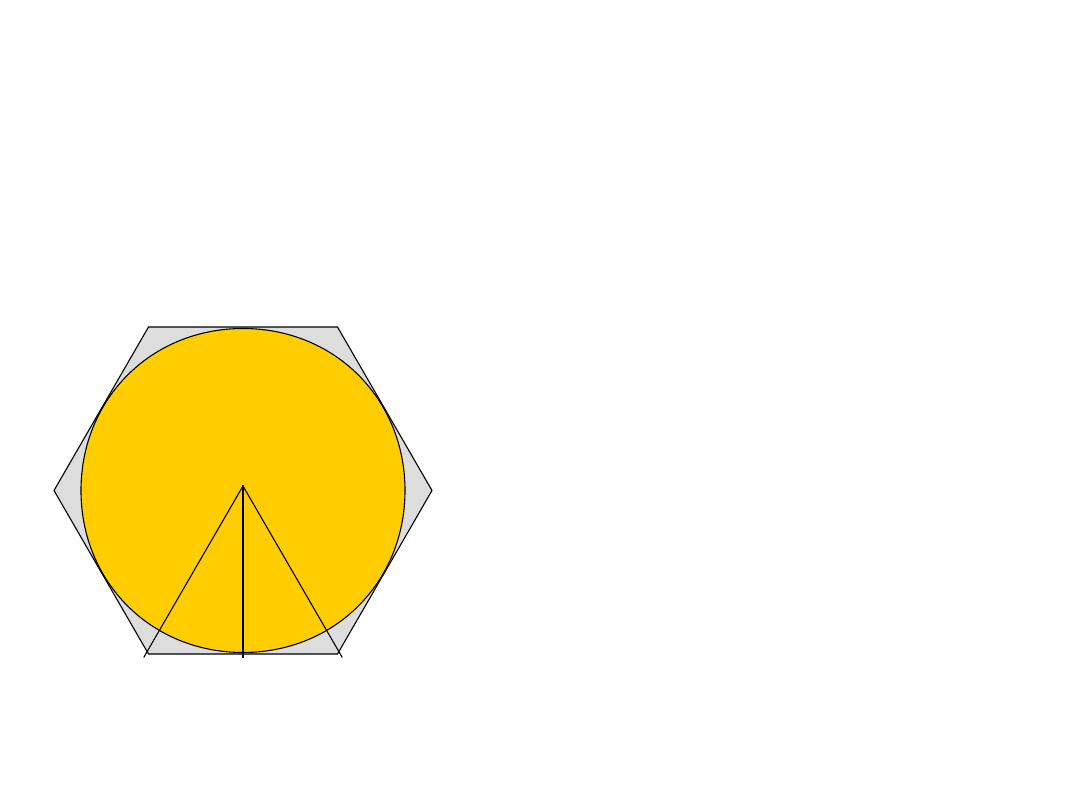
ZADANIE

8

Oblicz promień okręgu wpisanego w sześciokąt
foremny, którego bok jest równy 6cm.

ROZWIĄZANIE:

Sześciokąt foremny można podzielić
na sześć trójkątów równoramiennych o
boku równym bokowi sześciokąta
foremnego. Promień okręgu wpisanego
w ten sześciokąt dzieli bok sześciokąta
(trójkąta), na połowę i jest wysokością
trójkąta równoramiennego. Do
obliczenia promienia zastosować
można tw. Pitagorasa.

a=6cm

a

2

=r

2

+(1/2a)

2

r

2

=a

2

-1/4a

2

r

2

=3/4*6

2

r

a

a

a

a

a

O

Dalej

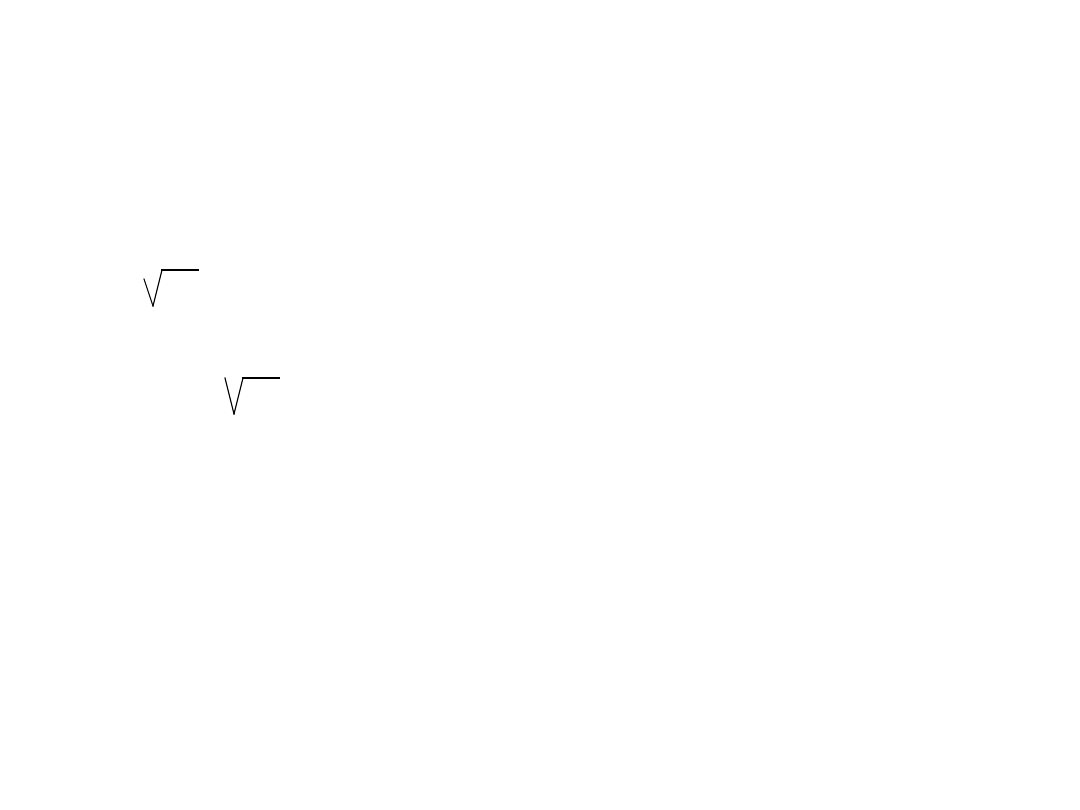
ciąg dalszy zadania 8

r

2

=3/4*36

r

2

=27

r=3 3

Odpowiedź

: Promień okręgu wpisanego w

sześciokąt foremny wynosi 3 3 cm.

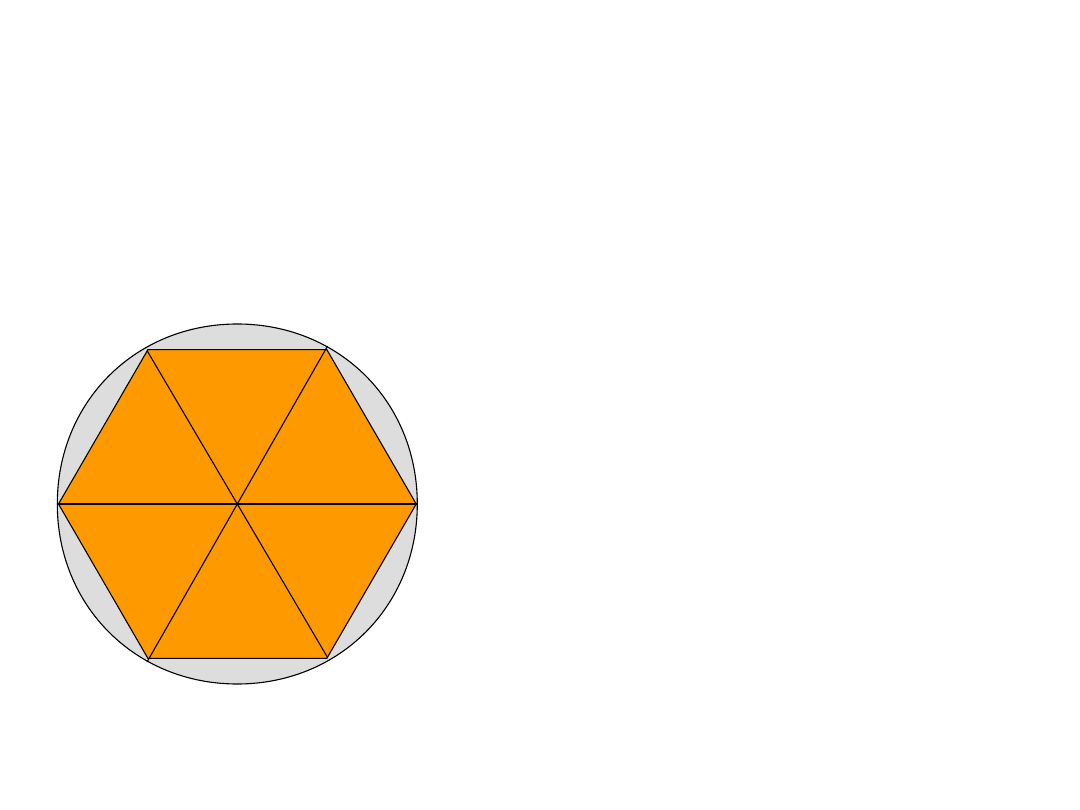
ZADANIE 9

Oblicz promień okręgu opisanego na sześciokącie
foremnym, którego bok jest równy 6cm.

ROZWIĄZANIE:

Sześciokąt foremny można podzielić
na sześć trójkątów równoramiennych o
boku równym bokowi sześciokąta
foremnego. Promień okręgu opisanego
na tym sześciokącie jest równy
długości boku sześciokąta. Jeżeli więc:

a=6cm, to r=6cm.

Odpowiedź

: Promień okręgu opisanego

na sześciokącie foremnym jest równy
bokowi tego sześciokąta, czyli 6cm.

a

a

r

a

O

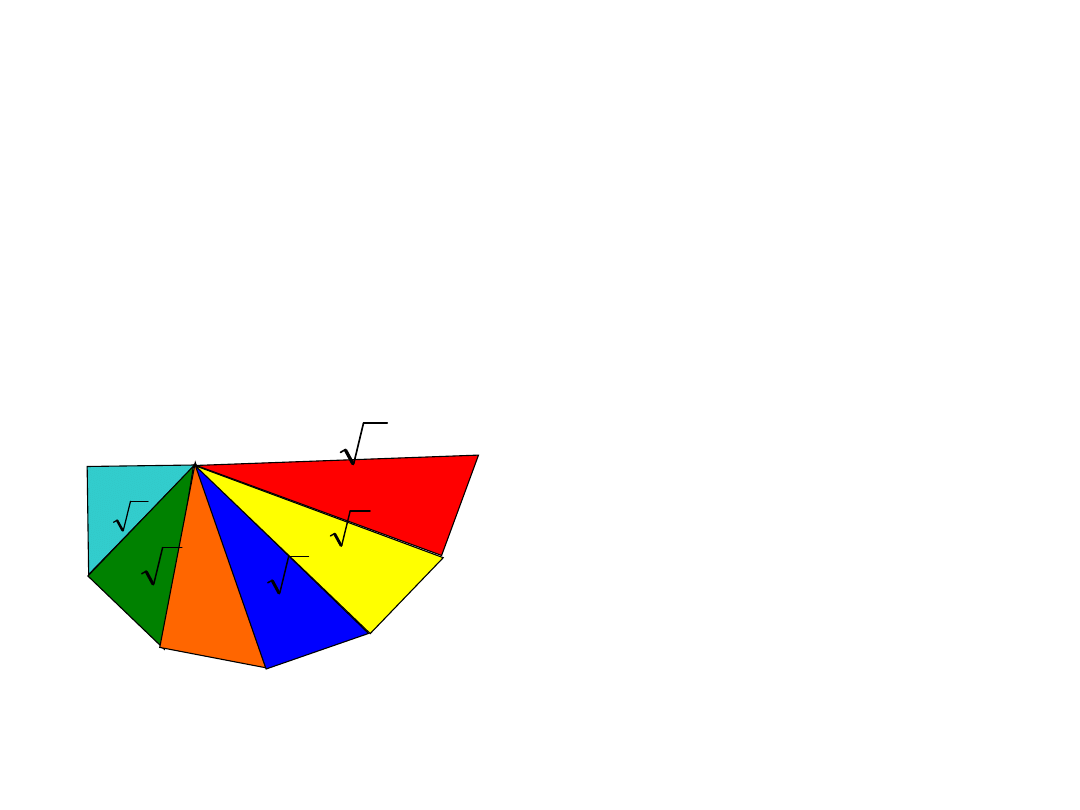
ZADANIE 10

Narysuj odcinki, których długość jest
pierwiastkiem kolejnych liczb naturalnych.

ROZWIĄZANIE:

Rysunek przedstawia metodę rysowania odcinków, będących
pierwiastkami kolejnych liczb naturalnych.

Wszystkie trójkąty prostokątne
jedną przyprostokątną mają o
długości 1 (pierwszy drugą
również). Wykorzystując wzór
Pitagorasa liczymy długość
przeciwprostokątnej. W ten
sposób można skonstruować
odcinek o dowolnej długości.

1

1

1

1

1

1

2

2

3

5

6

7

1

Koniec