Obwody rozgałęzione

prądu stałego

prof. dr hab. inż. Tadeusz NIEDZIELA

Kartkówka

Nazwisko, imię (nr. grupy)

1. Napisz wzory na zamianę układu rezystorów z

gwiazdy w trójkąt.

2. Napisz wzory na zamianę układu rezystorów z

trójkąta na gwiazdę .

3. Napisz wzory na dzielnik prądu.

Metody rozwiązywania obwodów rozgałęzionych prądu

stałego:

 

- metoda klasyczna

(zad. 5.3)

 

- metoda przekształcenia sieci

(zad. 5.1)

 
- metoda superpozycji

(zad. 5.2)

 
-metoda potencjałów węzłowych

(zad. 5.6, 5.7, 5.9)

 
-metoda superpozycji

[z metodą oczkową (5.10a, c)]

[z metodą węzłową (5.10b, c)]

 
- metoda z zastosowaniem twierdzenia Thevenina

(zad. 5.12,

5.14)

 
- metoda z zastosowaniem twierdzenie Thevenina i z metodą węzłową

(zad.

5.11)

 
- metoda z zastosowaniem twierdzenia Nortona

(zad. 5.13)

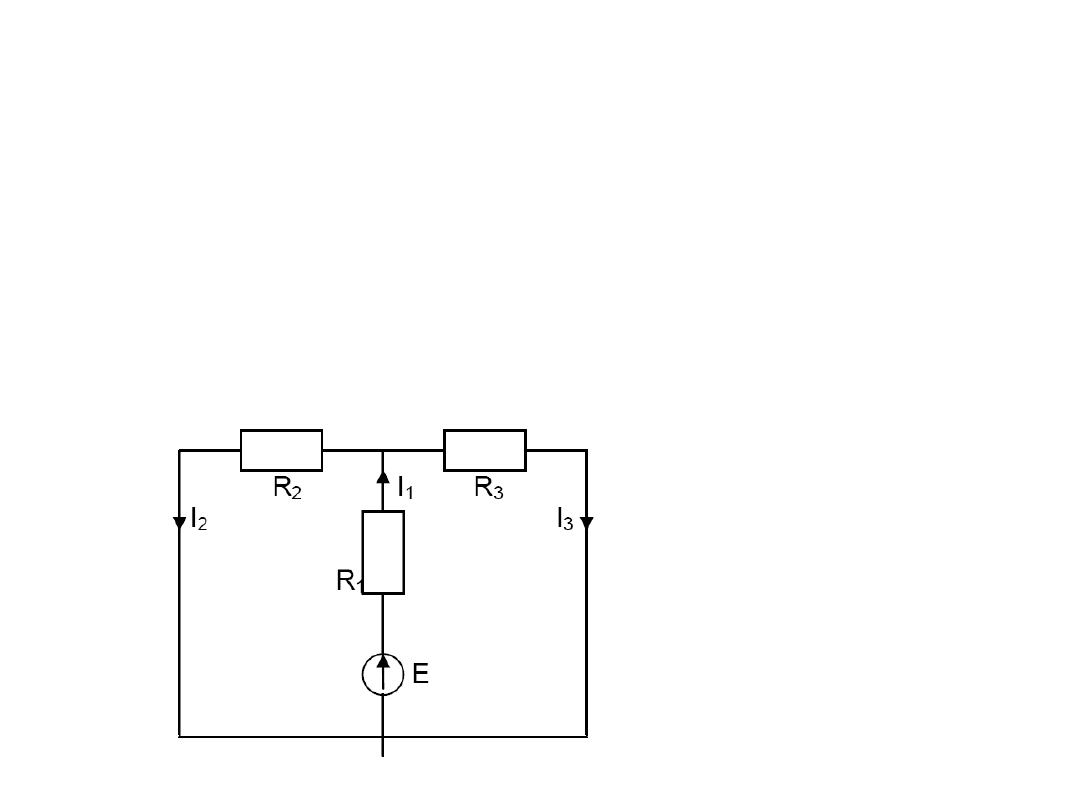
METODA KLASYCZNA

 

Zadanie 1

 Oblicz

wartości prądów gałęziowych

(I

1

, I

2

, I

3

) w danym

obwodzie

stosując metodą klasyczną

(równań

prądowych wg. I prawa Kirchhoffa oraz równań prądowych
wg. II prawa Kirchhoffa).

 Dane:

R

1

= 6 Ω, R

2

= 2 Ω, R

3

= 3 Ω, E = 36V

 

Dla obwodu zawierającego

v

węzłów można napisać,

zgodnie z I prawem Kirchhoffa

v-1

równań

niezależnych

=> 2-1 = 1

Dla obwodu zawierającego

b

gałęzi można napisać,

zgodnie z II prawem Kirchhoffa

b-(v-1)

równań

niezależnych =>

3-1 = 2

 

1

2

3

2 2

1 1

1 1

3 3

0

0

0

I

I

I

R I

I R E

RI

I R E

-

-

=

�

�

+

-

=

�

�

+

-

=

�

1

2

3

1 1

2 2

3

1 1

2

3 3

0

0

0

I

I

I

RI

R I

I

E

RI

I

R I

E

-

-

=

�

�

+

+ � =

�

�

+ � +

=

�

1

2

1

3

1

1

1

0

0

R R
R

R

-

-

�

�

�

�

�

�

�

�

�

�

1

2

3

I

I

I

� �

� �

� �

� �

� �

0

E
E

� �

� �

� �

� �

� �

1

1

1

6 2

0

6 0

3

-

-

�

�

�

�

�

�

�

�

�

�

1

2

3

I

I

I

� �

� �

� �

� �

� �

0

36
36

� �

� �

� �

� �

� �

1

1

1

6 2

0

6 0

3

-

-

�

�

�

�

�

�

�

�

�

�

2 0
0 3

�

�

�

�

�

�

6 0
6 3

�

�

�

�

�

�

6 2
6 0

�

�

�

�

�

�

0

1

1

36 2

0

36 0

3

-

-

�

�

�

�

�

�

�

�

�

�

36 0
36 3

�

�

�

�

�

�

36 2
36 0

�

�

�

�

�

�

1

1

180

5

36

I

A

W

W

=

=

=

=

·

=

W =

= 1

+1

-1

=1·6+1·18-1·(-
12)=6+18+12=36

= 1

-1=108-1·(-72) = 180

W

1

=

·

1 0

1

6 36 0
6 36 3

-

�

�

�

�

�

�

�

�

�

�

36 0
36 3

�

�

�

�

�

�

6 36
6 36

�

�

�

�

�

�

W

2

=

=1

-1 =108-1·(0) = 108

2

2

108

3

36

I

A

W

W

=

=

=

1

1 0

6 2 36
6 0 36

-

�

�

�

�

�

�

�

�

�

�

2 36
0 36

�

�

�

�

�

�

6 36
6 36

�

�

�

�

�

�

3

3

72

2

36

A

W

I

W

=

=

=

W

3

=

=1

+1

=2·36 = 72

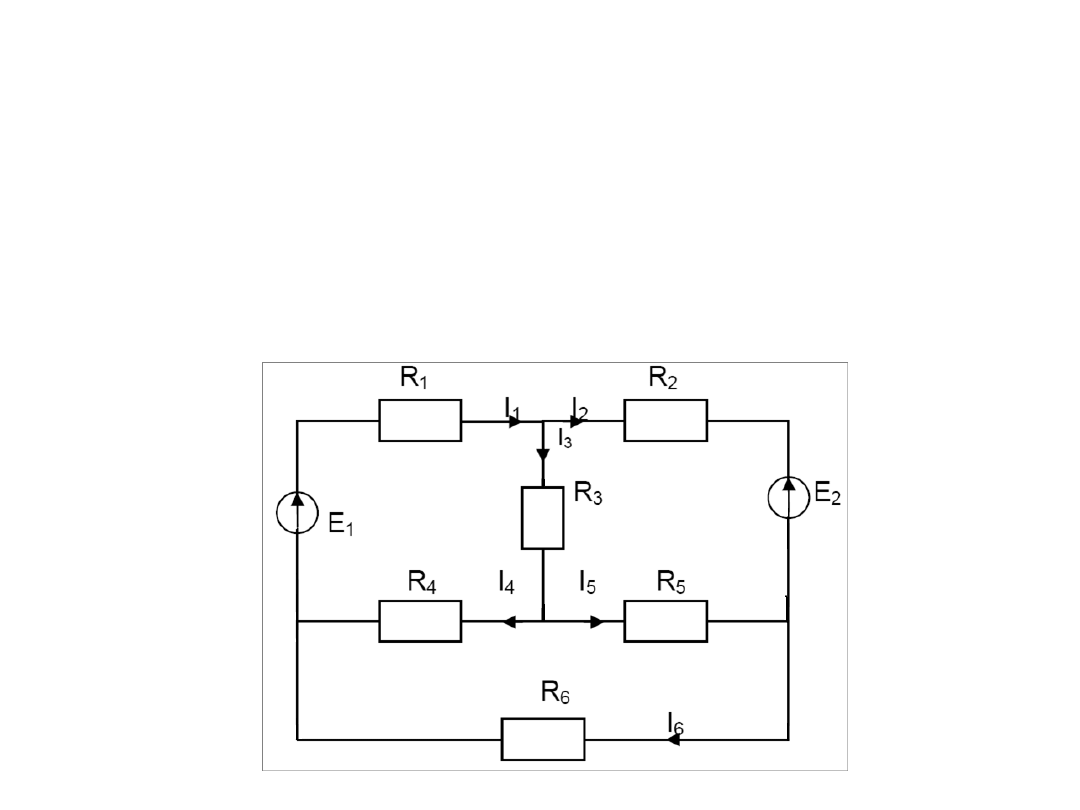
METODA PRZEKSZTALCENIA

SIECI

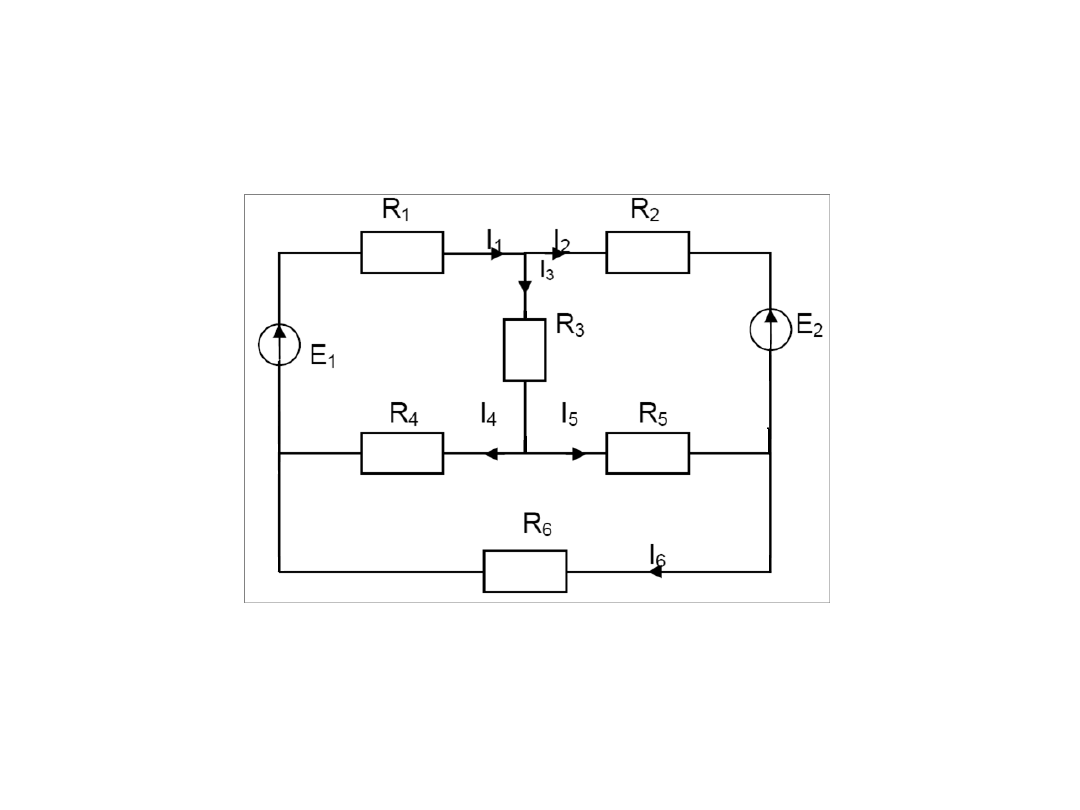
Zadanie 2

 

Oblicz

wartość prądów gałęziowych

(I

1

, I

2

, I

3

, I

4

, I

5

, I

6

) w

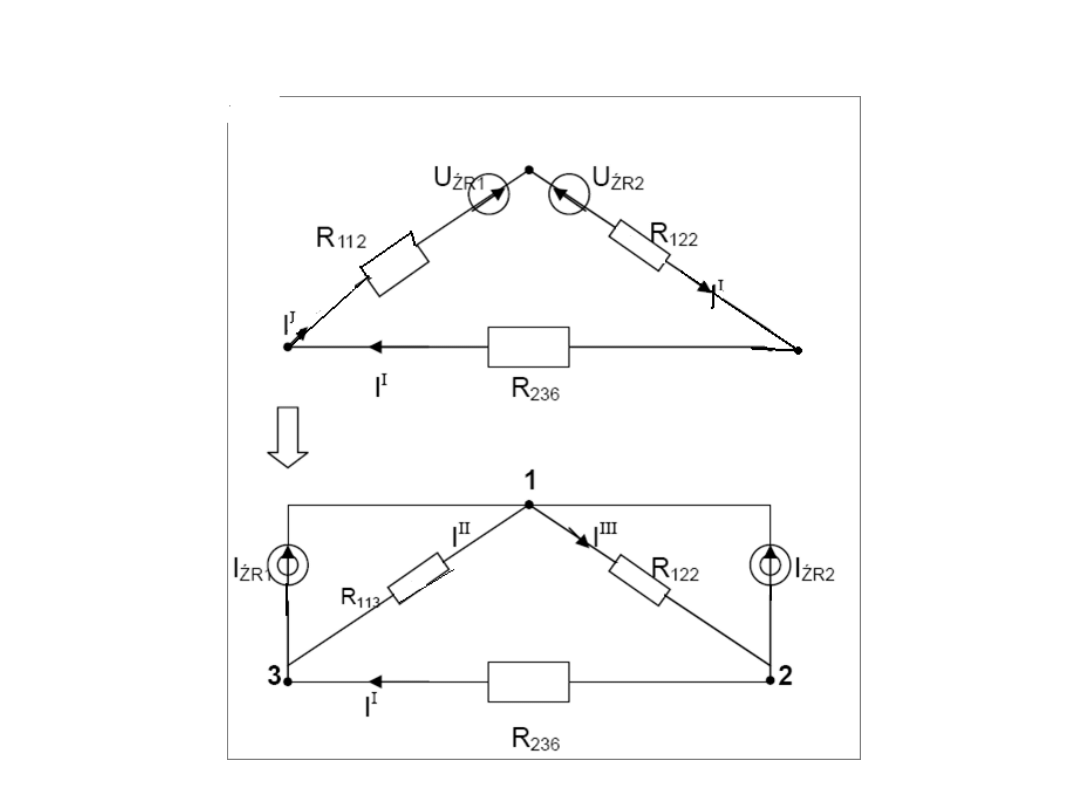
danym obwodzie posługując się

metodą przekształcania

sieci (z zamianą źródeł)

.

Dane: R

1

= 3 Ω, R

2

= 3 Ω, R

3

= 3 Ω, R

4

= 3 Ω, R

5

= 3 Ω, R

6

= 3

Ω, E

1

= 12V, E

2

= 6V

1

I

I

I

I

I

I

I

II

I

III

I

I

I

f

I

c

I

a

I

b

I

e

I

d

 

2 12 2 10

4

3

3 3

3

A

-

=

-

=

10

3

A

2 6 2 8

2

3 3 3 3

A

-

= + =

1 2

12

1

2

3

9

3 3

9

3

RR

R

R R

R

= + +

+ +

=

=

W

2 3

23

2

3

1

9

3 3

9

3

R R

R

R R

R

= + +

+ +

=

=

W

3 1

31

3

1

2

9

3 3

9

3

R R

R

R R

R

= + +

+ +

=

=

W

Dla węzła 3 z I prawa Kirchoffa

I’ + I’’ - I

ŹR1

= 0

, I

ŹR1

= 4A

I’’ = - I’+4 =

I’’ =

Dla węzła 2 z I prawa Kirchoffa

- I’ + I’’’ - I

ŹR2

= 0

, I

ŹR2

= 2A

I’’’ = 2+I’ =

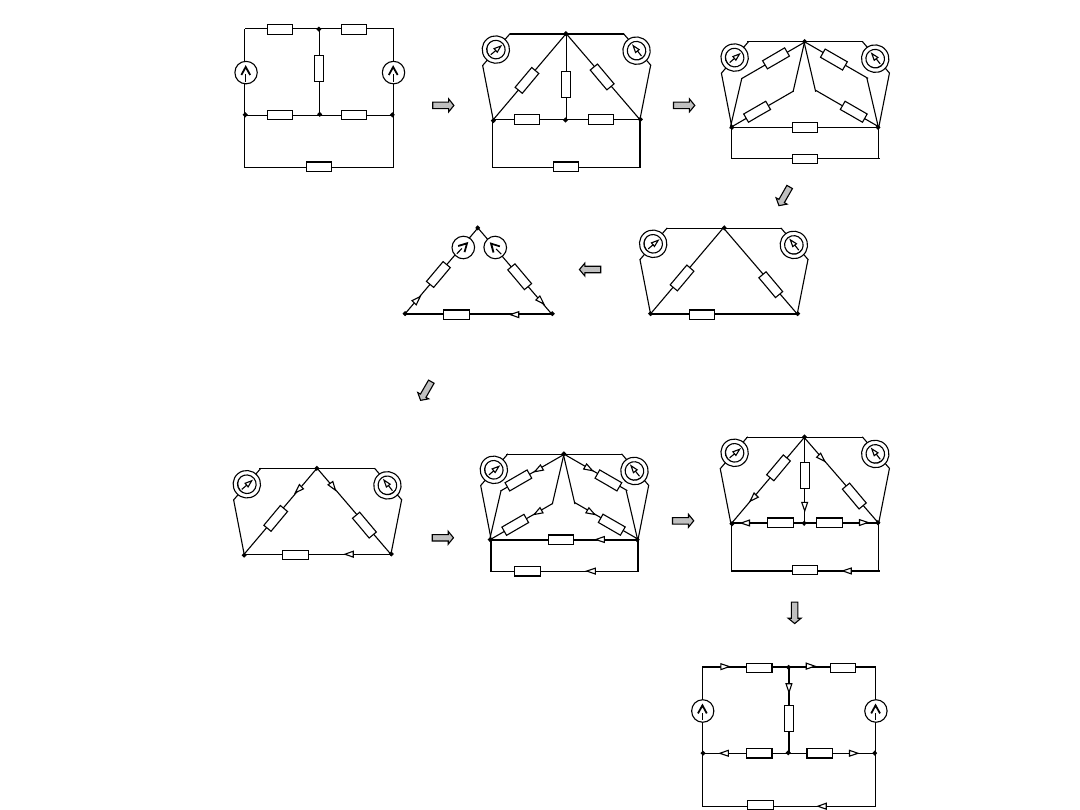
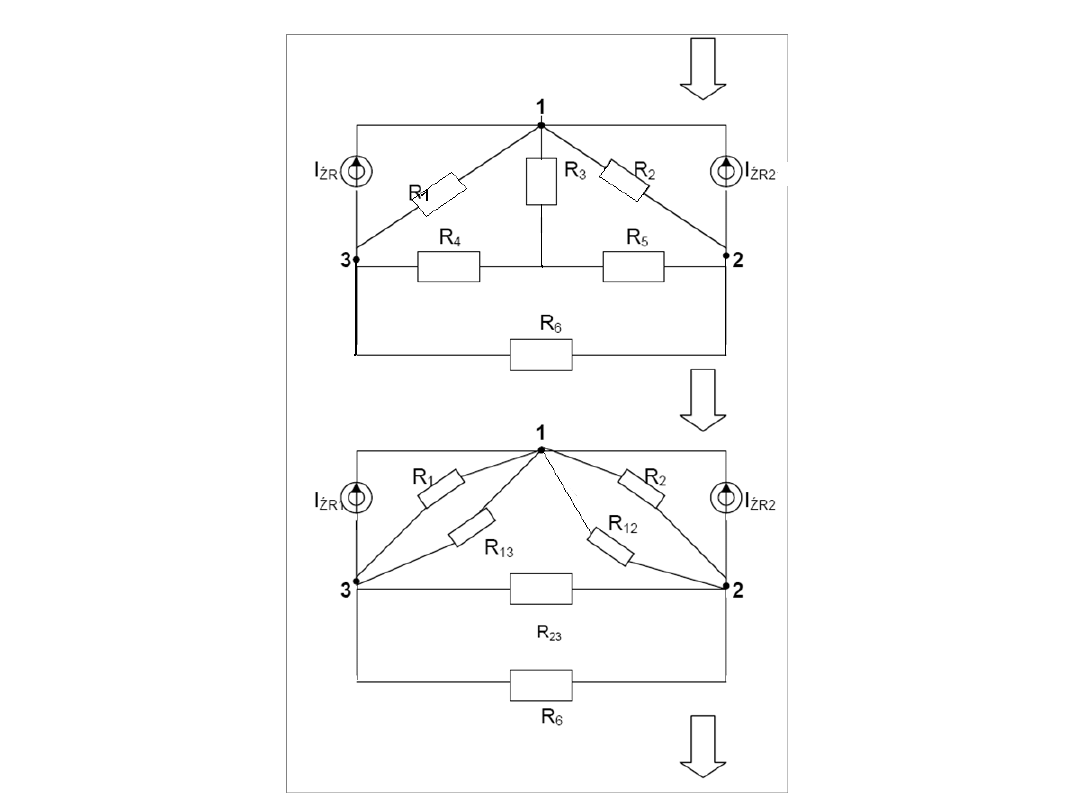
Przy zamianie λ na ∆ mają zastosowanie następujące
ogólne wzory „rezystancyjne”:

113

1

13

1

1

1

1 1 3 1 4

3 9

9

9

R

R

R

+

=

+

= + =

=

113

9

2,25

4

R = =

W

122

12

2

1

1

1

1 1 4
9 3 9

R

R

R

=

+

= + =

122

9

2,25

4

R = =

W

236

23

6

1

1

1

1 1 4
9 3 9

R

R

R

=

+

= + =

236

9

2,25

4

R = =

W

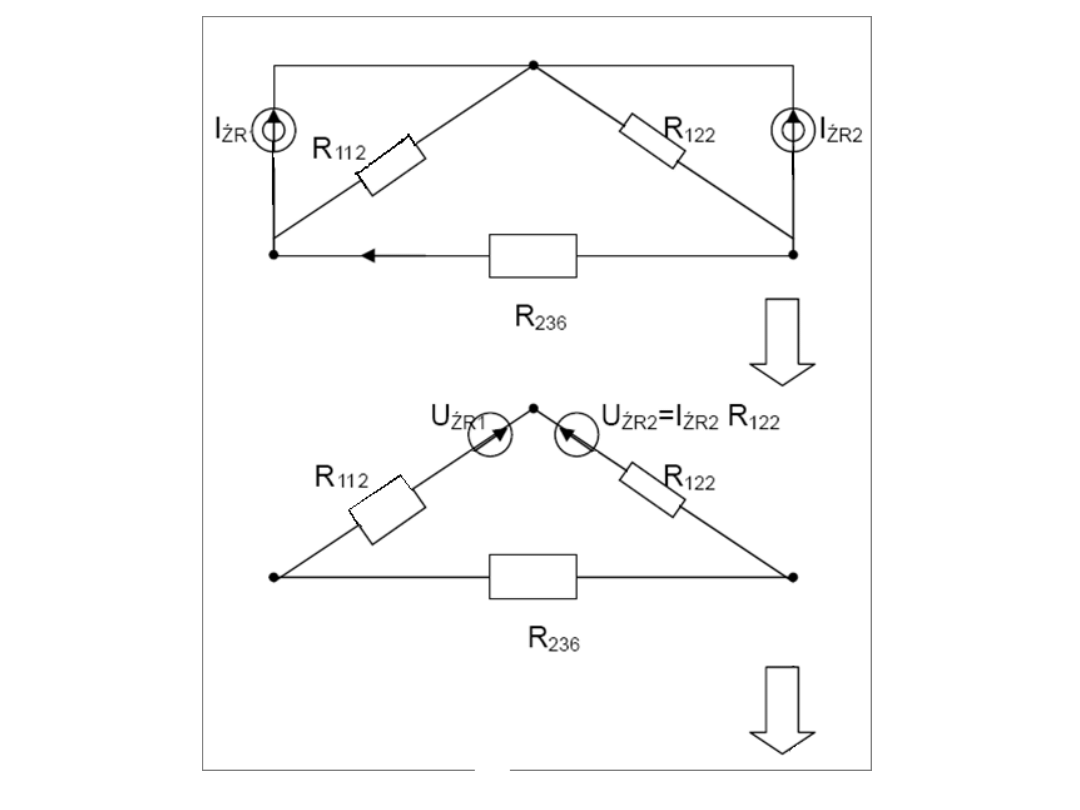
1

1

1

4

ŹR

E

I

R

A

=

=

2

2

2

6

2

3

ŹR

E

I

R

A

= =

=

=>

=>

=>

R

Z

= R

113

+ R

112

+ R

236

= 2,25 + 2,25 + 2,25 = 6,75 Ω

U

ŹR1

= I

ŹR1

·R

113

= 4·2,25 = 9V

U

ŹR2

= I

ŹR2

·R

122

= 2·2,25 = 4,5V

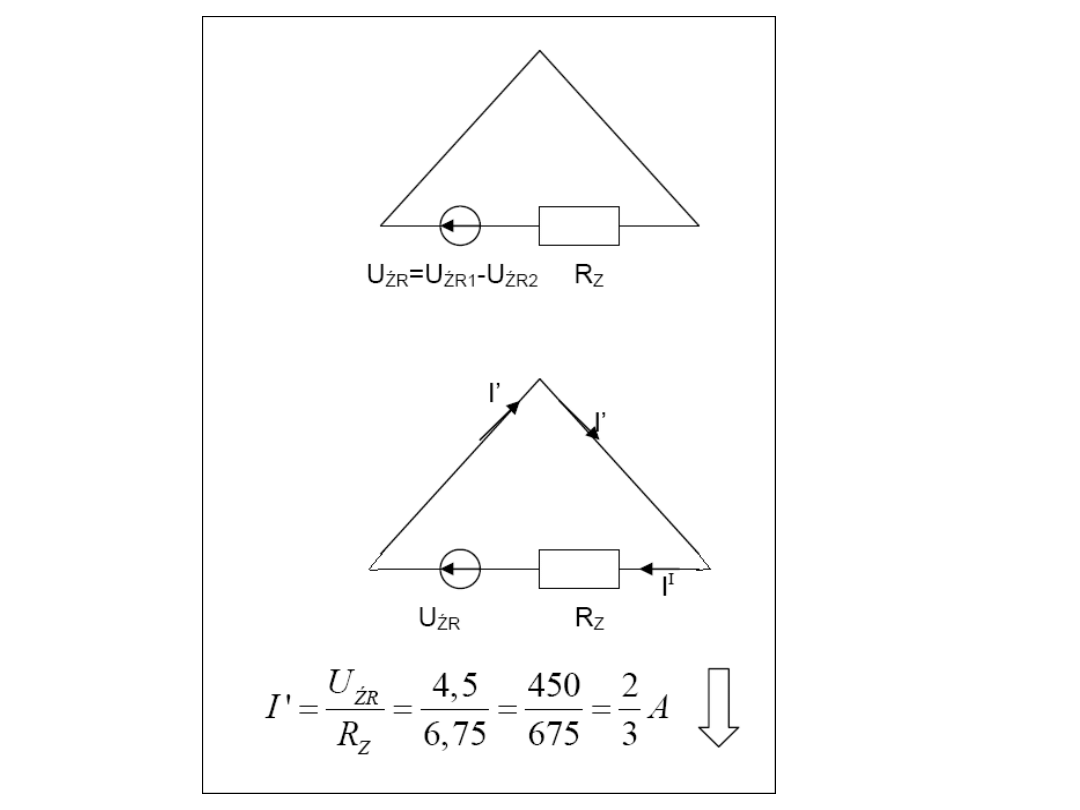
U

ŹR

= U

ŹR1

-U

ŹR2

= 9 – 4,5 = 4,5V

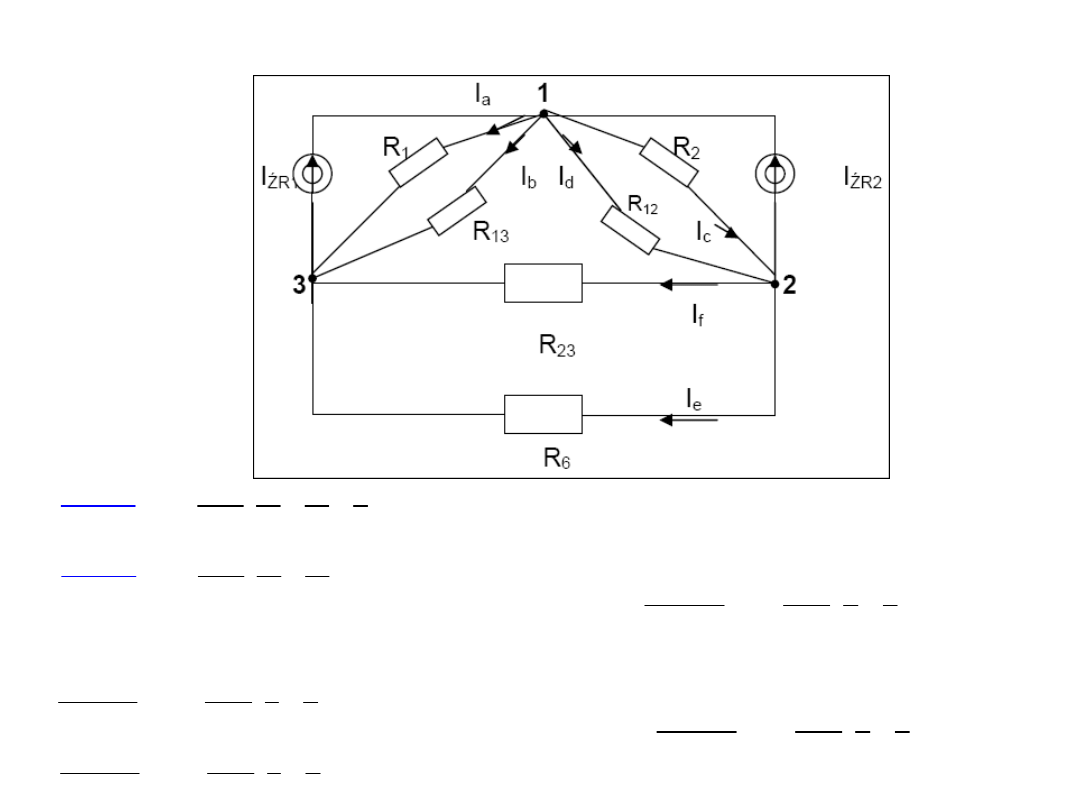
Korzystamy z r-ń na dzielnik prądu

1

1

13

13

1

13

3 10 10 5

3 9 3 12 6

9 10 15

2,5

3 9 3

6

II

b

II

a

R

I

I

R R

R

I

I

R

A

A

R

�

=

=

�

� =

=

�

+

�

�

�

=

� =

=

+

+

=

�

�

+

�

12

12

2

2

12

2

9

8 6

2

9 3 3 3

3 8 2

9 3 3 3

III

c

III

d

R

I

I

A

R

R

R

I

I

A

R

R

� =

� =

� = =

�

+

+

�

�

� =

� =

� =

�

+

+

�

23

23

6

9

2 3

0,5

9 3 3 6

I

e

R

I

I

A

R

R

=

� =

� = =

+

+

6

23

6

3

2 1

3 9 3 6

I

f

R

I

I

A

R

R

=

� =

� =

+

+

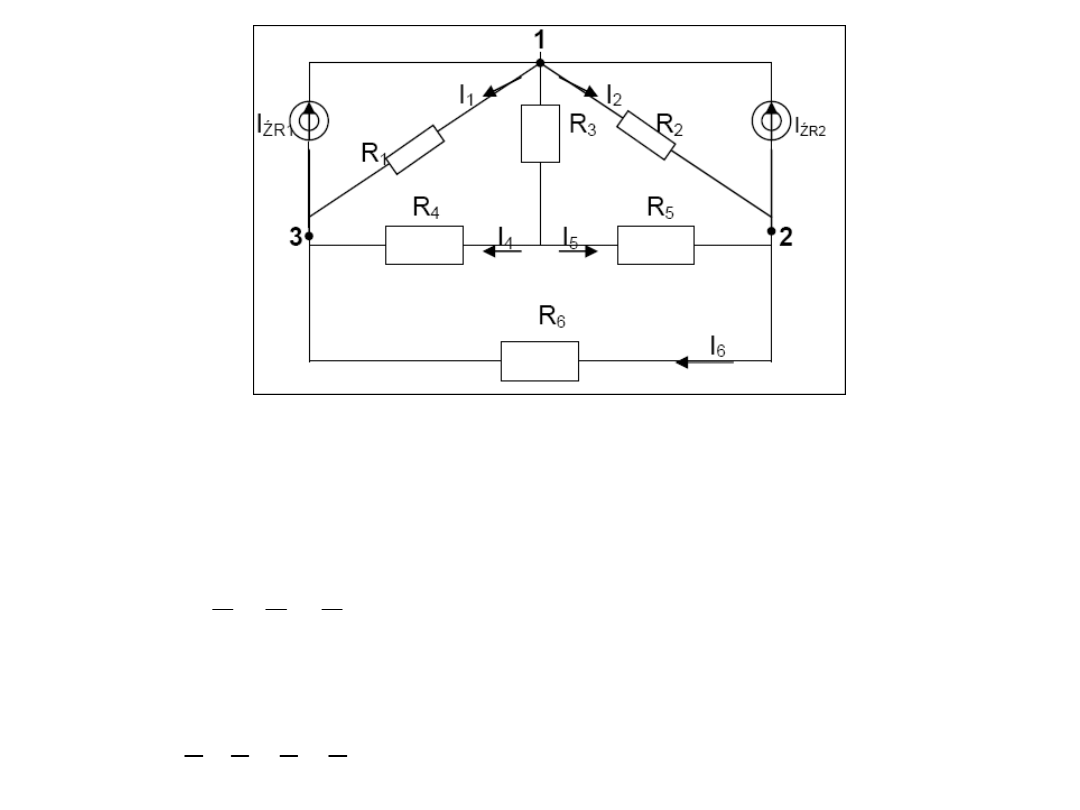
Zakładamy zwroty prądów

I

3

, I

5

, I

1

I

4

, I

2

, I

6

3

5 2 9

1,5

6 3 6

b

d

I

I

I

A

= + = + = =

(Przez rezystor R

3

płynie prąd I

b

oraz I

d

)

5

2 1 3 1

0,5

3 6 6 2

d

f

I

I

I

A

= -

= -

= = =

1

1

4 2,5 1,5

a

ŹR

I

I

I

A

=

-

= -

=

4

5 1

1

6 6

b

f

I

I

I

A

= + = + =

(Przez rezystor R

5

płynie prąd I

d

oraz I

f

)

(Przez rezystor R

4

płynie prąd I

b

oraz I

f

)

I

2

= I

c

– I

źr2

= 2-2 = 0

I

6

= I

e

= 0,5A

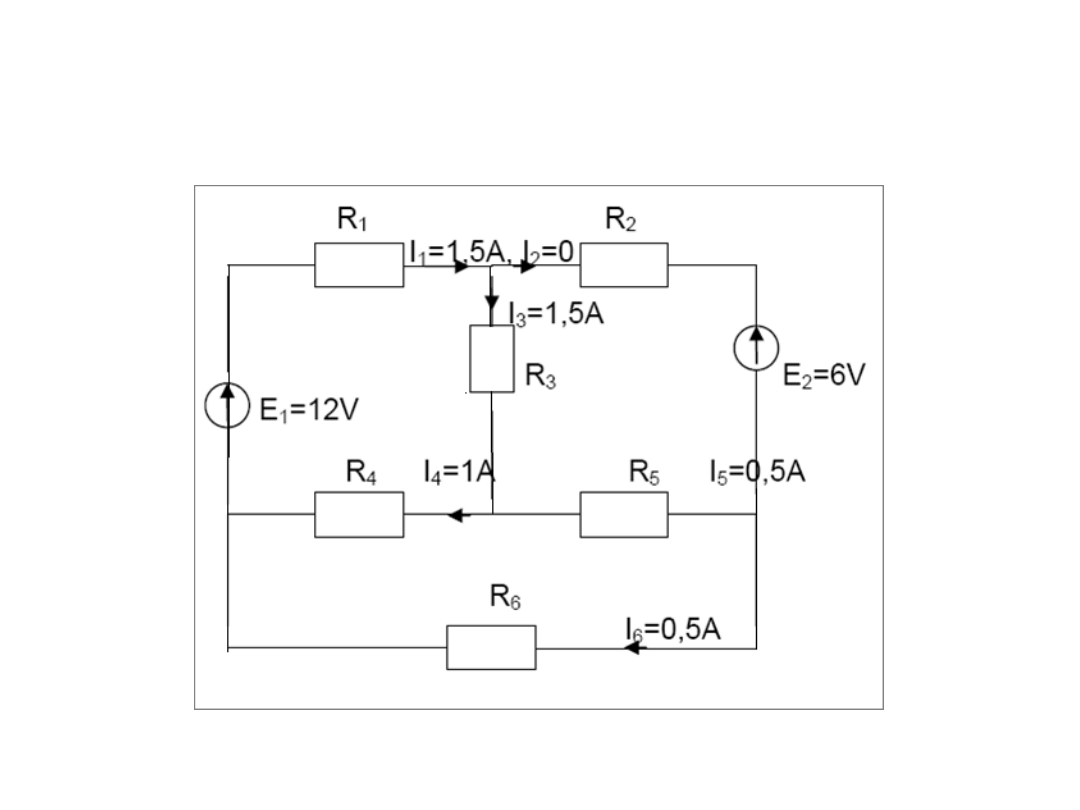
Rozwiązanie zadania

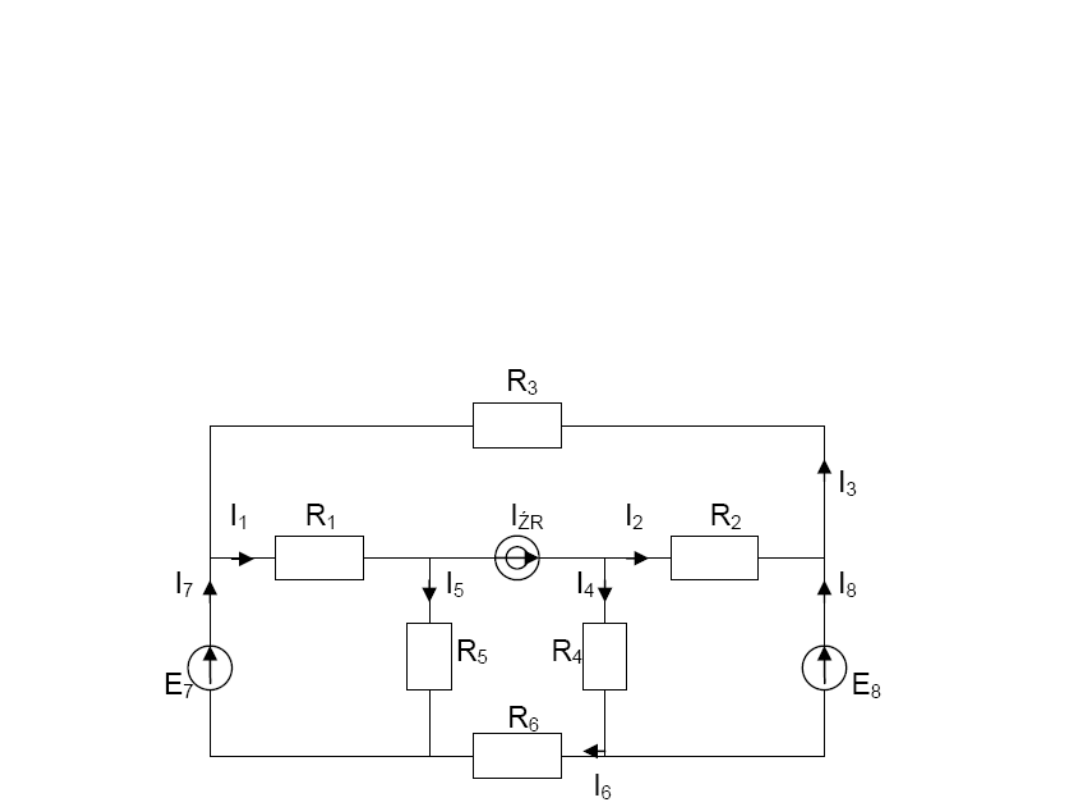
METODA SUPERPOZYCJI

Zadanie 3

Oblicz

wartość prądów gałęziowych

(I

1

, I

2

, I

3

, I

4

, I

5

, I

6

, I

7

, I

8

) w

danym obwodzie

stosując metodę superpozycji

.

Dane: R

1

= 1 Ω, R

2

= 2 Ω, R

3

= 4 Ω, R

4

= 4 Ω, R

5

= 5 Ω, R

6

= 6 Ω,

E

7

= 18V, E

8

= 36V, I

ŹR

= 12A

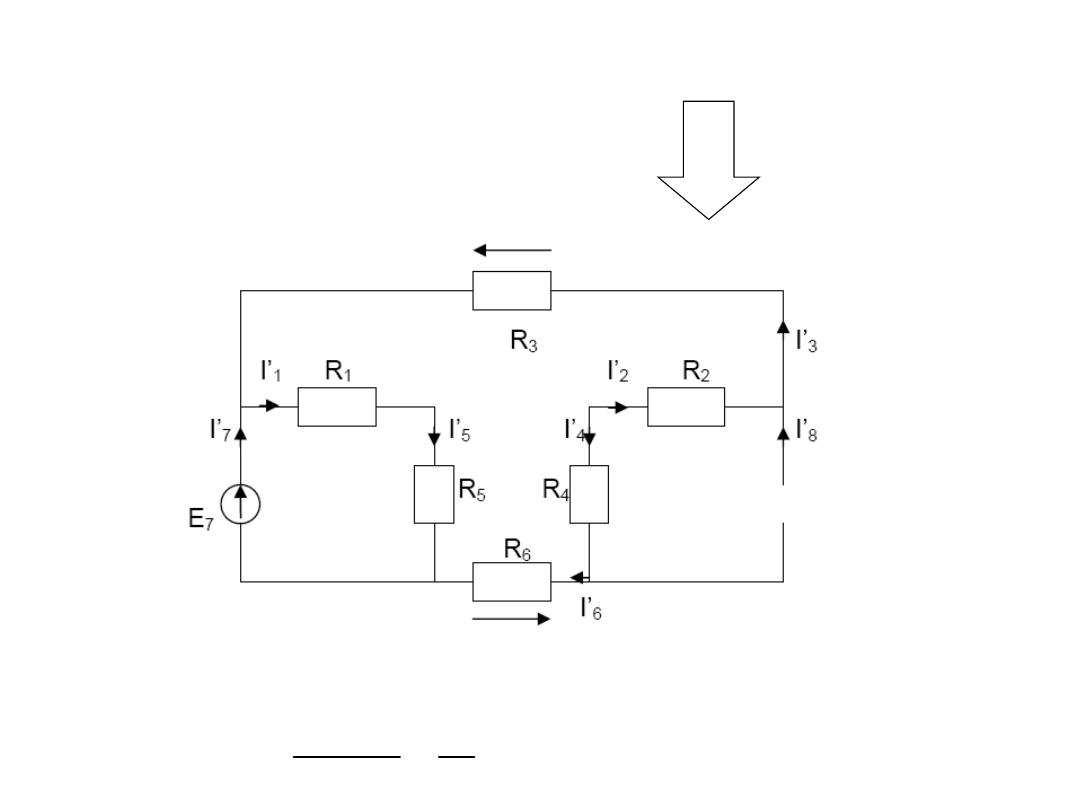
I

rozwiązanie

- rozwieramy źródło prądowe I

ŹR

- zwieramy źródło napięciowe E

8

- obliczamy wszystkie prądy gałęziowe

I

’

– Prąd w gałęziach dla I rozwiązania

'

'

7

1

5

1

5

18

3

6

E

I

I

A

R R

= =

=

=

+

(

)

2

4

24

2

4

2

4

2

4

1

1

1

1

1

1

1

R

R

R

R

R

R

R

R

R

+

+

�

�

=

+ =

+ =

+

+

+

�

(

)

2

4

2

4

24

2

4

2

4

0

1

1

R

R

R

R

R

R

R

R

R

+

+

�

=

=

=

+

+

�

+ +

�

'

7

3

3

6

18

2

3 6

E

I

A

R R

-

=

=

=

+

+

=>

I’

3

= -2A

Gałąź 8 nie stanowi żadnego oporu

, stąd prąd I’

8

= I’

3

= -2A, ponieważ w gałęzi 8 płynie

cały prąd I’

3

stąd w gałęzi drugiej i czwartej nie płynie żaden prąd.

I’

2

= 0 A , I’

4

= 0 A

I’

7

+ I’

3

- I’

1

= 0

I’

7

= I’

1

- I’

3

= 3 – (-2) = 5A

I’

6

= - I’

3

= -(-2) = 2A

W związku z powyższym prądy w gałęziach 1-8 dla I rozwiązania wynoszą
odpowiednio:

I’

1

= 3A, I’

2

= 0, I’

3

= -2A, I’

4

= 0, I’

5

= 3A, I’

6

= 2A, I’

7

= 5A, I’

8

= -2A

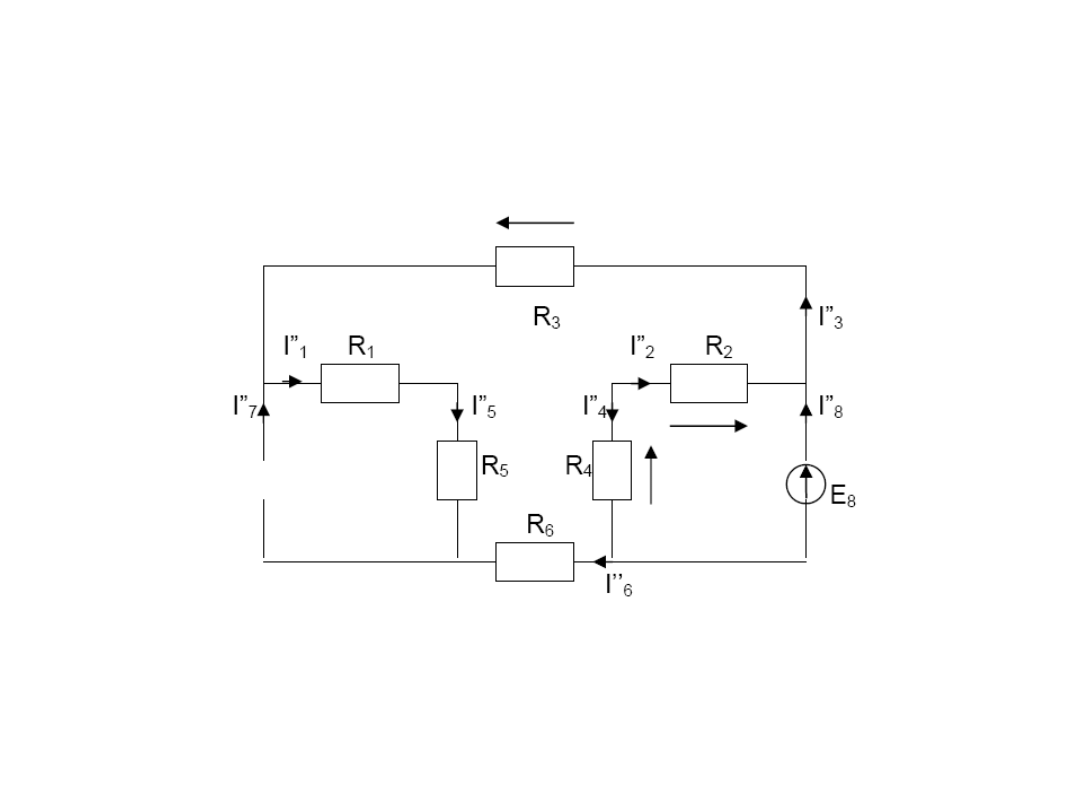
II rozwiązanie

Rozwieramy źródło prądowe I

ŹR

, zwieramy źródło napięciowe E

7

''

''

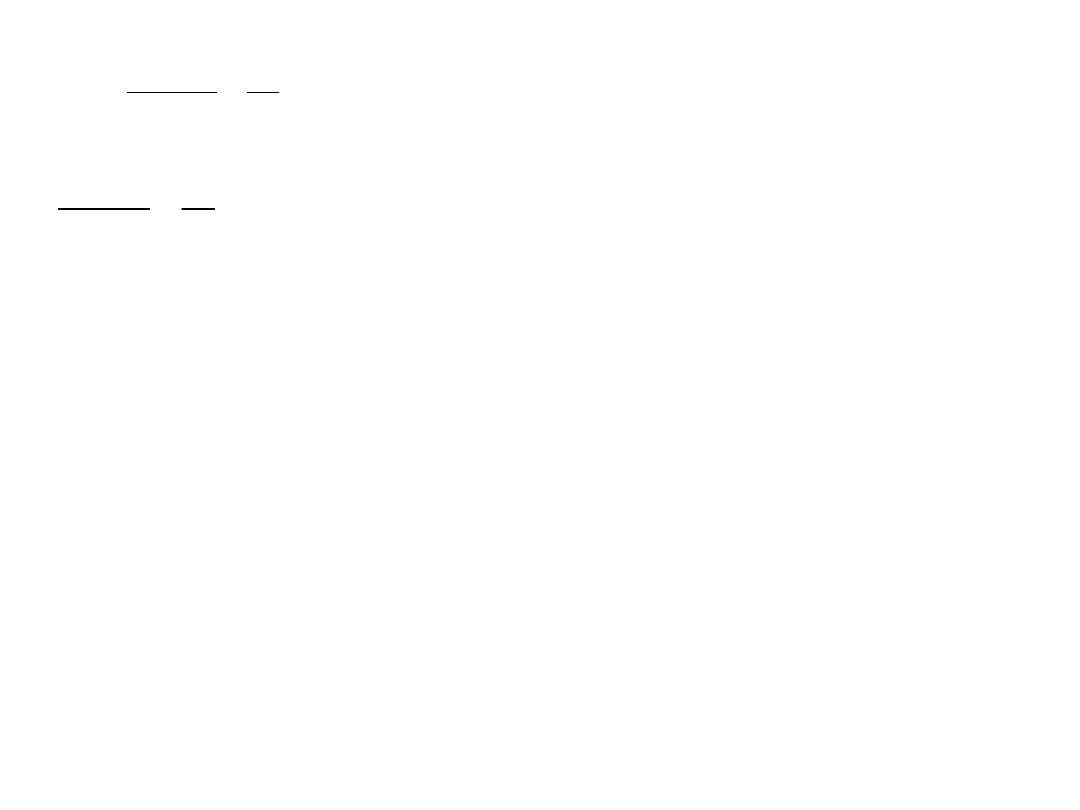
8

4

2

2

4

36

6

6

E

I

I

A

R

R

=-

=

=

=

+

''

8

3

3

6

36

4

9

E

I

A

R R

=

=

=

+

=>

I’’

2

= -6A

I’’

6

= -I’’

3

= -4A, I

7

’’

= -I

3

’’

= -4A,

I’’

1

= I’’

5

= 0

I’’

8

+ I’’

2

= I’’

3

I’’

8

= I’’

3

- I’’

2

= 4-(-6)=10A

Stąd prądy w gałęziach dla II rozwiązania wynoszą odpowiednio:

I’’

1

= 0, I’’

2

= -6A, I’’

3

= 4A, I’’

4

= 6A, I’’

5

= 0, I’’

6

= -4A, I’’

7

= -4A, I’’

8

= 10A

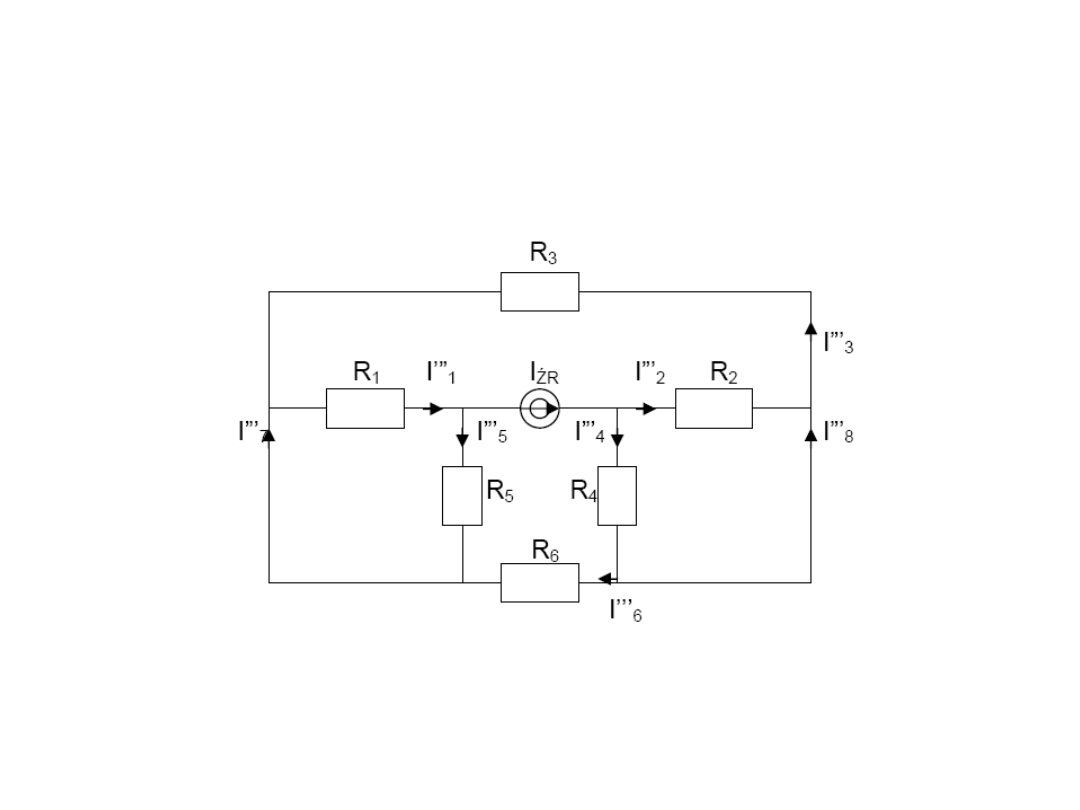
III rozwiązanie

Zwieramy źródła napięciowe E

7

i E

8

Korzystamy z wzorów na dzielnik prądu

'''

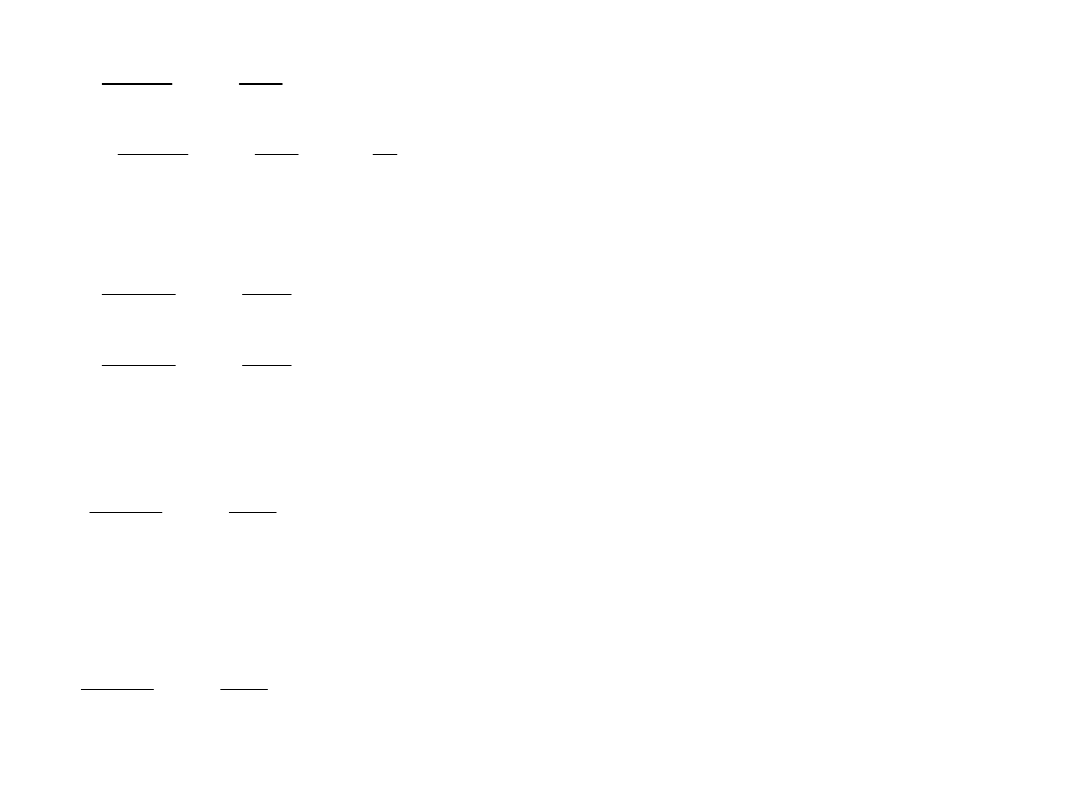
5

1

1

5

'''

1

5

1

5

5

12 10

1 5

1

12

12

2

1 5

6

ŹR

ŹR

R

I

I

A

R R

R

I

I

A

R R

� =

� =

� =

�

+

+

�

�

-

� =-

� =

� =-

=-

�

+

+

�

'''

4

2

4

2

'''

2

4

4

2

4

12 8

4 2

2

12 4

4 2

ŹR

ŹR

R

I

I

A

R

R

R

I

I

A

R

R

� =

� =

� =

�

+

+

�

�

� =

� =

� =

�

+

+

�

'''

6

3

3

6

6

12 8

3 6

ŹR

R

I

I

A

R R

=

� =

� =

+

+

'''

3

6

3

6

3

12 4

3 6

ŹR

R

I

I

A

R R

=

� =

� =

+

+

I’’’

7

= I’’’

5

+ I’’’

6

= -2 + 4 = 2A

I’’’

4

- I’’’

6

- I’’’

8

= 0

I’’’

8

= I’’’

4

- I’’’

6

= 4 – 4 = 0

Stąd prądy gałęziowe dla 3 rozwiązania

I’’’

1

= 10A, I’’’

2

= 8A, I’’’

3

= 8A, I’’’

4

= 4A, I’’’

5

= -2A, I’’’

6

= 4A, I’’’

7

= 2A, I’’’

8

= 0

Wyniki końcowe ( superpozycja rozwiązań)

I

1

= I’

1

+ I’’

1

+ I’’’

1

= 3 + 0 + 10 = 13A,

I

2

= I’

2

+ I’’

2

+ I’’’

2

= 0 - 6 + 8 = 2A,

I

3

= I’

3

+ I’’

3

+ I’’’

3

= -2 + 4 + 8 = 10A,

I

4

= I’

4

+ I’’

4

+ I’’’

4

= 0 + 6 + 4 = 10A,

I

5

= I’

5

+ I’’

5

+ I’’’

5

= 3 + 0 - 2 = 1A,

I

6

= I’

6

+ I’’

6

+ I’’’

6

= 2 – 4 + 4 = 2A,

I

7

= I’

7

+ I’’

7

+ I’’’

7

= 5 – 5 + 2 = 3A,

I

8

= I’

8

+ I’’

8

+ I’’’

8

= -2 + 10 + 0 = 8A

METODA PRĄDÓW OCZKOWYCH

Równanie macierzowe obliczania prądów oczkowych

R · I = E

R – macierz rezystancji własnych i wzajemnych,
I – macierz prądów oczkowych,
E – macierz napięć źródłowych oczkowych.

11

12

1

01

11

21

22

2

02

22

1

2

0

. . .
. . .

.

.

. . .

.

.

.

.

.

. . .

.

.

.

.

.

. . .

.

.

.

. . .

n

n

n

n

nn

n

nn

R

R

R

I

E

R

R

R

I

E

R

R

R

I

E

�

� � � � �

�

� � � � �

�

� � � � �

�

� � � � �

�

=

�

� � � � �

�

� � � � �

�

� � � � �

�

� � � � �

�

� � � � �

gdzie:

n- liczba oczek liniowo niezależnych
I

01

– prąd oczka 1-szego

E

KK

–

napięcie źródłowe k-tego oczka

jest równa sumie napięć

źródłowych należących do tego oczka.

R

KK

–

rezystancja własna k-tego oczka

jest równa sumie

rezystancji wszystkich gałęzi należących do tego oczka. Rezystancje
własne oczek przyjmujemy zawsze ze znakiem (+).

R

KL

–

rezystancja wzajemna oczka k-tego z oczkiem l-tym

jest

równa rezystancji gałęzi wspólnej oczka k-tego i l-tego.

Znak rezystancji wzajemnej zależy od zwrotów prądów
oczkowych w gałęzi wspólnej.

Jeżeli zwroty prądów oczkowych są

jednakowe to przyjmujemy znak (+) rezystancji wzajemnej.
Natomiast jeżeli zwroty prądów oczkowych są przeciwne to znak
rezystancji wzajemnej przyjmujemy (-).

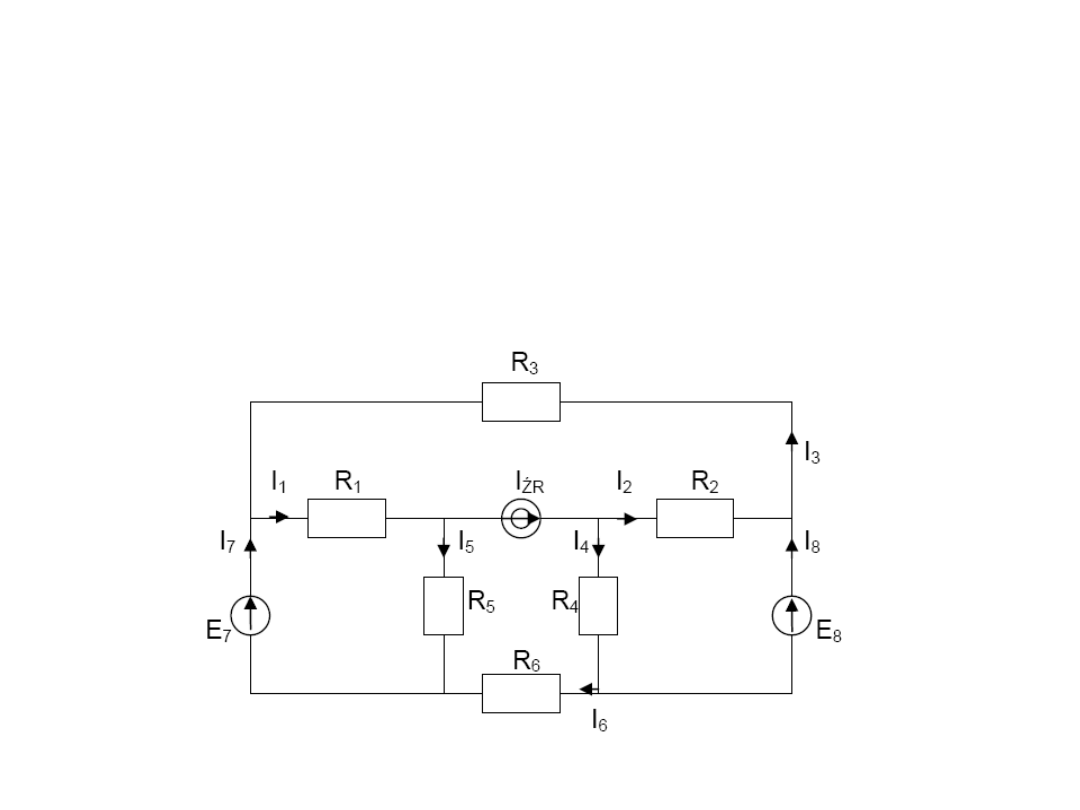
Zadanie 5

Oblicz

wartość prądów gałęziowych

(I

1

, I

2

, I

3

, I

4

, I

5

, I

6

, I

7

, I

8

) w

danym obwodzie

stosując metodę oczkową

.

Dane:
R

1

= 1 Ω, R

2

= 2 Ω, R

3

= 3 Ω, R

4

= 4 Ω, R

5

= 5 Ω,

R

6

= 6 Ω, E

7

= 18V, E

8

= 36V,

I

ŹR

= 12A

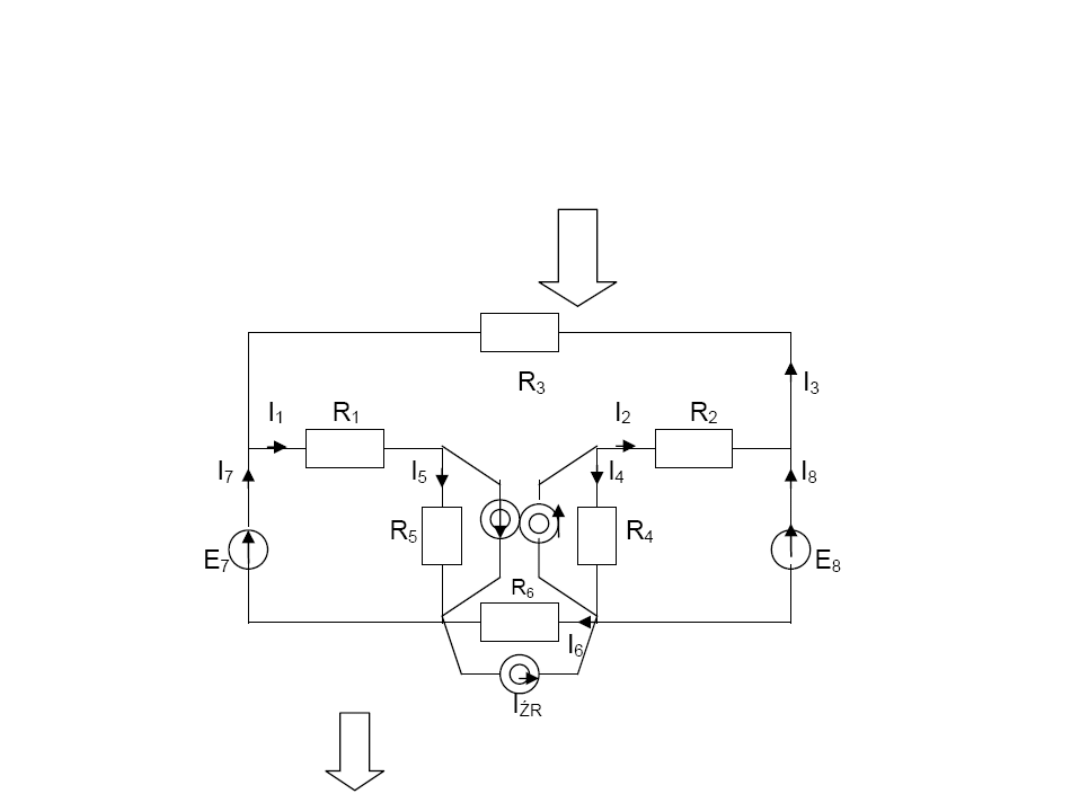
1. etap

– „Przenieść” występujące w obwodzie „samoistne”

źródła prądowe, a następnie sprowadzić wszystkie gałęzie do
postaci napięciowej.

2. etap

– Obliczyć prądy oczkowe a następnie prądy gałęziowe.

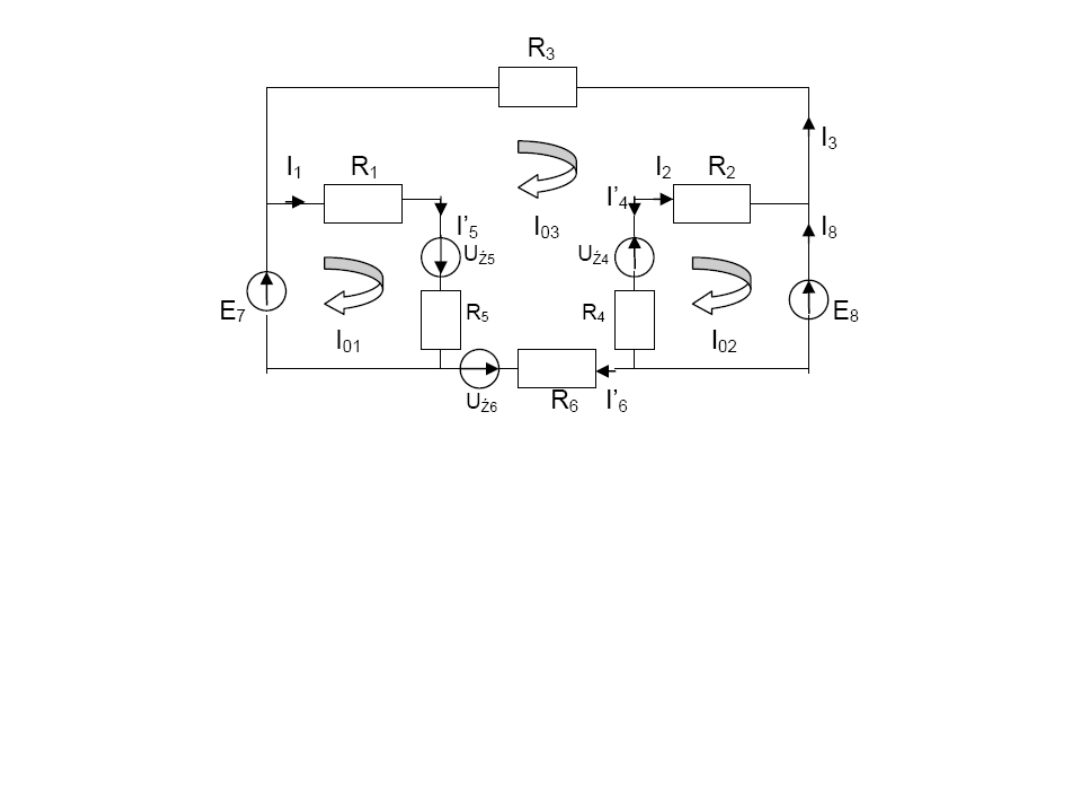
U

ŹR5

= R

5

·I

ŹR

= 5·12 = 60V,

U

ŹR6

= R

6

·I

ŹR

= 6·12 = 72V,

U

ŹR4

= R

4

·I

ŹR

= 4·12 = 48V.

R

11

= R

1

+R

5

= 1+5 = 6,

R

22

= R

4

+R

2

= 4+2 = 6,

R

33

= R

3

+R

2

+R

4

+R

6

+R

5

+R

1

= 3+2+4+6+5+1 = 21

R

12

= R

21

= 0,

R

31

= R

13

= -(R

1

+R

5

) = -(1+5) = -6,

R

23

= R

32

= -(R

4

+R

2

) = -(4+2) = -6,

E

11

= E

7

+U

Ź5

= 18+60 = 78V,

E

22

= U

Ź4

– E

8

= 48-36 = 12V,

E

33

= - (U

Ź4

+ U

Ź6

+ U

Ź5

) = - (48+72+60) = -180

01

02

03

6

0

6

78

0

6

6

12

6

6 21

180

I

I
I

-

�

� � � �

�

�

� � � �

�

-

�

=

�

� � � �

�

�

� � � �

�

-

-

-

�

� � � �

�

(

)

6

0

6

6

6

0 6

0

6

6

6

6

6 21

6 6

6

6 21

6 6 21 6 6 216 6 90 216 540 216 324 108 3

W

-

�

�

-

�

� �

�

�

�

=

-

=

-

=

�

� �

�

�

�

-

-

�

� �

�

�

�

-

-

�

�

� � - � -

= � -

=

-

=

=

�

(

)

(

)

1

78

0

6

6

6

12

6

12

6

6

78

6

78 6 21 36 6

12 6 6 180

6 21

180

6

180

6 21

78 90 6 ( 72 1080) 7020 6 (1080) 7020 6048 972 108 9

W

-

�

�

-

�

� �

�

�

�

=

-

=

-

= � � -

- �-

�+ �

=

�

� �

�

�

�

-

-

-

�

� �

�

�

�

-

-

�

�

= � - �-

+

=

- �

=

-

=

=

�

R·I

0

= E

W = 108·3

W

1

= 108·9

1

01

108 9

3

108 3

W

I

A

W

�

=

=

=

�

(

)

2

6

78

6

12

6

0

6

0

12

0

12

6

6

78

6

180 21

6 21

6

180

6

180 21

6 12 21 6 180 78 (36) 6 (6 12)

4968 2808 432 2592

108 24

W

-

�

�

-

-

�

�

�

� �

�

�

�

=

-

=

-

-

=

�

�

�

� �

�

�

�

-

-

-

-

�

�

�

� �

�

�

�

-

-

�

�

� � - �

+ �

- � � =-

+

-

=

=-

�

2

02

108 24

8

108 3

W

I

A

W

�

=

=-

=-

�

(

)

( )

3

6

0

78

6

12

0

6

0

6

12

6

78

6

6 180 6 12 78 36

6

180

6

6

6

6

180

6( 1008 72) 2808

6048 2808

108 30

W

-

�

�

�

�

�

�

�

�

=

=

+

= �- � + � +

=

�

�

�

�

�

�

-

-

-

-

�

�

�

�

�

�

-

-

-

�

�

= -

+

+

=-

+

=-

�

3

03

108 30

10

108 3

W

I

A

W

�

=

=-

=-

�

Prądy gałęziowe wyrażamy przez prądy oczkowe

I

1

= I

01

– I

03

= 3-(-10) = 13A,

I

2

= -(I

03

– I

02

)= -[-10-(-8)]) = 2A,

I

3

= -I

03

=-(-10) = 10A,

I

4

+ I

2

= I

żr

=>

I

4

= 12 – I

2

= 12 – 2 = 10A,

I

1

– I

5

– I

żr

= 0 =>

I

5

= I

1

– 12 = 13 – 12 = 1A,

I’

4

= - I

2

= -2A,

I’

6

= I

03

= -10A,

I’

5

= I

01

– I

03

= 3 – (-10) = 3 + 10 = 13A,

I’

6

= - I

03

= -10A,

I

7

+ I

3

= I

1,

Z I prawa Kirchhoffa

I

7

= I

1

- I

3

= 13 - 10 = 3A,

I

8

= I

3

- I

2

= 10 - 2 = 8, Z I prawa Kirchhoffa

I

4

- I

6

- I

8

= 0,

I

6

= I

4

– I

8

= 10 – 8 = 2A

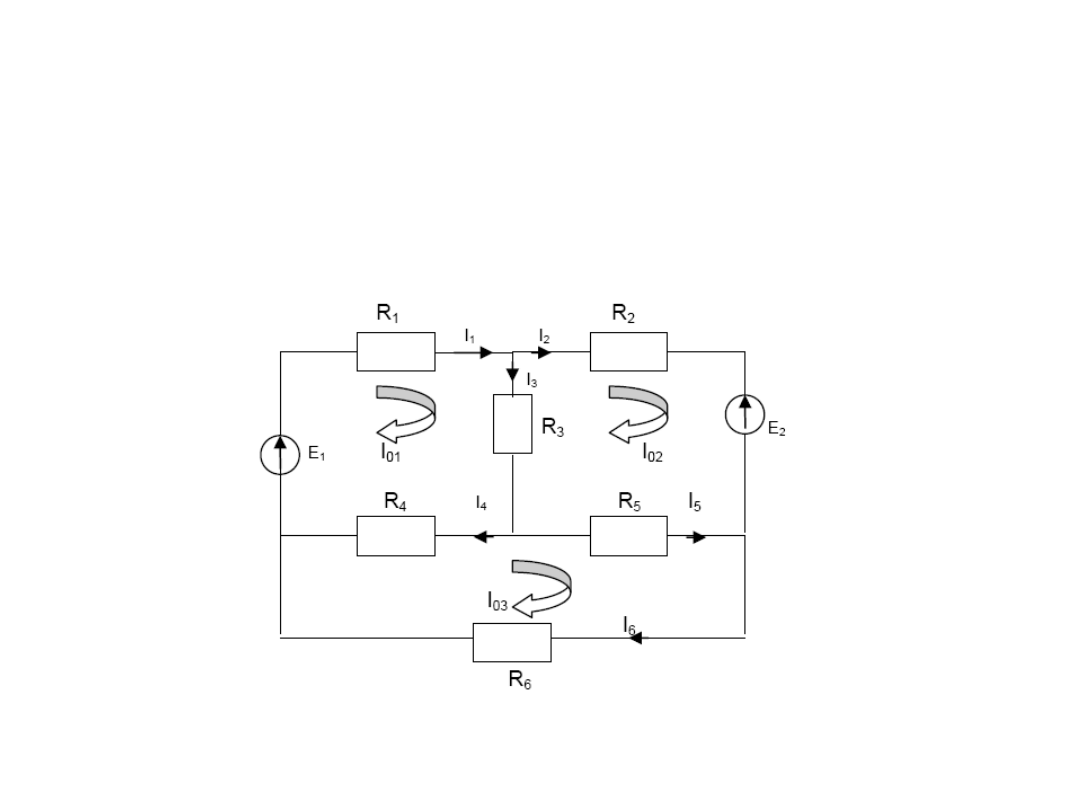
Zadanie 4

Oblicz

wartość prądów gałęziowych

(I

1

, I

2

, I

3

, I

4

, I

5

, I

6

) w danym

obwodzie

stosując metodę oczkową

.

Dane: R

1

= R

2

= R

3

= R

4

= R

5

= R

6

= 3 Ω, E

1

= 12V, E

2

= 6V,

R·I

0

= E

R

11

= R

1

+R

3

+ R

4

= 3 + 3 + 3 = 9 Ω,

R

22

= R

2

+R

5

+ R

3

= 3 + 3 + 3 = 9 Ω,

R

33

= R

4

+R

5

+ R

6

= 3 + 3 + 3 = 9 Ω

R

12

= R

21

= -R

3

= - 3 Ω,

R

13

= R

31

= -R

4

= - 3 Ω,

R

23

= R

32

= -R

5

= - 3 Ω

E

11

= E

1

= 12V,

E

22

= -E

2

= -6V,

E

33

= 0

11

12

13

01

11

21

22

23

02

22

31

32

33

03

33

01

02

03

9

3

3

12

3 9

3

6

3

3 9

0

R

R

R

I

E

R

R

R

I

E

R

R

R

I

E

I

I
I

�

� � � � �

�

� � � � �

�

=

�

� � � � �

�

� � � � �

�

� � � � �

-

-

�

� � � � �

�

� � � � �

-

-

�

= -

�

� � � � �

�

� � � � �

-

-

�

� � � � �

(

)

9

3

3

9

3

9

3

3 9

3 9

3

9

3

3

3 9

3 9

3

3

3

3 9

9 81 9 3 ( 27 9) 3 (9 27) 9 72 108 108 648 216 27 16

W

-

-

�

�

-

-

-

�

� �

� �

�

�

�

= -

-

=

+

-

=

�

� �

� �

�

�

�

-

-

-

-

�

� �

� �

�

�

�

-

-

�

�

� -

+ �-

-

- � +

= � -

-

=

-

= �

(

)

1

12

3

3

9

3

6

3

6 9

6 9

3

12

3

3

3 9

0

9

0

3

0

3 9

12 81 9 3 ( 54) 3 (18) 864 162 54 864 216 648 27 24

W

-

-

�

�

-

-

-

-

�

� �

� �

�

�

�

= -

-

=

+

-

=

�

� �

� �

�

�

�

-

-

�

� �

� �

�

�

�

-

�

�

� -

+ �-

- � =

-

-

=

-

=

= �

1

01

27 24

1,5

27 16

W

I

A

W

�

=

=

=

�

(

)

2

9 12

3

6

3

3

3

3

6

3

6

3

9

12

3

0

9

3 9

3 0

3 0

9

9

54 12 ( 27 9) 3 ( 18)

486 432 54 0

W

-

�

�

-

-

-

-

-

-

�

�

�

� �

�

�

�

= -

-

-

=

-

-

=

�

�

�

� �

�

�

�

-

-

�

�

�

� �

�

�

�

-

�

�

�-

-

�-

-

- �-

=-

+

+ =

2

02

0

0

27 16

W

I

A

W

=

=

=

�

(

)

3

9

3 12

9

6

3

6

3 9

3 9

6

9

3

12

3 0

3 0

3

3

3

3 0

9

18 3 ( 18) 12 (9 27)

162 54 432 216 27 8

W

-

�

�

-

-

-

-

�

� �

�

�

�

�

�

= -

-

=

+

+

=

�

� �

�

�

�

�

�

-

-

-

-

�

� �

�

�

�

�

�

-

-

�

�

�-

+ �-

+ � +

=-

-

+

=

= �

3

03

27 8

0,5

27 16

W

I

A

W

�

=

=-

=

�

Prądy gałęziowe wyrażamy przez prądy oczkowe

I

1

= I

01

= 1,5A,

I

2

= I

02

= 0A,

I

3

= I

01

– I

02

= 1,5 - 0 = 1,5A,

I

4

= I

02

– I

03

= 0 – 0,5 = -0,5A,

I

5

= I

01

– I

03

= 1,5 – 0,5 = 1,0A,

I

6

= I

03

= 0,5A

METODA POTENCJALÓW

WĘZLOWYCH

(metoda węzłowa)

Równanie macierzowe obliczania potencjałów węzłowych

Y · V = I

ŹR

Y – macierz admitancji własnych i wzajemnych,
V – macierz potencjałów węzłowych,
I

ŹR

– macierz prądów źródłowych.

11

12

1

01

1

21

22

2

02

2

1

2

0

. . .
. . .

.

.

.

. . .

.

.

.

.

.

. . .

.

.

.

.

.

. . .

.

.

. . .

n

ŹR

n

ŹR

n

n

nn

n

ŹRn

I

Y

Y

Y

V

I

Y

Y

Y

V

I

Y

Y

Y

V

� �

�

� � �

� �

�

� � �

� �

�

� � �

� �

�

� � �

�

=� �

�

� � �

� �

�

� � �

� �

�

� � �

� �

�

� � �

�

� � � � �

Y –

macierz admitancji własnych i wzajemnych

jest macierzą

kwadratową symetryczną, na głównej przekątnej występują
admitancje własne węzłów ze znakiem (+), poza główną przekątną
admitancje wzajemne węzłów ze znakiem (-).

Y

KK

–

admitancja własna k-tego węzła

jest równa sumie

admitancji gałęzi zbiegającej się w k-tym węźle. Admitancje własne
przyjmujemy ze znakiem (+).

Y

KL

–

admitancja k-tego węzła z węzłem l-tym

jest równa sumie

admitancji wszystkich gałęzi łączących bezpośrednio węzeł l-ty z l-
tym. Admitancje wzajemne przyjmujemy ze znakiem (-).

V –

macierz potencjałów węzłowych

jest macierzą kolumnową o

liczbie wierszy n, równej liczbie węzłów liniowo niezależnych.

I

ŹR

–

macierz prądów źródłowych wypadkowych

jest macierzą

kolumnową o liczbie wierszy n, równej liczbie węzłów liniowo
niezależnych.

I

ŹR

–

prąd źródłowy wypadkowy dla k-tego węzła

jest równy

sumie iloczynów admitancji gałęzi i napięć źródłowych gałęzi
należących do k-tego węzła









E

Y

METODA POTENCJALÓW

WĘZLOWYCH

(metoda węzłowa)

Równanie macierzowe obliczania potencjałów węzłowych

G · V = I

ŹR

G –

macierz konduktancji własnych i wzajemnych,

V –

macierz potencjałów węzłowych,

I

ŹR

–

macierz prądów źródłowych.

11

12

1

01

1

21

22

2

02

2

1

2

0

. . .
. . .

.

.

.

. . .

.

.

.

.

.

. . .

.

.

.

.

.

. . .

.

.

. . .

n

ŹR

n

ŹR

n

n

nn

n

ŹRn

I

G

G

G

V

I

G

G

G

V

I

G

G

G

V

� �

�

� � �

� �

�

� � �

� �

�

� � �

� �

�

� � �

�

=� �

�

� � �

� �

�

� � �

� �

�

� � �

� �

�

� � �

�

� � � � �

G –

macierz konduktancji własnych i wzajemnych

jest macierzą

kwadratową symetryczną, na głównej przekątnej występują
konduktancje własne węzłów ze znakiem (+), poza główną przekątną
konduktancje wzajemne węzłów ze znakiem (-).

G

KK

–

konduktancja własna k-tego węzła

jest równa sumie

konduktancji gałęzi zbiegającej się w k-tym węźle. Konduktancje
własne przyjmujemy ze znakiem (+).

G

KL

–

konduktancja k-tego węzła z węzłem l-tym

jest równa

sumie konduktancji wszystkich gałęzi łączących bezpośrednio węzeł l-
ty z l-tym. Konduktancje wzajemne przyjmujemy ze znakiem (-).

V –

macierz potencjałów węzłowych

jest macierzą kolumnową o

liczbie wierszy n, równej liczbie węzłów liniowo niezależnych.

I

ŹR

–

macierz prądów źródłowych wypadkowych

jest macierzą

kolumnową o liczbie wierszy n, równej liczbie węzłów liniowo
niezależnych.

I

ŹR

–

prąd źródłowy wypadkowy dla k-tego węzła

jest równy

sumie iloczynów konduktancj gałęzi i napięć źródłowych gałęzi
należących do k-tego węzła









E

Y

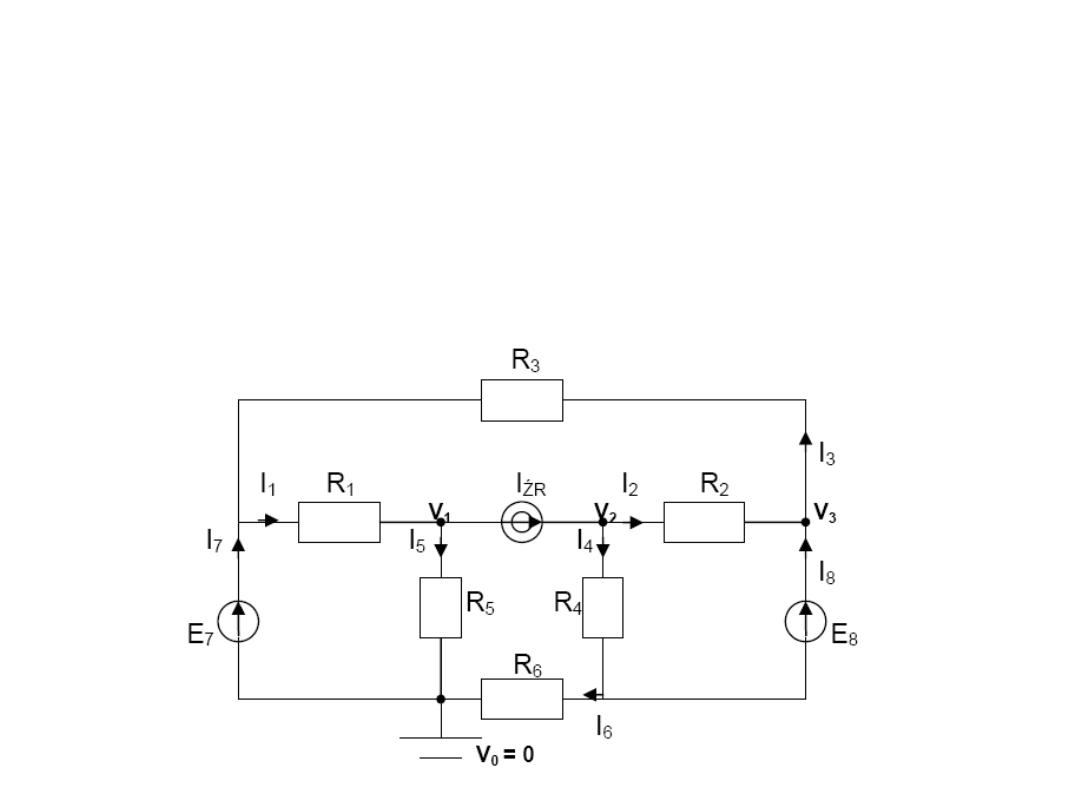
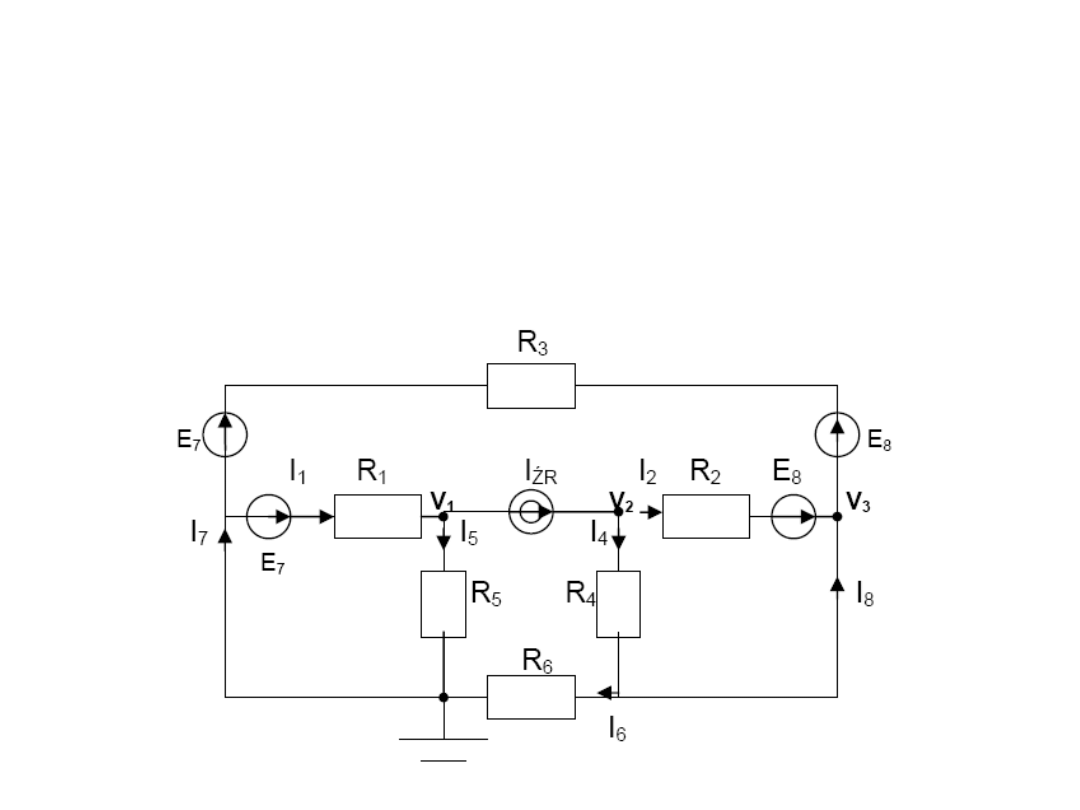
Zadanie 7

Oblicz

wartość prądów gałęziowych

(I

1

, I

2

, I

3

, I

4

, I

5

, I

6

, I

7

, I

8

) w

danym obwodzie stosując

metodę potencjałów węzłowych

.

Dane: R

1

= 1 Ω, R

2

= 2 Ω, R

3

= 3 Ω, R

4

= 4 Ω,

R

5

= 5 Ω, R

6

= 6 Ω, E

7

= 18V, E

8

=36V,

I

ŹR

= 12A.

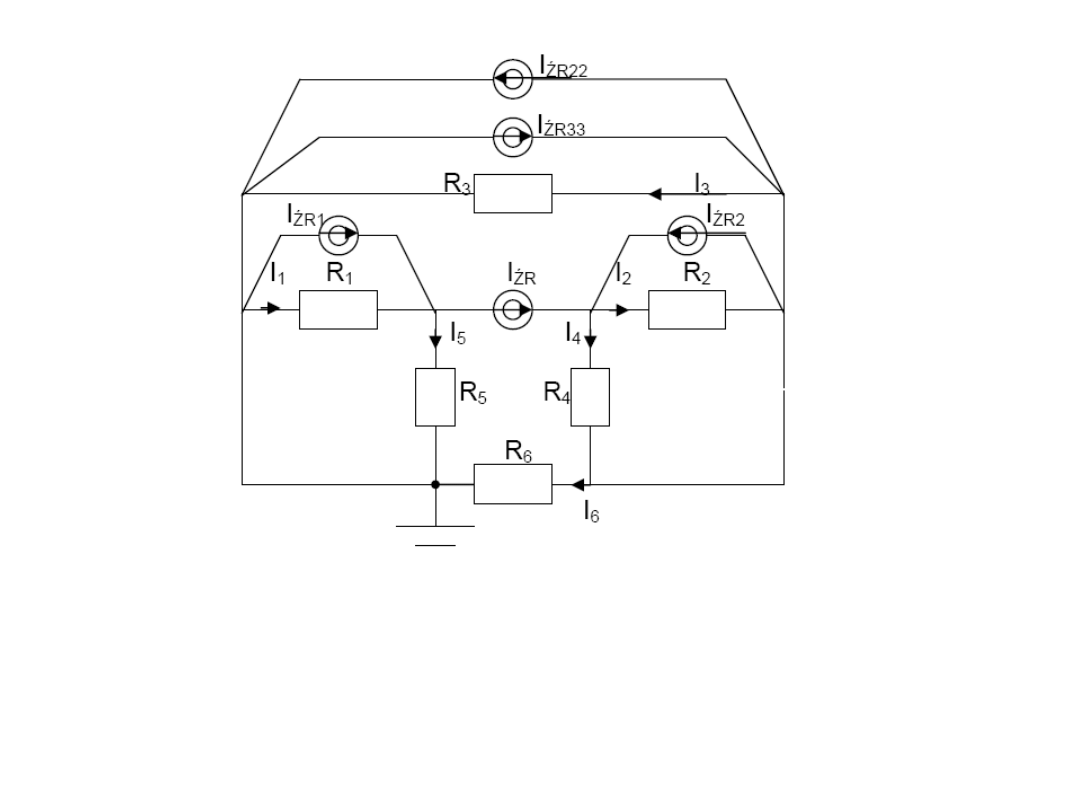
1 etap

–

„Przenieść” źródła napięciowe występujące

w gałęziach bezrezystancyjnych.

2 etap

–

„Sprowadzić” wszystkie gałęzie do postaci

prądowej.

3 etap

–

Rozwiązać przekształcony obwód tzn.

obliczyć prądy gałęziowe.

G·V = I

ŹR

G –

macierz konduktancji własnych i wzajemnych,

V –

macierz potencjałów węzłowych,

I

ŹR

–

macierz prądów źródłowych.

11

1

5

1 1 5 1

1

6

5

5

1

1

5

G

R

R

+

= + =

=

=

+

22

4

2

1 1 1 2

1

3

2

4

1

4

4

G

R

R

+

= + =

=

=

+

2

4

1 1

3

1

9

4

1

2

R

R

�

�

=-

+

=-

�

�

�

�

�

�

-

+

�

�

�

�

3

2

4

6

1 1 1 1

15 5

3 2 4

1

1

12 4

1

6

1

R

R

R

R

�

�

= + + +

=

�

�

+

+

+

�

�

�

�

=

�

�

�

�

G

12

= G

21

=

0,

G

13

= G

31

=

0,

G

23

= G

32

=

G

33

=

7

1

1

1

18

12 6

1

ŹW

ŹR

ŹR

ŹR

E

I

I

I

I

R

A

=

-

-

-

=

=

=

8

2

2

2

36

12

12 18 30

2

ŹW

ŹR

ŹR

ŹR

E

I

I

I

I

R

A

=

-

=

-

= -

= + =

8

7

8

3

22

33

2

3

3

2

36 18 36

12 6 18

24

3

3

2

ŹW

ŹR

ŹR

ŹR

E

E

E

I

I

I

I

R

R

A

R

=

=-

+

-

=-

+

-

+ -

=-

+ -

=-

-

11

12

13

1

1

21

22

23

2

2

31

32

33

3

2

ŹW

ŹW

ŹW

G

G

G

V

I

G

G

G

V

I

G

G

G

V

I

�

�

�

� � �

�

�

�

� � �

�

=� �

�

� � �

�

�

�

� � �

�

� � � � �

1

2

3

6

0

0

5

6

3

3

0

30

4

4

24

3

5

0

4

4

V

V

V

�

�

�

�

� � � �

�

�

� � � �

�

�

-

�

=

� � � �

�

�

� � � �

-

�

� � � � �

�

�

-

�

�

�

�

6

0

0

5

3

3

6 3 5 3 3

6 15 9

9

0

4

4

5 4 4 4 4

5 16 16

5 4

3

5

0

4

4

W

�

�

�

�

�

�

�

� �

�

�

�

=

-

=

� - � =

-

=

�

� �

�

�

�

�

�

� �

�

�

�

�

�

-

�

�

�

�

9

5 4

W =

�

1

6

0

0

3

3

3 5 3 3

15 9

36 9

30

6

6

4

4

4 4 4 4

16 16

16 4

3

5

24

4

4

W

�

�

�

�

�

�

�

� �

�

�

�

=

-

=

� - � =

-

=

=

�

� �

�

�

� �

� �

�

�

�

�

-

-

�

�

�

1

1

9 5 4

5

4 9

W

V

V

W

��

=

=

�

=

2

6

0

0

3

3

5

30

0

3

6

6 30 5 3

4

4

0 30

6

24

5

5

4

5

5

4

4

24

0

5

4

4

0

24

4

6 78 9 13
5 4

5

W

�

�

�

�

�

� �

�

�

�

-

-

�

� �

�

�

�

�

�

�

=

-

=

-

=

-

� =

�

� �

� �

�

�

�

�

�

�

� �

�

-

�

�

�

� �

�

�

� �

�

�

�

-

�

�

�

�

�

� =

2

2

9 13 5 4

52

5

9

W

V

W

V

�

=

�

=

=

�

3

6

0

6

5

3

6

3

3

6

72 90

3 9

0

30

24 30

4

5

4

4

5

4

4

5

3

0

24

4

W

�

�

�

�

�

�

�

�

� �

�

�

�

=

=

- � + � =

-

+

=

�

� �

�

�

� �

� �

�

�

�

�

�

-

-

�

�

�

�

3

3

3 9 5 4

12

5

9

W

V

W

V

� �

=

�

=

=

'

2

3

2

2

40

20

2

V V

I

A

R

-

=

=

=

V

2

– V

3

= 52 – 12 = 40V

I

2

= I

2

– I

ŹR2

= 2

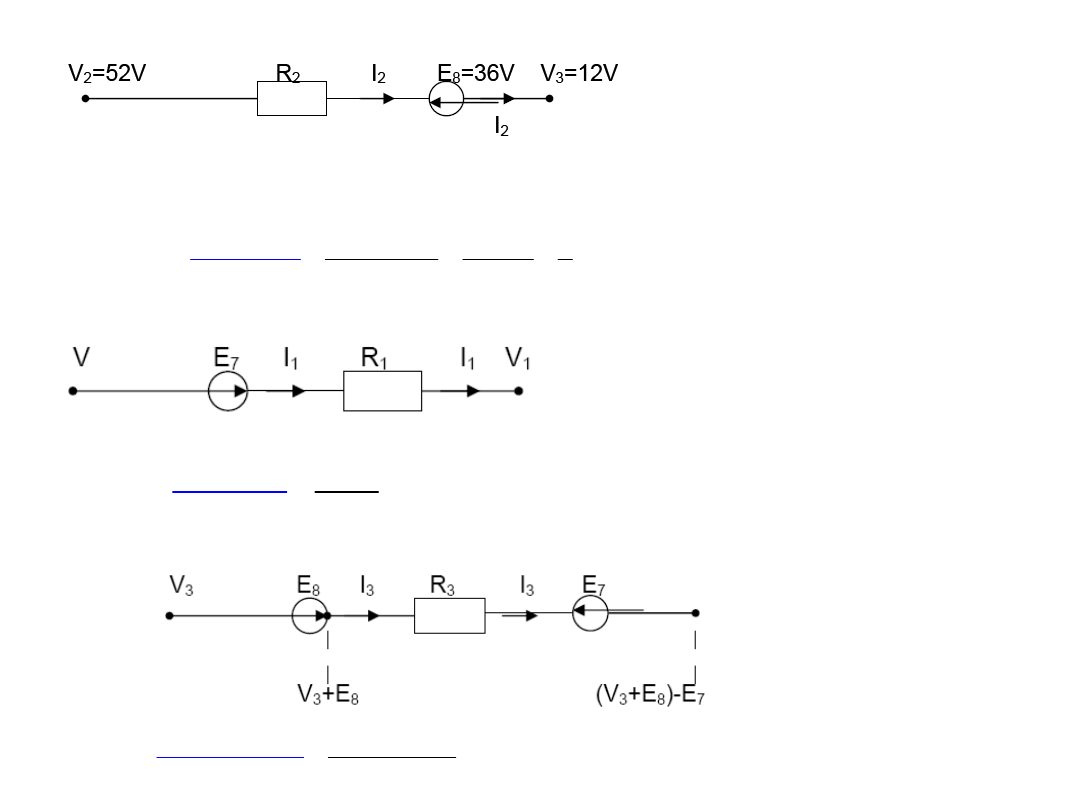
Gałąź 2

Prąd płynie od potencjału wyższego do niższego

2

8

3

2

2

52 36 12 52 48 4

2

2

2

2

V E V

I

A

R

-

-

-

=

=

-

=

=

-

=

Gałąź 1

7

1

1

1

18 5

13

0

1

E V

I

R

A

+

-

=

=

-

=

Gałąź 3

3

8

7

3

3

0

(12 36) 18

10

3

V E E

I

R

A

+

-

=

-

=

+ -

=

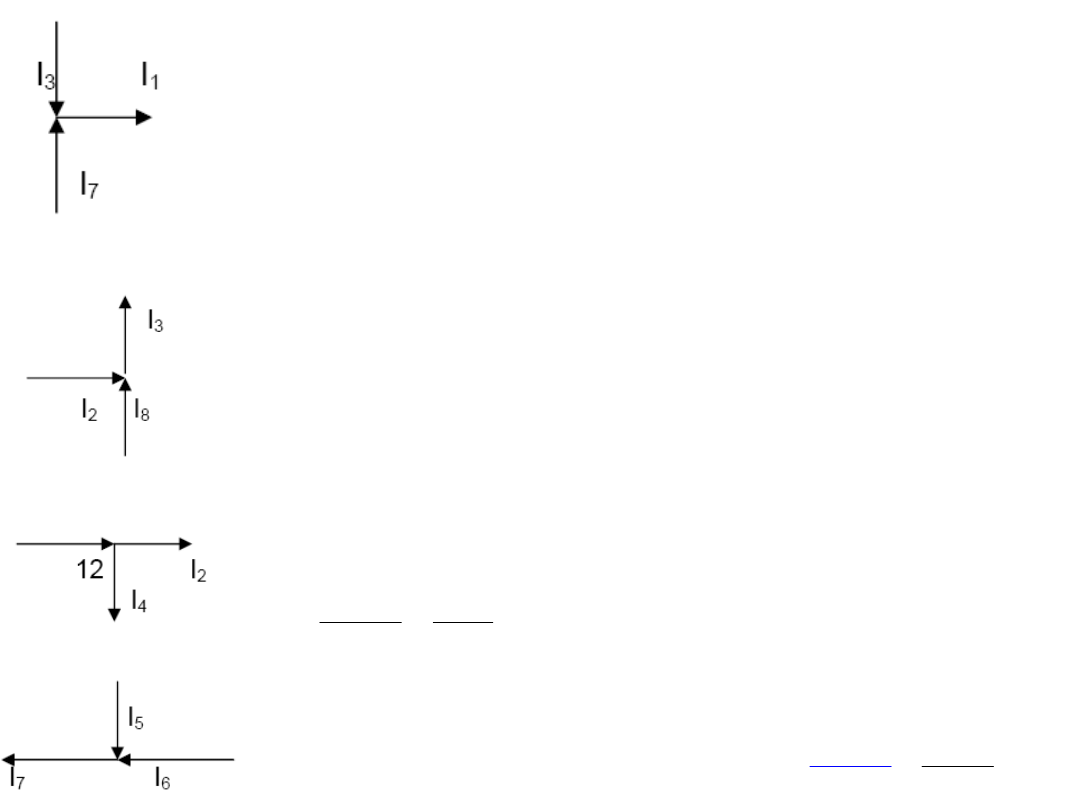
I

7

+ I

3

– I

1

= 0

,

I

7

= I

1

– I

3

= 13 – 10 = 3A

I

2

– I

3

+ I

8

= 0

,

I

8

= I

3

– I

2

= 10 – 2 = 8A

12 – I

2

– I

4

= 0

,

I

4

= 12 – I

2

= 12 – 2 = 10A

1

0

5

5

5 0

1

5

V V

I

A

R

-

-

=

=

=

I

6

+ I

5

= I

7

I

6

= I

7

– I

5

= 3 – 1 = 2A

lub

3

0

6

6

12 0

2

6

A

V V

I

R

-

-

=

=

=