Złożone schematy badawcze

c.d. Dwuczynnikowa analiza

wariancji

W schemacie 2 x 2
W schemacie 2 x 3

Efekty główne w SPSS

• Przykład analizy w schemacie 2x2:

– Badacz testował hipotezy czy patrzenie

w oczy (czynnik na dwóch poziomach:
patrzy w oczy vs. nie patrzy w oczy)
oraz temat rozmowy (czynnik drugi na
dwóch poziomach: temat przyjemny dla
badanego vs. temat nieprzyjemny)
wpływa na sympatię wobec
eksperymentatora.

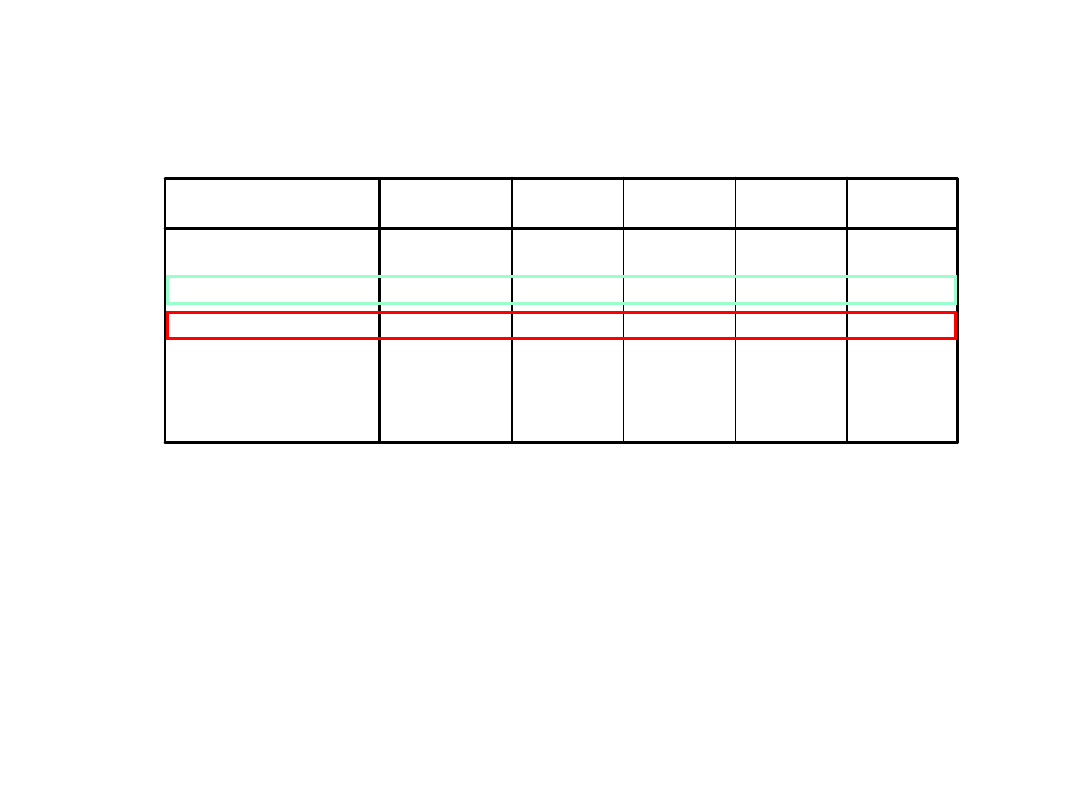
Analizujemy testy F

Testy efektów międzyobiektowych

Zmienna zależna: OCEN1

22,500

a

3

7,500

28,723

,000

504,100

1

504,100

1930,596

,000

10,000

1

10,000

38,298

,000

12,100

1

12,100

46,340

,000

,400

1

,400

1,532

,224

9,400

36

,261

536,000

40

31,900

39

Źródło zmienności
Model skorygowany
Stała
OCZY
TEMAT
OCZY * TEMAT
Błąd
Ogółem
Ogółem skorygowane

Typ III sumy

kwadratów

df

Średni

kwadrat

F

Istotność

R kwadrat = ,705 (Skorygowane R kwadrat = ,681)

a.

Zapisujemy:

Efekt główny patrzenia w oczy:

F(1,36) = 38,3; p<0,001 (M

patrzy

=4,05;

M

nie patrzy

=3,05)

Efekt główny tematu:

F(1,36) = 46,34; p<0,001 (M

przyjemny

=4,10;

M

nieprzyjemny

=3,00)

Efekt interakcji nieistotny

Który efekt silniejszy

• Gdy porównujemy efekty pochodzące z tego

samego badania wystarczy porównanie

wartości F

• Gdy chcemy porównywać wyniki pochodzące

z różnych badań obliczamy miarę siły efektu,

cząstkowe eta

2

–

Eta

2

– pokazuje jaki procent całkowitej wariancji

zmiennej zależnej jest wyjaśniony przez dany

efekt, definiowana:

η

2

=

SS

efektu

SS

efektu

+ SS

błędu

Korzystając z F i df

eta

2

=

Mając zatem standardowy zapis APA

możemy obliczyć ile wynosi eta

2

(F) (df
między)

(F) (df między) + df
wewnątrz

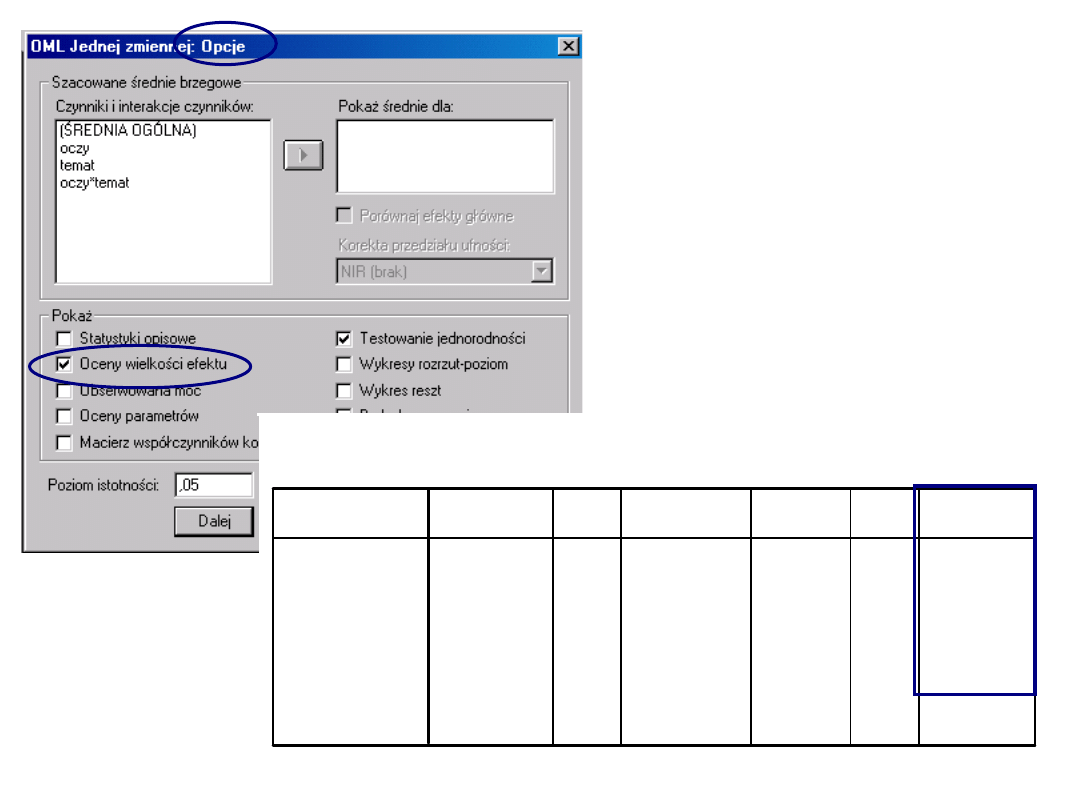
W SPSSie…

Tests of Between-Subjects Effects

Dependent Variable: OCEN1

22,500

a

3

7,500

28,723

,000

,705

504,100

1

504,100 1930,596

,000

,982

10,000

1

10,000

38,298

,000

,515

12,100

1

12,100

46,340

,000

,563

,400

1

,400

1,532

,224

,041

9,400

36

,261

536,000

40

31,900

39

Source
Corrected Model
Intercept
OCZY
TEMAT
OCZY * TEMAT
Error
Total
Corrected Total

Type III Sum

of Squares

df

Mean Square

F

Sig.

Partial Eta

Squared

R Squared = ,705 (Adjusted R Squared = ,681)

a.

Interpretacja efektów głównych w

schemacie 2x3

• W momencie gdy przynajmniej

jeden z czynników jest na więcej
niż dwóch poziomach nie
wystarczy sama informacja o
istotności testu F

• Powinniśmy wykonać dodatkowe

analizy

Interpretacja efektów głównych

• Przykład badania w schemacie 2x3

Badacz testował hipotezy czy:
– patrzenie w oczy (czynnik 1 na dwóch

poziomach: patrzy w oczy vs. nie patrzy w oczy)
oraz

– temat rozmowy (czynnik 2 na trzech poziomach:

temat neutralny dla badanego vs. temat
przyjemny vs. temat nieprzyjemny) wpływa na
sympatię wobec eksperymentatora.

• Ile grup w badaniu?
• Ile efektów prostych?

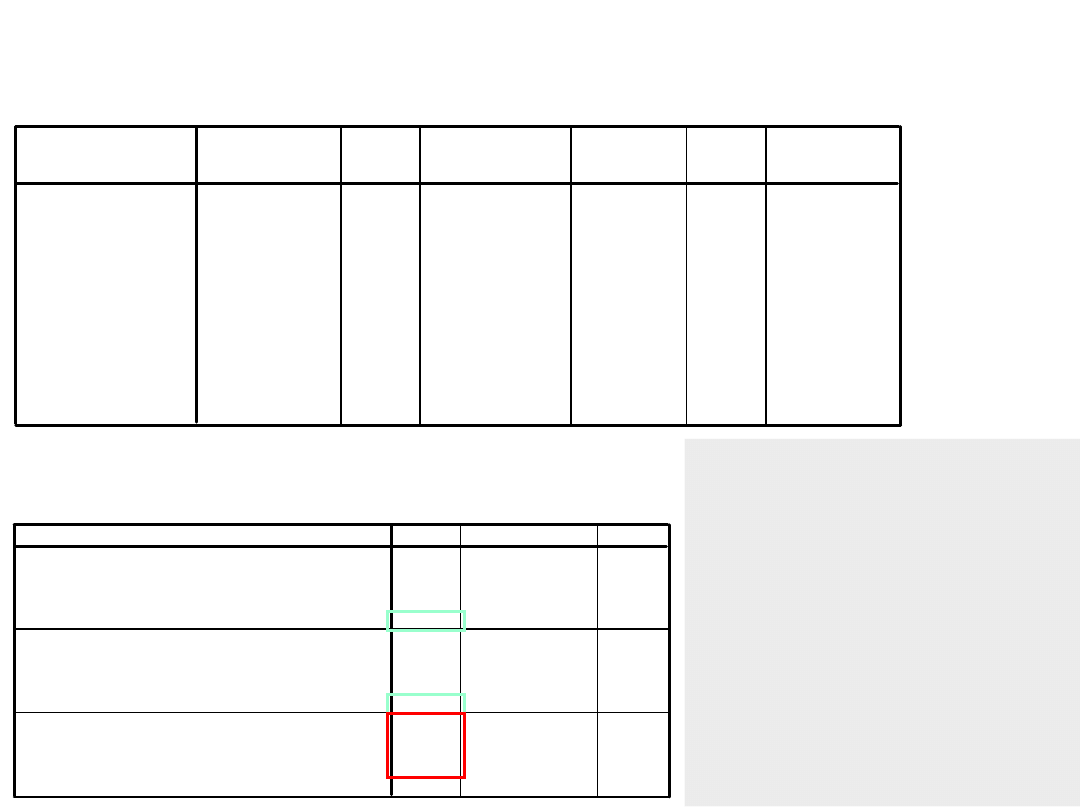
Tests of Between-Subjects Effects

Dependent Variable: OCEN1

29,250

a

5

5,850

22,809

,000

,679

821,400

1

821,400 3202,570

,000

,983

14,017

1

14,017

54,650

,000

,503

14,800

2

7,400

28,852

,000

,517

,433

2

,217

,845

,435

,030

13,850

54

,256

864,500

60

43,100

59

Source
Corrected Model
Intercept
OCZY
TEMAT
OCZY * TEMAT
Error
Total
Corrected Total

Type III Sum

of Squares

df

Mean Square

F

Sig.

Partial Eta

Squared

R Squared = ,679 (Adjusted R Squared = ,649)

a.

Testy F

Descriptive Statistics

Dependent Variable: OCEN1

4,50

,527

10

3,60

,516

10

4,45

,497

10

4,18

,650

30

3,70

,483

10

2,40

,516

10

3,55

,497

10

3,22

,762

30

4,10

,641

20

3,00

,795

20

4,00

,669

20

3,70

,855

60

TEMAT
1 temat przyjemny
2 temat nieprzyjemny
3 neutralny
Total
1 temat przyjemny
2 temat nieprzyjemny
3 neutralny
Total
1 temat przyjemny
2 temat nieprzyjemny
3 neutralny
Total

OCZY
1 patrzy w oczy

2 nie patrzy w oczy

Total

Mean Std. Deviation

N

Interpretacja efektu
głównego „patrzenia
w oczy” tak jak
poprzednio –
patrzymy na średnie i
wiemy, że się różnią,
nie możemy tak
postąpić z czynnikiem
„temat rozmowy”

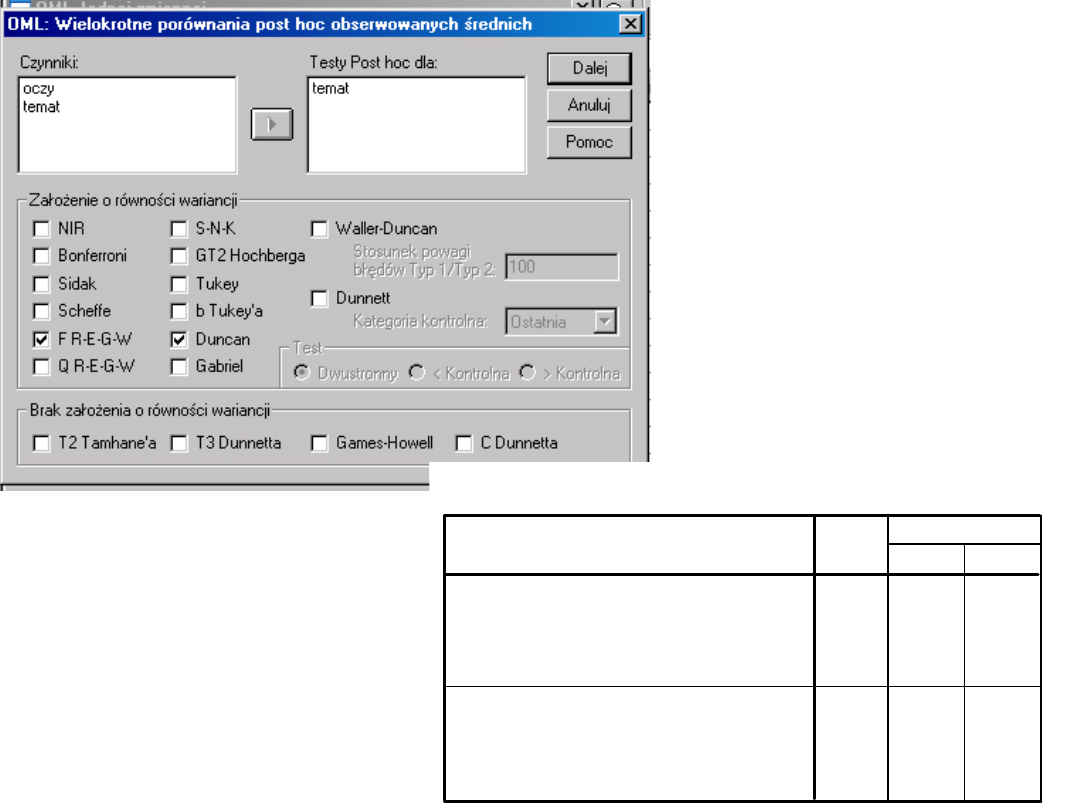
Testy post hoc

OCEN1

20

3,00

20

4,00

20

4,10

1,000

,535

20

3,00

20

4,00

20

4,10

1,000

,535

TEMAT
2 temat nieprzyjemny
3 neutralny
1 temat przyjemny
Sig.
2 temat nieprzyjemny
3 neutralny
1 temat przyjemny
Sig.

Duncan

a,b

Ryan-Einot-Ga
briel-Welsch F

b

N

1

2

Subset

Means for groups in homogeneous subsets are displayed.
Based on Type III Sum of Squares
The error term is Mean Square(Error) = ,256.

Uses Harmonic Mean Sample Size = 20,000.

a.

Alpha = ,05.

b.

Kontrasty SPSS

• Możliwe jest przeprowadzenie analizy

kontrastów dla podziału ze względu
na każdy analizowany czynnik (ale
tylko jeden w tym samym czasie)

• Brak zupełnej swobody w

konstruowaniu porównań, zamiast
tego możemy wybierać wśród
wbudowanych typów kontrastów

Kontrasty SPSS – które warto

znać?

•

Prosty. Wybranie tego typu kontrastu powoduje
porównanie średniej każdego poziomu ze średnią
odniesienia. Jako odniesienie wybrać można kategorię
pierwszą lub ostatnią. Ten typ kontrastu jest przydatny
szczególnie w przypadku korzystania z grupy kontrolnej.

•

Wielomianowy. Wybranie tego typu kontrastu powoduje
porównanie efektu liniowego, efektu kwadratowego,
sześciennego itd. Dla wszystkich kategorii efekt liniowy
zawarty jest w pierwszym stopniu swobody; efekt
kwadratowy - w drugim stopniu swobody itd. Tego typu
kontrasty używane są często do szacowania trendów
wielomianowych.

Efekty interakcji

Interpretacja efektów

interakcyjnych

• Konieczne obliczenie efektów prostych (w

schematach 2x2 wystarczające)

• W przypadku bardziej specyficznych hipotez

lub w bardziej złożonych schematach, gdy

istotny efekt prosty wykonujemy

porównania wielokrotne lub planowane

• Jak wykonać efekty proste oraz odpowiednie

dla nich porównania wielokrotne w SPSS?

Interakcje w SPSSie

• Brak opcji testujących efekty proste
• Przekształcamy dwa czynniki na

jedną zmienną kategorialną i
wykonujemy prostą
jednoczynnikowa ANOVAę lub

• Stosujemy filtry i wykonujemy testy

t lub jednoczynnikową ANOVAę lub

• Korzystamy z pomocy syntaxa

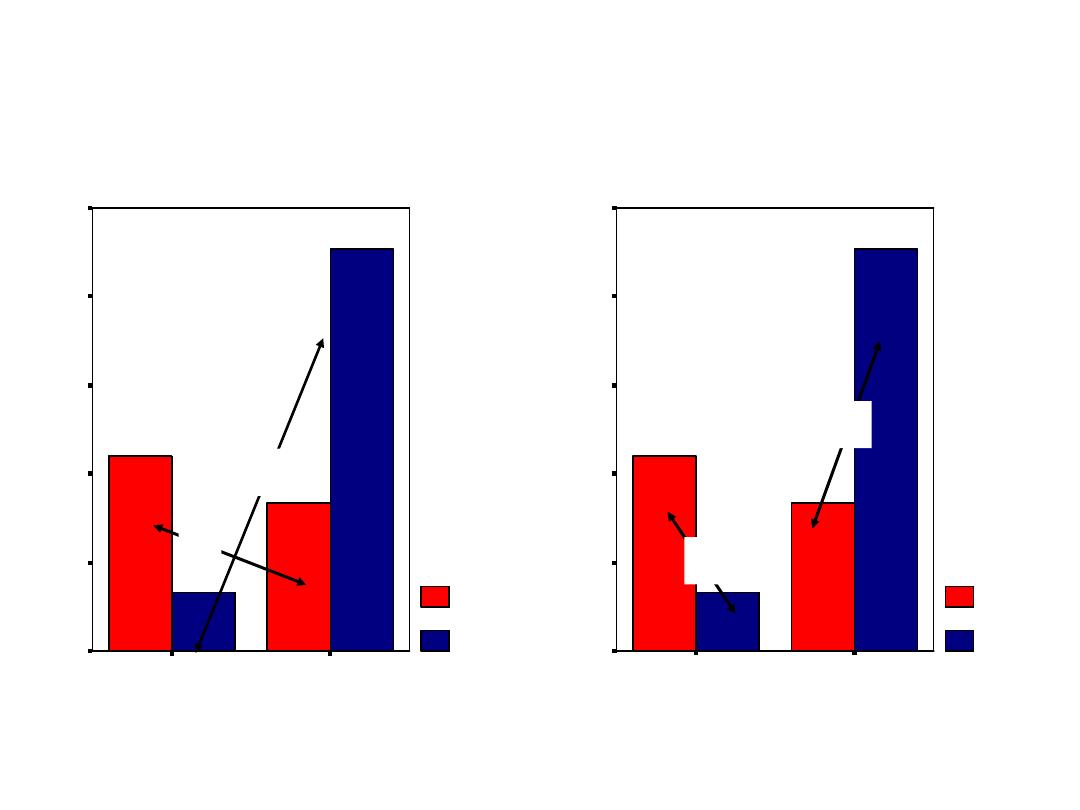
Jeszcze raz o chronopsychologii

• Wróćmy na chwilę do przykładu z

chronotypami

PORA

wieczorem

rano

po

zi

om

r

oz

w

ią

za

ni

a

za

da

ń

um

ys

ło

w

yc

h

8

7

6

5

4

3

ranne ptaszki

sowy

1

2

PORA

wieczorem

rano

po

zi

om

r

oz

w

ią

za

ni

a

za

da

ń

um

ys

ło

w

yc

h

8

7

6

5

4

3

ranne ptaszki

sowy

3

4

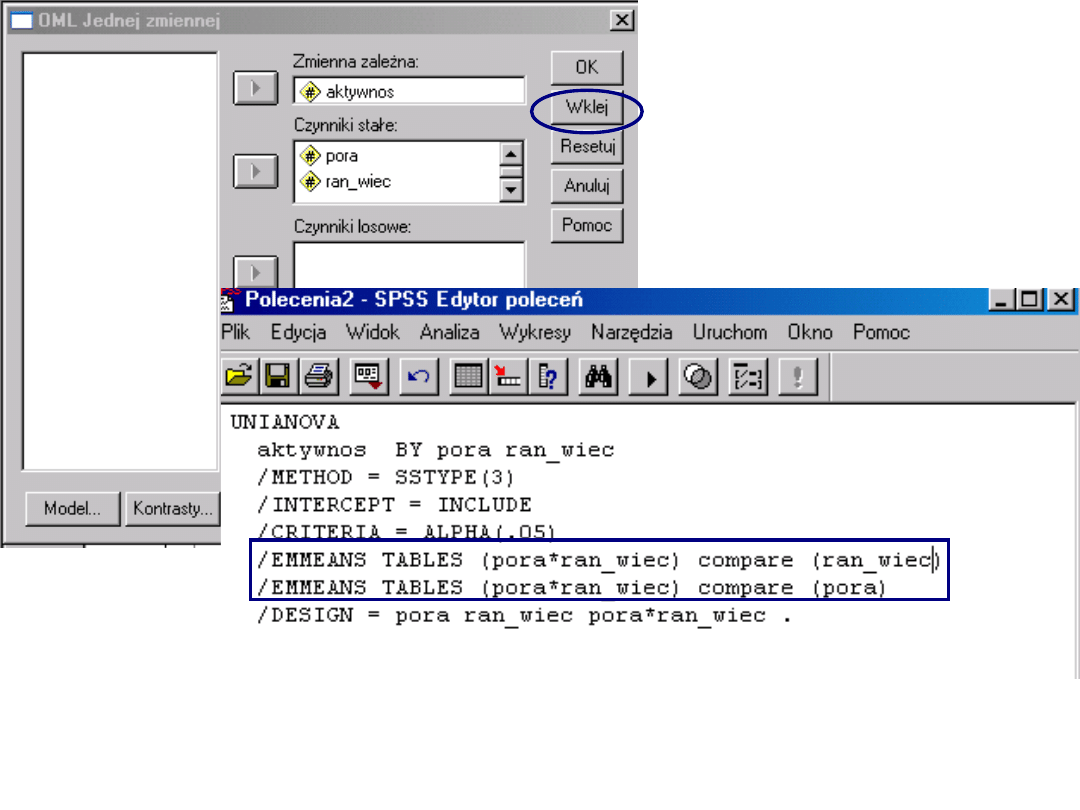
Efekty

proste w

SPSSie

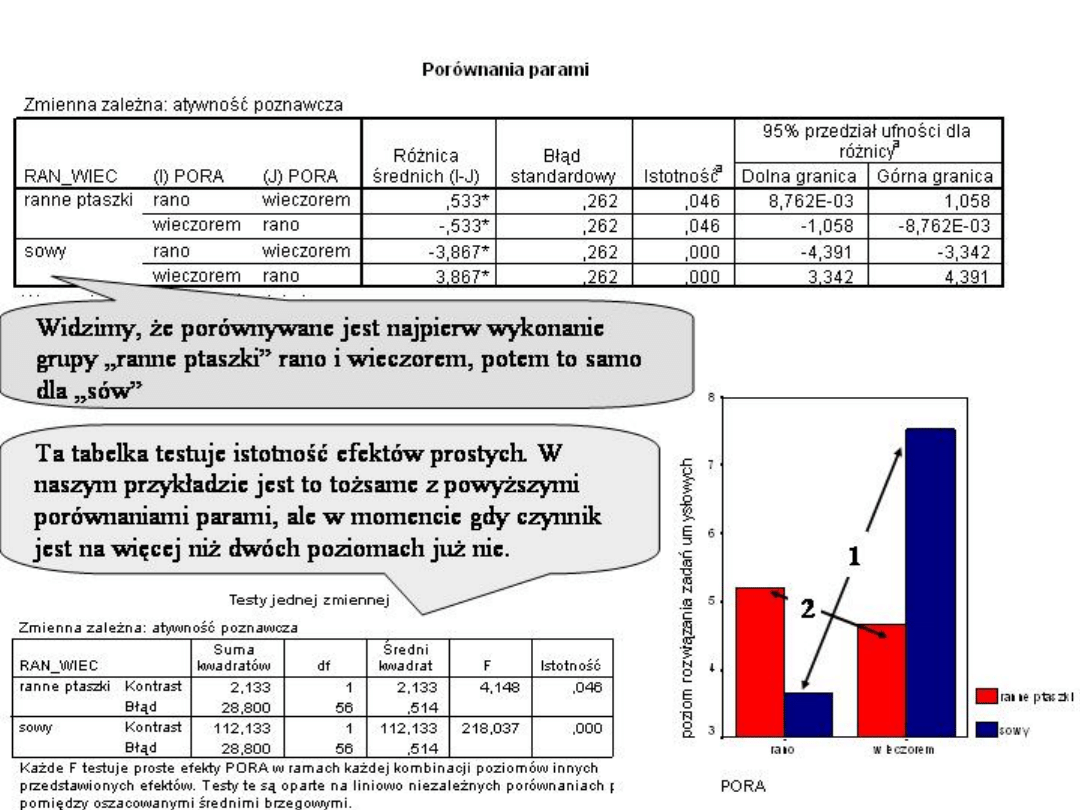
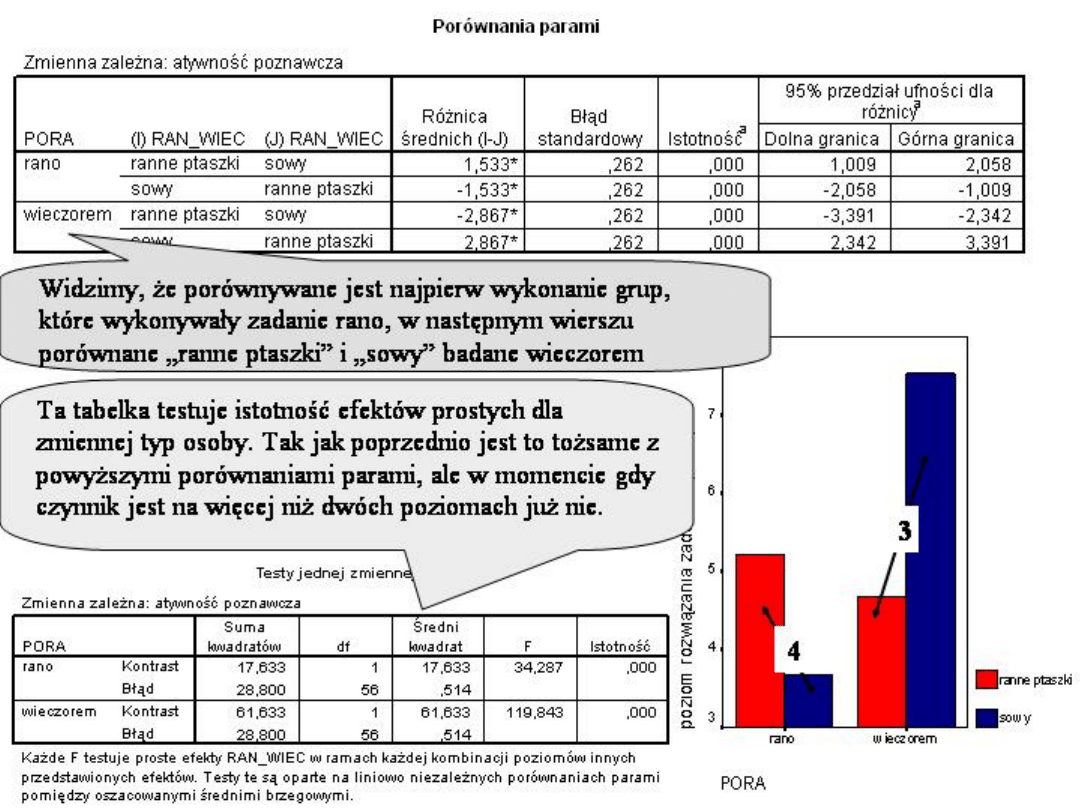
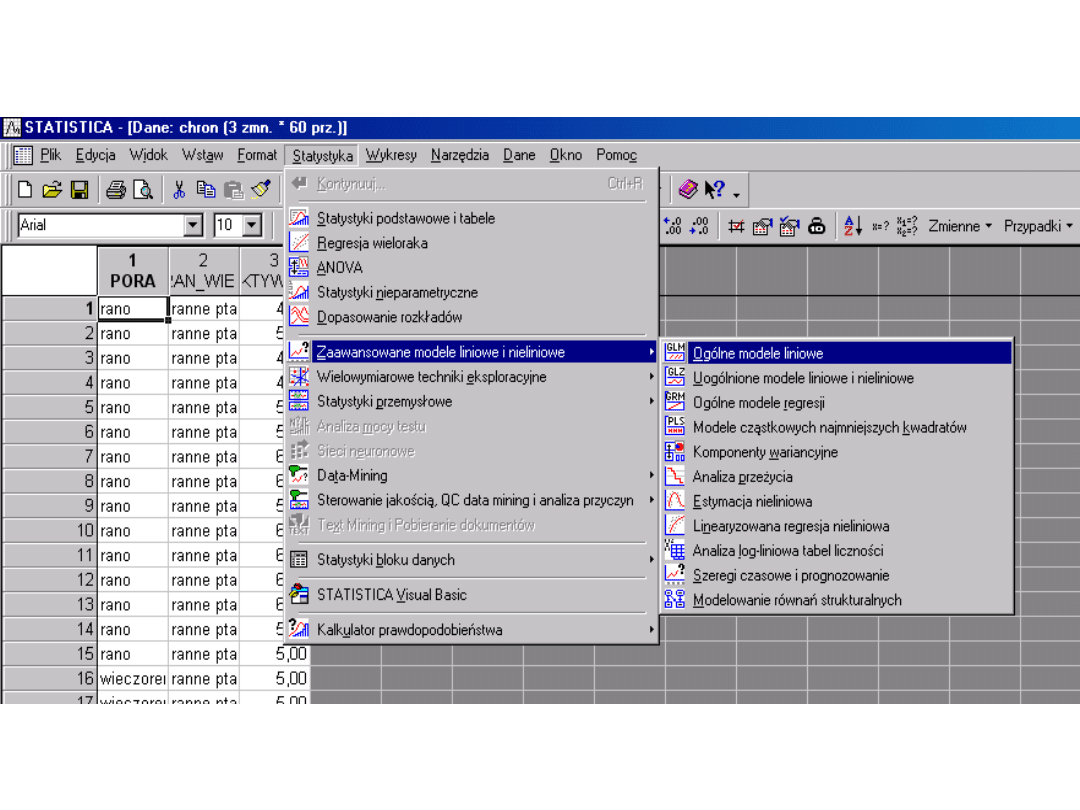
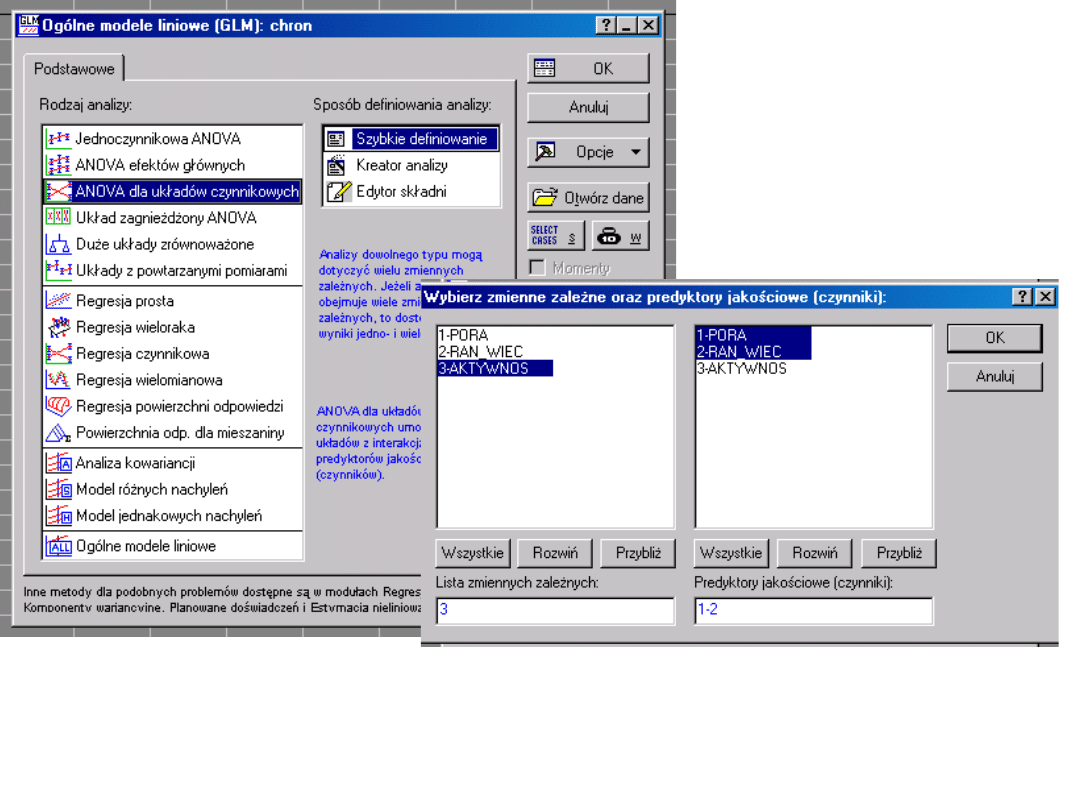
Interpretacja interakcji w

STATISTICE

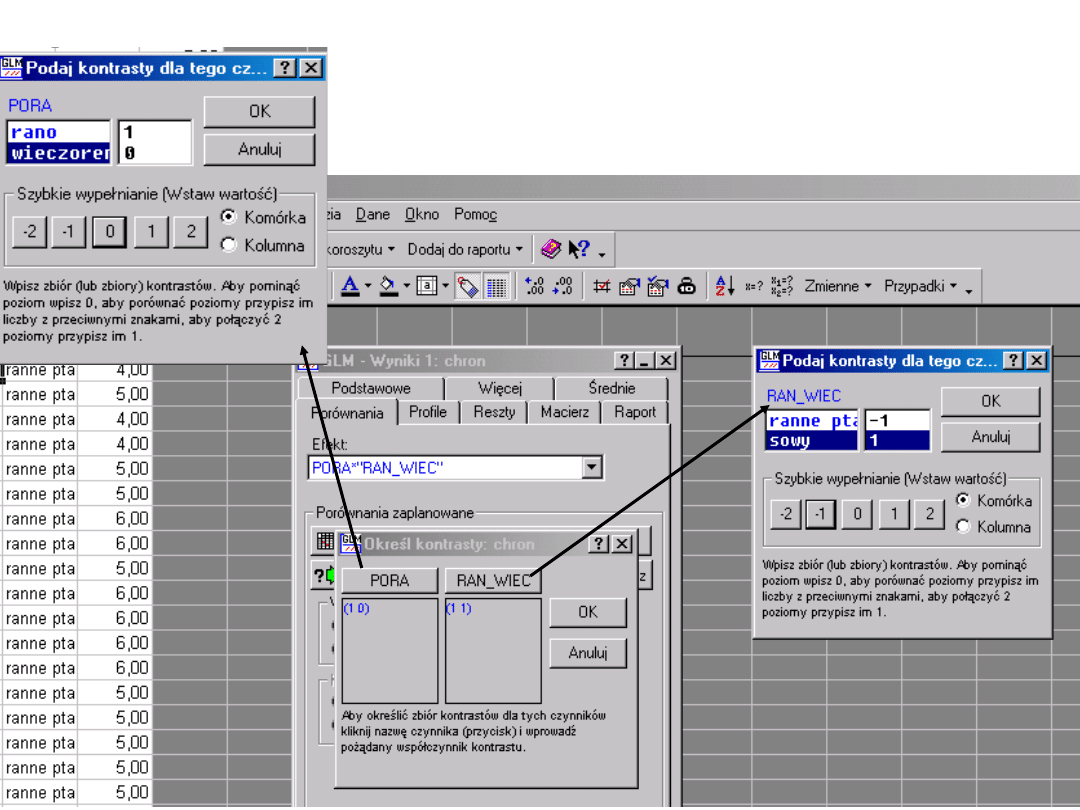
A jakie współczynniki kontrastu dla porównania
osób „porannych ptaszków” rozwiązujących
zadanie rano i wieczorem?

Kontrasty

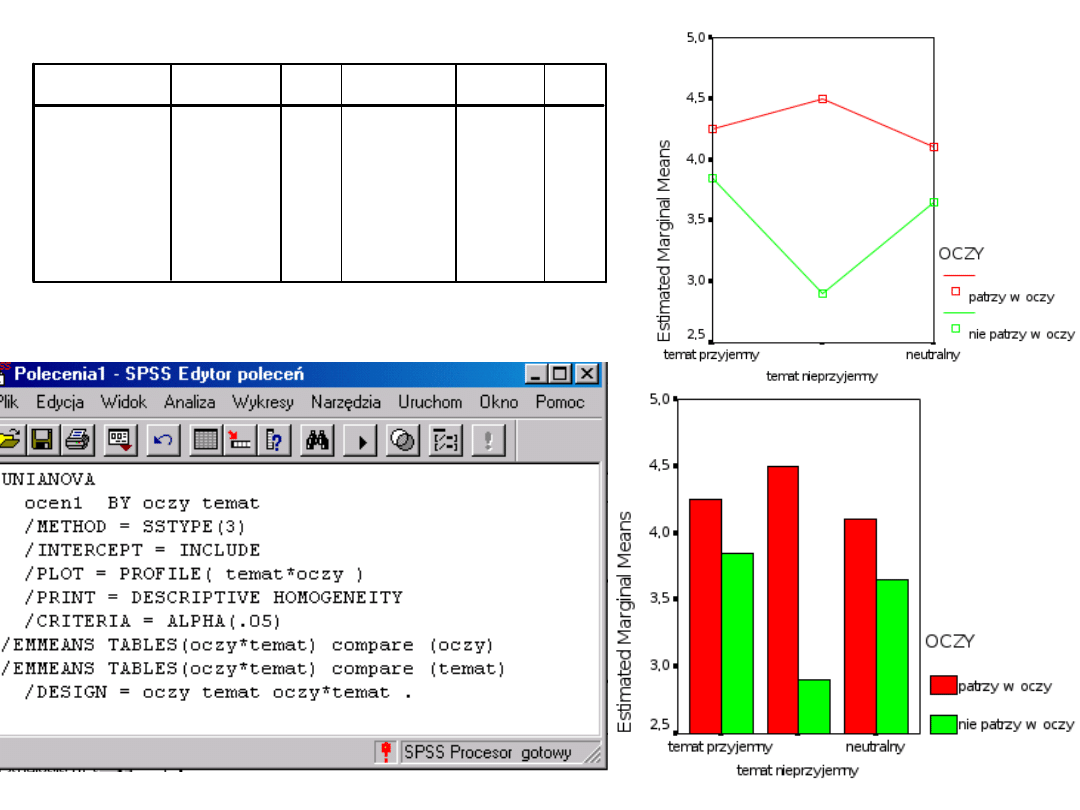
Interakcja w schemacie

2x3

• Ponownie:

– Badacz testował hipotezy czy patrzenie w

oczy (czynnik na dwóch poziomach: patrzy w
oczy vs. nie patrzy w oczy) oraz temat
rozmowy (czynnik drugi na trzech poziomach:
temat neutralny dla badanego vs. temat
przyjemny vs. temat nieprzyjemny) wpływa na
sympatię wobec eksperymentatora.

• Tym razem interesuje nas interakcja tych

czynników

Tests of Between-Subjects Effects

Dependent Variable: OCEN1

15,837

a

5

3,167

14,284

,000

900,938

1

900,938 4062,683

,000

10,004

1

10,004

45,113

,000

1,225

2

,613

2,762

,072

4,608

2

2,304

10,390

,000

11,975

54

,222

928,750

60

27,812

59

Source
Corrected Model
Intercept
OCZY
TEMAT
OCZY * TEMAT
Error
Total
Corrected Total

Type III Sum

of Squares

df

Mean Square

F

Sig.

R Squared = ,569 (Adjusted R Squared = ,530)

a.

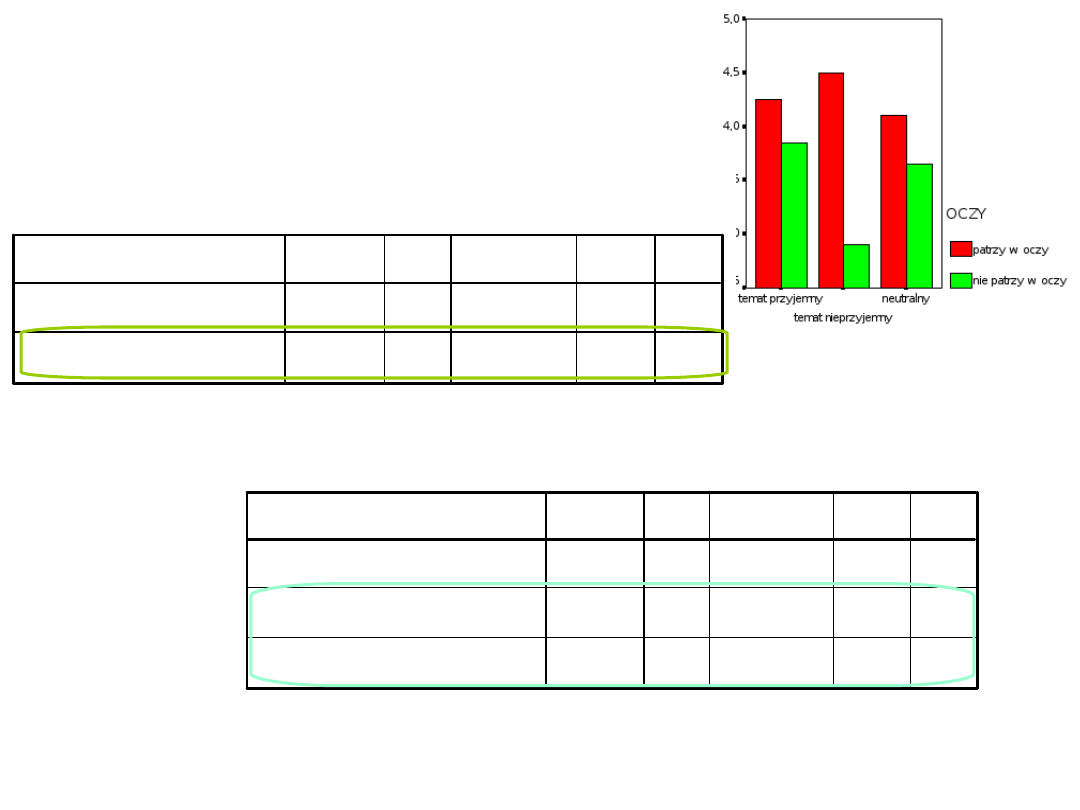
Które efekty proste

istotne?

Univariate Tests

Dependent Variable: OCEN1

,800

1

,800

3,608

,063

11,975

54

,222

12,800

1

12,800 57,720

,000

11,975

54

,222

1,013

1

1,013

4,566

,037

11,975

54

,222

Contrast
Error
Contrast
Error
Contrast
Error

TEMAT
1,00 temat przyjemny

2,00 temat nieprzyjemny

3,00 neutralny

Sum of

Squares

df

Mean Square

F

Sig.

Each F tests the simple effects of OCZY within each level combination of the other effects
shown. These tests are based on the linearly independent pairwise comparisons among the
estimated marginal means.

Univariate Tests

Dependent Variable: OCEN1

,817

2

,408

1,841

,168

11,975

54

,222

5,017

2

2,508 11,311

,000

11,975

54

,222

Contrast
Error
Contrast
Error

OCZY
1,0 patrzy w oczy

2,0 nie patrzy w oczy

Sum of

Squares

df

Mean Square

F

Sig.

Each F tests the simple effects of TEMAT within each level combination of the other effects
shown. These tests are based on the linearly independent pairwise comparisons among
the estimated marginal means.

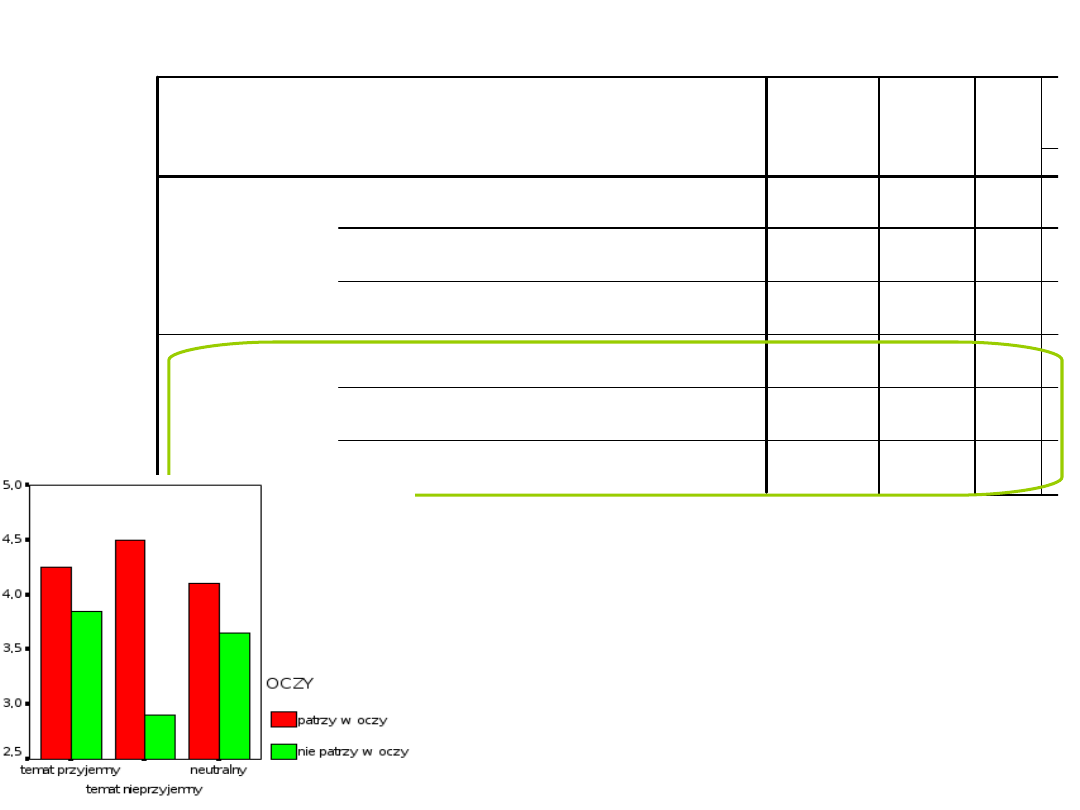
Które średnie się
różnią?

Pairwise Comparisons

Dependent Variable: OCEN1

-,250

,211

,240

-,672

,172

,150

,211

,479

-,272

,572

,250

,211

,240

-,172

,672

,400

,211

,063

-,022

,822

-,150

,211

,479

-,572

,272

-,400

,211

,063

-,822

,022

,950*

,211

,000

,528

1,372

,200

,211

,347

-,222

,622

-,950*

,211

,000

-1,372

-,528

-,750*

,211

,001

-1,172

-,328

-,200

,211

,347

-,622

,222

,750*

,211

,001

,328

1,172

(J) TEMAT
2,00 temat nieprzyjemny
3,00 neutralny
1,00 temat przyjemny
3,00 neutralny
1,00 temat przyjemny
2,00 temat nieprzyjemny
2,00 temat nieprzyjemny
3,00 neutralny
1,00 temat przyjemny
3,00 neutralny
1,00 temat przyjemny
2,00 temat nieprzyjemny

(I) TEMAT
1,00 temat przyjemny

2,00 temat nieprzyjemny

3,00 neutralny

1,00 temat przyjemny

2,00 temat nieprzyjemny

3,00 neutralny

OCZY
1,0 patrzy w oczy

2,0 nie patrzy w oczy

Mean

Difference

(I-J)

Std. Error

Sig.

a

Lower Bound Upper Bound

95% Confidence Interval for

Difference

a

Based on estimated marginal means

The mean difference is significant at the ,05 level.

*.

Adjustment for multiple comparisons: Least Significant Difference (equivalent to no adjustments).

a.

A gdybyśmy chcieli porównać dwie

grupy z jedną…?

• Czasami potrzebujemy wykonać porównania

niestandardowe

– Wśród osób, którym eksperymentator nie patrzy

w oczy, chcemy porównać grupę rozmawiającą na

temat nieprzyjemny z grupami rozmawiającymi o

temacie przyjemnym i neutralnym.

• Odpowiednie kontrasty

– Czynnik oczy
patrzy w oczy: 0; nie patrzy w oczy: 1
– Czynnik temat:
nieprzyjemny: 2; przyjemny: -1; neutralny: -1

Analiza wariancji z

powtarzanym pomiarem

Analiza wariancji z powtarzanym

pomiarem

Rozszerzenie testu T-Studenta dla prób

zależnych o dodatkowy trzeci pomiar

Mamy trzy pomiaru u jednej osoby – to może

być:

• trzykrotny pomiar tej samej zmiennej,
• pomiar trzech różnych zmiennych by określić

na przykład profil osobowości osób cierpiących
na alkoholizm

Zalety takiego schematu

• Możliwość wnioskowania o przyczynowo-skutkowych

powiązaniach między zmiennymi zależnymi. (słabo wypadają

w testach – dlaczego? bo zmniejsza się efektywność pamięci

operacyjnej)

• Unikamy problemu złego doboru osób do grup badawczych

(w jednej grupie sami optymiści a w drugiej sami

pesymiści)– poważny problem przy eksperymentach, gdzie

grupy są zwykle małoliczne

• „Oszczędzamy” osoby badane

• Duża moc takiego testu – bardzo czułe narzędzia do

wykrywania różnic

Wady – efekt kolejności („carry over

effect”)

• Efekt wprawy albo efekt pogorszenia

• Efekty symetryczne

– wtedy, gdy różnica między

wynikami w poziomie wykonania jest taka sama dla

każdej kolejności. Rozwiązanie - rotowanie kolejności

(counter-balance) lub losowa kolejność dla każdej osoby

1 kolejność: zadanie 1, zadanie 2
2 kolejność: zadanie 2, zadanie 1

• Efekty niesymetryczne

– wtedy, gdy różnica między

wynikami w poziomie wykonania jest różna dla każdej

kolejności. Pojawia się wtedy trudność w interpretacji

danych ale też źródło dalszych hipotez – nie powinno się
stosować schematu wewnątrz osób.

1 kolejność: zadanie 1, zadanie 2
2 kolejność: zadanie 2, zadanie 1

12

12

12

22

Założenia

• Rozkład normalny w każdym pomiarze

• Sferyczność

– wariancje wewnątrz pomiarów są

identyczne, korelacje wariancji różnic między wynikami

osób są zbliżone – bardzo ważne założenie

automatycznie testowane w SPSS-ie i od razu obliczane
specjalne poprawki na niespełnienie tego założenia.

Takane i Ferguson nazywają to założenie

symetrią złożoną

i uważają, że może być lekko złamane w

jednoczynnikowej analizie wariancji wtedy, gdy rozkłady

są normalne.

Sferyczność

• Gdy powtarzany pomiar ma dwa poziomy to nie ma

problemu sferyczności

• Gdy powtarzany pomiar występuje na trzech poziomach

wtedy musi zostać spełniony warunek polegający na tym, że

korelacje różnic między pomiarami mają być takie same.

Pomiar

1

Pomiar

2

Pomiar

3

P1-

p2

P2-

p3

P1-

p3

Osoba 1

3

2

4

1

-2

-1

Osoba 2

4

3

5

1

-2

-1

Osoba 3

5

6

6

-1

0

-1

Var1 Var2 Var1

Sumy kwadratów

Suma kwadratów całkowita (odległość wyników – np. pomiar 1 - od
średniej globalnej)

Suma kwadratów dla pomiaru (odległość średnich dla pomiarów
np. średnia p1 od średniej ogólnej)

Suma kwadratów dla osób (odległość średniej dla każdej osoby –
np. średnia 1- od średniej globalnej)

Suma kwadratów błedu jest obliczany jako efekt interakcyjny
pomiaru i osób. (pomiar x osoba)

1
osoba

2
osoba

Pomiar
1

Pomiar
2

Pomiar
3

Pomiar
1

Pomiar
2

Pomiar
3

średni
a 1

średni
a 2
średni
a
ogólna

średnia
p 1

średnia
p 2

średnia
p 3

Stopnie swobody i średnie kwadraty

Df błędu = (liczba osób – 1)*(liczba pomiarów –

1)

Df całkowite = liczba pomiarów * liczba osób –1
Df pomiar = liczba pomiarów –1
Df osoby = liczba osób –1

F = średni kwadrat pomiarów/ średni kwadrat błędu

Efekt interakcyjny pomiar x osoby jest silny –
niespójny wzorzec – średni kwadrat błędu duży

Pomiar 1 Pomiar 2 Pomiar 3 wyni

ki

Osoba 1

1

2

4

rosną

Osoba 2

4

3

2

malej

ą

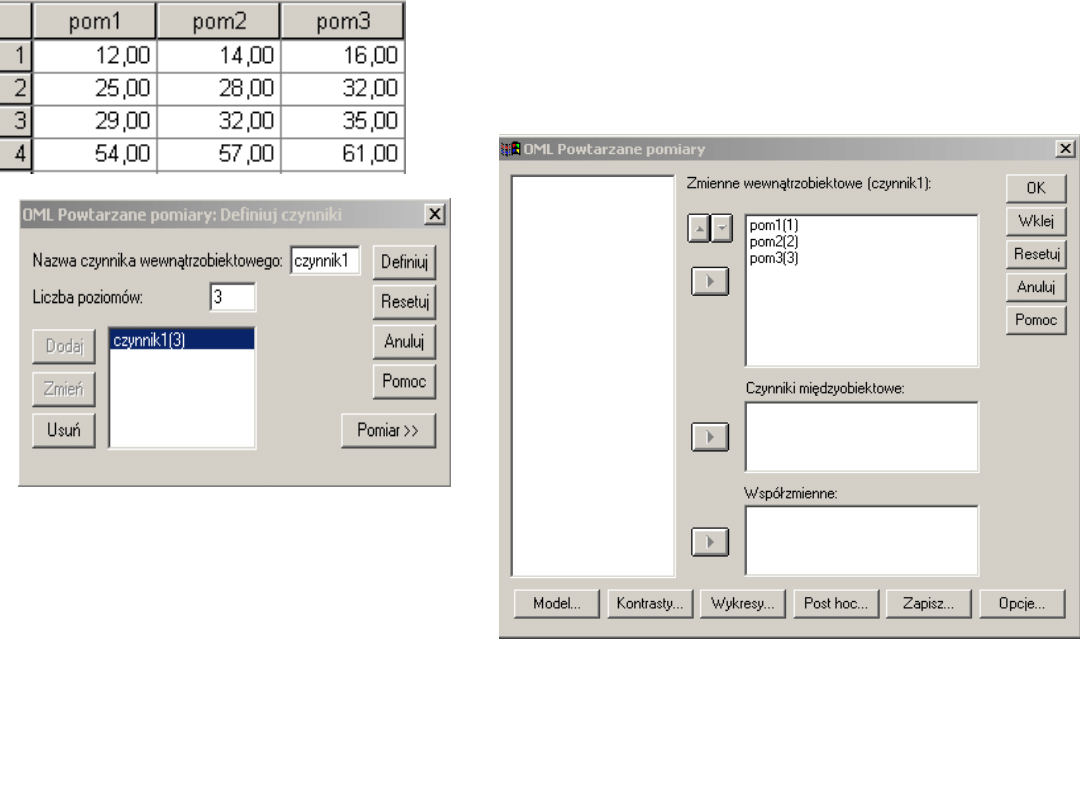
Jak w SPSS-ie

Definiujemy ile jest

poziomów
powtarzanego
czynnika oraz
wybieramy zmienne

Założenie o

sferyczności

Test sferyczności Mauchly'ego

Miara: MIARA_1

,066

5,422

2

,005

,517

,544

,500

Efekt wewnątrzobiektowy
CZYNNIK1

W

Mauchly'ego

Przybliżone

chi-kwadrat

df

Istotność

Greenhous

e-Geisser

Huynh-Feldt

Dolna granica

epsilon

Epsilon

Testy efektów wewnątrzobiektowych

Miara: MIARA_1

72,167

2

36,083

68,368

,000

72,167

1,034

69,768

68,368

,003

72,167

1,087

66,362

68,368

,003

72,167

1,000

72,167

68,368

,004

3,167

6

,528

3,167

3,103

1,020

3,167

3,262

,971

3,167

3,000

1,056

Sferyczność założona
Greenhouse-Geisser
Huynh-Feldt
Dolna granica epsilon
Sferyczność założona
Greenhouse-Geisser
Huynh-Feldt
Dolna granica epsilon

Źródło zmienności
CZYNNIK1

Błąd(CZYNNIK1)

Typ III sumy

kwadratów

df

Średni

kwadrat

F

Istotność

W jednoczynnikowej analizie wariancji z powtarzanym pomiarem
stosuje się najczęściej poprawki na niespełnione założenie o
sferyczności zawarte w tabeli „Testy efektów
wewnątrzobiektowych”:

Greenhouse Geisera wtedy, gdy duże liczebności, Huynha-Feldt’a
wtedy gdy małe liczebności w porównywanych grupach.
Najbardziej konserwatywna jest Dolna granica epsilon.

Odczytujemy, że są różnice między trzema pomiarami F(1,
6)=68,368; p<0,01

Testy efektów wewnątrzobiektowych

Miara: MIARA_1

72,167

2

36,083

68,368

,000

72,167

1,034

69,768

68,368

,003

72,167

1,087

66,362

68,368

,003

72,167

1,000

72,167

68,368

,004

3,167

6

,528

3,167

3,103

1,020

3,167

3,262

,971

3,167

3,000

1,056

Sferyczność założona
Greenhouse-Geisser
Huynh-Feldt
Dolna granica epsilon
Sferyczność założona
Greenhouse-Geisser
Huynh-Feldt
Dolna granica epsilon

Źródło zmienności
CZYNNIK1

Błąd(CZYNNIK1)

Typ III sumy

kwadratów

df

Średni

kwadrat

F

Istotność

Testy wielu zmiennych

b

,981

51,000

a

2,000

2,000

,019

,019

51,000

a

2,000

2,000

,019

51,000

51,000

a

2,000

2,000

,019

51,000

51,000

a

2,000

2,000

,019

Ślad Pillai
Lambda Wilksa
Ślad Hotellinga
Największy
pierwiastek Roy'a

Efekt
CZYNNIK1

Wartość

F

df hipotezy

df błędu

Istotność

Statystyka dokładna

a.

Plan: Intercept
Plan wewnątrzobiektowy: CZYNNIK1

b.

Założenie o sferyczności

Znacznie rzadziej stosuje się poprawkę wartości statystyki F.
Statystyka F jest obliczana na podstawie statystyk z lewej
strony tabeli. Najczęściej stosowane to Lambda Wilksa (dla
więcej niż dwóch pomiarów) oraz Ślad Hotellinga (dla dwóch
pomiarów).

Zapis w tym przypadku będzie wyglądał następująco:

F(2,2)=51; p<0,05

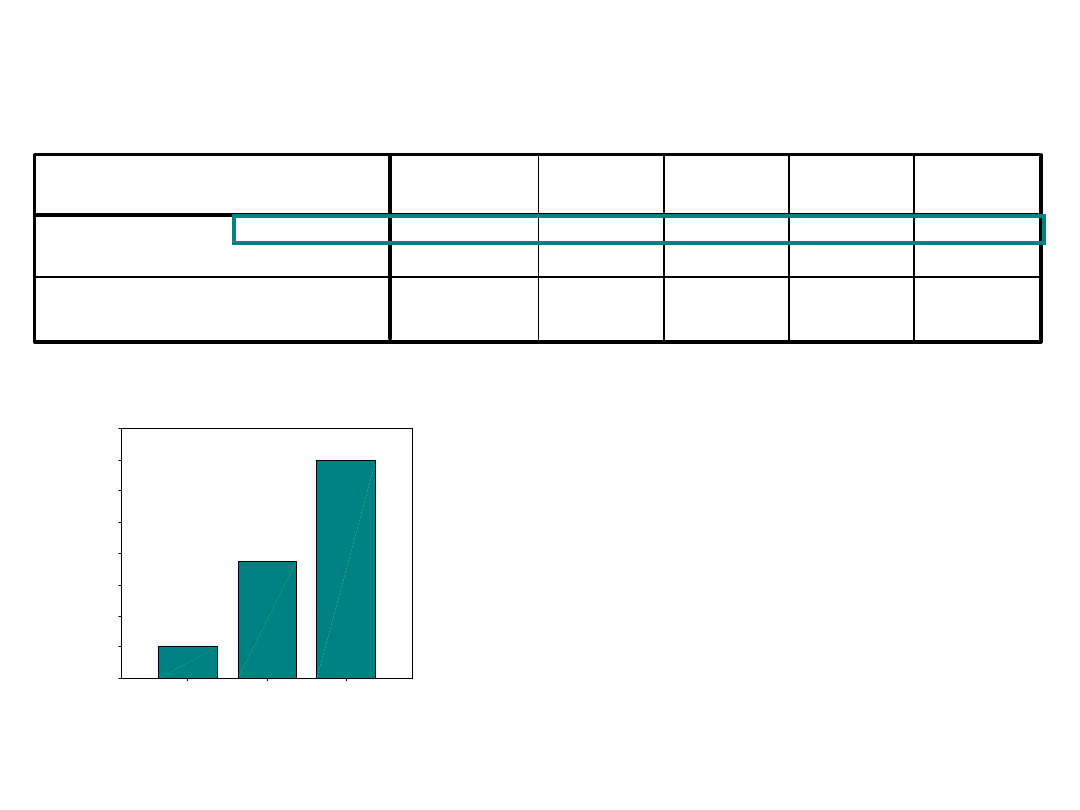
No, ale jak układają się średnie?

Kontrast liniowy okazał się

istotny F(1,3)=72;
p<0,01

i po obejrzeniu średnich na

wykresie uznajemy, że
dobrostan psychologiczny
systematycznie wzrasta
po psychoterapii.

Testy kontrastów wewnątrzobiektowych

Miara: MIARA_1

72,000

1

72,000

72,000

,003

,167

1

,167

3,000

,182

3,000

3

1,000

,167

3

,056

CZYNNIK1
Liniowy
Kwadratowy
Liniowy
Kwadratowy

Źródło zmienności
CZYNNIK1

Błąd(CZYNNIK1)

Typ III sumy

kwadratów

df

Średni

kwadrat

F

Istotność

Skuteczność terapii

pomiar

s kutki odroczone

s kutki bezpoś rednie

przed terapią

O

sz

ac

o

w

an

e

ś

re

d

n

ie

b

rz

e

g

o

w

e

37

36

35

34

33

32

31

30

29

A teraz

prościej

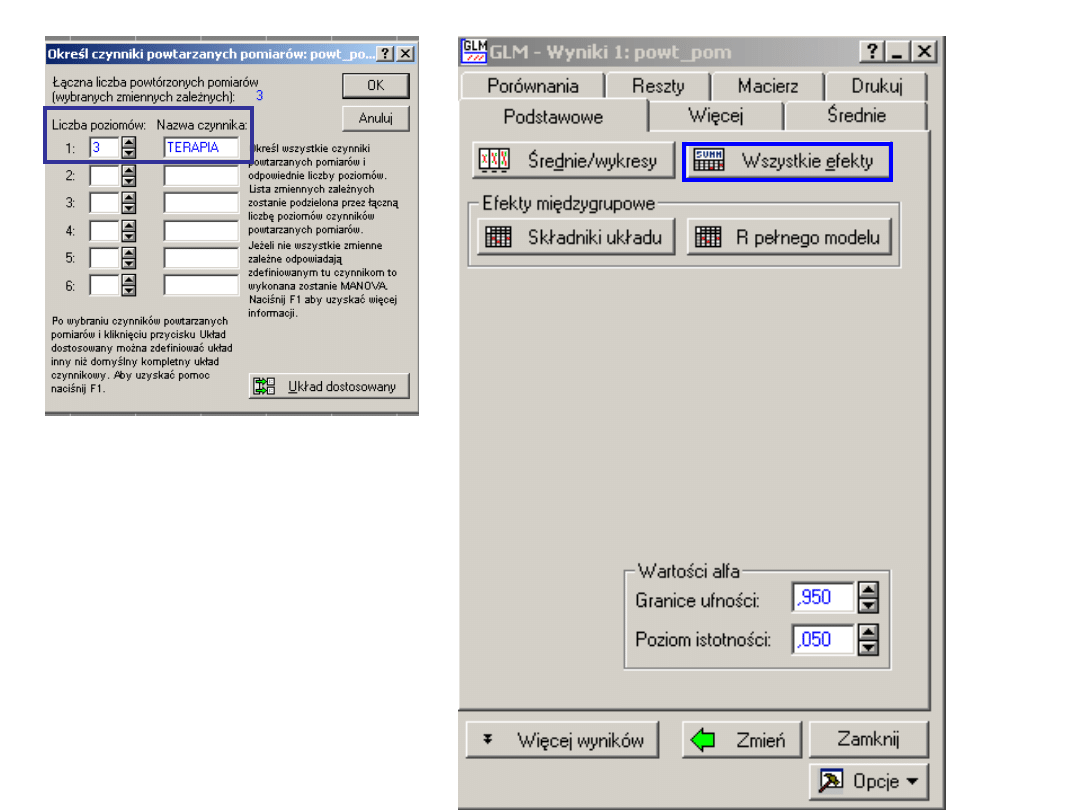
Wydruk

Uzyskano istotny efekt F(2, 6)=68; p<0,001

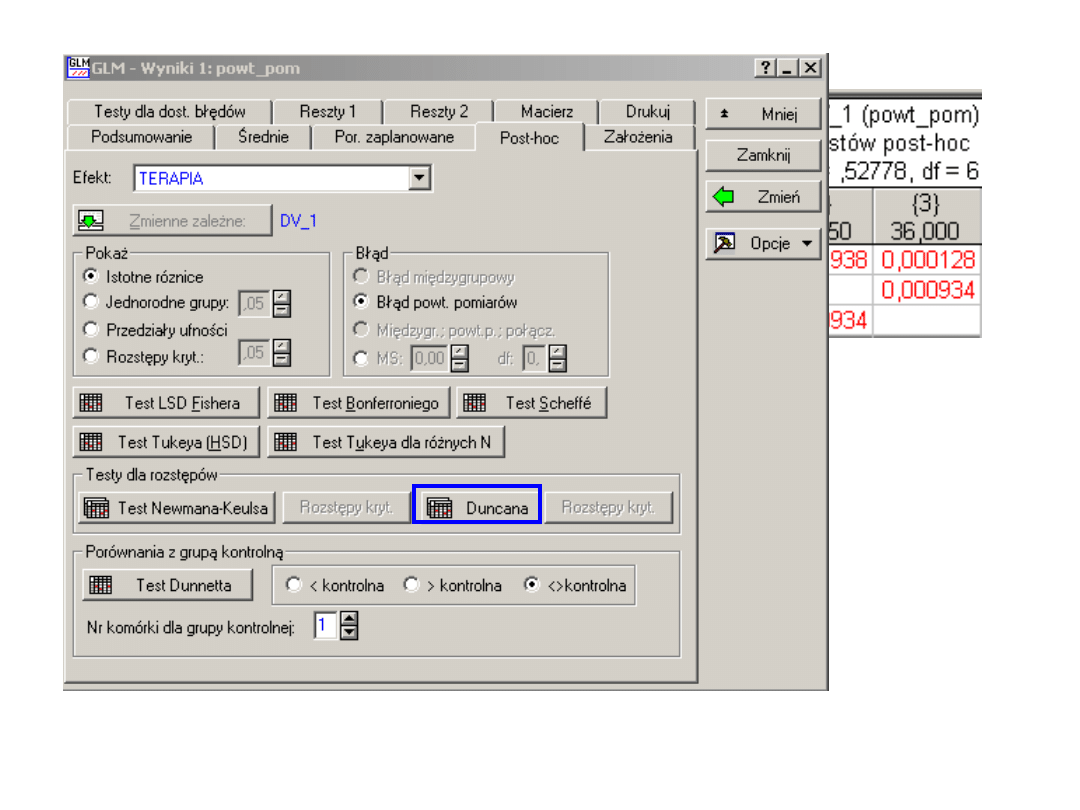
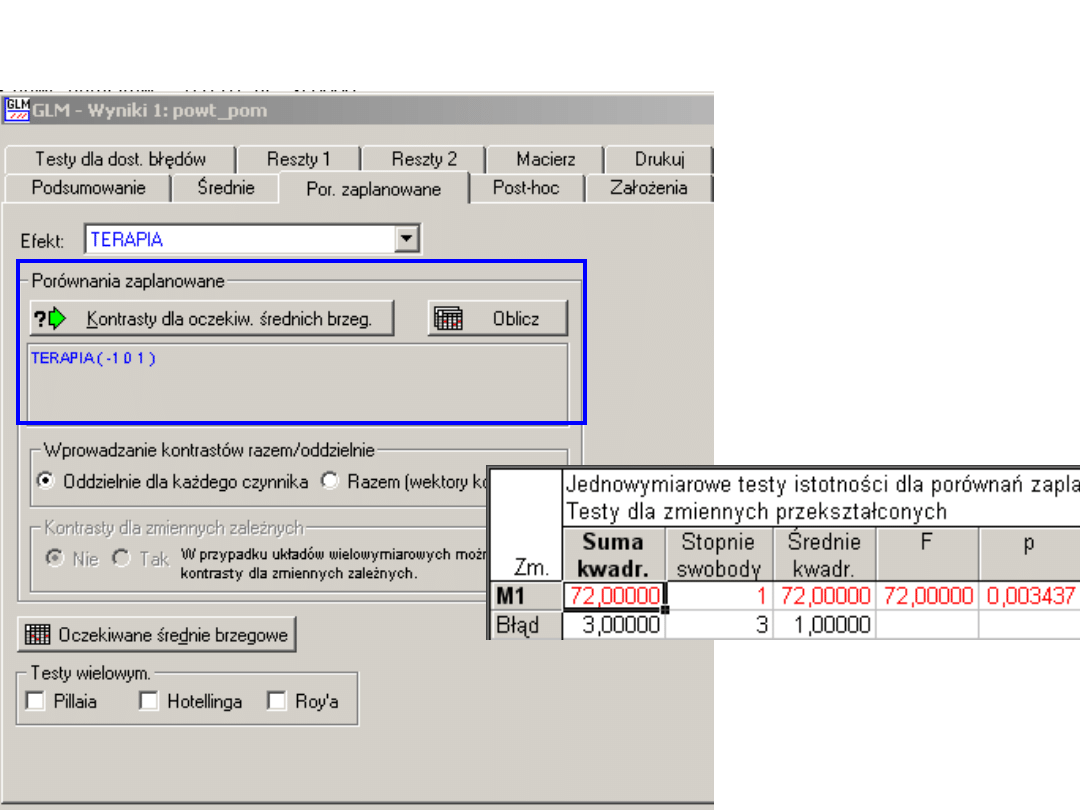
Kontrasty