W związku z tym, że przy ostatnich wyborach do

Samorządu Studentów Uniwersytetu Wrocławskiego

frekwencja wyniosła 2%, w tym roku powstała silna

grupa studentów, którzy chcą to zmienić.

Jeżeli jest to możliwe, prosimy o pomoc

polegającą na poinformowaniu studentów

Wydziału Fizyki, że

w najbliższy poniedziałek i wtorek, (2XI - 3XI)

na ich Wydziale przy pl. M. Borna 9 wystawione zostaną urny

wyborcze w związku z tegorocznymi wyborami do organów

regulaminowych Samorządu Studentów Uniwersytetu

Wrocławskiego, w skład których wchodzą:

-Parlament studentów,

-Wydziałowa rada samorządu studentów,

-Starosta wydziału

Samorząd to niesamowite miejsce do rozmów, od

niego zależy większość spraw dotyczących studentów.

W tych wyborach, realnie może się poprawić sposób

funkcjonowania organów administracji w społeczności

Studentów Uniwersytetu Wrocławskiego. Następne

wybory odbędą się dopiero za trzy lata.

Z poważaniem,

Anna Koropczuk, Wydział Prawa Administracji i

Ekonomii, UWr Krzysztof Parjaszewski, Wydział

Matematyki i Informatyki UWr

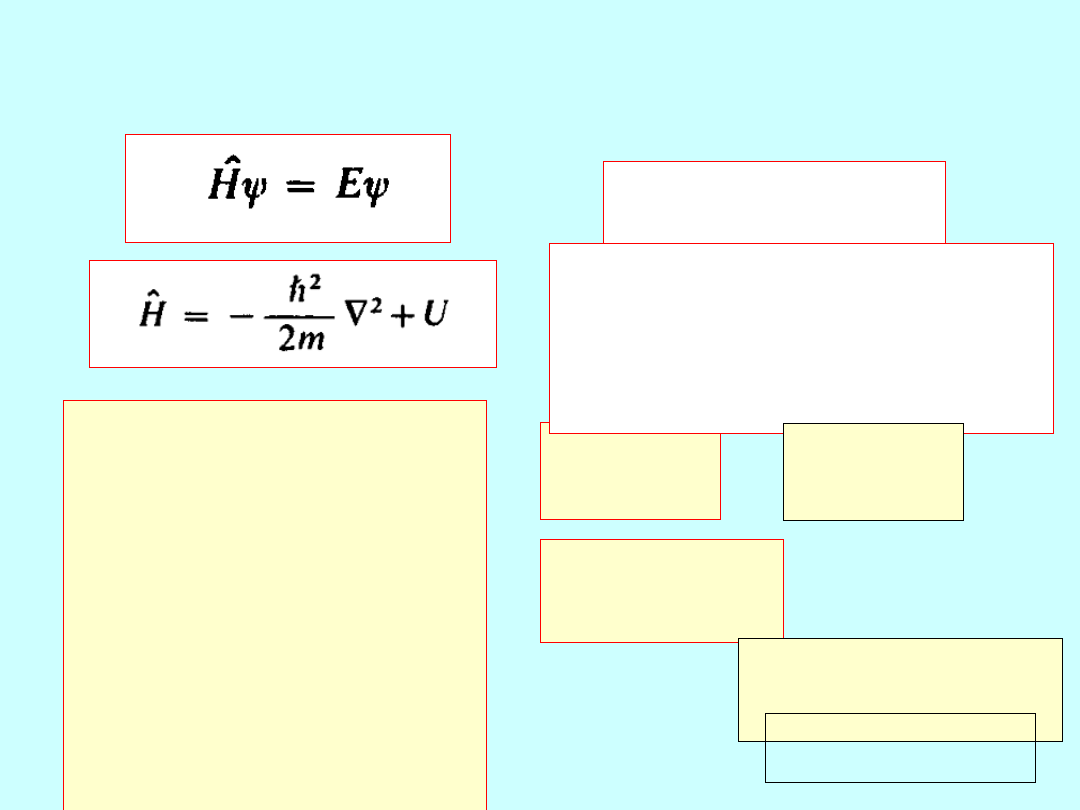
Atomy w mechanice kwantowej

1. Atom wodoru i

wodoropodobny

2. Atom

wieloelektronowy

- metale alkaliczne

Li, Na, K, Rb, Cs, Fr

- inne pierwiastki

E =

E(

n

)

ψ =

ψ(

n,l,m

l

,m

s

)

n = 1, 2, 3, ...; l = 0, 1,

.., n-1;

m

l

= -l, -l+1,..., l; m

s

=

-1/2, 1/2

E =

E(

n,l,m

s

)

E 

R/n

2

E  R/

(n+

α

(l,m

s

))

2

Rydberg,

α - defekt kwantowy

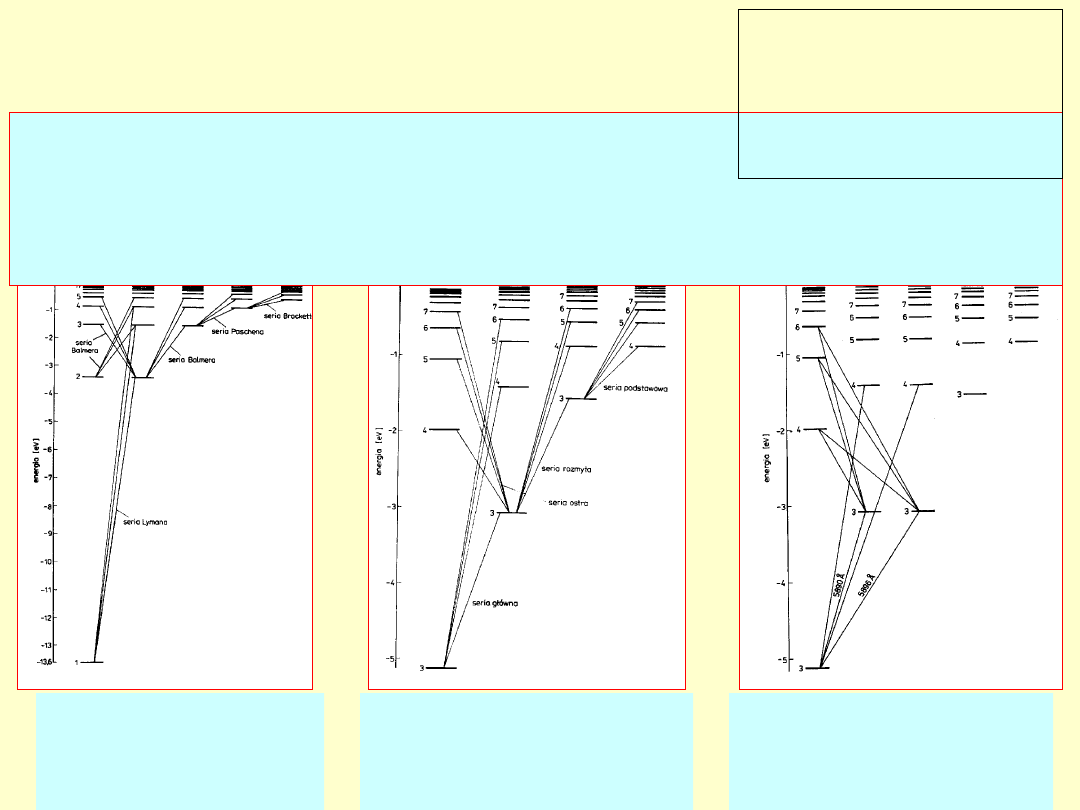
Poziomy struktury

energetycznej H

(krotność degen. =

2n

2)

Poziomy struktury

energetycznej Na

(krotność degen. =

2(2l+1))

Poziomy subtelnej

struktury

energetycznej Na

(krotność degen. =

2l+1)

Serie widmowe – reguły

wyboru

Wynik przejść między stanami o

różnych energiach

a także liczbach orbitalnego momentach pędu (l lub L) różniących się o 1

(

ΔL=±1

)

oraz równych liczbach całkowitego momentu pędu (j lub J) lub różniących

się o1 (

ΔJ=0,±1

).

Spin fotonu

Spin fotonu

=

1

(liczba spinowa

fotonu)

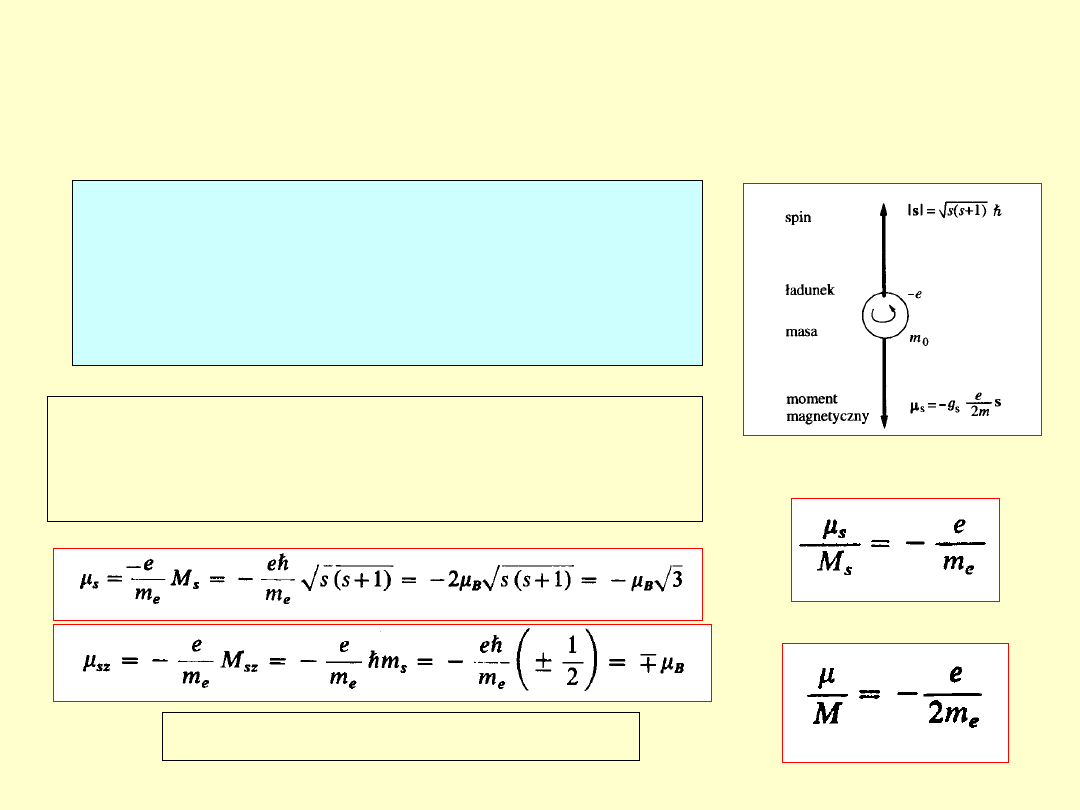
Spin elektronu

Spin elektronu

= ½

- liczba kwantowa s spinu elektronu czyli jego własnego

momentu pędu s (M

s

).

μ

B

– magneton Bohra = ½ eh/m

e

g

s

= 2 s =

1/2

Spinowy moment magnetyczny elektronu

μ

s

jest wprost proporcjonalny do jego spinu M

s

(s)

elektron

wirująca kula

Spin elektronu a właściwie

spinowy moment magnetyczny

spinowy moment magnetyczny

elektronu

elektronu

μ

μ

s

s

jest odpowiedzialny za

subtelną strukturę widm atomowych

subtelną strukturę widm atomowych

.

–

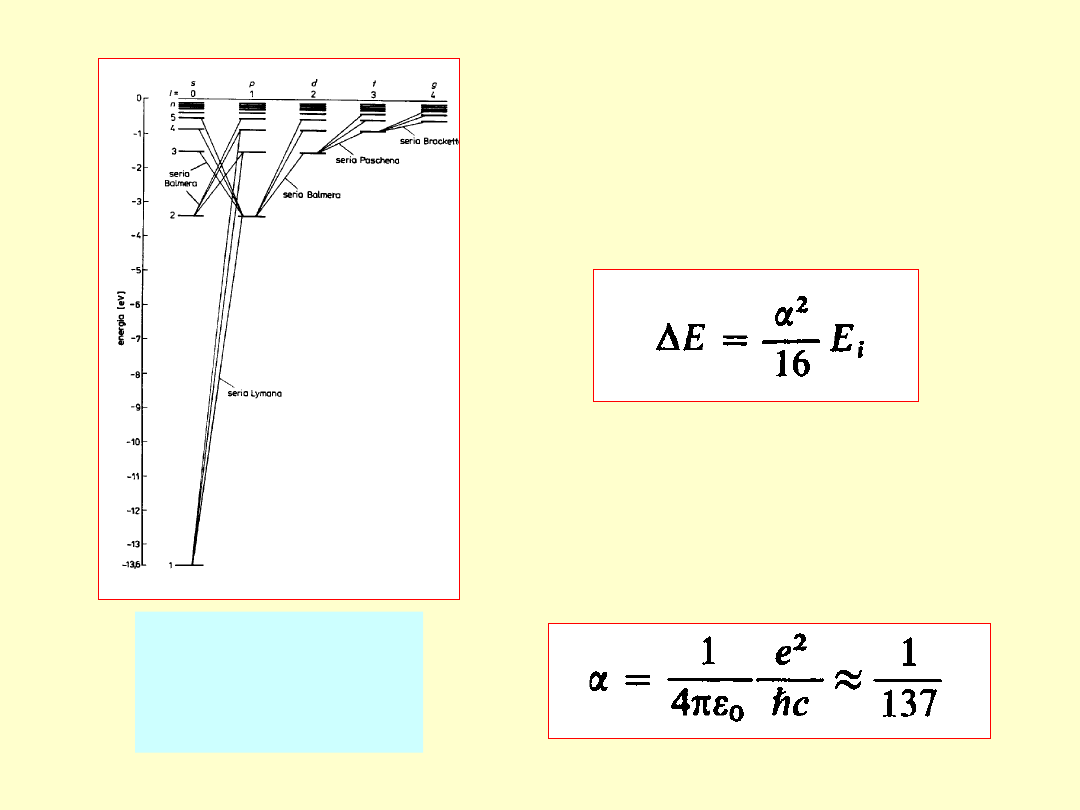
Odległość między

poziomami struktury

subtelnej atomu wodoru,

uwarunkowana spinem

elektronu (efekt

relatywistyczny):

E

i

– energia jonizacji (dla M

j

= )

Bezwymiarowa stała α -
stała struktury
subtelnej:

Poziomy struktury

energetycznej H

(krotność degen. =

2n

2)

Atomy
wieloelektronowe

1. Moment pędu.

2. Moment magnetyczny.

Moment pędu atomu

wieloelektronowego

(

suma momentów orbitalnych i spinowych wszystkich

elektronów)

- uwarunkowany oddziaływaniem momentów

magnetycznych

1. Sprzężenie Russela-Saundersa lub

sprzężenie L-S (

występuje najczęściej

).

J = Σl

i

+ Σs

i

, L = Σl

i

, S = Σs

i

,

(J = L+S)

2. Sprzężenie j-j (

ciężkie

atomy

).

J = Σ(l

i

+ s

i

),

j

i

=

l

i

+ s

i

Wektory momentu pędu:

orbitalnego – L (M

L

), własnego – S (M

S

),

całkowitego – J (M

J

).

M

J

= ΣM

l

+ ΣM

s

, M

L

= ΣM

l

, M

S

= ΣM

s

,

(M

J

= M

L

+M

S

)

M

J

= Σ(M

l

+ M

s

), M

j

= M

l

+ M

s

i i i i

i i i i
i

Sprzężenie Russela-

Saundersa

J = L+S, L+S–1, ... , |L–S|

2S+1 (S<L) lub 2L+1 (L<S) wartości całkowitych lub

połówkowych (decyduje wartość S, L zawsze całkowite)

Symbol
charakteryzujący stan
elektronów atomu –
term stanu tych
elektronów.

Liczby kwantowe:
S - spinowa
L – orbitalna,
J - całkowitego momentu
pędu

L = S (

L=0

), P (

L=1

), D (

L=2

), F

(

L=3

), itd.

Przykład.
S = 1
(2S+1=3)
L = 1,
J = 0, 1, 2

2S+1

L

J

3

P

0

,

3

P

1

,

3

P

2

Moment magnetyczny atomu

orbitaln

y

spinow

y

całkowi

ty

Magnet

on

Bohra

Czynnik

Landégo

Spinowy i orbitalny czynnik

Landégo elektronu nie są

jednakowe.

g

s

= 2g

l

(g

s

=2, g

l

=1)

W konsekwencji

μ

μ

j

j

i

i

J

J

nie są współliniowe.

nie są współliniowe.

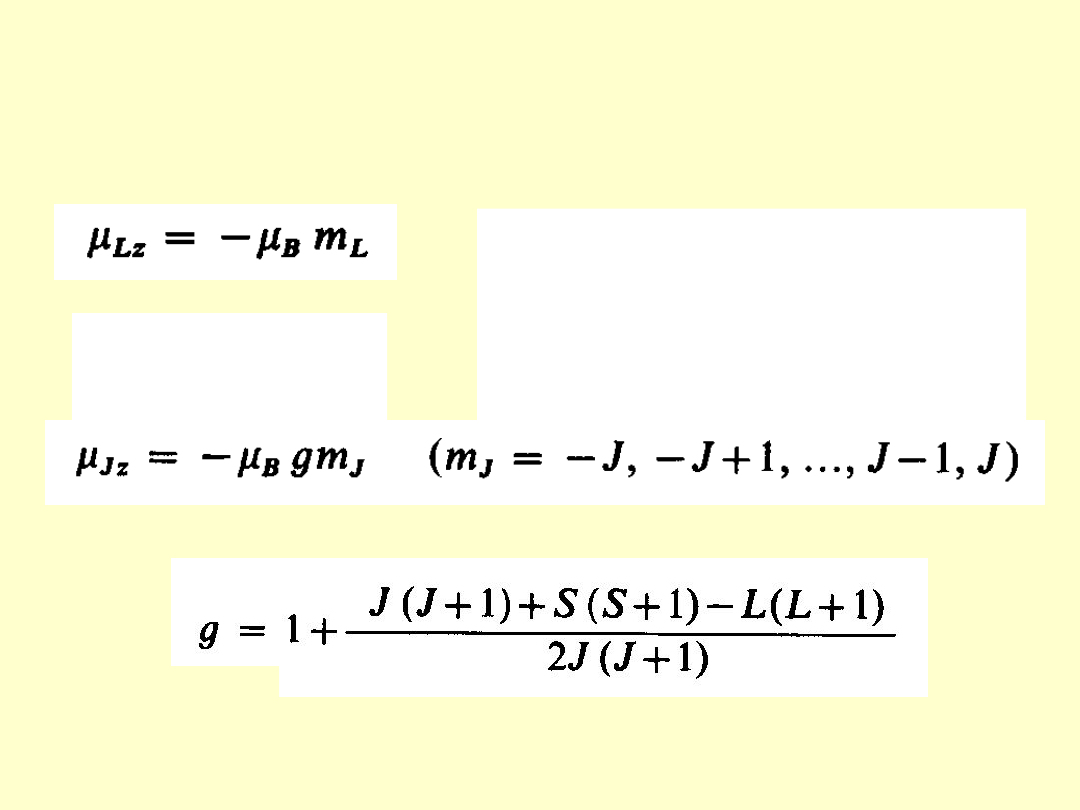
μ

Sz

= – 2 μ

B

m

S

Rzuty μ na wyróżnioną oś

(

z

)

(m

L

= – L, – L+1, ..., L

– 1, L)

(m

S

= – S, – S+1, ..., S

– 1, S)

Czynnik

Landégo

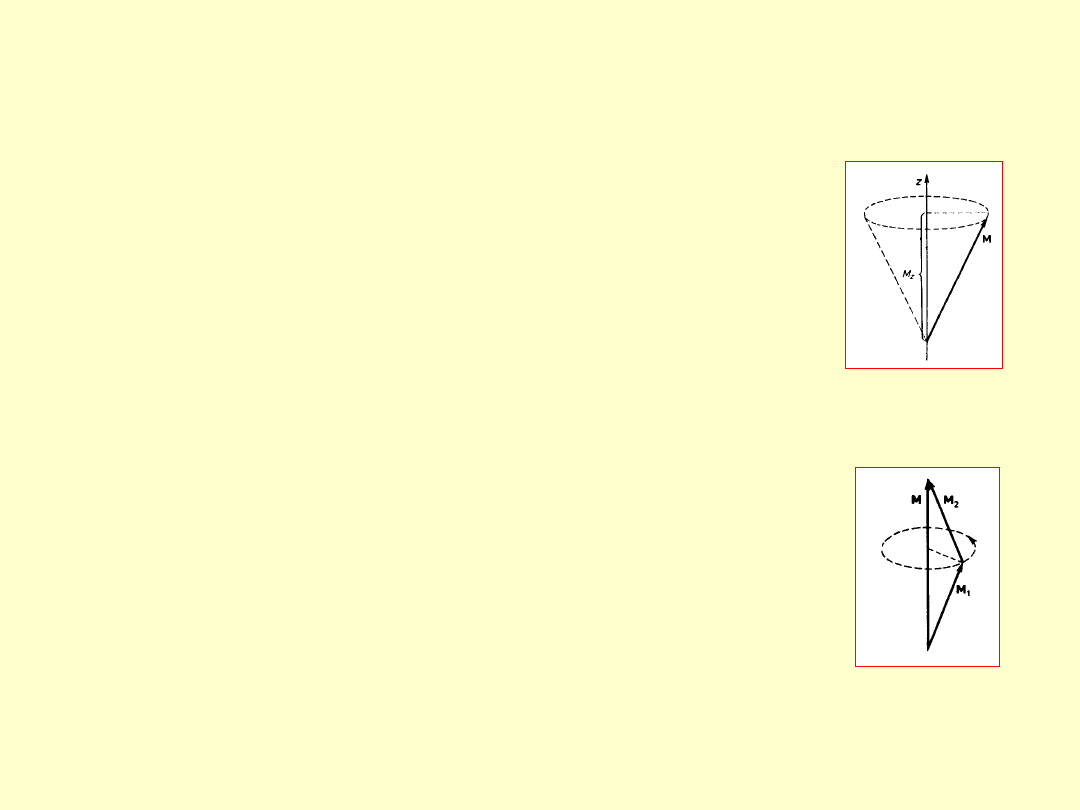
Wektorowy model

atomu

1. Jeżeli znany jest moment pędu M i jedna
z jego składowych M

z

(wzdłuż osi z) to

wektor M wykonuje ruch precesyjny wokół
osi z (dwie pozostałe jego składowe M

x

i M

y

są w tym przypadku nieokreślone).

2. Jeżeli moment pędu M jest
wypadkowym wektorem dwóch momentów
pędu M

1

i M

2

, oddziaływujących ze sobą za

pośrednictwem momentów magnetycznych
μ

1

i μ

2

, to M

1

i M

2

wykonują ruch

precesyjny wokół kierunku wektora M z
częstością proporcjonalną do energii
oddziaływania między μ

1

i μ

2

.

Jeżeli jednocześnie znany jest moment
pędu M i jedna z jego składowych M

z

to

wektor M wykonuje z kolei ruch
precesyjny wokół osi z (patrz pkt.1).

Atom w polu
magnetycznym.

1. Zjawisko Zeemana (1896) – normalne i
anomalne.

2. Zjawisko Paschena – Backa (1912).

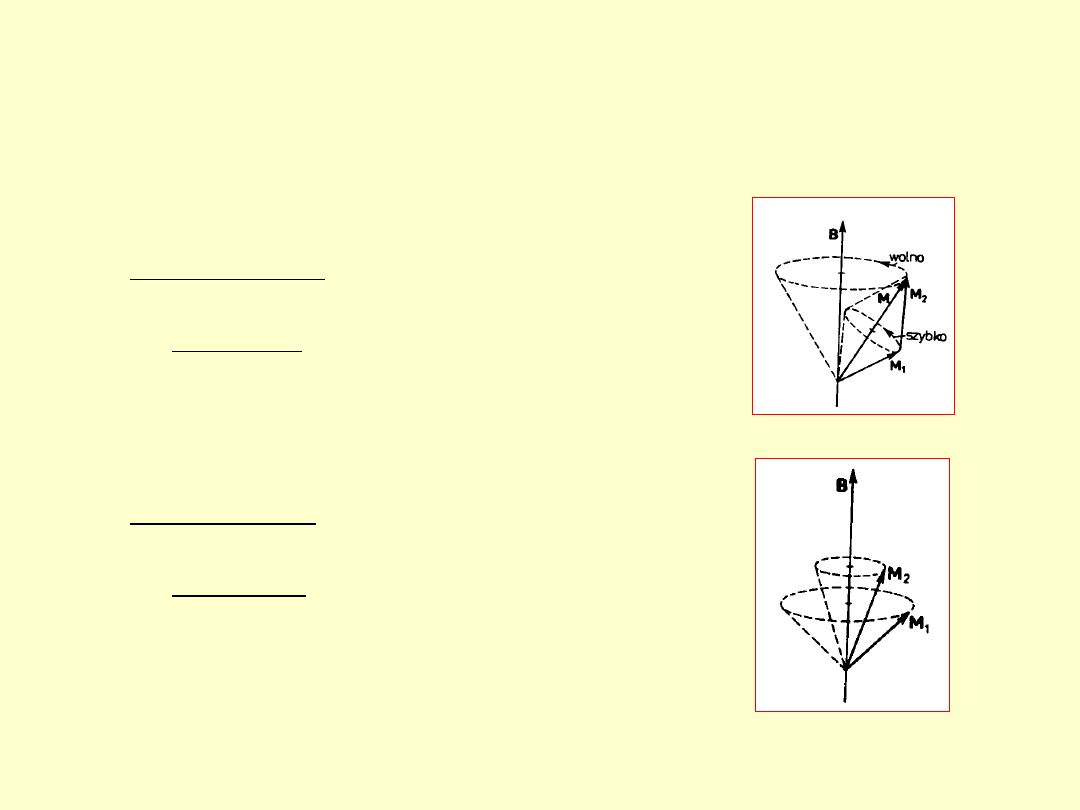
Pole magnetyczne B
wzdłuż osi z

1. Słabe pole B – oddziaływanie
momentów magnetycznych ze
sobą większe od oddziaływania
każdego z nich z polem
magnetycznym.

2. Silne pole B – oddziaływanie
momentów magnetycznych ze
sobą mniejsze od oddziaływania
każdego z nich z polem
magnetycznym.

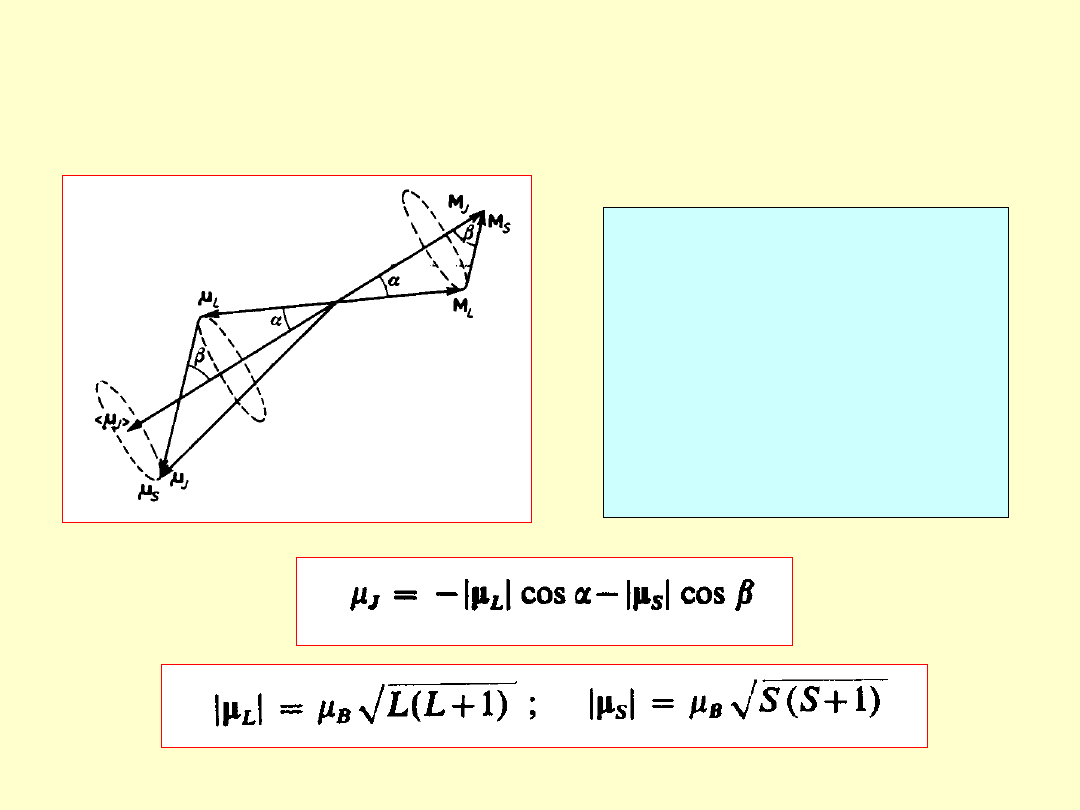
Czynnik

Landégo

Spinowy i orbitalny czynnik

Landégo elektronu nie są

jednakowe.

g

s

= 2g

l

(g

s

=2, g

l

=1)

W konsekwencji

μ

j

i M

j

nie są współliniowe.

2

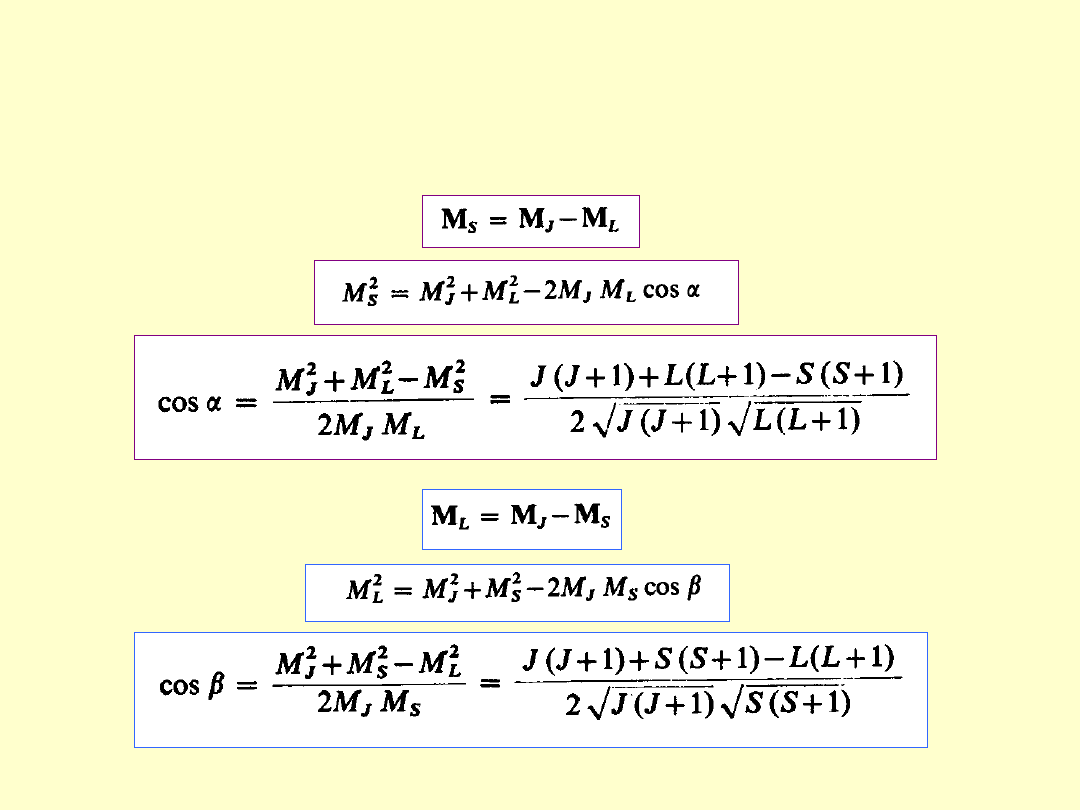
Czynnik Landégo c.d.

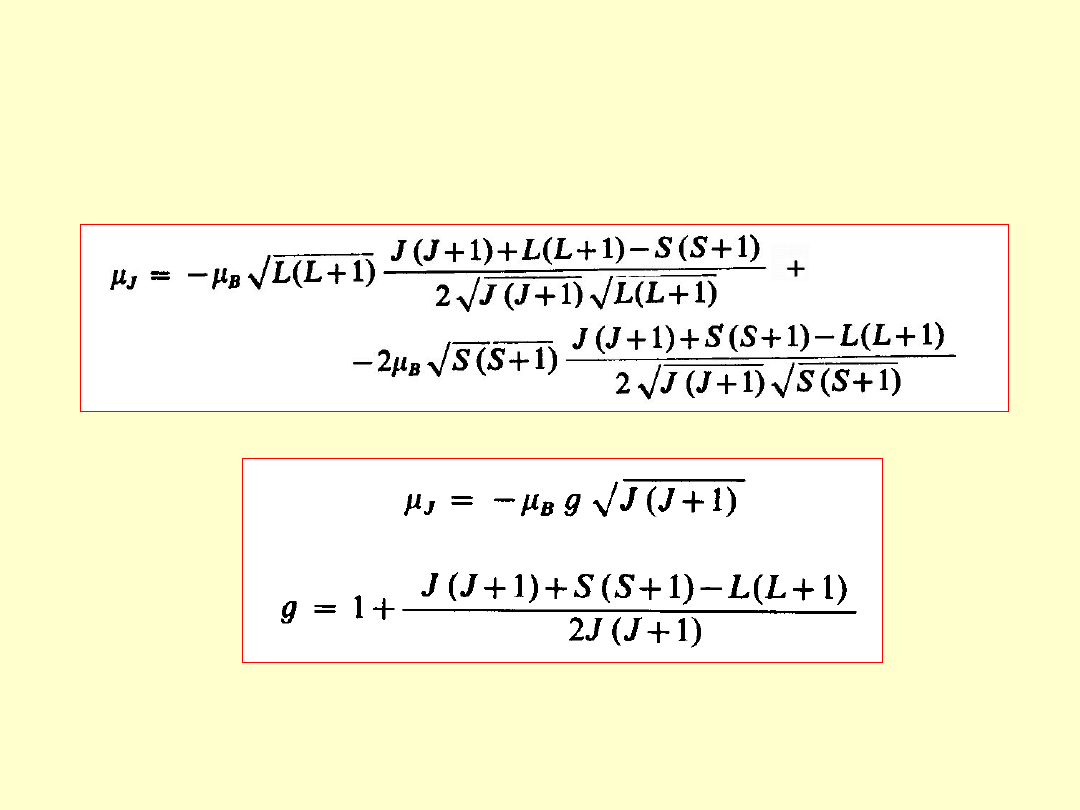
Czynnik Landégo

c.d.

Zjawisko Zeemana

Zeemana

- 1896

rozszczepienie poziomów energetycznych atomu

(i w konsekwencji linii widmowych)

pod wpływem zewnętrznego, słabego

słabego

pola

magnetycznego

(rozszczepienie magnetyczne mniejsze od

multipletowego – uwarunkowane subtelnym

oddziaływaniem spin-orbita)

ΔE = -μ

J

•B = -μ

J

B

cos(μ

J

,B)

Pole magnetyczne zdejmuje degeneracje stanów o różnej liczbie

kwantowej m

J

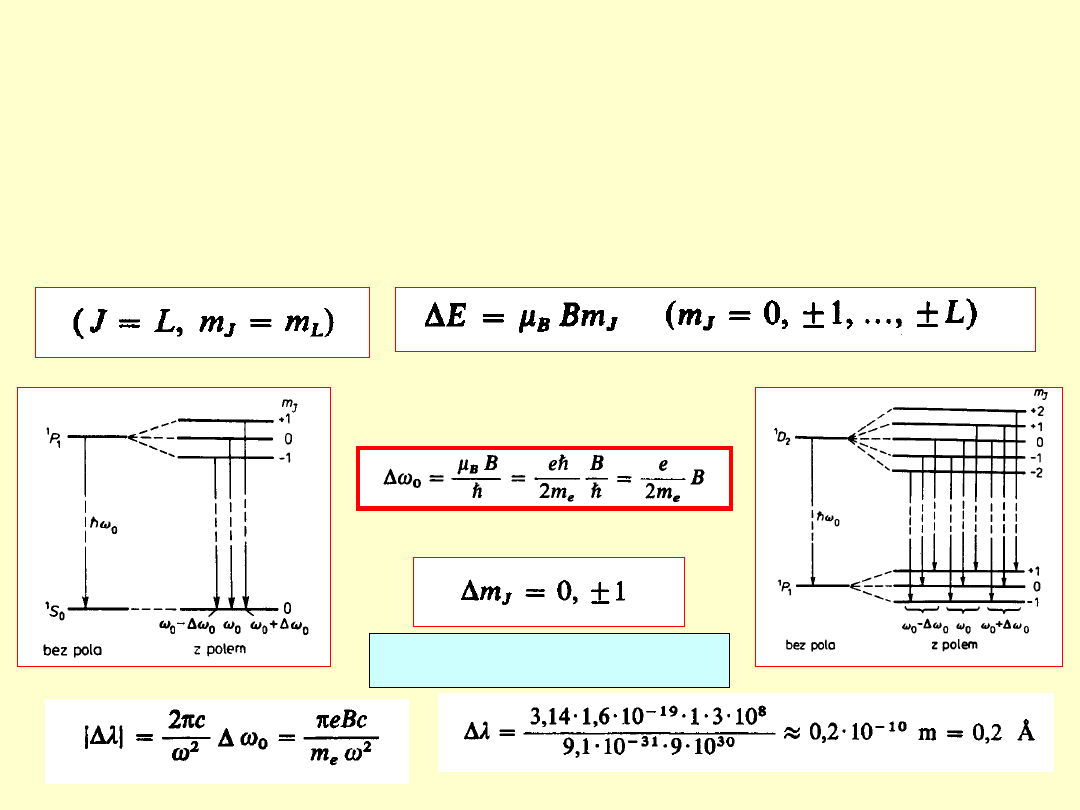
Normalne

Normalne

zjawisko Zeemana

– rozszczepienie magnetyczne

singletów

(linie widmowe nie mające struktury subtelnej –

wynik przejść między poziomami z S=0 czyli g=1)

Jednakowa odległość między kolejnymi

podpoziomami

Rozszczepienie zawsze tylko na 3

linie

Przesunięcie normalne

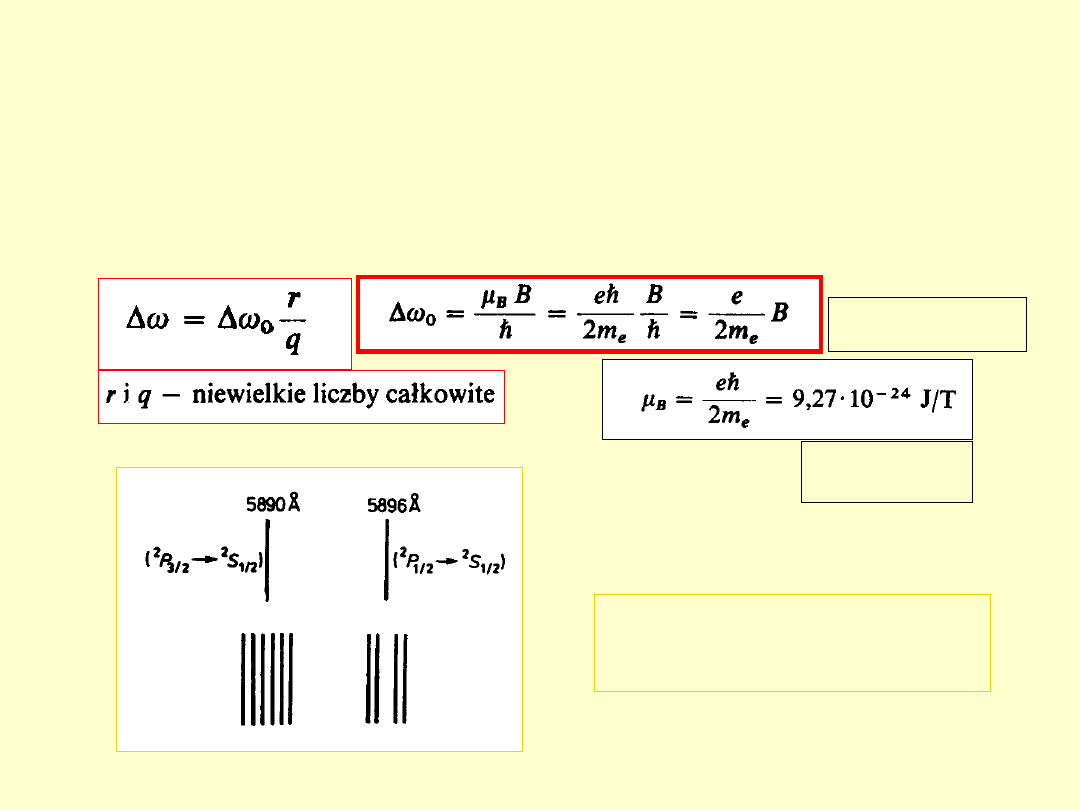
Anomalne

Anomalne

zjawisko Zeemana

– rozszczepienie magnetyczne

multipletów

(linie widmowe mające strukturę subtelną)

Przesunięcie

normalne

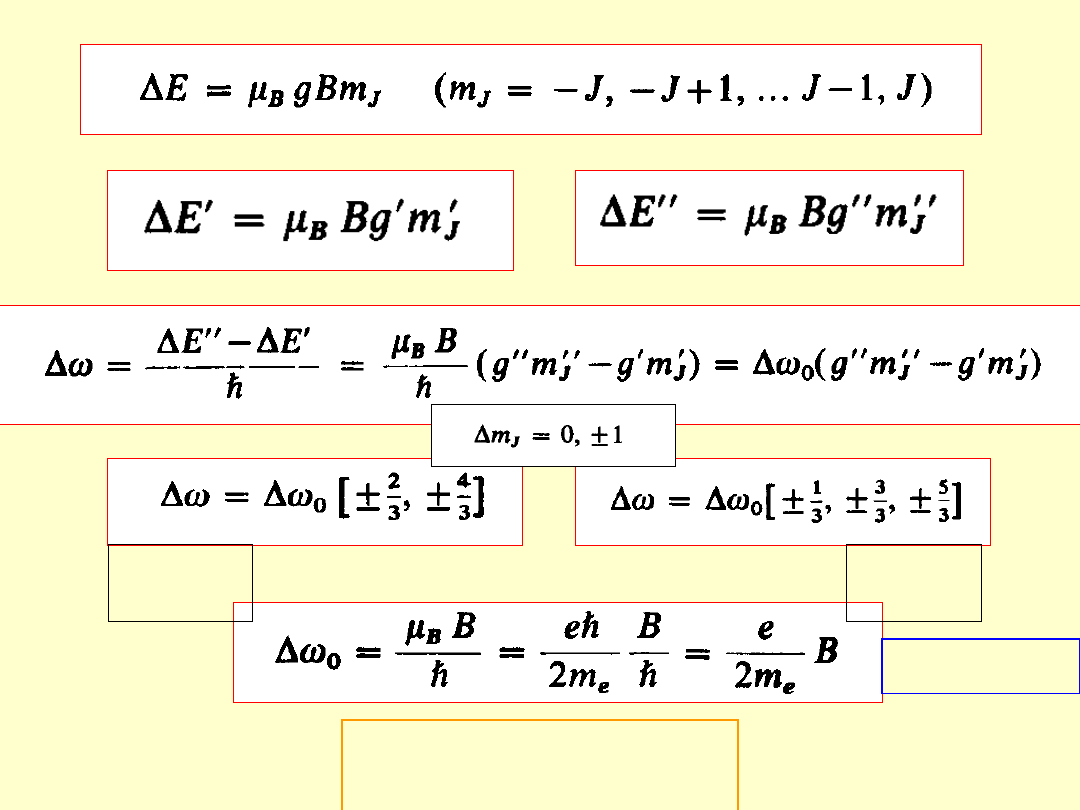
Rozszczepienie żółtego

dubletu sodu w słabym polu

magnetycznym

Magneton
Bohra

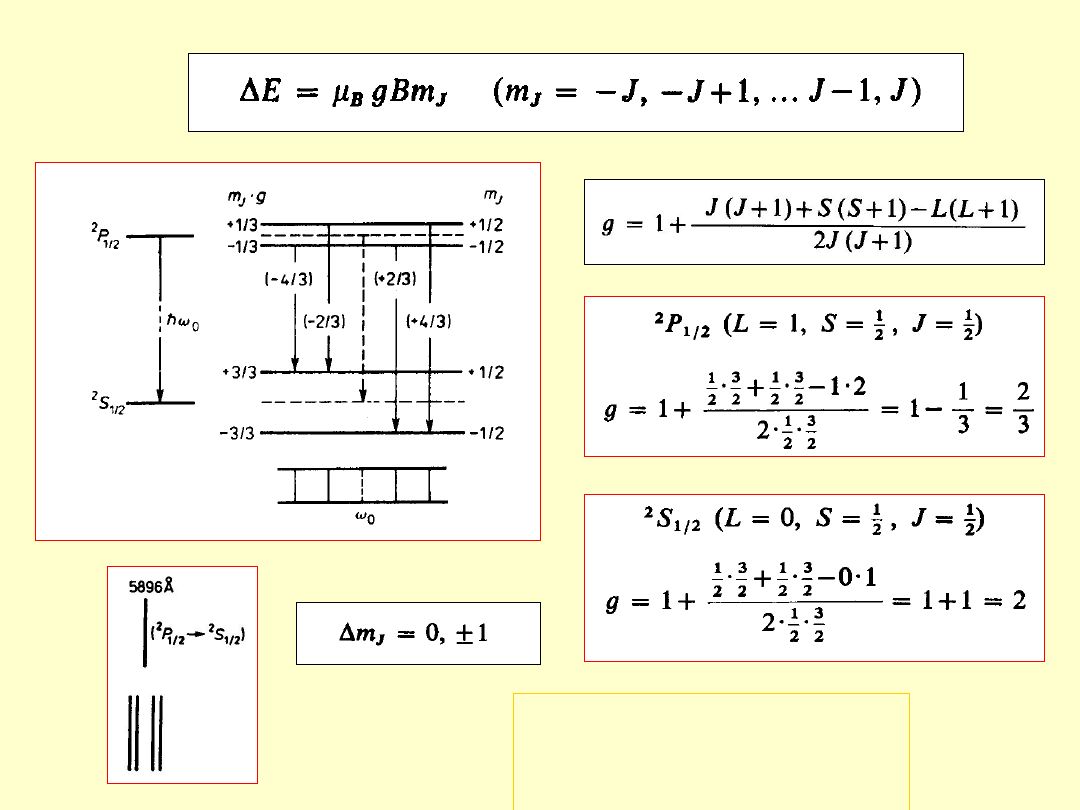
Rozszczepienie żółtego

dubletu sodu w słabym polu

magnetycznym – linia o

mniejszej energii

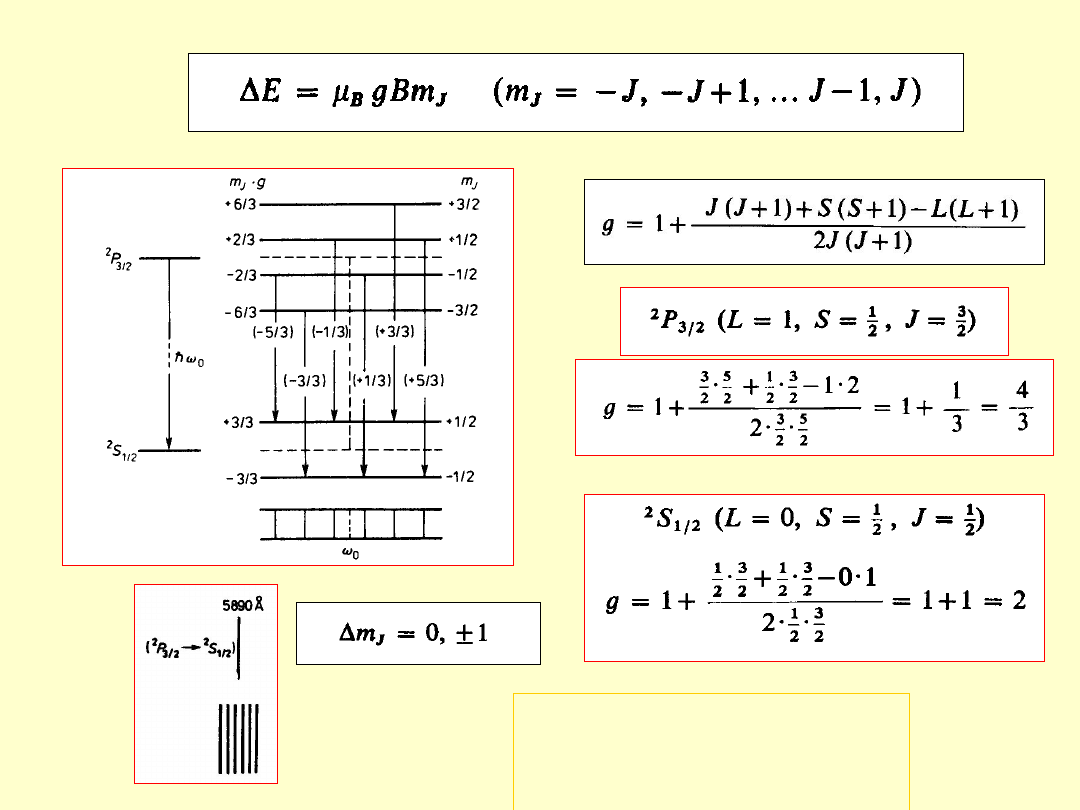
Rozszczepienie żółtego

dubletu sodu w słabym polu

magnetycznym – linia o

większej energii

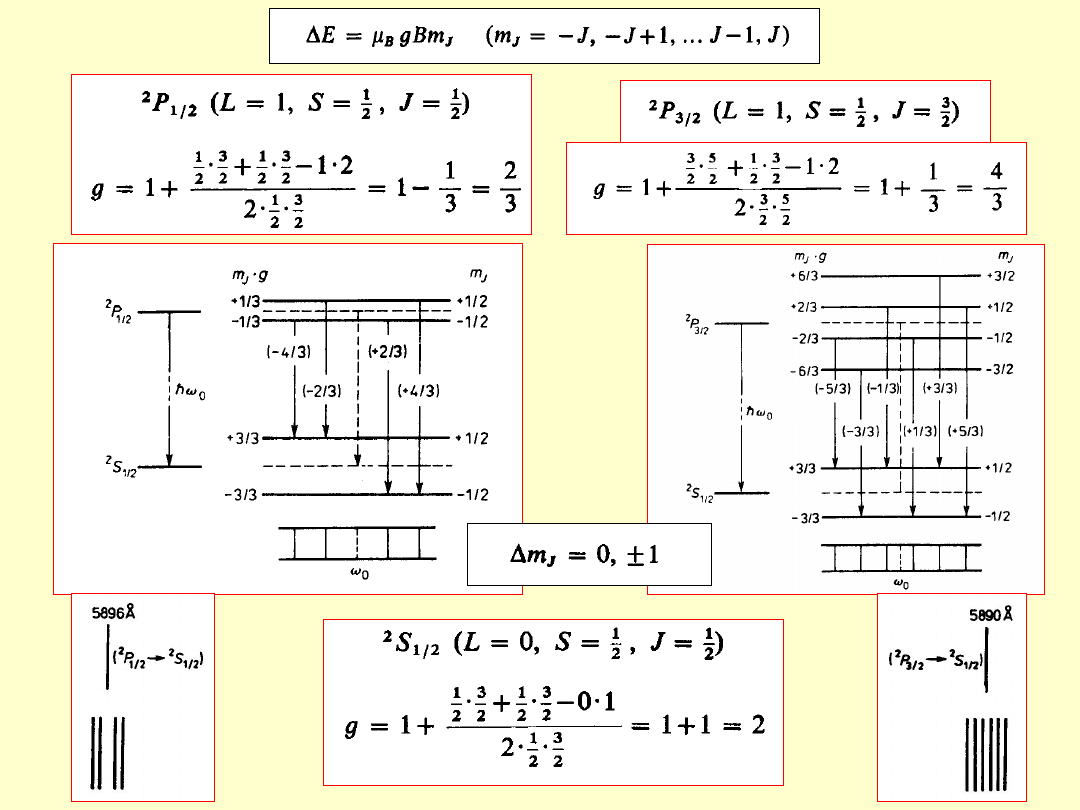
2

P

1/2

–

2

S

1/2

2

P

3/2

–

2

S

1/2

Rozszczepienie żółtego

dubletu sodu w słabym polu

magnetycznym

Przesunięcie

normalne

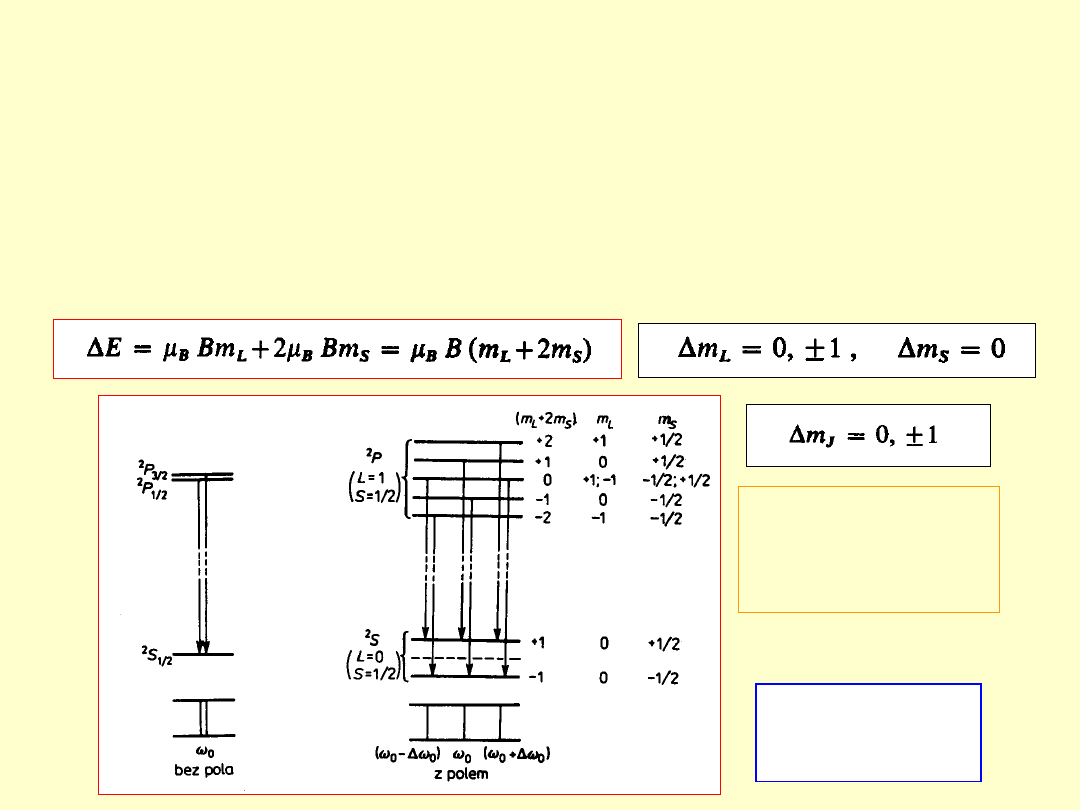
Zjawisko Paschena-Backa

Paschena-Backa

-

-

1912

1912

rozszczepienie poziomów energetycznych atomu

(i w konsekwencji linii widmowych)

pod wpływem zewnętrznego, silnego

silnego

pola

magnetycznego

(rozszczepienie magnetyczne większe od

multipletowego)

Rozszczepienie

żółtego dubletu

sodu w silnym polu

magnetycznym

Normalny

tryplet

zeemanowski

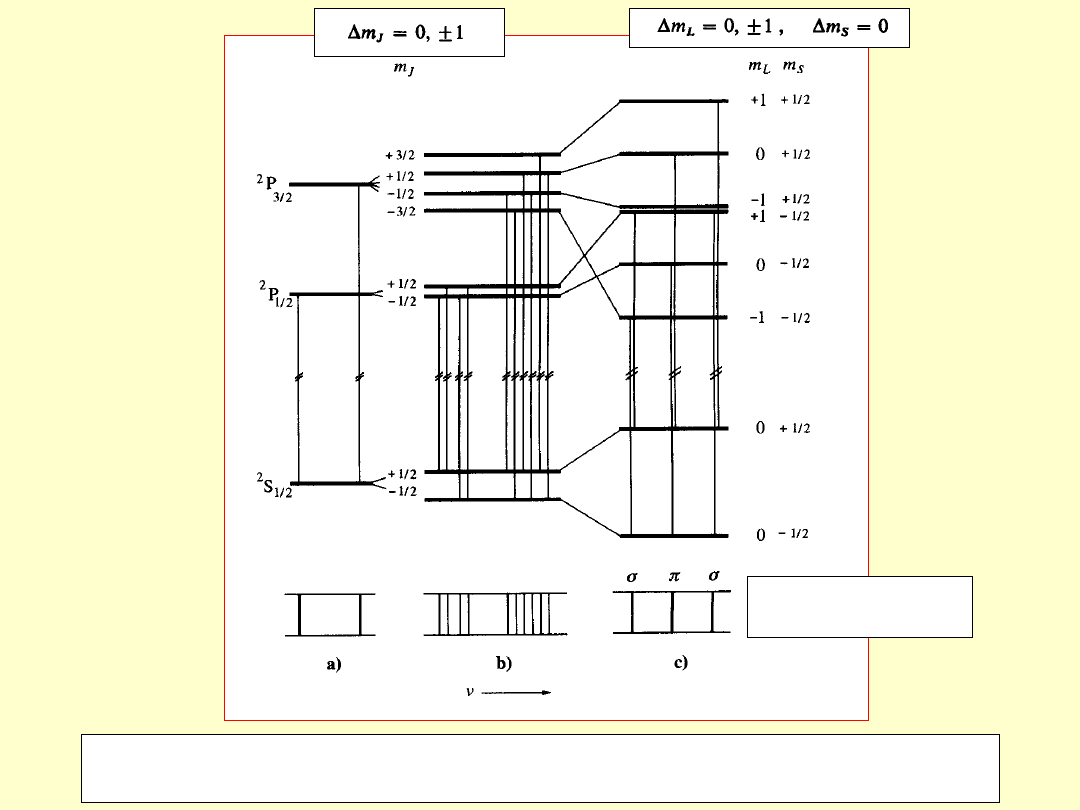
Rozszczepienie żółtego dubletu sodu (a) w słabym (b) i silnym (c) polu

magnetycznym

Normalny tryplet

zeemanowski

Konfiguracja elektronowa

atomu

1. Charakterystyki stanu elektronu.

2. Zakaz Pauliego.

3. Reguły Hunda

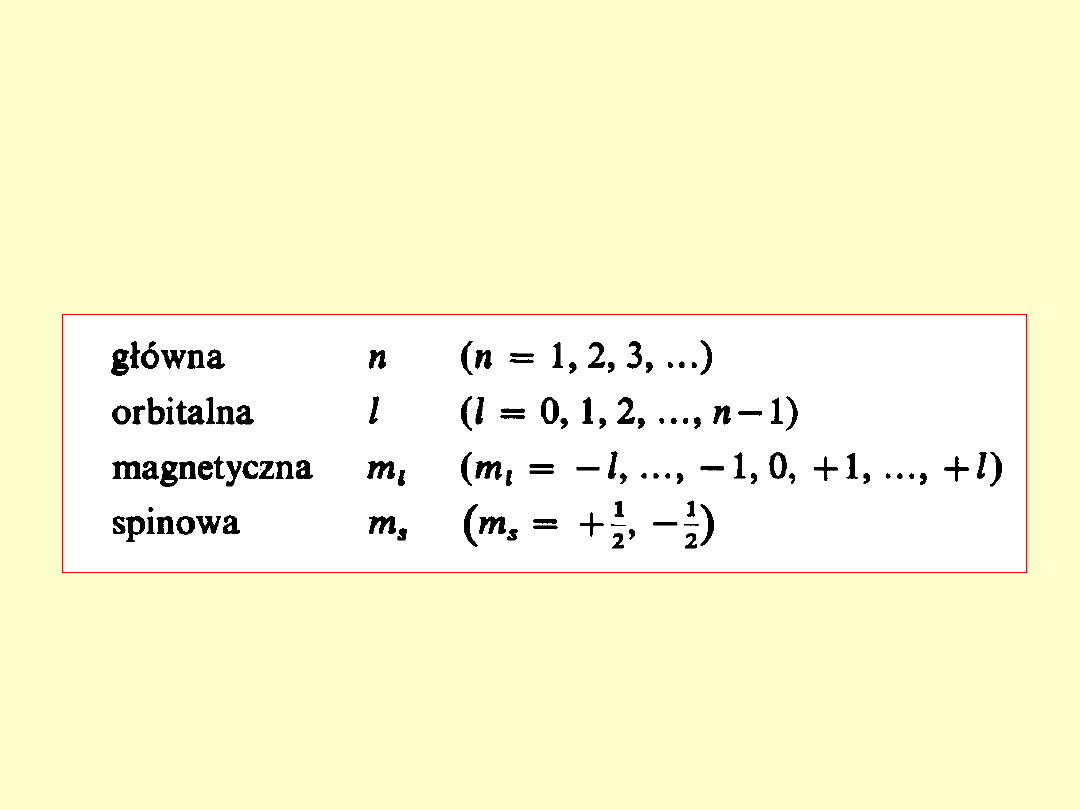
Stan każdego elektronu w atomie

charakteryzują cztery liczby

kwantowe:

Zakaz Pauliego:

W tym samym atomie nie może być dwóch

elektronów opisanych przez taki sam zbiór

czterech liczb kwantowych: n, l, m

l

i m

s

.

W stanach o danej wartości n
może być w atomie nie więcej
niż 2n

2

elektronów:

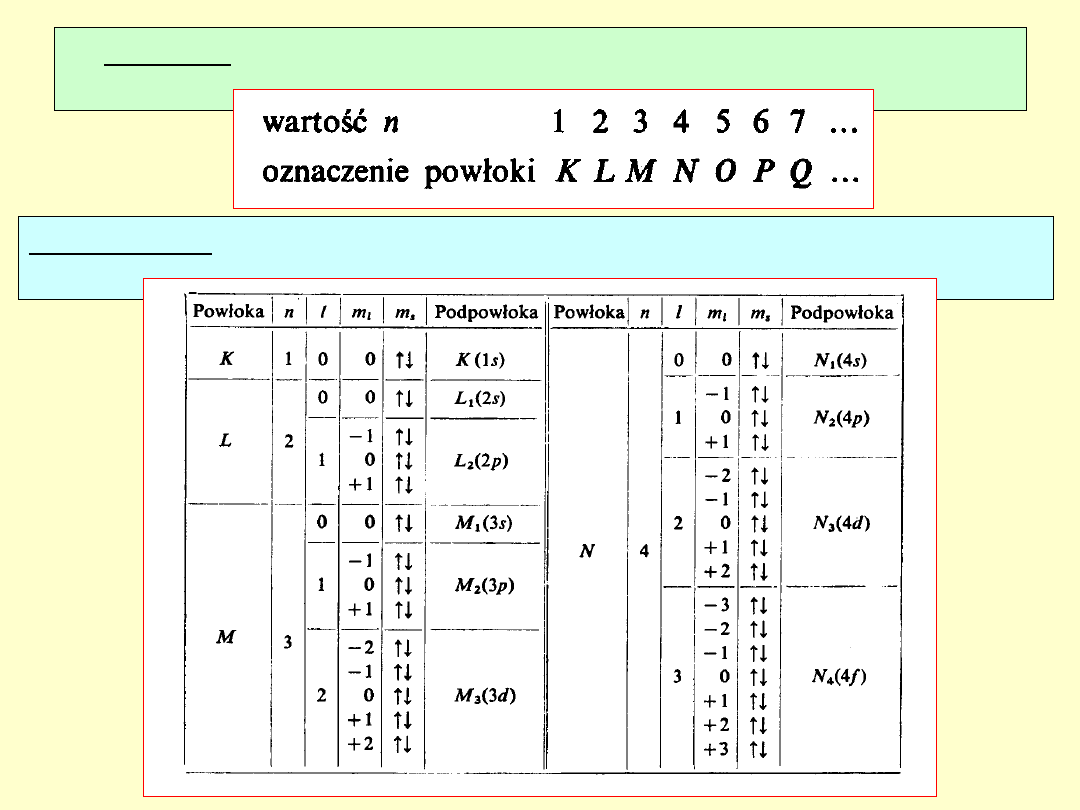
Powłoka: zbiór elektronów atomu o takiej samej wartości

liczby kwantowej n.

Podpowłoka: zbiór elektronów powłoki o takiej samej wartości
liczby kwantowej l.

Dla całkowicie zapełnionej

podpowłoki

jej sumaryczny spinowy moment

pędu S

i sumaryczny orbitalny moment

pędu L

są równe zeru tj.

S = 0

i

L = 0

stąd

J =

0.

Przy wyznaczaniu L i S

atomu można nie brać pod

uwagę zapełnionych

podpowłok.

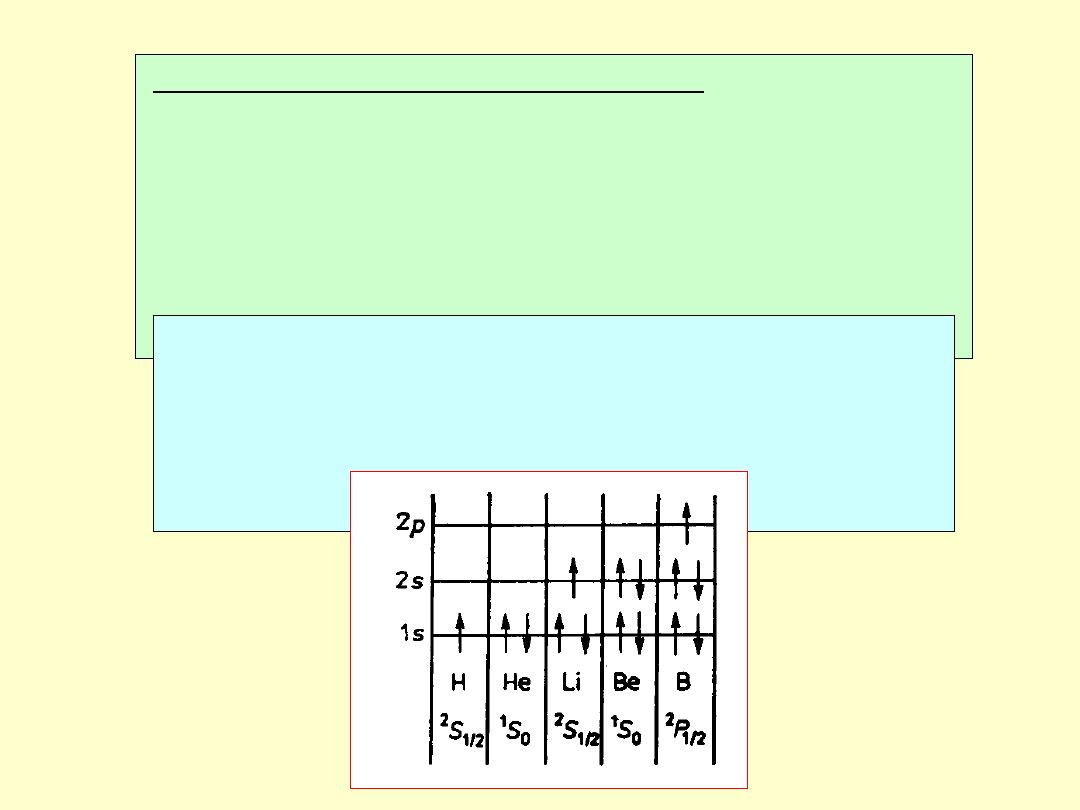
Konfiguracja elektronowa atomu zapisywana jest

przez podanie symboli wszystkich stanów

elektronowych nl obsadzonych przez elektrony

począwszy od podstawowego 1s, wraz z liczbą

elektronów k w poszczególnych stanach – ciąg

symboli nl

k

;

np. konfigurację elektronową atomu litu zapisujemy

w postaci: 1s

2

2s

1

.

Informacja o wartościach S, L i J dla danego

stanu elektronów atomu zawarta jest w symbolu

termu tego stanu:

2S+1

L

J

;

np. term podstawowego stanu atomu litu ma

postać:

2

S

1/2

.

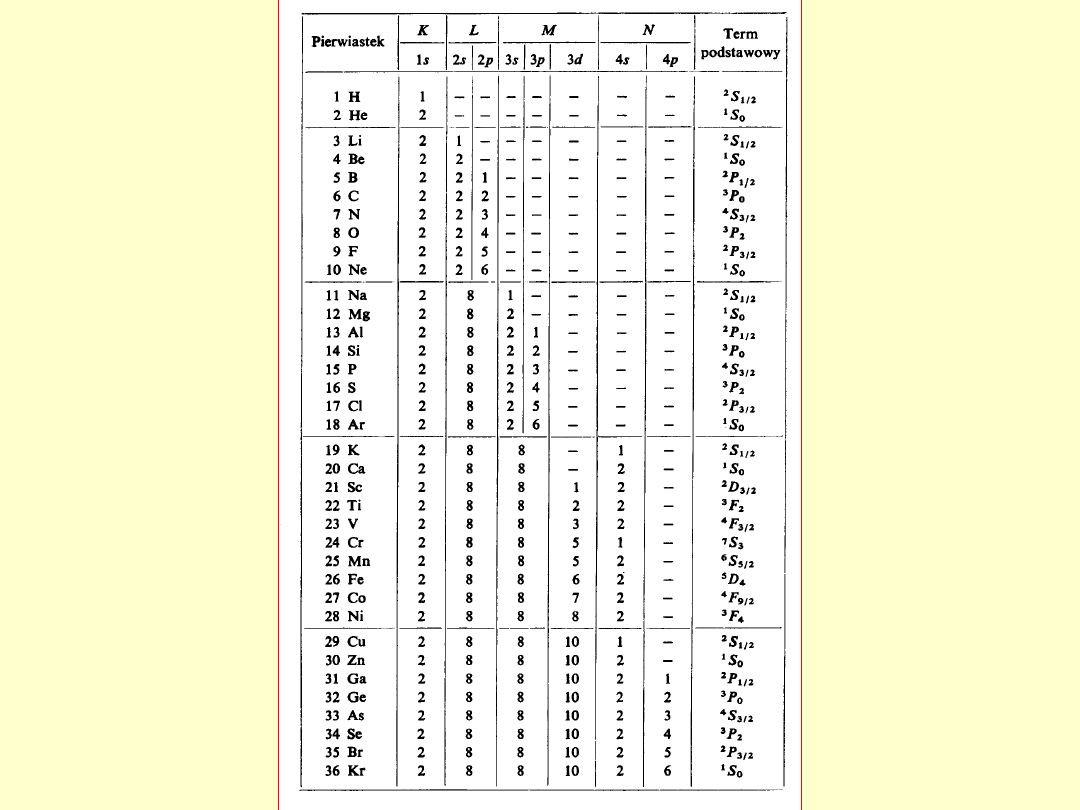
Reguły Hunda

1. Spośród termów odpowiadających danej
konfiguracji elektronowej najmniejszą energię ma
term o największej możliwej wartości S oraz o
największej wartości L możliwej przy takim S.

2. Multiplety utworzone przez elektrony równoważne
(takie samo nl) są regularne (ze wzrostem J rośnie
energia stanu), jeżeli zapełniona jest nie więcej niż
połowa podpowłoki, natomiast jeżeli zapełnienie
przekracza połowę podpowłoki to multiplety są
odwrócone (ze wzrostem J energia stanu maleje).

Wynika stąd, że dla multipletów regularnych J = |L-S| a
dla odwróconych J = L+S.

Liczba niesparowanych elektronów na podpowłokach
(nl) powinna być jak największa.

Promieniowanie

rentgenowskie

1. Generowanie.

2. Charakterystyczne promieniowanie
rentgenowskie.

3. Prawo H. Moseleya – 1913

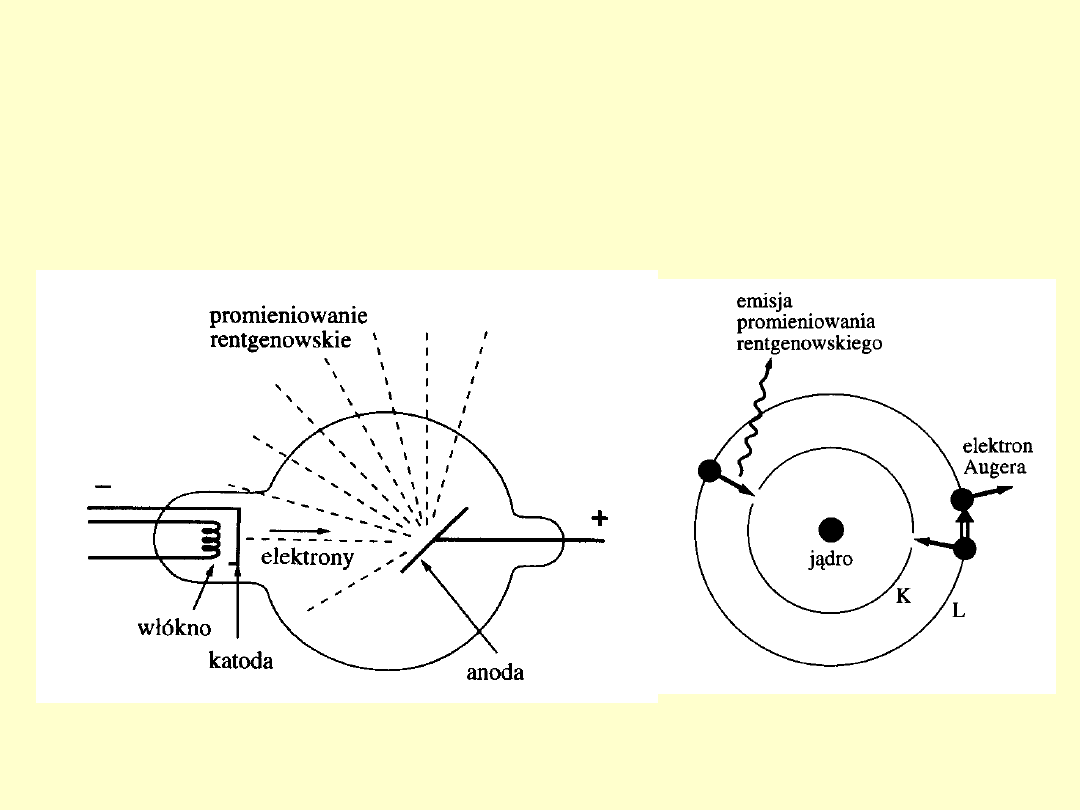
Charakterystyczne promieniowanie

rentgenowskie

- powstaje wówczas gdy wyrwany zostaje jakiś

elektron

z wewnętrznej powłoki atomu.

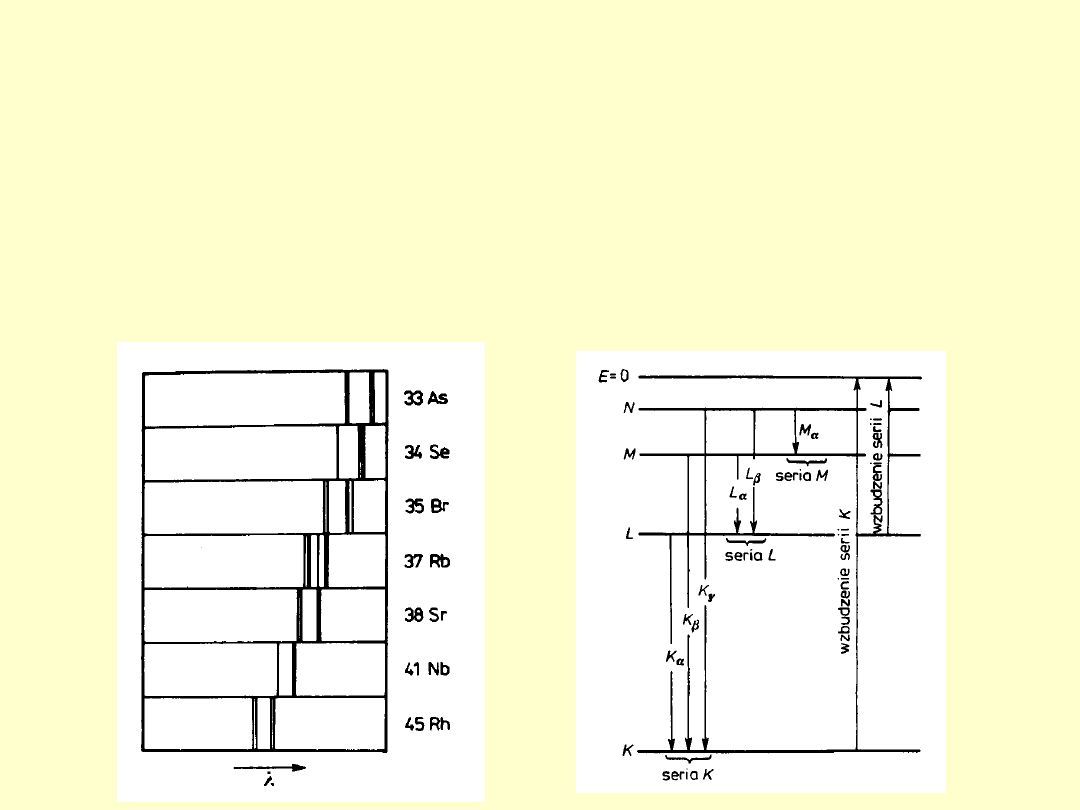
1. Charakterystyczne widma rentgenowskie składają się z
kilku serii oznaczonych literami K, L, M, N i O.
2. Liczba linii w każdej serii jest niewielka; oznaczone są one
w kolejności wzrostu częstości za pomocą greckich liter α, β,
γ, ... , np..: K

α

, K

β

, K

γ

, ... .

3. Widma różnych pierwiastków mają podobny charakter.
4. Ze wzrostem liczby atomowej Z pierwiastka jego widmo
rentgenowskie przesuwa się w stronę fal krótszych (wyższych
częstości).

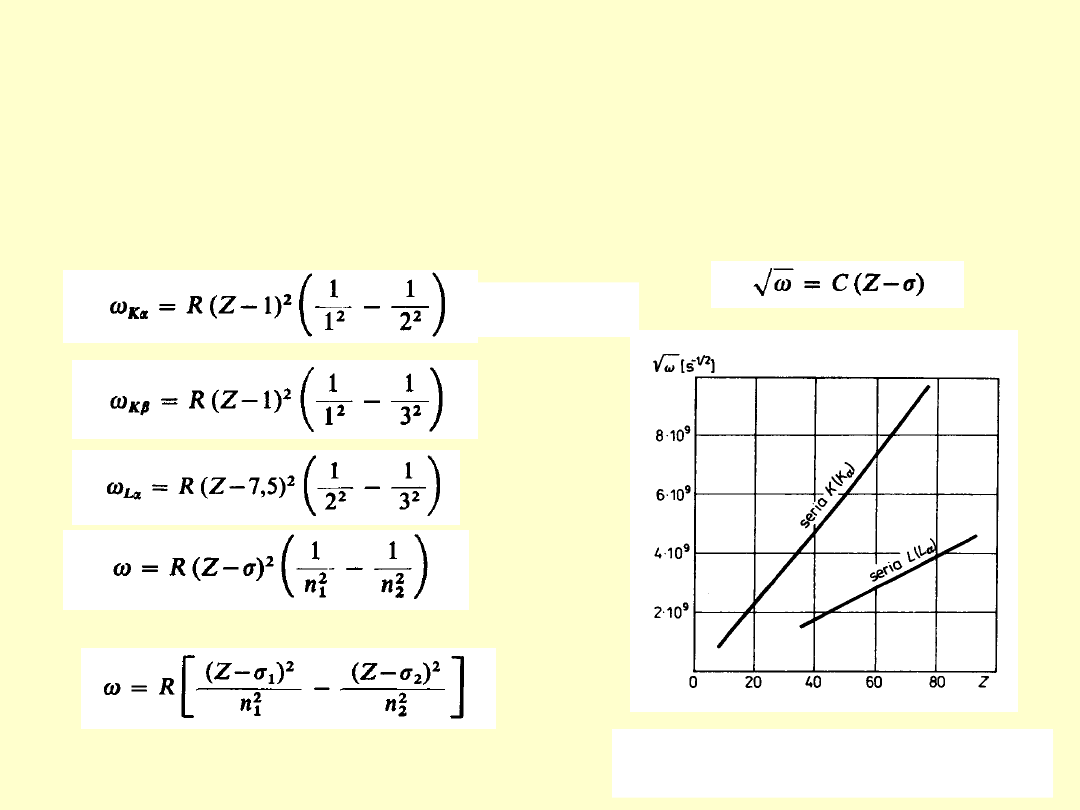
Prawo H. Moseleya – 1913

Wiąże liczbę atomową Z pierwiastka z częstością linii

emitowanego przezeń rentgenowskiego promieniowania

charakterystycznego.

R – stała
Rytberga

σ – stała ekranowania jądra przez
elektrony

Dziękuję za uwagę

Wymuszona emisja fotonów

Einstein – 1918

Zarówno przejścia absorpcyjne jak i emisyjne
atomu mogą być wywoływane przez
promieniowanie elektromagnetyczne.

Tego typu przejścia nazywamy wymuszonymi.

Promieniowanie emitowane w wyniku takich
przejść to promieniowanie wymuszone.

Promieniowania (fotony) wymuszające i
wymuszone mają taki sam kierunek rozchodzenia
się, częstość, fazę i polaryzację a zatem są
spójne.

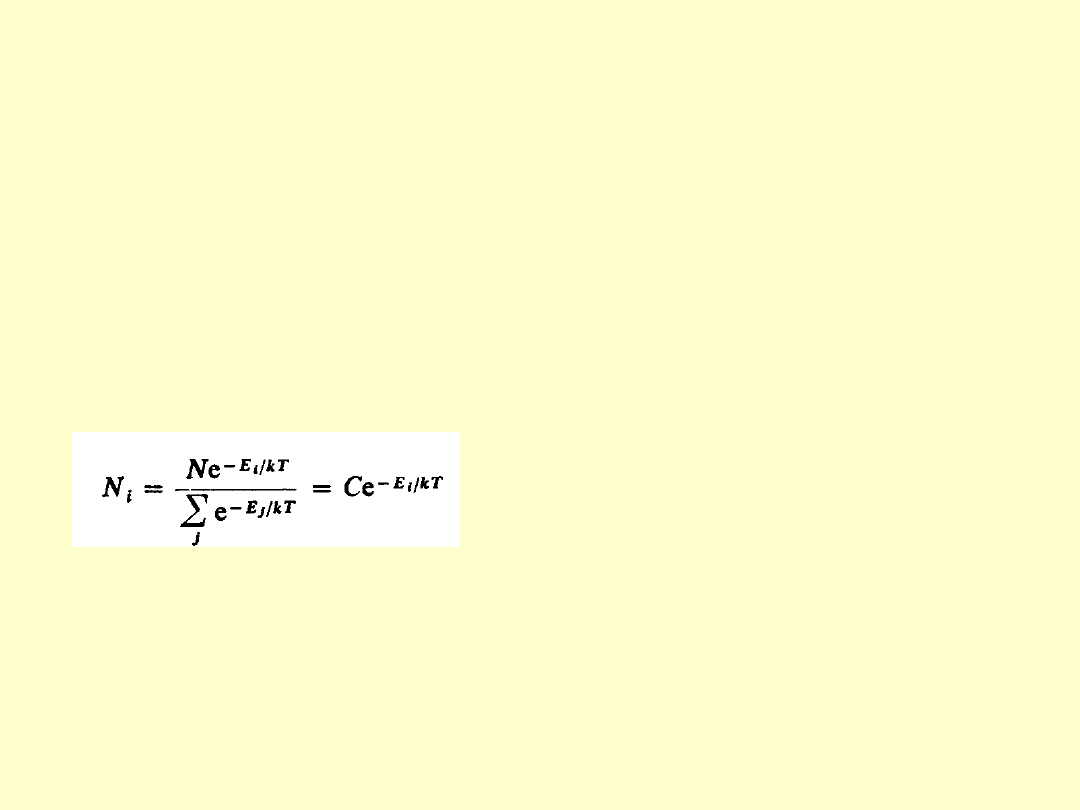
Lasery

(wzmacniacze światła za pomocą emisji wymuszonej)

1953 – MASER

(Microwave Amplification by Stimulated Emission

of Radiation)

1960 – LASER

(Light Amplification by Stimulated Emission

of Radiation)

W przypadku równowagi termodynamicznej liczbę atomów

N

i

, które w temperaturze T znajdują się w stanie o energii

E

i

opisuje prawo Boltzmana:

gdzie N jest całkowita liczbą
atomów.

Liczba przejść między dwoma poziomami jest
proporcjonalna do obsadzenia poziomu wyjściowego więc
dla atomów w równowadze termodynamicznej
pochłanianie padających fotonów przeważa nad emisją
wymuszoną i spada natężenie wiązki fotonów podczas ich
przechodzenia przez materię (w równowadze
termodynamicznej).

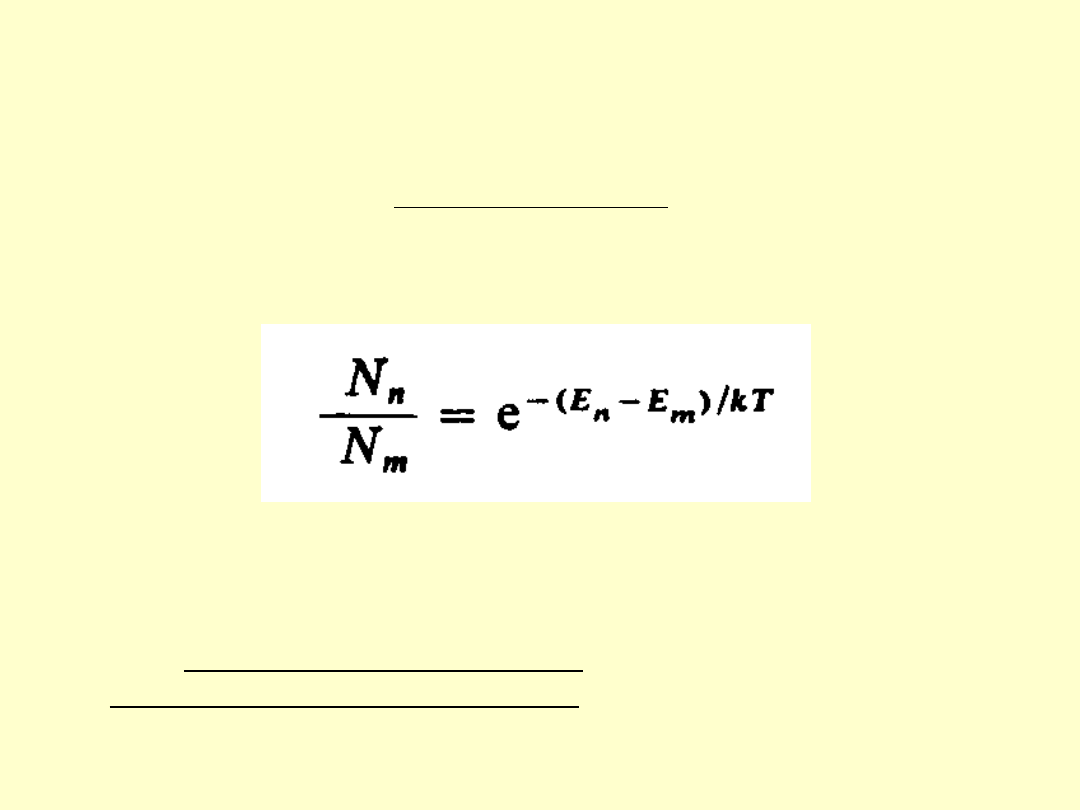
Wzmocnienie promieniowania padającego za pomocą
emisji wymuszonej w danym zespole atomów wymaga
wystąpienia w nim inwersji obsadzeń – sytuacji, w której
w stanie o większej energii E

n

jest więcej atomów niż w

stanie o mniejszej energii E

m

.

Opis takiej sytuacji (N

n

>N

m

gdy E

n

>E

m

) za pomocą

rozkładu Boltzmana wymaga by T miało wartość ujemną
stąd stany z inwersją obsadzeń nazywane są niekiedy
stanami z ujemną temperaturą.

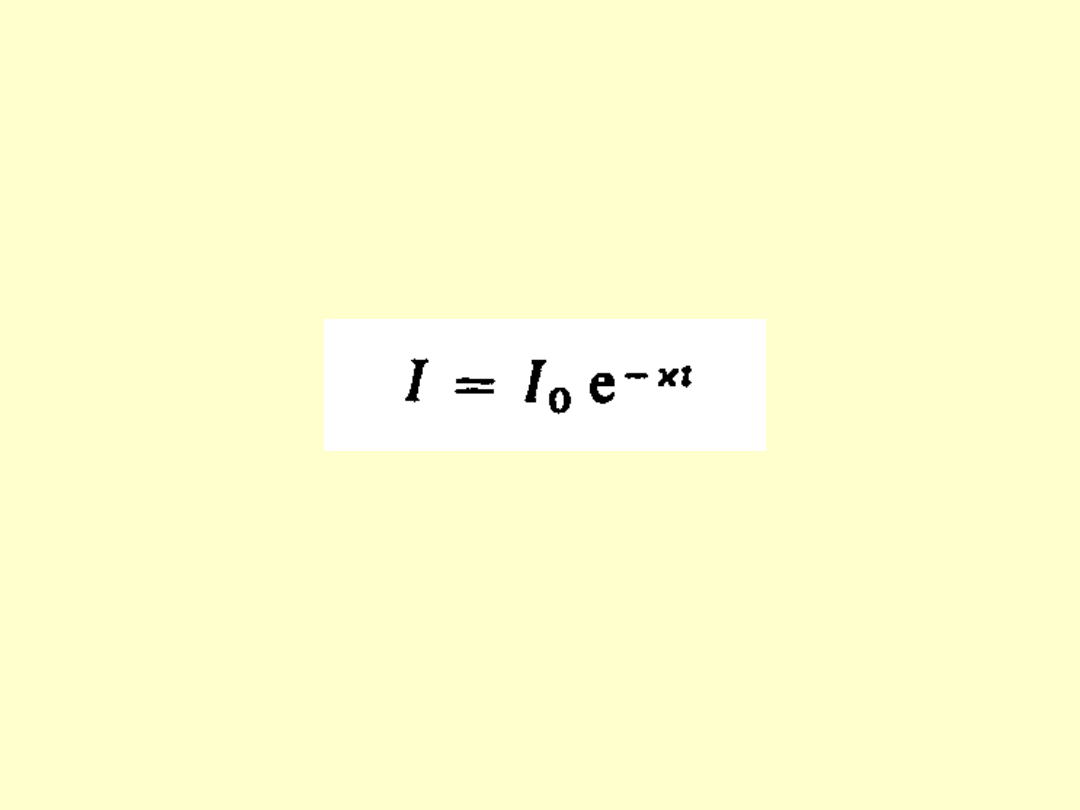
W substancji z inwersją obsadzeń, emisja
wymuszona może przewyższać pochłanianie światła
przez atomy na skutek czego padająca wiązka może
być wzmacniana przez tą substancję.

Opis takiej sytuacji za pomocą związku dla
ośrodka pochłaniającego światło wymaga
przyjęcia, że współczynnik pochłaniania ma
wartość ujemną.

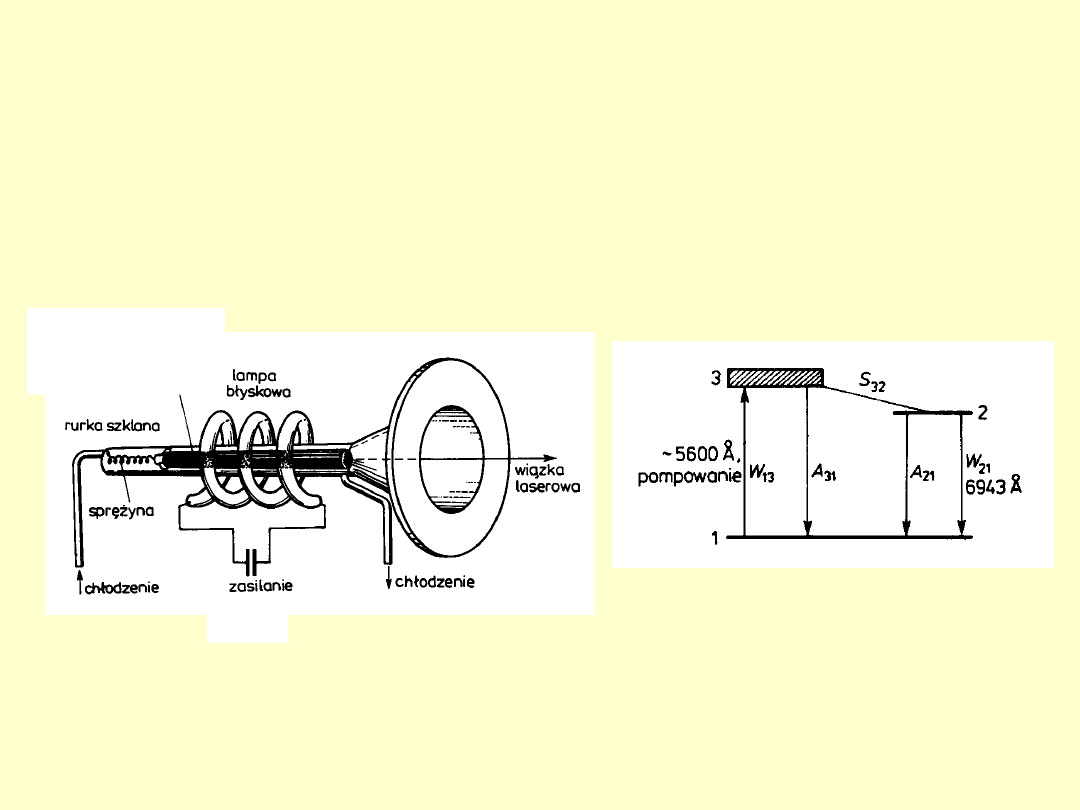
Laser rubinowy

(Al

2

O

3

, niektóre atomy Al zastąpione przez Cr

+++)

Cr

+++)

τ

2

=

~10

-3

s

1960 – T.H. Maiman
(USA)

walec,
Φ = 1 cm, l = 5
cm

1KV

ksenono
wa

τ

3

=

~10

-8

s

1961 – laser gazowy
He i N

2

1963 – lasery
półprzewodnikowe

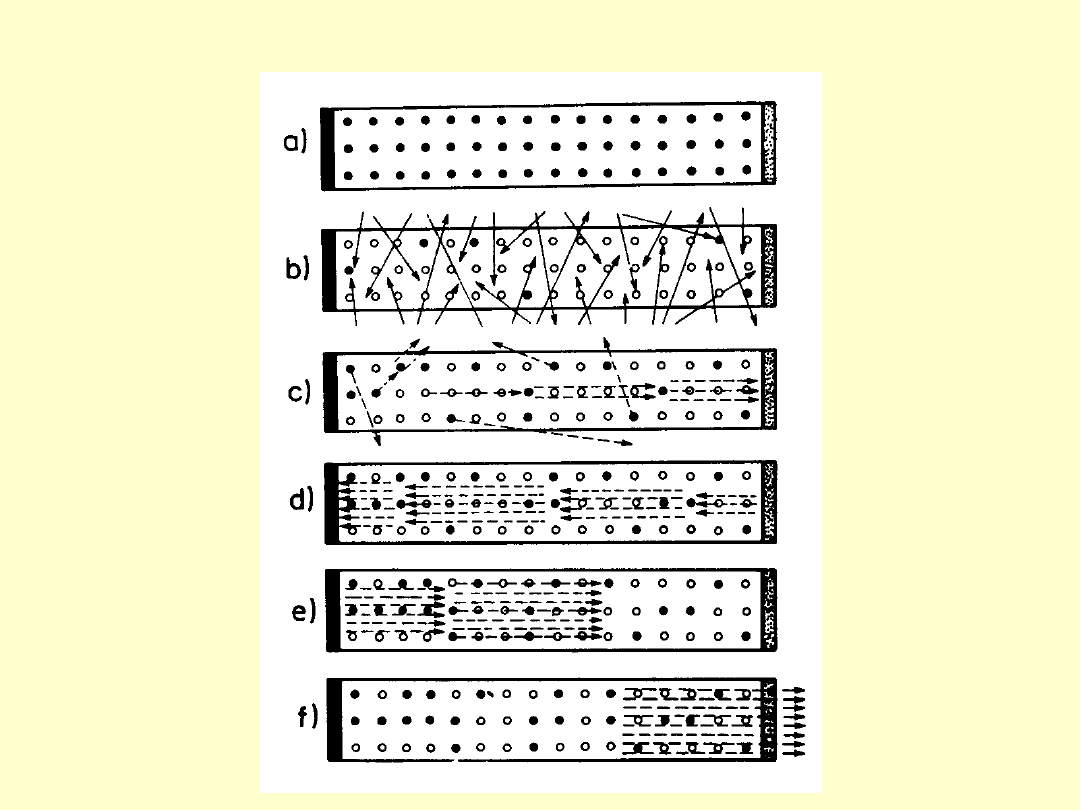
Ag

100
%

8%

Dziękuję za uwagę