Podstawy Sterowania Logicznego,

Funkcje Boolowskie cz. 3

Podstawy sterowania

logicznego

Funkcje boolowskie cz. 3

Funkcjonalność pełna zbioru funkcji

boolowskich

Liczba funkcji X→Y

Twierdzenie

Dla dowolnych zbiorów skończonych X i Y, jeśli X

zawiera k elementów i Y zawiera m elementów, to istnieje mk funkcji odwzorowujących zbiór X w Y.

Podstawy Sterowania Logicznego 2011/12, ©ZM

2/28

Liczba funkcji boolowskich X→Y

W przypadku funkcji boolowskich n zmiennych:

zbiór X (dziedzina) zawiera k=2n elementów,

zbiór Y (przeciwdziedzina) zawiera 2 elementy.

Stąd liczba możliwych do zdefiniowania funkcji boolowskich n zmiennych wynosi

n

2

2

Podstawy Sterowania Logicznego 2011/12, ©ZM

3/28

Elektrotechnika I st, rok 3, moduł C

1

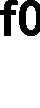
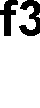
Podstawy Sterowania Logicznego,

Funkcje Boolowskie cz. 3

Liczba funkcji boolowskich X→Y

Liczba

Liczba funkcji

zmiennych

1

22 = 4

2

24 = 16

3

28 = 256

4

216 = 65536

5

232 = 4294967296

Podstawy Sterowania Logicznego 2011/12, ©ZM

4/28

Funkcje boolowskie 1 zmiennej

a

Funkcja

Wyrażenie

Nazwa funkcji

0

1

f0

0

0

0

Stała 0

f1

0

1

a

Przeniesienie

f2

1

0

a

Negacja (NOT)

f3

1

1

1

Stała 1

Podstawy Sterowania Logicznego 2011/12, ©ZM

5/28

Funkcje boolowskie 1 zmiennej

Podstawy Sterowania Logicznego 2011/12, ©ZM

6/28

Elektrotechnika I st, rok 3, moduł C

2

Podstawy Sterowania Logicznego,

Funkcje Boolowskie cz. 3

Funkcje boolowskie 2 zmiennych (1)

ab

Funk

Wyrażenie

Nazwa funkcji

cja

00

01

10

11

f0

0

0

0

0

0

Stała 0

f1

1

0

0

0

Funkcja Peierce’a (NOR)

a + b

f2

0

1

0

0

Iloczyn z zakazem

a ⋅ b

f3

1

1

0

0

Negacja (NOT)

a

Podstawy Sterowania Logicznego 2011/12, ©ZM

7/28

Funkcje boolowskie 2 zmiennych (2)

ab

Funk-

Wyrażenie

Nazwa funkcji

cja

00

01

10

11

f4

0

0

1

0

Iloczyn z zakazem

a ⋅ b

f5

1

0

1

0

Negacja (NOT)

b

f6

0

1

1

0

Nierówność (XOR)

a ⋅ b + a ⋅ b

f7

1

1

1

0

Funkcja Sheffera (NAND)

a ⋅ b

Podstawy Sterowania Logicznego 2011/12, ©ZM

8/28

Funkcje boolowskie 2 zmiennych (3)

ab

Funk

Wyrażenie

Nazwa funkcji

cja

00

01

10

11

f8

0

0

0

1

a ⋅ b

Iloczyn (AND)

f9

1

0

0

1

Równość (XNOR)

a ⋅ b + a ⋅ b

f10

0

1

0

1

Przeniesienie

b

f11

1

1

0

1

Implikacja (jeśli a, to b)

a + b

Podstawy Sterowania Logicznego 2011/12, ©ZM

9/28

Elektrotechnika I st, rok 3, moduł C

3

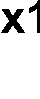
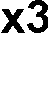
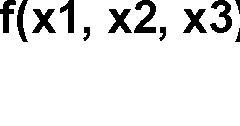
Podstawy Sterowania Logicznego,

Funkcje Boolowskie cz. 3

Funkcje boolowskie 2 zmiennych (4)

ab

Funk

Wyrażenie

Nazwa funkcji

cja

00

01

10

11

f12

0

0

1

1

a

Przeniesienie

f12

1

0

1

1

Implikacja (jeśli b, to a)

a + b

f14

0

1

1

1

Suma (OR)

a + b

f15

1

1

1

1

1

Stała 1

Podstawy Sterowania Logicznego 2011/12, ©ZM

10/28

Zasada superpozycji i podstawiania

W realizacji technicznej funkcji boolowskich stosuje się zasady:

• Superpozycji, która polega na łańcuchowym łączeniu funktorów,

• Podstawiania, która polega na doborze (zamianie) odpowiedniego wejścia funktora.

Podstawy Sterowania Logicznego 2011/12, ©ZM

11/28

Zasada superpozycji

f (

=

⋅

⋅

+

⋅

+

⋅

+

⋅

1

x , x2, x3 ) 1

x

x2 x3

1

x

x2 x2 x3

1

x

x3

Podstawy Sterowania Logicznego 2011/12, ©ZM

12/28

Elektrotechnika I st, rok 3, moduł C

4

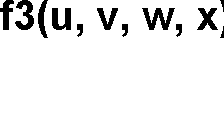
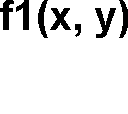
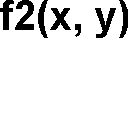
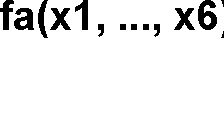
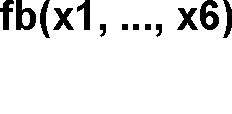
Podstawy Sterowania Logicznego,

Funkcje Boolowskie cz. 3

Zasada podstawiania

f

=

=

3 ( w, x, y, z ) f3 ( 1

x , 1

f ( x2, x3 ), x4, f2 ( x5 , x6 )

= f a ( 1

x , x2, x3, x4, x5, x6 ) f

=

=

3 ( w, x, y, z ) f3 ( x2 , 1

f ( 1

x , x3 ), x5 , f2 ( x3, x4 )

= f b ( 1

x , x2, x3 , x4 , x5, x6 ) Podstawy Sterowania Logicznego 2011/12, ©ZM

13/28

Funkcjonalność pełna zbioru funkcji

boolowskich

Dany jest zbiór F wszystkich funkcji boolowskich n

n

zmiennych:

F = f :

→

n

{ Qn Q }

Niech F b

:

k

ędzie podzbiorem zbioru Fn

k

F ⊂ F ,

n

k

F = {f0, 1

f , ..., f k −1}

Podstawy Sterowania Logicznego 2011/12, ©ZM

14/28

Funkcjonalność pełna zbioru funkcji

boolowskich

Problem

Jakie warunki powinny spełniać funkcje należące do zbioru F , aby stosuj

k

ąc zasadę superpozycji i

podstawiania można było uzyskać każdą funkcję ze zbioru F ?

n

Rozwiązanie

Zbiór F powinien by

k

ć funkcjonalnie pełny.

Podstawy Sterowania Logicznego 2011/12, ©ZM

15/28

Elektrotechnika I st, rok 3, moduł C

5

Podstawy Sterowania Logicznego,

Funkcje Boolowskie cz. 3

Funkcjonalność pełna zbioru funkcji

boolowskich

Twierdzenie

Zbiór funkcji F b

k

ędący podzbiorem zbioru funkcji

logicznych n zmiennych jest funkcjonalnie pełny, gdy zawiera co najmniej jedną funkcję:

nie zachowującą zera,

nie zachowującą jedynki,

nieliniową,

niemonotoniczą,

niesamodualną.

Podstawy Sterowania Logicznego 2011/12, ©ZM

16/28

Postać wielomianowa funkcji boolowskiej Twierdzenie

Każdą funkcję boolowską

n

f : Q → Q

można zapisać w postaci wielomianu

f ( x , ..., x

=

⊕

⊕ ⊕

⊕

1

n )

a

a x

...

a

0

1 1

n xn

⊕ a +

⊕

+

+

⊕

+

⊕

n

x x

a

1 1 2

n

x x

...

a

2 1 3

N x x ... x

1 2

n

gdzie: ai ∈ { a , ..., aN

ai = ∨

0

},

0

1

Podstawy Sterowania Logicznego 2011/12, ©ZM

17/28

Postać wielomianowa funkcji boolowskiej Aby funkcję:

f : Qn → Q

przekształcić do postaci wielomianowej należy: 1. Zapisać funkcję w normalnej postaci dysjunkcyjnej.

2. Zmienne zanegowane zapisać w postaci sumy modulo 2 zgodnie z tożsamością:

x = 1 ⊕ x

3. Działania sumy zastąpić działaniami sumy modulo 2

(+)→ (⊕)

Podstawy Sterowania Logicznego 2011/12, ©ZM

18/28

Elektrotechnika I st, rok 3, moduł C

6

Podstawy Sterowania Logicznego,

Funkcje Boolowskie cz. 3

Postać wielomianowa funkcji boolowskiej 4. Wykonać zaznaczone działania i zredukować wyrazy podobne zgodnie z zasadą sumowania modulo 2



a ⊕ a ⊕ ... ⊕ a = a

gdy n nieparzys e

t



1 4

4 2

4

4 3

0

gdy n parzyste

n razy

Podstawy Sterowania Logicznego 2011/12, ©ZM

19/28

Postać wielomianowa funkcji boolowskiej Przykład

Zamienić na postać wielomianową funkcje:

=

⋅

+

⋅

+

⋅

1

f ( 1

x , x2 ) 1

x

x2

1

x

x2

1

x

x2

f

=

+

2 ( 1

x , x2 ) 1

x

x2

f

=

⋅

⋅

+

⋅

3 ( 1

x , x2, x3 ) 1

x

x2 x3

1

x

x2

Podstawy Sterowania Logicznego 2011/12, ©ZM

20/28

Klasy funkcji boolowskich

Funkcja liniowa

Definicja

Funkcja boolowska

n

f : Q → Q

jest liniowa wtedy gdy może być przedstawiona w postaci wielomianu pierwszego stopnia: f ( x , x ,..., x

1

2

= a0 ⊕ a x

1

1 ⊕ a x

2

2 ⊕ ... ⊕ a x

n )

n

n

Podstawy Sterowania Logicznego 2011/12, ©ZM

21/28

Elektrotechnika I st, rok 3, moduł C

7

Podstawy Sterowania Logicznego,

Funkcje Boolowskie cz. 3

Klasy funkcji boolowskich

Funkcja zachowująca zero

Definicja

Funkcja boolowska

f : Qn → Q

jest funkcją zachowującą zero wtedy gdy:

∀ n x = 0 ⇒ f ( x) = 0

x∈ Q

Argument funkcji równy 0

∀

x

n

= ( x ... x x

x

n −

=

−

⇔ ∀ i∈

n −

i =

−

1

1

0 )

0

x∈ Q

{

∈

0,1, ...,

1}

0

Podstawy Sterowania Logicznego 2011/12, ©ZM

22/28

Klasy funkcji boolowskich

Funkcja zachowująca jeden

Definicja

Funkcja boolowska

f : Qn → Q

jest funkcją zachowującą jeden wtedy gdy:

∀ n x = 1 ⇒ f ( x) = 1

x∈ Q

Argument funkcji równy 1

∀

x

n

= ( x ... x x

x

n −

=

−

⇔ ∀ i∈

n−

i =

−

1

1

0 )

1

x∈ Q

{

∈

0,1, ...,

1}

1

Podstawy Sterowania Logicznego 2011/12, ©ZM

23/28

Klasy funkcji boolowskich

Funkcja monotoniczna

Definicja

Funkcja boolowska

f : Qn → Q

jest funkcją monotoniczną wtedy gdy:

∀

≤

⇔

≤

n

1

x

x2

f ( 1

x ) f ( x2 )

x ,

∈

1 x2

Q

Relacja porządkująca argumenty

∀

≤

⇔ ∀ ∈

∈

−

≤

n x

x

−

1

2

i

x

x

x , x

Q

∈

(0, ,1..., n 1) 1 i

2 i

1

2

Podstawy Sterowania Logicznego 2011/12, ©ZM

24/28

Elektrotechnika I st, rok 3, moduł C

8

Podstawy Sterowania Logicznego,

Funkcje Boolowskie cz. 3

Klasy funkcji boolowskich

Funkcja samodualna

Definicja

Funkcja boolowska

f : Qn → Q

jest funkcją samodualna wtedy gdy:

∀

=

⇔

=

n

1

x

x2

f

∈

( x f x

x , x

Q

∈

( 1) ( 2)

1

2

Argumenty przeciwne

∀

=

⇔ ∀ ∈

∈

−

=

n x

x

−

1

2

i

x

x

x , x

Q

∈

(0, ,1..., n 1) 1 i

2 i

1

2

Podstawy Sterowania Logicznego 2011/12, ©ZM

25/28

Funkcjonalność pełna zbioru funkcji

Przykład 1

x x

f1

f2

1 0

00

1

0

01

1

1

10

0

0

11

0

1

Funkcja

f1

f2

zachowująca 0

nie

TAK

zachowująca 1

nie

TAK

liniowa

TAK

TAK

monotoniczna

nie

TAK

samodualna

TAK

TAK

Podstawy Sterowania Logicznego 2011/12, ©ZM

26/28

Funkcjonalność pełna zbioru funkcji

Przykład 2

x x

NOT

AND

NAND

OR

NOR

XOR

XNOR

1 0

00

1

0

1

0

1

0

1

01

1

0

1

1

0

1

0

10

0

0

1

1

0

1

0

11

0

1

0

1

0

0

1

Funkcja

NOT

AND

NAND

OR

NOR

XOR

XNOR

zachow. 0

nie

TAK

nie

TAK

nie

TAK

nie

zachow. 1

nie

TAK

nie

TAK

nie

nie

TAK

liniowa

TAK

nie

nie

nie

nie

TAK

TAK

monoton.

nie

TAK

nie

TAK

nie

nie

nie

samodualna

TAK

nie

nie

nie

nie

nie

nie

Podstawy Sterowania Logicznego 2011/12, ©ZM

27/28

Elektrotechnika I st, rok 3, moduł C

9

Podstawy Sterowania Logicznego,

Funkcje Boolowskie cz. 3

Funkcje liniowe dwóch zmiennych

f (

=

⊕

⊕

1

x , x2 ) a0

1

a

1

x

a2 x2

a2

a1

a0

Funkcja

0

0

0

0

0

0

1

1

0

1

0

1

x

0

1

1

1 ⊕ 1

x = 1

x

1

0

0

x2

1

0

1

1 ⊕ x =

2

x2

1

1

0

1

x ⊕ x2

1

1

1

1 ⊕

⊕

=

⊕

1

x

x2

1

x

x2

Podstawy Sterowania Logicznego 2011/12, ©ZM

28/28

Elektrotechnika I st, rok 3, moduł C

10