Ćwiczenie 66

Wyznaczanie stałej Plancka

Wstęp:

Przedstawione

schematycznie

na

rys.1

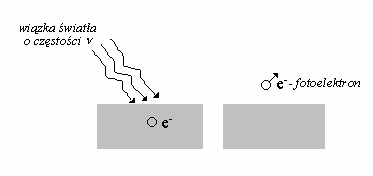
zjawisko,

nazywane

zjawiskiem

fotoelektrycznym zewnętrznym, polega na emisji elektronów z powierzchni niektórych metali lub

innych materiałów o małej pracy wyjścia, pod wpływem padającego na nie światła. Emitowane w

ten sposób elektrony (nazywane fotoelektronami) tworzą w określonych warunkach prąd

fotoelektryczny.

Rys.1

Zjawisko to, z zwłaszcza jego własności, do których należą

- niezależność energii fotoelektronów od natężenia padającego światła,

- występowanie częstości granicznej światła, poniżej której dla danego materiału zjawisko to

nie zachodzi,

- liniowa zależność natężenia prądu fotoelektrycznego od natężenia oświetlenia powierzchni,

- natychmiastowe pojawianie się prądu fotoelektrycznego po oświetleniu powierzchni

są niewytłumaczalne z punktu widzenia falowej teorii światła.

Wyjaśnienie zjawiska fotoelektrycznego zewnętrznego i jego własności stało się możliwe po

wprowadzeniu przez Plancka pojęcia kwantu energii promieniowania elektromagnetycznego o

wartości:

E = hν

f

gdzie: ν – częstość fali elektromagnetycznej,

h = 6,63·10-34 [Js] – stała Plancka

Wykorzystując pojęcie kwantu energii promieniowania elektromagnetycznego, Einstein

wprowadził postulat zgodnie, z którym energia fali świetlnej przenoszona jest w postaci

oddzielnych kwantów energii (tzw. fotonów) oraz, że w wyniku oddziaływania z elektronem

foton przekazuje mu cała swoją energię. W rezultacie pomiędzy energią padającego fotonu a

maksymalną energią kinetyczną fotoelektronów otrzymuje się prostą zależność, nazywaną

równaniem Einsteina – Milikana:

hν = W + E

(1)

k m

ax

gdzie: W – bariera potencjału jaką elektron musi pokonać aby opuścić powierzchnię danego

materiału, nazywana zwykle pracą wyjścia elektronu z danego materiału.

Z równania (1) wynika w szczególności, że dla fotonów o energii mniejszej od pracy wyjścia nie

można wywołać emisji fotoelektronów, a zatem praca wyjścia jest równa energii fotonów światła

o częstości równej częstości granicznej W = hνg.

Przedstawiony na rys.2 schemat układu pomiarowego pozwala badać zarówno własności zjawiska

fotoelektrycznego, jak i wyznaczyć stałą Plancka w oparciu o równanie (1).W skład układu

pomiarowego wchodzą:

źródło światła S o danej długości fali, którego natężenie można zmieniać od zera do pewnej

wartości maksymalnej,

próżniowa bańka szklana z wtopioną katodą światłoczułą K( fotokatodą) i elektrodą

zbierającą A (anodą),

elektryczny układ zasilania, utrzymujący napięcie o żądanej polaryzacji i wartości pomiędzy

elektrodami,

Rys.2.

Jeżeli pomiędzy elektrodami zostanie przyłożone napięcie o ujemnej polaryzacji tzw. napięcie

hamowania, to każdy fotoelektron emitowany z katody będzie hamowany polem elektrycznym,

którego praca Wel = eUh będzie równa ubytkowi energii kinetycznej fotoelektronów. Maksymalna

wartość napięcia hamowania Uhm, przy której prąd fotoelektryczny zaniknie odpowiada zatem

pracy pola elektrycznego równej maksymalnej energii kinetycznej fotoelektronów:

e U

= E

hm

k m

ax

W warunkach tych równanie (1) można zapisać w postaci:

h

W

U

= ν −

(2)

hm

e

e

Z powyższego równania wynika dalej, że dopasowanie prostej regresji (y=ax+b) do wykresu

eksperymentalnej zależności Uhm = Uhm (ν) pozwala, na podstawie wyznaczonych parametrów

a i b prostej, obliczyć stałą Plancka h i pracę wyjścia W:

h = e ⋅ a ; W = e ⋅ b (3)

Przebieg ćwiczenia.

Schemat elektryczny układu pomiarowego przedstawiono na poniższym rysunku. W układzie tym

prąd fotoelektryczny przepływa przez opornik R, wywołując spadek napięcia UR. Spadek ten

mierzony jest przy pomocy przyłączonego równolegle do opornika woltomierza cyfrowego, co

pozwala wyznaczyć natężenie prądu fotoelektrycznego zgodnie z prawem Ohma:

U

I

R

=

f

R

Drugi woltomierz cyfrowy służy do pomiaru wartości napięcia hamowania U, którego źródłem

jest zasilacz napięcia stałego i przykładanego pomiędzy anodę A i katodę K fotokomórki.

Rys.3.

Kolejność wykonywania czynnoś ci

1. Przy napięciu hamowania równym zero (U0 = 0) wyznaczyć charakterystykę prądową

fotokomórki If = If (v) zmieniając długość fali światła (λ) oświetlającego fotokatodę, co 20 nm

w przedziale od 400 do 660 nm

a) Dokonać pomiarów napięcia UR wywołanego przepływem prądu fotoelektrycznego If przy

podanych wyżej długościach fali świetlnej λ i zapisać je w tab.1.

b) Obliczyć wartości If z prawa Ohma przy wartości R = 2.49 MΩ. Wyniki zapisać w tab.1.

c) Obliczyć częstości ν odpowiadające długościom fali λ i zapisać wyniki w tab. 1

Tab.1.

λ [nm]

400 420 440 460 480 500 520 540 560 580 600 620 640 660

UR [V]

ν x 1015 [Hz]

If [nA]

2. Wyznaczyć krzywe "hamowania" If = If (Uh) dla trzech długości fali: 400, 500, 600.

a) Wybrać wiązkę światła o danej długości fali poczynając od najmniejszej (λ=400 nm)

b) Włączyć zasilacz napięcia hamowania, nastawić napięcie hamowania Uh na 0,1V i zmierzyć

napięcie UR

c) Zwiększając napięcie Uh, co 0,1 V zmierzyć kolejne wartości UR. Ostatni pomiar wykonać

przy takim napięciu hamowania Uhm, przy którym wartość napięcia UR spadnie do zera.

d) Wyniki pomiarów i obliczeń zestawić w tab.2.

Tab.2.

λ=400 nm

λ=500 nm

λ=600 nm

Uh [V]

UR [V]

If [nA]

Uh [V]

UR [V]

If [nA]

Uh [V]

UR [V]

If [nA]

0,1

0,1

0,1

0,2

0,2

0,2

0,3

0,3

itd.

itd.

itd.

0,000

0,000

…

0,000

0,000

...

…

0,000

0,000

...

0,000

0,000

3. Wyznaczyć doświadczalną zależność Uhm=Uhm (ν) dla częstości ν odpowiadającym

długościom fali λ: 600, 580, 560, 540, 520 itd., aż do 400 nm.

a) Wybrać wiązkę światła o danej długości fali 600 nm i ustalić takie napięcie hamowania Uhm,

przy którym spadek napięcia UR będzie równy zero; wartość napięcia hamowania Uhm

wpisać do tab.3.

b) Zmniejszać kolejno długość światła, co 20 nm (od 600 do 400 nm) i ustalać za każdym

razem nowe napięcia Uhm, przy których spadek napięcia UR będzie równy zero; wartości

kolejnych napięć Uhm wpisać do tab.3.

Tab.3.

λ [nm]

400 420

440

460

480

500

520

540

560

580

600

ν ×1017 [Hz]

Uhm [V]

ν1= ×1017[Hz]

U1= [V]

ν2= ×1017[Hz]

U2 [V]

1. Na podstawie wyników pomiarów z tab.1 sporządzić wykres zależności prądu

fotoelektrycznego od częstości fali padającego światła: If = If (λ).Na podstawie wykresu,

stosując ekstrapolacje liniową, wyznaczyć wartość graniczną λg1 długości fali światła,

powyżej której prąd fotoelektryczny w badanej fotokomórce nie powstaje. Wartość λg1

zapisać w tab.4.

2. Na podstawie wyników pomiarów z tab.2 wykreślić na wspólnym wykresie wyznaczone

krzywe hamowania: If = If (Uh ).

3. Na podstawie wyników pomiarów z tab.3 sporządzić wykres zależności: Uhm= Uhm(ν).

4. Obliczyć parametry a i b prostej regresji dopasowanej do wykresu z pkt.3 (obliczenia można

wykonać korzystając z dostępnego na pracowni arkusza kalkulacyjnego). Zapisać wartości

wyznaczonych parametrów wraz z ich błędami w tab.4.

5. Wykreślić prostą regresji na wykresie Uhm = Uhm(ν), korzystając z obliczonych parametrów:

a) Obliczyć wartości teoretyczne Uhm odpowiadające dwóm dowolnie wybranym wartościom ν.

Rezultaty obliczeń zamieścić w tab.3.

b) Nanieść znalezione (w sposób opisany powyżej) punkty teoretyczne na wykres Uhm = Uhm(ν)

i wykreślić przechodzącą przez nie prostą, ekstrapolując jej przebieg aż do przecięcia się z

osiami wykresu.

6. Określić z wykresu częstość graniczną νg, dla której Uhm=0 i obliczyć długość fali λg odpowiadającą wartości νg, tj. wynikającą z równania Einsteina – Milikana wartość

graniczną długości fali światła, powyżej której prąd fotoelektryczny w badanej fotokomórce

nie powinien powstawać; obliczoną wartość λg wpisać do tab.4.

7. Obliczyć stałą Plancka h, pracę wyjścia W wyrażoną w elektronowoltach wraz z błędami tych

wartości. Rezultaty obliczeń zamieścić w tab.4.

Tab.4.

a ± ∆a

b ± ∆b

λ

λ

gl

g

h ± ∆h

W ± ∆W

[...]

[...]

[nm]

[nm]

[Js]

[eV]

*Wyznaczanie zależności prądu fotoelektrycznego od natężenia oświetlenia*

Uwaga: Ta część ć wiczenia wykonywana jest tylko na polecenie prowadzą cego zaję cia

Wstęp

Natężenie fali elektromagnetycznej jest proporcjonalne do kwadratu wektora pola elektrycznego

tej fali, a zatem natężenie oświetlenia powierzchni prostopadłej do tej wiązki światła jest też

proporcjonalne do kwadratu wektora pola elektrycznego fali świetlnej:

Φ =

E

C 2 (r) c

os2 (

ω t − kr)

0

0

gdzie: C – stała proporcjonalności,

ω =2πν – kołowa częstość drgań,

k = 2π/λ – liczba falowa fali świetlnej o częstości ν i długości λ.

Jeśli światło oświetlające daną powierzchnię przechodzi wcześniej przez układ polaroidów

skręconych względem siebie o kąt α, to kwadrat amplitudy natężenia pola elektrycznego światła

po przejściu przez polaroidy zmienia się zgodnie z prawem Malusa wg zależności:

E 2 = E 2 (r) c

os2α

0p

0

W konsekwencji natężenie oświetlenia światłem przechodzącym przez układ polaroidów zmienia

się w ten sam sposób:

Φ =

B

2

Φ c

os2α

0

gdzie: B – stała proporcjonalności,

Φ0 – natężenie oświetlenia przy kącie skręcenia polaroidów równym zero.

Ponieważ iloczyn BΦ0 jest w danych warunkach pomiarów wartością stałą, to dla zbadania

zależności natężenia prądu fotoelektrycznego If od natężenia oświetlenia, wystarczy zbadać

zależność tego prądu od kwadratu kosinusa kąta skręcenia polaroidów, tj. zależność:

I = I (cos2α)

f

f

Przebieg ćwiczenia

Wykorzystywany w ćwiczeniu układ optyczny do wybierania wiązki światła o

określonej długości fali zakończony jest uchwytem, w którym zamocowana jest badana

fotokomórka. Uchwyt ten wyposażony jest w polaroidy, których kąt wzajemnego skręcenia

można regulować w przedziale od do 0 do 90o , co 1,8o , przy pomocy wystającego w górnej części uchwytu karbowanego pokrętła. Obrót o dwa karby równoważny jest przyrostowi kąta

skręcenia polaroidów o 3,6o. Wstawienie układu polaroidów w bieg wiązki światła padającego na

fotokomórkę dokonuje się przez przesunięcie poziomego suwaka uchwytu, w jego drugie skrajne

położenie tj. położenie przeciwne do tego, przy którym wykonywane były poprzednie części

ćwiczenia.

Kolejność wykonywania czynnoś ci

1. Sprawdzić czy zasilacz napięcia hamowania jest wyłączony i w razie potrzeby wyłączyć go.

2. Wprowadzić polaroidy w bieg wiązki światła oświetlającego fotokomórkę.

3. Korzystając z wyznaczonej uprzednio charakterystyki częstotliwościowej fotokomórki –

tab.1.

4. Wybrać wiązkę światła o długości fali odpowiadającej największemu prądowi

fotoelektrycznemu; wartość wybranej długości światła zanotować w tab.5.

5. Pokrętło polaroidów skręcić maksymalnie w prawo, co odpowiada zerowej wartości kąta

skręcenia polaroidów.

6. Odczytać wartość napięcia UR i obliczyć natężenie prądu If; wyniki wpisać do tab.5.

7. Obrócić w lewo pokrętło polaroidów o dwa karby, odczytać aktualną wartość napięcia UR i

obliczyć natężenie prądu If; wyniki zapisać w tab.5.

8. Wykonać serie 24 dalszych pomiarów napięcia UR obracając za każdym razem w lewo

pokrętło polaroidów o dwa karbu i obliczyć odpowiadające im wartości natężenia prądu If;

wyniki pomiarów i obliczeń wpisać do tab.5.

Tab.5.

λ= ...................... [nm]

α

cos2α

UR

If

α

cos2α

UR

If

α

cos2α

UR

If

[deg]

-

[V]

[nA]

[deg]

-

[V]

[nA]

[deg]

-

[V]

[nA]

0

32,4

64,8

3,6

36,0

68,4

7,2

39,6

72,0

10,8

43,2

75,6

14,4

46,8

79,2

18,0

50,4

82,8

21,6

54,0

86,4

25,2

57,6

90,0

28,8

61,2

Opracowanie wyników pomiarów

1. Na podstawie wyników zebranych w tab.5. sporządzić:

Wykres zależności prądu If od kąta α skręcenia polaroidów

Wykres zależności prądu If od kwadratu kosinusa kąta skręcenia polaroidów

2. Przeprowadzić aproksymacje liniową dla punktów pomiarowych badanej zależności

I = I (cos2α) tzn. obliczyć parametry prostej regresji dopasowanej do uzyskanego rozkładu

f

f

punktów pomiarowych; (obliczenia można wykonać przy pomocy dostępnego na pracowni

arkusza kalkulacyjnego),

3. Wykreślić wyznaczoną prostą regresji na wykresie I = I (cos2α) ; wartości parametrów

f

f

prostej regresji, ich błędów bezwzględnych i współczynnika R dopasowania prostej zamieścić

w legendzie wykresu