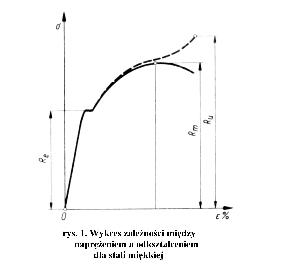
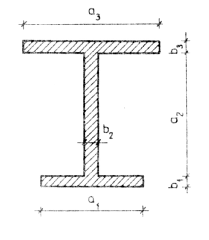
Materiały ( na prawach rękopisu) do zajęć z Wytrzymałości Materiałów II. Opracował dr inż. Jan Raczka . Luty 2004.
ROZDZIAŁ 5
METODA NOŚNOŚCI GRANICZNEJ
Poprawnie zaprojektowana konstrukcja powinna być bezpieczna. Rozróżniamy kilka metod sprawdzania bezpieczeństwa konstrukcji. Są to metody: naprężeń dopuszczalnych, naprężeń granicznych, odkształceń plastycznych, nośności granicznej i stanów granicznych.
Ogólnie metody te różnią się sposobem sprawdzania nośności konstrukcji czy też jej elementu Omawiamy tu bardzo krótko podstawy metody nośności granicznej w porównaniu z metodą naprężeń dopuszczalnych.
Nośność konstrukcji lub jej elementu, zgodnie z metodą naprężeń dopuszczalnych (dalej krótko MND), jest osiągnięta wtedy, gdy ekstremalne naprężenie choćby w jednym punkcie danego elementu konstrukcji osiągnie wartość dopuszczalną np. granicę plastyczności Re (Rpl).
Obciążenie, przy którym zostanie osiągnięta nośność będziemy oznaczali z indeksem s np. qs, Ps, Ms i nazywali obciążeniem dopuszczalnym. Obciążenie dopuszczalne nie jest obciążeniem niszczącym. Zwykle konstrukcja jest zdolna do przenoszenia większych obciążeń Nośność konstrukcji, zgodnie z metodą nośności granicznej (dalej krótko MNG) jest osiągnięta wtedy, gdy zostanie osiągnięta nośność w takiej liczbie przekrojów, że konstrukcja ulegnie zniszczeniu, czyli np. stanie się układem geometrycznie zmiennym. Obciążenie przy którym zostanie osiągnięta nośność będziemy oznaczali z indeksem n np. qn, Pn, Mn i nazywali obciążeniem granicznym lub niszczącym.
Rozciąganie (ściskanie) osiowe
s
2
1
Rpl = R0,002
stan
stan
sprężysty
plastyczny
ee
e
Uproszczony wykres rozciągania materiału sprężysto – plastycznego 1) materiał idealnie sprężysto-plastyczny
ε ≤ εe → σ = E · ε
ε > εe → σ = Re
2) materiał idealnie sprężysto-plastyczny ze wzmocnieniem
ε ≤ εe → σ = E · ε
ε > εe → σ = Re + E1 · ( ε - εe )
3) materiał sztywno-plastyczny
ε = 0 ⇒ σ < Re
ε → ∞ ⇒ σ = Re
Zgodnie MND:
σmax ≤ R ; σzast ≤ Re
PDF created with pdfFactory trial version www.pdffactory.com
Materiały ( na prawach rękopisu) do zajęć z Wytrzymałości Materiałów II. Opracował dr inż. Jan Raczka . Luty 2004.
Ze względu na równomierny rozkład naprężeń w przekroju pręta rozciąganego lub ściskanego stan uplastycznienia występuje równocześnie w całym przekroju i nośność określona wg MND i MNG jest identyczna.
P
P
n
s = Pn = A · Rpl ; Pd =
n
n – współczynnik bezpieczeństwa
Przykład 1
Dla pręta zawieszonego na trzech cięgnach wyliczyć siłę niszczącą Pn.
Dane: A; Rpl; dla pręta EJ = ∞; dla cięgien EA = const.
N 1
N 2
N 3
L
2a
a
0, 4a
E
P
D1
D2
D3
∑ Y
+
+
=
1
N N 2 N 3 P
∑ M
N 2
a − P ,
2 4 a + N
a
3
= 0
E
2
3
∆2 − 1
∆
∆3 − 1
∆
∑∆
=
2 a
3 a
N L
N
L
N L
1
1
∆ =
;
∆2
2
=
;
∆3
3
=
EA
EA
EA
N 1 =
P
071
,
0
N 2 = 386
,
0
P
N 3 = 543
,
0
P = Nn
R
pl A
N = R
A ⇒ 543
,
0
P = R
A ⇒ P =
= 1,841 N
n
pl
pl
n
543
,
0
Pomimo uplastycznienia pręta (3) układ pozostaje geometrycznie niezmienny.
PDF created with pdfFactory trial version www.pdffactory.com
Materiały ( na prawach rękopisu) do zajęć z Wytrzymałości Materiałów II. Opracował dr inż. Jan Raczka . Luty 2004.
N 1
N 2
N n
P
Zakładając, że pręt (3) osiągnie swoją nośność Nn, układ stanie się geometrycznie zmienny i konstrukcja ulegnie zniszczeniu gdy np. pręt (2) też osiągnie nośność Nn, czyli z warunków równowagi:
1
N 1 = N −
n
,
0 2 P
2
N 2 = − 5,
1 N
+
n
,
1 2 P
⇒
= 2 ⇒
= − 5
,
1
+
n
P
Nn
N
Nn
Nn
,
1 2 P
=
n
P 2,083 Nn
Przykład 2
Dla pręta jak na rysunku wyliczyć Ps, Pn oraz współczynnik m, czyli stosunek Pn/Ps .
Dane: A; Re; EA = const.
a)
b)
P / 4
R e * A
A
3 * a / 4
+
+
B
P
a / 4
P
-
-
C
3 * P / 4 = R e * A
- R e * A
X
a) obliczenie siły Ps (uplastyczniającej tylko część BC) czyli dopuszczalnej wg MND
PDF created with pdfFactory trial version www.pdffactory.com
Materiały ( na prawach rękopisu) do zajęć z Wytrzymałości Materiałów II. Opracował dr inż. Jan Raczka . Luty 2004.
3 P
σ max =
≤ R e
4 A
δ X
11
+
δ 10 = 0
X
P
L
∆ AB
+ ∆ L AB = L AB = 0
X
− X a
L
∆ AB = EA
P
3 Pa
L
∆
AB
= 4 EA
− X a
3 P a
+
= 0
EA
4 EA
3
X =
P
4
4 R e A
P ≤
= s
P
3
b) obliczenie siły Pn (uplastyczniającej cały pręt) czyli granicznej wg MNG
P = 2
=
e
R A
n
P
c) współczynnik m
P
3
m = n =
P
2
s
Skręcanie
Pręt o przekroju kołowym i pierścieniowym
a)
b)
c)
2r
Stan sprężysty Stan sprężysto-plastyczny Stan graniczny
Ms Mn
PDF created with pdfFactory trial version www.pdffactory.com
Materiały ( na prawach rękopisu) do zajęć z Wytrzymałości Materiałów II. Opracował dr inż. Jan Raczka . Luty 2004.
dr
r
dff
Wyznaczenie momentu uplastyczniającego włókna skrajne: Ms M ρ
R
s
t
pl
τ
=
=
−
−
max
R
( war. H
M
H )
pl
J 0
3
1 4
4 2 4
4 3
⇓
t
R π r 3
t
pl
τ
=
=
max
pl
R
M
s
2
Wyznaczenie momentu uplastyczniającego cały przekrój: Mn
t
t
dT =
=
ρ ϕ ρ
pl
R dA
pl
R
d d
t
dM = ρ dP =
ρ 2 ϕ ρ
s
pl
R
d d
π
2
r
t
2 R
r
π
3
t
2
pl
M =
ϕ ρ ρ =
n
pl
R
d
d
∫
∫
3
0
0
t
M =
n
pl
R pl
W
Porównując stwierdzamy, że Mn jest ponad 30% większe niż Ms .
Dla przekroju pierścieniowego na podobnej zasadzie otrzymujemy: 2 t
R
π
pl
M =
2 −
n
( 3
R
3
R
1
)
3
PDF created with pdfFactory trial version www.pdffactory.com
Materiały ( na prawach rękopisu) do zajęć z Wytrzymałości Materiałów II. Opracował dr inż. Jan Raczka . Luty 2004.
Pręty o przekrojach niekołowych
Wg analogii błonowej – wartość naprężeń stycznych jest proporcjonalna do tangensa kąta największego w danym punkcie spadku powierzchni, jaką tworzy błona rozpięta na konturze przekroju i obciążona jednostronnym stałym ciśnieniem. Moment skręcający jest proporcjonalny do podwojonej objętości bryły zawartej między płaszczyzną przekroju, a powierzchnią wygiętej błony.
wykres naprężeń stycznych
Przy uplastycznieniu przekroju naprężenia styczne są w każdym punkcie równe są Rtpl wobec czego wspomniana powierzchnia musi mieć jednakowy spadek. Warunek ten spełnia „wzgórze piaskowe” (analogia Nadaia). Jeżeli przyjmiemy, że tangens kąta nachylenia powierzchni równa się Rtpl , to moment skręcający będzie równy podwojonej objętości „nasypanego piasku”.
b
a
a
a
PDF created with pdfFactory trial version www.pdffactory.com
Materiały ( na prawach rękopisu) do zajęć z Wytrzymałości Materiałów II. Opracował dr inż. Jan Raczka . Luty 2004.
R
R
t
pl
pl
R =
= tg α
;
M =
pl
n
3
3
d
la tg α = 1
(
2
b (
3 a -
b )
t
W =
M =
R
W
pl
n
pl
pl
6
gdy
a
〉〉 b
1 n
2
W =
a
b
∑
pl
2
i
i
1
Przykład 1.
Dla danego pręta wyznaczyć obciążenie niszczące msn przyjmując do obliczenia t Rpl raz
hipotezę CTG i drugi raz hipotezę HMH.
Dane: L = 200cm; Rpl = 20kN/cm2; d1 = 4cm; d2 = 8cm.
d2
d1
L
m
s
0, 3L
0, 2L
0, 5L
M
n
M
n
R
t
pl
=
⇒
pl
R
HMH
3
t
kN
=
pl
R
55
,
11
2
cm
R
t
pl
=
⇒
pl
R
CTG
2
t
kN
=
pl
R 10
2
cm
2 M = ms ⋅ 0,2 L
n
n
t
M =
R
n
pl
pl
W
π
HMH ⇒ M
n =
55
,
11
⋅
⋅ (83 − 43)=
,
1354 65kNcm
12
2 M
2
n
⋅ 354
1
,65
kNcm
ms
n =
=
= ,
67 74
0,2 ⋅ L
0,2 ⋅ 200
cm
PDF created with pdfFactory trial version www.pdffactory.com
Materiały ( na prawach rękopisu) do zajęć z Wytrzymałości Materiałów II. Opracował dr inż. Jan Raczka . Luty 2004.
π
CTG ⇒ M
n = 10 ⋅
⋅ (83 − 43)=
86
,
1172
kNcm
12
2 M
2
n
⋅ 172
1
,86
kNcm
ms
n =
=
= ,
58 65
0,2 L
0,2 ⋅ 00
2
cm
Przykład 2
Dla skręcanego pręta o przekroju jak na rysunku stosując analogię Nadaia wyznaczyć wartość granicznego momentu skręcającego.
Dane: R t
pl = 12kN/cm2; a1 = 15cm; a2 = 25cm; a3 = 30cm; b1 = 0,3cm; b2 = 0,5cm; b3 = 0,4cm.
gdy
a
〉〉 b
1 n
2
1
W =
a
∑ h
i
i =
(15⋅ 3,02 +25⋅ 5,02 +20⋅ ,042)= ,54cm3
pl
2
2
1
M
t
n = R W
= 12 ⋅ ,
5 4 =
8
,
64
kNcm
pl
pl
Zginanie
a)
b)
L/ 2
Rp l
Rp l
P
x
y
Ps
Pn
y
z
L
a) Rozkład naprężeń w środku rozpiętości belki przy obciążeniu P = Ps uplastyczniającym tylko włókna skrajne przekroju. Moment uplastyczniający włókna skrajne przekroju oznaczamy przez Ms.
b) Rozkład naprężeń w środku rozpiętości belki przy obciążeniu P = Pn uplastyczniającym niemal cały przekrój pod siłą P. Moment uplastyczniający cały przekrój oznaczamy Mn i nazywamy momentem granicznym lub niszczącym.
PDF created with pdfFactory trial version www.pdffactory.com
Materiały ( na prawach rękopisu) do zajęć z Wytrzymałości Materiałów II. Opracował dr inż. Jan Raczka . Luty 2004.
Wyznaczanie momentu granicznego (niszczącego) przekroju
oraz wskaźnika zginania plastycznego
Przekrój z jedną osią symetrii
R pl
h g
d A g
-
y
h d
+
d A d
R pl
z
Z sumy rzutów na oś poziomą :
σ dA + σ dA = R A − R A =
∫
d
∫
g
pl
d
pl
g
0
Ad
Ag
A = A
d
g
wynika, że oś zginania plastycznego dzieli przekrój na dwie części o równych polach.
Moment Mn graniczny (niszczący), czyli uplastyczniający cały przekrój jest równy momentowi bryły naprężeń względem osi zginania plastycznego y :
h
h g
h
h g
d
d
M
= σ
+ σ
=
+
n
z
∫ d d
dA
z
∫ g dA
g
R pl z
∫ d d
dA
z
∫ g dA
g
0
0
1
0
4
4
4
2 0
4
4
4
3
Wpl = S d
+ S g
y
y
M
=
n
R pl W
pl
Przekrój z dwiema osiami symetrii
h
Oś zginania plastycznego jest drugą (poziomą) osią symetrii hg = hd =
i wtedy:
2
h
h
2
2
M = 2 σ
z
dA
R 2
z
n
pl
dA
∫
=
∫
0
4
1
0
4
23
d
S
y
PDF created with pdfFactory trial version www.pdffactory.com
Materiały ( na prawach rękopisu) do zajęć z Wytrzymałości Materiałów II. Opracował dr inż. Jan Raczka . Luty 2004.
M
= R
d
W
W
= 2 S
n
pl
pl
pl
y
Dla podstawowych przekrojów można wyznaczyć stosunek wskaźnika zginania plastycznego do wskaźnika zginania sprężystego:
Wpl
Dla prostokąta: ω =
=
5
,
1 , koła ω = 1,75 i dwuteownika ω ≈ 1,17
W
Wyznaczanie nośności granicznej układu prętowego na przykładzie belki
Obliczenia nośności granicznej można wykonywać dwiema metodami: statyczną i kinematyczną.
Algorytm dla metody statycznej jest następujący:
1. Ustalamy wielkości nadliczbowe (jeśli układ jest statycznie niewyznaczalny).
2. Sporządzamy wykresy momentów zginających od obciążenia zewnętrznego dla zastępczego układu statycznie wyznaczalnego.
3. Sporządzamy wykres momentów od obciążenia wielkościami nadliczbowymi.
4. Łączymy tak wykresy z punktów 2 i 3, aby w dostatecznej liczbie przekrojów został
osiągnięty warunek stanu granicznego.
Algorytm dla metody kinematycznej:
1. Ustalamy liczbę przegubów plastycznych.
2. Zakładamy możliwy kinematycznie schemat zniszczenia.
3. Obliczamy pracę sił zewnętrznych Lz i pracę sił wewnętrznych Lw dla przyjętego schematu zniszczenia.
4. Z warunku Lz + Lw = 0 obliczamy obciążenie niszczące.
W wypadku, gdy obciążenie niszczące wyznaczone obiema metodami jest jednakowe mówimy, że rozwiązanie zadania jest zupełne. Gdy rozwiązania są różne to mówimy o oszacowaniu dolnym (statycznym) i górnym (kinematycznym) nośności granicznej.
Przykład 1
Dla belki jak na rysunku wyznaczyć siłę Ps oraz Pn metodą statyczną. Dane: L, P, h, b, Rpl.
b
L/ 2
Rpl
Rpl
P
h
x
y
Ps
Pn
y
z
L
Pl / 4
PDF created with pdfFactory trial version www.pdffactory.com
Materiały ( na prawach rękopisu) do zajęć z Wytrzymałości Materiałów II. Opracował dr inż. Jan Raczka . Luty 2004.
PL h
2
M z
12 PL
2
4 2
R b h
σ =
=
=
=
pl
Rpl ⇒
Ps =
3
J y
b h
8
2
b h
3 L
12
2
2
R
b
h
R
b
h
pl
pl
M n =
= M ⇒
Pn =
4
L
= P
pl
m
n = W = ω = 5
,
1
P
W
s
Przykład 2
Dla belki jak na rysunku obliczyć Pn. Dane: L = 400cm; Rpl = 20kN/cm2.
6 cm
L
4 cm
P
3 cm
17 cm
z
3 cm
L / 3
2L / 3
10 cm
P
M
n
M
n
M
n
-
+
+
2 PL / 9
=
M
n
M
n
Wyznaczenie momentu granicznego (niszczącego) przekrój:
M
R W
n =
pl
pl
W =
d
S
S
y
+ g
pl
y
3 ⋅10 + 3 ⋅
z = 4 ⋅ 6 + 10
(
− z )
⋅ 3
czyli :
z = 4 cm
W = 3 ⋅10 ⋅ 5,5 + 4 ⋅ 3 ⋅
2 + 6 ⋅ 4 ⋅ (- )
8 + 3 ⋅ 6 ⋅ (- )
3 = 437
3
cm
pl
M n = 20 ⋅ 437 = 8740 kNcm
Warunek stanu granicznego i wyznaczenie obciążenia niszczącego: 2
PL − M
n = M n
9
9 M
9
n
⋅ 740
8
P = P
n =
=
=
65
,
196
kN
L
400
PDF created with pdfFactory trial version www.pdffactory.com
Materiały ( na prawach rękopisu) do zajęć z Wytrzymałości Materiałów II. Opracował dr inż. Jan Raczka . Luty 2004.
Przykład 3
Wyznaczyć maksymalną wartość siły P = Pn, przy której przedstawiona belka ulegnie zniszczeniu. Dane: L = 400cm; Rpl = 25kN/cm2; siły rozstawione są co L/4.
L
4P
3P
2P
2 cm
a
b
c
20 cm
y
4P
3P
2P
M
n
z
10 cm
M
n
-
+
5 PL / 4
PL
3 PL / 2
Wyznaczenie momentu granicznego (niszczącego) przekrój:
M n = R W
;
W
pl
pl
= 2 ⋅ S
;
y
z = 10
pl
cm
W = 2 ⋅ 10 ⋅10 ⋅ 5 − 6 ⋅ 8 ⋅
4 = 616 cm3
pl
M n = 25 ⋅ 16
6
= 15400 kNcm
Warunek stanu granicznego i wyznaczenie obciążenia niszczącego: 5
3
7 M
a
)
PL −
M
n = M
a
n ⇒ P
=
n
n
=
9
,
53
kN
4
4
5 L
3
1
M
b
)
PL − M
n = M
b
n ⇒ P
=
n
n
=
5
,
38
kN
2
2
L
1
5 M
c )
P
L −
M
n = M
a
n ⇒ P
=
n
n
=
1
,
48 kN
4
4 L
P
n = P (
min)
b
n
= P
n
=
5
,
38
kN
PDF created with pdfFactory trial version www.pdffactory.com
Materiały ( na prawach rękopisu) do zajęć z Wytrzymałości Materiałów II. Opracował dr inż. Jan Raczka . Luty 2004.
Przykład 4
Dla belki jak na rysunku określić obciążenie niszczące: qn.
L
a
x
q
B
A
a
0, 41 L
qx l
( − x)
M x
Moment zginający: M
A
α =
+
2
l
M
gdzie
A jest skierowaną w górę reakcją w podporze B.
l
Maksymalny moment zginający wystąpi w przekroju o odciętej x = xm obliczonej z równania: dM
1 M
α = ql − + M
qx
A = 0 czyli: x ≡ x = l
+
A
m
dx
2
l
2
2 ql
Podstawiając x = xm do równania na Mα i przyjmując Mα(xm)= Mn, MA = – Mn otrzymujemy: 2
ql
1
M
1
M
1
M
M =
(
n
−
)(
n
+
) − M (
n
−
)
n
n
2
2
2
ql
2
2
ql
2
2
ql
skąd po przekształceniach dochodzimy do równania kwadratowego na ql2 : ( ql )22−12 2
M n ⋅ ql + 4
2
M n = 0
z którego wyznaczamy dwa pierwiastki:
M
q
n
= 3
(
2
− 2 2)
przy x = −( 2 + l
1
m
)
1 czyli poza przedziałem określoności.
l 2
oraz
M
M
q ≡ q
n
n
= 3
(
2
+ 2 2)
= 66
,
11
przy
x = ( 2 − l
)
1 = ,
0
l
2
n
m
414
l 2
l 2
czyli właściwą wartość obciążenia niszczącego.
PDF created with pdfFactory trial version www.pdffactory.com
Materiały ( na prawach rękopisu) do zajęć z Wytrzymałości Materiałów II. Opracował dr inż. Jan Raczka . Luty 2004.
Przykład 5
Określić obciążenie niszczące P = Pn metodą kinematyczną belki z przykładu 2, czyli zakładając, że znana jest wartość momentu Mn uplastyczniającego przekrój.
L
P
L / 3
2L / 3
P
M
n
M
n
P
f1
f2
d
f
δ
3
δ
3
δ
3
δ
3
δ
ϕ =
,
=
=
+
=
1
ϕ
,
2
ϕ
5
,
4
l
l
2
l
l
2
l
Lz = Pn δ,
δ
3
δ
3
δ
5
,
4
L = − M
− M
− M
w
n
n
n
l
l
2
l
Z warunku Lz + Lw =0 otrzymujemy Pn = 9Mn/l czyli tak samo jak w przykładzie 2.
PDF created with pdfFactory trial version www.pdffactory.com