Rozciag-scisk staty niewyz

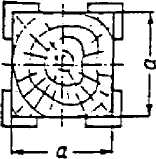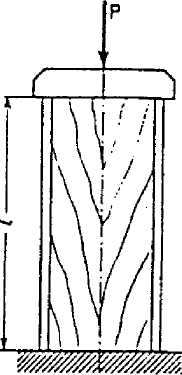
Rozciąganie i ściskanie statycznie niewyznaczalne 1. Na drewnianej kolumnie jak na rysunku, o wysokości l=1 m i przekroju kwadratowym o boku a = 250 mm, wzmocnionej czterema stalowymi kątownikami L40x40x4 ( AL=3.08 cm2) spoczywa ciężar P. Obliczyć jego dopuszczalną wartość, oraz skrócenie słupa (∆ l), jakie przy nim wystąpi, przyjmując dla stali kcst=160 MPa, Est=2·105 MPa, zaś dla drewna kcdr=12 MPa,

Edr=104 MPa.

2. Dla konstrukcji jak na rysunku dobrać średnice prętów (1) i (2) na których zawieszono sztywną belkę AB,

zamocowaną przegubowo w punkcie A, obciążoną na końcu siłą P = 180 kN. Założone stosunki przekrojów φ d1

φ d2

prętów: A2=1,5· A1, długości l=1 m, moduły Younga:

1= E2=2·105

MPa,

zaś

dopuszczalne

naprężenia

rozciągające kr = 160 MPa. Dla dobranych średnic d1 i d2

obliczyć pionowe przemieszczenie punktu B belki.

3. W konstrukcji jak na rysunku, ciężar G=10 kN podtrzymywany jest przez trzy pręty, z których środkowy (3) został wykonany 1

krótszy o δ=1 mm w stosunku do pr

ętów skrajnych (1 i 2).

Obliczyć naprężenia w prętach po zmontowaniu konstrukcji, jeśli: Α

2Α

2 Α

l=1 m, A1=A2=A=2 cm2, A3=2A, E=2·105 MPa.

4. Ciężar G=80 kN został podwieszony na konstrukcji jak na rysunku, 1

będącej symetrycznym układem trzech prętów, z których środkowy 2Α

ma dwukrotnie większe pole przekroju poprzecznego w stosunku do

ętów skrajnych. Obliczyć naprężenia powstałe w poszczególnych

prętach, oraz pionowe przemieszczenie punktu O konstrukcji, Α

wiedząc że: A=2 cm2, h=1 m, α=300, E=2·105 MPa.

5. Konstrukcja jak na rysunku, składająca się z prętów o jednakowym E

γ =600

przekroju A=5 cm2, została zmontowana bez naprężeń wstępnych.

Obliczy

ć naprężenia, jakie powstaną w poszczególnych prętach na

skutek wzrostu temperatury o ∆ t=30 0C, wiedząc, że wszystkie 1

3 C

pręty zostały wykonane ze stali, dla której moduł Younga wynosi D

E=2·105 MPa, zaś współczynnik rozszerzalności liniowej α=1,25·10-5 1/0C.